精编1.2.1-任意角的三角函数(优秀课件)_图文.ppt

高中数学三角函数121任意角的三角函数(一)PPT课件

6
6 62
3.已知角α的终边与单位圆的交点 P( 5 , 2 5 )，则
55
sinα+cosα= ( )
A . 5 B .5 C .25 D . 25
5
5
5
5
【解析】选B.因为 siny25,cosx5，
5
5
所以 sincos2555.
55 5
4.若角α终边上一点坐标为(-5,12),则cosα=
1.2 任意角的三角函数 1.2.1 任意角的三角函数(一)
整体概述
概况一
点击此处输入相关文本内容点击此处输入相关文本内容
概况二
点击此处输入相关文本内容点击此处输入相关文本内容
概况三
点击此处输入相关文本内容点击此处输入相关文本内容
【自主预习】主题1:任意角的三角函数的定义使锐角α的顶点与原点O重合,始边与x轴的非负半轴重合,在终边上任取一点P,作PM⊥x轴于M,设P(x,y), |OP|=r,据此回答下列问题:
主题2:三角函数值的符号法则及诱导公式一
1.设P(x,y)为α终边上任意一点(异于原点),记r=|OP|,
则 sin y,c o s x,ta n y(x 0 ),由此可知任意角α
r
r
x
的三角函数值的符号与谁有关?
提示:角α的三角函数值的符号与点P的坐标x,y的正负
有关.
2.取角α分别为30°,390°,-330°,它们的三角函数值是什么关系?为什么? 用文字语言描述:它们的同名三角函数值相等,因为三个角的终边相同.
2.已知角α,则角α的三角函数值符号确定,反之若角 α的某个三角函数值符号确定,则角α的终边所在象限确定吗? 提示:不一定,若已知角α的一个三角函数值的符号,则角α所在的象限可能有两种情况,若已知角α的两个三角函数值的符号,则角α所在的象限就唯一确定.

任意角的三角函数-课件1PPT课件一等奖新名师优质课获奖比赛公开课

m5
m5
m ________．
（4）若角旳终边过点 Pa，8，且 cos 3 ，
5
则 a ________．
（5）角旳终边在直线 y 2x上，求旳六个三
角函数值．
正弦上为正，余弦右为正，正切余切一三正，其他为负不为正
例２:
1、判断下列各三角函数旳符号 A.260 B. 4 C. 672 10 D.11 3
2、若sin 0且 tan 0，那么是第几象限角？
3、已知是第三象限角，试判定： sin( cos ) cos(sin )的符号
练习:
（1）若角终边上有一点P 3，0，则下列函数值不
§1.2.1 任意角旳三角函数
设是任意角，旳终边上任意一点 P旳坐标是x，y，
当角在第一、二、三、四象限时旳情形，它与原点
旳距离为 r ，则 r x 2 y 2 x2 y2 0 ．
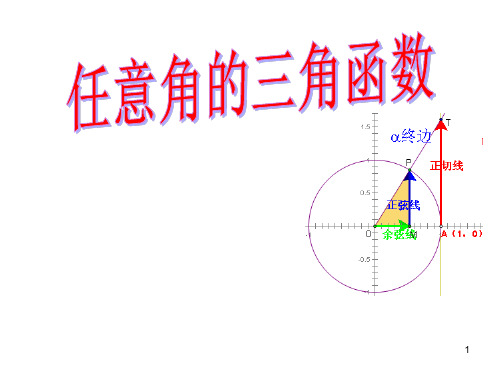
任意角旳三角函数
1、定义：
①比值 y 叫做旳正弦，记作sin ，即 sin y ．
r
r
x
②比值
叫做
旳余弦，记作cos ，即cos
Байду номын сангаас
x
．
r
r
③比值 y 叫做旳正切，记作tan，即 tan y ．
x
x
④比值 x 叫做旳余切，记作cot ，则 cot x ．
y
y
⑤比值 r 叫做旳正割，记作sec ，则 sec r ．
x
x
⑥比值 r 叫做旳余割，记作csc ，则csc r ．
y
y
我们把正弦、余弦，正切、余切，正割及余割都看成是以角为自变量，以比值为函数值旳函数，以上六种函数统称三角函数．

1.2.1任意角的三角函数优秀课件

实例剖析
例1：如图已知角α的终边与单位圆的交点是，P( 1 , 3 )
求角α的正弦、余弦和正切值。
22
y
解：根据任意角的三角函数定义：
sin 3
2
cos 1
2
P( 1 , 3 ) 22
tan 3
O
x
点评：若已知角α的终边与单位圆的交点坐标，则可直接利用定义求三角函数值。
y
上述等式中的绝对值
ห้องสมุดไป่ตู้
符号,能否给线段OM、 MP规定一个适当的方
M
A(1,0)
O
x
向,使它们的取值与点P α的 P
的坐标一致?
终边 (Ⅲ)
y
α的
终边
P
A(1,0)
OM x
(Ⅰ)
y
M A(1,0)
O
x
P
α的
(Ⅳ) 终边
【定义】有向线段
* 带有方向的线段叫有向线段. *有向线段的大小称为它的数量.
在坐标系中,规定:
例2、求 5 的正弦、余弦和正切值.
理论
3
迁移
解：在直角坐标系中，作 AOB 5 ，易知 AOB
31 3
的终边与单位圆的交点坐标为 ( , )
所以 sin5 3 cos5 1 2 tan25 3
y
32
32
3
，
思考：若把角 5 改为 7 呢?
5
3
6
7 1
（3）角的大小是任意的.
2.什么叫做1弧度的角？度与弧度是怎样换算的？
（1）等于半径长的圆弧所对的圆心角叫做1 弧度的角.
（2）180°＝ rad.

任意角的三角函数PPT优秀课件

2.确定下列三角函符数号值：的
(1)sin256;
(2)cos(406);
23
(3)tan .
3
3.角的终边 P (上 m ,5)且 ,有 co 一 sm (点 m 0),
13
求 sin co 值 s.
小结： 1．任意角的三角函数的定义； 2．三角函数的定义域； 3．正弦、余弦、正切函数的值在各象限的符号．
1．2．1任意角的三角函数（1）
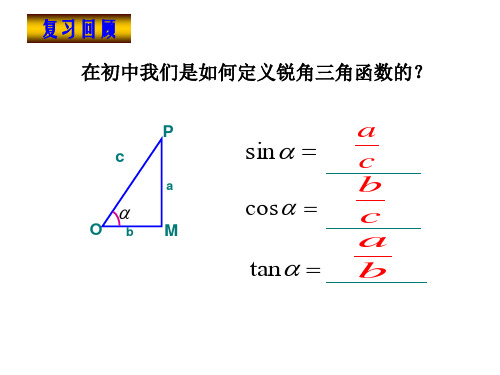
问题1:你能回忆一下初中里学过的锐角三角函数(正弦, 余弦,正切)的定义吗?
在RtPO中 M
如何将POM 放到平面直角坐标系中？
sin PM
P
OP
co sOM OP
tanPM OM

O
M
锐角三角函数
问题2：将POM 放到平面直角坐，标系中
87.当一切毫无希望时，我看着切石工人在他的石头上，敲击了上百次，而不见任何裂痕出现。但在第一百零一次时，石头被劈成两半。我体会到，并非那一击，而是前面的敲打使它裂开。――[贾柯·瑞斯] 88.每个意念都是一场祈祷。――[詹姆士·雷德非]
89.虚荣心很难说是一种恶行，然而一切恶行都围绕虚荣心而生，都不过是满足虚荣心的手段。――[柏格森] 90.习惯正一天天地把我们的生命变成某种定型的化石，我们的心灵正在失去自由，成为平静而没有激情的时间之流的奴隶。――[托尔斯泰]
(1)cos 7 ; (2)sin4(6)5; (3)tan11 .
12
3
解： (1) 7 是第二象限角 co， s7所 0.以
12
12
(2) 因为 4652360225,即465是第三象限角，所 sin(465)0.
(3) 因为 1125,即11 是第四象 ,所限以角

高中数学1.2.1任意角的三角函数优秀课件

其中: OM a
sin MP b
OP r
MP b OP r a2 b2
cos OM a
OP r
y
﹒Pa, b
r b
tan MP b
OM a
o
﹒
aMx
5
诱思探究
如果改变点Ｐ在终边上的位置，这三个比值会改变吗？
y
P
﹒ P(a,b)
O
M M
OMP ∽ OM P
sin MP M P
y
T
M
A(1,0)
O
x
α的 P终边ຫໍສະໝຸດ (Ⅲ)yTα的终边
P
A(1,0)
OM x
(Ⅰ)
y
M A(1,0)
O
x
PT
α的
(Ⅳ) 终边 34
这三条与单位圆有关的有向线段MP、OM、
AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线
当角α的终边与x轴重合时,正弦线、正切线,分别变成一个点,此时角α的正弦值和正切值都为0;
OP OP
cos OM
OP
OM OP
x
tan MP
OM
M P OM
能否通过|op|取特殊值将表达式简化呢？ 6
若OP r 1，则以原点为圆心,以单位
长度为半径的圆叫做单位圆.
Y
P(a,b)
O
M
sin
MP OP
b
cos OM a
X
OP
tan MP b a OM
7
1、任意角的三角函数第一定义
弦和正切值 .
解:由已知可得 OP0 (3)2 (4)2 5
y
设角的终边与单位圆交于 P(x, y) ，

1.2.1任意角的三角函数(一)PPT课件

解设
P(以x，αy＝)为32πα为＝例32π，上其任余一略点。，易知点
P(x，y)在
y
轴负半轴上。
∴x＝0，y<0，r＝ x2＋y2＝－y>0。
∴sin 32π＝yr＝－1；cos 32π＝-xr＝0；tan 32π＝yx，无意义。 7
1.2.1（一）
例1、已知角 α 的终边上一点 P(－15a,8a) (a∈R 且 a≠0)，求
-
12
1.2.1（一）
探究点四诱导公式一由任意角的三角函数的定义可以知道，终边相同的角的同
α 的各三角函数值。
解：∵x＝－15a，y＝8a ∴r＝－15a2＋8a2＝17|a| (a≠0) (1)若 a>0，则 r＝17a，于是sin α＝187 cos α＝－1157 tan α＝－185 (2)若 a<0，则 r＝－17a,于是sin α＝－187 cos α＝1157 tan α＝－185
tan B＝ba＝43.
-
2
1.2.1（一）
问题 2 如图，锐角 α 的顶点与原点 O 重合，始边与 x 轴的非负半轴重合，在 α 终边上任取一点 P(a，b)，它与原点的距离为 r，作 PM⊥x 轴，你能根据直角三角形中三角函数的定义求出 sin α，cos α，tan α 吗？
答 sin α＝br，cos α＝ar，tan α＝ba.
(2)∵285°是第四象限角，∴sin 285°<0，
∵－105°是第三象限角，∴cos(－105°)<0， ∴sin 285°·cos(－105°)>0。
随堂练习 2 (1)若 sin αcos α<0，则 α 是第__二__或__四___象限角。 (2)代数式：sin 2·cos 3·tan 4 的符号是_负___号____。

1.2.1 任意角的三角函数课件(共36张PPT)

栏目导引
第一章三角函数
做一做
2.下列函数值为正的是________． ①sin 171°；②cos 45π；③tan(－91°)．解析：∵171°是第二象限角，所以 sin 171°>0； ∵45π 是第二象限角，所以 cos 45π<0； ∵－91°是第三象限角，所以 tan(－91°)>0.
答案：①③
栏目导引
第一章三角函数
3．诱导公式终边相同的角的同一三角函数的值___相__等___，即 sin(α＋k·2π)＝___s_i_n_α____； cos(α＋k·2π)＝__c_o_s__α_____； tan(α＋k·2π)＝___t_a_n_α_____，其中k∈Z.
栏目导引
第一章三角函数
3．三角函数线四注意 (1)位置：三条有向线段中有两条在单位圆内，一条在单位圆外； (2)方向：正弦线由垂足指向α的终边与单位圆的交点；余弦线由原点指向垂足；正切线由切点指向切线与α的终边(或其延长线)的交点； (3)正负：三条有向线段中与x轴或y轴同向的为正值，与x轴或y轴反向的为负值； (4)书写：有向线段的起点字母在前，终点字母在后．
栏目导引
第一章三角函数
(2)原式＝sin(2π＋π3 )cos(－4π＋π6 )＋tan(－4π＋π4)·cos(4π＋π3 ) ＝sinπ3cosπ6＋tanπ4cosπ3 ＝ 23× 23＋1×12＝54.
【名师点评】由三角函数的定义可知，三角函数值的大小是由角的终边位置确定的．终边相同的角的同一三角函数值相等，而与角α终边相同的角总可以表示为α＋2kπ(α为弧度， k∈Z)或α＋k·360°(α为角度，k∈Z)的形式．
边的角 α 的正弦值为－ 22，求 cos α 和 tan α 的值．【解】设点 M 的坐标为(x1，y1)．

1.2.1任意角的三角函数.ppt1.ppt

解：在直角坐标系中，作AOB 5 ，易知 AOB
3
的终边与单位圆的交点坐标为 (1 , 3 )
22
y
所以 sin 5 3 cos 5 1
32
32
5
3
o
﹒
A
x
5 换成 4 呢？
3
3
﹒
B
tan 5 3
3
点评：若已知角α的大小求三角函数值时，可先求出角α 终边与单位圆的交点，然后再利用定义求三角函数值。
解：因为x=-4，y=-3,
r 42 32
sin a y 3 r5
cosa x 4 r5
tan a y 3 x4
25 5
练习：已知角的终边上一点P15a,8aaR且a 0，
求角的sin, cos, tan的值.
解：由于x -15a, y 8a,
所以r 15a2 8a2 17 a a 0
1.三角函数的定义域
三角函数
定义域
sin
cos
tan
R R
{ | k , k Z}
2
y 2.三角函数值在y各象限的符号 y
（）
（）（）（）（）
o
x
o
x
o
x
（
）（）
sin
（）（）
cos
（
）（
tan
）
归纳总结
本节课主要学习了那些内容?
①任意角三角函数的概念. ②三角函数的定义域及三角函数值在各象限的符号.
（2）x 叫做的余弦，记作 cos，即 cos x ；
y
（3）
叫做
的正切，记作tan ，即 tan y
(x 0)

1.2.1任意角的三角函数1.ppt

x
x
5
• 正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，统称为三角函数。
6
例题1:
1 求 5的正弦、余弦和正切值.
3
7
知识扩展
任意角的三角函数定义2
设是任意角，的终边上任意一点P 的坐标是x，y ，
当角在第一、二、三、四象限时的情形，它与原点的距
离为 r ，则 r x 2 y 2 x2 y2 0 ．
8
定义：
①比值 y 叫做的正弦，记作sin ，即 sin y ．
r
r
②比值 x 叫做的余弦，记作cos ，即cos x ．
r
r
③比值
y 叫做 x
的正切，记作tan，即 tan
y x
．
9
任意角的三角函数定义 y Α的终边
3
2
2
2
0
0 3
2
1
2
2
2
1 0 1
3 3
1
3 不存在 0 不存在 0
15
小结：
任意角的三角函数
sinα cosα
tanα
定义 sin y cos x
r
r
tan y
x
R 定义域
R

k

2
,k

Z

符号
数形结合来记忆
16

2
,k

Z

13
例3 确定下列三角函数值的符号：
(1)cos 7 ; (2)sin(465o ); (3)tan 11