第4章 参数估计
教育与心理统计学 第四章 抽样理论与参数估计考研笔记-精品
第四章抽样理论与参数估计第一节抽样理论的基本知识分层抽样，又叫分层随机抽样，这种抽样方法是按照总体已有的某些特征，承认总体中已有的差异，按差异将总体分为几个不同的部分，每一部分称为一个层，在每一个层中实行简单随机抽样。
它充分利用了总体的已知信息，因而是一种非常适用的抽样方法，其样本代表性及推论的精确性一般优于简单随机抽样。
分层的原则是层与层之间的变异越大越好，各层内的变异要小。
试述分层抽样的原则和方法？分层抽样是按照总体上已有的某些特征，将总体分成几个不同部分，在分别在每一部分中随机抽样。
分层的总的原则是：各层内的变异要小，而层与层之间的变异越大越好。
在具体操作中，没有一成不变的标准，研究人员可根据研究需要依照多个分层标准，视具体情况而定。
⑷两阶段随机抽样两阶段随机抽样首先将总体分成M个部分，每一部分叫做一个"集团"（或"群"），第一步从M个集团中随机抽取m个"集团”作为第一阶段样本，第二步是分别从所选取的m个"集团”中抽取个体（g构成第二阶段样本。
一般而言，两阶段抽样相对于简单随机抽样，标准误要大些，但是，两阶段抽样简便易行，节省经草贼，因而它是大规模调查研究中常被使用的抽样方法。
例如，如果我们要了解全国城市初中二年级学生的身高，第一步我们可以从全国几百个城市中随机抽取几十个城市作为第一阶段的样本。
第二步，在第一阶段随机抽取出来的城市中再随机抽取初中二年级的学生。
（二）非旃抽样非概率抽样不是完全按随机原则选取样本，有方便抽样、判断抽样。
方便抽样是由调查人员自由、方便地选择被调查者的非随机选样。
判断抽样是通过某些条件过滤，然后选择某些被调查者参与调查的抽样法。
当采取非概率抽样的方法选取样本时，研究者要说明采用此种方取样的原因以及对研究结果可能造成的影响。
第二节抽样分布［统计量分布、基本随机变量函数的分布］总体：又称母全体、全域，指具有某种特征的一类事物的全体。
第四章中心极限定理与参数估计
当 n 很大时,近似地服从正态分布.
第四章 中心极限定理与参数估计
例 1、对敌人的防御工事进行 80 次轰炸，每次轰炸命中目标炸弹 数目的数学期望为 2，方差为 0.8，且各次轰炸相互独立，求在 80 次轰炸中有 150 颗～170 颗炸弹命中目标的概率。 解：第 i 次轰炸命中目标炸弹的数目 X i (i 1,2,,80) 都是离散型随机
根据随机变量数学期望的性质，计算数学期望
80
80
80
E( X ) E( X i ) E( X i ) 2 160
i 1
i 1
i 1
第四章 中心极限定理与参数估计
由于离散型随机变量变量 X 1 , X 2 ,, X 80 相互独立，根据随机
变量方差的性质，计算方差
80
80
80
D( X ) D( X i ) D( X i ) 0.8 64 82
分大时，离散型随机变量 X 近似服从参数为 np, npq ( p q 1)
的正态分布，即近似有离散型随机变量 X ～ N(np, npq) 定理4.22表明:
正态分布是二项分布的极限分布, 当n充分大时, 可 以利用该定理来计算二项分布的概率.
随机变量 X 的取值在数学期望 E(X ) 附近的密集程度越低。
第四章 中心极限定理与参数估计
（3）在使用切贝谢夫不等式时，要求随机变量 X 的数学期望 E( X ) 与方差 D( X ) 一定存在，这时无论随机变量 X 的概率分布已知或未
知，都可以对事件 X E(X ) 发生的概率进行估计。 2、切贝谢夫不等式的应用举例 例1、 已知电站供电网有电灯 10000 盏，夜间每一盏灯开灯的概率 皆为 0.8，且它们开关与否相互独立，试利用切贝谢夫不等式估计夜 晚同时开灯的灯数在 7800 盏～8200 盏之间的概率。
参数估计的一般步骤
参数估计的一般步骤引言：参数估计是统计学中一项重要的任务，它用于根据样本数据来推断总体参数的值。
参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。
本文将详细介绍参数估计的一般步骤，并以人类的视角进行描述，使读者更好地理解和应用这些步骤。
一、确定估计方法在参数估计中，首先需要确定合适的估计方法。
估计方法可以分为点估计和区间估计两种。
点估计方法通过单个数值来估计参数的值，例如最大似然估计和矩估计。
区间估计方法则通过一个区间来估计参数的范围，例如置信区间估计。
选择合适的估计方法是参数估计的第一步。
二、选择样本在确定了估计方法后，接下来需要选择合适的样本进行参数估计。
样本应当具有代表性，能够反映总体的特征。
为了保证样本的代表性，可以使用随机抽样方法来选择样本。
通过合理选择样本，可以减小估计误差，提高参数估计的准确性。
三、计算估计值在选择好样本后，需要计算参数的估计值。
对于点估计方法，可以使用最大似然估计或矩估计等方法来计算参数的估计值。
对于区间估计方法，可以使用置信区间估计来计算参数的范围。
计算估计值时，需要根据样本数据和估计方法进行相应的计算，确保估计结果的准确性。
四、进行推断在计算得到估计值后，需要进行推断，即根据估计值对总体参数进行推断。
对于点估计方法，可以直接使用估计值作为总体参数的估计值。
对于区间估计方法，可以使用置信区间来表示总体参数的范围。
通过推断可以了解总体参数的可能取值范围，帮助做出正确的决策和预测。
总结：参数估计的一般步骤包括确定估计方法、选择样本、计算估计值和进行推断。
在进行参数估计时，需要选择合适的估计方法和样本，计算出估计值，并进行相应的推断。
参数估计在统计学中扮演着重要的角色，它帮助我们根据样本数据来推断总体参数的值，从而更好地了解和应用统计学。
通过本文的介绍，希望读者能够更好地理解和应用参数估计的一般步骤。
第四章 参数估计
x
n
总体标准差，若 未知，可用样本
标准差代替
36
总体均值的置信区间引例
(２ 未知)
例：某商场从一批袋装食品中随机抽取10袋，测得 每袋重量（单位：克）分别为789，780，794， 762，802，813，770，785，810，806，要 求以95%的把握程度，估计这批食品的平均每袋 重量的区间范围。假定食品重量服从正态分布。
0.95，Ｚ/2=1.96
x Z 2
n
,
x
Z
2
n
26 1.96 6 ,26 1.96 6
100
100
24.824,27.176
我们可以95％的概率保证平均每天 参加锻炼的时间在24.824～ 27.176 分钟之间。
一般置信水平
一般使用的置信水平是：90%, 95%, 99%
Confidence Level
▪ 总体服从正态分布,且总体方差（２）已知 ▪ 如果不是正态分布，可以由正态分布来近似 (n 30)
2. 使用正态分布统计量Ｚ
Z
x s
m ~ N (0,1)
n
3. 总体均值 在1-置信水平下的置信区间为
s
s
x
Za 2
,x n
Za 2 n
总体均值的置信区间
(２ 已知)
抽样极限误差:
s x Za 2 n
❖ 定理1
当总体 X ~ N ( m , s 2 ) 时，抽自该总体
的简单随机样本 x1 , x 2 , , x n 的样本平均数
服从数学期望为 ，方差为 s2的正态分布，
n
即 x ~ N (m, s2 ) 。
n
Z x ~ N (0,1) n
参数估计
（2）再用样本k阶矩代替相应的总体k阶矩
上一页
下一页
返回
设 总 体X ~ N ( , 2 ), , 2 未 知 ， 设 例1： ( X 1 , X 2 ,..., X n )为 来 自 总 体 的 样 本 ， 求 X 与 2的 矩 估 计 量 。
解：先建立待估参数与总体矩的关系
维随机变量，样本的联合概率密度为:
f ( x1 , x2 ,, xn ) f X 1 ( x1 ) f X 2 ( x2 ) f X n ( xn )
f ( x1 , ) f ( x2 , ) f ( xn , ) f ( xi , )
i 1
n
显然上式也为θ的函数，记作 L( )，即
L( ) f ( xi , )
i 1 n
我们称 L( ) 为似然函数。
小结：
似然函数
n p( x i ; ) i 1 L( ) n f ( x i ; ) i 1
由上可知，求极大似然估计值就是求使 L( ) 取最大的θ值。 下面我们用例子来说明求解极大似然估计值的步骤。
6
3
[ x dx x dx]
2 3 0 0
2
用样本k阶矩代替相应的总体k阶矩,得θ的矩估计量：
ˆ 2X
２）将数据代入，得θ的矩估计值为：
ˆ 2x 2 1 xi 8.9 8 i 1
8
计 算 器 的 使 用
例3：设总体X在区间[a,b]上服从均匀分布, a , b
实为 发生的概率。
根据极大似然原理，
概率大的事件在一次观测中更容易发生。
现在只做一次抽样， 事件 { X 1 x1 , X 2 x2 ,, X n xn } 故 认为其概率较大。 认为其概率较大。 也即我们应选择 使 L( ) 取最大值。 我们把使 L( ) 取最大值的 值称为 的极大 竟然发生了,
(04)第4章 参数估计
（2）99%的置信区间是多少？
（3）若样本容量为40，而观测的数据不变，则 95%的置信区间又是多少？
5 - 31
统计学
STATISTICS
总体均值的区间估计
(例题分析)
12, s 4.1
解:(1)已知n=15, 1- = 95%， =0.05 ，x
统计学
STATISTICS
总体均值的区间估计
统计学
STATISTICS
大样本的估计方法
不论总体是不是服从正态分布，在大样本 （n 30）时，样本均值均服从正态分布。 若已知 2 x
x ~ N ( ,
总体均值 在1- 置信水平下的置信区间为
n
)
z
n
~ N (0,1)
z 2
有效性：对同一总体参数的两个无偏点估计量， 有更小标准差的估计量更有效
ˆ P( )
ˆ1 的抽样分布
B A
ˆ2 的抽样分布
ˆ
5 - 11
ˆ ˆ1 是比 2 更有效，是一个更好的估计量
统计学
STATISTICS
有效性
(efficiency)
x1 x2 x3 样本均值 x 3 x1 2 x2 3x3 和 x1 6
统计学
STATISTICS
第 4 章 参数估计
4.1 参数估计的基本原理 4.2 一个总体参数的区间估计 4.4 样本容量的确定
5-1
统计学
STATISTICS
4.1 参数估计的一般问题
4.1.1 估计量与估计值 4.1.2 点估计与区间估计 4.1.3 评价估计量的标准
第四章线性系统参数估计的最小二乘法
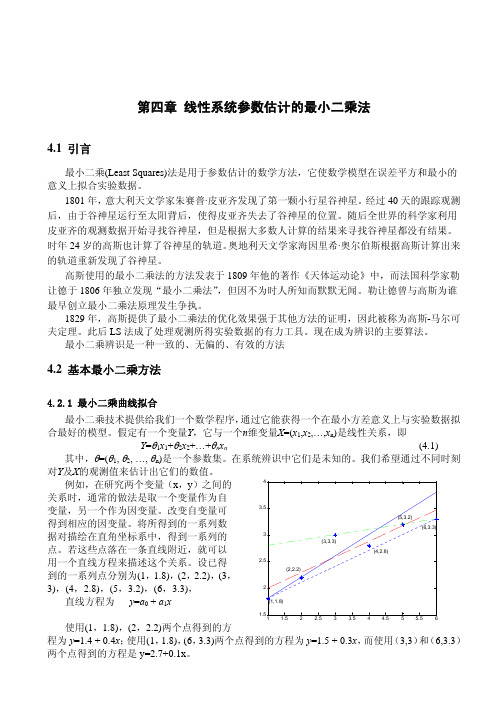
测得铜导线在温度Ti (o C) 时的电阻 Ri (Ω ) 如表 6-1，求电阻 R 与温度 T 的近似函数关系。
i
1
2
3
4
5
6
7
Ti (o C) Ri (Ω )
19.1 76.30
25.0 77.80
30.1 79.25
36.0 80.80
40.0 82.35
45.1 83.90
50.0 85.10
使用(1，1.8)，(2，2.2)两个点得到的方
1.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
程为 y=1.4 + 0.4x；使用(1，1.8)，(6，3.3)两个点得到的方程为 y=1.5 + 0.3x，而使用（3,3）和（6,3.3）
两个点得到的方程是 y=2.7+0.1x。
(4.1)
其中，θ=(θ1, θ2, …, θn)是一个参数集。在系统辨识中它们是未知的。我们希望通过不同时刻
对Y及X的观测值来估计出它们的数值。
例如，在研究两个变量（x，y）之间的
4
关系时，通常的做法是取一个变量作为自
变量，另一个作为因变量。改变自变量可
3.5
得到相应的因变量。将所得到的一系列数
据对描绘在直角坐标系中，得到一系列的
X T XΘˆ = X TY
(4.7)
得
Θˆ＝( X T X )−1 X TY
(4.8)
这样求得的Θˆ 就称为Θ的最小二乘估计(LSE)，在统计学上，方程(4.7)称为正则方程，称ε
为残差。
在前面讨论的例子中，把 6 个数据对分别代入直线方程y=a0 + a1x中可得到 1 个由 6 个直线
统计学(第三版)课后答案 袁卫等主编
统计学第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
3. 一组数据的分布特征可以从哪几个方面进行测度？答：数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
要求:(1)计算这一比值95%的置 信区间;
(2)得出上述结论时作了什么假 设;
(3)能否以95%的置信水平说明 新酵素的产出率提高了。
已知: x x 1.268, s 0.228 n
1 95%
1求 :
解 :由 95%知Z 1.96
2
: x
第四章
参 数估计
4.1 参数估计的一般问题 4.2 一个总体参数的区间估计 4.3 两个总体参数的区间估计 4.4 样本容量的确定
学习目标
1. 估计量与估计值的概念 2. 点估计与区间估计的区别 3. 评价估计量优良性的标准 4. 一个总体参数的区间估计方法 5. 两个总体参数的区间估计方法 6. 样本容量的确定方法
112.5 102.6 100.0 116.6 136.8
25袋食品的重量
101.0 103.0 102.0
107.5
95.0 108.8
123.5 102.0 101.6
95.4
97.8 108.6
102.8 101.5
98.4
100.5 115.6 102.2 105.0
93.3
解：已知Ｘ~N(，102)，n=25, 1- = 95%，z/2=1.96。根据
Z
2
S n
1.268
1.96
0.228 36
1.194,1.342
（2）假设36批的样本是随机的。
（3）（1.194,1.342)>1,说明新酵素 的产出率提高了。
P109~5.7
: x
Z
2
s n
450 1.96
已知 : n 400, x 20000, s 6000
1 95%,(大样本) 求:
解 :由1 95%知z 1.96
3. 估计值：估计参数时计算出来的统计量的具 体值
– 如果样本均值 x =80，则80就是的估计值
参数估计的方法
估计方法
点估计
区间估计
点估计
(point estimate)
1. 用样本的估计量直接作为总体参数的估计值
– 例如：用样本均值直接作为总体均值的估计 – 例如：用两个样本均值之差直接作为总体均值
参数估计在统计方法中的地位
统计方法
描述统计
推断统计
参数估计
假设检验
第一节
参数估计的一般问题
一、估计量与估计值
(estimator & estimated value)
1. 估计量：用于估计总体参数的随机变量
– 如样本均值，样本比率、样本方差等
– 例如: 样本均值就是总体均值 的一个估计量
2. 参数用 表示，估计量用 ˆ 表示
n
P
x
n
Z
1
2
Px Z
2
n
x Z
2
1
n
即 : 给定置信度1 就有 : 总体均值的置信区间为:
: x Z
2
n
x
Z
2
n
,x Z
2
n
52 100
439.808,460.192
N : 2199040 ,2300960
习题7： 某汽车轮胎厂欲估计 其轮胎的平均行驶里程，由于轮胎 行驶里程受汽车型号、行驶的路面 以及汽车前后轮位置等影响，因此 使用了大样本 n 400 进行随机配置， 试验结果 x 20000 公里，标准差为 6000公里。要求估计总体均值的置 信区间，置信系数为95%。
P110~5.9
: x
Z
2
n
21.8
1.96
0.3 5
21.55,22.05
（二）大样本 1、方差已知
重复抽样
:
x
Z
2
n
不重复抽样 : x Z
2
n
N N
n 1
2、方差未知
重复抽样 : x Z
2
S n
不重复抽样 : x Z
2
S n
N N
n 1
【例】一家保险公司收集到由36投保个人组成的随 机样本，得到每个投保人的年龄(周岁)数据如下表。 试建立投保人年龄90%的置信区间
36个投保人年龄的数据
23 35 39 27 36 44 36 42 46 43 31 33 42 53 45 54 47 24 34 28 39 36 44 40 39 49 38 34 48 50 34 39 45 48 45 32
已知 : x x 14.8 15.3 15.1 15
n
6
0.05
由1 0.95知Z Z 0.025 1.96
2
求:
解 : : x
Z
2
n
15
1.96
0.05 6
14.96,15.04
2. 表示为 (1 -
为是总体参数未在区间内的比率
3. 常用的置信水平值有 99%, 95%, 90%
相应的 为0.01，0.05，0.10
置信区间
(confidence interval)
1. 由样本统计量所构造的总体参数的估计区间称 为置信区间
2. 统计学家在某种程度上确信这个区间会包含真 正的总体参数，所以给它取名为置信区间
习题6： 某药厂在生产过程中改换了一 种新的酵素，测定了36批的产出率与理论 产出率的比值：
1.28 1.31 1.48 1.10 0.99 1.25 1.22 1.65 1.40 0.95 1.25 1.32 1.23 1.43 1.24 1.73 1.35 1.31 0.92 1.10 1.05 1.39 1.16 1.19 1.41 0.98 0.82 1.22 0.91 1.26 1.32 1.71 1.29 1.17 1.74 1.51
x 35, S 4.5,1 95.45%
求 : 1E 2
解:由1 95.45%知Z 2
2
1E Z
2
S n
N n N 1
2 4.5 1000 100 100 1000 1
0.86件
2 : x E 35 0.86 34.14,35.86
(1 - ) % 区间包含了 % 的区间未包含
影响区间宽度的因素
1.总体数据的离散程度，用 来测度
2. 3.
样本容量， x 置信水平 (1
-
n)，影响
z
的大小
评价估计量的标准
无偏性
(unbiasedness)
无偏性：估计量抽样分布的数学期望等于 被估计的总体参数
P(ˆ)
解：已知n=36, 1- = 90%，z/2=1.645。根据样本数
据计算得：
x 39.5 s 7.77
总体均值在1- 置信水平下的置信区间为
x z 2
s 39.5 1.645 7.77
n
36
39.5 2.13
37.37,41.63
投保人平均年龄的置信区间为37.37岁~41.63岁
参数估计（parameter estimation) 就是在抽样及抽样分布的基础上，
根据样本统计量来推断我们所关心 的总体参数。
统计推断的过程
总体
样
样本统计量
本
如：样本均值
、比率、方差
非参数统计是统计学的一个重要分支，它在实践中有着
广泛的应用。所谓统计推断就是由样本观察值去了解总体， 它是统计学的基本任务之一。若根据经验或某种理论我们能 在推断之前就对总体作一些假设，则这些假设无疑有助于提 高统计推断的效率。这种情况下的统计方法称为参数统计。 如果我们所知很少，以致于在推断之前不能对总体作任何假 设，或仅能作一些非常一般性(例如连续分布、对称分布等) 的假设，这时如果仍然使用参数统计方法，其统计推断的结 果显然是不可信的，甚至有可能是错的。在对总体的分布不 作假设或仅作非常一般性假设条件下的统计方法称为非参数 统计。
3. 用一个具体的样本所构造的区间是一个特定的 区间，我们无法知道这个样本所产生的区间是 否包含总体参数的真值
– 我们只能是希望这个区间是大量包含总体参数真值
的区间中的一个，但它也可能是少数几个不包含参 数真值的区间中的一个
置信区间与置信水平
样本均值的抽样分布
x
/2
1–
/2
x
x
为显著性水平 1 则称为置信度。
1. 在点估计的基础上，给出总体参数估计的一个区间 范围，该区间由样本统计量加减抽样误差而得到的
2. 根据样本统计量的抽样分布能够对样本统计量与总 体参数的接近程度给出一个概率度量
– 比如，某班级平均分数在75～85之间，置信水平是95%
置信区间
样本统计量 (点估计)
无偏
有偏
A
B
ˆ
有效性
(efficiency)