2018年浙江省高中数学竞赛预赛真题

合集下载

2018年浙江省高中数学联赛试题

2018年浙江省高中数学联赛试题一．填空题1. 已知a 为正实数，且11()1xf x a a =-+是奇函数，则()f x 的值域为______________. 2. 设数列{}n a 满足11151(12)n n a a a n +==+= ，，，，则20181n n a ==∑______________.3. 已知3()4παβπ∈，，，412cos()sin()5413παβα+=-=，，则cos()4πβ+=______________. 4. 在八个数字24678111213，，，，，，，中任取两个组成分数，则这些数中有_______文化既约分数. 5. 已知虚数z 满足310z +=，则20182018111z z z ⎛⎫⎛⎫+= ⎪⎪--⎝⎭⎝⎭_____________.6. 设||10AB = ，若平面上点P 满足，对于任意t R ∈，有||3AP t AB -≥，则当PA PB ⋅ 取得最小值时，||PA PB +=____________.7. 在ABC ∆中，7AB AC +=，且其面积4ABC S ∆=，则sin A 的最小值为____________. 8. 设()|1||||2|f x x x x =++--，则(())10f f x +=有__________个不同的解.9. 设x y R ∈，满足120x -=，则x 的取值范围为____________.10. 四面体P ABC -，PA BC ==PB AC ==PC AB ==则该四面体P ABC - 外接球的半径为____________. 二．解答题11. 已知动直线l 与圆221O x y +=：相切，与椭圆2219x y +=相交于不同的两点A B ，.求原点到线段AB 的中垂线的最大距离.12. 设a R ∈，且对任意实数b 均有2[01]max ||1x x ax b ∈++≥，，求a 的取值范围.13. 设实数122018x x x ，，，满足212(122016)n n n x x x n ++≤= ，，，和201811n n x ==∏，证明：100910101x x ≤.14. 将2(2)n n ≥个不同整数分成两组1212n n a a a b b b ，，，；，，，. 证明：111||(||||)ij i j i j i ni j nj nab a a b b n ≤≤≤<≤≤≤---+-≥∑∑.15. 如图所示将同心环均匀分成(3)n n ≥格，在内环中固定数字1~n .问能否将数字1~n 填入外环格内，使得外环旋转任意格后有且仅有一个格中内外环的数字相同？。

2018年浙江省高中数学竞赛预赛真题含答案

2 f (1) 1 a b f (0) b ，所以 f (1) 1 a b 1，
解得 a 1 . （2）当 0 a 1 时，即 1 a 0 ，此时函数 f (x) 的最值在抛物线的顶点和右端点取得，而对
22 b 0 有 f (1) 1 a 1， f ( a ) a2 1 .
24 （3）当 1 a 1时，即 2 a 1，此时函数 f (x) 的最值在抛物线的顶点和左端点取得，而对
22 b 0 有 f (0) b 1 ， f ( a ) a2 1 .
24 （4）当 a 1 时，即 a 2 ，此时函数 f (x) 的最值在抛物线的左右端点取得，对任意 b 1有
2018
13.设实数
x1
，
x2
，…，
x2018
满足
x2 n1

xn xn2 (n

1,
2, ,
2016)
和
xn 1，证明： x x 1009 1010 1.
n1
14.将 2n(n 2) 个不同整数分成两组 a1 ， a2 ，…， an ； b1 ， b2 ，…， bn .证明
．
8.设 f (x) x 1 x x 2 ，则 f ( f (x)) 1 0 有
个不同的解．
9.设 x, y R 满足 x 6 y 4 x y 12 0 ，则 x 的取值范围为
．
10.四面体 P ABC ， PA BC 6 ， PB AC 8 ， PC AB 10 ，则该四面体外接球的半径
2 f (0) b 1 ，所以 f (1) 1 a b 1，解得 a 3 .

2018年浙江省高中数学竞赛预赛真题

2018年浙江省高中数学竞赛试卷一、填空题1.已知a 为正实数，且11()1xf x a a =-+是奇函数，则()f x 的值域为． 2.设数列{}n a 满足11a =，151(1,2,)n n a a n +=+=⋅⋅⋅，则20181nn a==∑ ．3.已知3,,4παβπ⎛⎫∈⎪⎝⎭，4cos()5αβ+=，12sin 413πα⎛⎫-= ⎪⎝⎭，则cos 4πβ⎛⎫+= ⎪⎝⎭ ．4.在八个数字2，4，6，7，8，11，12，13中任取两个组成分数.这些分数中有个既约分数．5.已知虚数z 满足310z +=，则20182018111z z z ⎛⎫⎛⎫+= ⎪⎪--⎝⎭⎝⎭．6.设10AB =，若平面上点P 满足，对于任意t R ∈，有3AP t A B -≥，则P AP B ⋅的最小值为，此时PA PB += ．7.在ABC ∆中，7AB AC +=，且三角形的面积为4，则sin A ∠的最小值为． 8.设()12f x x x x =++--，则(())10f f x +=有个不同的解． 9.设,x y R ∈满足64120x y x y ---+=，则x 的取值范围为． 10.四面体P ABC -，6PA BC ==，8PB AC ==，10PC AB ==，则该四面体外接球的半径为．二、解答题11.已知动直线l 与圆O ：221x y +=相切，与椭圆2219x y +=相交于不同的两点A ，B .求原点到AB 的中垂线的最大距离.12.设a R ∈，且对任意实数b 均有2[0,1]max 1x x ax b ∈++≥，求a 的取值范围.13.设实数1x ，2x ，…，2018x 满足212(1,2,,2016)n n n xx x n ++≤=⋅⋅⋅和201811n n x ==∏，证明：100910101x x ≤.14.将2(2)n n ≥个不同整数分成两组1a ，2a ，…，n a ；1b ，2b ，…，n b .证明111()i j j i j i i n i j nj na b a a b b n ≤≤≤<≤≤≤---+-≥∑∑.15.如图所示将同心圆环均匀分成(3)n n ≥格.在内环中固定数字1n .问能否将数字1n 填入外环格内，使得外环旋转任意格后有且仅有一个格中内外环的数字相同？2018年浙江省高中数学竞赛试卷参考答案一、填空题1. 11(,)22-2. 2019580771616-3. 5665- 4. 36 5. 1- 6. 16-；6 7.728. 3 9. 1421314213x -≤≤+ 10. 3 二、解答题11.解：依题意可设l ：(0)y kx m k =+≠.因为直线l 与圆O 相切，所以，O 到直线l 的距离为1，即211m k=+.原点到AB 的中垂线的最大距离为43. 12.解1：设2()f x x ax b =++，对于1(0)1b f ≥⇒≥，所以只要考虑1b <. （1）当02a-≤时，即0a ≥.此时函数()f x 的最值在抛物线的左右端点取得，对任意1b <有(1)1(0)f a b f b =++>=，所以(1)11f a b =++≥，解得1a ≥. （2）当1022a <-≤时，即10a -≤<，此时函数()f x 的最值在抛物线的顶点和右端点取得，而对0b =有(1)11f a =+<，2()124a a f --=<. （3）当1122a<-≤时，即21a -≤<-，此时函数()f x 的最值在抛物线的顶点和左端点取得，而对0b =有(0)1f b =<，2()124a a f --=<. （4）当12a-≥时，即2a ≤-，此时函数()f x 的最值在抛物线的左右端点取得，对任意1b <有(0)1f b =<，所以(1)11f a b =++≤-，解得3a ≤-.综上1a ≥或3a ≤-.解2：设2[0,1]max x m x ax b ∈=++，则有m b ≥，1211m a b m b a b a ≥++⇒≥+++≥+依题意，1112aa +≥⇒≥，或3a ≤-. 13.证明：由条件n x ，2n x +同号.反证法，假设100910101x x >.（1）若1009x ，1010x 同为正数，由n x ，2n x +同号可知1x ，2x ，…，2018x 同号. 由212121n n n n n n n x x x x x x x +++++≤⇒≤100910101011100810091010x x xx x x ⇒≤≤ 1009101010111008101110081x x x x x x ⇒≤⇒>，同理100910091008101110121012100710081007101010111010x x x x x x x x x x x x =⋅≤⋅=100710121x x ⇒>. 类似可证明：100610131x x >，100510041x x >，…，120181x x >. 因此201811nn x=>∏，矛盾.（2）若1009x ，1010x 同为负数，由n x ，2n x +同号可知1x ，2x ，…，2018x 均为负数，仍然有212121n n n n n n n x x x x x x x +++++≤⇒≤，类似（1）可证得. 14.证明：令111()n i j j i j i i n i j nj nT a b a a b b ≤≤≤<≤≤≤=---+-∑∑，下面用归纳法证明n T n ≥.当2n =时，不妨设12a a <，12b b <，22a b <.2212211T b a b a b a =-+-+-122121b a a a b b +-----，当1121112122a b T b a b b b a <⇒=-+++->；当11222112a b T b a a b >⇒=-++>. 假设对正整数n 成立，对正整数1n +，不妨设121n a a a +<<⋅⋅⋅<，121n b b b +<<⋅⋅⋅<，11n n a b ++<.再设11k n k b a b ++<<，则有11111n n n n i n i i i T b a a b +++===-+-∑∑111111n nn i n i n n n i i a a b b b a T ++++==----+-+∑∑，下证1111nn n i n i i i ba ab ++==-+-∑∑11110n nn i n i i i a a b b ++==----≥∑∑.由（1）11(1,2,,)k n k b a b k n ++<<=⋅⋅⋅，得到1111nn n i n i i i ba ab ++==-+-∑∑1111n nn i n i i i a a b b ++==----∑∑112()0ni n i k b a +=+=->∑；（2）若11n a b +<，则1111nn n i n i i i ba ab ++==-+-∑∑1111n nn i n i i i a a b b ++==----∑∑11()0ni n i b a +==->∑.15.解：设对应于内环1，2，…，n 的外环数字为1i ，2i ，…，n i ，它是数字1，2，…，n 的一个排列.对1,2,,k n =⋅⋅⋅，记外环数字k i 在按顺时针方向转动k j 格时，和内环数字相同，即mod k k i k j n -=，1,2,,k n =⋅⋅⋅.根据题意，1j ，2j ，…，n j 应是0，1，2，…，1n -的排列.求和11()mod n nk k k k i k j n ==-=∑∑(012(1))mod n n =+++⋅⋅⋅+-1(1)mod 2n n n =-. 于是n 必须是奇数.对于奇数n ，我们取n i n =，m i n m =-，(1,2,,1)m n =⋅⋅⋅-，可以验证mod k k i k j n -=，0n j =，12n j -=，24n j -=，…，121n n jn --=-，12j n =-，14n j n -=-，36j n =-，…，121n j -=，符合题目要求！。

年全国高中数学联赛浙江省预赛试题及答案（word版本）

年全国高中数学联合竞赛浙江省预赛试卷一、选择题 1、下列三数16273,log 82,log 1242的大小关系正确的是（） A 、16273log 82log 1242<< B 、27163log 124log 822<<C 、27163log 124log 822<<D 、27163log 124log 822<<2、已知两点A （1,2），B （3,1）到直线L 252L 共有（）A 、1条B 、2条C 、 3条D 、 4条3、设()f n 为正整数n （十进制）的各数位上的数字的平方之和，比如()22212312314f =++=。

记1()()f n f n =，1()(())k k f n f f n +=，1,2,3...k =，则2006(2006)f =（）A 、20B 、4C 、42D 、1454、设在xOy 平面上，20y x <≤，01x ≤≤所围成图形的面积为13，则集合 {}{}2(,)|||||1,(,)|||1M x y y x N x y y x =-≤=≥+的交集M N ⋂所表示的图形面积为（）A 、13 B 、23 C 、1 D 、435、在正边形中，与所有边均不平行的对角线的条数为（）。

A 、B 、21003 C 、210031003- D 、210031002- 6、函数sin cos tan cot sin cos tan cot ()sin tan cos tan cos cot sin cot x x x x x x x x f x x x x x x x x x ++++=+++++++在(,)2x o π∈时的最小值为（）。

A 、2B 、4C 、6D 、8 二、填空题7、手表的表面在一平面上。

整点1,2,,12这12个数字等间隔地分布在半径为22的圆周上。

从整点i 到整点()1i +的向量记作1i i t t +，则1223233412112t t t t t t t t t t t t ⋅+⋅++⋅＝。

第九届陈省身杯全国高中数学奥林匹克竞赛(浙江预赛)试题及解答

令 f x
x
3
x 1
2
x
2
2 1 x 1 x2

x
3
x 1

2
2 1 x 1

0 ，则
x
2
2 1 x 1 x2
2
由于 x
2 1 x 1 0 。 2 1 x 1 0 的判别式小于 0 ，则该方程无实根。
1 1 2 ， t
2 2 1 1 2 1 f t 3 2 t 1 2 3 t 0 ，因此函数 f t 为凸函数，由琴生不等 t t t t
L, M , N , K ，则四面体 LMNK 的内切球的半径为
答
。
3 2 。 2
设四面体 LMNK 的内切球的半径为 r ，因为 NLK LNM 90 ，所以
1 2 2 。 S LMN S LNK 1 2 2 4
又因为 MLK MNK 90 ，所以 S LMK S MNK
5, 43+19
2 11 14 。
x 1 x 0 x 1 ，若 f x 的最大值为 f x0 x3 x 1
，则 x0

6.设函数 f x 。答
2 1 2 2 1 。 2
x 4 2 x3 x 2 2 x 1
式可得 f x f y 2 f
3 3
x y 2f 2
1 1 125 。当 x y 时等号成立，因此 4 2 2
125 1 1 。 x y 的最小值为 4 x y

2018年全国高中数学联赛浙江赛区预赛试题+答案

|m|
l
O
O
l
1√
= 1.
5
1+ k2
y = kx + m
A(x1, y1), B(x2, y2)
x2 + 9y2 − 9 = 0
(1 + 9k2)x2 + 18kmx + (9m2 − 9) = 0
第3页
(
)
18km
9km m
x1 + x2 = − 1 + 9k2
AB
(
− 1 +)9k2 , 1 + 9k2 .
f (x) = −2
x = −1 f (x) = 0
1
x = −3, x =
3
3
9. x, y ∈ R
x
−
6√y
−
√ 4x
−
y
+
12
=
0
x
√
√
答案 14 − 2 13 ≤ x ≤ 14 + 2 13.
解析
x
−
6√y
−
√ 4x
−
y
+
12
=
0
⇒
√ (x
−
y
−
2)2
+
(√y
−
3)2
=
1
.
. . √ x − y − 2 = cos θ
1≤i≤n,1≤j≤n
1≤i<j≤n
证明
∑
∑
Tn =
|ai − bj| −
(|aj − ai| + |bj − bi|)
1≤i≤n,1≤j≤n
1≤i<j≤n

2018年全国高中数学联赛浙江省预赛高三数学试题(解析版)

2018年全国高中数学联赛浙江省预赛高三数学试题一、填空题1 1= 一-；—1 .已知a 为正实数，且 “1是奇函数，则⑷的值域为.1111 1 1 ― --- ----------- =- - + f （x ）=--— 由小）为奇函数可知a - + 19「+ 1,解得a= 2,即 22、由此得f （x ）的值域为। 2 2'.2018「2%1.3 ) 鼻二1 3- 5a +1£ 南满足］一，n*i- a (n=1, 2,…)，则 n = 1520198077【答案】16 16 【解析】【详解】1 / 八■ +［二5皆十1小二1+『5阿+1=%由4" 4"56故答案为：.2.设数列所以 2018V Lu1<-2c201S=不5 +5 +... + S20185x c 2018 1t=—行口-162018 S 2019£07 71616(3n \小 4风0 E —cos(a + p)=3.已知 '4",56I 4.J 13,则【解析】【详解】%£ E (彳再)孙3 +位二Mi 7Tcos\p + —I = cos (a + 所以 sin(a + B)——，得.J71 a—4亡叫cr 一: 6二 - 13, 5665【解析】【详解】加索-34.在八个数字2, 4, 6, 7, 8, 11, 12, 13中任取两个组成分数.这些分数中有个既约分数.【答案】36【解析】【详解】在7, 11, 13中任取一个整数与在2, 4, 6, 8, 12中任取一个整数构成既约分数，共有3 5 种；在7, 11, 13中任取两个整数也构成既约分数，共有A3,6中.合计有36种不同的既约分数./ 1 ^2018 + (1/01S _5,已知虚数z满足P+1=Q,则上』H .【答案】I【解析】【详解】1 2018 上r , 3^72 2.1 之上[/ 1 \2018 + ( 1 JOIS _ 工 ,1 _(Z)- _ . . I _ 1I? - 1 l z _ 1 _ t2,2018 - t3,1345 _ z-所以^ .6.设明=1。

浙江省杭州市2018年高考数学命题比赛试题25(word版含答案)

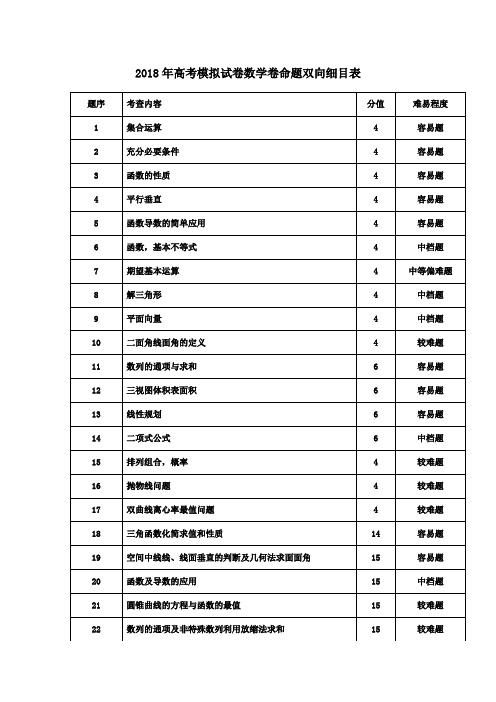
2018年高考模拟试卷数学卷命题双向细目表考试设计说明本试卷设计是在认真研读《2018年考试说明》的基础上精心编制而成，以下从三方面加以说明。

一、在选题上：（1）遵循“考查基础知识的同时，注重考查能力”的原则，确立以能力立意命题的指导思想，将知识、能力和素质融为一体，全面检测考生的数学素养。

（2）试卷保持相对稳定，适度创新，逐步形成“立意鲜明，背景新颖，设问灵活，层次清晰”的特色。

二、命题原则：（1）强化主干知识，从学科整体意义上设计试题．（2）注重通性通法，强调考查数学思想方法．（3）注重基础的同时强调以能力立意，突出对能力的全面考查．（4）考查数学应用意识，坚持“贴近生活，背景公平，控制难度”的原则．（5）结合运动、开放、探究类试题考查探究精神和创新意识．（6）体现多角度，多层次的考查，合理控制试卷难度。

2018年浙江省高考模拟试卷数学卷本试题卷分选择题和非选择题两部分．满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分（共40分）注意事项：1.答题前，考生务必将自己的姓名、准考证号用黑色的字迹的签字笔或钢笔填写在答题纸上。

2.每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

答在试题卷上无效。

参考公式：如果事件A ，B 互斥，那么棱柱的体积公式 ()()()P A B P A P B +=+ V Sh =如果事件A ，B 相互独立，那么其中S 表示棱柱的底面积，h 表示棱柱的高 ()()()P A B P A P B ⋅=⋅ 棱锥的体积公式如果事件A 在一次试验中发生的概率是p ，那么 13V S h =n 次独立重复试验中事件A 恰好发生k 次的概率其中S 表示棱锥的底面积，h 表示棱锥的高()()()1,0,1,2,,n kk kn n P k C p k k n -=-= 棱台的体积公式球的表面积公式 24S R π= ()1213V h S S =球的体积公式 343V R π= 其中12,S S 分别表示棱台的上底、下底面积，其中R 表示球的半径 h 表示棱台的高一、选择题：（本大题共10小题，每小题4分，共40分。

2018年浙江省高中数学竞赛预赛真题Word版含答案

2018年浙江省高中数学竞赛试卷一、填空题1.已知a 为正实数，且11()1x f x a a =-+是奇函数，则()f x 的值域为． 2.设数列{}n a 满足11a =，151(1,2,)n n a a n +=+=⋅⋅⋅，则20181nn a==∑ ．3.已知3,,4παβπ⎛⎫∈⎪⎝⎭，4cos()5αβ+=，12sin 413πα⎛⎫-= ⎪⎝⎭，则c o s 4πβ⎛⎫+= ⎪⎝⎭ ．4.在八个数字2，4，6，7，8，11，12，13中任取两个组成分数.这些分数中有个既约分数．5.已知虚数z 满足310z +=，则20182018111z z z ⎛⎫⎛⎫+= ⎪⎪--⎝⎭⎝⎭．6.设10AB =，若平面上点P 满足，对于任意t R ∈，有3AP t AB -≥，则PA PB ⋅的最小值为，此时PA PB += ．7.在ABC ∆中，7AB AC +=，且三角形的面积为4，则sin A ∠的最小值为． 8.设()12f x x x x =++--，则(())10f f x +=有个不同的解．9.设,x y R ∈满足120x -=，则x 的取值范围为．10.四面体P ABC -，PA BC =，PB AC ==PC AB ==接球的半径为．二、解答题11.已知动直线l 与圆O ：221x y +=相切，与椭圆2219x y +=相交于不同的两点A ，B .求原点到AB 的中垂线的最大距离.12.设a R ∈，且对任意实数b 均有2[0,1]max 1x x ax b ∈++≥，求a 的取值范围.13.设实数1x ，2x ，…，2018x 满足212(1,2,,2016)n n n xx x n ++≤=⋅⋅⋅和201811n n x ==∏，证明：100910101x x ≤.14.将2(2)n n ≥个不同整数分成两组1a ，2a ，…，n a ；1b ，2b ，…，n b .证明111()i j j i j i i n i j nj na b a a b b n ≤≤≤<≤≤≤---+-≥∑∑.15.如图所示将同心圆环均匀分成(3)n n ≥格.在内环中固定数字1n .问能否将数字1n 填入外环格内，使得外环旋转任意格后有且仅有一个格中内外环的数字相同？2018年浙江省高中数学竞赛试卷参考答案一、填空题1. 11(,)22-2. 2019580771616- 3. 5665- 4. 36 5. 1-6. 16-；67.728. 39. 1414x -≤+二、解答题11.解：依题意可设l ：(0)y kx m k =+≠.因为直线l 与圆O 相切，所以，O 到直线l 的距离为11=.原点到AB 的中垂线的最大距离为43. 12.解1：设2()f x x ax b =++，对于1(0)1b f ≥⇒≥，所以只要考虑1b <. （1）当02a-≤时，即0a ≥.此时函数()f x 的最值在抛物线的左右端点取得，对任意1b <有(1)1(0)f a b f b =++>=，所以(1)11f a b =++≥，解得1a ≥. （2）当1022a <-≤时，即10a -≤<，此时函数()f x 的最值在抛物线的顶点和右端点取得，而对0b =有(1)11f a =+<，2()124a a f --=<.（3）当1122a<-≤时，即21a -≤<-，此时函数()f x 的最值在抛物线的顶点和左端点取得，而对0b =有(0)1f b =<，2()124a a f --=<.（4）当12a-≥时，即2a ≤-，此时函数()f x 的最值在抛物线的左右端点取得，对任意1b <有(0)1f b =<，所以(1)11f a b =++≤-，解得3a ≤-. 综上1a ≥或3a ≤-.解2：设2[0,1]max x m x ax b ∈=++，则有m b ≥，1211m a b m b a b a ≥++⇒≥+++≥+依题意，1112aa +≥⇒≥，或3a ≤-. 13.证明：由条件n x ，2n x +同号.反证法，假设100910101x x >.（1）若1009x ，1010x 同为正数，由n x ，2n x +同号可知1x ，2x ，…，2018x 同号. 由212121n n n n n n n x x x x x x x +++++≤⇒≤100910101011100810091010x x xx x x ⇒≤≤ 1009101010111008101110081x x x x x x ⇒≤⇒>，同理100910091008101110121012100710081007101010111010x x x x x x x x x x x x =⋅≤⋅=100710121x x ⇒>. 类似可证明：100610131x x >，100510041x x >，…，120181x x >. 因此201811nn x=>∏，矛盾.（2）若1009x ，1010x 同为负数，由n x ，2n x +同号可知1x ，2x ，…，2018x 均为负数，仍然有212121n n n n n n n x x x x x x x +++++≤⇒≤，类似（1）可证得. 14.证明：令111()n i j j i j i i n i j nj nT a b a a b b ≤≤≤<≤≤≤=---+-∑∑，下面用归纳法证明n T n ≥.当2n =时，不妨设12a a <，12b b <，22a b <.2212211T b a b a b a =-+-+-122121b a a a b b +-----，当1121112122a b T b a b b b a <⇒=-+++->；当11222112a b T b a a b >⇒=-++>. 假设对正整数n 成立，对正整数1n +，不妨设121n a a a +<<⋅⋅⋅<，121n b b b +<<⋅⋅⋅<，11n n a b ++<.再设11k n k b a b ++<<，则有11111nnn n i n i i i T b a a b +++===-+-∑∑111111nnn i n i n n n i i a a b b b a T ++++==----+-+∑∑，下证1111nn n i n i i i ba ab ++==-+-∑∑11110n nn i n i i i a a b b ++==----≥∑∑.由（1）11(1,2,,)k n k b a b k n ++<<=⋅⋅⋅，得到1111nn n i n i i i ba ab ++==-+-∑∑1111n nn i n i i i a a b b ++==----∑∑112()0ni n i k b a +=+=->∑；（2）若11n a b +<，则1111nn n i n i i i ba ab ++==-+-∑∑1111n nn i n i i i a a b b ++==----∑∑11()0ni n i b a +==->∑.15.解：设对应于内环1，2，…，n 的外环数字为1i ，2i ，…，n i ，它是数字1，2，…，n 的一个排列.对1,2,,k n =⋅⋅⋅，记外环数字k i 在按顺时针方向转动k j 格时，和内环数字相同，即mod k k i k j n -=，1,2,,k n =⋅⋅⋅.根据题意，1j ，2j ，…，n j 应是0，1，2，…，1n -的排列.求和11()mod n nk k k k i k j n ==-=∑∑(012(1))mod n n =+++⋅⋅⋅+-1(1)mod 2n n n =-. 于是n 必须是奇数.对于奇数n ，我们取n i n =，m i n m =-，(1,2,,1)m n =⋅⋅⋅-，可以验证mod k k i k j n -=，0n j =，12n j -=，24n j -=，…，121n n jn --=-，12j n =-，14n j n -=-，36j n =-，…，121n j -=，符合题目要求！。

2018年数学竞赛预赛真题及答案解析内部流出，绝密必看！

2018年数学竞赛预赛真题及答案解析内部流出，绝密必看！
导读
近日，全国各省市的2018数学竞赛预赛正在如火如荼的进行中，目前北京、江苏、浙江、湖北、四川等10余个省市的初赛已经结束。

学科竞赛网第一时间，为大家汇总带来各省市的预赛真题与答案解析，供广大数学竞赛党学习参考。

（注：目前所有省市的预赛真题都没有官方发布，均为内部渠道获得，部分试题清晰度可能不佳，后续试题正式发布后，我们会及时更新高清版）
北京预赛真题及答案解析
江苏预赛真题与答案真题
答案解析
浙江预赛真题与答案
上海预赛真题与答案真题
答案解析
湖北预赛真题及参考答案
四川预赛真题与答案
重庆预赛真题及答案
福建初赛真题及参考答案
河南预赛真题与答案高一。

浙江省杭州市2018年高考数学命题比赛试题18(word版含答案)

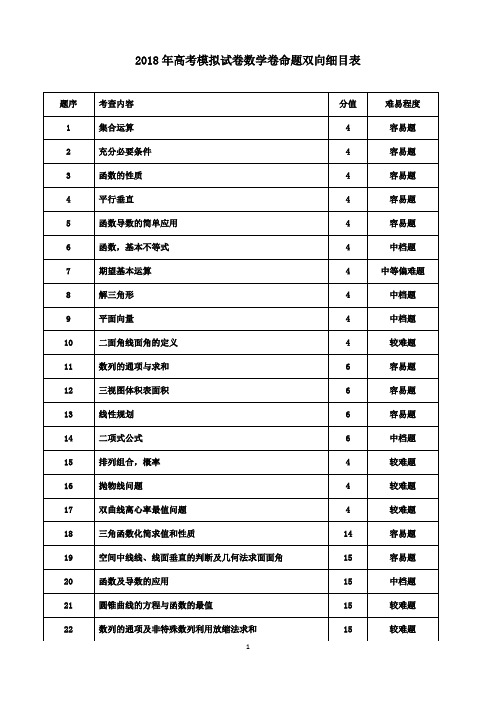
2018年高考模拟试卷数学卷命题双向细目表考试设计说明本试卷设计是在认真研读《2018年考试说明》的基础上精心编制而成，以下从三方面加以说明。

（2）试卷保持相对稳定，适度创新，逐步形成“立意鲜明，背景新颖，设问灵活，层次清晰”的特色。

2018年高考模拟试卷数学卷（时间 120 分钟满分150 分）参考公式：如果事件A ，B 互斥，那么()()()P A B P A P B +=+．如果事件A ，B 相互独立，那么()()()P A B P A P B ⋅=⋅．如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,...,)k k n kn n P k C p p k n -=-= ．球的表面积公式24S Rπ=，其中R 表示球的半径．球的体积公式343VRπ=，其中R 表示球的半径．柱体的体积公式V S h =，其中S 表示柱体的底面积，h 表示柱体的高．锥体的体积公式13V S h=，其中S 表示锥体的底面积，h 表示锥体的高．台体的体积公式121()3Vh S S =+，其中12,S S 分别表示台体的上、下底面积，h 表示台体的高．选择题部分一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若i 是虚数单位，复数z 满足(1－i)z ＝1，则|2z －3|＝( ) A ． 3 B ． 5 C ． 6 D ．7 2．已知条件p ：x ≤1，条件q ：＜1，则q 是￢p 成立的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既非充分也非必要条件3．已知，函数y=f （x+φ）的图象关于（0，0）对称，则φ的值可以是（） A ． B ．C ．D ．4．若直线xcos θ+ysin θ﹣1=0与圆（x ﹣cos θ）2+（y ﹣1）2=相切，且θ为锐角，则这条直线的斜率是（） A ．B ．C ．D ．5．若m 、n 为两条不重合的直线，α、β为两个不重合的平面，则下列命题中的真命题个数是（）①若m 、n 都平行于平面α，则m 、n 一定不是相交直线； ②若m 、n 都垂直于平面α，则m 、n 一定是平行直线；③已知α、β互相垂直，m 、n 互相垂直，若m ⊥α，则n ⊥β； ④m 、n 在平面α内的射影互相垂直，则m 、n 互相垂直．A ．1B ．2C ．3D ．46．设0,0),0,(),1,(),2,1(>>-=-=-=b a b OC a OB OA ，O 为坐标原点，若A 、B 、C 三点共线，则ba 21+的最小值是（）A ．2B ．4C ．6D ．87．将5名同学分到甲、乙、丙3个小组，若甲组至少两人，乙、丙组每组至少一人，则不同的分配方案的种数为( ) A ．50 B ．80 C ．120 D ．1408．已知F 1、F 2分别是双曲线的左右焦点，A 为双曲线的右顶点，线段AF 2的垂直平分线交双曲线与P ，且|PF 1|=3|PF 2|，则该双曲线的离心率是（） A ． B ． C ． D ．9．已知f (x )＝x 2＋3x ，若|x －a |≤1，则下列不等式一定成立的是( ) A ．|f (x )－f (a )|≤3|a |＋3 B ．|f (x )－f (a )|≤2|a |＋4 C ．|f (x )－f (a )|≤|a |＋5 D ．|f (x )－f (a )|≤2(|a |＋1)210．如图，棱长为4的正方体ABCD A 1B 1C 1D 1，点A 在平面α内，平面ABCD 与平面α所成的二面角为30°，则顶点C 1到平面α的距离的最大值是( )A ．2(2＋2)B ．2(3＋2)C ．2(3＋1)D ．2(2＋1)非选择题部分二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分） 11．设全集集U=R ，集合M={x|﹣2≤x ≤2}，N={x|y=}，那么M ∩N= ，C U N= ．12．一空间几何体的三视图如图所示，则该几何体的体积为，表面积为．13．已知{a n }为等差数列，若a 1+a 5+a 9=8π，则前9项的和S 9= ， cos （a 3+a 7）的值为．14．袋中有大小相同的3个红球，2个白球，1个黑球．若不放回摸球，每次1球，摸取3次，则恰有2 次红球的概率为________；若有放回摸球，每次1球，摸取3次，则摸到红球次数X 的期望为________．15. 已知变量x ，y 满足⎩⎪⎨⎪⎧x －4y ＋3≤0，x ＋y －4≤0，x ≥1，x 2＋y 2xy的取值范围为________．16.设max{a ，b }＝⎩⎪⎨⎪⎧aa ≥b b a <b已知x ，y ∈R ，m ＋n ＝6，则F ＝max{|x 2－4y ＋m |，|y 2－2x ＋n |}的最小值为________．17．已知函数f (x )＝x 2－x －4x x －1(x <0)，g (x )＝x 2＋bx －2(x >0)，b ∈R .若f (x )图象上存在A ，B 两个不同的点与g (x )图象上A ′，B ′两点关于y 轴对称，则b 的取值范围为________．三、解答题（本大题共5小题，共74分,解答应写出文字说明,证明过程或演算步骤.） 18．（本题满分14分）在∆A B C 中，a b c ，，分别是∠∠∠A B C ，，的对边长，已知a b c ，，成等比数列，且a c a cb c 22-=-，求∠A 的大小及b B csin 的值.俯视图19．（本题满分15分）如图，已知四棱锥P-ABCD ，底面ABCD 为菱形，PA ⊥平面ABCD ，∠ABC=60°，E ，F 分别是BC ，PC 的中点。

浙江省高中数学联赛试题及参考答案

n
n
n
n
∑ ∑ ∑ ∑ T= n+1
bn+1 − ai + an+1 − bi − an+1 − ai − bn+1 − bi + bn+1 − an+1 + Tn
解得 a ≥ 1。………………………………………………………………10 分
（2）当 0 < − a ≤ 1 时，即 −1 ≤ a < 0 ，此时函数 f (x) 的最值在抛物线的顶点和右 22
端点取得，而对 b = 0 有 f (1) = 1 + a < 1, f (− a ) = −a2 < 1。
x≤0 x≤2
由 f ( f (x)) +1 =0 得到
x + 3, x > 2
f (x) = −2, 或 f (x) = 0 。由 f (x) = −2, 得一个解 x = −1 ；由 f (x) = 0 得两个解
x = −3, x = 1 ，共 3 个解。 3
9. 设 x, y ∈ R 满足 x − 6 y − 4 x − y +12=0 ，则 x 的取值范围为 ______________。解由 x − 6 y − 4 x − y +12=0 ⇒ ( x − y − 2)2 + ( y − 3)2 =1。令
−
2018 4
=5 16
(52018
− 1)
−
2018 4
=52019 16
−
8077 16
。
3.
已知α , β
∈

3π 4
,π

， cos(α

浙江省杭州市2018年高考数学命题比赛试题21(word版含答案)

试卷设计说明结合《学科教学指导意见》、《2018年浙江省考试说明》及历年全国各地高考数学试卷，精心编撰了本试卷。

整个试卷的结构与新高考试卷结构一致，从题型，分数的分布与内容的选择力求与高考保持一致，在难度的把握上，基本介于以前文理科难度之间。

试卷强化基础知识，注重能力考查，重视通性通法。

命题、选题均从数学素养出发，侧重对知识的理解与应用，考查学生对于所学知识的迁移，考察学生思维的广度与深度，考察学生的数学能力，并在一定基础之上有所拔高，检验学生对于更高层次的数学思想方法的掌握程度。

试卷命题双向细目表本试卷分第（Ⅰ）卷（选择题）和第（Ⅱ）卷（非选择题）两部分．满分150分，考试时间120分钟请考生按规定用笔将所有试题的答案涂、写在答题纸上。

参考公式：球的表面积公式：，其中R 表示球的半径；球的体积公式：34π3VR=，其中R 表示球的半径；棱柱体积公式：V S h =，其中S 为棱柱的底面面积，h 为棱柱的高；棱锥体积公式：13V S h =，其中S 为棱柱的底面面积，h 为棱柱的高；台体的体积公式：()1213Vh S S =+其中12,SS 分别表示台体的上底、下底面积，h 表示台体的高．第Ⅰ卷（选择题共40分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

一. 选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1. [原创] 已知集合{|2}xP x R y =∈=，{|Q y R y =∈=，则P Q ⋂=（ ▲ ）A .[1,1]-B .[0,)+∞C .(,1][1,)-∞⋃+∞D .(0,1]2. [原创] 已知复数34i z i ⋅=+，其中i 为虚数单位，则z =（ ▲ ）A .43i -+B .43i --C .43i -D .43i +3. [原创] 若命题P ：对于任意的x ,有|1||21|x x a ++-≥恒成立，命题Q ：3a ≤，则P 是Q 的（ ▲ ）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. [原创] 在平面直角坐标系XOY 中，曲线()ln f x a x x =+在x a =处的切线过原点，则a =（ ▲ ）A .1B .eC .1eD .05. [原创] 已知正整数,x y 满足不等式组2252x y x y y -≤⎧⎪+≥⎨⎪≤⎩，则221x y x +++的取值范围为（ ▲ ）A .77[,]42B .7[2,]2C .7[,2]4D .57[,]226. [原创]袋中有大小相同的10个球，其中红球6个，白球4个.现从袋中随机摸出3个球，设摸取的3个球中所含红球数为X ,则()P X k =取最大值时，k 的值为（ ▲ ）A . 0B .1C .2D .37. [原创] 在三角形A B C ∆中，=4A B ，0A C λλ=>（），若2CA CB ⋅≥-对任意的0λ>恒成立，则角A 的取值范围为（ ▲ ）A .[]42ππ， B .3[]44ππ， C .3(0,]4π D .3[4ππ，） 8. [原创] 已知1(,0)F c -,2(,0)F c 分别为双曲线2222:1(,0)x y a b abΓ-=>的左、右焦点，过点1F 作直线l 切圆222()x c y r -+=于点P ,l 分别交Γ右支于A 、B 两点（A 、B 位于线段1F P 上），若1||:||:||2:2:1F A A B B P =,则双曲线Γ的离心率的值为（ ▲ ）A .5 B5C.+ D.9. [原创] 在四面体A B C D -中，,E F 分别为棱,A B C D 的中点，过E F 的平面α交,B C A D 于,G H ，则,E G F E H F S S ∆∆满足下列哪种关系（ ▲ ）A .E G F E H F S S ∆∆=B .E G F E H F S S ∆∆>C .E G F E H F S S ∆∆<D .,E GF E H F S S ∆∆随着平面α的变化而变化10. [原创]已知二次函数2(),,,f x a x b x c a b c N +=++∈,函数()f x 在11(,)44-上有两个零点，则a b c ++的最小值为（▲）A .38B .39C .40D .41第Ⅱ卷（非选择题共110分）注意事项：1．黑色字迹的签字笔或钢笔填写在答题纸上，不能答在试题卷上。

2018年浙江省高中数学联赛试题及参考答案

2018
1 + z −1
2018
z 2018 + 1 ( z 3 )672 z 2 + 1 z 2 + 1 = = = = −1 。 ( z 2 )2018 ( z 3 )1345 z −z
6. 设 AB = 10 。若平面上点 P 满足，对于任意 t ∈ R ，有 AP − t AB ≥ 3 ，则 PA ⋅ PB 的最小值为______________，此时 PA+ PB = _______________。解由 AP − t AB ≥ 3 可知点 P 到直线 AB 的距离为 3。
4. 在八个数字 2,4,6,7,8,11,12,13 中任取两个组成分数。这些分数中有个既约分数。解在 7,11,13 中任取一个整数与在 2,4,6,8,12 中任取一个整数构成既约分数，共
1 1 2 有 2C3 C5 = 30 种；在 7,11,13 中任取两个整数也构成既约分数，共有 A3 = 6 中。合
8. 设 f ( x) =| x + 1| + | x | − | x − 2 | , 则 f ( f ( x)) + 1 = 0 有__________个不同的解。
− x − 3, x ≤ −1 x − 1, −1 < x ≤ 0 因为 f ( x ) =| x + 1 | + | x | − | x − 2 |= 3x − 1,0 < x ≤ 2 x + 3, x > 2
解
由 f ( f ( x)) + 1 = 0 得到
f ( x ) = −2, 或 f ( x ) = 0 。由 f ( x ) = −2, 得一个解 x = −1 ；由 f ( x ) = 0 得两个解

浙江省高中数学联赛预赛试题

2018年浙江省高中数学竞赛一、填空题(每题8分，共80分)1.已知a 为正实数，且f (x )=1a －1a x +1是奇函数，则f (x )的值域为 . 2.设数列{a n }满足a 1=1，a n +1=5a n +1(n =1，2，…)，则∑n =12018a n = .3.已知α、β∈⎝⎛⎭⎫3π4，π，cos(α+β)=45，sin(α－β)=1213，则cos ⎝⎛⎭⎫β+π4= . 4.在八个数2，4，6，7，8，11，12，13中任取两个组成分数，这些分数中有个既约分数.5.已知虚数z 满足z 3+1=0，则⎝⎛⎭⎫z z －12018+⎝⎛⎭⎫1z －12018= . 6.设|AB |→=10.若平面上点P 满足对任意的t ∈R ，有||AP →－tAB →≥3，则P A →·PB →的最小值为，此时，|P A →+PB →|= .7.在△ABC 中，AB +AC =7，且三角形的面积为4，则sin A 的最小值为 .8.设f (x )=|x +1|+|x |－|x －2|，则f (f (x ))+1=0有个不同的解.9.设x ，y ∈R 满足x －6y －4x －y +12=0，则x 的取值范围为 .10.四面体P －ABC ，P A =BC =6，PB =AC =8，PC =AB =10，则该四面体外接球的半径为 .二、解答题：(11、12、13题各20分，14、15各30分)11.已知动直线l 与圆x 2+y 2=1相切，与椭圆x 29+y 2=1相交于不同的两点A 、B ，求原点到AB 的中垂线的最大距离.12.设a ∈R ，且对任意实数b 均有max x ∈[0，1]|x 2+ax +b |≥1，求a 的取值范围.13.设实数x 1，x 2，…，x 2018满足x 2n +1≤x n x n +2(n =1，2，…，2018)和 n =12018x n =1，证明：x 1009x 1010≤1.14.将2n (n ≥2)个数分成两组a 1，a 2，…，a n 和b 1，b 2，…，b n .证明：∑1≤i ≤n 1≤j ≤n |a i －b j |－∑1≤i <j ≤n(|a i －a j |+|b j －b i |)≥n .15.如图所示，将同心圆环均匀分成了n(n≥3)格.在内环中固定数字1~n.问能否将数字1~n 填入外环格内，使得外环旋转任意格后有且仅有一个格中内外环中数字相同?…n4321。

浙江省杭州市2018年高考数学命题比赛试题20(word版含答案)

2018年高考模拟试卷数学卷命题双向细目表考试设计说明本试卷设计是在认真研读《2018年考试说明》的基础上精心编制而成，以下从三方面加以说明。

（2）试卷保持相对稳定，适度创新，逐步形成“立意鲜明，背景新颖，设问灵活，层次清晰”的特色。

2018年高考模拟试卷数学卷本试题卷分选择题和非选择题两部分.全卷共4页，选择题部分1至2页，非选择题部分3至4页.满分150分.考试用时120分钟. 考生注意：1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上.2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效. 参考公式：球的表面积公式锥体的体积公式24S R=π 13V S h =球的体积公式其中S 表示棱锥的底面面积，h 表示棱锥的高343V R=π 台体的体积公式其中R 表示球的半径1()3a b V h S S =+柱体的体积公式其中S a ，S b 分别表示台体的上、下底面积V =Sh h 表示台体的高其中S 表示棱柱的底面面积，h 表示棱柱的高选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知}11|{<<-=x x A ，}20|{≥≤=x x x B 或，则=B C A R ( ) A ．)2,1(- B ．)1,0( C ．)0,1(-D ．)2,1(2．双曲线14522=-xy的焦点坐标是（）A ． ()0,1±B ．()0,3±C ．()1,0±D ．()3,0±3.一个几何体的三视图如图所示，则该几何体的体积是（）A ．64B ．72C ．80D ．4.若复数22i 1ia ++(a ∈R )是纯虚数,则复数i a 22+在复平面内对应的点在A ．第一象限 B ．第二象限C ．第三象限D5. 函数c o s ln ||x y x -=的图象大致是（）6.设R m ∈，实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥.0623,0632,y x y x m y ，若182≤+y x ，则实数m 的取值范围是（）A ．53≤≤-mB ．62≤≤-mC ．63≤≤-mD ．52≤≤-m7.已知52⎪⎭⎫⎝⎛-x a x 的常数项为15，则函数1)1(log )(31+-+=x a x x f 在区间⎥⎦⎤⎢⎣⎡-2,32上的最大值为（） A ．-10B ．0C ．10D ．232log31+8．已知等比数列{a n }的公比为q ，前n 项和为n S ，则“0>n S ”是“数列{}n S 单调递增”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件9.设5s in7a π=，2c o s 7b π=，2ta n7c π=，则（）A ．b a c <<B ．a c b <<C ．b c a <<D ．a b c <<10.如图，已知矩形ABCD ,1=AB ,2=BC ,F E ,分别为线段AD 与BC 上的点（不包括端点），沿直线BE 将ABE ∆旋转，沿直线DF 将DCF ∆旋转，在旋转的过程中，求AB 与CD 所成角的最大值是（） A ．3πB ．2πC ．32πD ．65π非选择题部分（共110分）第10题二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.11．我国古代数学著作《九章算术》有如下问题：“今有蒲（水生植物名）生一日，长三尺；莞（植物名，俗称水葱、席子草）生一日，长一尺．蒲生日自半，莞日自倍．问几何日而长等？”意思是：今有蒲生长1日，长为3尺；莞生长1日，长为1尺．蒲的生长逐日减半，莞的生长逐日增加1倍．若蒲、莞长度相等，则所需的时间约为___ __日．（结果保留一位小数，参考数据： lg 20.30≈， lg 30.48≈）12.已知随机变量x 的分布列，其中0,2πα⎛⎫∈ ⎪⎝⎭则sin α= ，()E x = . 13．在ABC∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且222sin sin sin sin sin0B C B C A +--=．（1）A = ；（2）若4B π=，则b c= ．14.已知集合N M ,是同一坐标平面内一些点组成的集合，若{}R y x y x M ∈=+=ααα,1sin cos |),(,且φ=⋂N M ,则原点到直线R y x ∈=+ααα,1sin cos 的距离是，集合N 所表示的区域的最大面积 .15．已知向量b a ,3==-_______，b 与b a -夹角的余弦值的最大值是_______.16.有4张分别标有数字1，2，3，4的红色卡片和4张分别标有数字1，2，3，4的蓝色卡片，从这8张卡片中取出4张卡片排成一行．如果取出的4张卡片所标的数字之和等于10，则不同的排法共有种（用数字作答）． 17. 平面直角坐标系xoy 中，已知椭圆()2222:10x y C a b ab+=>>左、右焦点分别是12,F F ，焦距为c 2，若曲线1C :m c x y ++=21满足对R m ∈∀,1C 与2C 至多2个公共点，求椭圆的离心率的范围是 .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤. 18．（本题满分14分）已知函数)0(1)sin (cos sin 3)(>+-=ωωωωx x x x f 相邻两条对称轴之间的距离为2π.（Ⅰ）求ω的值及函数()f x 的单调递减区间；（Ⅱ）已知,,a b c 分别为A B C ∆中角,,A B C的对边，且满足()1a f A ==，求A B C∆面积S 的最大值.19．（本题满分15分）如图，,,,,l A B αβαβαβ⊥=∈∈点A 在直线l 上的射影为1,A 点B 在l 上的射影为1.B已知112,1,A B A A B B ===求：（I ）直线AB 分别与平面,αβ所成角的大小；（II ）二面角11A A B B --的余弦值.20．（本题满分15分）已知函数()()215280815f x x x =->，()()0k g x x x=>，过点16161515f ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭，且与()f x 相切的直线与()g x 也相切（Ⅰ）求k 的值；（Ⅱ）若对任意0x >，都有()()f x a x b g x ≥+≥恒成立，求a 的取值范围.21．（本题满分15分）已知抛物线y x42=的焦点为F ，A 、B 是抛物线上的两动点，且)0(>=λλFB AF ．过A 、B 两点分别作抛物线的切线，设其交点为M ．（Ⅰ）证明AB FM ∙为定值；（Ⅱ）设ABM ∆的面积为S ，写出)(λf S =的表达式，并求S 的最小值．22．（本题满分15分）数列{}n a ，已知1=3a ，14=1n n n a a a +++，（Ⅰ）证明：()12(2)0n n a a +--< （Ⅱ）证明：1123n n a --≤（Ⅲ）已知n S 是数列{}n n a a -+1的前n 项和，求证：2≤n S .B 1A 1AB（第19题）βα2018年高考模拟试卷数学参考答案和评分标准选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（原创）A 【命题意图】考查集合、并集、补集的概念．解析：()2,0=B C R ，()2,1-=B C A R ，故选 A ． 2．（原创）D 【命题意图】考查双曲线焦点解析：焦点在y 轴上．945222=+=+=b a c ，3=c ，故选 D ．3. （原创）B 【命题意图】考查几何体的三视图和体积公式，同时考查空间想象能力．解析：这是“横躺”着的正方体和三棱锥,724432131444=⨯⨯⨯⨯+⨯⨯=V , 故选B ．4. （原创）D 【命题意图】考查复数的运算解析：22i 1ia ++i a a i i i i a )1(1)1)(1()1)(22(-++=-+-+=，所以1-=a ，故选B ．5. （改编）D 【命题意图】考查函数的图像解析：令6π=x ，0>y ，排除A,C;函数是偶函数，排除B.故选D ．6.（原创）C 【命题意图】考查线性规划解析：二元不等式（组）表示的区域如图所示（ABC ∆及其内部区域），52yx d +=表示原点)0,0(O 到直线02:=+y x l 的距离，点)6,6(A 到直线l 的距离5185612≤+=d 成立．点),263(m m B -到直线l的距离518563≤+-=mm d ，解得63≤≤-m ．故选C ．7. （原创）C 【命题意图】考查二项式定理和函数的最值解析：由题意rr rx xa C --52125)()(中0)5(212=-+-r r ，解得：r =1，则15)(115=-a C ，可得a =﹣3．那么可得函数13)1(log)(31+++=x x x f ，因为函数)(x f 在区间⎥⎦⎤⎢⎣⎡-2,32上是减函数,当32-=x时，函数)(x f 取得最大值为10．故选C ．8．（原创）B 【命题意图】考查等比数列通项与前n 项和之间的关系，充要条件解析：充分条件，举例21,11-==q a ，此时0211211>⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--=nn S ，数列{}n S 不单调递增，所以不充分；必要条件，因为数列{}n S 单调递增，)2(01≥>-=-n S S a n n n ，因为{a n }等比数列，所以01>a ，所以0>n S .故选B ． 9. （改编）A 【命题意图】考查比较大小与三角函数值解析：找中间变量4π，224sin72sin75sin1=>==>πππa ，224sin72cos =<=ππb ，14tan72tan=>=ππc .故选A ．10. （原创）B 【命题意图】考查立体几何综合问题解析：取极端位置，A 点不翻折，F 点在B 点位置，C 绕BD 翻折，观察C 在平面ABCD 内的投影可以落在AD 上，所以存在CD AB ⊥ 结合异面直线所成角范围.(体现浙江选择题的特色).故选B ．非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11．（改编） 2.6 【命题意图】考查数学文化，等差等比数列解析：设蒲的长度组成等比数列{}n a ，其前n 项和n A ；莞长度组成等比数列{}n b ，其前n 项和n B ；则1212211)211(3--==--=nn nn B A ，化简得7262=+nn，得62=n，即：6.22lg 3lg 12lg 6lg ≈+==n12.（原创）54；1 【命题意图】考查概率及数学期望的综合运用第10题解析：22sin sin c o s 144sin c o s 1ααααα⎧++=⎪⎨⎪+=⎩解得3c o s =5α，4s in 5α=，故()sin =2c o s 14E x αα-+=13．（原创）3π1- 【命题意图】考查正弦定理的应用及求值的思想解析：（1）由222sin sin sin sin sin 0B C B C A +--=及正弦定理得 2220b c b c a +--=，从而2221c o s 22b c aA b c+-==，3A π∴=（2）由（1）知23B C π+=，若4B π=，则512C π=，所以s in s in 415s in s in124b B cCππ=====14. （原创）1；π 【命题意图】考查集合，直线与圆解析：原点到直线R y x ∈=+ααα,1sin cos 的距离1sincos122=+=ααd ，所以M 是单位圆的切线上的点组成的集合，集合N 所表示的区域的最大面积π。

浙江省杭州市2018年高考数学命题比赛试题2(word版含答案)

2018年高考模拟试卷数学卷命题双向细目表考试设计说明本试卷设计是在认真研读《2018年考试说明》的基础上精心编制而成，以下从三方面加以说明。

（2）试卷保持相对稳定，适度创新，逐步形成“立意鲜明，背景新颖，设问灵活，层次清晰”的特色。

绝密★考试结束前2018年高考模拟试卷数学卷考生须知：1. 本卷满分150分，考试时间120分钟；2. 答题前务必将自己的姓名,准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的地方。

3. 答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范答题，在本试卷纸上答题一律无效。

4. 考试结束后，只需上交答题卷。

参考公式：如果事件,A B 互斥，那么柱体的体积公式()()()PABPA PB +=+VSh =如果事件,A B 相互独立,那么其中S 表示柱体的底面积，h 表示柱体的高()()()PA B PA PB = 锥体的体积公式如果事件A 在一次试验中发生的概率为p ,那么n 13V S h =次独立重复试验中事件A 恰好发生k 次的概率为其中S 表示锥体的底面积，h 表示锥体的高()()10,1,2),,(k k n knn P k C p p k n -==⋯－球的表面积公式台体的体积公式 24S R =π121()3V S S h =+球的体积公式其中12,S S 分别表示台体的上、下底面积， 343V R =πh 表示为台体的高其中R 表示球的半径选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。