第二十四章 圆检测参考答案
第二十四章 圆培优检测卷(解析版)(重点突围)

《第二十四章 圆》培优检测卷班级___________ 姓名___________ 学号____________ 分数____________考试范围:第二十四章; 考试时间:120分钟; 总分:120分一、选择题(本大题共6小题,每小题3分,共18分)1.(2021·浙江·杭州市建兰中学九年级期中)已知O e 的半径为3cm ,点A 到圆心O 的距离为2cm ,那么点A 与O e 的位置关系是( )A .点A 在O e 内B .点A 在O e 上C .点A 在O e 外D .不能确定【答案】A【分析】根据点到圆心的距离d 与圆的半径r 之间的数量关系进行判断即可.【详解】解:由题意得:2,3d r ==,故:d r <,∴点A 在O e 内,故选A .【点睛】本题考查点与圆的位置关系:点到圆心的距离大于圆的半径时,点在圆外,点到圆心的距离等于圆的半径时,点在圆上,点到圆心的距离小于圆的半径时,点在圆内.2.(2022·福建省福州延安中学九年级阶段练习)下列四个命题中,真命题是( )A .如果两条弦相等,那么它们所对的圆心角相等B .圆是轴对称图形, 任何一条直径都是圆的对称轴C .平分弦的直径一定垂直于这条弦D .等弧所对的圆周角相等【答案】D【分析】根据圆心角、弧、弦的关系对A 进行判断,根据对称轴的定义对B 进行判断,根据垂径定理的推论对C 进行判断,根据圆周角定理的推论对D 进行判断.【详解】解:A 、在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,故此选项错误,不符合题意;B 、圆是轴对称图形, 任何一条直径所在的直线都是圆的对称轴,故此选项错误,不符合题意;C 、平分弦(非直径)的直径一定垂直于这条弦,故此选项错误,不符合题意;D 、等弧所对的圆周角相等正确,故此选项正确,符合题意,故选:D .理及圆周角定理的推论.3.(2022·湖北孝感·九年级期末)点P 到⊙O 的最近点的距离为2cm ,最远点的距离为7cm ,则⊙O 的半径是( )A .5cm 或9cmB .2.5cmC .4.5cmD .2.5cm 或4.5cm【答案】D【分析】根据已知条件能求出圆的直径,即可求出半径,此题点的位置不确定所以要分类讨论.【详解】解:①当点在圆外时,∵圆外一点和圆周的最短距离为2cm ,最长距离为7cm ,∴圆的直径为7﹣2=5(cm ),∴该圆的半径是2.5cm ;②当点在圆内时,∵点到圆周的最短距离为2cm ,最长距离为7cm ,∴圆的直径=7+2=9(cm ),∴圆的半径为4.5cm ,故选:D .【点睛】本题考查了点和圆的位置关系的应用,能根据已知条件求出圆的直径是解此题的关键.4.(2022·北京·人大附中九年级阶段练习)如图,AB 为O e 的直径,点C ,D 在O e 上,若130ADC Ð=°,则BAC Ð的度数为( )A .25°B .30°C .40°D .50°【答案】C 【分析】根据圆内接四边形对角互补求得B Ð,根据直径所对的圆周角是直角可得=90°ACB Ð,根据直角三角形的两个锐角互余即可求解.【详解】解:∵AB 为O ⊙的直径,,60OA OB AOB =Ð=°Q ,AOB \ 是等边三角形,12,12OA AB AP AB \====,223OP OA AP \=-=,即这个正六边形的边心距为3,【点睛】本题考查了正多边形的中心角和边心距、等边三角形的判定与性质、勾股定理,熟练掌握正多边形的中心角和边心距的概念是解题关键.6.(2022·全国·九年级单元测试)如图,AB过半⊙O的圆心O,过点B作半⊙O的切线BC,切点为点C,连接AC,若∠A=25°,则∠B的度数是( )A.65°B.50°C.40°D.25°【答案】C【分析】连接OC,根据切线的性质,得出∠OCB=90°,再利用圆的半径相等,结合等边对等角,得出∠A =∠OCA,然后再利用三角形的外角和定理,得出∠BOC的度数,再利用直角三角形两锐角互余,即可得出∠B的度数.【详解】解:连接OC,∵BC与半⊙O相切于点C,∴∠OCB=90°,∵∠A=25°,∵OA=OC,∴∠A=∠OCA,∴∠BOC=2∠A=50°,∴∠B=90°﹣∠BOC=40°.故选:C【点睛】本题考查了切线的性质、等边对等角、三角形外角和定理、直角三角形两锐角互余,解本题的关键在熟练掌握相关的性质、定理.二、填空题(本大题共6小题,每小题3分,共18分)7.(2022·北京市朝阳区人大附中朝阳分校九年级阶段练习)如图,点A、B、C在⊙O上,∠C=45°,半径OB的长为3,则AB的长为_____.【答案】32【分析】首先根据圆周角定理求出∠【答案】1【分析】连接OA、OC、OD然后由含30°角的直角三角形的性质求解即可.【详解】解:连接OA、OC∵点O为正六边形ABCDEF【答案】15【分析】如图,连接CQ,然后求出【详解】解:如图,连接CQ.由题意CQ=CP,CDPQ=∴DQ=DP=12∵PA=QB,【答案】1或3或5e与坐标轴的切点为【分析】设PQ点D是切点,P e的半径是1Q,PB=2Q=,PC2\=+=,52 AP AC PC定及性质,利用分类讨论的思想求解.三、(本大题共5小题,每小题6分,共30分)(1)点M的坐标为 (2)点D(5,﹣2)在⊙M【答案】(1)(2,0)(2)内【分析】(1)由网络可得出线段(2)解:由图知,圆的半径AM∵2513>,∴点D在圆M内,(1)求正六边形的边长;(2)以A为圆心,AF为半径画弧【答案】(1)6(2)4π(1)求ACBÐ的度数;e的半径为3,求圆弧 AC的长.(2)若O【答案】(1)30°(2)2pe的切线∵AB是O^∴OA AB∴90Ð=OAB°∵90Ð=DAC°Ð=Ð∴DAC OAB(2)在(1)的基础上,连接BO 并延长与【点睛】本题考查了作图:无刻度直尺作图,考查了正五边形的对称性质,掌握正五边形的性质是解题的关键.17.(2022·湖南·长沙麓山国际实验学校九年级阶段练习)如图,与A ,B 重合),过O 作OC ⊥AP (1)试判断CD 与AB 的数量和位置关系?并说明理由;(2)若45B Ð=°,AP=4,则⊙∵45B Ð=°,四、(本大题共3小题,每小题8分,共24分)18.(2021·江苏·阜宁县实验初级中学九年级阶段练习)如图,⊙O 的弦AB 、DC 的延长线相交于点E .A D AE DE E E Ð=Ðìï=íïÐ=Ðî,∴△ACE ≌△DBE (ASA ),∴BE =CE ,∵AE =DE ,∴AE -BE =DE -CE ,即AB =CD .【点睛】本题考查了圆的相关计算与证明,三角形全等的判定和性质,正确理解圆心角、弧与弦的关系是解题的关键.19.(2021·广东惠州·九年级期末)如图在Rt ABC 中,∠C =90º,以AC 为直径作⊙O ,交AB 于D ,过O 作OE ∥AB ,交BC 于E .(1)求证:DE 是⊙O 的切线;(2)如果⊙O 的半径为3,DE =4,求AB 的长;(3)在(2)的条件下,求△ADO 的面积.【答案】(1)证明见解析(2)10AB =(3) 4.32ADO S =△【分析】(1)根据平行线的性质,得出123A Ð=ÐÐ=Ð,,再根据等边对等角,得出1A Ð=Ð,再根据等量代换,得出32Ð=Ð,再利用SAS ,得出OCE ODE ≌△△,进而得出OCE ODE Ð=Ð,进而得出OD DE ^,即可得出结论;(2)根据(1),得出ODE 是直角三角形,根据勾股定理,得出5OE =,再根据三角形的中位线定理,即可得出AB 的长;(3)连接CD ,根据圆周角定理,得出90ADC Ð=°,再根据等面积法,得出CD 的长,然后根据勾股定理,得出AD 的长,再根据三角形的面积公式,得出ADC 的面积,再根据三角形中线平分三角形的面积,即可得出ADO △的面积.(1)证明:如图,∵OE AB ∥,∴123A Ð=ÐÐ=Ð,,∵OA OD =,∴1A Ð=Ð,∴32Ð=Ð,∵OC OD OE OE ==,,∴()OCE ODE SAS △≌△,∴OCE ODE Ð=Ð,∵90C Ð=°,∴90OCE ODE Ð=Ð=°,即OD DE ^,∴DE 是⊙O 的切线.(2)解:由(1),可得:三角形ODE 是直角三角形,在Rt ODE △中,∵34OD DE ==,,∴5OE =,【点睛】本题考查了平行线的性质、等边对等角、全等三角形的性质与判定、切线判定定理、勾股定理、三角形的中位线定理、圆周角定理、三角形中线的性质,解本题的关键在熟练掌握相关的性质定理.20.(2022·江苏·泰州市姜堰区南苑学校九年级)如图,在圆心,OB为半径的圆与(1)如图1,若AP=DP,则⊙O的半径r值为_______;(2)求BC=6,求⊙O的半径r长;(3)若AD的垂直平分线和⊙O有公共点,求半径r的取值范围.【答案】(1)8 3(2)3∵Oe与AC相切于点∴AC OD^,∴∠ADO=90°,即∠PDO∵∠ABC =90°, AB =8,∴22AC AB BC =+=∵OD AC ^,AB BC ^∴1122AC OD BC OB ×+×∴AC OD BC OB ×+×=∵∠EFD=∠ODF=∠OEF=90°∴四边形ODFE是矩形,∵OD=OE,∴四边形ODFE是正方形,===∴AF DF OD r∵222,∵OD<OA,∴OB+OD<OB+OA,∴2r<8,∴r<4,∴r的取值范围是252-【点睛】本题主要考查了圆的切线的判定与性质、切线长定理、勾股定理、用不等式求取值范围等知识与方法,熟练掌握相关知识点是解题的关键,属于考试压轴题.五、(本大题共2小题,每小题9分,共18分)(1)求抛物线解析式及D 点坐标.(2)猜测直线CM 与D e 的位置关系,并证明你的猜想.(3)抛物线对称轴上是否存在点P ,若将线段上?若能,求点P 的坐标;若不能,说明理由.【答案】(1)()2125344y x =--+;(3,0)(2)相切;证明见解析;由抛物线的解析式得:M (3,254∵D (3,0),∴()22225225403416CM æö=-+-=ç÷èø∴222CM CD DM +=,根据题意得∠CP C¢=∠CGD=∠GDO ∴∠CPH+∠HP C¢=90°,∠GCP+∴∠GCD=∠HP C¢,OC=GD=4,∵CP=C¢P∴∆CGP≅∆PH C¢,∴PG=C¢H=GD-DP=4-k,CG=PH六、(本大题共12分)。
人教版(2024)数学九年级上册第二十四章 圆 本章复习与测试(含答案)

第二十四章圆一、选择题1. 已知⊙O的半径为3 cm,OP=4 cm,则点P与⊙O的位置关系是( )A.点P在圆内B.点P在圆上C.点P在圆外D.无法确定2. 已知圆锥的底面半径为3 cm,母线长为4 cm,则圆锥的全面积是( )A.15π cm2B.21π cm2C.20π cm2D.24π cm23. 下列说法:①平分弦的直径垂直于弦;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的内心到三条边的距离相等.其中不正确的有( )个.A.1B.2C.3D.44. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35∘,则∠CAB的度数为( )A.35∘B.45∘C.55∘D.65∘5. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,连接AD,若∠C=22∘,则∠CDA的大小为( )A.112∘B.124∘C.129∘D.136∘6. 如图,在⊙O中,OC⊥AB,∠ADC=32∘,则∠OBA的度数是( )A.64∘B.58∘C.32∘D.26∘7. 在截面为半圆形的水槽内装有一些水,如图,水面宽AB为6分米,如果再注入一些水后,水面上升1分米,此时水面宽变为8分米,则该水槽面半径为( )A.3分米B.4分米C.5分米D.10分米8. 设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )A.3B.2C.4或10D.2或59. 如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若的值为( )QP=QO,则QCQAA.23−1B.23C.3+2D.3+210. 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ,Q为切点,则线段PQ长度的最小值为( )A.5B.7C.23D.32二、填空题11. 如图,AB是⊙O的直径,C,D,E都是⊙O上的点,则∠1+∠2=.12. 如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n∘,则∠DCE=.13. 如图,CD是⊙O的直径,弦AB⊥CD于点E,若AB=6,CE:ED=1:9,则⊙O的半径是.14. 如图,菱形OABC的边长为2,且点A,B,C在⊙O上,则劣弧BC的长度为.15. 如图,AB是⊙O的直径,AC与⊙O相切于点A,CE∥AB交⊙O于点D,E,CD=2,AB=8.则AD=.16. 如图,矩形ABCD中,AB=2,BC=2,以B为圆心,BC为半径画弧,交AD于点E,则图中阴影部分的面积是.17. 如图所示,边长为2的正方形ABCD的顶点A,B在一个半径为2的圆上,顶点C,D在该圆内,将正方形ABCD绕点A逆时针旋转,当点D第一次落在圆上时,点C运动的路线长为.18. 在⊙O中,AB是⊙O的直径,AB=8 cm,AC=CD=BD,M是AB上一动点,CM+DM的最小值是cm.三、解答题19. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).(1) 请画出△ABC绕点O逆时针旋转90∘后的△A1B1C1;并写出A1,B1,C1三点的坐标.(2) 求出(1)中C点旋转到C1点所经过的路径长(结果保留π).20. 已知AB是半圆O的直径,OD⊥弦AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=2,求OF的长.21. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.(1) 求证:AD平分∠BAC.(2) 若∠BAC=60∘,OA=2,求阴影部分的面积(结果保留π).22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.(1) 求证:AE=ED;(2) 若AB=10,∠CBD=36∘,求AC的长.23. 如图,半圆O的直径DE=12 cm,△ABC中,∠ACB=90∘,∠ABC=30∘,BC=12 cm,半圆O以2 cm/s的速度从左向右运动,在运动的过程中,点D,E始终在直线BC上,设运动时间为t(s),当t=0 s时,半圆O在△ABC的左侧,OC=8 cm.(1) 当t=8(s)时,试判断点A与半圆O的位置关系;(2) 当t为何值时,直线AB与半圆O所在的圆相切.24. 如图,点A是半径为12cm的⊙O上的一点,动点P从点A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到A点立即停止运动.(1) 在点P运动过程中,当∠POA=90∘时,求点P的运动时间.(2) 如图,点B是OA延长线上一点,AB=OA,当点P运动的时间为2s时,试判断直线BP与⊙O的位置关系,并说明理由.25. 已知四边形ABCD内接于⊙O,BC=CD,连接AC,BD.(1) 如图①,若∠CBD=36∘,求∠BAD的大小.(2) 如图②,若点E在对角线AC上,且EC=BC,∠EBD=24∘,求∠ABE的大小.答案一、选择题1. C2. B3. D4. C5. B6. D7. C8. B9. D10. B二、填空题11. 90∘12. n13. 514. 23π15. 416. 22−1−π217. 2π318. 8三、解答题19.(1) 如图,△A1B1C1为所作,A1,B1,C1三点的坐标分别为(−4,2),(−1,1),(−3,4);(2) OC=32+42=5,所以C点旋转到C1点所经过的路径长=90×π×5180=52π.20. ∵OD⊥AC,AC=2,∴AD=CD=1,∵OD⊥AC,EF⊥AB,∴∠ADO=∠OFE=90∘,∵OE∥AC,∴∠DOE=∠ADO=90∘,∴∠DAO+∠DOA=90∘,∠DOA+∠EOF=90∘,∴∠DAO=∠EOF,在△ADO和△OFE中,{∠DAO=∠EFO,∠DAO=∠FOE,OA=OE,∴△ADO≌△OFE(AAS),∴OF=AD=1.21.(1) ∵⊙O切BC于D,∴OD⊥BC,∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB.(2) 设EO与AD交于点M,连接ED.∵∠BAC=60∘,OA=OE,∴△AEO是等边三角形,∴AE=OA,∠AOE=60∘,∴AE=AO=OD,又由(1)知,AC∥OD,即AE∥OD,∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60∘,∴S△AEM=S△DMO,∴S阴影=S扇形EOD=60π×22360=2π3.22.(1) ∵AB是⊙O的直径,∴∠ADB=90∘,∵OC∥BD,∴∠AEO=∠ADB=90∘,即OC⊥AD,∴AE=ED.(2) ∵OC⊥AD,∴AC=CD,∴∠ABC=∠CBD=36∘,∴∠AOC=2∠ABC=2×36∘=72∘,∴AC=72π×5180=2π.23.(1) ∵△ABC中,∠ACB=90∘,∠ABC=30∘,BC=12 cm,∴AC=tan30∘BC=43,当t=8时,如图,此时OC=8,在Rt△ACO中,AC=43,∴AO=AC2+OC2=47,∵半圆O的直径DE=12 cm,47>6,∴点A在半圆外;(2) ①如图1,过C点作CF⊥AB,交AB于F点;∵∠ABC=30∘,BC=12 cm,∴FO=6 cm;当半圆O与△ABC的边AB相切时,又∵圆心O到AB的距离等于6 cm,且圆心O又在直线BC上,∴O与C重合,即当O点运动到C点时,半圆O与△ABC的边AB相切;此时点O运动了8 cm,所求运动时间为t=82=4(s),②当点O运动到B点的右侧,且OB=12 cm时,如图2,过点O作OQ⊥直线AB,垂足为Q.在Rt△QOB中,∠OBQ=30,则OQ=6 cm,即OQ与半圆O所在的圆相切.此时点O运动了32 cm.所求运动时间为:t=32÷2=16 s,综上可知当t=4 s或16 s时,AB与半圆O所在的圆相切.24.(1) 当∠POA=90∘时,根据弧长公式可知点P运动的路程为⊙O周长的14或34,设点P运动的时间为t s,当点P运动的路程为⊙O周长的14时,2π⋅t=14⋅2π⋅12,解得t=3,当点P运动的路程为⊙O周长的34时,2π⋅t=34⋅2π⋅12,解得t=9,∴当∠POA=90∘时,点P运动的时间为3s或9s.(2) 如图,当点P运动的时间为2s时,直线BP与⊙O相切.理由如下:当点P运动的时间为2s时,点P运动的路程为4πcm,连接OP,PA,∵半径AO=12cm,∴⊙O的周长为24πcm,∴AP的长为⊙O周长的16,∴∠POA=60∘,∵OP=OA,∴△OAP是等边三角形,∴OP=OA=AP,∠OAP=60∘,∵AB=OA,∴AP=AB,∵∠OAP=∠APB+∠B,∴∠APB=∠B=30∘,∴∠OPB=∠OPA+∠APB=90∘,∴OP⊥BP,∴直线BP与⊙O相切.25.(1) ∵BC=CD,∴∠BDC=∠CBD=36∘,∴∠BAC=∠BDC=36∘,∵BC=CD,∴BC=CD,∴∠CAD=∠CBD=36∘,∠BAD=∠BAC+∠CAD=36∘+36∘=72∘.(2) ∠CEB=∠EAB+∠ABE(外角的应用),∵CE=CB,∴∠CEB=∠CBE=∠CBD+∠EBD,∴∠EAB+∠ABE=∠CBD+∠EBD,∵BC=CD,∴BC=CD,∴∠EAB=∠CBD,∴∠ABE=∠EBD=24∘.。
部编数学九年级上册第二十四章圆过关自测卷含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第二十四章过关自测卷(100分,45分钟)一、选择题(每题4分,共32分)1.〈重庆〉如图1,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A.40° B.图2.〈甘肃兰州〉如图2是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8 cm,水面最深地方的高度为2 cm,则该输水管的半径为()A.3 cm B.4 cm C.5 cm D.6 cm3.〈甘肃兰州〉圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥母线长为()A.3 cm B.6 cm C.9 cm D.12 cm图3 图44.如图3,边长为a的六角螺帽在桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为()A.6a B.5a C.2aπ D aπ5.〈山东泰安〉如图4,已知AB是⊙O的直径,AD切⊙O于点A,点C是⌒EB的中点,则下列结论不成立的是()A.OC//AE B.EC=BCC.∠DAE=∠ABE D.AC⊥OE6.〈2013,晋江市质检〉如图5,动点M,N分别在直线AB与CD上,且AB//CD,∠BMN与∠MND的平分线相交于点P,若以MN为直径作⊙O ,则点P与⊙O的位置关系是()A.点P在⊙O外 B.点P在⊙O内C.点P在⊙O上 D.以上都有可能7.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120° B.125° C.135° D.150°8.〈贵州遵义〉如图6,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为()图6A.32π cm B.322æö+ç÷èøπ cm C.43π cm D.3 cm二、填空题(每题4分,共24分)9.〈四川巴中〉如图7,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于________.图7 图810.〈重庆〉如图8,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为________(结果保留π).11.〈贵州遵义〉如图9,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为_______ _(结果保留根号).图12.如图10,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为每秒1个单位长度,以O为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.13.如图11,正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,则AP的长为________.图11 图1214.如图12,AB为半圆O的直径,C为半圆的三等分点,过B,C两点的半圆O的切线交于点P,若AB的长是2a,则PA的长是________.三、解答题(15题9分,16题10分,17题11分,18题14分,共44分)15. 如图13所示,△ABC中,∠ACB=90°,AC=2 cm,BC=4cm,CM是AB边上的中线,以C长为半径画圆,则点A,B,M与⊙C的位置关系如何?图1316.如图14,已知CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为2,求⌒BD的长.17.如图15,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.(1)求这个扇形的面积;(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形A BC围成一个圆锥?若不能,请说明理由;若能,请求出剪的圆的半径是多少.18.如图16,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;图16(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.参考答案及点拨一、1. C 点拨:∵AB是⊙O的切线,B为切点,∴OB⊥AB,即∠OBA=90°,∵∠BAO=40°,∴∠O=50°,∵OB=OC,∴∠OCB=12(180°-∠O)=65°.故选C.1所示,过圆心O作OD⊥AB于点D,连接OA.∵OD⊥AB,∴AD=12AB=12×8=4 (cm).设OA=r cm,则OD=(r-2 )cm,在Rt△AOD中,OA2=OD2+AD2,即r2=(r-2)2+42,解得r=5.故选C.3. B 点拨:解答本题运用了方程思想.由题意得圆锥的底面周长是6πcm,设母线长是l cm,则lπ=6π,解得:l=6.故选B.4. C 点拨:分析可知,六角螺帽在桌面上滚动(没有滑动)一周,它的中心O 点所经过的路径长为60180a π×6=2a π.故选C .5. D 点拨:A.∵点C 是⌒EB 的中点,∴OC ⊥BE ,∵AB 为圆O 的直径,∴AE ⊥BE ,∴OC ∥AE ,本选项正确;B.∵⌒ EC =⌒BC ,∴EC =BC ,本选项正确;C.∵AD 为圆O 的切线,∴AD ⊥OA ,∴∠DAE +∠EAB =90°,∵∠ABE +∠EAB =90°,∴∠DAE =∠ABE ,本选项正确;D.AC 不一定垂直于OE ,本选项错误.故选D.6. C 点拨:∵AB ∥CD ,∴∠BMN +∠MND =180°,∵∠BMN 与∠MND 的平分线相交于点P ,∴∠PMN =21∠BMN ,∠PNM =21∠MND ,∴∠PMN +∠PNM =90°.∴∠MPN =180°-(∠PMN +∠PNM )=180°-90°=90°.∴以MN 为直径作⊙O 时,OP =21MN =⊙O 的半径,∴点P 在⊙O 上.故选C .7. C 点拨:如答图2,连接IC .答图2∵CD 为AB 边上的高,∴∠ADC =90°,∴∠BAC +∠ACD =90°.∵I 为△ACD 的内切圆圆心,∴AI ,CI 分别是∠BAC 和∠ACD 的平分线,∴∠IAC +∠ICA =21(∠BAC +∠ACD )=21×90°=45°,∴∠AIC=135°.又∵AB =AC ,∠BAI =∠CAI ,AI =AI ,∴△AIB ≌△AIC ,∴∠AIB =∠AIC =135°.故选C .8. C 点拨:结合题图和已知条件,易知点B 经过的路径长=2×ππ341801120=⨯ (cm).故选C .二、9. 32° 点拨:∵AB 是⊙O 的直径,∴∠ADB =90°,∵∠ABD =58°,∴∠A =90°-∠ABD =32°,∴∠BCD =∠A =32°.10.π-2 点拨:S 扇形OAB =3604903602⨯=ππR n =π,S △AOB =21×2×2=2,则S 阴影=S 扇形OAB -S △AOB =π-2.11. ππ2 点拨:解答本题运用了方程思想.∵图中两个阴影部分的面积相等,∴S 扇形ADF =S △ABC ,即360452AF ∙π=21·AC ·BC ,又∵AC =BC =1,∴AF 2=π4,∴AF =ππ2.12. 4 点拨:如答图3所示,根据题意,作O′D⊥BC于D,则O′D=3.在Rt△O′CD中,∠C=60°,O′D=3,∴O′C=2,∴O′A=6-2=4.∴以O为圆心、3为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第4秒.答图3 答图413. 13点拨:连接AE,如答图4,由题意易得AE=23,EP=1, ∠AEP=90°.∴在Rt△AEP中,AP221)(=13.2+314. 7a 点拨:连接OC,OP,如答图5所示.∵C为半圆的三等分点,答图5∴∠BOC=120°,已知PC,PB都是半圆O的切线,由切线长定理可得:∠POB =21∠BOC =60°.在Rt △POB 中,OB =a ,∠P OB =60°,则PB =3a ;在Rt △ABP 中,由勾股定理得:AP =22BP AB +=7)3()2(22=+a a a.三、15. 解:∵CA =2cm <5cm ,∴点A 在⊙C 内;∵BC =4cm >5cm ,∴点B 在⊙C 外;在△ABC 中,∠ACB =90°,∴由勾股定理,得AB =222224+=+AC BC =25(cm ).∵ CM 是AB 边上的中线,∴CM =21AB =5cm ,∴CM =⊙C 的半径,∴点M 在⊙C 上.16.(1)证明:连接OB ,如答图6所示:答图6∵BC =AB ,∠CAB =30°,∴∠ACB =∠CAB =30°,又∵OC =OB ,∴∠CBO =∠ACB =30°,∴∠AOB =∠CBO +∠ACB =60°.在△ABO 中,∠CAB =30°,∠AOB =60°,可得∠ABO =90°,即AB ⊥OB ,∴AB 是⊙O 的切线.(2)解:∵OB=2,∠BOD=60°,∴⌒BD的长度l=32180260=∙ππ.点拨:此题考查了切线的判定,等腰三角形的性质,三角形的外角性质以及弧长公式的运用.切线的判定方法有两种:有切点连半径,证明垂直;无切点作垂线,证明垂线段等于半径.17. 解:(1)如答图7所示,连接BC.由∠BAC=90°得BC为⊙O的直径,∴BC=4.在Rt△ABC中,由勾股定理可得:AB=AC=22,∴S扇形ABC=36022902)(π⨯⨯=2π.答图7(2)不能.如答图7所示,连接AO并延长交⌒BC于点D,交⊙O于点E,则DE=4-22.而l⌒BC =18022902)(π⨯⨯=2π,设能与扇形ABC围成圆锥的底面圆的直径为d,则dπ=2π,∴d=2.又∵DE=4-22<d=2,即围成圆锥的底面圆的直径大于DE,∴不能围成圆锥.点拨:(1)由勾股定理求出扇形的半径,再根据扇形面积公式求值.(2)题需要求出③中最大圆的直径以及圆锥底面圆的直径(圆锥底面圆的周长即为弧BC的长),然后进行比较即可.18. 解:(1)线段AB长度的最小值为4.理由如下:连接OP,如答图8所示.答图8∵AB切⊙O于P,∴OP⊥AB.取AB的中点C,则AB=2OC;当OC=OP时,OC最短,即AB最短,此时AB=4.(2)设存在符合条件的点Q.答图9如答图9,设四边形APOQ为平行四边形,∵∠APO=90°,∴四边形APOQ为矩形,又∵OP=OQ,∴四边形APOQ为正方形,∴OQ=QA,∠QOA=45°.在Rt△OQA中,根据OQ=2,∠AOQ=45°,得Q点坐标为(2,-2);如答图10,设四边形APQO为平行四边形,答图10∵OQ∥PA,∠APO=90°,∴∠POQ=90°,又∵OP=OQ,∴∠PQO=45°,∵PQ∥OA,∴PQ⊥y轴.设PQ⊥y轴于点H,在Rt△OHQ中,根据OQ=2,∠HQO=45°,得Q点坐标为(-2,2).∴符合条件的点Q的坐标为(-2,2)或(2,-2).方法规律:解答本题运用了分类讨论思想.(1)如答图8,设AB的中点为C,连接OP,由于AB是⊙O的切线,故△OPC是直角三角形,所以当OC与OP重合时,OC最短,即AB最短.(2)分两种情况:如答图9,当四边形APOQ是正方形时,△OPA,△OAQ都是等腰直角三角形,可求得点Q的坐标为(2,-2);如答图10,可求得∠QOP=∠O PA=90°,由于OP=OQ,故△OPQ是等腰直角三角形,可求得点Q的坐标为(-2,2).。
人教版九年级数学下册第二十四章《圆》检测卷(含答案)
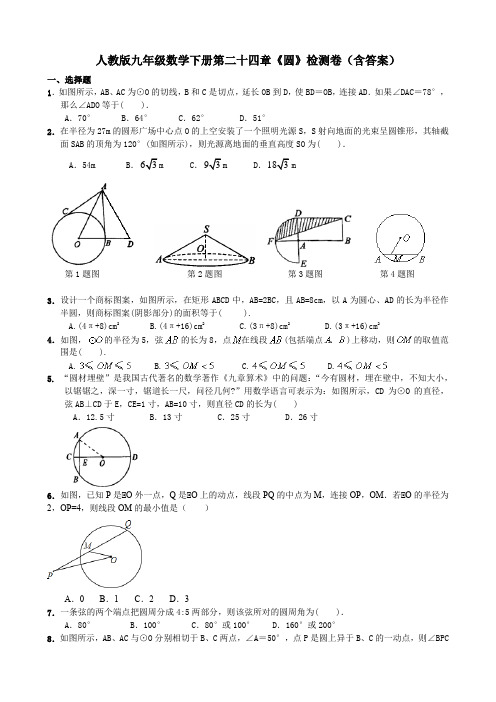
人教版九年级数学下册第二十四章《圆》检测卷(含答案)一、选择题 1.如图所示,AB 、AC 为⊙O 的切线,B 和C 是切点,延长OB 到D ,使BD =OB ,连接AD .如果∠DAC =78°, 那么∠ADO 等于( ).A .70°B .64°C .62°D .51°2.在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ,S 射向地面的光束呈圆锥形,其轴截面SAB 的顶角为120°(如图所示),则光源离地面的垂直高度SO 为( ). A .54m B ..m D .m第1题图 第2题图第3题图 第4题图3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm ,以A 为圆心、AD 的长为半径作半圆,则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm 2B.(4π+16)cm 2C.(3π+8)cm 2D.(3π+16)cm 24.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是( ). A. B. C. D. 5. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD 为⊙O 的直径,弦AB ⊥CD 于E ,CE=1寸,AB=10寸,则直径CD 的长为( )A .12.5寸B .13寸C .25寸D .26寸6.如图,已知P 是⊙O 外一点,Q 是⊙O 上的动点,线段PQ 的中点为M ,连接OP ,OM .若⊙O 的半径为2,OP=4,则线段OM 的最小值是( )A .0B .1C .2D .37.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为( ). A .80° B .100° C .80°或100° D .160°或200°的度数是( ).A .65°B .115°C .65°或115°D .130°或50°二、填空题 9.如下左图,是的内接三角形,,点P 在上移动(点P 不与点A 、C 重合),则的变化范围是__ ________.第9题图 第10题图10.如图所示,EB 、EC 是⊙O是两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,那么∠A 的度数是________________. 11.已知⊙O 1与⊙O 2的半径、分别是方程 的两实根,若⊙O 1与⊙O 2的圆心距=5.则⊙O 1与⊙O 2的位置关系是 __ __ .12.如图,AB 为⊙O 的直径,AB=AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,⊙BAC=45°,给出以下五个结论:①⊙EBC=22.5°;②BD=DC ;③AE=2EC ;④劣弧是劣弧的2倍;⑤AE=BC ,其中正确的序号是 .13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______ ________. 14.已知正方形ABCD ,截去四个角成一正八边形,则这个正八边形EFGHIJLK 的边长为____ ____,面积为_____ ___.15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形,分别以它们的各顶点为圆心,以l 为半径画弧与两邻边相交,得到3条弧,4条弧,……1r 2r 2680x x -+=d(1)图(1)中3条弧的弧长的和为___ _____,图(2)中4条弧的弧长的和为_____ ___;(2)求图(m)中n条弧的弧长的和为____ ____(用n表示).16.如图所示,蒙古包可以近似地看做由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为9πm2,高为3.5m,外围高4 m的蒙古包,至少要____ ____m2的毛毡.三、解答题17. 如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD.18.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:⊙A=⊙AEB;(2)连接OE,交CD于点F,OE⊙CD,求证:⊙ABE是等边三角形.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类似的思想提出了如下命题:③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:(1)请你从①②③三个命题中选择一个进行证明;(2)请你继续完成下面的探索;①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.参考答案一、选择题 1.【答案】B ;【解析】由AB 为⊙O 的切线,则AB ⊥OD .又BD =OB ,则AB 垂直平分OD ,AO =AD ,∠DAB =∠BAO .由AB 、AC 为⊙O 的切线,则∠CAO =∠BAO =∠DAB .所以,∠DAB =∠DAC =26°. ∠ADO =90°-26°=64°.本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.2.【答案】C ;【解析】圆锥的高、底面半径与母线组成直角三角形.由题意,SO ⊥AB 于O ,∴ ∠SOA =∠SOB =90°.又SA =SB ,∠ASB =120°,∴ ∠SAB =∠SBA =,设SO =x m ,则AS =2x m .∵ AO =27,由勾股定理,得(2x)2-x 2=272,解得(m).3.【答案】A.;【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系. ∵ 矩形ABCD 中,AB=2BC ,AB=8cm , ∴ AD=BC=4cm ,∠DAF=90°,,,又AF=AD=4cm , ∴,∴ .4.【答案】A ;【解析】OM 最长是半径5;最短是OM ⊥AB 时,此时OM=3,故选A. 5.【答案】D ;【解析】因为直径CD 垂直于弦AB ,所以可通过连接OA(或OB),求出半径即可. 根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”, 知(寸),在Rt △AOE 中,,即,解得OA=13,进而求得CD=26(寸).故选D. 6.【答案】B.【解析】设OP 与⊙O 交于点N ,连结MN ,OQ ,如图,⊙OP=4,ON=2, ⊙N 是OP 的中点, ⊙M 为PQ 的中点,⊙MN 为⊙POQ 的中位线,180120302=°-?°93x =⊙MN=OQ=×2=1,⊙点M 在以N 为圆心,1为半径的圆上,当点M 在ON 上时,OM 最小,最小值为1, ⊙线段OM 的最小值为1.故选B . 7.【答案】C ; 【解析】圆周角的顶点在劣弧上时,圆周角为;圆周角的顶点在优弧上时, 圆周角为.注意分情况讨论. 8.【答案】C ;【解析】连接OC 、OB ,则∠BOC =360°-90°-90°-50°=130°.点P 在优弧上时,∠BPC =∠BOC =65°;点P 在劣弧上时,∠BPC =180°-65°=115°. 主要应用了切线的性质定理、圆周角定理和多边形内角和定理.二、填空题 9.【答案】; 10.【答案】99°;【解析】由EB=EC ,∠E=46°知,∠ECB= 67°,从而∠BCD=180°-67°-32°=81°, 在⊙O 中,∠BCD 与∠A 互补,所以∠A=180°-81°=99°. 11.【答案】相交;【解析】求出方程 的两实根、分别是4、2,则-<<+,所以两圆相交.12.【答案】①①①;【解析】连接AD ,AB 是直径,则AD ⊙BC ,又⊙⊙ABC 是等腰三角形,故点D 是BC 的中点,即BD=CD ,故②正确; ⊙AD 是⊙BAC 的平分线,由圆周角定理知,⊙EBC=⊙DAC=⊙BAC=22.5°,故①正确;⊙⊙ABE=90°﹣⊙EBC ﹣⊙BAD=45°=2⊙CAD ,故④正确; ⊙⊙EBC=22.5°,2EC ≠BE ,AE=BE ,⊙AE ≠2CE ,③不正确; ⊙AE=BE ,BE 是直角边,BC 是斜边,肯定不等,故⑤错误. 综上所述,正确的结论是:①②④.13.【答案】7或3;【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,即另一圆半径为7或 3.5136010092⨯⨯=°°413608092⨯⨯=°°122680x x -+=1r 2r 1r 2r d 1r 2r14.【答案】; ;【解析】正方形ABCD 外接圆的直径就是它的对角线,由此求得正方形边长为a .如图所示,设正八边形的边长为x .在Rt △AEL 中,LE =x ,AE =AL,∴ ,, 即正八边形的边长为..15.【答案】(1)π; 2π; (2)(n-2)π;【解析】∵ n 边形内角和为(n-2)180°,前n 条弧的弧长的和为个以某定点为圆心,以1为半径的圆周长,∴ n 条弧的弧长的和为. 本题还有其他解法,比如:设各个扇形的圆心角依次为,,…,,则, ∴n 条弧长的和为.16.【答案】720π;【解析】∵ S =πr 2,∴ 9π=πr 2,∴ r =3.∴ h 1=4,∴ ,∴,.所求面积包括圆锥的侧面积和圆柱的侧面积,不包括底面积.1)a 22)a x 2x x a +=1)x a =1)a 2222241)]2)AEL S S S a x a a a =-=-=-=△正方形正八边形(2)1801(2)3602n n -=-121(2)(2)2n n ππ⨯⨯-=-1α2αn α12(2)180n n ααα+++=-…°1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-5l ==223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱2036720S ππ=⨯=总17.【答案与解析】(1)连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ,∴OF 垂直平分BC∴∴AF 平分∠BAC .(2)由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18.【答案与解析】 证明:(1)⊙四边形ABCD 是⊙O 的内接四边形, ⊙⊙A+⊙BCD=180°, ⊙⊙DCE+⊙BCD=180°, ⊙⊙A=⊙DCE , ⊙DC=DE ,⊙⊙DCE=⊙AEB , ⊙⊙A=⊙AEB ;(2)⊙⊙A=⊙AEB , ⊙⊙ABE 是等腰三角形, ⊙EO ⊙CD , ⊙CF=DF ,⊙EO 是CD 的垂直平分线, ⊙ED=EC , ⊙DC=DE , ⊙DC=DE=EC ,⊙⊙DCE 是等边三角形, ⊙⊙AEB=60°,⊙⊙ABE 是等边三角形.19.【答案与解析】解:∵公共弦AB =120 ∴==a R 46120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=2BF FC =A BCDE FO12345HA BCD EFO 12H()∴=-⎛⎝ ⎫⎭⎪=-==r R a O o 442422222602606090,∠S S S R a r AmB AO B AO B弓形扇形=-=-=-229036012180036004244∆ππS S S R a r AnB AO B AO B弓形扇形=-=-=-1160360122400360036266∆ππ()∴=+=-+S S S AmB AnB 阴影弓形弓形4200360013π()[]∴-+两圆相交弧间阴影部分的面积为42003600132πcm .20. 【答案与解析】 (1)如选命题①. 证明:在图(1)中,∵ ∠BON =60°,∴ ∠1+∠2=60°. ∵ ∠3+∠2=60°,∴ ∠1=∠3. 又∵ BC =CA ,∠BCM =∠CAN =60°, ∴ △BCM ≌△CAN ,∴ BM =CM . 如选命题②.证明:在图(2)中,∵ ∠BON =90°,∴ ∠1+∠2=90°. ∵ ∠3+∠2=90°,∴ ∠1=∠3. 又∵ BC =CD ,∠BCM =∠CDN =90°, ∴ △BCM ≌△CDN ,∴ BM =CN . 如选命题③.证明:在图(3)中,∵ ∠BON =108°,∴ ∠1+∠2=108°. ∵ ∠2+∠3=108°,∴ ∠1=∠3. 又∵ BC =CD ,∠BCM =∠CDN =108°, ∴ △BCM ≌△CDN ,∴ BM =CN . (2)①答:当∠BON =时结论BM =CN 成立.②答:当∠BON =108°时.BM =CN 还成立. 证明:如图(4),连接BD 、CE 在△BCD 和△CDE 中,∵ BC =CD ,∠BCD =∠CDE =108°,CD =DE , ∴ △BCD ≌△CDE .∴ BD =CE ,∠BDC =∠CED ,∠DBC =∠ECD . ∵ ∠CDE =∠DEN =108°, ∴ ∠BDM =∠CEM .∵ ∠OBC+∠OCB =108°,∠OCB+∠OCD =108°. (2)180n n-°又∵∠DBC=∠ECD=36°,∴∠DBM=∠ECM.∴△BDM≌△CEN,∴ BM=CN.。
-人教版九年级数学上第24章圆全章测试含答案.doc

第24章 圆 全章测试一、填空题(每题5分,计40分)1、已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( ) A .40° B .80° C .160° D .120°2.点P 在⊙O 内,OP =2cm ,若⊙O 的半径是3cm ,则过点P 的最短弦的长度为( ) A .1cmB .2cmCD.3.已知A 为⊙O 上的点,⊙O 的半径为1,该平面上另有一点P,PA =P 与⊙O 的位置关系是( )A .点P 在⊙O 内B .点P 在⊙O 上C .点P 在⊙O 外D .无法确定4.如图,A B C D ,,,为O 的四等分点,动点P 从圆心O 出发,沿O C D O ---路线作匀速运动,设运动时间为t (s ).()APB y =∠,则下列图象中表示y 与t 之间函数关系最恰当的是( )5. 在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( ) A .与x轴相离、与y 轴相切 B .与x 轴、y 轴都相离 C .与x轴相切、与y 轴相离 D .与x 轴、y 轴都相切6 如图,若⊙的直径AB 与弦AC 的夹角为30°,切线CD 与AB的延长线交于点D,且⊙O 的半径为2,则CD 的长为 ( )A.B.C.2D. 47.如图,△PQR 是⊙O 的内接三角形,四边形ABCD 是⊙O 的内接正方形,BC ∥QR,则∠DOR 的度数是 ( )A.60B.65C.72D. 75第4题图AB C DOP B .D .A .C .第6题图O P Q D B AC 第7题图 R8.如图,A ⊙、B ⊙、C ⊙、D ⊙、E ⊙相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是( )A .πB .1.5πC .2πD .2.5π 二 选择题(每题5分,计30分) 9.如图,直角坐标系中一条圆弧经过网格点A 、B 、C ,其中,B 点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .10. 如图,在ΔABC 中,∠A=90°,AB=AC=2cm ,⊙A 与BC 相切于点D ,则⊙A 的半径长为 cm.11.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB ⊥弦CD 于E ),设AE x =,BE y =,他用含x y ,的式子表示图中的弦CD 的长度,通过比较运动的弦CD 和与之垂直的直径AB 的大小关系,发现了一个关于正数x y ,的不等式,你也能发现这个不等式吗?写出你发现的不等式 .(12题图)12.如图,∠AOB=300,OM=6,那么以M 为圆心,4为半径的圆与直OA 的位置关系是_________________. 13.如图,△㎝,则AC的长等于_______㎝。
九年级数学上册《第二十四章 圆》单元检测卷及答案-人教版精选全文

可编辑修改精选全文完整版九年级数学上册《第二十四章圆》单元检测卷及答案-人教版学校:___________班级:___________姓名:___________考号:___________一、选择题:(本题共8小题,每小题5分,共40分.)1.下列命题中是假命题的是()A.直径是弦;B.等弧所在的圆是同圆或等圆C.弦的垂直平分线经过圆心;D.平分弦的直径垂直于弦2.Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为()A.2cm B.2.4cm C.3cm D.4cm3.如图,⊙O的直径CD垂直弦AB于点E,且CE=2, DE=8,则AB的长为()A.4 B.6 C.7 D.84.如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是()A.OC∥BD B.AD⊥OCC.△CEF≌△BED D.AF=FD5.如图,OA交⊙O于点B,AD切⊙O于点D,点C在⊙O上.若∠A=40°,则∠C为()A.20°B.25°C.30°D.35°6.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是()C.3+πD.πA.8﹣πB.5π47.如图,△ABC是⊙O的内接三角形,∠A=30°,BC=√2,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为()A.1 B.√2C.√3D.28.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE=DE,BC=CE过点O作OF⊥AC于点F,延长FO交BE于点G,若DE=3,EG=2则AB的长为()A.4√3B.7 C.8 D.4√5二、填空题:(本题共5小题,每小题3分,共15分.)9.在直径为10cm的圆中,弦AB的长为8cm,则它的弦心距为cm.10.如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA 的度数为度.11.如图,⊙I为△ABC的内切圆,AB=9,BC=8,AC=10,点D、E分别为AB、AC上的点,且DE 为⊙I的切线,则△ADE的周长为12.如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为.13.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,̂上的动点,连接PA、PD,则∠APD的大小是度.若点P为优弧ABD三、解答题:(本题共5题,共45分)⌢=AC⌢∠ADC=120°,求证:△ABC是等边三角形.14.已知四边形ABCD内接于⊙O,AB15.如图,在△ABC中AB=AC,以AC为直径的⊙O与AB交于点D,过点B作BE∥AC,与过点C的⊙O的切线相交于点E.求证:BD=BE.16.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D过D作直线DG∥BC.(1)若∠ACB=70°,则∠ADB=;∠AEB=.(2)求证:DE=CD;(3)求证:DG是⊙O的切线.⌢=BP⌢.17.已知,如图,⊙O的半径为2,半径OP被弦AB垂直平分,交点为Q,点C在圆上,且BC(1)求弦AB的长;(2)求图中阴影部分面积(结果保留π).18.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.(1)判断BC、MD的位置关系,并说明理由;(2)若AE=16,BE=4,求线段CD的长;(3)若MD恰好经过圆心O,求∠D的度数参考答案:1.D 2.B 3.D 4.C 5.B 6.A 7.D 8.B 9.310.7111.1112.413.2514.证明:∵四边形ABCD内接于⊙O∴∠ABC+∠ADC=180°∴∠ABC=180°﹣∠ADC=180°﹣120°=60°⌢=AC⌢∵AB∴AB=AC又∵∠ABC=60°∴△ABC是等边三角形.15.证明:如图,连接CD∵AC是直径∴∠ADC=90°∴∠ADC=∠BDC=90°∵CE是⊙O的切线∴AC⊥CE∴∠ACE=90°∵BE∥AC∴∠ACE+∠E=180°∴∠E=90°∴∠BDC=∠E.∵AB=AC∴∠ABC=∠ACB∵BE∥AC∴∠ACB=∠EBC∴∠DBC=∠EBC在△DCB和△ECB中∴△DCB≌△ECB(AAS)∴BD=BE16.(1)70º;125º(2)证明:连接BD∵点E是ΔABC的内心∴∠ABE=∠CBE,∠BAD=∠CAD∵∠DBC=∠DAC∴∠DBC=∠BAD∵∠DBE=∠DBC+∠CBE,∠DEB=∠BAD+∠ABE ∴∠DEB=∠DBE∴BD=DE∵∠BAD=∠CAD⌢=CD⌢∴BD∴BD=CD∴DE=CD;(3)证明:连接OD交BC于H,如图∵点E是ΔABC的内心∴AD平分∠BAC即∠BAD=∠CAD⌢=CD⌢∴BD∴OD⊥BC∴BH=CH∵DG//BC∴OD⊥DG∴DG是⊙O的切线;17.(1)解:连接OB,则OB=2∵弦AB垂直平分OP∴OQ=12OP=1.在Rt△OBQ中∵半径OP垂直AB∴AQ=BQ∴AB=2√3;(2)解:在Rt△OBQ中,cos∠POB=12∴∠POB=60°.连接OC,BC∵BC⌢=BP⌢∴BC=BP,∠BOC=∠POB=60°.又∵OC=OB∴△OBC是等边三角形.∴∠BCO=60°∵∠POB=60°,∠BOC=60°.∵∠BCO+∠POC=180∘∴BC∥OP∴S△PBC=S△OBC∴S阴=S扇形OBC=60360π⋅22=23π.18.(1)解:BC∥MD.理由:∵∠M=∠D,∠M=∠C,∠D=∠CBM ∴∠M=∠D=∠C=∠CBM∴BC∥MD.(2)解:∵AE=16,BE=4∴OB=16+42=10∴OE=10﹣4=6连接OC∵CD⊥AB∴CE=12CD在Rt△OCE中∵OE2+CE2=OC2,即62+CE2=102,解得CE=8 ∴CD=2CE=16.(3)解:如图2∵∠M=12∠BOD,∠M=∠D∴∠D=12∠BOD,∵AB⊥CD,∴∠D=13×90°=30°。
人教版九年级数学 上册 第二十四章 圆 单元综合与测试(含答案)

第二十四章圆单元复习与检测题(含答案)一、选择题1、点P在⊙O内,OP=2cm,若⊙O的半径是3cm,则过点P的最短弦的长度为()A.1cm B.2cm C. cm D. cm2、已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,,那么点P 与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.无法确定3、下列说法正确的是()A.三点确定一个圆 B.一个三角形只有一个外接圆C.和半径垂直的直线是圆的切线 D.三角形的内心到三角形三个顶点距离相等4、同一平面内两圆的半径是R和r,圆心距是d,若以R、r、d为边长,能围成一个三角形,则这两个圆的位置关系是()A.外离B.相切C.相交D.内含5、在⊙O中,圆心O到弦AB的距离为AB长度的一半,则弦AB所对圆心角的大小为()A.30° B.45° C.60° D.90°6、如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是()A.60 B.65C.72 D.757、在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定()A.与轴相离、与轴相切 B.与轴、轴都相离C.与轴相切、与轴相离 D.与轴、轴都相切8、如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积()A.等于24 B.最小为24B.C.等于48 D.最大为489、已知⊙O1与⊙O2外切于点A,⊙O1的半径R=2,⊙O2的半径r=1,若半径为4的⊙C与⊙O1、⊙O2都相切,则满足条件的⊙C有()A、2个B、4个C、5个D、6个10、已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是()A.24cm B.48cm C.96cm D.192cm二、填空题11、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为.12、如图,△ABC内接于⊙O,∠B=∠OAC,OA=8㎝,则AC的长等于_______㎝。
人教版九年级数学上册《第二十四章圆 》测试卷-附参考答案

人教版九年级数学上册《第二十四章圆》测试卷-附参考答案一、单选题1.已知AB是⊙O的直径,的度数为60°,⊙O的半径为2cm,则弦AC的长为()A.2cm B.cm C.1cm D.cm2.已知圆O的半径为5,同一平面内有一点P,且OP=4,则点P与圆O的关系是()A.点P在圆内B.点P在圆外C.点P在圆上D.无法确定3.如图,是的直径,若,则圆周角的度数是()A.B.C.D.4.如图,已知半圆O与四边形的边相切,切点分别为D,E,C,设半圆的半径为2,则四边形的周长为()A.7 B.9 C.12 D.145.如图,是的内接三角形,作,并与相交于点D,连接BD,则的大小为()A.B.C.D.6.如图,点A,B,C在上,四边形是平行四边形.若对角线,则的长为()A.B.C.D.7.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为()A.B.C.D.8.如图,半径为的扇形中,是上一点,垂足分别为,若,则图中阴影部分面积为( )A.B.C.D.二、填空题9.如图,是的弦,C是的中点,交于点D.若,则的半径为 .10.如图,是的直径,交于点,且,则的度数= .11.AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为.12.如图,为的外接圆,其中点在上,且,已知和则.13.如图,以正方形的顶点为圆心,以对角线为半径画弧,交的延长线于点,连结,若,则图中阴影部分的面积为.(结果用表示)三、解答题14.如图,CD是⊙O的直径,弦AB⊥CD于E,是的中点,连接BC,AO,BD.求的大小.15.如图,是的外接圆,且,点M是的中点,作交的延长线于点N,连接交于点D.(1)求证:是的切线;(2)若,求的半径.16.如图,等腰内接于,AC的垂直平分线交边BC于点E,交于F,垂足为D,连接AF并延长交BC的延长线于点P.(1)求证:;(2)若,求的度数.17.如图,在中,是边上一点,以为圆心,为半径的圆与相交于点,连接,且.(1)求证:是的切线;(2)若,求的长.18.如图,⊙O的半径OC垂直于弦AB于点D,点P在OC的延长线上,AC平分∠PAB.(1)判断AP与⊙O的位置关系,并说明理由;(2)若⊙O的半径为4,弦AB平分OC,求与弦AB、AC围成的阴影部分的面积.参考答案:1.A2.A3.B4.D5.A6.C7.D8.B9.510.24°11.12.13.14.解:又是中点在和中≌∴BD=OA是直径,OA是半径90°且30°. 15.(1)证明:∵∴∵点M是的中点∴∴∴∴是的直径∴∵∴∴是的切线;(2)解:如图所示,连接,设交于D∵∴设的半径为r,则∵∴在中,由勾股定理的∴∴∴的半径为.16.(1)证明:如图,连接BF.∵AC的垂直平分线交边BC于点E,交于F,且圆是轴对称图形,∴O,E,F三点共线,∴∴∴,∵,∴(2)解:如图,连接CF,设,则∵∴∵∴∴∴.∵∴,即易证(SAS),∴∵,∴,∴,∴,解得∴∴的度数为108°.17.(1)证明:连接OD.∵AC=CD∴∠A=∠ADC.∵OB=OD∴∠B=∠BDO.∵∠ACB=90°∴∠A+∠B=90°.∴∠ADC+∠BDO=90°.∴∠ODC=180°﹣(∠ADC+∠BDO)=90°.又∵OD是⊙O的半径∴CD是⊙O的切线.(2)解:∵AC=CD,∠A=60°∴△ACD是等边三角形.∴∠ACD=60°.∴∠DCO=∠ACB﹣∠ACD=30°.在Rt△OCD中,OD=CDtan∠DCO tan30°=2.∵∠B=90°﹣∠A=30°,OB=OD∴∠ODB=∠B=30°.∴∠BOD=180°﹣(∠B+∠BDO)=120°.∴的长18.(1)解:AP与⊙O的位置关系是相切,理由如下:连接平分垂直于弦,且是半径是的切线;(2)解:连接OB,如图所示:∵弦AB垂直平分OC∴∴∴∵OA=OC∴△OAC是等边三角形∴∴△OBD≌△CAD(ASA)∴。
人教版九年级数学上册《第二十四章圆》单元检测卷带答案

人教版九年级数学上册《第二十四章圆》单元检测卷带答案学校:___________班级:___________姓名:___________考号:___________知识点 1 正多边形和圆正多边形:各边相等,各角也相等的多边形叫做正多边形.把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距.要作半径为R 的正n 边形,只要把半径为R 的圆n 等分,然后顺次连接各部分点即可. 正多边形的有关计算:①正n 边形的每个内角都等于(n−2)⋅180o n =180∘−360∘n ;②正n 边形的每个中心角都等于 360∘n ;③正n 边形的每个外角都等于 360∘n .1. 如图,正六边形 ABCDEF 内接于⊙O,连接BD.则∠CBD 的度数是 ( ) A.30° B.45° C.60° D.90°2. 如图,在正六边形ABCDEF 中AC =2√3,则它的边长是 ( )A.1B.√2C.√3D.23. 如图,正五边形ABCDE 内接于⊙O,P 为 DÊ上的一点(点P 不与点D 重合),则∠CPD 的度数为 ( ) A.30° B.36° C.60° D.72°4. 如图,已知⊙O 的内接正六边形ABCDEF 的边心距OM=2,则该圆的内接正三角形ACE 的面积为( )A.2B.4C.6√3D.4√35. 如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是 ( )A.6√3−πB.6√3−2πC.6√3+πD.6√3+2π6. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是 ()A.弦AB的长等于圆内接正六边形的边长B.弦AC的长等于圆内接正十二边形的边长̂=BĈD.∠BAC=30°C.AC7. 若正六边形的边长为3,则其较长的一条对角线长为 .̂所对的圆心角∠BOD 的大8. 如图,⊙O 与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD小为度.9. 如图,五边形ABCDE是⊙O 的内接正五边形,AF是⊙O 的直径,则∠BDF 的度数是°.10. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为.11. 如图1,2,3,…,n,M,N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图1中. ∠MON的度数.(2)图2中∠MON的度数是,图3中∠MON的度数是 .(3)试探究∠MON的度数与正n边形边数n的关系.(直接写出答案)知识点2 弧长和扇形面积弧长公式:l=nπR180由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.扇形的面积公式:S扇形=nπR2360.连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.设圆锥的母线长为l,底面圆的半径为r,则圆锥的侧面积为πrl,全面积为πr(r+l).12. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是(结果保留π) ( )A.2πB.4πC.12πD.24π13. 如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )A.4π-8B.2πC.4πD.8π-814. 若扇形的圆心角为90°,,半径为6,则该扇形的弧长为 ( )A.32π B.2π C.3π D.6π15. 如图,在边长为4的正方形ABCD中,以点B 为圆心,AB为半径画弧,交对角线BD于点 E,则图中阴影部分的面积是(结果保留π) ( )A.8-πB.16-2πC.8-2πD.8−12π16. 如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则BĈ的长为 ( )A.4π3B.8π3C.2√3πD.2π17. 圆锥的底面半径是5cm,侧面展开图的圆心角是180°,圆锥的高是 ( )A.5√3cmB.10 cmC.6cmD.5cm18. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为 ( )A.6πB.3√3πC.2√3πD.2π19. 如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在AB̂上的点 D 处,且表示BD̂的长),若将此扇形OAB 围成一个圆锥,则圆锥的底面半径与母线长的比为 ( )A.1:3B.1:πC.1:4D.2:920. 如图,线段AB 经过⊙O 的圆心,AC,BD分别与⊙O 相切于点 C,D.若AC=BD=4,∠A =45°,则CD̂的长度为 ( )A.πB.2πC.2√2πD.4π21. 圆锥侧面展开图的圆心角的度数为216°,母线长为5,该圆锥的底面半径为 .22. 如图,在Rt△ABC中∠ACB=90∘,BC=√3,AB=2,以点A 为圆心,以AC 为半径画弧,交AB于D,则扇形 CAD 的周长是 .(结果保留π)23. 如图,AC是⊙O 的直径,B,D是⊙O上的点,若⊙O 的半径为3, ∠ADB=30°则BĈ的长为 .24. 在1 Rt△ABC中∠C=90°,AC=3,BC=4,把它沿斜边AB 所在直线旋转一周,所得几何体的侧面积是 .(结果保留π)25. 如图,在平行四边形ABCD中AB<AD,∠A=150°,CD=4,以 CD 为直径的⊙O交AD 于点 E,则图中阴影部分的面积为 .26. 如图, △ABC内接于⊙O,AD与BC是⊙O 的直径,延长线段AC 至点G,使AG=AD,连接DG交⊙O于点 E,EF∥AB交AG于点 F.(1)求证:EF与⊙O 相切.(2)若EF=2√3,AC=4,求扇形OAC 的面积.参考答案1. A2. D3. B4. D5. A6. D7.68.1449.54 10.5√211.解:(1)如图,连接OB,OC,∵点O是正三角形ABC的中心∴OB=OC,∠BOC=360∘3=120∘,OB,OC 分别平分∠ABC 和∠ACB ∵AB =AC,∴∠ABC = ∠ACB,∴∠OBM =∠OCB又∵OB=OC,BM=CN,∴△OBM≌△OCN,∴∠BOM =∠CON ∴∠MON=∠BOM+∠BON=∠CON+∠BON=∠BOC= 120°.(2)90°;72°.(3)∠MON=360∘n.12. C 13. A 14. C 15. C 16. B 17. A 18. A19. D20. B 21.3 22.π3+2 23.2π24.84π525.2π3+√326.(1)证明:如图1,连接OE,∵OD=OE,∴∠D=∠OED.∵AD=AG,∴∠D=∠G,∴∠OED=∠G,∴OE∥AG∵BC是⊙O的直径,∴∠BAC=90°,∵EF∥AB∴∠EFG=90°,∵OE∥AG,∴∠OEF=90°,∴OE⊥EF∴EF与⊙O 相切.(2)解:如图 2,连接 OE,过点 O 作 OH ⊥AC 于点 H∴∠OHF=90∘,∵OA=OC,∴CH=12AC,∵AC=4∴CH=2,由(1)知∠HFE=∠OEF=90°∴四辺形OEFH 是矩形, ∴OH=EF=2√3,在Rt△OHC中OC=√CH2+OH2=√22+(2√3)2=4∵OA=AC=OC=4∴△AOC是等边三角形∴∠AOC=60°∴S扇形OAC=60π×42360=83π.。
2023年春学期沪科版九年级数学下册第二十四章【圆】检测卷附答案解析

2023年春学期九年级数学下册第二十四章【圆】检测卷一、单选题1.北京教育资源丰富,高校林立,下面四个高校校徽主题图案中,既不是中心对称图形,也不是轴对称图形的是()A .B .C .D .2.如图,在正方形网格中,点A ,B ,C ,D ,O 都在格点上.下列说法正确的是()A .点O 是ABC 的内心B .点O 是ABC 的外心C .点O 是ABD 的内心D .点O 是ABD 的外心3.如图,BC 为直径,35ABC ∠=︒,则D ∠的度数为()A .35︒B .45︒C .55︒D .65︒4.如图,若O 的半径为5,圆心O 到一条直线的距离为2,则这条直线可能是()A .1lB .2l C .3l D .4l 5.底面半径为3,高为4的圆锥侧面积为()A .15πB .20πC .25πD .30π6.如图,圆的两条弦AB ,CD 相交于点E ,且 AD CB=,∠A =40°,则∠DEB 的度数为()A .50°B .100°C .70°D .80°7.下列条件中,不能确定一个圆的是()A .圆心与半径B .直径C .平面上的三个已知点D .三角形的三个顶点8.若一个正n 边形的每个内角为144°,则这个正n 边形的边数为()A .8B .9C .10D .119.如图,正六边形ABCDEF 的边长为6,以顶点A 为圆心,AB 的长为半径画圆,用图中阴影部分围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为()A .4B .32C .2D .1010.如图,已知AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,且∠BCD =30°,CD =3部分的面积S 阴影=()A .2πB .83πC .43πD .38π二、填空题11.正十边形的中心角等于度.12.若O 的半径为5cm ,点A 到圆心O 的距离为4cm ,那么点A 与O 的位置关系是.13.若一个正多边形的一个外角等于36°,则这个正多边形的边数是.14.如图,在边长为4的等边△ABC 中,以B 为圆心、BA 为半径画弧,再以AB 为直径画半圆,则阴影部分的面积为.三、计算题15.如图,AB 是⊙O 的直径,点D 在⊙O 上,∠DAB =45°,BC ∥AD ,CD ∥AB .若⊙O 的半径为1,求图中阴影部分的面积(结果保留π).16.计算高为4cm ,底面半径为3cm 的圆锥的体积.(圆锥的体积=13×底面积×高,π取3)四、解答题17.如图扇形纸扇完全打开后,外侧两竹条AB 、AC 的夹角为120°,AB 长为30cm ,贴纸部分BD 长为20cm ,求贴纸部分的面积.18.在一个3m×4m 的矩形地块上,欲开辟出一部分作花坛,要使花坛的面积为矩形面积的一半,且使整个图案绕它的中心旋转180°后能与自身重合,请给出你的设计方案.19.如图,已知O ,A 是 BC的中点,过点A 作AD BC .求证:AD 与O 相切.20.如图,AB 是O 的直径,弦CD AB ⊥于点E ,若8AB =,6CD =,求OE 的长.21.已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=12BC.22.如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.五、综合题23.如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.(1)求证:直线AE是⊙O的切线.(2)若∠BAC=30°,BC=4,cos∠BAD=34,CF=103,求BF的长.答案解析部分1.【答案】D【解析】【解答】解:A 、不是中心对称图形,是轴对称图形,故该选项不符合题意;B 、是中心对称图形,不是轴对称图形,故该选项不符合题意;C 、不是中心对称图形,是轴对称图形,故该选项不符合题意;D 、既不是中心对称图形,也不是轴对称图形,故该选项符合题意.故答案为:D.【分析】轴对称图形:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;中心对称图形:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此一一判断得出答案.2.【答案】D【解析】【解答】解:根据点A ,B ,C ,D ,O 都在正方形网格的格点上.可知:点O 到点A ,B ,D 的三点的距离相等,所以点O 是△ABD 的外心.故答案为:D.【分析】根据图形可得点O 到点A 、B 、D 的距离相等,然后结合外心的概念进行判断.3.【答案】C【解析】【解答】解:∵CB 是直径,∴∠BAC=90°,∵∠ABC=35°,∴∠ACB=90°-35°=55°,∴∠D=∠C=55°,故答案为:C .【分析】先利用圆周角的性质和三角形的内角和求出∠ACB=90°-35°=55°,再利用圆周角的性质可得∠D=∠C=55°。
2023-2024学年九年级数学上册《第二十四章 圆》单元测试卷有答案(人教版)

2023-2024学年九年级数学上册《第二十四章圆》单元测试卷有答案(人教版)学校:___________班级:___________姓名:___________考号:___________知识点归纳1、圆在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作⊙O,读作“圆O”。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆上任意两点间的部分叫做圆弧,简称弧。
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
小于半圆的弧叫做劣弧。
大于半圆的弧叫做优弧。
能够重合的两个圆叫做等圆。
在同圆或等圆中,能重合的弧叫等弧。
2、垂径定理垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;弦的垂直平分线过圆心,且平分弦对的两条弧.3、弧、弦、圆心角之间的关系定义:顶点在圆心的角叫做圆心角。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等。
注:在同圆或等圆中,如果两个圆心角,两条弦,两条弧、两个弦的弦心距中,有一组量相等,那么其余各组量也分别相等4、圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等。
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
圆内接四边形的性质:圆内接四边形的对角互补。
5、点和圆的位置关系设⊙O 的半径为r ,点P 到圆心的距离为OP=d ,则有:点P 在圆外⇔d >r ;点P 在圆上⇔d=r ;点P 在圆内⇔d <r 。
性质:不在同一条直线上的三个点确定一个圆。
人教版九年级数学上册第二十四章圆测试题(含答案)(含知识点)

数学第二十四章圆测试题附参考答案时间:45分钟分数:100分一、选择题(每小题3分,共33分)1.(2005·资阳)若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为()A.2ba+B.2ba-C.22baba-+或D.baba-+或2.(2005·浙江)如图24—A—1,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是()A.4 B.6 C.7 D.83.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为()A.40°B.80°C.160°D.120°4.如图24—A—2,△ABC内接于⊙O,若∠A=40°,则∠OBC的度数为()A.20°B.40°C.50°D.70°5.如图24—A—3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为()A.12个单位B.10个单位C.1个单位D.15个单位6.如图24—A—4,AB为⊙O的直径,点C在⊙O上,若∠B=60°,则∠A等于()A.80°B.50°C.40°D.30°7.如图24—A—5,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为()A.5 B.7 C.8 D.108.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m,母线长为3m,为防雨需图24—A—5图24—A—1 图24—A—2 图24—A—3 图24—A—4在粮仓顶部铺上油毡,则这块油毡的面积是( )A .26m B .26m π C .212m D .212m π 9.如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切于点P ,大圆的弦CD 经过点P ,且CD=13,PC=4,则两圆组成的圆环的面积是( )A .16πB .36πC .52πD .81π10.已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为( ) A .310 B .512 C .2 D .3 11.如图24—A—7,两个半径都是4cm 的圆外切于点C ,一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm 后才停下来,则蚂蚁停的那一个点为( ) A .D 点 B .E 点 C .F 点 D .G 点 二、填空题(每小题3分,共30分) 12.如图24—A —8,在⊙O 中,弦AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点C ,则∠AOC= 。
初中数学人教版九年级上册-第二十四章-圆单元测试卷(含答案)

人教版数学九上圆一、单选题1.下列语句中正确的是( )A.长度相等的两条弧是等弧B.圆上一条弧所对的圆心角等于它所对圆周角的一半C.垂直于圆的半径的直线是圆的切线D.三角形有且只有一个外接圆2.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( )A.42°B.21°C.84°D.60°3.如图,在矩形ABCD中,AD=8,以AD的中点O为圆心,以OA长为半径画弧与BC相切于点E,则阴影部分的面积为( )A.8−4πB.16−4πC.32−4πD.32−8π4.如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接CE,若AB=4,CD=1,则CE的长为( )A.13B.4C.10D.155.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )A .B .C .D .6.如图.将扇形AOB 翻折,使点A 与圆心O 重合,展开后折痕所在直线l 与AB 交于点C ,连接AC .若OA =2,则图中阴影部分的面积是( )A .2π3−32B .2π3−3C .π3−32D .π37.如图,⊙O 是正△ABC 的外接圆,△DOE 是顶角为120°的等腰三角形,点O 与圆心重合,点D ,E 分别在圆弧上,若⊙O 的半径是6,则图中阴影部分的面积是( )A .4πB .12π−9 3C .12π−923D .24π− 9 38.如图,在正方形ABCD 中,点E ,F 分别是边BC 和CD 上的动点(不与端点重合),∠EAF =45°,AF 、AE分别与对角线BD交于点G和点H,连接EG.以下四个结论:(1)BE+DF=EF;(2)△AGE是等腰直角三角形;(3)S△AGH:S△AEF=1:2;(4)AB+BE=2BG,其中正确结论的个数是( )A.1B.2C.3D.49.【情境】如图是某数学项目学习小组设计的“鱼跃龙门”徽章图案,已知A,B,C,D,E是圆的5个等分点,连结BD,CE交于点F.设鱼头部分的四边形ABFE的面积为S1,鱼尾部分的△CDF的面积为S2.【问知】设S1:S2=n:1,则n的值为( )A.43−1B.3+5C.1+25D.35−110.如图,半径为5的圆中有一个内接矩形ABCD,AB>BC,点M是ABC的中点,MN⊥AB于点N,若矩形ABCD的面积为30,则线段MN的长为()A.10B.522C.702D.210二、填空题11.如图,在⊙O的内接五边形ABCDE中,∠EBD=31°,则∠A+∠C= °.12.如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 cm.13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=2,则⊙O的直径为 .14.如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与AB交于点C,若OA=2,则OC的长为 .15.如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C 为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为 .16.如图,已知△ABC是⊙O的内接三角形,⊙O的半径为2,将劣弧AC沿AC折叠后刚好经过弦BC的中点D.若∠ACB=60°,则弦AC的长为 .三、解答题17.如图,直径为1m的圆柱形水管有积水(阴影部分),水面的宽度AB为0.8m,求水的最大深度CD.18.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.19.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连结BD.(1)求证:∠BAD=∠CBD.(2)若∠AEB=125°,求BD的长.(结果保留π)20.如图,AB为⊙O的直径,弦CD⊥AB于E,连接AC,过A作AF⊥AC,交⊙O于点F,连接DF,过B作BG⊥DF,交DF的延长线于点G.(1)求证:BG是⊙O的切线:(2)若∠DFA=30°,DF=4,求阴影部分的面积.21.在直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.其中C点坐标为(0,4).(1)求点A坐标.(2)如图,过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,求AN的长度.(3)在⊙M上,若∠CPM=45°,求出点P的坐标.22.圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形.(1)如图1,四边形ABCD为等邻边圆内接四边形,AD=CD,∠ADC=60°,直接写出∠ABD的度数;(2)如图2,四边形ADBC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,若四边形ADBC为等邻边圆内接四边形,AD=BD,求CD的长.(3)如图3,四边形ABCD为等邻边圆内接四边形,BC=CD,AB为⊙O的直径,且AB=48.设BC=x,四边形ABCD的周长为y,试确定y与x的函数关系式,并求出y的最大值.答案解析部分1.【答案】D2.【答案】A3.【答案】D4.【答案】A5.【答案】D6.【答案】B7.【答案】B8.【答案】D9.【答案】B10.【答案】A11.【答案】21112.【答案】1613.【答案】2214.【答案】2π315.【答案】53316.【答案】621717.【答案】解:∵⊙O的直径为1m,∴OA=OD=0.5m.∵OD⊥AB,AB=0.8m,∴AC=0.4m,∴OC=OA2−AC2=0.52−0.42=0.3m,∴CD=OD−OC=0.5−0.3=0.2m.答:水的最大深度为0.2m.18.【答案】解:∵OA⊥OB,∴∠AOB=90°,∴∠A=90°﹣∠B=90°﹣28°=62°,∵OA=OC,∴∠ACO=∠A=62°,而∠ACO=∠BOC+∠B,∴∠BOC=62°﹣28°=34°.19.【答案】(1)证明:∵AD平分∠BAC,∴∠CAD=∠BAD.∵∠CAD=∠CBD,∴∠BAD=∠CBD;(2)解:如图,连结OD.∵∠AEB= 125°,∴∠AEC= 55°.∵AB为⊙O的直径,∴∠ACE=90°,∴∠CAE= 35°,∴∠DAB=∠CAE=35°,∴∠BOD=2∠BAD=70°,∴BD的长为70×π×3180=7 6π.20.【答案】(1)证明:∵C,A,D,F在⊙O上,AF⊥AC,∴∠D=∠CAF=90°,∵AB⊥CD,BG⊥DF,∴∠BED=∠G=90°,∴四边形BEDG中,∠ABG=90°,∴半径OB⊥BG,∴BG是⊙O的切线;(2)解:连接CF,∵∠CAF=90°,∴CF是⊙O的直径,∴OC=OF,∵直径AB⊥CD于E,∴CE=DE,∴OE是△CDF的中位线,∴OE=12DF=2,∵∠AFD=30°,∴∠ACD=∠AFD=30°,∴∠CAE=90°−∠ACE=60°,∵OA=OC,∴△AOC是等边三角形,∵CE⊥AB,∴E为AO的中点,∴OA=2OE=4,OB=4,AE=2,∴BE=OB+OE=6,DE=CE=23,∵∠BED=∠D=∠G=90°,∴四边形BEDG是矩形,∴S阴影=S矩形BEDG−S梯形OEDF−S扇形BOF=6×23−12×(2+4)×23−60π⋅42360=63−83π.21.【答案】(1)解:连接CM,∵M(3,0),C(0,4),∴OM=3,OC=4,∴CM=5,即⊙M的半径为5,∴MA=5,∴AO=AM-OM=2,∴A(−2,0);(2)连接CM,作MH⊥AN于H,∵CE为⊙M的切线,∴MC⊥EC,即∠MCE=90°.∵AN⊥CE于F,即∠AFC=90°.又∵MH⊥AN于H,即∠MHA=90°.∴在四边形FHMC中,∠CMH=90°=∠CMO+∠AMH.∵在Rt△AHM中,∠HAM+∠AMH=90°,∴∠HAM=∠CMO.∵在Rt△COM中,∠CMO+∠OCM=90°,∴∠OCM=∠AMH.∵在△AMH与△MCO中,∠HAM=∠CMOMC=MA∴△AMH≌△MCO(ASA),∠OCM=∠AMH故AH=MO=3.即AN=HN+AH=3+3=6;(3)解:结合题意,可知PM=CM,△CMP为等腰三角形,同时因为∠CPM=45°=∠PCM,因此△CMP也是等腰直角三角形,即∠CMP=90°且CM=PM=5.①当P在CM右侧时,作PE垂直x轴于E.∵∠CMP=90°,∴∠CMO+∠PME=90°.又∵在Rt△PEM中,∠PME+∠MPE=90°,∴∠CMO=∠MPE.∴同理可得∠MCO=∠PME.在△MCO与△PME中,∠CMO=∠MPECM=PM∴△MCO≌△PME(ASA)∠MCO=∠PME∴OM=PE=3,ME=OC=4,即存在P1(7,3);②当P在CM左侧时(设为P2),作PF垂直x轴于F.根据圆的对称性,结合①的结论,易证:△MCO≌△PMF,∴OM=PF=3,FM=OC=4,即存在P2(−1,−3).22.【答案】(1)解:60°(2)解:连接CD,过点A作AH⊥CD,交CD于点H.如图:在Rt△AHC中,∵∠ACH=∠ABD=45°,AC=6,∴CH=AH=32,此时△ADB为等腰直角三角形,AD=BD=52,在Rt△AHD中,∵AH=32,AD=52,∴DH=42,∴CD=CH+DH=72.(3)解:如图,连接OC,BD.∵BC=CD,OB=OD,∴OC垂直平分BD,∵O为AB中点,∴OF为△BDA的中位线,有OF=12AD,OF//AD,设OF=t,则CF=24−t,AD=2t,y=48+x+x+2t=2t+2x+48,在Rt△BFC中,B F2=B C2−C F2=x2−(24−t)2,在Rt△BFO中,B F2=B O2−O F2=242−t2,于是有:x2−(24−t)2=242−t2,整理得,t=−148x2+24,∴y=−124x 2+2x+96=−124(x−24)2+120,当x=24时,y max=120。
第24章 圆 人教版数学九年级上册单元闯关双测A卷(含答案)

第二十四章圆(测基础)——2023-2024学年人教版数学九年级上册单元闯关双测卷【满分:120】一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)1.下列说法中,不正确的是( )A.圆既是轴对称图形,又是中心对称图形B.圆有无数条对称轴C.圆的每一条直径都是它的对称轴D.圆的对称中心是它的圆心2.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )A.①B.②C.③D.④3.如图,P是外一点,PA,PB分别和切于A,B两点,C是弧AB上任意一点,过点C作的切线分别交PA,PB于点D,E.若的周长为12,则PA的长为( )A.12B.6C.8D.44.如图, 四边形 OABC是菱形, 连接AC, 则的度数是( )A. B. C. D.5.如图, AB是的直径, 点C,D是上的点, 且,DO的延长线交于点E, 若, 则的度数为( )A. B. C. D.6.如图,BD是的直径,点A,C在上,,交BD于点G.若,则的度数为( )A. B. C. D.7.如图,正六边形ABCDEF内接于,若的半径等于2,则图中阴影部分的面积是( ).A. B. C. D.8.如图, 是的内接三角形, 过点C 的的切线交BO的延长线于点P, 若, 那么的度数为( )A. B. C. D.9.如图, 在中, , 用尺规按①到②的步骤操作:①作的平分线交BC于点D;②在AC上找一点O, 以点O为圆心, OA长为半径画圆, 使经过点D, 交 AB于点E, 交 AC于另一点F.结论 I : BC一定是的切线;结论 II : 顺次连接点O,E,D,F, 必得菱形OEDF.对于结论 I 和 II, 下列判断正确的是( )A. I 和 II 都对B. I 和 II 都不对C. I 不对 II 对D. I 对 II 不对10.如图, 在中, ,, 点D为 AB的中点, 点P在AC上, 且, 将CP 绕点C 在平面内旋转, 点P的对应点为点Q, 连接AQ,DQ. 当时, 对于AQ的长, 甲、乙两人有不同的结果:甲: ;乙. 则下列说法正确的是( )A. 甲对, 乙错B. 甲错, 乙对C.甲、乙合在一起才正确D.甲、乙合在一起也不正确二、填空题(每小题4分,共20分)11.现有圆周的一个扇形彩纸片,该扇形的半径为,小红同学为了在“六一”儿童节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为的圆锥形纸帽接缝处不重叠,那么剪去的扇形纸片的圆心角为______.12.如图所示,,是中两条互相垂直的直径,点P在上,且不与点A,M重合,过点P作,的垂线,垂足分别是D,C.当点P在上移动时,的值__________.(填“逐渐变大”“逐渐变小”或“不变”)13.已知的半径为6,则的内接正方形的边长为_________.14.如图, 在矩形ABCD中, ,, 点E 是矩形ABCD 内部一动点, 且, 点P是AB边上一动点, 连接PD,PE, 则的最小值为________.15.的半径为,AB,CD是的两条弦,,,.则AB和CD之间的距离_____.三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)16.(8分)如图,在一座圆弧形拱桥,它的跨度AB为,拱高PM为,当洪水泛滥到跨度只有时,就要采取紧急措施,若某次洪水中,拱顶离水面只有,即PN=4m时,试通过计算说明是否需要采取紧急措施.17.(8分)如图,⊙O是的外接圆,,延长BC到D,连接AD,使.AB交OC于E.(1)求证:AD与相切;(2)若,.求的半径.18.(10分)如图,A,B是上两点,,C为弧AB上一点.(1)写出弦AB对的弧的度数;(2)若C是劣弧的中点,判断四边形OACB的形状,并说明理由.19.(10分)在中,,点A在以BC为直径的半圆外.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)在图①中作弦EF,使;(2)在图②中以BC为边作一个的圆周角.20.(12分)如图,以的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且.(1)试判断的形状,并说明理由;(2)已知半圆的半径为5,,求BD的长.21.(12分)如图,为的外接圆,AB为的直径,点D为的中点,连接OD.(1)求证:;(2)设OD交BC于E,若,.求阴影部分面积.答案以及解析1.答案:C解析:A选项,圆既是轴对称图形,又是中心对称图形,此选项正确;B选项,圆有无数条对称轴,此选项正确;C选项,圆的每一条直径所在的直线都是它的对称轴,此选项错误;D选项,圆的对称中心是它的圆心,此选项正确.故选C.2.答案:C解析:要恢复圆形镜子,则碎片中必须有一段完整的弧,才能确定这条弧所在的圆的圆心和半径,只有③符合题意,故选C3.答案:B解析:PA,PB分别和切于A,B两点,,DE是O的切线,,,的周长为12,即,.故选B.4.答案:B解析:如图,连接OB.四边形OABC是菱形, ,AC平分,,是等边三角形,,.5.答案:C解析:连接,,,,,6.答案:B解析:是的直径,.,,.,,,.7.答案:C解析:正六边形ABCDEF内接于,,,,,图中阴影部分的面积故选:C.8.答案:B解析:如图, 连接OC, 设点 E是优弧BC上任一点,连接CE,BE. CP是的切线,,,四边形ABEC是圆内接四边形9.答案:D解析:连接OD,,.AD平分,,,,,BC是的切线.由题意得,. 易知仅当时,, 即四边形OEDF为菱形,此时,,故四边形OEDF不一定为菱形.10.答案:C解析:,,. 连接 CD,点D为AB 的中点, , ,,点Q在以点C为圆心, 1 为半径的圆上运动. 分两种情况讨论:①当点Q在线段CD上时, 如图(1), 则,;②当点Q在线段DC 的延长线上时, 如图(2),,. 综上所述, AQ的长为或.11.答案:解析:解得:,扇形彩纸片是圆周,因而圆心角是剪去的扇形纸片的圆心角为.剪去的扇形纸片的圆心角为.故答案为.12.答案:不变解析:连接,,,,,四边形是矩形,,,是半径,长度不变,的值不变.故答案为:不变.13.答案:解析:如图,连接,的半径为6,四边形ABCD是正方形,,是的直径,.,,,解得,即的内接正方形的边长等于.14.答案:8解析:设点O为BC的中点. 由题意可知, 点E 在以BC为直径的半圆O上运动, 作半圆O关于AB的对称图形 (半圆 ), 点E的对称点为, 连接,, 则. 易知当点 D,P,,共线时, 的值最小, 为的长, 如图所示. 在中,,,. 又,, 即的最小值为 8 .15.答案:或解析:作于E,交CD于F,连接OA、OC,如图,,,,,在中,,,,在中,,,,当圆心O在AB与CD之间时,;当圆心O不在AB与CD之间时,;即AB和CD之间的距离为或.故答案为或.16.解析:设圆弧所在圆的圆心为O,连接OA、,设半径为x米,则OA=OA′=OP,由垂径定理可知AM=BM,A′N=B′N,米,∴AM=30米,且OM=OP―PM=(x―18)米,在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,即x2=(x―18)2+302,解得x=34,∴ON=OP―PN=34―4=30((米),在Rt△A′ON中,由勾股定理可得(A′N=OA′2―ON2=342―302=16(米),∴A′B′=32米>30米,∴不需要采取紧急措施.17.解析:(1)如图,连接,由圆周角定理得:,,,即,又是的半径,与相切;(2)设的半径为r,则,,,在中,,即,解得或(不符题意,舍去),故的半径为4.18.答案:(1)60或120(2)菱形,见解析解析:(1)在优弧AB上取一点D,连接AD,BD,如图1所示:,,,;弦AB对的弧的度数为或;(2)菱形,理由:连接OC,是弧AB的中点,,又,和都是等边三角形,,四边形OACB是菱形.19.解析:(1)如图:连接DE,DE即为EF,在中,,,又四边形BCEF是圆内接四边形,,,;(2)如图:过点A作BC的垂线AO,交半圆于P点,连接BP,,,又,.20.答案:(1)为等腰三角形(2)解析:(1)为等腰三角形.理由如下:连接AE,如图,,,即AE平分.为直径,,.,,,为等腰三角形.(2)由(1)知,,.在中,,,.为直径,,,.21.答案:(1)见解析;(2);解析:(1)证明:AB是的直径,,点E是BC的中点,,,,,;(2)设,,,,,,解得:,,,,,,,阴影部分的面积.。
第24章 圆 人教版数学九年级上册单元测试卷(含答案)

第二十四章 圆一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)1.(2022·北京通州区期末)如图,若OA⊥OB,则∠C=( )A.22.5°B.67.5°C.90°D.45°(第1题) (第2题)2.(2022·江苏镇江润州区段考改编)如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是( )A.3B.4C.5D.63.(2021·江苏常熟期中)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(-3,0),B(-1,2),C(3,2),则△ABC的外心的坐标是( )A.(1,-2)B.(0,0)C.(1,-1)D.(0,-1)(第3题) (第4题)4.(2021·山东寿光期中)如图,若正方形ABCD的边长为6,则其外接圆半径OA与内切圆半径OE的比值为( )A.3B.2C.2D.35.(2022·湖北十堰期末)如图,点A,B,C,D都在☉O上,OA⊥BC,∠OBC=40°,则∠ADC 的度数为( ) A.40° B.30° C.25° D.50°6.(2022·浙江金华期中改编)如图,☉O 与正六边形OABCDE 的边OA ,OE 分别交于点F ,G ,点M 为劣弧FG 的中点.连接FM ,GM ,若FM=22,则☉O 的半径为( )A.2B.6C.22D.26(第6题) (第7题)7.(2022·浙江宁波江北区期末)如图,AB 是半圆O 的直径,C ,D 是半圆上两点,连接CA ,CD ,AD.若∠ADC=120°,BC=1,则BC 的长为( )A.π3B.π4C.π6D.2π38.(2022·江苏镇江期中)简易直尺、含60°角的直角三角板和量角器如图摆放(无重叠部分),A 为三角板与直尺的交点,B 为量角器与直尺的接触点,C 为量角器与三角板的接触点.若点A 处刻度为4,点B 处刻度为6,则该量角器的直径长为( )A.2B.23C.4D.439.如图,四边形ABCD 内接于☉O ,AD ∥BC ,直线EF 是☉O 的切线,B 是切点.若∠C=80°,∠ADB=54°,则∠CBF=( )A.45°B.46°C.54°D.60°10.如图(1),AB是半圆O的直径,点C是半圆O上异于A,B的一点,连接AC,BC.点P从点A出发,沿A→C→B以1 cm/s的速度运动到点B.图(2)是点P运动时,△PAB 的面积y(cm2)随时间x(s)变化的图象,则点D的横坐标为( )A.a+2B.2C.a+3D.3二、填空题(共5小题,每小题3分,共15分)11.(2022·山东济南天桥区期末)如图,☉A,☉B,☉C两两相离,且半径都为2,则图中阴影部分的面积之和为 .(结果保留π)(第11题) (第12题)12.(2022·江苏苏州姑苏区期中)如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 .13.(2022·河北唐山期末改编)如图,△ABC内接于☉O,过点A作直线EF,已知∠B=∠EAC,根据弦AB的位置变化,试探究直线EF与☉O的位置关系.甲:如图(1),当弦AB过点O时,EF与☉O相切;乙:如图(2),当弦AB不过点O时,EF也与☉O相切.你认为 的判断正确.14.新风向关注数学文化在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,则直径AB的长为 寸.(第14题) (第15题)15.如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与点A,B重合),当PA= 时,△PAD为等腰三角形.三、解答题(共6小题,共55分)16.(7分)(2022·北京四中期中改编)某游乐园的摩天轮采用了国内首创的横梁结构,如图,摩天轮半径为44 m,中心O距离地面56 m,匀速运行一圈的时间为18 min.由于受到周边建筑物的影响,乘客与地面之间超过一定距离时,可视为最佳观赏位置.已知在运行的一圈里最佳观赏时长为12 min,求最佳观赏位置与地面的最小距离(即BD的长).17.(8分)(2021·浙江温州模拟)如图,已知AB是☉O的直径,弦CD⊥AB于点E,点M 是☉O上一动点,∠M=∠D,连接BC.(1)判断BC与MD的位置关系,并说明理由;(2)若MD恰好经过圆心O,求∠D的度数.18.(8分)(2022·山东临沂期末)如图,AB为☉O的直径,AC,DC为弦,∠ACD=60°,P 为AB延长线上的点,连接PD,∠APD=30°.(1)求证:DP是☉O的切线.(2)若☉O的半径为2,求图中阴影部分的面积.19.(10分)[与特殊平行四边形综合](2021·河南驻马店二模)如图,已知☉O的直径AB=2,C是AB上一个动点(不与点A,B重合),切线DC交AB的延长线于点D,连接AC,BC,OC.(1)请添加一个条件使△BAC≌△ODC,并说明理由.(2)若点C关于直线AB的对称点为E.①当AD= 时,四边形OCDE为正方形.②当∠CDB= °时,四边形ACDE为菱形.20.(10分)新风向探究性试题如图,已知AB是☉O的直径,BC与☉O相切于点B,CD 与☉O相切于点D,连接AD,OC.(1)求证:AD∥OC.(2)小聪与小明在做这个题目的时候,对∠CDA+∠AOC的值进行了探究:小聪说,∠CDA+∠AOC的值是一个固定值;小明说,∠CDA+∠AOC的值随∠A的度数的变化而变化.若∠CDA+∠AOC的值为y,∠A的度数为x,你认为他们之中谁的说法正确?若小聪的说法正确,请求出y;若小明的说法正确,请求出y与x之间的关系.21.(12分)新风向探究性试题【问题呈现】阿基米德折弦定理:如图(1),AB和BC是☉O的两条弦(即折线ABC是☉O的一条折弦),BC>AB,M是ABC的中点,则从点M 向BC作垂线,垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的过程. 图(1) 图(2) 图(3) 图(4)证明:如图(2),在CD上截取CG=AB,连接MA,MB,MC和MG.∵M是ABC的中点,∴MA=MC.①∵∠A=∠C,②∴△MAB≌△MCG,∴MB=MG.又MD⊥BC,∴BD=DG,∴CD=CG+DG=AB+BD,即CD=AB+BD.根据证明过程,分别写出步骤①,②的理由:① .② .【理解运用】在图(1)中,若AB=4,BC=6,则BD= .【变式探究】如图(3),AB,BC是☉O的两条弦,点M是AC的中点,MD⊥BC于点D,请写出CD,DB,BA之间存在的数量关系: .【实践应用】如图(4),△ABC内接于☉O,BC是☉O的直径,点D为圆周上一动点,满足∠DAC=45°.若AB=6,☉O的半径为5,求AD的长.第二十四章 圆·B卷1.D ∵OA⊥OB,∴∠AOB=90°,∴∠C=12∠AOB=【技巧】同圆中,同弧所对的圆周角等于圆心角的一半45°.2.B 连接BD,由勾股定理可得BD=AB2+AD2=42+32=5,由题意可知,3<r<5,因此只有B选项符合.3.A 如图,∵三角形的外心到三角形三个顶点的距离相等,∴线段BC,AB的垂直平分线的交点即为外心P,由图可知,点P的坐标为(1,-2).4.B 由题意结合题图可知,内切圆直径等于正方形边长,则OE=3.由正方形的性质可得OA=32,则OAOE =323=2.5.C ∵OA ⊥BC ,∴AC =AB .∵∠OBC=40°,∴∠AOB=50°,∴∠ADC=12∠AOB=12×50°=25°.6.C 连接OM ,由题意知∠FOG=120°.∵点M 为劣弧FG 的中点,∴∠FOM=60°.∵OM=OF ,∴△OFM 是等边三角形,∴OM=OF=FM=22,则☉O 的半径为22,故选C .7.A 如图,连接OC.∵∠ADC=120°,∴∠ABC=60°.∵OB=OC ,∴△OBC 为等边三角形,∴∠COB=60°,OB=OC=BC=1,∴BC 的长=60π·1180=π3.8.D 如图,添加点D ,连接OA ,OB ,由题意得AB=6-4=2,∵∠CAD=60°,∴∠BAC=120°.∵AB 与半圆O 相切于点B ,AC 与半圆O 相切于C ,∴∠BAO=60°,∠AOB=30°,∴OA=2AB=4,∴OB=OA 2-AB 2=42-22=23,∴量角器的直径长为43.9.B 如图,连接OD ,OB ,则∠BOD=2∠C=160°.∵OB=OD ,∴∠OBD=180°―160°2=10°.∵四边形ABCD 内接于☉O ,∴∠A=180°-∠C=100°.∵AD ∥BC ,∴∠A+∠ABC=180°,∴∠ABC=80°.在△ABD 中,∠ADB=54°,∴∠ABD=180°-54°-100°=26°,∴∠OBC=80°-26°-10°=44°.∵EF 是☉O 的切线,∴∠OBF=90°,∴∠CBF=90°-∠OBC=90°-44°=46°.故选B .∵AD ∥BC ,∴∠ADB+∠BDC+∠C=180°.∵∠C=80°,∠ADB=54°,∴∠BDC=46°.∵∠CBF 是弦切角,∴∠CBF=∠BDC=46°.(弦切角定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数)10.A 从题图(2)看,当x=a 时,y 取得最大值a ,此时点P 运动到点C 处,即AC=a.∵∠ACB=90°,∴y=12×AC×BC=12BC×a=a ,解得BC=2.当点P 运动到点B 处时,y=0,即AC+BC=OD ,∵AC+BC=a+2,∴点D 的横坐标为a+2.11.2π 因为∠A+∠B+∠C=180°,所以阴影部分的面积之和等于半径为2的半圆的面积,为2π.12.10 如图,连接OA ,OB ,由题意知点A ,B ,C ,D 在以点O 为圆心,OA 的长为半径的同一个圆上.∵∠ADB=18°,∴∠AOB=2∠ADB=36°,∴这个正多边形的边数=360°÷36°=10.13.甲、乙 题图(1)中,∵AB 是☉O 的直径,∴∠C=90°,∴∠B+∠CAB=90°.∵∠EAC=∠B ,∴∠EAC+∠CAB=90°,∴EF ⊥AB.∵OA 是半径,∴EF 是☉O 的切线,故甲的判断正确.如图,作直径AM ,连接CM ,则∠ACM=90°,∠B=∠M.∵∠EAC=∠B ,∴∠EAC=∠M.∵∠CAM+∠M=90°,∴∠CAM+∠EAC=90°,∴EF 是☉O 的切线,故乙的判断正确.14.26 连接OC.∵CD ⊥AB ,AB 为☉O 的直径,CD=10,∴CE=12CD=5. 设OC=OA=x ,则OE=x-1.由勾股定理得OE 2+CE 2=OC 2,即(x-1)2+52=x 2,解得x=13,∴AB=26寸.15.22或85516.【参考答案】由题意得AB⊥OM,BO=44,×360°=120°,∠AOB=18―1218∴∠BOC=60°,∠OBC=30°,∴OC=1OB=22.2∵中心O距离地面56 m,∴OM=56,∴CM=OM-OC=34,∴BD=34 m,故最佳观赏位置与地面的最小距离为34 m.(7分) 17.【参考答案】(1)BC∥MD.(1分)理由:∵∠MBC=∠D,∠M=∠D,∴∠M=∠MBC,∴BC∥MD.(4分) (2)∵AB是☉O的直径,CD⊥AB于点E,∴∠D+∠EOD=90°.(6分)∵MD过圆心O,∴∠BOD=2∠M=2∠D,∴∠D+2∠D=90°,∴∠D=30°.(8分) 18.【参考答案】(1)证明:如图,连接OD.∵∠ACD=60°,∴∠AOD=120°,∴∠BOD=60°.∵∠APD=30°,∴∠ODP=90°,即PD⊥OD.∵OD是半径,∴PD是☉O的切线.(4分)(2)∵在Rt △POD 中,OD=2,∠OPD=30°,∴OP=4.由勾股定理得PD=23.∴S 阴影部分=S △POD -S扇形ODB =12×2×23-60π·22360=23-2π3.(8分)19.【参考答案】(1)添加条件∠A=30°.(1分)理由:∵AB 是☉O 的直径,∴∠ACB=90°.∵DC 是☉O 的切线,∴∠DCO=90°,∴∠ACB=∠DCO.(3分)∵OA=OC ,∴∠A=∠OCA=30°,∴∠BOC=60°.∵OC=OB ,∴△BOC 是等边三角形,∴BC=OC ,∠ABC=∠DOC=60°,∴△BAC ≌△ODC (ASA).(6分)或添加条件BC=1.(1分)∵AB 是☉O 的直径,∴∠ACB=90°.∵DC 是☉O 的切线,∴∠DCO=90°,∴∠ACB=∠DCO.(3分)∵OC=OB=12AB=1=BC ,∴△BOC 是等边三角形,∴∠ABC=∠DOC=60°,∴△BAC ≌△ODC (ASA).(6分)(答案不唯一,正确即可给分)(2)①2+1(8分)解法提示:∵AB=2,∴OA=OC=1.连接OE ,DE ,若四边形OCDE 是正方形,则△OCD 是等腰直角三角形,易得OD=2,∴AD=OD+OA=2+1.②30(10分)解法提示:∵DC 是☉O 的切线,∴∠DCO=90°,∴∠COD=90°-∠CDB.∵OC=OA ,∴∠CAB=12∠COD=90°―∠CDB2.连接AE ,若四边形ACDE 是菱形,则CA=CD ,∴∠CAB=∠CDB ,即90°―∠CDB2=∠CDB ,解得∠CDB=30°,∴当∠CDB=30°时,四边形ACDE 是菱形.20.【思路导图】(1)连接ODRt △ODC ≌Rt △OBC →∠DOC=∠BOC →∠DAO=∠BOC →AD ∥CO【参考答案】(1)如图,连接OD.(1分)∵BC 与☉O 相切于点B ,CD 与☉O 相切于点D ,∴∠ODC=∠OBC=90°.(2分)在Rt △ODC 和Rt △OBC 中,OD =OB ,OC =OC ,∴Rt △ODC ≌Rt △OBC ,∴∠DOC=∠BOC.(4分)∵∠DAO=12∠DOB ,∴∠DAO=∠BOC ,∴AD ∥CO.(5分)(2)小聪的说法正确.(6分)∵∠CDA+∠AOC=y ,∠A=x ,∴∠ODC+∠ODA+∠AOC=y ,∠ODA=∠OAD=x.∵∠ODC=90°,∴90°+x+∠AOC=y.由(1)得AD ∥CO ,∴∠OAD+∠AOC=180°,即x+∠AOC=180°,∴y=90°+x+∠AOC=90°+180°=270°.(10分)21.【参考答案】【问题呈现】①在同圆中,如果两条弧相等,那么它们所对的弦相等②同弧所对的圆周角相等(4分)【理解运用】1(6分)解法提示:∵CD=AB+BD ,∴CD=12(AB+BC )=12×(4+6)=5,∴BD=BC-CD=6-5=1.【变式探究】DB=AB+CD(8分)解法提示:如图,在DB 上截取BG=BA ,连接MA ,MB ,MC ,MG.∵M 是AC 的中点,∴AM=MC ,∠MBA=∠MBG.又MB=MB ,∴△MAB ≌△MGB ,∴MA=MG ,∴MC=MG.又DM ⊥BC ,∴DC=DG ,∴AB+DC=BG+DG ,即DB=AB+CD.【实践应用】∵BC是☉O的直径,∴∠BAC=90°.∵AB=6,☉O的半径为5,∴易得AC=8.(分类讨论思想)如图,连接AD,当∠DAC=45°时,有两种情况.①∠D1AC=45°,则D1是BC的中点.过点D1作D1G1⊥AC于点G1,则CG1+AB=AG1.∴AG1=1(6+8)=7,∴AD1=72.2②∠D2AC=45°,过点D2作D2G2⊥AC于点G2,同理易得CG2=AB+AG2,∴CG2=7,AG2=1,∴AD2=2.综上,AD的长为72或2.(12分)。
2023-2024学年人教版九年级数学上册第二十四章圆单元检测题(含答案)

第二十四章圆单元检测题一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列说法中,正确的是( )A.过圆心的线段叫直径B.长度相等的两条弧是等弧C.与半径垂直的直线是圆的切线D.圆既是中心对称图形,又是轴对称图形2.已知☉O的半径为6,圆心O到直线l的距离为7,则直线l与☉O的位置关系是( )A.相离B.相交C.相切D.无法确定3.(2023自贡)如图所示,△ABC内接于☉O,CD是☉O的直径,连接BD,∠DCA=41°,则∠ABC的度数是( )第3题图A.41°B.45°C.49°D.59°4.圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )A.10πB.15πC.30πD.45π5.如图所示,☉O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的取值范围是( )第5题图A.3<OP<5B.3≤OP≤5C.4<OP<5D.4≤OP≤56.如图所示,四边形ABCD内接于☉O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )A.45°B.50°C.55°D.60°7.如图所示,☉O是△ABC的外接圆,∠BAC=60°,若☉O的半径OC为2,则弦BC的长为( )第7题图A.4B.23C.338.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )2 B.22-22 D.2-29.(2022娄底改编)如图所示,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC 的内心成中心对称,则圆中的黑色部分的面积与△ABC 的面积之比是( )第9题图3π18 B.3183π9 D.3910.(2022广大附中一模)如图所示,点A,B 的坐标分别为A(2,0), B(0,2),点C 为坐标平面内一点,BC=1,点M 为线段AC 的中点,连接OM,则OM 的最大值为( )2+1 B.2+12C.22+1D.22-12二、填空题:本大题共5小题,每小题3分,共15分.11.用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设 .12.如图所示,C为AB的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= cm.13.已知圆心角为120°的扇形的面积为12π cm2,则扇形的弧长是 cm.14.如图所示,☉O的半径为1,PA,PB是☉O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,若∠APB=60°,则△PAB的周长为 .第14题图15.小明很喜欢钻研问题,一次数学老师拿来一个残缺的圆形瓦片(如图所示),让小明求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量得AB的中点C到AB的距离CD=1.6 cm,AB=6.4 cm,则求得圆形瓦片所在圆的半径为 cm.第15题图三、解答题(一):本大题3小题,第16题10分,第17,18题各7分,共24分.16.(1)(2022湘潭节选)如图所示,在☉O中,直径AB与弦CD相交于点E,连接AC,BD,AD.若AD=3,∠C=30°,求☉O的半径.(2)如图所示,扇形OAB的圆心角为120°,半径OA为6 cm.若把扇形纸片OAB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.17.如图所示,四边形ABCD内接于☉O,AB=AD,∠C=110°,若点E在AD 上,求∠E的度数.18.(2022珠海一模改编)如图所示,已知AB是☉O的直径,直线CD是☉O的切线,过点A作AD⊥CD,垂足为D,直线CD与AB的延长线交于点E.当AB=2BE,且CE=3时,求AD的长.四、解答题(二):本大题3小题,每小题9分,共27分.19.(原创)综合与实践素材:一张三角形纸板.操作:如图(1)所示,将一块三角形纸板ABC,准备裁剪成一个面积最大的圆形,已知∠C=90°,BC=3,AC=4.如图(2)所示,作△ABC的内切圆☉O,切点分别为D,E,G,连接OG,OD,OE.解决问题:请求出裁剪出的最大圆形面积.20.(2022眉山改编)如图所示,AB为☉O的直径,点C是☉O上一点,CD 与☉O相切于点C,过点B作BD⊥DC,连接AC,BC.(1)求证:BC平分∠ABD;(2)若BC=23,AB=4,求阴影部分的面积.21.(2022新疆节选)如图所示,☉O是△ABC的外接圆,AB是☉O的直径,点D在☉O上,AC=CD,连接AD,延长DB交过点C的切线于点E.求证:(1)∠ABC=∠CAD;(2)BE⊥CE.五、解答题(三):本大题2小题,每小题12分,共24分.22.(2022金华)综合探究如图(1)所示,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:作法如图(2)所示.1.作直径AF.2.以F为圆心,FO为半径作圆弧,与☉O交于点M,N.3.连接AM,MN,NA.(1)求∠ABC的度数;(2)△AMN是正三角形吗?请说明理由;(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.23.(2022宁波)综合运用如图(1)所示,☉O为锐角三角形ABC的外接圆,点D在BC上,AD交BC 于点E,点F在AE上,满足∠AFB-∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连接BD,DG.设∠ACB=α.(1)用含α的代数式表示∠BFD;(2)求证:△BDE≌△FDG;(3)如图(2)所示,若AD为☉O的直径,当AB的长为2时,求AC的长.答案:一、选择题1.D2.A3.C4.B5.D6.B7.B8.B9.A 10.B二、填空题11.∠B≥90° 12.2 13.4π 14.33 15.4三、解答题(一)16.(1)解:∵∠C=∠B,∠C=30°,∴∠B=30°.∵AB是☉O的直径,AD=3,∴∠ADB=90°.∴AB=6.∴☉O的半径为3.(2)如图所示,设圆锥底面圆的半径为r,所以2πr=4π,解得r=2,在Rt△OHC中,HC=2,OC=6,所以OH=OC2-H C2=42(cm).17.解:如图所示,连接BD,∵∠C+∠BAD=180°,∠C=110°,∴∠BAD=180°-110°=70°.∵AB=AD,∴∠ABD=∠ADB.×(180°-70°)=55°.∴∠ABD=12∵四边形ABDE是☉O的内接四边形,∴∠E+∠ABD=180°.∴∠E=180°-55°=125°.18.解:如图所示,连接OC,∵直线CD为☉O的切线,∴∠OCE=90°.∵AB=2BO,AB=2BE,∴BO=BE=CO.设BO=BE=CO=x,∴OE=2x.在Rt△OCE中,根据勾股定理,得OC2+CE2=OE2,即x2+(3)2=(2x)2.∴x=1.∴AE=3,∠E=30°.∴AD=32.四、解答题(二)19.解:∵∠C=90°,BC=3,AC=4,OG=OE=OD,∴AB=32+42=5.∴S △ABC =12AC×BC=12AC×OG+12BC×OE+12AB×OD=12OG×C △ABC ,即12AC×BC=12OG×C △ABC .∴12×3×4=12×OG×(3+4+5),解得OG=1,∴裁剪出的最大圆形面积为π×12=π.20.(1)证明:连接OC,如图所示,∵CD 与☉O 相切于点C,OC 为半径,∴OC ⊥CD.∵BD ⊥CD,∴OC ∥BD.∴∠OCB=∠DBC.∵OC=OB,∴∠OCB=∠OBC.∴∠DBC=∠OBC.∴BC 平分∠ABD.(2)解:如图所示,作CE ⊥AO 于点E,∵AB是直径,AB=4,∴∠ACB=90°,OA=OC=2.在Rt△ABC中,AC=AB2-B C2=42-(23)2=2,∴AO=CO=AC=2.∴△AOC是等边三角形.∴∠AOC=60°.∵CE⊥OA,∴OE=12OA=1.∴CE=3.∴阴影部分的面积S=60×π×22360-12×2×3=2π3-3.21.证明:(1)∵AC=CD,∴∠CAD=∠ADC.∵∠ABC=∠ADC,∴∠ABC=∠CAD.(2)如图所示,连接OC,∵CE与☉O相切于点C,∴∠OCE=90°.∵四边形ADBC是圆内接四边形,∴∠CAD+∠DBC=180°.∵∠DBC+∠CBE=180°,∴∠CAD=∠CBE.∵∠ABC=∠CAD,∴∠CBE=∠ABC.∵OB=OC,∴∠OCB=∠ABC.∴∠OCB=∠CBE.∴OC∥BE.∴∠E=180°-∠OCE=90°.∴BE⊥CE.五、解答题(三)22.解:(1)∵五边形ABCDE是正五边形,∴∠ABC=(5-2)×180°=108°,5即∠ABC=108°.(2)△AMN是正三角形.理由如下:如图所示,连接ON,NF,由题意,得FN=ON=OF,∴△FON是等边三角形.∴∠NFA=60°.∴NMA=60°.同理,得∠ANM=60°,∴∠MAN=60°.∴△MAN是正三角形.(3)∵∠AMN=60°,∴∠AON=120°.×2=144°,∵∠AOD=360°5∴∠NOD=∠AOD-∠AON=144°-120°=24°.∵360°÷24°=15,∴n的值是15.23.(1)解:∵∠AFB-∠BFD=∠ACB=α,①又∵∠AFB+∠BFD=180°,②②-①,得2∠BFD=180°-α,.∴∠BFD=90°-α2,(2)证明:由(1),得∠BFD=90°-α2∵∠ADB=∠ACB=α,.∴∠FBD=180°-∠ADB-∠BFD=90°-α2∴∠BFD=∠FBD.∴DB=DF.∵FG∥AC,∴∠CAD=∠DFG.∵∠CAD=∠DBE,∴∠DFG=∠DBE.在△BDE 和△FDG 中,{DB =DF ,∠DBE =∠DFG ,BE =FG ,∴△BDE ≌△FDG(SAS).(3)解:∵△BDE ≌△FDG,∴∠FDG=∠BDE=α,DE=DG.∴∠BDG=∠BDF+∠EDG=2α.∵DE=DG,∴∠DGE=12(180°-∠FDG)=90°-α2.∴∠DBG=180°-∠BDG-∠DGE=90°-3α2.∵AD 是☉O 的直径,∴∠ABD=90°.∴∠ABC=∠ABD-∠DBG=3α2.∴AC 与AB 所对的圆心角度数之比为3∶2.∴AC 与AB 的长度之比为3∶2.∵AB =2,∴AC =3.。
人教版九年级数学上册《第二十四章圆》单元检测卷带答案

人教版九年级数学上册《第二十四章圆》单元检测卷带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.已知点A为⊙O内的一点,且⊙O的半径为5cm,则线段OA的长度可能是()A.3cm B.5cm C.6cm D.7cm⌢的中点,半径OC交弦AB于点D,已知OC=5,AB=8,则CD的长为()2.如图,在⊙O中,点C为ABA.2B.√5C.√7D.33.如图,点A、B、C在⊙O上∠ACB=55°,则∠ABO的度数是()A.30°B.35°C.40°D.55°4.如图,⊙O中,CD是切线,切点是D,直线CO交⊙O于B、A,∠A=15°,则∠C的度数是()A.45°B.65°C.60°D.70°5.如图,点O是△ABC内切圆的圆心,已知∠ABC=50°,∠ACB=80°,则∠BOC的度数是()A.100°B.115°C.125°D.130°6.如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为()A.100°B.110°C.120°D.130°7.如图,过正六边形内切圆圆心的两条直线夹角为60°,圆的半径为√3,则图中阴影部分面积之和为()A.π−√3B.π−23√3C.√3−23πD.√3−12π8.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则BC⌢的长为()A.6πB.2πC.32πD.π二、填空题9.如图,AB是⊙O的直径,弦CD⊥AB交于点E,若OE=4,CE=3,则⊙O的半径为.10.如图,四边形ABCD内接于⊙O,点M在AD的延长线上∠CDM=71°,则∠AOC=.11.如图,AB是⊙O的直径,DE切⊙O于点E,BD⊥DE于点D,交⊙O于点C.若AB=5,BC=3,则CD=.12.如图,在正八边形ABCDEFGH中,连接AC、AE,则∠CAE的度数是.13.如图:一把折扇的骨架长是 30 厘米,扇面宽为 20 厘米,完全展开时圆心角为135°,扇面的面积为平方厘米.三、解答题14.如图,在△ABC中AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.(1)求证:BE=CE;(2)若AB=6,∠BAC=54°,求AD⏜的长.15.如图,AB是⊙O的直径,C是BD⏜的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF.(2)若CD=6,AC=8,求⊙O的半径及CE的长.16.如图,在△ABC中BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.(1)求证:AD=CD;(2)求证:DE为⊙O的切线.17.如图,水平放置的圆柱形排水管的截面半径为12cm,截面中有水部分弓形的高为6cm.(1)求截面中弦AB的长;(2)求截面中有水部分弓形的面积.18.如图,直角三角形ABC中,∠C=90°,点E为AB上一点,以AE为直径的⊙O上一点D在BC上,且AD平分∠BAC.(1)证明:BC是⊙O的切线;(2)若BD=4,BE=2,求AB的长.参考答案1.A2.A3.B4.C5.B6.B7.D8.D9.510.142°11.112.45°13.187.5π14.(1)证明:如图,连接AE.∵AB是圆O的直径∴∠AEB=90°即AE⊥BC.又∵AB=AC∴AE是边BC上的中线∴BE=CE;(2)解:∵AB=6∴OA=3.又∵OA=OD,∠BAC=54°∴∠AOD=180°−2×54°=72°∴AD⏜的长为:72×π×3180=6π5.15.(1)证明:∵AB是⊙O的直径∴∠ACB=90°∴∠A=90°-∠ABC.∵CE⊥AB∴∠ECB=90°-∠ABC∴∠ECB=∠A.又∵C是BD⌢的中点∴CD⌢=BC⌢∴∠DBC=∠A∴∠ECB=∠DBC∴CF= BF ;(2)解:∵BC⌢=CD ⌢ ∴BC=CD=6.在Rt △ABC 中,AB= √BC 2+AC 2=√62+82=10 ∴⊙O 的半径为5;∵S △ABC = 12AB ×CE= 12BC ×AC∴CE= BC×AC AB =6×810=245.16.(1)证明:∵AB 为直径∴∠ADB =90° ∵BA =BC ∴AD =CD ;(2)证明:连接OD ,如图∵AD =CD ,AO =OB∴OD 为△BAC 的中位线∴OD ∥BC ∴DE ⊥BC ∴OD ⊥DE ∴DE 为⊙O 的切线.17.(1)解:如图:作OC ⊥AB 交⊙O 于D ,连结OB∴OB=12cm.∵O是圆心OC⊥AB∴AB=2BC∵CD=6cm∴OC=OD−CD=12−6=6(cm)∴BC=√OB2−OC2=√122−62=6√3(cm)∴AB=2BC=12√3cm.即弦AB长12√3cm.(2)解:连结OA∵OC⊥AB,OB=2OC∴∠BOC=60°∴∠AOB=120°∴S弓形=120360π×122−12×12√3×6=48π−36√3(cm2).即截面中有水部分弓形的面积为(48π−36√3)cm2.18.(1)证明:连接ODAD平分∠BAC ∴∠1=∠2∵OA=OD ∴∠2=∠3 ∴∠1=∠3∴AC//OD∵∠C=90°∴∠ODE=90°,即OD⊥BC ∵OD是半径∴BC是⊙O的切线(2)解:设OD=OE=r在Rt△ODB中,BD=4,BE=2,故OB=r+2由勾股定理,得:r2+42=(r+2)2解之,得:r=3故OD=OA=OE=3,AB=6+2=8.。
人教版九年级上册《第二十四章圆》综合检测试卷(含答案).docx

第二十四章综合检测试卷(满分:100分时间:90分钟)一、选择题(每小题2分,共20分)1.下列命题中正确的有(A )(1)平分弦的直径垂直于弦;(2)经过半径一端且与这条半径垂直的直线是圆的切线;(3)在同圆或等圆中,圆周角等于圆心角的一半;(4)平面内三点确定一个圆;(5)三角形的外心到各个顶点的距离相等.A. 1个B. 2个C. 3个D. 4个2. [2016-江苏南京甲考】C知止7X以形旳垃氏为2,则匕旳内切圆旳半彳仝为(B )A. 1B.书C. 2D. 2羽3. [2017-江苏宿迁中考】若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是(D )A. 2 cmB. 3 cmD. 6 cm4. [2016-福建三明中考】如图,AB是的弦,半径OC丄A3于点ZZ若OO的半径B. 3D・5的延长线于点& 若ZE=50°,则ZCDB等于(A )A.20°D. 40°6.如图,直线BA、PB是OO的两条切线,A、3分别为切点,ZAPB=120°, OP=10cm,则弦A3的长为(D )B.IO\/3 cmC. 4 cm为5, AB=S,则CQ的长是(A )A.C.5. 如图, 点C、D为OO上的点,过点C作(DO的切线交ABB. 25°C. 30°笫4题第5题cmC. 5 cmD. 5羽 cm7. 【辽宁营口中考】将弧长为2^cm,圆心角为120。
的扇形围成一个圆锥的侧面,则这个圆锥的髙及侧面积分别是(B)A.迈 cm,3^ cm2C. 2y[2 cm,6^ cm 2 B. 2y[2 cm,3^ cm 2D. cm,6n- cm 28.小明想用直角尺检查某些工件是否恰好是半圆形,下列几个图形是半圆形的是9.如图,OC 过原点O,且与两坐标轴分别交于点A. C. 610•【贵州遵义中考】将正方形ABCD 绕点A 按逆时针方向旋转30。
第二十四章 圆检测参考答案10.doc

第二十四章圆检测参考答案1. B 解析:选项A中有4条对称轴,选项B中有6条对称轴,选项C 中有3条对称轴,选项D 中有2条对称轴,故选B.2. D 解析:依据垂径定理可得,选项A、B> C都正确,选项D是错误的.3. A4. D 解析:= = ・5. D 解析:因为5 —2V3,5V5 + 2»所以两圆相交.6. D 解析:如图所示,由题意得4D = Z乩= 由勾股定理得ric=v^« ffiacf =4^* 由三角形面第6题答图积公式,得S =吉』E・恥=令3尺7. A 解析:由勾股定理知,43 = 5 cm,又1+4=5・所以两圆外切.&B 解析:本题考查了圆的周长公式C = 2»fl. V 00的半径0A = 6, ZA0B = 90°, 弧4B的长为-C = 3^1.240TIX5 「、9. B 解析:分针40分钟旋转240°,则分针针端转过的弧长是------ =—(cm).ISO 310. B 解析:设点0到直线d的距离为d,\- PS切。
于点E ,:.卩护=PQTQ2•••直线外一点与直线上的点的所有连线中,垂线段最短,••• PEnBO2 = ¥_22 = 5.11.30 解析:由垂径定理= yl, ZffES = 9CT. = Z :. QE = 1,•••= 6旷,又00 = 0C, /. ZffCff = 3(T.12.25013.3 解析:在弦力B的两侧分别有一个和两个点符合要求.14.相交解析:GX4由图示位置沿直线4B向右平移3cmJ&,此时圆心距为Zcm,2-K2<2 + L 所以此时两圆相交.15.40°解析:I Z4OC = 1GL , Z5OC = 80°, AZD =4(T .16.10 100 n 解析:C3 = 2rt«Cg =4n«C t = 6TI ・■—* C10a= 200ir ,C a +C2 + C s +■•• ■+C aoo=10 IOO TI.17. 16 解析:连接0G OB,贝ijOCJ. AB. •:= 10= 6cm. ?. BC = 8cm>AB = 16 cm.18.9vl-3x H析.连临0儿WaPA , PB切OO于4, B两点,所以ZOXF= ZOBP = 90-,所以ZAOB = 120", AP = 所以%散倔=珈所以阴影部分的面积为9y^ —3x .19.解:过点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四章 圆检测参考答案
1.B 解析:选项A 中有4条对称轴,选项B 中有6条对称轴, 选项C 中有3条对称轴,选项D 中有2条对称轴,故选B.
2.D 解析:依据垂径定理可得,选项A 、B 、C 都正确,选项D 是错误的.
3.A
4.D 解析:
5.D 解析:因为所以两圆相交.
6.D 解析:如图所示,由题意得由勾股定理得
,由三角形面
积公式,得
.
7.A 解析:由勾股定理知,
,又
所以两圆外切.
8.B 解析:本题考查了圆的周长公式 .∵ O ⊙的半径6OA =,90AOB ∠=°,
∴ 弧AB 的长为. 9.B 解析:分针
分钟旋转
º,则分针针端转过的弧长是
. 10.B 解析:设点到直线的距离为
∵
切⊙于点,∴
∵ 直
线外一点与直线上的点的所有连线中,垂线段最短,∴
11.30 解析:由垂径定理得∴
,
∴ ∠
∴ ∠
.
12.250
13.3 解析:在弦AB 的两侧分别有一个和两个点符合要求. 14.相交 解析:A ⊙由图示位置沿直线AB 向右平移,此时圆心距为
,
所以此时两圆相交.
15.40° 解析:∵∠ ,∴ ∠,∴∠ . 16.10 100
解析:
,
10 100.
17.16 解析:连接,则
.∵
∴
∴ 18. PA ,PB 切⊙于A ,B 两点 ,所以∠
=
∠
,所以∠
所以
所以阴
影部分的面积为.
19.解:过点作,垂足为. ∵
,∴
.
E
A
B
C D
• O
第6题答图
∵ ∠
,∴ ,
∴ =215. 20.解:如图,∵ ,∴ △是等边三角形,
∴∠=60°, ∴
,.
∴ 弦所对的弧所对的圆周角的度数为30°或150°. 21.解:∵ ∠=,∴=. 又∵为直径,∴ ∠=,∴∠=. ∵ ,∴ ,∴//,
∴ 四边形是等腰梯形,∴ .
22.解:作,则即为边上的高. 设圆心到的距离为,则依据垂径定理得.
当圆心在三角形内部时,边上的高为
;
当圆心在三角形外部时,边上的高为 .
23.解:直线BD 与相切.证明如下: 如图,连接OD 、ED .
OA OD =Q ,∴ A ADO ∠=∠.
90C ∠=o Q ,∴ 90CBD CDB ∠+∠=o .
又CBD A ∠=∠Q ,∴ 90ADO CDB ∠+∠=o . ∴ 90ODB ∠=o .∴ 直线BD 与相切.
24.解: (1) CD 与⊙O 的位置关系是相切.理由如下: 作直径CE ,连接AE . ∵ 是直径,∴ ∠
90°,∴ ∠∠
°.
∵
,∴ ∠
∠
.
∵ AB ∥CD ,∴ ∠ACD =∠CAB . ∵ ∠∠,∴ ∠
∠,
∴∠
+∠ACD = 90°,即∠DCO = 90°,∴
,∴ CD 与⊙O 相切.
(2)∵
∥
,
,∴
D
C
O
A
E
第23题答图
第22题答图
C
B
A O
D D
O C B
A
B
O
A
D
第20题答图
又∠°,∴ ∠∠°.
∵
,∴ △
是等边三角形,∴ ∠
°,
∴ 在Rt△DCO 中, ,∴ .
25.(1)证明:连接O C . ∵ CD
AC =,120A C D ︒
∠=,∴ 30A D ︒∠=∠=. ∵ OC
OA =, ∴ 230A ︒∠=∠=. ∴ 290O C D A C D ︒
∠=∠-∠=. ∴ C D 是O ⊙的切线.
(2)解: ∵
, ∴
. ∴
.
在Rt △OCD 中, tan 6023CD OC =⋅︒=.
∴Rt 11
2232322
OCD S OC CD ∆=
⨯=⨯⨯=. ∴ 图中阴影部分的面积为-322
3
π.
26.证明:(1)由同弧所对的圆周角相等,知∠∠
.
∵,,∴ ∠∠∠∠,∴ ∠∠
, ∴ ∠∠
.又∵,
, ∴ △
≌△
. ∴
.
(2) ∵ ,∴ .
∵
,∴ ∠
, ∴ ∠
∠
.
由勾股定理,得 又∵, ∴
,∴
, ∴
.。
