§96第一型曲线积分的计算.ppt
第一型曲线积分

L xyds
2 0
a cos t b sin t ( a sin t )2 (b cos t )2 dt
ab02 sin t cos t a 2 sin 2 t b 2 cos2 t dt
ab 02 (a 2 b 2 ) sin 2 t b 2 d (sin 2 t ) 2
( x ) 0.
L ( x y )ds
2 ( x 0 ) 1 0 dx 0
2
0 x dx
2
2.
(2) L: x ( y ) 2, 0 y 3.
( x ) 0.
L ( x y )ds
2 ( 2 y ) 1 0 dy 0
x2 y2
x2 y2
ds. 其中曲线 x 2 y 2 a 2 , 直
线 x 0, y x 在第一象限中所围的图 形边界。
解
Le
ds ds AB e
x2 y2
oA e
x2 y2
ds oB e
x2 y2
ds
oA : x 0, 0 y a .
I xyz ds
0 a 2 cos sin k ( a sin )2 (a cos )2 k 2 d
2 2 2 a k a k 2
2Байду номын сангаас
0 sin 2 d
2
1 ka 2 a 2 k 2 . 2
例5
计算
Le
0
ab(a 2 ab b 2 ) . 3(a b )
y
例2
计算
L ( x y ) ds.
第一型曲线积分

Li
L
k
也存在,且 f ( x, y)ds
f ( x, y)ds
L
i 1 Li
3 保号性若L f ( x, y)ds与L g( x, y)ds都存在,
且在 L上 f ( x, y) g( x, y),
则L f ( x, y)ds L g( x, y)ds
4 积分绝对值 若L f ( x, y)ds存在,则 L f ( x, y)ds也存在,且| L f ( x, y)ds | L f ( x, y)ds
2(t) 2(t) 2(t)dt;
例1. 计算L yds. 其中 L 为y2=2x自点(0, 0)到点(2, 2)
的一段弧. 解1:
y 2
y2=2x
ds
1
dy dxyds 2 2x 1 1 dx
L
0
2x
0
2x
2 2x+1dx 1 (5 5 1)
0
3
解2: L : x y2 , 0≤y≤2 2
f ( (t ), (t ))关于t 连续, 则
M>0, 使得 f ( (t ), (t )) M .
又 2(t) 2(t)在[, ]上一致连续
。
即 0, 0,使当t<时有
2( ) 2( ) 2( ) 2( ) ,
从而
n
M ti M (b a) 0. i 1
由定积分的定义
5 平均值公式 若L f ( x, y) d存s在,L的弧长为s,
则存在常数c,使得L f ( x, y)ds cs。
其中inf f ( x, y) c sup f ( x, y)
L
L
二 第一型曲线积分的计算
定理 20.1
第一型曲线积分的定义

第一型曲线积分的定义第一型曲线积分,是微积分中的一种重要概念与计算方法,它涉及曲线和向量场之间的积分。
本文将介绍第一型曲线积分的定义、性质和计算方法。
一、第一型曲线积分的定义第一型曲线积分,也称为曲线的线积分,是指在曲线上某个有向长度元素$\mathrm{d}s$上的函数值与该长度元素的乘积$d\boldsymbol{s}$在整个曲线上的积分。
设$C$是曲线,其参数方程为$\boldsymbol{r}(t)=(x(t), y(t), z(t)), t\in[a,b]$,则$C$的长度由公式:$$ L(C)=\int_{C}\mathrm{d}s=\int_{a}^{b}\left[\ left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\r ight)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\f rac{1}{2}} \mathrm{d}t $$计算曲线$C$上的一个标量函数$f(x,y,z)$在曲线上的第一型曲线积分,即为:$$ \int_{C} f(x, y, z) \mathrm{d}s=\int_{a}^{b}f\left(\boldsymbol{r}(t)\right)\left[\left(x^{\prim e}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}\right]^{\frac{1}{2}}\mathrm{d}t $$若积分路径可以看成向量值函数$\boldsymbol{r}(t)$的积分,第一型曲线积分就可以写作:$$ \int_{\boldsymbol{r}}\boldsymbol{F}(\boldsymbol{r}) \cdot \mathrm{d}\boldsymbol{r}=\int_{a}^{b}\boldsymbol{F}\left(\boldsymbol{r}(t)\right) \cdot \boldsymbol{r}^{\prime}(t) \mathrm{d}t=\int_{a}^{b} \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{s} $$其中$\boldsymbol{F}(\boldsymbol{r})$是向量场,$\mathrm{d}\boldsymbol{r}$表示一个有向长度元素,$\cdot$表示向量内积运算,$\mathrm{d}\boldsymbol{s}=\boldsymbol{r}^{\prime}(t ) \mathrm{d} t$表示线元素。
高等数学课件 §9.6第一型曲线积分计算

R
xds
L
R
xR
R2x2
dx 0
R2 x2
(法二 ):L: xy R Rcsion s ,0
ds R2sin2R2co2sd
xd R s2co d sR 2 sin 0
L
0
0
例 2 L (x y )d,L s :连接 O (0 ,0 )A 三 ,( 1 ,0 )B ,( 点 0 ,1 ) 的.
§9.6 第一型曲线积分的计算
一、第一型曲线积分的概念 曲线形物体的质量
设 曲 线 形 物 体 在 x平 o 面 上 占 y 有 可 求 长 曲 线 L ,
其 线 密 度 为 连 续 函 数 f ( x , y ) , 求 该 物 体 的 质 量 m 。
y
M1 M2 A
M i1MiBiblioteka (i,i) LM n1
解
OA
:
y
0
0 x
1
ds dx
y
B
y 1 x
AB
:
0
x
1
ds
2 dx
x 0
o
OB
:
0
y 1
ds dy
Ax
1
1
1
L(xy)ds0xdx0 2dx 0ydy
1x2 1 21y2 1 1 2
20
20
例 3 计L算 (x2y2z2)d,其 s L:中 x2 xy 2 z z2 19 2.
B
o
x
( 1 ) 分 割 在 L 上 任 取 点 列 M 1,M 2, M n 1, 把 L分n小 为 段
si(i 1 ,2 , ,n ), 同 时 也 以 si 表 示 第 i小 段 弧 长 。 ( 2 ) 近 似
§9.6第一型曲线积分的计算

(4)取极限 令 d = max {∆si } ,则 m = lim ∑ f (ξ i , ηi )∆si 。
1≤ i ≤ n
n
d →0 i =1
2.第一型曲线积分的定义
面内的一条光滑(或分段光滑)曲线弧, 设 L 为 xoy 面内的一条光滑(或分段光滑)曲线弧, 有界。 f ( x , y ) 在 L 上有界。任取点列 M 1 , M 2 ,L M n−1 ,把 L 分 为 n 小 段 ∆si ( i = 1, 2, L, n) , 同时也以 ∆si 表示第 i 小 段的弧长。 段的弧长。任取 (ξ i , ηi ) ∈ ∆si ,作和式 ∑ f (ξ i , ηi )∆si ,
L
+∫
.
4. 当f ( x , y ) ≡ 1时,
∫L ds 等于L的长度.
5. 设在 L 上 f ( x , y ) ≤ g( x , y ), 则
∫L f ( x , y )ds ≤ ∫L g( x , y )ds.
特殊地
∫L f ( x , y )ds ≤ ∫L f ( x , y ) ds.
连续的一阶导数,且 x ′ 2 ( t ) + y′ 2 ( t ) ≠ 0 ,则 连续的一阶导数,
ds = x ′ 2 ( t ) + y′ 2 ( t )dt ,
∫L
f ( x , y )ds = ∫ f [ x ( t ), y( t )] x ′ 2 ( t ) + y′ 2 ( t )dt 。
km µ o y dV
3 ( x2 + y2 + z2 ) 2
km µ o x dV
3 ( x2 + y2 + z2 )2
第一型曲线积分的计算方法

第一型曲线积分的计算方法
1. 嘿,你知道直接法吗?就像我们要数清楚一堆糖果有多少颗一样直接!比如计算曲线 y=x^2 从 0 到 1 那一段的第一型曲线积分,咱就直接把函数的值代进去算,简单粗暴有木有!
2. 还有参数法呢!这就像给曲线找到一个特别的密码来解题呀!比如说一个圆的曲线,用参数表示出来再去计算积分,超有意思的咧!
3. 利用对称性来计算也很棒哦!这就好像发现了一个隐藏的小技巧。
像计算关于 x 轴对称的曲线的积分,有些部分咱直接就可以简化啦,多方便呀!
4. 想想看,换元法也不错呀!就如同给问题变个魔法一样。
比如把很难的式子通过换元变得简单易懂,然后轻松算出积分,多牛呀!
5. 哇塞,格林公式也能助力第一型曲线积分的计算哦!这就像是给我们开了一扇快捷之门呀。
特别是在一些复杂图形中,简直是救星呀!
6. 别忘了分块计算呀!这就好比把一个大难题拆分成好多小部分来解决。
遇到复杂的曲线,咱就一块块来,总能搞定的嘛!
总之,第一型曲线积分的计算方法多种多样,每一种都有它独特的魅力和用处,就看你怎么去运用啦!。
第一类曲线积分

f ( x , y )ds lim f [ ( t ), ( t )]si
0
n i 1 i 1
n
lim f [ ( t ), ( t )] [ ( t )]2 [ ( t )]2 t i
f [ ( t ), ( t )] [ ( t )]2 [ ( t )]2 dt
例 2: 计算
L
R 2 x 2 y 2 ds,其中 L 是上半圆弧
x 2 y 2 Rx, y 0 。
解1 :参数方程
R R x 2 2 cos L: , 0 R y sin o 2
解:设 M i ( i ,i ) , 则
z
h( x , y )
Ai h( i ,i )si
则曲面的面积为:
A h( i ,i )si
i 1 n
o x
Ai 1 MBiblioteka Ai iny令 max{si }, 并令 0,则 A lim h( i ,i )si
: x ( t ), y ( t ), z ( t ). ( t )
其中 ( t ), ( t ), ( t ) 在 [ , ] 上具有连续的一阶 导数 , 则
f ( x , y, z )ds
f [ ( t ), ( t ), ( t )] 2 ( t ) 2 ( t ) 2 ( t )dt
L2
机动 目录 上页 下页 返回 结束
4. (比较性质) :若在曲线 L 上, f ( P ) g( P ) ,则
L f ( P )ds L g( P )ds
特别地,若存在一点 P0 L,使得 f ( P0 ) g( P0 ) ,则
高数9-1(第一型曲线积分)

(3) L : r r( ),
L f ( x, y)ds
f [r ) cos, r( )sin ]
r2 ( ) r2 ( )d
推广 : x (t), y (t), z (t) ( t )
f ( x, y, z)ds
f [(t), (t),(t)] 2(t) 2(t) 2(t)dt ( )
2 f ( x, y)ds,当f ( x, y) 是L上关于x (或y)的偶函数 L1
L1是曲线L落在y (或x)轴一侧的部分.
运用对称性简化对弧长的曲线积分 计算时, 应同时考虑被积函数 f ( x, y)与积 分曲线L的对称性.
6/19
例 计算 ( x y3 )ds. 其中L是圆周 x2 y2 R2. L
(对路径具有可加性)
4/19
5.性质
(1) [ f ( x, y, z) g( x, y, z)]ds
f ( x, y, z)ds g( x, y, z)ds
(2) kf ( x, y, z)ds k f ( x, y, z)ds (k为常数)
(3) 与积分路径的方向无关, 即
(
⌒ f
f ( x, y)ds
b
f [ x, ( x)]
1 2( x)dx (a b)
L
a
ds 1 2( x)dx
(2) L : x ( y), c y d
f ( x, y)ds
d
f [( y), y]
1 2( y)dy (c d )
L
c
ds 1 2( y)dy
10/19
解 对称性,得
y x2 y2 R2
( x y3 )ds xds y3ds 0
L
《曲线积分》课件

换元法
总结词
换元法是通过引入新的变量替换原变量,将曲线积分转化为更容易计算的定积分的方法。
详细描述
换元法的基本思想是通过引入新的变量替换原变量,将曲线积分转化为定积分。通过选择合适的换元函数,可以 将曲线积分的积分路径转化为直线或简单的几何形状,从而简化计算过程。这种方法在处理复杂的曲线积分时非 常有效。
经济学中的应用
在经济学中,曲线积分可以用于研究商品价格变动对需求量 的影响,以及投资回报率等问题。
曲线积分的分类
第一型曲线积分
第一型曲线积分是计算函数在曲线上 的定积分,用于计算曲线下的面积和 长度等。
第二型曲线积分
第二型曲线积分是计算函数关于某个 变量的变差,用于计算速度和加速度 等物理量。
02
曲线积分背景
曲线积分是微积分学中的重要概 念,它与定积分、重积分等概念 有密切联系,是解决许多实际问 题的重要工具。
曲线积分的应用
1 2
3
物理学中的应用
曲线积分在物理学中有广泛的应用,如计算曲线运动的轨迹 长度、速度和加速度等。
工程学中的应用
在工程学中,曲线积分被广泛应用于计算各种曲线形状的物 体在运动过程中的物理量,如管道流速、机械零件的振动等 。
电场线的积分与电荷量
电场线的积分
电场线是描述电场分布的几何图形,电 场线的积分可以用来计算电场中的电荷 量。通过曲线积分的方法,可以计算出 电场线上各点的电场强度,从而得到整 个电场的电荷量分布。
VS
电荷量
电荷量是描述电场中电荷数量的物理量, 它表示电场中电荷的多少。在物理学中, 电荷量可以通过电场线的积分来计算,并 用于研究电场的性质和行为。
06
曲线积分的综合应用
理学第一型曲线积分的计算
M ( x, y,z) ,取包含点 M 的一体积微元dV ,
则质量微元为 dm f ( x, y,z)dV ,点M 到 x 轴 的距离
为 y2 z2 ,于是点M 处 的质量微元关于 x 轴 的转
动惯量为 dJ x ( y2 z2 ) f ( x, y,z)dV ,从而
J x ( y2 z2 ) f ( x, y,z)dV ,
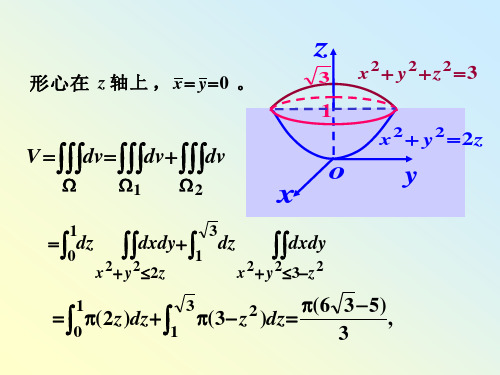
形心在 z 轴上 ,x y0 。
z
3 x2 y2z23
V dvdvdv
1 2
1
o
x
x2 y2 2z
y
1
3
0dz dxdy1 dz dxdy
x2 y22z
x2 y23z2
1
0(2z)dz 1
3(3 z2 )dz (6
3 5), 3
zdv zdv zdv
1
2
1
3
0 zdz dxdy1 zdz dxdy
同理可得 J y (z2 x2 ) f ( x, y,z)dV ,
J z ( x2 y2 ) f ( x, y,z)dV 。
若 是平面区域 D,面密度函数为 f ( x, y) ,则平面 薄片对 x 轴 、 y 轴 的转动惯量为
J x y2 f ( x, y)d , J y x2 f ( x, y)d 。
x2 y22z
x2 y23z2
1
0 z(2z)dz1
3 z(3 z2 )dz 5 3
5
z 1 V
zdv
(6
3 3 5)
5(6
3 5) 83
,
3
∴形心的坐标为(0,0, 5(6 3 5) )。
83
二.物体的转动惯量
设在 R3 上 有 n 个质量为 m1, m2 , , mn 的质点组, 它们的坐标分别为 ( xi , yi , zi ) (i 1, 2, , n) ,这个 质点组绕着某一条直线 l 旋转,设这 n 个质点到直线 l 的距离分别是 d1, d2, , dn ,由力学可知,质点组 对直线l 的转动惯量为
八.第一类曲线积分计算

Mk Mskk1
称为被积函数, 称为积分弧段 .
曲线形构件的质量 M (x, y, z) ds
4
如果 L 是 xOy 面上的曲线弧, 则定义对弧长的曲线积
分为
n
L
f
(x,
y) ds
lim
0 k 1
f
(k
,k
)sk
被积函数 弧微分
n
L
f
( x,
y)d s
注意 φ2(t) ψ2(t )连续
n ຫໍສະໝຸດ limλ0 k1f [φ(τk ),ψ (τk )]
因此
13
注 1º sk 0, tk 0, 因此积分限必须满足下限小于上限:
α β ! 2º 注意到
ds (d x)2 (d y)2
φ2(t ) ψ2(t )d t
[α f ( x, y) β g( x, y)]ds α f ( x, y)ds β g( x, y)ds
L
L
L
2º可加性: L由L1和L2组成
f (x, y)ds f (x, y)ds f (x, y)ds
L
L1
L2
3º 保序性:
特别的有 | f ( x, y)ds | f ( x, y)ds
y
ds dy dx
o xx
因此上述计算公式相当于“换元法”.
14
推广 1º如果曲线 L 的方程为
y ψ( x) (a x b ),
则
b
f ( x,ψ( x)) a
1 ψ2(x)dx
2º 如果L为极坐标形式
( ) ( ),
考研数学-第一型曲线曲面积分

3 2 C在xoy面上投影D xy {( x , y ) x y 1} 4
2
2x 2 y z z z 1 1 x y y 2z y 2z
2
2
2
2
4 y 2 z 2 4 yz y 2z
2 2
8 16 8 5 5 R R R 5 15 5 3
例14
练习十二/五
设有一个由曲线y ln x, y 0, x e所围成的 均匀薄片, 其面密度为 1, 若此薄片关于直线 x t的转动惯量为I (t ), 求使I (t )取得最小值的t. y 2 解:I (t ) ( x t ) d
dx 2 2 解 : ds 1 ( ) dy dy 2 dy 4 y
( x y 1)ds
L
2
2
( 4 y y 1)
2
2 4 y
2
dy
8 2
例2 练习十三/二(2)
x2 y 2 设L为椭圆 1,已知其周长为a, 2 3 则 (3x 2 5 xy 2 y 2 )ds _______ .
λ 0
i 1
n
2. 计算:
: z z( x , y ) , ( x , y ) D x y , 则
f ( x , y, z )dS
Dxy
f [ x, y, z( x , y )]
1 zx zy dxdy;
2 2
方法:一投、二代、三换.
3. 对称性
对面积的曲面积分 f ( x , y , z ) d S,
第十节 第一型曲线曲面积分 积分应用
1 第一型曲线积分解析

y
R cos R sin
( )
O
L Rx
R2 sin 2 (R sin )2 (R cos )2d
R3 sin 2
d
2
R3
2
sin 2
4
0
R3( sin cos )
例8. 设均匀螺旋形弹簧L的方程为
解
I y L
x2 y 1 x2
ds
2 1
x2 ln x 1 x2
1 1 x2 dx
2
1
x
ln
xdx
ln
4
3 4
.
例7. 计算半径为R ,中心角为
的圆弧 L 对于它的对
称轴的转动惯量 I (设线密度 = 1).
解: 建立坐标系如图, 则
y
I y2 ds L
L
:
x
2π
cos t d t 0
0
a
a2 k2
2π
sin t d t
0
0
k
a2 k2
2π
tdt
2π2k
0
a2 k2
故质心坐标为 ( 0, 0, k π )
内容小结
1. 定义 f (x, y) ds L
f (x, y, z)ds
2. 性质
(1) f (x, y, z) g(x, y, z) ds g(x, y, z)ds (, 为常数)
2 (
i)
2 (
i
)ti
.
§6.4第一型曲线积分的计算

故 ( x2 y2 z2 )ds 9 ds 2 9 2dt 18 .
L
L2
02
例 4.设 L 为椭圆 x2 y2 1 ,其周长为 a, 43
求 (3x 2 4 y 2 2xy)ds 的值. L
解:∵ x2 y2 1 ,∴ 3 x2 4 y2 12 , 43
∴ (3x 2 4 y 2 2xy)ds (代入L的方程) L
L
x2 y2 z2 9 与平面x z1 的交线. 2
解: L
:x2 y2Biblioteka x z1z29 2
(x 1)2 2
2 z1 x.
y2 4
1,
其参数方程为:
x 1 2cost, 2
y 2sint,
z
1 2
2 cos t .
(0t 2 ) ,
ds ( 2 sint)2 (2cos t)2 ( 2 sint)2 dt 2dt,
ds 1 y2 (x)dx R dx
R2 x2
R xR
xds
dx 0
L
R R2 x2
(法二)
:
L
:
x
y
R R
cos s in
,0
ds R 2 sin 2 R 2 cos2 d
xds R 2 cosd R 2 sin 0
L
0
0
例 2 L (x y)ds, L : 连接三点O(0,0), A(1,0), B(0,1)的折线.
而平面 x y z0 通过原点,
∴ L 为平面 x y z 0 上半径为 R 的圆,其周长为 2R .
∵曲线 L 的 方程对 x,y,z 具有轮换对称性,
∴ zds xds yds 1 ( x y z)ds 0 ,
第一型曲线积分计算公式

第一型曲线积分计算公式:第一型曲线积分也称为路径积分或弧长积分,用于计算向量场沿着曲线的积分。
其计算公式如下:∫C F · dr其中,C 是曲线,F 是向量场,dr 是曲线上的微元弧长向量。
以下是两个实例:实例1:考虑曲线C,由参数方程r(t) = (cos(t), sin(t)),其中0 ≤ t ≤ π/2。
向量场F(x, y) = (x, y)。
我们可以首先计算曲线的切向量r'(t) = (-sin(t), cos(t))。
然后计算F · dr:F · dr= (x, y) · (dx, dy) = (x, y) · (dx/dt, dy/dt) dt [使用链式法则将dr 转换为dt] = (cos(t), sin(t)) · (-sin(t), cos(t)) dt = -sin(t)cos(t) + sin(t)cos(t) dt = 0由于F · dr = 0,因此该曲线上的第一型曲线积分为0。
实例2:考虑曲线C,由参数方程r(t) = (t, t^2),其中0 ≤ t ≤ 1。
向量场F(x, y) = (y, x)。
首先计算曲线的切向量r'(t) = (1, 2t)。
然后计算F · dr:F · dr = (y, x) · (dx, dy) = (y, x) · (dx/dt, dy/dt) dt = (t^2, t) · (1, 2t) dt = t^2 + 2t^2 dt = 3t^2 dt要计算第一型曲线积分,我们需要将积分限从参数t 转换为实际的曲线长度。
曲线长度由下式给出:s = ∫[a, b] ||r'(t)|| dt计算曲线长度:s = ∫[0, 1] ||r'(t)|| dt = ∫[0, 1] ||(1, 2t)|| dt = ∫[0, 1] sqrt(1^2 + (2t)^2) dt = ∫[0, 1] sqrt(1 + 4t^2) dt = ∫[0, 1] sqrt(4t^2 + 1) dt现在我们可以计算第一型曲线积分:∫C F · dr = ∫[0, 1] 3t^2 dt = 3∫[0, 1] t^2 dt = 3[t^3/3] [0, 1] = 1因此,该曲线上的第一型曲线积分为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长. 任取 (i ,i ) si ,作和式 f ( i ,i )si ,设
i 1
d max {si } ,如果当d 0时 ,和式的极限总存在,
1in
则称此极限为 f ( x, y) 在曲线弧 L 上的第一型曲线积分
或对弧长的曲线积分,记作 f ( x, y)ds ,即 L
被积函数
弧长元素
n
n
m f (i ,i )si .
i 1
y
A o
B
L Mn1
(i ,i ) Mi
M2
M1
M i 1
x
n
取极限
令 d max{si },
1in
m lim f ( i ,i )si .
d 0i1
2.第一型曲线积分的定义
设 L 为oxy 面上的一条光滑(或分段光滑)曲线弧,
f ( x, y) 在 L 上有界.任取点列 M1 , M 2 , , M n1 ,把 L 分为 n 小 段 li (i 1, 2, , n) ,并以si 表示 li 的弧
L
f (x, y)
ds lim f (i ,i )si
d 0i1
注:
积分弧
(1)当 f ( x, y) 在光滑曲线 L 上连续时, f ( x, y)ds 存在. L
(2)将上述定义推广,可得空间曲线 L 上的第一型曲线
n
积分:
L
f
( x,
y, z)ds
lim
d 0i1
f
( i
,i
,
i
)si
ห้องสมุดไป่ตู้
.
第一型曲线积分的性质
性质1 (线性性质) 设 f , g 可积, 又, 为常数, 则有
L[ f ( x, y) g( x, y)]ds L f ( x, y)ds L g( x, y)ds .
性质2 (可加性) 设 L1 与 L2 首尾相接成 L, 则有
L f ( x, y)ds L1 f ( x, y)ds L2 f ( x, y)ds ,
f ( x, y, z)ds f [x(t), y(t), z(t)] x2 (t) y2 (t) z2 (t)dt
L
注意:
(1)第一型曲线积分与曲线的方向无关,化为关于 参数的定积分计算时,上限必须大于下限.
(2)对 f ( x, y)ds 来说, f ( x, y) 是定义在 L 上的, L 被积函数中的 x,y 应满足 L 的方程,故可利 用 L 的方程化简被积函数.
1
y2 ( x)dx.
若 L由 方 程 x x( y) (c y d ) 给 出, 则 取 y 为 参 数,
ds 1 x2 ( y)dy,
d
L f ( x, y)ds c
f [x( y), y]
1 x2 ( y)dy.
3.若 L由方程 ( ) ( ) 给出,则取 为参数,
9-5-1第一类曲线积分
引例 1.曲线形物体的质量
设曲线形物体在 oxy 面上是一段曲线弧 L, 它的端点为 A、B,其线密度为连续函数 f (x, y) , 求该物体的质量 m.
分割 M1 ,M 2 , ,M n1 li ,
近似 ( i ,i )li ,
mi f ( i ,i )si .
求和
y x, ds 1 4x2 dx,
0 x 1
故 L yds OA AB B⌒O
1
0 dx
1
ydy
1
x
1 4x 2 dx
0
0
0
0 2 1 (5 5 1) 1 (5 5 7).
3 12
12
y
B
y x2 x1
o y0 A x
例2. 计算 xe x 2 y 2 ds, 其中L 是从 A( 0, 1 ) 沿圆周
ds 2 ( ) 2 ( )d ,
f ( x, y)ds f [( )cos, ( )sin] 2 ( ) 2 ( )d
L
4. 若空间光滑曲线 L的参数方程为
x x(t) , y y(t) , z z(t) ( t ) ,则
ds x2 (t) y2 (t) z2 (t)dt ,
ds x2 (t) y2 (t)dt,
L f (x, y)ds
f [x(t), y(t)]
x2(t) y2 (t)dt.
2. 若 L由 方程 y y( x) (a x b) 给 出, 则 取 x 为 参数,
ds 1 y2 ( x)dx,
b
L f ( x, y)ds a f [ x, y( x)]
2
A
被积函数 xe x 2 y 2 e 1 y2 ,
o
x
B
xy
y ,
1 y2
ds
1
x
2 y
dy
dy , 1 y2
xe
x2 y2 ds e
1 2
L
2
1 y2
dy
(1
1 y2
2 )e. 2
例 3. 计 算 ( x 2 y 2 z 2 )ds , 其 中 L 为 球 面
L
x 2 y 2 1 到 B( 2 , 2 )处的一段劣弧. 22
解法 1 L : x cost , y sint , t ,
42
y
被积函数 xe x 2 y 2 e cos t,
A
ds ( sint)2 (cost)2 dt dt,
o
x
B
xe
L
x2 y2 ds e
例 1.计算 yds ,其中 L 为抛物线 y x2 ,直线 L x1 及 x 轴所围成的曲边三角形的整个边界.
解:L
OA
AB
⌒
BO
y
B
OA :
y0 ,
y 0, ds dx,
0 x 1
y x2 x1
AB :
x1
,
y
o
y , ds dy,
0 y 1
y0 A x
⌒
BO :
y
x2
,
简记为 L f ( x, y)ds L1 L2 .
性质 3 L ds L的长度.
f ( x, y)在闭曲线L上对弧长的曲线积分记为L f ( x, y)ds.
第一型曲线积分的计算
1.设 f ( x, y) 在曲线 L 上连续,L 的参数方程为 x x(t) ,
y y(t) ( t ) ,其中 x(t) , y(t) 在[ , ]上有 连续的一阶导数,且 x2(t) y2(t) 0,则
2
cos tdt
(1
4
2 )e. 2
解法 2 L 的极坐标方程为 1 , ,
42
被积函数 xe x 2 y 2 e cos ,
y A
ds 2 2 d d ,
o
x
B
xe
x2 y2 ds e
2
cos d (1
2 )e. 2
L
4
解法 3 L : x 1 y2 , 2 y1 , y
