46--质点系的角动量
角动量及其守恒定律

m r2 r1 J0
22
因为 1 2, 1 1 2 E k 1 J 1 1 ( J 1 1 ) 1 2 2 相 E k1 E k 2 等 1 1 2 E k 2 J 2 2 ( J 2 2 ) 2 2 2 即系统的机械能不守恒。
23
人双臂收回过程中,内力做功,
J 2
l/2
r dr
2
1 12
l
3
0
1 12
ml
2
如转轴过端点垂直于棒 l 1 2 J r d r ml 2 0 3
例3 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 , 在盘上取半径为 r ,宽为 d r 的圆环
v M (2 gh )
u l 2
1 2
M
h N
B
l 2 1 12
2
2
把M、N和跷板作为 一个系统, 角动量守恒
mvM l 2 J 2 mu
C l
m l 1 2 1 6 m ( 2 gh )
A l/2
ml
2
解得
mvMl 2 m l
2
2
12 ml
2
2 2 2
质量连续分布刚体的转动惯量
J
m
j
j j
r
2
r dm
2
d m :质量元
例2 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
dr
l 2
r
dr
O´
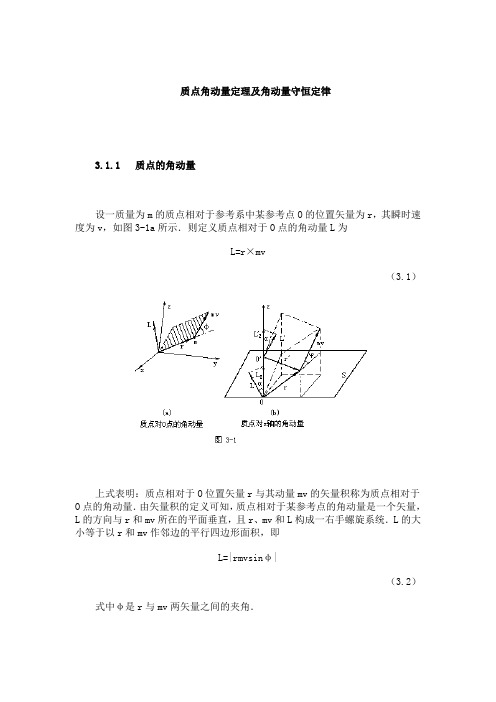
第二章第四节 质点的角动量 角动量定理

dLi = dL dt dt
即质点系对给定点(参考点)的角动量的时间变化率等于作用 在体系上所有外力对该点力矩矢量和.
质点的角动量 角动量定理
概要
1 质点的角动量 2 力对一参考点的力矩 3 质点对参考点的角动量定理和守恒定律
1 角动量
角动量是描述物体的转动特征的物理量.
定义
L
=
r
×
mv
=
r
×
p
L 是质点对参考点的动量矩(角动量)
r 是参考点指向质点的矢量.
大小:L = rp sinθ
方向: r × mv
×
FN
= r × (F1 + F2 + + FN )
=
r
×
∑
Fi
即诸力对参考点的力矩的矢量和等于合力对同 一参考点的力矩.
说明:力矩与参考点的选择有关.
3 质点角动量定理
M
=
dL
dt
质点对任一固定点的角动量的时间变化率 等于合外力对该 点的力矩.
质点系对参考点的角动量定理
∑ ∑ M i外 =
2 力对一参考点的力矩
定义
M
=
r
×
F
r ——参考点指向质点
的位置矢量.
大小: M = rF sinα
z
M
O x
F
α
r
P
y
方向:
r
Hale Waihona Puke × F M
单位:N·m 量纲:ML2T-2
r
F
若质点受N个力同时作用时
M
=
质点角动量定理及角动量守恒定律
在远地点径矢的大小
设卫星在远地点的速度为v2因远、近地点的速度与该处径矢垂直,放由的动量守恒定律可得
r1mv1=r2mv2
由此得
求卫星的运行周期T.由开普勒第二定律可知
由几何关系知,椭圆面积=πab,其中a、b分别为椭圆的半长、短轴,它们可由远、近地点的径矢求出
我们把质点对z轴上任意一点的角动量L在z轴上的投影,叫做质点对于z轴的角动量,用Lx表示.上面已证明,Lz的数值是与参考点无关的.
在国际单位制中,角动量的单位为千克·米2/秒(kg·m2·s-1).
例1如图3-2所示,质量为m的质点以速率v绕半径为r的圆轨道作匀速率运动.求此质点相对于圆心O点的角动量.
解已知氢原子中电子的质量为9.11×10-31kg,它绕原子核运动的平均半径为5.29×10-11m,角速度为4.13×1016s-1,所以它对原子核中心的角动量为
L=mr2ω=(9.11×10-31)×)5.29×10-11)2×(4.13×1016)kg·m2·s-1
=1.05×10-34kg·m2·s-1.
质点在有心力作用下的运动是一种重要的运动形式.有心力运动的上述特征既不能用动量也不能用能量概念来说明,但利用角动量守恒却给出了简洁而中肯的描述.从这里我们也可以看到力学中引入角动量概念的必要性.
例5我国在1971年发射的科学实验卫星在以地心为焦点的椭圆轨道上运动.已知卫星近地点高度为h1=266km,远地点高度为h2=1826km,卫星经过近地点时速率为v1=8.13km·s-1,试求卫星通过远地点时的速度和卫星运行周期.计算中取地球半径R=6.37×103km,空气阻力不计.
角动量

M z = m2 gR − m1 gR = 0
系统的总角动量守恒:
m2 v2 R − m1v1 R = 0
m1=m2,所以v1=v2
同高从静态开始 往上爬
L − L0 = m1v1 R − m2 v2 R > 0 ∴ m1v1 R > m2 v2 R ⇒ v1 > v2
体重轻的先到顶点
dL M z = m2 gR − m1 gR = >0 dt
∫ =∫
∫
L 2 L − 2
L
0
L
x dm
mL x λ dx = 3
2
2
A L/2
C
0
IC =
x 2 λ dx = mL 2 / 12
例、求质量为m、半径为R的均匀圆环的转 动惯量。轴与圆环平面垂直并通过圆心。
O
R dm
解: I = R2dm = R2 dm = mR2
∫
∫
例:求质量为m、半径为R均匀圆盘的转动惯量。轴 与盘平面垂直并通过盘心。
ωB
⎧ J Aω A + J Bω B = ( J A + J B )ω ⎨ 2 2 J A = m A RA 2 , J B = m B RB 2 ⎩ 2 2 m A RAω A + m B RBω B ω= 2 2 m A RA + m B RB = 100 rad⋅ s −1
A
B
ω
例、如图所示,一质量为m的小球以水平速度射入一静止悬于顶 端长棒的下端,碰后以速度v’反向运动,已知棒长为l,质量为M。 设碰撞前后杆视为一直保持竖直位置,求碰撞后杆的角速度 解:由小球和杆组成的系统受到的外力有重 力和轴对杆的作用,它们对O轴的力矩分量 为零,所以系统对O轴的角动量分量守恒
第三章 动量和角动量

mi
由n个质点组成的质点系: dpi Fi F外i F内i dt i i i i
质点系
F外i
F内i mi
合外力 F外 零 dp 质点系的动量定理 dpi d dp F外 pi 右边: (微分形式) dt dt dt dt i i p2 持续一段时间: F外dt dp p2 p1
弹性碰撞 碰撞
动量守恒,机械能守恒 动量守恒 动量守恒
非完全弹性碰撞
完全非弹性碰撞
3)若某一方向合外力为零, 则此方向动量守恒 .
F外x 0 , F外y 0 , F外z 0 ,
px mi vix C x pz mi viz C z p y mi viy C y
解:由质点的动量定理,
t1
t2 I Fdt p2 p1
F t mgt p2 p1
4m / s
F/N 30
0-4s: I
t=4s时: v
0
1 0-7s: I (4 7) 30 mg t p2 p1 2
t=7s时: v
x2 x1
x
解得:x1 3.33m, x2 1.67m
小结
动量定理及动量守恒定律 1. 动量定理
t2 对 质 点: I F dt P2 P1 t1 Fdt dP t2 对 质 点 系 I F外 dt P2 P1 t1 F外 dt dP
第三章 动量和角动量
力的累积效应
力对时间的累积冲量 力对空间的累积做功
动量 能量
3-1 质点的动量定理
1、冲量 动量定理 牛顿第二定律
质点系角动量守恒定律

dL τ ,再考虑诸质点所受惯性力的力矩,即得 dt
dL τ i外 ri (mi ac ) dt 式中惯性力矩又可写作 mi ri dL ( mi ri) ac ( ) mac τ i外 m dt
此即质点系对质心的角动量定理,与惯性系中角动量定理具有完 全相同的形式。是表明质心系特殊和重要性的又一个例子。
第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系,在研究物体的运动 时,人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况,并且在这类运动中也存在着某些共同的重要规律。例 如,天文观测表明,行星绕日运动遵从开普勒第二定律,在近 日点附近绕行速度较快,远日点速度较慢,这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
当τ iz 0时,
Lz 常量.
§5.4 质点系对质心的角动量定理和 守 恒 定 律
前面给出的角动量定理和角动量守恒定律都相对于惯性系 而言,现在研究质心参考系中质点系角动量的变化规律。如图 (a),C xyz 即质心参考系。C 为质心,x ' , y ' 和 z 坐标轴
与惯性参考系 O xyz 的 x, y 和 z 轴总保持平行,而质心具有 加速度 ac 。 z
四、质点对轴的角动量定理和守恒定律(自阅)
§5.3 质点系的角动量定理及角动量守恒定 律
一、质点系角动量定理
设质点系由 N 个质点组成,对选定的某固定参考点,第 i 个 质 点的角动量定理的表达式为τ dLi
§5.2 角动量定理及其守恒律

f2
r2
内容
⒈质点系对点的角动量定理:
M外 dL dt
质点系在碰撞过程中对o轴的角动量守恒
o
⊙ 正方向
胶泥碰前速度
v0 2gh
h
m'
v m vo
m v
据角动量守恒
m' 2ghR (m'm)vR mvR
v
m' 2 gh m ' 2m
例1:人造地球卫星,绕地球作椭圆轨道运动, 地球在椭圆的一个焦点上,则卫星的( (A)动量不守恒,动能守恒. (B)动量守恒,动能不守恒. (C)对地心的角动量守恒,动能不守恒. (D)对地心的角动量不守恒,动能守恒. )
⒋质点对轴的角动量守恒定律:
若M z 0,则Lz = C
说 明
在应用角动量定理或角动 量守恒定律时,力矩和角动 量必须选取惯性系中的同一 参考点或同一参考轴.
o'
α L
T
o
F
mg
角动量守恒与选取的参考点或参考轴有关。
M o
Fl cos
L o'
mvl ,
例1
解得:v1 5.91104 m / s; v2 3.88 104 m / s
二、质点系的角动量
第i个质点对o点的角动量
Li ri P i
P2
r2
P 1
质点系对o点的角动量
dLi ri Fi ri f i 对 mi 使用角动量定理: dt
质点系统的角动量

质点系统的角动量角动量是物体旋转时所具有的性质,质点系统的角动量是由其中所有质点的角动量之和组成的。
质点系统的角动量具有许多重要的特性和应用,如守恒定律和撞击问题。
本文将探讨质点系统的角动量及其相关概念和应用。
一、质点系统的角动量定义质点系统的角动量是由其中每个质点的质量、速度和与某一旋转轴的距离共同决定的。
对于一个质量为m的质点,其角动量可以用以下公式表示:L = m * r * v * sinθ其中L表示角动量,m表示质点的质量,v表示质点的速度,r表示质点与旋转轴的距离,θ表示速度方向和质点距离旋转轴的夹角。
二、质点系统的角动量守恒定律质点系统的角动量守恒定律是指在没有外力和外力矩作用下,质点系统的总角动量保持不变。
这意味着在系统内部发生作用时,质点系统整体的角动量不会改变。
例如,考虑一个由两个质点组成的系统,当两个质点之间的距离发生变化时,一个质点靠近旋转轴,另一个质点离开旋转轴。
质点的速度会相应改变,但是质点系统的总角动量保持不变。
三、质点系统的角动量守恒的应用质点系统的角动量守恒定律在解决撞击问题时发挥了重要的作用。
当两个物体发生碰撞时,守恒定律可用于计算碰撞前后物体的角动量变化。
考虑一个由两个质点组成的系统,在碰撞前,两个质点的角动量分别为L1和L2。
碰撞发生后,两个质点的角动量分别为L1'和L2'。
根据角动量守恒定律,可以得到:L1 + L2 = L1' + L2'通过对碰撞前后质点的速度和质量进行分析,可以解出碰撞后质点的速度和角动量变化。
四、实际示例:自行车轮转动中的角动量进一步说明质点系统的角动量,我们可以以自行车轮的转动为例。
当自行车轮旋转时,每个质点在轮辐上的角动量会以一定的方式组合成轮子整体的角动量。
当骑行者使自行车轮旋转速度加快时,轮子的角动量也将相应增加。
这可以通过调整骑行者身体的位置来实现。
如果骑行者将身体朝轮子的一个方向倾斜,轮子会产生相反方向的反作用力,从而改变了质点系统的角动量。
质点系的角动量定理

质点系的角动量定理质点系的角动量定理引言角动量是物理学中一个非常重要的概念,它描述了物体围绕某一轴旋转时所具有的特定性质。
在实际应用中,我们经常需要研究由多个质点组成的系统的角动量变化,这就涉及到了质点系的角动量定理。
定义首先,我们来回顾一下单个质点的角动量定义:对于一个质量为m、速度为v、距离某一轴距离为r的质点,它的角动量L可以表示为L = mvr sinθ,其中θ是速度方向与轴线方向之间的夹角。
然后再考虑由N个质点组成的系统,每个质点都有自己的速度和位置。
此时,整个系统所具有的总角动量可以表示为L = Σi=1N L_i,即每个质点所具有的角动量之和。
推导接下来我们来推导一下质点系的角动量定理。
假设一个由N个质点组成的系统,在某一瞬间t1时刻它们所具有的总角动量为L1,在另一瞬间t2时刻它们所具有的总角动量为L2。
那么根据牛顿第二定律和牛顿运动定律,我们可以得到以下的式子:F = ma = m(dv/dt) = d(mv)/dt其中F是质点所受的合力,m是质量,v是速度。
将上式两边同时乘以r sinθ,再对所有质点的角动量求和,可以得到:Σi=1N (r_i x F_i) = d/dt (Σi=1N L_i)其中r_i是第i个质点距离某一轴的距离向量,F_i是它所受的合力向量。
右边表示总角动量随时间的变化率。
根据矢量积的性质,r_i x F_i可以表示为m_iv_ir_isinθ_i,其中θ_i是速度方向与轴线方向之间的夹角。
将其代入上式中可得:Σi=1N m_iv_ir_isinθ_i = d/dt (Σi=1N L_i)这就是质点系的角动量定理。
应用利用质点系的角动量定理,我们可以研究各种旋转系统中角动量随时间变化的规律。
例如,在自由陀螺运动中,陀螺在自身重力作用下绕着固定轴线旋转。
由于陀螺具有一定的自旋角速度,它的角动量会随时间变化。
根据质点系的角动量定理,我们可以推导出陀螺的进动和章动规律。
5-2 质点系的角动量定理及角动量守恒定律

若质点系的所有质点均分别在与 z 轴垂直的平 面内运动,且一共同的角速度绕 z 轴作圆周运动, 则质点系对 z 轴的角动量为
Lz ri mi vi mi ri
i i
2
当质点系对轴的角动量守恒时:
ri 变小,则
M z 0 ,Lz 常量
增大;
ri 变大,则
减小.
质点系对轴的角动量定理
质点系对轴的角动量定理
dLz Mz dt
如果在一个过程中,质点系所受的外力 对 z 轴的力矩始终保持为零,则质点系对该 轴的角动量守恒.
M z 0 ,Lz 常量
质点系对轴的角动量守恒定律
当内力矩远大于外力矩时,质点系对轴的角动量 也是守恒的. (例:P170例1)
在直角坐标系中,上式沿三个坐标轴的投影式为
dLy dLx dLz M x M ix , My , Mz . dt dt dt
• 如果只考虑上式中某一个分量,例如 z 分量,则 表现为对轴的特征:即质点系对于 z 轴的角动量对时 间的变化率等于质点系所受一切外力对 z 轴力矩的代 数和,叫做质点系对 z 轴的角动量定理。
ri fij rj f ji (ri rj ) fij 0
ri fij 0
i i j
成对出现的内力对参考点的力矩矢量和为零. 由于系统内力总是成对出现,则系统内力矩的矢量和为零. • 可见,系统的内力矩只能使系统内各质点的角动量改变, 但不能改变质点系总的角动量。
如果在一个过程中,始终无外力矩作用或所受 的外力矩为零,则质点系的总角动量守恒 .
M外 0 ,L 常矢量
质点系对某一固定点的角动量守恒定律
角动量、刚体

归纳
质点的
角动量定理 归纳
所受的合外力矩
角动量的时间变化率
冲量矩
当 即
角动量的增量
0
时, 有
0
物理意义:当质点不受外力矩或合外力矩为零 (如有心力作用)时,质点的角动量 前后不改变。
(后面再以定律的形式表述这一重要结论)
质点角动量守恒
根据质点的 角动量定理
若 即
则
常矢量 当质点 所受的合外力对某参考点 的力矩 为 守恒。
用力上爬者先到; ( 2)
一 人 用 力 上 爬
一 人 握 绳 不 动
握绳不动者先到; ( 3)
可能出现的情况是
(请点击你要选择的项目)
(4)以上结果都不对。
两人质量相等 小议链接2
既忽略 滑轮质量 终点线
又忽略 轮绳摩擦
终点线
两人同时到达; ( 1)
用力上爬者先到; ( 2)
一 人 用 力 上 爬
内
得
质点系的角动量 的时间变化率
内
外
质点受外力 矩的矢量和
微分形式
外 外
称为
内力矩在求矢 量和时成对相消
微、积分形式
将
外
对时间求导 的微分形式
质点系的角动量 的时间变化率
质点受外力 某给定 参考点 矩的矢量和
的积分形式
内
外 外 外 质点系的 内
内
得
内 质点系所受的
冲量矩 质点系的角动量
矩的矢量和 的时间变化率 若各质点的速度或所受外力与参考点共面,则其角动量或力矩只含正反 内力矩在求矢 两种方向,可设顺时针为正向,用代数和代替矢量和。 量和时成对相消 微分形式 称为
小球被绳子拴着,绳子穿过光滑水平桌面上的小孔,向 下拉绳子,小球的速度怎样变化?动量、角动量改变吗?
5.3质点系对质心的角动量定理和守恒定理

m 2 r12 m1 m2
( u)( u)
r12 u r12 ( u )
上页
下页
返回
结束
m 1m 2 m1 m2
上页
u u
返回 结束
下页
第五章 角动量 关于对称性
(2) rc m 1 r1 m 2 r2 m1 m2
m 2 ( r1 r2 ) m1 m2 m 1 ( r2 r1 )
r1 rc r1
dL M外 dt
——质点系对质心的角动量定理.
上页
下页
返回
结束
第五章 角动量 关于对称性
质点系对质心的角动量的时间变化率等于外力
相对质心的力矩的矢量和.
在质心系中角动量定理同样适用.
§5.3 2 质点系对质心的角动量守恒定律
当
M 外 0时, L ' 恒矢量
如跳水运动员等在空中翻筋斗.
同样
M i 外 z 0, L z 常量
动画演示
上页
下页
返回
结束
第五章 角动量 关于对称性
[例题]质量为m1和m2的两个质点,其位矢和速度分
别为 ,试求: (1)每个质点相对于它们质心的动量.
r1、 v 1
和 r 2、 v 2
(2)两质点相对于它们的质心的角动量. [解](1)在质心系中两质点的速度分别为
上页
下页
返回
结束
第五章 角动量 关于对称性
L 质点系相对质心的角动 量, M 外 诸外力对质心的力矩 , M 惯 惯性力对质心的力矩 .
质点的角动量

2、质点的角动量定理
设质点的质量为m,在合力F 的作用下,运动方程
d mv F ma dt
d mv r F r dt
考虑到
d d dr r mv r mv mv dt dt dt
dr v v v 0 dt
r1 1 m r2 2 r 2
2
得: 2 r1 1 r 2
2
r 1 1 2 2 1 1 m(r11 ) 2 m r 1 1 2 2 r 2
2 1
4、推广到质点系情形
利用牛顿第三定律,我们还可以将质点角动量定律推广到质 点系的情况,得到质点系总角动量的时间变化率与合外力 矩的简单关系,即质点系的角动量定理。 我们定义质点系对给定参考点O的总角动量为系统内所有质 点对选定参考点O的角动量的矢量和,即 :
L Li ri pi ,
M r F r F1 r F2 r FN M1 M 2 MN ,
3、质点的角动量守恒定律
若质点所受的合外力矩为零,即 M=0,则
v
L
L=r mv=恒矢量
角动量守恒定律:当质点所受的对参考点的合外力
矩为零时,质点对该参考点的角动量为一恒矢量。 两种情况: a、质点所受的外力为零 b、外力不为零,合力矩为零 特例: •在向心力的作用下,质点对力心的角动量都是守恒的
由于质点i与质点j的相互作用内力与它们的连线矢量互相 平行,即
rij // fij
所以质点系的角动量定理可以表示为
dL M外 , dt
其中合外力矩定义为所有外力矩的矢量和,即
角动量

内力对体系的总力矩为零,上式变为
dL ri Fi M i M dt i i
体系角动量定理的微分形式
8
体系角动量定理的积分形式
t L L0 Mdt
0
体系对给定点角动量的增量等于外力对该点的总冲量矩 质点系角动量定理指出,只有外力矩才对体系的角动量变化 有贡献.内力矩对体系角动量变化无贡献,但对角动量在体系内 的分配是有作用的.
解:⑴ 对于由两个质点构成的质点系,引入相对速度u
v2 u v12 v1 v2 v1
考虑到质心系是零动量参考系,即 可得
m2v2 0 m1v1
v2 m1 u m1 m2
15
v1
m2 u m1 m2
7
㈡
质点系角动量定理
一、质点系角动量定理
质点系对给定点的角动量等于各质点对该点的矢量和:
L li ri pi ri mi vi
i i i
对t求导,利用质点角动量定理,则得
dL dli ri Fi fi dt i dt i
1,开普勒行星运动定律 (1)轨道定律:行星沿椭圆轨道运行,太阳位于椭圆的一
个焦点上;
(2)面积定律:对任一行星,它的矢径在相等的时间内扫过 的面积相等;
(3)周期定律:行星绕太阳运动轨道半长轴a的立方正比 于公转周期T的平方.即 T a 3 2 22
利用角动量守恒定律证明开普勒面积定律
有心力对原点的力矩为零,故质点对原点的角动量守恒. 对②式两边乘r,再对时间积分得
r m 2rr r 2 0 mr 2r d 0 mr 2 dt Lconst mr 2
质点系的角动量定理

质点系的角动量定理介绍质点系的角动量定理是力学中的一项基本原理,用于描述质点系在外力作用下角动量的变化规律。
本文将全面、详细、完整地探讨质点系的角动量定理。
角动量的定义角动量是描述物体旋转状态的物理量,表示物体围绕某一轴旋转时具有的转动能力。
对于一个质点,其角动量可以定义为质点的质量乘以质点的位置矢量与旋转轴之间的叉乘。
角动量的数学表达式为:L=r×p其中,L表示角动量,r表示质点相对于某一轴的位置矢量,p表示质点的动量。
角动量定理的表述质点系的角动量定理可以表示为:dLdt=M其中,dLdt表示角动量的变化率,M表示作用在质点系上的合外力矩。
角动量定理的推导为了推导角动量定理,我们需要使用牛顿第二定律和角动量的定义。
考虑一个质点系,由n个质点组成。
对于其中的第i个质点,根据牛顿第二定律,可以得到:m i d2r idt2=F i其中,m i表示第i个质点的质量,r i表示第i个质点的位置矢量,F i表示作用在第i个质点上的合外力。
将角动量的定义代入上式可得:m i d 2r i dt 2=d dt (r i ×m i dr i dt) 对上式进行展开和简化可以得到:m i d 2r i dt 2=m i dr i dt ×dr i dt +r i ×m i d 2r i dt 2 根据向量恒等式A ×(B ×C )=B (A ⋅C )−C (A ⋅B ),可以得到:m i d 2r i dt 2−r i ×m i d 2r i dt 2=m i dr i dt ×dr i dt将上式对所有质点求和,并利用质点系的总动量定义p =∑m in i=1dr i dt 和质点系的质心位置矢量定义R =1M ∑m i n i=1r i (其中M =∑m i n i=1),可以得到:dp dt=F −R ×F 其中,F 表示质点系的合外力。
力学智慧树知到答案章节测试2023年德州学院

绪论单元测试1.设函数在点处可导,则等于( )A:B:C:0D:答案:D2.在x=3处的微分dy= ( )A:6dxB:dxC:3dxD:9dx答案:A3.的值为( )A:1B:2C:0D:答案:A4.矢量的标积满足结合律,即。
( )A:对B:错答案:B5.。
( )A:对B:错答案:B第一章测试1.下列关于质点的说法正确的是()。
A:只要物体的体积足够小,就可将物体视为质点B:研究地球自转可将地球视为质点C:只要物体的质量足够小,就可将物体视为质点D:研究地球公转时可将地球视为质点答案:D2.关于参考系和坐标系下列说法错误的是:( )A:参考系和坐标系的选则原则上是任意的B:参考系不同,对同一运动的描述不同C:描述物体运动必须选定参考系,否则对运动的描述没有意义D:参考系相同,坐标系不同时对同一运动的描述不同答案:D3.运动是绝对的,但是运动的描述具有相对性。
()A:对B:错答案:A4.选择不同的参考系,对同一物体运动的描述是相同的。
()A:错B:对答案:A5.地球很大不能视为质点,电子很小可以视为质点。
()A:错B:对答案:A第二章测试1.车厢正作匀速直线运动,从车厢上掉下一物体A,若忽略空气阻力,从地面上观察者看去,A物体的运动是:()A:匀加速直线运动B:自由落体运动C:平抛运动D:斜抛运动答案:C2.下列说法错误的是:( )A:质点作直线运动,加速度的方向和运动方向总是一致的B:质点作斜抛运动,加速度的方向恒定C:质点作曲线运动,速度的法向分量总是零,但加速度的法向分量总不为零D:质点作曲线运动,加速度的方向总是指向曲线凹的一边答案:A3.物体自某一时刻开始运动,经Δt时间后沿一曲线又回到出发点,此时的速度大小与初速度相同,但方向不同,则()。
A:在Δt时间内的平均速度为零B:在Δt时间内的平均加速度为零C:在Δt时间内的路程为零D:在Δt时间内的平均速率为零立答案:A4.已知质点的运动学方程,可以通过求一阶导数得到质点的速度,求二阶导数得到质点的加速度。
第2章 动量和角动量

L
质点的动量p和 矢径r不互相垂直
L
O
m r
2
p
O
90
0
r
90 0
p
m
d
L pr mvr mr
L pd pr sin mvr sin 2 mr sin
用叉积定义
角动量
v
L
m r
p
r
方向用右手螺旋法规定 角动量方向
一、质点的动量定理
1、动量 (描述质点运动状态,矢量)
P=m v
大小:mv 单位:kgm/s
方向:速度的方向 量纲:MLT-1
2、冲量 (力的作用对时间的积累,矢量) I 方向:速度变化的方向 单位:Ns
(1) 常力的冲量
量纲:MLT-1
I Ft
(2) 变力的冲量
F1 t1
F2 t 2
Mv ( M dM )(v dv) dM(v u) Mv vdM Mdv dMdv vdM udM
Mdv udM 0 v M dM M0 v v0 u ln dv u M v0 M0 M
§3.5 质心**
n 个质点组成质点系的质量中心
Fz dt
t1
t2
4、质点的动量定理的应用
例:逆风行舟 f u
m
v
p1
p
p2
例1、质量为2.5g的乒乓球以
10 m/s 的速率飞来,被板推
v2 30o 45o n
挡后,又以 20 m/s 的速率飞
出。设两速度在垂直于板面 的同一平面内,且它们与板 面法线的夹角分别为 45o 和
大学物理-角动量守恒定律 PPT

dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
37
例6 一杂技演员M由距水平跷板高为h 处 自由下落到跷板的一端A,并把跷板另一端 的演员N弹了起来.问演员N可弹起多高?
M
h
N
C
A
B
l/2
l
38
设跷板是匀质的,长度为l,质量为m',
6mv0
(M 3m)l
v0 m
31
例3 摩擦离合器 飞轮1:J1、 w1 摩擦轮2: J2 静止,两轮沿轴向结合,结合后两轮达到 的共同角速度。 解:两轮对共同转轴的角动量守恒
21
试与下例的齿轮啮合过程比较。
32
例4 两圆盘形齿轮半径r1 、 r2 ,对通过盘心
垂轮直以于0 盘转面动转,轴然的后转两动轮惯正量交为啮J1合、,J2求,啮开合始后1
点o的矢径为 r ,动量为 p ,如下图。在计算其
角动量时,注意有两个特点:
(1) o点到 p 方向的垂直距离 r sin 不变;
(2) L 方向不变;
p2
假如 p 的大小也不变, 显然L 的大小不变。这表
明,自由质点对任意参考 点的角动量保持不变。
p1
1 r1
2
r2
r sin o
5
1.5.2 质点角动量定理
必须指明是对哪个点而言的
注意两点:
(1) 质点的角动量是相对某一参考点而言的,因此
对不同的参考点,角动量 L 不同;
(2) L 的大小在0~ rp 之间变化,如果把动量分解
为径向分量 pcos 和横向分量 psin ,则仅横
角动量

※匀速直线运动质点相对任意固定点 的角动量守恒
如图, 圆锥摆. 例: 如图, 圆锥摆. 点的角动量是否守恒? 是 m对于 o 点的角动量是否守恒? (是) 点的角动量是否守恒? 否 m对于 o’ 点的角动量是否守恒?(否) m动量是否守恒? (否) 动量是否守恒? 否 质点绕行半周时间内的绳的张 力冲量是多少?(A --B ?(A点 力冲量是多少?(A点--B点) mA r v
r r r Lo' = l × m v
≠0
方向随时间变化, 大小 Lo’=mvl 方向随时间变化 不守恒 *合外力矩、角动量均对同一点而言 合外力矩、角动量均对同一点而言 均对同一点
解: 绕行半周时间
∆t =
πR
v
r r rr 绕行半周动量增量为: 绕行半周动量增量为 − m v k − mv k = −2mv k
r r
(4)行星在公转轨道上的角动量 行星在公转轨道上的角动量
r p r p
ϕ
ϕ
r r
d
O
dr r
L= pd = pr sinϕ
质点做直线运动时, 质点做直线运动时,该质点对直线上 一点和直线外一点的角动量分别是多 少?
在讲力矩和角动量时一定指明对那一个点而言. 在讲力矩和角动量时一定指明对那一个点而言.
2-7质点的角动量与角动量守恒定律
一、力矩
r M
r r
o
r F
α
r r r M = r ×F
※力矩大小 ※力矩方向 右手螺旋法 的选择(点力矩) ※取决于固定点 的选择(点力矩) 单位: ※单位:
质点系角动量

i
r
T
二者获得相等相反的角动量; 而动量相同! Fi 0!
iቤተ መጻሕፍቲ ባይዱ
27
例2 轻质杆,端部固结一小球,另一小球以水 平速度碰杆中部,碰撞时间极短,后粘合。 已知:m1,m2 v0 l 求ω o 解: 选 m1 (含杆 ) m2 v
0
碰撞时重力和轴力都通过 o,对o力矩为零,故L守恒
11
质点角动量推导
大小: r F rF sin Fd
方向:服从右手螺旋法则
dL r F dt
F
o
r
d
m
力矩
对参考点的力矩
定义: M r F
大小: Fd Fr sin 方向: 垂直于r 和F组成的平面 服从右手螺旋法则
l l l m2v0 lm1l m2 2 2 2
m2
l
m
1
2m 2 v 0 4m1 m2 l
存在水平轴力 由结果验算!
思考:对m1+m2 为什么不用水平动量守恒? 28
质点系动量与角动量对比: 动量
p m v
i i
i
角动量 L r p
i i
22
质量 m' 在 A 点和 B 点只受有心力作用 , 角动量守恒
mv0 ( R h) mvB R 1 vB ( R h)v0 R 1 709 m s
飞船在 A点喷出气体后,在到达月球的 过程中,机械能守恒
1 mM m 1 mM m 2 2 mv A G mvB G 2 Rh 2 R
m1
(不爬)
m2
(爬 )
m1= m2 把小孩看成质点, 以滑轮中心为“固定点”,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对各质点求和 得到
质点系角动量定理
质点系角动量定理 质点系角动量守恒定律
46--质点系的角动量
2020/9/12
一、作用于质点系的力矩 设质点系中第 i个质点受外力 Fi 作用则质点系受 到外力对固定参考点O的力矩矢量和应为:
1、重力的力矩
ห้องสมุดไป่ตู้
在重心和质心重合的情况下,可将总重力作用 点放在质心上来计算重力的力矩。 2、内力力矩
质点系内力力矩的矢量和为0。
二、质点系角动量定理和角动量守恒定律 根据质点角动量定理,第 i 个质点受到的力矩为
