第23章 旋转 教学课件 PPT (1)
合集下载
人教版九年级初中数学上册第二十三章旋转-图形的旋转1PPT课件

新知探究
旋转的性质 (1)旋转前、后的图形全等. (2)对应点到旋转中心的距离相等. (3)对应点与旋转中心所连线段的夹角等于旋转角.
新知探究
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺 时针旋转90°,画出旋转后的图形.
A
D
E
FB
C
新知探究
【分析】关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
第二十三章 旋转
23.1.1 图 形 的 旋 转
—-第一课时
人教版九年级(初中)数学上册 授课老师:XX
前言
学习目标
1.认识旋转,熟悉现实生活中的旋转现象。 2.理解图形旋转的基本性质。
重点难点
重点:分析研究旋转现象,探索旋转的性质。 难点:图形旋转的变换关系。
生活中常见的旋转
新课引入
电风扇
摩天轮
解:因为点A是旋转中心,所以它的对应点是它本身. 正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后D与B 重合。 设点E的对应点F. ∵△ADE≌△ABF ∴∠ABF=∠ADE,BF=DE. 因此在CB的延长线上取点F,使BF=DE, 则△ABF为旋转后的图形.
课堂练习
如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达 △ACE的位置.
① 试说出旋转中心、旋转方向及旋转角度? 点A、逆时针、60°
A
② ∠DAE等于多少度? 60° ③ △DAE是什么三角形? 等边三角形 ④ 如果M是AB的中点,那么经过上述旋转后,点 M转到了什么位置? AC边中点
M
E
BD
C
课堂练习
如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达
人教版数学九年级上册第二十三章 旋转数学活动课件(共13张PPT)
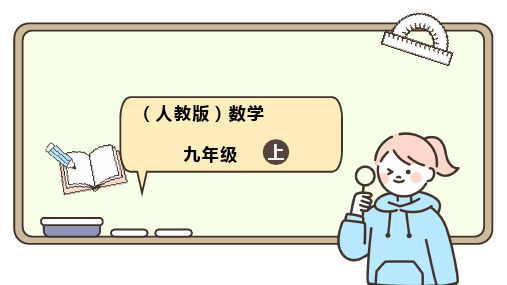
点的坐标依次是什么?
y
3 P3(-2, 1 )2
PP((11,,22))
1
· -4
-3
-2
-1
O -1
x 1234
-2 P2(-1,-2-3)
P1(2, -1 )
原坐标
90°
180°
270°
360°
(1,2) (2, -1 ) (-1, -2 )(-2,1 ) (1, 2 )
5.点P(x, y)绕原点分别逆时针旋转90°, 180°, 270°, 360°后的对应
(y,-x),(-x,-y),(-y,x),(x,y)
归纳总结
点P(x,y)绕原点分别顺时针旋转 旋转的角度 90° 180° 270° 360°
对应点的坐标 (y,-x) (-x,-y) (-y,x) (x,y)
3.点P(1,2)绕原点分别逆时针旋转90°, 180°, 270°, 360°后的对应
234
猜测这些点和分
P3(2, -1 ) 别关于y轴,原 点,x轴对称的
规律一样
原坐标
90°
180°
270°
360°
(1,2) (-2,1 ) (-1, -2 ) (2, -1 ) (1, 2 )
3.点P(x, y)绕原点分别顺时针旋转90°, 180°, 270°, 360°后的对应
点的坐标依次是什么?
-1
O -1
1
-2
-3
x 234
C(3-x,,-2-y))
观察这两个点的坐标有
什么特征?把对应数字 分别换成x、y你发现了 什么?
问题一:A、C两点的坐标关系是什么? 坐标互为相反数
问题二:A、C两点的位置关系是什么?
人教课标版初中数学九年级上册第二十三章23.1 图形的旋转(共22张PPT)
• 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
•
O
点A的对应点是 A' ;
点B的对应点是 B' ;
A'
B'
若OA=2,则OA'= 2 ;
若OB=1.5,则OB'= 1.5 ;
猜想:对应点到旋转中心的距离相等?
O
B'
点A的对应点是 A' ; 点B的对应点是 B' ;
A'
若∠AOA'=100°,则∠BOB'= 100° ;
猜想:对应点与旋转中心所连线段的夹 角相等?
B
美丽的旋转
风车旋转 重复着历史的记忆 木马旋转 幻想着青春的旋律 钟摆旋转 追赶着时间的极限 地球旋转 带来日夜的交替
……
你可曾 感到 旋转与我们 息息相关 美丽的旋转 让我们的生活 一片灿烂!
这节课中, 有什么收获 ? 还有什么疑惑呢?
在变中寻找不变
人类永恒的追求
1、练习第2题,习题第3题。
猜想:旋转性质 对应点到旋转中心的距离相等? 对应点与旋转中心所连线段的夹角相等?
验证:旋转性质
小试牛刀
A 1、如图,△ABC绕点M旋 转得到△ DEF,则:
B
点C的对应点是___点__F___; 旋转中心是__点__M____;
E
C D
M
23-1 图形的旋转 课件(共20张PPT)

按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在
同一条直线上,那么旋转角等于(C )。
A.55° B.70°
C.125° D.145°
解析:知道∠B=35°,∠C=90°,所以∠BAB1=55°。 也就是旋转角是180°-55°=125°。
教学新知
知识点2:旋转的性质特征。 (1)对应点对应点到旋转中心的距离相等。 (2)对应点与旋转中心所连线段的夹角等于旋转角。 (3)旋转前、后的图象全等。
BC=5,BD=4。则下列结论错误的是( B )。
A.AE//BC
B.∠ADE=∠BDC
C.△BDE是等边三角形 D.△ADE的周长是9
小练习
解析:∵△ABC是等边三角形,∴∠ABC=∠C=60°, ∵将△BCD绕点B逆时针旋转60°,得到△BAE, ∴AEB=∠C=60°,∴AE//BC,故选项A正确; ∵△ABC是等边三角形,∴AC=AB=BC=5,∵△BAE由△BCD逆时针旋转60°得 出,∴AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°, BE=BD,∴△BDE是等边三角形,故选择C正确;∴DE=BD=4,∴△AED的周长 =AE+AD+DE=AC+BD=9,故选项D正确;而选项B没有条件证明∠ADE=∠BDC,∴ 结论错误的是B。
小练习
如图所示,已知△ABC是直角三角形,∠ACB=90°, AB=5cm,BC=3cm,△ABC绕点C逆时针方向旋转90°
后得到△DEC,则∠D=∠__A__,∠B=_∠_D__EC___, DE=__5__cm,EC=__3__cm,AE=_1__cm,DE与AB的 位置关系为_垂__直__。
人教版数学九年级上册第二十三章《23.1 图形的旋转》课件

= 3 ,OA ′ =5 ,旋转角等于44 ° .
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt
△ADE,点B的对应点D恰好落在BC边上.若AC= ,
∠B=60 °,则CD的长为(D )
A. 0.5
B. 1.5 C.
D. 1 E
C
A
D B
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转 45°而成的. (1)若AB=4,则S正方形A′B′C′D1′=6 ; (2) ∠BAB ′= 45°, ∠B′AD= 45.°
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
风车风轮的每个叶片在风的吹动下转动到新的位置.
旋转的定义
把一个图形绕着平面内某点O沿 某个方向转动一个角度的图形变 换叫做旋转.
P
对应点
O
旋转中心
旋转角
P′
1.这个定点O称为旋转中心.
2.转动的角称为旋转角. 3.如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点. 4.转动的方向分为顺时针与逆时针.
B
A C
O
F
D
E
二、旋转的性质
活动:如图,在硬纸板上,挖出一 个△ABC,再挖一个小洞O作为旋转 中心,硬纸板下面放一张白纸.先在 纸上描出这个挖掉的三角形图案 (△ABC),然后围绕旋转中心转动 硬纸板,再描出这个挖掉的三角形 (△DEF),移开硬纸板.
A
B C
D O
F
E
问题1 在图形的旋转过程中,线段OA A
归纳总结
确定一次图形的旋转时, 必须明确 旋转中心 旋转角 旋转方向
温馨提示:①旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度” 称之为旋转的三要素;②旋转变换同样属于全等变换.
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt
△ADE,点B的对应点D恰好落在BC边上.若AC= ,
∠B=60 °,则CD的长为(D )
A. 0.5
B. 1.5 C.
D. 1 E
C
A
D B
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转 45°而成的. (1)若AB=4,则S正方形A′B′C′D1′=6 ; (2) ∠BAB ′= 45°, ∠B′AD= 45.°
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
风车风轮的每个叶片在风的吹动下转动到新的位置.
旋转的定义
把一个图形绕着平面内某点O沿 某个方向转动一个角度的图形变 换叫做旋转.
P
对应点
O
旋转中心
旋转角
P′
1.这个定点O称为旋转中心.
2.转动的角称为旋转角. 3.如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点. 4.转动的方向分为顺时针与逆时针.
B
A C
O
F
D
E
二、旋转的性质
活动:如图,在硬纸板上,挖出一 个△ABC,再挖一个小洞O作为旋转 中心,硬纸板下面放一张白纸.先在 纸上描出这个挖掉的三角形图案 (△ABC),然后围绕旋转中心转动 硬纸板,再描出这个挖掉的三角形 (△DEF),移开硬纸板.
A
B C
D O
F
E
问题1 在图形的旋转过程中,线段OA A
归纳总结
确定一次图形的旋转时, 必须明确 旋转中心 旋转角 旋转方向
温馨提示:①旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度” 称之为旋转的三要素;②旋转变换同样属于全等变换.
2018年秋人教版九年级上数学第23章 旋转 23.1图形的旋转课件(1)(20张PPT)
温故而知新:
这种图形变换叫什么?
平移的定义:
平移变换
在平面内,将一个图形沿某个方向移 动一定的距离,叫做图形的平移.
平移的特征: 平移前后图形是全等的.
下面的图形变换属于平移吗? 这些图形变换叫做什么呢?
第二十三章 旋转
23.1 图形的旋转(1)
1.创设情境,导入新知
指针式钟表的指针在不停地转动,风 扇扇叶的每个叶片转动到新的位置.这些 现象有哪些共同特点?
2.定义
把一个平面图形绕着平面内某一点 O
转动一个角度,叫做图形的旋转.
点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过 旋转变为点 P′,那么这 两个点叫做这个旋转的 对应点.
P
O 120° P′
3.小试牛刀
(1)下列现象中属于旋转的有( C)个
①地下水位逐年下降; ②传送带的移动; ③方向盘的转动; ④水龙头开关的转动; ⑤钟摆的运动; ⑥荡秋千运动. A.2 B.3 C.4 D.5
(2)时钟的时针在不停地转动,从 上午 6 时到上午 9 时,时针旋转的旋 转角是多少度?从上午 9 时到上午 10 时呢?
(3)如图,杠杆绕支点转动撬起 重物,杠杆的旋转中心在哪里?旋转 角是哪个角?
(4)填空
O 45°
B
A
点A绕_O_点,往_顺_时_针方向,
转动了_4_5 度到点B.
B′
7.应用
例 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形 吗?试一试你有几种方法?
A
D
E
B
C
方法1:
ADLeabharlann EFBC图中 △ABF 为所求图形.
这种图形变换叫什么?
平移的定义:
平移变换
在平面内,将一个图形沿某个方向移 动一定的距离,叫做图形的平移.
平移的特征: 平移前后图形是全等的.
下面的图形变换属于平移吗? 这些图形变换叫做什么呢?
第二十三章 旋转
23.1 图形的旋转(1)
1.创设情境,导入新知
指针式钟表的指针在不停地转动,风 扇扇叶的每个叶片转动到新的位置.这些 现象有哪些共同特点?
2.定义
把一个平面图形绕着平面内某一点 O
转动一个角度,叫做图形的旋转.
点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过 旋转变为点 P′,那么这 两个点叫做这个旋转的 对应点.
P
O 120° P′
3.小试牛刀
(1)下列现象中属于旋转的有( C)个
①地下水位逐年下降; ②传送带的移动; ③方向盘的转动; ④水龙头开关的转动; ⑤钟摆的运动; ⑥荡秋千运动. A.2 B.3 C.4 D.5
(2)时钟的时针在不停地转动,从 上午 6 时到上午 9 时,时针旋转的旋 转角是多少度?从上午 9 时到上午 10 时呢?
(3)如图,杠杆绕支点转动撬起 重物,杠杆的旋转中心在哪里?旋转 角是哪个角?
(4)填空
O 45°
B
A
点A绕_O_点,往_顺_时_针方向,
转动了_4_5 度到点B.
B′
7.应用
例 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形 吗?试一试你有几种方法?
A
D
E
B
C
方法1:
ADLeabharlann EFBC图中 △ABF 为所求图形.
人教课标版初中数学九年级上册第二十三章23.1 图形的旋转(共20张PPT)

C
⊙初始设置⊙窗口左上⊙窗口中央
Байду номын сангаас
图形变换是思想
例2 如图所示,点p为等边△ABC内一点,AP=3cm, BP=4cm(, C1P)=5求cm∠,APB; 解:如图,把△ABP以点B为中心顺
时针旋转60°,到△BCP1,连接PP1, ∴△ABP≌△BCP1 ∴BP=BP1=4,AP=CP1=3, 又∵∠PBP1=60°,CP=5 ∴△BPP1为等边三角形,
图形变换是经验
图形变换是经验
A1
A
P1
60°
P
B
C
图形变换通过实践、应用,形成一种经验, 我们可以有意识地应用于数学解题之中.
史话费马
且走且思的升华 本节课你有哪些收获,哪些感想?
今天我们学了什么?
今天我们悟到什么? 今天的质疑和发现?
A1
A
P1
60°
P
B
C
学习延伸
1.巩固性作业
(必做)
课本P63 第10、11题
图形变换
几何变换是知识
图形变换
基本的图形变换
平移变换
轴对称变换
旋转变换
共性:改变__位__置____; 不变___形__状__、__大__小__; 本质上都是__点__的变换.
图形变换是知识
图形的 变化
示例图形
与对应线段有关的 与对应点有关的
结论(数量、位置)
结论
平移
AB=A′B′, AB∥A′B′
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。21.8.2521.8.2506:22:4006:22:40August 25, 2021 14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年8月25日星期三上午6时22分40秒06:22:4021.8.25 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年8月上午6时22分21.8.2506:22August 25, 2021 16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年8月25日星期三6时22分40秒06:22:4025 August 2021 17、儿童是中心,教育的措施便围绕他们而组织起来。上午6时22分40秒上午6时22分06:22:4021.8.25
⊙初始设置⊙窗口左上⊙窗口中央
Байду номын сангаас
图形变换是思想
例2 如图所示,点p为等边△ABC内一点,AP=3cm, BP=4cm(, C1P)=5求cm∠,APB; 解:如图,把△ABP以点B为中心顺
时针旋转60°,到△BCP1,连接PP1, ∴△ABP≌△BCP1 ∴BP=BP1=4,AP=CP1=3, 又∵∠PBP1=60°,CP=5 ∴△BPP1为等边三角形,
图形变换是经验
图形变换是经验
A1
A
P1
60°
P
B
C
图形变换通过实践、应用,形成一种经验, 我们可以有意识地应用于数学解题之中.
史话费马
且走且思的升华 本节课你有哪些收获,哪些感想?
今天我们学了什么?
今天我们悟到什么? 今天的质疑和发现?
A1
A
P1
60°
P
B
C
学习延伸
1.巩固性作业
(必做)
课本P63 第10、11题
图形变换
几何变换是知识
图形变换
基本的图形变换
平移变换
轴对称变换
旋转变换
共性:改变__位__置____; 不变___形__状__、__大__小__; 本质上都是__点__的变换.
图形变换是知识
图形的 变化
示例图形
与对应线段有关的 与对应点有关的
结论(数量、位置)
结论
平移
AB=A′B′, AB∥A′B′
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。21.8.2521.8.2506:22:4006:22:40August 25, 2021 14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年8月25日星期三上午6时22分40秒06:22:4021.8.25 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年8月上午6时22分21.8.2506:22August 25, 2021 16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年8月25日星期三6时22分40秒06:22:4025 August 2021 17、儿童是中心,教育的措施便围绕他们而组织起来。上午6时22分40秒上午6时22分06:22:4021.8.25
人教X课标版初中数学九年级上册第二十三章23.1 图形的旋转(共28张PPT)

17、一个人即使已登上顶峰,也仍要 自强不 息。2021/8/32021/8/32021/8/32021/8/3
谢谢观赏
You made my day!
我们,还在路上……
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB, ∠DAB=90°, 所以旋转后点D与点B重合.
设点E的对应点为点E′,因为旋转后
E′
的图形与旋转前的图形全等,所以
∠ABE′= ∠ADE=90°,BE′=DE
因此,在CB的延长线上取点E′,使BE′=DE, 则 △ABE′为旋转后的图形.
作业.
谢谢大家!
1.钟表的分针匀速旋转一周需要60分. (1)指出它的旋转中心; (2)经过20分,分针旋转了多少度?
2.如图,小明坐在秋千上,秋千旋转了80°,请在图中小明身上 任意选一点P,利用旋转性质,标出点P的对应点.
P′
P
3. 如图,杠杆绕支点转动撬起重物,杠杆的旋转 中心在哪里?旋转角是哪个角?
A
B/ O
B
A/
旋转中心在支点O 旋转角为∠AOA/ 或∠BOB/
A
P B P CB
9、有时候读书是一种巧妙地避开思考 的方法 。2021/8/32021/8/3T uesday, August 03, 2021
10、阅读一பைடு நூலகம்好书如同和过去最杰出 的人谈 话。2021/8/32021/8/32021/8/38/3/2021 3:33:41 PM
生活中的旋转:
自转与公转
世界如此美丽
活动一: 探究旋转性质:
在硬纸板上,挖一个三角形洞,再挖一个小 洞O作为旋转中心,硬纸板下面放一张白纸. 先在纸上描出这个挖掉的三角形图案 (△ABC),然后围绕旋转中心转动硬纸板, 再描出这个挖掉的三角形(△A′B′C′) ,移 开硬纸板.
九年级数学上册 第二十三章 旋转 23.1 图形的旋转(第1

关闭
由旋转的性质,可得
△BCD≌△BAE,∴∠ห้องสมุดไป่ตู้AE=∠BCD=∠ABC=60°,∴AE∥BC,故选项A正确;
不能说明∠ADE=∠BDC,故选项B不正确;又知∠DBE=60°,BD=BE,可得 关闭 △B BDE是等边三角形,故选项C正确;DE=BD=4,因此△ADE的周长
=AD+AE+DE=BD+AC=9,故选项D正确.
关闭
C
答案
1
2
3
4
5
6
7
3.下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的 是( )
关闭
B
答案
1
2
3
4
5
6
7
4.在等边三角形ABC中,D是AC上一点,连接BD,将△BCD绕点B逆时 针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的 是( ) A.AE∥BC B.∠ADE=∠BDC C.△BDE是等边三角形 D.△ADE的周长是9
解析 答案
1
2
3
4
5
6
7
5.如图,将左边的矩形绕点B旋转一定角度后,位置如右边的矩形,则
∠ABC=
.
90°
关闭
答案
7.0°
旋转的性质 【例】 如图,△ABC是等边三角形,D是BC边上一点,△ABD经过 旋转后到达△ACE的位置. (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB边的中点,那么经过上述旋转后,点M转到了什么 位置? 分析确定这个图形的旋转中心是解决问题的关键. 解:(1)旋转中心是点A. (2)旋转角∠BAC=60°. (3)点M转到了AC的中点处. 点拨在旋转过程中,不动的点与其本身是对应点,且该点即为旋 转中心.一对对应点与旋转中心连线的夹角是旋转角,对应线段的 夹角也是旋转角.
由旋转的性质,可得
△BCD≌△BAE,∴∠ห้องสมุดไป่ตู้AE=∠BCD=∠ABC=60°,∴AE∥BC,故选项A正确;
不能说明∠ADE=∠BDC,故选项B不正确;又知∠DBE=60°,BD=BE,可得 关闭 △B BDE是等边三角形,故选项C正确;DE=BD=4,因此△ADE的周长
=AD+AE+DE=BD+AC=9,故选项D正确.
关闭
C
答案
1
2
3
4
5
6
7
3.下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的 是( )
关闭
B
答案
1
2
3
4
5
6
7
4.在等边三角形ABC中,D是AC上一点,连接BD,将△BCD绕点B逆时 针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则下列结论错误的 是( ) A.AE∥BC B.∠ADE=∠BDC C.△BDE是等边三角形 D.△ADE的周长是9
解析 答案
1
2
3
4
5
6
7
5.如图,将左边的矩形绕点B旋转一定角度后,位置如右边的矩形,则
∠ABC=
.
90°
关闭
答案
7.0°
旋转的性质 【例】 如图,△ABC是等边三角形,D是BC边上一点,△ABD经过 旋转后到达△ACE的位置. (1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB边的中点,那么经过上述旋转后,点M转到了什么 位置? 分析确定这个图形的旋转中心是解决问题的关键. 解:(1)旋转中心是点A. (2)旋转角∠BAC=60°. (3)点M转到了AC的中点处. 点拨在旋转过程中,不动的点与其本身是对应点,且该点即为旋 转中心.一对对应点与旋转中心连线的夹角是旋转角,对应线段的 夹角也是旋转角.
人教版九年级上册第23章旋转(复习课件) (共36张PPT)

5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
例4.下列图形中,中心对称图形是
()
答案B
下列图形中,既是中心对称又是轴对称 的图形是( )
答案C
2.中心对称和对称中心:
把一个图形绕着某一点旋转 180°后,如果它能和另一个图形完 全重合,那么称这两个图形成中心 对称,这个点叫做对称中心.这两个 图形中的对应点,叫做关于中心的 对称点.
3.中心对称和中心对称图形的关系:
∵∠EDF=45°, ∴∠FDM=45°. ∴△DEF与△DMF关于DF成 轴对称, ∴EF=FM. △BEF的周长=BE+EF+BF
=BE+(FC+CM)+BF=BE+FC+AE+BF
=(BE+AE)+(FC+BF)=BA+BC=2,
所以△BEF的周长为2.
例7.如图,水渠旁有一大块L形耕 地,要画一条直线为分界线,把耕 地平均分成两块,分别承包给两个
正八边形呢?正n边形呢?
正n边形 都是旋转对称图形,其旋转中心是 它们的中心,旋转角为 3 6 0 .
n
圆 的旋转角是任意角度
(二)中心对称 1.中心对称图形与对称中心:
在平面内,某一图形绕某一点旋 转180°后能与原来的图形互相重合, 那么这个图形叫做中心对称图形,这 个点叫做对称中心.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.旋转改变图形的形状和大小 B.平移改变图形的位置 C. 图形可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到
3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图
形所在的平面上可以作为旋转中心的点共有__3_个___个.
A
D
E
●
B C
F
4、 如图:P是等边ABC内的一点,把ABP按不同的方向通过 旋转得到BQC和ACR,
B C
旋转中心是___点__O___;
O
旋转角是___∠_A_O__C___∠_B__O_D___;
D
A E
F
B
问题: D
旋转的性质:
O
C
1改.在变图?旋形转的前旋后转的过图程形中全,哪等些;发生了改变?哪些没有发生
2线.分段别O对连D应结,它点对们到应有旋点什转A么、中关D心与系的?旋距任转离意中相找心等一O;对,对量应一点量,量线一段下OA与
将△CDE逆时针旋转90°画出旋转后的图形.
等腰直角三角形 如连结EM,那么△CEM是怎样的三角形?
D
C
E
A
BM
随堂练习
1.下列现象中属于旋转的有( C )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动; ④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动. A.2 B.3 C.4 D.5
2. 下列说法正确的是( B )
定点,沿某个方向转动一个角度,
像(C这ir样c你u的mr能图ot给形at变i旋o换n转)称. A´
这个定B 点称为旋转中心,
所转动的角称B为O旋转角O. A C´
旋转的三要素:
旋转中心, 旋转方向,
旋B转/ 角度.
找一找
请仔细观察此图, 点A,线段AB,∠ABC分 别转到了什么位置?
(第一课时)
平移变换
轴对称变换
转转刮动水动荡器的的秋时车千针轮
这些运动有什么共同的特征?
认识旋转 图形的旋转
O
0
45
B
A
点A绕_O_点,往_顺_时_针方向,转动了_4_5 度到点B.
认识旋转
B/
B
A
0
/
A
0 60
35
O
认识旋转
A
B
B´
C0
100
A´
O
C´
认旋识转旋的转概念
B´ 在平面内A,把一A个图形O绕一个
◆图形的旋转是由旋转中心和旋转的角度决定.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心; (2)经过20分,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60 分,因此旋转20分,分针
360 20 120
旋转的角度为
60
例2.如图,正方形ABCD中,E是AD上一点,以点C为中心
什么位置?
A
(5)若点G是线段BE的中点,经过旋转
后,点G移到了什么位置?请在图形
. 上作出.
(6)连结EF,请判断△AEF的形状,并说明理由. D
(7)试判断四边形ABCD与AFCE面积的大小关系.H
F
G. E
B
C
6.已知,如图边长为1的正方形EFOG绕与之边长相 等的正方形ABCD的中心O旋转任意角度,求图中阴 影部分的面积.
(3)旋转角是什么? ∠AOD和∠BOE都是旋转角
③ 对应点到旋转中心的距离相等.
(第二课时)
1这. 旋某节转个课的方定向你义转学:动在一到平定了面的内角什,度么将,一这知个样识图的形图?绕形一运个动定称点为沿旋着转. 你这是个用定点什称么为方旋转法中获心,得转这动的些角知称为识旋的转角?.
2. 旋转的性质:
本①节旋课转你不改还变有图形什的么大小地与方形状没,有但可解改决变定吗向?;
B
对应点
点A
对应线段 线段AB
对应角 ∠ABC
B´ A
C A´
点A´ O
C´
线段A´ B´
∠ A´B´ C´
试一试
如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是___点__D___;
A
线段OB的对应线段是_线__段__O_D__;
线段CD的对应线段是_线__段__A_B__; ∠AOB的对应角是_∠__C_O_D___; ∠B的对应角是___∠__D___;
它们与旋转中心的连线段,你能发现什么规律? 3.量一对下应∠A点O与D旋的转度中数心,连再线任段意的找夹几角对等对于应旋点转,角分.别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
旋转的基本性质 ◆旋转前、后的图形全等. ◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此 相等.
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角,
③ 对应点到旋转中心的距离相等.
议一议
1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋 转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
旋转中心是O
(2)经过旋转,点A、B分别移动到什么位置? 点D和点E的位置
2.本图案可以看做是一个菱形通过几次旋转得到的?每 次旋转了多少度?
5次
600, 1200, 1800, 2400, 3000
也可以看做是二个相邻菱形通 过几次旋转得到的?每次旋转 了多少度?
2次 1200 , 2400
还可以看做是几个菱形通过几 次旋转得到的?每次旋转了多 少度?
33个个 1次1次1806000
(1)指出旋转中心、旋转方向和旋转角度? (2)ACR是否可以直接通过把BQC旋转得到?
A
●O
R
P
B
C
Q
5.如图,在正方形ABCD中,E是CB延长线上一
点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点? (2)旋转角是多少度?
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别移动到
1这. 旋节转课的定你义学:在到平了面内什,么将一知个识图形?绕一个定点沿着 某个方向转动一定的角度,这样的图形运动称为旋转.
你这是个用定点什称么为方旋转法中获心,得转这动的些角知称为识旋的转角?.
2. 旋转的性质:
本①节旋课转你不改还变有图形什的么大小地与方形状没,有但可解改决变定吗向?;
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角,
G
A
D
O E
B
C
F
6.已知,如图边长为1的正方形EFOG绕与之边长相等的正方 形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
G
A
D
O E
B
C
F
1.香港区徽可以看作是什么“基本图案”通过怎样的旋转而 得到的?
可以看作是一个花瓣连续4次旋转所形成的,每 次旋转分别等于720 , 1440 , 2160 , 2880
3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图
形所在的平面上可以作为旋转中心的点共有__3_个___个.
A
D
E
●
B C
F
4、 如图:P是等边ABC内的一点,把ABP按不同的方向通过 旋转得到BQC和ACR,
B C
旋转中心是___点__O___;
O
旋转角是___∠_A_O__C___∠_B__O_D___;
D
A E
F
B
问题: D
旋转的性质:
O
C
1改.在变图?旋形转的前旋后转的过图程形中全,哪等些;发生了改变?哪些没有发生
2线.分段别O对连D应结,它点对们到应有旋点什转A么、中关D心与系的?旋距任转离意中相找心等一O;对,对量应一点量,量线一段下OA与
将△CDE逆时针旋转90°画出旋转后的图形.
等腰直角三角形 如连结EM,那么△CEM是怎样的三角形?
D
C
E
A
BM
随堂练习
1.下列现象中属于旋转的有( C )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动; ④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动. A.2 B.3 C.4 D.5
2. 下列说法正确的是( B )
定点,沿某个方向转动一个角度,
像(C这ir样c你u的mr能图ot给形at变i旋o换n转)称. A´
这个定B 点称为旋转中心,
所转动的角称B为O旋转角O. A C´
旋转的三要素:
旋转中心, 旋转方向,
旋B转/ 角度.
找一找
请仔细观察此图, 点A,线段AB,∠ABC分 别转到了什么位置?
(第一课时)
平移变换
轴对称变换
转转刮动水动荡器的的秋时车千针轮
这些运动有什么共同的特征?
认识旋转 图形的旋转
O
0
45
B
A
点A绕_O_点,往_顺_时_针方向,转动了_4_5 度到点B.
认识旋转
B/
B
A
0
/
A
0 60
35
O
认识旋转
A
B
B´
C0
100
A´
O
C´
认旋识转旋的转概念
B´ 在平面内A,把一A个图形O绕一个
◆图形的旋转是由旋转中心和旋转的角度决定.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心; (2)经过20分,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60 分,因此旋转20分,分针
360 20 120
旋转的角度为
60
例2.如图,正方形ABCD中,E是AD上一点,以点C为中心
什么位置?
A
(5)若点G是线段BE的中点,经过旋转
后,点G移到了什么位置?请在图形
. 上作出.
(6)连结EF,请判断△AEF的形状,并说明理由. D
(7)试判断四边形ABCD与AFCE面积的大小关系.H
F
G. E
B
C
6.已知,如图边长为1的正方形EFOG绕与之边长相 等的正方形ABCD的中心O旋转任意角度,求图中阴 影部分的面积.
(3)旋转角是什么? ∠AOD和∠BOE都是旋转角
③ 对应点到旋转中心的距离相等.
(第二课时)
1这. 旋某节转个课的方定向你义转学:动在一到平定了面的内角什,度么将,一这知个样识图的形图?绕形一运个动定称点为沿旋着转. 你这是个用定点什称么为方旋转法中获心,得转这动的些角知称为识旋的转角?.
2. 旋转的性质:
本①节旋课转你不改还变有图形什的么大小地与方形状没,有但可解改决变定吗向?;
B
对应点
点A
对应线段 线段AB
对应角 ∠ABC
B´ A
C A´
点A´ O
C´
线段A´ B´
∠ A´B´ C´
试一试
如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是___点__D___;
A
线段OB的对应线段是_线__段__O_D__;
线段CD的对应线段是_线__段__A_B__; ∠AOB的对应角是_∠__C_O_D___; ∠B的对应角是___∠__D___;
它们与旋转中心的连线段,你能发现什么规律? 3.量一对下应∠A点O与D旋的转度中数心,连再线任段意的找夹几角对等对于应旋点转,角分.别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
旋转的基本性质 ◆旋转前、后的图形全等. ◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此 相等.
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角,
③ 对应点到旋转中心的距离相等.
议一议
1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋 转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
旋转中心是O
(2)经过旋转,点A、B分别移动到什么位置? 点D和点E的位置
2.本图案可以看做是一个菱形通过几次旋转得到的?每 次旋转了多少度?
5次
600, 1200, 1800, 2400, 3000
也可以看做是二个相邻菱形通 过几次旋转得到的?每次旋转 了多少度?
2次 1200 , 2400
还可以看做是几个菱形通过几 次旋转得到的?每次旋转了多 少度?
33个个 1次1次1806000
(1)指出旋转中心、旋转方向和旋转角度? (2)ACR是否可以直接通过把BQC旋转得到?
A
●O
R
P
B
C
Q
5.如图,在正方形ABCD中,E是CB延长线上一
点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点? (2)旋转角是多少度?
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别移动到
1这. 旋节转课的定你义学:在到平了面内什,么将一知个识图形?绕一个定点沿着 某个方向转动一定的角度,这样的图形运动称为旋转.
你这是个用定点什称么为方旋转法中获心,得转这动的些角知称为识旋的转角?.
2. 旋转的性质:
本①节旋课转你不改还变有图形什的么大小地与方形状没,有但可解改决变定吗向?;
② 旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角,
G
A
D
O E
B
C
F
6.已知,如图边长为1的正方形EFOG绕与之边长相等的正方 形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
G
A
D
O E
B
C
F
1.香港区徽可以看作是什么“基本图案”通过怎样的旋转而 得到的?
可以看作是一个花瓣连续4次旋转所形成的,每 次旋转分别等于720 , 1440 , 2160 , 2880
