SAS高级统计分析教程(包括代码,超详细)
SAS统计分析报告教程方法总结材料

SAS统计分析报告教程方法总结材料统计分析是对数据进行理性、全面和深入的分析,以发现其中的规律、趋势和关联性。
SAS(Statistical Analysis System)是一个流行的统计分析软件,广泛应用于数据分析、研究和报告编制领域。
本文将介绍SAS统计分析报告的编制方法,帮助读者了解如何利用SAS软件进行统计分析,并撰写专业的统计分析报告。
一、数据导入与准备在进行统计分析之前,首先需要导入数据并对数据进行清洗和准备。
SAS软件支持多种数据格式的导入,包括CSV、Excel、数据库等。
可以使用PROC IMPORT或DATA STEP语句来将数据导入SAS环境中,并使用DATA STEP或PROC SQL语句对数据进行清洗和准备,包括删除缺失值、解决数据异常值等。
二、描述性统计分析描述性统计分析是对数据集中的变量进行统计概括和描述。
在SAS中,可以使用PROCMEANS、PROCFREQ、PROCUNIVARIATE等过程来计算变量的均值、标准差、中位数、众数、频数分布等描述性统计指标。
通过描述性统计分析可以初步了解数据的分布情况,为后续的统计测试和模型建立奠定基础。
三、统计检验统计检验是用来检验数据之间的关系或差异是否显著的一种方法。
在SAS中,可以使用PROCTTEST、PROCANOVA、PROCCORR等过程进行假设检验,检验两组或多组数据之间的显著性差异或相关性。
在进行统计检验时,需要设置显著性水平和备择假设,以便进行准确的统计分析。
四、图形展示图形展示是将数据通过图表的形式呈现出来,更直观地展示数据的特征和规律。
在SAS中,可以使用PROCGPLOT、PROCSGPLOT、PROCGCHART等过程来绘制各种类型的图表,包括直方图、散点图、折线图、饼图等。
通过图形展示,可以更清晰地了解数据的分布情况和变量之间的关系,为数据分析和报告提供有力支持。
五、报告编制报告编制是统计分析的最后一步,将分析结果整理成报告文档,进行数据解释和结论归纳。
SAS数据分析与统计

一、数据集的建立1.导入Excel数据表的步骤如下:1) 在SAS应用工作空间中,选择菜单“文件”→“导入数据”,打开导入向导“Import Wizard”第一步:选择导入类型(Select importtype)。
2) 在第二步的“Select file”对话框中,单击“Browse”按钮,在“打开”对话框中选择所需要的Excel文件,返回。
然后,单击“Option”按钮,选择所需的工作表。
(注意Excel文件要是2003的!!)3) 在第三步的“Select library and member”对话框中,选择导入数据集所存放的逻辑库以及数据集的名称。
4 ) 在第四步的“Create SAS Statements”对话框中,可以选择将系统生成的程序代码存放的位置,完成导入过程。
2.用INSIGHT创建数据集1)启动SAS INSIGHT模块,在“SAS INSIGHT:Open”对话框的”逻辑库“列表框中,选定库逻辑名2)单击“新建”按钮,在行列交汇处的数据区输入数据值(注意列名型变量和区间型变量,这在后面方差分析相关性分析等都要注意!!)3)数据集的保存:•“文件”→“保存”→“数据”;•选择保存的逻辑库名,并输入数据集名;•单击“确定”按钮。
即可保存新建的数据集。
3.用VIEWTABLE窗口建立数据集1)打开VIEWTABLE窗口2)单击表头顶端单元格,输入变量名3)在变量名下方单元格中输入数据4)变量类型的定义:右击变量名/column attributes…4.用编程方法建立数据集DATA 语句; /*DATA步的开始,给出数据集名*/Input 语句;/*描述输入的数据,给出变量名及数据类型和格式等*/(用于DATA步的其它语句)Cards; /*数据行的开始*/[数据行]; /*数据块的结束*/RUN; /*提交并执行*/例子:data=数据集名字;input name$ phone room height; ($符号代表该列为列名型,就是这一列是文字!!比如名字,性别,科目等等)cards;rebeccah 424 112 (中间是数据集,中间每一行末尾不要加逗号,但是carol 450 112 数据集最后要加一个分号!!)louise 409 110gina 474 110mimi 410 106alice 411 106brenda 414 106brenda 414 105david 438 141betty 464 141holly 466 140;proc print data=; (这一过程步是打印出数据集,可要可不要!)run;*数据集中的框架我会用加粗来显示,大家主要记加粗的,下面的编程部分都是这样!!二、基本统计分析1.用INSIGHT计算统计量1)在INSIGHT中打开数据集在菜单中选择“Solution(解决方案)”→“Analysis(分析)”“Interactive Data Analysis(交互式数据分析)”,打开“SAS/INSIGHT Open”对话框,在对话框中选择数据集,单击“Open(打开)”按钮,即可在INSIGHT中打开数据窗口2)选择菜单“Analyze(分析)”→“Distribution (Y)(分布)”,打开“Distribution (Y)”对话框。
SAS软件及统计应用教程

第i特征根 1CCaani2nRi2R
上式可以理解为第i对典型变量表示观测变量总方差 作用的指标,它的值越大说明表示作用越大。
SAS软件与统计应用教程
6. 典型相关系数的标准误
STAT
SECaniR1Cna1ni2R
7. 典型相关系数的假设检验
典型相关系数的假设检验包括对全部总体典型相关系
数的检验和对部分总体典型相关系数的检验。对数据的
前两个典型相关系数比形态指标和机能指标两组间的 任何一个相关系数都大。
SAS软件与统计应用教程
STAT
(2) 典型变量所解释的变异 第二部分是的5个特征根(Eigenvalues),包括:特
征根、相邻两个特征根之差、特征根所占方差信息量的
比例和累积方差信息量的比例。从中可以看出,前两对
典型变量所能解释的变异占总变异(方差)的91.18%, 如图7-4所示。其它三个典型相关变量的作用很小,一 共只解释了总变异的9%,可以不予考虑。
1 ,i j
C( U o i,U j r ) r 0 ,i j C( V o i,V j) r r 0 ,i j
SAS软件与统计应用教程
STAT
2) 同 一 对 典 型 相 关 变 量 Ui 和 Vi 之 间 的 相 关 系 数 为 CanRi,不同对的典型相关变量之间互不相关,即:
Co(U ri,V rj) C0ai nii Rjj
Ui = ai'X* = ai1X1* + ai2X2* + … + aipXp* Vi = bi'Y* = bi1Y1* + bi2Y2* + … + biqYq* i = 1,2,…,m = min(p,q);其中X*,Y*为原变量组
SAS统计分析教程方法总结

对定量结果进行差异性分析1. 单因素设计一元定量资料差异性分析1.1. 单因素设计一元定量资料 t 检验与符号秩和检验T 检验前提条件: 定量资料满足独立性和正态分布, 若不满足则进行单 因素设计一元定量资料符号秩和检验。
1.2. 配对设计一元定量资料 t 检验与符号秩和检验配对设计:整个资料涉及一个试验因素的两个水平,并且在这两个水 平作用下获得的相同指标是成对出现的,每一对中的两个数据来自于同一 个个体或条件相近的两个个体。
1.3. 成组设计一元定量资料 t 检验成组设计定义:A 有A1, A2个水平,将全部n (n 最好是偶数)个受试对 元分析的问题。
配对,无法消除个体差异对观测结果的影响,因此,其试验效率低于配对 设计。
T 检验分析前提条件:独立性、正态性和方差齐性。
14成组设计一元定量资料Wilcoxon 秩和检验不符合参数检验的前提条件,故选用非参数检验法,即秩和检验。
设试验因素象随机地均分成2 组, 分别接受 A1, A2, 2种处理。
再设每种处理下观测 的定量指标数为k ,当 k=1时,属于一元分析的问题;当 k >2时,属于多在成组设计中,因2 组受试对象之间未按重要的非处理因素进行两两1.5.单因素k (k>=3)水平设计定量资料一元方差分析方差分析是用来研究一个控制变量的不同水平是否对观测变量产生了显著影响。
这里,由于仅研究单个因素对观测变量的影响,因此称为单因素方差分析。
方差分析的假定条件为:各处理条件下的样本是随机的。
各处理条件下的样本是相互独立的,否则可能出现无法解析的输出结果。
各处理条件下的样本分别来自正态分布总体,否则使用非参数分析。
各处理条件下的样本方差相同,即具有齐效性。
16单因素k(k>=3)水平设计定量资料一元协方差分析协方差分析(Analysis of Covarianee是将回归分析与方差分析结合起来使用的一种分析方法。
在这种分析中,先将定量的影响因素(即难以控制的因素)看作自变量,或称为协变量(Covariate),建立因变量随自变量变化的回归方程,这样就可以利用回归方程把因变量的变化中受不易控制的定量因素的影响扣除掉,从而,能够较合理地比较定性的影响因素处在不同水平下,经过回归分析手段修正以后的因变量的样本均数之间的差别是否有统计学意义,这就是协方差分析解决问题的基本计算原理。
《SAS统计分析介绍》PPT课件

精选ppt
19
FORMAT语句可以为变量输出规定一个输出格式,比如 proc print data=score;
format math 5.1 chinese 5.1;
run;
使得列出的数学、语文成绩宽度占5位,带一位小数。 事实上,在生成数据集的DATA步中也可以用FORMAT语句规 定变量的输出格式,用LABEL 语句规定变量的标签,用LENGTH 语句规定变量的存贮长度,用ATTRIB语句同时规定变量的各属 性。在数据步中规定的变量属性是附属于数据集本身的,是永 久的;在过程步中规定的变量属性(标签、输出格式等)只用 于此过程的本次运行。
关 分 析
定性资料 ( R*C表)
双向无序 双向有序、属性不同
双向有序、属性相同
直线相关分析 Spearman秩相关 c2检验 Spearman秩相关、线性趋势检验 一致性检验(kappa系数的假设检验)
一个应变量,一个自变量:直线回归分析
回 归
应变量为连续型定量变量,服从正态分 布
一个应变量,多个自变量:多重线性回归 分析
在VAR后面给出变量列表:
VAR 变量名1 变量名2 … 变量名n;
变量名列表可以使用省略的形式,如X1-X3,
math-chinese等。
如果数据集中有几个变量依次为
math,english,chinese,则
var math-chinese 与
var math english chinese 等价。
5.304312 标准误差均 值
3645 584713.9 72.40189 0.56804 263832.5
0.140937
99% 95% 90% 75% Q3 50% 中位数
Sas代码作图详解(图文并茂)

Sas代码作图详解SAS/Graph太强大了,本文主要讲一些常用且功能强大的Graph相关的过程步。
1 proc gplot的简单例子proc gplot data=sashelp.shoes;plot Returns * Sales ;run;结果:2 我们也可以只画出符合条件的数据的图形。
proc gplot data=sashelp.shoes;where Region in("United States", "Eastern Europe");plot Returns * Sales ;run;结果:3 输出的图像都是默认的黑色的小十字,因此我们不能区分来自不同地区的数据,下面的程序就是为了解决这一问题proc gplot data=sashelp.shoes;where Region in("United States", "Eastern Europe");plot Returns * Sales= Region;run;结果:这里红色的来自美国,黑色的来自东欧,当然我们也可以自己设定颜色(SAS基本颜色有:black, red, green, blue, cyan, magenta, grey, pink, orange, brown, and yellow)。
4 设定坐标轴和所有文字和颜色proc gplot data=sashelp.shoes;where Region in("United States", "Eastern Europe");plot Returns * Sales= Region/caxis=bluectext=redgrid;run;结果:5 如果要对网格进行更精细地设置,则要用到AUTOHREF和AUTOVREF选项。
AUTOHREF中,LHREF设置水平线的线类型,CHREF设置水平线的线颜色;AUTOVREF中,LVREF设置垂直线的线类型,CVREF设置垂直线的线颜色。
SAS软件和统计应用教程

2.1.3 表示数据分散程度的统计量
1. 极差(Range)与半极差(Interquartile range)
极差就是数据中的最大值和最小值之间的差:
极差 = max{xi} – min{xi} 上、下四分位数之差Q3 – Q1称为四分位极差或半极
差,它描述了中间半数观测值的散布情况。
2. 方差(Variance或Var)
RUN;
显示结果如图所示。
2. MEANS过程
(1) 语法格式 MEANS过程的一般格式:
PROC MEANS DATA=<数据集名>[<统计量关键字列表>]; [VAR <分析变量列表>;] [BY <分组变量名>;] [CLASS <分组变量名>;]
RUN;
PROC MEANS语句后的选项主要用来指定所要计算 的统计量,默认情况下,MEANS过程会给出频数、均 数、标准差、最大值和最小值等,其余统计量的计算均 需要在选项中指定。
中位数 x12((n2x1()n2)
x(n1)) 2
n为奇数 n为偶数
3. 众数(Mode)
观测值中出现最多的数称为众数。众数用得不如均值 和中位数普遍。在属性变量分析中,常需考虑频数,因 此众数用得多些。
4. 百分位数(Percentile)
分位数也是描述数据分布和位置的统计量。0.5分位 数就是中位数,0.75分位数和0.25分位数又分别称为上、 下四分位数,并分别记为Q3和Q1。
单击“OK”按钮,即可得到关于变量Income的矩统计 量和基本统计测度
2.2.3 编程实现描述性统计
SAS提供有多个不同的过程来实现统计量的计算,它 们 在 功 能 范 围 上 有 许 多 的 重 复 , 下 面 介 绍 用 FREQ 、 MEANS和UNIVARIATE这三个过程来计算简单的描述 统计量。
统计软件SAS使用教程

统计软件SAS使用教程第1章SAS系统简介§1.1 SAS发展概况SAS(Statistical Analysis System)是一个大型的数据管理与数据统计分析处理的软件包。
1966年由美国North Carolina州立大学开始研制,1976年在美国成立了SAS研究所。
SAS主要用于数据处理和统计分析领域,是一个功能齐全、使用方便灵活。
只须要有少量的、简单的语句、写出SAS程序,进行运行,就可以满足拥护要求,一些特殊的计算或处理方式可以通过选项来指定。
从而达到且让用户将SAS程序在SAS环境下提高运行,及时了解到程序运行情况及出现的错误,程序可以方便的编辑修改和运行,直到用户得出满意的计算结果。
目前,SAS已经发展成为一个功能齐全、应用范围广泛、使用灵活方便的数据库管理和数据分析的标准软件系统。
其统计分析部分,在数据处理和统计分析领域,被业界和国际上公认为标准软件和最权威的统计软件包。
SAS应用广泛,其应用范围涉及到理、工、农、林、医、管理、商业、行政事物等各个领域。
国际上成立了专门的SAS协会SUGI (SAS User Group International),每年有学术会议讨论研究有关SAS的问题。
SAS在我国的应用。
SAS的主要版本。
§1.2 SAS的结构、功能、特点一、SAS结构与功能:SAS软件包由多个大的功能模块组成,用户可以根据需要,选择安装部分或全部SAS功能模块来组成一个运行系统。
SAS系统的核心(基本)部分是SAS/BASE模块,其功能是承担数据管理,管理用户使用环境,进行用户语言的处理,调用其他模块。
在SAS/BASE模块的基础上,还可以增加如下不同的模块、从而实现不同的功能。
⑴SAS/BASE⑵SAS/STAT⑶SAS/AF⑷SAS/FSP⑸SAS/GRAPH⑹SAS/ETS⑺SAS/IML⑻SAS/OR⑼SAS/QC二、SAS的特点:l 实用性强、功能完善、使用方便、编程简单、容易学习。
SAS统计分析与应用(第四讲)

详细描述
多元线性回归分析通过建立多元线性方程组来描述多个因变量与多个自变量之间的关系,并利用最小二乘法来估计回归系数。这种方法可以用于预测多个因变量的值,并评估多个自变量对因变量的影响程度。
数学模型
Y1 = β01 + β11X1 + β21X2 + ... + ε1
多元线性回归分析
Y2 = β02 + β12X1 + β22X2 + ... + ε2
01
双因素方差分析是用于比较两个分类变量对数值型因变量的影响的统计方法。
02
它通过分析两个分类变量对数值型因变量的交互作用和单独作用,判断两个分类变量对数值型因变量的影响是否显著。
双因素方差分析
04
回归分析
总结词
一元线性回归分析是用来研究一个因变量与一个自变量之间的线性关系的回归分析方法。
数学模型
01
02
03
04
t检验
用于比较两组Biblioteka 据的均值是否存在显著差异,如独立样本t检验和配对样本t检验。
方差分析
用于比较两组或多组数据的方差是否存在显著差异,如单因素方差分析和多因素方差分析。
卡方检验
用于比较实际观测频数与期望频数之间的差异,如拟合优度检验和独立性检验。
非参数检验
不依赖于总体分布的假设检验方法,如符号检验、秩次检验等。
Y = β0 + β1X + ε
参数解释
Y是因变量,β0是截距,β1是斜率,X是自变量,ε是误差项。
详细描述
一元线性回归分析通过建立线性方程来描述因变量和自变量之间的关系,并利用最小二乘法来估计回归系数。这种方法可以用于预测因变量的值,并评估自变量对因变量的影响程度。
SAS统计分析(第七讲)汇总

15
例11-6 data ex11_6;
infile 'e:\sasx\sas7\ex11_5.txt';
input x1-x4 y @@; proc reg; model y=x1-x4/stb selection=cp aic adjrsq; model y=x1-x4/tol vif collin collinoint R;
2018/10/30
3
四、分类变量的数量化
在实际研究中,自变量常常会是分类变量,主要包括三
种类型的分类变量:①两分类变量,如性别(男、女);② 有序分类变量,如病情(轻度、中度、重度);③无序分类 变量,如职业(干部、职员、工人、农民)。进行多元回归 分析,必须将这样的指标数量化,常用的数量化方法有:
自变量间的多重共线性(multicollinearity)
多重共线性是指在进行多元回归时,自变量间存在线性相关 关系。共线关系存在,可使估计系数方差加大,系数估计不稳 定,结果分析困难。出现以下现象提示可能存在自变量之间的 共线关系。
2018/10/30 14
整个回归方程的统计检验P<α,而各偏回归系数的检验均出 现P> α的矛盾现象。 偏回归系数的估计值明显与实际情况不符,或者是偏回归系 数的符号与专业知识的情况相反。据专业知识,该自变量与应 变量间关系密切,而偏回归系数检验结果P> α。
修正均数间比较的F值
F
MS 修正均数 MS 组内剩余
如修正均数间有差别,必要 时再作两两比较。
公共回归系数 bc
bc
组内(或误差)的l xy 组内(或误差)的l xx
各修正均数的计算
Yi Yi bc ( X i X )
SAS软件及统计应用教程3

μ1 -
t=
X Y ( 1 2 ) S w 1 n1 + 1 n 2
~ t ( n1 + n 2 2 )
X Y ± tα 2 ( n1 + n 2 2 ) S w 1 n 1 + 1 n 2
Sw = ( n1 1) S + ( n2 1) S n1 + n2 2
n
2
n n ∑(X i X )2 ∑(X i X )2 i =1 , i =1 2 2 χ α 2 (n 1) χ 1α 2 ( n 1)
SAS软件与统计应用教程 SAS软件与统计应用教程
STAT
正态总体参数的各种置信区间见表3-1。 正态总体参数的各种置信区间见表 。
被估参数
STAT
4. 总体比例与比例差的置信区间
实际应用中经常需要对总体比例进行估计, 实际应用中经常需要对总体比例进行估计,如产品的 合格率、大学生的就业率和手机的普及率等。 合格率、大学生的就业率和手机的普及率等。记π和P分 和 分 别表示总体比例和样本比例, 则当样本容量n很大时 别表示总体比例和样本比例 , 则当样本容量 很大时 一般当nP和 均大于5时 (一般当 和n(1 – P)均大于 时,就可以认为样本容量 均大于 足够大) 样本比例P的抽样分布可用正态分布近似 的抽样分布可用正态分布近似。 足够大), 样本比例 的抽样分布可用正态分布近似 。 总体比例与比例差的置信区间如表3-2所示 所示。 总体比例与比例差的置信区间如表 所示。
SAS软件与统计应用教程 SAS软件与统计应用教程
STAT
第三章 区间估计与假设检验
3.1 区间估计与假设检验的基本概念 3.2 总体均值的区间估计与假设检验的 总体均值的区间估计与假设检验的SAS实现 实现 3.3 总体比例的区间估计与假设检验的 总体比例的区间估计与假设检验的SAS实现 实现 3.4 总体方差的区间估计与假设检验的 总体方差的区间估计与假设检验的SAS实现 实现 3.5 分布检验
SAS统计分析教程方法总结

SAS统计分析教程方法总结SAS(Statistical Analysis System)是一种流行的统计分析软件,被广泛应用于各个领域的数据分析和决策支持中。
本文将总结SAS统计分析教程的方法,以帮助读者更好地理解和应用SAS软件。
1.数据导入与数据清洗:在进行统计分析之前,首先需要将数据导入SAS软件中。
SAS支持多种数据格式,如Excel、CSV等。
可以使用INFILE和INPUT语句读取数据,并使用DATA步骤定义变量。
在导入数据后,通常需要对数据进行清洗,包括处理缺失值、异常值等。
SAS提供了多种数据处理函数,如MEAN、SUM等,可以帮助完成数据清洗和处理工作。
2.描述性统计分析:描述性统计分析可以了解数据的特征和分布情况。
例如,可以使用PROCMEANS计算数据的均值、标准差、最小值、最大值等;使用PROCFREQ计算离散变量的频数和频率等。
此外,SAS还提供了PROCUNIVARIATE、PROCSUMMARY等过程,可以方便地进行更加复杂的描述性统计分析。
3.统计图表绘制:统计图表是数据分析中常用的可视化工具,能够直观地展示数据的特征和趋势。
SAS提供了PROC SGPLOT和PROC GPLOT等过程,可以绘制各种类型的统计图表,如直方图、散点图、柱状图等。
通过调整图形参数,可以使图表更加美观和易读。
此外,SAS还支持使用ODS(OutputDelivery System)输出图表到不同的输出格式中。
4.假设检验与推断统计:假设检验是统计分析中常用的方法,可以用来判断数据之间是否存在显著差异。
在SAS中,可以使用PROCTTEST、PROCANOVA等过程进行单样本、双样本和多样本假设检验。
此外,SAS还支持非参数检验方法,如PROCNPAR1WAY等。
除了假设检验,推断统计也是重要的统计分析方法,用于对总体参数进行估计和推断。
在SAS中,可以使用PROCMEANS、PROCREG等过程进行点估计和区间估计。
使用SAS进行数据挖掘与统计分析技巧

使用SAS进行数据挖掘与统计分析技巧第一章:介绍SAS软件及其应用领域SAS(Statistical Analysis System)是一款功能强大的统计分析软件,被广泛应用于数据挖掘、数据处理和统计分析等领域。
本章将介绍SAS软件的概述、应用领域以及一些常用的SAS功能。
第二章:SAS基本操作及数据准备在使用SAS进行数据挖掘和统计分析之前,首先需要了解SAS 的基本操作和数据准备工作。
本章将介绍如何运行SAS软件、创建和管理数据集、导入和导出数据、数据清洗和缺失值处理等相关技巧。
第三章:数据预处理与变量选择数据预处理是进行数据挖掘和统计分析的重要步骤。
本章将介绍如何进行数据缺失值处理、异常值处理、数据平滑和标准化等预处理技术。
同时,还将探讨如何进行变量选择,以提高模型的准确性和可解释性。
第四章:常用的数据挖掘技术SAS提供了丰富的数据挖掘技术,能够帮助分析人员从大量数据中挖掘出有价值的信息。
本章将介绍常用的数据挖掘技术,包括分类和回归分析、聚类分析、关联规则挖掘以及文本挖掘等,并结合实例演示如何使用SAS实现这些技术。
第五章:统计分析方法及应用统计分析是了解数据分布、发现规律和得出结论的重要手段。
本章将介绍常用的统计分析方法,包括假设检验、方差分析、卡方检验和回归分析等,并结合实例演示如何使用SAS进行统计分析,并解读分析结果。
第六章:SAS与其他数据挖掘工具的整合除了SAS软件本身提供的功能外,还可以将SAS与其他数据挖掘工具进行整合,以扩展分析的能力和应用范围。
本章将介绍如何使用SAS进行数据交互和整合,包括使用SAS与R、Python 和Excel等工具进行数据交互和集成分析。
第七章:高级技术与应用实例在掌握了SAS的基本操作和常用技巧后,我们可以进一步学习一些高级技术和实际应用案例,以解决更复杂的问题。
本章将介绍SAS的高级数据处理技术,如宏语言编程、SQL查询和图形分析等,并结合实例演示其应用。
SAS统计分析教程

SAS高级统计分析教程(包括代码,超详细)
程序实现
PROC UNIVARIATE; BY variables ; CLASS variable(s); ; FREQ variable ; HISTOGRAM; ID variables ; OUTPUT ; PROBPLOT < variables >; QQPLOT < variables >; VAR variables ; WEIGHT variable ; RUN;
程序实现
PROC CORR < options > ; BY variables ; FREQ variable ; PARTIAL variables ; VAR variables ; WEIGHT variable ; WITH variables ; RUN;
系统抽样(systematic sampling):先把总体中的每个个体编号,然后随机选取其中 之一作为抽样的开始点进行抽样,可以想象,如果编号是随机的,系统抽样与简单随机 抽样是等价的。
程序实现
PROC SURVEYSELECT options; STRATA variables ; CONTROL variables ; SIZE variable ; ID variables;
3.EM工具插补:补缺节点(包含单一插补和多重插补)
第二章 双变量分析
培训目的: 1. 理解中心极限定理;参数估计和假设检验理论; 2. 掌握相关分析的方法; 4. 掌握列联表分析的方法.
第一节 基本理论
中心极限定理
设随机变量 X1, X2, , Xn, 相互独立,服从同一分布且具
有期望 E Xi 和方差 D Xi 2 ,则随机变量
4.1.基本理论 4.2.建模流程 4.3.数据探索 4.4. 简单线性回归 4.5. 多元线性回归 4.6.残差检测 4.7.强影响点判断 4.8.共线性诊断 4.9.模型预测
SAS数据分析与统计

一、数据集的建立1.导入Excel数据表的步骤如下:1) 在SAS应用工作空间中,选择菜单“文件”→“导入数据”,打开导入向导“Import Wizard”第一步:选择导入类型(Select import type)。
2) 在第二步的“Select file”对话框中,单击“Browse”按钮,在“打开”对话框中选择所需要的Excel文件,返回。
然后,单击“Option”按钮,选择所需的工作表。
(注意Excel文件要是2003的!!)3) 在第三步的“Select library and member”对话框中,选择导入数据集所存放的逻辑库以及数据集的名称。
4 ) 在第四步的“Create SAS Statements”对话框中,可以选择将系统生成的程序代码存放的位置,完成导入过程。
2.用INSIGHT创建数据集1)启动SAS INSIGHT模块,在“SAS INSIGHT:Open”对话框的”逻辑库“列表框中,选定库逻辑名2)单击“新建”按钮,在行列交汇处的数据区输入数据值(注意列名型变量和区间型变量,这在后面方差分析相关性分析等都要注意!!)3)数据集的保存:•“文件”→“保存”→“数据”;•选择保存的逻辑库名,并输入数据集名;•单击“确定”按钮。
即可保存新建的数据集。
3.用VIEWTABLE窗口建立数据集1)打开VIEWTABLE窗口2)单击表头顶端单元格,输入变量名3)在变量名下方单元格中输入数据4)变量类型的定义:右击变量名/column attributes…4.用编程方法建立数据集DATA 语句; /*DATA步的开始,给出数据集名*/Input 语句;/*描述输入的数据,给出变量名及数据类型和格式等*/(用于DATA步的其它语句)Cards; /*数据行的开始*/[数据行]; /*数据块的结束*/RUN; /*提交并执行*/例子:data=数据集名字;input name$ phone room height; ($符号代表该列为列名型,就是这一列是文字!!比如名字,性别,科目等等)cards;rebeccah 424 112 (中间是数据集,中间每一行末尾不要加逗号,但是carol 450 112 数据集最后要加一个分号!!)louise 409 110gina 474 110mimi 410 106alice 411 106brenda 414 106brenda 414 105david 438 141betty 464 141holly 466 140;proc print data=; (这一过程步是打印出数据集,可要可不要!)run;*数据集中的框架我会用加粗来显示,大家主要记加粗的,下面的编程部分都是这样!!二、基本统计分析1.用INSIGHT计算统计量1)在INSIGHT中打开数据集在菜单中选择“Solution(解决方案)”→“Analysis(分析)”“Interactive Data Analysis(交互式数据分析)”,打开“SAS/INSIGHT Open”对话框,在对话框中选择数据集,单击“Open(打开)”按钮,即可在INSIGHT中打开数据窗口2)选择菜单“Analyze(分析)”→“Distribution (Y)(分布)”,打开“Distribution (Y)”对话框。
学会使用SAS进行数据分析与统计

学会使用SAS进行数据分析与统计第一章:SAS简介与安装1.1 SAS的定义与发展历程1.2 SAS的应用领域与优势1.3 SAS的安装与配置步骤第二章:SAS基本语法与数据处理2.1 SAS数据集的创建与导入2.2 数据集的基本操作(查询、排序、合并等)2.3 数据集的转换与处理(缺失值处理、变量转换等)第三章:SAS统计分析3.1 描述性统计分析(中心趋势与离散程度测量)3.2 统计图表(直方图、散点图、箱线图等)3.3 参数检验方法(t检验、方差分析等)3.4 非参数检验方法(秩和检验、卡方检验等)3.5 回归分析(线性回归、逻辑回归等)第四章:SAS数据挖掘与建模4.1 数据挖掘的概念与方法论4.2 数据挖掘过程与流程4.3 数据探索与预处理4.4 分类与预测模型的建立4.5 模型评估与应用第五章:SAS与大数据分析5.1 大数据与SAS的关系与发展趋势5.2 大数据的存储与处理5.3 大数据分析的典型方法与应用5.4 SAS在大数据分析中的优势与应用案例第六章:SAS与业务决策支持6.1 SAS在决策支持系统中的作用6.2 基于SAS的数据驱动决策方法6.3 风险管理与预警系统的建立6.4 模拟与优化决策的实现6.5 基于SAS的智能决策系统案例分析第七章:SAS的应用案例分析7.1 金融行业中的风险控制与信用评估7.2 医疗保险领域中的疾病预测与费用预测7.3 零售行业中的用户行为分析与精准营销7.4 制造业中的质量控制与生产优化7.5 市场调研与品牌分析中的应用案例第八章:SAS的发展与前景展望8.1 SAS在数据科学领域的地位与作用8.2 SAS的发展趋势与技术创新8.3 SAS对于人才发展的需求8.4 对于SAS未来的个人职业规划建议总结:本文分析了SAS的基础语法与数据处理、统计分析、数据挖掘与建模、大数据分析、业务决策支持以及应用案例等多个方面。
SAS作为一种功能强大的数据分析与统计工具,在各行各业的实际应用中发挥着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
给每一个缺失数据一 些替代值,如此得到 “完全数据集”后,再使用完全数据统计 分析方法分析数据并进行统计推断。
近年来,人们开始重视数据缺失问题,着 力研究插补方法。迄今为 止,提出并发展 了30多种的插补方法。在抽样调查中应用 的主要是单一插补和多重插补。
特别注意:插补的目的并不是预测单个缺 失值,而是预测缺失数据所服从的分布.
RUN;
第二节 数据探索
数据特征 均值 中位数 众数 方差 标准差
标准误差
定义 -- 观测值升序排列 出现频率最高的数 -- 方差的平方根 --
公式
x
1 n
n i 1
xi
N为奇数: x2 n
N为偶数:
x2
n
x2
n1
2Leabharlann s2 1 n n 1 i1
2
xi x
--
s n
程序实现
PROC MEANS; BY <DESCENDING> variable-1 <... >; CLASS variable(s); FREQ variable; ID variable(s); OUTPUT ; VAR ; WEIGHT variable; RUN;
PROC UNIVARIATE; BY variables ; CLASS variable(s); ; FREQ variable ; HISTOGRAM; ID variables ; OUTPUT ; PROBPLOT < variables >; QQPLOT < variables >; VAR variables ; WEIGHT variable ; RUN;
第三节 缺失值填充
在许多实际问题的研究中,有一些数据 无法获得或缺失。当缺失比例很小时,可 直接对完全记录进行数据处理,舍弃缺失 记录。 但在实际数据中,往往缺失数据占
有相当的比重,尤其是多元数据。这时前 述的处理将是低效率的,因为这样做丢失 了大量信息,并且会产生偏倚,使不完全 观测数据与完全观测数据间产生系统差异.
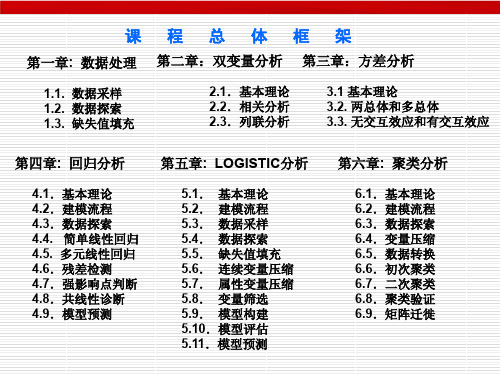
课程总体框架
第一章: 数据处理 第二章:双变量分析 第三章:方差分析
1.1. 数据采样 1.2. 数据探索 1.3. 缺失值填充
2.1.基本理论 2.2.相关分析 2.3.列联分析
3.1 基本理论 3.2. 两总体和多总体 3.3. 无交互效应和有交互效应
第四章: 回归分析
第五章: LOGISTIC分析
系统抽样(systematic sampling):先把总体中的每个个体编号,然后随机选取其中 之一作为抽样的开始点进行抽样,可以想象,如果编号是随机的,系统抽样与简单随机 抽样是等价的。
程序实现
PROC SURVEYSELECT options; STRATA variables ; CONTROL variables ; SIZE variable ; ID variables;
4.1.基本理论 4.2.建模流程 4.3.数据探索 4.4. 简单线性回归 4.5. 多元线性回归 4.6.残差检测 4.7.强影响点判断 4.8.共线性诊断 4.9.模型预测
5.1. 基本理论 5.2. 建模流程 5.3. 数据采样 5.4. 数据探索 5.5. 缺失值填充 5.6. 连续变量压缩 5.7. 属性变量压缩 5.8. 变量筛选 5.9. 模型构建 5.10.模型评估 5.11.模型预测
PROC FREQ < options > ; BY variables ; OUTPUT; TABLES requests; WEIGHT variable; RUN;
PROC BOXPLOT < options > ; PLOT analysis-variable*group-variable; BY variables; ID variables; RUN;
单一插补指对每个缺失值,从其预测分布 中取一个值填充缺失值后,使用标准的完 全数据分析进行处理。
插补方法:业务逻辑;均值法;最小邻居法; 比率/回归法;决策数法等。
单一插补往往会低估估计量的方差,为改 善这一弊病,80年代前后,Rubin提出了 多重插补。多重插补是一种以模拟为基础 的方法,对每个缺失值产生m个合理的插 补值,这样插补后,得到m组完全数据, 使用标准的完全数据方法分析每组数据并 融合分析结果。
程序实现
1.单一插补: PROC STDIZE < options > ; BY variables ; FREQ variable ; LOCATION variables ; SCALE variables ; VAR variables ; WEIGHT variable ; RUN;
2.多重插补: PROC MI < options > ; BY variables ; CLASS variables ; EM < options > ; FREQ variable ; MCMC < options > ; MONOTONE < options > ; VAR variables ; RUN;
分层抽样(stratified sampling):对总体按照某些性质分类,再从类别中随机抽取样 本。显然,分层抽样考虑到了总体要分层的性质上差异性。
整群抽样(cluster sampling):先把总体分成若干群,再从这些群中抽取几个群;然 后再在这些抽取的群中对个体进行简单随机抽样。整群抽样一般要求群之间的差异不能 太大,否则会增大误差。
第一节 数据采样
总体(population):包含所要研究的个体的集合,现实世界一般不可获取。
样本(sample):总体中的部分,一般通过抽查获取。
样本量(sample size):样本中个体的数量。
随机样本:总体中每个个体以等概率选入所获得的样本。
抽样方法:
简单随机抽样(simple random sampling):对总体每一个体以同等概率抽取。
第六章: 聚类分析
6.1.基本理论 6.2.建模流程 6.3.数据探索 6.4.变量压缩 6.5.数据转换 6.6.初次聚类 6.7.二次聚类 6.8.聚类验证 6.9.矩阵迁徙
第一章 数据处理
培训目的: 1.掌握数据建模前数据预处理的必要工作; 2.掌握数据采样的方法; 3.掌握数据探索的方法; 4.掌握数据缺失值填充的方法
