55曲线与方程
ProeCreoUG曲线方程大全及关系式、函数的说明资料

Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程:r = 5 theta = t*3600z =(sin(3.5*theta-90))+24*t图1圆柱坐标(cylindrical ) 方程: r=ttheta=10+t*(20*360) z=t*3图34.蝴蝶曲线 球坐标方程:rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8图4图5笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合(二)Array22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta) Array图23 24.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图2627.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图3637.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合(三)42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图4243.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图4647.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图4950 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图5354.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图5556.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图5758.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图5859.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图6061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合(四)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图6263.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图6364.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图6465.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线). 球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图6768.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
曲线与方程 知识讲解(非常有用)

曲线与方程编稿:辛文升审稿:孙永钊【考纲要求】1.了解轨迹的背景、含义和概念2.能根据所给的条件,选择恰当的直角坐标系求出曲线的轨迹方程,画出某些简单方程所表示的曲线;3.在形成概念的过程中,培养分析、抽象和概括等思维能力,4.掌握形数结合、函数与方程、化归与转化等数学思想,以及坐标法、待定系数法等常用的数学方法;渗透数形结合思想。
【知识网络】轨迹数学思想与方法求轨迹方程的常用方法轨迹的概念、意义【考点梳理】【高清课堂:曲线与方程408396知识要点】考点一:曲线与方程的定义1.“曲线的方程”、“方程的曲线”的定义:在直角坐标系中,如果某曲线C 上的点与一个二元方程0),(=y x f 的实数解建立了如下关系:(1)曲线上的点的坐标都是这个方程的解(轨迹的纯粹性);(2)以这个方程的解为坐标的点都是曲线上的点(轨迹的完备性);那么,这个方程叫做曲线的方程;这条曲线叫做方程的曲线。
2.定义的理解:设P={具有某种性质(或适合某种条件)的点},{(,)|(,)0}Q x y f x y ==,若设点00(,)M x y ,用集合的观点,上述定义中的两条可以表述为:(1)00(,)M P x y Q ∈⇒∈,即P Q ⊆;(2)00(,)x y Q M P ∈⇒∈,即Q P ⊆。
以上两条还可以转化为它们的等价命题(逆否命题):(1)00(,)x y Q M P ∉⇒∉;(2)00(,)M P x y Q ∉⇒∉。
显然,当且仅当P Q ⊆且Q P ⊆,即Q P =时,才能称方程0),(=y x f 为曲线C 的方程;曲线C 为方程0),(=y x f 的曲线(图形).要点诠释:在领会定义时,要牢记关系(1)、(2)两者缺一不可,它们都是“曲线的方程”和“方程的曲线”的必要条件.两者满足了,“曲线的方程”和“方程的曲线”才具备充分性.只有符合关系(1)、(2),才能将曲线的研究转化为方程来研究,即几何问题的研究转化为代数问题.这种“以数论形”的思想是解析几何的基本思想和基本方法考点二:求曲线方程的一般步骤求简单的曲线方程的一般步骤:(1)建立适当的坐标系,用有序实数对表示曲线上任意一点M 的坐标;(2)写出适合条件P 的点M 的集合()P M ;(3)用坐标表示条件()P M ,列出方程0),(=y x f ;(4)化方程0),(=y x f 为最简形式;(5)证明以化简后的方程的解为坐标的点都是曲线上的点上述方法简称“五步法”,在步骤④中若化简过程是同解变形过程;或最简方程的解集与原始方程的解集相同,则步骤⑤可省略不写,因为此时所求得的最简方程就是所求曲线的方程。
ProeCreoUG曲线方程大全及关系式、函数的说明资料

Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t图12.葉形线.圆柱坐标(cylindrical ) 方程: r=ttheta=10+t*(20*360) z=t*3图3图5笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合(二)Array22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图23 24.长短幅圆内旋轮线卡笛尔坐标b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图24 25.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图32 33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图33 34.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图35 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图36 37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图38 39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2phi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合(三)42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图42 43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图44 45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图45 46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图46 47.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图51 52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图53 54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图55 56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图58 59.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图59 60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图60 61.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合(四)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图64 65.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线)球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
第3讲空间解析几何—曲面、曲线及其方程

第3讲 空间解析几何—曲面、曲线及其方程本节主要内容第三节 曲面及其方程1 曲面方程的概念2 旋转曲面3 柱 面 4二次曲面第四节 空间曲线及其方程1 空间曲线的一般方程2 空间曲线的参数方程3 空间曲线在坐标面上的投影讲解提纲:第七章 空间解析几何与向量代数第三节 曲面及其方程一、 曲面方程的概念空间曲面研究的两个基本问题是:1.已知曲面上的点所满足的几何条件,建立曲面的方程;2.已知曲面方程,研究曲面的几何形状.二、旋转曲面以一条平面曲线绕其平面上的一条直线旋转一周形成的曲面叫做旋转曲面,旋转曲线和定直线分别叫做旋转曲面的母线和轴。
三、柱面平行于定直线并沿定曲线C 移动的直线L 形成的轨迹叫做柱面,定曲线C 叫做柱面的准线,动直线L 叫做柱面的母线。
四、二次曲面三元二次方程0),,(=z y x F 所表示的曲面称为二次曲面。
例题选讲:曲面方程的概念例1 建立球心在点),,(0000z y x M 、半径为R 的球面方程. 解:易得球面方程为2222000()()()x x y y z z R -+-+-=例2 求与原点O 及)4,3,2(0M 的距离之比为1:2的点的全体所组成的曲面方程. 解:易得曲面方程为22224116()(1)()339x y z +++++=。
例3 已知()1,2,3,A ()2,1,4,B - 求线段AB 的垂直平分面的方程.解:设点(,,)M x y z 为所求平面上的任一点,由 A M B M ==整理得26270x y z -+-=。
例4方程2222440x y z x y z ++-++=表示怎样的曲面?旋转曲面例5 将xOz 坐标面上的抛物线25z x =分别绕x 轴旋转一周,求所生成的旋转曲面的方程.解:易得旋转曲面的方程225y z x +=例6 直线L 绕另一条与L 相交的定直线旋转一周, 所得旋转曲面称为叫圆锥面. 两直线的交点称为圆锥面的顶点, 两直线的夹角α)20(πα<<称为圆锥面的半顶角. 试建立顶点在坐标原点, 旋转轴为z 轴, 半顶角为α的圆锥面方程解:在yoz 坐标平面上,直线L 的方程为 c o tz y α= 可得圆锥面的方程为2222()z x y α=+柱面例7 分别求母线平行于x 轴和y 轴,且通过曲线222222216x y z x y z ⎧++=⎨-+=⎩的柱面方程.解:母线平行于x 轴的柱面方程:22316y z -= 母线平行于y 轴的柱面方程:223216x z += 二次曲面.椭球面:1222222=++cz b y a x )0,0,0(>>>c b a抛物面椭圆抛物面 qy p x z 2222+= (同号与q p )双曲抛物面 z qy p x =+-2222 ( p 与q 同号)双曲面单叶双曲面 1222222=-+c z b y a x )0,0,0(>>>c b a双叶双曲面 1222222-=-+c z b y a x )0,0,0(>>>c b a二次锥面 0222222=-+cz b y a x例8 由曲面,0,0,0===z y x 1,122=+=+z y y x 围成的空间区域(在第一卦限部分), 作它的简图.课堂练习 1.求直线11:121x y z L --==绕z 轴旋转所得到的旋转曲面的方程. 2.指出方程221x y -=及22z x =-所表示的曲面. 3 方程()()22234z x y =-+--的图形是怎样的?第四节 空间曲线及其方程一、 空间曲线的一般方程 ⎩⎨⎧==0),,(0),,(z y x G z y x F二、空间曲线的参数方程 ⎪⎩⎪⎨⎧===)()()(t z z t y y t x x三、 空间曲线在坐标面上的投影⇒⎩⎨⎧==.0),,(,0),,(z y x G z y x F ⇒=0),(y x H ⎩⎨⎧==00),(z y x H例题选讲:空间曲线的一般方程例1方程组 221493x y y ⎧+=⎪⎨⎪=⎩表示怎样的曲线?空间曲线的参数方程例2 若空间一点M 在圆柱面222a y x =+上以角速度ω绕z 轴旋转, 同时又以线速度v 沿平行于z 轴的正方向上升 (其中ω、v 是常数), 则点M 构成的图形叫做螺旋线. 试建立其参数方程.解:取时间t 为参数,在t=0时,动点位于x 轴上的一点(,0,0)A a 处。
圆锥曲线方程知识点总结

圆锥曲线方程知识点总结一、圆锥曲线的基本方程椭圆的标准方程如下:$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. (a > b > 0)$$其中椭圆的长轴为$2a$,短轴为$2b$,焦距为$\sqrt{a^2 - b^2}$,离心率为$c/a$。
双曲线的标准方程如下:$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1. (a > 0, b > 0)$$其中双曲线的两个分支的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$。
抛物线的标准方程如下:$$x^2 = 4ay. (a > 0)$$其中抛物线的焦点为$(0, a)$,顶点为$(0, 0)$。
二、圆锥曲线的参数方程圆锥曲线还可以用参数方程表示。
以椭圆为例,其参数方程为:$$\begin{cases}x = a \cos \theta, \\y = b \sin \theta. \\\end{cases}$$其中$\theta$的取值范围为$[0, 2\pi]$。
双曲线和抛物线的参数方程也可以类似地表示。
三、圆锥曲线的极坐标方程圆锥曲线还可以用极坐标方程表示。
以椭圆为例,其极坐标方程为:$$r = \frac{ab}{\sqrt{a^2 \sin^2 \theta + b^2 \cos^2 \theta}}.$$其中$r$为极径,$\theta$为极角。
双曲线和抛物线的极坐标方程也可以类似地表示。
四、圆锥曲线的性质1. 圆锥曲线关于坐标轴的对称性:- 椭圆关于$x$轴和$y$轴都对称;- 双曲线关于$x$轴和$y$轴都对称;- 抛物线关于$y$轴对称。
2. 圆锥曲线的焦点、直径、离心率等:- 椭圆的焦点到中心的距离为$c = \sqrt{a^2 - b^2}$,离心率为$e = c/a$;- 双曲线的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$,离心率为$e = c/a$;- 抛物线的焦点到中心的距离为$c = a$,离心率为$e = 1$。
各种曲线的方程

1.碟形弹簧圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t2.葉形线.笛卡儿坐標标方程:a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3.螺旋线(Helical curve)圆柱坐标(cylindrical)方程:r=ttheta=10+t*(20*360)z=t*34.蝴蝶曲线球坐标方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 85.渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=06.螺旋线.笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t7.对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t+0.0001)8.球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*209.双弧外摆线卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)10.星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^311.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*36012.圆内螺旋线采用柱座标系方程:theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)13.正弦曲线笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=014.太阳线(这本来是做别的曲线的,结果做错了,就变成这样了)15.费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做16.Talbot 曲线卡笛尔坐标方程:theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b17.4叶线(一个方程做的,没有复制)18.Rhodonea 曲线采用笛卡尔坐标系方程:theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)19. 抛物线笛卡儿坐标方程:x =(4 * t)y =(3 * t) + (5 * t ^2) z =020.螺旋线圓柱坐标方程:r = 5theta = t*1800z =(cos(theta-90))+24*t21.三叶线圆柱坐标方程:a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta) y=(a+b)*sin(theta)-b*sin((a/b+1)*theta) z=023. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c) y=b*sin(theta)24.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)25.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)柱坐标a=100theta = t*400r = a*theta30.对数螺线柱坐标theta = t*360*2.2 a = 0.005r = exp(a*theta)31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x) for x32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/234.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/235.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+137.八字曲线x = 2 * cos ( t *(2*180)) y = 2 * sin ( t *(5*360)) z = 038.螺旋曲线r=t*(10*180)+1 theta=10+t*(20*180) z=t39.圆x = cos ( t *(5*180)) y = sin ( t *(5*180)) z = 040.封闭球形环绕曲线rho=2theta=360*tphi=t*360*1041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 042.蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)柱坐标theta = t*360r=10+(8*sin(theta))^244.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)45.梅花曲线柱坐标r=10+(3*sin(theta*2.5))^246.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^247.改一下就成为空间感更强的花曲线了;) theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^248.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*1249.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2 z = t*1650 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+t theta=t*360*10z=t*1051 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*1053.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*2055. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)56.梅花曲线theta=t*360r=100+50*cos(5*theta) z=2*cos(5*theta)57.桃形曲线rho=t^3+t*(t+1) theta=t*360phi=t^2*360*10*1058.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+2459.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2) z=sin(ang2)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*664.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8) y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*865.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)66. ufo (漩涡线)球坐标:rho=t*20^2 theta=t*log(30)*60 phi=t*720067. 手把曲线thta0=t*360 thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1) x=r*cos(thta0)y=r1*sin(thta1)z=068.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*569. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
双曲线的简单几何性质(直线与双曲线的位置关系)

焦点坐标,离心率.渐近线方程。 解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3 半焦距c=
42 32 5
焦点坐标是(0,-5),(0,5) 离心率:
e
4 渐近线方程: y x 3
c 5 a 4
5 例2:已知双曲线顶点间的距离是16,离心率e , 4 焦点在x轴上,中心在原点,写出双曲线的方 程,并且求出它的渐近 线和焦点坐标 . 2 2
解: 椭圆的焦点在x轴上,且坐标为
F , 0),F ( , 0) 1 (2 2 2 2 2
双曲线的焦点在x轴上,且c 2 2
3 双曲线的渐近线方程为 y x 3 b 3 ,而c 2 a 2 b 2 , a 2 b 2 8 a 3 解出 a 2 6,b 2 2 x2 y2 双曲线方程为 1 6 2
xa
x a
ya
或
或
y a
b c 关于 ( a,0) y x e 坐标 a a 轴和 (其中 原点 都对 a c 2 a 2 b2 ) 称 (0, a) y x b
例题讲解
例1 :求双曲线
9y2 16x2 144 的实半轴长,虚半轴长,
y2 x2 2 1 2 4 3
. .
B2 A2
图形
. .
F1(-c,0)
F1
y
y
F2
A1 A2
O
F2(0,c)
B1
B1 F2(c,0)
F2
x
A1 O F1
x F1(0,-c)
方程 范围 对称性 顶点 离心率 渐近线
பைடு நூலகம்
x y 1 (a b 0) 2 2 a b
高中数学必修一《双曲线及其标准方程》课件

2R
又∵|BC|-|AC|=±8,
∴sin
A-sin sin C
B=±180=±45.]
31
(2)[解] 因为 P 是双曲线左支上的点,所以|PF2|-|PF1|=6,两 边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,所以|PF1|2+|PF2|2=36+ 2|PF1|·|PF2|=36+2×32=100.
16
(2)法一:∵焦点相同, ∴设所求双曲线的标准方程为ax22-by22=1(a>0,b>0),
∴c2=16+4=20,即 a2+b2=20.
①
∵双曲线经过点(3 2,2),∴1a82-b42=1.
②
由①②得 a2=12,b2=8,∴双曲线的标准方程为1x22 -y82=1.
17
法二:设所求双曲线的方程为16x-2 λ-4+y2 λ=1(-4<λ<16). ∵双曲线过点(3 2,2),∴161-8 λ-4+4 λ=1, 解得 λ=4 或 λ=-14(舍去). ∴双曲线的标准方程为1x22 -y82=1.
所以双曲线的标准方程为x32-y52=1.
23
(2)因为焦点在 x 轴上,且 c= 6, 所以设双曲线的标准方程为ax22-6-y2a2=1,0<a2<6. 又因为过点(-5,2),所以2a52 -6-4 a2=1, 解得 a2=5 或 a2=30(舍去). 所以双曲线的标准方程为x52-y2=1.
(2)双曲线的定义中,F1、F2 分别为双曲线的左、右焦点,若|MF1| -|MF2|=2a(常数),且 2a<|F1F2|,则点 M 的轨迹是什么?
[提示] (1)当距离之差的绝对值等于|F1F2|时,动点的轨迹是两 条射线,端点分别是 F1,F2,当距离之差的绝对值大于|F1F2|时,动 点的轨迹不存在.
曲线与方程知识点总结

曲线与方程知识点总结一、直线的方程1. 斜截式方程直线的斜率k为非零常数,截距b为任意实数,直线方程可表示为:y = kx + b2. 截距式方程过点A(a,b)且与x轴、y轴交点分别为A,B的直线方程为:\frac{x}{a} + \frac{y}{b} = 13. 两点式方程经过两点A(x1,y1)和B(x2,y2)的直线方程为:\frac{y-y1}{y2-y1} = \frac{x-x1}{x2-x1}4. 四个参数式方程经过点A(x1,y1)且斜率为k的直线方程为:(y-y1) = k(x-x1)5. 我国教科书通常在中学阶段只讲解前三种方程的形式,但四个参数式方程在高等数学的微积分、解析几何等课程中非常常见。
6. 平面直角直线方程通常可写为y = kx + b,其中k为直线的斜率,b为截距。
二、曲线的方程1. 平面曲线方程:对于任一平面曲线,通常可以写成y=f(x)的形式。
其中,f(x)是x的函数,描述了y与x 的关系。
2. 参数式方程:有时,平面曲线不方便用y=f(x)的形式描述,而可以使用参数式方程。
参数式方程是一对函数x(t),y(t)关于参数t的表达式。
3. 极坐标方程:在极坐标系中,平面曲线可以写成r=f(θ)的形式。
其中,r是极径,θ是极角。
三、曲线的性质1. 曲线的对称性:关于x轴对称、y轴对称、原点对称、关于直线y=x对称等。
2. 曲线的周期性:函数f(x)具有周期T的性质,如果满足f(x+T) = f(x)。
曲线在点(x,f(x))和点(x+T,f(x))上有相同的函数值。
3. 曲线的单调性:函数f(x)在区间I上单调递增或单调递减。
4. 曲线的凹凸性:函数f(x)在区间I上凹函数或凸函数。
5. 曲线的渐近线:直线y=kx+b与曲线f(x)有以下情形:a) f(x)在正无穷大的地方与y=kx+b趋近同一数值。
b) f(x)在正无穷大的地方与y=kx+b趋近无穷大。
c) f(x)在正无穷大的地方与y=kx+b有交点但同时趋于正无穷大和负无穷大。
双曲线方程推导步骤

双曲线方程推导步骤宝子,今天咱来唠唠双曲线方程的推导哈。
咱先从双曲线的定义说起,双曲线就是平面内到两个定点F1、F2的距离之差的绝对值是常数(这个常数要小于F1F2哦)的点的轨迹。
那咱就设这两个定点F1、F2在x轴上,坐标分别是(-c,0)和(c,0),然后设双曲线上任意一点P的坐标是(x,y)。
根据定义,PF1 - PF2 = 2a(a是个正数呢)。
那PF1的长度就是根号下[(x + c)² + y²],PF2的长度就是根号下[(x - c)²+ y²]。
这时候就有两种情况啦。
当PF1 - PF2 = 2a的时候,也就是根号下[(x + c)² + y²] - 根号下[(x - c)² + y²]=2a。
这个式子看起来有点复杂,咱得想办法把根号去掉。
那就把后面那个带根号的式子移到右边,然后两边同时平方。
这样就得到(x + c)² + y² = 4a²+ (x - c)² + y²+4a根号下[(x - c)² + y²]。
展开式子,x²+2cx + c²+y² = 4a²+x² - 2cx + c²+y²+4a根号下[(x - c)² + y²]。
一些项可以消掉啦,就剩下4cx - 4a² = 4a根号下[(x - c)² + y²]。
再化简一下,cx - a² = a根号下[(x - c)² + y²]。
再平方一次,(cx - a²)² = a²[(x - c)² + y²]。
展开又能得到好多项,c²x² - 2a²cx + a⁴ = a²(x² - 2cx + c²+ y²)。
高考数学二轮复习考点知识与题型专题讲解41---圆锥曲线的方程与性质

高考数学二轮复习考点知识与题型专题讲解第41讲圆锥曲线的方程与性质[考情分析]高考对这部分知识的考查侧重三个方面:一是求圆锥曲线的标准方程;二是求椭圆的离心率、双曲线的离心率以及渐近线问题;三是抛物线的性质及应用问题.考点一圆锥曲线的定义与标准方程核心提炼1.圆锥曲线的定义(1)椭圆:|PF1|+|PF2|=2a(2a>|F1F2|).(2)双曲线:||PF1|-|PF2||=2a(0<2a<|F1F2|).(3)抛物线:|PF|=|PM|,l为抛物线的准线,点F不在定直线l上,PM⊥l于点M.2.求圆锥曲线标准方程“先定型,后计算”“定型”:确定曲线焦点所在的坐标轴的位置;“计算”:利用待定系数法求出方程中的a2,b2,p 的值.例1(1)(2022·衡水中学模拟)已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,以线段F1A为直径的圆交线段F1B的延长线于点P,若F2B∥AP且线段AP的长为2+2,则该椭圆方程为()A.x 24+y 22=1B.x 28+y 23=1 C.x 25+y 24=1 D.x 28+y 24=1 答案 D解析 设椭圆的半焦距为c ,因为点P 在以线段F 1A 为直径的圆上,所以AP ⊥PF 1.又因为F 2B ∥AP ,所以F 2B ⊥BF 1.又因为|F 2B |=|BF 1|,所以△F 1F 2B 是等腰直角三角形,于是△F 1AP 也是等腰直角三角形,因为|AP |=2+2,所以|F 1A |=2(2+2),得a +c =2(2+2),又b =c ,所以a =2c ,解得a =22,c =2,得b 2=a 2-c 2=4,所以椭圆方程为x 28+y 24=1. (2)(2022·荆州模拟)已知双曲线C :x 216-y 29=1的左、右焦点分别是F 1,F 2,点P 是C 右支上的一点(不是顶点),过F 2作∠F 1PF 2的角平分线的垂线,垂足是M ,O 是原点,则|MO |=________. 答案 4解析 延长F 2M 交PF 1于点Q ,由于PM 是∠F 1PF 2的角平分线,F 2M ⊥PM ,所以△QPF 2是等腰三角形,所以|PQ |=|PF 2|,且M 是QF 2的中点.根据双曲线的定义可知|PF 1|-|PF 2|=2a ,即|QF 1|=2a ,由于O 是F 1F 2的中点,所以MO 是△QF 1F 2的中位线,所以|MO |=12|QF 1|=a =4. 易错提醒 求圆锥曲线的标准方程时的常见错误双曲线的定义中忽略“绝对值”致错;椭圆与双曲线中参数的关系式弄混,椭圆中的关系式为a 2=b 2+c 2,双曲线中的关系式为c 2=a 2+b 2;圆锥曲线方程确定时还要注意焦点位置.跟踪演练1 (1)已知双曲线的渐近线方程为y =±22x ,实轴长为4,则该双曲线的方程为( ) A.x 24-y 22=1 B.x 24-y 28=1或y 24-x 28=1 C.x 24-y 28=1 D.x 24-y 22=1或y 24-x 28=1 答案 D解析 设双曲线方程为x 22m -y 2m=1(m ≠0), ∵2a =4,∴a 2=4,当m >0时,2m =4,m =2;当m <0时,-m =4,m =-4.故所求双曲线的方程为x 24-y 22=1或y 24-x 28=1. (2)已知A ,B 是抛物线y 2=8x 上两点,当线段AB 的中点到y 轴的距离为3时,|AB |的最大值为( )A .5B .5 2C .10D .10 2答案 C解析 设抛物线y 2=8x 的焦点为F ,准线为l ,线段AB 的中点为M .如图,分别过点A ,B ,M 作准线l 的垂线,垂足分别为C ,D ,N ,连接AF ,BF .因为线段AB 的中点到y 轴的距离为3,抛物线y 2=8x 的准线l :x =-2,所以|MN |=5.因为|AB |≤|AF |+|BF |=|AC |+|BD |=2|MN |=10,当且仅当A ,B ,F 三点共线时取等号,所以|AB |max =10.考点二 椭圆、双曲线的几何性质 核心提炼1.求离心率通常有两种方法(1)求出a ,c ,代入公式e =c a. (2)根据条件建立关于a ,b ,c 的齐次式,消去b 后,转化为关于e 的方程或不等式,即可求得e 的值或取值范围.2.与双曲线x 2a 2-y 2b 2=1(a >0,b >0)共渐近线bx ±ay =0的双曲线方程为x 2a 2-y 2b 2=λ(λ≠0).考向1 椭圆、双曲线的几何性质例2(2022·河南五市联考)设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,以F 2为圆心的圆恰好与双曲线C 的两条渐近线相切,且该圆恰好经过线段OF 2的中点,则双曲线C 的渐近线方程为( )A .y =±3xB .y =±33x C .y =±233x D .y =±2x答案 B解析 由题意知,渐近线方程为y =±b ax , 焦点F 2(c ,0),c 2=a 2+b 2,因为以F 2为圆心的圆恰好与双曲线C 的两渐近线相切,则圆的半径r 等于圆心到切线的距离,即r =⎪⎪⎪⎪±b a ·c 1+⎝⎛⎭⎫±b a 2=b , 又该圆过线段OF 2的中点,故c 2=r =b , 所以b a =b 2a 2=b 2c 2-b2=33. 所以渐近线方程为y =±33x . 考向2 离心率问题例3(多选)(2022·全国乙卷)双曲线C 的两个焦点为F 1,F 2,以C 的实轴为直径的圆记为D ,过F 1作D 的切线与C 交于M ,N 两点,且cos ∠F 1NF 2=35,则C 的离心率为( ) A.52B.32 C.132 D.172 答案 AC解析 不妨设双曲线的标准方程为x 2a 2-y 2b2=1(a >0,b >0),F 1(-c ,0),F 2(c ,0). 当两个交点M ,N 在双曲线两支上时,如图1所示,图1设过F 1的直线与圆D 相切于点P ,连接OP ,由题意知|OP |=a ,又|OF 1|=c ,所以|F 1P |=b .过点F 2作F 2Q ⊥F 1N ,交F 1N 于点Q .由中位线的性质,可得|F 2Q |=2|OP |=2a ,|PQ |=b .因为cos ∠F 1NF 2=35, 所以sin ∠F 1NF 2=45, 故|NF 2|=52a ,|QN |=32a , 所以|NF 1|=|F 1Q |+|QN |=2b +32a . 由双曲线的定义可知|NF 1|-|NF 2|=2a ,所以2b +32a -52a =2a ,所以2b =3a . 两边平方得4b 2=9a 2,即4(c 2-a 2)=9a 2,整理得4c 2=13a 2,所以c 2a 2=134, 故c a =132,即e =132. 当两个交点M ,N 都在双曲线上的左支上时,如图2所示,图2同理可得|F 2Q |=2|OP |=2a ,|PQ |=b .因为cos ∠F 1NF 2=35, 所以sin ∠F 1NF 2=45, 可得|NF 2|=52a ,|NQ |=32a , 所以|NF 1|=|NQ |-|QF 1|=32a -2b , 所以|NF 2|=|NF 1|+2a =72a -2b , 又|NF 2|=52a ,所以72a -2b =52a , 即a =2b ,故e =1+⎝⎛⎭⎫b a 2=52.故选AC.规律方法 (1)在“焦点三角形”中,常利用正弦定理、余弦定理,结合椭圆(或双曲线)的定义,运用平方的方法,建立与|PF 1|·|PF 2|的联系.(2)求双曲线渐近线方程的关键在于求b a 或a b的值,也可将双曲线方程中等号右边的“1”变为“0”,然后因式分解得到.跟踪演练2 (1)(2022·全国甲卷)椭圆C :x 2a 2+y 2b2=1(a >b >0)的左顶点为A ,点P ,Q 均在C 上,且关于y 轴对称.若直线AP ,AQ 的斜率之积为14,则C 的离心率为( ) A.32 B.22 C.12 D.13答案 A解析 设P (m ,n )(n ≠0),则Q (-m ,n ),易知A (-a ,0),所以k AP ·k AQ =n m +a ·n -m +a =n 2a 2-m 2=14.(*) 因为点P 在椭圆C 上,所以m 2a 2+n 2b 2=1,得n 2=b 2a2(a 2-m 2),代入(*)式,得b 2a 2=14, 所以e =c a =1-b 2a 2=32.故选A. (2)(多选)(2022·衡水中学模拟)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过点F 2的直线与双曲线的右支交于A ,B 两点,若|AF 1|=|BF 2|=2|AF 2|,则( )A .∠AF 1B =∠F 1ABB .双曲线的离心率e =333C .双曲线的渐近线方程为y =±63x D .原点O 在以F 2为圆心,|AF 2|为半径的圆上答案 AB解析 设|AF 1|=|BF 2|=2|AF 2|=2m ,则|AB |=|AF 2|+|BF 2|=3m ,由双曲线的定义知,|AF 1|-|AF 2|=2m -m =2a ,即m =2a ,|BF 1|-|BF 2|=2a ,即|BF 1|-2m =2a ,∴|BF 1|=3m =|AB |,∠AF 1B =∠F 1AB ,故选项A 正确;由余弦定理知,在△ABF 1中,cos ∠AF 1B =|AF 1|2+|BF 1|2-|AB |22|AF 1|·|BF 1|=4m 2+9m 2-9m 22·2m ·3m =13, 在△AF 1F 2中,cos ∠F 1AB =|AF 1|2+|AF 2|2-|F 1F 2|22·|AF 1|·|AF 2|=4m 2+m 2-4c 22·2m ·m =cos ∠AF 1B =13, 化简整理得12c 2=11m 2=44a 2,∴离心率e =c a =4412=333,故选项B 正确; 双曲线的渐近线方程为y =±b ax =±c 2-a 2a 2x =±e 2-1x =±263x , 故选项C 错误;若原点O 在以F 2为圆心,|AF 2|为半径的圆上,则c =m =2a ,与c a =333相矛盾,故选项D 错误. 考点三 抛物线的几何性质核心提炼抛物线的焦点弦的几个常见结论设AB 是过抛物线y 2=2px (p >0)的焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则(1)x 1x 2=p 24,y 1y 2=-p 2. (2)|AB |=x 1+x 2+p .(3)当AB ⊥x 轴时,弦AB 的长最短为2p .例4 (1)(2022·泰安模拟)已知抛物线C :y 2=2px (p >0)的焦点为F ,点M 在抛物线C 上,射线FM 与y 轴交于点A (0,2),与抛物线C 的准线交于点N ,FM →=55MN →,则p 的值等于( )A.18 B .2 C.14D .4 答案 B解析 设点M 到抛物线的准线的距离为|MM ′|,抛物线的准线与x 轴的交点记为点B.由抛物线的定义知,|MM ′|=|FM |.因为|FM ||MN |=55, 所以|MM ′||MN |=55, 即cos ∠NMM ′=|MM ′||MN |=55, 所以cos ∠OF A =cos ∠NMM ′=55, 而cos ∠OF A =|OF ||AF |=p 2⎝⎛⎭⎫p 22+22=55,解得p =2. (2)(多选)(2022·新高考全国Ⅱ)已知O 为坐标原点,过抛物线C :y 2=2px (p >0)焦点F 的直线与C 交于A ,B 两点,其中A 在第一象限,点M (p ,0).若|AF |=|AM |,则( )A .直线AB 的斜率为2 6B .|OB |=|OF |C .|AB |>4|OF |D .∠OAM +∠OBM <180°答案 ACD解析 对于A ,由题意,得F ⎝⎛⎭⎫p 2,0. 因为|AF |=|AM |,且M (p ,0), 所以x A =x F +x M 2=34p ,将其代入抛物线方程y 2=2px ,得y A =62p , 所以A ⎝⎛⎭⎫34p ,62p ,所以直线AB 的斜率k AB =k AF =62p -034p -p 2=26,故A 正确;对于B ,由选项A 的分析,知直线AB 的方程为y =26⎝⎛⎭⎫x -p2,代入y 2=2px ,得12x 2-13px +3p 2=0,解得x =34p 或x =13p ,所以x B =13p ,所以y B =-63p ,所以|OB |=x 2B +y 2B =73p ≠|OF |,故B不正确;对于C ,由抛物线的定义及选项A ,B 的分析, 得|AB |=x A +x B +p =1312p +p =2512p >2p ,即|AB |>4|OF |,故C 正确; 对于D ,易知|OA |=334p ,|AM |=54p , |OB |=73p ,|BM |=103p , 则cos ∠OAM =|OA |2+|AM |2-|OM |22|OA |·|AM |=3316p 2+2516p 2-p 22×334p ·54p=21533>0,cos ∠OBM =|OB |2+|BM |2-|OM |22|OB |·|BM |=79p 2+109p 2-p 22×73p ·103p=470>0,所以∠OAM <90°,∠OBM <90°,所以∠OAM +∠OBM <180°,故D 正确.综上所述,选ACD.规律方法 利用抛物线的几何性质解题时,要注意利用定义构造与焦半径相关的几何图形(如三角形、直角梯形等)来沟通已知量与p 的关系,灵活运用抛物线的焦点弦的特殊结论,使问题简单化且减少数学运算.跟踪演练3 (1)(2021·新高考全国Ⅰ)已知O 为坐标原点,抛物线C :y 2=2px (p >0)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ ⊥OP .若|FQ |=6,则C 的准线方程为________. 答案 x =-32解析 方法一 (解直角三角形法)由题易得|OF |=p2,|PF |=p ,∠OPF =∠PQF ,所以tan ∠OPF =tan ∠PQF , 所以|OF ||PF |=|PF ||FQ |,即p 2p =p 6,解得p =3,所以C 的准线方程为x =-32.方法二 (应用射影定理法)由题易得|OF |=p 2,|PF |=p ,|PF |2=|OF |·|FQ |,即p 2=p2×6,解得p =3或p =0(舍去),所以C 的准线方程为x =-32.(2)(2022·济宁模拟)过抛物线y 2=4x 的焦点F 的直线与该抛物线及其准线都相交,交点从左到右依次为A ,B ,C .若AB →=2BF →,则线段BC 的中点到准线的距离为( ) A .3 B .4 C .5 D .6 答案 B解析 由抛物线的方程可得焦点F (1,0),渐近线的方程为x =-1,由AB →=2BF →,可得|AB ||BF |=2,由于抛物线的对称性,不妨假设直线和抛物线位置关系如图所示,作BE 垂直准线于点E , 准线交x 轴于点N ,则|BF |=|BE | ,故|AB ||BF |=|AB ||BE |=2,故∠ABE =π4 , 而BE ∥x 轴,故∠AFN =π4,所以直线AB 的倾斜角为π4,所以直线AB 的方程为y =x -1, 设B (x 1,y 1),C (x 2,y 2),联立⎩⎪⎨⎪⎧y =x -1,y 2=4x ,整理可得x 2-6x +1=0,则x 1+x 2=6,所以BC 的中点的横坐标为3, 则线段BC 的中点到准线的距离为3-(-1)=4.专题强化练一、单项选择题1.(2022·中山模拟)抛物线C :y 2=2px 上一点(1,y 0)到其焦点的距离为3,则抛物线C 的方程为( ) A .y 2=4x B .y 2=8x C .y 2=12x D .y 2=16x 答案 B解析 因抛物线C :y 2=2px 上一点(1,y 0)到其焦点的距离为3,则p >0,抛物线准线方程为x =-p2,由抛物线定义得1-⎝⎛⎭⎫-p2=3,解得p =4, 所以抛物线C 的方程为y 2=8x .2.已知双曲线x 2m -y 2=1(m >0)的一个焦点为F (3,0),则其渐近线方程为( )A .y =±24x B .y =±22xC .y =±2xD .y =±12x答案 A解析 因为双曲线x 2m -y 2=1(m >0)的一个焦点为F (3,0),所以由m +1=32,得m =8, 所以双曲线方程为x 28-y 2=1,所以双曲线的渐近线方程为y =±24x .3.(2022·全国乙卷)设F 为抛物线C :y 2=4x 的焦点,点A 在C 上,点B (3,0),若|AF |=|BF |,则|AB |等于( ) A .2 B .2 2 C .3 D .3 2 答案 B解析 方法一由题意可知F (1,0),抛物线的准线方程为x =-1.设A ⎝⎛⎭⎫y 24,y 0, 则由抛物线的定义可知|AF |=y 204+1.因为|BF |=3-1=2,所以由|AF |=|BF |,可得y 204+1=2,解得y 0=±2,所以A (1,2)或A (1,-2).不妨取A (1,2),则|AB |=(1-3)2+(2-0)2=8=22,故选B. 方法二 由题意可知F (1,0),故|BF |=2, 所以|AF |=2.因为抛物线的通径长为2p =4, 所以AF 的长为通径长的一半, 所以AF ⊥x 轴,所以|AB |=22+22=8=2 2.故选B.4.(2022·潍坊模拟)如图,某建筑物白色的波浪形屋顶像翅膀一样漂浮,建筑师通过双曲线的设计元素赋予了这座建筑以轻盈、极简和雕塑般的气质,该建筑物外形弧线的一段可以近似看成焦点在y 轴上的双曲线y 2a 2-x 2b 2=1(a >0,b >0)上支的一部分.已知该双曲线的上焦点F 到下顶点的距离为36,F 到渐近线的距离为12,则该双曲线的离心率为( )A.53B.54C.43D.45 答案 B解析 点F (0,c )到渐近线y =±ab x ,即ax ±by =0的距离d =|±bc |a 2+b 2=b =12, 又由题意知⎩⎪⎨⎪⎧a +c =36,a 2+122=c 2, 解得⎩⎪⎨⎪⎧a =16,c =20,所以e =c a =2016=54.5.(2022·福州质检)已知点F 1,F 2分别是椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过点F 2的直线交椭圆于A ,B 两点,且满足AF 1⊥AB ,|AF 1||AB |=43,则该椭圆的离心率是( )A.23B.53C.33D.63 答案 B解析 如图所示,设|AF 1|=4x ,则|AB |=3x ,因为AF 1⊥AB ,则|BF 1|=|AB |2+|AF 1|2=5x , 由椭圆的定义可得|AF 1|+|AB |+|BF 1|=(|AF 1|+|AF 2|)+(|BF 2|+|BF 1|)=4a =12x ,则x =a 3,所以|AF 1|=4x =4a 3, 则|AF 2|=2a -4a 3=2a3,由勾股定理可得|AF 1|2+|AF 2|2=|F 1F 2|2, 则⎝⎛⎭⎫4a 32+⎝⎛⎭⎫2a 32=4c 2,则c =53a , 因此该椭圆的离心率为e =c a =53.6.如图,圆O 与离心率为32的椭圆T :x 2a 2+y 2b 2=1(a >b >0)相切于点M (0,1),过点M 引两条互相垂直的直线l 1,l 2,两直线与两曲线分别交于点A ,C 与点B ,D (均不重合).若P 为椭圆上任意一点,记点P 到两直线的距离分别为d 1,d 2,则d 21+d 22的最大值是( )A .4B .5 C.163 D.253答案 C解析 易知椭圆C 的方程为x 24+y 2=1,圆O 的方程为x 2+y 2=1, 设P (x 0,y 0), 因为l 1⊥l 2,则d 21+d 22=|PM |2=x 20+(y 0-1)2,因为x 204+y 20=1,所以d 21+d 22=4-4y 20+(y 0-1)2=-3⎝⎛⎭⎫y 0+132+163, 因为-1≤y 0≤1,所以当y 0=-13,即点P ⎝⎛⎭⎫±423,-13时,d 21+d 22取得最大值163. 二、多项选择题7.(2022·临沂模拟)2022年4月16日9时56分,神舟十三号返回舱成功着陆,返回舱是宇航员返回地球的座舱,返回舱的轴截面可近似看作是由半圆和半椭圆组成的“曲圆”,如图在平面直角坐标系中半圆的圆心在坐标原点,半圆所在的圆过椭圆的焦点F (0,2),椭圆的短轴与半圆的直径重合,下半圆与y 轴交于点G .若过原点O 的直线与上半椭圆交于点A ,与下半圆交于点B ,则( )A .椭圆的长轴长为4 2B .|AB |的取值范围是[4,2+22]C .△ABF 面积的最小值是4D .△AFG 的周长为4+4 2 答案 ABD解析 由题意知,椭圆中的几何量b =c =2, 得a =22,则2a =42,A 正确; |AB |=|OB |+|OA |=2+|OA |, 由椭圆性质可知2≤|OA |≤22, 所以4≤|AB |≤2+22,B 正确; 记∠AOF =θ, 则S △ABF =S △AOF +S △OBF=12|OA |·|OF |sin θ+12|OB |·|OF |sin(π-θ) =|OA |sin θ+2sin θ =(|OA |+2)sin θ, 取θ=π6,则S △ABF =1+12|OA |≤1+12×22<4,C 错误;由椭圆定义知|AF |+|AG |=2a =42, 所以△AFG 的周长L =|FG |+42=4+42, D 正确.8.(2022·济宁模拟)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,左、右顶点分别为A 1,A 2,点P 是双曲线C 上异于顶点的一点,则( ) A .||P A 1|-|P A 2||=2aB .若焦点F 2关于双曲线C 的渐近线的对称点在C 上,则C 的离心率为 5 C .若双曲线C 为等轴双曲线,则直线P A 1的斜率与直线P A 2的斜率之积为1D .若双曲线C 为等轴双曲线,且∠A 1P A 2=3∠P A 1A 2,则∠P A 1A 2=π10答案 BCD解析 对于A ,在△P A 1A 2中,根据三角形两边之差小于第三边, 可知||P A 1|-|P A 2||<|A 1A 2|=2a ,故A 错误; 对于B ,焦点F 2(c ,0),渐近线不妨取y =bax ,即bx -ay =0,设F 2关于双曲线C 的渐近线的对称点为(m ,n ),则⎩⎨⎧n m -c ×ba =-1,b ×m +c 2-a ×n2=0,得⎩⎨⎧m =a 2-b 2c,n =2abc ,即F 2关于双曲线C 的渐近线的对称点为⎝⎛⎭⎫a 2-b 2c ,2ab c , 由题意知该点在双曲线上,故(a 2-b 2)2a 2c 2-(2ab )2b 2c 2=1,将c 2=a 2+b 2 代入,化简整理得b 4-3a 2b 2-4a 4=0,即b 2=4a 2,∴e 2=c 2a 2=a 2+b 2a 2=1+b 2a 2=5,得e =5,故B 正确;对于C ,双曲线C 为等轴双曲线, 即C :x 2-y 2=a 2(a >0), 设P (x 0,y 0)(y 0≠0),则x 20-y 20=a 2, 则x 20-a 2=y 20,故12·PA PA k k =y 0x 0+a ·y 0x 0-a=y 20x 20-a2=1,故C 正确; 对于D ,双曲线C 为等轴双曲线, 即C :x 2-y 2=a 2(a >0), 且∠A 1P A 2=3∠P A 1A 2, 设∠P A 1A 2=θ,∠A 1P A 2=3θ, 则∠P A 2x =4θ,根据C 的结论12·PA PA k k =1, 即有tan θ·tan 4θ=1, ∴sin θcos θ·sin 4θcos 4θ=1, ∴cos 5θ=0, ∵θ+3θ∈(0,π), ∴θ∈⎝⎛⎭⎫0,π4, ∴5θ=π2,∴∠P A 1A 2=θ=π10.三、填空题9.写出一个满足以下三个条件的椭圆的方程:______________.①中心为坐标原点;②焦点在坐标轴上;③离心率为13.答案x 29+y 28=1(答案不唯一)解析 只要椭圆方程形如x 29m +y 28m =1(m >0)或y 29m +x 28m=1(m >0)即可.10.(2022·淄博模拟)已知P 1,P 2,…,P 8是抛物线x 2=4y 上不同的点,且F (0,1).若FP 1--→+FP 2--→+…+FP 8--→=0,则|FP 1--→|+|FP 2--→|+…+|FP 8--→|=________.答案 16解析 设P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3),…,P 8(x 8,y 8),P 1,P 2,P 3,…,P 8是抛物线x 2=4y 上不同的点,点F (0,1),准线为y =-1,则FP i --→=(x i ,y i -1)(i =1,2,…,8),所以FP 1--→+FP 2--→+…+FP 8--→=(x 1+x 2+…+x 8,(y 1-1)+(y 2-1)+…+(y 8-1))=0,所以(y 1-1)+(y 2-1)+…+(y 8-1)=0,即y 1+y 2+y 3+…+y 8=8,∴|FP --→1|+|FP 2--→|+…+|FP 8--→|=(y 1+1)+(y 2+1)+…+(y 8+1)=y 1+y 2+…+y 8+8=16.11.(2022·济南模拟)已知椭圆C 1:x 236+y 2b 2=1(b >0)的焦点分别为F 1,F 2,且F 2是抛物线C 2:y 2=2px (p >0)的焦点,若P 是C 1与C 2的交点,且|PF 1|=7,则cos ∠PF 1F 2的值为________.答案57解析 依题意,由椭圆定义得|PF 1|+|PF 2|=12,而|PF 1|=7,则|PF 2|=5,因为点F 2是抛物线C 2:y 2=2px (p >0)的焦点,则该抛物线的准线l 过点F 1,如图,过点P 作PQ ⊥l 于点Q ,由抛物线定义知|PQ |=|PF 2|=5,而F 1F 2∥PQ ,则∠PF 1F 2=∠F 1PQ ,所以cos ∠PF 1F 2=cos ∠F 1PQ =|PQ ||PF 1|=57. 12.(2022·福州质检)已知O 为坐标原点,F 是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左焦点,A 为C 的右顶点,过F 作C 的渐近线的垂线,垂足为M ,且与y 轴交于点P .若直线AM 经过OP 的中点,则C 的离心率是________.答案 2解析 由题意可知,F (-c ,0),A (a ,0),渐近线不妨设为y =-b ax , 则k FM =a b, 直线FM 的方程为y =a b(x +c ), 令x =0,可得y =ac b, 则P ⎝⎛⎭⎫0,ac b , 则OP 的中点坐标为⎝⎛⎭⎫0,ac 2b , 联立⎩⎨⎧ y =-b a x ,y =a b (x +c ),解得M ⎝⎛⎭⎫-a 2c ,ab c , 因为直线AM 经过OP 的中点,所以ac 2b -00-a =ab c -0-a 2c-a ,则2b 2=ac +c 2,2(c 2-a 2)=ac +c 2, 即c 2-ac -2a 2=0,则e 2-e -2=0,解得e =-1 (舍)或e =2.四、解答题13.(2022·衡水中学模拟)双曲线x 2-y 2b 2=1(b >0)的左、右焦点分别为F 1,F 2,直线l 过F 2且与双曲线交于A ,B 两点.(1)若l 的倾斜角为π2,△F 1AB 是等边三角形,求双曲线的渐近线方程; (2)设b =3,若l 的斜率存在,且(F 1A --→+F 1B --→)·AB →=0,求l 的斜率.解 (1)设A (x A ,y A ).由题意知,F 2(c ,0),c =1+b 2,y 2A =b 2(c 2-1)=b 4,因为△F 1AB 是等边三角形, 所以2c =3|y A |,即4(1+b 2)=3b 4,解得b 2=2⎝⎛⎭⎫b 2=-23舍去. 故双曲线的渐近线方程为y =±2x .(2)由已知,F 1(-2,0),F 2(2,0). 设A (x 1,y 1),B (x 2,y 2),直线l :y =k (x -2).显然k ≠0.由⎩⎪⎨⎪⎧x 2-y 23=1,y =k (x -2),得(k 2-3)x 2-4k 2x +4k 2+3=0. 因为l 与双曲线交于两点,所以k 2-3≠0,且Δ=36(1+k 2)>0. 设AB 的中点为M (x M ,y M ). 由(F 1A --→+F 1B --→)·AB →=0,即F 1M →·AB →=0, 知F 1M ⊥AB ,故1· 1.F M k k =-而x M =x 1+x 22=2k 2k 2-3,y M =k (x M -2)=6k k 2-3,1F M k =3k 2k 2-3, 所以3k 2k 2-3·k =-1,得k 2=35, 故l 的斜率为±155.。
人教A版高中数学选修2-1第二章 圆锥曲线与方程-圆锥曲线基本题型总结习题

圆锥曲线基本题型总结:提纲:一、定义的应用:1、定义法求标准方程:2、涉及到曲线上的点到焦点距离的问题:3、焦点三角形问题:二、圆锥曲线的标准方程:1、对方程的理解2、求圆锥曲线方程(已经性质求方程)3、各种圆锥曲线系的应用:三、圆锥曲线的性质:1、已知方程求性质:2、求离心率的取值或取值范围3、涉及性质的问题:四、直线与圆锥曲线的关系:1、位置关系的判定:2、弦长公式的应用:3、弦的中点问题:4、韦达定理的应用:一、定义的应用:1.定义法求标准方程:(1)由题目条件判断是什么形状,再由该形状的特征求方程:(注意细节的处理)1.设F1,F2为定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则动点M的轨迹是()A.椭圆B.直线C.圆D.线段【注:2a>|F1 F2|是椭圆,2a=|F1 F2|是线段】A.x 225+y 29=1 (y ≠0) B.y 225+x 29=1 (y ≠0) C.x 216+y 216=1 (y ≠0) D.y 216+x 29=1 (y ≠0) 【注:检验去点】3.已知A (0,-5)、B (0,5),|P A |-|PB |=2a ,当a =3或5时,P 点的轨迹为( ) A.双曲线或一条直线 B.双曲线或两条直线 C.双曲线一支或一条直线D.双曲线一支或一条射线 【注:2a<|F 1 F 2|是双曲线,2a=|F 1 F 2|是射线,注意一支与两支的判断】4.已知两定点F 1(-3,0),F 2(3,0),在满足下列条件的平面内动点P 的轨迹中,是双曲线的是( ) A.||PF 1|-|PF 2||=5 B.||PF 1|-|PF 2||=6 C.||PF 1|-|PF 2||=7D.||PF 1|-|PF 2||=0 【注:2a<|F 1 F 2|是双曲线】5.平面内有两个定点F 1(-5,0)和F 2(5,0),动点P 满足|PF 1|-|PF 2|=6,则动点P 的轨迹方程是( ) A.x 216-y 29=1(x ≤-4)B.x 29-y 216=1(x ≤-3) C.x 216-y 29=1(x ≥4)D.x 29-y 216=1(x ≥3) 【注:双曲线的一支】 6.如图,P 为圆B :(x +2)2+y 2=36上一动点,点A 坐标为(2,0),线段AP 的垂直平分线交直线BP 于点Q ,求点Q 的轨迹方程.7.已知点A(0,3)和圆O 1:x 2+(y +3)2=16,点M 在圆O 1上运动,点P 在半径O 1M 上,且|PM|=|PA|,求动点P 的轨迹方程.(2)涉及圆的相切问题中的圆锥曲线:8.已知圆A :(x +3)2+y 2=100,圆A 内一定点B (3,0),圆P 过B 且与圆A 内切,求圆心P 的轨迹方程. 已知动圆M 过定点B (-4,0),且和定圆(x -4)2+y 2=16相切,则动圆圆心M 的轨迹方程为( ) A.x 24-y 212=1 (x >0)B.x 24-y 212=1 (x <0) C.x 24-y 212=1D.y 24-x 212=1 【注:由题目判断是双曲线的一支还是两支】 9.若动圆P 过点N (-2,0),且与另一圆M :(x -2)2+y 2=8相外切,求动圆P 的圆心的轨迹方程. 【注:双曲线的一支,注意与上题区分】10.如图,已知定圆F 1:x 2+y 2+10x +24=0,定圆F 2:x 2+y 2-10x +9=0,动圆M 与定圆F 1、F 2都外切,求动圆圆心M 的轨迹方程.11.若动圆与圆(x -2)2+y 2=1相外切,又与直线x +1=0相切,则动圆圆心的轨迹是( ) A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线12.已知动圆M 经过点A (3,0),且与直线l :x =-3相切,求动圆圆心M 的轨迹方程. 【注:同上题做比较,说法不一样,本质相同】13.已知点A (3,2),点M 到F ⎝⎛⎭⎫12,0的距离比它到y 轴的距离大12.(M 的横坐标非负) (1)求点M 的轨迹方程; 【注:体现抛物线定义的灵活应用】(2)是否存在M ,使|MA |+|MF |取得最小值?若存在,求此时点M 的坐标;若不存在,请说明理由. 【注:抛物线定义的应用,涉及抛物线上的点到焦点的距离转化成到准线的距离】(3)其他问题中的圆锥曲线:14.已知A ,B 两地相距2 000 m ,在A 地听到炮弹爆炸声比在B 地晚4 s ,且声速为340 m/s ,求炮弹爆炸点的轨迹方程. 【注:双曲线的一支】2.15.如图所示,在正方体ABCD —A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与到直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是( )A .直线B .圆C . 双曲线D .抛物线【注:体现抛物线定义的灵活应用】2.涉及到曲线上的点到焦点距离的问题:16.设椭圆x 2m 2+y 2m 2-1=1 (m >1)上一点P 到其左焦点的距离为3,到右焦点的距离为1,则椭圆的离心率为( )A.22 B.12 C.2-12 D.3417.椭圆x 216+y 27=1的左右焦点为F 1,F 2,一直线过F 1交椭圆于A 、B 两点,则△ABF 2的周长为( )A .32B .16C .8D .418.已知双曲线的方程为x 2a 2-y 2b2=1,点A ,B 在双曲线的右支上,线段AB 经过双曲线的右焦点F 2,|AB |=m ,F 1为另一焦点,则△ABF 1的周长为( )A .2a +2mB .4a +2mC .a +mD .2a +4m19.若双曲线x 2-4y 2=4的左、右焦点分别是F 1、F 2,过F 2的直线交右支于A 、B 两点,若|AB |=5,则△AF 1B 的周长为________.20.设F 1、F 2是椭圆x 216+y 212=1的两个焦点,P 是椭圆上一点,且P 到两个焦点的距离之差为2,则△PF 1F 2是( )A .钝角三角形B .锐角三角形C .斜三角形D .直角三角形21.椭圆x 29+y 22=1的焦点为F 1、F 2,点P 在椭圆上.若|PF 1|=4,则|PF 2|=________,∠F 1PF 2的大小为________.【注:椭圆上的点到焦点的距离,最小是a -c ,最大是a+c 】22.已知P 是双曲线x 264-y 236=1上一点,F 1,F 2是双曲线的两个焦点,若|PF 1|=17,则|PF 2|的值为________.【注:注意结果的取舍,双曲线上的点到焦点的距离最小为c -a 】23.已知双曲线的方程是x 216-y 28=1,点P 在双曲线上,且到其中一个焦点F 1的距离为10,点N 是PF 1的中点,求|ON |的大小(O 为坐标原点). 【注:O 是两焦点的中点,注意中位线的体现】24.设F 1、F 2分别是双曲线x 25-y 24=1的左、右焦点.若点P 在双曲线上,且1PF u u u u r ·2PF u u u u r =0,则|1PF u u u u r +2PF u u u u r |等于( ) A .3 B .6 C .1 D .225.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值是( ) A.172B.3C. 5D.92【注:抛物线定义的应用,将抛物线上的点到焦点的距离转化成到准线的距离】26.已知抛物线y 2=4x 上的点P 到抛物线的准线的距离为d 1,到直线3x -4y +9=0的距离为d 2,则d 1+d 2的最小值是( ) A.125 B.65 C .2 D.55【注:抛物线定义的应用,将抛物线上的点到准线的距离转化成到焦点的距离】27.设点A 为抛物线y2=4x 上一点,点B(1,0),且|AB|=1,则A 的横坐标的值为( )A .-2B .0C .-2或0D .-2或2 【注:抛物线的焦半径,即定义的应用】3.焦点三角形问题:椭圆的焦点三角形周长2c 2a 2C PF PF C 21F PF 21+∆=++= 椭圆的焦点三角形面积:推导过程:2tan sin cos 121sin 21cos 1 -)cos (12 (1)-(2)(2)2a (1)COS 2-2 1 b 2b PFPF S 2bPFPF 4c 4a PFPF PF PF 4c PF PF PF PF 2221F PF 22122212212212221θθθθθθθ=+==+==+⎪⎩⎪⎨⎧=+=+∆得双曲线的焦点三角形面积:2tanbS 2F PF 21θ=∆28.设P 为椭圆x 2100+y 264=1上一点,F 1、F 2是其焦点,若∠F 1PF 2=π3,求△F 1PF 2的面积.【注:小题中可以直接套用公式。
混凝土强度与温度和龄期增长曲线图
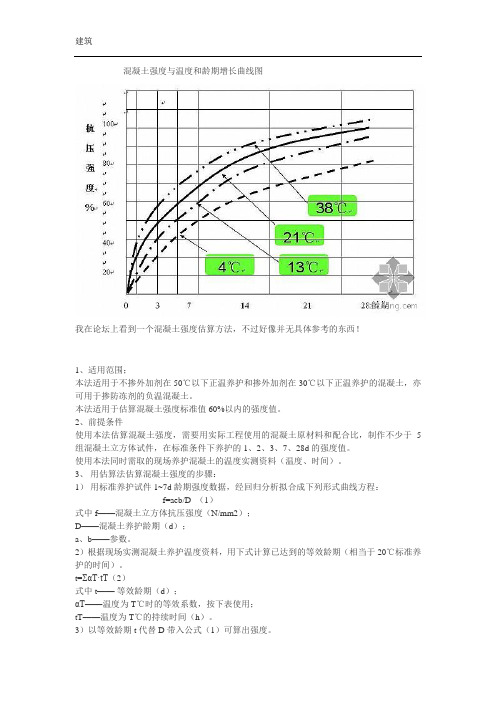
混凝土强度与温度和龄期增长曲线图我在论坛上看到一个混凝土强度估算方法,不过好像并无具体参考的东西!1、适用范围;本法适用于不掺外加剂在50℃以下正温养护和掺外加剂在30℃以下正温养护的混凝土,亦可用于掺防冻剂的负温混凝土。
本法适用于估算混凝土强度标准值60%以内的强度值。
2、前提条件使用本法估算混凝土强度,需要用实际工程使用的混凝土原材料和配合比,制作不少于5组混凝土立方体试件,在标准条件下养护的1、2、3、7、28d的强度值。
使用本法同时需取的现场养护混凝土的温度实测资料(温度、时间)。
3、用估算法估算混凝土强度的步骤:1)用标准养护试件1~7d龄期强度数据,经回归分析拟合成下列形式曲线方程:f=aeb/D (1)式中f——混凝土立方体抗压强度(N/mm2);D——混凝土养护龄期(d);a、b——参数。
2)根据现场实测混凝土养护温度资料,用下式计算已达到的等效龄期(相当于20℃标准养护的时间)。
t=ΣαT·tT(2)式中t——等效龄期(d);αT——温度为T℃时的等效系数,按下表使用;tT——温度为T℃的持续时间(h)。
3)以等效龄期t代替D带入公式(1)可算出强度。
等效系数αT温度等效温度系数αT温度等效温度系数αT温度等效温度系数αT 50 3.16 28 1.45 6 0.4349 3.07 27 1.39 5 0.4048 2.97 26 1.33 4 0.3747 2.88 25 1.27 3 0.3546 2.80 24 1.22 2 0.3245 2.71 23 1.16 1 0.3044 2.62 22 1.11 0 0.2743 2.54 21 1.05 1 0.2542 2.46 20 1.00 -2 0.2341 2.38 19 0.95 -3 0.2140 2.30 18 0.91 -4 0.2039 2.22 17 0.86 -5 0.1838 2.14 16 0.81 -6 0.1637 2.07 15 0.77 -7 0.1536 1.99 14 0.73 -8 0.1435 1.92 13 0.68 -9 0.1334 1.85 12 0.64 -10 0.1233 1.78 11 0.61 -11 0.1132 1.71 10 0.57 -12 0.1131 1.65 9 0.53 -13 0.1030 1.58 8 0.50 -14 0.1029 1.52 7 0.46 -15 0.09一、普通混凝土达到1.2N/mm2强度所需龄期参考对照表注:水灰比:采用普通水泥为0.65-0.8;采用矿渣水泥为0.56-0.68。
高二数学上 第七章 直线和圆的方程 : 7.5曲线的方程(一)

之间的关系: 只具备性质(2) 即具备完备性,
但不具备性质(1) 即不具纯粹备性.l2
l1
因为到两坐标轴距离相等的点的
轨迹有 两条直线l1 和 l2 ,
直线 l1 上的点的坐标都是方程y=x 的解,
但直线 l2 上的点(除原点外)的坐标不是方程y=x
的解,
y=x只是直线l1的方程,它不是所求轨迹的方程.
(2)“以这个方程的解为坐标的点都在曲线上”阐 明符合条件的所有点都在曲线上而毫无遗(漏完备性).
由曲线的方程的定义可知,
如果曲线C的方程是 f(x,y)=0,那么点P0(x0 ,y0) 在曲线C 上的充要高条二数件学上是第七f章(x直0线,和圆y的0方)=0 .
程 : 7.5曲线的方程(一)
例如,过点A(2,0)平行于y轴的直线L(如 图)与方程|x|=2 之间的关系:
高二数学上 第七章 直线和圆的方 程 : 7.5曲线的方程(一)
例1 证明圆心为 半坐 径5标 的 等原 圆 于点 的x2, 方 y2程 2, 5是
并判M 断 1(3, 点 4)、 M 2(25, 2)是否在.这个圆
证明: (1)设M(x0, y0)是圆上任意 , 则 一点
由题意知 |MO|5即 x02 y02 5.
高二数学上 第七章 直线和圆的方
(D)曲线C是方程f(x,y)=程0的: 7曲.5曲线线的的方程一(一部) 分或是全部
作业:
P69 练 习:1,2,3 作业: P72 1,2
高二数学上 第七章 直线和圆的方 程 : 7.5曲线的方程(一)
高二数学上 第七章 直线和圆的方 程 : 7.5曲线的方程(一)
高二数学上 第七章 直线和圆的方 程 : 7.5曲线的方程(一)
高考数学一轮复习 8.9 曲线与方程精品教学案(教师版) 新人教版

【考纲解读】了解方程的曲线与曲线的方程的对应关系.【考点预测】高考对此部分内容考查的热点与命题趋势为:1.平面解析几何是历年来高考重点内容之一,经常与逻辑、不等式、三角函数等知识结合起来考查,在选择题、填空题与解答题中均有可能出现,在解答题中考查,一般难度较大,与其他知识结合起来考查,在考查平面解析几何基础知识的同时,又考查数形结合思想、转化思想和分类讨论等思想,以及分析问题、解决问题的能力.2.2013年的高考将会继续保持稳定,坚持考查解析几何与其他知识的结合,在选择题、填空题中继续搞创新,命题形式会更加灵活.【要点梳理】1.已知曲线形状,求方程:可以用待定系数法.2.未知曲线的形状,求方程:(1)直接法:直接由条件列式,化简整理即可;(2)代入法:明确主动点与被动点;(3)定义法:利用圆或圆锥曲线的定义求轨迹方程.【例题精析】考点一求曲线方程例1.(2012年高考湖北卷文科21)设A是单位圆x2+y2=1上任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足丨DM丨=m丨DA丨(m>0,且m≠1).当点A在圆上运动时,记点M的轨迹为曲线C。
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标。
(2)过原点且斜率为K的直线交曲线C于P,Q两点,其中P在第一象限,且它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的K>0,都有PQ⊥PH?若存在,请说明理由.因为P,H两点在椭圆C上,所以222211222222,,m x y mm x y m⎧+=⎪⎨+=⎪⎩两式相减可得222221212()()0m x x y y -+-=. ③【名师点睛】本小题主要考查直线与圆以及圆锥曲线等基础知识,考查函数与方程思想、分类讨论思想、数形结合思想等数学思想方法,考查同学们分析问题和解决问题的能力. 【变式训练】1.(2012年高考辽宁卷文科20)(本小题满分12分)如图,动圆2221:C x y t +=,1<t<3,与椭圆2C :2219x y +=相交于A ,B ,C ,D 四点,点12,A A 分别为2C 的左,右顶点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第55课时 曲线与方程
编者:陈彩余 审核:陆海蓉 第一部分 预习案
一、学习目标
1.理解坐标法研究解析几何问题的基本思想,会根据条件求曲线的轨迹方程;
2.掌握常用的几种求轨迹方程的方法.
二、知识回顾
1.曲线与方程
如果曲线C 上点的坐标(x ,y )都是方程f (x ,y )=0的解,且以方程f (x ,y )=0的解(x ,y )为坐标的点都在曲线C 上,那么,方程f (x ,y )=0叫做曲线C 的方程,曲线C 叫做方程f (x ,y )=0的曲线.
2.求动点的轨迹方程的一般步骤
(1)建系——建立适当的坐标系.
(2)设点——设轨迹上的任一点P (x ,y ).
(3)列式——列出动点P 所满足的关系式.
(4)代换——依条件式的特点,选用距离公式、斜率公式等将其转化为x ,y 的方程式,并化简.
(5)证明——证明所求方程即为符合条件的动点轨迹方程.
3.两曲线的交点
(1)由曲线方程的定义可知,两条曲线交点的坐标应该是两个曲线方程的公共解,即两个曲线方程组成的方程组的实数解;反过来,方程组有几组解,两条曲线就有几个交点;方程组无解,两条曲线就没有交点.
(2)两条曲线有交点的充要条件是它们的方程所组成的方程组有实数解.可见,求曲线的交点问题,就是求由它们的方程所组成的方程组的实数解问题.
4.注意点
求轨迹方程的常用方法
(1)直接法:直接利用条件建立x ,y 之间的关系F (x ,y )=0;
(2)待定系数法:已知所求曲线的类型,求曲线方程——先根据条件设出所求曲线的方程,再由条件确定其待定系数;
(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程;
(4)代入法(相关点法):动点P (x ,y )依赖于另一动点Q (x 0,y 0)的变化而变化,并且Q (x 0,y 0)又在某已知曲线上,则可先用x ,y 的代数式表示x 0,y 0,再将x 0,y 0代入已知曲线得要求的轨迹方程;
(5)参数法:当动点P (x ,y )坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将x ,y 均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程.
班级_________ 学号_________
姓名_________
三、基础训练
1.已知点A (-2,0)、B (3,0),动点P (x ,y )满足P A →·PB →=x 2-6,则点P 的轨迹方程是__________.
2.已知两定点A (-2,0)、B (1,0),如果动点P 满足P A =2PB ,则点P 的轨迹所包围的图形的面积
为________.
3.方程(2x +3y -1)(x -3-1)=0表示的曲线是__________________.
4.已知点P 是直线2x -y +3=0上的一个动点,定点M (-1,2),Q 是线段PM 延长线上的一点,
且PM =MQ ,则Q 点的轨迹方程是______________.
5.若点P 到直线x =-1的距离比它到点(2,0)的距离小1,则点P 的轨迹为__________.
第二部分 探究案
探究一 直接法求轨迹方程
问题1已知M (4,0),N (1,0),若动点P 满足MN →·MP →=6|NP →|.
(1)求动点P 的轨迹C 的方程;
(2)设Q 是曲线C 上任意一点,求Q 到直线l :x +2y -12=0的距离的最小值.
问题2、如图所示,过点P (2,4)作互相垂直的直线l 1,l 2,若l 1交x 轴于A ,l 2交y 轴于B ,求线段AB 中点M 的轨迹方程.
探究二 定义法求轨迹方程
问题3、已知两个定圆O 1和O 2,它们的半径分别是1和2,且O 1O 2=4.动圆M 与圆O 1内切,又与圆O 2外切,建立适当的坐标系,求动圆圆心M 的轨迹方程,并说明轨迹是何种曲线.
问题4、已知点F ⎝⎛⎭⎫14,0,直线l :x =-14
,点B 是l 上的动点.若过B 垂直于y 轴的直线与线段BF 的垂直平分线交于点M ,则点M 的轨迹方程是________.
探究三 相关点法求轨迹方程
问题5、设F (1,0),M 点在x 轴上,P 点在y 轴上,且MN →=2MP →,PM →⊥PF →,当点P 在y 轴上运动
时,求点N 的轨迹方程.
问题6、已知长为1+2的线段AB 的两个端点A 、B 分别在x 轴、y 轴上滑动,P 是AB 上一点,
且AP →=22
PB →,求点P 的轨迹C 的方程.
探究四 利用参数法求轨迹方程
问题7、已知抛物线y 2=4px (p >0),O 为顶点,A 、B 为抛物线上的两动点,且满足OA ⊥OB ,如果OM ⊥AB 于M 点,求点M 的轨迹方程.
我的收获
第三部分 训练案 见附页。
