高等数学典型例题与应用实例(重积分B部分)

高等数学第九章重积分第四节重积分应用

x= z=
∫∫∫Ω xd xd y d z ∫∫∫Ω
V zd x d y d z V
∫∫∫Ω yd xd y d z
V
,
( V = ∫∫∫ d x d y d z为Ω的体积 ) Ω
上页下页返回结束
若物体为占有xOy 面上区域 D 的平面薄片其面密度的平面薄片, 若物体为占有则它的质心坐标质心坐标为则它的质心坐标为
上页下页返回结束
三、物体的质心
设空间有n个质点设空间有个质点, 分别位于 (xk , yk , zk ) , 其质量分别个质点为 mk ( k =1, 2, L, n ) ,由力学知该质点系的质心坐标由力学知,
∑xk mk
为
n
x=
k =1 n
∑yk mk
, y=
k =1 n
n
∑zk mk
∴ dA = 1 + f x2 + f y2 dσ 曲面S的面积元素曲面S
∴ A = ∫∫ 1 + f x2 + f y2 dσ ,
D
∂z ∂z A = ∫∫ 1 + (∂x )2 + (∂y )2dxdy 曲面面积公式为：曲面面积公式为： Dxy
上页
下页
返回
结束
小结 1. 设曲面 S 的方程为：z = f ( x , y ) 的方程为：
设曲面的方程为：３．设曲面的方程为：y = h( z , x ) 则曲面面积公式为：则曲面面积公式为： A =
∫∫
Dzx
1+ (
∂y 2 ∂z
) + ( ) dzdx.
∂y 2 ∂x
上页下页返回结束
例 4. 求球面 x 2 + y 2 + z 2 = a 2 含在圆柱体 2 2 x + y = ax 内部的那部分面积内部的那部分面积.

重积分典型例题

重积分典型例题
重积分典型例题
例 1 在下列积分中改变累次积分的次序： (1) 解 (2) 解
ò
b a
dx ò f ( x , y ) dy ， ( a < b ) ；
a
x
ò
b a
dx ò f ( x , y ) dy = ò dy ò f ( x , y ) dx ．
a a y 2 ax 2 ax - x 2 2 ax 2 ax - x 2
òò ( x - a )( y - b ) dxdy £ òò | x - a | | y - b | dxd y £ òò
D D
| x - a || y - b | dxdy
[ a ,b ]´[ c , d }
= ò | x - a | dx × ò | y - b | dy
a c b =æ - x ) dx + ò ( x - a ) dx ö ç òa (a ÷× a è ø
2 2
f ( x , y ) dx + ò dy ò x , y ) dy ． y f (
2
2 a
2 a
a
2 a
例 2 计算下列重积分：
(1)
òò xy dxdy ，D 为抛物线 y
D p 2 òò xy dxdy = ò 2 xdx ò 0 D p 4 p 2 p 2 7 p 5 2 2 = × x 0 = ． 3 7 21 2 px - 2 px
解
令 x = ar cos q ， y = br sin q ，则 0 £ q £ 2 p ， 0 £ r £ 1 ，
¶ ( x, y ) = abr ．有 ¶ ( r , q )

数学分析21.6重积分的应用(含习题及参考答案)

第二十一章重积分 6重积分的应用一、曲面的面积问题：设D 为可求面积的平面有界区域，函数f(x,y)在D 上具有连续的一阶偏导数，讨论由方程z=f(x,y), (x,y)∈D 所确定的曲面S 的面积.分析：对区域D 作分割T ，把D 分成n 个小区域σi (i=1,2,…,n). 曲面S 同时也被分割成相应的n 个小曲面片S i (i=1,2,…,n). 在每个S i 上任取一点M i , 作曲面在这一点的切平面πi , 并在πi 上取出一小块A i , 使得A i 与S i 在xy 平面上的投影都是σi . 现在M i 附近，用切平面A i 代替小曲面片S i . 则当T 充分小时，有 △S=∑=∆ni i S 1≈∑=∆ni i A 1, 这里的△S, △S i , △A i 分别表示S, S i 和A i 的面积.∴当T →0时，可用和式∑=∆ni i A 1的极限作为S 的面积.建立曲面面积计算公式：∵切平面πi 的法向量就是曲面S 在点M i (ξi ,ηi ,ζi )处的法向量，记其与z 轴的夹角为γi , 则|cos γi |=),(),(1122i i yi i xf f ηξηξ++.∵A i 在xy 平面上投影为σi , ∴△A i =iiγσcos ∆=i i i y i i x f f σηξηξ∆++),(),(122. 又和数∑=∆ni i A 1=∑=∆++ni i i i y i i x f f 122),(),(1σηξηξ是连续函数),(),(122y x f y x f y x ++在有界闭区域D 上的积分和，∴当T →0时，有△S=∑=→∆++ni i i i y i i x T f f 1220),(),(1lim σηξηξ=⎰⎰++Dy x dxdy y x f y x f ),(),(122, 或△S=∑=→∆ni i iT 1cos limγσ=⎰⎰∧Dz n dxdy ),cos(,其中),cos(∧z n 为曲面的法向量与z 轴正向夹角的余弦.例1：求圆锥z=22y x +在圆柱体x 2+y 2≤x 内那一部分的面积. 解：由x 2+y 2≤x, 得D={(r,θ)|0≤r ≤21, 0≤θ≤2π}, 又z x =22y x x +=r r θcos =cos θ, z y =22yx y+=r r θsin =sin θ, ∴△S=⎰⎰++Dyxdxdy z z 221=⎰⎰πθ202102rdr d =π42.例2：设平面光滑曲线的方程为y=f(x), x ∈[a,b] (f(x)>0). 求证：此曲线绕x 轴旋转一周得到的旋转曲面的面积为： S=⎰'+ba dx x f x f )(1)(22π.证：由上半旋转面方程为z=22)(y x f -, 得 z x =22)()()(yx f x f x f -', z y =22)(yx f y --. 即有221yxz z ++=2222222)()()()(1yx f y y x f x f x f -+-'+=2222)())(1)((yx f x f x f -'+. ∴S=⎰⎰--'+b a x f x f dy y x f x f x f dx )()(222)()(1)(2=⎰⎰-'+b a x f dyy x f dx x f x f )(0222)(1)(1)(4=⎰⎰---'+ba x f x yf d x f y dx x f x f )(01222))(()(11)(1)(4=⎰⎰-'+b a dt tdx x f x f 102211)(1)(4=⎰'+b adx x f x f )(1)(22π.注：若空间曲面S 由参量方程：x=x(u,v),y=y(u,v),z=z(u,v),(u,v)∈D 确定, 其中x(u,v), y(u,v), z(u,v)在D 上具有连续一阶偏导数，且),(),(v u u y x ∂,),(),(v u u z y ∂,),(),(v u u x z ∂中至少有一个不等于0，则曲面S 在点(x,y,z)的法线方向数为⎝⎛∂),(),(v u u z y ,),(),(v u u x z ∂,⎪⎪⎭⎫∂),(),(v u u y x , 则它与z 轴的夹角的余弦的绝对值为：),cos(∧z n =222),(),(),(),(),(),(),(),(⎪⎪⎭⎫ ⎝⎛∂+⎪⎪⎭⎫ ⎝⎛∂+⎪⎪⎭⎫ ⎝⎛∂∂v u u y x v u u x z v u u z y v u u y x=2222222)())((),(),(v u v u v u vvvuuuz z y y x x z y x z y x v u u y x ++-++++∂=21),(),(FEG v u u y x -∂,其中E=222u u u z y x ++,G=222v v v z y x ++,F=v u v u v u z z y y x x ++.当),(),(v u u y x ∂≠0，则有△S=⎰⎰∧Dz n dxdy ),cos(=dudv z n v u u y x D ⎰⎰'∧∂),cos(),(),(=dudv F EG D ⎰⎰'-2.例3：求球面上两条纬线和两条经线之间的曲面的面积(图中阴影部分). 解：设球面方程为：(R 为球的半径). x=Rcos ψcos φ,y=Rcos ψsin φ, z=Rsin ψ.由E=222ψψψz y x ++=R 2, G=222ϕϕϕz y x ++=R 2cos 2ψ, F=ϕψϕψϕψz z y y x x ++=0，得2F EG -=R 2cos ψ. ∴△S=⎰⎰2121cos 2ψψϕϕψψϕd R d =R 2(φ2-φ1)(sin ψ2-sin ψ1).二、质心引例：设V 是密度函数为ρ(x,y,z)的空间物体，ρ(x,y,z)在V 上连续. 为求得V 的质心坐标公式，先对V 作分割T ，在属于T 的每一小块v i 上任取一点(ξi ,ηi ,ζi )，则小块v i 的质量可用ρ(ξi ,ηi ,ζi )△v i 近似代替. 若把每一小块看作质量集中在(ξi ,ηi ,ζi )的质点时，整个物体就可用这n 个质点的质点系来近似代替. 由于质点系的质心坐标公式为：∑∑==∆∆=ni iiiini iiiiin v v x 11),,(),,(ζηξρζηξρξ, ∑∑==∆∆=ni iiiini iiiiin v v y 11),,(),,(ζηξρζηξρη, ∑∑==∆∆=n i iiiini ii i i in v v z 11),,(),,(ζηξρζηξρζ.当T →0时，n x , n y , n z 的极限x , y , z 就定义为V 的质心坐标，即⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x x x ),,(),,(ρρ, ⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x y y ),,(),,(ρρ, ⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x z z ),,(),,(ρρ.当物体V 的密度均匀即ρ为常数时，则有⎰⎰⎰∆=VxdV Vx 1, ⎰⎰⎰∆=VydV Vy 1, ⎰⎰⎰∆=VzdV Vz 1, 这里△V 为V 的体积.又密度分布为ρ(x,y)的平面薄板D 的质心坐标为：⎰⎰⎰⎰=DDd y x d y x x x σρσρ),(),(, ⎰⎰⎰⎰=DDd y x d y x y y σρσρ),(),(. 当平面薄板的密度均匀时，即ρ为常数时，则有⎰⎰∆=Dxd D x σ1, ⎰⎰∆=D yd D y σ1, △D 为薄板D 的面积.例4：求密度均匀的上半椭球体的质心.解：设椭球体由不等式a x 2+by 2+c z 2≤1表示.由对称性知x =0, y =0, 又由ρ为常数，得z =⎰⎰⎰⎰⎰⎰VVdVdVz ρρ=abc abc ππ3242=83c .三、转动惯量质点A 对于轴l 的转动惯量J 是质点A 的质量m 和A 与转动轴l 的距离r 的平方的乘积，即J=mr 2.设ρ(x,y,z)为空间物体V 的密度分布函数，它在V 上连续. 对V 作分割T ，在属于T 的每一小块v i 上任取一点(ξi ,ηi ,ζi )，则v i 的质量可用ρ(ξi ,ηi ,ζi )△v i 近似代替. 当以质点系{(ξi ,ηi ,ζi ), i=1,2,…, n}近似替代V 时，质点系对于x 轴的转动惯量为：i i i i ni i i x v J n∆+=∑=),,()(122ζηξρζη.当T →0时，上述积分和的极限就是物体V 对于x 轴的转动惯量 J x =⎰⎰⎰+VdV z y x z y ),,()(22ρ. 类似地,V 对于y 轴与z 轴的转动惯量分别为：J y =⎰⎰⎰+VdV z y x x z ),,()(22ρ, J z =⎰⎰⎰+VdV z y x y x ),,()(22ρ.同理，V 对于坐标平面的转动惯量分别为：J xy =⎰⎰⎰VdV z y x z ),,(2ρ, J yz =⎰⎰⎰VdV z y x x ),,(2ρ, J xz =⎰⎰⎰VdV z y x y ),,(2ρ.平面薄板对于坐标轴的转动惯量分别为：J x =⎰⎰Dd y x y σρ),(2, J y =⎰⎰Dd y x x σρ),(2. 以及有J l =⎰⎰Dd y x y x r σρ),(),(2,其中l 为转动轴, r(x,y)为D 中点(x,y)到l 的距离函数.例5：求密度均匀的圆环D 对于垂直于圆环面中心轴的转动惯量. 解：设圆环D 为R 12≤x 2+y 2≤R 22, 密度为ρ, 则D 中任一点(x,y)与转轴的距离平方为x 2+y 2, 于是转动惯量为：J=⎰⎰+Dd y x σρ)(22=⎰⎰21320R R dr r d πθρ=2πρ(R 24-R 14)=例6：求均匀圆盘D 对于其直径的转动惯量.解：设D 为x 2+y 2≤R 2, 密度为ρ, D 内任一点(x,y)与y 轴的距离为|x|, 于是转动惯量为：(m 为圆盘质量) J=⎰⎰Dd x σρ2=⎰⎰Rdr r d 02320cos θθρπ=⎰πθθρ2024cos 4d R =44R ρπ=42mR .例7：设某球体的密度与球心的距离成正比，求它对于切平面的转动惯量.解：设球体由x 2+y 2+z 2≤R 2表示，密度为k 222z y x ++, k 为比便常数. 切平面方程为x=R, 则球体对于平面x=R 的转动惯量为： J=k ⎰⎰⎰-++VdV x R z y x 2222)(=k ⎰⎰⎰-ππϕθϕϕθ003220sin )cos sin (Rdr r r R d d=kR 6⎰⎰⎪⎭⎫ ⎝⎛+-ππϕθϕθϕθ023220cos sin 61cos sin 5241d d =⎰πθθ2026cos 911d kR =911k πR 6.四、引力求密度为ρ(x,y,z)的立体对立体外质量为1的质点A 的引力.设A 的坐标为(ξi ,ηi ,ζi )，V 中点的坐标用(x,y,z)表示. V 中质量微元dm=ρdV 对A 的引力在坐标轴上的投影为 dF xyz其中K 为引力系数， r=222)()()(ζηξ-+-+-z y x 是A 到dV 的距离，于是力F 在三个坐标轴上的投影分别为： F x =K ⎰⎰⎰-VdV r x ρξ3, F y =K ⎰⎰⎰-V dV r y ρη3, F z =K ⎰⎰⎰-VdV r z ρζ3, 所以F=F x i+F y j+F z k.例8：设球体V 具有均匀的密度ρ, 求V 对球外一点A(质量为1)的引力(引力系数为k).解：设球体为x 2+y 2+z 2≤R 2，球外一点坐标为(0,0,a) (R<a). 则F x =F y =0,F z =k ⎰⎰⎰-++-V dV a z y x a z ρ2/3222])([=k ρ⎰⎰⎰-++--zD R R a z y x dxdydz a z 2/3222])([)(, 其中D z ={(x,y)|x2+y2≤R 2-z 2}. 运用极坐标计算得： F z =k ρdr a z r rd dz a z z R RR ⎰⎰⎰---+-2202/32220])([)(πθ =2πk ρ⎰-+----R R dz aaz R a z )21(22=2πk ρ⎪⎪⎭⎫⎝⎛+--++-+-⎰-R R dz a az R R a a az R a R 22222222212= 2πk ρ⎥⎦⎤⎢⎣⎡-+----+---⎰⎰--RRRRaz d a az R a R a az d a az R a R )2(214)2(241222222222=2πk ρ⎥⎦⎤⎢⎣⎡+---+-----RRRRa az R a R a a az R a R 22222322222)2(612 =2πk ρ⎥⎦⎤⎢⎣⎡-++----222233)(6)()(2a R a R a a R R a R=2πk ρ⎪⎪⎭⎫⎝⎛-+++-232332a R R a R R R =2334a R k ρπ-. (注：z ≤R<a)习题1、求曲面az=xy 包含在圆柱x 2+y 2=a 2内那部分的面积.解：∵z x =a y, z y =ax , D={(r,θ)|0≤r ≤a, 0≤θ≤2π}, ∴曲面面积为： S=⎰⎰⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+Ddxdy a x a y 221=⎰⎰+a dr a r r d 022201πθ=)122(322-a π.2、求锥面z=22y x +被柱面z 2=2x 所截部分的曲面面积. 解：且面在xy 平面的投影区域为：D={(r,θ)|0≤r ≤1, 0≤θ≤2π}, 且z x =22yx x +, z y =22yx y +, ∴曲面面积为：S=⎰⎰⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++Ddxdy y x y y x x 2222221=⎰⎰10202rdr d πθ=π2.3、求下列均匀密度的平面薄板质心：(1)半椭圆2222by a x +≤1, y ≥0；(2)高为h, 底分别为a 和b 的等腰梯形.解：(1)设质心位置为(x ,y ), 由对称性得x =0.y =⎰⎰⎰⎰DDd yd σρσρ=⎰⎰⎰⎰DDd yd σσ=⎰⎰Dyd ab σπ2=dr r ab d ab ⎰⎰πθθπ122sin 2=π34b . (2)不妨设a 为下底，以下底中点为原点建立直角坐标系，则 D={(x,y)|l 1(y)≤x ≤l 2(y),0≤y ≤h}.设质心位置为(x ,y ), 由对称性得x =0.又等腰三角形的面积为2)(hb a +, ∴y =⎰⎰+D yd h b a σ)(2=⎰⎰+h y l y l dx ydy h b a 0)()(21)(2=⎰⎥⎦⎤⎢⎣⎡+---+--+h ydy a h y h a b a h y h b a h b a 02)(22)(2)(2=⎰⎥⎦⎤⎢⎣⎡+--+h ydy a h y h b a h b a 0)()(2=⎰⎪⎭⎫ ⎝⎛+-+h dy by y h b a h b a 02)(2=h b a a b )(32++. 其中：l 1(y): x=2)(2a h y h a b ---; l 2(y): x=2)(2ah y h b a +--.4、求下列均匀密度物体的质心.(1)z ≤1-x 2-y 2, z ≥0；(2)由坐标面及平面x+2y-z=1所围的四面体. 解：(1)设质心为(x ,y ,z ), 由对称性x =y =0, 应用柱面坐标变换有,z =⎰⎰⎰⎰⎰⎰VVdV dV z ρρ=⎰⎰⎰⎰⎰⎰--221020110201r r dz r d r d zdz r d r d ππθθ=dr r r dr r r )1()1(212102210--⎰⎰=31. (2)设质心为(x ,y ,z ),∵V=⎰⎰⎰VdV =121， ∴x =⎰⎰⎰--+21001211x y x dz dy xdx V =⎰⎰---2101)21(12x dy y x xdx =⎰-1024)1(12dx x x =41. y =⎰⎰⎰--+yy x dz dx ydy V 210122101=⎰⎰---ydx x y ydy 210210)21(12=⎰-21022)21(12dy y y =81. z =⎰⎰⎰--+yy x zdz dx dy V21012211=⎰⎰--+-ydx y x dy 2102210)12(6=⎰--21033)21(6dy y =41-.5、求下列均匀密度的平面薄板的转动惯量： (1)半径为R 的圆关于其切线的转动惯量；(2)边长为a 和b, 且夹角为φ的平行四边形，关于底边b 的转动惯量.解：(1)设切线为x=R, 密度为ρ.则对任一点P(x,y)∈D, P 到x=R 的距离为R-x ，从而转动惯量 J=ρ⎰⎰-Dd x R σ2)(=ρ⎰⎰+-Rdr r Rr R r d 022220)cos cos 2(θθθπ=ρ⎰+-πθθθ2024)cos 41cos 3221(d R= R 4. (2)设密度为ρ. 以底边为x 轴，左端点为原点，则转动惯量 J=⎰⎰Dd y σ2=ρ⎰⎰+by y a dx dy y ϕϕϕcot cot sin 02=3sin 33ϕρb a .6、计算下列引力：(1)均匀薄片x 2+y 2≤R 2, z=0对于轴上一点(0,0,c) (c>0)处的单位质量的引力；(2)均匀柱体x 2+y 2≤a 2, 0≤z ≤h 对于点P(0,0,c) (c>h)处的单位质量的引力；(3)均匀密度的正圆锥体(高h, 底半径R)对于在它的顶点处质量为m 的质点的引力.解：(1)根据对称性知引力方向在z 轴上，∴F z =0, F y =0.F z =k ρ⎰⎰++Ddxdy c y x c 2/3222)(=kc ρ⎰⎰+R dr c r r d 02/32220)(πθ=2k .∴F={0,0,2k }.(2)根据对称性知引力方向在z 轴上，∴F z =0, F y =0. F z =k ρ⎰⎰⎰-++-VdV c z y x c z 2/3222])([=k ρ⎰⎰⎰-+-a h dr c z r rd dz c z 02/322200])([)(πθ=-2k πρdz c z a c z h⎰⎥⎥⎦⎤⎢⎢⎣⎡-+-+022)(1=2k πρ[]h c h a c a --+-+2222)(. ∴F={0,0,2k πρ[]h c h a c a --+-+2222)(}.(3)以圆锥体的顶点为原点, 对称轴为z 轴建立xyz 三维直角坐标系. 根据对称性知引力方向在z 轴上，∴F z =0, F y =0.F z =k ρm ⎰⎰⎰++V dV z y x z 2/3222)(=k ρm ⎰⎰⎰+R hrR dz z r zrdr d 02/322020)(πθ=2k πR ρm ⎪⎪⎭⎫⎝⎛++-22221R h R h R . ∴F={0,0, 2k πR ρm ⎪⎪⎭⎫ ⎝⎛++-22221R h R h R }.7、求曲面⎪⎩⎪⎨⎧=+=+=ψϕψϕψsin sin )cos (cos )cos (a z a b y a b x (0≤φ≤2π, 0≤ψ≤2π) 的面积，其中常数a,b 满足0≤a ≤b.解：∵x φ=-(b+acos ψ)sin φ, y φ=(b+acos ψ)cos φ, z φ=0; x ψ=-asin ψcos φ, y ψ=-asin ψsin φ, z ψ=acos ψ.∴E=222ϕϕϕz y x ++=(b+acos ψ)2, G=222ψψψz y x ++=a 2, F=ψϕψϕψϕz z y y x x ++=0. ∴S=σd F EG D ⎰⎰'-2=σψd a b a D ⎰⎰'+)cos (=⎰⎰+ππψψϕ2020)cos (d a b d a =4ab π2.8、求螺旋面⎪⎩⎪⎨⎧===ϕϕϕb z r y r x sin cos (0≤r ≤a, 0≤φ≤2π) 的面积.解：∵x r =cos φ, y r =sin φ, z r =0; x φ=-rsin φ, y φ=rcos φ, z φ=b.∴E=222r r r z y x ++=1, G=222ϕϕϕz y x ++=r 2+b 2, F=ϕϕϕz z y y x x r r r ++=0.∴S=σd F EG D ⎰⎰'-2=σd b r D ⎰⎰'+22=⎰⎰+πϕ20022d dr b r a=π⎪⎪⎭⎫⎝⎛++++b b a a b b a a 22222ln .9、求边长为a 密度均匀的正方体关于其任一棱边的转动变量. 解：以正方体的一个顶点为原点，顶点上方的棱为z 轴，使正方体处于第一卦限中，则正方体对z 轴上的棱的转动变量为： J z =ρ⎰⎰⎰+V dV y x )(22=ρ⎰⎰⎰+aaadz y x dy dx 00220)(=a ρ⎰⎰+aady y x dx 0220)(=a ρ⎰+adx a ax 032)31(=32a 5ρ. (ρ为正方体密度)。

高数D10.4重积分的应用

练习. 计算三重积分
其中为由
柱面 x2 y2 2x 及平面 z 0, z a (a 0), y 0 所围
成半圆柱体.
0 2cos z
解: 在柱面坐标系下 :
0
2
a
0 z a
原式 z 2 d dd z
a
zdz
2 d
2cos 2 d
0
0
0
o y
2 x 2cos
4a2
上连续，求平面薄片的质心的坐标.
在D上任取一直径很小的闭区域d ,(面积也记作d )，
(x, y)是d上的一个点。由于d的直径很小，且(x, y)
在D上连续，所以薄片中相应于d的部分的质量近似
V D f (x, y)dxd y
• 占有空间有界域的立体的体积为
V dxdydz
z f (x, y)
D
z f (x, y)
D
P158
P158
P168
作业
• P167 • P177
12 （1）（3） 1、2
例1. 求曲面
任一点的切平面与曲面
所围立体的体积 V .
解: 曲面 S1在点
D
a dxdy
a2 x2 y2
2
a
2a d
1
d
0
0 a2 2
z
2
a
2a d
1
( 1)d(a2 2)
0
0 a2 2 2
ao
2a[ 1
1
a2 2 ]0a 4a2 .
x
y
2
例 2 设有一颗地球的同步轨道通讯卫星，轨道位于地
球的赤道平面内，且可近似认为是圆轨道．通讯卫星运
行的角速率与地球自转的角速率相同，即人们看到它在

数学分析21.6重积分的应用(含习题及参考答案)

第二十一章重积分 6重积分的应用一、曲面的面积问题：设D 为可求面积的平面有界区域，函数f(x,y)在D 上具有连续的一阶偏导数，讨论由方程z=f(x,y), (x,y)∈D 所确定的曲面S 的面积.分析：对区域D 作分割T ，把D 分成n 个小区域σi (i=1,2,…,n). 曲面S 同时也被分割成相应的n 个小曲面片S i (i=1,2,…,n). 在每个S i 上任取一点M i , 作曲面在这一点的切平面πi , 并在πi 上取出一小块A i , 使得A i 与S i 在xy 平面上的投影都是σi . 现在M i 附近，用切平面A i 代替小曲面片S i . 则当T 充分小时，有 △S=∑=∆ni i S 1≈∑=∆ni i A 1, 这里的△S, △S i , △A i 分别表示S, S i 和A i 的面积.∴当T →0时，可用和式∑=∆ni i A 1的极限作为S 的面积.建立曲面面积计算公式：∵切平面πi 的法向量就是曲面S 在点M i (ξi ,ηi ,ζi )处的法向量，记其与z 轴的夹角为γi , 则|cos γi |=),(),(1122i i yi i xf f ηξηξ++.∵A i 在xy 平面上投影为σi , ∴△A i =iiγσcos ∆=i i i y i i x f f σηξηξ∆++),(),(122. 又和数∑=∆ni i A 1=∑=∆++ni i i i y i i x f f 122),(),(1σηξηξ是连续函数),(),(122y x f y x f y x ++在有界闭区域D 上的积分和，∴当T →0时，有△S=∑=→∆++ni i i i y i i x T f f 1220),(),(1lim σηξηξ=⎰⎰++Dy x dxdy y x f y x f ),(),(122, 或△S=∑=→∆ni i iT 1cos limγσ=⎰⎰∧Dz n dxdy ),cos(,其中),cos(∧z n 为曲面的法向量与z 轴正向夹角的余弦.例1：求圆锥z=22y x +在圆柱体x 2+y 2≤x 内那一部分的面积. 解：由x 2+y 2≤x, 得D={(r,θ)|0≤r ≤21, 0≤θ≤2π}, 又z x =22y x x +=r r θcos =cos θ, z y =22yx y+=r r θsin =sin θ, ∴△S=⎰⎰++Dyxdxdy z z 221=⎰⎰πθ202102rdr d =π42.例2：设平面光滑曲线的方程为y=f(x), x ∈[a,b] (f(x)>0). 求证：此曲线绕x 轴旋转一周得到的旋转曲面的面积为： S=⎰'+ba dx x f x f )(1)(22π.证：由上半旋转面方程为z=22)(y x f -, 得 z x =22)()()(yx f x f x f -', z y =22)(yx f y --. 即有221yxz z ++=2222222)()()()(1yx f y y x f x f x f -+-'+=2222)())(1)((yx f x f x f -'+. ∴S=⎰⎰--'+b a x f x f dy y x f x f x f dx )()(222)()(1)(2=⎰⎰-'+b a x f dyy x f dx x f x f )(0222)(1)(1)(4=⎰⎰---'+ba x f x yf d x f y dx x f x f )(01222))(()(11)(1)(4=⎰⎰-'+b a dt tdx x f x f 102211)(1)(4=⎰'+b adx x f x f )(1)(22π.注：若空间曲面S 由参量方程：x=x(u,v),y=y(u,v),z=z(u,v),(u,v)∈D 确定, 其中x(u,v), y(u,v), z(u,v)在D 上具有连续一阶偏导数，且),(),(v u u y x ∂,),(),(v u u z y ∂,),(),(v u u x z ∂中至少有一个不等于0，则曲面S 在点(x,y,z)的法线方向数为⎝⎛∂),(),(v u u z y ,),(),(v u u x z ∂,⎪⎪⎭⎫∂),(),(v u u y x , 则它与z 轴的夹角的余弦的绝对值为：),cos(∧z n =222),(),(),(),(),(),(),(),(⎪⎪⎭⎫ ⎝⎛∂+⎪⎪⎭⎫ ⎝⎛∂+⎪⎪⎭⎫ ⎝⎛∂∂v u u y x v u u x z v u u z y v u u y x=2222222)())((),(),(v u v u v u vvvuuuz z y y x x z y x z y x v u u y x ++-++++∂=21),(),(FEG v u u y x -∂,其中E=222u u u z y x ++,G=222v v v z y x ++,F=v u v u v u z z y y x x ++.当),(),(v u u y x ∂≠0，则有△S=⎰⎰∧Dz n dxdy ),cos(=dudv z n v u u y x D ⎰⎰'∧∂),cos(),(),(=dudv F EG D ⎰⎰'-2.例3：求球面上两条纬线和两条经线之间的曲面的面积(图中阴影部分). 解：设球面方程为：(R 为球的半径). x=Rcos ψcos φ,y=Rcos ψsin φ, z=Rsin ψ.由E=222ψψψz y x ++=R 2, G=222ϕϕϕz y x ++=R 2cos 2ψ, F=ϕψϕψϕψz z y y x x ++=0，得2F EG -=R 2cos ψ. ∴△S=⎰⎰2121cos 2ψψϕϕψψϕd R d =R 2(φ2-φ1)(sin ψ2-sin ψ1).二、质心引例：设V 是密度函数为ρ(x,y,z)的空间物体，ρ(x,y,z)在V 上连续. 为求得V 的质心坐标公式，先对V 作分割T ，在属于T 的每一小块v i 上任取一点(ξi ,ηi ,ζi )，则小块v i 的质量可用ρ(ξi ,ηi ,ζi )△v i 近似代替. 若把每一小块看作质量集中在(ξi ,ηi ,ζi )的质点时，整个物体就可用这n 个质点的质点系来近似代替. 由于质点系的质心坐标公式为：∑∑==∆∆=ni iiiini iiiiin v v x 11),,(),,(ζηξρζηξρξ, ∑∑==∆∆=ni iiiini iiiiin v v y 11),,(),,(ζηξρζηξρη, ∑∑==∆∆=n i iiiini ii i i in v v z 11),,(),,(ζηξρζηξρζ.当T →0时，n x , n y , n z 的极限x , y , z 就定义为V 的质心坐标，即⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x x x ),,(),,(ρρ, ⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x y y ),,(),,(ρρ, ⎰⎰⎰⎰⎰⎰=VVdVz y x dVz y x z z ),,(),,(ρρ.当物体V 的密度均匀即ρ为常数时，则有⎰⎰⎰∆=VxdV Vx 1, ⎰⎰⎰∆=VydV Vy 1, ⎰⎰⎰∆=VzdV Vz 1, 这里△V 为V 的体积.又密度分布为ρ(x,y)的平面薄板D 的质心坐标为：⎰⎰⎰⎰=DDd y x d y x x x σρσρ),(),(, ⎰⎰⎰⎰=DDd y x d y x y y σρσρ),(),(. 当平面薄板的密度均匀时，即ρ为常数时，则有⎰⎰∆=Dxd D x σ1, ⎰⎰∆=D yd D y σ1, △D 为薄板D 的面积.例4：求密度均匀的上半椭球体的质心.解：设椭球体由不等式a x 2+by 2+c z 2≤1表示.由对称性知x =0, y =0, 又由ρ为常数，得z =⎰⎰⎰⎰⎰⎰VVdVdVz ρρ=abc abc ππ3242=83c .三、转动惯量质点A 对于轴l 的转动惯量J 是质点A 的质量m 和A 与转动轴l 的距离r 的平方的乘积，即J=mr 2.设ρ(x,y,z)为空间物体V 的密度分布函数，它在V 上连续. 对V 作分割T ，在属于T 的每一小块v i 上任取一点(ξi ,ηi ,ζi )，则v i 的质量可用ρ(ξi ,ηi ,ζi )△v i 近似代替. 当以质点系{(ξi ,ηi ,ζi ), i=1,2,…, n}近似替代V 时，质点系对于x 轴的转动惯量为：i i i i ni i i x v J n∆+=∑=),,()(122ζηξρζη.当T →0时，上述积分和的极限就是物体V 对于x 轴的转动惯量 J x =⎰⎰⎰+VdV z y x z y ),,()(22ρ. 类似地,V 对于y 轴与z 轴的转动惯量分别为：J y =⎰⎰⎰+VdV z y x x z ),,()(22ρ, J z =⎰⎰⎰+VdV z y x y x ),,()(22ρ.同理，V 对于坐标平面的转动惯量分别为：J xy =⎰⎰⎰VdV z y x z ),,(2ρ, J yz =⎰⎰⎰VdV z y x x ),,(2ρ, J xz =⎰⎰⎰VdV z y x y ),,(2ρ.平面薄板对于坐标轴的转动惯量分别为：J x =⎰⎰Dd y x y σρ),(2, J y =⎰⎰Dd y x x σρ),(2. 以及有J l =⎰⎰Dd y x y x r σρ),(),(2,其中l 为转动轴, r(x,y)为D 中点(x,y)到l 的距离函数.例5：求密度均匀的圆环D 对于垂直于圆环面中心轴的转动惯量. 解：设圆环D 为R 12≤x 2+y 2≤R 22, 密度为ρ, 则D 中任一点(x,y)与转轴的距离平方为x 2+y 2, 于是转动惯量为：J=⎰⎰+Dd y x σρ)(22=⎰⎰21320R R dr r d πθρ=2πρ(R 24-R 14)=例6：求均匀圆盘D 对于其直径的转动惯量.解：设D 为x 2+y 2≤R 2, 密度为ρ, D 内任一点(x,y)与y 轴的距离为|x|, 于是转动惯量为：(m 为圆盘质量) J=⎰⎰Dd x σρ2=⎰⎰Rdr r d 02320cos θθρπ=⎰πθθρ2024cos 4d R =44R ρπ=42mR .例7：设某球体的密度与球心的距离成正比，求它对于切平面的转动惯量.解：设球体由x 2+y 2+z 2≤R 2表示，密度为k 222z y x ++, k 为比便常数. 切平面方程为x=R, 则球体对于平面x=R 的转动惯量为： J=k ⎰⎰⎰-++VdV x R z y x 2222)(=k ⎰⎰⎰-ππϕθϕϕθ003220sin )cos sin (Rdr r r R d d=kR 6⎰⎰⎪⎭⎫ ⎝⎛+-ππϕθϕθϕθ023220cos sin 61cos sin 5241d d =⎰πθθ2026cos 911d kR =911k πR 6.四、引力求密度为ρ(x,y,z)的立体对立体外质量为1的质点A 的引力.设A 的坐标为(ξi ,ηi ,ζi )，V 中点的坐标用(x,y,z)表示. V 中质量微元dm=ρdV 对A 的引力在坐标轴上的投影为 dF xyz其中K 为引力系数， r=222)()()(ζηξ-+-+-z y x 是A 到dV 的距离，于是力F 在三个坐标轴上的投影分别为： F x =K ⎰⎰⎰-VdV r x ρξ3, F y =K ⎰⎰⎰-V dV r y ρη3, F z =K ⎰⎰⎰-VdV r z ρζ3, 所以F=F x i+F y j+F z k.例8：设球体V 具有均匀的密度ρ, 求V 对球外一点A(质量为1)的引力(引力系数为k).解：设球体为x 2+y 2+z 2≤R 2，球外一点坐标为(0,0,a) (R<a). 则F x =F y =0,F z =k ⎰⎰⎰-++-V dV a z y x a z ρ2/3222])([=k ρ⎰⎰⎰-++--zD R R a z y x dxdydz a z 2/3222])([)(, 其中D z ={(x,y)|x2+y2≤R 2-z 2}. 运用极坐标计算得： F z =k ρdr a z r rd dz a z z R RR ⎰⎰⎰---+-2202/32220])([)(πθ =2πk ρ⎰-+----R R dz aaz R a z )21(22=2πk ρ⎪⎪⎭⎫⎝⎛+--++-+-⎰-R R dz a az R R a a az R a R 22222222212= 2πk ρ⎥⎦⎤⎢⎣⎡-+----+---⎰⎰--RRRRaz d a az R a R a az d a az R a R )2(214)2(241222222222=2πk ρ⎥⎦⎤⎢⎣⎡+---+-----RRRRa az R a R a a az R a R 22222322222)2(612 =2πk ρ⎥⎦⎤⎢⎣⎡-++----222233)(6)()(2a R a R a a R R a R=2πk ρ⎪⎪⎭⎫⎝⎛-+++-232332a R R a R R R =2334a R k ρπ-. (注：z ≤R<a)习题1、求曲面az=xy 包含在圆柱x 2+y 2=a 2内那部分的面积.解：∵z x =a y, z y =ax , D={(r,θ)|0≤r ≤a, 0≤θ≤2π}, ∴曲面面积为： S=⎰⎰⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+Ddxdy a x a y 221=⎰⎰+a dr a r r d 022201πθ=)122(322-a π.2、求锥面z=22y x +被柱面z 2=2x 所截部分的曲面面积. 解：且面在xy 平面的投影区域为：D={(r,θ)|0≤r ≤1, 0≤θ≤2π}, 且z x =22yx x +, z y =22yx y +, ∴曲面面积为：S=⎰⎰⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++Ddxdy y x y y x x 2222221=⎰⎰10202rdr d πθ=π2.3、求下列均匀密度的平面薄板质心：(1)半椭圆2222by a x +≤1, y ≥0；(2)高为h, 底分别为a 和b 的等腰梯形.解：(1)设质心位置为(x ,y ), 由对称性得x =0.y =⎰⎰⎰⎰DDd yd σρσρ=⎰⎰⎰⎰DDd yd σσ=⎰⎰Dyd ab σπ2=dr r ab d ab ⎰⎰πθθπ122sin 2=π34b . (2)不妨设a 为下底，以下底中点为原点建立直角坐标系，则 D={(x,y)|l 1(y)≤x ≤l 2(y),0≤y ≤h}.设质心位置为(x ,y ), 由对称性得x =0.又等腰三角形的面积为2)(hb a +, ∴y =⎰⎰+D yd h b a σ)(2=⎰⎰+h y l y l dx ydy h b a 0)()(21)(2=⎰⎥⎦⎤⎢⎣⎡+---+--+h ydy a h y h a b a h y h b a h b a 02)(22)(2)(2=⎰⎥⎦⎤⎢⎣⎡+--+h ydy a h y h b a h b a 0)()(2=⎰⎪⎭⎫ ⎝⎛+-+h dy by y h b a h b a 02)(2=h b a a b )(32++. 其中：l 1(y): x=2)(2a h y h a b ---; l 2(y): x=2)(2ah y h b a +--.4、求下列均匀密度物体的质心.(1)z ≤1-x 2-y 2, z ≥0；(2)由坐标面及平面x+2y-z=1所围的四面体. 解：(1)设质心为(x ,y ,z ), 由对称性x =y =0, 应用柱面坐标变换有,z =⎰⎰⎰⎰⎰⎰VVdV dV z ρρ=⎰⎰⎰⎰⎰⎰--221020110201r r dz r d r d zdz r d r d ππθθ=dr r r dr r r )1()1(212102210--⎰⎰=31. (2)设质心为(x ,y ,z ),∵V=⎰⎰⎰VdV =121， ∴x =⎰⎰⎰--+21001211x y x dz dy xdx V =⎰⎰---2101)21(12x dy y x xdx =⎰-1024)1(12dx x x =41. y =⎰⎰⎰--+yy x dz dx ydy V 210122101=⎰⎰---ydx x y ydy 210210)21(12=⎰-21022)21(12dy y y =81. z =⎰⎰⎰--+yy x zdz dx dy V21012211=⎰⎰--+-ydx y x dy 2102210)12(6=⎰--21033)21(6dy y =41-.5、求下列均匀密度的平面薄板的转动惯量： (1)半径为R 的圆关于其切线的转动惯量；(2)边长为a 和b, 且夹角为φ的平行四边形，关于底边b 的转动惯量.解：(1)设切线为x=R, 密度为ρ.则对任一点P(x,y)∈D, P 到x=R 的距离为R-x ，从而转动惯量 J=ρ⎰⎰-Dd x R σ2)(=ρ⎰⎰+-Rdr r Rr R r d 022220)cos cos 2(θθθπ=ρ⎰+-πθθθ2024)cos 41cos 3221(d R= R 4. (2)设密度为ρ. 以底边为x 轴，左端点为原点，则转动惯量 J=⎰⎰Dd y σ2=ρ⎰⎰+by y a dx dy y ϕϕϕcot cot sin 02=3sin 33ϕρb a .6、计算下列引力：(1)均匀薄片x 2+y 2≤R 2, z=0对于轴上一点(0,0,c) (c>0)处的单位质量的引力；(2)均匀柱体x 2+y 2≤a 2, 0≤z ≤h 对于点P(0,0,c) (c>h)处的单位质量的引力；(3)均匀密度的正圆锥体(高h, 底半径R)对于在它的顶点处质量为m 的质点的引力.解：(1)根据对称性知引力方向在z 轴上，∴F z =0, F y =0.F z =k ρ⎰⎰++Ddxdy c y x c 2/3222)(=kc ρ⎰⎰+R dr c r r d 02/32220)(πθ=2k .∴F={0,0,2k }.(2)根据对称性知引力方向在z 轴上，∴F z =0, F y =0. F z =k ρ⎰⎰⎰-++-VdV c z y x c z 2/3222])([=k ρ⎰⎰⎰-+-a h dr c z r rd dz c z 02/322200])([)(πθ=-2k πρdz c z a c z h⎰⎥⎥⎦⎤⎢⎢⎣⎡-+-+022)(1=2k πρ[]h c h a c a --+-+2222)(. ∴F={0,0,2k πρ[]h c h a c a --+-+2222)(}.(3)以圆锥体的顶点为原点, 对称轴为z 轴建立xyz 三维直角坐标系. 根据对称性知引力方向在z 轴上，∴F z =0, F y =0.F z =k ρm ⎰⎰⎰++V dV z y x z 2/3222)(=k ρm ⎰⎰⎰+R hrR dz z r zrdr d 02/322020)(πθ=2k πR ρm ⎪⎪⎭⎫⎝⎛++-22221R h R h R . ∴F={0,0, 2k πR ρm ⎪⎪⎭⎫ ⎝⎛++-22221R h R h R }.7、求曲面⎪⎩⎪⎨⎧=+=+=ψϕψϕψsin sin )cos (cos )cos (a z a b y a b x (0≤φ≤2π, 0≤ψ≤2π) 的面积，其中常数a,b 满足0≤a ≤b.解：∵x φ=-(b+acos ψ)sin φ, y φ=(b+acos ψ)cos φ, z φ=0; x ψ=-asin ψcos φ, y ψ=-asin ψsin φ, z ψ=acos ψ.∴E=222ϕϕϕz y x ++=(b+acos ψ)2, G=222ψψψz y x ++=a 2, F=ψϕψϕψϕz z y y x x ++=0. ∴S=σd F EG D ⎰⎰'-2=σψd a b a D ⎰⎰'+)cos (=⎰⎰+ππψψϕ2020)cos (d a b d a =4ab π2.8、求螺旋面⎪⎩⎪⎨⎧===ϕϕϕb z r y r x sin cos (0≤r ≤a, 0≤φ≤2π) 的面积.解：∵x r =cos φ, y r =sin φ, z r =0; x φ=-rsin φ, y φ=rcos φ, z φ=b.∴E=222r r r z y x ++=1, G=222ϕϕϕz y x ++=r 2+b 2, F=ϕϕϕz z y y x x r r r ++=0.∴S=σd F EG D ⎰⎰'-2=σd b r D ⎰⎰'+22=⎰⎰+πϕ20022d dr b r a=π⎪⎪⎭⎫⎝⎛++++b b a a b b a a 22222ln .9、求边长为a 密度均匀的正方体关于其任一棱边的转动变量. 解：以正方体的一个顶点为原点，顶点上方的棱为z 轴，使正方体处于第一卦限中，则正方体对z 轴上的棱的转动变量为： J z =ρ⎰⎰⎰+V dV y x )(22=ρ⎰⎰⎰+aaadz y x dy dx 00220)(=a ρ⎰⎰+aady y x dx 0220)(=a ρ⎰+adx a ax 032)31(=32a 5ρ. (ρ为正方体密度)。

高等数学典型例题与应用实例(重积分B部分)

例利用二重积分的性质，估计积分2222(2)d Dx y x y σ+-⎰⎰ 的值，其中D 为半圆形区域224,0x y y +≤≥．解我们先求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值．由22220,420,x yf x xy f y x y '⎧=-=⎪⎨'=-=⎪⎩解得D 内驻点为(2,1)±，(2,1)2f ±=．在边界1:0L y =(22)x -≤≤上，2()(,0)g x f x x ==在1L 上(,)f x y 的最大值为4，最小值为0．在边界222:4L x y +=(0)y ≥上，242()(,4)58(22)h x f x x x x x =-=-+-≤≤由3()4100h x x x '=-=得驻点123550,,22x x x ==-=，(0)(0,2)8h f ==． 5537()(,)2224h f ±=±=．综上，(,)f x y 在D 上的最大值为8，最小值为0．又D 的面积为2π，所以由二重积分的估值性质知222202(2)d 82Dx y x y πσπ⋅≤+-≤⋅⎰⎰，即22220(2)d 16Dx y x y σπ≤+-≤⎰⎰．例设D 为xoy 平面上以(1,1),(1,1),(1,1)---为顶点的三角形区域，1D 为D 在第一象限的部分，则(cos sin )()Dxy x y dxdy +=⎰⎰．（A ）12cos sin D x y dxdy ⎰⎰ （B ）12D xy dxdy ⎰⎰（C ）14(cos sin )D xy x y dxdy +⎰⎰ （D ）0解区域D 如图所示，并记0D 为以(1,1),(1,1),(0,0)-为顶点的三角形区域，则0D 关于y 轴对称，且1D 为0D 在y 轴右侧的部分区域，区域0D D -关于x 轴对称．又xy 关于x 和y 均为奇函数；而cos sin x y 关于x 为偶函数．关于y 为奇函数，由二重积分的奇偶对称性得0,0D D D xy dxdy xy dxdy -==⎰⎰⎰⎰，故0Dxy dxdy =⎰⎰；1cos sin 2cos sin ,cos sin 0D D D D x ydxdy x y dxdy x y dxdy -==⎰⎰⎰⎰⎰⎰，故1cos sin 2cos sin DD x y dxdy x y dxdy =⎰⎰⎰⎰．所以1(cos sin )cos sin 2cos sin DDDD xy x y dxdy xy dxdy x y dxdy x y dxdy +=+=⎰⎰⎰⎰⎰⎰⎰⎰．因此我们选（A ）．例设区域}0,0,4),{(22≥≥≤+=y x y x y x D ，()f x 为D 上的正值连续函数，,a b 为常数，则Dσ= ．解由题意知，D 关于直线y x =对称，由二重积分轮换对称性得DσDσ=12D d σ=⎰⎰ 211()π2π22242D D a b a b a b a b d d σσ+++=+==⋅⋅=⎰⎰⎰⎰．因此，我们应填“π2a b+．”例计算二次积分220sin xydx dy yππ⎰⎰解积分区域如图，则原式20sin yydy dx yπ=⎰⎰2200sin sin sin y dy ydy ydy ππππ==+-⎰⎰⎰4=；例设D为椭圆区域22(1)(2)149x y--+≤，计算二重积分()Dx y dxdy+⎰⎰．解令12cos,23sin,x ry r=+⎧⎨=+⎩θθ则D的极坐标表示为01,02r≤≤≤≤θπ，且(,)6(,)x yrrθ∂=∂．由式(10.2.8)，可得2100()6(32cos3sin)Dx y dxdy d r r rdr+=++⎰⎰⎰⎰πθθθ2326(cos sin)1823d=++=⎰πθθθπ．例计算二重积分⎰⎰+Dyxyx dd)(，其中D为.122++≤+yxyx解解法1 D的边界曲线为,2/3212122=⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-yx这是一个以⎪⎭⎫⎝⎛21,21为圆心，23为半径的圆域，采用一般的变量代换，令⎪⎪⎩⎪⎪⎨⎧-=-=,21,21yvxu即作变换⎪⎪⎩⎪⎪⎨⎧+=+=,21,21vyux于是D变为.2/3:22≤+'vuD.111),(),(==∂∂=vuyxJ所以，()d d(1)1d dD Dx y x y u v u v'+=++⋅⋅⎰⎰⎰⎰（再用极坐标）.23023d d )cos (sin d d d )1sin cos (d 222/30202/3020ππθθθθθθθππ=+⎪⎪⎭⎫ ⎝⎛⋅=++=++=⎰⎰⎰⎰⎰⎰r r r r rr r r D解法2 由于积分区域D ：23212122≤⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 关于21=x （即)021=-x 对称，故⎰⎰=⎪⎭⎫ ⎝⎛-D y x x .0d d 21 类似地，由于D 关于⎪⎭⎫⎝⎛=-=02121y y 即对称，故 ⎰⎰=⎪⎭⎫ ⎝⎛-D y x y .0d d 21 从而.2323d d d d 1d d 21d d 21d d )(2ππ=⎪⎪⎭⎫ ⎝⎛⋅===⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰面积D y x y x y x y y x x y x y x D D D DD例计算y x e I Dy xd d },max{22⎰⎰=，其中，}10,10|),{(≤≤≤≤=y x y x D解 D 由x y =分为D 2，D 2两部分，如图.⎪⎩⎪⎨⎧≤≤≤≤≤≤≤≤=1,10:,0,10:,21},max{2222y x x D e x y x D e e y x y x x e y y e x y x e y x e I yy xx D y D x d d d d d d d d 01010222212⎰⎰⎰⎰⎰⎰⎰⎰+=+=21110d d 2d d 2222x e x xe y e x x x xx ⎰⎰⎰⎰===.1102-==e e x例利用二重积分计算定积分1(,0)ln b ax x I dx a b x-=>⎰解因为1ln ln bb a btt aa x x x dt x x x-==⎰所以 ⎰⎰⎰⎰⎰⎪⎭⎫⎝⎛++=+=+===bab aba batta b t dt t dx x dt dx dt x I 11ln )1ln(11)(11例 ],[)(b a x f 为上的连续函数，且0)(>x f ，试利用二重积分证明.)()(1d )(2a b x f x x f baba-≥⎰⎰证因为x x f y y f x x f x x f b a b a babad )(1d )(d )(1d )(⎰⎰⎰⎰=,d d )()(d d )()(y x y f x f y x x f y f DD⎰⎰⎰⎰≥= 其中所以},,|),{(b y a b x a y x D ≤≤≤≤=⎰⎰⎰⎰⎰⎰+=DD bab ay x y f x f y x x f y f x x f x x f d d )()(d d )()(d )(1d )(2 y x y f x f y f x f y x y f x f x f y f DDd d )()()()(d d )()()()(22⎰⎰⎰⎰≥+=,)(2d d 22a b y x D-==⎰⎰亦即.)(d )(1d )(2a b x x f x x f baba-≥⎰⎰例计算⎰1d )(x x xf ，其中⎰=21d int)(x t tS x f 解当10,102≤≤≤≤x x 时⎰⎰⎰-===111222,d sin d sin d sin )(x x x y yy y y y t t tx f从而x y y y x x x xf x d d sin d )(101102⎰⎰⎰⎥⎦⎤⎢⎣⎡-= 图y x y yx y y y x x xDd d sin d sin d 1102⎰⎰⎰⎰-=⋅-=，其中D 曲线1,2==y x y ，和0=x 所围成，如图10-8。

高等数学重积分 (9.4.2)--重积分的应用

习题 9.41. 求下列平面闭区域D 的面积.(1) D 由曲线e ,e x x y y -==及1x =围成；(2) D 由曲线21,1y x y x =+=--围成；(3) D 由双纽线22222()4()x y x y +=-围成；(4) {(cos ,sin )|24sin }D r r r θθθ=≤≤；(5) 1(cos ,sin )1cos 2D r r r θθθ⎧⎫=≤≤+⎨⎬⎩⎭； (6) D 由曲线2223()2(0)x y ax a +=>围成；(7) D 由椭圆22(234)(567)9x y x y +++++=围成；(8) D 是由曲线3y x =，34y x =，3x y =，34x y =所围成的位于第一象限部分;2. 利用二重积分计算下列各题中立体Ω的体积.(1) Ω为第一卦限中由圆柱面224y z +=与平面2,0,0x y x z ===所围成；(2) Ω由平面0,0,y z y x ===及6236x y z ++=围成；(3) 22{(,,)|1x y z x y z Ω=+≤≤+；(4) 222{(,,)|1,11}x y z x y z z Ω=+≤+-≤≤;(5) Ω由平面0,0,0,1x y z x y ===+=及抛物面226x y z +=-围成.3. 设平面薄片所占的闭区域是由直线2,x y y x +==和x 轴所围成，它的面密度22(,)x y x y ρ=+，求该薄片的质量.4. 在一半径为R 的球体内，以某条直径为中心轴用半径为r 的圆柱形钻孔机打一个孔(r R <)，求剩余部分的体积. 若圆柱形孔的侧面高为h ，证明所求体积只与h 有关，而与r 和R 无关.5. 利用三重积分求所给立体Ω的体积.(1) Ω是由柱面2x y =和平面0z =及1x z +=所围成的立体；(2) Ω是由抛物面22z x y =+和所2218z x y =--围成的立体；(3) Ω为圆柱体cos r a θ≤内被球心在原点、半径为a 的球所割下的部分;(4) Ω是由单叶双曲面2222x y z R +-=和平面0,z z H ==围成的立体;(5) 1Ω是Oxyz 坐标系中体积为5的立体，Ω为1Ω在变换448u x y z =++，274v x y z =++，43w x y z =++下的像.6. 已知物体Ω的底面是xOy 平面上的圆域222{(,)|}x y x y R +≤，当用垂直于x 轴的平面截Ω均得到正三角形, Ω的体密度函数为(,,)1x x y z Rρ=+，试求其质量. 7. 计算下列曲面的面积.(1) 平面63212x y z ++=位于第一卦限部分的曲面;(2) 正弦曲线的一拱sin y x =(0πx ≤≤)绕x 轴旋转一周而成的曲面;(3) 球面2222x y z a ++=含在圆柱面22x y ax +=内部的曲面;(4) 曲面222z x y =+被柱面22222()x y x y +=-所截下部分的曲面;(5) 抛物面22z y x =-夹在圆柱面221x y +=和224x y +=之间部分的曲面;(6) 球面22223x y z a ++=(0z >)和抛物面222x y az +=(0a >)所围成立体的表面;(7) 圆柱面229x y +=，平面4312y z +=和4312y z -=所围成立体的表面;(8) 两个底面半径都为R , 轴相互正交的圆柱所围立体的表面.8. 求占有下列区域D , 面密度为(,)x y μ的平面薄片的质量与质心：(1) D 是以(0,0),(2,1),(0,3)为顶点的三角形闭区域, (,)x y x y μ=+；(2) D 是第一象限中由抛物线2y x =与直线1y =围成的闭区域, (,)x y xy μ=；(3) D 是由心脏线1sin r θ=+所围成的闭区域, (,)2x y μ=；(4) 22{(,)|(1)1}D x y x y =+-≤, (,)|1|x y y y μ=+-.9. 计算下列立体Ω的体积和形心：(1) 2222{(,,)|3633}x y z x y z x y Ω=+≤≤--；(2) 2222(,,)1x y x y z z a b ⎧⎫⎪⎪Ω=+≤≤⎨⎬⎪⎪⎩⎭; (3) Ω位于锥面3πϕ=上方，球面4cos ρϕ=下方.10. 若半径为R 的半球体上任一点密度与该点到底面之距离成正比(比例系数为k ), 求其质量与质心.11. 求下列平面薄片或物体对指定轴的转动惯量.(1) 均匀薄片{(cos ,sin )|2sin 4sin }D r r r θθθθ=≤≤(面密度为1)对极轴;(2) 底长为a ，高为h 的等腰三角形均匀薄片(面密度为1)对其高;(3) 质量为M , 半径为R 的非均匀球体(其上任一点的密度与球心到该点的距离成正比)对其直径;(4) 密度为1的均匀物体2222x y z ++≤，222x y z +≥对Oz 轴.12. 设物体Ω占有的区域为222{(,,)|,||}x y z x y R z H +≤≤，其密度为常数. 已知Ω关于x 轴及z 轴的转动惯量相等. 证明:2H R =.13. 求下列密度为1的均匀物体对指定质点的引力(引力常数为k ).(1) 高为h ，半顶角为α的圆锥体对位于其顶点的单位质量质点;(2) 柱体222x y R +≤(0z h ≤≤)对位于点0(0,0,)()M a a h >处的单位质量质点;(3) 半径为R 的球体对球内的单位质量质点P .。

高等数学典型例题与应用实例(重积分B部分)

例利用二重积分的性质，估计积分2222(2)d Dx y x y σ+-⎰⎰ 的值，其中D 为半圆形区域224,0x y y +≤≥．解我们先求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值．由22220,420,x yf x xy f y x y '⎧=-=⎪⎨'=-=⎪⎩解得D内驻点为(，(2f =．在边界1:0L y =(22)x -≤≤上，2()(,0)g x f x x ==在1L 上(,)f x y 的最大值为4，最小值为0．在边界222:4L x y +=(0)y ≥上，42()(58(22)h x f x x x x ==-+-≤≤由3()4100h x x x '=-=得驻点1230,x x x ===(0)(0,2)8h f ==．7((4h f ==．综上，(,)f x y 在D 上的最大值为8，最小值为0．又D 的面积为2π，所以由二重积分的估值性质知222202(2)d 82Dx y x y πσπ⋅≤+-≤⋅⎰⎰，即22220(2)d 16Dx y x y σπ≤+-≤⎰⎰．例设D 为xoy 平面上以(1,1),(1,1),(1,1)---为顶点的三角形区域，1D 为D 在第一象限的部分，则(cos sin )()Dxy x y dxdy +=⎰⎰．（A ）12cos sin D x y dxdy ⎰⎰ （B ）12D xy dxdy ⎰⎰（C ）14(cos sin )D xy x y dxdy +⎰⎰ （D ）0解区域D 如图所示，并记0D 为以(1,1),(1,1),(0,0)-为顶点的三角形区域，则0D 关于y 轴对称，且1D 为0D 在y 轴右侧的部分区域，区域0D D -关于x 轴对称．又xy 关于x 和y 均为奇函数；而cos sin x y 关于x 为偶函数．关于y 为奇函数，由二重积分的奇偶对称性得0,0D D D xy dxdy xy dxdy -==⎰⎰⎰⎰，故0Dxy dxdy =⎰⎰；1cos sin 2cos sin ,cos sin 0D D D D x ydxdy x y dxdy x y dxdy -==⎰⎰⎰⎰⎰⎰，故1cos sin 2cos sin DD x y dxdy x y dxdy =⎰⎰⎰⎰．所以1(cos sin )cos sin 2cos sin DDDD xy x y dxdy xy dxdy x y dxdy x y dxdy +=+=⎰⎰⎰⎰⎰⎰⎰⎰．因此我们选（A ）．例设区域}0,0,4),{(22≥≥≤+=y x y x y x D ，()f x 为D 上的正值连续函数，,a b 为常数，则Dσ= ．解由题意知，D 关于直线y x =对称，由二重积分轮换对称性得DσDσ=12D d σ=⎰⎰ 211()π2π22242D D a b a b a b a b d d σσ+++=+==⋅⋅=⎰⎰⎰⎰．因此，我们应填“π2a b+．”例计算二次积分220sin xydx dy yππ⎰⎰解积分区域如图，则原式20sin yydy dx yπ=⎰⎰2200sin sin sin y dy ydy ydy ππππ==+-⎰⎰⎰4=；例设D 为椭圆区域22(1)(2)149x y --+≤，计算二重积分()Dx y dxdy +⎰⎰．解令12cos ,23sin ,x r y r =+⎧⎨=+⎩θθ则D 的极坐标表示为01,02r ≤≤≤≤θπ，且(,)6(,)x y r r θ∂=∂．由式(10.2.8)，可得21()6(32cos 3sin )Dx y dxdy d r r rdr +=++⎰⎰⎰⎰πθθθ20326(cos sin )1823d =++=⎰πθθθπ．例计算二重积分⎰⎰+Dy x y x d d )(，其中D 为.122++≤+y x y x解解法1 D 的边界曲线为,2/3212122=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 这是一个以⎪⎭⎫ ⎝⎛21,21为圆心，23为半径的圆域，采用一般的变量代换，令⎪⎪⎩⎪⎪⎨⎧-=-=,21,21y v x u 即作变换⎪⎪⎩⎪⎪⎨⎧+=+=,21,21v y u x 于是D 变为.2/3:22≤+'v u D.11001),(),(==∂∂=v u y x J所以，()d d (1)1d d DD x y x y u v u v '+=++⋅⋅⎰⎰⎰⎰（再用极坐标）.23023d d )cos (sin d d d )1sin cos (d 222/30202/3020ππθθθθθθθππ=+⎪⎪⎭⎫ ⎝⎛⋅=++=++=⎰⎰⎰⎰⎰⎰r r r r rr r r D解法2 由于积分区域D ：23212122≤⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 关于21=x （即)021=-x 对称，故⎰⎰=⎪⎭⎫ ⎝⎛-D y x x .0d d 21 类似地，由于D 关于⎪⎭⎫⎝⎛=-=02121y y 即对称，故 ⎰⎰=⎪⎭⎫ ⎝⎛-D y x y .0d d 21 从而.2323d d d d 1d d 21d d 21d d )(2ππ=⎪⎪⎭⎫ ⎝⎛⋅===⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰面积D y x y x y x y y x x y x y x D D D DD例计算y x e I Dy xd d },max{22⎰⎰=，其中，}10,10|),{(≤≤≤≤=y x y x D解 D 由x y =分为D 2，D 2两部分，如图.⎪⎩⎪⎨⎧≤≤≤≤≤≤≤≤=1,10:,0,10:,21},max{2222y x x D e x y x D e e y x y x x e y y e x y x e y x e I yy xx D y D x d d d d d d d d 01010222212⎰⎰⎰⎰⎰⎰⎰⎰+=+=21110d d 2d d 2222x e x xe y e x x x xx ⎰⎰⎰⎰===.1102-==e ex例利用二重积分计算定积分1(,0)ln b ax x I dx a b x-=>⎰解因为1ln ln bb a btt aa x x x dt x x x-==⎰所以 ⎰⎰⎰⎰⎰⎪⎭⎫⎝⎛++=+=+===bab aba batta b t dt t dx x dt dx dt x I 11ln )1ln(11)(11例 ],[)(b a x f 为上的连续函数，且0)(>x f ，试利用二重积分证明.)()(1d )(2a b x f x x f baba-≥⎰⎰证因为x x f y y f x x f x x f b a b a babad )(1d )(d )(1d )(⎰⎰⎰⎰=,d d )()(d d )()(y x y f x f y x x f y f DD⎰⎰⎰⎰≥= 其中所以},,|),{(b y a b x a y x D ≤≤≤≤=⎰⎰⎰⎰⎰⎰+=DD bab ay x y f x f y x x f y f x x f x x f d d )()(d d )()(d )(1d )(2 y x y f x f y f x f y x y f x f x f y f DDd d )()()()(d d )()()()(22⎰⎰⎰⎰≥+=,)(2d d 22a b y x D-==⎰⎰亦即.)(d )(1d )(2a b x x f x x f baba-≥⎰⎰例计算⎰1d )(x x xf ，其中⎰=21d int)(x t tS x f 解当10,102≤≤≤≤x x 时⎰⎰⎰-===111222,d sin d sin d sin )(x x x y yy y y y t t tx f从而x y y y x x x xf x d d sin d )(101102⎰⎰⎰⎥⎦⎤⎢⎣⎡-= 图y x y yx y y y x x xDd d sin d sin d 1102⎰⎰⎰⎰-=⋅-=，其中D 曲线1,2==y x y ，和0=x 所围成，如图10-8。

高等数学第九章重积分

第9章重积分典型例题一、二重积分的概念、性质 1、二重积分的概念：d 01(,)lim(,)niiii Df x y f λσξησ→==∆∑⎰⎰其中：D ：平面有界闭区域，λ：D 中最大的小区域的直径（直径：小区域上任意两点间距离的最大值者），i σ∆：D 中第i 个小区域的面积2、几何意义：当(,)0f x y ≥时，d (,)Df x y σ⎰⎰表示以曲面(,)z f x y =为曲顶，D 为底的曲顶柱体的体积。

所以d 1Dσ⎰⎰表示区域D 的面积。

3、性质（与定积分类似）：:线性性、对积分区域的可加性、比较性质、估值性质、二重积分中值定理二、二重积分的计算1、在直角坐标系下计算二重积分（1）若D 为X 型积分区域：12,()()a x b y x y y x ≤≤≤≤，则21()()(,)(,)by x ay x Df x y dxdy dx f x y dy =⎰⎰⎰⎰（2）若D 为Y 型积分区域：12,()()c y d x y x x y ≤≤≤≤，则21()()(,)(,)dx y cx yf x y dxdy dy f x y dx =⎰⎰（3X －型或者Y －型区域之和，如图，则123(,)(,)(,)(,)D D D f x y d x d y f x y d x d y f x y d x d y f x y d x d=++⎰⎰⎰⎰⎰⎰⎰（4（5）对称性的应用1(,)2(,),(,)0(,)DD f x y dxdy f x y dxdy f x y y D x f x y y ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称，关于为奇函数1(,)2(,),(,)0(,)D D f x y dxdy f x y dxdy f x y x D y f x y x ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称，关于为奇函数（6）积分顺序的合理选择：不仅涉及到计算繁简问题，而且又是能否进行计算的问题。

08 第四节重积分应用举例

2 I x 轴的转动惯量 y ( x , y )dxdy . D
薄片对于原点的转动惯量 I o ( x 2 y 2 ) ( x , y )dxdy .
D
事实上: 平面薄片D对某点M 或某直线L 的转动惯量
I d 2 ( x , y ) ( x , y )dxdy .
2 2 Dxy

2
,
S 4 1 z x z y dxdy
同理可得
2. 若曲面的方程为：x = x(y,z), (y,z)Dyz, 其中 Dyz 是在 yoz 面的投影区域. 则曲面面积公式为： S
D yz

2 1 x2 x y z dydz;
3. 若曲面的方程为： y = y(z,x), (z,x)Dzx, 其中 Dzx是在 zox 面的投影区域. 则曲面面积公式为：S
例 1 求体密度为常量的均匀圆柱筒： a 2 x 2 y 2 b2, 0 z h 对位于原点处的一质量为 m 的质点的引力． (b a 0)
Fx Fy 0, 解由积分区域的对称性及物体匀质可知：
( x2 y2 z ) b 2 b h z mk d d ) d 3 dz mk (1 2 2 a 0 a 0 h ( 2 z 2 )2

空间物体对某点M 或某直线L 的转动惯量
I d 2 ( x , y , z ) ( x , y , z )dxdydz .
其中 d 2 ( x , y , z ) 为点 ( x , y , z ) 到点M (或直线 L)的距离.

例 3 设一匀质物体占空间区域, 其中由 x +y =1, z 1 x 2 y 2 , z =1 围成, 求物体的形心及关于 z z 轴的转动惯量.

重积分经典例题

郑州大学重积分经典例题1．（P148,第2题）求函数()yx y x f 22sin.sin,=在闭正方形区域:D ()ππ≤≤≤≤y x 0,0上的函数值的平均值.解：()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎰⎰⎰⎰ππ22sin.sin,ydy xdx dxdy y x f D202sin⎥⎦⎤⎢⎣⎡=⎰πxdx ；又.22sin 41222cos 1sin|02ππππ=⎥⎦⎤⎢⎣⎡-=-=⎰⎰x x dx xxdx所以().4,2π=⎰⎰dxdyy x f D故()y x f ,在闭正方形区域D 上的函数值的平均值为 ()().414,122===⎰⎰ππσdxdy y x f D S D2．（P148,第3题）设函数()x f 在闭区间[]b a ,上连续，证明不等式 ()()().22dx x fa b dx x f bab a ⎰⎰-≤⎥⎦⎤⎢⎣⎡证明：考虑积分 ()()[]d x d y y f x f I D⎰⎰-=2一方面 ()()()()dxdy y fdxdy y f x f dxdyx fI DDD⎰⎰⎰⎰⎰⎰+-=22.2 （1）其中()()()();222dx x fa b dyx fdx dxdyx fbababaD⎰⎰⎰⎰⎰-==（2）()()()()dy y fa b dyy fdx dxdyy fbababaD⎰⎰⎰⎰⎰-==222()();2dx x f a b ba⎰-= （3）()()()()()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==⎰⎰⎰⎰⎰⎰ba b a b a baDdy y f dx x f dxdy y f x f dx dxdy y f x f ...().2⎥⎦⎤⎢⎣⎡=⎰ba dx x f （4）将（2）、（3）、（4）代入（1）得 ()()().2222⎥⎦⎤⎢⎣⎡--=⎰⎰ba badx x f dx x f a b I（5）另一方面显然0≥I ，即()()()02222≥⎥⎦⎤⎢⎣⎡--⎰⎰ba badx x f dx x f a b ，故()()().22dx x fa b dx x f bab a ⎰⎰-≤⎥⎦⎤⎢⎣⎡3．（P149,第4题）设()x f 在闭区间[]b a ,上为正值连续函数.证明不等式()()()2..b b aa dx fx dx b a f x ⎡⎤⎡⎤≥-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰证法一：考虑到定积分与变量的记号无关.故有：()()⎰⎰=babay f dy x f dx ----（1）以及()().dy y f dx x f baba⎰⎰=-----（1）所以，()()()()..⎰⎰⎰⎰=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡Db a b a dxdy y f x f x f dx dx x f ---------------（2）其中，⎩⎨⎧≤≤≤≤.,:b y a b x a D同理，()()()()..⎰⎰⎰⎰=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡Db a b a dxdy x f y f x f dx dx x f -----------------（3），（2）+（3），得：()()()()()()()()()().2.2⎰⎰⎰⎰⎰⎰≥⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡DDb a b a dxdy y f x f x f y f dxdy y f x f x f y f x f dx dx x f()222.Dd x d y b a ==-⎰⎰ 即：()()()2..bba adx f x dx b a f x ⎡⎤⎡⎤≥-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰ 证法二：因为()0≥x f ，所以，20ba dx λ⎡⎤⎢≥⎢⎣⎰，即： ()()()220.bb aadx f x dx b a fx λλ⎡⎤+-+≥⎢⎥⎣⎦⎰⎰------（1）（1）式左边是λ的非负二次三项式，因此必有判别式()()()20b ba adx b a fx dx f x ⎡⎤⎡⎤∆=--≤⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰，故 ()()()2..b b aa dx f x dxb a f x ⎡⎤⎡⎤≥-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰4．（书p149页习题8）设函数()x f 在[]b a ,上连续，证明：()()().dx x b x f dx x f dy ba baya-=⎰⎰⎰证法一：与累次积分()dx x f dy b ay a⎰⎰对应的二重积分的积分区域 ⎩⎨⎧≤≤≤≤.,:b x a b y x D交换积分次序后，重新计算()dx x f dy baya⎰⎰，则有()=⎰⎰dx x f dy baya()dy x f dx babx⎰⎰()().dx x b x f ba-=⎰.证法二：记()()dx x f y F ya⎰=，则()()dy y F dx x f dy babaya⎰⎰⎰=()[]()dy y F y y F y baba⎰'-=|.()()()dy y f y a aF b bF ba⎰--=.()()dx x f x dx x f b bab a⎰⎰--=.0.()().dx x b x f ba-=⎰5．（书p149页习题10）设()x f 为[]1,1-上的连续函数，证明： ().4210⎥⎦⎤⎢⎣⎡=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎰⎰⎰≤≤dx x f ab dxdy b y f a x f by ax 证明：因为⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎰⎰⎰⎰--≤≤b b a aby ax dy b y f dx a x f dxdy b y f a x f .（1）其中对于dx a x f aa⎰-⎪⎭⎫ ⎝⎛，令,ax u =则()()()dxx f a du u f a du u f a dx a x f aa⎰⎰⎰⎰===⎪⎭⎫⎝⎛--10101122；（2）同理，对于dy b y f bb⎰-⎪⎭⎫⎝⎛，令,by v =则()()()dxx f b dv v f b dv v f b dy b y f bb⎰⎰⎰⎰===⎪⎭⎫⎝⎛--1010112.2；（3）故().4210⎥⎦⎤⎢⎣⎡=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎰⎰⎰≤≤dx x f ab dxdy b y f a x f by a x6．（书p158页习题3）证明：dy yxdx xx⎰⎰2sin21π().242sin3242+=+⎰⎰πππdy yxdx x证明：（一）记⎩⎨⎧≤≤≤≤.,21:1x y x x D ，⎩⎨⎧≤≤≤≤2,42:2y x x D .分别画出草图.则12.D D D = （二）按所给积分次序很困难，故更换积分次序，即要将积分区域视为-Y 型区域：⎩⎨⎧≤≤≤≤.,21:2y x y y D ，此时无须分块. 原式dx yxdy y y⎰⎰=22sin21π⎪⎪⎭⎫⎝⎛=⎰⎰y x d y x dy yy y22sin2221πππdy y x y y y ⎰⎥⎦⎤⎢⎣⎡-=21|22cos 2ππdyy y ⎰-=212cos2ππ⎪⎭⎫ ⎝⎛-=⎰y d y 2sin 4212ππ⎥⎦⎤⎢⎣⎡--=⎰212122sin2sin 4|ydy y y πππ⎥⎦⎤⎢⎣⎡+--=|2122cos .214y πππ().2421432+=⎥⎦⎤⎢⎣⎡---=ππππ 7．（书p158页习题4）求⎰⎰-=112.2xydy edx x I解：按所给积分次序很困难，画出积分区域D 的图形，交换积分次序.dx x dy eI yy⎰⎰-=212⎰-=13231dy y ey()⎰--=12261yed y()⎥⎦⎤⎢⎣⎡-+-=⎰--1210222|61yd eey yy[]().216116161111101|2------=-+-=⎥⎦⎤⎢⎣⎡+-=e e e e e y8．（书p158页习题5）利用极坐标，求下面的二重积分：（ⅰ）()D dxdy yxy xI D,22⎰⎰++=为由上半圆周122=+yx（0≥y ）与直线x y ±=围成的圆扇形；（ⅱ）Ddxdy y x y x I D,112222⎰⎰++--=为单位圆（122≤+y x ）；（ⅲ）D dxdy y x I D,sin22⎰⎰+=为圆环域（22224ππ≤+≤y x ）；（ⅳ）Ddxdy xy I D,arctan ⎰⎰=为单位圆（122≤+y x ）含在第一象限内的部分.解：（ⅰ）()=++=⎰⎰dxdy y xy xI D22()022++⎰⎰dxdyyxD.841422.22412πππθππ=⨯⎪⎭⎫⎝⎛-⨯==⎰⎰dr r r d （ⅱ）rdrrr d dxdy y x y x I D ⎰⎰⎰⎰+-=++--=20122222211411πθrdrr r ⎰+-=122112π（令t r =2）dt tt ⎰+-=111πdt tt ⎰--=1211πdt t⎰-=1211πdttt ⎰--121π|10arcsin t π=()210211121t d t --⎪⎭⎫ ⎝⎛--⎰π2.ππ=|1021t-+π2.ππ=π-.12⎪⎭⎫⎝⎛-=ππ （ⅲ）⎰⎰⎰⎰=+=20222.sin 4sinπππθrdrr d dxdy y x I D⎰⎪⎭⎫⎝⎛=πππ2.sin .2.4rdr r ()⎰-=πππ2cos .2r rd .6sin 6cos cos 222222||πππππππππ-=--=⎥⎦⎤⎢⎣⎡--=⎰r rdr r r（ⅳ）rdrr r d dxdy xy I D.cos sin arctanarctan21⎰⎰⎰⎰==πθθθ==⎰⎰rdr d .21πθθ .1621.21.21022022010||πθθθππ=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎰⎰r dr r d9．（书p158页习题6）计算下面的二重积分：（ⅰ）D dxdy x y I D,2⎰⎰-=为正方形（20,11≤≤≤≤-y x ）；（ⅱ）Ddxdy yxI D,422⎰⎰-+=为圆域（922≤+y x ）；（ⅲ）()Ddxdy y x I D,cos ⎰⎰+=为正方形（20,20ππ≤≤≤≤y x ）.解：（ⅰ）此题中积分区域本来是非常规范的矩形域⎩⎨⎧≤≤≤≤-.20,11:y x D （画图）但由于被积函数为分段函数2||y x -2222,,.,y x y x x y y x⎧-≥⎪=⎨-≤⎪⎩，故需要用抛物线2y x =将积分区域分成两个小区域.即12D D D = ，则原式=()()1222.D D y x dxdy x y dxdy -+-⎰⎰⎰⎰其中，⎩⎨⎧≤≤-≤≤,11,2:21x y x D ， ⎩⎨⎧≤≤-≤≤,11,0:22x x y D于是，有()dy x y dx I x⎰⎰--=11222().15465115431122=+=-+⎰⎰-dy y xdx x（ⅱ）设222212:04,:49.D x y D x y ≤+≤≤+≤则12.D D D = 所以，()()12222244D D I xyd xy d σσ=--++-⎰⎰⎰⎰()()22232224144.2d r rdr d rrdr πππθθ=-+-=⎰⎰⎰⎰（ⅲ）以直线2π=+y x 将区域D 分成两个子区域，12D D D =其中，⎪⎩⎪⎨⎧≤≤-≤≤,20,20:1ππx x y D ， ⎪⎩⎪⎨⎧≤≤≤≤-,20,22:2πππx y x D()dy y x dx I x⎰⎰-+=22cos ππ()dyy x dx x⎰⎰-+-+222cos πππ其中()=+⎰⎰-dy y x dx x2020cos ππ()dx y x x ⎰⎥⎦⎤⎢⎣⎡+-220|sin ππ()12s i n 120-=-=⎰ππdxx ；()dy y x dx x⎰⎰-+-222cos πππ()dxy x x ⎰⎥⎦⎤⎢⎣⎡+-=-222|sin πππ().121c o s 20-=--=⎰ππdx x所以 .21212-=⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-=πππI 10．（书p159页习题7）求(),t F '其中()()0002>=⎰⎰≤≤≤≤-t dxdy et F ty tx ytx .解：（一）()dxedy dxdy e t F ttytx ty tx ytx ⎰⎰⎰⎰-≤≤≤≤-==0022dy y tx d e t y t t y tx⎰⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-00222dy et y tty tx⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=-002|2dy e t y tyt⎰⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-02122t d y e t y tyt⎰⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-022122令,tu y =则,tdu dy =()()du t e u t F u 2101212⎰⎪⎪⎭⎫ ⎝⎛--=-()du e u tu ⎰⎪⎪⎭⎫⎝⎛--=-1012212 （1）（二）)()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--='⎰⎰--101221012121222uu e u t t du e u t t F（因为（1）式）().2t F t=11．（书p159页习题8）根据⎰⎰=DD dxdy 的面积，求下面曲线围成图形的面积：（ⅰ）由抛物线x y =2与半圆周22yx -=围成的图形；（ⅱ）曲线()xy y x =+222围成的图形. 解：（ⅰ）联立⎩⎨⎧-==.2,22y x x y 得⎩⎨⎧==.1,1y x 或⎩⎨⎧-==.1,1y x 故两曲线的交点为()1,1及()1,1-.化出区域D 的草图，并视之为-Y 型区域. 则所求面积为[]⎰⎰⎰⎰⎰-----===1122112222yydx dy dxdy A y yD32222a r c s i n .2223222|10212-⎥⎥⎦⎤⎢⎢⎣⎡-+=--=⎰y y y d y y .312+=π （ⅱ）解法一：由()xy y x =+222，知0xy ≥，即图形分布在第一及第三象限.化为极坐标方程表示为()θθθsin .cos 2=r（1）故 ()θθθs i n .c o s =r ⎥⎦⎤⎢⎣⎡--∈2,ππθ或.2,0⎥⎦⎤⎢⎣⎡∈πθ （2）所以，所求面积为()⎰⎰=⎥⎦⎤⎢⎣⎡⨯==22021cos .sin sin cos 2122ππθθθθθθd d A A().21sin21sin .sin |2022===⎰ππθθθd解法二：记1D 为D 在第一象限内的那部分区域，则⎰⎰⎰⎰===20sin cos 01221πθθθrdrd dxdy A A D.21c o s .s i n 22202s i nc o s 02|⎰⎰==⎥⎦⎤⎢⎣⎡=ππθθθθθθd d r12．（书p159页习题9）求下面立体图形的体积（ⅰ）球面()02222>=++a az z y x 的上半部分与圆锥面222y x z +=围成的图形；（ⅱ）圆柱面222a z y =+与222a z x =+围成的立体的图形. （ⅰ）解法一：画出积分区域Ω的草图. 联立⎩⎨⎧+==++.,2222222y x z az z y x ，消去z ，即得Ω在xoy 面上的投影区域为.:222a yx D ≤+所以，所求立体的体积为 ()[]d x d y y x yx a a V D⎰⎰+---+=22222()[]⎰⎰--+====πθ2022ar d r r ra a d 极⎥⎦⎤⎢⎣⎡-+-=⎰⎰⎰aaar d rr a dr r ardr 02222π().32.21.23.22.23232233|a ra aaaππππ=---=解法二：画出积分区域Ω的草图，显然见Ω的体积为球体az z y x 2222≤++的体积的上半部分体积加上锥体()a z y x z ≤≤+≥0222的体积故 ..3134.2132321a a a a V V V πππ=+=+= （ⅱ）解法一：()()(),22222z a za D S z A z -=-==所以，()().31688322a dz z a dzz A V a a=-==⎰⎰解法二：()()().316338888333000222221111a a a dx y a dy dy x a dx V V V V a xay=⎪⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-+-=+==⎰⎰⎰⎰解法三：（切片法）[].3168883220a dz z a D dxdy dzdv V aaz=-===⎰⎰⎰⎰⎰⎰⎰Ω13．（P159,第12题）根据下面的提示，证明贝塔函数()t s ,β与伽马函数()t Γ之间的关系为()()()()t s t s t s +ΓΓΓ=,β ()0,0>>t s其中()(),1,111dx x xt s t s --⎰-=β()dx ext xt -+∞-⎰=Γ01提示：（ⅰ）在()t Γ中用2x 替换x ，得()dx ext xt .20122-+∞-⎰=Γ.（ⅱ）()()()dxdy y x f t s Da ⎰⎰+∞→=ΓΓ,lim4，其中()a y a x D ≤≤≤≤0,0为正方形，函数()().,221212yx s t eyxy x f +---= （ⅲ）如图所示，()a K 表示半径为a 的圆)(222a y x ≤+含在第一象限的部分，()aK2表示半径为a 2的圆)2(222a yx ≤+含在第一象限的部分.由于函数()y x f ,的非负性，()()≤⎰⎰dxdyy x f a K ,()≤⎰⎰dxdyy x f D,()().,2d x d y y x f aK⎰⎰（ⅳ）计算上述不等式两端的积分，并让.+∞→a证明：（ⅰ）令2u x =，则 udu dx 2=，故()()udu eu t ut 22012-+∞-⎰=Γdueuut .20122-+∞-⎰=换记为 ()dx ext xt .20122-+∞-⎰=Γ. （1）（ⅱ）()()⎥⎦⎤⎢⎣⎡=ΓΓ⎰--+∞→dx ext s axt a 0122lim2⎥⎦⎤⎢⎣⎡⎰--+∞→dy eyays a 0122lim2.()d x d yy x f Da ⎰⎰+∞→=,lim 4. （2）其中(){}a y a x y x D ≤≤≤≤=0,0|,为正方形区域，()().,221212yx s t eyxy x f +---= （ⅲ）显然，由于()0,≥y x f ，故有 ()()≤⎰⎰dxdyy x f a K ,()≤⎰⎰dxdyy x f D,()().,2d x d y y x f aK⎰⎰ （3）其中()(){}222|,a y x y x a K ≤+= ；()(){}2222|,2a y x y x a K ≤+=分别是半径为a 及的a 2圆含在第一象限的部分. （3）式左端积分()dxdyeyxyx a K s t 221212----⎰⎰=（改为极坐标）()()⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡=-----⎰⎰rdr e r r d rs a t s t .sin cos 212012121220θθθπ（4）其中()()θθθπd s t 121220sin cos --⎰()()()θθθθθπd s t sin .cos 2sincos 21121202--=--⎰（令u =θ2cos ，则du d =-θθθsin cos 2）()du u us t 111121----=⎰()().,21121111t s duu us t β=-=--⎰；（5）其中rdrerr rs t a.212120---⎰（令u r =2，则du rdr =）du eu us a--+⎰=120221dxex xt s a--+⎰=1221；（6）故由（5）、（6）两式，得（3）式左端积分().,21⎥⎦⎤⎢⎣⎡=t s β⎥⎦⎤⎢⎣⎡--+⎰dx ex xs a120221()dxe x t s xa t s --+⎰=201,41β. （7）同理得（3）式右端积分()dxext s xat s --+⎰=2201,41β. （8）故（3）化为()dxext s xat s --+⎰21,41β ()dxdyy x f D⎰⎰≤,()dxext s xat s --+⎰≤2201,41β （9）（9）式两边令,+∞→a 有 ()()()()≤ΓΓ≤+Γt s t s t s .41.,41β()()t s t s +Γ.,41β故()()()()t s t s t s ΓΓ=+Γ.41..,41β （10）（10）化简，即得： ()()()().,t s t s t s +ΓΓΓ=β14．（书p166页习题1）引入适当的变换，将下面的二重积分化为一重积分：（ⅰ）()dxdy y x f I y x ⎰⎰≤++=1；（ⅱ）()D dxdy xy f I D,⎰⎰=为双曲线1=xy和2=xy （0,0>>y x ）与直线x y =和xy 4=围成的区域；（ⅲ）dxdy x y f I xy x ⎰⎰≤+⎪⎭⎫⎝⎛=22；（ⅳ）()dxdyc by ax f I y x ⎰⎰≤+++=122（022≠+b a ）.解：（ⅰ）画出积分区域D （如图，为一个正方形区域）. 作变量代换：⎪⎩⎪⎨⎧-=+=⇒⎩⎨⎧-=+=.2,2.,v u y v u x y x v y x u由二重积分的换元法 ()()dudvJu f dxdyy x f I D y x ⎰⎰⎰⎰'≤+=+=1. （1）其中()()2121212121,,-=-=∂∂∂∂∂∂∂∂=∂∂=vy uy v xu x v u y x J ；（2）⎩⎨⎧≤≤-≤≤-'.11,11:u v D （3）故()()dv u f dududvu f I D ⎰⎰⎰⎰--'==11112121()()⎰⎰--==1111.221du u f du u f（ⅱ）画出积分区域D （如图）.作变量代换：⎪⎩⎪⎨⎧==⇒⎪⎩⎪⎨⎧==..,.,v u y v ux x y v xy u由二重积分的换元法 ()()dudvJu f dxdyxy f I D D⎰⎰⎰⎰'==. （1）其中()()v vu uv vv u uv v y uy v xuxv u y x J 1.2121212121,,=-=∂∂∂∂∂∂∂∂=∂∂=（2）⎩⎨⎧≤≤≤≤'.21,41:u v D （3）故()()dvvdu u f dudv v u f I D ⎰⎰⎰⎰=='21411.211.21()⎰=21..2ln du u f （ⅲ）画出积分区域D （如图）.作变量代换：⎩⎨⎧==.s i n ,c o sθθr y r x由二重积分的换元法()θθd r d J f d x d y x y f I D D⎰⎰⎰⎰'=⎪⎭⎫⎝⎛=tan . （1）其中()()rr r y ry xr x r y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,, （2）⎪⎩⎪⎨⎧≤≤-≤≤'.22,cos 0:πθπθr D （3）故()θθr d r df d x d y x y f I D D⎰⎰⎰⎰'=⎪⎭⎫⎝⎛=tan ()r d r f d ⎰⎰-=22c o st a n ππθθθ().cos .tan 21222⎰-=ππθθθd f（ⅳ）作正交变量代换：..,22222222v u y x b a a vb u y ba b v a u x +=+⇒⎪⎪⎩⎪⎪⎨⎧+-=++=由二重积分的换元法 ()()dudvJ c ba uf dxdy c by axf I D y x ⎰⎰⎰⎰'≤+++=++=22122. （1）其中()().1,,22222222=+-+++=∂∂∂∂∂∂∂∂=∂∂=ba aba b ba b b a a vy uy v x u xv u y x J （2）.1:22≤+'vuD或⎪⎩⎪⎨⎧≤≤--≤≤--'.11,11:22u u v uD （3）故()d udvc ba uf I D ⎰⎰'++=22()d vc ba u f du uu⎰⎰----++=11112222().1211222⎰-++-=du c ba uf u15．（书p167页习题2）引入适当的变换，求下列曲线所围成图形的面积：（ⅰ）()222a x y x =+-；（ⅱ）ky hx by ax +=+2222（0,0,0,0>>>>k h b a ）；（ⅲ）0,0,144===+y x by ax .)0,0(>>b a ；（ⅳ）()()122222111=+++++c y b x a c y b x a （01221≠-b a b a ）.解：（ⅰ）作变量代换：⎩⎨⎧-==⇒⎩⎨⎧=-=.,.,u v y v x x v y x u则原方程化为222a v u =+. （1）于是，曲线所围成的面积为 d x d y S D⎰⎰=1dudvJD ⎰⎰'=1其中()().11110,,=-=∂∂∂∂∂∂∂∂=∂∂=vy uy v x u xv u y x J （2）222a v u ≤+ （3）所以.12a dudvS D π==⎰⎰'（ⅱ）令⎩⎨⎧==.sin ,cos θθbr y ar x则原方程化为 .s i n c o s θθkb ha r +=（1）由于0≥r ，故有0s i n c o s ≥+θθkb ha . （2）为使（2）式有解，首先要求θ不能落在第三象限（否则，.0sin cos ≤+θθkb ha）因此确定θ不能超出⎥⎦⎤⎢⎣⎡-∈ππθ,2的范围. 下面进一步讨论θ的取值范围.().a 若.2,20cos ⎥⎦⎤⎢⎣⎡-∈⇒≥ππθθ，则由（2）式，得： bh ak-≥θtan ，（3）由（3）式解得：2a r c t a n πθ≤≤-bh ak ；（4）().b 若.,20cos ⎥⎦⎤⎢⎣⎡∈⇒≤ππθθ，则由（2）式，得： bhak -≤θtan ，（5）由（3）式解得：.a r c t a n 2bh ak -≤≤πθπ（6）综合（4）、（6）两式，知θ的取值范围为 .a r c t a n a r c t a n bhakbhak-≤≤-πθ于是，曲线所围成的面积为 d x d y S D⎰⎰=1θd r d JD ⎰⎰'=1其中()()abrbr b ra a y ry xr xr y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,, （7）⎪⎩⎪⎨⎧-≤≤-≤≤'.arctan arctan ,cos 0:bh ak bh ak r D πθθ （8）故 θd r d abr S D ⎰⎰'=drr d ab bhak bhak kb ha⎰⎰--+=arctanarctansin cos 0πθθθ⎰--⎪⎭⎫⎝⎛+=bhak bhak d k b h a ab arctanarctan2sin cos 2πθθθ⎰--⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+=bhakbhak d k b h a kb ha kb ha ab arctan arctan 222222222sin cos 1.2πθθθ⎰--⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++⎪⎪⎭⎫ ⎝⎛+=bhakbhak d kb ha kbkb ha h a kb ha ab arctan arctan 2222222222222sin cos .2πθθθ （9）令 .tan ,.cos sin 02222022220bhak kb ha kb k b h a ha =⇒⎪⎪⎩⎪⎪⎨⎧+=+=ααα（10）则()⎰--+⎪⎪⎭⎫ ⎝⎛+=bhakbhak d k b ha ab S arctan arctan 022222sin .2πθαθ()⎰--+-⎪⎪⎭⎫ ⎝⎛+=bh akbhakd k b ha ab arctan arctan 0222222cos 1.2πθαθ⎰--⎪⎪⎭⎫ ⎝⎛+=bh akbhak d k b h a ab arctan arctan 2222.4πθ()⎰--+⎪⎪⎭⎫⎝⎛+-bhakbhak d k b h a ab arctan arctan 0222222cos .4πθαθπ.42222⎪⎪⎭⎫ ⎝⎛+=k b h a ab ()|arctan arctan0222222sin .21.4bh akbhak k b ha ab --+⎪⎪⎭⎫ ⎝⎛+-παθπ.42222⎪⎪⎭⎫ ⎝⎛+=k b h a ab 0-.42222⎪⎪⎭⎫⎝⎛+=k b ha ab π （（ⅲ））令⎩⎨⎧==.sin ,cos 88θθbr y ar x 则原方程化为.1=r （1）于是，曲线所围成的面积为 d x d y S D⎰⎰=1θd r d JD ⎰⎰'=1其中()().sin.cos 8cos .sin8sin sin .cos 8cos ,,777878θθθθθθθθθθθabr br b ra a y ry x r xr y x J =-=∂∂∂∂∂∂∂∂=∂∂=（2）⎪⎩⎪⎨⎧≤≤≤≤'.20,10:πθr D （3）故 θθθd r d a b r S D 77s i n.c o s 8⎰⎰'=dr r d ab ⎰⎰=20177sin .cos 8πθθθ⎰=2077sin .cos 4πθθθd ab （令θsin =u ）()⎰-=2032714πdu u u ab()⎰-+-=20131197334πdu u u u u ab.7014141103814abab =⎪⎭⎫ ⎝⎛-+-= （ⅳ）()()122222111=+++++c y b x a c y b x a （01221≠-b a b a ）.令⎩⎨⎧++=++=.,222111c y b x a v c y b x a u即⎪⎪⎩⎪⎪⎨⎧-+--=-+--=.,12212121211221122112b a b a a c c a u a v a v b a b a b c b c v b u b x则原方程化为.122=+v u （1）于是，曲线所围成的面积为 d x d y S D⎰⎰=1dudvJD ⎰⎰'=1其中()().1,,122112211122121221112212b a b a b a b a a b a b a a b a b a b b a b a b vy uy v x u xv u y x J -=------=∂∂∂∂∂∂∂∂=∂∂=（2）.1:22≤+'v u D （3）故 dudvb a b a S D 122111-=⎰⎰'..11221πb a b a -=（令θsin =u ）16．（书p167页习题3）求由下列曲面包围的立体的体积：（ⅰ）1222222=++c z b y a x （椭球面）；（ⅱ）1222222-=-+c z b y a x （双叶双曲面），12222=+by ax （椭圆柱面）；（ⅲ）12222=++c zby ax ，.0,13232==⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛z b y a x 解：（ⅰ）根据对称性及二重积分的几何意义，知 ⎰⎰--==122221144D dxdyby ax c V V （1）其中 .0,0,1:22221>>≤+y x by ax D为计算方便，特引入变量替换令⎩⎨⎧==.sin ,cos θθbr y ar x则被积函数化为2222211rc by ax c z -=--= （2）积分区域1D 化为 .20.1:21⎪⎭⎫⎝⎛≤≤≤'πθr D（3）于是⎰⎰'-==121144D drd J rc V V θ其中()()abrbr b ra a y ry xr xr y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,, （4）故⎰⎰'-==D drd J r c V V θ21144⎰⎰'-=D rdrd r abcθ214⎰⎰-=201214πθrdr r d abc().341322|10232abc r ab ππ=⎥⎦⎤⎢⎣⎡--=（ⅱ）根据对称性及二重积分的几何意义，知 ⎰⎰++==Ddxdyby ax c V V 2222122上（1）其中 .1:2222≤+by ax D为计算方便，特引入变量替换令⎩⎨⎧==.sin ,cos θθbr y ar x则被积函数化为2222211rc by ax c z +=++= （2）积分区域D 化为 .1:2≤'r D （3）于是⎰⎰'+==D drd J rc V V θ21122其中()()abrbr b ra a y ry xr xr y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,, （4）故⎰⎰'+==D drd J r c V V θ21122⎰⎰'+=D rdrd r abcθ212⎰⎰+=πθ201212rdr r d abc()().122341322|10232-=⎥⎦⎤⎢⎣⎡+=abc r ab ππ（ⅲ）12222=++c zby ax ，.0,13232==⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛z b y a x 根据对称性及二重积分的几何意义，知 ⎰⎰⎪⎪⎭⎫⎝⎛--=1222214D dxdyb y a xc V （1）其中 ()0,0,1:32321≥≥≤⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛y x b y a x D 为计算方便，特引入变量替换令⎩⎨⎧==.sin ,cos 33θθbr y ar x 则被积函数化为().s i n c o s 16262θθr r c z --= （2）积分区域1D 化为 ⎪⎭⎫⎝⎛≤≤≤'20.1:1πθr D （3）于是()⎰⎰'--=16262sin cos 14D drd J r r c V θθθ其中()().sin.cos 3cos .sin3sin sin .cos 3cos ,,222323θθθθθθθθθθθabr br b ra a y ry xr xr y x J =-=∂∂∂∂∂∂∂∂=∂∂=（4）故()⎰⎰'--=16262sin cos 14D drd J r r c V θθθ()⎰⎰--=201226262sin .cos sin cos 112πθθθθθrdr r r d abc⎰⎰=192022sin .cos 12rdr d abc πθθθdr r d abc ⎰⎰-132028.sin .cos 12πθθθdr r d abc ⎰⎰-13228.cos .sin 12πθθθ⎰=2022sin .cos 6πθθθd abc ⎰-2028sin .cos 3πθθθd abc⎰-2028cos .sin 3πθθθd abc()⎰-=2042cos cos 6πθθθd abc ()⎰--20108cos cos 3πθθθd abc()⎰--20108sinsin 3πθθθd abc⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛-=2.!!10!!9!!8!!732.!!4!!346πππabc abc ⎪⎭⎫ ⎝⎛--2.!!10!!9!!8!!73πabc.25675abc π=17.（书p174页习题2）计算下列各三重积分（先画出积分区域的草图）：（ⅰ）()dzdxdy z y x dxdydz⎰⎰⎰Ω+++31，其中Ω为由坐标平面0,0,0===z y x 和平面1=++z y x 围成的四面体；（ⅱ）dz dxdy z xy ⎰⎰⎰Ω32，Ω为由曲面xy z =和平面0,1,===z x x y 围成的区域；（ⅲ）dz xyzdxdy ⎰⎰⎰Ω，Ω为单位球1222≤++z y x 位于第一卦限的那部分区域；（ⅳ）dz zdxdy ⎰⎰⎰Ω，Ω为圆锥面()0,022>>+=R h yx Rh z 与平面h z =围成的区域；解：（ⅰ）()dzdxdy z y x dxdydz⎰⎰⎰Ω+++31；Ω在xoy 坐标面上的投影区域为三角形区域.10,10:⎩⎨⎧≤≤-≤≤x x y D 故()d x d y d z z y x ⎰⎰⎰Ω+++311=()dzz y x dy dx xyx ⎰⎰⎰---+++101010311()()z y x d z y x dy dx xyx ++++++=⎰⎰⎰---111110103()⎰⎰---⎥⎦⎤⎢⎣⎡+++-=110102|11.21xy x dy z y x dx()⎰⎰-⎥⎦⎤⎢⎣⎡-++=1102411121xdy y x dx⎰-⎪⎪⎭⎫ ⎝⎛-++-=1010|411121dx y y x x⎰⎪⎭⎫ ⎝⎛+++-=101144321dx x x().1652ln 21811ln 4321|102-=⎪⎭⎫ ⎝⎛+++-=x x x（ⅱ）dz dxdy z xy ⎰⎰⎰Ω32；Ω在xoy 坐标面上的投影区域为三角形区域.10,0:⎩⎨⎧≤≤≤≤x x y D 故d x d y d z z xy ⎰⎰⎰Ω32=dz z dy y xdx xxy⎰⎰⎰132⎰⎰⎥⎦⎤⎢⎣⎡=1042|41x xy dyz y xdx ⎰⎰=16441xdyy x xdx⎰⎪⎭⎫ ⎝⎛=175|7141dx y x x ⎰=112281dxx.3641131.281|1013==x（ⅲ）dz xyzdxdy ⎰⎰⎰Ω；Ω在xoy 坐标面上的投影区域为.10,10:2⎪⎩⎪⎨⎧≤≤-≤≤x x y D 故dx d y d z x y z ⎰⎰⎰Ω=dzz ydyxdx xyx ⎰⎰⎰---11010222⎰⎰---⎥⎦⎤⎢⎣⎡=110102222|21xy x dy z y xdx ()⎰⎰---=110222121xdy yx y xdx()()⎰⎰-----⎪⎭⎫ ⎝⎛-=11022222112121xy x d y x x d x()⎰⎥⎦⎤⎢⎣⎡---=-110222|212141dx y x x x()⎰-=122181dxxx()()⎰--⎪⎭⎫ ⎝⎛-=1022211.2181x d x x ().481131.161|1032=--=x（ⅳ）由对称性知，dz zdxdy ⎰⎰⎰Ωdz zdxdy ⎰⎰⎰Ω=14其中1Ω为Ω在第一卦限内的那部分区域，1Ω在xoy 坐标面上的投影区域为.0,0:221⎪⎩⎪⎨⎧≤≤-≤≤Rx x R y D 故d x d y d z z ⎰⎰⎰Ω=⎰⎰⎰+-R hyx RhxR zdzdy dx 022224⎰⎰-+⎥⎦⎤⎢⎣⎡=R xR hy x R hdy z dx 0022222|214()⎰⎰-⎥⎦⎤⎢⎣⎡+-=RxR dy y x R h h dx 022222222dxy y x R y hRx R ⎰⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=-003222|223112()dx xR xR x R x R hR⎰⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+---=032222222223112⎰-=Rdx x R h2222dxx R xRh R⎰--0222222()dx xR Rh R⎰--3222232其中22222222141.22R h Rh dx x R h R ππ==-⎰ ；=--⎰dx x R xRh R222222tdtR t tR R Rh cos .cos sin222222⎰-πdt t t Rh ⎰-=22222cossin2π()dtt t Rh ⎰--=204222sinsin2π222282.!!4!!32.!!2!!2R h R h πππ-=⎥⎦⎤⎢⎣⎡--=；()=--⎰dx xR Rh R3222232⎰-23322c o s .c o s 32πt d t R t R Rh⎰-=2422c o s 32πt d t Rh .82.!!4!!3322222R h Rh ππ-=-= 所以d x d y d zz ⎰⎰⎰Ω222Rh π=228Rh π-=-228Rh π.422R h π=18（书p174页习题3）利用改变积分次序的方法，将下面的三次积分表示成一重积分（ⅰ）()ρρηξξηd f d d I x⎰⎰⎰=；（2）().110dz z f dy dx I yx ⎰⎰⎰+=解：（1）先将后两次积分()ρρηξηd f d ⎰⎰0中的积分次序进行变换：()()()[]()()ρρξρρηρηρρρρηξξρξξξρξηd f d f d f d d f d -===⎰⎰⎰⎰⎰⎰0|---（14）所以，()()()()ξρξρρρρξρξρξd f d d f d I xxx-=-=⎰⎰⎰⎰0()()ρρρρρρρξξρρd x x f d f xxx ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=⎰⎰22202222|()().220ρρρd x f x-=⎰（2）先将后两次积分()dz z f dy yx ⎰⎰+10中的积分次序进行变换：()()()dy z f dz dy z f dz dz z f dy x z x xxyx ⎰⎰⎰⎰⎰⎰-+++=11101()()()dz x z z f dz z f x x x+-+=⎰⎰+11所以， ()()()∏+I =+-+=∧+⎰⎰⎰⎰dz x z z f dx dz z f dx I x xx11011----（15）.其中，()()()dz z z f dx z f dz z -==I ⎰⎰⎰1111--------（16）， ()()()()dx x z z f dz dx x z z f dz z z+-++-=∏⎰⎰⎰⎰-11211110()()()dzz z f dz z z z f 22222121-+⎪⎪⎭⎫⎝⎛-=⎰⎰，。

高数重积分-重积分的应用

由元素法
x ( x, y )d x , ( x, y )d
D D
y ( x, y )d y . ( x , y )d
D D
当薄片是均匀的，重心称为形心.
1 x xd , AD 1 y yd . 其中 A d AD D

2 d
2 0
b cos
a cos
r cos rdr
D

D 8 4
(b 3 a 3 ) b 2 ba a 2 . 2 2 (b a ) 2(b a )
20
对 y 轴的转动惯量为
y
b
o
a
x
I y x 2dxdy,
D
0 dy 0
b
y a ( 1 b )
1 3 x dx a b . 12
2
同理：对x 轴的转动惯量为
I x y 2dxdy 1 ab3 .
D
12
14
例 5 已知均匀矩形板（面密度为常数）的长 b h 和宽分别为和，计算此矩形板对于通过其形心且分别与一边平行的两轴的转动惯量.
2 2
1 2 故S a 4 x 2 4 y 2 dxdy 2dxdy D a Dxy
xy
d
0
2
a
0
1 2 a 4r 2 rdr 2a 2 a
a 2 (6 2 5 5 1). 6
7
三、平面薄片的重心 ( x , y )
n 设 xoy 平面上有个质点，它们分别位于
5
例 2 求由曲面 x 2 y 2 az 和 z 2a (a 0) 所围立体的表面积.

重积分计算及应用.pptx

所围成的闭区域.
提示: 利用极坐标
D
:
02
R
2
cos
原式
y Rcos o D Rx
2 R3
2 (1 sin3 ) d
30
第7页/共41页
P183 7. 把积其中由分曲面
所围成的闭区域 . 提示: 积分域为
化为三次积分, 及平面
:
1 1 x2y2
原式 dx dy f (x, y, z)dz 1 x2 0
D2
1 x2 d x
x
dy 00
1
1
y
yx
o D2
D1
1x
1 y x
第22页/共41页
例9. 计算二重积
分 (1) I D sgn( y x2 )dxdy, D : 1 x 1，0 y 1
(2) I ( x2 y2 2xy 2) dxdy, 其中D 为圆域 D
在第一象限部分.
D
1 dx 1 x2
1 0
f ( x, y) dy.
第13页/共41页
例6. 交换下列二次积分的顺序: y
y sin x
解: 如图所示
o
D1
2
D2 x
I
dx
sin x
f (x, y) d y
2
dx
0
f (x, y) d y
00
sin x
D1 f (x, y) d D2 f (x, y) d
R
R2 x2
0 D yd x dy R d xb ydy
2 R3 R b2 3
由此解得 b 2R
y
y R2 x2
b ? Do
R
Rx

高等数学第四节重积分的应用

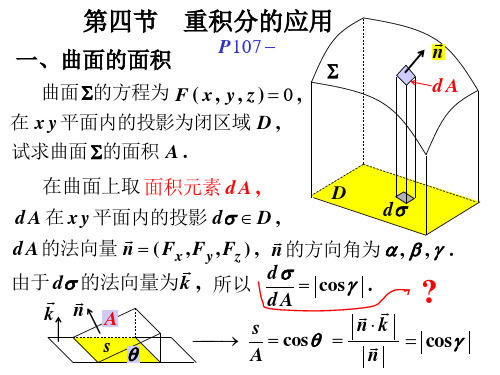
d A d xy Fx2 Fy2 Fz2 d xy .
cos
Fz
曲面 z f ( x , y ) , n ( fx , f y , 1) ,
cos
1
1
f
2 x
f
2 y
d A dxy cos
1
f
2 x
f
2 y
d xy
.
2
圆柱面
xy
a a
cos sin
z z
x2 y2 a2
0 2 0
A R2 sin d d
cos R
Rh
R2 2 0
d
0
sin
d
R2 2 (1 cos )
所求比值
三颗同步卫星
k
R2
2 (1 cos 4 R2
)
可覆盖除两极外的地球全表面 .
1 cos h
2
2(R h)
42.5%
用投影方法计算卫星覆盖面积见 P1089 .
2. 球坐标 f ( x, y, z)dv
f (r sin cos , r sin sin , r cos) r 2 sin dr d d
的质量, 重心坐标, 转动惯量 . 27
曲面的面积
d A d xy cos
z f (x, y)
dA
1
f
2 x
f
2 y
d
A
1
f
2 x
f
2 y
d
x a cos
b
dx
2(x)
a 1( x)
f
( x,
y)dy
2 画 D图,向Y 轴投影,
c y d
D 1( y) x 2( y)

重积分的运用举例

r2 a z z 2a r
2a
解得交线 L： r a z a
a
z 2a r
L
r 2 az
.
0
2a
y
x
例3. 求曲面 x y az (a ) 与 z a x y 所围体积
用哪种坐标？柱面坐标 z 联立
r 2 az z 2a r
§4 重积分应用举例
• 立体体积 • 曲面的面积 • 物体的质量 • 物体的质心 • 物体的转动惯量 • 物体对质点的引力
一. 体积
1. 二重积分可求曲顶柱体的体积： f ( x , y )dxdy
D
z f ( x , y ) 为柱体的顶.
2. 空间区域的体积： dv .
y 2 x
若光滑曲面方程为隐式
且 Fz 0, 则
Fy z Fx z , , x Fz y Fz
( x , y ) Dx y
2
A Dx y
Fx Fy Fz
2 2
Fz
dx d y
1. 锥面 z x y 被圆柱面 x y x 所割下部分的曲面面积
x
y z z 联立 y z x
消y得
x 2z
x z
得 z=2
. . . .
y z z 又由 y
Dxz : x 2 2z , z 2
o
S y z y x dxdz

求体积时应注意： 1. 立体由哪些曲面围成；
2. 体积必须是正值，如图形具有对称性，可利用对称性简化。
例1.求半径为R的球面与半顶角为的内接锥面所围成的立体的体积

887-4重积分的应用举例

是闭区域D上的连续函数, 则该平面薄片的质心坐标为
类似地, 设一物体占有空间闭区域, 其密度(x, y, z)是闭区域上的连续函数, 则该物体的质心坐标为
(3) 物体的转动惯量
设一平面薄片占有xOy面上的闭区域D, 其面密度(x, y) 是D上的连续函数, 则该平面薄片对x、y轴的转动惯量为
D
首页
上页
返回
下页
结束
铃
设光滑曲面则面积 S 可看成曲面上各点 P(x, y, z)
z n SP
处小切平面的面积 d S 无限积累而成.
o
设它在 D 上的投影为 d , 则
x
d y
d cos d S
cos
1
1 fx2 (x, y) f y2 (x, y)
nz
dS
首页
上页
返回
下页
结束
铃
(2)质心设一平面薄片占有xOy面上的闭区域D, 其面密度(x, y)
是闭区域D上的连续函数, 则该平面薄片的质心坐标为
分析
•P点对x轴的静矩为dMxy(x, y)d.
•薄片对x轴的静矩为
•设质心的横坐标为y, 薄片的质量为M, 则yMMx.
P(x,y)
z x2 3y2
z

8

x2

y2

x2 y2 1,
42
于是
{( x, y, z) | D : x2 y2 1, x2 3y2 z 8 x2 y2}. 42
V
dv
8x2 y2
dxdy x2 3y2

z
2 y

R. R2 x2

高等数学典型例题与应用实例(重积分B部分)

高等数学 第九章 重积分 第四节 重积分应用

重积分典型例题

数学分析21.6重积分的应用(含习题及参考答案)

高数D10.4重积分的应用

数学分析21.6重积分的应用(含习题及参考答案)

高等数学典型例题与应用实例(重积分B部分)

高等数学 重积分 (9.4.2)--重积分的应用

高等数学典型例题与应用实例(重积分B部分)

高等数学第九章 重积分

08 第四节 重积分应用举例

重积分经典例题

高数重积分-重积分的应用

重积分计算及应用.pptx

高等数学 第四节 重积分的应用

重积分的运用举例

887-4重积分的应用举例

高等数学第九章重积分第四节重积分应用

高等数学重积分 (9.4.2)--重积分的应用

高等数学第九章重积分

08 第四节重积分应用举例

高等数学第四节重积分的应用