介质平板波导建模过程
用周期性边界条件模拟导波介质的传播模式及其模式常数的后续分析计算

用周期性边界条件模拟导波介质的传播模式及其模式常数的后续分析计算 例子:平板波导基本参数:光波长1064nm ,导波介质为钕玻璃(n=1.54),介质厚度1000nm 。
波导中传播模式的理论值:通过理论计算(见附录),可知该频率的TE 光在这个波导中存在两个模式。
基模(m=0)的角度θ为74.533°,即β=k*n*sin74.533°,传播方向x 上的空间波长为x sin λλθ==1064nm/1.54/sin74.533°=716.871nm 。
1模(m=1)的角度θ为42.192°,传播方向x 上的空间波长为x sin λλθ==1064nm/1.54/sin42.192°=1028.72nm 。
在例子中我们就将通过数值模拟,处理得到空间波长从而得到各个模式的角度。
STEP1:建立EastFDTD 文档。
设置合适的参数:选择合适的单位:本例子的波导厚1微米,脉冲中心波长1.064微米,故长度单位取0.01微米比较合适。
选择边界类型:为了节省计算空间,边界条件x 方向为周期性的边界条件。
Y 方向为PML 吸收边界条件。
由于是2D 模型,Z 方向为周期性边界条件。
由于本例子的计算空间是相当大的2000*200,为保证y 方向上吸收干净,PML 吸收边界设置多一些,本例子用32层。
设置计算区域:为了避免脉冲在传播过一个周期长度后头尾相干叠加影响计算结果,x方向一个周期的长度不能小于光源脉冲的长度。
而且为了空间分辨率提高,要尽可能的增加一个周期的长度,但x方向越长计算时间也越长,所以要适当取舍。
本例子中的2D结构计算时间短,x方向不妨设得长一些,这里设为正负1000。
由于波导厚度为1微米,故y方向设置正负100。
为了达到平衡后,只留下导模的光,计算时间设得较长,为15000步。
STEP2:建立材料。
这个例子只有两种材料:空气和钕玻璃。
空气不用新建,所以只新建一个材料。
光纤结构、波导原理和制造

其中h = 6.63 10-34 J·s为普朗克常数
在光的照射下,金属是否发射电子,仅与光的频率相关,而 与光的亮度和照射时间无关。不同的金属材料要求不同的光 照频率。
2 基本的光学定律和定义
光速 c = 3 108 m/s 波长:l = c/v 当光在媒介中传播时,速度cm = c/n 常见物质的折射率:空气 1.00027;
光纤结构、波导原理和制造
主要内容
回顾光的特性、基本的光学定律和定义
介绍光纤结构、分类、特性和射线光学解 释
圆波导模式及其理论简介* 单模光纤的特性、材料以及制造工艺 光纤的几种成缆方式
光的波动性 1 光的基本特性
- 17世纪意大利格里马蒂和英国胡克 观测到光的衍射现象
- 1690年海牙物理学家惠更斯提出光 的波动性学说
光纤的分类
按传输的模式数目分 • 单模光纤 • 多模光纤
按折射率的变化分 • 阶跃光纤 • 梯度光纤
ITU-T官方定义 • G.651光纤 (渐变型多模光纤) • G.652光纤 (常规单模光纤) • G.653光纤 (色散位移光纤) • G.654光纤 (衰减最小光纤) • G.655光纤 (非零色散位移光纤)
光传播的入射角条件 将s1和s2的值代入相位关系式并简化可以得到:
2pn1d sin mp l
假如只考虑波的电场分量垂直于入射面的情况,那么因发射带
来的相移为:
2arctan
cos2
n22 / n12
s in
代入简化式中可以得到:
tan pn1d
s in
kp
n12
cos2
水 1.33; 玻璃 (SiO2) 1.47; 钻石 2.42; 硅 3.5 折射率大的媒介称为光密媒介,反之称为光疏媒介
平面介质波导建模过程

©2013 COMSOL
1 |
DIELECTRIC SLAB WAVEGUIDE
Solved with COMSOL Multiphysics 4.3b
The analytic solution is found by assuming that the electric field along the direction of propagation varies as Ez = E(y)exp(-ikxx), where E(y) = C1cos(kyy) inside the dielectric slab, and E(y) = C0exp(−α(|y| − (hslab/2)) in the cladding. Because the electric and magnetic fields must be continuous at the interface, the guidance condition is t slab α = k y tan k y --------- 2 where ky and α satisfy k y = k core – k cladding – α
Figure 1: The guided modes in a dielectric slab waveguide have a known analytic solution.
Model Definition
A dielectric slab of thickness hslab = 1 μm and refractive index ncore = 1.5 forms the core of the waveguide, and sits in free space with ncladding = 1. Light polarized out of the plane of propagation, of wavelength λ = 1550 nm, is perfectly guided along the axis of the waveguide structure, as shown in Figure 1. Here, only the TE0 mode can propagate. The structure varies only in the y direction, and it is infinite and invariant in the other two directions.
对称平板波导的模式计算课程设计(论文)

目录摘要 (I)Abstract (II)1 设计目的及任务要求 (1)1.1 设计目的 (1)1.2 任务要求 (1)1.3 软件简介 (1)2原理分析 (2)2.1 均匀介质薄膜波导 (2)2.2 平面光波导 (3)2.3 平板波导的波动理论 (5)3 对称平面波导的BeamPROP仿真设置 (7)4 平面波导仿真图 (12)4.1 波导结构观察 (12)4.2 波导传输仿真 (12)4.3 不同模式仿真图 (13)5 总结 (17)参考文献 (18)摘要能够引导光束的传播,从而使光束的能量在横的方向上受到限制,并使损耗和噪声降到最小,这种器件通常称为光波导,简称波导光束在介质中传输时,由于介质的吸收和散射而引起损耗,由于绕射而引起发散,这些情况都会导致光束中心部分的强度不断地衰减。
因此,有必要设计制作某种器件,它能够引导光束的传播,从而使光束的能量在横的方向上受到限制,并使损耗和噪声降到最小,这种器件通常称为光波导,简称波导。
结构最简单的波导是由三层均匀介质组成的,中间的介质层称为波导层或芯层,芯两侧的介质层称为包层。
芯层的介电常数比芯两侧包层的介电常数稍高,使得光束能够集中在芯层中传输,因而起到导波的作用。
这种波导的介电常数分布是陡变的,也称为阶梯变化的,常称这种波导为平板波导。
最简单的平板型光波导是由沉积在衬底上的一层均匀薄膜构成,因而又叫做薄膜波导。
正如大家所熟悉的单层电路板,所有电路都位于基板的一个平面内一样。
本文从理论上推导了对称平板波导的模式计算,利用BeamPROP软件仿真,探究了对称平板波导的模式分类及各自特点,得到了其仿真特性和一些仿真图,验证了相关理论,并且加深了对对称平板波导的模式的理解。
关键词:波导模式计算仿真AbstractPropagating light beams can be guided, so that the energy of the beam in the horizontal direction is restricted, and to minimize losses and noise, such devices commonly referred to as an optical waveguide, the waveguide shortWhen the beam propagating in a medium, the medium due to absorption and scattering caused by the loss, due to the divergence caused by diffraction, these conditions could result in the central portion of the intensity of the beam attenuation constant. Therefore, it is necessary to design a device which can guide the propagating light beams, so that the energy of the beam in the horizontal direction is restricted, and to minimize losses and noise, such devices commonly referred to as an optical waveguide, the waveguide short . The simplest structure of the waveguide is formed by three homogeneous medium, the dielectric layer is called an intermediate layer or a dielectric layer of the waveguide core layer on both sides of the core is called the cladding. Dielectric constant than the dielectric constant of the core layer is clad on both sides of the core is slightly higher, so that the beam can be concentrated in the core layer transmission, and thus acts as guided waves. This distribution is steep waveguide dielectric constant change, also called step change, often referred to as a slab waveguide such a waveguide. The simplest type optical waveguide plate is deposited on the substrate by a layer of a uniform thin film, which is also known as a thin film waveguide.As you are familiar with the single circuit board, all circuits are located within the same plane of the substrate. Theoretically derived from the symmetric slab waveguide mode is calculated using BeamPROP software simulation, explores the symmetrical slab waveguide pattern classification and their characteristics, got some of its characteristics and simulation diagram simulation to verify the theory, and deepened the symmetry understanding slab waveguide modes.Keywords: computer simulation waveguide mode1 设计目的及任务要求1.1 设计目的培养较为扎实的光电子的理论知识及较强的实践能力;加深对光电器件的选型及光路形式的选择的了解;强化使用实验仪器进行电路的调试检测能力。
平板介质光波导理论

(3,1 -5a )
(3.1 - 5b )
可以得出:Hy = Ex = 0 因此,只有y方向电场存在 利用分离变量法对波动方程(3.1 – 13)求解,便可得到平板 介质波导的场模表示式为
E y(x, z,t) E y(x)exp j t z
其中Ey(x)及模传播常数满足
(3.2 – l)
(3.1 - 12) (3.1 - 13)
(3.1 - 14)
• 最简单的情况是设光波的电矢量 沿y方向偏振、沿z方向传播的平 面电磁波,即有 • E = Ey、Ex = Ez = 0。
• Ey在z方向以角频率 = 2发生 周期变化, • 因为只在z方向有空间变化,故 有/x = /y = 0 • 由式(3.1 – 13)可以得到以z和t作 为函数的Ey:
3.1 光波的电磁场理论
• 一、基本的电磁场理论
•
麦克斯韦方程组
B E t D H J t B 0
(3,1 -1a )
(3.1 - 1b ) (3.1 - 1c ) (3.1 - 1d )
D
• 设介质是均匀且各向同性的,且假设在低场强下不足以 产生非线性效应,并且不考虑在半导体介质中实际存在 的色散效应,而认为和与光波的频率无关。 (3.1 - 3a ) D E
第三章 平板介质光波导理论
引言 3.1 光波的电磁场理论 3.2 光在平板介质波导中的传输特性
引言
• 从理论上说,平板介质光波导是一种最简单的光波导形式, 可以运用电磁场的基本理论,将平板介质波导处理为边界 条件,从而得到数学上简单、物理上容易理解的基本光波 导的有关方程。一旦熟悉了这种介质光波导的一般方法, 就不难从数学上深入认识圆形光波导(如光纤)和其它形 状的光波导. • 分析介质波导的一般方法是根据介质波导的边界条件求解 麦克斯韦方程,得出有关光场传播模式的表示式; • 传播模式可以分为偶阶的和奇阶的横电波( TE )和横磁 波 ( TM ) ; • 由传播模式的本征方程或特征方程得出与模有关的传播常 数。然后求出传输模的截止条件、相位延迟等与波导有关 的参数, • 分析平板介质波导的实际意义在于,许多半导体光电子器 件和集成光学是以平板介质波导作为工作基础的。如,异 质结半导体激光器和发光二极管正是利用异质结所形成的 光波导效应将光场限制在有源区内并使其在输出方向上传 播。
FEKO应用10_1_三层介质平板
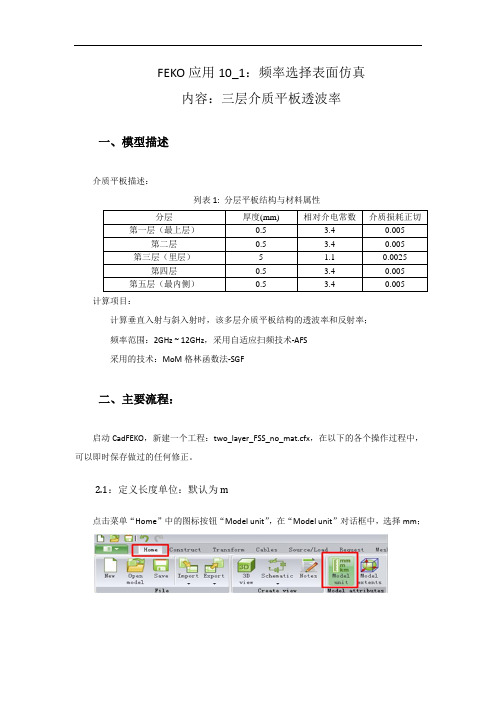
FEKO应用10_1:频率选择表面仿真内容:三层介质平板透波率一、模型描述介质平板描述:列表1: 分层平板结构与材料属性分层厚度(mm) 相对介电常数介质损耗正切第一层(最上层)0.5 3.4 0.005第二层0.5 3.4 0.005 第三层(里层) 5 1.1 0.0025第四层0.5 3.4 0.005 第五层(最内侧)0.5 3.4 0.005 计算项目:计算垂直入射与斜入射时,该多层介质平板结构的透波率和反射率;频率范围:2GHz ~ 12GHz,采用自适应扫频技术-AFS采用的技术:MoM格林函数法-SGF二、主要流程:启动CadFEKO,新建一个工程:two_layer_FSS_no_mat.cfx,在以下的各个操作过程中,可以即时保存做过的任何修正。
2.1:定义长度单位:默认为m点击菜单“Home”中的图标按钮“Model unit”,在“Model unit”对话框中,选择mm;2.2:定义变量:在CadFEKO中左侧的树型浏览器中双击“Variables”节点,依次定义如下变量:最小工作频率:fmin=2e9最大工作频率:fmax=12e9相对介电常数:epsr1=3.4相对介电常数:epsr2=1.1介质损耗正切:tand1=0.005介质损耗正切:tand2=0.0025介质层厚度(第一、二、四、五层):h1=0.5,h2=0.5介质层厚度(中间层):h3=52.3:定义材料:在CadFEKO中左侧的树型浏览器中选中“Media”节点,点击鼠标右键,选择“Dielectric”,在弹出的“Dielectric medium properties”对话框中:定义相对介电常数(Relative permittivity):epsr1介质损耗正切值(Dielectric loss tangent):tand1名称定义为:mat1点击“Add”;定义相对介电常数(Relative permittivity):epsr2介质损耗正切值(Dielectric loss tangent):tand2名称定义为:mat2点击“Create”;2.4:模型建立(略):2.5:定义无限大多层介质平板点击菜单“Construct->Planes/arrays->Plane/Ground”,弹出“Plane/ground”对话框:选择“Planar multilayer substrate”点击“Add”按钮两次Layer1层:Ground plane修改为“None”,Thickness修改为h1+h2, Medium为:mat1;Layer2层:Ground plane修改为“None”,Thickness修改为h3, Medium为:mat2;Layer3层:Ground plane修改为“None”,Thickness修改为h1+h2, Medium为:mat1;点击“OK”按钮。
光波导数值模拟方法

光波导数值模拟方法介质光波导是利用介质的折射率差来限制光场,从而引导和控制光波传播的一种结构,是光波导器件中的最基本构成成分。
常见的波导主要有光纤和平面波导两种,本文主要针对应用于平面集成光路的平面光波导进行讨论。
平面光波导主要有两种结构,即平板波导(二维结构)和条形波导(三维结构)两种[46], 如图2.1所示。
平板波导如图2.1a 所示,在垂直于光波传播方向(z 方向)的截面上,只在纵向(x 方向)上受到限制,而在横向上(y 方向)可以无限延伸,是完全均匀的。
而条形波导,如图2.1b ,则是在两个方向(x ,y 方向)同时受到限制。
通常实际光器件都是建立在条形波导的基础上的,平板波导由于在横向上缺乏对光的约束,只在很少情况下(如AWG 的自由传输区)才会用到。
但是从平板这种更加简单的二维结构入手,可以更方便于对波导特性的研究。
图2.1 两种平面波导结构:(a )平板波导,(b )条形波导平板光波导理论假设现有一平板波导由三种介质组成,如图2.2所示,上包层折射率为n c (x >a ),衬底折射率n s ,(x <-a ),芯层折射率n f (-a <x <a ),平板芯层厚度为2a 。
传统的射线理论认为,光线在波导中传播时,将会在上下两个界面中发生全反射,以此也可得出波导存在导波模式的最基本条件:n f >n s ,n c 。
那么,当光线入射到界面的角度满足max(sin(),sin())c f s f arc n n arc n n θ>,光线就能同时在两个界面都发生全内反射,从而被束缚在波导之中。
同时,为了使得光线能在波导中稳定传输,还必需满足光线在两个界面之间往返一次的总相位变化是2π的整数倍。
于是根据以上这些条件,就可以求出对应于某一波长(真空中波矢为k 0)的光线所需满足的入射角θ,从而求出其传播常数,即传播方向上的波矢分量,0sin f k n βθ=,以及与该传播模式对应的等效折射率0eff n k β=,在此不再赘述。
实验指导书--介质填充波导本征模研究.docx

上机实验二:介质填充波导的本征模研究一、实验目的微波在某个特定的导波结构中是以模式的形式存在的。
模式是麦克斯韦方程组在相应波导结构截面中的本征解,所以也叫本征模。
另外,矩形波导因其加工方便,且具有损耗小和双极化特性,常用于要求双极化模的天线的馈线中,也广泛用作各种谐振腔、波长计,是一种较常用的规则金属波导。
本次实验利用HFSS/CST 平台实现介质填充的矩形波导的设计与仿真,通过改变矩形波导内部介质的形状、填充位置、介电常数及磁导率,观察其本征模的相位常数,截止波长以及横截面上的电场矢量分布的变化,并进行横向比较,总结规律。
二、实验原理现阶段,能够容易得到波导内部各参量解析解的矩形波导模型(如图1)大致为一无限长矩形截面直波导管,管的轴线与z 轴方向一致,它的内壁坐标分别为x=0,x=a,y=0,y=b,假设波导管材料为理想导体,内部填充参量为ε和μ的理想介质。
已知矩形波导内部TE 波和TM 波的场分量表达式及相关特性。
图1 矩形波导结构1、 矩形波导内的TE 模⑴.场分量表达式z E =0coscos zz m x n y H H e a b γππ-=02cos sin x c zn m x n y E H b a b j k eγπππωμ-= 02sin cos z y c j m m x n y E H e k a a b γωμπππ-=-02-sin cos c m mpx npy zH H e x k a a b γπγ= 02cossin zy c n m x n y H H e k ba b γγπππ-=-其中γ==2222222c x ym n k k k a b ππγωμε⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭⑵.TE 模的主要参数截止频率mn f ==截止波长mn mnf νλ==相位常数mn β=导波波长g λ=2、 矩形波导内的TM 模⑴.场分量表达式0coscos zz m x n y E E e a b γππ-=0z H =02cossin x czm m x n y E E k a a b eγγπππ-=-02sin cos zy c n m x n y E E ek b a b γγπππ-=-02-E sin cos c n mpx npy zHe xb a b j k πγωε=02cos sin zy c m m x n y H E e a a b j k γπππωε-=-⑵.TM 模的主要参数TM 模的主要参数均与上述TE 模的计算公式相同。
第3章 电介质平板和光纤中的导波

个方程能够合并成一个简单的方程(见习题3.14) 2hq 1 (3.1-16) tan hd = 2 2 2 h −q TE模的解可分成两类,第一类, 1 A = 0, C = D, h tan hd = q (3.1-17) 2 第二类 1 B = 0, C = − D, h cot hd = − q (3.1-18) 2 第一类解对应对称的波函数,第二类解则对应非对称的波函数。
下面的方程描述了对称介质波导的折射率分布
n2 , x < d 2 n( x) = n1 , 其他地方
(3.1-1)
n 式中, 是导波层(芯层)的厚度, 2 是芯层的折射率,而 n1 是 d n 包层媒质的折射率。为了实现传导,2 必须比n1大。接下来的问
题就是找出这些传导模式。 由于媒质在电介质结构中是均匀分布的,所以处理这类问 题的电磁方法相对比较简单。另外,均匀介质中的麦克斯韦方 程的解是简单的平面波。因而所要做的就是写出每个部分平面 波方程,在界面满足边界条件从而确保波函数的连续性。现在 计算沿z 轴方向传播的单色光波。麦克斯韦方程可以写成
β>
n2ω (3.1-6) c 因此将会得到满足这些传播条件,方程式(3.1-5)和式(3.16),的受限模式。这些模式同样可以被归类为TE或者TM模。TE模的 电场垂直于xz 平面(入射面或传播面)并仅包括了模场的 E , 和 H Hx y z 分量。而TM模包含模场的 H , E 和 E 分量。 y x z
p
β ω c
(3.1-20)
β
n
有效
n2
n1
波导中的TM,模式
现在考虑TM模,其磁场矢量垂直于传播面(xz 平面)。TM模 的推导原则跟TE模相近似。场振幅可以写成
1.2-介质板波导

k k0 n2
应有K 2 k0 2 n2 2 2 0, 令 2 2 k0 2 n2 2
D ( x d ) e i D x ( x d ) ( )e x
12
(3) 边界条件和特征方程式
当x d 时, 应有E y1 E y 2 , H z1 H z 2 A(1 K
1.2 介质平板波导
1
主要内容
1.
基本波动方程和波导方程式
2.
3.
对称介质平板波导的传输模式
介质板波导中的多模群时延
2
1、波动方程和波导方程式
1)波动方程:由麦克斯韦方程组推导出
B E t E ( B ) t D 2 ( E ) E ( ) t t D ( E ) E E 0 E E
准备2
i E z H z Ex 2 ( ) K x y i H z E z Hx ( ) 2 K x y i E z H z E y 2 ( ) K y x i H z E z Hy ( ) 2 K y x K 2 k 2 2 2 2
两个平面波的传输方向与介质板的法线夹角
tan
K
在介质板上,两个平面波满足内部全反射条件, 它们对介质板入射角度是由模式传输矢量的分量β、K所决定。
21 结论:模式截止的情况与以临界角入射到介质板上的平面波相对应
3)TM模式(以TE分析类似) 3.介质板波导中的多模群时延
d dL dH K 2 k0 2 n12 2 f 0
得 令
平板光波导

根据边界条件,在x=a,-a处,有 E y , H z 连续(E y 和它的偏导数)
tan(ha ) q
h
tan(ha ) p
h
h(2a) m arctan(q ) arctan(p )
h
h
这就是TE模的特征方程
13
类似地,再研究TM模
To explain metal’s dispersion regulation, another more precise mode was demonstrate called Drude mode.
Where,
()
p2 2 i
p
Is totally caused by the transition of
令
2 1
k021
2
2 2
2
k02 2
在X=a处利用
1
dH y (x) dx
可以得到
tan( 1a)
1 2 2 1
T
1a m arctan(T )
16
对于奇对称的情况:
Hy(x)
Asin(1a)e 2 (xa) , x a Asin(1x),| x | a Asin(1a)e 2 (xa) , x a
2h 212 210
5
如果相干相长,即满足谐振条件,则此入射角对应的光 线(模式)可以被导波所接受
2h 212 210 2m
物理意义:在波导厚度h确定的情况下,平板波导所能 维持的导模模式数量是有限的,此时m只能取有限个整 数值,这个方程也称作平板波导的本征方程
每一模式对应的锯齿光路和横向光场分布
6
对于特征方程中的 12 10 是上下界面处全反射所引起的相移,那 么具体可根据菲涅尔公式求出。
第4章-介质波导
Ae
be
e r
A
g
b
ar
x y z
a
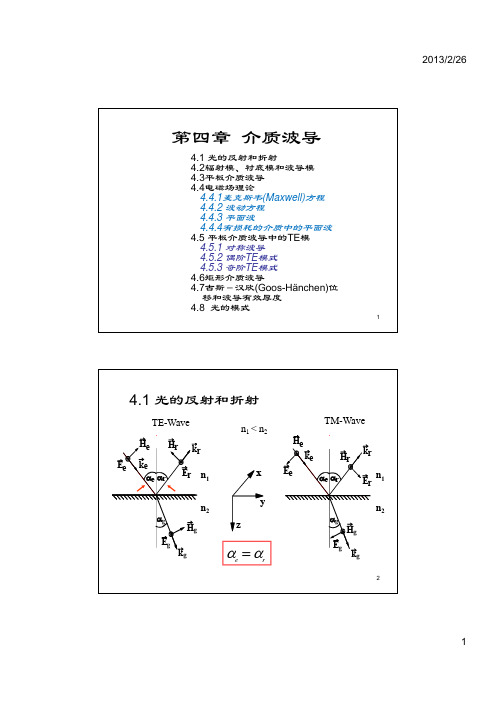
n1 n2 plane l of f incidence i id
a e a cos e a r a cos r a g a cos g b e br bg b Poyntingvector S E H
2 n1 cos g 1 2 sin 2 e n2 Eg 2n1 cos e Ee n1 cos e n 2 cos g
rTE
2 2 2 Er n1 cos e n 2 n1 sin e 2 2 Ee n1 cos e n 2 2 n 1 sin e
r cs e e
e
e
cc r
导波模
两个界面处全内反射 nf > ns > nc
2ΦS
17
nc nf ns
h
z
nc
z=h
cc
s
c e
radiation mode
x
y n=0
nf
ns
e
h
cc
r
substrate mode
h
s
2ΦC
e
h
e
cc r
rcs e
1
4.1 光的反射和折射
TE-Wave
He Ee ke e r Hr Er kr
n1 < n2
He
ke
TM-Wave
kr Er
Hr
n1 n2
x y z
Ee
e r
n1 n2
g
Eg
Hg kg
g
1.1平板波导几何光学分析1102

1 1
1 1
导模
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
波导的n1、n2界面的全反射临界角 波导的n1、n3界面的全反射临界角 因为 n2 n3,所以 C12 C13
C 12 arcsin
C 13 arcsin
n2 n1
n3 n1
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
X 覆盖层 薄膜层 衬底层
Z
n3 n1 n2
Y
平板波导
Z-光波传输方向
从物理量随着指标变化来看,平板波导只与X、Z两 个指标波导。又可称平板波导为二维波导。
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
设n1 > n2 n3
n2= n3-对称平板波导; n2 n3-非对称平板波导;
sin 1 sin C 12 sin C 13
将
sin C 12
n2 n1
代入
n1sin 1 n2
n2 sin1 n1
k0n1sin 1 k0n2
而传播常数
k1z k0 n1 sin 1
n2 k0
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
1、导模 (1)传播常数 因为是导模,所以 1 > C12 C13, 定义:传播常数-薄膜层中,沿Z方向的波数。
k1z k0 n1 sin 1
n1k0
1
Z
=k1z =n1k0 sin1
§1.1 平板波导几何光学分析 2011年2月
第一章 平板波导
覆盖层中,
平板波导理论

P
c
T
漏泄光线
z
zp1
3
3.1 均匀介质薄膜波导中光线的传播 方程
n0
d
n1
n2
❖ 厚度d很薄,约为数微米; ❖ 芯层折射率(n1)大于衬底折射率(n2)和敷层折
射率(n3); ❖ y方向比x方向尺度大得多。
4
3.1.1 光线的传播路径及光线的分类
t
n3
i r
z
n1
d d s
n
(
x
)
dx d s
d n1( x ) dx
d d s
n
(
x
)
dz ds
0
x
ds dx
z(x) dz
z(0) z
积分上面第二式得
n ( x ) d z const ds
由几何关系得
dz ds
cos
z
故
n(x) dz ds
n 1 ( x ) cos
z ( x ) n 1 ( 0 ) cos
)
0
所以
A
n
2 1
(
x
x tp )
cos
2 2 z ( x tp
)
2
即
dx dz
n
2 1
(
x
)
2
1/2
再次积分得
z(x)
x 0
n
2 1
(
x
)
2
1/2 d x
即 x 0时 , z 0的前提下 ,
给定 n1 ( x ) 和 z ( 0 ), 即可确定传播路径
14
3.2.2 传播时延及时延差 n2
第一讲介质平板波导基础理论(PDF)

多模情况下的本征方程为(TE 模 ):
tan(κh)
=
κ ( p + q) κ 2 − pq
• 实线与虚线的交点给出模式
本征方程的解。由这些交点
可以得到一系列(κ m h) 值,再
利用关系式
κ
2 m
+
β
2 m
=
k
2 0
n12
可得到导模的传播常数 βm
• 曲线 F (κh)在下式解出的点
上终止:
κh = (n12 − n22 )1/ 2 k0h
夹角 θ 只能取有限个离散值。薄膜中
的波动场按以下方式变化:
exp[i(±κx + βz)]
κ = k0n1 cosθ , β = k0n1 sinθ
平板波导的模式本征方
程: 2kh − 2φ13 − 2φ12 = 2mπ
• 只有满足本征方程的入射角θ才为波导所接受。在厚度确定的情况
下,平板波导所能维持的导模数量是有限的,因此m只能取有限
k02n12 − β 2
式中 β = k 0 n 1 sin θ1 , k 0 = 2π / λ
图1.3 TE模的相移作为入射角的 函数的曲线图
平板波导的模式
图1.4 在平板波导中的图像
(a)辐射模的折线图像;(b)衬 底辐射模的折射图像;(c)导 模的z字型图像
图1.5 平板波导的俯视图
平板波导的导模可以用锯齿形光线图 像描述,并且锯齿光线与界面法线的
•
个正整数。
对TE模, κh = mπ
+ tan −1 ( p ) + tan−1 ( q )
式中:
κ
κ
κ
=
(k
平板波导

H y ( x)
H 然后,根据边界条件,x=a,-a处, y , Ez 分量连续
n2 q f tan(ha ) 2 ns h n2 p f tan(ha ) 2 nc h
n2 q n2 p f f 2ha m arctan( 2 ) arctan( 2 ) ns h nc h 这就是TM模的特征方程
D 0 B 0 B t D H t E
B 0 H 0 H 0e i ( k r t ) D E E0e i ( k r t )
E -i0 H H i E
E z E y i0 H x y z Ex E z i0 H y z x E y E x i0 H z x y
Why free electrons will oscillate with the light wave excitation?
Hy 是SPP的本征模式. 然而, Ey 并不存在于表面等离子波 中. 所以只用讨论Hy 模式 如图所示,Hy Ex k 三者满足右手定则,Ex的正负半轴 激起金属中自由电子的震荡。
E y
z E x E z i0 H y z x E y i0 H z x
假设:
E E(x, y)e -iz H H ( x , y ) e i z
Ey E y x
0 Hx
Hy
Ex
i0 H z H z iE y x
As e
q ( x a )
, x a
根据边界条件,在x=a,-a处,有 E y , H z连续(E y 和它的偏导数)
q h p t an(ha ) h t an( ha )
介质平板波导建模过程
6转到重命名材料对话框,并在新名称编辑字段中键入核心。
7单击确定。
MESH 1
大小
1在模型构建器窗口中,模型1下右键单击网格1,选择自由
三角。
2在尺寸设置窗口中,找到晶片尺寸部分。
3单击自定义按钮。
4定位元素尺寸参数部分。在最大元素大小编辑字段,
输入lambda0/n_cladding/8。
3在端口设置窗口,找到端口属性一节。
4从端口类型列表中,选择数值。
材料
材料1
1在模型构建器窗口中,模型1下右键单击材料和选择材料。
2在材质的设置窗口中,找到材料的内容部分。
3在该表中,输入以下设置:
PropertyNameValue
Refractive indexnn_cladding
4右键单击模型1>材料>材料1,选择重命名。
4在相关的编辑字段中,键入传播常数,beta_1。
5单击评价按钮。
6在模型构建器窗口中,右键单击派生值,并选择全球评估。
7在全球评估的设置窗口中,单击右上角的替换表达式
拐角表达部分的。从菜单中,选择电磁波,
频域>港口>传播常数(ewfd.beta_2)。
8找到了表达的部分。选择说明复选框。
9在相关的编辑字段中,键入传播常数,beta_2。
4在模型构建器窗口中,右键单击研究2,选择计算。
最后,比较分析和计算的传播常数。
结果
派生值
1在模型构建器窗口中,在结果右键单击派生值,然后选择
全球评估。
2在全球评估的设置窗口中,单击右上角的替换表达式
拐角表达部分的。从菜单中,选择电磁波,
平板介质波导特征方程几何光学推导的一种修正

24(1): 28-32.
【5】吴金克 ,王彬 .超滤膜截留性能测定方法 [J】.天津化 工,
2000(2): 24-26.
作者简介:赵朔 (1985-),女,河北人,工程师,现从事分析
【6]于 小焱,张 晓慧,庞永超 .凝胶 排 阻 色谱 法测定 中空纤维 测试工作
39
信 息 记录材料 2 01 8年 11月 第 1 9卷 第11期
under norm ]. circumst ̄nces
处理虽然简单 明了,却在推更为普 适和全 面 的理解 。如 文献 [10] 2推导方法修正
中采用 了单条光线 自身相长干涉 的推导方法,此种情况只
为 了使推导过程更具 一般性 ,本文试图对 已有推导方
解准确,被广泛应用于各种波 导材料光场求解及特性分析
中。然而电磁场方法推导过程较为复杂,且在分析和推导
相应规律时较为抽象 ,不易与物理模型进行直观 的对应。
波导介质特征方程 的推导 以及光线特性分析可 以利用几何
光学的分析方法 ,使求解过程变得简单清晰,且能与物理
模型直接对应 ,易于理解 。因此 ,在很多 已有 的文献资料
波导条件 )是研究其光束传输行为和规律 的基本理论公式 。 方程进 行了讨论,对加深波导特征方程 的理解提供 了有益
在 目前 已有 的报道 中,对于波导特 征方程 的推导 ,主 的帮助 。同时也为学 习者和教学者在涉及该理论规律 的讨
要有几何光学和 电磁场理论两种方法 。电磁场理论因其求 论时,提供了一种更为全 面和透彻的解释 。
导条件,并没有给 出推导过程。 本文分析了已有方法在推 面是一个 比较一般 情况下 的波 阵面 B’F,而推 导利用 的
第二讲 介质平板波导电磁理论

2 • 再利用 (1 / n j )(∂H y / ∂x) 在导波层— 衬底界面上连续的条件,可得
2 2 n12κ ( n3 p + n2 q) tan(κh) = 2 2 2 4 n2 n3 κ − n1 pq
• 上式也可以写成:κh = mπ + φ12 + φ13 式中:
n 2 p 1 φ12 = tan n κ 2
TE导模
• 平板波导三层介质中的电场分布 :
A exp( −qx ) E y ( x ) = Bcos(κx) + C sin(κx) D exp[ p( x + h)] 0 < x < +∞ -h < x < 0 - ∞ < x < -h
图4介质平板波导以及 所选用的坐标系
• 利用利用Ey(x)在导波层— 衬底界面和导波层— 覆盖层界面处连 续以及 ∂E y / ∂x 在导波层— 覆盖层界面连续的边界条件,可得 :
heff = h +
p
+
q
TM导模
C exp( − qx) 2 n1 q H y ( x) = C[cos(κx) − sin(κx)] n κ 3 2 n C[cos(κh) + 1 q sin(κh)] exp[ p( x + h)] n κ 3 0 < x < +∞ −h<x <0 − ∞ < x < -h
第二章
麦克斯韦方程:
∂B (r , t ) ∂t ∂D( r , t ) ∇ × H (r , t ) = ∂t ∇ × E (r , t ) = −
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最后,比较分析和计算的传播常数。
结果
派生值
1在模型构建器窗口中,在结果右键单击派生值,然后选择
全球评估。
2在全球评估的设置窗口中,单击右上角的替换表达式
拐角表达部分的。从菜单中,选择电磁波,
频域>港口>传播常数(ewfd.beta_1)。
3找到表达的部分。选择说明复选框。
8单击Build All按钮。
研究1
第1步:边界模式分析
1在模型构建器窗口中,右键单击研究1,选择研究步骤>边界
模式分析。
2在边界模式分析设置窗口中,找到研究设置部分。
3在搜索周边的编辑字段中,键入n_core模式。此值应在
附近您所期望的基本模式具有的价值。
4在模态分析频率编辑字段中,键入F0。此频率的精确值
解析解是通过假设发现,电场沿的方向传播变化作为Ez=E(y)exp(-i ),其中 内,和 在包层,由于电场和磁场必须是连续的界面,引导条件是
其中KY和α满足
其中 和 .因此能够通过牛顿-拉夫逊法找到解决方案,上述两个方程用于每当COMSOL Multiphysics软件检测非线性方程组时,唯一的要求被认为有足够初步猜测。
电磁波,频率域
波被激发时在左侧的端口。
端口1
1在模型构建器窗口中,右键单击电磁波,频域
并选择端口。
2选择边界1,3,只有5。
3在端口设置窗口,找到端口属性一节。
4从端口类型列表中,选择数值。
5从波激励在这个端口列表中,选择开。
现在,添加了出口。
端口2
1右键单击电磁波,频域,然后选择端口。
2选择边界仅8-10(在右侧的边界)。
5右键单击模型1 >材料>材料2,选择重命名。
6转到重命名材料对话框,并在新名称编辑字段中键入核心。
7单击确定。
MESH 1
大小
1在模型构建器窗口中,模型1下右键单击网格1,选择自由
三角。
2在尺寸设置窗口中,找到晶片尺寸部分。
3单击自定义按钮。
4定位元素尺寸参数部分。在最大元素大小编辑字段,
输入lambda0/n_cladding/8。
k_yk_y^2-(k_core^2-k_cladding^2-alpha^2)k_core/2
研第1步下:固定。
2在固定的设置窗口中,找到物理和变量选择部分。
3在该表中,输入以下设置:
PhysicsSolve for
Electromagnetic Waves, Frequency Domain×
5转到重命名材料对话框,并在新名称编辑字段中键入覆层。
6单击OK(确定)。
默认情况下,添加的第一个材料适用于所有领域。加芯材。
材料2
1右键单击材料和选择材料。
2只选择域2。
3在材质的设置窗口中,找到材料的内容部分。
4在表中,输入以下设置:
PropertyNameValue
Refractive indexnn_core
4在相关的编辑字段中,键入传播常数,beta_1。
5单击评价按钮。
6在模型构建器窗口中,右键单击派生值,并选择全球评估。
7在全球评估的设置窗口中,单击右上角的替换表达式
拐角表达部分的。从菜单中,选择电磁波,
频域>港口>传播常数(ewfd.beta_2)。
8找到了表达的部分。选择说明复选框。
9在相关的编辑字段中,键入传播常数,beta_2。
造型说明
模型向导
1转到模型向导窗口。
2单击2D按钮。
3单击下一步。
4在添加物理树中,选择光学>波光学>电磁波,频率
域(ewfd)。
5单击添加所选。
6单击下一步。
7查找该研究小节。在树中,选择自定义研究>空研究。
8单击Finish(完成)。
全球释义
参数
1在模型构建器窗口中,右键单击全局定义和选择参数。
6单击Build按钮选择。
矩形2
1在模型构建器窗口中,右键单击几何体1,选择矩形。
2在矩形的设置窗口中,找到尺寸段。
3在宽度编辑字段中,键入w_slab。
4在身高编辑字段中,键入h_cladding。
5找到位置部分。从基础列表中,选择中心。
6单击Build All按钮。
7单击绘图工具栏上的最大化按钮。
15选择说明复选框。
16在相关的编辑字段中,键入传播常数,计算出来的。
17单击评价按钮。
一些物理>固定。
6单击完成。
全球常微分方程和DAES
全球方程1
1在模型构建器窗口中,模型1下>全球常微分方程和微分代数方程单击全局
方程1。
2在全球方程设置窗口中,找到全球方程部分。
3在该表中,输入以下设置:
Namef(u,ut,utt,t)Initial value (u_0)
alphaalpha-k_y*tan(k_y*h_core/2)k_core/2
并不重要。重要的是,它应该是高于截止频率为
的基本模式,但低于该下一个模式。此设置可确保
边界模式分析发现基本模式。
添加另一个边界模式的分析,对于第二个端口。
第2步:边界模式分析2
1右击研究1,选择研究步骤>边界模式分析。
2在边界模式分析设置窗口中,找到研究设置部分。
3在搜索周边的编辑字段中,键入n_core模式。
4在端口名称编辑字段中,键入2。
5在模态分析频率编辑字段中,键入F0。
最后,添加对在波导中的传播波的研究步骤。
步骤3:频域
1右击研究1,选择研究步骤>频域。
2在频域中的设置窗口中,找到研究设置部分。
3在频率编辑字段中,键入F0。
4右键单击研究1,选择计算。
结果
电场(ewfd)
默认的图显示了电场的常态。修改剧情表演的
几何1
1在模型构建器窗口中,在模型1单击几何1。
2在几何设置窗口中,找到单位部分。
3从长度单位列表中,选择微米。
矩形1
1右键单击模型1>几何1,选择矩形。
2在矩形的设置窗口中,找到尺寸段。
3在宽度编辑字段中,键入w_slab。
4在身高编辑字段中,键入h_core。
5找到位置部分。从基础列表中,选择中心。
尺寸1
1在模型构建器窗口中,模型1下>网1右键单击Free三角1和
选择尺寸。
2在尺寸设置窗口中,找到几何实体选择部分。
3从几何实体级别列表中,选择域名。
4选择域2只。
5定位元素尺寸段。点击自定义按钮。
属性名值
折射率n n_core
6定位元素尺寸参数部分。选择最大元素大小检查
框。
7在相关的编辑字段中,键入lambda0/n_core/8。
后者,加上全球常微分方程和微分代数方程的接口,然后设置和解决有关
方程。
模型1
在模型构建器窗口中,右键单击模型1,然后选择添加物理。
模型向导
1转到模型向导窗口。
2在添加物理树中,选择数学>常微分方程和DAE接口>全球常微分方程和
微分代数方程(GE)。
3单击添加所选。
4单击下一步。
5找到研究小节。在树中,选择自定义研究>预设的研究
该模型考虑了电介质平板波导的截面在x和y方向上是有限的。因为该领域在波导外呈指数分布,领域在一定距离可以被认为是零。这是方便的,因为假设它们被施加足够远则边界条件与y方向无关。
使用数值端口的边界条件在x方向上建立在正x方向上传播的波导。这些边界条件首先要求解决本征值问题这解决了在边界的领域和传播常数问题。
10右键单击结果>派生值>全球评估4,选择评估>表1
-全球评估3(ewfd.beta_1)。
11右键单击派生值,并选择全球评估。
12在全局评估设置窗口中,找到数据部分。
13从数据集列表中,选择解决方案4。
14找到表达部分。在表达式编辑字段中,键入
SQRT(k_core ^ 2 - k_y ^ 2)。
2在参数设置窗口中,找到参数部分。
3在该表中,输入以下设置:
NameExpressionDescriptionlambda01550[nm]Wave lengthn_core1.5Refractive index,core n_claddin g1Refractive index, cladding h_core1[um]Thickness, core h_claddin g7[um]Thickness, cladding w_slab5[um]Slab widthk_core2*pi[rad]*n_core/lambda0Wave number, core k_cladding2*pi[rad]*n_cladding/lambda0 Wave number, cladding f0c_const/lambda0Frequency
z分量(与图2比较)。
1在模型构建器窗口中,展开电场(ewfd)节点,然后单击曲面。
2在表面设置窗口,单击窗口右上角的替换表达式
表达部分。从菜单中,选择电磁波,频率
域>电>电场>电场z分量(ewfd.Ez)。
3找到着色和样式部分。从颜色表列表中,选择WaveLight。
4单击Plot按钮。
由仿真结果比较来解析解完成。计算
结果与讨论
图2示出了结果。在左边的数值端口的边界条件激发了在x方向传播的模块和是完全由在右侧的数值端口所吸收的一个模式。分析和数值计算传播常量是一致的。
图2:在电介质平板波导的电场。
模型库路径:Wave_Optics_Module/Verification_Models/ dielectric_slab_waveguide
