最新中考数学必会几何模型
2024年中考数学常见几何模型最值模型之瓜豆模型(原理)圆弧轨迹型

最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
掌握该压轴题型的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径。
本专题就最值模型中的瓜豆原理(动点轨迹为圆弧型)进行梳理及对应试题分析,方便掌握。
【模型解读】模型1、运动轨迹为圆弧模型1-1. 如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.Q点轨迹是?如图,连接AO,取AO中点M,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.则动点Q是以M为圆心,MQ为半径的圆。
模型1-2. 如图,△APQ是直角三角形,∠PAQ=90°且AP=k⋅AQ,当P在圆O运动时,Q点轨迹是?如图,连结AO,作AM⊥AO,AO:AM=k:1;任意时刻均有△APO∽△AQM,且相似比为k。
则动点Q是以M为圆心,MQ为半径的圆。
模型1-3. 定义型:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧。
(常见于动态翻折中)如图,若P为动点,但AB=AC=AP,则B、C、P三点共圆,则动点P是以A圆心,AB半径的圆或圆弧。
模型1-4. 定边对定角(或直角)模型1)一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.如图,若P为动点,AB为定值,∠APB=90°,则动点P是以AB为直径的圆或圆弧。
2)一条定边所对的角始终为定角,则定角顶点轨迹是圆弧.如图,若P为动点,AB为定值,∠APB为定值,则动点P的轨迹为圆弧。
【模型原理】动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。
1(2023·山东泰安·统考中考真题)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=43,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是()A.3B.62-4C.213-2D.22(2023·四川广元·统考一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为.3(2023·四川宜宾·统考中考真题)如图,M是正方形ABCD边CD的中点,P是正方形内一点,连接BP,线段BP以B为中心逆时针旋转90°得到线段BQ,连接MQ.若AB=4,MP=1,则MQ的最小值为.4(2023·湖南·统考中考真题)如图,在矩形ABCD中,AB=2,AD=7,动点P在矩形的边上沿B→C→D→A运动.当点P不与点A、B重合时,将△ABP沿AP对折,得到△AB P,连接CB ,则在点P的运动过程中,线段CB 的最小值为.5(2023·山东·统考中考真题)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD< BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,则线段BF的最小值为.6(2023·浙江金华·九年级校考期中)如图,点A,C,N的坐标分别为(-2,0),(2,0),(4,3),以点C为圆心、2为半径画⊙C,点P在⊙C上运动,连接AP,交⊙C于点Q,点M为线段QP的中点,连接MN,则线段MN的最小值为.7(2023上·江苏连云港·九年级校考阶段练习)已知矩形ABCD,AB=6,BC=4,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为.8(2023下·陕西西安·九年级校考阶段练习)问题提出:(1)如图①,在△ABC中,AB=AC,∠BAC=120°,BC=43,则AB的长为;问题探究:(2)如图②,已知矩形ABCD,AB=4,BC=5,点P是矩形ABCD内一点,且满足∠APB= 90°,连接CP,求线段CP的最小值;问题解决:(3)如图③所示,我市城市绿化工程计划打造一片四边形绿地ABCD,其中AD∥BC,AD= 40m,BC=60m,点E为CD边上一点,且CE:DE=1:2,∠AEB=60°,为了美化环境,要求四边形ABCD的面积尽可能大,求绿化区域ABCD面积的最大值.课后专项训练1(2023·安徽合肥·校考一模)如图,在△ABC中,∠B=45°,AC=2,以AC为边作等腰直角△ACD,连BD,则BD的最大值是()A.10-2B.10+3C.22D.10+22(2023春·广东·九年级专题练习)已知:如图,在△ABC中,∠BAC=30°,BC=4,△ABC面积的最大值是( ).A.8+43B.83+4C.83D.8+833(2022秋·江苏扬州·九年级校考阶段练习)如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为()A.43+4B.4C.43+8D.64(2023·山东济南·一模)正方形ABCD中,AB=4,点E、F分别是CD、BC边上的动点,且始终满足DE=CF,DF、AE相交于点G.以AG为斜边在AG下方作等腰直角△AHG使得∠AHG=90°,连接BH.则BH的最小值为()A.25-2B.25+2C.10-2D.10+25(2023上·江苏连云港·九年级统考期中)如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接CM,则CM的最小值为.6(2023春·广东深圳·九年级专题练习)如图,点G是△ABC内的一点,且∠BGC=120°,△BCF是等边三角形,若BC=3,则FG的最大值为.7(2023·江苏泰州·九年级专题练习)如图,在矩形ABCD中,AD=10,AB=16,P为CD的中点,连接BP.在矩形ABCD外部找一点E,使得∠BEC+∠BPC=180°,则线段DE的最大值为.8(2023·陕西渭南·三模)如图,在矩形ABCD中,AB=6,BC=5,点E在BC上,且CE=4BE,点M 为矩形内一动点,使得∠CME=45°,连接AM,则线段AM的最小值为.9(2023江苏扬州·三模)如图,在等边△ABC和等边△CDE中,AB=6,CD=4,以AB、AD为邻边作平行四边形ABFD,连接AF.若将△CDE绕点C旋转一周,则线段AF的最小值是.10(2023秋·湖北武汉·九年级校考阶段练习)如图,△ABC为等腰直角三角形,∠BAC=90°,AB= AC=22,点D为△ABC所在平面内一点,∠BDC=90°,以AC、CD为边作平行四边形ACDE,则CE的最小值为.11(2023·福建泉州·统考模拟预测)如图,点E是正方形ABCD的内部一个动点(含边界),且AD= EB=8,点F在BE上,BF=2,则以下结论:①CF的最小值为6;②DE的最小值为82-8;③CE= CF;④DE+CF的最小值为10;正确的是.12(2021·广东·中考真题)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为.13(2023·广东·深圳市二模)如图,在矩形ABCD中,AB=3,BC=4,E为边BC上一动点,F为AE 中点,G为DE上一点,BF=FG,则CG的最小值为.14(2023秋·广东汕头·九年级校考期中)如下图,在正方形ABCD中,AB=6,点E是以BC为直径的圆上的点,连接DE,将线段DE绕点D逆时针旋转90°,得到线段DF,连接CF,则线段CF的最大值与最小值的和.15(2023·陕西渭南·统考一模)如图,在矩形ABCD中,AB=2,BC=4,Q是矩形ABCD左侧一点,连接AQ、BQ,且∠AQB=90°,连接DQ,E为DQ的中点,连接CE,则CE的最大值为.16(2023·安徽亳州·统考模拟预测)等腰直角△ABC 中,BAC =90°,AB =5,点D 是平面内一点,AD =2,连接BD ,将BD 绕D 点逆时针旋转90°得到DE ,连接AE ,当DAB =(填度数)度时,AE 可以取最大值,最大值等于.17(2023·河北廊坊·统考二模)已知如图,△ABC 是腰长为4的等腰直角三角形,∠ABC =90°,以A 为圆心,2为半径作半圆A ,交BA 所在直线于点M ,N .点E 是半圆A 上仟意一点.连接BE ,把BE 绕点B 顺时针旋转90°到BD 的位置,连接AE ,CD .(1)求证:△EBA ≌△DBC ;(2)当BE 与半圆A 相切时,求弧EM的长;(3)直接写出△BCD 面积的最大值.18(2022·北京·中考真题)在平面直角坐标系xOy 中,已知点M (a ,b ),N .对于点P 给出如下定义:将点P 向右(a ≥0)或向左(a <0)平移a 个单位长度,再向上(b ≥0)或向下(b <0)平移b 个单位长度,得到点P ',点P '关于点N 的对称点为Q ,称点Q 为点P 的“对应点”.(1)如图,点M (1,1),点N 在线段OM 的延长线上,若点P (-2,0),点Q 为点P 的“对应点”.①在图中画出点Q;②连接PQ,交线段ON于点T.求证:NT=12 OM;(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t12<t<1,若P为⊙O外一点,点Q为点P的“对应点”,连接PQ.当点M在⊙O上运动时直接写出PQ长的最大值与最小值的差(用含t的式子表示)19(2023下·广东广州·九年级校考阶段练习)如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)连接CD,延长ED交BC于点F,若△ABC的边长为2;①求CD的最小值;②求EF的最大值.20(2023·江苏常州·统考二模)如图,在平面直角坐标系中,二次函数y=-13x2+bx-3的图像与x轴交于点A和点B9,0,与y轴交于点C.(1)求二次函数的表达式;(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)若点Q在第四象限内,且cos∠AQB=35,点M在y轴正半轴,∠MBO=45°,线段MQ是否存在最大值,如果存在,直接写出最大值;如果不存在,请说明理由.最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
2024年中考数学几何模型(全国通用):三角形中的重要模型-垂美四边形与378、578模型(学生版)

专题10三角形中的重要模型-垂美四边形与378、578模型模型1、垂美四边形模型规定:对角线互相垂直的四边形叫做“垂美”四边形图1图2图3条件:如图1,已知四边形ABCD ,对角线AC 、BD 交于点O ,且AC ⊥BD ;结论:①AB 2+CD 2=AD 2+BC 2;②“垂美”四边形的面积等于对角线乘积的一半。
【变形1】条件:如图2,在矩形ABCD 中,P 为CD 边上有一点,连接AP 、BP ;结论:DP 2+BP 2=AP 2+PC 2【变形2】条件:如图3,在矩形ABCD 中,P 为矩形内部任意一点,连接AP 、BP ,CP ,DP ;结论:AP 2+PC 2=DP 2+BP 2用处:①对角线垂直的四边形对边的平方和相等;②已知三边求一边的四边形,可以联想到垂美四边形。
例1.(2023·山东枣庄·统考模拟预测)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD ,对角线AC 、BD 交于点O .若AD =3,BC =5,则22AB CD ____________.例2.(2023秋·河北石家庄·八年级统考期末)如图所示,四边形ABCD 的对角线AC ,BD 互相垂直,若2AD ,4AB ,5BC 则CD 的长为()A .2.5B .3C .4D例3.(2023·湖北武汉·九年级校考阶段练习)如图,四边形ABCD 的两条对角线互相垂直,AC 、BD 是方程216600x x 的两个解,则四边形ABCD 的面积是()A .60B .30C .16D .32例4.(2023·湖北·九年级专题练习)学习新知:如图1、图2,P 是矩形ABCD 所在平面内任意一点,则有以下重要结论:AP 2+CP 2=BP 2+DP 2.该结论的证明不难,同学们通过勾股定理即可证明.应用新知:如图3,在△ABC 中,CA =4,CB =6,D 是△ABC 内一点,且CD =2,∠ADB =90°,则AB 的最小值为_____.例5.(2022·山东济宁·统考一模)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称________,________.(2)如图(1),已知格点(小正方形的顶点)(0,0)O ,(3,0)A ,(0,4)B ,请你直接写出一个以格点为顶点,OA ,OB 为勾股边且对角线相等的勾股四边形OAMB 的顶点M 的坐标为________;(3)如图(2),将ABC 绕顶点B 按顺时针方向旋转60°,得到DBE ,连接AD ,DC ,30DCB .求证:222DC BC AC ,即四边形ABCD 是勾股四边形;(4)若将图(2)中ABC 绕顶点B 按顺时针方向旋转a 度)090(a ,得到DBE ,连接AD ,DC ,则DCB ________°,四边形BECD 是勾股四边形.例6.(2022秋·江西抚州·九年级校考阶段练习)(1)【知识感知】如图1,我们把对角线互相垂直的四边形叫做垂美四边形,在我们学过的:①平行四边形②矩形③菱形④正方形中,能称为垂美四边形是______;(只填序号)(2)【概念理解】如图2,在四边形ABCD 中,=AB AD ,=CB CD ,问四边形ABCD 是垂美四边形吗?请说明理由.(3)【性质探究】如图1,垂美四边形ABCD 的两对角线交于点O ,试探究AB ,CD ,BC ,AD 之间有怎样的数量关系?写出你的猜想,并给出证明;(4)【性质应用】如图3,分别以Rt ACB △的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连接CE ,BG ,GE ,已知8AC ,10AB ,求GE .模型2、378和578模型当我们遇到两个三角形的三边长分别为3,7,8和5,7,8的时候,通常不会对它们进行处理,实际是因为我们对于这两组数字不敏感,但如果将这两个三角形拼在一起,你将惊喜地发现这是一个边长为8的等边三角形。
2024年中考数学几何模型归纳(全国通用):全等与相似模型-一线三等角(K字)模型(学生版)

专题14全等与相似模型-一线三等角(K 字)模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角:锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B +CE=DE证明思路:,A B C BED +任一边相等BED ACE异侧型一线三等角:锐角一线三等角直角一线三等角钝角一线三等角条件:FAC ABD CED +任意一边相等证明思路:,A B C BED +任一边相等BED ACE例1.(2021·山东日照·中考真题)如图,在矩形ABCD 中,8cm AB ,12cm AD ,点P 从点B 出发,以2cm/s 的速度沿BC 边向点C 运动,到达点C 停止,同时,点Q 从点C 出发,以cm/s v 的速度沿CD 边向点D 运动,到达点D 停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v 为_____时,ABP △与PCQ △全等.例2.(2022·黑龙江·九年级期末)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.例3.(2022·广东·汕头市潮阳区一模)(1)模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;,OB=4,将线段AB绕(2)模型应用:①已知直线AB与y轴交于A点,与x轴交于B点,sin∠ABO=35点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x 5上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.例4.(2023·湖南岳阳·统考一模)如图,在ABC 中,AB =AC =2,∠B =40°,点D 在线段BC 上运动(点D 不与点B 、C 重合),连接AD ,作∠ADE =40°,DE 交线段AC 于点E .(1)当∠BDA =115°时,∠EDC =______°,∠AED =______°;(2)线段DC 的长度为何值时,△ABD ≌△DCE ,请说明理由;(3)在点D 的运动过程中,△ADE 的形状可以是等腰三角形吗?若可以,求∠BDA 的度数;若不可以,请说明理由.例5.(2022·浙江杭州·一模)老师在上课时,在黑板上写了一道题:“如图,ABCD 是正方形,点E 在BC 上,DF ⊥AE 于F ,请问图中是否存在一组全等三角形?”小杰同学经过思考发现:△ADF ≌△EAB .理由如下:因为ABCD 是正方形(已知)所以∠B =90°且AD =AB 和AD ∥BC又因为DF ⊥AE (已知)即∠DFA =90°(垂直的意义)所以∠DFA =∠B (等量代换)又AD ∥BC 所以∠1=∠2(两直线平行,内错角相等)在△ADF 和△EAB 中12DFA B AD AB所以△ADF ≌△EAB (AAS )小胖却说这题是错误的,这两个三角形根本不全等.你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF 全等的三角形,请能说出此线段的做法吗?并说明理由.例6.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,90ACB ,AC BC ,AD CE ,BE CE ,垂足分别为D ,E , 2.5cm AD , 1.7cm DE .求BE 的长”,请直接写出此题答案:BE 的长为________.(2)探索证明:如图②,点B ,C 在MAN 的边AM 、AN 上,AB AC ,点E ,F 在MAN 内部的射线AD 上,且BED CFD BAC .求证:ABE CAF ≌.(3)拓展应用:如图③,在ABC 中,AB AC ,AB BC .点D 在边BC 上,2CD BD ,点E 、F 在线段AD 上,BED CFD BAC .若ABC 的面积为15,则ACF 与BDE 的面积之和为________.(直接填写结果,不需要写解答过程)例7.(2023·贵州遵义·八年级统考期末)过正方形ABCD (四边都相等,四个角都是直角)的顶点A 作一条直线MN .(1)当MN 不与正方形任何一边相交时,过点B 作BE MN 于点E ,过点D 作DF MN 于点F 如图(1),请写出EF ,BE ,DF 之间的数量关系,并证明你的结论.(2)若改变直线MN 的位置,使MN 与CD 边相交如图(2),其它条件不变,EF ,BE ,DF 的关系会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明;(3)若继续改变直线MN 的位置,使MN 与BC 边相交如图(3),其它条件不变,EF ,BE ,DF 的关系又会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明.模型2.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,ABC,为等边三角形,点D,E分别在边BC,AB上,60ADE若4DE ,则AD的长为()BD DC, 2.4A.3B.5C.2例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在 ABC中,∠BAC=90°,ABAC=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:BDAE=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在 ABC中,ABAC=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在 ABC中,沿 ABC的边AB、AC向外作矩形ABDE和矩形ACFG,ABAE=ACAG=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.问题探究:(1)先将问题特殊化,如图(2),当90 时,直接写出GCF 的大小;(2)再探究一般情形,如图(1),求GCF 与 的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120 时,若12DG CG ,求BE CE 的值.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在ABC中,90ACB,AC BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:ADC CEB△≌△.(1)探究问题:如果AC BC,其他条件不变,如图②,可得到结论;ADC CEB△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x与直线CD交于点 2,1M,且两直线夹角为 ,且3tan2,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,3AB ,5BC ,点E为BC边上—个动点,连接AE,将线段AE绕点E顺时针旋转90 ,点A落在点P处,当点P在矩形ABCD 外部时,连接PC,PD.若DPC△为直角三角形时,请你探究并直接写出BE的长.【观察与猜想】(1)如图1,在正方形ABCD中,E,F分别是AB,AD则DECF的值为___________;(2)如图2,在矩形ABCD中,7AD ,BD,若CE BD,则CEBD的值为___________;【类比探究】(3)如图3,在四边形ABCD中,90A B,E为线交ED的延长线于G,交AD的延长线于F,求证:DE AB CF课后专项训练1.(2022·湖南·长沙市二模)如图,等腰直角三角形ABC 的直角顶点C 与坐标原点重合,分别过点A 、B 作x 轴的垂线,垂足为D 、E ,点A 的坐标为(-2,5),则线段DE 的长为()A .4B .6C .6.5D .72.(2022·贵州·凯里一模)如图,在平面直角坐标系中 0,4A 、 6,0C ,BC x 轴,存在第一象限的一点 ,25P a a 使得PAB △是以AB 为斜边的等腰直角三角形,则点P 的坐标().A . 3,1或 3,3B . 5,5C . 3,1或 5,5D .3,3A . 9,3B . 9,24.(2023·湖南长沙·九年级专题练习)如图,在矩形CD 或延长线上运动,且∠BEF5.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.7.(2022·安徽·九年级专题练习)如图,矩形取BE的中点G,点G绕点E运动路径=,△CEF10.(2023·浙江·九年级期末)如图,已知ABC 和CDE 均是直角三角形,Rt ACB CED ,AC CE ,AB CD 于点F .(1)求证:ABC ≌CDE ;(2)若点B 是EC 的中点,10cm DE ,求AE 的长.11.(2022·江苏·九年级专题练习)【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF ,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l 于E ,CF l 于F .若1AE ,2CF ,则EF 的长为________.【模型应用】(2)如图4,将正方形OABC 放在平面直角坐标系中,点O 为原点,点A 的坐标为 ,则点C 的坐标为________.【模型变式】(3)如图5所示,在ABC 中,90ACB ,AC BC ,BE CE 于E ,AD ⊥CE 于D ,4cm DE ,6cm AD ,求BE 的长.12.(2022·江苏镇江·二模)模型构建:如图1,AM MN 于点M ,BN MN 于点N ,AB 的垂直平分线交MN 于点P ,连接AP 、BP .若90APB ,求证:AM BN MN .数学应用:如图2,在ABC 中,D 是BC 上一点,AC AD BD ,90CAD ,8AB ,求ABC 的面积.实际运用:建设“交通强国”是满足人民日益增长的美好生活需要的必然要求.建设“美丽公路”是落实美丽中国建设、回应人民日益增长的美好生活对优美生态环境的需要.如图3是某地一省道与国道相交处的示意图,点Q 处是一座古亭,鹅卵石路QA 、QB 以及 AB 两旁栽有常青树,其它区域种植不同的花卉;设计要求QA QB ,QA QB , AB 是以Q 为圆心、QA 为半径的圆弧(不计路宽,下同).请在图4中画出符合条件的设计图,要求尺规作图,保留作图痕迹,标注必要的字母,写出详细的作法,不要求说明理由;13.(2022·黑龙江·桦南县九年级期中)如图1,在ABC 中,90ACB ,AC BC ,直线MN 经过点C ,且AD MN 于D ,BE MN 于E .(1)由图1,证明:DE AD BE ;(2)当直线MN 绕点C 旋转到图2的位置时,请猜想出DE ,AD ,BE 的等量关系并说明理由;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).14.(2022·黑龙江佳木斯·三模)在ABC 中,90ABC ,AB BC ,D 为直线AB 上一点,连接CD ,过点B 作BE CD 交CD 于点E ,交AC 于点F ,在直线AB 上截取AM BD ,连接FM .(1)当点D ,M 都在线段AB 上时,如图①,求证:BF MF CD ;(2)当点D 在线段AB 的延长线上,点M 在线段BA 的延长线上时,如图②;当点D 在线段BA 的延长线上,点M 在线段AB 的延长线上时,如图③,直接写出线段BF ,MF ,CD 之间的数量关系,不需要证明.15.(2022·安徽·合肥二模)(1)如图1,等腰直角ABC 中,90ACB ,CB CA ,线段ED 经过点C ,过A 作AD ED 于点D ,过B 作BE ED 于.E 求证:BEC △≌CDA .(2)如图2,已知在平面直角坐标系xOy 中,O 为坐标原点,点A 的坐标为 0,4,点C 的坐标为 3,0 ,点B 是平面直角坐标系中的一点,若ABC 是以AC 为直角边的等腰直角三角形,求点B 的坐标;(3)如图3,已知在平面直角坐标系xOy 中,O 为坐标原点,在等腰直角OAB 中,90OAB ,4OA AB ,点M 在线段OB 上从O 向B 运动(运动到点B 停止),以点M 为直角顶点向右上方做等腰直角AMN ,求点N 移动的距离.(3)【拓展探究】在整个运动过程中,请直接写出N 点运动的路径长,及CN 的最小值.(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当FEC ②如图2,当2tan 3FCE 时,求AF 的长;(2)如图3,延长CF ,DA 交于点时,求证:AE AF .18.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ,8cm BC ,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ,交线段AB 于点D .(1)求证:BDE CEA △∽△(2)设BE x ,AD y ,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.19.(2023·浙江·九年级专题练习)在平面直角坐标系中,O 为坐标原点,直线AB 与y 轴交于点A ,与x 轴交于点B ,2OA ,AOB 的面积为2.(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k ,AD y 轴,将BC 绕点B 顺时针旋转90 ,交AD 于点D ,求点D 的坐标.(用含k 的式子表示)(3)如图3,在(2)的条件下,连接OD ,交直线BC 于点E ,若345ABC BDO ,求点E 的坐标.20.(2022·湖南郴州·中考真题)如图1,在矩形ABCD 中,4AB ,6BC .点E 是线段AD 上的动点(点E 不与点A ,D 重合),连接CE ,过点E 作EF CE ,交AB 于点F .(1)求证:AEF DCE ∽;(2)如图2,连接CF ,过点B 作BG CF ⊥,垂足为G ,连接AG .点M 是线段BC 的中点,连接GM .①求AG GM 的最小值;②当AG GM 取最小值时,求线段DE 的长.。
2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
模型1:高分线模型条件:AD 是高,AE 是角平分线结论:∠DAE=2B C∠∠-例1.(2023秋·浙江·八年级专题练习)如图,在ABC 中,30A ∠=︒,50B ∠=︒,CD 为ACB ∠的平分线,CE AB ⊥于点E ,则ECD ∠度数为()A .5︒B .8︒C .10︒D .12︒【答案】C 【分析】依据直角三角形,即可得到40BCE ∠=︒,再根据30A ∠=︒,CD 平分ACB ∠,即可得到BCD ∠的度数,再根据DCE BCD BCE ∠=∠-∠进行计算即可.【详解】解:50,B CE AB ∠=︒⊥ ,40BCE ∴∠=︒,又30A ∠=︒ ,CD 平分ACB ∠,1118050305022()BCD BCA ∴∠=∠=⨯︒-︒-︒=︒,504010DCE BCD BCE ∴∠=∠-∠=︒-︒=︒,故选:C .【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180︒是解答此题的关键.例2.(2023春·河南南阳·七年级统考期末)如图,在△ABC 中,∠1=∠2,G 为AD 的中点,BG 的延长线交AC 于点E ,F 为AB 上的一点,CF 与AD 垂直,交AD 于点H ,则下面判断正确的有()①AD 是△ABE 的角平分线;②BE 是△ABD 的边AD 上的中线;③CH 是△ACD 的边AD 上的高;④AH 是△ACF 的角平分线和高A .1个B .2个C .3个D .4个【答案】B【详解】解:①根据三角形的角平分线的概念,知AG 是△ABE 的角平分线,故此说法错误;②根据三角形的中线的概念,知BG 是△ABD 的边AD 上的中线,故此说法错误;③根据三角形的高的概念,知CH 为△ACD 的边AD 上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH 是△ACF 的角平分线和高线,故此说法正确.故选:B .【点睛】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.例3.(2023·安徽合肥·七年级统考期末)如图,已知AD 、AE 分别是Rt △ABC 的高和中线,AB =9cm ,AC =12cm ,BC =15cm ,试求:(1)AD 的长度;(2)△ACE 和△ABE 的周长的差.【答案】(1)AD 的长度为365cm ;(2)△ACE 和△ABE 的周长的差是3cm .【分析】(1)利用直角三角形的面积法来求线段AD 的长度;(2)由于AE 是中线,那么BE =CE ,再表示△ACE 的周长和△ABE 的周长,化简可得△ACE 的周长﹣△ABE 的周长=AC ﹣AB 即可.【详解】解:(1)∵∠BAC =90°,AD 是边BC 上的高,∴S △ACB =12AB•AC =12BC•AD ,∵AB =9cm ,AC =12cm ,BC =15cm ,∴AD =AB AC CB ⋅=91215⨯=365(cm ),即AD 的长度为365cm ;(2)∵AE 为BC 边上的中线,∴BE =CE ,∴△ACE 的周长﹣△ABE 的周长=AC+AE+CE ﹣(AB+BE+AE )=AC ﹣AB =12﹣9=3(cm ),即△ACE 和△ABE 的周长的差是3cm .【点睛】此题主要考查了三角形的面积,关键是掌握直角三角形的面积求法.例4.(2023·广东东莞·八年级校考阶段练习)如图,在ABC 中,AD ,AE 分别是ABC 的高和角平分线,若30B ∠=︒,50C ∠=︒.(1)求DAE ∠的度数.(2)试写出DAE ∠与C B ∠-∠关系式,并证明.(3)如图,F 为AE 的延长线上的一点,FD BC ⊥于D ,这时AFD ∠与C B ∠-∠的关系式是否变化,说明理由.【答案】(1)10︒(2)()12DAE C B ∠=∠-∠(3)不变,理由见解析【分析】(1)根据三角形内角和求出BAC ∠,根据角平分线的定义得到50BAE ∠=︒,根据高线的性质得到90ADE ∠=︒,从而求出60BAD ∠=︒,继而根据角的和差得到结果;(2)根据角平分线的定义得到12BAE BAC ∠=∠,根据三角形内角和求出119022EAC B C ∠=︒-∠-∠,根据角的和差得到结果;(3)过A 作AG BC ⊥于G ,结合(2)知1()2EAG C B ∠=∠-∠,证明FD AG ∥,得到AFD EAG ∠=∠,即可证明.【详解】(1)解:∵30B ∠=︒,50C ∠=︒,∴1805030100BAC ∠=︒-︒-︒=︒,∵AE 平分BAC ∠,∴1502BAE CAE BAC ∠=∠=∠=︒,∵AD 是高,∴90ADE ∠=︒,∵30B ∠=︒,∴60BAD ∠=︒,∴10DAE BAD BAE ∠=∠-∠=︒;(2)()12DAE C B ∠=∠-∠,证明如下:∵AE 平分BAC ∠,∴12EAC BAC ∠=∠,∵180BAC B C ∠=︒-∠-∠,∴()11101902822B C B C EAC ︒-∠-∠-∠︒-==∠∠,∴EAD EAC DAC ∠=∠-∠()11090922B C C =︒∠---∠︒-∠()12C B =∠-∠;(3)不变,理由是:如图,过A 作AG BC ⊥于G ,由(2)可知:1()2EAG C B ∠=∠-∠,AG BC ⊥ ,90AGB ∠=︒,FD BC ⊥ ,90FDC ∴∠=︒,AGD FDC ∴∠=∠,FD AG ∴∥,AFD EAG ∴∠=∠,1()2AFD C B ∴∠=∠-∠.【点睛】本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质,熟练掌握三角形的内角和定理和角平分线的性质是解题的关键.模型2:双垂直模型结论:①∠A =∠C ;②∠B =∠AFD =∠CFE ;③AB CD AE BC ⋅=⋅。
中考几何48个模型及题型

中考几何48个模型及题型中考几何常见的48个模型及题型主要包括以下几类:
1. 直线与角。
a. 直线与角的性质,如同位角、对顶角等。
b. 直线间的夹角关系,如邻补角、对顶角等。
2. 三角形。
a. 三角形的性质,如三角形内角和为180度、三角形的外角性质等。
b. 三角形的全等与相似,如全等三角形的判定条件、相似三角形的性质等。
c. 三角形的高、中线、角平分线等线段的性质。
3. 四边形。
a. 平行四边形的性质,如对角线互相平分、对角线长度关系等。
b. 矩形、菱形、正方形和长方形的性质,如对角线长度关系、边长关系等。
c. 梯形的性质,如梯形的中位线、高的性质等。
4. 圆。
a. 圆的性质,如圆心角、弧、切线等。
b. 圆的相交关系,如相交弦定理、相交弧的性质等。
5. 相似。
a. 图形的相似性质,如相似三角形的判定条件、相似多边形的性质等。
b. 相似三角形的应用,如相似三角形的边比例定理、高线定理等。
6. 地理中的几何。
a. 地图的比例尺计算。
b. 方位角的计算。
c. 测量角度、距离等。
以上是中考几何常见的48个模型及题型,涵盖了直线与角、三角形、四边形、圆、相似和地理中的几何等多个方面。
希望这些信息能够帮助到你。
2023中考数学常见几何模型《全等模型-倍长中线与截长补短》含答案解析

专题01 全等模型--倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析,方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
【常见模型及证法】1、基本型:如图1,在三角形ABC 中,AD 为BC 边上的中线.证明思路:延长AD 至点E ,使得AD =DE . 若连结BE ,则BDE CDA ∆≅∆;若连结EC ,则ABD ECD ∆≅∆;2、中点型:如图2,C 为AB 的中点.证明思路:若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.3、中点+平行线型:如图3, //AB CD ,点E 为线段AD 的中点.证明思路:延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.1.(2022·山东烟台·一模)(1)方法呈现:如图①:在ABC 中,若6AB =,4AC =,点D 为BC 边的中点,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E 使DE AD =,再连接BE ,可证ACD EBD △≌△,从而把AB 、AC ,2AD 集中在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是_______________,这种解决问题的方法我们称为倍长中线法;(2)探究应用:如图②,在ABC 中,点D 是BC 的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,判断BE CF +与EF 的大小关系并证明;(3)问题拓展:如图③,在四边形ABCD 中,//AB CD ,AF 与DC 的延长线交于点F 、点E 是BC 的中点,若AE 是BAF ∠的角平分线.试探究线段AB ,AF ,CF 之间的数量关系,并加以证明.2.(2022·河南南阳·中考模拟)【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:如图,在ABC 中,D 是边BC 的中点,过点C 画直线CE ,使//CE AB ,交AD 的延长线于点E ,求证:AD ED=证明∵//CE AB (已知)∴ABD ECD ∠=∠,BAD CED ∠=∠(两直线平行,内错角相等).在ABD △与ECD 中,∵ABD ECD ∠=∠,BAD CED ∠=∠(已证),BD CD =(已知),∴()A.A.S ABD ECD △△≌,∴AD ED =(全等三角形的对应边相等).(1)【方法应用】如图①,在ABC 中,6AB =,4AC =,则BC 边上的中线AD 长度的取值范围是______.(2)【猜想证明】如图②,在四边形ABCD 中,//AB CD ,点E 是BC 的中点,若AE 是BAD ∠的平分线,试猜想线段AB 、AD 、DC 之间的数量关系,并证明你的猜想;(3)【拓展延伸】如图③,已知//AB CF ,点E 是BC 的中点,点D 在线段AE 上,EDF BAE ∠=∠,若5AB =,2CF =,求出线段DF 的长.3.(2022·河北·中考模拟)倍长中线的思想在丁倍长某条线段(被延长的线段a 要满足两个条件:①线段a 一个端点是图中一条线段b 的中点;②线段a 与这条线段b 不共线),然后进行连接,构造三角形全等,再进一步将某些线段进行等量代换,再证明全等或其他的结论,从而解决问题.【应用举例】如图(1),已知:AD 为ABC ∆的中线,求证:2AB AC AD +>.简证:如图(2),延长AD 到E ,使得DE AD =,连接CE ,易证ABD ECD ∆≅∆,得AB = ,在ACE ∆中,AC CE +> ,2AB AC AD +>.【问题解决】(1)如图(3),在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =.(2)如图(4),在ABC ∆中,90,A D ∠=︒是BC 边的中点,E F 、分别在边AB AC 、上,DE DF ⊥,若3,4BE CF ==,求EF 的长.(3)如图(5),AD 是ABC ∆的中线,,AB AE AC AF ==,且90BAE FAC ∠=∠=︒,请直接写出AD 与EF 的数量关系_ 及位置关系_ .模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。
初中数学必学48个几何模型

初中数学必学48个几何模型
1. 直线和线段
2. 射线
3. 角
4. 直角
5. 锐角和钝角
6. 平行线
7. 等腰三角形
8. 等边三角形
9. 直角三角形
10. 直角坐标系
11. 等比例线段
12. 外接圆和内切圆
13. 弧和扇形
14. 正方形
15. 长方形
16. 平行四边形
17. 梯形
18. 圆
19. 半圆
20. 圆周角
21. 正多边形
22. 立方体
23. 长方体
24. 正方体
25. 球体
26. 圆锥
27. 圆柱
28. 右锥和右圆锥
29. 高锥和高圆锥
30. 正棱柱
31. 正棱锥
32. 正六面体
33. 正八面体
34. 正十二面体
35. 菱形
36. 菱形组合
37. 等角三角形
38. 曲线
39. 等腰梯形
40. 对称图形
41. 平行四边形法则
42. 夹角
43. 三角形中位线定理
44. 三角形中心
45. 三角形外角和
46. 面积公式
47. 三分点
48. 垂线定理。
2024年中考数学常见几何模型全归纳(全国通用)专题31 圆中的重要模型之四点共圆模型(解析版)

专题31圆中的重要模型之四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
【答案】2【分析】首先连接OE,由角器上对应的读数.【详解】解:连接OE,A .13B .52∵在ABC 中,90BAC【答案】30【分析】连接AC 与BD 又易知在Rt ACD △中,【详解】解:连接AC 与∵四边形形ABCD 是矩形,12OA OB OC OD AC又∵DE BF 于E ,即是直角三角形,∴12OE BD ,∴OA OC OD OE ,∴点A B 、、,由旋转的性质可知:AF AB ,【答案】122【分析】(1)根据条件,证明AOD COD△△△△,代入推断即可.(2)通过AOG ABC证明ODF CBF△△,代入推断即可.又∵∵CE CF∴CEF CFE模型2、定边对双直角共圆模型C同侧型异侧型1)定边对双直角模型(同侧型)条件:若平面上A、B、C、D四个点满足90ABD ACD,结论:A、B、C、D四点共圆,其中AD为直径。
2)定边对双直角模型(异侧型)条件:若平面上A、B、C、D四个点满足90ABC ADC,结论:A、B、C、D四点共圆,其中AC为直径。
【点睛】本题考查了圆的直径所对的圆周角为【点睛】此题主要考查圆内接四边形,直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键是添加辅助线构造特殊三角形,求出线段.模型3、定边对定角共圆模型条件:如图1,平面上A 、B 、C 、D 四个点满足ADB ACB ,结论:A 、B 、C 、D 四点共圆.条件:如图2,AC 、BD 交于H ,AH CH BH DH ,结论:A B C D 、、、四点共圆.例1.(2023·江苏·九年级假期作业)如图,在Rt ABC 中,∠BAC =90°,∠ABC =40°,将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上.(1)求∠BAD 的度数;(2)求证:A 、D 、B 、E 四点共圆.【答案】(1)10°;(2)见解析【分析】(1)由三角形内角和定理和已知条件求得∠C 的度数,由旋转的性质得出AC =AD ,即可得出∠ADC =∠C ,最后由外角定理求得∠BAD 的度数;(2)由旋转的性质得到∠ABC =∠AED ,由四点共圆的判定得出结论.【详解】解:(1)∵在Rt ABC 中,∠BAC =90°,∠ABC =40°,∴∠C =50°,∵将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上,∴AC =AD ,∴∠ADC =∠C =50°,∴∠ADC =∠ABC +∠BAD =50°,∴∠BAD =50°-40°=10°证明(2)∵将 ABC 绕A 点顺时针旋转得到 ADE ,∴∠ABC =∠AED ,∴A 、D 、B 、E 四点共圆.【点睛】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定,解题的关键是理解旋转后的图形与原图形对应边相等,对应角相等.例3.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=________°;现将△DCE 绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是________.【答案】804##4【分析】利用SAS 证明△BDC ≌△AEC ,得到∠DBC =∠EAC =20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB =60°,推出A 、B 、C 、F 四个点在同一个圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,此时线段AF 长度有最小值,据此求解即可.【详解】解:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠BAC =∠ACB =∠DCE =60°,∴∠DCB +∠ACD =∠ECA +∠ACD =60°,即∠DCB =∠ECA ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC,∴△ACE ≌△BCD (SAS ),∴∠EAC =∠DBC ,∵∠DBC =20°,∴∠EAC =20°,∴∠BAF =∠BAC +∠EAC =80°;设BF 与AC 相交于点H,如图:∵△ACE ≌△BCD ∴AE =BD ,∠EAC =∠DBC ,且∠AHF =∠BHC ,∴∠AFB =∠ACB =60°,∴A 、B 、C 、F 四个点在同一个圆上,∵点D 在以C 为圆心,3为半径的圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,∴此时线段AF 长度有最小值,在Rt △BCD 中,BC =5,CD =3,∴BD 4,即AE =4,∴∠FDE =180°-90°-60°=30°,∵∠AFB =60°,∴∠FDE =∠FED =30°,∴FD =FE ,过点F 作FG ⊥DE 于点G ,∴DG =GE =32,∴FE =DF =cos 30DG∴AF =AE -FE 80;【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.例4.(2022·贵州遵义·统考中考真题)探究与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC 同侧有两点B ,D ,连接AD ,AB ,BC ,CD ,如果B D ,那么A ,B ,C ,D 四点在同一个圆上.探究展示:如图2,作经过点A ,C ,D 的O ,在劣弧AC 上取一点E (不与A ,C 重合),连接AE ,CE 则180AEC D (依据1)B D ∵180AEC B点A ,B ,C ,E 四点在同一个圆上(对角互补的四边形四个顶点共圆)点B ,D 在点A ,C ,E 所确定的O 上(依据2)点A ,B ,C ,E 四点在同一个圆上(1)反思归纳:上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:__________;依据2:__________.(2)图3,在四边形ABCD 中,12 ,345 ,则4 的度数为__________.(3)拓展探究:如图4,已知ABC 是等腰三角形,AB AC ,点D 在BC 上(不与BC 的中点重合),连接AD .作点C 关于AD 的对称点E ,连接EB 并延长交AD 的延长线于F ,连接AE ,DE .①求证:A ,D ,B ,E与判定,掌握以上知识是解题的关键.模型4、对角互补共圆模型P条件:如图1,平面上A、B、C、D四个点满足ABC ADC,结论:A、B、C、D四点共圆.条件:如图2,BA、CD的延长线交于P,PA PB PD PC,结论:A、B、C、D四点共圆.A.2B.22【答案】A【分析】先根据等腰三角形的性质可得,,,A B E D四点共圆,在以BE为直径的圆上,连接【答案】43/113【分析】过点B作BH AM交F,点A,M,B,C四点共圆,得法求解,12AMBS AM DE△【详解】解析:过点B作BH 于点,如图所示:【答案】52 2【分析】连接BD并延长,利用四点共圆的判定定理得到的性质和圆周角定理得到DBF性质解答即可得出结论.(1)求证:A ,E ,B ,D 四点共圆;(2)如图2,当AD CD 时,O 是四边形AEBD O 的切线;(3)已知1206BC ,,点M 是边BC 的中点,此时P 是四边形出圆心P 与点M 距离的最小值.【答案】(1)证明见解析(2)证明见解析(3)32(3)解:如图所示,作线段AB 的垂直平分线,分别交∵120AB AC BAC ,,∴B课后专项训练1.(2023秋·河北张家口·九年级校考期末)如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为()A.2B.3C.4D.6【答案】D【分析】根据两个直角三角形公共斜边时,四个顶点共圆,结合图形求解可得.【详解】解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选D.【点睛】本题考查四点共圆的判断方法.解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆.,.下2.(2023·安徽合肥·校考一模)如图,O是AB的中点,点B,C,D到点O的距离相等,连接AC BD列结论不一定成立的是()A .12B .3=4C .180ABC ADCD .AC 平分BAD【答案】D 【分析】以点O 为圆心,OA 长为半径作圆.再根据圆内接四边形的性质,圆周角定理逐项判断即可.【详解】如图,以点O 为圆心,OA 长为半径作圆.由题意可知:OA OB OC OD .即点A 、B 、C 、D 都在圆O 上.A .∵ AB AB ,∴12 ,故A 不符合题意;B .∵ BCBC ,∴3=4 ,故B 不符合题意;C .∵四边形ABCD 是O 的内接四边形,∴180ABC ADC ,故C 不符合题意;D .∵ BC 和CD不一定相等,∴BAC 和DAC 不一定相等,∴AC 不一定平分BAD ,故D 符合题意.故选:D .【点睛】本题考查圆周角定理及其推论,充分理解圆周角定理是解答本题的关键.3.(2023·江苏宿迁·九年级校考期末)如图,在Rt ABC △中,90ACB ,3BC ,4AC ,点P 为平面内一点,且CPB A ,过C 作CQ CP 交PB 的延长线于点Q ,则CQ 的最大值为()【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.4.(2023·北京海淀·九年级校考期中)如图,点接AC,BD.请写出图中任意一组互补的角为【答案】DAB【分析】首先判断出点【答案】130【分析】根据题意得到四边形【详解】解:由题意得到∴四边形ABCD为圆∵∠ABC=50°,∴∠【点睛】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.6.(2023·浙江金华·A.3B.1∵PE AB 于点E ,PD AC 于点,∴90AEP ADP ,∴180AEP ADP ,∴A 、E 、D 四点共圆,PA 是直径,在Rt PDC 中,45C ,∴△是等腰直角三角形,45APD ∴APD △也是等腰直角三角形,45PAD ,∴PED PAD ∴45AED ,∴AED C ,∵EAD CAB ,∴AED ∽设2AD x ,则2PD DC x ,22x ,如图2,取AP 的中点O 则2AO OE OP x ,∵604515EAP BAC PAD ,过E 作EM AP 于M ,则EM x,cos30OM OE ,∴36222OM x x ,∴6226222AM x x x ,由勾股定理得: 222226222AE AM EM x x +【答案】3632 /323 【分析】数形结合,根据动点的运动情况判断点【详解】解:如图旋转,连接以BC 为直径作O ,以AE 为半径作在ABD △和ACE △中AB AC AD AE BAD CAEPBC PBA ACB PBC 90BAC BPC EAD ∵,122AB ∵,A 的半径为62∴又∵90BAC EAD ,CAD,∵33BC ,OP BC∵MQ,MC与圆O相切,1QOM COM COP 【答案】(1)见详解(2)证明:如下图所示由题意可知AC 逆时针旋转90得到边AE ,90E ACB ,则90ACB ∵,AE BF ∥,90 ∵,90EFC ,,F ,E 四点共圆..∵四边形ABCD是菱形,AC,且 GOC GCO90==∵, 点90DHC DOC=BDF OCH=,且BF OM ∵, 点==90AED AOD尝试应用如图2,点D 为等腰Rt ABC △外一点,AB AC ,BD CD ,过点A 的直线分别交DB 的延长线和CD 的延长线于点N ,M ,求证:12ABN ACM S S AN AM △△.问题拓展如图3,ABC 中,AB AC ,点D ,E 分别在边AC ,BC 上,60BDA BEA ,AE ,BD ,直接写出BE 的长度(用含a ,b 的式子)∵ABC 为等腰直角三角形,∴AB AC , 又∵BD CD ,即:=90BDC ,∴A 、B 在ABN 与ACE △中,AB AC ABN ACE BN CE,∴∴BAN BAE CAE BAE BAC ∴1122AME AMC S AE AM AN AM S S △△∴60AFB BAF ABF ,AB AF AC ,∵60BDA BEA ,∴A 、D 、E 、B 、F 五点共圆,则:13 ,24 ,60BEF AEB ,【答案】问题情境:见解析;问题解决:(1)102;(2)13522【分析】[问题情境]连结AC ,取AC 的中点O ,连结OB 、OD ,根据直角三角形斜边上的中线等于斜边的一半,可得OD OA OC OB ,以此即可证明;[问题解决](1)根据题意可得225AE AD DE ,由[问题情境]结论可知A 、D 、E 、据圆周角定理以及正方形的性质可得45PDE PAE ,则PAE △为等腰直角三角形,设AP 长为a ,根据勾股定理列出方程,求解即可;(2)由[问题情境]结论可知A 、D 、E 、P 四点共圆,过点O 作OG AD 于点G ,作OH 接OB 交O 于点P ,连接PB ,根据题意可得四边形MBNP 为矩形,则要求MN 的最小值,即求值,根据平行线的性质和中点的定义可得OG 为ADE V 的中位线,得1AG ,12OG ,同理可证四边形1【翻折】(1)如图1,将DEF 沿线段AB 翻折,连接CF ,下列对所得四边形ACBF 的说法正确的是平分CBF 、CAF ,②AB 、CF 互相平分,③12ACBF S AB CF 四边形,④A 、C 、B 、F 四点共圆.AB 垂直平分CF ,故②ABC ABF ACBF S S S 四边形1122AB AB FG 12AB CG 取AB 的中点O ,连接CO FO ,ABC ABF △、△均为直角三角形,∴OB OC OA OF ,∴A 、B 、F 四点共圆,故()沿线段向左平移,∴AB CF ,CF BE 的中点,∴BE BD BF特殊情况分析:(1)如图1,正方形ABCD 中,点P 为对角线时针旋转ADC 的度数,交直线BC 于点Q .小明的思考如下:连接DQ ,∵AD CQ ∥,90ADC DCQ ,∴ACQ DAC ∵90DPQ ,∴180DPQ DCQ ,∴点D P Q 、、PDQ PCQ DQP PCD∵在菱形ABCD 中BC AD ∥,180ADC DCQ ,DPQ ADC ,∵180DPQ DCQ ,∴点P C Q 、、、共圆,∴DQP ACD ,ACB PDQ ,∵AC 为菱形ABCD 的对角线,ACB ACD ,∴PDQ DQP ,∴ DP PQ ;(3)解:3PQ 或3.由于点P 为对角线AC 上一个动点,分两类情况讨论如下:所示:180302ADC ACD,。
中考数学题中的几何模型

有关“中考数学题”中的几何模型
有关“中考数学题”中的几何模型如下:
1.直角三角形模型:直角三角形是初中数学中常见的几何模型之一,它涉及到勾股定
理、直角三角形的性质等知识点。
在中考数学题中,直角三角形模型通常会出现在与三角形、四边形、圆等相关的题目中。
2.相似三角形模型:相似三角形是初中数学中另一个重要的几何模型,它涉及到相似三
角形的性质、相似三角形的判定条件等知识点。
在中考数学题中,相似三角形模型通常会出现在与三角形、四边形、圆等相关的题目中。
3.梯形模型:梯形是初中数学中常见的几何图形之一,它涉及到梯形的性质、梯形的面
积计算等知识点。
在中考数学题中,梯形模型通常会出现在与四边形、圆等相关的题目中。
4.圆与扇形模型:圆与扇形是初中数学中常见的几何图形之一,它涉及到圆的性质、扇
形的面积计算等知识点。
在中考数学题中,圆与扇形模型通常会出现在与圆、扇形、三角形等相关的题目中。
全等模型-角平分线模型—2024年中考数学常见几何模型全归纳(全国通用)(解析版)

全等模型-角平分线模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各类模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的几类全等模型作相应的总结,需学生反复掌握。
模型1.角平分线垂两边(角平分线+外垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线、CA OA ⊥于点A 时,过点C 作CA OB ⊥.结论:CA CB =、OAC ∆≌OBC ∆.图1 图2常见模型1(直角三角形型)条件:如图2,在ABC ∆中,90C ∠=︒,AD 为CAB ∠的角平分线,过点D 作DE AB ⊥.结论:DC DE =、DAC ∆≌DAE ∆.(当ABC ∆是等腰直角三角形时,还有AB AC CD =+.)图3常见模型2(邻等对补型)条件:如图3,OC 是∠COB 的角平分线,AC =BC ,过点C 作CD ⊥O A 、CE ⊥OB 。
结论:①180BOA ACB ∠+∠=︒;②AD BE =;③2OA OB AD =+.例1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,∵AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,∴1DF DE ==, ∴1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1. 【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键. 例2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A .40°B .45°C .50°D .60°【答案】C 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,∴∠CAF=100°,在Rt△PFA和Rt△PMA中,{PA PA PM PF==,∴Rt△PFA≌Rt△PMA(HL),∴∠FAP=∠PAC=50°.故选C.【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM=PN=PF是解题的关键.八年级校联考期中)如图,ABC中,ACF∠A.①②B.①③C.②③④D.①②③④【答案】D【分析】过点P作PD AC⊥于D,根据角平分线的判定定理和性质定理即可判断①结论;证明()Rt Rt HLPAM PAD≌,()Rt Rt HLPCD PCN≌,得出APM APD∠=∠,CPD CPN∠=∠,进而得到2MPN APC∠=∠,再利用四边形内角和,即可判断②结论;根据角平分线的定义和三角形的外角性质,即可判断③结论;根据全等三角形的性质,即可判断④结论.【详解】解:①如图,过点P作PD AC⊥于D,BP 平分ABC ∠,PM BE ⊥,PN BF ⊥,PM PN ∴=, AP 平分EAC ∠,PM BE ⊥,PD AC ⊥,PM PD ∴=,PN PD ∴=,PN BF ⊥,PD AC ⊥,CP ∴平分ACF ∠,①结论正确;②PM BE ⊥,PD AC ⊥,PN BF ⊥,90PMA PDA PNB ∴∠=∠=∠=︒,在Rt PAM 和Rt PAD △中,PM PD PA PA =⎧⎨=⎩,()Rt Rt HL PAM PAD ∴≌,APM APD ∴∠=∠,同理可得,()Rt Rt HL PCD PCN ≌,CPD CPN ∴∠=∠,()22MPN APM APD CPD CPN APD CPD APC ∴∠=∠+∠+∠+∠=∠+∠=∠,360ABC PNB MPN PMA ∠+∠+∠+∠=︒,360180ABC MPN PNB PMA ∴∠+∠=︒−∠−∠=︒,2180ABC APC ∴∠+∠=︒,②结论正确;③AP 平分EAC ∠, 2CAE MAP ∴∠=∠,CAE ABC ACB ∠=∠+∠,MAP ABP APB ∠=∠+∠,()2ABC ACB ABP APB ∴∠+∠=∠+∠, BP 平分ABC ∠,2ABC ABP ∴∠=∠,222ABP ACB ABP APB ∴∠+∠=∠+∠,2ACB APB ∴∠=∠,③结论正确; ④由②可知,Rt Rt PAM PAD ∴≌,Rt Rt PCD PCN ≌,PAM PAD SS ∴=,PCD PCN S S =, PAC PAD PCD S S S =+,PAC PAM PCN S S S =+APM CPN APC S S S ∴+=△△△,④结论正确,∴正确的结论是①②③④,故选:D【点睛】本题考查了角平分线的平分线的判定定理和性质定理,全等三角形的判定和性质,四边形内角和,三角形的外角性质,熟练掌握角平分线上的点到角两边的距离相等是解题关键. 例4.(2023秋·浙江·八年级专题练习)如图,四边形ABDC 中,90D ABD ∠=∠=︒,点O 为BD 的中点,且OA平分BAC ∠.(1)求证:OC 平分ACD ∠;(2)求证:OA OC ⊥;(3)求证:AB CD AC +=.【答案】(1)见解析(2)见解析(3)见解析【分析】(1)过点O 作OE AC ⊥于E ,根据角平分线上的点到角的两边的距离相等,可得OB OE =,从而求出OE OD =,然后根据到角的两边距离相等的点在角的平分线上证明即可;(2)利用HL ,证明Rt Rt ABO AEO ≌,根据全等三角形对应角相等,可得AOB AOE ∠=∠,同理可得COD COE ∠=∠,然后求出=90AOC ∠︒,再根据垂直的定义即可证明;(3)根据全等三角形对应边相等,可得AB AE =,CD CE =,然后根据线段之间的数量关系,即可得出结论.【详解】(1)证明:过点O 作OE AC ⊥于E ,∵90ABD Ð=°,OA 平分BAC ∠∴OB OE =,∵点O 为BD 的中点,∴OB OD =,∴OE OD =,又∵90D Ð=°,∴OC 平分ACD ∠;(2)证明:在Rt ABO △和Rt AEO △中,AO AO OB OE =⎧⎨=⎩,∴()Rt Rt HL ABO AEO △≌△,∴AOB AOE ∠=∠,在Rt CEO △和Rt CDO △中,CO CO OE OD =⎧⎨=⎩,∴()Rt Rt HL CEO CDO ≌,∴COD COE ∠=∠,∴1180902AOC AOE COE ∠=∠+∠=⨯︒=︒,∴OA OC ⊥;(3)证明:∵Rt Rt ABO AEO ≌,∴AB AE =,∵Rt Rt CEO CDO ≌,∴CD CE =,∵AE CE AC +=,∴AB CD AC +=.【点睛】本题考查了角平分线的判定与性质、全等三角形的判定与性质、垂线的定义,熟记性质并作辅助线构造出全等三角形是解题的关键.例5.(2022·河北·九年级专题练习)已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;(2)如图2,若∠AOB=120°,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.【答案】(1)CF=CG;(2)CF=CG,见解析【分析】(1)结论CF=CG,由角平分线性质定理即可判断.(2)结论:CF=CG,作CM⊥OA于M,CN⊥OB于N,证明△CMF≌△CNG,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF=CG;证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,∴CF=CG(角平分线上的点到角两边的距离相等);(2)CF=CG.理由如下:如图,过点C作CM⊥OA,CN⊥OB,∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120°,∴CM=CN(角平分线上的点到角两边的距离相等),∴∠AOC=∠BOC=60°(角平分线的性质),∵∠DCE=∠AOC,∴∠AOC=∠BOC=∠DCE=60°,∴∠MCO=90°-60° =30°,∠NCO=90°-60° =30°,∴∠MCN=30°+30°=60°,∴∠MCN=∠DCE,∵∠MCF=∠MCN-∠DCN,∠NCG=∠DCE-∠DCN,∴∠MCF=∠NCG,在△MCF和△NCG中,CMF CNGCM CNMCF NCG∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MCF≌△NCG(ASA),∴CF=CG (全等三角形对应边相等).【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等.模型2.角平分线垂中间(角平分线+内垂直)【模型解读与图示】条件:如图1,OC 为AOB ∠的角平分线,AB OC ⊥,结论:△AOC ≌△BOC ,OAB ∆是等腰三角形、OC 是三线合一等。
中考数学必学几何模型大全(含解析)

中考数学必学几何模型大全(含解析)模型一:截长补短模型如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短法。
截长法:如图①,在EF上截取EG=AB,再证明GF=CD即可。
补短法:如图①,延长AB至H点,使BH=CD,再证明AH=EF即可。
模型分析截长补短的方法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段。
该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程。
例题精讲1、如图,AC平分①BAD,CE①AB于点E,①B+①D=180°,求证:AE=AD+BE.解析:如图,在EA上取点F,使EF=BE,连接CF,①CE①AB,①CF=CB,①CFB=①B①①AFC+①CFB=180°,①D+①B=180°,①①D=①AFC①AC平分①BAD,即①DAC=①F AC在①ACD和①ACF中,①D=①AFC,①DAC=①F AC,AC=AC①ACD①①ACF(AAS),①AD=AF,①AE=AF+EF=AD+BE2、如图,已知在①ABC中,①C=2①B,①1=①2,求证:AB=AC+CD解析:在AB上取一点E,使AE=AC,连接DE,①AE=AC,①1=①2,AD=AD,①①ACD①①AED,①CD=DE,①C=①3①①C=2①B,①①3=2①B=①4+①B,①①4=①B,①DE=BE,CD=BE①AB=AE+BE,①AB=AC+CD3、如图,在五边形ABCDE中,AB=AE,BC+DE=CD,①B+①E=180°,求证:AD平分①CDE.解析:延长CB至点F,使BF=DE,连接BF=DE,连接AF,AC①①1+①2=180°,①E+①1=180°,①①2=①E①AB=AE,①2=①E,BF=DE,①①ABF①①AED,①F=①4,AF=AD①BC+BF=CD,即FC=CD又①AC=AC,①①ACF①①ACD,①①F=①3①①F=①4,①①3=①4,①AD平分①CDE.4、已知四边形ABCD中,①ABC+①ADC=180°,AB=BC,如图,点P,Q分别在线段AD,DC上,满足PQ=AP+CQ,①ADC求证:①PBQ=90°-12解析:如图,延长DC,在上面找一点K,使得CK=AP,连接BK,①①ABC+①ADC=180°,①①BAD+①BCD=180°①①BCD+①BCK=180°,①①BAD=①BCK在①BAP和①BKC中AP =CK ,①BAP =①BCK ,AB =BC ,①①BP A ①①BKC (SAS ),①①ABP =①CBK ,BP =BK①PQ =AP +CQ ,①PQ =QK①在①BPQ 和①BKQ 中,BP =BK ,BQ =BQ ,PQ =KQ①①BPQ ①①BKQ (SSS ),①①PBQ =①KBQ ,①①PBQ =12①ABC ①①ABC +①ADC =180°,①①ABC =180°-①ADC①12①ABC =90°-12①ADC ,①①PBQ =90°-12①ADC5、如图,在①ABC 中,①B =60°,①ABC 的角平分线AD 、CE 相交于点O ,求证:AE +CD =AC .解析:由题意可得①AOC =120°①①AOE =①DOC =180°-①AOC =180°-120°=60°在AC 上截取AF =AE ,连接OF ,如图在①AOE 和①AOF 中,AE =AF ,①OAE =①OAF ,OA =OA①①AOE ①①AOF (SAS ),①①AOE =①AOF ,①①AOF =60°,①①COF =①AOC -①AOF =60°又①COD =60°,①①COD =①COF同理可得:①COD ①①COF (ASA ),①CD =CF又①AF =AE ,①AC =AF +CF =AE +CD ,即AE +CD =AC6、如图所示,AB ①CD ,BE ,CE 分别是①ABC ,①BCD 的平分线,点E 在AD 上,求证:BC =AB +CD .解析:在BC 上取点F ,使BF =AB①BE ,CE 分别是①ABC ,①BCD 的平分线,①①ABE =①FBE ,①BCE =①DCE①AB ①CD ,①①A +①D =180°在①ABE和①FBE中,AB=FB,①ABE=①FBE,BE=BE①①ABE①①FBE(SAS),①①A=①BFE,①①BFE+①D=180°①①BFE+①EFC=180°,①①EFC=①D在①EFC和①EDC中,①EFC=①D,①BCE=①DCE,CE=CE ①①EFC①①EDC(AAS),①CF=CD①BC=BF+CF,①BC=AB+CD7、四边形ABCD中,BD>AB,AD=DC,DE①BC,BD平分①ABC (1)证明:①BAD+①BCD=180°(2)DE=3,BE=6,求四边形ABCD的面积.【解析】(1)过点D作BA的垂线,得①DMA①DEC(HL)①①ABC+①MDE=180°,①ADC=①MDE①①ABC+①ADC=180°,①①BAD+①BCD=180°(2)S四边形ABCD=2S①BED=188、已知:在①ABC中,AB=CD-BD,求证:①B=2①C.【解析】在CD上取一点M使得DM=DB则CD-BD=CM=AB①①AMD=①B=2①C模型二:倍长中线法模型分析:①ABC中AD是BC边中线方式1:延长AD到E,使DE=AD,连接BE方式2:间接倍长,作CF①AD于F,作BE①AD的延长线于E,连接BE方式3:延长MD到N,使DN=MD,连接CD例题精讲:1、已知,如图①ABC中,AB=5,AC=3,则中线AD的取值范围是.【解答】1<AD<4.2、如图,①ABC 中,E ,F 分别在AB ,AC 上,DE ①DF ,D 是中点,试比较BE +CF 与EF 的大小.【解答】解:BE +CF >FP =EF .延长ED 至P ,使DP =DE ,连接FP ,CP ,①D 是BC 的中点,①BD =CD ,在①BDE 和①CDP 中,{DP =DE∠EDB =∠CDP BD =CD①①BDE ①①CDP (SAS ),①BE =CP ,①DE ①DF ,DE =DP ,①EF =FP ,(垂直平分线上的点到线段两端点距离相等)在①CFP 中,CP +CF =BE +CF >FP =EF .3、已知:在①ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF .【解答】证明:如图,延长AD 到点G ,使得AD =DG ,连接BG .①AD 是BC 边上的中线(已知),①DC =DB ,在①ADC 和①GDB 中,{AD =DG∠ADC =∠GDB(对顶角相等)DC =DB,①①ADC ①①GDB (SAS ),①①CAD =①G ,BG =AC又①BE =AC ,①BE =BG ,①①BED =①G ,①①BED =①AEF ,①①AEF =①CAD ,即:①AEF =①F AE ,①AF =EF .4、已知:如图,E 是BC 的中点,点A 在DE 上,且①BAE =①CDE .求证:AB =CD .【解答】证明:延长DE 到F ,使EF =DE ,连接BF ,①E 是BC 的中点,①BE =CE ,①在①BEF 和①CED 中{BE =CE ∠BEF =∠CED EF =DE,①①BEF ①①CED .①①F =①CDE ,BF =CD .①①BAE =①CDE ,①①BAE =①F .①AB =BF ,又①BF =CD ,①AB =CD .5、如图,①ABC 中,AB =AC ,点D 在AB 上,点E 在AC 的延长线上,DE 交BC 于F ,且DF =EF ,求证:BD =CE .【解答】证明:如图,过点D 作DG ①AE ,交BC 于点G ;则①DGF ①①ECF ,①DG :CE =DF :EF ,而DF =EF ,①DG =CE ;①AB =AC ,①①B =①ACB ;①DG ①AE ,①①DGB =①ACB ,①①DBG =①DGB ,①DG =BD ,①BD =CE .模型三:角平分线四大模型1、角平分线的性质2、角平分线的对称性3、角平分线+平行线,等腰现4、角平分线+垂线,等腰归例题精讲:1、如图,D是①EAF平分线上的一点,若①ACD+①ABD=180°,请说明CD=DB的理由.【解答】解:过点D分别作AE,AF的垂线,交AE于M,交AF于N,则①CMD=①BND=90°,①AD是①EAF的平分线,①DM=DN,①①ACD+①ABD=180°,①ACD+①MCD=180°,①①MCD=①NBD,在①CDM和①BDN中,①CMD=①BND=90°,①MCD=①NBD,DM=DN,①①CDM①①BDN,①CD=DB.2、如图,BD和CD分别平分①ABC的内角①EBA和外角①ECA,BD交AC于点F,连接AD.(1)求证:①BDC=12∠BAC;(2)若AB=AC,请判断①ABD的形状,并证明你的结论.【解答】(1)证明:①BD和CD分别平分①ABC的内角①EBA和外角①ECA,①①ABC=2①DBC,①ACE=2①DCE,①①ACE=①BAC+①ABC,①DCE=①BDC+①DBC,①2①DCE=2①BDC+2①DBC,①①BAC=2①BDC,即①BDC=12①BAC;(2)①ABD是等腰三角形,证明:①AB=AC,①①ABC=①ACB,过D作DQ①AB于Q,DR①BC于R,DW①AC于W,①BD和CD分别平分①ABC的内角①EBA和外角①ECA,①DQ=DR,DW=DR,①DQ=DW,①DQ①AB,DW①AC,①①GAC=2①GAD=2①CAD,①①GAC=①ABC+①ACB,①①GAD=①ABC,①AD①BC,①①ADB=①DBC,①①ABD=①DBC,①①ADB=①ABD,①AB=AD,即①ABD是等腰三角形.3、如图,在①ABC中,①ABC=90°,AB=7,AC=25,BC=24,三条角平分线相交于点P,求点P到AB的距离.【解答】解:过点P作PD①AB于D,PE①BC于E,PF①AC于F,①点P是①ABC三条角平分线的交点,①PD=PE=PF①S ①ABC =S ①P AB +S ①PBC +S ①P AC =12PD •AB +12PE •BC +12PF •AC =12PD •(AB +BC +AC )=12PD •(7+25+24)=28PD 又①①ABC =90°,①S ①ABC =12AB •BC =12×7×24=7×12,①7×12=28PD ,①PD =3 答:点P 到AB 的距离为3.4、如图,AD 是①ABC 中①BAC 的平分线,P 是AD 上的任意一点,且AB >AC ,求证:AB −AC >PB −PC .【解答】证明:如图,在AB 上截取AE ,使AE =AC ,连接PE ,①AD 是①BAC 的平分线,①①BAD =①CAD ,在①AEP 和①ACP 中,{AE =AC ∠BAD =∠CAD AP =AP,①①AEP ①①ACP (SAS ),①PE =PC ,在①PBE 中,BE >PB −PE 即AB −AC >PB −PC .5、在①ABC 中,AD 是①BAC 的外角平分线,P 是AD 上的任意一点,试比较PB +PC 与AB +AC 的大小, 并说明理由.【解答】解:PB +PC >AB +AC如图,在BA 的延长线上取一点E ,使AE =AC ,连接EP .由AD 是①BAC 的外角平分线,可知①CAP =①EAP ,又AP 是公共边,AE =AC ,故①ACP ①①AEP从而有PC =PE ,在①BPE 中,PB +PE >BE而BE =AB +AE =AB +AC ,故PB +PE >AB +AC ,所以PB +PC >AB +AC6、已知:如图,在①ABC 中,①A =2①B ,CD 平分①ACB ,且AC =6,AD =2.求BC 的长.【解答】解:如图,在BC 上截取CE =CA ,连接DE ,①CD平分①ACB,①①1=①2,在①ACD和①ECD中{CA=CE∠1=∠2CD=CD,①①ACD①①ECD(SAS),①AD=ED,①A=①CED,①①A=2①B,①①CED=2①B,①①CED=①B+①BDE,①①BDE=①B,①BE=ED,①AC=6,AD=2,①AD=BE=2,AC=CE=6,①BC=BE+CE=2+6=8.7、如图,①AOB=30°,OD平分①AOB,DC①OA于点C,DC=4cm,求OC的长.【解答】过点D作DE//OB,交OA于点E.OC=CE+OE=CE+DE=8+43.8、(1)如图①ABC中,BD、CD分别平分①ABC,①ACB,过点D作EF①BC交AB、AC于点E、F,试说明BE+CF=EF的理由.(2)如图,①ABC中,BD、CD分别平分①ABC,①ACG,过D作EF①BC交AB、AC于点E、F,则BE、CF、EF有怎样的数量关系?并说明你的理由.【解答】解:(1)①BD平分①ABC,①①ABD=①CBD,①EF①BC,①①EDB=①DBC,①①ABD=①EDB,①BE=ED,同理DF=CF,①BE+CF=EF;(2)BE−CF=EF,由(1)知BE=ED,①EF①BC,①①EDC=①DCG=①ACD,①CF=DF,又①ED−DF=EF,①BE−CF=EF.9、如图,在①ABC ,AD 平分①BAC ,E 、F 分别在BD 、AD 上,且DE =CD ,EF =AC ,求证:EF ①AB .【解答】解:过E 作AC 的平行线于AD 延长线交于G 点, ①EG ①AC在①DEG 和①DCA 中,{∠ADC =∠GDE CD =ED ∠DEG =∠DCA,①①DEG ①①DCA (ASA ), ①EG =EF ,①G =①CAD ,又EF =AC ,故EG =AC ①AD 平分①BAC ,①①BAD =①CAD ,①EG =EF ,①①G =①EFD ,①①EFD =①BAD ,①EF ①AB .10、已知等腰直角三角形ABC ,BC 是斜边.①B 的角平分线交AC 于D ,过C 作CE 与BD 垂直且交BD 延长线于E ,求证:BD =2CE .【解答】证明:如图,分别延长CE ,BA 交于一点F . ①BE ①EC ,①①FEB =①CEB =90°, ①BE 平分①ABC ,①①FBE =①CBE , 又①BE =BE ,①①BFE ①①BCE (ASA ). ①FE =CE .①CF =2CE .①AB =AC ,①BAC =90°,①ABD +①ADB =90°,①ADB =①EDC , ①①ABD +①EDC =90°.又①①DEC =90°,①EDC +①ECD =90°,①①FCA =①DBC =①ABD . ①①ADB ①①AFC .①FC =DB ,①BD =2EC .11、如图.在①ABC 中,BE 是角平分线,AD ①BE ,垂足为D ,求证:①2=①1+①C .【解答】证明:如图,延长AD 交BC 于点F ,①BE 是角平分线,AD ①BE ,①①ABF 是等腰三角形,且①2=①AFB , 又①①AFB =①1+①C ,①①2=①1+①C .12、(1)如图(a )所示,BD 、CE 分别是①ABC 的外角平分线,过点A 作AD ①BD ,AE ①CE ,垂足分别为D 、E ,连接DE ,求证:DE ①BC ,DE =12(AB +BC +AC );(2)①如图(b )所示,BD 、CE 分别是①ABC 的内角平分线,其他条件不变;①如图(c )所示,BD 为①ABC 的内角平分线,CE 为①ABC 的外角平分线,其他条件不变;则在图(b )、图(c )两种情况下,DE 与BC 还平行吗?它与①ABC 三边又有怎样的数量关系?请写出你的猜测,并对其中一种情况进行证明.【解答】解:(1)如图1,分别延长AE 、AD 交BC 于H 、K , 在①BAD 和①BKD 中,{∠ABD =∠DBK BD =BD ∠BDA =∠BDK ,①①BAD ①①BKD (ASA ), ①AD =KD ,AB =KB ,同理可证,AE =HE ,AC =HC ,①DE =12HK ,又①HK =BK +BC +CH =AB +BC +AC ,①DE =12(AB +AC +BC ); (2)①猜在想结果:图2结论为DE =12(AB +AC −BC ). 证明:分别延长AE 、AD 交BC 于H 、K , 在①BAD 和①BKD 中,{∠ABD =∠DBK BD =BD ∠BDA =∠BDK,①①BAD ①①BKD (ASA ),①AD =KD ,AB =KB , 同理可证,AE =HE ,AC =HC ,①DE =12HK ,又①HK =BK -BH =AB +AC -BC ,①DE =12(AB +AC −BC ); ①图3的结论为DE =12(BC +AC −AB ).证明:分别延长AE 、AD 交BC 或延长线于H 、K , 在①BAD 和①BKD 中,{∠ABD =∠DBK BD =BD ∠BDA =∠BDK,①①BAD ①①BKD (ASA ),①AD =KD ,AB =KB 同理可证,AE =HE ,AC =HC ,①DE =12KH又①KH =BC -BK +HC =BC +AC -AB .①DE =12(BC +AC −AB ).模型四:手拉手模型模型:如图,①ABC 是等腰三角形、①ADE 是等腰三角形,AB =AC ,AD =AE , ①BAC =①DAE = 。
2024年中考数学总复习初中数学常考10个几何模型汇总

2024年中考数学总复习初中数学常考10个几何模
型汇总
模型一:“12345”模型
模型二:“半角”模型
对称半角模型
旋转半角模型
模型三:“角平分线”模型
角平分线定理角平分线+垂线=等腰三角形角分线+平行线=等腰三角必呈现
角平分线+垂线=等腰三角形
模型四:“手拉手”模型
条件:1、两个等腰三角形;2、顶角相等;3、顶点重合。
结论:1、手相等;2、三角形全等;3、手的夹角相等;
4、顶点连手的交点得平分。
模型五:“将军饮马”模型
模型六:“中点”模型
【模型1】倍长
1、倍长中线;
2、倍长类中线;
3、中点遇平行延长相交
【模型2】遇多个中点,构造中位线
1.直接连接中点;
2.连对角线取中点再相连
模型七:“邻边相等的对角互补”模型
【模型1】
【条件】如图,四边形ABCD中,AB=AD,∠BAD+∠BCD=∠ABC+∠ADC=180°
【结论】AC平分∠BCD
【模型2】
【条件】如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°【结论】①∠ACB=∠ACD=45°②BC+CD=V2AC
模型八:“一线三角”模型
【条件】∠EDF=∠B=∠C,且DE=DF
【结论】△BDE=△CFD
模型九:“弦图”模型
【条件】正方形内或外互相垂直的四条线段【结论】新构成了同心的正方形
模型十:费马点。
2024中考数学常见几何模型归纳总结—三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-“8”字模型、“A”字模型与三角板模型近年来各地中考中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题“8”字模型、“A ”字模型与三角板模型进行梳理及对应试题分析,方便掌握。
模型1、“8”字模型图1图28字模型(基础型)条件:如图1,AD 、BC 相交于点O ,连接AB 、CD ;结论:①A B C D ∠+∠=∠+∠;②AB CD AD BC +<+。
8字模型(加角平分线)条件:如图2,线段AP 平分∠BAD ,线段CP 平分∠BCD ;结论:2∠P =∠B +∠D例1.(2021·河北·统考中考真题)下图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且A ∠,B ∠,E ∠保持不变.为了舒适,需调整D ∠的大小,使110EFD ∠=︒,则图中D ∠应(填“增加”或“减少”)度.【答案】减少10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系,进行计算即可判断.【详解】解:∵∠A+∠B=50°+60°=110°,∴∠ACB=180°-110°=70°,∴∠DCE=70°,如图,连接CF并延长,∴∠DFM=∠D+∠DCF=20°+∠DCF,∠EFM=∠E+∠ECF=30°+∠ECF,∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD=110°,则∠EFD减少了10°,若只调整∠D的大小,由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°,因此应将∠D减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.例2.(2023·浙江·八年级假期作业)如图,求∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠K 的度数.【答案】540°【分析】如图所示,由三角形外角的性质可知:∠A +∠B =∠IJL ,∠C +∠D =∠MLJ ,∠H +∠K =∠GIJ ,∠E +∠F =∠GML ,然后由多边形的内角和公式可求得答案.【详解】解:如图所示:由三角形的外角的性质可知:∠A +∠B =∠IJL ,∠C +∠D =∠MLJ ,∠H +∠K =∠GIJ ,∠E +∠F =∠GML ,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠K =∠IJL +∠MLJ +∠GML +∠G +∠GIJ =(5-2)×180°=3×180°=540°.【点睛】本题主要考查的是三角形外角的性质和多边形的内角和公式的应用,利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键例3.(2023·山东德州·八年级校考阶段练习)如图1,已知线段,AB CD 相交于点O ,连接,AC BD ,则我们把形如这样的图形称为“8字型”.(1)求证:A C B D ∠+∠=∠+∠;(2)如图2,若CAB ∠和BDC ∠的平分线AP 和DP 相交于点P ,且与,CD AB 分别相交于点M N 、.①若100,120B C ∠=︒∠=︒,求P ∠的度数;②若角平分线中角的关系改为“11,33CAP CAB CDP CDB ∠=∠∠=∠”,试探究P ∠与,B C ∠∠之间的数量关系.【答案】(1)见解析(2)①110︒;②()123P B C ∠=∠+∠【分析】(1)利用三角形内角和定理和对顶角相等即可证明;(2)①根据角平分线的定义得到CAP BAP ∠=∠,BDP CDP ∠=∠,再根据“8字形”得到,CAP C CDP P BAP P BDP B ∠+∠=∠+∠∠+∠=∠+∠,两等式相减得到C P P B ∠-∠=∠-∠,即()12P B C ∠=∠+∠,即可求解.②根据11,33CAP CAB CDP CDB ∠=∠∠=∠,可得23BAP BAC ∠=∠,23BDP BDC ∠=∠,再由三角形内角和定理和对顶角相等,可得()2C P P B ∠-∠=∠-∠,即可求解.【详解】(1)证明:在AOC 中,180A C AOC ∠+∠=︒-∠,在BOD 中,180B D BOD ∠+∠=︒-∠,∵AOC BOD ∠=∠,∴A C B D ∠+∠=∠+∠;(2)解:①∵CAB ∠和BDC ∠的平分线AP 和DP 相交于点P ,∴,CAP BAP BDP CDP ∠=∠∠=∠,∵CAP C CDP P ∠+∠=∠+∠①,BAP P BDP B ∠+∠=∠+∠②,由-①②,得:C P P B ∠-∠=∠-∠,即()12P C B ∠=∠+∠,∵100,120B C ∠=︒∠=︒,∴()11001201102P ∠︒=︒︒=+;②∵11,33CAP CAB CDP CDB ∠=∠∠=∠,∴23BAP BAC ∠=∠,23BDP BDC ∠=∠,∵CAP C CDP P ∠+∠=∠+∠,BAP P BDP B ∠+∠=∠+∠,∴()111333C P BDC BAC BDC BAC ∠-∠=∠-∠=∠-∠,()222333P B BDC BAC BDC BAC ∠-∠=∠-∠=∠-∠,∴()2C P P B ∠-∠=∠-∠,∴()123P B C ∠=∠+∠),故答案为:()123P B C ∠=∠+∠.【点睛】本题考查了三角形内角和、有关角平分线的计算,解题的关键是灵活运用“8字形”求解.例4.(2023春·广东深圳·七年级统考期末)定理:三角形任意两边之和大于第三边.(1)如图1,线段AD ,BC 交于点E ,连接AB ,CD ,判断AD BC +与AB CD +的大小关系,并说明理由;(2)如图2,OC 平分AOB ∠,P 为OC 上任意一点,在OA ,OB 上截取OE OF =,连接PE ,PF .求证:PE PF =;(3)如图3,在ABC 中,AB AC >,P 为角平分线AD 上异于端点的一动点,求证:PB PC BD CD ->-.【答案】(1)AD BC AB CD +>+;理由见详解(2)证明见详解(3)证明见详解【分析】(1)根据三角形任意两边之和大于第三边知,AE BE AB +>,CE ED CD +>,两式相加即可得出结论;(2)根据SAS 证OEP OFP △≌△即可得出结论;(3)在AB 上取一点E ,使AE AC =,连接DE 交BP 于点F ,证APE APC ≌,即PC PE =,同理证CD DE =,然后同理(1)得PB CD PC BD +>+,变形不等式即可得出结论.【详解】(1)解:AD BC AB CD +>+,理由如下:AE BE AB +> ,CE ED CD +>,AE BE CE ED AB CD ∴+++>+,即AD BC AB CD +>+;(2)证明:OC 平分AOB ∠,EOP FOP ∴∠=∠,在OEP 和OFP △中,OE OF EOP FOP OP OP =⎧⎪∠=∠⎨⎪=⎩,()OEP OFP SAS ∴ ≌,PE PF ∴=;(3)证明:在AB 上取一点E ,使AE AC =,连接DE 交BP 于点F,AD 是BAC ∠的角平分线,EAP CAP ∴∠=∠,在APE V 和APC △中,AE AC EAP CAP AP AP =⎧⎪∠=∠⎨⎪=⎩,()APE APC SAS ∴ ≌,PE PC ∴=,同理可证DE DC =,EF PF EP +> ,BF FD BD +>,EF PF BF FD EP BD ∴+++>+,即PB DE EP BD +>+,PB CD PC BD ∴+>+,PB PC BD CD ∴->-.【点睛】本题主要考查三角形的综合题,熟练掌握三角形的三边关系和全等三角形的判定和性质等知识是解题的关键.例5.(2023春·江苏苏州·七年级校联考期中)阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论A B C D ∠+∠=∠+∠.我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论AOC A C P ∠=∠+∠+∠.(1)直接利用上述基本图形中的任意一种,解决问题:如图2,AP 、CP 分别平分BAD ∠、BCD ∠,说明:()12P B D ∠=∠+∠.(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:①如图3,直线AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠,若30B ∠=︒,20D ∠=︒,求P ∠的度数.②在图4中,AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠,猜想P ∠与B ∠、D ∠的关系(直接写出结果,无需说明理由).③在图5中,AP 平分BAD ∠,CP 平分BCD ∠的外角BCE ∠,猜想P ∠与B ∠、D ∠的关系(直接写出结果,无需说明理由).【答案】(1)见解析(2)①25︒;②()11802P B D ∠=︒-∠+∠;③()190+2P B D ∠=︒∠+∠【分析】(1)根据角平分线的定义可得1234∠=∠∠=∠,,再根据题干的结论列出3214P ABC P ADC ∠+∠=∠+∠∠+∠=∠+∠,,相加得到22314P ABC ADC ∠+∠+∠=∠+∠+∠+∠,继而得到2P ABC ADC ∠=∠+∠,即可证明结论;(2)①如图所示,分作BAD BCD ∠∠,的角平分线交于H ,根据(1)的结论得到()1252H B D ∠=∠+∠=︒,再由角平分线的定义和平角的定义证明90PCH ∠=︒,90PAH ∠=︒,再根据题干的结论可推出25P H ==︒∠∠;②如图所示,分作BAD BCD ∠∠,的角平分线交于H ,由(1)的结论可知()12H B D ∠=∠+∠,,同理可得90PCH ∠=︒,90PAH ∠=︒,则由四边形内角和定理可得()11802P B D ∠=︒-∠+∠;③由题干的结论可得P B BAP BCP =++∠∠∠∠,由角平分线的定义得到1122BAP BAO BCP BCE ==∠,∠,再求出1902BCP BCD =︒-∠,由题干的结论可知B BAO D BCD +=+∠∠∠∠,由此可得()1902P B BAP BCP B D =++=︒++∠∠∠∠∠∠.【详解】(1)解:∵AP CP 、分别平分BAD BCD ∠∠、,∴1234∠=∠∠=∠,,∴2314∠+∠=∠+∠,由题干的结论得:32P ABC ∠+∠=∠+∠,∠14P ADC +∠=∠+∠,∴21324P ABC ADC ∠+∠+∠=∠+∠+∠+∠,∴2P ABC ADC ∠=∠+∠,∴()12P ABC ADC ∠=∠+∠,即()12P B D ∠=∠+∠;(2)解:①如图所示,分作BAD BCD ∠∠,的角平分线交于H ,由(1)的结论可知()1252H B D ∠=∠+∠=︒,∵PC HC ,分别平分BCE BCD ∠,∠,∴1122BCP BCE BCH BCD ==∠,∠,∵180BCD BCE ∠+∠=︒∴119022BCP BCH BCD BCE +=+=︒∠∠∠∠,∴90PCH ∠=︒,同理可得90PAH ∠=︒,由题干的结论可得P PAH H PCH +=+∠∠∠∠,∴25P H ==︒∠∠;②如图所示,分作BAD BCD ∠∠,的角平分线交于H ,由(1)的结论可知()12H B D ∠=∠+∠,,同理可得90PCH ∠=︒,90PAH ∠=︒,∴()13601802P PAH PCH H B D =︒---=︒-+∠∠∠∠∠∠;③由题干的结论可得P B BAP BCP =++∠∠∠∠,∵AP 平分BAD ∠,CP 平分BCD ∠的外角BCE ∠,∴1122BAP BAO BCP BCE ==∠∠,∠∠,∵180BCE BCD =︒-∠∠,∴1902BCP BCD =︒-∠∠,由题干的结论可知B BAO D BCD +=+∠∠∠∠,∴BAO D BCD B =+-∠∠∠∠,∴P B BAP BCP =++∠∠∠∠119022B BAO BCD =++︒-∠∠1111902222B D BCD B BCD =++-+︒-∠∠∠∠()1902B D =︒++∠∠.【点睛】本题考查了三角形的内角和定理,角平分线的定义,多边形内角和定理,准确识图并运用好“8”字形的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.模型2、“A ”字模型结论:①∠3+∠4=∠D +∠E ;②∠1+∠2=∠A +180°。
2024年中考数学几何模型(全国通用):三角形中的导角模型飞镖模型、风筝模型、角内翻模型(原卷版)
专题02三角形中的导角模型-飞镖模型、风筝模型、角内翻模型近年来各地中考中常出现一些几何导角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题就飞镖型、风筝模型进行梳理及对应试题分析,方便掌握。
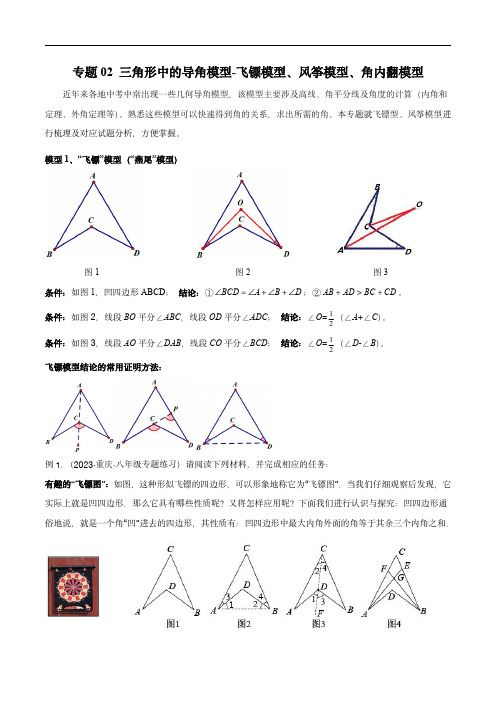
模型1、“飞镖”模型(“燕尾”模型)图1图2图3条件:如图1,凹四边形ABCD;结论:①BCD A B D;②AB AD BC CD。
(∠A+∠C)。
条件:如图2,线段BO平分∠ABC,线段OD平分∠ADC;结论:∠O=12条件:如图3,线段AO平分∠DAB,线段CO平分∠BCD;结论:∠O=1(∠D-∠B)。
2飞镖模型结论的常用证明方法:例1.(2023·重庆·八年级专题练习)请阅读下列材料,并完成相应的任务:有趣的“飞镖图”:如图,这种形似飞镖的四边形,可以形象地称它为“飞镖图”.当我们仔细观察后发现,它实际上就是凹四边形.那么它具有哪些性质呢?又将怎样应用呢?下面我们进行认识与探究:凹四边形通俗地说,就是一个角“凹”进去的四边形,其性质有:凹四边形中最大内角外面的角等于其余三个内角之和.A.19 B.20例4.(2023·广东·八年级期中)如图,在三角形ABC 中,AB AC BC ,为三角形内任意一点,连结AP ,并延长交BC 于点D .求证:(1)AB AC AD BC ;(2)AB AC AP BP CP . AB D CP 探究:(1)观察“箭头四角形”,试探究BDC 与A 、B 、C 之间的关系,并说明理由;应用:(2)请你直接利用以上结论,解决以下两个问题:①如图2,把一块三角尺XYZ 放置在ABC 上,使三角尺的两条直角边XY 、XZ 恰好经过点B 、则ABX ACX ;②如图o 3,ABE 、ACE 的2等分线(即角平分线)BF 点F ,若60BAC ,130BEC ,求BFC 的度数;模型2、风筝模型(鹰爪模型)图1图21)风筝(鹰爪)模型:结论:∠A +∠O =∠1+∠2;2)风筝(鹰爪)模型(变形):结论:∠A +∠O=∠2-∠1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录将军饮马模型 (3)模型1:直线与两定点 (3)模型2/角与定点 (10)模型3两定点一定长 (15)第十二章辅助圆 (20)模型1 共端点,等线段模型 (20)模型2 直角三角形共斜边模型 (23)半角模型 (32)模型实例 (33)8字模型与飞镖模型 (50)模型1:角的8字模型 (50)模型2:角的飞镖模型 (54)模型3 边的“8”字模型 (57)模型4 边的飞镖模型 (58)中点四大模型 (63)模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 (63)模型2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (66)模型3 已知三角形一边的中点,可考虑中位线定理 (71)模型4 已知直角三角形斜边中点,可以考虑构造斜边中线 (78)二次函数 (85)圆中的辅助线 (91)模型1 连半径构造等腰三角形 (91)模型2 构造直角三角形 (94)模型3 与圆的切线有关的辅助线 (100)相似模型 (111)模型1:A、8模型 (111)模型2 共边共角型 (116)模型3 一线三等角型 (121)模型4 倒数型 (127)模型5 与圆有关的简单相似 (132)模型6 相似和旋转 (136)1.2空间几何体的三视图和直观图 (145)1.3 空间几何体的表面积与体积 (145)手拉手模型 (147)模型手拉手 (147)三垂直全等模型 (158)模型三垂直全等模型 (158)蚂蚁行程 (170)模型立体图形展开的最短路径 (170)截长补短辅助线模型 (180)模型:截长补短 (180)角平分线四大模型 (192)模型1 角平分线的点向两边作垂线 (192)模型2 截取构造对称全等 (194)模型3 角平分线+垂线构造等腰三角形 (198)模型4 角平分线+平行线 (200)将军饮马模型“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现. 模型1:直线与两定点模型 作法 结论lBA当两定点A 、B 在直线l 异侧时,在直线l 上找一点P ,使PA +PB 最小.lPAB连接AB 交直线l 于点P ,点P 即为所求作的点.PA +PB 的最小值为ABl AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA +PB 最小.lPB'AB作点B 关于直线l 的对称点B ', 连接AB '交直线l 于点P ,点P 即为所求作的点.PA +PB 的最小值为AB 'l AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA PB -最大. lPAB连接AB 并延长交直线l 于点P ,点P 即为所求作的点.PA PB -的最大值为ABlAB当两定点A 、B 在直线l 异侧时,在直线l 上找一点P ,使得PA PB -最大.lB'ABP作点B 关于直线I 的对称点B ',连接AB '并延长交直线l 于点P ,点P 即为所求作的点.PA PB -的最大值为AB 'l AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA PB -最小. lPAB连接AB ,作AB 的垂直平分线交直线l 于点P ,点P 即为所求作的点.PA PB -的最小值为0模型实例例1:如图,正方形ABCD 的面积是12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,则PD +PE 最小值是 .EBC ADP解答:如图所示,∵点B 与点D 关于AC 对称,∴当点P 为BE 与AC 的交点时,PD +PE 最小,且线段BE 的长. ∵正方形ABCD 的面积为12,∴其边长为3∵△ABE 为等边三角形,∴BE =AB =23.∴PD +PE 的最小值为3例2:如图,已知△ABC 为等腰直角三角形,AC =BC =4,∠BCD =15°,P 为CD 上的动点,则PA PB的最大值是多少?DPPA'B解答:如图所示,作点A 关于CD 的对称点A ′,连接A ′C ,连接A ′B 并延长交CD 于点P ,则点P 就是PA PB -的值最大时的点,PA PB -=A ′B .∵△ABC 为等腰直角三角形,AC =BC 等于4,∴∠ACB =90°. ∵∠BCD =15°,∴∠ACD =75°.∵点A 、A ′关于CD 对称,∴AA ′⊥CD ,AC =CA ′, ∵∠ACD =∠DCA ′=75°,∴∠BCA ′=60°.∵CA ′=AC =BC =4,∴△A ′BC 是等边三角形,∴A ′B =BC =4.∴PA PB -的最大值为4. 练习1.如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上一动点,则EC +ED 的最小值是 .DACB E解:解:过点C 作CO ⊥AB 于O ,延长CO 到C ',使O C '=OC ,连接D C ',交AB 于E ,连接C 'B ,此时DE+CE=DE+E C '=D C '的值最小.连接B C ',由对称性可知∠C 'BE=∠CBE=45°,∴∠CB C '=90°,∴B C '⊥BC , ∠BC C '=∠B C 'C=45°,∴BC=B C '=2,∵D 是BC 边的中点,∴BD=1, 根据勾股定理可得:D C '5EC+ED 5 2.如图,点C 的坐标为(3,y ),当△ABC 的周长最短时,求y 的值.xyB (2,0)A (0,3)O解:解:(1)作A 关于x=3的对称点A ′,连接A ′B 交直线x=3与点C . ∵点A 与点A ′关于x=3对称,∴AC=A ′C .∴AC+BC=A ′C+BC .当点B 、C 、A ′在同一条直线上时,A ′C+BC 有最小值,即△ABC 的周长有最小值. ∵点A 与点A ′关于x=3对称,∴点A ′的坐标为(6,3).设直线BA ′的解析式y=kx+b ,将点B 和点A ′的坐标代入得:k =34,b =−32. ∴y=34x-32. 将x=3代入函数的解析式,∴y 的值为343.如图,正方形ABCD 中,AB =7,M 是DC 上的一点,且DM =3,N 是AC 上的一动点,求|DN -MN |的最小值与最大值.C A N解:解:当ND=NM时,即N点DM的垂直平分线与AC的交点,|DN-MN|=0,因为|DN-MN|≤DM,当点N运动到C点时取等号,此时|DN-MN|=DM=3,所以|DN-MN|的最小值为0,最大值为3PB OAQ点P 、Q 在∠AOB 内部,在OB 边上找点D ,OA 边上找点C ,使得四边形PQDC 周长最小.分别作点P 、Q 关于OA 、OB 的对称点P ′、Q ′,连接P ′Q ′,分别交OA 、OB 于点C 、D ,点C 、D 即为所求.PC +CD +DQ 的最小值为P ′Q ′,所以四边形PQDC 周长的最小值为PQ +P ′Q ′模型实例如图,∠AOB=30°,∠AOB 内有一定点P ,且10OP =.在OA 上有一点Q ,OB 上 一点R .若立△PQR 周长最小,则最小周长是多少?解答如图,作点P 分别关于OA 、OB 的对称点E 、F ,连接EF ,分别交OA 、OBAPOB 于点Q 、R ,连接OE 、OF 、PE 、PF .EQ OP =,FR RP =.△PQR 的周长的最小值为EF 的长.由对称性可得∠EOQ=∠POQ ,∠FOR=∠POR , ∠EOF=2∠AOB=60°. △EOF 是正三角形.10EF OE OP ===.即△PQR 周长最小值为10.模型2/角与定点 1.已知,40MON°?,P 为MON Ð内一定点,A 为OM 上的点,B 为ON 上的点,当△PAB 的周长取最小值时: (1)找到A 、B 点,保留作图痕迹;(2)求此时APB Ð等于多少度.如果∠MON =θ,∠APB 又等于多少度?ONMP1.解答(1)做点P 分别关于OM ON 、的对称点E F 、,连接EF 分别交OM ON 、于点A B 、.点A B 、即为所求,此时△PAB 的周长最小.(2)∵点E 与点P 关于直线OM 对称,点F 与点P 关于ON 对称, ∴∠E =∠APE ,∠F =∠BPF ,∠CPD =180°-∠MON =140°. ∴在△EFP 中,∠E +∠F =180°-140°=40°,∴∠CPA +∠BPD =40°.∴∠APB =100°.如果∠MON =θ, ∴∠CPD =180°-θ,∠E +∠F =θ. 又∵∠PAB =2∠E ,∠PBA =2∠F ∴∠PAB +∠PBA =2(∠E +∠F )=2θ ∴∠APB =180°-2θ.ONE2.如图,四边形中ABCD ,110BAD °?,90B D °??,在BC 、CD 上分别找 一点M 、N ,使△AMN 周长最小,并求此时+AMN ANM ∠∠的度数.A D BMN2.解答如图,作点A 关于BC 的对称点A ',关于CD 的对称点A '',连接A A '''与BC 、CD 的交点即为所求的点M 、N .此时△AMN 周长最小. ∵∠BAD =110°,∴∠A '+∠A ''=180°-110°=70°. 由轴对称的性质得:∠A '=∠A AM ',∠A ''=∠A AN '', ∴∠AMN +∠ANM =2(∠A '+∠A '')=2×70°=140°.3.如图,在x 轴上找一点C ,在y 轴上找一点D ,使AD CD BC ++最小,并求直 线CD 的解析式及点C 、D 的坐标.3.解答作点A关于y轴的对称点A',点B关于x轴的对称点B',连接A B''分别交x轴、y轴于点C、D,此时AD CD BC++最小.由对称性可知A'(-1,3),B'(3,-1).易求得直线A B''的解析式为2=-+.y xy x=-+,即直线CD的解析式2当0x=,∴点C坐标为(2,0).y=时,2当0x=时,2y=,∴点D坐标为(0,2).4.如图,20MON°?,A、B占分别为射线OM、ON上两定点,且2OB=,OA=,4点P、Q分别为射线OM、ON上两动点,当P、Q运动时,线段AQ PQ PB++的最小值是多少?ONB4.解答作A 点关于ON 的对称点A ',点B 关于OM 的对称点B ',连接A B '',分别交OM ON 、于点P Q 、,连接OA '、OB '.则AQ PQ PB A Q PQ PB A B ''''++=++=,此时AQ PQ PB ++最小. 由对称可知,PB PB '=,AQ A Q '=,2OA OA '==,4OB OB '==,20MOB NOA MON ''∠=∠=∠=︒. 60A OB ''∠=︒.作A D '⊥OB '于点D , 在Rt △ODA '中, ∴1OD =,A D '=∴413B D '=-=,A B ''=∴AQ PQ PB ++的最小值是模型3两定点一定长模型作法结论如图,在直线l上找M、N两点(M在左),使得AM+MN+NB 最小,且MN=d. 将A向右平移d个单位到A′,作A′关于l的对称点A",连接A"B与直线l交于点N,将点N向左平移d个单位即为M,点M,N即为所求.AM+MN+NB的最小值为A"B+dBAlM NA′A"BAld如图,l1∥l2,l1、l2间距离为d,在l1、l2分别找M、N两点,使得MN⊥l1,且AM+MN+NB最小.将A向下平移d个单位到A,连接A′B交直线l2于点N,过点N作MN⊥l1,连接AM.点M、N即为所求.AM+MN+NB的最小值为A'B+d.例题:在平面直角坐标系中,矩形OABC如图所示,点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,求点E的坐标.解答:如图,将点D向右平移2个单位得到D'(2,2),作D'关于x轴的对称点D"(2,-2),连接BD"交x轴于点F,将点F向左平移2个单位到点E,此时点E和点F为所求作的点,且四边形BDEF周长最小.理由:ABl2l1A′NMABl2l1∵四边形BDEF 的周长为BD +DE +EF +BF ,BD 与EF 是定值. ∴BF +DE 最小时,四边形BDEF 周长最小, ∵BF +ED =BF +FD '=BF +FD "=BD "设直线BD "的解析式为y =kx +b ,把B (6,4),D "(2,-2)代入,得6k +b =4,2k +b =-2,解得k =32,b =-5,∴直线BD "的解析式为y =32x -5.令y =0,得x =103,∴点F 坐标为(103,0).∴点E 坐标为(43,0).练习1.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,A (3,0),B (0,4),D 为边OB 的中点. (1)若E 为边OA 上的一个动点,求△CDE 的周长最小值;(2)若E 、F 为边OA 上的两个动点,且EF =1,当四边形CDEF 的周长最小时,求点E 、F 的坐标.解答:(1)如图,作点D 关于x 轴的对称点D ',连接CD '与x 轴交于点E ,连接DE ,由模型可知△CDE 的周长最小.∵在矩形OACB 中,OA =3,OB =4,D 为OB 的中点, ∴D (0,2),C (3,4),D '(0,-2).设直线CD '为y =kx +b ,把C (3,4),D '(0,-2)代入, 得3k +b =4,b =-2,解得k =2,b =-2, ∴直线CD '为y =2x -2. 令y =0,得x =1, ∴点E 的坐标为(1,0). ∴OE =1,AE =2. 利用勾股定理得CD =13,DE =5,CE =25,∴△CDE 周长的最小值为13+35.(2)如图,将点D 向右平移1个单位得到D '(1,2),作D '关于x 轴的对称点D ″(1,-2),连接CD ″交x 轴于点F ,将点F 向左平移1个单位到点E ,此时点E 和点F 为所求作的点,且四边形CDEF 周长最小.理由:∵四边形CDEF 的周长为CD +DE +EF +CF ,CD 与EF 是定值,∴DE +CF 最小时,四边形BDEF 周长最小,∴DE +CF =D 'F +CF =FD ″+CF =CD ″, 设直线CD ″的解析式为y =kx +b ,把C (3,4),D (1,-2)代入,得3k +b =4,k +b =-2,解得k =3,b =-5.∴直线CD ″的解析式为y =3x -5, 令y =0,得x =53,∴点F 坐标为(53,0),∴点E 坐标为(23,0).2.村庄A和村庄B位于一条小河的两侧,若河岸彼此平行,要架设一座与河岸垂直的桥,桥址应如何选择,才使A与B之间的距离最短?解答:设l1和l2为河岸,作BD⊥l2,取BB'等于河宽,连接AB'交l1于C1,作C1C2⊥l2于C2,则A→C1→C2→B为最短路线,即A与B之间的距离最短.AB l2 l1第十二章 辅助圆模型1 共端点,等线段模型图①O AC B图②BOC A图③OABC如图①,出现“共端点,等线段”时,可利用圆定义构造辅助圆.如图②,若OA =OB =OC ,则A 、B 、C 三点在以O 为圆心,OA 为半径的圆上.如图③,常见结论有:∠ACB =12∠AOB ,∠BAC =12∠BOC .模型分析∵OA =OB =OC .∴A 、B 、C 三点到点O 的距离相等.∴A 、B 、C 三点在以O 为圆心,OA 为半径的圆上. ∵∠ACB 是»AB 的圆周角,∠AOB 是»AB 的圆心角,∴∠ACB =12∠AOB .同理可证∠BAC =12∠BOC .(1)若有共端点的三条线段,可考虑构造辅助圆. (2)构造辅助圆是方便利用圆的性质快速解决角度问题. 模型实例如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.求证:∠1+∠2=90°.21 B C DA证明证法一:如图①,∵AB=AC=AD.∴B、C、D在以A为圆心,AB为半径的⊙A上.∴∠ABC=∠2. 在△BAC中,∵∠BAC+∠ABC+∠2=180°,∴2∠1+2∠2=180°.∴∠1+∠2=90°.证法二:如图②,∵AB=AC=AD.∴∠BAC=2∠1.∵AB=AC,∴B、C、D在以A为圆心,AB为半径的⊙O上.延长BA与圆A相交于E,连接CE.∴∠E=∠1.(同弧所对的圆周角相等.)∵AE=AC,∴∠E=∠ACE.∵BE为⊙A的直径,∴∠BCE=90°.∴∠2+∠ACE=90°.∴∠1+∠2=90°.图①21CDAB小猿热搜1.如图,△ABC 为等腰三角形,AB =AC ,在△ABC 的外侧作直线AP ,点B 与点 D 关于AP 轴对称,连接BD 、CD ,CD 与AP 交于点E .求证:∠1=∠2.12PBACE DA D21PE CB证明∵A 、D 关于AP 轴对称,∴AP 是BD 的垂直平分线. ∴AD =AB ,ED =EB .又∵AB =AC .∴C 、B 、D 在以A 为圆心,AB 为半径的圆上.∵ED =EB ,∴∠EDB =∠EBD . ∴∠2=2∠EDB .又∵∠1=2∠CDB . ∴∠1=∠2.2.己知四边形ABCD ,AB ∥CD ,且AB =AC =AD =a ,BC =b ,且2a >b ,求BD 的长.A CBDBCEDA解答以A 为圆心,以a 为半径作圆,延长BA 交⊙A 于E 点,连接ED . ∵AB ∥CD ,∴∠CAB =∠DCA ,∠DAE =∠CDA . ∵AC =AD , ∴∠DCA =∠CDA . ∴∠DAE =∠CAB .在△CAB 和△DAE 中. AD AC DAE CAB AE AB =⎧⎪∠=∠⎨⎪=⎩∴△CAB ≌△DAE . ∴ED =BC =b ∵BE 是直径,∴∠EDB =90°. 在Rt △EDB 中,ED =b ,BE =2a , ∴BD模型2 直角三角形共斜边模型模型分析如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边中线等于斜边一半,可得:OC=OD=OA=OB,∴A、B、C、D四点共圆.(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;(2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.模型实例例1 如图,AD、BE、CF为△ABC的三条高,H为垂线,问:(1)图中有多少组四点共圆?(2)求证:∠ADF=∠ADE.解答(1)6组①C、D、H、E四点共圆,圆心在CH的中点处;②D、B、F、H四点共圆,圆心在BH的中点处;③A、E、H、F四点共圆,圆心在AH的中点处;④C、B、F、E四点共圆,圆心在BC的中点处;⑤B、A、E、D四点共圆,圆心在AB的中点处;⑥C、D、F、A四点共圆,圆心在AC的中点处.(2)如图,由B、D、H、F四点共圆,得∠ADF=∠1.同理:由A、B、D、E四点共圆,得∠ADE=∠1.∴∠ADF=∠ADE.例2 如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F,求证:FE=DE.解答如图,连接DB、DF.∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,∴∠CBF=45°,∠DBC=45°,∴∠DBF=90°.又∵∠DEF=90°,∴D、E、B、F四点共圆.∴∠DFE=∠DBE=45°(同弧所对的圆周角相等).∴△DEF是等腰直角三角形.∴FE=DE.P1.如图,锐角△ABC中,BC.CE是高线,DG⊥CE于G,EF⊥BD于F,求证:FG BCB证明:由于Rt△BCE与Rt△BCD共斜边BC,∴B、C、D、E四点共圆.∴∠DBC=∠DEG,同理,Rt∠EDF与Rt△DGE共斜边DE,∴D、E、F、G四点共圆.于是∠DEG=∠DFG,因此,∠DBC=∠DFG.于是FG∥BC2. 如图,BE.CF为△ABC的高,且交于点H,连接AH并延长交于BC于点D,求证:AD⊥BC.HEFB C3.如图,等边△PQR内接于正方形ABCD,其中点P,Q,R分别在边AD,AB,DC上,M是QR 的中点.求证:不论等边△PQR怎样运动,点M为不动点.RQA4.如图,已知△ABC 中,AH 是高,AT 是角平分线,且TD ⊥AB,TE ⊥AC.求证:∠AHD=∠AHE.EHDBC补充:半角模型已知如图:①∠2=12∠AOB;②OA=OB.OAB EF123连接FB,将△FOB绕点O旋转至△FOA的位置,连接F′E,FE,可得△OEF≌△OEF′4321F'FE BAO模型分析∵△OBF≌△OAF′,∴∠3=∠4,OF=OF′.∴∠2=12∠AOB,∴∠1+∠3=∠2∴∠1+∠4=∠2又∵OE是公共边,∴△OEF ≌△OEF ′.(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; (3)常见的半角模型是90°含45°,120°含60°. 模型实例例1 已知,正方形ABCD 中,∠MAN=45°,它的两边分别交线段CB 、DC 于点M 、N . (1)求证:BM+DN=MN .(2)作AH ⊥MN 于点H ,求证:AH=AB .证明:(1)延长ND 到E ,使DE=BM , ∵四边形ABCD 是正方形,∴AD=AB . 在△ADE 和△ABM 中, ⎪⎩⎪⎨⎧=∠=∠=BM DE B ADE ABAD∴△ADE ≌△ABM .∴AE=AM ,∠DAE=∠BAM∵∠MAN=45°,∴∠BAM+∠NAD=45°. ∴ ∠MAN=∠EAN=45°. 在△AMN 和△AEN 中, ⎪⎩⎪⎨⎧=∠=∠=AN AN EAN M AN EA M A∴△AMN ≌△AEN . ∴MN=EN .∴BM+DN=DE+DN=EN=MN .(2)由(1)知,△AMN ≌△AEN . ∴S △AMN =S △AEN .即EN AD 21MN AH 21⋅=⋅.又∵MN=EN , ∴AH=AD . 即AH=AB .例2 在等边△ABC的两边AB、AC上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在线段AB、AC上移动时,BM、NC、MN之间的数量关系.(1)如图①,当DM=DN时,BM、NC、MN之间的数量关系是_______________;(2)如图②,当DM≠DN时,猜想(1)问的结论还成立吗?写出你的猜想并加以证明.图①图②解答(1)BM、NC、MN之间的数量关系是BM+NC=MN.(2)猜想:BM+NC=MN.证明:如图③,延长AC至E,使CE=BM,连接DE.∵BD=CD,且∠BDC=120°,∴∠DBC=∠DCB=30°.又∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∴∠MBD=∠NCD=90°.在△MBD与△ECD中,∵DB=DC,∠DBM=∠DCE=90°,BM=CE,∴△MBD≌△ECD(SAS).∴DM=DE,∠BDM=∠CDE.∴∠EDN=∠BDC-∠MDN=60°.在△MDN和△EDN中,∵MD=ED,∠MDN=∠EDN=60°,DN=DN,∴△MDN≌△EDN(SAS).∴MN=NE=NC+CE=NC+BM.图③例3 如图,在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是BC、CD延长线上的点,且∠EAF=21∠BAD .求证:EF=BE-FD .证明:在BE 上截取BG ,使BG=DF ,连接AG . ∵∠B+∠ADC=180°,∠ADF+∠ADC=180°, ∴∠B=∠ADF . 在△ABG 和△ADF 中, ⎪⎩⎪⎨⎧=∠=∠=DF BG ADF B AD AB∴△ABG ≌△ADF (SAS ). ∴∠BAG=∠DAF ,AG=AF . ∴∠GAF=∠BAD . ∴∠EAF=21∠BAD=21∠GAF . ∴∠GAE=∠EAF . 在△AEG 和△AEF 中,⎪⎩⎪⎨⎧=∠=∠=AE AE FAE GAE AF AG∴△AEG ≌△AEF (SAS ). ∴EG=EF . ∵EG=BE-BG , ∴EF=BE-FD .跟踪练习:1.已知,正方形ABCD ,M 在CB 延长线上,N 在DC 延长线上,∠MAN=45°. 求证:MN=DN-BM .【答案】证明:如图,在DN 上截取DE=MB ,连接AE , ∵四边形ABCD 是正方形, ∴AD=AB ,∠D=∠ABC=90°. 在△ABM 和△ADE 中, ⎪⎩⎪⎨⎧=∠=∠=DE BM ABM D AB AD∴△ABM ≌△ADE .∴AM=AE , ∠MAB=∠EAD . ∵∠MAN=45°=∠MAB+∠BAN , ∴∠DAE+∠BAN=45°.∴∠EAN=90°-45°=45°=∠MAN . 在△AMN 和△AEN 中, ⎪⎩⎪⎨⎧=∠=∠=AN AN EAN M AN AE AM∴△ABM ≌△ADE . ∴MN=EN . ∵DN-DE=EN . ∴DN-BM=MN .2.已知,如图①在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°,探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D使问题得到解决.请你参考小明的思路探究并解决以下问题:(1)猜想BD、DE、EC三条线段之间的数量关系式,并对你的猜想给予证明;(2)当动点E在线段BC上,动点D运动到线段CB延长线上时,如图②,其他条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明.图①图②【答案】解答:(1)猜想:DE2=BD2+EC2.证明:将△AEC绕点A顺时针旋转90°得到△ABE′,如图①∴△ACE≌△ABE′.∴BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB.在Rt△ABC中,∵AB=AC,∴∠ABC=∠ACB=45°.∴∠ABC+∠ABE′=90°,即∠E′BD=90°.∴E′B2+BD2=E′D2.又∵∠DAE=45°,∴∠BAD+∠EAC=45°.∴∠E′AB+∠BAD=45°,即∠E′AD=45°.∴△AE′D≌△AED.∴DE=DE′.∴DE2=BD2+EC2.图①(2)结论:关系式DE2=BD2+EC2仍然成立.证明:作∠FAD=∠BAD,且截取AF=AB,连接DF,连接FE,如图②∴△AFD≌△ABD.∴FD=DB,∠AFD=∠ABD.又∵AB=AC,∴AF=AC.∵∠FAE=∠FAD+∠DAE=∠FAD+45°,∠EAC=∠BAC-∠BAE=90°-(∠DAE-∠DAB )=90°-(45°-∠DAB)=45°+∠DAB,∴∠FAE=∠CAE.又∵AE=AE,∴△AFE≌△ACE.∴FE=EC,∠AFE=∠ACE=45°.∠AFD=∠ABD=180°-∠ABC=135°.∴∠DFE=∠AFD-∠AFE=135°-45°=90°.在Rt△DFE中,DF2+FE2=DE2.即DE2=BD2+EC2.图②3.已知,在等边△ABC中,点O是边AC、BC的垂直平分线的交点,M、N分别在直线AC、BC上,且∠MON=60°.(1)如图①,当CM=CN时,M、N分别在边AC、BC上时,请写出AM、CN、MN 三者之间的数量关系;(2)如图②,当CM≠CN时,M、N分别在边AC、BC上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3)如图③,当点M在边AC上,点N在BC的延长线上时,请直接写出线段AM、CN、MN三者之间的数量关系.图①图②图③【答案】结论:(1)AM=CN+MN;如图①图①(2)成立;证明:如图②,在AC上截取AE=CN,连接OE、OA、OC.∵O是边AC、BC垂直平分线的交点,且△ABC为等边三角形,∴OA=OC,∠OAE=∠OCN=30°,∠AOC=120°.又∵AE=CN,∴△OAE≌△OCN.∴OE=ON,∠AOE=∠CON.∴∠EON=∠AOC=120°.∵∠MON=60°,∴∠MOE=∠MON=60°.∴△MOE≌△MON.∴ME=MN.∴AM=AE+ME=CN+MN.图②(3)如图③,AM=MN-CN.图③4.如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E、F分别是线段BC、CD上的1∠BAD.点,且BE+FD=EF.求证:∠EAF=2【答案】证明:如图,把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG,AD旋转到AB,AF旋转到AG,∴AG=AF ,BG=DF ,∠ABG=∠D ,∠BAG=∠DAF . ∵∠ABC+∠D=180°, ∴∠ABC+∠ABG=180°. ∴点G 、B 、C 共线. ∵BE+FD=EF , ∴BE+BG=GE=EF . 在△AEG 和△AEF 中, ⎪⎩⎪⎨⎧===EF EG AE AE AF AG ∴△AEG ≌△AEF . ∴∠EAG=∠EAF . ∴∠EAB+∠BAG=∠EAF . 又∵∠BAG=∠DAF , ∴∠EAB+∠DAF=∠EAF . ∴∠EAF=21∠BAD .5.如图①,已知四边形ABCD,∠EAF的两边分别与DC的延长线交于点F,与CB的延长线交于点E,连接EF.(1)若四边形ABCD为正方形,当∠EAF=45°时,EF与DF、BE之间有怎样的数量关系?(只需直接写出结论)(2)如图②,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=1∠BAD2时,EF与DF、BE之间有怎样的数量关系?请写出结论并证明.(3)在(2)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结论)解答:(1)EF=DF-BE(2)EF=DF-BE证明:如图,在DF上截取DM=BE,连接AM,∵∠D+∠ABC=∠ABE+∠ABC=180°∵D=ABE∵AD=AB在△ADM 和△ABE 中,DM BE D ABE AD AB =⎧⎪∠=∠⎨⎪=⎩∴△ADM ≌△ABE∴AM=AE ,∠DAM=∠BAE∵∠EAF=∠BAE+∠BAF=12∠BAD , ∴∠DAM+∠BAF=12∠BAD ∴∠MAF=12∠BAD ∴∠EAF=∠MAF 在△EAF 和△MAF 中AE AM EAF MAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△MAF ∴EF=MF∵MF=DF-DM=DF-BE , ∴EF=DF-BE (3)∵EF=DF-BE∴△CEF 的周长=CE+EF+FC=BC+BE+DC+CF-BE+CF=BC+CD+2CF=158字模型与飞镖模型模型1:角的8字模型如图所示,AC、BD相交于点O,连接AD、BC.结论:∠A+∠D=∠B+∠C.ADOCB模型分析证法一:∵∠AOB是△AOD的外角,∴∠A+∠D=∠AOB.∵∠AOB是△BOC的外角,∴∠B+∠C=∠AOB.∴∠A+∠D=∠B+∠C.证法二:∵∠A+∠D+∠AOD=180°,∴∠A+∠D=180°-∠AOD.∵∠B+∠C+∠BOC=180°,∴∠B+∠C=180°-∠BOC.又∵∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.(1)因为这个图形像数字8,所以我们往往把这个模型称为8字模型.(2)8字模型往往在几何综合题目中推导角度时用到.模型实例观察下列图形,计算角度:。
