半导体物理第六章 pn结
合集下载
半导体物理作业(六)答案

两边杂质浓度为 N A = 1016 cm −3 , N D = 1020 cm −3 ,求温度 300K 时的势垒高度和势 垒宽度。
VD = kT N A N D 1016 × 10 20 0 . 026 ln = ln = 0.026 × ln 9.61168781× 1015 =0.9568 (V) 2 2 10 q ni 1.02 × 10
τp
半导体物理作业(六)
学号:
姓名:
4/6 页
(1.02 ×10 ) =
9 × 10
14
10 2
× 1.602 × 10 −19 ×
0.026 × 460 =6.40×10-11(A/cm2) −6 10
.3 ⎛ qV ⎞ ⎛ 0.0026 ⎞ -6 2 kT ⎜ ⎟ ⎜ 3) J = J s ⎜ e − 1⎟ = 0.16 × ⎜ e − 1⎟ ⎟ =6.5×10 (A/cm ) ⎝ ⎠ ⎝ ⎠
qD p pn 0 Lp =
=
μ p N A μ nτ n N A μ pτ n 5 × 1017 × 460 × 1 = =508 = μ n N D μ pτ p N D μ nτ p 9 × 1014 × 550 × 1
q kTμ p
2) J s ≈
Dp kTμ p ni2 n2 n2 = i q = i q τp qτ p ND ND ND
qD p qDn n p0 + pn 0 Ln Lp
半导体物理作业(六)
学号:
姓名:
2/6 页
2. 若 N D = 5 ×1015 cm −3 , N A = 1017 cm−3 ,求室温下 Ge 突变 pn 结的 VD。(300K 时锗 的本征载流子浓度为 2.33×1013 cm-3) 解: VD =
半导体物理基础(6)PN结

外加电场与内建电场方向相反,削弱了内建电场,因而使势 垒两端的电势差由VD减小为(VD-Vf),相应地势垒区变薄。
XD
VD
(
q
2 r
0
)(
NA ND NAND
)
由于电场作用而使非平衡载流子进入半导体的过程称为-电注入
np0
nn0
Space charge region
Diffusion region
1. Alloyed Junctions (合金结)
合金温度
降温再结晶
2. Diffused Junctions (扩散结)
Conceptual example of the use of photolithography to form a pn junction diode.
3. Ion Implantation (离子注入)
p x pn0e k0T
I-V characteristic of a p-n junction
现假设:
1. 势垒区的自由载流子全部耗尽,并忽略势垒区中 载流子的产生和复合。
2. 小注入:注入的少数载流子浓度远小于半导体中 的多数载流子浓度。在注入时,扩散区的漂移电场 可忽略。
(1) 正向偏置 ( Forward bias)
刚接触,扩散》漂移
内建电场
漂移 扩散=漂移
(达到动态平衡)
漂移运动
P型半导体
---- - - ---- - - ---- - - ---- - -
内电场E N型半导体 + +++++ + +++++ + +++++ + +++++
XD
VD
(
q
2 r
0
)(
NA ND NAND
)
由于电场作用而使非平衡载流子进入半导体的过程称为-电注入
np0
nn0
Space charge region
Diffusion region
1. Alloyed Junctions (合金结)
合金温度
降温再结晶
2. Diffused Junctions (扩散结)
Conceptual example of the use of photolithography to form a pn junction diode.
3. Ion Implantation (离子注入)
p x pn0e k0T
I-V characteristic of a p-n junction
现假设:
1. 势垒区的自由载流子全部耗尽,并忽略势垒区中 载流子的产生和复合。
2. 小注入:注入的少数载流子浓度远小于半导体中 的多数载流子浓度。在注入时,扩散区的漂移电场 可忽略。
(1) 正向偏置 ( Forward bias)
刚接触,扩散》漂移
内建电场
漂移 扩散=漂移
(达到动态平衡)
漂移运动
P型半导体
---- - - ---- - - ---- - - ---- - -
内电场E N型半导体 + +++++ + +++++ + +++++ + +++++
半导体物理 第六章 pn结

nn 0 1 ln ( EFn EFp ) n p 0 k0T
nn 0 1 ln ( EFn EFp ) n p 0 k0T
nn 0 N D , n p 0
ni NA
2
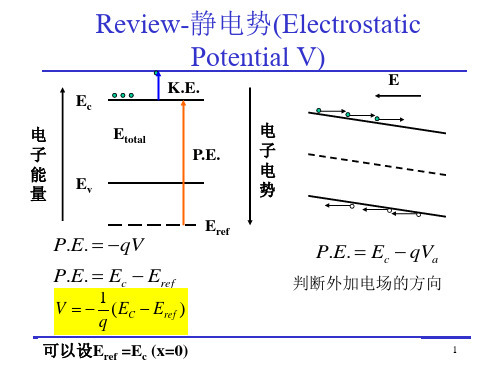
qVD=EFn-EFp
k0T nn 0 1 VD ( EFn EFp ) (ln ) q q n p0
6.1.4
VD称为pn结的接触电势差或内建 电势差. qVD为pn结的势垒高度. 平衡时pn结的费米能级处处 相等. qVD=EFn-EFp nn0、np0分别为平衡时n、p区 的电子浓度
EFn Ei nn 0 ni exp( ) k0T
n p 0 ni exp( EFp Ei k0T )
外加正向偏 压下,非平 衡少数载流 x p x 子在两边扩 qV 同理: n p ( x) n p 0 n p 0 [exp( ) 1] exp( ) 散区的分布 k0T Ln
xn x qV pn ( x) pn 0 pn 0 [exp( ) 1] exp( ) k0T Lp
正向偏移下,非平衡状态
N区电子扩散 向P区; P 区空穴扩散 向N区
PP’处电子浓度〉P区空穴浓度, 形成向P区的电子扩散流。
非平衡少子(电子或空穴)在扩散过程中, 不断与多子复合,直到复合完毕,这段 扩散过程称为扩散长度。
一定正向偏压下,单位时间从n区扩散到pp’边界的电子 浓度时一定的,并在p区形成稳定分布(空穴一样)。 非平衡载流子的电注入:正向偏压使非平衡载流子 进入半导体的过程。
产生漂移电流
6.1.3
电子从费米能级高的n区流 向费米能级低的p区, 空穴从p流到n区。
最后,Pn具有统一费米能级EF,
半导体物理_第六章_pn结

Jn dEF dx n n
qDp dEF J p p0 kT dx
电流密度与费米能级的关系 对于平衡的pn结,Jn, Jp均为零,因此,
Jp dEF dx p p
EF=常数
qDp dEF J p p0 kT dx
当电流密度一定时,载流子浓度大的地方, EF随 位置变化小,而载流子浓度小的地方, EF随位置 变化较大。
非平衡载流子的电注入:正向偏压使非平衡载流子进入半导 体的过程。
注入到p区的电子断与空穴复合,电子流不断转化 为空穴流,直到全部复合为止。
扩散电流〉漂移电流
根据电流连续性原理,通过pp’(或nn’)任何一个界 面的总电流是相等的。只是电子电流和空穴电流 的比例不同。 总电流=扩散电流+漂移电流
反向偏移下,非平衡状态 外加反向电场与内建势场方向一致。
1. pp’处注入的非平衡少数载流子浓度:
EFn Ei n p ni exp( ) k0T EFn EFP n p p p ni exp( ) k0T
2
p p ni exp(
Ei EFp k0T
)
在pp’边界处, x=-xp, qV=Efn-Efp,
qV n p ( x p ) p p ( x p ) ni exp( ) k0T
电子电势能-q V(x)由n到p不断升高 P区能带整体相对n区上移。n区能带整体相对p区下移。 直到具有统一费米能级 pn结费米能级处处相等标志pn结达到动态平衡,无扩散、 漂移电流流过。
动态平衡时
本征费米能级Ei的变化与-qV(x)一致
k0T n Dn q
k0T n Dn q
同理,空穴电流密度为:
qV x p ( ) 0 2. 加反向偏压下,如果qV>>k0T, e k0T
半导体物理第6章

非平衡载流子的电注入
在一定的正向偏压下,单位时间内从n区来到pp’处的非 平衡少子浓度是一定的,并在扩散区内形成一稳定的 分布。
在pp’处有一不变的向p区内部流动的电子扩散流。
同理,在边界nn’处也有一不变的向n区内部流动的空穴 扩散流。
当增大偏压时,势垒降得更低,增大了流入p区的电子 流和流入n区的空穴流
,
qVD E Fn E Fp
对于非简并半导体,n区和p区的平衡电子浓度
nn 0 E Fn Ei ni exp( ) k 0T
n p 0 ni exp( E Fp E i k 0T )
两式相除取对数得
nn 0 1 ln ( E Fn E Fp ) n p 0 k 0T
x
p
n
线性缓变结 N D N A j ( x x j ), j 杂质浓度梯度
6.1.2 空间电荷区
半导体中载流子有扩散运动和漂移运动两种运 动方式。 载流子在电场作用下的定向运动称为漂移运动. 在半导体中,如果载流子浓度分布不均匀,因 为浓度差,载流子将会从浓度高的区域向浓度 低的区域运动,这种运动称为扩散运动。
p(x)
n(x) p n x
nno pno
npo
平衡p-n结中载流子的分布
利用上述公式计算电势能比n区导带底高0.1eV 的点x处的载流子浓度,假设势垒高度为0.7eV, 则
n( x ) n n 0 e
0.1 0.026
ND 50
0.6
qV ( x) qVD qV ( x) p( x) p n 0 exp( ) p p 0 exp( ) p p 0 e 0.026 10 10 N A k 0T k 0T
半导体物理 第六章 PN结

主要内容:
1、非平衡PN结能带图 2、PN结电流电压方程
1、非平衡PN结
(1)PN 结正偏、反偏
• 平衡PN结
P
N
• 正偏PN结
P
N
• 反偏PN结
P
N
哈尔滨工业大学微电子科学与技术系
(2)非平衡PN能带图
EC
E
n F
空穴 EFP
能量 EV
qVD q(VD-V)
E
p F
电子
EC
能量
EFn
EV
EC
空穴 EFP
扩散电容:
(2)突变结势垒电容
CTA2(NA r 0 N qD)A N V N (D DV)AX rD 0
XD
2r0(NAND)V (DV) qN AND
(3)线性缓变结势垒电容
CT
A3
qjr202 12(VDV)
r0A XD
XD
3
12r0(VD qj
V)
(4)扩散电容
CDa2q(np0Lnk 0Tpn0Lp)exk q p 0TV
x
x
qVD ECn EFn
电子 能量
EVn
哈尔滨工业大学微电子科学与技术系
• 本征费米能级 Ei 随位置 x 的变化
dEi qdV(x)
dx
dx
(3)平衡PN结的载流子分布
n ( xP) n n 0 exp
xp
qV
( x ) qV
k
xn
0
TN
D
ห้องสมุดไป่ตู้
pp0
p(x)
p n 0 expn(x )qV
§6.1 PN结及其能带图
P-N Junction and its energy band diagram
1、非平衡PN结能带图 2、PN结电流电压方程
1、非平衡PN结
(1)PN 结正偏、反偏
• 平衡PN结
P
N
• 正偏PN结
P
N
• 反偏PN结
P
N
哈尔滨工业大学微电子科学与技术系
(2)非平衡PN能带图
EC
E
n F
空穴 EFP
能量 EV
qVD q(VD-V)
E
p F
电子
EC
能量
EFn
EV
EC
空穴 EFP
扩散电容:
(2)突变结势垒电容
CTA2(NA r 0 N qD)A N V N (D DV)AX rD 0
XD
2r0(NAND)V (DV) qN AND
(3)线性缓变结势垒电容
CT
A3
qjr202 12(VDV)
r0A XD
XD
3
12r0(VD qj
V)
(4)扩散电容
CDa2q(np0Lnk 0Tpn0Lp)exk q p 0TV
x
x
qVD ECn EFn
电子 能量
EVn
哈尔滨工业大学微电子科学与技术系
• 本征费米能级 Ei 随位置 x 的变化
dEi qdV(x)
dx
dx
(3)平衡PN结的载流子分布
n ( xP) n n 0 exp
xp
qV
( x ) qV
k
xn
0
TN
D
ห้องสมุดไป่ตู้
pp0
p(x)
p n 0 expn(x )qV
§6.1 PN结及其能带图
P-N Junction and its energy band diagram
微电子学 半导体物理学 第六章pn结
(N
2 x 2 + N D xn ) A p
x D = xn + x p N A x p = N D xn
NA ND xn = xD x p = xD NA + ND NA + ND
1/ 2
1/ 2
2ε 0ε r 2ε ε N + N D 代入 VD 得 x D = 0 r A VD = qN VD N AN D q eff q2 N A (x + x p )2 (-xp<x<0) EC ( x ) = EC ( p ) − 2ε 0ε r q2 N D ( x − xn )2 − 2011 EC ( x ) = E复旦大学半导体物理 -qV D (0<x<xn) + C ( p) 2ε 0ε r
复旦大学半导体物理 - 2011
14
平衡时的费米能级
J n = J n扩 + J n漂 = 0
dn 0 J n = qn 0 µ n E + qDn dx
dn0 1 dEi 1 dE F = − n0 + n0 dx k BT dx k BT dx dV ( x ) 1 dEi E=− = dx q dx
NDNA越大,VD越大;Eg越大,ni越小,VD越大。 NA=1017cm-3, ND=1015cm-3, Si的VD=0.70V. 复旦大学半导体物理 - 2011
17
平衡时,
qVD = Ecp − Ecn = E g + ( EFn − Ec ) + ( Ev − EFp )
对于非简并半导体,势垒高度会大于禁带宽度Eg吗?
耗尽层近似
从N区到P区,随着电子势能的升高,电子浓度 迅速下降,由于Vd(~1V),在势垒区的大部 分范围内,电子极为稀少,可视为电子耗尽, N侧空间电荷区的电荷基本是由电离施主贡献 的。同理,P侧空间电荷区的电荷有电离受主 贡献。 认为,在空间电荷区载流子被耗尽了
半导体物理_第6章_pn结

+ + + + + + + + + + + +
+ + + + + +
n型半导体
空间电荷区, 也称耗尽层。
扩散运动
扩散的结果是使空间 电荷区逐渐加宽。
5
注意:
1、空间电荷区中没有载流子。 2、空间电荷区中内电场阻碍p区中的空穴、n 区中的电子(都是多子)向对方运动(扩 散运动)。
3 、 p 区中的电子和 n 区中的空穴(都是少 子),数量有限,因此由它们形成的电流 很小。
qVD k 0T
加正向偏置V后,结电压为(VD-Vf),
n p x p nn0e
q (V D V f ) k0T
qV f
n p0e
k0T
p n xn p p 0 e
q (VD V f ) k 0T
qV f
pn 0 e
k 0T
在xp处注入的非平衡电子浓度为:
2
d 2 pn p x Dp 0 2 dx p
x x p x A exp( ) B exp( ) Lp Lp
p x pno [exp( qV f k0T xn x ) Lp
) 1]exp(
Jp
Dp dpx qDp q px dx Lp
D1,D2是积分常数,由边界条件确定。设p型中性 区的电势为零,则在热平衡条件下边界条件为: 代入有:
V1(xp ) 0,V2 (xn ) VD
2 qN D xn D1 , D2 VD 2 r 0 2 r 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两式相除取对数得:
ln nno 1 np0 k0T
EFn EFp
若半导体处于强电离区,则
nno
ND , npo
ni2 NA
VD
1 q
EFn EFp
k0T q
ln
NDNA ni2
接触电势差VD和pn结两边的掺杂浓度、温度、材料的 禁带宽度有关。一定温度下,突变结两边掺杂浓度越 高,VD越大;禁带宽度越大,ni越小,VD也越大.
dx
k0T dx dx
Jn
nqn
1 dEF q dx
dEi dx
而本征费米能级Ei的变化与电子电势能-qV(x)的变 化一致,所以:
dEi q dV x q
dx
dx
11
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
带入后得到电子总电流密度:
区是逐渐变化的, 为缓变结.若杂质分布可用x=xj 处杂质分布曲线的切线表示,则称为线性缓变结,可 表示为:
ND N A j x x j
式中的αj是x=xj处切线的斜率,称为杂质浓度梯度.
4
§6.1 pn结及其能带图 §6.1.2 平衡pn结的形成
5
§6.1 pn结及其能带图 §6.1.2 平衡pn结的形成
载流子的两种运动:
扩散运动:多子在浓度差作用下定向移动
漂移运动:在内建电场的作用下载流子的定向移动,阻 碍了扩散运动的进行.
空间电荷区(pn结、势垒区、耗尽层):
由带正电的电离施主和带负电的电离受主杂质构成,存 在内建电场,电场方向由n区指向p区.当pn结达到平衡时,净 电流为零,空间电荷区宽度一定。
合金结和高表面浓度的浅扩散结一般可认为是 突变结,结中杂质分布表示为:
x xj, Nx NA x xj , Nx ND
边界两侧可认为只含有一种导电类型的杂质.
3
§6.1 pn结及其能带图 §6.1.1 pn结中的杂质分布
⒉线性缓变结 低表面浓度的深扩散结中,杂质浓度从p区到n
从能带图中可以看出,势垒高度正好补偿了两个 半导体的费米能级的差异,即
qVD EFn EFp
令nn0和np0分别表示n区和p区平衡电子浓度,则
nno
ni
exp
EFn Ei k0T
np0
ni
exp
EFp k0T
Ei
14
§6.1 pn结及其能带图 §6.1.4 pn结接触电势差 dx
dEF Jn
dx nn
同理,空穴总电流密度为:
Jp
p p
dEF dx
dEF J p
dx p p
12
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
上两式表示了费米能级随位置的变化和电流密度之间 的关系.对于平衡pn结,Jn和Jp均为零,因此有:
dEF dx
0, EF
常数
上述关系式还说明当电流密度一定时,载流子浓度大 的地方,EF随位置变化小,而载流子浓度小的地方,EF 随位置变化较大。
13
§6.1 pn结及其能带图 §6.1.4 pn结接触电势差
平衡pn结的空间电荷区两端的电势差VD称为pn结 接触电势差或内建电势差,相应的qVD称为pn结势垒高 度.
在一块n型(或p型)半导体单晶上,用合金法、 扩散法、生长法、离子注入法等方法将另一种导电 类型的杂质掺入其中,使这块单晶的不同区域分别 具有n型和p型的导电类型~,在两者的交界面处就形 成了pn结.
2
§6.1 pn结及其能带图 §6.1.1 pn结中的杂质分布
根据pn结中杂质分布的不同, pn结可分为突变 结和线性缓变结两种. ⒈突变结
平衡pn结中费米能级处处相等恰好标志了每一 种载流子的扩散电流和漂移电流相互抵消,没有净电 流流过pn结,这一结论也可从电流密度方程式推出。
9
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
证明如下:
考虑电子电流,流过pn结的电子总电流密度为:
Jn
nqn
qDn
dn dx
由爱因斯坦关系,则
返回1 返回2 返回3 8
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
当两块半导体形成pn结时,电子将从费米能级高 的n区流向费米能级低的p区。当pn结处于平衡状态 时,两者的费米能级达到一致.此时,n区整个能带比 p区整个能带低,空间电荷区内的能带产生弯曲,弯曲 的高度即为qVD.当电子从势能低的n区向势能高的p 区运动时,必须克服这一势能高坡,对空穴也一样,所 以也称空间电荷区为势垒区.
Jn
qn n
k0T q
dn dx
nqn
k0T q
d dx
ln
n
由平衡非简并半导体电子浓度公式:
n
ni
exp
EF Ei k0T
10
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
得到:
d ln n 1 dEF dEi
中性区+空间电荷区+中性区
6
§6.1 pn结及其能带图 §6.1.2 平衡pn结的形成
空间电荷区内的电势分布:
由于内建电场的存在,空间电荷区内电势V(x)由n区向p 区不断降低,而电子的电势能-qV(x)则由n区向p区不断升高 (电势越高的地方电子的能量越低)。
返回
7
§6.1 pn结及其能带图 §6.1.3 平衡pn结的能带图
15
§6.1 pn结及其能带图 §6.1.5 pn结载流子分布
取p区电势为零,并且p区导带底能量为零,势垒区 中一点x的电势V(x)为正值,且越接近n区的点电势越 高.到势垒区靠近n一侧边界xn处的电势最高为VD,用xn 和-xp分别代表n区和p区势垒区的边界.势垒区内点x 处的电子的附加电势能为E(x)=-qV(x).
对非简并半导体,考虑内建电场的附加电势后:
第六章 pn结
在同一块半导体材料中若同时有两种不同的导电 类型时,交界面处形成了pn结。pn结是很多半导体器 件如结型晶体管、集成电路等的基本结构,了解和掌 握其性质具有重大意义。
本章重点讨论了pn结的形成过程和能带情况,并 对其电流电压特性、电容效应及击穿特性等性质进行 了介绍。
1
§6.1 pn结及其能带图 §6.1.1 pn结中的杂质分布
