微专题五 利用轴对称解决最值问题
利用“轴对称变换”解决最值问题(1)

初中数学动点典型题分析
所谓“动点问题”是指图形中有一个或多个动点,在线段、射线或者弧线上
运动的一类开放性题目,而解决这类题的关键是动中取静,让动点定下来,灵活地运用相关数学知识解决问题.在变化中找到不变的性质是解决数“动点”问题的基本思路.
数学压轴题正逐步转向数形结合、动态几何、动手操作、实验探究等方向,
加强了对几何图形运动变化的考核,从变化的角度来研究三角形、四边形、函数图象等,通过“对称”“翻折”“平移”“旋转”等研究手段和方法来探究图形
性质及变化.让学生经历探索的过程,培养学生分析问题、解决问题的能力,把
运动观点、方程思想、数形结合思想、分类思想、转化思想有机地结合起来.目录正在整理之中....
QQ资料群:453495932,微信:2781202173.公众号:初中数学解题思路(lishi_shuxue).
一、利用“垂线段最短”解决最值问题
二、利用“三点共线”解决最值问题
三、利用“轴对称变换”解决最值问题
【典型例题1】难度★★
【思路分析】利用轴对称的性质解决一动点到两定点距离和最小的问题,辅助线方法是作某一定点的对称点(本题做C点的对称点,与A连接确定点D),熟练运用此方法是本例题和变式的主要目的,同时运用到勾股定理、三角函数等相关知识.本题做C点的对称点
【答案解析】解:。
利用轴对称性质求几何最值

利用轴对称性质求几何最值————————————————————————————————作者: ————————————————————————————————日期:ﻩ轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。
比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个:(1)两点之间线段最短;(2)三角形两边之和大于第三边;(3)垂线段最短。
初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的最值问题。
下面对三类线段和的最值问题进行分析、讨论。
(1)两点一线的最值问题:(两个定点+ 一个动点)问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。
核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于直线的对称点,连结这个对称点与另一定点,交直线于一点,交点即为动点满足最值的位置。
变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
1. 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为()A.4 B.8 C.D.2.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15°B.22.5° C.30° D. 45°3.如图,Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE 最小,则这个最小值是_____________.4.(2006•河南)如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB 边上一动点,则EC+ED的最小值是_____________.5.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )A.B.C. D. 106..(2009•抚顺)如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )A.2√3 B. 2√6C.3D. √6(2)一点两线的最值问题:(两个动点+一个定点)问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
利用轴对称解决最值问题

九年级数学专题复习利用轴对称解决最值问题学案学习目标:1.借助中考真题的探究,掌握处理最值问题的基本知识源,明确解决图形几何最值问题的思考方向、思路方法,并感受体验其解题策略;2.体验变化中寻找不变性的数学思想方法, 能将最值问题化归与转化为相应的数学模型进行分析与突破.学习重难点:1.借助相关概念、图形性质、定理,探寻几何图形最值问题中化归与转化的关键.2.知识溯源,借助中考真题的研究,从知识转化角度,掌握处理最值问题的基本知识源,归纳总结其解题策略.教学过程:一、真题探究真题示例1(2016•福建龙岩)如图1,在周长为12的菱形ABCD 中,AE=1,AF=2,若P 为对角线BD 上一动点,则EP+FP 的最小值为( )A .1B .2 C.3 D .4【基本模型(一)】变式1:正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上的一动点,DN +MN 的最小值为_________变式2:在等边三角形ABC 中,AB =4,点E 是AB 的中AD 是高,在AD 上找一点P ,使BP +PE 的值最小 .变式3:已知二次函数的图象与坐标轴交于点 A (-1, 0)点B (0,-5)和点C .(1)求抛物线的解析式;(2)已知该函数图象的对称轴上存在一点P ,使 的周长最小,求出点P 的坐标。
(1) (2) (3)(图1) c x ax y +-=42PAB ∆N M D C B A真题示例2(2016•四川内江)如图2所示,已知点C(1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值是______.【基本模型(二)】变式:45AOB ∠=°,P 是AOB ∠内一点,10PO =,Q R 、分别是OA OB 、上的动点,则PQR△周长的最小值为_________.真题示例3(2012•浙江宁波)如图4,△ABC 中,︒=∠60BAC ,︒=∠45ABC ,AB=22,D 是线段BC 上的一个动点,以AD 为直径画⊙O 分别交AB ,AC 于E ,F ,连接EF ,则线段EF 长度的最小值为 .【基本模型(三)】变式:如图,在△ABC 中,AB=3,AC=4, BC=5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,则EF 的最小值为 .(图3) (图2)【拓展延伸】如图,在等边三角形ABC 中,AB=4,点D 、P 、E 分别为边BC 、AB 、AC 上(均不与端点重合)的动点 则 的周长的最小值是________.三、专题总结1.收获哪些解题方法?2.体验哪些解题策略?DEP课后自测题1.(2013•江苏宿迁)在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x 轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是.变式: 在平面直角坐标系xOy中,已知点A(2,-1),B(1,2),点P在x轴上运动,当|PA﹣PB|最大时,点P的坐标是.2.(2016•四川泸州)如图6,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .3.(2016•江苏常州)如图7,在平面直角坐标系xOy中,一次函数y=x与二次函数y=x2+bx 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.(1)求二次函数的表达式;(2)长度为2的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;(图7)(图6)。
中考数学几何模型专题专题五—轴对称

专题五轴对称模型21 将军饮马之“两点一线”模型模型故事唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.如图,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营.请问怎样走才能使总的路程最短?模型展现基础模型怎么用?1.找模型遇到两个定点和一条定直线,求定直线上一点,与两点的连线和最小,考虑“两点一线”求最值模型2.用模型异侧两点则直接连接,同侧两点,则需要通过轴对称性质转化为异侧,利用“两点之间线段最短”求最值结论分析结论1:连接AB交直线l于点P,此时P A+PB值最小,最小值为AB的长证明:当点A,B,P共线时,P A+PB=AB,当点A,B,P不共线时,P A+PB>AB,∴P A+PB≥AB,∴当点A,B,P共线时,P A+PB的值最小,最小值是线段AB的长.结论2:作点B关于直线∴的对称点B',连接AB',交直线l于点P,此时P A+PB值最小,最小值为AB'的长证明:由轴对称性质可知,PB=PB',∴P A+PB=P A+PB'≥AB',∴当点A,B' ,P共线时,P A+PB的值最小,最小值是线段AB'的长.(也可以作点A关于直线l的对称点A',同理也可求出P A+PB的最小值)满分技法1.两点之间,线段最短.如图,点A和点B之间的3条线中,线段AB的距离最短,是线路∴.2.对称的性质.如图,若点A,A’关于直线l对称,P是直线l上一点,则P A= P A'.模型拓展模型拓展巧学巧记“两点一线”型问题简记为:线段和最小时,异侧直接连,同侧找对称;线段差最大时,同侧直接连,异侧找对称.典例小试例1 (2020贺州)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=6√3,BD=6,点P是AC上一动点(点拨:一动点P),点E是AB的中点,则PD+PE(点拨:两定点D,E,一定线AC,求线段和最小值)的最小值为_________.考什么?轴对称的性质,两点之间线段最短(三角形三边关系),菱形的性质,勾股定理,等边三角形的判断与性质思路点拨线段和最值问题,先根据已知条件判断定点、动点的个数及定点与定线的位置关系,确定模型,再按照模型结论确定最值点。
轴对称中几何动点最值问题总结

轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。
比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个:正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
1.如图,直线l和l的同侧两点A、B,在直线l上求作一点P,使PA+PB最小。
(2)一点两线的最值问题:(两个动点+一个定点)问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。
变异类型:1.如图,点P是∠MON内的一点,分别在OM,ON上作点A,B。
使△PAB的周长最小。
x轴()3.(4)两点两线的最值问题:(两个动点+两个定点)问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另一动点的距离和最小。
核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最短),且这条线段垂直于另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线段中,垂线段最短)时,两线段和最小,最小值等于这条垂线段的长。
变异类型:演变为多边形周长、折线段等最值问题。
1.如图,点A是∠MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
12.31。
2.,341.11.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上秱动,则当PA +PD 取最小值时,△APD中边AP 上的高为()Part6、一次函数一次函数b kx y +=的图象与y x ,轴分别交于点).4,0(),0,2(B A(1)求该函数的解析式;(2)O。
函数利用对称解决最值

利用对称解决函数的最值问题例1、抛物线2,两点,交y轴于点C,y ax bx c=++交x轴于A B Array对称轴为直线1x=。
且A、C两点的坐标分别为(10)A-,、,.C-(03)(1)求抛物线2=++的解析式;y ax bx c(2)求A O C△和BO C△的面积的比;(3)在对称轴上是否存在一个点P,使P A C△的周长最小.若存在,请求出点P的坐标;若不存在,请说明理由.例2、24.已知:抛物线m-=与x轴的一个交点为A(1,0).y2+ax4ax(1)求抛物线与x轴的另一个交点B的坐标;(2)点C是抛物线与y轴的交点,且△ABC的面积为3,求此抛物线的解析式;(3)点D是(2)中开口向下的抛物线的顶点.抛物线上点C的对称点为Q,把点D沿对称轴向下平移5个单位长度,设这个点为P;点M、N分别是x轴、y轴上的两个动点,当四边形PQMN的周长最短时,求PN+MN+QM的长.(结果保留根号)例3、25、已知:抛物线c=2过点A(-1,0)、B(-2,-5),与y轴交-xbxy++于点C,顶点为D.(1)求该抛物线的解析式;(2)某直线过点A(-1,0),且与抛物线只有一个交点,求此直线的解析式;(3)直线l过点C,且l∥x轴,E为l上一个动点,EF⊥x轴于F.求使DE+EF+BF的和为最小值的E、F两点的坐标,并直接写出DE+EF+BF的最小值.例4、24.已知:抛物线n mx x y ++=2与x 轴交A 、B 两点(A 点在B 点左侧),B (3,0),且经过C (2,-3),与y 轴交于点D ,(1)求此抛物线的解析式及顶点F 的坐标;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物于E 点,求线段PE 长度的最大值;(3)在(1)的条件下,在x 轴上是否存在两个点G 、H (G 在H 的左侧),且GH=2,使得线段GF+FC+CH+HG 的长度和为最小;如果存在,求出G 、H的坐标;如果不存在,说明理由。
中考数学知识点考点复习指导利用轴对称求最值

中考数学知识点考点复习指导利用轴对称求最值利用轴对称求最值是高中数学中的一个重要的知识点,也是中考数学中经常考察的内容之一、下面我将从以下几个方面为你详细介绍如何利用轴对称求最值。
1.轴对称性的概念轴对称性是指对于平面上的一个图形,如果沿条直线旋转180度后,旋转后的图形与原图形重合,那么我们就说这个图形具有轴对称性。
轴对称的直线称为轴线。
轴对称的图形的特点是:图形的任意一点关于轴线对称的点也在图形内部。
2.利用轴对称求最值的一般步骤求解最值的一般步骤为:首先明确最值是指最大值还是最小值,然后利用轴对称性把问题转化为一个等价的问题,利用已知条件求解这个等价问题,最后还原到原问题中,得到最值。
3.利用轴对称求最值的具体方法在具体的问题中,可以根据实际的情况,运用合适的方法进行求解。
下面是常见的一些方法:(1)利用轴对称线上的点求最值:对于轴对称的图形,如果可以确定图形上的其中一点关于轴线的对称点是最值点,那么这个最值点的横坐标就可以作为最值的解。
(2)利用轴对称图形的特点求最值:对于具有轴对称性的图形,如果能够找到一些特殊的点,使得这些点关于轴线对称,而且能够确定这些点是最值点,那么这个最值点就可以作为最值的解。
(3)利用轴对称图形的性质求最值:对于轴对称的图形,如果能够利用对称性与其他已知条件建立等式或不等式,然后求解这个等式或不等式的解,就可以得到最值的解。
(4)利用轴对称折线的特点求最值:对于轴对称的折线图,可以利用折线图的性质,比如单调性,交点等,将问题转化为求解折线的最值的问题,然后利用已知条件求解最值。
4.练习题示例为了更好地理解和掌握利用轴对称求最值的方法,我们可以通过一些练习题来加深印象。
下面是一些练习题的示例:(1)求函数y=2x^2-3x+1在区间[-1,2]上的最大值和最小值。
解:首先,求函数的极值点,对应的x值是-1/4、然后,将-1/4代入函数,得到y=-1/8、所以在[-1,2]上,最大值为1,最小值为-1/8(2)求函数y=x^3-3x^2+3x的最大值和最小值。
轴对称中几何动点最值问题总结

轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。
比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个:(1)两点之间线段最短;(2)三角形两边之和大于第三边;(3)垂线段最短。
初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的最值问题。
下面对三类线段和的最值问题进行分析、讨论。
(1)两点一线的最值问题:(两个定点+ 一个动点)问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。
核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于直线的对称点,连结这个对称点与另一定点,交直线于一点,交点即为动点满足最值的位置。
方法:1.定点过动点所在直线做对称。
2.连结对称点与另一个定点,则直线段长度就是我们所求。
变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
1.如图,直线l和l的同侧两点A、B,在直线l上求作一点P,使PA+PB最小。
(2)一点两线的最值问题:(两个动点+一个定点)问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。
变异类型:1.如图,点P 是∠MON 内的一点,分别在OM ,ON 上作点A ,B 。
使△PAB 的周长最小。
2.如图,点A 是∠MON 外的一点,在射线OM 上作点P ,使PA 与点P 到射线ON 的距离之和最小。
(3) 两点两线的最值问题: (两个动点+两个定点)问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。
专题:轴对称模型求最值
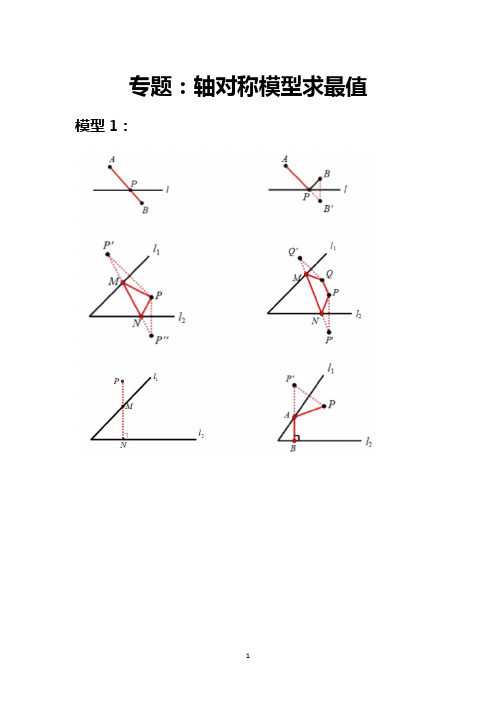
专题:轴对称模型求最值模型1:模型3:模型例题:例题1.如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN 的周长的最小值为___________.解答:如图,作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长.△点P 关于OA 的对称点为C ,△PM=CM ,OP=OC ,△COA=△POA ; △点P 关于OB 的对称点为D ,△PN=DN ,OP=OD ,△DOB=△POB ,△OC=OD=OP=3,△COD=△COA+△POA+△POB+△DOB=2△POA+2△POB=2△AOB=60°,△△COD是等边三角形,△CD=OC=OD=3.△△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=3.例题2.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,求△PMN周长的最小值2解:作N关于AB的对称点N′,连接MN′,NN′,ON′,OM,ON,∵N关于AB 的对称点为N′,∴MN′与AB的交点P′即为△PMN 周长最小时的点,∵N是弧MB 的中点,∴∠A=∠NOB=∠MON=20°,∴∠MON′=60°∴△MON′为等边三角形,∴MN′=OM=4,∴△PMN周长的最小值为4+1=5例题3.如图,在平面直角坐标系中,有A(1,2),B(3,3)两点,现另取一点C(a,1),当a =时,AC+BC的值最小.例题3如图,在矩形ABCD中,AB=10,AD=6,动点P满足S△P AB=S矩形ABCD,则点P 到A,B两点距离之和P A+PB的最小值为2.3解:设△ABP中AB边上的高是h.∵S△P AB=S矩形ABCD,∴AB•h=AB•AD,∴h=AD=4,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.在Rt△ABE中,∵AB=10,AE=4+4=8,∴BE===2,即P A+PB的最小值为2.例题4:如图所示,凸四边形ABCD中,∠A=90°,∠C=90°,∠D=60°,AD=3,AB =,若点M、N分别为边CD,AD上的动点,求△BMN的周长的最小值.4解:作点B关于CD、AD的对称点分别为点B'和点B'',连接B'B''交DC和AD于点M和点N,DB,连接MB、NB;再DC和AD上分别取一动点M'和N'(不同于点M和N),连接M'B,M'B',N'B和N'B'',如图1所示:∵B'B''<M'B'+M'N'+N'B'',B'M'=BM',B''N'=BN',∴BM'+M'N'+BN'>B'B'',又∵B'B''=B'M+MN+NB'',MB=MB',NB=NB'',∴NB+NM+BM<BM'+M'N'+BN',∴C△BMN=NB+NM+BM时周长最小;连接DB,过点B'作B'H⊥DB''于B''D的延长线于点H,如图示2所示:∵在Rt△ABD中,AD=3,AB=,∴==2,∴∠2=30°,∴∠5=30°,DB=DB'',又∵∠ADC=∠1+∠2=60°,∴∠1=30°,∴∠7=30°,DB'=DB,∴∠B'DB''=∠1+∠2+∠5+∠7=120°,DB'=DB''=DB=2,又∵∠B'DB''+∠6=180°,∴∠6=60°,∴HD=,HB'=3,在Rt△B'HB''中,由勾股定理得:===6.∴C△BMN=NB+NM+BM=6,例题5:如图,矩形ABCD中,AB=4,BC=8,E为CD的中点,点P、Q为BC上两个动点,且PQ=3,当CQ=时,四边形APQE的周长最小.:5解:点A向右平移3个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,此时MQ+EQ最小,∵PQ=3,DE=CE=2,AE==2,∴要使四边形APQE的周长最小,只要AP+EQ最小就行,即AP+EQ=MQ+EQ,过M作MN⊥BC于N,设CQ=x,则NQ=8﹣3﹣x=5﹣x,∵△MNQ∽△FCQ,∴=,∵MN=AB=4,CF=CE=2,CQ=x,QN=5﹣x,解得:x=,则CQ=例题6:如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,求PM+PN的最小值6解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,则此时PM+PN最小,∵点A坐标(2,3),∴点A′坐标(2,﹣3),∵点B(3,4),∴A′B==5,∴MN=A′B﹣BN﹣A′M=5﹣3﹣1=5﹣4,∴PM+PN的最小值为5﹣4.精品变式练习:1.如图,正方形ABCD 的边长为4,∠DAC 的平分线交DC 于点E ,若点P ,Q 分别是AD 和AE 上的动点,求DQ +PQ 的最小值为 .2.如图,圆柱形玻璃杯高为12cm 、底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为 cm .2如图,在正方形ABCD 中,AB=3,点M 在CD 的边上,且DM=1,ΔAEM 与ΔADM 关于AM 所在的直线对称,将ΔADM 按顺时针方向绕点A 旋转90°得到ΔABF,连接EF ,则线段EF 的长为3.图所示,30AOB ∠=,点P 为AOB ∠内一点,8OP =,点,M N 分别在,OA OB 上,求PMN ∆周长的最小值为:4.在矩形ABCD中,AB=8,BC=10,G为AD边的中点.如图,若E、F为边AB上的两个动点,且EF=4,当四边形CGEF的周长最小时,则求AF的长为.5如图,已知点D,E分别是等边三角形ABC中BC,AB边的中点,BC=6,点F是AD边上的动点,则BF+EF的最小值为.6.如图,长为1的线段AB在x轴上移动C(0,1)、D(0,2),则AC+BD的最小值是.7 (1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为.(2)如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN 的最小值.(3)如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD 的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.8如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;(2)请问AC+CE的值是否存在最小值?若存在,请求出这个最小值;若不存在请说明理由.(3)根据(2)中的规律和结论,请直接写出出代数式+的最小值为.9如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B两点(点A 在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ 为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.11 10已知,如图,二次函数()2230y ax ax a a =+-≠图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A 点右侧),点H 、B 关于直线l:y x =+对称.(1)求A 、B 两点的坐标,并证明点A 在直线l 上;(2)求二次函数解析式;(3)过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连结HN 、NM 、MK ,求HN+NM+MK 的最小值.。
中考数学复习---《利用对称求最值问题》知识点总结与专项练习题(含答案)
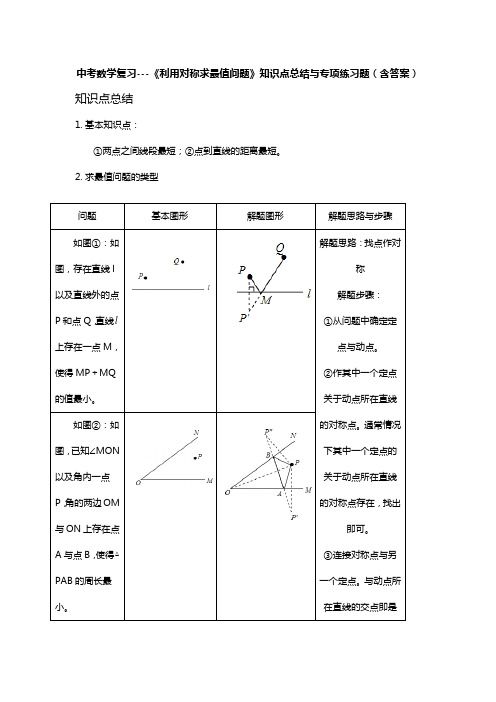
中考数学复习---《利用对称求最值问题》知识点总结与专项练习题(含答案)知识点总结1.基本知识点:①两点之间线段最短;②点到直线的距离最短。
2.求最值问题的类型问题基本图形解题图形解题思路与步骤如图①:如图,存在直线l 以及直线外的点P和点Q,直线l 上存在一点M,使得MP+MQ 的值最小。
解题思路:找点作对称解题步骤:①从问题中确定定点与动点。
②作其中一个定点关于动点所在直线的对称点。
通常情况下其中一个定点的关于动点所在直线的对称点存在,找出即可。
③连接对称点与另一个定点。
与动点所在直线的交点即是如图②:如图,已知∠MON 以及角内一点P,角的两边OM 与ON上存在点A与点B,使得△PAB的周长最小。
微专题1.(2022•德州)如图,正方形ABCD 的边长为6,点E 在BC 上,CE =2.点M 是对角线BD 上的一个动点,则EM +CM 的最小值是( )A .62B .35C .213D .413【分析】要求ME +MC 的最小值,ME 、MC 不能直接求,可考虑通过作辅助线转化ME ,MC 的值,从而找出其最小值求解.【解答】解:如图,连接AE 交BD 于M 点, ∵A 、C 关于BD 对称, ∴AE 就是ME +MC 的最小值,如图③:如图:已知∠AOB 以及角内两点点P 与点Q ,角的两边上分别存在M 、N 使得四边形PQMN 的周长最小。
动点的位置。
然后解题。
∵正方形ABCD中,点E是BC上的一定点,且BE=BC﹣CE=6﹣2=4,∵AB=,∴AE==2,∴ME+MC的最小值是2.故选:C.2.(2022•资阳)如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点.若AB=4,则AE+OE的最小值是()A.42B.25+2 C.213D.210【分析】本题为典型的将军饮马模型问题,需要通过轴对称,作点A关于直线BC的对称点A',再连接A'O,运用两点之间线段最短得到A'O为所求最小值,再运用勾股定理求线段A'O的长度即可.【解答】解:如图所示,作点A关于直线BC的对称点A',连接A'O,其与BC的交点即为点E,再作OF⊥AB交AB于点F,∵A与A'关于BC对称,∴AE=A'E,AE+OE=A'E+OE,当且仅当A',O,E在同一条线上的时候和最小,如图所示,此时AE+OE=A'E+OE=A'O,∵正方形ABCD,点O为对角线的交点,∴,∵A与A'关于BC对称,∴AB=BA'=4,∴FA'=FB+BA'=2+4=6,在Rt△OFA'中,,故选:D.3.(2022•菏泽)如图,在菱形ABCD中,AB=2,∠ABC=60°,M是对角线BD上的一个动点,CF=BF,则MA+MF的最小值为()A.1 B.2C.3D.2【分析】当MA+MF的值最小时,A、M、F三点共线,即求AF的长度,根据题意判断△ABC为等边三角形,且F点为BC的中点,根据直角三角形的性质,求出AF的长度即可.【解答】解:当A、M、F三点共线时,即当M点位于M′时,MA+MF的值最小,由菱形的性质可知,AB=BC,又∵∠ABC=60°,∴△ABC为等边三角形,∵F点为BC的中点,AB=2,∴AF⊥BC,CF=FB=1,∴在Rt△ABF中,AF==.故选:C.4.(2022•广安)如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE+PF的最小值是()A.2 B.3C.1.5 D.5【分析】如图,取AB的中点T,连接PT,FT.首先证明四边形ADFT是平行四边形,推出AD=FT=2,再证明PE+PF=PT+PF,由PF+PT≥FT=2,可得结论.【解答】解:如图,取AB的中点T,连接PT,FT.∵四边形ABCD是菱形,∴CD∥AB,CD=AB,∵DF=CF,AT=TB,∴DF=AT,DF∥AT,∴四边形ADFT是平行四边形,∴AD=FT=2,∵四边形ABCD是菱形,AE=DE,AT=TB,∴E,T关于AC对称,∴PE=PT,∴PE+PF=PT+PF,∵PF+PT≥FT=2,∴PE+PF≥2,∴PE+PF的最小值为2.故选:A.5.(2022•赤峰)如图,菱形ABCD,点A、B、C、D均在坐标轴上.∠ABC=120°,点A (﹣3,0),点E是CD的中点,点P是OC上的一动点,则PD+PE的最小值是()3A.3 B.5 C.22D.32【分析】根据题意得,E点关于x轴的对称点是BC的中点E',连接DE'交AC与点P,此时PD+PE有最小值,求出此时的最小值即可.【解答】解:根据题意得,E点关于x轴的对称点是BC的中点E',连接DE'交AC与点P ,此时PD +PE 有最小值为DE ',∵四边形ABCD 是菱形,∠ABC =120°,点A (﹣3,0), ∴OA =OC =3,∠DBC =60°, ∴△BCD 是等边三角形, ∴DE '=OC =3,即PD +PE 的最小值是3, 故选:A .6.(2022•安顺)已知正方形ABCD 的边长为4,E 为CD 上一点,连接AE 并延长交BC 的延长线于点F ,过点D 作DG ⊥AF ,交AF 于点H ,交BF 于点G ,N 为EF 的中点,M 为BD 上一动点,分别连接MC ,MN .若91=∆∆FCEDCG S S ,则MC +MN 的最小值为 .【分析】由正方形的性质,可得A 点与C 点关于BD 对称,则有MN +CM =MN +AM ≥AN ,所以当A 、M 、N 三点共线时,MN +CM 的值最小为AN ,先证明△DCG ∽△FCE ,再由=,可知=,分别求出DE =1,CE =3,CF =12,即可求出AN .【解答】解:如图,连接AM,∵四边形ABCD是正方形,∴A点与C点关于BD对称,∴CM=AM,∴MN+CM=MN+AM≥AN,∴当A、M、N三点共线时,MN+CM的值最小,∵AD∥CF,∴∠DAE=∠F,∵∠DAE+∠DEH=90°,∵DG⊥AF,∴∠CDG+∠DEH=90°,∴∠DAE=∠CDG,∴∠CDG=∠F,∴△DCG∽△FCE,∵=,∴=,∵正方形边长为4,∴CF=12,∵AD∥CF,∴==,∴DE=1,CE=3,在Rt△CEF中,EF2=CE2+CF2,∴EF==3,∵N是EF的中点,∴EN=,在Rt△ADE中,EA2=AD2+DE2,∴AE==,∴AN=,∴MN+MC的最小值为,故答案为:,7.(2022•内江)如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是.【分析】延长BC到G,使CG=EF,连接FG,则四边形EFGC是平行四边形,得CE=FG,则AF+CE=AF+FG,可知当点A、F、G三点共线时,AF+CE的值最小为AG,利用勾股定理求出AG的长即可.【解答】解:延长BC到G,使CG=EF,连接FG,∵EF∥CG,EF=CG,∴四边形EFGC是平行四边形,∴CE=FG,∴AF+CE=AF+FG,∴当点A、F、G三点共线时,AF+CE的值最小为AG,由勾股定理得,AG===10,∴AF+CE的最小值为10,故答案为:10.8.(2022•贺州)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为.【分析】如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.利用勾股定理求出FT=,EF=5,证明PE+PF=PF+PT≥FT,可得结论.【解答】解:如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.∵四边形ABCD是矩形,∴∠A=∠ADT=90°,∵∠AHT=90°,∴四边形AHTD是矩形,∵AE=DE=AD=3.AF=FB=AB=4,∴AH=DT=3,HF=AF﹣AH=4﹣3=1,HT=AD=6,∴FT===,∵DG平分∠ADC,DE=DT,∴E、T关于DG对称,∴PE=PT,∴PE+PF=PF+PT≥FT=,∵EF===5,∴△EFP的周长的最小值为5+,故答案为:5+.9.(2022•娄底)菱形ABCD的边长为2,∠ABC=45°,点P、Q分别是BC、BD上的动点,CQ+PQ的最小值为.【分析】连接AQ,作AH⊥BC于H,利用SAS证明△ABQ≌△CBQ,得AQ=CQ,当点A、Q、P共线,AQ+PQ的最小值为AH的长,再求出AH的长即可.【解答】解:连接AQ,作AH⊥BC于H,∵四边形ABCD是菱形,∴AB=CB,∠ABQ=∠CBQ,∵BQ=BQ,∴△ABQ≌△CBQ(SAS),∴AQ=CQ,∴当点A、Q、P共线,AQ+PQ的最小值为AH的长,∵AB=2,∠ABC=45°,∴AH=,∴CQ+PQ的最小值为,故答案为:.10.(2022•眉山)如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=43,则PE+PB的最小值为.【分析】作点B关于AC的对称点B',交AC于点F,连接B′E交AC于点P,则PE+PB的最小值为B′E的长度;然后求出B′B和BE的长度,再利用勾股定理即可求出答案.【解答】解:如图,作点B关于AC的对称点B',交AC于点F,连接B′E交AC于点P,则PE+PB的最小值为B′E的长度,∵四边形ABCD为矩形,∴AB=CD=4,∠ABC=90°,在Rt△ABC中,AB=4,BC=4,∴tan∠ACB==,∴∠ACB=30°,由对称的性质可知,B'B=2BF,B'B⊥AC,∴BF=BC=2,∠CBF=60°,∴B′B=2BF=4,∵BE=BF,∠CBF=60°,∴△BEF是等边三角形,∴BE=BF=B'F,∴△BEB'是直角三角形,∴B′E===6,∴PE+PB的最小值为6,故答案为:6.11.(2022•滨州)如图,在矩形ABCD中,AB=5,AD=10.若点E是边AD上的一个动点,过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F,则在点E移动的过程中,AF+FE+EC的最小值为.【分析】如图,过点E作EH⊥BC于点H.利用相似三角形的性质求出FH,EF,设BF =x,则DE=10﹣x﹣=﹣x,因为EF是定值,所以AF+CE的值最小时,AF+EF+CE 的值最小,由AF+CE=+,可知欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交x轴于点P,连接AP,此时PA+PB的值最小,最小值为线段A′B的长,由此即可解决问题.【解答】解:如图,过点E作EH⊥BC于点H.∵四边形ABCD是矩形,∴∠B=∠BAD=∠BHE=90°,∴四边形ABHE是矩形,∴EH=AB=5,∵BC=AD=10,∴AC===5,∵EF⊥AC,∴∠COF=90°,∴∠EFH+∠ACB=90°,∵∠BAC+∠ACB=90°,∴∠EFH=∠BAC,∴△EHF∽△CBA,∴==,∴==,∴FH=,EF=,设BF=x,则DE=10﹣x﹣=﹣x,∵EF是定值,∴AF+CE的值最小时,AF+EF+CE的值最小,∵AF+CE=+,∴欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交xz轴于点P,连接AP,此时PA+PB的值最小,最小值为线段A′B的长,∵A′(0,﹣5),B(,5),∴A′B==,∴AF+CE的最小值为,∴AF+EF+CE的最小值为+.解法二:过点C作CC′∥EF,使得CC′=EF,连接C′F.∵EF=CC′,EF∥CC′,∴四边形EFC′C是平行四边形,∴EC=FC′,∵EF⊥AC,∴AC⊥CC′,∴∠ACC=90°,∵AC′===,∴AF+EC=AF+FC′≥AC′=,∴AF+EF+CE的最小值为+.故答案为:+.12.(2022•自贡)如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为.【分析】解法一:利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.解法二:设AE=x,则BF=3﹣x,根据勾股定理可得:EG+CF=+,由勾股定理构建另一矩形EFGH,根据线段的性质:两点之间线段最短可得结论.【解答】解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,∵CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4﹣1=3,由勾股定理得:HG'==3,即GE+CF的最小值为3.解法二:∵AG=AD=1,设AE=x,则BF=AB﹣EF﹣AE=4﹣x﹣1=3﹣x,由勾股定理得:EG+CF=+,如图,矩形EFGH中,EH=3,GH=2,GQ=1,P为FG上一动点,设PG=x,则FP=3﹣x,∴EP+PQ=+,当E,P,Q三点共线时,EP+PQ最小,最小值是3,即EG+CF的最小值是3.故答案为:3.13.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为()A.2B.2 C.22D.4【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.【解答】解:如图,连接AE,∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=EF+CF+AE,∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,连接AC,∴d1+d2+d3最小值为AC,在Rt△ABC中,AC=AB=2,∴d1+d2+d3最小=AC=2,故选:C.14.(2022•安徽)已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA的面积分别记为S0,S1,S2,S3.若S1+S2+S3=2S0,则线段OP 长的最小值是()A.233B.235C.33D.237【分析】如图,不妨假设点P在AB的左侧,证明△PAB的面积是定值,过点P作AB的平行线PM,连接CO延长CO交AB于点R,交PM于点T.因为△PAB的面积是定值,推出点P的运动轨迹是直线PM,求出OT的值,可得结论.【解答】解:如图,不妨假设点P在AB的左侧,∵S△PAB+S△ABC=S△PBC+S△PAC,∴S1+S0=S2+S3,∵S1+S2+S3=2S0,∴S1+S1+S0=2,∴S1=S0,∵△ABC是等边三角形,边长为6,∴S0=×62=9,∴S1=,过点P作AB的平行线PM,连接CO延长CO交AB于点R,交PM于点T.∵△PAB的面积是定值,∴点P的运动轨迹是直线PM,∵O是△ABC的中心,∴CT⊥AB,CT⊥PM,∴•AB•RT=,CR=3,OR=,∴RT=,∴OT=OR+TR=,∵OP≥OT,∴OP的最小值为,当点P在②区域时,同法可得OP的最小值为,如图,当点P在①③⑤区域时,OP的最小值为,当点P在②④⑥区域时,最小值为,∵<,故选:B.。
初中数学几何模型与最值问题05专题-费马点中的对称模型与最值问题(含答案)

初中数学最值问题专题5 费马点中的对称模型与最值问题【专题说明】【例题】1、如图,在△ABC 中,△ACB =90°,AB =AC =1,P 是△ABC 内一点,求P A +PB +PC 的最小值.【分析】如图,以AD 为边构造等边△ACD ,连接BD ,BD 的长即为P A +PB +PC 的最小值.至于点P 的位置?这不重要!如何求BD ?考虑到△ABC 和△ACD 都是特殊的三角形,过点D 作DH △BA 交BA 的延长线于H 点,根据勾股定理,222BD BH DH =+即可得出结果.C2、如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.3、如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN的周长的最小值为___________.4、如图,点都在双曲线上,点,分别是轴,轴上的动点,则四边形周长的最小值为( )A .B .C .D .5、如图所示,30AOB ∠=,点P 为AOB ∠内一点,8OP =,点,M N 分别在,OA OB 上,求PMN ∆周长的最小值.ABCDME6、如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接P C,P E.当△P CE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是C P上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.7、已知,如图,二次函数()2230y ax ax a a =+-≠图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A点右侧),点H 、B 关于直线l :y x =+对称.(1)求A 、B 两点的坐标,并证明点A 在直线l 上; (2)求二次函数解析式;(3)过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连结HN 、NM 、MK ,求HN +NM +MK 的最小值.专题5 费马点中的对称模型与最值问题 答案【专题说明】【例题】1、如图,在△ABC 中,△ACB =90°,AB =AC =1,P 是△ABC 内一点,求P A +PB +PC 的最小值.【分析】如图,以AD 为边构造等边△ACD ,连接BD ,BD 的长即为P A +PB +PC 的最小值.至于点P 的位置?这不重要!如何求BD ?考虑到△ABC 和△ACD 都是特殊的三角形,过点D 作DH △BA 交BA 的延长线于H 点,根据勾股定理,222BD BH DH =+即可得出结果.C2、如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.【分析】依然构造60°旋转,将三条折线段转化为一条直线段. 分别以AD 、AM 为边构造等边△ADF 、等边△AMG ,连接FG ,易证△AMD △△AGF ,△MD =GF △ME +MA +MD =ME +EG +GF过F 作FH △BC 交BC 于H 点,线段FH 的长即为所求的最小值.ABCDMEHFGE MDCBA3、如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN 的周长的最小值为___________.【解析】如图,作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△P MN 的周长最短,最短的值是CD 的长.△点P 关于OA 的对称点为C , △P M =CM ,O P=OC ,△COA =△P OA ; △点P 关于OB 的对称点为D , △P N =DN ,O P=OD ,△DOB =△P OB ,△OC =OD =O P=3,△COD =△COA +△P OA +△P OB +△DOB =2△P OA +2△P OB =2△AOB =60°, △△COD 是等边三角形, △CD =OC =OD =3.△△P MN 的周长的最小值=P M +MN +P N =CM +MN +DN ≥CD =3.4、如图,点都在双曲线上,点,分别是轴,轴上的动点,则四边形周长的最小值为()A.B.C.D.【解析】分别把点A(a,3)、B(b,1)代入双曲线y=得:a=1,b=3,则点A的坐标为(1,3)、B点坐标为(3,1),作A点关于y轴的对称点P,B点关于x轴的对称点Q,所以点P坐标为(﹣1,3),Q点坐标为(3,﹣1),连结P Q分别交x轴、y轴于C点、D点,此时四边形ABCD的周长最小,四边形ABCD周长=DA+DC+CB+AB=D P+DC+CQ+AB=P Q+AB==4+2=6,故选B.5、如图所示,30AOB ∠=,点P 为AOB ∠内一点,8OP =,点,M N 分别在,OA OB 上,求PMN ∆周长的最小值.【解析】如图,作P 关于OA 、OB 的对称点12P P 、,连结1OP 、2OP ,12PP 交OA 、OB 于M 、N ,此时PMN ∆周长最小,根据轴对称性质可知1PMPM =,2PN P N =,1212PMN PM MN P N PP ∴∆=++=,且1AOP AOP ∠=∠,2BOP BOP ∠=∠,12260POP AOB ∠=∠=︒,128OP OP OP ===,12PP O ∆为等边三角形,1218PP OP ==即PMN ∆周长的最小值为8.6、如图,在平面直角坐标系中,抛物线y =x 2﹣x ﹣与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,点E (4,n )在抛物线上.(1)求直线AE 的解析式;(2)点P 为直线CE 下方抛物线上的一点,连接P C ,P E .当△P CE 的面积最大时,连接CD ,CB ,点K是线段CB的中点,点M是C P上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.【解析】(1)△y=x2﹣x﹣,△y=(x+1)(x﹣3).△A(﹣1,0),B(3,0).当x=4时,y=.△E(4,).设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:,解得:k=,b=.△直线AE的解析式为y=x+.(2)设直线CE的解析式为y=mx﹣,将点E的坐标代入得:4m﹣=,解得:m=.△直线CE的解析式为y=x﹣.过点P作P F△y轴,交CE与点F.设点P的坐标为(x,x2﹣x﹣),则点F(x,x﹣),则F P=(x﹣)﹣(x2﹣x﹣)=x2+x.△△E P C的面积=×(x2+x)×4=﹣x2+x.△当x=2时,△E P C的面积最大.△P(2,﹣).如图2所示:作点K关于CD和C P的对称点G、H,连接G、H交CD和C P与N、M.△K是CB的中点,△k(,﹣).△点H与点K关于C P对称,△点H的坐标为(,﹣).△点G与点K关于CD对称,△点G(0,0).△KM+MN+NK=MH+MN+GN.当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.△GH==3.△KM+MN+NK的最小值为3.(3)如图3所示:△y ′经过点D ,y ′的顶点为点F ,△点F (3,﹣).△点G 为CE 的中点,△G (2,).△FG =.△当FG =FQ 时,点Q (3,),Q ′(3,).当GF =GQ 时,点F 与点Q ″关于y =对称,△点Q ″(3,2).当QG =QF 时,设点Q 1的坐标为(3,a ).由两点间的距离公式可知:a +=,解得:a =﹣.△点Q 1的坐标为(3,﹣).综上所述,点Q 的坐标为(3,),Q ′(3,)或(3,2)或(3,﹣). 7、已知,如图,二次函数()2230y ax ax a a =+-≠图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A=+对称.点右侧),点H、B关于直线l:y x(1)求A、B两点的坐标,并证明点A在直线l上;(2)求二次函数解析式;BK AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连结HN、NM、(3)过点B作直线//MK,求HN+NM+MK的最小值.【解析】(1)依题意,得ax2+2ax−3a=0(a≠0),两边都除以a得x2+2x−3=0,解得x1=−3,x2=1,△B点在A点右侧,△A点坐标为(−3,0),B点坐标为(1,0),答:A.B两点坐标分别是(−3,0),(1,0).证明:△直线l:y x+-=,△点A在直线l上.当x=−3时,y(3)0(2)△点H、B关于过A点的直线l:y x+对称,△AH=AB=4,过顶点H作HC△AB交AB于C点,则AC=12,2AB HC==△顶点H(1,-,代入二次函数解析式,解得a=,△二次函数解析式为2y x=,答:二次函数解析式为2y x=+.(3)直线AH的解析式为y=+,直线BK的解析式为y=-y xy⎧=⎪⎨⎪=-⎩,解得3xy=⎧⎪⎨=⎪⎩K),则BK=4,△点H、B关于直线AK对称,K,△HN+MN的最小值是MB,过K作KD△x轴于D,作点K关于直线AH的对称点Q,连接QK,交直线AH于E,则QM=MK,QE=EKAE△QK,△根据两点之间线段最短得出BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,△BK△AH,△△BKQ=△HEQ=90△,由勾股定理得QB8==△HN+NM+MK的最小值为8,。
轴对称中几何动点最值问题总结

轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。
比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个:(1)两点之间线段最短;(2)三角形两边之和大于第三边;(3)垂线段最短。
初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的最值问题。
下面对三类线段和的最值问题进行分析、讨论。
(1)两点一线的最值问题:(两个定点+ 一个动点)问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。
核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于直线的对称点,连结这个对称点与另一定点,交直线于一点,交点即为动点满足最值的位置。
方法:1.定点过动点所在直线做对称。
2.连结对称点与另一个定点,则直线段长度就是我们所求。
变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
1.如图,直线l和l的同侧两点A、B,在直线l上求作一点P,使PA+PB最小。
(2)一点两线的最值问题:(两个动点+一个定点)问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。
变异类型:1.如图,点P 是∠MON 内的一点,分别在OM ,ON 上作点A ,B 。
使△PAB 的周长最小。
2.如图,点A 是∠MON 外的一点,在射线OM 上作点P ,使PA 与点P 到射线ON 的距离之和最小。
(3) 两点两线的最值问题: (两个动点+两个定点)问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。
