八年级数学上学期人教版优质课件-12.3 第2课时 角平分线的判定
合集下载
人教版数学八年级上册12.3.2 角平分线的判定课件(共22张PPT)

BE=CF,
E
B
D
┐
A
FC
DB=DC,
∴Rt△BDE≌Rt△CDF(HL). ∴DE=DF.
∴即AD是∠BAC的平分线.
12.3.2 角平分线的判定
二 三角形的内角平分线
探究1
分别画出以下三角形的三个内角的角平分线,你发现了什么?
A
A
A
B
C
┐
B
C
B
C
三角形的三条角平分线相交于一点,且交点位于三角形的内部.
针对训练
1.如图,在直角△ABC 中,AC=BC,∠C =90°,AP 平分∠BAC,BD
平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC 于点 M,若 OM
=4.
(1) 求点 O 到△ABC 三边的距离和;
B
解:如图,过点 O 作 ON⊥BC 于点 N,过点
O 作 OE⊥AB 于点 E,
A. 110° B. 120° C. 130°
D. 140°
解析:由于 O 到△ABC 三边的距离相等, 故 O 是三条内角平分线的交点, 即 BO,CO 都是内角的平分线,
12.3.2 角平分线的判定
则∠OBC=1∠ABC,∠OCB=1∠ACB.
2
2
∵∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴FG=FM.
G
同理可得∴FM=FH. ∴FG=FH, ∴点F在∠BAC的平分线上.
M H
12.3.2 角平分线的判定
3.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC. 求证:AM是∠DAB的平分线. 解:如图,作MN⊥AD于N,
∵DM平分∠ADC,∠C=∠DNM=90°
E
B
D
┐
A
FC
DB=DC,
∴Rt△BDE≌Rt△CDF(HL). ∴DE=DF.
∴即AD是∠BAC的平分线.
12.3.2 角平分线的判定
二 三角形的内角平分线
探究1
分别画出以下三角形的三个内角的角平分线,你发现了什么?
A
A
A
B
C
┐
B
C
B
C
三角形的三条角平分线相交于一点,且交点位于三角形的内部.
针对训练
1.如图,在直角△ABC 中,AC=BC,∠C =90°,AP 平分∠BAC,BD
平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC 于点 M,若 OM
=4.
(1) 求点 O 到△ABC 三边的距离和;
B
解:如图,过点 O 作 ON⊥BC 于点 N,过点
O 作 OE⊥AB 于点 E,
A. 110° B. 120° C. 130°
D. 140°
解析:由于 O 到△ABC 三边的距离相等, 故 O 是三条内角平分线的交点, 即 BO,CO 都是内角的平分线,
12.3.2 角平分线的判定
则∠OBC=1∠ABC,∠OCB=1∠ACB.
2
2
∵∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴FG=FM.
G
同理可得∴FM=FH. ∴FG=FH, ∴点F在∠BAC的平分线上.
M H
12.3.2 角平分线的判定
3.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC. 求证:AM是∠DAB的平分线. 解:如图,作MN⊥AD于N,
∵DM平分∠ADC,∠C=∠DNM=90°
人教版八年级上册第12章全等三角形12.3角的平分线的判定课件(共21张PPT)
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 4:30:01 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
知识点:角的平分线的判定 【例1】课本练习题
课堂导学
【答案】证明:过点P作PD⊥AN, PE⊥AM, PF⊥CB,垂足分别为D,E,F. ∵CP平分∠MCB,PE⊥AM,PF⊥CB. ∴PE=PF,同理,PD=PF. ∴PD=PE,∴AP平分∠BAC. 【点拔】涉及证角平分线问题,常作角两边 的垂线段.再推证两条垂线段相等.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
人教版八年级数学上册12.3.2角平分线的判定课件
D NP
F M
同理,PE=PF.
B
E
C
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
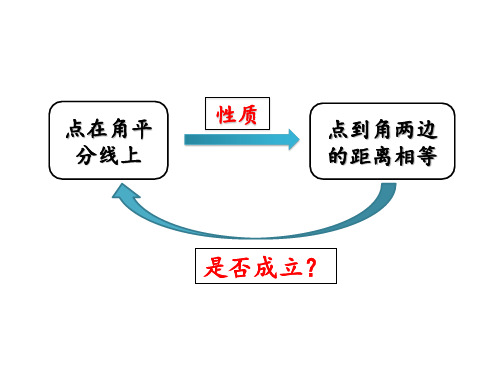
结论想:一三想,角点形P在的∠三A的条平角分平线上分吗线?交这说于明一三点角, 并形且的三这条点角到平分三线边有的什距么关离系相?等.
3、如图所示是一块三角形的草坪,现要在草坪上建 一凉亭供大家休息,要使凉亭到草坪三条边的距离相
∵BD=CD,BE=CF ∴ Rt△BDE ≌ Rt△CDF(HL) ∴DE=DF ∴ AD平分∠BAC
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF (1)求证:AD平分∠BAC; (2)猜想写出AB+AC与AE之间的
等量关系并给予证明.
(2)猜想:AB+AC=2AE 证明:由(1)得AD平分∠BAC
等,凉亭的位置应选在( C )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点 C.△ABC三条角平分线的交点 D.△ABC三条高所在直线的交点 4、如图,∠AOB=70°,QC⊥OA于C, QD⊥OB于D,若QC=QD,则∠AOQ=__3_5_°
1.角的内部到角的两边的距离相等的点在角的平分线上
解得x 2.5 在图上取OD 2.5cm, A
DS
B
C
D点即为集贸市场的位置
2、如图,△ABC的角平分线BM,CN相交于点P。 求证:点P到三边AB、BC、CA的距离相等
证明:过点P作PD⊥AB于D, PE⊥BC于E,PF⊥AC于F
∵BM是△ABC的角平分线, 点P在BM上, ∴PD=PE.
A
用符号语言表示为:
A
∵ PD⊥OA,PE⊥OB, PD=PE.
人教版八年级上册12.3 第2课时 角平分线的判定 课件(共13张PPT)

第十二章 全等三角形
12.3 角的平分线的性质 第2课时
角平分线的判定
学习目标
1.理解角的内部到角两边距离相等的点在角的平分线上(角的判定); 2.能利用角的判定定理解决简单的几何问题。
复习回顾
问题1:关于角平分线,你知道什么? 问题2:角平分线性质的文字语言和几何语言?
复习回顾
角的平分线的性质: 角的平分线上的点到角的两边的距离相等.
. 一处
B. 两处
C. 三处
D. 四处
分析: 由于没有限制在何处选址,故要求的地址共有四处.
巩固新知
2. 如图,△ABC 中,∠C = 90°,AD 是△ABC 的角平分线, DE⊥AB 于 E,F 在 AC 上 BD=DF. 求证:CF=EB.
证明:∵AD 平分∠CAB, DE⊥AB,∠C= 90°(已知),
角的平分线上的点到角的两边的距离相等.
O
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点 Q 在∠AOB 的平分线上.
∴ QD=QE.
A D
Q EB
探究新知
证明: ∵ PD⊥OA,PE⊥OB(已知), ∴ ∠PDO=∠PEO= 90°(垂直的定义) . 在Rt△PDO 和Rt△PEO 中 PO=PO(公共边), PD=PE, ∴ Rt△PDO ≌ Rt△PEO(HL) . ∴ ∠ POD=∠POE. ∴点P在∠AOB 的平分线上.
总结新知
结论: 角的内部到角的两边距离相等的点在角的平分线上.
几何语言:
∵OC 是∠AOB 的平分线,PD⊥OA,PE⊥OB, ∴PD=PE (角的平分线上的点到角的两边的距离相等).
探究新知
反过来,到一个角的两边的距离相等的点是否一定在这个 角的平分线上呢?
12.3 角的平分线的性质 第2课时
角平分线的判定
学习目标
1.理解角的内部到角两边距离相等的点在角的平分线上(角的判定); 2.能利用角的判定定理解决简单的几何问题。
复习回顾
问题1:关于角平分线,你知道什么? 问题2:角平分线性质的文字语言和几何语言?
复习回顾
角的平分线的性质: 角的平分线上的点到角的两边的距离相等.
. 一处
B. 两处
C. 三处
D. 四处
分析: 由于没有限制在何处选址,故要求的地址共有四处.
巩固新知
2. 如图,△ABC 中,∠C = 90°,AD 是△ABC 的角平分线, DE⊥AB 于 E,F 在 AC 上 BD=DF. 求证:CF=EB.
证明:∵AD 平分∠CAB, DE⊥AB,∠C= 90°(已知),
角的平分线上的点到角的两边的距离相等.
O
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,点 Q 在∠AOB 的平分线上.
∴ QD=QE.
A D
Q EB
探究新知
证明: ∵ PD⊥OA,PE⊥OB(已知), ∴ ∠PDO=∠PEO= 90°(垂直的定义) . 在Rt△PDO 和Rt△PEO 中 PO=PO(公共边), PD=PE, ∴ Rt△PDO ≌ Rt△PEO(HL) . ∴ ∠ POD=∠POE. ∴点P在∠AOB 的平分线上.
总结新知
结论: 角的内部到角的两边距离相等的点在角的平分线上.
几何语言:
∵OC 是∠AOB 的平分线,PD⊥OA,PE⊥OB, ∴PD=PE (角的平分线上的点到角的两边的距离相等).
探究新知
反过来,到一个角的两边的距离相等的点是否一定在这个 角的平分线上呢?
八年级数学上册 第十二章 《角平分线的判定》课件 人教版

A
B
P
D
C
挑战自我
5、如图,点A、点B、点C分别是三位同学所在座 位,要在三点构成的△ABC内部确定一个点P存放 一个神秘礼盒,使点P到三边AB、AC、BC的距离 相等,这个点应取于何处?
三角形的三条角平分线 交于一点,这个点到三角形 三边的距离相等。
D F
.P
E
挑战自我
6、如图,BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,
作业布置:创优P31-32
谢谢指导!
A M
Q
O
N
B
小试锋芒
判断正误:
2、已知:Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上. A
M
Q
O
N
B
小试锋芒
3、如图,DE⊥AB于点E,DF⊥BC于点F, 且DE=DF,若∠DBC=55°,则∠ABC=______.
小试锋芒
4、如图,已知AB//CD,∠BCD=100°,点P到 AB、BC的距离相等,则∠PBC=______.
已知:PD⊥OA,PE⊥OB,垂足分 别为D,E,PD =PE.
求证:P在∠AOB的平分线上.
新知探究
角平分线的判定
角的内部到角的两边的距离相等的 点在角的平分线上
几何语言 ∵PD⊥OA,PE⊥OB, PD = PE ∴点P 在∠AOB的平分线上 (OP 平分 ∠AOB).
小试锋芒
判断题:
1、如图,若QM =QN,则OQ 平分∠AOB。
§12.3.2 角平分线的判定
情境引入
如图,长沙最近多雨水天气,要在S 区一点P放 置一个雨量器测量降水量,使它到两条路的距离相 等. 这个放置点应取于何处?
人教版八年级上册 12.3 角的平分线的判定(共18张PPT)

•
填空:
A
练一练 12
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
E
∴__D_C__=_D_E____
(__在__角__平__分___线__上__的___点__到__角___的__两__边__的_C__距__离__相D___等__)
B
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴_∠__1_=_∠__2___
B
等的点在角的平分线上
。 ∵ PDOA PEOB
PD = PE
\ OP 是 AOB的平分线
用途:判定一条射线是角平分线
•
9、要学生做的事,教职员躬亲共做; 要学生 学的知 识,教 职员躬 亲共学 ;要学 生守的 规则, 教职员 躬亲共 守。20 21/8/10 2021/8/10Tues day , August 10, 2021
(_到__一__个__角__的__两__边__的__距__离__相__等__的__点__,__在__这__个__角__平__分__线__上__。)
应用角平分线性质定理的逆定理
判断题: (1)如图,若QM =QN,则OQ 平分∠AOB;( X )
A M
Q
O
N
B
应用角平分线性质定理的逆定理
判断题:
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四
新人教版八年级上册课件:第12章 12.3角平分线的性质和判定(共66张PPT)

D
A
证明:作射线OP
∵
PD ^ OA
\
PE ^ OB
O E
P
PDO PEO 90
OP = OP (公共边) PD = PE ( 已 知 )
在 Rt△PDO 和Rt△PEO 中,
B
\ RtPDO≌ RtPEO ( HL) \ AOP BOP (全等三角形的对应角相等) \ 点P在 AOB 角的平分线上
OM=ON, MC=NC, OC=OC, ∴ △OMC≌ △ONC(SSS) ∴∠MOC=∠NOC B 即:OC平分∠AOB
A M
C
N
O
角的平分线上的点到这个角的两边的距离相等。 已知:如图,OC是∠AOB的平分线,点P在OC上,
PD⊥OA,PE⊥OB,垂足分别是D,E。 求证:PD=PE 证明:∵ PD⊥OA,PE⊥OB(已知)
D
C
F A E B N
课堂小结
1、画一个已知角的角平分线; 及画一条已知直线的垂线;
2、角平分线的性质:
角的平分线上的点到角的两边的距离相等. 3、角平分线的判定结论: 到角的两边的距离相等的点在角平分线上。
判定:到角的两边的距离相 等的点在角的平分线上。
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,QD=QE ∴点Q在∠AOB的平分线上. 性质:角的平分线上的点到角的两边的距离 相等. 用数学语言表示为: ∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上 ∴ QD=QE
B C E
怎样找三角形内到三角形三边距离相等的点?
如图,△ABC的∠B的外角的平分线BD与∠C 的外角的平分线CE相交于点P.
求证:点P到三边AB、BC、CA所在直线的距离 相等.
人教版八年级数学上册12.3 角的平分线的性质 课件

【课本P50 练习 第1题】
随堂演练
4.已知:如图,在△ABC中,AD是∠BAC的角平分线,且 BD=CD,DE⊥AB,DF⊥AC.垂足分别为E、F.求证:EB=FC. 证明:∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC
∴ DE=DF, ∠DEB=∠DFC=90 °, 在Rt△BDE 和 Rt△CDF中,
BD=CD, DE=DF , ∴ Rt△BDE ≌ Rt△CDF(HL). ∴ EB=FC.
课堂小结
角平分线
尺规 作图
性质
依据:SSS
一个点: 角平分线上的点 二距离: 点到角两边的距离 两相等: 两条垂线段相等
添加辅助 线解题
过角平分线上一点向 两边作垂线段
12.3 角的平分线的性质
角平分线的判定
(2) 分别以点M,N为圆心.大于 1 MN的长为半径画弧,两弧在 2 ∠AOB的内部交于点C.
A M
(3) 画射线OC.射线OC即为所求.
C
O
B
N
思考
1.为什么以大于
1 2
MN的长为半径作弧?
2.两弧的交点一定在∠AOB的内部吗?
A M
C
O
NB
结论
1.如果以小于 1 MN的长为半径作弧,所作的两弧
AD=AB,
CD=CB,
D
∴△ACD≌△ACB(SSS)
∴∠DAC=∠BAC.
∴AE平分∠DAB.
A
B C E
知识点一 用尺规作角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
A
思考 如果没有平分角的仪器, 我们用尺规作图也能画 出一个角的平分线吗?
O
B
知识点一 用尺规作角的平分线
随堂演练
4.已知:如图,在△ABC中,AD是∠BAC的角平分线,且 BD=CD,DE⊥AB,DF⊥AC.垂足分别为E、F.求证:EB=FC. 证明:∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC
∴ DE=DF, ∠DEB=∠DFC=90 °, 在Rt△BDE 和 Rt△CDF中,
BD=CD, DE=DF , ∴ Rt△BDE ≌ Rt△CDF(HL). ∴ EB=FC.
课堂小结
角平分线
尺规 作图
性质
依据:SSS
一个点: 角平分线上的点 二距离: 点到角两边的距离 两相等: 两条垂线段相等
添加辅助 线解题
过角平分线上一点向 两边作垂线段
12.3 角的平分线的性质
角平分线的判定
(2) 分别以点M,N为圆心.大于 1 MN的长为半径画弧,两弧在 2 ∠AOB的内部交于点C.
A M
(3) 画射线OC.射线OC即为所求.
C
O
B
N
思考
1.为什么以大于
1 2
MN的长为半径作弧?
2.两弧的交点一定在∠AOB的内部吗?
A M
C
O
NB
结论
1.如果以小于 1 MN的长为半径作弧,所作的两弧
AD=AB,
CD=CB,
D
∴△ACD≌△ACB(SSS)
∴∠DAC=∠BAC.
∴AE平分∠DAB.
A
B C E
知识点一 用尺规作角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
A
思考 如果没有平分角的仪器, 我们用尺规作图也能画 出一个角的平分线吗?
O
B
知识点一 用尺规作角的平分线
数学人教版八年级上册数学第十二章12.3角的平分线的判定 PPT课件

新知应用
例3 如图, ∠B=∠C=90°, M是BC的中点, DM平分∠ADC. (2) 线段CD、AB、AD间有怎样的关系?
解: (2)CD+AB=AD; 理由如下: ∵ME⊥AD, MC⊥CD, ∴∠C=∠DEM=90°, 在Rt△DCM和Rt△DEM中
DM=DM,
MC=ME, ∴Rt△DCM≌Rt△DEM(HL), ∴CD=DE,
新知应用
例2 如图, 已知∠CBD和∠BCE的平分线相交于点F, 求证: 点F在∠DAE的平分线上.
证明: 过点F作FG⊥AE, FH⊥AD, FM⊥BC, 垂足为G, H, M.
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
A
同理可得, ∴FM=FH,
∴FH =FG , ∴点F在∠DAE的平分线上.
课堂总结
内容
角平分线的 判定定理
作用
结论
角的内部到角两边距离相等的点在 这个角的平分线上.
判断一个点是否在角的平分线上.
三角形的三条角平分线相交于三角 形内一点.
感谢聆听
D N
P
∴PD=P点EP. 在∠A的平分线上.
B
同理PE=PF.
E
结∴论P:D=三PE角=形PF的. 三条角平分线交于一点, 称为三角
即点P形到的三边内A心B,, B并C,且CA这的点距到离三相边等.的距离相等.
F M
C
新知应用
例1 如图, 在△ABC中, 点O是△ABC内一点, 且点O到△ABC三边 的距离相等.若∠A=40°, 则∠BOC的度数为( )A
A D
则∠AOC与∠BOC 是否相等?
C
P
O
E
人教版八年级上册数学精品系列角平分线的判定PPT

D
A
在Rt△PDO和Rt△PEO 中,
OP=OP,
O
P
PD= PE,
∴Rt△PDO≌Rt△PEO( HL).
E B
∴∠AOP=∠BOP(全等三角形的对应角相等).
∴点P在∠AOB 的平分线上.
★判定定理: 角的内部到角的两边的距离相等的点在角的平分线上.
▼应用所具备的条件: (1)位置关系:点在角的内部;
CN相交
证明:过点P作PD、PE,PF分 别垂直于AB、BC,CA,垂足 分别为D、E、F.
A
ND
F
P
M
∵BM是△ABC的角平分线,
点P在BM上,
B
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
C E
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
(2)若△ABC的周长为32,求△ABC的面积.
解:连接OC.
SABC SAOC SBOC SAOB
1 AB OE 1 BC ON 1 AB OM
2
2
2
1 OM (AB BC OM ) 2
1 4 32 64
A
2
B
O
P
DM
C
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
(2)数量关系:该点到角两边的距离相等.
A
▼定理的作用:判断点是否在角平分线上. D
C
▼应用格式:
P
∵ PD⊥OA,PE⊥OB,PD=PE. O
E
B
∴点P 在∠AOB的平分线上.
人教版八年级上册数学课件 12.3 第2课时 角平分线的判定(共23张PPT)
人教版八年级数学上册1角平分线的性质与判定课件

角平分线的性质:在角的平分线上的点到这
个角的两边的距离相等。
D
∵ OP 是 AOB 的平分线
PD ^ OA PE ^ OB
O
\ PD = PE
用途:证线段相等
E
角平分线的判定到一个角的两边的距离相等的
点, 在这个角的平分线上。
∵ PD ^ OA PE ^ OB
A C
P B
PD = PE
\ OP 是 AOB 的平分线
(点D到AB的距离是3)
C
D
A
E
B
如图,由 PD ^ OA 于点 D , PE ^ OB
于点 E,PD= PE , 可以得到什么结论 ?
到一个角的两边的距离相等 的点, 在这个角的平分线上。
已知:如图, PD ^ OA ,
D
A
PE ^ OB ,垂足分别是
O
A、B,PD=PE ,
求证:点P在AOB 的角平分线上。
• ∵BM是△ABC的角平分线,点P在BM
上(已知)
A
• ∴PD=PE(在角平分线上的点到角的
两边的距离相等)
D
F
• 同理 PE=PF.
N PM
• ∴ PD=PE=PF.
B
C
• 即点P到边AB、BC、CA的距离相等
E
练习:
如图,三条公路相交,现在要修建一加 油站,使加油站到三条公路的距离相等, 问加油站该选在什么位置上?
A
C C′
B
课堂练习
5已知:如图,BE⊥AC于E, CF⊥AB于F, BE、CF相交于D, BD=CD 。 求证: AD平分∠BAC 。
B
F
A
D
E
人教版八年级数学上册《12.3第2课时角平分线的判定》

角的内部到角两边距离相等的 点在这个角的平分线上
角平分线 作 用 的判定定理
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
灿若寒星
O 解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
灿若寒星
D S
C
典例精析
例2已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
A
N
P
M
B
C
灿若寒星
证明:过点P作PD,PE,PF分
别垂直于AB,BC,CA,垂足 分别为D,E,F.
A
D
N
F
P
M
∵BM是△ABC的角平分线,
点BM上,
B
∴PD=PE.同理PE=PF.
C E
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
想一想:点P在∠A的平分线上吗?这说明三角形的三条角 平分线有什么关系? 点P在∠A的平分线上.
这说明三角形的三条角平分线相交于一点,这一点到三角 形三边的距离相等.
相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
A
(
∴点D在∠EPF的平分线上. ∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
34 P
12 B E DFC
∴∠3=∠4,∴AD平分∠BAC.
灿若寒星
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F, 求证:点F在∠DAE的平分线上.
灿若寒星
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.
人教版八年级上册数学123角的平分线的性质优秀课件

OP=OP(公共边),
O
P
PD= PE(已知 ),
∴Rt△PDO≌Rt△PEO( HL).
E B
∴∠AOP=∠BOP (全等三角形的对应角相等).
∴点P在∠AOB的平分线上.
探究新知
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上. 应用所具备的条件:
(1)位置关系:点在角的内部; (2)数量关系:该点到角两边的距离相等.
BC=DC.将点A放在角的顶点,AB和AD沿着角的两边
放下,沿AC画一条射线AE,AE就是角平分线,你能
说明它的道理吗?
A
其依据是SSS,两全等三角形的 对应角相等.
D
B
(E)C
探究新知
【思考】如果没有此仪器,我们用数学作图做 请大家找到用尺规作角的平分线的方法,并说明
第一课时
角的平分线的性质
导入新知
下图是一个平分角的仪器,其中AB= AD,BC=DC. 将点A放在角的顶点,AB和AD 沿着角的两边放下,沿 AC画一条射线AE,AE 就是这个角的平分线,你能说
A
明它的道理吗?
D
B
C E
素养目标
3. 熟练地运用角平分线的性质解决实际 问题. 2. 探究并认知角平分线的性质.
P在∠AOB的平分线上.
3
2.如图,AB∥CD,点P到AB,BC,CD的距离相等,则
点P是 ∠ABC的平分线与 ∠BCD 的平分线的交点.
探究新知
知识点 2 三角形的内角平分线
分别画出下列三角形三个内角的平分线,你发现 了什么?
发现:三角形的三条角平分线相交于一点.
探究新知 分别过交点作三角形三边的垂线,用刻度尺量一
角平分线的性质(课件)人教版数学八年级上册

拓展训练 2.如图,△ABC 中,∠C = 90°,AD 是△ABC 的角
平分线,DE⊥AB 于 E,F 在 AC 上 BD=DF.求证:CF=EB.
证明:∵AD 平分∠CAB,DE⊥AB,∠C= 90°(已知), ∴CD=DE (角的平分线的性质). 在Rt △CDF 和 Rt△EDB 中, CD=DE (已证),DF=DB(已知), ∴ Rt△CDF ≌ Rt△EDB(HL). ∴ CF=EB (全等三角形对应边相等).
互动新授 思考
如图,要在S区建一个集贸市场,使它到公路、铁路的距 离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建 于何处(在图上标出它的位置,比例尺为1:20000)?
S
互动新授
解:在Rt△ABC与Rt△ABD中:
AB=AB
BC=BD
∴ Rt△ABC ≌ Rt△ABD(HL).
∴∠CAB=∠DAB
M
即点B在∠CAD的角平分线上
你能得出什 A么结论呢?
C
D
B S
N
角的平分线的判定: 角的内部到角的两边的距离相等的点在 角的平分线上.
典例精析
例:如图,△ABC的角平分线BM,CN相交于点P.求证:点P 到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB交于点D,PE⊥BC交于点E,
PF⊥AC交于点F.
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE.
∵AC=BC,
∴AE=BC,
∴△DEB的周长为8cm.
课堂小结
三角形的角 平分线
角的平分线上的点到角的两边的距离相等.
角的内部到角的两边的距离相等的点在 角的平分线上.
人教版八年级(上)角平分线的判定PPT-公开课

【名师示范课】人教版八年级上册12. 3.2角 平分线 的判定 课件-公 开课课 件(推 荐)
3.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在 OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
证明:∵OD平分线∠POQ, ∴∠AOD=∠BOD. 在△AOD与△BOD中, ∵OA=OB,∠AOD=∠BOD,OD=OD, ∴△AOD≌△BOD. ∴∠ADO=∠BDO. ∵CM⊥AD,CN⊥BD, ∴CM=CN.
C
温馨提示:不存在垂线段———构造应用
变式1:如图,在直角△ABC中,∠C=900,AP平分∠BAC,BD平分 ∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4. (2)若△ABC的周长为32,求△ABC的面积.
解:连接OC
SABC SAOC SBOC SAOB
1 AB OE 1 BC ON 1 AB OM
讲授新课
一 角平分线的判定 问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这
个新结论正确吗?
角平分线的性质: 角的平分线上的点到角的两边的距离相等. 几何语言:
A
D C
∵ OC平分∠AOB, 且PD⊥OA, PE⊥OB
P
O
E
B
∴ PD= PE 猜想:
思考:这个结论正 确吗?
角的内部到角的两边距离相等的点在角的平分线上.
O
∴点P 在∠AOB的平分线上.
A D
C
P
E
B
典例精析
例1:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰ 20000)?
O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何语言描述: ∵ OC平分∠AOB, 且PD⊥OA, PE⊥OB.
∴ PD= PE. 不必再证全等
A D
P到OA的距离
C 角平分线上的点
P
O
E
B P到OB的距离
2.我们知道,角平分线上的点到角的两边的距离相 等.那么到角的两边的距离相等的点是否在角的平 分线上呢?
到角的两边的距离相等的点在角的平分线上.
PE的距离与到PF的距离相等,判断AD是否平分
∠BAC,并说明理由.
解:AD平分∠BAC.理由如下: ∵D到PE的距离与到PF的距离相等, ∴点D在∠EPF的平分线上. ∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3. B E
(
A
34 P
12 DFC
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
3.已知:如图,OD平分∠POQ,在OP、OQ边上取 OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于 N.求证:CM=CN. 证明:∵OD平分线∠POQ, ∴∠AOD=∠BOD. 在△AOD与△BOD中, ∵OA=OB,∠AOD=∠BOD,OD=OD, ∴△AOD≌△BOD. ∴∠ADO=∠BDO. ∵CM⊥AD,CN⊥BD, ∴CM=CN.
你能证明这 个结论吗? 发现:过交点作三角形三边的垂线段相等
证明结论
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,
PF分别垂直于AB,BC, CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
A
ND
F
P
M
点P在BM上,
周长
2
例2 如图,在△ABC中,点O是△ABC内一点,且点O
到△ABC三边的距离相等.若∠A=40°,则∠BOC的
度数为( A ) A.110° B.120°
C.130°
解D析.:14由0°已知,O到三角形三边的距离
相等,所以O是内心,即三条角平分线
的交点,AO,BO,CO都是角平分线, 所∠B以C有O=∠C∠BAOC=O=∠AB∠12 OAC=B,∠12 ABC, ∠ABC+∠ACB=180°-40°=140°,
八年级数学上(RJ)
第十二章 全等三角形
12.3 角的平分线的性质
第2课时 角平分线的判定
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解角平分线判定定理.(难点) 2.掌握角平分线判定定理内容的证明方法并应用其解题. (重点) 3.学会判断一个点是否在一个角的平分线上.
导入新课
复习回顾
1.叙述角平分线的性质定理 角的平分线上的点到角的两边的距离相等.
讲授新课
一 角平分线的判定 问题:交换角的平分线的性质中的已知和结论,你能
得到什么结论,这个新结论正确吗?
角平分线的性质:
A
角的平分线上的点到角的两边的距离相等. D
几何语言:
C
∵ OC平分∠AOB,
O
且PD⊥OA, PE⊥OB
P
E
B
∴ PD= PE 猜想:
思考:这个结 论正确吗?
角的内部到角的两边距离相等的点在角的平分线上.
P
∵ PD⊥OA,PE⊥OB,PD=PE. O
E
B
∴点P 在∠AOB的平分线上.
典例精析
例1:如图,要在S区建一个贸易市场,使它到铁路 和公路距离相等, 离公路与铁路交叉处500米,这 个集贸市场应建在何处(比例尺为1︰20000)?
O
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
D S
C
方法点拨:根据角平分线的判定定理,要求作的点到 两边的距离相等,一般需作这两边直线形成的角的平 分线,再在这条角平分线上根据要求取点.
二 三角形的内角平分线 活动1 分别画出下列三角形三个内角的平分线,你 发现了什么?
发现:三角形的三条角平分线相交于一点
活动2 分别过交点作三角形三边的垂线,用刻度尺量一 量,每组垂线段,你发现了什么?
B
∴PD=PE.同理PE=PF.
C E
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
想一想:点P在∠A的平分线上吗?这说明三角形
的三条角平分线有什么关系?
A
点P在∠A的平分线上.
D
N
F
P
M
B
C
E
结论:三角形的三条角平分线交于一点,并且
这点到三边的距离相等.
变式1:如图,在直角△ABC中,∠C=90°,AP平分
P E
B
∴∠AOP=∠BOP(全等三角形的对应角相等).
∴点P在∠AOB 角的平分线上.
知识总结
判定定理:
角的内部到角的两边的距离相等的点在角的平分线上.
应用所具备的条件: (1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
A
定理的作用:判断点是否在角平分线上. D
C
应用格式:
∠OBC+∠OCB=70°, ∠BOC=180°-70°=110°.
方法总结
由已知,O 到三角形三边的距离相等,得O是 内心,再利用三角形内角和定理即可求出∠BOC的 度数.
归纳总结
角的平分线的性质 角的平分线的判定
图形C PFra bibliotekC P
已知 条件
结论
OP平分∠AOB PD⊥OA于D PE⊥OB于E
PD=PE
PD=PE PD⊥OA于D PE⊥OB于E
OP平分∠AOB
当堂练习
1. 如图,某个居民小区C附近有三条两两相交的道路 MN、OA、OB,拟在MN上建造一个大型超市,使得 它到OA、OB的距离相等,请确定该超市的位置P.
A
M
小区C
P
O
N
B
2. 如图所示,已知△ABC中,PE∥AB交BC于点E,
PF∥AC交BC于点F,点P是AD上一点,且点D到
证明猜想
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E, PD=PE.求证:点P在∠AOB的角平分线上.
证明:作射线OP,∵PD⊥OA,PE⊥OB. ∴∠PDO=∠PEO=90
D
A
在°R,t△PDO和Rt△PEO 中,
OP=OP(公共边),O PD= PE(已知 ),
∴Rt△PDO≌Rt△PEO( HL).
解:连接OC
SABC SAOC SBOC SAOB
1 AB OE 1 BC ON 1 AB OM
2
2
2
1 OM ( AB BC OM ) 2
1 4 32 64
A
2
B
O
P
DM
C
知识与方法
1.应用角平分线性质: 存在角平分线 条件 涉及距离问题
2.联系角平分线性质:
距离
面积 s 1 ch
∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作 OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
B
12
O
P
A
DM
C
温馨提示:不存在垂线段———构造应用
变式1:如图,在直角△ABC中,∠C=900,AP平分 ∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作 OM⊥AC,若OM=4. (2)若△ABC的周长为32,求△ABC的面积.
