第六章-3菲涅尔衍射和波带片
合集下载
菲涅尔衍射.ppt

当波长、P点的位置r0、 圆孔位置R给定后,由
N
2 N
(1
1)
r0 R
N与圆孔的大小ρN有关,孔大,露出的的波带多, 衍射效应不显著,孔小,露出的的波带少,衍射效
应显著;
当孔趋于无限大- -即 没有光阑时,
播到任一点P时的振幅,只要把球面波相对于P分成半
波带,将第一个和最后一个(第N个)带所发出的次
波的振幅相加或相减即可。
12/28/2019
返回
(3) N与ρN间的关系
D
图示O为点光源,DD’ 为光阑,其上有一半径 为ρN的圆孔,S为通过
圆孔的波面-球冠(球 冠的高为h),P为圆孔
对称由上任意一点。
半波带与观察点P的位置、圆孔的大小、波长等有关。
12/28/2019
返回
S BnN
(2) 合振幅的计算
Rh
rN
O R B0
r0
P
N个半波带的发次波在P点叠加
的合振幅AN
AN a1 a2 a3 a4 a5 ... (1) N 1 aN
aN:第N个半波带所发在P点的次波振幅 “-”:相邻两个半波带所发次波到达P点相位差为
(4)轴外点Q的衍射
12/28/2019
返回
(1)r0对衍射现象的影 响
当波长、圆孔位置R、大 小ρh给定后,由
N
2 N
(1
1)
r0 R
P点的振幅与P点的位置r0有关,即移动观察屏,P
点出现明暗交替变化;
随r0增大,N减小,菲涅耳衍射效应显著;
当r0大到一定程度时,r0→∞,露出的波带数N不 变化,且为
惠更斯菲涅耳衍射课件

生物医学成像
X射线成像
X射线在穿过人体组织时发生衍射 ,通过分析衍射产生的图像可以 诊断疾病。
超声成像
超声波在遇到人体组织时发生衍射 ,通过分析衍射产生的回波可以生 成人体内部结构的图像。
光学显微镜
光学显微镜利用光的衍射和干涉现 象来观察细胞和组织的结构。
04 实验演示
单缝衍射实验
总结词
通过单缝衍射实验,观察光通过单缝产生的衍射现象,了解衍射的基本原理。
的变化引起的,而物理衍射是由于波动性质引起的。
按光强分布分类
02
根据光强分布的不同,衍射可以分为会聚衍射、发散衍射和干
涉衍射等类型。
按波长与障碍物尺寸关系分类
03
根据波长与障碍物或孔缝尺寸的关系,衍射可以分为小孔衍射
、大孔衍射和多缝衍射等类型。
0动现象的基本方程,其形式为$frac{partial^2 Phi}{partial t^2} = c^2 nabla^2 Phi$,其中$Phi$是波动场,$c$是波速。
透镜制造
在制造透镜时,需要考虑 到材料的衍射特性,以消 除或减少像差。
干涉仪
干涉仪利用衍射原理来测 量波长和相干长度。
雷达 and sonar
目标识别
雷达和声纳通过分析衍射 产生的回波来识别目标。
距离测量
通过测量衍射回波的时间 差,可以计算出目标与探 测器之间的距离。
速度测量
通过分析衍射回波的多普 勒频移,可以测量目标的 速度。
实现更高效的衍射器件
利用衍射现象,可以设计出各种光学器件,如光束整形器 、光束分束器等。未来可以通过优化设计,提高这些器件 的效率和稳定性。
探索其他物理场的衍射现象
除了光学领域,其他物理场如电磁波、声波等也存在衍射 现象。未来可以进一步探索这些物理场的衍射现象及其应 用。
菲涅尔圆孔衍射和圆屏衍射(修正版)
就形成菲涅耳波带片。
2)例题:
波带片的孔径内有20个半波带,遮挡偶数的 半波带,求轴上场点P0处的光强比自由传播 时大多少倍? 解:
A' A1 A3 A5 A19 10 A1 20 A0
I ' A' 400 A0 400 I 0
2 2
波带片相当于透镜,可以会聚光波。
(4)求露出前n个半波带的圆孔衍射中心场点Po 处的合振幅
取:
A1
A3 Ak A(P) A4
· · ·
…
A2 A1
则有:
(a) k为奇数 A3 Ak A(P)
1 A( P0 ) [ A1 (1) ( n 1) An ] 2
I A ( P0 )
2
A2 (b) k为偶数 波带法中的振幅矢量
2R (1 cos )
2
,
S
R
M
O
r
b
P0
R 2 ( R b) 2 r 2 其中:cos 2 R ( R b)
d 2R sin d
2
得: d 2Rdr
rdr sin d R ( R b)
r
Rb
把 d 看成半波带面积
半波带法1要解决的问题求菲涅耳衍射中心场点p处的光强度2解决方法采用近似处理的方法updupup3步骤1把波前分割成为一系列环形半波带使得相邻两个波带的边缘点到p点的光程差等于半个波长圆孔的菲涅耳衍射与波带分割原则upape30304比较各个振幅的大小球冠面积
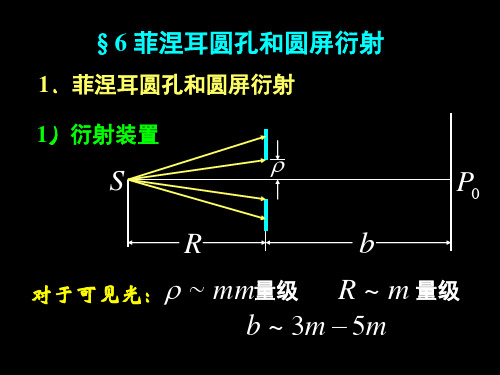
§6 菲涅耳圆孔和圆屏衍射
1.菲涅耳圆孔和圆屏衍射
3) 菲涅耳波带片的半径公式
M R k S hO
2)例题:
波带片的孔径内有20个半波带,遮挡偶数的 半波带,求轴上场点P0处的光强比自由传播 时大多少倍? 解:
A' A1 A3 A5 A19 10 A1 20 A0
I ' A' 400 A0 400 I 0
2 2
波带片相当于透镜,可以会聚光波。
(4)求露出前n个半波带的圆孔衍射中心场点Po 处的合振幅
取:
A1
A3 Ak A(P) A4
· · ·
…
A2 A1
则有:
(a) k为奇数 A3 Ak A(P)
1 A( P0 ) [ A1 (1) ( n 1) An ] 2
I A ( P0 )
2
A2 (b) k为偶数 波带法中的振幅矢量
2R (1 cos )
2
,
S
R
M
O
r
b
P0
R 2 ( R b) 2 r 2 其中:cos 2 R ( R b)
d 2R sin d
2
得: d 2Rdr
rdr sin d R ( R b)
r
Rb
把 d 看成半波带面积
半波带法1要解决的问题求菲涅耳衍射中心场点p处的光强度2解决方法采用近似处理的方法updupup3步骤1把波前分割成为一系列环形半波带使得相邻两个波带的边缘点到p点的光程差等于半个波长圆孔的菲涅耳衍射与波带分割原则upape30304比较各个振幅的大小球冠面积
§6 菲涅耳圆孔和圆屏衍射
1.菲涅耳圆孔和圆屏衍射
3) 菲涅耳波带片的半径公式
M R k S hO
6.3 菲涅耳半波带法和振幅矢量图解法ppt课件

ds2R2sind
sind rkdkr
R(Rr0)
物理科学与信息工程学院
5
由上两式可得:
ds 2Rdrk
rk R r0
因为rk>>,故可将drk看着相邻半波带间r的差值/2,ds看着半波带的面积, 于是有
由此可见:
Sk R
rk R r0
Sk
与k无关
rk
即它对每一个半波带都是相同的,这样影响a k的大小因素中,只剩下倾斜因 子 K( k)了。
I0
1 4
a12
物理科学与信息工程学院
9
三、矢量合成法
各半波带在P点引起的振动可以用上下交 替的矢量来表示。为清楚起见,将各矢量 彼此错开,如图
矢量a1的起点在某一水平基线上,其余各 矢量的起点都与前一矢量的终点等高,从 基线指向最末一矢量ak终点的即为合振动 Ak的振动矢量。
a1
a2
a 3 a 5 Ak a4
1例说明惠更斯-菲涅耳原理的应用。如图:
O为点光源,S为任一时刻的波面,R为半 径。
S
为了确定光波到达对称轴
上任一点P时,波面S所起 o 的作用,连O,P与球面
相交于B点,B点称为P点
对于波面的极点。
R
r4 r3 B r0 r2
r1
P
令PB0=r0,
设想将波面分为许多环形带,使从每两个相邻带的相应边缘 到P点的距离相差半个波长。
a4
a3 2
a5 2
, ak
ak1 2
ak1 2
物理科学与信息工程学院
7
当k为奇数时,则
A k a 2 1 (a 2 1 a 2 a 2 3 ) (a 2 3 a 4 a 2 5 ) .. .a 2 . k.
第六章-3菲涅尔衍射和波带片

A' =
光强比等于振幅比的平方
A1 2
I 波带片 I自由传播
=(
A 2 ) = 400 A'
82
(6-27)
1 1 kλ + = R b ρ k2
令
(a)偶数半波带涂黑的波带片
(b)奇数半波带涂黑的波带片
图 6-27 波带片
81
第六章 光的衍射与光学仪器的分辨本领
f = ρ k2 / k λ = ρ12 / λ
则有
(6-28)
1 1 1 + = R b f
(6-29)
这一公式与高斯成像公式(2-8)的形式相同,说明波带片的成像作用与透镜相似。 从式(6-28)可以看出,波带片的焦距与波长成反比,如果用白光照明,会出现色差。 我们可以把波带片看作一个特殊的光栅, 对于入射的平行光, 这一光栅的零级衍射光位 于式(6-29)确定的焦点上,光栅还有其它级次的衍射,所以波带片有多个实焦点,分别位于 、-f /7,…。这些次焦点的 f,f /3,f /5,f /7,…;还有多个虚焦点,分别位于-f,-f /3,-f /, 光强比主焦点的光强弱很多。 与光学透镜相比,不论加工成本,还是加工周期,波带片都有优势,所以在一些特殊光 学系统中,可以用波带片取代传统的光学透镜。 例题 一块波带片的孔径内有 20 个半波带,奇数露出,偶数挡住,轴上场点的强度比自由传 播时大多少倍? 解:波带片在轴上场点产生的振幅为 A=A1+A3+A5+…+A19≈10A1 自由传播时的振幅为
1 [ A1 ( P0 ) − An ( P0 )] 。 2
图 6-26 半波带法中的矢量图
菲涅耳衍射现象分析 1)、自由传播 最后一个半波带上f (θn)=0,因此An=0,于是
菲涅尔衍射

• P2点与S的连线交波面于C2点。
–C2以下的半个波面被直边屏 遮挡,C2以上的半个波面也
有一部分被遮挡。
–P2点的合光场振幅矢量的一 端为Z,另一端为M1”,即为 M1”Z,
–P2点的光强度正比于(M1”Z)2。
M1”
• M1”随P2点的位置不同,沿着螺
线移动,
–P2离P0愈远,其上光强愈小; –当P2离P0足够远时,光强度
波带特点 P点的振幅
• 条状波带面积随波带 序数N的增大而快速 减小。
• 各波带在P点的光场复振幅, 当波带序数N的增大时,迅速 下降;
–波带面积减小、到P点的距 离增大、倾角加大。
• 不能应用环形波带的有关公式 进行讨论。如何做?
• 微积分思想:
–将每个直条波带按相邻波 带间相位差相等的原则,再 分成若干个波带元。
菲涅尔波带
2、菲涅尔透镜的焦距
若波带片是对应距离为z1的轴上点P0设计的, 当单色光 垂直照射波带片时,P0 为一亮点,称为波带片的焦点, z1 即为波带片的焦距。
由公式 得:
N
2 N
(1
1)
r0 R
f
z1
N2 N
1 R
1 r0
N
2 N
3、菲涅尔透镜的成像关系
s ﹣l
An (P)
a1 2
二.振幅矢量法 考虑每一个半波带分为更小的子波带—
r0
2
r0
i
2N
一个均匀的振幅矢量对P点的贡献 第一半波带分成N个子带
S
O
r0
P 第一半波带中心到边缘划分的各相 邻子带对应点相同的光程差 / 2N
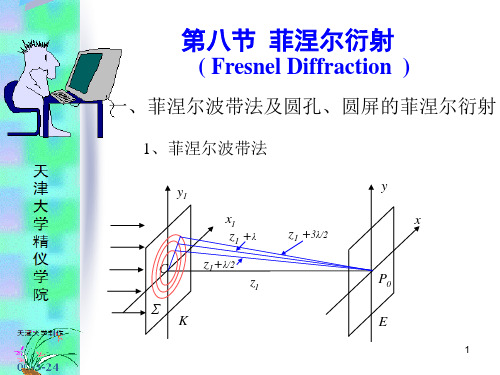
菲涅尔衍射
y x
P0
讨论:
Σ
K
E
1、圆屏较小时,轴上点P0总是亮点;
2、随P点离开P0点逐渐向外,其光强将时大时小变化,由于系统的 对称性,距离P0相同的点P有相同的光强。故衍射图样为同心圆。
3、圆屏较大时,P0点的光强度接近于0。
6
二、菲涅尔透镜
1、菲涅尔透镜
已知菲涅尔圆孔衍射P0点复振幅为:
E~ E~1 E~2 E~3 E~4 1n E~n
ei
k 2z
2
d
iz
e e 1
2
i 2
1 d
x
iz
1 d
2
e i 2
1 d
x ei
k 2z
2
d
iz
e e 1
2
i
2
1 d
x
iz
1 d
2
代入原式得:
E~(x, y
)
1
e
iz
1 d
2
cos 2
x
d
15
z
定义:不用透镜可对周期性物体成像的方法成为泰伯效应或泰伯 自成像(Selfimaging)。
12
说明: (以振幅型正弦光栅为例)
设光栅的振幅透射系数为
x1,y1
2
t(x1, y1) 1 cos d x1
z
若单位平面波垂直照射,刚刚透过光栅的光场为: E~(x1, y1) t(x1, y1)
13
被光栅调制的光场 E~(x1, y1) 传播到菲涅尔衍射区到达距离z
时的复振幅分布为:
E~x, y eikz iz
菲涅耳波带片PPTppt

制作步骤与注意事项
03
04
05
06
总结与展望
研究总结
在光学、声学、水文学等领域,菲涅耳波带片的研究已经取得了一些重要的成果,如在光学领域研究光的干涉和衍射等现象。
菲涅耳波带片在理论研究和实验研究方面都取得了一定的进展,但仍存在很多挑战和需要深入研究的问题。
菲涅耳波带片是一种由两个或多个同心环状波带构成的波动现象,具有较高的学术研究价值和应用价值。
高效去污
使用菲涅耳波带片可以快速清洁光学元件,提高生产效率
快速清洁
菲涅耳波带片可以有效地保护光学元件,延长其使用寿命
高效保护
03
医疗设备
菲涅耳波带片在医疗设备领域也有着广泛的应用,如眼科仪器、显微镜等
应用领域
01
光学制造
菲涅耳波带片在光学制造领域中得到了广泛应用,如相机、望远镜、激光器等
02
科学研究
特点
菲涅耳波带片具有结构简单、制造成本低、易于调整等优点,在光谱分析和光学通信等领域得到广泛应用。
03
菲涅耳波带片的特点
Байду номын сангаас
菲涅耳波带片是一种用于光学和光电子学中的元件,它通过将入射光波分解为一系列不同频率的波带,实现对光的衍射和散射。
菲涅耳波带片具有高透光性、高反射性和高定向性等特点,可广泛应用于光学干涉仪、光谱分析、光学显微镜、光信息处理等领域。
组装仪器
03
将制作好的波带片放置在显微镜的载物台上,并调整显微镜的倍数,使得可以清晰地观察到干涉现象。
01
02
准备材料
制作菲涅耳波带片需要准备透明介质、精密刻刀、尺子、显微镜等工具和材料。
绘制圆环
使用精密刻刀在透明介质上绘制多个同心圆环,每个圆环的宽度要非常窄,通常需要使用高精度的测量仪器进行测量。
《物理光学》菲 涅 耳 衍 射

变化, 且为
N
Nm
2 N
R
该波带数称为菲涅耳数,它是一个描述圆孔衍射效应的很重要 的参量。此后,随着r0的增大,P0点光强不再出现明暗交替的 变化,逐渐进入夫朗和费衍射区。而当r0很小时,N很大,衍 射效应不明显。当r0小到一定程度时,可视光为直线传播。
(2) N对衍射现象的影响
R和r0一定时,圆孔对P0露出的波带数N与圆孔半径有关, N∝ρ2 N 。 于是,孔大,露出的波带数多,衍射效应不显著; 孔小,露出的波带数少,衍射效应显著。当孔趋于无限大时,
它的一个优点是,适应波段范围广。比如用金属薄片制作的 波带片,由于透明环带没有任何材料,可以在从紫外到软X射 线的波段内作透镜用,而普通的玻璃透镜只能在可见光区内 使用。 此外, 还可制作成声波和微波的波带片。
4.5.1 菲涅耳半波带法
下图绘出了一个单色点光源S照射圆孔衍射的情况, P0是圆孔中 垂线上的一点,在某时刻通过圆孔的波面为MOM′, 半径为R。
M
S
R
P0
M‘
现在以P0为中心,以r1, r2, …, rN为半径,在波面上作圆, 把MOM′分成N个环带, 所选取的半径为 :
r1
r0
2
r2
r0
2
这样,相邻2个半波带(2,3),(8,9),(14,15)对场 点的贡献彼此抵消,只剩下1,7,13半波带,它们彼此的光程 差为3λ,在场点相干叠加增强,形成一个焦点。 菲涅耳波带片与普通透镜相比,还有另外一个差别:波带片的焦 距与波长密切相关,其数值与波长成反比,这就使得波带片的色 差比普通透镜大得多, 色差较大是波带片的主要缺点。
4.5.2菲涅耳波带片
在利用菲涅耳波带法讨论菲涅耳圆孔衍射时已经知道,由于相 邻波带的相位相反,它们对于观察点的作用相互抵消。因此, 当只露出一个波带时,光轴上P0点的光强是波前未被阻挡时的 四倍。对于一个露出 20 个波带的衍射孔,其作用结果是彼此 抵消,P0为暗点。现在如果让其中的1、3、5、……、19 等 10 个奇数波带通光, 而使 2、 4、 6、 ……、 20 等 10 个偶 数波带不通光, 则P0点的合振幅为
《菲涅耳衍射》PPT课件

N
2 N
(1
R)
2 N
(78)
R r0 r0
AN
a1 2
aN 2
(76)
a1 a2 a3 aN
(4)轴外点的衍射
对于轴外任意点 P 的光强度,原则上也可以用同样 的方法进行讨论。
M
P
M0M2M
S
O1M 1
2
P
0
MN R N hN
rN=r0+N /
2
S
S O O
r0
P
0
(4)轴外点的衍射
通常在半定量处理菲涅耳衍射现象时,均采用比较 简单、物理概念很清晰的菲涅耳波带法或图解法。
4.3.1 菲涅耳圆孔衍射—菲涅耳波带法(Fresnel diffraction by a circular aperture — Fresnel's zone construction )
1. 菲涅耳波带法
N
1
2 2
(73)
(3)倾斜因子 由上图可见,倾斜因子为
K( ) 1 cos (74)
2
将(72)-(74)式代入(66)式,可以得到各个波带在 P0 点产生的光振动振幅
aN
πR
R r0
1
cos N
2
(75)
可见,各个波带产生的振幅 aN 的差别只取决于倾角
N。
aN
SN rN
K ( )
(66)
这说明,当孔小到只露出一个波带时,P0 点的光强 度由于衍射效应,增为无遮挡时 P0 点光强度的四倍。
I1 a12
只露出一个波带时的光强
A
a1 2
(80)
无遮挡时的光强
菲涅耳波带片ppt

03
提高人们的生活品质。
THANKS
谢谢您的观看
光学仪器装配
在光学仪器装配过程中,菲涅耳波带片可以用来检测光学元件的表面平整度 和光学性能,以确保仪器装配的质量。
光学特性研究
光的干涉和衍射
通过使用菲涅耳波带片,可以研究光的干涉和衍射现象,例如观察彩色干涉条纹 和衍射花样,有助于理解光的行为和性质。
光的偏振
菲涅耳波带片可以用来研究光的偏振现象,例如观察偏振光的干涉和衍射,有助 于了解光偏振的特性和应用。
高精度切割机
用于精确切割菲涅尔波带片,通常采用 激光或机械切割方式。
光学平台
用于支撑和固定光学元件,通常由低膨 胀系数玻璃和金属框架组成。
光学胶水
用于将菲涅尔波带片粘合到光学平台上 。
制作步骤
1. 在光学平台上固定光学元件,确保表面平整、 无划痕和气泡等缺陷。
3. 将切割好的菲涅尔波带片粘合到光学平台上, 使用光学胶水进行固定。
2. 使用高精度切割机按照设计好的尺寸和形状切 割菲涅尔波带片,确保边缘平整、无毛刺。
4. 进行光学性能测试,检查波带片的透光性和反 射性是否符合设计要求。
调整与优化
01
调整菲涅尔波带片的角度
通过调整菲涅尔波带片的角度,可以改变光的透射和反射方向,以达
到预期的光学效果。
02
优化光学胶水的选择
不同的光学胶水会对光学性能产生影响,因此需要选择适合的光学胶
现代光学技术应用
高精度光学测量
在高精度光学测量中,如光学元件表面质量检测、光学波前 检测和光学表面形貌测量等领域,菲涅耳波带片可以作为干 涉仪的核心元件,提高测量精度和可靠性。
光学通信和传感
在光学通信和传感技术中,菲涅耳波带片可以用来实现光束 整形、光束调制和光束耦合等功能,提高通信和传感的效率 和精度。
光的衍射现象

S
观察比较方便,但定量计算却很复杂(需完成复杂 的Fresnel积分)。
2.Fraunhofer衍射(远场衍射)
光源和光屏到障碍物或孔隙的距离可以认为是无限远 的,即实际上使用的是平行光束。比Fresnel衍射更重 要。
L2
L1பைடு நூலகம்
S
o
Fraunhofer衍射可通过使用简单实用的方法——半波带 法得到重要而近似准确的结果。
a
a
2
U ( ) C eikr dx
a
2
C eikxsin dx
a
C
eikx sin
ik sin
x a
|2
x a 2
2
2
C
1
ika sin
ika sin
[e 2 e 2 ]
ik sin
C 1 2i sin( ka sin )
ik sin
2
2C
sin(
ka
sin
2
)
ac
sin
k sin
d
在光孔和接收范围满足傍轴条件情况下, 0 0,
r r0 (场点到光孔中心的距离)
U (P) i U 0(Q)eikrd
r0 (0 )
三、衍射现象的分类
分类的标准——按光源和考察点(光屏)到障 碍物距离的不同进行分类。
1 Fresnel衍射(近场衍射)
障碍物(孔隙)距光源和光屏的距离都是有限的,或 其中之一是有限的。
A
(b) n为偶数
半波带法中的振动矢量图
A(P0 )
1 2
[ A1
(1)n1
An
]
讨论:1)自由传播情形,整个波前裸露
f (n ) 0,从而An 0
观察比较方便,但定量计算却很复杂(需完成复杂 的Fresnel积分)。
2.Fraunhofer衍射(远场衍射)
光源和光屏到障碍物或孔隙的距离可以认为是无限远 的,即实际上使用的是平行光束。比Fresnel衍射更重 要。
L2
L1பைடு நூலகம்
S
o
Fraunhofer衍射可通过使用简单实用的方法——半波带 法得到重要而近似准确的结果。
a
a
2
U ( ) C eikr dx
a
2
C eikxsin dx
a
C
eikx sin
ik sin
x a
|2
x a 2
2
2
C
1
ika sin
ika sin
[e 2 e 2 ]
ik sin
C 1 2i sin( ka sin )
ik sin
2
2C
sin(
ka
sin
2
)
ac
sin
k sin
d
在光孔和接收范围满足傍轴条件情况下, 0 0,
r r0 (场点到光孔中心的距离)
U (P) i U 0(Q)eikrd
r0 (0 )
三、衍射现象的分类
分类的标准——按光源和考察点(光屏)到障 碍物距离的不同进行分类。
1 Fresnel衍射(近场衍射)
障碍物(孔隙)距光源和光屏的距离都是有限的,或 其中之一是有限的。
A
(b) n为偶数
半波带法中的振动矢量图
A(P0 )
1 2
[ A1
(1)n1
An
]
讨论:1)自由传播情形,整个波前裸露
f (n ) 0,从而An 0
菲涅耳波带片PPT

历史背景
菲涅耳波带片是由法国物理学家奥古斯丁·菲涅耳在19世纪 初提出和研究的。
菲涅耳波带片是波动光学中的一个重要概念,自提出以来 一直被广泛研究和发展。
现实应用
菲涅耳波带片在光学领域有着 广泛的应用,例如在全息技术 中制作全息图和全息干涉仪。
在声学领域,菲涅耳波带片可 以用来分析和设计声学系统, 例如在音乐和音响工程中。
光学通信和网络
光学加密和安全
波带片可以用来实现高速、高效的光束耦合 和整形,提高光学通信和网络的性能和效率 。
波带片可以用来实现复杂的光学加密技术, 保护信息安全。
光束质量优化
光学信息处理
波带片可以用来改善激光等光源光束的质量 和聚焦性能,提高光学仪器和应用的精度和 灵敏度。
波带片可以用来实现光束的快速、灵活和高 效变换,促进光学信息处理技术的发展。
THANK YOU.
制作方法
材料
需要一片透明的硬质材料,如玻璃或塑料,以及一些精细的切割工具。
步骤
首先在硬质材料上绘制一个圆,并按照所需的环数将圆划分成若干个等分的 扇形;然后在每个扇形中以不同的半径向外切割,直至达到圆的边界;最后 将中心圆形区域保留作为波带片的基底。
应用领域
光学研究
菲涅耳波带片常用于光学研究 中,例如光的衍射、散射和干
如果发现有缺陷,需要重新制作 菲涅耳波带片。
在确定菲涅耳波带片质量合格后 ,可以使用其他检测设备进行性 能测试,例如光谱仪、拉曼光谱
仪等。
04
实验:菲涅耳波带片的应用
双缝实验
实验原理
双缝实验是用来研究光的波动 特性的实验,通过双缝的干涉 和衍射现象来证明光的波动性
。
实验装置
双缝实验装置包括光源、狭缝 、屏幕和观察装置。
菲涅耳波带片依据菲涅耳圆孔衍射的讨论

a1 a2 a3 aN
由于这种变化比较缓慢, 所以近似有:
a1 a3 a2 2 a3 a5 a4 2
a2m
a 2 m 1 a 2 m 1 2
AN a1 a2 a3 a4 aN
则N为奇数时
N为偶数时
a1 a N AN 2 2
一般情况下 r0 >> N ,故
R Nr0 R r0
2 N
2 N
也可表示成
R N 1 R r 0
2.
(1) r0对衍射现象的影响
(2) N 对衍射现象的影响 (3) 波长对衍射现象的影响
(4) 轴外点的衍射
(1) r0对衍射现象的影响
2 N R N 1 R r0
r0+3/2
N
S
R d
M
r0+
r0+/2 P0
M
h
r0
以P0为中心、r1, r2, …, rN为半径,在波面上作圆。
① 菲涅耳半波带的划分
MOM 分成 N 个环带,所选取的半径为 :
2 2 r2 r0 2 N rN r0 2
相邻两环带上的相应两点到 P0 点的光程差为半个波长, 这样的环带叫菲涅耳半波带。
N 和 R 一定,随 r0 的增大,N 减小,菲涅耳衍射效应显著。
r0 很大时,可视为 r0 ,露出的波带数 N 不再变化,且
ΔS N aN K ( ) rN
③ 半波带面积ΔSN 的计算
r0+N/2 M
N
S
点共露出 N 个波带,这 N 个波带相应的
波面面积是:
光学 菲涅耳衍射

sin u u
B'
dx
θ
b
x
B
θ
P0
P F
三、光强分布特点
sin 2 u 由 I P = I 0 2 可知 : 不同的θ对应着不同的观察点 也对应着不同的光强值 , . u dI P d sin 2 u 2 sin u (u cos u sin u ) = 0 时, I P取得极值,即 : 2 = =0 当: 3 u du du u πb ① λ sin θ 0 = 0 u0 = 0 sin u = 0 uk = kπ πb sin θ = kπ ② 时取得极值. k λ tgu = u ③
决定,在居间位置,光强介于最大值和最小值之间。对线光源,整个花样 为平行于缝、并以中央条纹为中心、对称展开的明暗相间的直线状条纹。 2 2、各级亮条纹(最大值)光强不等。中央亮条纹强度最强;其余亮 条纹 (次最大)光强远小于中央条纹,并随级数的增大而很快减小。
λ
P0
3、条纹宽度—角宽度θ
亮条纹宽度—相邻暗条纹间的间隔。
L2
MD N
dx
θ
b
x
B
θ
P0
P
dE 0 =
A0 dx cos ω t b
F
由惠—菲原理可知: BB‘上所有窄带发出的次波在屏上叠加,就形成了衍射花样。 现取一束与原入射方向成θ角(称为衍射角)的光束,并作辅助平面BD垂直于衍 射方向,则BD面上任一点到P点的光程相等。
∴ M , B 两点沿 θ 方向到 P 点的光程差 δ = M N = x sin θ 又 : N 点的振动表达式为 A dx 复数式为 : dE = 0 e b dE = A0 dx 2π x sin θ ω t cos b λ ~ A0 dx i , 复振幅 d E = e b
菲涅耳衍射
五、波带片
设想制造这种屏,露出的半波带只让奇数(或偶 数)带透光。
1.合振幅:
a1 a3 a5 ... a2 k 1 A k
k
or : A a a a ... a
k 2 4 6 k
2k
2.制作: ①照相
②摄取牛顿环
③镀膜光刻
3.形状 10
3 2 10
2 563310
1.5m
0.75m
向后移动0.5m 向前移动0.25m
r0
'
3 2
4 56631010
rk2 r02 kr0 h 2( R r0 ) 2( R r0 )
kr0 kr0 R R kr0 2r0 2( R r0 ) R r0
2 h
2 2 Rh ( R r0 ) Rh 1 1 即k ( ) r0 R r0 R
讨论: 1)平行光照射
菲涅耳衍射
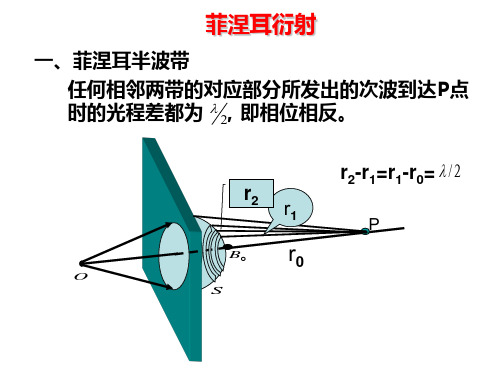
一、菲涅耳半波带 任何相邻两带的对应部分所发出的次波到达P点 时的光程差都为 2 ,即相位相反。 r2-r1=r1-r0= / 2 r1
P
r2
B
O S
0
r0
二、合振幅的计算:
Ak a1 a2 a3 a4 a5 ... (1)k 1 ak
S k ak K ( k ) rk
解: 半径为1mm的圆孔包含的波带数为:
R R r0 k r0 R
2 h
1m m 1000m m 1000m m 4 6 1000m m 1000m m 50010 m m
2
半径为0.5mm的圆屏挡住的波带数为:
2 0 . 5 m m 1000 m m 1000 m m ' k 1 6 1000m m 1000m m 50010 m m
菲涅尔衍射-菲涅尔衍射课件

实验结果分析
分析衍射条纹的形状和分布规律, 理解光的波动性和衍射原理。
比较不同障碍物(如狭缝、圆孔) 对衍射条纹的影响,探究衍射现
象与障碍物形状的关系。
通过实验数据,计算出光的波长 等参数,进一步验证光的波动性。
04
菲涅尔衍射的应用实例
光栅的制造
菲涅尔衍射在光栅制造中的应用
光栅是一种重要的光学元件,用于分光和光谱分析。 在光栅制造过程中,菲涅尔衍射原理被用来控制光束 的衍射方向和模式,从而实现精确的光束分离和光谱 分析。
行性和性能指标。
全息摄影技术
菲涅尔衍射在全息摄影技术中的应用
全息摄影技术是一种记录和重现三维图像的技术。在全息摄影过程中,菲涅尔衍射原理被用来控制光的衍射和干 涉,从而实现三维图像的记录和再现。
全息摄影技术的过程
全息摄影技术通常包括记录和再现两个步骤。在记录步骤中,利用菲涅尔衍射原理和干涉原理,将三维物体发出 的光波分散并记录在感光材料上。在再现步骤中,通过特定的衍射结构将记录的光波重新组合并投影到空气中或 特定的观察屏幕上,以重现三维图像。
THANKS
感谢观看
菲涅尔衍射公式
菲涅尔衍射公式描述了光波在遇到边缘或障碍物时,衍射光强度的分布情况。 该公式基于波动理论,能够准确预测衍射现象。
菲涅尔半波带法
菲涅尔半波带法是一种分析衍射现象 的方法,通过将衍射区域划分为一系 列半波带,分析各半波带的贡献来解 释衍射现象。
该方法有助于直观理解衍射现象,简 化分析过程。
菲涅尔衍射的应用
光学仪器设计
菲涅尔衍射在光学仪器设计中具有重 要应用,如透镜、反射镜、光栅等光 学元件的设计,都需要考虑菲涅尔衍 射的影响。
干涉测量
光信息处理
菲涅耳圆孔衍射
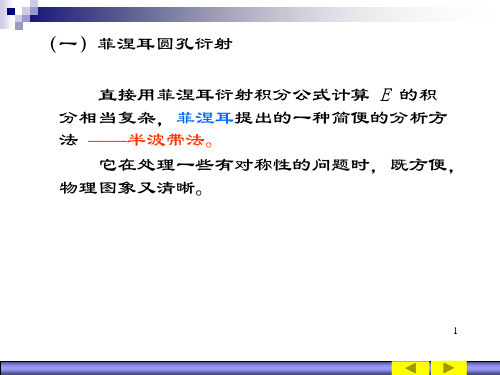
B2
B1
S
R
B0 r0
r1=r0+λ/2
●
P
B0P r0 B1P B0P B2P B1P B3P B2P
…
BK
P
BK 1P
2
这样分成的环形波带称为菲涅耳半波带,任何相邻两波
带以相反的相位(相位相差)同时到达 P 点(光程差λ/2 )。 2
二、合振幅的计算
用 a1、a2、…、an分别表示各波带在 P 点的振幅,由于 相邻波带相位相差,有:
n
n2
1 r0
1 R
R→∞(平行光入射) n n2 , r0
n nr0
可见,n 与P0在轴上的位置r0有关。
8
讨论:
▲ 对 P0 点若 S 恰好分成 n 个半波带时:
An
1 2
(a1
an )
n 为偶数
An
1 2
(a1
an )
最大
n 为奇数
An
1 2 (a1
an )
最小
▲ 对 P0 点若 S 中还含有不完整的半波带时:
rk r0
·P0
▲ 计算P点的光强 首先考虑通过圆孔的K个完整菲涅耳半波带数:
在ΔBAP0中:
k 2 rk 2 (r0 h)2 rk 2 r02 2r0h h2 rk 2 r02 2r0h
rk r0 k 2 ,
忽略 k 22 项
4
k2
r0 2
k r0
k 22
4
r0
2r0h
例:某一波带片只让5个奇数带通过,则
A5
5a1
10
a1 2
,
I5
100I0
即:此时光强是无光阑时光强的100倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 6-22 菲涅耳衍射实验装置示意图
图 6-23 菲涅耳衍射图样
2. 半波带法 公式(6-1)要求对波前作无限分割, 积分后得到观察点的光强。 半波带法是一种近似的计 算方法,将积分运算变成非常简洁的求和公式。 这一方法首先将衍射屏划分成若干个同心圆环,如图 6-24 所示,相邻同心圆环的光程 相差半个波长,这样划分的同心圆环称为半波带。
图 6-24 半波带法
78
第六章 光的衍射与光学仪器的分辨本领
通过每个半波带的子光束在P0点产生的复振幅为
% ( P ) = A ( P )eiϕ1 ΔU 1 0 1 0 % ( P ) = A ( P )ei (ϕ1 +π ) ΔU
2 0 2 0
% ( P ) = A ( P )ei (ϕ1 + 2π ) ΔU 3 0 3 0 ....................................
1 A( P0 ) = [ A1 ( P0 ) + (−1) n +1 An ( P0 )] 2
(6-25)
将式(6-25)绘制成矢量图, 如图 6-26 所示, 当 n 为奇数时, A( P0 ) = 当 n 为偶数时, A( P0 ) =
1 [ A1 ( P0 ) + An ( P0 )] , 2
1 [ A1 ( P0 ) − An ( P0 )] 。 2
图 6-26 半波带法中的矢量图
菲涅耳衍射现象分析 1)、自由传播 最后一个半波带上f (θn)=0,因此An=0,于是
A( P0 ) =
看到的是亮点。 2)、圆孔衍射 当圆孔中包含奇数个半波带时,中心是亮点;当圆孔中包含偶数个半波带时,中心是暗 点。 3)、圆屏衍射 设圆屏遮挡住前 k 个半波带,那么有
(6-16)
如图 6-25 所示, Ak(P0)是角度θ的函数,与半波带的面积ΔΣ成正比,与半波带到观 察点P0的距离成反比,因此,可以写成一个与Ak(P0)成正比的函数f(θk) 与
ΔΣ 乘积的形式 r
(6-17)
Ak ( P0 ) ∝ f (θ k )
ΔΣ k rk
图 6-25 半波带法中的几何关系
Rb k λ = k ρ1 R+b Rbλ R+b
(6-26)
) − [b + R(1 − cos α )]2
cos α =
= =
k 2λ 2 4
可以得到 1 − co按式(6-26)和(6-27)制 作的波带片如图 6-27 所 示,图 6-27(a)是偶数半波 带涂黑的波带片,图 6-27(b)是奇数半波带涂黑 的波带片。 将式(6-26)改写成
ρ k2 = r 2 − [b + R (1 − cos α )]2 kλ 2
=(b +
2 = bk λ − R 2 (1 − cos α ) 2 − 2bR (1 − cos α )
R 2 + ( R + b) 2 − r 2 2 R ( R + b) 2 R 2 + 2 Rb + b 2 − b 2 − bk λ − 2 R ( R + b) 2 R 2 + 2 Rb − bk λ 2 R ( R + b) bk λ 2 R ( R + b)
说明在λ<<r0 的条件下,
ΔΣ k 与k无关,Ak(P0)仅与倾斜因子f(θk)有关。 rk
由于衍射屏上的孔径与光源到衍射屏的距离、 与衍射屏到观察屏的距离相比都很小, 所 以f (θk)随θk 的增加而缓慢单调递减变化,可以作为线性变化的参数来处理,除了首项和 尾项之外,中间各项写为 Ak =
Ak −1 Ak +1 + 的形式,则式(6-16)简化为 2 2
球冠面积为
Σ = 2π R 2 (1 − cos α )
R 2 + ( R + b) 2 − r 2 cos α = 2 R ( R + b)
对式(6-18)和(6-19)分别取微分
(6-18) (6-19)
d Σ = 2π R 2 sin α dα sin a dα =
将式(6-21)代入式(6-20)中
(6-20) (6-21)
rdr R ( R + b)
d Σ 2π Rdr = r R+b
取 dr ≈λ/2, 则
(6-22)
ΔΣ k π Rλ = rk R+b
(6-23)
79
第六章 光的衍射与光学仪器的分辨本领
代入式(6-17)
Ak ( P0 ) ∝ f (θ k )
ΔΣ k rk
(6-24)
80
1 A1 ( P0 ) 2
第六章 光的衍射与光学仪器的分辨本领
A( P0 ) = Ak +1 ( P0 ) − Ak +2 ( P0 ) + ... + (−1) n +1 An ( P0 ) = 1 Ak +1 ( P0 ) 2
无论 k 是奇数还是偶数,中心总是亮的。 3.菲涅耳波带片 从半波带法出发,将奇数半波带或偶数半波带涂黑,剩余部分透光,就构成了菲涅耳波 带片。 在图(6-25) 中,令r=b+kλ/2,ρ= ρk,则根据余弦定理可以导出
A' =
光强比等于振幅比的平方
A1 2
I 波带片 I自由传播
=(
A 2 ) = 400 A'
82
(6-27)
1 1 kλ + = R b ρ k2
令
(a)偶数半波带涂黑的波带片
(b)奇数半波带涂黑的波带片
图 6-27 波带片
81
第六章 光的衍射与光学仪器的分辨本领
f = ρ k2 / k λ = ρ12 / λ
则有
(6-28)
1 1 1 + = R b f
(6-29)
这一公式与高斯成像公式(2-8)的形式相同,说明波带片的成像作用与透镜相似。 从式(6-28)可以看出,波带片的焦距与波长成反比,如果用白光照明,会出现色差。 我们可以把波带片看作一个特殊的光栅, 对于入射的平行光, 这一光栅的零级衍射光位 于式(6-29)确定的焦点上,光栅还有其它级次的衍射,所以波带片有多个实焦点,分别位于 、-f /7,…。这些次焦点的 f,f /3,f /5,f /7,…;还有多个虚焦点,分别位于-f,-f /3,-f /, 光强比主焦点的光强弱很多。 与光学透镜相比,不论加工成本,还是加工周期,波带片都有优势,所以在一些特殊光 学系统中,可以用波带片取代传统的光学透镜。 例题 一块波带片的孔径内有 20 个半波带,奇数露出,偶数挡住,轴上场点的强度比自由传 播时大多少倍? 解:波带片在轴上场点产生的振幅为 A=A1+A3+A5+…+A19≈10A1 自由传播时的振幅为
第六章 光的衍射与光学仪器的分辨本领
§6.3 菲涅耳衍射和波带片 本节从实验现象出发, 首先介绍菲涅耳衍射的实验装置和实验结果, 然后用半波带法导 出计算公式,最后用菲涅耳衍射理论计算波带片的参数。 1. 实验装置 菲涅耳衍射实验装置如图 6-22 所示,光源S与衍射屏的距离R为米的数量级,衍射屏与 观察屏之间的距离b为 3~5 米,衍射屏为一圆孔,圆孔半径ρ为毫米数量级,衍射屏与观察 屏平行,光源S、衍射屏上圆孔的圆心、观察屏中心P0共线。 实验现象 衍射图样是以点P0为中心的一组亮暗相间的同心圆环,中心点可能是亮的,也可能是暗 的;当ρ变化时,衍射图样中心亮暗交替变化;沿轴向移动观察屏时,衍射图样中心亮暗交 替变化;把衍射屏上的圆孔换成圆屏(圆盘),则衍射图样中心总是亮点。衍射图样如图 6-23 所示。
P0点的合成复振幅为 (6-15)
% ( P ) = [ A ( P ) − A ( P ) + A ( P ) − ... + (−1) n +1 A ( P )]eiϕ1 U 0 1 0 2 0 3 0 0 n
复振幅的绝对值为
% ( P ) = A ( P ) − A ( P ) + A ( P ) − ... + (−1) n +1 A ( P ) A( P0 ) = U 0 1 0 2 0 3 0 n 0
