石墨烯理论(中)
石墨烯综述

1、石墨烯的介绍1.1石墨烯的发现回顾石墨烯的发展史,从理论上对其特性的预言到实验上的成功制备经历了近60年的时间,它的发展史是一部符合科学发展规律的发展史。
早在1947年菲利普·华莱士(Philip Wallace)就开始研究石墨烯的电子结构,麦克鲁(J.W.McClure)在1956年推导出了相应的波函数方程[1]。
但那个时期由于受到早期朗道(L.D.Landau)和佩尔斯(R.E.Peierls)[2]提出的准二维晶体材料由于其自身的热力学不稳定性,在常温常压下会迅速分解的理论的影响,石墨烯的研究只是停留在理论上。
后来实验物理学家们虽经过几次实验上的探索,但很遗憾他们离石墨烯的发现仅一步之遥。
直到2004年安德烈·盖姆和康斯坦丁·诺沃肖罗夫[3]以石墨为原料,通过微机械力剥离法得到一系列叫作二维原子晶体的新材料——“石墨烯(graphene ) ”。
石墨烯的发现打破了禁锢人们几十年的理论——热力学涨落不允许二维晶体在有限温度下自由存在,震撼了整个物理界。
他们因此也获得2008年诺贝尔物理学奖的提名。
1.2 石墨烯的结构石墨烯是指紧密排列成二维蜂巢状晶体点阵的单层碳原子,又名“单层石墨片”。
一般认为1-10层是二维石墨烯。
在单层石墨烯中,每个碳原子通过sp2杂化与邻近的三个碳原子形成十分牢固的σ键,构成稳定的六边形。
每个碳原子贡献剩余一个p z轨道电子形成垂直于晶面方向的大π键,π电子可以自由移动,赋予石墨烯优异的导电性能[4]。
石墨烯还是构筑其他维度碳材料的基本单元。
它可以团聚成零维的富勒烯,卷曲成一维的碳纳米管,堆叠成三维的石墨[5]。
1.3 石墨烯的性能1.3.1 石墨烯的物理性能石墨烯具有优异的力学性能。
它是已知材料中强度和硬度最高的晶体材料。
其断裂强度(强度极限)为42N/m2,抗拉强度和弹性模量分别为130Gpa和1.0TPa[6]如果将普通钢换算成和石墨烯一样的厚度,其二维强度极限为0.084~0.40 N/m2。
石墨烯简单介绍ppt课件
填充在信号中,它们被要求使用越来越高的频率,然而手机的工作频
率越高,热量也越高,于是,高频的提升便受到很大的限制。由于石 墨烯的出现,高频提升的发展前景似乎变得无限广阔了。 这使它在
微电子领域也具有巨大的应用潜力。
26
石墨烯应用
透明电极
石墨烯
和
,使它在透明电
导电极方面有非常好的应用前景。触摸屏、液晶显示、有机光伏电池、
有机发光二极管等等,都需要良好的透明电导电极材料。特别是,
。由于氧化铟锡脆度较高,比较容易损毁。在溶液
内的石墨烯薄膜可以沉积于大面积区域 。
通过化学气相沉积法,可以制成大面积、连续的、透明、高电导 率的少层石墨烯薄膜,主要用于光伏器件的阳极,并得到高达1.71% 能量转换效率;与用氧化铟锡材料制成的元件相比,大约为其能量转 换效率的55.2%。
石墨烯
1
什 么 是 石 墨 烯?
石墨烯(英文名Graphene)是一种由C原子 形成的蜂窝状的准二维结构,是C的另外一种 同素异形体。
。例如,在计算石墨和碳纳米 管特性时,通常都是从石墨烯这个基本结构单 元出发的。
石墨烯:基本结构单元
2
石墨烯的来源?
实际上石墨烯本来就存在于自然界,只是难以剥离出 单层结构。石墨烯一层层叠起来就是石墨。1mm厚的石墨 大约包含300万层石墨烯。
14
结构与性能
力学性能
石墨烯是已知材料中强度和硬度最高的晶体结构。其
和
分别为125GPa和1.1TPa。石墨烯的
(抗拉强度)为42N/M2。
普通钢的强度极限大多分布在250~1200MPa范围内,即 0.25ӽ109~1.2ӽ109N/m2。如果钢具有同石墨烯一样的厚度(约 0.335nm),则可推算出其二维强度极限0.084~0.40N/m。由 此可知,
权健自然医学藏象石墨烯原理解析

权健自然医学藏象石墨烯原理解析历史来源:2004年,英国曼彻斯特大学的两位科学家Andre Geim(安德烈·盖姆)和Konstantin Novoselov(克斯特亚·诺沃消洛夫)发现他们能用一种非常简单的方法得到越来越薄的石墨薄片。
他们从高定向热解石墨中剥离出石墨片,然后将薄片的两面粘在一种特殊的胶带上,撕开胶带,就能把石墨片一分为二。
不断地这样操作,于是薄片越来越薄,最后,他们使用普通胶带获得了只有一个原子厚度的一小片碳,这就是石墨烯。
只有一个原子厚度,看似普通的一层薄薄的碳,缔造了2010年度的诺贝尔物理学奖。
安德烈·盖姆和康斯坦丁·诺沃肖罗夫向世人展现了形状如此平整的碳元素在量子物理学的神奇世界中所具有的杰出性能。
力学特性:石墨烯是目前已知强度最高的材料之一,同时还具有很好的韧性,石墨烯的理论杨氏模量达1.0TPa,固有的拉伸强度为130GPa。
而利用氢等离子改性的还原石墨烯也具有非常好的强度,平均模量可大0.25TPa。
因此将石墨烯按比例置入纤维中,可以赋予纺织产品很好的弹性且不易变形。
导热特性:石墨烯具有非常好的热传导性能。
纯的无缺陷的单层石墨烯的导热系数高达5300W/mK,是目前为止导热系数最高的碳材料,因此藏象石墨烯纤维织物与人体体温结合能自动导热,从而促进人体毛细血管血液循环,能活化细胞组织、加快新陈代谢、活血通络、快速祛湿除菌、保持身体持久干爽。
电子特性:石墨烯在室温下的载流子迁移率约为15000cm2/(V-s),这一数值超过了硅材料的10倍,是目前已知载流子迁移率最高的物质锑化铟(InSb)的两倍以上,且电子迁移率受温度变化的影响较小。
而石墨烯中的载流子遵循一种特殊的量子隧道效应,在碰到杂质时不会产生背散射,这是石墨烯局域超强导电性以及很高的载流子迁移率的原因。
因此藏象石墨烯纤维织物的导电特性可以避免织物静电的产生,如果将藏象石墨烯纤维织物生产成服装用作加油站、加气站、危化品仓库等场所作业人员的工作服装,可以有效防止静电带来的危险发生。
石墨烯电阻率和热导率

石墨烯电阻率和热导率石墨烯是一种由碳原子形成的单层薄膜,具有非常高的强度、导电性和热导率。
它的独特性质使其成为材料科学领域的热点之一。
在本文中,我们将重点讨论石墨烯的电阻率和热导率的特性。
首先,我们来看一下石墨烯的电阻率。
电阻率是描述材料电阻能力的量,它与材料的电导率成反比。
对于大多数材料来说,电阻率是与温度呈正相关的。
然而,石墨烯是一种特殊的材料,它的电子输运行为与传统材料有很大不同。
石墨烯的电子输运是由其特殊的带电载流子行为驱动的。
石墨烯中的电子具有质量非常小的二维费米子行为,类似于相对论性粒子。
这意味着石墨烯中的电子在低能量下表现出非常高的电导率。
实际上,石墨烯的电导率可以达到3.28×105 S/m,是铜的200倍。
这种高导电性是由于石墨烯中的电子在平面中的传输速度非常快,而且几乎没有散射。
石墨烯的高电导率使其在电子器件中具有巨大的潜力。
石墨烯的高电导率意味着它可以传输更多的电荷,并且可以实现更高的工作电流密度。
这使石墨烯成为高频率电子器件和高速电子通信中的理想材料。
此外,石墨烯的电导率还使其在电磁屏蔽、导电涂层和传感器等领域有广泛的应用。
接下来,我们来讨论石墨烯的热导率。
石墨烯的热导率非常高,理论上可以达到5300 W/m·K。
这种高热导率是由于石墨烯中的碳原子只在二维平面上排列,形成了高度有序的晶格结构。
这种结构使石墨烯中的声子(热传导的主要载体)具有非常长的自由路径,并且几乎没有散射。
石墨烯的高热导率使其成为高效的热管理材料。
它可以在非常短的时间内将热量从一个区域传导到另一个区域,使设备保持较低的温度。
这种特性使石墨烯在电子器件的散热和热管理中有广泛的应用。
此外,石墨烯的高热导率还有助于制备高性能的热界面材料和热传导纳米材料。
石墨烯的电阻率和热导率在很大程度上受其纯度和晶格结构的影响。
较高纯度的石墨烯具有更好的电导性和热导性能。
目前,石墨烯的制备技术正在不断改进,石墨烯的纯度和晶格结构也在逐渐提高。
石墨烯

石墨烯石墨烯声明:百科词条人人可编辑,词条创建和修改均免费,绝不存在官方及代理商付费代编,请勿上当受骗。
详情>> 石墨烯(二维碳材料)编辑本词条由“科普中国”百科科学词条编写与应用工作项目审核。
石墨烯(Graphene)是一种由碳原子以sp2杂化方式形成的蜂窝状平面薄膜,是一种只有一个原子层厚度的准二维材料,所以又叫做单原子层石墨。
英国曼彻斯特大学物理学家安德烈·盖姆和康斯坦丁·诺沃肖洛夫,用微机械剥离法成功从石墨中分离出石墨烯,因此共同获得2010年诺贝尔物理学奖。
石墨烯常见的粉体生产的方法为机械剥离法、氧化还原法、SiC外延生长法,薄膜生产方法为化学气相沉积法(CVD)。
[1] 由于其十分良好的强度、柔韧、导电、导热、光学特性,在物理学、材料学、电子信息、计算机、航空航天等领域都得到了长足的发展。
作为目前发现的最薄、强度最大、导电导热性能最强的一种新型纳米材料,石墨烯被称为“黑金”,是“新材料之王”,科学家甚至预言石墨烯将“彻底改变21世纪”。
极有可能掀起一场席卷全球的颠覆性新技术新产业革命。
中文名石墨烯外文名Graphene 发现时间2004年主要制备方法机械剥离法、气相沉积法、氧化还原法、SiC外延法主要分类单层、双层、少层、多层(厚层)基本特性强度柔韧性、导热导电、光学性质应用领域物理、材料、电子信息、计算机等目录1 研究历史2 理化性质? 物理性质? 化学性质3 制备方法? 粉体生产方法? 薄膜生产方法4 主要分类? 单层石墨烯? 双层石墨烯? 少层石墨烯? 多层石墨烯5 主要应用? 基础研究? 晶体管? 柔性显示屏? 新能源电池? 航空航天? 感光元件? 复合材料6 发展前景? 中国? 美国? 欧洲? 韩国? 西班牙? 日本研究历史编辑实际上石墨烯本来就存在于自然界,只是难以剥离出单层结构。
石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯。
石墨烯

Байду номын сангаас
其中
H0 单层石墨烯的有效哈密顿量,V 狄拉克锥的带速度
U 双层石墨烯转移位移δ的层间交错 ,V 晶格扭曲矩阵
结论
• 电子的跃迁概率是与电子能量和入射角有关的 • 电子的输运对晶体边界的方向和里面的原子组态有很 强的依赖 • 在低能部分,扶手椅AA和锯齿SP边界几乎是绝缘的, 而在扶手椅SP和锯齿AA边界输运能力很强 • 在绝缘情况下, 当费米能增加到一定值时,它的输运 急速增加 • 这表明在电流通过边界的时候可以通过场效应来控制 • 锯齿形边缘一般在两个谷之间有不同的传输特性,这 使一个谷在某个特定的情况下能生成极化电流
原 子 结 构
扶手椅边界这两个坐标系的关系是 (x,y) = (x`,y`) 定义石墨烯的晶格向量 晶格常数a 定义 0.246nm 作为B原子到最近邻的A原子的向量 =0.142nm为石墨烯中最近的碳原子之间的距离 和
有效连续模型
• 哈密顿量
• 有效近似
• 当W远远大于晶格常数时, 两个狄拉克点附近的态 不杂化,然后我们可以分别构造两个狄拉克点的哈 密顿量
石墨烯中电子在AB-BA边界的输运
理论物理 李丛丛 2013-12-19
• 电子的输运对晶体边界的方向和里面的原子组态 有很强的依赖 • 多层石墨烯中层间相互作用比较弱,它会出现各 种不同的叠加方式 • 二维晶体中,几何边界会大大的影响电子传输
• 这篇文章通过研究没有层间电压并且不对称的特 殊的原子排布结构,计算双层石墨烯AB-BA域边界 的电子传输性质。
石墨烯

2.双层石墨烯与石墨烷
• 小结 优点:文章利用第一性原理计算,首先利用已有 的实验数据判断利用哪种计算方法。 不足:仅对双层石墨烯吸附氢方面进行讨论,作为 良好的褚氢材料还要能快速的释放氢。 ps:石墨烯变成石墨烷的过程是可逆的,将石墨烷在 450℃加热12个小时,石墨烷就转化成了石墨烯。 参考:Ryu S.Han M Y,Maultzs ch J, et al.Reversible Basal Plane Hydrogenation of Graphene[J].NanoLett,2008,8(12);4597
石墨烯掺杂
Suzuki T,Hasegawa T, Mukai S,et al.A theoretical study on storage states of Li ions in carbon anodes of Li ion batteries using molecular orbital calculations[J].Carbon,2003,41(10):1933 用B3LYP/6-13G(d)//HF/6-31G*标准和PM3理论研 究了Li+与多环烃分子的相互作用,其结构为18个氢 原子在C架的四周,Li+分散于C和H原子上,距石墨 烯表面h=1.812Å处
2.双层石墨烯与石墨烷
在早期的理论和实 验工作中,发现了 两种二聚物氢化后 的石墨烯表面。这 两种二聚物的效果 也可以等效为一种 三聚物。
2.双层石墨烯与石墨烷
双层石墨烯全部氢 化以后能量相比石 墨烯和氢原子为负, 因此这是一种非常 稳定的结构。 所以,氢原子的覆 盖率可达50%
2.双层石墨烯与石墨烷
• 参考文献: • D.W.Boukhvalov and M.I.Katsnelson.Phys.Rev.B 78.085413(2008). • Z.Lou,T.Yu,K.j.Kim,Z.Ni,Y.You,S.Lim,Z.Shen,S.W ang.and J.Lin,ACS N ano 3,1781(2009). • J.O.Sofo,A.S.Chaudhari,and G.D.Barber.Phys.Rev.B 75,153401(2007) • J.Kanasaki,E.Inami,K.Tanimura,H.Ohnishi,and K.Nasu,Phys.Rev.Lett.102,087402(2009)
cvd_铜箔_连续生长石墨烯_理论说明

cvd 铜箔连续生长石墨烯理论说明1. 引言1.1 概述在过去几十年中,石墨烯作为一种具有出色的物理和化学特性的二维材料,在科学界引起了巨大的关注。
它具有高导电性、高透明性、稳定性等优点,可以应用于电子器件、能源储存、催化和生物医学等领域。
尽管石墨烯的制备方法有很多种,但化学气相沉积(CVD)是一种最常用且有效的方法之一。
本文将重点介绍CVD铜箔连续生长石墨烯的理论说明。
首先,我们将介绍CVD 方法及其在石墨烯生长中的应用。
然后,我们将探讨铜箔作为衬底材料的优势以及该材料对石墨烯生长的影响。
最后,我们将详细解析石墨烯生长的机制,并分析其中涉及的关键因素。
1.2 文章结构本文共分为五个主要部分。
本引言部分是第一部分,主要对全文进行概述和总体框架的介绍。
接下来第二部分将详细讲解CVD铜箔连续生长石墨烯的理论说明。
第三部分将介绍我们的实验设计以及对实验结果的详细分析和讨论。
第四部分将解释和讨论实验结果,同时探讨CVD铜箔连续生长石墨烯所具有的优势和挑战。
最后,第五部分是结论部分,总结全文内容,并对未来研究方向进行展望。
1.3 目的本文的主要目的是通过理论说明和实验结果分析,深入了解CVD铜箔连续生长石墨烯的过程以及其中涉及的关键因素。
通过对铜箔作为衬底材料的优势进行探讨,希望能够进一步推动石墨烯在各领域中的应用。
此外,本文还旨在总结目前CVD方法制备石墨烯所面临的挑战,并提出未来研究方向,为相关领域的学者提供参考和启示。
以上就是“1. 引言”部分内容的详细描述,请按需使用。
2. CVD铜箔连续生长石墨烯理论说明:2.1 CVD方法介绍:CVD(化学气相沉积)是一种常用的合成石墨烯的方法之一。
该方法基于在高温下通过加热并使其分解的碳源与金属衬底反应,从而在表面上连续生长单层或多层石墨烯薄膜。
CVD方法具有可扩展性、过程参数可调控以及高质量等优点,因此被广泛应用于石墨烯的制备。
2.2 铜箔作为衬底材料的优势:在CVD法中,铜箔是最常用的衬底材料之一。
石墨烯以及导热性质的有关介绍
石墨烯以及导热性质的有关介绍石墨烯( Graphene)又叫单层石墨,是构造其他石墨材料的最基本的材料单元。
石墨稀是由sp2碳原子以蜂窝状晶格构成的二维单原子层结构。
每个碳原子周围有3个碳原子成键,键角120°;每个碳原子均为sp2杂化,并贡献剩余一个p轨道上的电子形成大π键。
在石墨烯中,碳原子在不停的振动,振动的幅度有可能超过其厚度。
其中最重要的石墨烯的晶格振动,不仅仅影响石墨烯的形貌特征,还影响的石墨烯的力学性质、输运特性、热学性质和光电性质。
对石墨烯的热学性质的影响主要是由于石墨烯晶格振动。
根据有关资料的显示,对石墨烯晶格振动的研究可利用价力场方法。
在价力场方法中,石墨烯内所有原子间的相互作用力可以分为键的伸缩力和键的弯曲力。
从经典的热学理论出发,对石墨烯的导热系数进行研究。
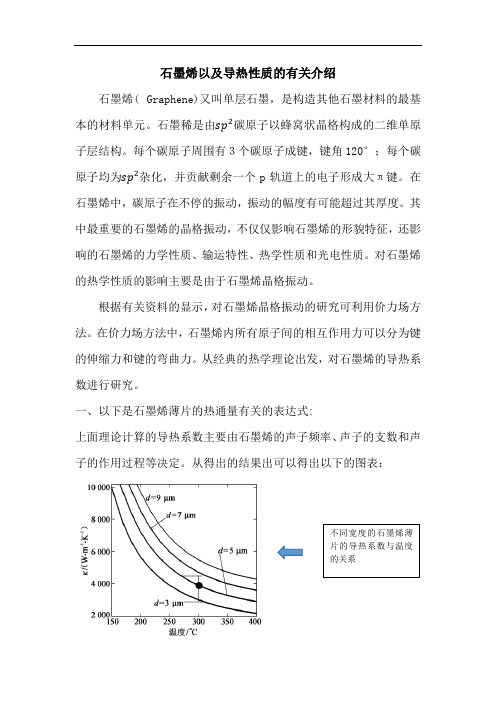
一、以下是石墨烯薄片的热通量有关的表达式:上面理论计算的导热系数主要由石墨烯的声子频率、声子的支数和声子的作用过程等决定。
从得出的结果出可以得出以下的图表:不同宽度的石墨烯薄片的导热系数与温度的关系从图中看出来石墨烯的导热系数随温度的增加而减小。
在同一温度下,导热系数随石墨烯的宽度的增加而增加。
由经典的热传导理论可知,随着温度的升高,晶格振动加强,声子运动剧烈,热流中的声子数目也增加。
声子间的相互作用或碰撞更加频繁,原子偏离对平衡位置的振幅增大,引起的声子散射加剧,使导热载体(声子)的平均自由程减小。
这是石墨烯的导热系数随温度升高而降低的主要原因。
对于石墨烯,电子的运动对导热也有一定的贡献,但在高温情况下,晶格振动对石墨烯的导热贡献是主要的,起主导作用。
二、石墨烯的导热系数经验公式式中Xg是温度系数,L是单层石墨烯的中间部分与散热片之间的距离,h是单层石墨烯厚度,d 为单层石墨烯的宽度,δf是G峰位移,δP是样品的热功率的变化。
从经验公式可以看出,石墨烯的导热系数主要受3个因数的影响: 单层石墨烯的尺寸效应,温度,石墨烯生长的基底材料。
石墨烯

石墨烯xxx长沙理工大学物理与电子科学学院摘要:分析了石墨烯的结构,介绍石墨烯的电子能带结构和量子力学对它的理论描述,并阐述了石墨烯的一些特性。
另外也讲述制备石墨烯的几种方法和特性表征。
最后是对石墨烯近几年的发展了解并展望未来。
引言:自从2004年石墨烯被发现以来,获得了科学界广泛关注。
石墨烯作为一种新型炭质材料,由单层碳原子紧密堆积成二维晶格结构。
它的理论比表面积达2600 m2/g,热导率为3 kw/m·K,室温下平面上的电子迁移率为1.5×10 cm2/V·s,拉伸模量和本征强度分别为1000 GPa和130 GPa。
石墨烯是零带隙半导体,其载流子迁移率比硅高100倍,在室温下具有微米级自由程和大的相干长度,是纳米电路的理想材料。
此外,石墨烯还具有完美的量子隧道效应及半整数的量子霍尔效应等一系列性质[1-2]。
这些优异的性能使得石墨烯在纳米电子器件、气体传感器、电池,超级电容器和储氢方面及纳米复合材料等领域有光明的应用前景。
一、石墨烯的结构石墨烯为复式六角晶格(图1),每个六边形结构中有两个碳原子,每个原子与最近邻的三个原子间形成三个盯键。
由于每个碳原子有四个价电子,所以每个碳原子又会贡献出一个剩余的P电子,它垂直于石墨烯平面,与周围原子形成未成键的电子。
这些1r电子在晶体中自由移动,赋予了石墨烯良好的导电性。
二、石墨烯的特点——电子能带结构石墨烯是二维碳原子蜂巢晶格,是由两个A型或B型的三角布拉维晶格(三角子晶格)组成.其载流子(电子和空穴)波函数具有双旋量,也就是说载流子除了通常的1/2自旋外,还有与它的子格自由度相联系的1/2赝自旋.石墨烯的电子能带结构可由最近邻紧束缚模型得到[3].导带电子(π电子)能从一个碳原子的2p 轨道跃迁到与它最近邻的3个碳原子之一,跃迁振幅(共振积分)为γ≡t ≈3eV.色散关系(能量和动量的关系)为:E=±γ√‾(1+4cos(k₂•а)+4cos(k₂•а)cos(k₁•√‾₃•а )), (1)其中,晶格常数а=0.246nm,碳原子的间距为а∕√‾₃=0.143nm.导带(CB,а= +1)和价带(VB,а=一1)分别对应上述色散关系中的不同正负号.导带和价带接触处为不等价的Dirac 点(分别对应能谷K和K´),如图2所示[3].能量E作为二维布洛赫波矢(也是动量)(k₁,k₂)的函数.六边形布里渊区上K或点K´(Dirac点)附近,色散关系是线性的,从局部来看相当于圆锥(见图2放大区).费米能级位于Dirac点处,费米面也由Dirae点构成.价带(VB)填满电子,导带(CB)是空的.由此可见,未参杂石墨烯是无带隙的.在Dirae点附近,电子的能量只依赖动量且成线性关系,类似于无质量的相对论粒子.因此,在低能且靠近K和K´点时,电子由二维无质量Dirac本征方程描述:−ίhυσ•▽φ(r)∕2π=Εφ(r), (2)这里,V =√‾₃•aπ/h≈1000000m/s是石墨烯电子的传输速度,相当于有效光速;φ(r)是电子波函数,E是能量,p→ίh∕2π▽是坐标表象下的动量算符.图2 紧束缚模型计算的石墨烯能带结构三、石墨烯的特性石墨烯最大的特性是室温下传递电子的速度比已知导体都快,运动速度为光速的1/300,远远超过了电子在一般导体中的运动速度,具有优良的导电性。
石墨烯

引言石墨烯是单层碳原子紧密堆积成单层二维蜂窝状晶体结构的一种炭质材料,碳原子排列与石墨的单原子层一样。
石墨烯是碳原子以sp2杂化连接的单原子层构成的, 其基本结构单元为有机材料中最稳定的苯六元环, 这种石墨晶体薄膜的厚度只有0.335nm,仅为头发的二十万分之一,是目前所发现的最薄的二维材料,是构建其他维数炭质材料(如零维富勒烯,一维纳米碳管、三维石墨)的基本单元,具有极好的结晶性及电学质量和优异的电学、力学性能和结晶性。
2004 年, Manchester 大学的Geim 小组首次用机械剥离法获得了单层或薄层的新型石墨烯.石墨烯是一种没有能隙的半导体,具有比硅高 100 倍的载流子迁移率 (2 × 10 5cm 2/v),在室温下具有微米级自由程和大的相干长度,因此石墨烯是纳米电路的理想材料,石墨烯还具有良好的导热性[3000W /(m ·K)] 、高强度(110GPa) 和超大的比表面积(2630mZ /g) 。
这些优异的性能使得石墨烯在纳米电子器件、气体传感器、能量存储及复合材料等领域有光明的应用前景。
一、石墨烯的合成目前制备石墨烯的主要方法有: 化学气相沉积法, 微机械剥离法以及液相条件下的有机分子分散法, 溶剂热法和氧化还原法等.化学气相沉积法是以能量激化气体反应先驱物发生化学反应在基底表面形成石墨烯薄膜的一种薄膜成长方法. Keun 等,Kim 等通过 CH4分解,还原 CO等反应生成气态碳原子, 产物沉积在基底表面,生成二维石墨烯薄膜,然而现阶段工艺不成熟及较高的成本限制了其规模应用。
微机械剥离法是采用离子束对物质表面刻蚀,并通过机械力对物质表面进行剥离制备石墨烯 .Geim 等用微机械剥离法从高定向热解石墨上剥离得到单层石墨烯,但由于工艺复杂制备的石墨烯产率低不能够满足工业化需求。
在一定程度上限制了规模化生产。
有机分子分散法是将石墨在有机溶剂中超声分散得到石墨烯的一种方法。
石墨烯基础知识简介

1.石墨烯(Graphene)的结构石墨烯是一种由碳原子以sp²杂化轨道组成六角型呈蜂巢状晶格的平面薄膜,是一种只有一个原子层厚度的二维材料。
如图1.1所示,石墨烯的原胞由晶格矢量a1和a2定义每个原胞内有两个原子,分别位于A和B的晶格上。
C原子外层3个电子通过sp²杂化形成强σ键(蓝),相邻两个键之间的夹角120°,第4个电子为公共,形成弱π键(紫)。
石墨烯的碳-碳键长约为0.142nm,每个晶格内有三个σ键,所有碳原子的p轨道均与sp²杂化平面垂直,且以肩并肩的方式形成一个离域π键,其贯穿整个石墨烯。
如图1.2所示,石墨烯是富勒烯(0维)、碳纳米管(1维)、石墨(3维)的基本组成单元,可以被视为无限大的芳香族分子。
形象来说,石墨烯是由单层碳原子紧密堆积成的二维蜂巢状的晶格结构,看上去就像由六边形网格构成的平面。
每个碳原子通过sp²杂化与周围碳原子构成正六边形,每一个六边形单元实际上类似一个苯环,每一个碳原子都贡献一个未成键的电子,单层石墨烯的厚度仅为0.335nm,约为头发丝直径的二十万分之一。
图 1.1(a)石墨烯中碳原子的成键形式(b)石墨烯的晶体结构。
图1.2石墨烯原子结构图及它形成富勒烯、碳纳米管和石墨示意图石墨烯按照层数划分,大致可分为单层、双层和少数层石墨烯。
前两类具有相似的电子谱,均为零带隙结构半导体(价带和导带相较于一点的半金属),具有空穴和电子两种形式的载流子。
双层石墨烯又可分为对称双层和不对称双层石墨烯,前者的价带和导带微接触,并没有改变其零带隙结构;而对于后者,其两片石墨烯之间会产生明显的带隙,但是通过设计双栅结构,能使其晶体管呈示出明显的关态。
单层石墨烯(Graphene):指由一层以苯环结构(即六角形蜂巢结构)周期性紧密堆积的碳原子构成的一种二维碳材料。
双层石墨烯(Bilayer or double-layer graphene):指由两层以苯环结构(即六角形蜂巢结构)周期性紧密堆积的碳原子以不同堆垛方式(包括AB堆垛,AA堆垛,AA‘堆垛等)堆垛构成的一种二维碳材料。
石墨烯导热原理(一)

石墨烯导热原理(一)什么是石墨烯?石墨烯是一种单层碳原子网格,具有非常高的强度和导电性。
它是由一系列碳原子组成的2D平面结构,是碳纳米材料的一种。
石墨烯具有许多不同的应用,其中最重要的是其出色的导电和导热性能。
石墨烯导热的原理石墨烯的导热原理因其非常复杂而成为了物理学家和科学家之间的热门话题。
石墨烯导热的原理主要基于几个原因:•石墨烯具有非常高的热传导性。
这是由于它的结构导致电子在石墨烯中的移动很快,因此它们可以在石墨烯中很容易地传输热量。
•石墨烯的非常薄的结构意味着热量可以很快地从一侧传输到另一侧。
•石墨烯的高度结晶性质也是导致其高导热性的重要原因。
在石墨烯中,碳原子排列成了一种有序的二维结构,因此电子在其中的运动路径也是有序的。
这种有序结构能够有效地传递热量和电流。
总之,石墨烯之所以具有出色的导热性,是由于其独特的结构和电子特性,以及其非常窄的厚度等结构因素所致。
石墨烯导热的应用石墨烯导热的应用非常广泛。
以下是其一些主要的应用领域:•热导材料:由于石墨烯的导热性能,它可以被用作高性能的热导材料。
这种材料在高温环境下具有出色的耐用性和稳定性。
•电子设备散热器:由于石墨烯的导热性能,它可以被用作电子设备散热器。
这种散热器可以更有效地将电子设备中产生的热量分散出去,从而降低设备发生过热的风险。
•生物医疗应用:石墨烯导热性能的优越性使其成为一种有前途的医疗应用材料,例如治疗肿瘤的纳米微粒,或是用于改善患者血液流动性的医疗器械。
总之,石墨烯导热的能力被广泛利用于各种不同的应用领域,对我们生活中的许多方面产生了深远的影响。
石墨烯与传统散热材料的比较石墨烯与传统散热材料相比,具有不同的优点和缺点。
以下是两者的比较:石墨烯的优点•石墨烯具有非常高的导热性,能够更有效地传递热量,因此能够更快地将电子设备产生的热量散热出去。
•石墨烯的稳定性高,能够在高温、密闭环境下发挥更好的散热效果。
•石墨烯比传统的金属材料更轻薄,能够更轻松地应用在微型设备或二维器件中。
石墨烯中的声子学效应研究

石墨烯中的声子学效应研究石墨烯是一种由碳原子组成的二维晶体材料,具有高强度、高导电性、高热传导性等优异的物理性质。
近年来,石墨烯的研究引起了极大的关注,而石墨烯中的声子学效应则成为了一个研究热点。
声子是指固体中传递热能和声波的元激发,是固体的基本激发。
声子能量与波矢的关系称为声子色散关系,它是描述固体热学和光学性质的基础。
在石墨烯中,声子性质独特,因此对其进行研究有重要的理论和实用价值。
石墨烯中的声子学效应主要涉及声子的色散关系、声子热导率、声子振动模式等问题。
其中,声子的色散关系是石墨烯中声子学效应研究的重点之一。
石墨烯的声子能带与传统三维材料有很大不同,因为石墨烯具有二维结构和独特的晶格形态。
在石墨烯中,由于支配声子色散关系的是矢量波动方程,因此存在两种不同的声子:纵声子和横声子。
纵声子的色散关系是线性的,而横声子的色散关系则是非线性的,因此在石墨烯中存在声子塞曼效应(Phonon Zeeman effect)。
这一效应意味着在石墨烯中,外加磁场可以使纵声子和横声子的能量产生分裂,从而影响材料的电学和热学性质。
另一个关注的问题是石墨烯中的声子热导率。
声子热导率通常被定义为物质中热流密度和温度梯度之比,是描述固体热传导性质的基础物理量。
在石墨烯中,由于其二维结构和高度有序的晶格结构,声子的热传导性质受到了极大的关注。
实验和理论研究表明,石墨烯中的声子热导率较低,通常在几十瓦特/米-K以下。
这种低声子热导率是由于石墨烯中声子的散射机制和晶格缺陷所导致的。
此外,石墨烯中的声子振动模式也是研究的一个重要问题。
在石墨烯中,由于其二维结构,声子的振动模式比较简单。
近年来的研究表明,石墨烯中存在多种振动模式,包括纵波、横波和弹性波等。
这些振动模式的研究有助于深入理解石墨烯的声子学性质。
总之,石墨烯中的声子学效应是一个复杂而有趣的研究领域。
对于深入理解石墨烯的物理性质以及开发新的石墨烯电子学器件,这一研究领域具有重要的意义。
石墨烯百科

石墨烯百科石墨烯石墨烯不仅是已知材料中最薄的一种,还非常牢固坚硬;作为单质,它在室温下传递电子的速度比已知导体都快。
简介石墨烯(Graphene)是一种由碳原子构成的单层片状结构的新材料。
是一种由碳原子以sp2杂化轨道组成六角型呈蜂巢晶格的平面薄膜,只有一个碳原子厚度的二维材料[1]。
石墨烯一直被认为是假设性的结构,无法单独稳定存在[1],直至2004年,英国曼彻斯特大学物理学家安德烈·海姆和康斯坦丁·诺沃肖洛夫,成功地在实验中从石墨中分离出石墨烯,而证实它可以单独存在,两人也因“在二维石墨烯材料的开创性实验”为由,共同获得2010年诺贝尔物理学奖[2]。
石墨烯目前是世上最薄却也是最坚硬的纳米材料[3] ,它几乎是完全透明的,只吸收2.3%的光"[4];导热系数高达5300 W/m·K,高于碳纳米管和金刚石,常温下其电子迁移率*超过15000 cm²/V·s,又比纳米碳管或硅晶体*高,而电阻率只约10-6 Ω·cm,比铜或银更低,为目前世上电阻率最小的材料[1]。
因为它的电阻率极低,电子迁移的速度极快,因此被期待可用来发展出更薄、导电速度更快的新一代电子元件或晶体管。
由于石墨烯实质上是一种透明、良好的导体,也适合用来制造透明触控屏幕、光板、甚至是太阳能电池。
石墨烯另一个特性,是能够在常温下观察到量子霍尔效应。
石墨烯的碳原子排列与石墨的单原子层雷同,是碳原子以sp2混成轨域呈蜂巢晶格(honeycomb crystal lattice)排列构成的单层二维晶体。
石墨烯可想像为由碳原子和其共价键所形成的原子尺寸网。
石墨烯的命名来自英文的graphite(石墨) + -ene(烯类结尾)。
石墨烯被认为是平面多环芳香烃原子晶体。
石墨烯的结构非常稳定,碳碳键(carbon-carbon bond)仅为1.42Å。
石墨烯-PPT

4,电子的相互作用
石墨烯中电子间以及电子与蜂窝状栅格 间均存在着强烈的相互作用。 石墨烯中的电子不仅与蜂巢晶格之间相 互作用强烈,而且电子和电子之间也有很 强的相互作用。
5、其它特殊性质 ① 石墨烯具有明显的二维电子特性。 ② 在石墨烯中不具有量子干涉磁阻 ③ 石墨烯电子性质用量子力学的迪拉克方程来描 述比薛定谔方程更 ④ 好可控渗透性 ⑤ 离子导电体各向异性 ⑥ 超电容性 ………………
实现人类梦想
Dreams: Dreams:对于强度比世界上最好的钢铁还要高 上百倍的石墨烯,如果能加以利用, 上百倍的石墨烯,如果能加以利用,不仅可以造 出纸片般薄的超轻型飞机材料、超坚韧的防弹衣, 出纸片般薄的超轻型飞机材料、超坚韧的防弹衣, 甚至还可以制作23000英里长伸入太空的电梯, 23000英里长伸入太空的电梯 甚至还可以制作23000英里长伸入太空的电梯, 实现人类坐电梯进入太空的梦想。 实现人类坐电梯进入太空的梦想。 美国国家航空航天局(NASA)悬赏400万美金 美国国家航空航天局(NASA)悬赏400万美金 400 鼓励科学家们进行这种电梯的开发
二、石墨烯材料的制备
1、机械剥离法 通过机械力从新鲜石墨晶体的表面剥离石墨烯片层。 加热SiC SiC法 2、加热SiC法 通过加热单晶SiC脱除Si,在单晶(0001)面上分解出石墨烯片层。Berger 等人已经能可控地制备出单层. 或是多层石墨烯 。据预测这种方法很可能是 未来大量制备石墨烯的主要方法之一。 3、热膨胀法 4、化学法
三、石墨烯材料的性质
1、力学性质——比钻石还要硬 力学性质——比钻石还要硬 ——
数据转换分析:在石墨烯样品微粒开始碎裂前, 数据转换分析:在石墨烯样品微粒开始碎裂前,它们每 100纳米距离上可承受的最大压力居然达到了大约2.9微 纳米距离上可承受的最大压力居然达到了大约2.9 100纳米距离上可承受的最大压力居然达到了大约2.9微 牛。 据科学家们测算,这一结果相当于要施加55牛顿的 据科学家们测算,这一结果相当于要施加55牛顿的 55 压力才能使1米长的石墨烯断裂。 压力才能使1米长的石墨烯断裂。如果物理学家们能制 取出厚度相当于普通食品塑料包装袋的(厚度约100 100纳 取出厚度相当于普通食品塑料包装袋的(厚度约100纳 石墨烯, 米)石墨烯,那么需要施加差不多两万牛的压力才能将 其扯断。换句话说,如果用石墨烯制成包装袋, 其扯断。换句话说,如果用石墨烯制成包装袋,那么它 将能承受大约两吨重的物品。 将能承受大约两吨重的物品。 打个比方说单层石墨烯的强度, 打个比方说单层石墨烯的强度,就像把大象的重量 加到一支铅笔上, 加到一支铅笔上,才能够用这支铅笔刺穿仅像保鲜膜一 样厚度的单层石墨烯。 样厚度的单层石墨烯。
石墨烯性能简介

第一章石墨烯性能及相关概念1 石墨烯概念石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体。
石墨烯狭义上指单层石墨,厚度为0.335nm,仅有一层碳原子。
但实际上,10层以内的石墨结构也可称作石墨烯,而10层以上的则被称为石墨薄膜。
单层石墨烯是指只有一个碳原子层厚度的石墨,碳原子-碳原子之间依靠共价键相连接而形成蜂窝状结构。
完美的石墨烯具有理想的二维晶体结构,由六边形晶格组成,理论比表面积高达2.6×102m2 /g。
石墨烯具有优异的导热性能(3×103W/(m•K))和力学性能(1.06×103 GPa)。
此外,石墨烯稳定的正六边形晶格结构使其具有优良的导电性,室温下的电子迁移率高达1.5×104 cm2 / (V·s)。
石墨烯特殊的结构、突出的导热导电性能和力学性能,引起科学界巨大兴趣,成为材料科学研究热点。
石墨烯结构图2 石墨烯结构石墨烯指仅有一个原子尺度厚单层石墨层片,由 sp2 杂化的碳原子紧密排列而成的蜂窝状晶体结构。
石墨烯中碳 -碳键长约为 0.142nm。
每个晶格内有三个σ键,连接十分牢固形成了稳定的六边状。
垂直于晶面方向上的π键在石墨烯导电的过程中起到了很大的作用。
石墨烯是石墨、碳纳米管、富勒烯的基本组成单元,可以将它看做一个无限大的芳香族分子,平面多环烃的极限情况就是石墨烯。
形象来说,石墨烯是由单层碳原子紧密堆积成二维蜂窝状晶格结构,看上去就像一张六边形网格构成的平面。
在单层石墨烯中,每个碳原子通过 sp2 杂化与周围碳原子成键给构整流变形,每一个六边单元实际上类似苯环,碳原子都贡献出个一个未成键电子。
单层石墨烯厚度仅0.35nm ,约为头发丝直径的二十万分之一。
石墨烯的结构非常稳定,碳原子之间连接及其柔韧。
受到外力时,碳原子面会发生弯曲变形,使碳原子不必重新排列来适应外力,从而保证了自身的结构稳定性。
石墨烯性能简介

第一章石墨烯性能及相关概念1石墨烯概念石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体。
石墨烯狭义上指单层石墨,厚度为0.335nm,仅有排列而成的蜂窝状晶体结构。
石墨烯中碳-碳键长约为0.142nm。
每个晶格内有三个σ键,连接十分牢固形成了稳定的六边状。
垂直于晶面方向上的π键在石墨烯导电的过程中起到了很大的作用。
石墨烯是石墨、碳纳米管、富勒烯的基本组成单元,可以将它看做一个无限大的芳香族分子,平面多环烃的极限情况就是石墨烯。
形象来说,石墨烯是由单层碳原子紧密堆积成二维蜂窝状晶格结构,看上去就像一张六边形网格构成的平面。
在单层石墨烯中,每个碳原子通过sp2杂化与周围碳原子成键给构整流变形,每一个六边单元实际上类似苯环,碳原子都贡献出个一个未成键电子。
单层石墨烯厚度仅0.35nm,约为头发丝直径的二十万分之一。
100倍,在室温下可以达到15000cm2/(V·s)。
电阻率比铝、铜和银低很多,只有10~6Ω·cm左右。
二是具有超强的导热性。
石墨烯的导热性能优于碳纳米管,是铜、铝等金属的数10倍,导热系数高达5300W/m?K。
三是具有超强的力学性,石墨烯的硬度超过金刚石,断裂强度达到钢铁的100倍。
四是具有超强的透光性。
石墨烯的吸光率非常小,透光率高达97.7%。
五是具有超强的比表面积。
石墨烯的比表面积每克比普通活性炭高出1130m2,达到2630m2/g。
3.1石墨烯的光学性能石墨烯是已知的世上最薄、最坚硬的纳米材料,它几乎是完全透明的,只吸收2.3%的光,具有优异的光学性能。
理论和实验结果表明,单层石墨石饱和。
这一非线性光学行为成为饱和吸收。
在近红外光谱区,在强光辐照下,由于其宽波段吸收和零带隙的特点,石墨烯会慢慢接近饱和吸收。
利用这一性质,石墨烯可用于超快速光子学,如光纤激光器等。
3.2石墨烯的电学性能石墨烯的每个碳原子均为sp2杂化,并贡献剩余一个p轨道电子形成π键,π电子可以自由移动,赋予石墨烯优异的导电性。
石墨烯 中心孔径

石墨烯中心孔径石墨烯是一种由碳原子组成的单层晶体结构,具有独特的力学、电学、光学等特性。
与其他材料相比,石墨烯的中心孔径是一个非常独特的属性,这使得它成为了许多研究领域的热点。
石墨烯的中心孔径首先由理论计算所预测,在接下来的实验中得到了证实。
中心孔径是指石墨烯中心的空隙或缺陷,呈现出六个连续的碳原子共面排列。
另外,通过在石墨烯中引入不同数量和形状的中心孔径,可以控制石墨烯的层间距、能隙、电荷转移、机械强度等特性,从而在电子学、电磁学、力学、能源等多个领域中发挥其独特的应用价值。
在石墨烯中引入中心孔径的方法主要有两种:机械方法和化学方法。
机械方法是指通过使用原子力显微镜(AFM)或扫描探针显微镜(STM)等手段,在石墨烯表面施加力,从而在石墨烯中心形成孔洞。
与机械法相比,化学法可以更加精确地控制中心孔径的大小和形状,这通常是通过退火、氧化、还原、电化学腐蚀等方法来实现的。
石墨烯的中心孔径主要可以分为两类:规则孔径和不规则孔径。
规则孔径是指中心孔径呈现出规则的形状,如圆形、方形、六边形等,其大小可以通过调整化学反应条件、原材料形态、催化剂类型等方法来控制。
不规则孔径则是指中心孔径的形状较为复杂或者随机,如多边形、星形、蜂窝状等,这些形态可以通过控制反应参数和流动条件来实现。
石墨烯的中心孔径在电子学和纳米技术领域中有着广泛的应用前景。
例如,在电子学领域中,中心孔径可以用于制备低功耗、高稳定性和高速度的晶体管;而在纳米技术领域中,中心孔径可以用于制备具有定向导电性能的纳米导线、纳米传感器和纳米机械器件。
总之,石墨烯的中心孔径是石墨烯研究领域中一个非常重要的方向,它不仅能够深入理解石墨烯的结构和性质,而且还可以为我们开辟出一些新的应用领域。
随着技术的不断发展,石墨烯的中心孔径相关研究将会得到更加深入的研究和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
石墨烯理论(中)值得注意,Dirac点必须是偶数个,这时Hall电导才会呈整数量子化;如果有奇数个Dirac 点,则会出现半整数量子化,而具有时间反演对称性的晶格系统保证了Dirac点是成对出现(Nielssen提出的“费米子加倍定理”)。
*费米子加倍定理:一个局域自由费米子晶格系统,若其作用量具有手征性以及平移对称性则费米子数会加倍。
我们不妨先考察量子场论中自由费米子作用量现在将d维空间连续费米子场引入到离散晶格系统(表示晶格格点),作用量变为为晶格常数,为晶格键方向上的单位矢量。
计算动量空间上系统的Green函数动量限制在Brillouin区中离散化,在离散取值附近展开Green函数,Green函数的极点代表粒子激发,我们会发现只有在Brillouin区顶点上的位置时Green函数才会得到与连续时候一致,并且这时候发现Brillouin区并不只包含一个费米子极点,计算每个顶点上对应的每个动量分量都会得到一个费米子传播函数,譬如一维晶格Brillouin区上有两个顶点上的费米子(注意这时符号改变,正好会消除手征反常);四维晶格格点中,动量分量取值,共十六个费米子。
对于d维空间晶格,则有个费米子。
因此在理想离散晶格中费米子数目成倍增加。
2.石墨烯中的量子自旋Hall效应最初量子自旋Hall效应的构造是C.L.Kane和Mele的从石墨烯结构引入了次邻近格点间电子的内禀自旋轨道耦合,和的Dirac点因为自旋轨道耦合会打开体能隙,此时体态就变成了绝缘体;假设自旋守恒,Kane-Mele模型为不难发现这个模型正是前面讨论过的Haldane模型的叠加,其中自旋向上和自旋向下的电子分别处于一个Haldane模型晶格中,跃迁矩阵元互为共轭。
以为基,则哈密顿量是两个自旋部分的直和计算半有限系统会出现两条手征边缘态,穿过费米能级的四条边缘态,分别代表两个边缘上的上下自旋。
石墨烯系统里的自旋轨道耦合作用是个复杂的事情,一方面碳原子质量数小,因此自旋耦合轨道作用比较弱。
另一方面,多体格点系统里面,价电子自旋可以和本格点(on-site)碳原子,邻近原子间的价键轨道乃至次邻近的价键轨道动量进行耦合。
一般我们关心的是轨道上价电子输运性质,尤其是在Dirac点处低能电子受到这种弱的自旋轨道耦合作用影响产生的不同的电子结构性质;在Dirac点处的零能态因为时间反演对称性是Krames二重简并的。
在石墨烯平面系统中,价层原子轨道是形成的轨道,形成碳骨架的键是杂化轨道。
成分与三个成分之间有能量(键能),还有价键轨道的能量。
紧束缚模型的哈密顿量里面的电子跃迁能量自然也需要考虑这些不同原子轨道、价键轨道间的跃迁能量。
从Thomas自旋轨道耦合项出发,由于自旋轨道耦合比较弱,我们可以将自旋耦合轨道作用项视为微扰项,可以在一个Brillouin区中考察Wannie表象下基态波函数完备集,两个顶点处也即Ferimi面附近的四重(包含了自旋简并)零能简并的轨道波函数(即A,B两个碳原子上的原子轨道组合成)与其他不与轨道简并的波函数()进行简并微扰计算,到二级近似,当然也可以用Bloch表象波函数进行近似展开,那就是Dresselhaus计算石墨系统自旋耦合作用所采用的办法。
算出来在点的微扰矩阵元为:写出系统的低能有效自旋轨道耦合作用的哈密顿量这是个很有意思的结果,第一项是平庸的对角项耦合能量,可以忽略;微扰的一级项是较为常见的Rashba自旋轨道耦合项,来源于电子自旋与相应原子轨道动量耦合,在无外场时候这个项不重要;微扰二级项是所谓内禀自旋耦合,由晶格对称性与碳原子轨道几何性质决定。
三个类似“自旋”的Pauli矩阵算符分别代表着电子真实自旋、石墨烯晶格结构(与A和B 原子轨道之间的耦合轨道运动自由度相关)的晶格赝自旋以及二重简并的谷自由度赝自旋(Brillouin区中包含和两个对称性不等价的简并能谷——二重谷简并) 。
石墨烯中的这两个谷由时间反演对称性相联系,这与电子自旋十分类似,所以石墨烯的谷自由度可视为赝自旋)以及真实的电子自旋,从构造上可以明显看出这个作用由晶格对称性和碳原子轨道几何性质所决定;这个项的出现在物理上的原因是轨道轨道之间混合的结果,换言之单纯的原子轨道混合对此没什么贡献,轨道混合才有净贡献,这一点也从Haldane模型的对这个内禀自旋轨道耦合项写法中间接体现出来:跃迁格点间的两个键的单位矢量(从格点指向相邻的格点)叉乘后再和轨道上的电子自旋矢量点乘我们说过这个内禀自旋轨道耦合将打开大小的能隙,这个能隙有多大?具体是需要去像上面那样微扰计算。
简便地估算我们可以选择简化的波函数。
前面第一节在二次量子化中对A,B原子的轨道进行叠加得到波函数,我们采用Nambu表象:。
是四分量波函数,这里我们不妨将之视为模恒定的包络函数;是A,B原子的处的波函数的模函数:为Brillouin区中等价于或者的另外三个顶点位置处的晶格动量,是从A到B格点的基矢。
这样微扰矩阵元也可以得到相同结果。
简单地引入晶格间的Coulomb作用能,这时粗略估计得到能隙大小约为上面的估算并没有考虑电子间的长程Coulomb相互作用,在石墨烯中进一步计入Coulomb 相互作用需要进行微扰计算。
现考虑无掺杂纯石墨烯晶格系统中的理想二维电子气体,引入Coulomb相互作用后变会变成某种Fermi液体系统哈密顿量为其中是电子密度算符石墨烯中的二维Coulomb相互作用电子液体理论和QED的情形很不同。
由于接近光速,因此认为Coulomb相互作用推迟效应很小几乎是瞬时。
而不想QED中光子是三维空间中传播,二维电子系统相互作用是限制于二维空间的,从哈密顿量可知Coulomb作用会破坏Lorentz对称。
正如同QED中l哈密顿量的两个参数是,二维电子系统理论也依赖于两个参数,并且在标度变化下不变。
以RG(重整化群)的语言来说,Coumlomb 作用是“临界变量”,与动能有关而不随标度变换改变。
在QED中的电磁作用耦合常数,在石墨烯二维电子系统中,能标下的耦合常数则是。
人们通常对Green函数微扰计算,对相互作用进行自能修正。
在Hartree-Fock近似下计算自能图,得到HF自能修正,是动量截断,依据Dirac方程的低能有效范围而设定。
我们看到当,能谱将是对数发散的,因为二维电子系统的Coulomb作用是长程的因此有必要引入屏蔽来避免发散,我们在无规相位近似(RPA)下计算出极化函数是因此在情况下,零频极化率将消失,得到动态介电函数后将抵消掉原本真空Coulomb作用的发散源;这就是耦合常数重整化后得到计入真空极化屏蔽的耦合常数:。
以上是对于小耦合常数情形,而上面得到的结果有更深的含义。
原本长程Coulomb相互作用经过屏蔽后变成短程作用,Thomas-Fermi屏蔽长度为,为电子数密度,可以看到在二维电子系统中屏蔽长度很小。
弱的相互作用微扰过程中是稳定不会发散的,因此能谱在重整化群的标度变换下是不变的,重整化流方程:重整化群方程依赖于重整化参数的标度,依据原来未重整化的作用顶点,我们可单单以来表征标度特征。
在长波极限很小接近为零,从方程可知此即为重整化流的不动点(即重整化参数的鞍点)。
变小,微扰性质将更好。
这意味着即使在强关联作用情形,系统依旧会流向长波微扰极限。
这告诉人们是临界无关的。
因此一定动量截断,小的色散关系将由上面重整化群方程给出,得到关于Fermi速度在下的对数重整化。
临界无关的含有对数修正项且在低能标下依然存在,这时我们的系统在低能情形变成一种临界Fermi液体。
在能标截断下有,,解重整化方程得到重整化参数。
该结果与大N极限展开(N是电子规范自由度,类似“味”)得到的结果相同。
我们把这些方法应用到自旋耦合轨道能的修正上去。
下面这个就是对具有自旋轨道耦合顶点项的传播子加上Coulomb作用的正规自能1PI图:重整化流方程:在能标的重整化为,选定一定截断有效作用,得到重整化自旋轨道耦合能,比较可知引入电子间相互作用后将会更明显地拉大能隙。
有界石墨烯晶格系统会产生两条无能隙螺旋边缘态,它们在边界上会形成一些没有“背散射”的导电通道(也就是不受杂质散射影响的理想导体)。
这是由于体态的非平庸拓扑性保护而对各种非磁性杂质具有鲁棒性。
考虑由于杂质导致的Krames对,之间的散射矩阵元。
对1/2自旋的电子时间反演算符为,其中是取复共轭操作算符,是自旋投影算符,且有。
非磁性杂质散射势满足,,Krames对之间,,即对于互为时间反演共轭的两个边缘态在保持时间反演对称的散射势下,其跃迁矩阵元为零。
也可以用Büttiker-Floquet 散射矩阵理论描述:考虑向左、向右运动的边缘态组成的入射态以及出射态, 时间反演对称将联系入射态和出射态,散射矩阵为,因此推得时间反演对称性使得, 这么一来,描述背向散射的矩阵元消失。
因此输运中是完美地穿过势垒,不存在非弹性背向散射。
很重要的一点情况是时间反演对称性依旧存在,而且在极化情况下自旋在方向是守恒的,也就是是个好量子数。
而当加入外电场(实际上材料也往往存在破坏自旋守恒的因素,譬如应变导致结构反演对称受破坏),那么这时候一级作用——Rashba自旋轨道耦合也就起很大影响。
而由于不是守恒的好量子数,也就无法定义自旋流了也就不再有量子自旋Hall 电导,因而不再处于QSH相。
然而值得庆幸的是,Rashba耦合项只是破坏空间反演对称性并没破坏时间反演对称性,那么作为边缘态出现的一对无质量Dirac费米子依旧会保留下来(这固然需要依据情况适当调节Fermi面与边缘态相交)。
当Rashba耦合能增大到比内禀耦合能大时,这时候边缘态不再是无能隙的,即打开了整个系统的能隙,这是意味着这是个量子相变临界点。
相变后变成弱的时间反演对称保护的二维非平庸拓扑绝缘体相,只不过自旋不守恒而失去QSH相。
当系统进入拓扑平庸相的参数区,边缘态也不再具有鲁棒性(从能谱中可看到,当Fermi 面移动不与边缘态谱线相交时候就不再有无质量Dirac费米子出现,杂质的干扰可以把这种边缘态可以拉进体态中)。
综上所述,我们明白了具有时间反演对称性的二维系统绝缘体有两类:拓扑非平庸相和拓扑平庸的普通绝缘体相。
当然,要判断系统处于何种相就要计算自旋陈数之差,也就是拓扑不变量。
当哈密顿量存在时间反演对称性,系统不存在Hall电流而Hall电导为零。
因此不论系统是否具有其他的拓扑性质第一陈数都等于零,这样就不能用第一陈数来对具有时间反演对称性的系统进行拓扑分类。
然而量子自旋Hall系统却具有净自旋流输运:,自旋Hall电导为:。
于2006年,Liang Fu和Kane提出了用时间反演极化定义拓扑数的方法来刻画系统的拓扑序。
