六度分离理论
通过6个人,你就能认识世界上任何一个人,偶绝对相信!

通过6个⼈,你就能认识世界上任何⼀个⼈,偶绝对相
信!
周末下班前有惊喜,和认识很久的朋友在开⼼⽹相认了,除了发现是同⼀届的,同⼀个城市的以外,还发现互相都有很多认识的朋友,⽽且还是不同渠道互相认识的朋友,世界真是⼩啊,怪不得说这个世界任何两个⼈之间相隔的⼈数最多不超过6个,绝对相信这个理论!
补⼀下课外知识啦,什么叫做六度分隔理论:
六度分隔(Six Degrees of Separation)理论。
1967年,哈佛⼤学的⼼理学教授Stanley Milgram(1933-1984)想要描绘⼀个连结⼈与社区的⼈际连系⽹。
做过⼀次连锁信实验,结果发现了“六度分隔”现象。
简单地说:“你和任何⼀个陌⽣⼈之间所间隔的⼈不会超过六个,也就是说,最多通过六个⼈你就能够认识任何⼀个陌⽣⼈。
”
“六度分隔”说明了社会中普遍存在的“弱纽带”,但是却发挥着⾮常强⼤的作⽤。
有很多⼈在找⼯作时会体会到这种弱纽带的效果。
通过弱纽带⼈与⼈之间的距离变得⾮常“相近”。
所谓“六度分隔”,⽤最简单的话描述就是:在⼈际脉络中,要结识任何⼀位陌⽣的朋友,这中间最多只要通过六个朋友就能达到⽬的。
六度空间理论

一、理论提出者斯坦利·米尔格兰姆(Stanley Milgram,1933-1984)出生于美国纽约市,毕业于昆斯学院,后赴哈佛大学深造。
1960年在哈佛大学获得哲学博士学位,同年转入耶鲁大学。
1963年回到哈佛大学,担任该校社会关系系国际比较研究课题的行政负责人。
米尔格兰姆是美国科学促进会的会员,1965年获该会社会心理学奖,1972年成为古根海姆的一名研究人员,1980年应聘于纽约市立大学任心理学教授。
斯坦利·米尔格兰姆在《美国名人录》中谈到他的成功秘诀时说:“作为一名社会心理学,我是这样看待世界的:我们不应试图控制任何实际感觉,而是应该了解它。
人与人之间应相互沟通、相互了解。
”米尔格兰姆对服从问题的实验研究,使他的这一主张得到了普遍的赞同。
他揭示了由于对权力主义的服从,使得一些人对另一些清白无辜的人所赞成的痛苦。
他认为他的实验还可以说明为什么会出现纳粹害关押在集中营里的受害者的残暴行为。
米尔格兰姆的主要著作有:《对权力的服从》、《电视与孤僻行为》(与R.肖特兰合著)、《社会生活中的个体》。
二、理论内容六度分割理论,Six Degrees of Separation,又称六度空间理论以及小世界理论等。
六度分割理论指出:你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过六个人你就能够认识任何一个陌生人。
两个小故事(1)1967年,美国社会心理学家米尔格伦设计了一个连锁信件实验。
他将一套连锁信件随机发送给居住在内布拉斯加州奥马哈的160个人,信中放了一个波士顿股票经纪人的名字,信中要求每个收信人将这套信寄给自己认为是比较接近那个股票经纪人的朋友,朋友收信后照此办理。
最终,大部分信在经过五、六个步骤后抵达了该股票经纪人。
(2)一家德国报纸接受了一项挑战,要帮法兰克福的一位土耳其烤肉店老板,找到他和他最喜欢的影星马龙·白兰度的关联。
结果经过几个月,报社的员工发现,这两个人只经过不超过六个人的私交,就建立了人脉关系。
六度分隔理论

六度分隔理论一、六度分隔假说(Six Degrees of Separation)1967年,美国哈佛大学的心理学教授Stanley Milgram(1933-1984)想要描绘一个连结人与社区的人际联系网,做过一次连锁信实验,结果发现了"六度分隔"现象。
六度分隔(Six Degrees of Separation)现象(又称为“小世界现象”small world phenomenon),可通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过六个人你就能够认识任何一个陌生人。
”“六度分隔”说明了社会中普遍存在的“弱纽带”,但是却发挥着非常强大的作用。
有很多人在找工作时会体会到这种弱纽带的效果。
通过弱纽带人与人之间的距离变得非常“相近”。
二、其数学解释如下:若每个人平均认识260人,其六度就是2606=1,188,137,600,000。
消除一些节点重复,那也几乎复盖了整个地球人口若干多多倍。
——摘录自wikilab三、六度分隔实验:Degrees of separation = no. of steps to go half way round circle1967年,美国哈佛大学社会心理学教授斯坦利·米尔格兰姆对这个问题做了一个著名的实验,他从内布拉斯加州和堪萨斯州招募到一批志愿者,随机选择出其中的三百多名,请他们邮寄一个信函。
信函的最终目标是米尔格兰姆指定的一名住在波士顿的股票经纪人。
由于几乎可以肯定信函不会直接寄到目标,米尔格兰姆就让志愿者把信函发送给他们认为最有可能与目标建立联系的亲友,并要求每一个转寄信函的人都回发一个信件给米尔格兰姆本人。
出人意料的是,有六十多封信最终到达了目标股票经济人手中,并且这些信函经过的中间人的数目平均只有5个。
也就是说,陌生人之间建立联系的最远距离是6个人。
1967年5月,米尔格兰姆在《今日心理学》杂志上发表了实验结果,并提出了著名的“六度分隔”假说。
六度分离文档

六度分离1. 简介六度分离是一种理论概念,描述了社交网络中人与人之间联系的短途路径。
该概念源自弗里曼·戴克曼于1967年提出的「小世界网络」理论,并在1990年由哈佛大学心理学家斯坦利·米尔格拉姆的实验中进一步得到验证。
六度分离指的是任意两个社交网络中的人之间,平均只需通过不超过六个人的中间人即可建立联系。
这意味着,世界上任何两个陌生人之间,通过不超过六个中间人,就可以建立起联系。
2. 六度分离的实验证据斯坦利·米尔格拉姆的实验是六度分离概念得到验证的重要实证之一。
他在1960年代进行了一系列的社交实验,被称为「小世界实验」。
在这个实验中,米尔格拉姆要求参与者通过写信方式将一封信寄给陌生人,而这封信的目标接收者并未提供。
实验参与者只能基于自己的社交网络和认识的人来选择发送该信的目标。
结果显示,平均只需要通过三到六个中间人,这封信最终就能被送到目标接收者手中。
这个实验结果引起了广泛的关注,并且成为了后来「六度分离」理论的重要依据。
除了米尔格拉姆的实验,现代社交网络的发展也进一步证实了六度分离的概念。
社交媒体平台如Facebook和LinkedIn 让人们更容易建立联系,扩大了我们的社交网络。
通过这些平台,人们可以迅速找到共同的朋友或认识的人,从而帮助他们建立新的联系。
这种联系的建立速度和范围也证明了六度分离的存在。
3. 六度分离的应用六度分离的概念在各个领域都有广泛的应用。
以下是一些典型的应用场景:社交网络分析社交网络分析是一种研究社交关系及其网络结构的方法。
六度分离理论对社交网络分析起到了重要的指导作用。
通过研究人与人之间的连接关系,可以深入了解信息传播、意见领袖和社交集团等社交现象。
营销和市场推广六度分离的理论对于营销和市场推广策略的制定非常有帮助。
通过了解目标顾客的社交网络,可以利用六度分离的原理,通过目标顾客的社交联系,快速传播产品或服务的信息。
这种方式的推广效果往往比传统的广告渠道更加高效和成功。
六度分离理论

社会效率
人际网络
六度分离促进社会网络化和“地球村” 六度分离促进社会网络化和“地球村”的形成
六度分离研究与社会网络和网络社会
其他
网络社会更证明并应用者六度分离理论
Title in 同学 here
Title in 亲人 here
各种社会软件联系着我们, 各种社会软件联系着我们,如QQ,MSN,UC, , 旺旺等交流软件 各种社区网站等如开心,人人,猫扑, 各种社区网站等如开心,人人,猫扑,博 客,微博等 电脑数码等的普及, 电脑数码等的普及,网游等等更能鲜明 证明六度分离理论 同时,人员管理,国家政治活动, 同时,人员管理,国家政治活动,国家经 济管理都有六度分离理论的应用。 济管理都有六度分离理论的应用。
六度分离理论
现今的网络在以六度分离理论为基础的同时, 现今的网络在以六度分离理论为基础的同时,不断验 证和完善着六度分离, 证和完善着六度分离,也通过理论的完善而不断改善 着自身,如此下去形成了一个良性的循环过程, 着自身,如此下去形成了一个良性的循环过程,使得 理论与服务一起得到升华! 理论与服务一起得到升华
六度分离研究与社会网络和网络社会
社会人际关系就是一个庞大的网络,现实社会中, 社会人际关系就是一个庞大的网络,现实社会中,人与人的交流是通过人与人 之间的介绍、握手来形成一个朋友圈、联系圈的, 之间的介绍、握手来形成一个朋友圈、联系圈的,每个人不需要直接认识所有 只需要通过他的朋友,朋友的朋友,就能促成一次握手。 人,只需要通过他的朋友,朋友的朋友,就能促成一次握手。而普通的网络交 则大多数通过某些平台来实现,比如将自己放到一个平台中去, 际,则大多数通过某些平台来实现,比如将自己放到一个平台中去,让很多人 看到,并且联系你认识你。两者的优缺点明显,社会性交际优点是可靠, 看到,并且联系你认识你。两者的优缺点明显,社会性交际优点是可靠,彼此 关系建立在可靠的人际网络上,缺点是产生握手的时间长、代价较高; 关系建立在可靠的人际网络上,缺点是产生握手的时间长、代价较高;平台式 的网络交际优点是成本低,但不可靠。 的网络交际优点是成本低,但不可靠。
六度分离理论

六度分离理论应用
网络中六 度分离的 应用 SNS与六 度分离理 论
物理、化学、 生物、交通、 影视传媒等 领域
,“六度分隔”和互联网的亲密结合,已 经开始显露出商业价值。人们在近几年越 来越关注社会网络的研究,很多网络软件 也开始支持人们建立更加互信和紧密的社 会关联,这些软件被统称为“社会性软件 ”。 人与人的交流是通过人与人之间的介绍、 握手来形成一个朋友圈、联系圈的,每个 人不需要直接认识所有人,只需要通过他 的朋友,朋友的朋友,就能促成一次握手 。 六度分离理论在各社会学科,个领域的经 济价值文化价值等都具有非常重大的意义 例如经济活动中的商业联系网络结构、生 态系统中的食物链结构,甚至人类脑神经 元结构,以及细胞内的分子交互作用网络 结构。
.
六度分离研究与社会网络和网络社会
这个看似非常简单,却又很玄妙的理论引起了数学家、物理学家, 这个看似非常简单,却又很玄妙的理论引起了数学家、物理学家,以及电脑科学家们的 关注。他们研究发现世界上许多其它的网络也有极相似的“六度分离”结构, 关注。他们研究发现世界上许多其它的网络也有极相似的“六度分离”结构,例如经济活动 中的商业联系网络结构、生态系统中的食物链结构,甚至人类脑神经元结构, 中的商业联系网络结构、生态系统中的食物链结构,甚至人类脑神经元结构,以及细胞内的 分子交互作用网络结构
人际
信息
六度分离原则

六度分离原则在社交网络领域中,有一个著名的理论被广为人知,那就是“六度分离”原则。
根据这个原理,任何两个人之间最多只需要通过六个中间人,就能够建立联系。
这个理论的背后蕴含着人类社会的网络结构和人际关系的奥秘。
尽管六度分离原则最初是由米尔格拉姆在20世纪60年代提出的,但是它的影响力却远远超过了学术界。
在现代社会中,我们经常听到有关“六度分离”的说法,而它也成为了社交网络和社会媒体平台的重要基础之一。
那么,为什么我们需要关注六度分离原则呢?它有什么实际意义呢?首先,六度分离原则揭示了人际关系网络的庞大性和复杂性。
人类社会是由一个个紧密相连的个体组成的,每个个体又处于多重社交圈中。
通过六度分离原则,我们意识到即使与我们直接接触的人数有限,但是通过他们我们可以间接接触到整个世界。
这种联系的广度和深度展示了人类社会的庞杂和错综复杂的结构。
其次,六度分离原则突显了社交网络和社会媒体的重要性和潜力。
在过去的几十年中,互联网的迅速发展使得人们之间的联系更加紧密。
社交网络平台如Facebook、Twitter等成为了人们交流、分享信息和建立联系的重要工具。
通过这些平台,我们可以轻松地与世界各地的人相连,通过朋友的朋友迅速建立联系。
六度分离原则的实践,正是由于互联网的普及和社交网络的繁荣。
然而,我们也要看到六度分离原则存在的一些潜在问题。
首先,虽然理论上说通过六个中间人可以建立联系,但在现实生活中,这并不一定容易实现。
由于人际关系的复杂性和网络平台的局限性,可能会遇到信息损失、误传等问题。
此外,由于社交网络的私密性和保护个人信息的需求,人们也可能对建立过多的联系感到困扰。
鉴于上述问题,有些人提出了对六度分离原则的质疑。
他们认为,在特定环境下,六度分离原则可能不适用。
比如,在某些社群中,人们的人际关系网可能更加紧密,可以迅速建立联系。
而在另一些特殊场景下,由于地理、文化等因素的限制,建立联系可能要比六度更多。
尽管如此,六度分离原则仍然成为了许多社会和学术研究的基础。
六度分隔理论名词解释

六度分隔理论名词解释六度分隔理论是指一个人可以通过六个人或更少的节点来联系任意两个人,让他们之间形成一个简单的社交网络。
六度分隔理论的研究可以帮助我们了解地球上最大的社交网络是如何形成的。
六度分隔理论最早由美国社会学家夏威夷大的斯蒂芬迪克斯(StephenD.Dicks)提出,他认为人们之间的社会联系可以通过六度距离产生化学效应。
这一理论被称为“六度分隔理论”,也可以说是迪克斯推论。
六度分隔理论意味着任何两个人之间都可以通过六度内的任何一个人介绍彼此。
意味着,通过六度分隔的这些人构成了一个大的社会网络,所有人彼此之间的关系都可以推断出来。
此,我们可以说,六度分隔理论可以帮助我们推断和探究社会网络的性质。
学者们也研究发现,六度分隔的理论并不是如迪克斯所认为的那样,一个人可以通过六度内的任何一个人来联系任意两个人,而是通过社会网络分析,发现各不相同的社会网络中,各个节点之间通过跳转节点最多需要几步,才能实现全球联通,这个值称为全球最少跳转路径。
同时,六度分隔理论的研究也可以用来帮助预测社会关系的变化。
如果一个人的关系网络中有一个关系节点变化,或者有其他节点加入或离开,那么这种变化可能会影响他在六度内分隔的节点,从而改变社会关系。
迪克斯的六度分隔理论也可以用来帮助把握社会趋势,特别是在分析新兴技术在社会中传播的过程中。
比如,在信息技术发展的时代,新信息技术可以通过六度内的节点传播到社会的其他节点,从而形成一个新的社会关系。
综上所述,六度分隔理论是一个重要的概念,可以帮助我们了解地球上最大的社会网络是如何形成的,并可以用来帮助我们推断和探究社会网络的性质,同时也可以用来预测社会关系的变化。
六度分隔理论的研究可以帮助我们更深刻地理解社会网络是如何运作的,以及新兴技术如何能够在社会中迅速扩散的本质原理。
六度分隔

六度空间应用
兴趣爱好搜寻
任何两位素不相识的人之间,通过一定的联系方式,总能够产生必然联系或关系。 - 六度分隔论
六度分隔理论
六度分隔理论表达了一个重要的
概念:任何两位素不相识的人之间, 通过一定的联系方式,总能够产生必 然联系或关系。也即是说通过朋友 目标人物
传朋友的方式可以发展更多的
于“朋友传朋友”的方式来发展业 务的,它们属于广义六度分隔理论, 或称小世界效应。
爱好
六度空间应用
来访好友
我的好友
用户注册微博以后,可根据来
访好友、同城好友、兴趣好友等条 件查找好友,与好友在线@或发私信 沟通
互为好友的两个人其好友资
料彼此共享,实现“朋友传朋友” 互粉关系应该获得更大的权
限,以激励用户互粉
无论这两个人是否认识,生活在地球上任何地方,他们之间最多只有六度分割。 - 六度分隔论
六度分隔 Six Degrees
六度分隔概述
意义:
世界上所有互不相识的人只需要很少(6位)中 间人就能建立起联系。称为小世界现象(又称小 世界效应)
源起:
1967哈佛大学心理学教授 Stanley Milgram 为 了解人际网络所进行的连锁信实验。发现了人与 任何陌生人之间的间隔,平均來说不会超过6个。
六度分隔理论
小世界网络同时具有“高网络聚集度”和 “低平均路径”的特性:
聚集意味着如果个体有共同的朋友,则两个个体 更有可能成为朋友 “低平均路径”意味着任意两个人可以通过比较 短的中间连接取得联系
拓展:
Watts与Strogatz也先后在疾病传播、昆虫神经 系统和电力系统中揭示出现实网络确实符合小世 界模型
六度分隔理论
六度分离理论在网络深度营销中的价值体现

六度分离理论在网络深度营销中的价值体现摘要:目前,电子商务已经深刻地改变了人们的生活和思维方式,网络和现代电子商务技术以一种新型的、互动的、更加人性化的营销新模式出现了。
以六度分离理论、小世界模型为基础,解释了基于电子商务平台的深度营销中顾客间建立联系的规律,从总结的规律出发,深入探讨了对网络深度营销启示,以及企业内外部营销价值。
电子商务已经将全球变成了一个真正意义上的大市场,世界上任何入网的企业和个人都可以通过网络进行资源共享、信息交流、电子商务等活动。
电子商务已经深刻地改变了人们的生活和思维方式,而且将继续改变下去。
而传统的营销观念都是建立在工业经济时代基础上的,随着科学技术的发展,已经不能完全适应网络经济时代的需要了。
所以,我们需要一种全新的营销观念,即基于电子商务技术与平台的深度营销,这种营销观念以网络和现代电子商务技术为基础,以企业和顾客之间的深度沟通为目标,从关心人的显性需求转向关心人的隐性需求的一种新型的、互动的、更加人性化的营销新模式。
一、六度分离理论及小世界网络模型的基本原理(一)六度分离理论的基本原理1969年,美国社会心理学家斯坦利•米尔格伦(Stanley•Milgram)做了一个定量试验:指定一名最终收信人,然后随机派发一定量的邮件给称为发信者的人,请这些发信人通过自己的关系网络传递这封信,并尽最大可能保证这封信能递送到指定的最终收信人手中。
虽然发信人与最终收信人互不相识,但最终试验证明,所有信件通过平均6次的传递,送到了最终收信人处[1]。
因此,米尔格伦得出结论:你和任何一个陌生人之间所间隔的人不会超过六个,也就是说最多通过六个人你就能够认识任何一个陌生人。
这就是闻名的“六度分离理论”(Six Degrees of Separation)。
此理论提出后虽然没有得到学术界完全的认可,但给人文学、经济学界带来了全新的灵感和研究思路。
(二)小世界网络模型的基本原理1998年,美国哥伦比亚大学社会学系任教的年轻学者Duncan Watts与其博士论文导师数学家Strogatz基于前人的理论提出了“Small-World Networks”(SWN),即W-S小世界网络模型[2]。
六度分离

六度分离“六度分离”是社会学家在研讲究社会网络(social networks)时提出的一个概念。
“六度分离”在学术上称为“小世界现象”或“小世界问题”。
该问题源于社会学家、哈弗大学的心理学教授Stanley Milgram(1934~1984)在1967年作的实验:“追踪美国社交网络中的最短路径”。
他要求每个参与者设法寄信给一个住在波士顿附近的“目标人物”,规定每个参与者只能转发给一个他们认识的人。
Milgram发现完整的链平均长度为6个人。
比如我们可以设想寄一封信给“莱温斯基”,够远吧?我设想的路径是:首先,我寄信给我的同学,他的父亲是外交官,由他寄信给他的父亲,外交官自然认识我国的外交部长,我国的外交部长一定认识克林顿,最后由克林顿寄信给莱温斯基即可。
正好是6个人。
按照这个概念,生活在这个世界上的每个人只需要很少的中间人(平均6个)就可以和全世界的任何一个人建立起联系。
我们可以把每个人看作是一个节点(node),认识的人之间可以画上一条边(side),最后会形成一个网络(net)。
每个节点可以有多少条边?或者每个人可以有多少个朋友?如果我们做这个调查的话,可能很困难,每个人对朋友的定义不一样,你认为是朋友,但我认为不是,这样获得的数据是有疑问的,有很多说不清楚的地方。
不过,现在有互联网,就好办多了,只要加在QQ好友栏的就算好友,假使我们真的做这样一个统计的话,我估计这个数字可能会比6 大,可能是8、9等等。
毕竟有不少人QQ上只几个名字,而现实生活中,我们认识的人肯定比“几个”要多多了。
现在,有不少人琢磨利用“六度分离”作交友网站。
另外P2P软件的下载也利用了“六度分离”,全世界的电脑连成了一个网络,网络上任意两台电脑,通过一个包含6台电脑的路径就可互相下载对方的资源了。
电影:六度分离(1993)Six Degrees ofSeparation,片子对六度分离的理论有提及,但是并没有通篇去阐述。
六度分割理论

“六度分割理论”马克思主义哲学认为,世界是一个普遍联系的有机整体,没有一个事物是孤立存在的。
在自然界、人类社会和人的思维中,到处都充满着体现客观事物之间普遍联系的事例。
例如在数学中有个著名的“六度分割理论”(英文翻译Six Degrees of Separation)又称为“六度空间理论”、“小世界理论”等。
早在1929年,匈牙利作家F Karinthy就做出了“小世界现象”论断,认为地球上的任何两个人都可以平均通过一条由六位联系人组成的链条而联系起来。
1967年,美国著名社会心理学家、斯坦利米尔格兰姆教授(Stanley Milgram)提出了“六度分割理论”。
它指出,世界上任何无论多么陌生两个人之间所间隔的人不会超过六个人,也即是说我们至多通过六个人就可以认识想要结识的人。
“六度分隔”现象,是米尔格兰姆教授在一次连锁信实验中发现的。
他将一套连锁信件随机发送给内布拉斯加州奥马哈的160个人,信中写有一个波士顿股票经纪人的名字。
在信中他要求每位收信人将这封信寄给自己认为是比较接近那个股票经纪人的朋友。
朋友收信后照此办理。
最终,大部分信件都寄到了这名股票经纪人手中,每封信在经过平均经手6.2次到达。
同年5月,米尔格兰姆在《今日心理学》杂志上发表了实验结果,并提出了著名的“六度分割理论”。
为验证理论的正确性,一家德国报纸曾接受了这样一项挑战:一位法兰克福的土耳其烤肉店老板,很希望结识影星马龙白兰度。
于是该报就要帮助老板找到他和马龙白兰度之间的“关系链”。
经过了几个月的努力,报社员工终于发现,其实这两个人之间只需要不超过六个人的联系,就可以建立人脉关系。
原来烤肉店老板是伊拉克移民,他有一个朋友住在加州,刚好这个朋友的同事,是电影制作人的女儿在女生联谊会的结拜姐妹的男朋友,而马龙白兰度正好主演了这部片子。
通过上述人脉关系,使得烤肉店老板在不超过六个人的间隔就建立两者之间的结识渠道。
“六度分割理论”内容及其验证事例,表明事情之间是存在普遍联系的。
六度分离理论

六度分离理论人们都说,好事不出门,坏事传千里。
那么为什么人们总是爱把坏事传的那么快呢?原来,这也是“六度分离”理论在起作用。
它是20世纪中叶提出来的,其内容为:任何两个人之间所间隔的人不会太多,最多不过六个。
这就是著名的六度分离理论。
这个理论告诉我们,任何两个人之间都可以通过一定的渠道(媒介)联系到,只要这种联系足够强大、及时,信息就会迅速传播开去。
美国曾经做过这样一个实验:在地球上选择100名记忆力超常的学生,给他们每人一本字典,并告诉他们,他们必须在5天内背完字典里的全部词条,而且不许查字典,不许问别人。
试验结果表明: 5天后,背完字典里所有词条的学生达90%。
但如果继续这项试验,当这些学生被要求再背一遍时,大部分人竟然无法再背下来了!显然,如果没有外界的监督和检查,几乎所有人都难以坚持到最后。
同样,在信息化社会里,没有管制的行业或者不负责任的人都很容易导致一些乱象。
就像最近被报道的英国禁止卖酒给年龄小于18岁的少女、阿富汗呼吁年轻人出国打工,而又有人揭发这些人才是专门欺骗外国人的商人一样,看似是不同的行业,其实背后都有相似的根源。
很快,整个欧洲的教育家们得出结论:一个孩子的知识程度与他和父母亲的关系密切相关。
不仅如此,与他亲近的同学、老师甚至邻居等,对他的影响也是极其巨大的。
而六度分离理论中提到的媒介则是指人际交往中使用的各种信息传播手段,包括书信、电话、广播、电视、报刊杂志等。
在我们身边,六度分离理论还体现在以下几个方面:学校老师的态度,对待不同成绩的学生有所差别,从而使班级形成良好的学习氛围;农民伯伯对待庄稼的态度不同,导致种植出来的粮食品质也大不相同。
一个人的朋友圈越大,他所能影响的人也就越多。
比如说,人们经常称赞一个人“真牛”,意思就是“真正的伟人”,虽然表面上说他是虚张声势,但心里还是挺佩服他的。
六度分离理论认为,任何两个人之间都可以通过一定的渠道(媒介)联系到,只要这种联系足够强大、及时,信息就会迅速传播开去。
六度空间理论分析报告

六度空间理论分析报告六度空间理论又称六度分割理论或小世界理论,你和任何一个陌生人之间所间隔的人不会超过六个(也就是说,最多通过五个中间人你就能够认识任何一个陌生人)涵义:假设世界上所有互不相识的人只需要很少中间人就能建立起联系。
后来1967年哈佛大学的心理学教授斯坦利·米尔格拉姆根据这概念做过一次连锁信件实验,尝试证明平均只需要五个中间人就可以联系任何两个互不相识的美国人。
价值:不管理论如何深奥,“六度分割”和互联网的亲密结合,已经开始显露出商业价值。
人们在近几年越来越关注社会网络的研究,很多网络软件也开始支持人们建立更加互信和紧密的社会关联,这些软件被统称为“社会性软件”(Social Software)。
例如Blog就是一种社会性软件,因为Blog写作所需要的个性和延续性,已使Blogger圈这种典型的物以类聚的生态形式,越来越像真实生活中的人际圈。
据致力于研究社会软件的毛向辉介绍,国外当今更流行的是一种快速交友,或者商业联系的工具,例如LinkedIN。
人们可以更容易在全球找到和自己有共同志趣的人、更容易发现商业机会、更容易达到不同族群之间的理解和交流,等等。
20世纪60年代,美国心理学家米尔格兰姆设计了一个连锁信件实验。
米尔格兰姆把信随机发送给住在美国各城市的一部分居民,信中写有一个波士顿股票经纪人的名字,并要求每名收信人把这封信寄给自己认为是比较接近这名股票经纪人的朋友。
这位朋友收到信后,再把信寄给他认为更接近这名股票经纪人的朋友。
最终,大部分信件都寄到了这名股票经纪人手中,每封信平均经手6.2次到达。
于是,米尔格兰姆提出六度分割理论,认为世界上任意两个人之间建立联系,最多只需要6个人分析应用关系强弱——权值问题我们一生可能会认识千百人,他们有的对我极其重要,有的对我无足轻重,我们联系建立的原因和方法也是千差万别的。
有父母亲属这类生而固有的联系,也有因为地理位置接近发展出来的。
六度理论学习计划作文

六度理论学习计划作文一、理论概述六度理论,也被称为“六度分隔”理论,是由美国心理学家斯坦利·米尔格拉姆在1967年提出的。
该理论认为,任何两个地球上的人之间只需要通过六个人的联系,就能够建立起直接的联系。
这个理论引起了广泛的关注,被认为是社交网络和人际关系研究的基础。
六度理论的提出,对我们认识社交网络和人际关系产生了深远的影响。
它使得我们更深刻地理解了人与人之间的联系,同时也为人际交往和社会关系的研究提供了新的视角。
二、学习目标1. 了解六度理论的历史背景和基本概念;2. 掌握六度理论在社交网络和人际关系中的运用;3. 深入理解六度理论对人际交往和社会关系的启示。
三、学习内容1. 六度理论的历史与背景- 理论提出者斯坦利·米尔格拉姆的生平及成就;- 六度理论的起源和发展过程;- 六度理论在心理学、社会学和传播学等领域的影响。
2. 六度理论的基本概念- 六度理论的概念由来和内涵;- 六度理论的实验和研究方法;- 六度理论的实际应用和案例分析。
3. 六度理论在社交网络中的应用- 社交网络的基本原理和结构;- 社交网络中的“小世界现象”与六度理论的关系;- 社交网络中的信息传播与影响力分析。
4. 六度理论在人际关系中的运用- 人际关系的形成和变化规律;- 人际关系网络的构建和维护;- 人际关系的质量和稳定性分析。
5. 六度理论对人际交往和社会关系的启示- 六度理论对人与人之间的联系和交流的意义;- 六度理论对社会网络和组织行为的影响;- 六度理论对人际交往和社会关系的指导意义。
四、学习方法1. 阅读相关文献和资料,包括经典著作、学术论文、案例分析等;2. 参与学术讨论和学术交流,积极参加学术研讨会和学术交流会;3. 深入实地调研和实践,结合实际情况进行个案分析和实证研究;4. 积极参与学术实践和社会实践,提升理论应用能力和实际操作技能。
五、学习步骤1. 第一阶段:对六度理论的历史与背景进行了解和分析;2. 第二阶段:掌握六度理论的基本概念和研究方法;3. 第三阶段:了解六度理论在社交网络中的应用和实际案例;4. 第四阶段:深入研究六度理论在人际关系中的运用和实际效果;5. 第五阶段:分析六度理论对人际交往和社会关系的启示和影响。
六度空间理论
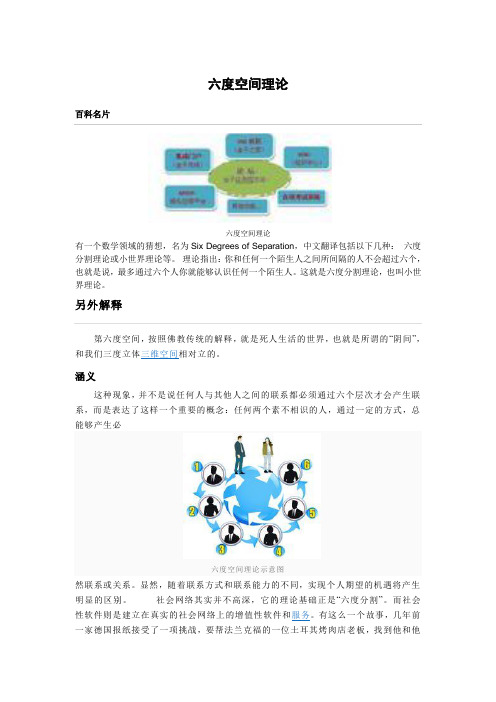
六度空间理论百科名片六度空间理论有一个数学领域的猜想,名为Six Degrees of Separation,中文翻译包括以下几种:六度分割理论或小世界理论等。
理论指出:你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过六个人你就能够认识任何一个陌生人。
这就是六度分割理论,也叫小世界理论。
另外解释第六度空间,按照佛教传统的解释,就是死人生活的世界,也就是所谓的“阴间”,和我们三度立体三维空间相对立的。
涵义这种现象,并不是说任何人与其他人之间的联系都必须通过六个层次才会产生联系,而是表达了这样一个重要的概念:任何两个素不相识的人,通过一定的方式,总能够产生必六度空间理论示意图然联系或关系。
显然,随着联系方式和联系能力的不同,实现个人期望的机遇将产生明显的区别。
社会网络其实并不高深,它的理论基础正是“六度分割”。
而社会性软件则是建立在真实的社会网络上的增值性软件和服务。
有这么一个故事,几年前一家德国报纸接受了一项挑战,要帮法兰克福的一位土耳其烤肉店老板,找到他和他最喜欢的影星马龙·白兰度的关联。
结果经过几个月,报社的员工发现,这两个人只经过不超过六个人的私交,就建立了人脉关系。
原来烤肉店老板是伊拉克移民,有个朋友住在加州,刚好这个朋友的同事,是电影《这个男人有点色》的制作人的女儿在女生联谊会的结拜姐妹的男朋友,而马龙·白兰度主演了这部片子。
价值不管理论如何深奥,“六度分割”和互联网的亲密结合,已经开始显露出商业价值。
人们在近几年越来越关注社会网络的研究,很多网络软件也开始支持人们建立更加互信和紧密的社会关联,这些软件被统称为“社会性软件”(Social Software)。
例如Blog就是一种社会性软件,因为Blog写作所需要的个性和延续性,已使Blogger圈这种典型的物以类聚的生态形式,越来越像真实生活中的人际圈。
据致力于研究社会软件的毛向辉介绍,国外现在更流行的是一种快速交友,或者商业联系的工具,例如LinkedIN。
SixDegreeofSeparation

SixDegreeofSeparation本博客的代码的思想和图⽚参考:好⼤学慕课浙江⼤学陈越⽼师、何钦铭⽼师的《数据结构》题⽬:六度空间”理论⼜称作“六度分隔(Six Degrees of Separation)”理论。
这个理论可以通俗地阐述为:“你和任何⼀个陌⽣⼈之间所间隔的⼈不会超过六个,也就是说,最多通过五个⼈你就能够认识任何⼀个陌⽣⼈。
”如图1所⽰。
图1 六度空间⽰意图“六度空间”理论虽然得到⼴泛的认同,并且正在得到越来越多的应⽤。
但是数⼗年来,试图验证这个理论始终是许多社会学家努⼒追求的⽬标。
然⽽由于历史的原因,这样的研究具有太⼤的局限性和困难。
随着当代⼈的联络主要依赖于电话、短信、微信以及因特⽹上即时通信等⼯具,能够体现社交⽹络关系的⼀⼿数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你⼀个社交⽹络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分⽐。
输⼊格式:输⼊第1⾏给出两个正整数,分别表⽰社交⽹络图的结点数NNN(1<N≤1041<N\le 10^41<N≤10输出格式:对每个结点输出与该结点距离不超过6的结点数占结点总数的百分⽐,精确到⼩数点后2位。
每个结节点输出⼀⾏,格式为“结点编号:(空格)百分⽐%”。
输⼊样例:10 91 22 33 44 55 66 77 88 99 10输出样例:1: 70.00%2: 80.00%3: 90.00%4: 100.00%5: 100.00%6: 100.00%7: 100.00%8: 90.00%9: 80.00%10: 70.00%We use two kinds of method to store the graph:adjacnet matrix and adjacnet tableThe code is followed:1/*2 * sixDigreeSeparation.c3 *4 * Created on: 2017年5⽉8⽇5 * Author: ygh6*/7 #include <stdio.h>8 #include <stdlib.h>910/*11 * Algorithm thought:12 * We easily know this question is BFS.13 * we access the first level nodes, then access second level nodes14 * until we reach the sixth level.15 * We let every node to BFS until it reach the sixth level,then we record the total nodes M16 * it can reach, calculate the M/N(The total point the test data gives) .17*/19#define MAX_VERTEX_MUM 1000120 typedef int vertex; /*vertex is the index of point in the graph*/21 typedef int dataType; /*dataType is the data type of vertex */22 typedef int weightType; /*The data type of weight */2324/*25 * Define a data structure to edge26*/27 typedef struct eNode *ptrToENode;28 typedef struct eNode {29 vertex v1, v2;30 weightType wight;31 };32 typedef ptrToENode edge;3334/*35 * Define a data structure for adjacent table node36*/37 typedef struct adjNode *ptrToAdjNode;38 typedef struct adjNode {39 vertex adjVertex; /*The index of vertex in the graph*/40 weightType weight; /*the value of the weight*/41 ptrToAdjNode next; /*A point to point next node*/42 };4344/*45 * Define a data structure for adjacent table head point46*/47 typedef struct vNode *ptrToVNode;48 typedef struct vNode {49 dataType data; /*The value of every vertex,some times it will be ignore*/50 ptrToAdjNode head;/*The point to point the adjacent table first element*/51 } adjList[MAX_VERTEX_MUM];5253/*Define a data structure for graph*/54 typedef struct gNode *ptrToGNode;55 typedef struct gNode {56int vertex_num;57int edge_num;58 adjList g;59 };60 typedef ptrToGNode adjacentTableGraph; /*a graph show by adjacent table*/ 6162/*63 create a graph given the vertex number.64 @param vertexNum The verter number of the graph65 @return a graph with vertex but no any egdgs66*/67 ptrToGNode createGraph(int vertexNum) {68 vertex v;69 adjacentTableGraph graph = (adjacentTableGraph) malloc(70sizeof(struct gNode));71 graph->vertex_num = vertexNum;72 graph->edge_num = 0;73for (v = 1; v <= graph->vertex_num; v++) {74 graph->g[v].head = NULL;75 }76return graph;77 }7879/*80 insert a edge to graph.We will distinct oriented graph and undirected graph81 The e->v1 and e->v2 are the vertexs' indexs in the adjacent table82 @param graph The graph you want to insert edge83 @param e The edge you want to insert the graph84 @param isOriented Whether the graph is oriented graph.If the graph is oriented85 we will set adjacent table graph[v1]->head=v2 and set graph[v1].head=v286 otherwise we only set graph[v1].head=v287*/88void insertEdge(adjacentTableGraph graph, edge e, int isOriented) {89 ptrToAdjNode newNode;90 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode));91 newNode->adjVertex = e->v2;92 newNode->weight = e->wight;93 newNode->next = graph->g[e->v1].head;94 graph->g[e->v1].head = newNode;95if (!isOriented) {96 newNode = (ptrToAdjNode) malloc(sizeof(struct adjNode));97 newNode->adjVertex = e->v1;98 newNode->weight = e->wight;99 newNode->next = graph->g[e->v2].head;100 graph->g[e->v2].head = newNode;101 }103104 adjacentTableGraph buildGraph() {105 adjacentTableGraph graph;106 edge e;107 vertex v;108int vertex_num;109 scanf("%d", &vertex_num);110 graph = createGraph(vertex_num);111 scanf("%d", &(graph->edge_num));112if (graph->edge_num) {113 e = (edge) malloc(sizeof(struct eNode));114for (v = 0; v < graph->edge_num; v++) {115 scanf("%d %d", &e->v1, &e->v2);116 e->wight = 1;117 insertEdge(graph, e, 0);118 }119 }120return graph;121 }122123/*==============================define a queue=====================================================*/ 124/*define a list to store the element in the queue*/125 typedef vertex elementType;126 typedef struct node *pList;127 typedef struct node {128 elementType element;129struct node *next;130 };131132/*define a queue to point the list*/133 typedef struct node2 *pQueue;134 typedef struct node2 {135 pList front; /*the front point to point the head of the list*/136 pList rear; /*the rear point to point the rear of of the list*/137 };138139/*create a empty list to store the queue element*/140 pList createEmptyList() {141 pList list;142 list = (pList) malloc(sizeof(struct node));143 list->next = NULL;144return list;145 }146/*create a empty queye*/147 pQueue createEmptyQueue() {148 pQueue queue = (pQueue) malloc(sizeof(struct node2));149 queue->front = NULL;150 queue->rear = NULL;151return queue;152 }153154/*155 Wether the queue is empty156 @param queue The queue need to adjust157 @return If the queue is null,return 1 otherwise return 0158*/159int isQueueEmpty(pQueue queue) {160return (queue->front == NULL);161 }162163/*164 Add a element to a queue,If the queue is null,we will create a new queue165 @parama queue The queue we will add elememt to166 @prama element The element we will add to queue167*/168void addQueue(pQueue queue, elementType element) {169if (isQueueEmpty(queue)) {170 pList list = createEmptyList();171 list->element = element;172 queue->front = queue->rear = list;173 } else {174 pList newNode = (pList) malloc(sizeof(struct node));175 newNode->element = element;176 newNode->next = queue->rear->next;177 queue->rear->next = newNode;178 queue->rear = newNode;179 }180 }181182/*183 delete a element from a queue184 @param queue The queue will be deleted a element185 @return The element has been deleted187 elementType deleteEleFromQueue(pQueue queue) {188if (isQueueEmpty(queue)) {189 printf("the queue is empty,don't allow to delete elemet from it!"); 190 } else {191 pList oldNode = queue->front;192 elementType element = oldNode->element;193if (queue->front == queue->rear) {194 queue->rear = queue->front = NULL;195 } else {196 queue->front = queue->front->next;197 }198free(oldNode);199return element;200 }201 }202203/*204 * Initialize a visited array that make them all to zero205*/206void initVisited(adjacentTableGraph graph, int *visited) {207int i;208for (i = 0; i <= graph->vertex_num; i++) {209 visited[i] = 0;210 }211 }212213/*214 Breadth first search215 @param graph The graph stored by the adjacent table216 @param startPoint The point we start search217 @param visited A array to tag the elemeent whether has been visited 218*/219int BFS(adjacentTableGraph graph, vertex startPoint, int *visited) { 220 ptrToAdjNode p;221int count = 0;222int level = 0;223int last = startPoint, tail;224 visited[startPoint] = 1;225 count++;226 pQueue queue = createEmptyQueue();227 addQueue(queue, startPoint);228while (!isQueueEmpty(queue)) {229 elementType element = deleteEleFromQueue(queue);230for (p = graph->g[element].head; p; p = p->next) {231if (visited[p->adjVertex] == 0) {232 visited[p->adjVertex] = 1;233 addQueue(queue, p->adjVertex);234 count++;235 tail = p->adjVertex;236 }237 }238if (last == element) {239 level++;240 last = tail;241 }242if (level == 6) {243return count;244 }245 }246return count;247 }248249/*250 *Prove the six degree of separation251*/252void SDS(adjacentTableGraph graph) {253 vertex v;254int count;255int visited[graph->vertex_num+1];256float result;257for (v = 1; v <= graph->vertex_num; v++) {258 initVisited(graph, visited);259 count = BFS(graph, v, visited);260 result = (float)((float)count / graph->vertex_num)*100;261 printf("%d: %0.2f", v, result);262 printf("%%");263 printf("\n");264 }265 }266267int main() {268 adjacentTableGraph graph = buildGraph();269 SDS(graph);Adjacnet Table1/*2 * sixDigreeSeparation.c3 *4 * Created on: 2017年5⽉9⽇5 * Author: ygh6*/7 #include <stdio.h>8 #include <stdlib.h>910/*11 * Algorithm thought:12 * We easily know this question is BFS.13 * we access the first level nodes, then access second level nodes14 * until we reach the sixth level.15 * We let every node to BFS until it reach the sixth level,then we record the total nodes M16 * it can reach, calculate the M/N(The total point the test data gives) .17*/1819#define MAX_VERTEX_NUM 10001 /*define the max number of the vertex*/20#define INFINITY 65535 /*define double byte no negitive integer max number is 65535*/2122 typedef int vertex; /*define the data type of the vertex*/23 typedef int weightType; /*define the data type of the weight*/24 typedef char dataType; /*define the data type of the vertex value*/2526/*define the data structure of the Edge*/27 typedef struct eNode *ptrToENode;28 typedef struct eNode {29 vertex v1, v2; /*two vertex between the edge <v1,v2>*/30 weightType weight; /*the value of the edge's weigth */31 };32 typedef ptrToENode edge;3334/*define the data structure of the graph*/35 typedef struct gNode *ptrToGNode;36 typedef struct gNode {37int vertex_number; /*the number of the vertex*/38int edge_nunber; /*the number of the edge*/39 weightType g[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*define the adjacent matrix of graph*/40 dataType data[MAX_VERTEX_NUM]; /*define the dataType array to store the value of vertex*/41 };42 typedef ptrToGNode adjacentMatrixGraph; /*a graph show by adjacent matrix*/4344/*45 create a graph given the vertex number.46 @param vertexNum The verter number of the graph47 @return a graph with vertex but no any egdgs48*/49 adjacentMatrixGraph createGraph(int vertexNum) {50 vertex v, w;51 adjacentMatrixGraph graph;52 graph = (adjacentMatrixGraph) malloc(sizeof(struct gNode));53 graph->vertex_number = vertexNum;54 graph->edge_nunber = 0;55/*initialize the adjacent matrix*/56for (v = 1; v <= graph->vertex_number; v++) {57for (w = 1; w <= graph->vertex_number; w++) {58 graph->g[v][w] = 0;59 }60 }6162return graph;63 }6465/*66 insert a edge to graph.We will distinct oriented graph and undirected graph67 @param graph The graph you want to insert edge68 @param e The edge you want to insert the graph69 @param isOriented Whether the graph is oriented graph.If the graph is oriented70 we will set adjacent matrix [n][m]=[m][n]=edge's weight,else we only set71 the adjacent matrix [n][m]=edge's weight72*/73void inserEdge(adjacentMatrixGraph graph, edge e, int isOriented) {74 graph->g[e->v1][e->v2] = e->weight;75if (!isOriented) {76 graph->g[e->v2][e->v1] = e->weight;7980/*81 construct a graph according user's input8283 @return a graph has been filled good84*/85 adjacentMatrixGraph buildGraph() {86 adjacentMatrixGraph graph;87 edge e;88int vertex_num, i;89 scanf("%d", &vertex_num);90 graph = createGraph(vertex_num);91 scanf("%d", &(graph->edge_nunber));92if (graph->edge_nunber) {93 e = (edge) malloc(sizeof(struct eNode));94for (i = 0; i < graph->edge_nunber; i++) {95 scanf("%d %d", &e->v1, &e->v2);96 e->weight = 1;97 inserEdge(graph, e, 0);98 }99 }100101return graph;102103 }104105/*=====================define a queue used BFS================================*/ 106/*107 * The elementType is element which the following list store.108*/109 typedef int elementType;110111/*112 * Define a list to store the queue elements113*/114 typedef struct node1 *pList;115 typedef struct node1 {116 elementType element;117struct node1 *next;118 };119120/*121 * Define a queue used to BFS122*/123 typedef struct node2 *pQueue;124 typedef struct node2 {125 pList font;126 pList rear;127 };128129/*130 * Create a empty list131*/132 pList createEmptyList() {133 pList list = (pList) malloc(sizeof(struct node1));134 list->next = NULL;135return list;136 }137138/*139 * Create a empty queue140*/141 pQueue createEmptyQueue() {142 pQueue queue = (pQueue) malloc(sizeof(struct node2));143 queue->font = queue->rear = NULL;144return queue;145 }146147/*148 * Whether the queue is empty149*/150int isQueueEmpty(pQueue queue) {151return (queue->font == NULL);152 }153154/*155 * Insert a element to a queue156*/157void insertQueue(pQueue queue, elementType element) {158159if (isQueueEmpty(queue)) {160 pList list = createEmptyList();162 queue->font = queue->rear = list;163 } else {164 pList newNode = (pList) malloc(sizeof(struct node1));165 newNode->element = element;166//newNode->next = queue->rear->next;167 queue->rear->next = newNode;168 queue->rear = newNode;169 }170 }171172 elementType deleteElementQueue(pQueue queue) {173if (isQueueEmpty(queue)) {174return -1;175 } else {176if (queue->font == queue->rear) {177 pList temp = queue->font;178 elementType elememt = temp->element;179free(temp);180 queue->font = queue->rear = NULL;181return elememt;182 } else {183 pList temp = queue->font;184 elementType elememt = temp->element;185free(temp);186 queue->font = queue->font->next;187return elememt;188 }189190 }191192 }193194/*195 *Breath first search a graph which store in form of adjacent matrix 196 *@param graph The graph stored with adjacent matrix197 *@param startPoint The start point we start search198 *@param visited A array to tag whether element has been accessed 199*/200int BFS(adjacentMatrixGraph graph, vertex startPoint, int *visited) { 201 vertex v, w;202/*203 * count:to record the total nodes the start point can access204 * level:to record the level the current node accessed205 * tail:to record the every node's index, every access it will be flush 206 * last:to record last lever latest accessed node,we can use it to 207 * let level add.208*/209int count = 0;210int level = 0, last = startPoint;211int tail = last;212 pQueue queue = createEmptyQueue();213 count++;214 visited[startPoint] = 1;215 insertQueue(queue, startPoint);216while (!isQueueEmpty(queue)) {217 w = deleteElementQueue(queue);218for (v = 1; v <= graph->vertex_number; v++) {219if (graph->g[w][v] != 0 && visited[v] == 0) {220 visited[v] = 1;221 insertQueue(queue, v);222 tail = v;223 count++;224 }225 }226if (w == last) {227 level++;228 last = tail;229 }230231if (level == 6) {232return count;233 }234 }235return count;236237 }238239/*240 * Initialize a visited array that make them all to zero241*/242void initVisited(adjacentMatrixGraph graph, int *visited) {243int i;244for (i = 1; i <= graph->vertex_number; i++) {246 }247 }248249/*250 *Prove the six degree of separation251 *@param graph A graph prepared252*/253void SDS(adjacentMatrixGraph graph) {254int visited[graph->vertex_number + 1];255 vertex v;256int count;257float result;258for (v = 1; v <= graph->vertex_number; v++) {259 initVisited(graph, visited);260 count = BFS(graph, v, visited);261 result = (float) ((float) count / graph->vertex_number * 100);262 printf("%d: %0.2f", v, result);263 printf("%%");264 printf("\n");265 }266 }267268int main() {269 adjacentMatrixGraph graph = buildGraph();270 SDS(graph);271return0;272 }Adjacnet MatrixFrom PTA test result,we find the adjacent matrix effective is more high than adjacent table.But the adjacent matrix take more memory.Is it use spaceto swap the timethe test result is follow。
什么是六度分隔理论?

什么是六度分隔理论?六度分隔理论(英语:Six Degrees of Separation)认为世界上任何互不相识的两人,只需要很少的中间人就能够建立起联系。
哈佛大学心理学教授斯坦利·米尔格拉姆于1967年根据这个概念做过一次连锁信实验,尝试证明平均只需要6步就可以联系任何两个互不相识的人。
这种现象,并不是说任何人与人之间的联系都必须要经过6步才会达到,而是表达了这样一个重要的概念:在任何两位素不相识的人之间,通过一定的联系方式,总能够产生必然联系或关系。
显然,随着联系方式和联系能力的不同,实现个人期望的机遇将产生明显的区别。
但是,超过40年来,此理论仍然有所争议。
虽然最初的论文发表后至今,很少有这方面的研究,但该理论仍然得到广泛应用,特别是在保险及直销业的从业员。
米尔格拉姆连锁信实验经过米尔格拉姆的小世界实验研究本来在无特定的市民大众进行,而不是在专业的、需要高度合作的数学界及演艺界进行(参见下)。
然而仍遭受不少抨击。
于首次连锁信实验(纪录于未注明日期论文"Results of Communication Project"),米尔格拉姆寄出60封信给堪萨斯州威奇塔市自愿参加者,请他们转交到麻萨诸塞州剑桥市某指定地点的股票经纪人。
参加者只能把信交给他认为有可能把信送到目的地的熟人,可以亲自送或者通过他的朋友。
虽然有50个人参与了实验,但组中只有3封信送到了目的地。
米尔格拉姆在他1967年的那篇著名论文[1]中提到在最初的实验中,其中的一封信在不到4日的时间内,就被传达到了目的地,但是他却忽略了一个重要事实,那就是实际上只有不到5%的信件最终被送达了。
在随后两次连锁信实验,因完成连锁的比例太低,实验结果未被发表。
但是幸运的是,研究者发现很多微妙的因素会对连锁信实验的结果产生极大的影响。
研究者尝试在不同种族和不同收入人群中来重复实验,他们发现巨大的差异。
事实上,在米尔格拉姆合著的一篇论文中揭示如果信件的最终接受者为黑人,实验的送达率为13%,而如果是白人,则送达率上升为33%,尽管实验者开始的时候并不知道接受者的种族。
六度分离理论

在数学模型方面,科学家们提出 了一些基于网络的模型来解释六 度分离现象。其中最著名的是 Barabasi-Albert 模型。这个模 型基于优先连接的原则,即新节 点更倾向于连接已经有很多连接 的节点。这个模型能够产生类似 于真实世界的网络结构,其中任 意两个节点之间平均只需要很少 的连接就可以建立联系
六度分离理论
xxxxxxxxxxx
六度分离理论,也称为六度区隔理论,是1967年由美国社会心理学家米尔格 伦提出的一种理论
这个理论的基本思想是,在人际交往的脉络中,任意两个陌生人都可以通过" 亲友的亲友"建立联系,这中间最多只要通过五个朋友就能达到目的
简单来说,六度分离理论认为地球上所有的人都可以通过五层关系来连接
此外,科学家们还提出了其他一 些模型,如基于社区的模型、基 于搜索的模型等来解释六度分离 现象。这些模型各有其特点和局 限性,但都从不同角度提供了对 六度分离现象的深入理解
PART 4
结论
六度分离理论是一个引人注目的理论和思想, 1 它揭示了人际网络的一种基本特征:任意两个
陌生人之间只隔着少数几层关系
PART 1
米尔格伦的六度分离实验
5
米尔格伦的六度分离理论是基于一个实验提出的。在这个实验中,米 尔格伦选择了一些志愿者,并给其中的一些人寄出了信件。这些信件 的目标是随机选择的,没有任何社会联系的陌生人。每一封信件都附 上回信地址,并要求收信人将这个信件寄给米尔格伦指定的下一个朋 友,可以是他们的朋友、同事、家庭成员等。这个过程被重复了几次, 直到最终这个信件到达了最初的目标
米尔格伦发现,平均而言,这个信件只需要通过五次传递就可以从发 信人到达收信人。这表明,在人际网络中,我们与任何陌生人之间只 隔着五个人的距离。这就是六度分离理论的基本原理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
张三
李四
显然,随着联系方式和联系能力的不同,实现个 人期望的机遇将产生明显的区别。
只需要小小的六步, 你就可以认识这个地球的每一个人!
1967年美国社会心理学家米尔格兰姆 (Stanley Milgram)提出了一个“六度分离”理论。该理论认 为在人际交往的脉络中,任意两个陌生人都可以 通过“亲友的亲友”建立联系,这中间最多只要 通过五个朋友就能达到目的。 虽然世界很大,但是如果将每个人 的人际关系网考虑进去,人与人的
距离其实很小 。生人搭上关系
?
六度分离理论(Six Degrees of Separation)
) “你和任何一个陌生人之间所间隔的人不会超 过五个,也就是说,最多通过五个人你就能够认 识任何一个陌生人。”根据这个理论,你和世界 上的任何一个人之间只隔着 五个人,不管对方在哪 个国家,属哪类人种, 是哪种肤色。
按照这种理论,每个人都可以利用自己的关系网 与完全陌生的人搭上关系,甚至像麦当娜、英国 女王伊丽莎白二世和奥巴马这样的名人从某种意 上来说都是我们的“熟人”。
六度分隔的现象,并不是说任何人与人之间的联 系都必须要通过六个层次才会产生联系,而是表 达了这样一个重要的概念:任何两位素不相识的 人之间,通过一定的联系方式,总能够产生必然 联系或关系。
微软公司的研究人员为证实这种理论的可行性而 专门开展实验,他们随意挑选了2006年的某一月, 记录下当月所有通过微软网络发送短信的用户地 址,分析了300多亿条地址信息,最终统计得出, 多达78%的用户仅仅通过发送平均6.6条短信,或 者说通过6.6步, 就可以和一个陌生人建 立起联系。
有人把世界65亿人开了7次方根,结果是25.2257, 从不科学方式说,我们每个人只要认识20几个 人就可以满足此理论。
2001年哥伦比亚大学社会学系的一个研究小组开 始在互联网上进行了这个实验:
他们建立了一个实验网站,终点是分布在不同国 家的18个人(包括纽约的一位作家、澳大利亚的一名警察以及巴黎的 一位图书管理员等等),志愿者通过这个网站把电子邮件 发给最可能实现任务的亲友。 结果一共有384个志愿者的邮件抵达了目的地, 电子邮件大约只花了五到七步就传递到了目标。 这个活动现在还在继续。
