医院排队模型
排队模型(掌握mm1,mmc,mm1k)

(1) (2) (3) (4) (5) (1) (2) (3) (4) (5) (1) (2) (3) (4) (5) i τi si ti wi i τi si ti wi i τi si ti wi 13 49 1 3 5 23 86 6 2 2 33 117 4 4 7
现实生活中的排队系统序Leabharlann 到达的顾客 号要求服务内容
服务机构
1 不能运转的机器 修理
修理技工
2 修理技工
领取修配零件 发放修配零件的管理员
3 病人
诊断或做手术 医生(或包括手术台)
4 电话呼唤
通话
交换台
5 文件搞
打字
打字员
6 提货单
提取存货
仓库管理员
7 驶入港口的货船 装(卸)货
装(卸)货码头(泊位)
二、排队系统的特征及其组成
1、排队系统的特征即拥挤现象的共性 1)、有请求服务的人或物 2)、有为顾客服务的人或物 3)、具有随机性 4)、服务的数量超过服务机构的容量
2、排队系统的三大基本组成部分
1)、输入过程(顾客到达的方式) a、顾客的总体(顾客源)的组成可能是有限的,也
可能是无限的; b、顾客相继到达的时间间隔可以是确定的,也可以
平均服务率: 41/127=0.32(人/分钟)
六、典型排队系统模型的结构及应用
M/M/C等待制排队模型研究要点: a、系统意义 b、状态转移速度图与状态转移速度矩阵 c、状态概率方程 d、系统的基本数量指标
Passion分布
设N(t)表示在时间[0, t)内到达顾客数; 令Pn(t1, t2)表示在时间区间[t1, t2)(t2 > t1)内有n(0) 个顾客到达的概率,即 Pn(t1, t2)=P{ N(t2) –N(t1)=n } (t2>t1,n0) Passion分布的三条件:
排队论模型

排队论模型随机服务系统理论是研究由顾客、服务机构及其排队现象所构成的一种排队系统的理论,又称排队论。
排队现象是一种经常遇见的非常熟悉的现象,例如:顾客到自选商场购物、乘客乘电梯上班、汽车通过收费站等。
随机服务系统模型已广泛应用于各种管理系统,如生产管理、库存管理、商业服务、交通运输、银行业务、医疗服务、计算机设计与性能估价,等等。
随机服务系统模拟,如存储系统模拟类似,就是利用计算机对一个客观复杂的随机服务系统的结构和行为进行动态模拟,以获得系统或过程的反映其本质特征的数量指标结果,进而预测、分析或估价该系统的行为效果,为决策者提供决策依据。
排队论模型及其在医院管理中的作用每当某项服务的现有需求超过提供该项服务的现有能力时,排队就会发生。
排队论就是对排队进行数学研究的理论。
在医院系统内,“三长一短”的现象是司空见惯的。
由于病人到达时间的随机性或诊治病人所需时间的随机性,排队几乎是不可避免的。
但如何合理安排医护人员及医疗设备,使病人排队等待的时间尽可能减少,是本文所要介绍的。
一、医院系统的排队过程模型医院是一个复杂的系统,病人在医院中的排队过程也是很复杂的。
如图1中每一个箭头所指的方框都是一个服务机构,都可构成一个排队系统,可见图2。
图1 医院系统的多级排队过程模型二、排队系统的组成和特征一般的排队系统都有三个基本组成部分:1. 输入过程其特征有:顾客源(病人源)的组成是有限的或无限的;顾客单个到来或成批到来;到达的间隔时间是确定的或随机的;顾客的到来是相互独立或有关联的;顾客相继到达的间隔时间分布和所含参数(如期望值、方差等)都与时间无关或有关。
2. 排队规则其特征是对排队等候顾客进行服务的次序有下列规则:先到先服务,后到先服务,有优先权的服务(如医院对于病情严重的患者给予优先治疗,在此不做一般性的讨论),随机服务等;还有具体排队(如在候诊室)和抽象排队(如预约排队)。
排队的列数还分单列和多列。
3. 服务机构其特征有:一个或多个服务员;服务时间也分确定的和随机的;服务时间的分布与时间有关或无关。
排队模型——精选推荐
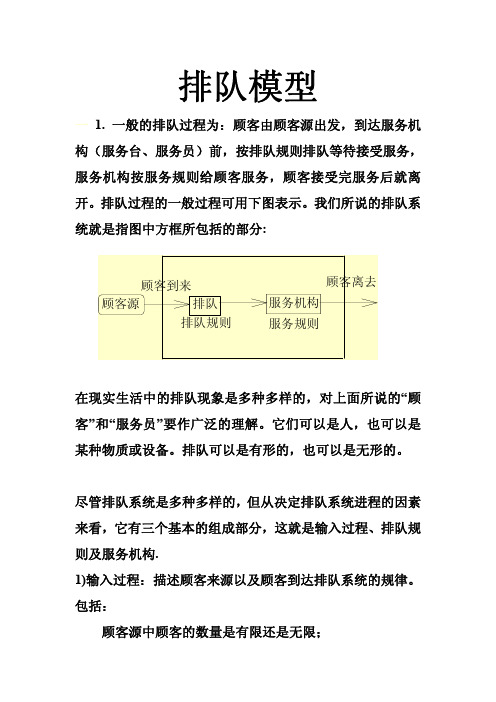
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
医院管理系统中排队模型的优化决策分析

患者希望 服 务 台越 多 、 服务效 率越 高、 逗 留时间越 短越好 使 自己的损失 达最小 , 为此 医院就要增加 医 生和设备 而医院也不可能无 限投入。为此就需要优化设计 , 其 目的就 是使患者 损失 费用和 医院服务 成本之 和达到最小
,
。
假设服务 台的个数为
,
为每个服务台单位 时间服务 台的成
加c [。! ) (一‘ ! ) 去( + 走
一P J
弋( c )一 ]
( 1 )
一 丢 2 及 疗 ,院 盲 加 和 薹菜要 L 1 ;’ 一, 2 其 囊使 不 目 医 设 】 1 : 医 医 会 增 生 备 不 设 备 造必 成 一 ,: …
13 排队系统 的最优化 . 在排 队系统 中
, ,
. , + _ , ( 4
‘
测、 分析或评价 , 最大 限度地 满足患者及 其家 属 的需求 , 将有 效避 免资源浪费。 1 随机模型
11 系统描述 . 以医院门诊为研究对象 , 它有如下特征 : ① 输入过程 : 患者的到达是相互独立 , 相继到达的n l e]间 1
L () 化简得 L ( 。 一L (’ ) |c ) |c +1≤ ,c ( 一1 一L( ’ 5 ) c )(
通过计算机模 拟依次 算 出 L () 上 ( )上 () … 相邻 ,1 ,吖 2 ,吖 3 , 两项之差 , 看常数落在哪两者之 间, 从而确定使患者损失 费用 和医院服务成本之 和达 到最优化 服务 台个数 C 的最优解 C’ 。 1 4 关 于服务方案问题优 化 . 当患者平均到达率上升 引起 服务强度增加致使平 均 队长
医院是一个 复杂 的系统 , 人从挂号 、 病 就诊 、 划价 、 药每 取
排队问题-数学建模

第九届“新秀杯”校园数学建模竞赛摘要医院有一位医生值班,经长期观察,每小时平均有4个病人,医生每小时可诊断5人,病人的到来服从Poisson流,诊断时间服从负指数分布。
根据题目所给信息,可以很明显看出本题是单服务台的排队模型,因此需要用到排队理论来求解这些问题。
本题需要用到排队理论中最简单的M/M/1/∞/∞模型,通过对病人到来及诊断时间的统计研究,得出这些数量指标的统计规律。
针对问题一,通过分析任意时刻t内到达的病人数为n的概率,使用数学期望的方法,,可以得出平均病人数及等待的平均病人数。
由题目给出条件病人的到来服从参数为λ的泊松分布,诊断时间服从参数为μ负指数分布,可以得出病人的平均看病所需时间及病人平均排队等待时间。
以及分析该医院的服务强度,可以粗略的分析该科室的工作状况。
针对问题二,在问题一的条件基础下,要求99%的病人有座位。
可以先假设出座位个数,由于每个时刻病人到来的个数是随机且独立,不可能同时到达两批病人,考虑到来病人的个数与座位之间的关系,考虑病人数不同时,有座位的概率不同。
所以用独立事件概率的加法可以得出概率需要大于等于0.99,从而反推出所需座位数。
针对问题三,分析问题可得,需要求出单位平均损失可以通过题目每小时病人到来数可以得出平均每天医院到来数。
根据问题一结论,可以得出平均看病所花时间,从而求出每天的平均损失。
针对问题四,只需要利用问题一,问题二,问题三的结论并改变医生每小时诊断时间,嵌套进来就能求解。
关键字:排队理论M/M/1/∞/∞模型数学期望Poisson流负指数分布一、问题提出某单位医院的一个科室有一位医生值班,经长期观察,每小时平均有4个病人,医生每小时可诊断5人,病人的到来服从Poisson流,诊断时间服从负指数分布。
(1)试分析该科室的工作状况:(2)如要求99%以上的病人有座,该科室至少设多少座位?(3)如果该单位每天24小时上班,病人因看病1小时而耽误工作单位要损失30元,这样单位平均损失多少元?(4)如果该科室提高看病速度,每小时平均可诊断6人,单位每天可减少损失多少?可减少多少座位?二、模型的准备根据题目所给信息,可以很明显看出本题是单服务台的排队模型,日常生活中存在大量有形和无形的排队或拥挤现象,如旅客购票排队,市内电话占线等现象。
医院病床安排的数学模型及算法分析

信 息 技 术
医院病 床 安排 的数学模 型及 算法分析
顿 毅 杰 马 明
( 西北民族 大学 计算机科学与信 息3 程学院 , - " 甘肃 兰州 7 0 3 ) 30 0
摘 要: 医院病 床 的合理 安排 是病人 和 医 院共 同关注 的问题 。 理论 上这 一 问题 有排 队论 和规 划论 的特 点。 考虑 到病 人 、 床和 手术之 病 间的 流程 关 间 、 平 平均 逗 留时 间 、 均等待 队 长和 住 院率 来作 为评 价指 标 . 些指标 可以 充 平 这
分 反 映 医 院病 床 安 排 的 优 劣 。
关键词 : 排队模 型 ; 系统 仿真 ; 支限界 算法 分 1问题简述 当前医院实行 的 F F 规则可 看作是一个 CS 单 队列 多服务 台的排 队模型 ,不能有效地分配 医院资源 。 因此我们把病 人按照手术类 型分 为 4 个 队列 , 将病床 当作服务 台, 建立 了一个 4 队列 多服务 台的具有优先权 的排队模型急症优先权 是非强拆型的。 型中的服务规 则为“ 模 当前选 中 的病人总平均逗 留时 间最 短” 同类 型内部先 和“ 果暂时没有病床 , 则等待住院 , 因而等待 的人 数 及空间在理论上是无 限制 的。病人按 照先 到先 服务 的规则 , 排成 一队 , 依次 住院 ; 病人住 院 从 到出院表示服务完 成, 离开排队系统。 先到先服 其 中 , 1 , o … ,J 选 中住 院的 , j , x = …4 = 表示 务规则可看作是一个单 队列多服务 台的排 队系 第 i 类病人中第 i 个病人的逗 留时间 ,规定 c i o = 统 , 中, 其 服务台 即为病床。因此 。 问题构成了一 0 ( l ,i , = …4 o 个具有 2 队列 ,9 个 7 个服务台的排 队系统 。 假设 5模型 的求解 f急症病人具有 优先权的 , 2 】 是非强拆 晴形 急症 ( 利用计算机编程对周六 、 日可安排手术 周 病人有优先住院权 ,但无权赶走正住 院的其 它 与周六 、 日 周 不安排手术 的两种情况 分别进行 病人 )但按照先到先服务的规则进行排队会导 模拟 解 。 。 致等待住院病人 队列越来越长 , 不能有效 的利 5 算法描述 . 1 用医院资源。 整个过程用 计算机 , 照模 拟计算完成 , 仿 其 4模型的建立与求 解 计算原则概括如下 : 显然 ,医院的病床服 务系统既有 离散 时间 5. .1初始 状态 ; 1 初始 日期天 数设 置为 l , 排队系统 的特点又有规划模 型的特点 , 但在 服 用 1 来递增 天数循环 开始模拟 ; 务的时间约束方面不 同于服务 系统 , 在动态性 5. . 1 2一旦 有 出院 , 出现空床 位 , 开始进 则 质上又 区别于线性规划结构 , 因此 , 建模时 既要 行床铺分 配 , 分配时优先考虑 急症 , 选择总 然后 考虑系统 结构 , 又要考虑 内部的优化选择。 逗 留时 间小 的人数 分配原则进 行分配 ,若无床 4 . 1系统结构模型的建立 位则加入等待队列 ; 因为各 类病 人服 务方 式与 服务 时 间的不 5 3 对每 个进 入到及 出院 的人 的信息 进 . 1 同 , 以我们把病人分为 四大类 , 所 建立一个 四队 行记 录, 随后天数增一继续模 拟第 二天的情况 , 列多服务台的具有 优先权 的非强拆排 队模型。 以此类推 ; 急症 病 人 ( 优先 权 )白 内障 、 内障 ( 、 白 双 5 4 天数到达所设 定的数值后结束循 环 , . 1 眼) 、 其他病人 病床 出院 对记录到的数据进行计算 分析。 4 . 院病床安排模型 2住 5 . 2参数 的确定 根据问题要求 ,我们对不 同的眼科疾病所 在进行仿真时 , 要用 到一些 参数来计算 评 花费的时间进行分析 ,总结 出两个可有效 降低 价指标 , 中包括 其 住院病人总逗 留时间,从而提高对 医院资源的 病人的住院时间 : z : sz y s b+ zs ls+ e s c s+ W 有效利用的两个规则。 规则 1 :当前选中住 院的病 人的总逗 留时 动手术 日期 : 间最小( 最小逗 留规则 ) sd = b sz zs s sb ls 规则 2 :每类病人 内部遵循 先到先服务 原 出院时间 : c = sd+e S y s C S+ W 则 在 4队列多服务台 的具有优先权 的病房排 逗留时间 : d = d l r+ s z - l s e s s b4 zs + c s+ w 队模型 内部需要进行住 院病 床安排 , 下面我们 干用以上两规则建立住 院病床安排模 型。 U 分别给 出周六 、 日可安排手术和周六 、 周 周 设 某天( 例如 b日 这一 天 ) 一些病 人出院后 日 不安排手术情形 下的距 离可动手术时间。分 共有 N个 空床 ( 腾出的和原 空的 )目前等 待 析可知 , 、 日 新 , 周六 周 不安排手术在住院安排模 型 住院的外科 急症病人 ( 第一类 病人 ) 共有 n 个 , 中仅对急症 和其它疾病距 离可 动手术时间有影 白内障 ( 眼 ) 人( 单 病 第二类病 人 ) 共有 n个 , 响 , 以可 预测其 它疾病 对 白内障的队长不影 白 所 内障( 双眼 ) 病人 ( 三类病 人 ) 第 共有 n个 , 他 响 , 固定其 它疾病和急 症情况 下 , 其 在 周六 、 日是 病人 ( 四类病人 ,包括视网膜疾病 和青光 眼 否安排手术对 白内障无影响。 第 等) 共有 n个 , 4 现要从四类等待住院的病人中分 6结果 分析 别选出 x,, , 位病人住 院, l 4 x xx 当然要遵循 急症 6 . 1评价指标选择 优先的原则 , 显然 , n n n N条件 下 , 在 柙 + - 应 对两个方案建立评 价指标 体系 ,评价这 两 满足 x x x N且 n n n 4 l + 4 = t 2 n N条 件下 , + + < 应 个方案 的优 劣。因该 问题 是一个 整体排 队的问 满足 X n X H,- 34 ̄即( l l2 23lX 1 = ,= X l,-  ̄ - 床铺 满员原则 ) 题 , , 对于一个排 队方案 的优劣主要由该排队系 则在规则 2 和规则 3 条件下可建立病床安排 模 统 的平均 等待时间 、 平均服 务时间 、 逗留时 平均 型 : mn if: 间和平均等待队长等主要 因素决 定日 所 以决定 。 对该 问题 的评 价指标 体 系 由平均 等待 入 院时 St 间、 平均住院时 间 、 平均逗 留时 间和平 均等待队 长和住院率构成。 + + N 若∑忙≥ + _= N ①{ 6 . 2结果对 比 l‘= , 1 , 若 ni , 4 ∑_< =… N 使用 M t b 件按 照上述 过程 进行 编程 aa 软 l
flexsim建模案例

flexsim建模案例以flexsim建模案例为题,我们将列举一些典型的案例来展示flexsim的建模能力和应用场景。
1. 物流仓库优化模型在这个案例中,我们使用flexsim建立一个物流仓库的模型,通过优化仓库布局、设备配置和作业流程,实现仓库运营的最佳化。
通过模拟不同的仓库布局和作业策略,我们可以评估不同方案下的仓库效率和成本,从而提出改进方案。
2. 生产线调度模型这个案例中,我们使用flexsim建立一个生产线调度模型,通过模拟不同的生产调度策略,评估不同方案下的生产效率和资源利用率。
通过灵活调整生产线的节拍、资源分配和工人安排,我们可以优化生产线的生产能力和效率。
3. 医院排队模型这个案例中,我们使用flexsim建立一个医院排队模型,通过模拟不同的排队策略和资源配置,评估不同方案下的患者等待时间和医疗资源利用率。
通过调整医生的工作量、诊断流程和资源分配,我们可以优化医院的排队系统,提升患者的就诊体验。
4. 供应链模型在这个案例中,我们使用flexsim建立一个供应链模型,模拟供应链中不同环节的物流流程和库存管理。
通过优化供应链中的运输路线、库存水平和订单处理流程,我们可以降低供应链的成本,提高供应链的响应速度和灵活性。
5. 机场运营模型这个案例中,我们使用flexsim建立一个机场运营模型,模拟机场的航班调度、旅客流动和行李运输。
通过优化航班的调度安排、旅客的流动路径和行李的运输流程,我们可以提高机场的运营效率和旅客的出行体验。
6. 货物分拣系统模型在这个案例中,我们使用flexsim建立一个货物分拣系统模型,模拟货物的分拣流程和设备利用率。
通过优化货物的分拣路径和设备的配置,我们可以提高分拣系统的效率和准确率,降低分拣成本。
7. 铁路调度模型这个案例中,我们使用flexsim建立一个铁路调度模型,模拟列车的运行和交路调度。
通过优化列车的运行路径、发车间隔和交路安排,我们可以提高铁路的运行效率和安全性,减少列车的延误和碰撞风险。
基于排队论的医院急诊模型

基于排队论的医院急诊模型作者:曾华;孙霞林来源:《价值工程》2010年第10期摘要: 本文用排队论的方法对医院急诊室排队系统进行分析,确定了该系统的的排队模型。
给出了统计平衡条件的排队系统的主要指标。
讨论了该排队系统的最优化,并进行了实例分析。
Abstract: The article gives the queue model of queue system in emergency Dept. of hospital based on the analysis of queue service system with the method of queue. It also determines the main parameters of queue system in balance conditions. The optimization of the system is also discussed. Several practical applications are discussed with the method.关键词: 医院急诊;排队论;最优化Key words: emergency in hospital;queue theory;optimization中图分类号:O141,O142文献标识码:A文章编号:1006-4311(2010)10-0127-020引言医院急诊工作的特点是病患者发病急,患者流量不稳定,随机性大,可控性小[1]。
因此,合理安排急诊室工作,充分利用医院急诊室资源,使得患者等待时间缩短,是目前需要解决的重要问题[2]。
本文主要考虑的是急诊室的排队问题,在综合考虑各种排队因素的基础上,优化排队系统各项指标,缩短排队时间,提高服务效率[3]。
1假设及说明假设急诊患者随机到达医院急诊室。
医院则根据患者的伤病的轻重和紧急性,依据事先确定的方法,将患者分配到几个优先等级中的其中之一。
排队论方法讲解

M-负指数分布 D-确定型分布 Ek k阶爱尔朗分布 - 阶爱尔朗分布
GI -一般相互独立的时间间隔分布 G -一般服务时间的分布
如 D/M/10/1000/∞ / F
排 队 论 方 法 讲 解
1.3 排队系统的运行指标
⑴ Ls: 队长 -系统中顾客数的期望 : ⑵ Lq: : 排队长 -系统中等待服务的顾客数 Ln: :正在接受服务的顾客数 Ls=Lq+Ln ⑶ Ws:逗留时间 :
排 队 论 方 法 讲 解
(3)普通性: 普通性: 普通性
内有2个或 对于充分小的△t,在[t,t+△t]内有 个或 , 内有 多个顾客到达的概率极小,可以忽略不 多个顾客到达的概率极小 可以忽略不 计,即 ∞ 即
∑ P (t , t + ∆t ) = o(∆t )
n=2 n
下面研究系统状态为n的概率分布:
= 1 − λ∆t − o(∆t )
P0 ( t , t + ∆ t ) = 1 − P1 ( t , t + ∆ t ) − ∑ Pn ( t , t + ∆ t )
n=2
∞
分为[0,t)和[t,t+△t), 将[0,t+△t)分为 分为 和 则在时间段[0,t+△t)内到达 个顾客的 内到达n个顾客的 则在时间段 内到达 概率为
n
由上结果可知,在长度为 的时间段内到达 由上结果可知 在长度为t的时间段内到达 在长度为 n个顾客的概率 服从泊松分布 个顾客的概率,服从泊松分布 个顾客的概率 服从泊松分布. 其中期望、 其中期望、方差为 E[ N (t )] = D[ N (t )] = λt
排 队 论 方 法 讲 解
1.5.2 负指数分布
排队论医院应用

医院排队论模型医院排队论模型医院就医排队是一种经常遇见的非常熟悉的现象.它每天以这样或那样的形式出现在我们面前. 例如,患者到医院就医,患者到药房配药、患者到输液室输液等,往往需要排队等待接受某种服务.这里,护士台、收费窗口、输液护士台及其服务人员都是服务机构或服务设备.而患者与商店的患者一样, 统称为患者.以上排队都是有形的,还有些排队是无形的.由于患者到达的随机性,所以排队现象是不可避免的.排队系统模拟所谓排队系统模拟,就是利用计算机对一个客观复杂的排队系统的结构和行为进行动态模拟,以获得反映其系统本质特征的数量指标结果,进而预测、分析或评价该系统的行为效果,为决策者提供决策依据.如果医院增添服务人员和设备,就要增加投资或发生空闲浪费;如果减少服务设备,排队等待时间太长,对患者和社会都会带来不良影响.因此,医院管理人员要考虑如何在这两者之间取得平衡,以便提高服务质量,降低服务费用.医院排队论,就是为了解决上述问题而发展起来的一门科学.它是运筹学的重要分支之一.在排队论中,患者和提供各种形式服务的服务机构组成一个排队系统,称为随机服务系统.这些系统可以是具体的,也可以是抽象的.排队系统模型已广泛应用于各种管理系统.如手术管理、输液管理、医疗服务、医技业务、分诊服务,等等.医院排队系统的组成排队系统的基本结构由四个部分构成:来到过程(输入)、服务时间、服务窗口和排队规则.1、来到过程(输入)是指不同类型的患者按照各种规律来到医院.2、服务时间是指患者接收服务的时间规律.3、服务窗口则表明可开放多少服务窗口来接纳患者.4、排队规则确定到达的患者按照某种一定的次序接受服务.⑴来到过程常见的来到过程有定长输入、泊松(Poisson)输入、埃尔朗(A. K. Erlang)输入等,其中泊松输入在排队系统中的应用最为广泛.所谓泊松输入即满足以下4个条件的输入:①平稳性:在某一时间区间内到达的患者数的概率只与这段时间的长度和患者数有关;②无后效性:不相交的时间区间内到达的患者数是相互独立的;③普通性:在同时间点上就诊或手术最多到达1个患者, 不存在同时到达2个以上患者的情况;④有限性:在有限的时间区间内只能到达有限个患者, 不可能有无限个患者到达.患者的总体可以是无限的也可以是有限的;患者到来方式可以是单个的,也可以是成批的;相继到达的间隔时间可以是确定的,也可是随机的;患者的到达可以是相互独立的,也可以是关联;到来的过程可以是平稳的,也可是非平稳的;⑵服务时间患者接受服务的时间规律往往也是通过概率分布描述的. 常见的服务时间分布有定长分布、负指数分布和埃尔朗分布.一般来说, 简单的排队系统的服务时间往往服从负指数分布, 即每位患者接受服务的时间是独立同分布的, 其分布函数为t (tμB ( t ) = 1- e - ≥0).其中μ>0为一常数, 代表单位时间的平均服务率. 而μ1/ 则是平均服务时间.⑶服务窗口服务窗口的主要属性是服务台的个数. 其类型有:单服务台、多服务台.多服务台又分并联、串联和混合型三种. 最基本的类型为多服务台并联.⑷排队规则分为三类:损失制、等待制、混合制.损失制:患者到达时,如果所有服务台都没有空闲,该患者不愿等待,就随即从系统消失.等待制:患者到达时,如果所有服务台都没有空闲,他们就排队等待. 等待服务的次序又有各种不同的规则:①先到先服务,如就诊、排队取药等;②后到先服务,如医院处理急症病人;③随机服务, 服务台空闲时,随机挑选等待的患者进行服务;④优先权服务,如照顾号.混合制:既有等待又有损失的情况,如患者等待时考虑排队的队长、等待时间的长短等因素而决定去留.队列的数目可是单列,也可是多列的;容量可能是有限的,也可能是无限的排队系统的分类排队系统模型主要可以由输入过程(患者到达时间间隔分布)、服务时间分布、服务台个数特征来描述.根据这些特征,可用符号进行分类, 用以表示不同的模型. 例如,利用一定的符号规则将上述特征按顺序用符号列出,并用竖线隔开,即输入过程| 服务分布| 服务台个数例如, M|M|S表示输入过程为泊松输入、服务时间服从负指数分布、S个服务台的排队系统模型; M|G|1则表示泊松输入、一般服务分布、单个服务台的排队系统.排队系统的主要数量指标评价和优化排队系统,需要通过一定的数量指标来反映.建立排队系统模型的主要数量指标有三个:等待时间、忙期与队长.⑴等待时间指患者从到达系统时起到开始接受服务时止这一段时间. 显然患者希望等待时间越短越好.用Wq 表示患者在系统中的平均等待时间.若考虑到服务时间,则用Ws 表示患者在系统中的平均逗留时间(包括等待时间和服务时间).⑵忙期指服务台连续繁忙的时间长度.该指标反映服务台的工作强度和利用程度.用B表示忙期的平均长度.与忙期相应的是闲期,闲期是指服务台一直空闲的时间长度.用I 表示闲期的平均长度.⑶队长指系统中的患者数(包括排队等候的和正在接受服务的所有患者).用Ls表示平均队长.若不考虑接受服务的患者, 则将系统中排队等候的患者数称为队列长.用Lq表示平均队列长.此外, 用ρ表示服务强度,其值为有效的平均到达率λ与平均服务率μ之比,即 .μ/λ =ρM | M | 1 模型M|M|1模型是输入过程为泊松输入,服务时间为负指数分布并具有单服务台的等待制排队系统模型,这是最简单的排队系统模型.假定系统的患者源和容量都是无限的,患者单队排列,排队规则是先到先服务.设在任意时刻t系统中有n个患者的概率Pn(t). 当系统达到稳定状态后,Pn(t)趋于平衡Pn且与t无关. 此时,称系统处于统计平衡状态,并称Pn为统计平衡状态下的稳态概率.n, n = 0, 1, 2, … .ρ )ρPn=(1-其中μ/λ =ρ表示有效的平均到达率λ与平均服务率μ之比(0<ρ<1).M | M | 1 模型的几个主要指标⑴在系统中的平均患者数(平均队长)Ls⑵在队列中等待的平均患者数(平均队列长)Lq⑶患者在系统中平均逗留时间Ws⑷患者在队列中平均等待时间Wq⑸闲期的平均长度I⑹忙期的平均长度B例某MRI室配有一位专业医师,负责核磁共振拍摄工作.已知每天平均有6名患者前来, 每人平均时间为1小时,前来的患者按泊松分布到达,服务时间服从负指数分布,每天按8小时计. 试求:①医师工作空闲的概率;②MRI室有两台患者同时到达的概率;③MRI室至少有1人来的概率;④MRI室逗留的患者的平均人数;⑤患者在MRI室的平均逗留时间;⑥MRI室等待患者的平均人数;⑦待拍摄的患者平均等待时间;⑧MRI室忙期的平均长度.解平均到达率= 6/8 = 0.75λ人/小时,平均服务率= 1μ人/小时,服务强度=0.75/1 = 0.75.ρ①MRI室没有拍摄患者的概率为= 1 - 0.75 = 0.25.ρP0 = 1 -即工作人员有25%的时间空闲.②MRI室有2名等候患者的概率为2 = 0.14.ρ ) ρP2 = (1 -③MRI室至少有1等候患者的概率为P = P (n≥1) = 1 - P0 ) = 0.75 .ρ= 1 - (1 -即有75%的时间, MRI室至少有1名等候患者.④MRI室逗留的患者的平均人数为M | M | C模型M|M| C(C≥2)是多服务台的等待制排队系统,它的各种特征的规定和假设与M|M|1模型基本相同.并假定C 个服务台并联排列,各服务台独立工作,其平均服务率相同,即 .μ C = μ1 = … = μ 1 = μ因此,该系统的平均服务率为 .μCM | M | C模型主要指标为:⑴平均队列长Lq⑵平均队长Ls.ρLs = Lq + C⑶患者在系统中平均逗留时间Ws⑷患者在队列中平均等待时间Wq。
医院病床安排的数学模型及算法分析

医院病床安排的数学模型及算法分析作者:顿毅杰马明来源:《中国新技术新产品》2010年第11期摘要:医院病床的合理安排是病人和医院共同关注的问题。
理论上这一问题有排队论和规划论的特点。
考虑到病人、病床和手术之间的流程关系,确定出使用平均等待时间、平均住院时间、平均逗留时间、平均等待队长和住院率来作为评价指标,这些指标可以充分反映医院病床安排的优劣。
关键词:排队模型;系统仿真;分支限界算法1 问题简述当前医院实行的FCFS规则可看作是一个单队列多服务台的排队模型,不能有效地分配医院资源。
因此我们把病人按照手术类型分为4个队列,将病床当作服务台,建立了一个4队列多服务台的具有优先权的排队模型急症优先权是非强拆型的。
模型中的服务规则为“当前选中的病人总平均逗留时间最短”和“同类型内部先到先服务”。
为了实现该排队系统中的实时病床分配,在系统中嵌入了一个规划模型,模型目标是使“当前选中病人总平均逗留时间”最短,约束条件中考虑了急症优先原则和床铺满员原则。
可以证明该规划模型满足“同类型内部先到先服务”规则。
我们使用计算机系统仿真求解模型,在仿真算法中嵌入了求解规划模型的逐步搜索算法,间与急症到达规律和病人的术后观察时间有关。
我们假设急症按泊松流到达、术后观察时间服从相互独立的均匀分布,在给定置信水平条件下给出了估计住院时间的置信区间。
此外,在该假设下也可由模拟算法求出病人的住院时间。
在前述规划模型的基础上加一比例约束条件即可得到病床比例分配模型。
2 模型的假设与符号说明2.1 模型的假设每个病人到达医院是随机的;外伤急症具有优先住院权;白内障手术仅安排在周一、周三,且对双眼白内障手术在同一周的周一做第一次手术、周三做第二次手术;其它眼科疾病不考虑急症;其它眼科疾病不安排周一、周三;假设手术设备和医生足够多,即只要住院的病人准备好,就可随时进行手术;假设每一种病的手术准备时间是固定的,观察时间是服从均匀分布的;假设入院当天即可进行术前准备;2.2 符号说明zy住院时间sszb手术准备时间zlss距离可动手术时间ecss二次手术延长时间w术后观察时间ssd动手术日期cy出院日期dy等待住院时间dl逗留时间cij表示选中住院的第i类病人中第j个病人的逗留时间N病房的空床数ni当前等待住院的第i类病人的个数xi从当前第i类等待病人中选出住院的病人的个数zzi当前第i类正在住院的病人的总数3 问题分析医院的病床服务系统具有以下特点:病人来源是无限的,以病人到达门诊登记等待为标志,进入待床住院排队系统;排队等待的病人如果暂时没有病床,则等待住院,因而等待的人数及空间在理论上是无限制的。
基于大数据分析的医院门急诊排队模型研究

基于大数据分析的医院门急诊排队模型研究医院门急诊排队问题一直是医院工作中的重要难点之一,尤其是在繁忙的时段,患者需要长时间等待才能得到就诊。
这种情况不仅影响了医院的服务质量,也让患者感到不满和疲惫。
为了解决这个问题,许多医院开始尝试使用大数据分析技术,寻找最佳的门急诊排队模型。
这个模型可以根据患者的信息和医疗资源的分配情况,提出最优的排队方案,降低等待时间和排队长度,提高就诊效率,提升医院服务水平。
本文就基于大数据分析的医院门急诊排队模型进行了研究,围绕几个关键问题展开讨论。
一、如何建立门急诊排队模型?建立门急诊排队模型需要利用大量的历史数据和实时数据,对患者的排队行为和医院的资源变化进行深入研究。
通常可以采用排队理论、模拟方法、统计分析等多种手段,对现有数据进行建模和分析,建立起科学可靠的门急诊排队模型。
其中,排队理论可以通过算法和模型,研究排队系统的运行机制和规律,确定排队长度、排队平均时间、等待人数等指标;模拟方法则可以通过模拟完整的排队场景,分析每个患者的排队时间和医疗资源利用情况;统计方法则可以根据历史数据和实时数据,建立患者到达和医生服务的概率分布模型,作为分析和预测排队情况的依据。
二、如何收集和处理门急诊排队的数据?医院门急诊排队数据的收集和处理对于建立科学有效的排队模型至关重要。
一般来说,可以通过医院的信息系统、大屏幕监控、问诊系统、移动应用等多种途径,收集到每个患者的个人信息、待就诊时间、就诊科室、医生资源、诊断结果等数据,以支持后续的数据分析和建模工作。
在收集和处理数据的过程中,需要考虑到数据的规范化、整合、去重、清洗等问题,以保证数据的高质量和可用性。
此外,对于敏感数据(如个人隐私信息等),还要加强安全和保护措施,防止泄露和误用。
三、如何提高门急诊就诊效率?基于大数据分析的门急诊排队模型不仅可以帮助医院优化排队方案,还可以提高就诊效率,缩短等待时间。
其中,提高就诊效率的方法包括:1.合理调配医疗资源,如医生、护士、设备等;2.为医生提供方便快捷的诊疗工具,如智能化问诊系统、移动助手等;3.对于常见疾病和就诊流程,可以引入自助诊疗设备和流程,让患者自行完成问诊和检查等环节,保证就诊效率;4.对于紧急病人和优先病人,应该优先安排,并尽快安排就诊。
排队论模型

排队论模型1. 引言排队论是运筹学中的一个重要分支,研究的是排队系统中顾客的到达、等待和服务过程。
在现实生活中,我们经常会遇到排队的场景,如银行、超市、医院等。
通过排队论模型的分析,可以帮助我们优化服务过程,提高效率和顾客满意度。
本文将介绍排队论模型的基本概念和常用模型。
2. 基本概念2.1 排队系统排队系统是指顾客到达一个系统,并等待被服务的过程。
一个排队系统通常包含以下几个要素:•到达过程:顾客到达系统的时间间隔可以是随机的,也可以是确定的。
•排队规则:系统中的顾客通常按照先来先服务原则排队。
•服务过程:系统中的服务员或服务设备为顾客提供服务,服务时间也可以是随机的或确定的。
•系统容量:排队系统中通常有一定的容量限制,即同时能够容纳的顾客数量。
2.2 基本符号在排队论中,通常使用以下符号来表示不同的概念:•λ:到达率,表示单位时间内系统的平均到达顾客数量。
•μ:服务率,表示单位时间内系统的平均服务顾客数量。
•ρ:系统利用率,表示系统的繁忙程度,计算公式为ρ = λ / μ。
•L:系统中平均顾客数,包括正在排队等待服务的顾客和正在接受服务的顾客。
•Lq:系统中平均等待队列长度,即正在排队等待服务的顾客数。
•W:系统中平均顾客逗留时间,包括等待时间和服务时间。
•Wq:系统中平均顾客等待时间,即顾客在排队等待服务的平均时间。
3. 常用模型3.1 M/M/1模型M/M/1模型是排队论中最简单的模型之一,其中M表示指数分布。
M/M/1模型满足以下几个假设:•顾客到达率λ满足均值为λ的指数分布。
•服务率μ满足均值为μ的指数分布。
M/M/1模型的特点是顾客到达率和服务率是独立的,且符合指数分布。
根据排队论的理论分析,可以计算出系统的性能指标,如系统利用率、平均顾客数、平均等待队列长度等。
3.2 M/M/c模型M/M/c模型是M/M/1模型的扩展,其中c表示服务员的数量。
M/M/c模型满足以下假设:•顾客到达率λ满足均值为λ的指数分布。
排队论模型求解就医排队问题

逗留的患者的平均人数: Ls= 3人 患者的平均逗留时间: Ws=4小时 等待患者的平均人数: Lq=2.25人 患者的平均排队等待时间: Wq=3小时
由此可知,K个M/M/1模型中患者的平均排 队等待时间为3小时。
假设:各种特征的规定和假设与模型1相同,假定K 个服务台并联排列,各服务台独立工作,其平均服 务率相同,即μ1=μ2=…=μk=μ因此,该系统的平均 服务率为kμ。 1 P 1 1 k 在M/M/K模型中: ( ) ( )(
[1]吴希.医院门诊系统的排队过程模型[J].中国 医药导报,2007,4(25):131—132. [2]彭迎春,董斯彬,常文虎.运用排队论模型测量 医 院 门 诊 流 程 效 率 [J]. 中 华 医 院 管 理 杂 志,2005,21(12):806—809. [3]李军,徐玖.运筹学一非线性系统优化[M].北京: 科学出版社2003:42 —50. [4]钱颂迪.运筹学[M].清华大学出版社,2005. [5]唐应辉,唐小我.排队论——基础与分析技术[M] 科学出版社,2006.
模型1OR模型2?
假设:该诊疗室每天平均有6名患者前来,每人平 均服务时间为l小时,前来的患者按泊松分布到达, 服务时间服从指数分布,每天按8小时计。则平均 到达率=6/8=0.75人/小时,平均服务率=1人/小 时,服务强度=0.75/1=0.75 在M/M/1模型中:
即如果一个诊室内有数名医生应把病案放在门口排队由一名护士按次序送到空闲的医生处而不是把病案放在各个医生处排队
资源学院2010级本科生 朱南华诺娃 201011191012
带优先权排队论_模型简介+应用案例分享

模型简介 1
模型假设:
1. 两个模型都存在N个优先级(1级代表最高) 2. 服务顺序首先基于优先级,同一优先级内,依据“先到先服务” 3. 对任意优先级,顾客到达服从Poisson分布,服务时间服从负指数分布 4. 对任意优先级顾客的服务时间相同 5. 不同优先级顾客的平均到达率可以不同
计算公式 2
Nonpreemptive Priorities
s=1
s=2
s=1
s=2
0.024 hour 0.154 hour
0.00037 hour 0.00793 hour
0.238 hour 0.325 hour
0.029 hour 0.033 hour
1.033 hour 0.06542 hour 0.889 hour
两种最基本的优先权排队模型:
非强占性优先权(Nonpreemptive Priorities)——即使一个高优先级
的顾客到达,也不能强制让一个正在接受服务的低优先级顾客返回排队。
强占性优先权(Preemptive Priorities)——若有高优先级的顾客到达,
服务员即中断对低优先级顾客的服务,并马上开始为高优先级顾客服务。
s=1
s=2
0.024 hour
0.154 hour
1.033 hour
Nonpreemptive Priorities
s=1
s=2
0.238 hour
0.029 hour
0.325 hour
0.033 hour
0.889 hour
0.048 hour
案例求解 3
即
W1
=W
= Wq
+
1 m
排队论模型PPT课件

0 0 0
顾客离去
10%
(
调试 0 检验
)
90
%
第8页/共40页
(5)匹配排队模型
煤矿 火车 煤仓
汽车(或火车)
港口
轮船
另外还有
(6)优先权的排队系统 (7)成批排队模型 (8)有限源排队模型
我们讨论(1)(2)两种
第9页/共40页
(三)、建立排队模型步骤 1.确定表达排队问题各个变量并建立它们之间的相互
时解,一般这种瞬时解是难以求得的
第14页/共40页
3.统计平衡下的极限解
实际应用中,关心的是t 时,方程的解称
为
生
灭
lim t
过程微
pn(t) pn
分由p差n' (t)分 0方
程
组
的
极
限
解
。
令
及(9.1)(9.2)式得当S
为有n1限pn状1 态(n集 时n ),pn (9.n11)p式n1 变 0为
2.几种重要的排队模型 (1)单服务台系统
顾客到达
排队
00…00
服务台
(2)多服务台的平衡系统
顾客离去
顾客到达 排队 服务台
00…00
顾客离去
顾客离去 服务台
服务机构
第7页/共40页
(3)串联排队系统
顾客到达 排队 00…00
0
0
顾客离去
M1
M2
…
Mn
0
(4)排队网络模型
顾客到达 排队 00…00
第2页/共40页
输入过程一样,服务时间都是随机的,且我们假设,设
n表示服务员为n个顾客提供服务所需的时间,则服务
基于排队论模型的门诊CT 检查排队优化设计

管理科◎张清芝1何雅静2岳萍3王琨4郑二维1基于排队论模型的门诊CT 检查排队优化设计(作者单位:1.哈尔滨医科大学附属第一医院;2.哈尔滨医科大学附属第二医院;3.黑龙江省卫生厅;4.哈尔滨医科大学附属第四医院)随着经济社会的不断发展,人们对健康的需求也在不断的提升。
公立医院,尤其是大型三级公立医院,其资源效率与患者的需求之间不平衡的矛盾依旧存在。
漫长的排队等待现象严重地影响了患者的就医体验,耗费着巨大的时间成本。
医院中的检查科室又是患者聚集最多,等候时间最长的部门。
为了进一步落实《关于印发进一步改善医疗服务行动计划(2018—2020年)的通知》(国卫办医函(2018)894号)文件的要求,切实提高群众的就医体验,本研究应用排队论去解决某省三级公立医院的门诊CT 检查等候时间过长的问题,通过优化其检查流程,以提高CT 设备的使用效率。
排队论是研究如何以最经济的方式控制排队的一种方法,能够有效地找到服务成本和等待量之间的平衡。
由于当前公立医院的规模不可能随着患者需求的增加而无限制的扩大,因此研究有限的医疗资源如何能提供尽可能多的服务就变得非常具有实际意义。
一、问题的提出1.CT 检查的排队现象。
患者从医生开具CT 检查处方到获得检查结果要经历大致五个步骤:开检查、排队缴费、排队预约,排队检查,报告获取。
由于整个检查过程是面向整个门诊的所有诊室患者,因此患者在每一个步骤都要经历过一次排队才能获得相应的服务。
由于一般患者对大型三级医院CT 检查的需求量往往大于CT 的实际服务提供能力,因而造成检查的等候时间过于漫长。
当前样本医院配置了门诊CT 机器3台,以每个工作日8小时计算,平均每台的日均工作量为140人,而实际上日均需求在200人次以上。
一方面医务人员不得不延长工作时间以满足患者需求,另一方面,患者的等候时间也必然增加。
2.CT 检查流程的改造设想。
解决CT 检查排队问题可以从两个方面入手:一是增加购置CT 设备。
医院就诊服务系统排队模型分析

过程的转移矩阵, 并利用矩阵分析方法进行求解 , 得到 了该系统的稳 态概率解及其它相关指标。 关键词 : 串联排 队; 稳态解 ; 转移 密度矩 阵
di1 .9 9 .s .1 0 -3 7 2 1. 4 0 2 o:0 3 6 /Ji n 0 44 3 . 0 0 0 . 0 s
医院是一个 由许 多科 室部 门组成 的复杂 的系统 , 人就 病 医必须经历挂号 、 就诊 、 划价 和取药 每一 个机构 , 由于 每个部
S ti n u e h tn t r o v r e c o t eg o a p i u i r a r b bl y,a d i o ec me h Oi se s r d t a ewo k c n eg n et h lb l t m ag e tp o a i t o m n i n t v r o st诊 的医生是有限的 , 当病 人达到一定数 量时 , 就会 出
现排 队就 医现象 , 就诊 病人 的数量 和每个 病人 就诊 的时间都 是随机 的, 当诊 室不多 , 患者过 多时 , 而 就会 出现病 人等 待时
科 渗 卜 就 人 厂.-0 I 到 l ] i 2P : 一 室就 ' 2诊 {科
Z a ayn h o Xio a
( o n ain d c lC l g f Not ih a d c lC le e tf o of Mah m t sa d F u d t i ol eo rh S c u nMe ia olg ,S a f Rom te a i n o Me a e c
・ 医学数 学模型探讨 ・
医 院 就 诊 服 务 系 统 排 队模 型分 析
王 松 建
( 州 医学 院数 理教研 室 徐
医院排队论模型(1)

医院排队论模型(1)医院排队论模型指的是人在医院排队就诊的过程中,如何利用排队论模型来优化排队过程,提高就诊效率,降低排队时间。
下面从排队论模型的三要素(到达率、服务率、队列容量)出发,探讨在医院排队过程中如何优化流程。
第一、到达率到达率指的是单位时间内到达就诊的人数。
在医院排队过程中,到达率的分析可以帮助医院预测每天需要接待的患者数量,从而根据就诊人数、科室人员数量等资源来合理安排诊疗流程,避免出现拥堵的情况。
在医院安排就诊计划时,可以根据就诊需求、人员数量、诊室开放时长等来制定排班计划,如早上安排主诊医生接待复杂病人,下午安排副诊医生接待一般患者等。
第二、服务率服务率指的是单位时间内完成服务的人数。
在医院排队过程中,每个病人的就诊时间不同,有的患者需要进行详细检查、化验,需要较长时间,有的患者可能只需要短暂检查,大约十几分钟左右。
因此,为了提高个体效率,医院可以根据病人种类、健康状况等特不同性制定不同的服务时间,避免患者等待时间过久。
医院服务行业,提高服务水平可以吸引更多患者就诊,轻松排队也能提高了患者就诊时的舒适度和安全感。
第三、队列容量队列容量指的是医院可以容纳等待就诊人数和等待空间。
医院到达的患者数量与就诊人数不匹配,往往会造成人流混乱,交通拥堵等问题。
因此,医院应该合理利用队列容量,充分利用场地现有资源,设置等待区域、设立排队标识等措施,通过这些技术手段,既可以避免人流混乱,也可以避免就诊过程中因不注意安全方面出现不必要的伤害。
以上是基本的医院排队论模型,通过对到达率,服务率和队列容量的分析可以合理安排医院就诊计划,优化流程,提高服务水平、减少等待时间,使得医院就诊流程得到良性循环。
8.2-单服务台排队模型PPT课件
4
10
0.0992
9.92
0.0006
5 ≥6
6
0.0416
1 7
0.0207
24..01 766.2 3
0.0952
∑
100
1.0000
100
1.3026
k
2
(A iTi)2,
k1a a为参数的个数
T i1
i
2021/7/23
13
2、计算公式
k
2
(Ai Ti)2 1.3026
T i1
i
k 1 a 6 1 1 4
(2)队长
L242020( 5人 )
2021/7/23
23
20人 /小 时 24人/小 时
(3)等待队长
L q( 2)24(2 2 0 4 220)4.16( 7人 )
(4)平均等待时间
W q L q 4 .2 1 0 6 7 0 .2 0 8 ( 3小 时 ) 1 2 .5 ( 分 钟 )
1
2
3
4
5
6
≧7
28
29
16
10
6
1
0
x nfn2.( 1人 /小 时 ) 100
2021/7/23
11
1、原理 判断样本观察频数(A)与理论(期望)频数(T )
之差是否由抽样误差所引起。
类别或组段 观察频数
理论频数
1
A1
T1
2
A2
T2k
Tk
问题:试判断这份样本,是否来自该理论分布?
注意:理论频数Ti不宜过小(如不小于5),否则需要合并组段!
3
排队模型的符号定义为: A/B/C/m/N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑵ 服务时间
患者接受服务的时间规律往往也是通过概率分布描 述的. 常见的服务时间分布有定长分布, 述的. 常见的服务时间分布有定长分布,负指数分布和埃 尔朗分布. 尔朗分布. 一般来说, 简单的排队系统的服务时间往往服从负指 一般来说, 数分布, 即每位患者接受服务的时间是独立同分布的, 数分布, 即每位患者接受服务的时间是独立同分布的, 其 分布函数为 B ( t ) = 1- e - t (t ≥0). 为一常数, 代表单位时间的平均服务率. 其中>0为一常数, 代表单位时间的平均服务率. 而1/ 则是平均服务时间. 则是平均服务时间.
如果医院增添服务人员和设备,就要增加投资或发生空闲浪费; 如果医院增添服务人员和设备,就要增加投资或发生空闲浪费; 如果减少服务设备,排队等待时间太长, 如果减少服务设备,排队等待时间太长,对患者和社会都会带来不良 影响. 影响. 因此,医院管理人员要考虑如何在这两者之间取得平衡, 因此,医院管理人员要考虑如何在这两者之间取得平衡,以便 提高服务质量,降低服务费用. 提高服务质量,降低服务费用. 医院排队论,就是为了解决上述问题而发展起来的一门科学. 医院排队论,就是为了解决上述问题而发展起来的一门科学.它 是运筹学的重要分支之一. 是运筹学的重要分支之一. 在排队论中,患者和提供各种形式服务的服务机构组成一个 和提供各种形式服务的服务机构组成一个排 在排队论中,患者和提供各种形式服务的服务机构组成一个排 队系统,称为随机服务系统 随机服务系统. 队系统,称为随机服务系统. 这些系统可以是具体的,也可以是抽象的. 这些系统可以是具体的,也可以是抽象的. 排队系统模型已广泛应用于各种管理系统.如手术管理, 排队系统模型已广泛应用于各种管理系统.如手术管理,输液 管理,医疗服务,医技业务,分诊服务,等等. 管理,医疗服务,医技业务,分诊服务,等等.
n=1
⑶
患者在系统中平均逗留时间W 患者在系统中平均逗留时间 s
1 Ls Ws = = λ λ
患者在队列中平均等待时间W ⑷ 患者在队列中平均等待时间 q
W =W q s 1
=
Lq
λ
闲期的平均长度I ⑸ 闲期的平均长度
I= 1
λ
忙期的平均长度B ⑹ 忙期的平均长度
1 B = Ls I = = λ λ λ
排队系统模拟 所谓排队系统模拟, 所谓排队系统模拟,就是利用计算机对一个客 观复杂的排队系统的结构和行为进行动态模拟, 观复杂的排队系统的结构和行为进行动态模拟,以 获得反映其系统本质特征的数量指标结果, 获得反映其系统本质特征的数量指标结果,进而预 分析或评价该系统的行为效果, 测,分析或评价该系统的行为效果,为决策者提供 决策依据. 决策依据.
排队系统的分类
排队系统模型主要可以由输入过程(患者到达时间间隔分布) 排队系统模型主要可以由输入过程(患者到达时间间隔分布), 服务时间分布,服务台个数特征来描述. 服务时间分布,服务台个数特征来描述. 根据这些特征,可用符号进行分类, 用以表示不同的模型. 根据这些特征,可用符号进行分类, 用以表示不同的模型. 例 利用一定的符号规则将上述特征按顺序用符号列出, 如,利用一定的符号规则将上述特征按顺序用符号列出,并用竖线 隔开,即 隔开, 输入过程 | 服务分布 | 服务台个数 例如, | | 表示输入过程为泊松输入 表示输入过程为泊松输入, 例如, M|M|S表示输入过程为泊松输入,服务时间服从负指 数分布, 个服务台的排队系统模型 个服务台的排队系统模型; | |1则表示泊松输入, |1则表示泊松输入 数分布,S个服务台的排队系统模型; M|G|1则表示泊松输入, 一般服务分布,单个服务台的排队系统. 一般服务分布,单个服务台的排队系统.
M | M | 1 模型
M|M|1模型是输入过程为泊松输入,服务时间为负指数分 | |1模型是输入过程为泊松输入, |1模型是输入过程为泊松输入 布并具有单服务台的等待制排队系统模型, 布并具有单服务台的等待制排队系统模型,这是最简单的排队系 统模型. 统模型. 假定系统的患者源和容量都是无限的,患者单队排列, 假定系统的患者源和容量都是无限的,患者单队排列,排队 规则是先到先服务. 规则是先到先服务. 设在任意时刻t系统中有 个患者的概率P . 系统中有n个患者的概率 设在任意时刻 系统中有 个患者的概率 n(t). 当系统达到稳 定状态后, 趋于平衡P 无关. 定状态后,Pn(t)趋于平衡 n且与 无关. 此时,称系统处于统计平衡 趋于平衡 且与t无关 此时, 状态,并称P 为统计平衡状态下的稳态概率. 状态,并称 n为统计平衡状态下的稳态概率. Pn=(1- ρ )ρ n, n = 0, 1, 2, … . (1(1 之比(0 (0< 其中ρ =λ/ 表示有效的平均到达率λ与平均服务率 之比(0<ρ < 1).
患者的总体可以是无限的也可以是有限的; 患者的总体可以是无限的也可以是有限的; 患者到来方式可以是单个的,也可以是成批的; 患者到来方式可以是单个的,也可以是成批的; 相继到达的间隔时间可以是确定的, 相继到达的间隔时间可以是确定的,也可是随机 的; 患者的到达可以是相互独立的,也可以是关联; 患者的到达可以是相互独立的,也可以是关联; 到来的过程可以是平稳的,也可是非平稳的; 到来的过程可以是平稳的,也可是非平稳的;
指服务台连续繁忙的时间长度. ⑵ 忙期 指服务台连续繁忙的时间长度.
该指标反映服务台的工作强度和利用程度. 该指标反映服务台的工作强度和利用程度.用B表示忙期的 表示忙期的 平均长度. 平均长度. 与忙期相应的是闲期,闲期是指服务台一直空闲的时间长度. 与忙期相应的是闲期,闲期是指服务台一直空闲的时间长度. 表示闲期的平均长度. 用I 表示闲期的平均长度. 指系统中的患者数( ⑶ 队长 指系统中的患者数(包括排队等候的和正在接受服务 的所有患者). 的所有患者). 表示平均队长.若不考虑接受服务的患者, 用Ls表示平均队长.若不考虑接受服务的患者, 则将系统中排 队等候的患者数称为队列长. 表示平均队列长. 队等候的患者数称为队列长.用Lq表示平均队列长. 此外, 表示服务强度, 此外, 用ρ 表示服务强度,其值为有效的平均到达率λ与平均 服务率 之比, 即ρ =λ/ .
M | M | 1 模型的几个主要指标 模型的几个主要指标 ⑴
在系统中的平均患者数(平均队长) 在系统中的平均患者数(平均队长)Ls
∞
ρ λ = Ls = ∑nP = n 1 ρ λ n=1
∞
⑵
在队列中等待的平均患者数(平均队列长) 在队列中等待的平均患者数(平均队列长)Lq
Lq = ∑(n 1)P = Ls ρ = ρLs n
⑴ 来到过程
常见的来到过程有定长输入,泊松(Poisson)输入,埃尔朗 常见的来到过程有定长输入,泊松( )输入, (A. K. Erlang)输入等,其中泊松输入在排队系统中的应用最为广 )输入等, 泛. 所谓泊松输入即满足以下4个条件的输入: 所谓泊松输入即满足以下4个条件的输入: 平稳性: ① 平稳性:在某一时间区间内到达的患者数的概率只与这段 时间的长度和患者数有关; 时间的长度和患者数有关; 无后效性: ② 无后效性:不相交的时间区间内到达的患者数是相互独立 的; ③ 普通性:在同时间点上就诊或手术最多到达1个患者, 不 普通性:在同时间点上就诊或手术最多到达1个患者, 存在同时到达2个以上患者的情况; 存在同时到达2个以上患者的情况; 有限性:在有限的时间区间内只能到达有限个患者, ④ 有限性:在有限的时间区间内只能到达有限个患者, 不可 能有无限个患者到达. 能有无限个患者到达.
排队系统的主要数量指标
评价和优化排队系统,需要通过一定的数量指标来反映. 评价和优化排队系统,需要通过一定的数量指标来反映. 建立排队系统模型的主要数量指标有三个:等待时间, 建立排队系统模型的主要数量指标有三个:等待时间,忙期 与队长. 与队长. ⑴ 等待时间 指患者从到达系统时起到开始接受服务时止这 一段时间. 显然患者希望等待时间越短越好. 一段时间. 显然患者希望等待时间越短越好. 表示患者在系统中的平均等待时间.若考虑到服务时间, 用Wq 表示患者在系统中的平均等待时间.若考虑到服务时间, 则用W 表示患者在系统中的平均逗留时间( 则用 s 表示患者在系统中的平均逗留时间(包括等待时间和服务 时间). 时间).
λ
1
MRI室配有一位专业医师 负责核磁共振拍摄工作. 室配有一位专业医师, 例 某MRI室配有一位专业医师,负责核磁共振拍摄工作.已 知每天平均有6名患者前来, 每人平均时间为1小时, 知每天平均有6名患者前来, 每人平均时间为1小时,前来的患者 按泊松分布到达,服务时间服从负指数分布,每天按8小时计. 按泊松分布到达,服务时间服从负指数分布,每天按8小时计. 试 求: 医师工作空闲的概率; ①医师工作空闲的概率; ②MRI室有两台患者同时到达的概率; MRI室有两台患者同时到达的概率; 室有两台患者同时到达的概率 ③MRI室至少有1人来的概率; 室至少有1人来的概率; ④ MRI室逗留的患者的平均人数; 室逗留的患者的平均人数; 患者在MRI室的平均逗留时间; ⑤患者在 室的平均逗留时间; 患者的平均人数; ⑥ MRI室等待患者的平均人数; 室等待患者的平均人数 ⑦待拍摄的患者平均等待时间; 待拍摄的患者平均等待时间; ⑧ MRI室忙期的平均长度. 室
医院排队系统的组成
排队系统的基本结构由四个部分构成: 排队系统的基本结构由四个部分构成:来到过 输入),服务时间,服务窗口和排队规则. ),服务时间 程(输入),服务时间,服务窗口和排队规则. 来到过程(输入) 1,来到过程(输入)是指不同类型的患者按照各 种 规律来到医院. 规律来到医院. 服务时间是指患者接收服务的时间规律. 2,服务时间是指患者接收服务的时间规律. 3,服务窗口则表明可开放多少服务窗口来接纳患 者. 4,排队规则确定到达的患者按照某种一定的次序 接 受服务. 受服务.
⑶ 服务窗口 服务窗口的主要属性是服务台的个数. 服务窗口的主要属性是服务台的个数. 其类 型有:单服务台,多服务台. 型有:单服务台,多服务台. 多服务台又分并联,串联和混合型三种. 多服务台又分并联,串联和混合型三种. 最 基本的类型为多服务台并联. 基本的类型为多服务台并联.
