第四章-特殊函数(上)-勒让德多项式和球谐函数
第四章-特殊函数(上)-勒让德多项式和球谐函数

2ll!dxl
k0
2lk!(lk)!
[2 l]
(1)k
k0
(2l2k)! xl2k 2lk!(lk)!(l2k)!
Pl(x).
3.勒让德多项式的积分表示
根据柯西积分公式的高阶导数,并取正方向积分有
i f(l)(z) l!
f() d
2πi C(z)l1
容易证明微分表示(4.1.10)也可表示为环路积分形式
4.2.1 勒让德多项式的性质 1. 勒让德多项式的零点 对于勒让德多项式的零点,有如下结论:
(i) P n ( x ) 的 n个零点都是实的,且在 (1,1) 内;
(ii) Pn 1 ( x ) 的零点与 P n ( x ) 的零点互相分离.
2. 奇偶性 根据勒让德多项式的定义式,作代换 x (x), 容易得到
P2n(0)(1)n2(22 nn n!)n !!(1)n(2 (n 2n )1 !)!!! (4.1.9)
式中记号 ( 2 n ) ! ! ( 2 n ) ( 2 n 2 ) ( 2 n 4 ) L 6 4 2
而 ( 2 n 1 ) ! ! ( 2 n 1 ) ( 2 n 3 ) ( 2 n 5 ) L 5 3 1
的项,即 k l
2
的项,应取 k m ax
[l] 2
,并且注意到
d l x 2 l 2 k ( 2 l 2 k ) ( 2 l 2 k 1 )[ 2 l 2 k ( l 1 ) ] x l 2 k d x l
因此有
1
dl
(x21)l
[2 l]
(1)k
(2l2k)(2l2k1)L(l2k1)xl2k
本章主要内容:勒让德多项式的来源、定 义、性质、生成与递推公式,球谐函数。
勒让德多项式

k 2 3P3 ( x) 5xP2 ( x) 2P ( x) 15 x3 9 x 1 2 2
勒让德多项式的性质
奇偶性
Pl(-x) = (-1)l Pl(x) 零点定理 L阶勒让德多项式为L次多项式,有L个零点。 正交性
– 正交性公式 – 模 – 正交性应用例题
完备性
(35cos 4 20cos 2 9)
勒让德多项式的图象
勒 让 德 多 项 式 的 图 象
母函数和递推公式
母函数 – 定义:u(x, r) =∑ Pl (x) r l – 形式:u(x, r) = ( 1-2rx + r2 )-1/2 – 推导 – 应用 递推公式 – 基本递推公式 – 证明 – 应用
球内解要求u (0, )有界,半通解化为 u
l 0
Al r l Pl (cos )
2
由边界条件得: Ax
l 0
Al a l Pl ( x )
Ax2 P ( x)dx k
2k 1 根据完备性:Ak 2a k
1
1
勒让德多项式的应用
例题 2
半径为a的球面上电势分布为 f = Acos2θ,确定球外空 间的电势 u 。
2
由边界条件得: Ax
l 0
Bl a l 1Pl ( x )
2k 1 k 1 根据完备性: k B a 2
1
1
Ax2 P ( x)dx k
勒让德多项式的应用
例题 3
一空心圆球区域,内半径为a,外半径为b,内球面上电势为 f = cosθ,外球面上电势为零,确定区域内电势u 。
解:定解问题为:u 0, a r b u |r a cos , u |r b 0
SphericalHarmonics球谐函数的理解与使用

SphericalHarmonics球谐函数的理解与使用球谐函数(Spherical Harmonics)是用于描述球对称性的函数。
它在数学、物理、计算机图形学等领域中具有广泛的应用。
本文将对球谐函数的理解与使用进行详细介绍。
首先,我们来了解球谐函数的定义。
给定单位球面上的点(x,y,z),球谐函数Yₗⁿ(x,y,z)定义如下:Yₗⁿ(x, y, z) = (-1)^m * sqrt((2ℓ+1)/(4π)*(ℓ-,m,)!/(ℓ+,m,)!)*Pₗ,m,(cosθ)*e^(imφ)其中,Yₗⁿ表示度为ℓ,阶为,m,的球谐函数;ℓ是非负整数,表示球谐函数的度;,m,<=ℓ,m是整数,表示球谐函数的阶;Pₗ,m,(cosθ)是勒让德多项式;θ是点(x, y, z)相对于x轴的极角;φ是点(x, y, z)相对于x轴的方位角;e是自然对数的底。
球谐函数具有下述性质:1.球谐函数是单位球面上的正交基,即不同的球谐函数之间在单位球面上的内积等于0。
2.Yₗⁿ(x,y,z)关于极角θ是奇函数,关于方位角φ是偶函数。
3.在单位球面上,球谐函数Yₗⁿ(x,y,z)的绝对值平方是一个常数,即,Yₗⁿ(x,y,z),²在球面上处处相等。
在物理学中,球谐函数被广泛应用于描述球对称的物理场。
例如,在量子力学中,球谐函数用于描述原子中的电子波函数;在电动力学中,球谐函数用于展开电磁场的球谐分量;在量子力学中,球谐函数用于描述自旋等。
在计算机图形学中,球谐函数也被广泛应用于实时渲染、全局光照以及球形图像处理等领域。
通过将光照场或图像投影到球谐函数系数上,可以实现基于球面光照的实时渲染。
球谐函数还可以用于创建全局光照环境贴图,用于增强场景的真实感。
此外,球谐函数还可以用于球形图像处理,例如球形全景图像的压缩和展开。
值得注意的是,球谐函数展开的精度和复杂度有一定的关系。
一般来说,较高阶的球谐函数能够更准确地近似光照场或图像,但计算复杂度也会增加。
球谐函数ylm

球谐函数ylm1. 什么是球谐函数球谐函数(Spherical Harmonics)是描述在球面上的物理和数学问题的一组函数。
球谐函数可以用于描述轴对称的空间分布,例如电荷分布、电磁场等。
球谐函数是平面波的三维推广,它描述了球对称下的波函数形式。
它在物理学、数学和计算机图形学等领域有广泛的应用。
球谐函数通常用Ylm(θ, φ)表示,其中θ是极角,φ是方位角。
2. 球谐函数的性质球谐函数具有以下一些重要的性质:2.1 正交性球谐函数在单位球面上是正交的,即不同的球谐函数之间的内积为零。
这个性质在解决物理和数学问题的时候是非常有用的,可以用来展开复杂的函数。
2.2 归一性球谐函数在单位球面上是归一的,即其平方的积分等于1。
这个性质保证了球谐函数在描述物理问题时的准确性,可以确保物理量的总能量是保持不变的。
2.3 奇偶性球谐函数具有奇偶性。
对于函数Ylm(θ, φ),当l为偶数时,其函数值是关于θ对称的;当l为奇数时,其函数值是关于θ反对称的。
2.4 旋转对称性球谐函数具有旋转对称性,即在球面上进行旋转变换后,球谐函数的形式不变。
这个性质保证了球谐函数在描述旋转对称系统时的准确性,如原子轨道和电磁场分布。
3. 球谐函数的计算球谐函数的计算可以通过递推关系或者数值方法来进行。
3.1 递推关系球谐函数Ylm(θ, φ)可以通过递推关系来计算,公式为:Ylm(θ, φ) = (-1)^m sqrt((2l+1) / (4π) (l-m) / (l+m)) Pnm(cosθ) e^(imφ)其中,Pnm(x)是勒让德多项式,可以通过递推关系Pnm(x) = (2n-1) * x * Pn-1m(x) - (n+m-1) * Pn-2m(x)来计算。
3.2 数值方法除了递推关系,还可以使用数值方法来计算球谐函数。
常用的数值方法包括插值法和数值积分法,可以根据具体问题的要求来选择合适的方法进行计算。
4. 球谐函数的应用球谐函数广泛应用于物理学、数学和计算机图形学等领域。
球谐函数 偏导

球谐函数偏导
球谐函数是一类特殊的函数,它们是由勒让德多项式和三角函数的乘
积组合而成的。
球谐函数在物理学的各个领域都有广泛的应用,如热
力学、电动力学、量子力学等。
此外,球谐函数也在图像与信号处理、计算机图形学中得到了应用。
首先,球谐函数的导数也十分重要。
球谐函数的定义域是单位球面上
的点,因此球谐函数的导数会在单位球面上产生向内或向外的法向量。
球谐函数和它们的导数在物理学中被广泛应用于描述旋转对称性、自
旋角动量和磁场等领域。
在这些应用中,球谐函数的导数被用于计算
旋转矩阵的元素、各向异性之间的耦合等问题。
其次,由于球谐函数具有特殊的正交性质,因此它们可以用来展开各
种函数。
这种展开叫做球谐函数展开。
球谐函数展开在图像与信号处理、计算机图形学中被广泛应用。
例如在计算机图形学中,球谐函数
展开被用来照亮、渲染物体,同时也被用来压缩和储存高动态范围图像。
此外,球谐函数展开也被用来进行信号分析和处理,如声音、图
像和视频信号的分析和压缩等。
最后,球谐函数还具有一系列的性质。
例如在三维空间中,球谐函数
可以用来描述电磁波、声波等的空间分布。
此外,在量子力学中,球
谐函数被用来描述粒子的自旋、角动量等,是量子力学中具有重要意义的函数。
总之,球谐函数作为一类特殊的函数,在物理学与计算机科学等领域都有广泛的应用。
球谐函数的偏导数、展开和性质等方面也具有重要意义。
因此,深入理解和应用球谐函数对于相关领域的研究和实践都具有十分重要的作用。
特殊函数
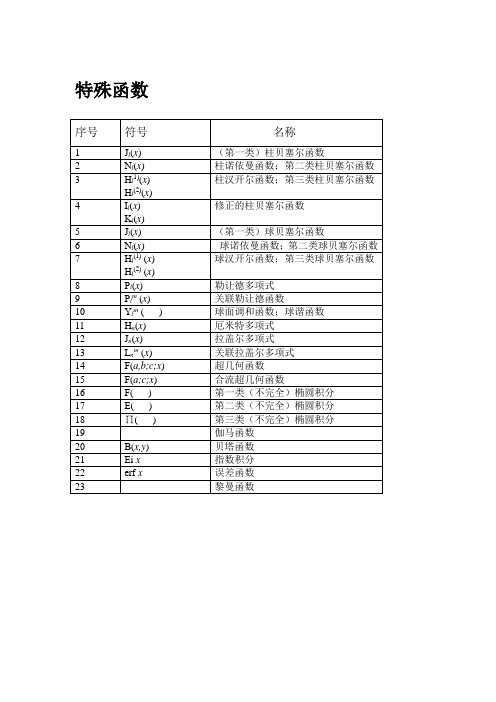
序号
符号
名称
1
Jl(x)
(第一类)柱贝塞尔函数
2
Nl(x)
柱诺依曼函数;第二类柱贝塞尔函数
3
Hl1)(x)
Hl(2)(x)
柱汉开尔函数;第三类柱贝塞尔函数
4
Il(x)
Kl(x)
修正的柱贝塞尔函数
5
Jl(x)
(第一类)球贝塞尔函数
6
Nl(x)
球诺依曼函数;第二类球贝塞尔函数
7
Hl(1)(x)
Hl(2)(x)
球汉开尔函数;第三类球贝塞尔函数
8
Pl(x)
勒让德多项式
9
Plm(x)
关联勒让德函数
10
Ylm()
球面调和函数;球谐函数
11
Hn(x)
厄米特多项式x)
关联拉盖尔多项式
14
F(a,b;c;x)
超几何函数
15
F(a;c;x)
合流超几何函数
16
F()
第一类(不完全)椭圆积分
17
E()
第二类(不完全)椭圆积分
18
∏()
第三类(不完全)椭圆积分
19
伽马函数
20
B(x,y)
贝塔函数
21
Eix
指数积分
22
erfx
误差函数
23
黎曼函数
北科大数理方程 4+ch4+勒让德(Legendre)多项式

dy dx
d ( sin
2
d (sin dx
dy dx
d dx
)
(sin
)
dx d
dx
dy dx ] d dx
2
( sin )
[(co s 1)
]
d dx
[(1 co s )
[(1 x )
dy dx
]
12
方程
d d 2 2 sin sin l ( l 1) sin m 0 d d 有限值 0 ,
2
2
0
d dr
r
(r
2
dR dr
) R r
1
2
sin
d
(sin
d d
) R r
2
sin
2
d
2
0,
2
以
R
1 d R dr (r
乘上式,得
2
dR dr
)
1
d
sin d
(sin
d d
)
1 sin
2
d
2
d
2
0,
4
1 d R dr
第四章 勒让德多项式
本章介绍另一类重要的特殊函数—勒让德函数。 勒让德函数是勒让德方程
(1 x )
2
d y dx
2
2
2x
dy dx
y 0
的解。 勒让德方程在区间[-1,1]上的有界解组成一类用途广泛的 正交函数系―勒让德多项式。 利用勒让德多项式,可以求出许多数学物理问题的解。
最新勒让德(legendre)多项式及其性质资料

勒让德(legendre )多项式及其性质一. 勒让德多项式勒让德多项式是由勒让德方程的通解推导出来的,所以我们首先引入勒让德方程,以及勒让德方程的幂级数解,勒让德方程的表达式如下:2'''(1)2(1)0x y xy n n y --++= 其中n 为非负实数 (1.1)它的幂级数解如下:12y y y =+ (1.2)其中:2241200(1)(2)(1)(3)[1]2!4!kk k n n n n n n y a x a x x ∞=+-++==-+⋅⋅⋅∑(1.3)213522110(1)(2)(1)(3)(2)(4)[]3!5!k k k n n n n n n y a xa x x x ∞++=-+--++==-++⋅⋅⋅∑ (1.4)由达朗贝尔判别法可知,当0n ≥不为整数时,这两个级数的收敛半径为1,在(1.3)式和(1.4)式中,0a 与1a 可以任意取值,它们起着任意常数的作用,显然,在区间(-1,1)内1y 和2y 都是方程(1.1)的解,所以(1.2)是(1.1)的通解。
上面(1.3)和(1.4)幂级数当||1x <时级数收敛,此外级数是发散的。
并且,我们发现,当n 取非负整数时,1y 和2y 中有一个便退化为n 次多项式,它就是方程(1.1)在闭区间[-1,1]上的有界解。
此时,适当的选定这个多项式的最高次幂系数n a ,所得的多项式称为n 阶勒让德多项式或第一类勒让德函数,记作()n P x ,下面我们来推导勒让德多项式()nP x 的表达式。
① 当n 为正偶数时1y 退化为n 次多项式。
为求得()n P x 的表达式,在1y 中我们通过n a 来表示其它各项的系数。
为此,将系数递推关系式改写成下列形式:2(2)(1)()(1)k k k k a a k n k n +++=-++ (1.5)在(1.5)式中取2kn =-,得:2(1)2(21)n n n n a a n --=-- (1.6)习惯上取n a 为 2(2)2(!)n nn a n = (1.7)于是有:2(1)2(21)(22)!2(21)2(1)!(1)(2!)n n n n n n n a n n n n n n ----=-----(22)!2(1)!(2)!nn n n -=--- (1.8)在(1.5)式中取4kn =-,并利用2n a -之值得:42(2)(3)4(23)n n n n a a n ----=--2(2)(3)(22)!(1)4(23)2(1)!(2)!n n n n n n n ---=---- 2(24)!(1)2(2!)(2)!(4)!nn n n -=--- (1.9)一般地,我们有()()222!12!()!(2)!mn m n n m a m n m n m --=--- (0,1,,2nm =⋅⋅⋅⋅⋅⋅) (1.10)我们将这些系数带入(1.3)中,并把此时的1y 记作()n P x ,可得:220(22)!()(1)2!()!(2)!nmn m n n m n m p x x m n m n m -=-=---∑ (1.11)这就是当n 为正偶数时勒让德多项式。
勒让德多项式及球函数共53页文档

勒让德多项式及球函数
11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
END
勒让德多项式是区间什么的正交函数

勒让德多项式是一类具有重要性质的正交函数,它们在数学和工程领域中有着广泛的应用。
本文将介绍勒让德多项式的定义、性质、正交关系以及其在实际问题中的应用。
一、勒让德多项式的定义勒让德多项式是勒让德微分方程的解,该微分方程形式如下:\[ (1-x^2)y''-2xy'+n(n+1)y=0 \]其中n为非负整数。
根据其定义,勒让德多项式可以通过勒让德微分方程的解出来。
勒让德多项式的具体形式可以表示为:\[ P_n(x)= \frac{1}{2^n n!} \frac{d^n}{dx^n}(x^2-1)^n \]其中n为非负整数,P_n(x)表示第n阶的勒让德多项式。
二、勒让德多项式的性质勒让德多项式具有许多重要的性质,例如:1. 勒让德多项式是正交的,即对于不同的n和m,有以下正交性质成立:\[ \int_{-1}^{1}P_n(x)P_m(x)dx=0, \quad(n\neq m) \]2. 勒让德多项式满足勒让德微分方程,这也是它的定义所在。
3. 勒让德多项式具有递推关系,即通过递推关系可以方便地计算高阶的勒让德多项式。
三、勒让德多项式的正交关系及应用勒让德多项式的正交性质在数学和工程领域中有着重要的应用。
在数学分析中,勒让德多项式的正交性质可以用来进行函数的展开和逼近,例如在傅立叶级数、泰勒级数及函数的插值逼近中。
在数值计算和数值分析中,勒让德多项式的正交特性也被广泛应用,例如在数值积分方法中,通过勒让德多项式的正交性质可以得到高效的数值积分算法。
勒让德多项式还具有广泛的物理应用,例如在量子力学中,勒让德多项式常常用来描述原子轨道的形状。
在实际问题中,勒让德多项式的正交性质为我们提供了一种简便而有效的数学工具,通过利用勒让德多项式的正交性质,我们可以更加方便地解决各种数学和工程问题。
勒让德多项式作为一类重要的正交函数,在数学和工程领域中具有着广泛的应用。
通过深入研究勒让德多项式的定义、性质、正交关系及其应用,我们可以更好地理解和运用这一类特殊的函数,从而为解决各种实际问题提供更加有效的数学工具。
球谐函数定义

球谐函数定义球谐函数是一种数学函数,通常用于描述三维空间中与球对称相关的问题。
在物理、工程和天文学等领域,球谐函数被广泛用于描述和分析各种现象,如电磁波、量子力学和天体物理学等。
本文将介绍球谐函数的定义、特点、形式、应用领域以及函数组合等方面的内容。
一、函数定义球谐函数是定义在三维空间中的函数,具有球对称性。
具体来说,如果一个函数满足对于空间中任意一点P和单位球心O有相同的函数值,即f(r, θ, φ) = f(r', θ', φ'),其中r、θ和φ分别是点P与球心O的距离、极角和方位角,则称该函数为球谐函数。
其中,r'、θ'和φ'分别是点P'与球心O的距离、极角和方位角。
二、特点1.球对称性:球谐函数描述的函数图像在三维空间中具有球对称性,即函数值在球面上均匀分布。
2.无奇异性:球谐函数在球面上没有奇异点,即函数值在整个球面上连续且可微。
3.完备性:在一定的边界条件下,球谐函数的集合是完备的,即任何具有球对称性的函数都可以由球谐函数展开。
三、形式球谐函数有多种形式,其中最常用的是连带勒让德函数。
连带勒让德函数的一般形式为P(n, m)(θ, φ)或P(n, m)(θ, φ),其中n和m是整数,θ和φ分别是极角和方位角。
这些函数的性质与普通的勒让德函数类似,但适用于球面坐标系。
四、应用领域1.电磁波:在电磁波传播过程中,球谐函数被用于描述电磁波的电场和磁场分量。
2.量子力学:在量子力学中,波函数通常是球谐函数的形式,用于描述粒子的波状行为。
3.天体物理学:在天体物理学中,球谐函数被用于描述天体的磁场、电场以及其它物理量。
4.其他领域:除了上述领域外,球谐函数还被应用于地球物理学、声学等领域。
五、函数组合在某些情况下,两个或多个球谐函数可以组合在一起形成一个新的球谐函数。
这些组合方式通常是基于特定的数学关系和物理规律,例如线性组合、乘积等。
通过合理的组合,可以构造出满足特定需求的球谐函数,进一步拓展了其在各个领域的应用范围。
球面谐波函数

球面谐波函数概述球面谐波函数是球坐标系下的一组正交函数,常用于描述球面上的物理问题。
它们在数学物理、电磁学、量子力学等领域有广泛的应用。
本文将详细介绍球面谐波函数的定义、性质和应用。
定义球面谐波函数是指满足拉普拉斯方程在球坐标系下的分离变量解。
球面谐波函数通常用符号Y lm (θ,ϕ)表示,其中l 和m 分别表示角动量量子数和磁量子数。
球面谐波函数可以通过以下公式表示:Y lm (θ,ϕ)=(−1)m √(2l +1)(l −m )!4π(l +m )!P lm (cosθ)e imϕ 其中,P lm (cosθ)是勒让德多项式,θ和ϕ分别表示球坐标系下的极角和方位角。
性质球面谐波函数具有许多重要的性质,下面列举了其中一些常见的性质:1. 正交性:不同的球面谐波函数之间满足正交归一关系,即∫Y lm ∗(θ,ϕ)Y l′m′(θ,ϕ)sinθdθdϕ=δll′δmm′其中,δll′和δmm′分别表示克罗内克δ符号。
2. 归一化:球面谐波函数可以通过归一化系数使其满足归一化条件,即∫|Y lm (θ,ϕ)|2sinθdθdϕ=1这样可以保证球面谐波函数的模长为1。
3. 递推关系:球面谐波函数之间存在递推关系,可以通过递推关系计算不同角动量量子数和磁量子数的球面谐波函数。
4. 旋转性质:球面谐波函数在球坐标系下具有良好的旋转性质,可以通过旋转矩阵与球面谐波函数之间的关系进行描述。
应用球面谐波函数在许多领域有广泛的应用,下面介绍其中几个重要的应用:1.量子力学:球面谐波函数是描述氢原子和其他球对称势场中的粒子的波函数的基础。
它们可以用来计算能级、波函数和选择规则等量子力学性质。
2.电磁学:球面谐波函数可以用于描述电磁场在球面上的分布。
它们在电磁辐射、天线理论和散射等问题中有广泛的应用。
3.地球物理学:球面谐波函数可以用于描述地球重力场和磁场的变化。
地球重力场和磁场的球谐展开可以帮助我们了解地球内部的结构和物理特性。
勒让德多项式球函数

第十一章勒让德多项式球函数本章讨论三维拉普拉斯方程在球坐标下的分离变量法,由此得到特殊函数:勒让德多项式、连带勒让德多项式和球谐函数,然后讨论它们的性质,最后讨论球函数的应用。
大纲要求:1.掌握球坐标下拉普拉斯方程的分离变量法2.掌握常点邻域的幂级数解法。
3.掌握勒让德多项式连带勒让德多项式,球函数的定义及基本性质4.掌握球函数在求解数理方程中的应用重点难点:1.球坐标下的分离变量法2.勒让德多项式的定义和基本性质3.连带勒让德多项式,球函数的定义4.球函数的应用第一节勒让德微分方程及勒让德多项式一、勒让德微分方程的导出考察三维拉普拉斯方程采用球坐标系,即:拉氏方程就变为:(1)首先,用分离变数法把表示距离的变数r与表示方向的变数θ和分离。
为此令代入(1)式得:用r2/RY遍乘各项并适当移项,即得:左边是r的函数,跟θ和无关。
右边定θ和的函数,跟r无关,两边相等。
只有同时等于一个常数,记为n(n+1),这就分离出两个方程:(2)(3)微分方程(2)即为欧勒型常微分方程,其解为:偏微分方程(3)叫做球函数方程,Y(θ,)称为球函数,进一步分离变数,以:代入球函数方程(3)得:用遍乘各项并适当移项,即得:左边是θ的函数,与无关,右边定的函数,跟θ无关,两边相等,只有等于一常数,记为l。
这样就分解为两个常微分方程。
(4)(5)先看关于Φ的方程,注意到自然周期条件:(6)方程(4)与自然周期条件(6)构成本征值问题,本征值是l=m2(m=0,1,2,3……)本征函数是:这样方程(5)应为:(7)通常令而代入(7)得:(8)一般将记为y(x).方程(8)为连带(缔合)勒让德微分方程。
如果球坐标的极轴是对称轴,则u与无关,从而Φ()与无关,即:m=0.在m=0的情况下,方程(8)成为:(9)这叫勒让德方程。
二、幂级数解和勒让德多项式的定义1、常点邻域上的级数解法在常微分方程理论中,对于二阶常微方程是存在一种解法,称为级数解法,把二阶常微分方程的解表为系数待定的幂级数,代入方程以逐个确定系数,这是一个比较普遍的方法,对方程并无特殊要求。
第四章-特殊函数(上)-勒让德多项式和球谐函数

因此,(2 n )!(2 n )!!(2 n 1 )!!
2、勒让德多项式的微分表示
Pl(x)21ll!ddxll (x21)l
(4.1.10)
上式通常又称为勒让德多项式的罗德里格斯(Rodrigues) 表示式.
下面证明表达式 (4.1.10) 和(4.1.7)是相同的.
【证明】 用二项式定理把 (x2 1)l展开
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 4.1
计算 P l ( 0 ) ,这应当等于多项式 P l ( x ) 的常数项.
如 l 为 2n 1(即为奇数)时, 则 P2n1 ( x)
只含奇 数次幂,不含常数项,所以
P2n1(0)0
(4.1.8)
l 2n (即为偶数)时.,则 P 2 n ( x ) 含有常数项,即 (4.1.7)中 k l 2 n 的那一项,所以
P2n(0)(1)n2(22 nn n!)n !!(1)n(2 (n 2n )1 !)!!! (4.1.9)
式中记号 ( 2 n ) ! ! ( 2 n ) ( 2 n 2 ) ( 2 n 4 ) L 6 4 2
而 ( 2 n 1 ) ! ! ( 2 n 1 ) ( 2 n 3 ) ( 2 n 5 ) L 5 3 1
(4.1.2) 式的解 Y ( , ) 与半径 r 无关,称为球谐函数
பைடு நூலகம்
,或简称为球函数.
球谐函数方程进一步分离变量,令 Y(,) () ()
得到关于 的常微分方程
sin 1 d d sind d l(l 1 )sim n2 2 0 (4.1.3)
称为 l 阶连带勒让德l 方程或缔合勒让德方程
.
令 xcos和 y(x)(x)
勒让德多项式及性质

例题2、以勒让德多项式为基本函数族,将函数
f ( x) 2 x 3 3x 4 在区间(-1,+1)上进行广义傅立叶展开。
1 1 2 P2 ( x) (3x 1) (3cos 2 1) 2 4 1 1 3 P3 ( x) (5x 3x) (5cos3 3cos ) 2 8 1 1 4 2 P4 ( x) (35x 30 x 3) (35cos 4 20cos 2 9) 8 64 1 1 P5 ( x) (63x5 70 x3 15x) (63cos5 35cos3 30cos ) 8 128 1 1 P6 ( x) (231x6 315x4 105x 2 5) (231cos 6 126cos 4 105cos 2 50) 16 512
前面已学:勒让德方程在x 1有自然边界条件: x 1 有限,从而构成 y 本征值问题,本征值是l (l 1), l 0,1, 2, 3..., 在l为整数条件下,勒让德方程 的两个线性独立特解y ( x ) a0 y0 ( x ) a1 y1 ( x )之一退化为l次多项式。 z l为2k (偶数): a y ( x) ~
l 2n (n 0,1, 2, ) l 2n 1
上式具有多项式的形式,故称
Pl ( )
为
l
阶勒让德多项式.勒让德多项式也称为第一类勒让德函数.
二、勒让德多项式
1、前几个勒让德多项式: (注意到 x cos ) P0 ( x) 1
P1 ( x) x cos
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 11.1
2、勒让德多项式的微分表示
1 dl Pl ( x) l ( x 2 1)l 2 l ! dx l
工程数学2012-CH10-勒让德多项式和球谐函数

由
2 d dy m 2 2 y=0 (1 − x ) + ω − 2 dx dx 1− x
令ω 2 =l (l + 1), 得
2 2 d y dy m 2 y=0 (1 − x ) 2 − 2 x + l (l + 1) − 2 dx dx (1 − x )
勒让德方程的通解为:
y ( x) = c0 y0 ( x) + c1 y1 ( x)
( −l )(l + 1) 2 (2 − l )(−l )(l + 1)(l + 3) 4 y0 ( x) = 1 + x + x + ⋅⋅⋅ + 2! 4! (2k − 2 − l )(2k − 4 − l ) ⋅⋅⋅ ( −l )(l + 1)(l + 3) ⋅⋅⋅ (l + 2k − 1) 2 k x + ⋅⋅⋅ (2k )! (1 − l )(l + 2) 3 (3 − l )(1 − l )(l + 2)(l + 4) 5 y1 ( x) = x + x + x − ⋅⋅⋅ + 3! 5! (2k − 1 − l )(2k − 3 − l ) ⋅⋅⋅ (1 − l )(l + 2)(l + 4) ⋅⋅⋅ (l + 2k ) 2 k +1 x + ⋅⋅⋅ (2k + 1)! (n − l )( n + l + 1) cn , 由达朗贝尔判别法和cn 递推关系cn + 2 = (n + 2)(n + 1) 对l ≠ 整数, 得泰勒级数的收敛半径 R = lim
球谐函数的性质

目录一般背景及注示正交变换加法定理表示定理加法定理的应用Rodrigues公式Funk-Hecke公式球谐函数的积分表示连带勒让德函数勒让德函数的性质微分方程球谐函数的拓展参考文献基本背景和记号:令()1,,q x x 是q 维欧几里得空间的一组笛卡尔坐标,这时我们有()()22221qx r x x ==++。
表达式 x r ξ= 这里 ()1,,1q ξξξξ==和 1)表示的是q 维单位球面上的笛卡尔系的点,记为q Ω,它的曲面元素为q d ω,其全部曲面为q ω,是由qq qd ωωΩ=⎰表示出来的。
由定义我们设2q ω=,接着我们有232;4ωπωπ==。
如果向量1,,q εε可以构成一个正交系,我们可以用<1>1;11,q q q q q t t t ξεεξ-=⋅-≤≤= 来表示q Ω上的点,而1q ξ-是由1,,q εε张成的空间的单位向量。
这时单位球面上的曲线元素可以写成()3211q q q d t dtd ωω--=-我们由上面可以得到 ()3122111q q q q t dtd ωω-+-Ω-=-⎰⎰上面积分式子的右边可以转化为()312120112212q q d q μμμ---⎛⎫⎛⎫ΓΓ ⎪ ⎪⎝⎭⎝⎭-=⎛⎫Γ ⎪⎝⎭⎰,当q=2,3,…。
<2>()21111222222qq q q q q q πωωω--⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭===⎛⎫⎛⎫⎛⎫ΓΓΓ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭记<3> 22212q q x x x ⎛⎫⎛⎫⎛⎫∂∂∂∆=+++ ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭为拉普拉斯算子,这时我们引入定义1:令()n H x 为q 维的n 次齐次多项式,同时满足()0q n H x ∆=这时称()1()()n n n nS H r H r ξξξ==为q 维的n 次(规则)球面调和函数。
由此我们马上可以得到:引理1: ()()()1nn n S S ξξ-=-令()n H x 和()m H x 是两个次数分别为n 和m 的齐次调和多项式,由格林定理我们可以得到()()()()10qnqm mqn n m q x H H H H d V H H m n d ξξω≤Ω=∆-∆=-⎰⎰, 同样地,在q Ω上n H 和m H 的法向导数分别为()()()()11m m n n r r H r mH H r nH r r ξξξξ==∂∂⎧⎫⎧⎫==⎨⎬⎨⎬∂∂⎩⎭⎩⎭和因此由定义(1)我们可以得到 引理2:对于m ≠n 时,有()()0qnmqS S d ξξωΩ=⎰,任何q 维的齐次多项式可以由下面式子代替(4) 110()(,,)()nj qn jq n j x Ax x H x --==∑其中11(,,)n j q A x x --是在点11,,q x x -的()n j -阶齐次多项式,应用拉普拉斯算子的形式 21()q q qx -∂∆=+∆∂ 得到(5) 2212()(1)()()jnn j q n qn j q q n j j j H x j j x A x A -----==∆=-+∆∑∑由系数相等我们的得到:12(2)(1)q n j n j A j j A ----∆=-++,因此,若已知n A 和1n A -,则所有的多项式j A 都可以知道,且线性无关的齐次调和多项式的数量与n A 和1n A -的系数的数量相等。
实球谐函数

实球谐函数
实球谐函数是一种特殊的函数,它在物理学、数学和工程学等领域中都有广泛的应用。
实球谐函数是一种描述三维空间中球对称性的函数,它可以用来描述球体内部和外部的物理现象,如电场、磁场、声波等。
实球谐函数是由勒让德多项式和球面谐函数组成的。
勒让德多项式是一种描述球对称性的函数,它可以用来描述球体内部和外部的物理现象。
球面谐函数是一种描述球面上的物理现象的函数,它可以用来描述球面上的电场、磁场、声波等。
实球谐函数的定义是:在三维空间中,如果一个函数满足以下条件,那么它就是实球谐函数:
1. 在球面上,函数的值是常数。
2. 在球面上,函数的梯度垂直于球面。
3. 在球面上,函数的拉普拉斯算子等于常数乘以函数本身。
实球谐函数在物理学中有广泛的应用。
例如,在电场中,实球谐函数可以用来描述电荷分布的形状和大小。
在磁场中,实球谐函数可以用来描述磁场的形状和大小。
在声波中,实球谐函数可以用来描述声波的传播方向和强度。
实球谐函数在数学中也有广泛的应用。
例如,在微积分中,实球谐
函数可以用来描述球体的体积和表面积。
在概率论中,实球谐函数可以用来描述球体内部的随机变量分布。
实球谐函数是一种非常重要的函数,它在物理学、数学和工程学等领域中都有广泛的应用。
通过研究实球谐函数,我们可以更好地理解三维空间中的物理现象,从而为科学技术的发展做出更大的贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 d ( x 1) d ( x 1) 1 2l 2 2l 2 2 (l !) dxl dxl 1 1 2 (l !)
d l 1 ( x 2 1)l d d l ( x 2 1)l 1 dxl 1 dx dxl dx
1 1 4 2 P4 ( x) (35 x 30 x 3) (35cos 4 20cos 2 9) 8 64 1 1 5 3 P5 ( x) (63x 70 x 15 x) (63cos 5 35cos 3 30cos ) 8 128
P6 ( x) 1 1 (231x 6 315 x 4 105 x 2 5) (231cos 6 126cos 4 105cos 2 50) 16 512
(4.1.2) 式的解 Y ( , ) 与半径 ,或简称为球函数.
(4.1.2)
r
无关,称为球谐函数
球谐函数方程进一步分离变量,令
Y ( , ) ( )( )
得到关于 的常微分方程
1 d d m2 sin l (l 1) 2 0 sin d d sin
称为 l 阶连带勒让德方程或缔合勒让德方程 l . 令
(4.1.3)
x cos
和
y( x) ( x)
把自变数从
换为
x ,则方程(4.1.3)可以化为下列
形式的 l 阶连带勒让德方程
d2 y dy m2 (1 x 2 ) 2 2 x l (l 1) y0 2 dx dx 1 x
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 4.1
计算 Pl (0) ,这应当等于多项式
Pl ( x) 的常数项.
则
如 l 为
2n 1(即为奇数)时,
P2 n 1 ( x)
只含奇 数次幂,不含常数项,所以
P2 n1 (0) 0
.
(4.1.8)
则 l 2n (即为偶数)时, P2 n ( x) 含有常数项,即 (4.1.7)中
2
(4.1.12)
,半径为
x2 1
zx
i
x x 1e
d i x 2 1ei d i( x)d
并注意到
2 1 ( x x 2 1ei )2 1 ( x 2 1)(1 ei2 ) 2 x x 2 1ei
2 x 2 1ei ( x x 2 1cos ) 2( x)( x x 2 1cos 让德多项式的积分表示
根据柯西积分公式的高阶导数,并取正方向积分有
f
(l )
l! f ( ) ( z) C ( z)l 1 d 2πi
容易证明微分表示(4.1.10)也可表示为环路积分形式
1 1 Pl ( x) 2πi 2l
C为
( 2 1)l C ( x)l 1 d
(2)模 (利用分部积分法证明)
N [Pl ( x)]2 dx
2 l 1 1
为了分部积分的方便,把上式的 Pl (x)用微分表示给出,则有
1 N 2l 2 2 (l !)
2 l
d l ( x 2 1)l d d l 1 ( x 2 1)l 1 dxl dx dxl 1 dx
(4.1.11)
z 平面上围绕 z x 点的任一闭合回路,
并取正方向.这叫作勒让德多项式的施列夫利积分表示式.
式(4.1.11)还可以进一步表为下述拉普拉斯积分.
1 π Pl ( x) ( x i 1 x 2 cos )l d π 0
【证明】 取 C 为圆周,圆心在 在 C 上有:
代入(4.1.11)得到
1 2π Pl ( x) ( x x 2 1 cos )l d 2π 0 1 π ( x i 1 x 2 cos )l d (4.1.12) π 0
这即为勒让德多项式的拉普拉斯积分表示. 从该积分还很容易看出
Pl (1) 1 Pl (1) (1)l
无关,则 m 0,即有
(4.1.4)
若所讨论的问题具有旋转轴对称性,即定解问题的解与
1 d d sin l (l 1) 0 sin d d
称为 l 阶勒让德 (legendre)方程.
(4.1.5)
同样若记
arc cos x, y( x) ( x)
1
[n(n 1) l (l 1)] Pl ( x)Pn (x)dx
1 1
因为上面等式左边的积分值为
(1 x 2 )[Pn ( x)Pl( x) Pl ( x)Pn ( x)] |1 1 0
所以当 n l 时,必然有
1
1 l
P ( x)Pn ( x)dx 0 成立.
d [(1 x 2 )Pl( x)] l (l 1)Pl ( x) 0 dx d [(1 x 2 )Pn ( x)] n(n 1)Pn ( x) 0 dx
两式相减,并在[-1,1] 区间上对x积分,得
d d 2 ( x)] Pl ( x) [(1 x 2 )Pn ( x)]}dx 1{Pn ( x) dx [(1 x )Pl dx
式(4.1.7)即为勒让德多项式的级数表示. 注意到 x cos , 故可方便地得出前几个勒让德多项式:
P0 ( x) 1
P1 ( x) x cos
1 1 2 P2 ( x) (3x 1) (3cos 2 1) 2 4 1 1 P3 ( x) (5 x3 3x) (5cos 3 3cos ) 2 8
2 l
dl 1 ( x 2 1)l dl 1 ( x 2 1)l dx l 1 1 dxl 1 dx
k l 2n
的那一项,所以
(2n)! n (2n 1)!! (4.1.9) P2 n (0) (1) 2 n (1) 2 n !n ! (2n)!! 式中记号 (2n)!! (2n)(2n 2)(2n 4)6 4 2
n
而 (2n 1)!! (2n 1)(2n 3)(2n 5)5 3 1
(2 因此, n)! (2n)!! (2n 1)!!
2、勒让德多项式的微分表示
1 dl Pl ( x) l ( x 2 1)l 2 l ! dxl
(4.1.10)
上式通常又称为勒让德多项式的罗德里格斯(Rodrigues) 表示式.
下面证明表达式 (4.1.10) 和(4.1.7)是相同的.
l 次求导过程中成为零,所以只需保留幂次 (2l 2k ) l l l k 的项,即 的项,应取 kmax [ ] ,并且注意到 2 2
dl 2l 2 k l 2k x (2l 2k )(2l 2k 1) [2l 2k (l 1)]x l dx
则上述方程也可写为下列形式的 l 阶勒让德方程
d 2 dy [(1 x ) ] l (l 1) y 0 dx dx
(4.1.6)
4.1.2 勒让德多项式的表示 1. 勒让德多项式的级数表示
我们知道:在自然边界条件下,勒让德方程的解 Pl ( x ) 为
l [ ] 2
(2l 2k )! l 2k Pl ( x) (1) l x 2 k !(l k )!(l 2k )! k 0
第四章 特殊函数(上)
——勒让德多项式 球函数
本章主要内容:勒让德多项式的来源、定 义、性质、生成与递推公式,球谐函数。
在球坐标系下对拉普拉斯方程分离变量径向部分得到 欧拉型常微分方程
d2 R dR 2 r 2r l (l 1) R 0 2 dr dr
和球谐函数方程
(4.1.1)
1 Y 1 2Y l (l 1)Y 0 sin 2 2 sin sin
n ,l
1 0
1 1
(4.2.2)
(n l ) (n l )
(4.2.3)
n l 时满足 Pn ( x)Pl ( x)dx 0 ,
称为正交性. 相等时可求出其模
Nl
2 1 l
1
2 P ( x)dx 2l 1
(l 0,1,2,)
(4.2.4)
下面给出公式(4.2.2),及其模(4.2.4)的证明 【证明】 (1)正交性 勒让德多项式必然满足勒让德方程(4.1.6),故有
【证明】 用二项式定理把
( x 2 1) l展开
l 1 2 l 1 l l! 1 2 l k k k ( x 1) l ( x ) (1) (1) l x 2l 2 k 2 l l! 2 l! k 0 (l k )!k! 2 k!(l k )! k 0
把上式对x求导 l 次.凡是幂次 (2l 2k ) l 的项在
(4.1.13)
利用拉普拉斯积分表示(4.1.12),还可以证明
Pl ( x) 1
,
(1 x 1)
x
(4.1.14)
【证明】 如从 ,则
回到原来的变量 , x
cos
1 π l Pl (cos ) cos i sin cos d π 0 1 π l Pl (cos ) cos i sin cos d π 0 l /2 1 π 2 2 2 0 cos sin cos d π l /2 1 π 1 π 2 2 0 cos sin d π 0 d 1 π
4.2 勒让德多项式的性质
