专升本 高数.ppt
合集下载
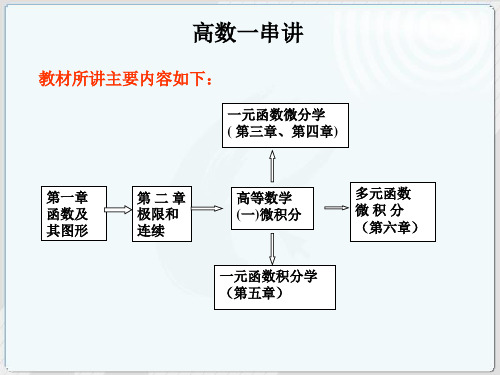
专升本高等数学(文史财经类)复习课件

第二节.函数的性质 一带而过
1. 函数的奇偶性 注意:定义域关于原点对称
奇函数:f (x) f (x) 图像关于原点对称
偶函数:f (x) f (x) 图像关于y轴对称
2. 函数的单调性
已知 y 当 x1 x2 当 x1 x2
f (x), xa,b, 若有
时,若有f x1 f x2
运算顺序:1 x2 3 2正弦函数sin 3指数运算e 分解顺序:1 y e 2 sin 3 x2 3
(反过来)
方法:从最后一层运算开始分解,每分解一步去掉一 层运算,分解到基本初等函数的和差积商为止。
例2 将下列复合函数分解为简单函数
1.y cos2 x
2.y x2 2x
3 y cos 2x 1 4 y ln sin x3
lim ex , 即当x 时,ex为正无穷大
x
lim 1 , 即当x 0时,1 为无穷大
x0 x
x
关于无穷大的说明
1、f (x) ,即f (x) 或
2、函数f (x)无穷大,不仅与函数有关,还与
变化趋势有关。如lim 1 ,而lim 1 1
x0 x
x3 x 3
3、无穷大实际上极限是不存在
1、只有0是可以作为无穷小的唯一的常数
2、无穷小与自变量的变化趋势有关,
例如:
lim
1
1
x1 x
例2:自变量x在怎样的变化过程中,下列函数为无穷小
(1)y 3x 1 无穷小的性质
(2) y 2x
(3) y (1)x 3
性质1 有限个无穷小的代数和为无穷小
性质2 有界函数与无穷小的乘积为无穷小
性质3 有限个无穷小的乘积为无穷小
例3
第一章函数、极限、连续(专升本专用PPT)-文档资料

2
六个常见函数的有界性: | sin x | 1; | cos x | 1; ( , ) | | arcsinx | | arctanx |
2
; | arccosx | ;[1,1] ; | arc cot x | ; ( , )
2
x 例2.判断函数f ( x) 的有界性 2 1 x x | x| | x| 1 解: 因为| f ( x) || | 2 2 1 x 1 x 2| x| 2 (1 x 2 2 | x |).所以函数f ( x)有界 .
y u是中间变量,y是因变量.
u , u 1 x 2
4 y就不是x的复合函数;复 合函数可分解为蕳单的函数
( 2)反函数 : 设函数y f ( x )的值域为Z f , 如果对Z f 中 任一y值从关系式y f ( x )中可确定惟一的一个 x值, 则称变量x为变量y的函数, 记为 : x ( y ), 其中 ( y )称为y f ( x )的反函数,习惯上y f ( x )的反 函数记为: y f 1 ( x )
f n ( x), y lim f (t , x) (1)极限形式的函数:y lim n tx
(2)积分形式的函数: y
5.非初等函数
x
0
f (t )dt ( f (t )连续 )
6.函数的简单性质 (1)奇偶性 设函数 f ( x )在区间x上有定义,如果对x X 恒有 f ( x ) f ( x ) (或f ( x ) f ( x )) 则称f(x)为偶函数(或f(x)为奇函数).偶函数f(x)的 图形对称于y轴,奇函数f(x)的图形对称于原点.
13ቤተ መጻሕፍቲ ባይዱ
六个常见函数的有界性: | sin x | 1; | cos x | 1; ( , ) | | arcsinx | | arctanx |
2
; | arccosx | ;[1,1] ; | arc cot x | ; ( , )
2
x 例2.判断函数f ( x) 的有界性 2 1 x x | x| | x| 1 解: 因为| f ( x) || | 2 2 1 x 1 x 2| x| 2 (1 x 2 2 | x |).所以函数f ( x)有界 .
y u是中间变量,y是因变量.
u , u 1 x 2
4 y就不是x的复合函数;复 合函数可分解为蕳单的函数
( 2)反函数 : 设函数y f ( x )的值域为Z f , 如果对Z f 中 任一y值从关系式y f ( x )中可确定惟一的一个 x值, 则称变量x为变量y的函数, 记为 : x ( y ), 其中 ( y )称为y f ( x )的反函数,习惯上y f ( x )的反 函数记为: y f 1 ( x )
f n ( x), y lim f (t , x) (1)极限形式的函数:y lim n tx
(2)积分形式的函数: y
5.非初等函数
x
0
f (t )dt ( f (t )连续 )
6.函数的简单性质 (1)奇偶性 设函数 f ( x )在区间x上有定义,如果对x X 恒有 f ( x ) f ( x ) (或f ( x ) f ( x )) 则称f(x)为偶函数(或f(x)为奇函数).偶函数f(x)的 图形对称于y轴,奇函数f(x)的图形对称于原点.
13ቤተ መጻሕፍቲ ባይዱ
专升本高数多元函数微分PPT课件

开 域 :不 包 括 边 界 在 内 的 区 域 称 为 开 域 .
无 界 区 域 有 界 区 域 :如 果 区 域 延 伸 到 无 穷 远 处 , 则称为无界区域,否则称为有界区域.
邻 域 :把 满 足 不 等 式 (x x0)2 ( y y0)2 ( 0) 的 点 P (x, y ) 的 全 体 称 为 点 P0 ( x0 , y0 ) 的 邻 域 . 它 是 以 点 P0 为 中 心 , 为 半 径 的 圆 形 开 区 域 , 称 不 包 含 点 P0 的 邻 域 为 无 心 邻 域 .
数的极限 lim f (x, y) A存在.反过来,如果当 P(x, y) 沿 xx0
y y 0
两条不同路径趋近于点 P0 (x0, y0 )时,函数 f (x, y) 趋近于不 同的值, 则可以断定函数的二重极限不存在.
y
Байду номын сангаас
P0
p o
x
2 . 多元函数的连续性
定义 设二元函数 z f (x, y)在点 P0 (x0 , y0 )的某个 邻域内有定义,若
点M (x, y,z).所有这样确定的点的集 x
合就是二元函数 z f (x, y)的图形,由 上一章知,通常是一张空间曲面(如 图 11.1-3 所示).
z zf(x,y) M(x,y,z)
o y
P(x,y) 图11.1-3
11.1.2 二元函数的极限与连续
1. 二 元 函 数 的 极 限
定 义 设 二 元 函 数 z f (x, y) , 如 果 当 点(x, y) 以 任 何
lim f (x, y) f (x0 , y0 )
(1)
xx0
y y0
则称二元函数 z f (x, y)在点 P0 (x0 , y0 )处连续.若函数
专转本高数知识点 讲义课件 第一讲:极限、洛比塔法则

n 例如, 数列 x n ; 有界 数列 x n 2 n . 无界 n1 数轴上对应于有界数列的点 x n 都落在闭区间
[ M , M ]上.
2.唯一性
定理2 每个收敛的数列只有一个极限.
问题: 函数 y f ( x ) 在 x 的过程中, 对应 函数值 f ( x ) 无限趋近于确定值 A.
1
y x2 1
o
x
分x 0和x 0两种情况分别讨论
x从左侧无限趋近 x0 , 记作x x0 0; x从右侧无限趋近 x0 , 记作x x0 0;
左极限
0, 0, 使当x0 x x 0时,
恒有 f ( x ) A . 记作 lim f ( x ) A 或 f ( x 0 0) A.
A
o
x0
x0
x0
x
显然, 找到一个后, 越小越好.
x 1 2. 例4 证明 lim x 1 x 1
2
证
函数在点x=1处没有定义.
任给 0,
x2 1 f ( x) A 2 x 1 x 1
要使 f ( x ) A ,只要取 ,0
x
0, X 0, 使当x X时, 恒有 f ( x ) A .
lim f ( x ) A且 x lim f ( x ) A. 定理 : lim f ( x) A x x
二、自变量趋向有限值时函数的极限
问题: 函数 y f ( x ) 在 x x0 的过程中 , 对应 函数值 f ( x ) 无限趋近于确定值 A.
满足不等式 f ( x ) A ,那末常数 A 就叫函数
专升本高数定积分的应用PPT课件

d
面积 A [( y) ( y)]dy . c
图6.1.3
图6.1.4
例 1. 求 y sin x , y cos x , x 0, x π 所围图形的面积.
2
解 作出简图(如图 6.1.5 所示),利用微元法求面积 A
π
π
A
4 0
(cos
x
sin
x)dx
2 π
(sin
x
cos
2
2
2
因此
V
R
A(x)dx
R 1 (R2 x2 ) tandx
R
R 2
1 2
tan
R2
x
1 3
x3
R R
=
2 3
R3
tan
.
注意,此题也可以用过 y轴上的点 y作垂直于 y轴的平面截
立体所得的截面来计算.
6.1.4 用定积分求平面曲线的弧长
设 一 曲 线 yf(x )在 [a ,b ]上 具 有 一 阶 连 续 的 导 数 f'(x ), 我 们 来 计 算 从 x a 到 x b 的 一 段 弧 的 长 s 度 ( 如 图 8 . 1 . 1 0所 示 ) .
A 1
r2 ( )d .
2
图6.1.6
图6.1.7
例 4 求由曲线r 2cos 2 所围图形的面积.
解 作简图(如图 6.1.7 所示),由于图形的对称性,
只需计算S1,再 8 倍即可,点 A的幅角为0,点 O的幅角为
π ,且 由 0变到 π 时,恰好画出弧 AO.所以
4
4
π
π
S
8S1
仍采用微元法,取 x为积分变 量 , x [a,b] , 在 微 小 区 间 [x, x dx]内,用切线段 MT 近似 代替小弧段 MN ,得弧长微元为
面积 A [( y) ( y)]dy . c
图6.1.3
图6.1.4
例 1. 求 y sin x , y cos x , x 0, x π 所围图形的面积.
2
解 作出简图(如图 6.1.5 所示),利用微元法求面积 A
π
π
A
4 0
(cos
x
sin
x)dx
2 π
(sin
x
cos
2
2
2
因此
V
R
A(x)dx
R 1 (R2 x2 ) tandx
R
R 2
1 2
tan
R2
x
1 3
x3
R R
=
2 3
R3
tan
.
注意,此题也可以用过 y轴上的点 y作垂直于 y轴的平面截
立体所得的截面来计算.
6.1.4 用定积分求平面曲线的弧长
设 一 曲 线 yf(x )在 [a ,b ]上 具 有 一 阶 连 续 的 导 数 f'(x ), 我 们 来 计 算 从 x a 到 x b 的 一 段 弧 的 长 s 度 ( 如 图 8 . 1 . 1 0所 示 ) .
A 1
r2 ( )d .
2
图6.1.6
图6.1.7
例 4 求由曲线r 2cos 2 所围图形的面积.
解 作简图(如图 6.1.7 所示),由于图形的对称性,
只需计算S1,再 8 倍即可,点 A的幅角为0,点 O的幅角为
π ,且 由 0变到 π 时,恰好画出弧 AO.所以
4
4
π
π
S
8S1
仍采用微元法,取 x为积分变 量 , x [a,b] , 在 微 小 区 间 [x, x dx]内,用切线段 MT 近似 代替小弧段 MN ,得弧长微元为
专升本(高数—)第五章多元函数微积分学PPT课件

第七节 二重积分的应用
*
2
考试点津:
• 本讲出题在18分—26分之间,本讲内容是 一元函数微分内容的延伸,一般在选择题、 填空题、解答题中出现。
• 本讲重点:
(1)二元函数的偏导数和全微分。
(2)二元函数的有关极值问题及应用。 (3)会计算二重积分
• 建议重点复习前几年考过的试题,把握考 试重心和知识点,重在模仿解题。
成人高考高数一辅导
•
College of Agriculture & Biological Engineering
*
1
第五章 多元函数微积分学 (11年考了22分)
第一节 多元函数、极限和连续 第二节 偏导数与全微分 第三节 二元函数的极值 第四节 二重积分的概念和性质 第五节 直角坐标系下二重积分的计算 第六节 极坐标系下二重积分的计算
可 以 证 明 ,一 元 函 数 关 于 极 限 的 运 算 法 则 仍 适 用 于 多 元 函 数 ,即 多 元 连 续 函 数 的 和 、差 、积 为 连 续 函 数 ,在 分 母 不 为 零 处 ,连 续 函 数 的 商 也 是 连 续 函 数 ,多 元 函 数 的 复 合 函 数 也 是 连 续 函 数 .由 此 还 可 得 出 如 下 结 论 : 一 切 多 元 初等函数在其定义区域内是连续的.
(4)最大值和最小值定理
在有界闭区域D上的多元连续函数,在D上至少取得它的最大 值和最小值各一次.
(5)介值定理
在有界闭区域D上的多元连续函数,如果在D上取得两个不同的
函数值,则它在D上取得介于这两值之间的任何值至少一次.分
(一) 偏导数
1. 偏导数的定义
定义 设函数 z f (x, y)在点(x0, y0 )的某一邻域内有 定义,当 y固定在 y0,而 x在 x0处有增量x时,相应地函 数有增量 f (x0 x, y0 ) f (x0, y0 ),如果极限
专升本高数多元函数微分ppt

z f (x, y) 在区域 D 上每一点都连续,则称函数 f (x, y) 在
区域 D 上连续.
若令 x x0 x , y y0 y ,则上述定义中的( 1)式 可写成
lim [ f ( x0 x, y0 y ) f ( x0 , y0 )] 0 x0 y0
d f ( x, y0 ) x x0 即 dx
f x ( x0 ,y0 ) ,就是这条曲线 Cx 在点 M0 处的切线 M 0 Tx 对 x 轴的
斜率(如图 11.2-1),即
f x ( x0 , y0 ) tan .
f 同理, y ( x0 ,y0 ) 是曲面 z f (x, y) 与平面 x x0 的交线 C y
2011年
2010年
x z 25.设函数 z ln(x y ) ,则 y y
A.
x y( x y)
B.
xln( x y ) y2
ln( x y) x C. y y( x y)
xln( x y ) x D. 2 y y( x y)
x 37.函数 z (1 y) 在点 (1, 1) 处的全微分 dz ________.
z f , , z y , f y ( x, y ) . y y
显然,偏导数的概念可推广到三元和三元以上的函数.
求多元函数的偏导数的方法:因为这里只有一个自变量在 变化,可以把其它自变量被看成是固定的常数,所以仍然是 一元函数的导数.
例
z z x 求 z xy 的偏导数 , . x y y
即பைடு நூலகம்
lim z 0 . x0 y0
这里 z 为函数 f (x, y) 点 ( x0 , y0 ) 处的全增量,即 z f ( x0 x, y0 y ) f ( x0 , y0 ) .
区域 D 上连续.
若令 x x0 x , y y0 y ,则上述定义中的( 1)式 可写成
lim [ f ( x0 x, y0 y ) f ( x0 , y0 )] 0 x0 y0
d f ( x, y0 ) x x0 即 dx
f x ( x0 ,y0 ) ,就是这条曲线 Cx 在点 M0 处的切线 M 0 Tx 对 x 轴的
斜率(如图 11.2-1),即
f x ( x0 , y0 ) tan .
f 同理, y ( x0 ,y0 ) 是曲面 z f (x, y) 与平面 x x0 的交线 C y
2011年
2010年
x z 25.设函数 z ln(x y ) ,则 y y
A.
x y( x y)
B.
xln( x y ) y2
ln( x y) x C. y y( x y)
xln( x y ) x D. 2 y y( x y)
x 37.函数 z (1 y) 在点 (1, 1) 处的全微分 dz ________.
z f , , z y , f y ( x, y ) . y y
显然,偏导数的概念可推广到三元和三元以上的函数.
求多元函数的偏导数的方法:因为这里只有一个自变量在 变化,可以把其它自变量被看成是固定的常数,所以仍然是 一元函数的导数.
例
z z x 求 z xy 的偏导数 , . x y y
即பைடு நூலகம்
lim z 0 . x0 y0
这里 z 为函数 f (x, y) 点 ( x0 , y0 ) 处的全增量,即 z f ( x0 x, y0 y ) f ( x0 , y0 ) .
专升本高等数学课件 第一章

称为由①, ②确定的复合函数, u 称为中间变量.
[说明] 通常 f 称为外层函数,g 称为内层函数.
注意:1.不是任何两个函数都可以复合成一个复 合函数的;
例如 y arcsin u, u 2 x2; y arcsin(2 x2 )
2.复合函数可以由两个以上的函数经过复 合构成.
例如 y cot x , y u, u cot v, v x .
例如,
2x 1,
f
(
x)
x2
1,
x0 x0
y x2 1
y 2x 1
• 隐函数:函数 y 与自变量 x 的对应法则用一个方程 F(x, y) 0
表示的函数,如x2 y2 1 0 .
二、函数的性质
1.函数的单调性
设函数 f ( x)的定义域为D, 区间I D, 如果对于区间 I 上任意两点 x1及 x2 , 当x1 x2时, (1) 若恒有 f ( x1 ) f ( x2 ),
o
例如,x2 y2 a2.
(x, y)
x
x
D
定义: 点集C {( x, y) y f ( x), x D} 称为
函数y f ( x)的图形.
3、函数的表示法
解析法:用解析表达式表示函数关系
表格法:用列表的方法来表示函数关系
图示法:用平面直角坐标系上的曲线来 表示函数关系
几个特殊的函数举例
反余弦函数 y arccos x
y arccos x
反正切函数 y arctan x
y arctan x
反余切函数 y arccot x
y arccot x
幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数.
专升本-高数一-PPT课件
例 2.下列各函数中,互为反函数的是(
n t, x o t cy (1 ) . y a x
)
1 x , 1 y ( ) 1 - x (2) .y2 2
知识点:反函数 求反函数的步骤是:先从函数 y f ( x ) 中解出 x f 1 ( y ) ,再置换 x 与
y ,就得反函数 y f 1 ( x ) 。
故函数的定义域为:{( x , y ) | x 0 且 x y 0} (2)要使函数有意义必须满足
故
x2 x 2 0 x 1 或 x 2 ,即 , x 2 x20 D ( 2, 1) (2, ) .
二、 极限
1.概念回顾
2、 极限的求法
利用极限四则运算、 连续函数、重要极限、无穷小代换、洛比达法则等 例 5: 求 lim
x
x5 . x2 9
1 5 1 5 2 lim( 2 ) x5 x x x 0 0. 解: lim 2 lim x x x x 9 x 9 9 1 1 2 lim(1 2 ) x x x 知识点:设 a0 0, b0 0, m, n N ,
数。
: D g ( D ) D f: D f( D ) g 1 1 1
f g : D f [ g ( D ) ]
例 1.下列函数中,函数的图象关于原点对称的是( (1) y 2 x 2 1 ; (3) y x 1 . 知识点: 函数的奇偶性 (2) y x 3 2sin x ;
则 lim
am x x b x n n
m
m a bn a1 x a0 0 b1 x b0
mn mn mn
专升本高等数学课件 第三章

满足 F(x) f (x) 或 dF(x) f (x) dx,则称 F (x) 为f (x) (或 f (x)dx)在区间 I 上的一个原函数 .
[例] sin x cos x sin x 是cos x 的原函数. ln x 1 ( x 0)
x ln x 是 1 在区间(0,)内的原函数.
(11) csc x cot xdx csc x C
(12) exdx ex C
(13)
axdx
ax C ln a
[例5]求积分
dx x3
.
[解]
dx x3
x3dx x31 C 31
1 2x2 C.
[例6]求积分 x2 xdx.
5
[解]
x2 xdx x2dx
x
1 2
d(1 2ln x)
1 2ln x
du u
ln
|
u
|
C
[例10] 求
e3
x
dx .
x
[解] 原式 = 2 e3 x d x
凑
2 e3 x d(3 x ) 3
2e3 x C 3
eudu eu C
[例11] 求 sin3 xdx . [解] 原式 = sin2 x sin x dx (1 cos2 x) dcos x
第三章 一元函数积分学
微分法: F(x) ( ? ) 互逆运算
积分法: ( ? ) f (x)
第一节 不定积分的概念与性质
一、原函数与不定积分的概念 二、基本积分表 三、不定积分的性质 四、小结
一、原函数与不定积分的概念
1.[定义1] 若在区间 I 上定义的两个函数 F (x) 及 f (x)
(
x
a)
[例] sin x cos x sin x 是cos x 的原函数. ln x 1 ( x 0)
x ln x 是 1 在区间(0,)内的原函数.
(11) csc x cot xdx csc x C
(12) exdx ex C
(13)
axdx
ax C ln a
[例5]求积分
dx x3
.
[解]
dx x3
x3dx x31 C 31
1 2x2 C.
[例6]求积分 x2 xdx.
5
[解]
x2 xdx x2dx
x
1 2
d(1 2ln x)
1 2ln x
du u
ln
|
u
|
C
[例10] 求
e3
x
dx .
x
[解] 原式 = 2 e3 x d x
凑
2 e3 x d(3 x ) 3
2e3 x C 3
eudu eu C
[例11] 求 sin3 xdx . [解] 原式 = sin2 x sin x dx (1 cos2 x) dcos x
第三章 一元函数积分学
微分法: F(x) ( ? ) 互逆运算
积分法: ( ? ) f (x)
第一节 不定积分的概念与性质
一、原函数与不定积分的概念 二、基本积分表 三、不定积分的性质 四、小结
一、原函数与不定积分的概念
1.[定义1] 若在区间 I 上定义的两个函数 F (x) 及 f (x)
(
x
a)
高升专 数学课件

2
a 2 2ab b 2
(a b)(a ab b ) a b
2 2 3
3
第一章
基础知识
,
(3)因式分解(整式乘法的逆运算) 因式分解的含义 将一个多项式转化成单项式或几个整式相乘的 形式,叫因式分解。如 a 2 b 2 (a b)( a b) 因式分解的原则: 1.从加减形式化简为乘除形式; 2.结果是否使最简形式(不能再约分)。 因式分解的方法: 主要有公式法、十字相乘法、分组分解法等。
,
当n>3时,使用分组分解法,分组后,再按 照n=2、n=3的方法继续分解。 第三步:检查因式分解是否完成,结果是否是最简 形式。 注意:并不是所有的多项式都能够在实数范围内分解。
高升专《 数学》 第一讲 (上)
第一章 基础知识
讲师:张国强
第一章 基础知识
例1-1:对下列式子迚行因式分解:
①
, ,
,
,
第一章
基础知识
,
因式分解的步骤 第一步:提取公因式,将共同的部分提取出来。 第二步:按照项数的多少使用不同的方法; 当n=2时,使用公式法为主,主要运用平方差、 立方差立方和公式; 当n=3时,使用完全平方公式与十字相乘法为主。 如果这两种方法无法使用,在求助于求根公式法, 其结果带有根号。
,
第一章
基础知识
(2)整式乘法:用乘法法则和乘法公式进行运算。 乘法法则:(a b)( m n)
a ( m n) b( m n) am an bm bn
平方差公式: (a b)( a b) a 2
b
2
( 完全平方公式: a b)
立方和(差)公式:
专升本 高数 PPT课件

二、极限 4.极限存在准则
单调有界数列必有极限 两面夹定理
5.两个重要极限
6.无穷小与无穷大:定义、关系、性质、无穷小的比较
极限与无穷小关系、等价无穷小替换定理(整式替换、 常见等价无穷小代换)
Hale Waihona Puke 第一章 函数、极限与连续 知识梳理
三、连续 1.定义:两个定义、左右连续、连续充要条件 2.运算性质:四则运算
定义域 自变量 因变量(函数) 函数值 值域
第一章 函数、极限与连续 知识梳理
一、函数 1.概念 (2)函数三要素
定义域 对应法则 值域 (3)函数的表示方法
图像法 表格法
分段函数 公式法用参数方程确定的函数
隐函数(显函数)
第一章 函数、极限与连续
知识梳理
定义域D关于原点对称
一、函数
高等数学辅导讲义(专升本)
• 第一章 函数、极限与连续 15%
• 第二章 一元函数的微分学 20%
• 第三章 一元函数的积分学 20%
• 第四章 多元函数微积分 15%
• 第五章 常微分方程
15%
• 第六章 无穷级数
10%
• 第七章 向量代数与空间解析几何5%
第一章 函数、极限与连续
(重点)
第一章 函数、极限与连续
复合函数的连续性 3.间断点及其分类:第一类:可去、跳跃
第二类 4.闭区间上连续函数的性质:最值性
介值性 零点定理
5. 初等函数 六种基本初等函数:
第一章 函数、极限与连续 知识梳理
六种基本初等函数 • 常数函数:定义域、值域、奇偶性、周期性、单调性 • 幂函数: • 指数函数: • 对数函数: • 三角函数:六个(正割函数、余割函数) • 反三角函数:四个
专升本高数第二章导数-PPT课件

f( x )f( x ) 0 导数的一个等价定义: f ( x )lim 0 x x 0 x x 0
左、右导数
设函数 y f (x )在点 x 如果 0的某个邻域内有定义
f (x x ) f (x y 0 0) 左极限 lim lim 存在,那 x 0 x 0 x x 称此极限值为函数 y f (x )在点 x 0 处的左导数。
2 x e b( 1 b ) f ( 0 ) l i m 2 x 0 x
f ( 0 ) f ( 0 ) , a 2
(二) 曲线的切线方程及法线方程
设 曲 线 的 方 程 为 y f() x , 若 f() x在 x 处 可 导 , 0 则 曲 线 在 点 M ( x ,y ) 处 的 切 线 方 程 为 0 0 y y f ( x ) ( x x ) 0 0 0
仍是 x 的函数,称为 f (x)的导函数。
1. 基本导数表
x x
1 c 0 , ( x ) x
x x
( aa ) l n a , ( e ) e
1 1 ( l o g x ) , ( l n x ) a x l n a x
( s i n x ) c o s( x , c o s x )s i n x 2 2 ( t a n x ) s e c x , ( c o t x ) c s c x ( s e c x ) s e c x t a n x , ( c s c x ) c s c x c o t x
第二章 一元函数微分学
§2.1. 导数与微分
(一) 导数的概念
我们再用极限来研究变量变化 的快慢程度,这即是微分学中 的重要概念—导数。
左、右导数
设函数 y f (x )在点 x 如果 0的某个邻域内有定义
f (x x ) f (x y 0 0) 左极限 lim lim 存在,那 x 0 x 0 x x 称此极限值为函数 y f (x )在点 x 0 处的左导数。
2 x e b( 1 b ) f ( 0 ) l i m 2 x 0 x
f ( 0 ) f ( 0 ) , a 2
(二) 曲线的切线方程及法线方程
设 曲 线 的 方 程 为 y f() x , 若 f() x在 x 处 可 导 , 0 则 曲 线 在 点 M ( x ,y ) 处 的 切 线 方 程 为 0 0 y y f ( x ) ( x x ) 0 0 0
仍是 x 的函数,称为 f (x)的导函数。
1. 基本导数表
x x
1 c 0 , ( x ) x
x x
( aa ) l n a , ( e ) e
1 1 ( l o g x ) , ( l n x ) a x l n a x
( s i n x ) c o s( x , c o s x )s i n x 2 2 ( t a n x ) s e c x , ( c o t x ) c s c x ( s e c x ) s e c x t a n x , ( c s c x ) c s c x c o t x
第二章 一元函数微分学
§2.1. 导数与微分
(一) 导数的概念
我们再用极限来研究变量变化 的快慢程度,这即是微分学中 的重要概念—导数。
专升本高等数学课件 第四章

当n 2时,n元函数统称为多元函数.
多元函数中同样有定义域、值域、自变量、因变量 等概念.
【例1】求 f ( x, y) arcsin(3的定x义2 域y2.) x y2
【解】 3 x2 y2 1 x y2 0
2 x2 y2 4
x
y2
所求定义域为 D {(x, y) | 2 x2 y2 4, x y2}.
偏导数 , 记为
z , y
f , y
zy ,
f y ( x, y) , f2( x, y)
(2)【多元函数的偏导数】
偏导数的概念可以推广到二元以上函数
[例如] 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的
偏导数定义为
x x
x
x
x
fy(x, y, z) ? fz(x, y, z) ?
f (x x, y) f (x, y) A x o(| x |),
lim f (x x, y) f (x, y) A z ,
x0
x
x
同理可得
B z . y
故
dz z x z y
x y
由此可见:可微 连续;可微 可偏导
⑵可导与可微的关系: ①一元函数:在某点 可导
可微.
②多元函数:各偏导数存在
2. 【混合偏导数相等的条件】
(1)【问题】 混合偏导数都相等吗? 答: 不一定相等
【补例】设
f
( x,
y)
x3 y x2 y2
0
( x, y) (0,0) ( x, y) (0,0)
求 f ( x, y)在点(0,0)的二阶混合偏导数.
[注意]分段函数
在分界点的偏导 数要用定义求得.
多元函数中同样有定义域、值域、自变量、因变量 等概念.
【例1】求 f ( x, y) arcsin(3的定x义2 域y2.) x y2
【解】 3 x2 y2 1 x y2 0
2 x2 y2 4
x
y2
所求定义域为 D {(x, y) | 2 x2 y2 4, x y2}.
偏导数 , 记为
z , y
f , y
zy ,
f y ( x, y) , f2( x, y)
(2)【多元函数的偏导数】
偏导数的概念可以推广到二元以上函数
[例如] 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的
偏导数定义为
x x
x
x
x
fy(x, y, z) ? fz(x, y, z) ?
f (x x, y) f (x, y) A x o(| x |),
lim f (x x, y) f (x, y) A z ,
x0
x
x
同理可得
B z . y
故
dz z x z y
x y
由此可见:可微 连续;可微 可偏导
⑵可导与可微的关系: ①一元函数:在某点 可导
可微.
②多元函数:各偏导数存在
2. 【混合偏导数相等的条件】
(1)【问题】 混合偏导数都相等吗? 答: 不一定相等
【补例】设
f
( x,
y)
x3 y x2 y2
0
( x, y) (0,0) ( x, y) (0,0)
求 f ( x, y)在点(0,0)的二阶混合偏导数.
[注意]分段函数
在分界点的偏导 数要用定义求得.
专升本 高等数学 第三章 PPT

M 0 M 的极限位置 M 0T 就定义为曲
L M0
y
y f (x) M N B T
o
线 L 在点 M 0 处的切线 . 设函数 y f ( x) 的图像为曲线 L(如上图) , M 0 ( x0 , f ( x0 )) 和 M ( x, f ( x)) 为曲线 L 上的两点,它们到 x 轴的垂足分别为 A 和 B,作 M 0 N 垂直 BM 并交 BM 于 N, 则 M 0 N Δx x x0 ,
也记为
f ( x0 Δx) f ( x0 ) Δy lim 即 f ( x0 ) lim x0 Δx x0 Δx
df ( x) dy y ' x x0 , 或 , dx xx0 dx xx
0
.
如果极限不存在,我们说函数 y f ( x) 在点 x0 处不可导. 如果固定 x0 ,令 x0 Δx = x ,则当 Δx 0 时, 有 x x0 ,故函数在 x0 处的导数 f ( x0 ) 也可表为
(3)取极限: y lim
y . x 0 x
例 7 求函数 y C (C 是常数)的导数. 解 (1)求增量:因为 y C ,即不论 x 取什么值, y 的值总等于 C ,所以 y 0 ;
y (2) 算比值: 0 ; x y lim 0 0 . x 0 x x 0
二、导数的概念
1.导数的定义
设函数 y f ( x) 在点 x0 的某一邻域内有定义,当自 变量 x 在 x0 处有增量 Δx (Δx 0, x0 Δx 仍在该邻域内)时, 相应地函数有增量 Δy f ( x0 Δx ) f ( x0 ) ,如果 Δ y 与 Δy Δ x 之比 当 Δ x 0 时,极限 Δx f ( x0 Δx) f ( x0 ) Δy lim lim Δx0 Δx Δx0 Δx 存在,那么这个极限值称为函数 y f ( x) 在点 x0 的导数. 并且说,函数 y f ( x) 在点 x0 处可导,记作 f ( x0 ) ,
L M0
y
y f (x) M N B T
o
线 L 在点 M 0 处的切线 . 设函数 y f ( x) 的图像为曲线 L(如上图) , M 0 ( x0 , f ( x0 )) 和 M ( x, f ( x)) 为曲线 L 上的两点,它们到 x 轴的垂足分别为 A 和 B,作 M 0 N 垂直 BM 并交 BM 于 N, 则 M 0 N Δx x x0 ,
也记为
f ( x0 Δx) f ( x0 ) Δy lim 即 f ( x0 ) lim x0 Δx x0 Δx
df ( x) dy y ' x x0 , 或 , dx xx0 dx xx
0
.
如果极限不存在,我们说函数 y f ( x) 在点 x0 处不可导. 如果固定 x0 ,令 x0 Δx = x ,则当 Δx 0 时, 有 x x0 ,故函数在 x0 处的导数 f ( x0 ) 也可表为
(3)取极限: y lim
y . x 0 x
例 7 求函数 y C (C 是常数)的导数. 解 (1)求增量:因为 y C ,即不论 x 取什么值, y 的值总等于 C ,所以 y 0 ;
y (2) 算比值: 0 ; x y lim 0 0 . x 0 x x 0
二、导数的概念
1.导数的定义
设函数 y f ( x) 在点 x0 的某一邻域内有定义,当自 变量 x 在 x0 处有增量 Δx (Δx 0, x0 Δx 仍在该邻域内)时, 相应地函数有增量 Δy f ( x0 Δx ) f ( x0 ) ,如果 Δ y 与 Δy Δ x 之比 当 Δ x 0 时,极限 Δx f ( x0 Δx) f ( x0 ) Δy lim lim Δx0 Δx Δx0 Δx 存在,那么这个极限值称为函数 y f ( x) 在点 x0 的导数. 并且说,函数 y f ( x) 在点 x0 处可导,记作 f ( x0 ) ,
专升本高数讲义课件PPT第十一讲和第十二讲__向量代数和空间解析几何

b
b
c
a
b
c
a
(b )
ab
三、向量与数的乘法
设 是一个数,向量a 与 的乘积a 规定为
(1) 0,
a
与a
同向,|
a
|
|
a
|
(2) 0,
a
0
(3) 0,
a
与a
反向,|
a
||
|
|
a
|
a
2a
1
a
2
数与向量的乘积符合下列运算规律:
(1)结合律:(a) ( a) ()a
例 1 求过三点A(2,1,4)、B(1,3,2)和 C (0,2,3)的平面方程.
解 AB {3, 4,6}
AC {B AC
{14, 9,1},
所求平面方程为 14( x 2) 9( y 1) (z 4) 0,
化简得 14x 9 y z 15 0.
1 空间平面及方程 2 空间直线及方程 3 空间曲面及方程 4 空间曲线方程
1.1、平面的点法式方程z
如果一非零向量垂直
于一平面,这向量就叫做
该平面的法线向量.
o
y
x
法线向量的特征: 垂直于平面内的任一向量.
已知
n {A, B, C},
M0( x0 , y0 , z0 ),
设平面上的任一点为 M( x, y, z)
求此平面方程.
解 设平面为 Ax By Cz D 0,
aA D 0, 将三点坐标代入得 bB D 0,
,
ay,
az },
b {bx , by , bz },
a b {ax bx ,ay by , az bz }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A,
收敛数列,发散数列
A lim f (x) A lim f (x)
x
x
A lim f (x) A lim f (x)
xa
xa
唯一性:limf (x) A, limf (x) B A B
性质保号性:flim( xf)
(x) A 0 f (x) 0 0且limf (x) limf
2.函数的简单性质 (1)函数的奇偶性
偶 偶 偶,偶 偶 偶,偶 偶 偶 奇偶性奇奇函偶数关奇于,原奇点对偶称 奇,偶函数关于y轴对称
(2)函数的有界性 上界、下界
(3)函数的周期性
可导奇函数的导函数是偶函数 可导偶函数的导函数是奇函数 奇函数的原函数是偶函数 偶函数的原函数不一定是奇函数
可导周期函数的导数是周期函数
第一章 函数、极限与连续 知识梳理
二、极限 4.极限存在准则
单调有界数列必有极限 两面夹定理
5.两个重要极限
6.无穷小与无穷大:定义、关系、性质、无穷小的比较
极限与无穷小关系、等价无穷小替换定理(整式替换、 常见等价无穷小代换)
第一章 函数、极限与连续 知识梳理
三、连续 1.定义:两个定义、左右连续、连续充要条件 2.运算性质:四则运算
(
x)
0
第一章 函数、极限与连续 知识梳理
二、极限 3.四则运算
注意:(1)有限次运算 (2) 若limf (x) A, limg (x)不存在,
则lim[f (x) g(x)]不存在
又若A 0,则lim[f (x)g(x)]不存在, lim[g (x) / f (x)]不存在
若limf (x),limg(x)都不存在, 则lim[f (x) g(x)],lim[f (x)g(x)], lim[f (x) / g(x)]不确定
定义域 自变量 因变量(函数) 函数值 值域
第一章 函数、极限与连续 知识梳理
一、函数 1.概念 (2)函数三要素
定义域 对应法则 值域 (3)函数的表示方法
图像法 表格法
分段函数 公式法用参数方程确定的函数
隐函数(显函数)
第一章 函数、极限与连续
知识梳理
定义域D关于原点对称
一、函数
奇 奇 奇,奇 奇 奇,奇 奇 奇
高等数学辅导讲义(专升本)
• 第一章 函数、极限与连续 15%
• 第二章 一元函数的微分学 20%
• 第三章 一元函数的积分学 20%
• 第四章 多元函数微积分 15%
• 第五章 常微分方程
15%
• 第六章 无穷级数
10%
• 第七章 向量代数与空间解析几何5%
第一章 函数、极限与连续
(重点)
第一章 函数、极限与连续
• 知识结构
概念
初等函数
函数
性质
复合函数
反函数
第一章 函数、极限与连续
• 知识结构
概念
无穷小 无穷大
性质
极限
重要极限
四则运算
存在准则
第一章 函数、极限与连续
• 知识结构
概念
闭区间 连续函数
性质
连续性
运算性质
间断点 及分类
第一章 函数、极限与连续 பைடு நூலகம்识梳理
一、函数 1.概念 (1)定义:y f (x), x D
复合函数的连续性 3.间断点及其分类:第一类:可去、跳跃
第二类 4.闭区间上连续函数的性质:最值性
介值性 零点定理
第一章 函数、极限与连续 知识梳理
六种基本初等函数 • 常数函数:定义域、值域、奇偶性、周期性、单调性 • 幂函数: • 指数函数: • 对数函数: • 三角函数:六个(正割函数、余割函数) • 反三角函数:四个
积化和差公式、和差化积公式
第一章 函数、极限与连续 知识梳理
二、极限
21.极.极限限的的性概质概念念函数数列极极限限::nlillxxmiimmaxffn((xx))
周期函数的原函数不一定是周期函数
(4)函数的单调性
第一章 函数、极限与连续 知识梳理
一、函数 3.反函数 定义域 值域 互换
y f (x), x D 与 y f 1(x), x M 关于 y x 对称
4.复合函数 外函数、内函数、中间变量 外函数的定义域与内函数的值域交集非空
5. 初等函数 六种基本初等函数:
