填数字问题乘除法

(小学奥数)乘除法数字谜(二)

5-1-2-3.乘除法數字謎（二）教學目標數字謎是杯賽中非常重要的一塊，特別是迎春杯，數字謎是必考的，一般學生在做數字謎的時候都採用嘗試的方式，但是這樣會在考試中浪費很多時間．本模組主要講乘除豎式數字謎的解題方法，學會通過找突破口來解決問題．最後通過例題的學習，總結解數字謎問題的關鍵是找到合適的解題突破口．在確定各數位上的數字時，首先要對填寫的數字進行估算，這樣可以縮小取值範圍，然後再逐一檢驗，去掉不符合題意的取值，直到取得正確的解答．知識點撥1.數字謎定義:一般是指那些含有未知數字或未知運算符號的算式．2.數字謎突破口：這種不完整的算式，就像“謎”一樣，要解開這樣的謎，就得根據有關的運算法則，數的性質（和差積商的位數，數的整除性，奇偶性，尾數規律等）來進行正確的推理，判斷．3.解數字謎：一般是從某個數的首位或末位數字上尋找突破口．推理時應注意：⑴數字謎中的文字，字母或其他符號，只取0~9中的某個數字；⑵要認真分析算式中所包含的數量關係，找出盡可能多的隱蔽條件；⑶必要時應採用枚舉和篩選相結合的方法（試驗法），逐步淘汰掉那些不符合題意的數字；⑷數字謎解出之後，最好驗算一遍．模組一、與數論結合的數字謎（1）、特殊數字【例 1】如圖，不同的漢字代表不同的數字，其中“變”為1，3，5，7，9，11，13這七個數的平均數，那麼“學習改變命運”代表的多位數是．1999998⨯学习改变命运变【考點】與數論結合的數字謎之特殊數字【難度】2星【題型】填空【關鍵字】學而思杯，4年級，第9題【解析】 “變”就是7，19999987285714÷=【答案】285714【例 2】右邊是一個六位乘以一個一位數的算式，不同的漢字表示不同的數，相同的漢字表示相同的數，其中的六位數是______ 。

杯小9望99999×赛赛希学【考點】與數論結合的數字謎之特殊數字【難度】3星【題型】填空【關鍵字】希望杯，4年級，初賽，20題【解析】賽×賽的個位是9，賽=3或7，賽=3，小學希望杯賽=333333，不合題意，舍去；故賽=7，小學希望杯賽=999999÷7=142857【答案】142857【例 3】右面算式中相同的字母代表相同的數字，不同的字母代表不同的數字，問A 和E 各代表什麼數字？E AE D E E E E E ×3C B【考點】與數論結合的數字謎之特殊數字【難度】3星【題型】填空例題精講【解析】由於被乘數的最高位數字與乘數相同，且乘積為EEEEEE ,是重複數字根據重複數字的特點拆分，將其分解質因數後為：=37111337EEEEEE E ⨯⨯⨯⨯⨯，所以3A =或者是7A =①若A ＝3，因為3×3＝9，則E ＝1，而個位上1×3＝3≠1，因此，A≠3。

乘除法数字谜(一)(含详细解析)

【考点】乘法数字谜【难度】2星【题型】填空
【关键词】走美杯，四年级，初赛，第12题，五年级，初赛，第11题
【解析】由知，“美”不为1，且“美”×“妙”<10，如果“美”为2，根据“美”×“学”的个位数为“妙”，那么“妙”为偶数，即为4，推出“学”为7，又由“Байду номын сангаас”+“学”=“数”，可知“数”为9，所以 2497。
【解析】因为竖式中五位数乘4仍是五位数，所以“客”是人于0小于3的偶数，只能是2，并推知“居” 8。因为“上”乘4不向上进位，且是奇数，所以“上” 1，并推知“然” 7。则所表示的三位数是978。
【答案】
【例 4】下面算式(1)是一个残缺的乘法竖式，其中□≠2，那么乘积是多少？
【考点】乘法数字谜【难度】2星【题型】填空
【答案】
【例 16】如图所示的除法算式中，每个各代表一个数字，则被除数是。
【考点】除法数字谜【难度】3星【题型】填空
【关键词】希望杯，4年级，初赛，8题
【解析】先确定商首位是8，再估量出除数首位是5，确定商的末位1，得到被除数为4620.
【答案】
【例 17】右边的除法算式中，商数是。
【考点】除法数字谜【难度】3星【题型】填空
【考点】乘法数字谜【难度】3星【题型】填空
1【解析】首先从式子中可以看出“思” ，另外第三个部分积的首位只能为9，所以“学”只能为3．由于3个部分积都是四位数，而且第三个部分积的首位为9，所以它比其它两个部分积要大，从而“学”比“而”和“杯”都大，所以“而”和“杯”只能分别为1和2，这样“学而思杯”就可能为3102或3201．分别进行检验，发现，与算式不相符，而符合，所以“学而思杯”代表的数字分别为3、2、0、1．

乘除法找规律填数题

乘除法找规律填数题在数学学习中，乘除法是我们经常遇到的数学运算，它们有着自己的规律和特点。

本文将以乘除法找规律填数题为主题，介绍一些有趣且具有挑战性的题目，并探讨它们的解题思路和相关规律。

题目一：填入适当的数字：4 × 3 ÷ 6 = ？解析：首先进行乘法运算 4 × 3 = 12，然后再进行除法运算 12 ÷ 6 = 2。

所以答案为2。

题目二：填入适当的数字：9 ÷ 3 × 2 = ？解析：根据运算顺序，我们先进行除法运算 9 ÷ 3 = 3，然后再进行乘法运算 3 × 2 = 6。

所以答案为6。

题目三：填入适当的数字：18 ÷ 9 × 3 = ？解析：同样按照运算顺序进行，首先进行除法运算 18 ÷ 9 = 2，然后再进行乘法运算 2 × 3 = 6。

所以答案为6。

通过以上三道题目的解析，我们可以发现乘除法在运算时有着一定的规律。

根据运算顺序的不同，最终的结果也会不同。

乘除法的运算顺序遵循先乘后除的原则，即先进行乘法运算，再进行除法运算。

这是因为乘法和除法之间有一个优先级的问题，乘法具有比除法更高的优先级。

在解决乘除法找规律填数题时，我们可以通过观察和总结规律来快速得到答案。

下面将进一步举例说明。

题目四：填入适当的数字：12 ÷ 2 × 4 = ？解析：根据运算顺序，首先进行除法运算 12 ÷ 2 = 6，然后再进行乘法运算 6 × 4 = 24。

所以答案为24。

题目五：填入适当的数字：20 ÷ 10 × 5 = ？解析：按照运算顺序进行，首先进行除法运算 20 ÷ 10 = 2，然后再进行乘法运算 2 × 5 = 10。

所以答案为10。

通过以上两道题目的解析，我们可以看到除法和乘法的运算顺序是有着一定的影响的。

小学奥数系列：第07讲乘除法填空格

第07讲数字谜问题第02讲乘除法填空格例1把1～9这九个不同的数字分别填在图7—1的各个方格内，可使加法和乘法两个算式都成立．现有三个数字的位置已确定，请你填上其他数字．答案17×4=68，68+25=93．分析在解乘法竖式的数字谜问题时，会经常使用枚举法试算．本题中，很重要的一个条件就是九个数字各不相同．知道了这一点，再使用枚举法就好了很多．‘详解因为九个数字各不相同，所以第一个乘数的十位只可能填1，如果填2、4、5都不可能使第一个乘法竖式成立，而17×4=68满足第一个乘法竖式．此时，数字谜变为一个加法竖式．因为和数的个位为3，所以第二个加数的个位为5．在九个数字中，现在只有2和9没有填过，因此可以很容易的知道68+25=93．评注此题关键是第一个乘法竖式，一个两位数乘一个一位数等于六十多，那么枚举的情况就很少了．况且所填的数字中不能有3，即情况就更少了．于是就可以比较容易地得出答案．例2请补全如图7-2所示的残缺算式．问其中的被乘数是多少?答案47568．分析在解乘法竖式数字谜问题时，要特别注意首位和末位，也要注意进位．此时的进位比加法要复杂一些，因此使用枚举法．详解先看末位：一个数字乘以7，个位是6，那么这个数只能是8.7×8=56，向十位进了“5”．而6×7：42。

因此积数的十位等于7，并且向百位进了“4”.9-4=5，因此乘数的百位数字乘以7所得的积的个位数字为5，所以乘数的百位数字只能是5．5×7=35，向干位进“3”.7×7=49，49+3=52，向万位进了“5”．因此乘数的万位数字乘以7所得的积大于25小于35，只有4×7=28满足条件．因此整个算式为：47568 × 7=322976．评注乘法的进位比加法复杂得多．两个数字相乘，可以向高位进位，而且在本题中还需要根据积的个位数字来推断乘数，而个位数字的确定也与进位有关．由此可知进位的重要性．例3 图7—3是一个残缺的乘法算式，只知道其中一个位置上数字为8，那么这个算式的乘积是多少?答案 1068．分析这个问题未知数很多，表面看上去很难，突破口就是“8”这个数字．第一个乘数乘以8是一个两位数，那么这个乘数的范围就很小了，而且这个乘数乘上第二个乘数的个位数字是一个三位数，所以第二个乘数的个位数字一定大于8，只可能是9．详解由分析可知，第二个乘数等于89．而第一个乘数只可能是10、ll或12，否则乘8后所得的积就是一个三位数，而11乘以9等于99，是_个两位数，不满足题中的要求．所以第一个乘数一定是12．12×89=1068评注解题时要善于找到突破口，这要求同学们具有很强的分析和推理能力，并且要对题中所涉及的知识点非常熟悉，运用自如．有些问题已知条件较少，那么这不多的几个条件往往就是突破口，它们包含了很重要的信息，应格外注意．例4在图7—4所示的残缺算式中只知道三个位置上的数字是4，那么补全后它的乘积是多少?答案 3243．分析这里只给出了三个4，第一个乘数首位为4，它乘上第二个乘数的个位数字所得的积为一个首位为4的三位数．这个条件很重要．利用枚举法和反证法推出所有的需要补伞的数字．使得竖式成立．详解第一个乘数最大是49，如果第二个乘数的个位为8，那么49×8=392，小于400．所以第二个乘数的个位数字只可能等于9．进一步可以推出第一个乘数的个位数字一定大于或等于5，否则第一个乘数乘上9以后肯定小于400．于是第一个乘数的个位数字只可能是5、6、7、8、9中的一个．如果第一个乘数的个位是5，那么45×9=405．因此第二个乘数的十位数字乘上45所得的积的个位数字应该等于4(否则两个乘数的积的十位数字就不可能等于4)，而45乘任何一个数之后，个位只能等于0或5，不等于4，所以第一个乘数的个位不等于5．同样可以知道第一个乘数的个位也不可能等于6、8和9．而当第一个乘数的个位数字等于7时，47×9=23，并且47×6=282，正好可以满足两个乘数的积的十位等于4．我们还可以知道47乘上6以外的其他任何一个数字，个位都不可能等于2，因此答案是惟一的：47×69=3243．评注这道题对分析能力要求很高，首先要推出第二个乘数的个位为9，然后再推出第一个乘数的个位等于7．在详解中，只用反证法证明了第一个乘数的个位不等于5，大家可以类似地证明它不可能等6、8和9．例5图7-5是一个残缺的乘法算式，补全后这个算式的乘积应是多少?答案1862．分析本题和上一题的解法是类似的，要用到枚举法和反证法．详解因为20×90=1800，所以第二个乘数的十位只能是9，否则最后的结果就小于1800．而18×99<1800，所以第一个乘数只能是19．再根据乘法算式的第3行，容易判断出第二个乘数的个位是8．所以这个算式的乘积应该是19×98=1862．评注这道题使用了枚举法，而且计算量很大，枚举法使用了很多次．这种思路比较简单，计算也不是很复杂，认真地计算，不怕麻烦，多试几次就可以很容易地得出答案．例6在图7-6所示除法竖式的每个方框中填人适当的数字，使算式成立，那么算式中的被除数是多少?。

小学奥数教程：乘除法数字谜(二)全国通用(含答案)

【答案】159
【例 12】一个六位数，如果满足，则称为“迎春数”(如，则就是“迎春数”).请你求出所有“迎春数”的总和.
【考点】与数论结合的数字谜之整除性质【难度】4星【题型】填空
【解析】方法一：显然，不小于4，原等式变形为
化简得，当时，，于是为．同理．，6，7，8，9，可以得到为，，，， .
①若“ ”=3，则盼盼盼盼盼盼盼盼盼÷3的商出现循环，且周期为3，这样就出现重复数字，
因此“ ”≠3。
②若“ ”=9，因为盼盼盼盼盼盼盼盼盼÷9=盼×（111111111÷9）=盼×12345679
若“盼”=1，则“开放的中国盼奥运”=12345679×1=12345679，“盼”=6，前后矛盾，所以“盼”≠1。
【答案】
【例 6】“迎杯×春杯=好好好”在上面的乘法算式中,不同的汉字表示不同的数字,相同的汉字表示相同的数字。那么“迎+春+杯+好”之和等于多少?
【考点】与数论结合的数字谜之特殊数字【难度】3星【题型】填空
1【解析】好好好=好×111=好×3×37，100以内37的倍数只有37和74，所以“迎杯”或“春杯”中必有1个是37或74，判断出“杯”是7或4。若杯=7，则好=9，999/37=27，所以，迎+春+杯+好=3+2+7+9=21若杯=4，则好=6，666/74=9，不是两位数，不符合题意。迎+春+杯+好=3+2+7+9=21。
【关键词】希望杯，4年级，初赛，20题
【解析】赛×赛的个位是9，赛=3或7，赛=3，小学希望杯赛=333333，不合题意，舍去；故赛=7，小学希望杯赛=99999母代表相同的数字，不同的字母代表不同的数字，问A和E各代表什么数字？

小学思维数学讲义乘除法数字谜-带详解

乘除法数字谜（一）教学目标数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突破口来解决问题．最后通过例题的学习，总结解数字谜问题的关键是找到合适的解题突破口．在确定各数位上的数字时，首先要对填写的数字进行估算，这样可以缩小取值范围，然后再逐一检验，去掉不符合题意的取值，直到取得正确的解答．知识点拨1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．2.数字谜突破口：这种不完整的算式，就像“谜”一样，要解开这样的谜，就得根据有关的运算法则，数的性质（和差积商的位数，数的整除性，奇偶性，尾数规律等）来进行正确的推理，判断．3.解数字谜：一般是从某个数的首位或末位数字上寻找突破口．推理时应注意：⑴数字谜中的文字，字母或其它符号，只取0~9中的某个数字；⑵要认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件；⑶必要时应采用枚举和筛选相结合的方法（试验法），逐步淘汰掉那些不符合题意的数字；⑷数字谜解出之后，最好验算一遍．例题精讲模块一、乘法数字谜【例1】下面是一个乘法算式：问：当乘积最大时，所填的四个数字的和是多少？×5【考点】乘法数字谜【难度】1星【题型】填空【关键词】华杯赛，初赛，第2题【解析】乘积是两位数并且是5的倍数，因而最大是95.95÷5＝19，所以题中的算式实际上是19×595所以，所填四个数字之和便是1＋9＋9＋5＝24【答案】24【例2】下面两个算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字．美⨯妙数学=数数妙，1□， c美+妙数学=妙数数。

美妙数学 = ___________【考点】乘法数字谜【难度】2 星【题型】填空【关键词】走美杯，四年级，初赛，第 12 题，五年级，初赛，第 11 题【解析】由美 ⨯ 妙数学 = 数数妙知，“美”不为 1，且“美”×“妙”<10，如果“美”为 2，根据“美”×“学”的个位数为“妙”，那么“妙”为偶数，即为 4，推出“学”为 7，又由 “美”+“学”=“数”，可知“数”为 9，所以美妙数学 = 2497。

(完整版)三年级数字谜加减法,乘除法

数字谜思维训练一、加减竖式数字谜例 1 在下面算式的空格中,各填入一个合适的数字,使算式成立.(1)□4 □(2) □□4＋□8 ＋ 1 □□□ 1 5 □□□ 3(3)□0 □6 (4) 1 □5 □－7 □4 □－□□9□6 7 8 6 7例 2 下面每个汉字代表一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字, 这些汉字各代表哪些数字?(1) 成都(2) 助成都市助人＋爱成都市助人为1 9 9 9 ＋助人为乐19 9 3例3 相同的汉字代表相同的数字，不同的汉字代表不同的数字，这些汉字各代表哪些数字?节童儿际国一六祝庆＋8 6 4 1 9 7 5 3 2庆祝六一国际儿童节二、乘法竖式数字谜例4 在下面算式的空格中,各填入一个合适的数字,使算式成立（1）□□ 8 （2）□□ 9 ×□×□79 2 1 □ 5 2（３）4 3 7 □(４) □□4 ×□×□□□□0 0 5 2 □2例5相同的汉字代表相同的数字，不同的汉字代表不同的数字，这些汉字各代表哪些数字?１数学俱乐部×３数学俱乐部１三、练习题1、在下面的空格中,各填入一个适当的数字,使式子成立.(1) □8 □(2) □1＋□6 □ 3 ＋□9 □□□1 2 8 □□9 □(3) □□4 （4）□0 0 1－□□－20 □79 □9 □(5)□□８(6) □ □ 9×□ × □３１□２ 1 8 3 22、下面的式子中相同的字母代表相同的数字,不同的字母代表不同的数字,式中的字母ABCD各代表哪些数字?A B C D×9D C B A3、在下面的式子里,6个小纸片各盖住了一个数字,问:被盖住的6个数字总和是多少?□□□＋□□□1 9 9 1。

乘除法数字谜(一)

第一讲乘除法数字谜（一）专题简析：解决算式谜题，关键是找准突破口，推理时应注意以下几点：1.认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；2.利用列举和筛选相结合的方法，逐步排除不合理的数字；3.试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4.算式谜解出后，要验算一遍。

例1.在下面的方框中填上合适的数字。

分析：由积的末尾是0，可推出第二个因数的个位是5；由第二个因数的个位是5，并结合第一个因数与5相乘的积的情况考虑，可推出第一人个因数的百位是3；由第一个因数为376与积为31□□0，可推出第二个因数的十数上是8。

题中别的数字就容易填了。

练习一第二讲乘除法数字谜（二）例1.下面算式中的a、b、c、d这四个字母各代表什么数字？分析：因为四位数abcd乘9的积是四位数，可知a是1；d和9相乘的积的个位是1，可知d只能是9；因为第二个因数9与第一个因数百位上的数b相乘的积不能进位，所以b只能是0（1已经用过）；再由b＝0，可推知c＝8。

练习二第三讲图形的个数例1.下面图形中有多少个正方形？分析：图中的正方形的个数可以分类数，如由一个小正方形组成的有6×3＝18个，2×2的正方形有5×2＝10个，3×3的正方形有4×1＝4个。

因此图中共有18＋10＋4＝32个正方形。

例2.下图中共有多少个三角形？分析：为了保证不漏数又不重复，我们可以分类来数三角形，然后再把数出的各类三角形的个数相加。

（1）图中共有6个小三角形；（2）由两个小三角形组合的三角形有3个；（3）由三个小三角形组合的三角形有4个；（4）由六个小三角形组合的三角形有1个。

所以共有6＋3＋4＋1＝14个三角形。

练习三1.下图中共有多少个正方形？2.下图中共有多少个正方形？3.下图中共有多少个正方形，多少个三角形？4.下面图中共有多少个三角形？第四讲找出数字的排列规律（一）找规律是我们在生活、学习、工作中经常使用的一种思想方法，在解数学题时人们也常常使用它，下面我们利用找规律的方法来解一些简单的数列问题。

乘除法数字谜(一)

第一讲乘除法数字谜（一）专题简析：解决算式谜题，关键是找准突破口，推理时应注意以下几点：1.认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；2.利用列举和筛选相结合的方法，逐步排除不合理的数字；3.试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4.算式谜解出后，要验算一遍。

例1.在下面的方框中填上合适的数字。

分析：由积的末尾是0，可推出第二个因数的个位是5；由第二个因数的个位是5，并结合第一个因数与5相乘的积的情况考虑，可推出第一人个因数的百位是3；由第一个因数为376与积为31□□0，可推出第二个因数的十数上是8。

题中别的数字就容易填了。

练习一第二讲乘除法数字谜（二）例1.下面算式中的a、b、c、d这四个字母各代表什么数字？分析：因为四位数abcd乘9的积是四位数，可知a是1；d和9相乘的积的个位是1，可知d只能是9；因为第二个因数9与第一个因数百位上的数b相乘的积不能进位，所以b只能是0（1已经用过）；再由b＝0，可推知c＝8。

练习二第三讲图形的个数例1.下面图形中有多少个正方形？分析：图中的正方形的个数可以分类数，如由一个小正方形组成的有6×3＝18个，2×2的正方形有5×2＝10个，3×3的正方形有4×1＝4个。

因此图中共有18＋10＋4＝32个正方形。

例2.下图中共有多少个三角形？分析：为了保证不漏数又不重复，我们可以分类来数三角形，然后再把数出的各类三角形的个数相加。

（1）图中共有6个小三角形；（2）由两个小三角形组合的三角形有3个；（3）由三个小三角形组合的三角形有4个；（4）由六个小三角形组合的三角形有1个。

所以共有6＋3＋4＋1＝14个三角形。

练习三1.下图中共有多少个正方形？2.下图中共有多少个正方形？3.下图中共有多少个正方形，多少个三角形？4.下面图中共有多少个三角形？第四讲找出数字的排列规律（一）找规律是我们在生活、学习、工作中经常使用的一种思想方法，在解数学题时人们也常常使用它，下面我们利用找规律的方法来解一些简单的数列问题。

乘除法数字谜

第一讲乘除法数字谜（一）专题简析：解决算式谜题，关键是找准突破口，推理时应注意以下几点：1.认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；2.利用列举和筛选相结合的方法，逐步排除不合理的数字；3.试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4.算式谜解出后，要验算一遍。

例1.在下面的方框中填上合适的数字。

分析：由积的末尾是0，可推出第二个因数的个位是5；由第二个因数的个位是5，并结合第一个因数与5相乘的积的情况考虑，可推出第一人个因数的百位是3；由第一个因数为376与积为31□□0，可推出第二个因数的十数上是8。

题中别的数字就容易填了。

练习一第二讲乘除法数字谜（二）例1.下面算式中的a、b、c、d这四个字母各代表什么数字？分析：因为四位数abcd乘9的积是四位数，可知a是1；d和9相乘的积的个位是1，可知d只能是9；因为第二个因数9与第一个因数百位上的数b相乘的积不能进位，所以b只能是0（1已经用过）；再由b＝0，可推知c＝8。

练习二第三讲图形的个数例1.下面图形中有多少个正方形？分析：图中的正方形的个数可以分类数，如由一个小正方形组成的有6×3＝18个，2×2的正方形有5×2＝10个，3×3的正方形有4×1＝4个。

因此图中共有18＋10＋4＝32个正方形。

例2.下图中共有多少个三角形？分析：为了保证不漏数又不重复，我们可以分类来数三角形，然后再把数出的各类三角形的个数相加。

（1）图中共有6个小三角形；（2）由两个小三角形组合的三角形有3个；（3）由三个小三角形组合的三角形有4个；（4）由六个小三角形组合的三角形有1个。

所以共有6＋3＋4＋1＝14个三角形。

练习三1.下图中共有多少个正方形？2.下图中共有多少个正方形？3.下图中共有多少个正方形，多少个三角形？4.下面图中共有多少个三角形？第四讲找出数字的排列规律（一）找规律是我们在生活、学习、工作中经常使用的一种思想方法，在解数学题时人们也常常使用它，下面我们利用找规律的方法来解一些简单的数列问题。

乘除法算式谜

乘除法算式谜1、乘除法算式谜 [问题一] 在右面的?里填上合适的数字。

想:因为积的个位是6，那么两个因数个位相乘的积的个位也是6;一个因数十位上是6，如果它与比1大的数相乘，所得的积肯定是三位数，但两次乘得的积都是两位数，那另一个因数的十位和个位都只能填1。

解:[试一试]1、在下面的?里填上合适的数字。

,、在下面的?里填上合适的数字。

[问题二] 下列算式中不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立。

想:(,)由积的个位是,，一个因数是,，推出另一个因数的各位数“杯”是,。

(,),×,,,,，在积的个位上写,，向十位进,，因为积的十位数“杯”为,，所以“金”×,的积的个位数是,，由此“金”是,。

(,)“金”是,，积的百位数为,，所以“庚”×,的积的末位数应是,，由此“庚”是,。

(,),×,,,,，在积的百位上写1，向千位进2，因为积的千位数为7，所以“罗”×3的积的末位数应是5，由此“罗”是5。

(5)由积的万位数“罗”是5，可推得“华”为8。

解:答:华,,，罗=5，庚=7，金=1，杯=4。

[试一试]1、下面算式中的a、b、c、d这四个字母各应代表什么数字,2、下式中“数学俱乐部”分别代表哪些数字,[问题三] 右面的乘法算式中，算、式、谜各代表一个互不相同的数字。

它们各代表什么数字时算式成立。

想:由算式谜×谜=???谜，可知谜不等于1或0，因此移只等于5或6。

(1)若谜=5，由于算式谜×算的乘积是三位数，所以“算”不大于3，且算式谜×算的乘积的百位上的数字大于等于3小于等于5，所以算=2。

由于算式谜×式=??5，可知式是奇数，且小于5。

(2)若谜=6，同理，算式谜×算的乘积的百位上的数字，必须大于等于4且小于等于6，所以算=2，由于2式6×式=??6，所以式=1，但216×216=46656，不符合题意。

华数思维训练导引三年级上学期第07讲数字谜问题第02讲乘除法填空格

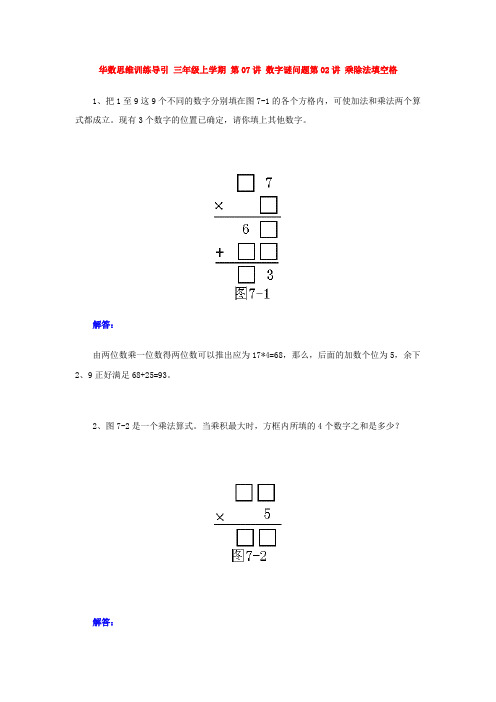
华数思维训练导引三年级上学期第07讲数字谜问题第02讲乘除法填空格1、把1至9这9个不同的数字分别填在图7-1的各个方格内，可使加法和乘法两个算式都成立。

现有3个数字的位置已确定，请你填上其他数字。

解答：由两位数乘一位数得两位数可以推出应为17*4=68，那么，后面的加数个位为5，余下2、9正好满足68+25=93。

2、图7-2是一个乘法算式。

当乘积最大时，方框内所填的4个数字之和是多少？解答：一个两位数乘5得两位数，那么个位只能是1；要使乘积最大，个位当然应该是9；即算式为19*5=95；那么，所填的四个数字之和为：1+9+9+5=24。

3、请补全图-3所示的残缺算式，问其中的被乘数是多少？解答：由个位往前分析，容易得到被乘数个位为8，积十位为7，被乘数百位为5，万位为4，积万位为3；即整个算式为：47568*7=332976。

所以，被乘数为47568。

4、图7-4是一个残缺的乘法竖式，那么乘积是多少？解答：由乘积的最高位不难看出积应该是10?2，且在它上面的乘积应该是9？；因为加2后有进位，所以，个位只有8、9两种可能；又第一个乘积的十位为2，个位也是2，说明被乘数为22，乘数个位为1；或者被乘数为11，乘数个位为2；如果被乘数为22，乘数个位为1，乘数的个位只能是4，显然不行；那么，被乘数为11，乘数个位为2，这样，乘数个位就为9，即整个算式为11*92=1012。

所以，乘积是1012。

5、图7-5是一个残缺的乘法算式，只知道其中一个位置上数字为8，那么这个算式的乘积是多少？解答：由被乘数乘8后得两位数容易得出被乘数应该为12，乘数个位则必定为9，那么结果为12*89=1068。

6、图7-6是一个残缺的乘法算式，补全后它的乘积是多少？解答：由乘积个位得5，那么被乘数的个位也必定是5；由乘数的十位乘被乘数时十位为0，可知乘数的十位是4或8；由积的千位为5，推得被乘数百位为3，并由此推出乘数十位为4；所以，算式为325*47=15275，即乘积是15275。

小学奥数填算式(乘除法)专项练习30题(有答案)

第8 讲填算式二专项练习30题（有答案）1．右图是三位数与一位数相乘的乘法竖式，每个方框填入一个数字，不同的填法有_________种．2．右面乘法竖式的积是_________．3．在一个一位数乘三位数的算式中，只出现2，3，5，7，8这五个数字．乘积的个位数是_________．4．完成右面的算式．5．在如图所示的方框中填入数字，使算式成立．6．在下面的算式的口里填上合适的数字，使算式成立．7．在□里填上合适的数字，使竖式成立．8．先在“□”里填上适当的数，然后在横线里填上恰当的数．（1）_________÷_________=_________（2）_________×_________=_________．9．在图的残缺算式中，只写出3个数字1，其余的数字都不是1．那么这个算式的乘积是_________．10．在下面算式的□内，填上适当的数字，使算式成立．11．在方框中填入适当的数，使得竖式成立．12．如图，在每个方框中填入一个数字，使得乘法竖式成立．两个乘数的和是_________．13．在□里填上合适的数字．14．在□中填上适当的数，使下面的竖式成立．15．在括号内填上适当的数，使竖式成立．16．在□里填上合适的数，使竖式成立．17．在算式的空格里填入一个合适的数字，使算式成立．18．如图所示的除法算式中，每个□各代表一个数字，则被除数是_________．19．，算式应为_________÷_________=_________．20．填数：21．在每个方框中填入一个数字，使得乘法竖式成立．已知乘积有两种不同的得数，那么这两个得数的差是_________．22．23．在下面的□里填上合适的数字．24．在横线里填上合适的数字．25．□里应填几才能使算式成立，算式为：_________÷_________=37．26．根据如图竖式中给出的数，在各个小方框内填上合适的数，使这个多位数乘法竖式完整．那么，乘积为_________．27．在下面算式的空格内，各填入一个合适的数字，使算式成立．28．在下面的□里填上合适的数．29．填入适当的数字使竖式成立．30．填出如图方框中的数．参考答案：1．因为1998=2×3×3×3×37，竖式中有一个因数是一位，1998的一位因数有：1，2，3，6，9；所以这个一位数可能是：1，2，3，6，9；当一个因数是1时，另一个因数是：1998÷1=1998，是四位数，不符合题意；当一个因数是2时，另一个因数是：1998÷2=999，符合题意；当一个因数是3时，另一个因数是：1998÷3=666，符合题意；当一个因数是6时，另一个因数是：1998÷6=333，符合题意；当一个因数是9时，另一个因数是：1998÷9=222，符合题意；由以上分析可得：999×2=1998，666×3=1998，333×6=1998，9×222=1998，共有4种不同的填法．故答案为：42．根据竖式可知，积的末尾是7，由3×9=27可得被乘数是13；由被乘数乘乘数的十位上的数的积的末尾是9，根据3×3=9可得乘数是39；由以上分析可得竖式是：所以，乘法竖式的积是5073．根据题意可知，一个一位数乘三位数积的个位数，就是这个一位数与三位数个位上数字相乘的积的末尾，因为只出现2，3，5，7，8这五个数字，只有3×5=15、5×5=25，7×5=35的末尾数字符合，并且末尾都是5；其它的都不符合，所以这个乘积的个位数是5．假设这个一位数字是3，那么这个三位数的个位数字是5，积的最高位最小是2，所以，三位数的最高位上的数大于5，那么是7或8；个位上，5×3=15，向十位进1；十位上，2×3+1=7，而3×7=21，3×8=24，都会出现其它数字不符合，8×3+1=25，向百位进2；百位上，7×3+2=23，符合题意；那么可得785×3=2355．根据以上分析可得竖式是：故填：5．4．根据竖式可知，7×□7的末尾是9，第二步中，□□7﹣□□9=□，因为17﹣9=8，所以最后一步可得出87，因为只有87×1=87，所以，除数是87，因为87×7=609，609+8=617，在第一步中7﹣6=1，所以，87乘商的最高位的末尾是6，因87×8=696，可以推出商是871，那么被除数是：871×87=75777；由以上分析可得竖式是：对应数字填入方框即可．6．7．根据题意，由竖式可得：除数□9与商的个位上的数相乘的积的末尾是6，因为9×4=36，所以，商的个位上的数是4；又因为□9×4的积是两位数，19×4=76，符合，29×4=116不符合，因此，除数是19；除数19与商的十位上的数相乘的积小于4□，并且它们的差小于10，因为19×1=19，4□﹣19相差大于10，不符合；19×2=38，4□﹣38相差不到10，符合，因此商的十位上的数是2；由以上推算可得：商是24，除数是19；那么被除数是：24×19=456；由以上推算可得竖式是：8．（1）所以9919÷91=109，（2）所以81×11=891，9．10．11．12．解：根据题意，由竖式可得：第一个因数与2相乘，是一个三位数，并且末尾数是0，5×2=10，所以，第一个因数的个位上的数是5，第一个因数百位数字最大是4，因为最后的结果是六位数，那么，只能是4；可以得到第一个因数是4□5；又因为4□5与第二个因数十位数数相乘的积是□1□，那么第二个因数十位数是1或2；假设是1，415×1=415，那么第一个因数是415，第二个因数最大是219，415×219=90885，不是六位数，那么第二个因数十位数是2；只有455×2=910，所以，第一个是455，又因为455×9=4095，所以，第二个因数是229；由以上可得：；所以，两个乘数的和是：455+229=684．故答案为：684．13．（1）根据竖式可知，□×7的末尾是4，只有2×7=14的末尾是4，所以被乘数的个位是2；因为3×7=21，向上一位进2，□×7+2=5□，因为7×7+2=51，8×7+2=58，所以被乘数的百位是7或8；竖式是：7 3 2×7﹣﹣﹣﹣﹣﹣﹣﹣5 1 2 4或×7﹣﹣﹣﹣﹣﹣﹣﹣5 8 2 4（2）根据三位数乘一位数积是四位数，并且是4□7□，乘数大于等于4，；假设乘数是4，5×4=20，进2，□×4+2的末尾是7，找不到一个数与4相乘再加2的末尾是7的数，不符合；假设乘数是5，5×5=25，进2，，□×5+2的末尾是7，可知□=1，3，5，7，9，所以，当十位的数是1时，1×5+2=7，□×5=4□，8×5=40，9×5=45，所以被乘数的百位可以填8或9；当十位的数是3时，3×5+2=17，进1，□×5+1=4□，8×5+1=41，9×5+1=46，所以被乘数的百位可以填8或9；当十位的数是5时，5×5+2=27，进2，□×5+2=4□，8×5+2=42，9×5+2=47，所以被乘数的百位可以填8或9；当十位的数是7时，7×5+2=37，进3，□×5+3=4□，8×5+3=43，9×5+3=48，所以被乘数的百位可以填8或9；当十位的数是9时，9×5+2=47，进4，□×5+4=4□，8×5+4=44，9×5+4=49，所以被乘数的百位可以填8或9；假设乘数是6，5×6=30，进3，□×6+3的末尾是7，因为4×6+3=27，进2，□×6+2=4□，7×6+2=44，所以被乘数的百位可以填7；因为9×6+3=57，进5，□×6+2=4□，6×6+5=41，7×6+5=47，所以被乘数的百位可以填6或7；假设乘数是7，5×7=35，进3，□×7+3的末尾是7，2×7+3=17，进1，□×7+1=4□，6×7+1=43，所以被乘数的百位可以填6；假设乘数是8，5×8=40，进4，□×8+4的末尾是7，找不到一个数与8相乘再加4的末尾是7的数，不符合；假设乘数是9，5×9=45，进4，□×9+4的末尾是7，7×9+4=67，进6，□×9+6=4□，4×9+6=42，所以被乘数的百位可以填4；所以，本题的答案为：815×5=4075，835×5=4175，855×5=4275，875×5=4375，895×5=4475，915×5=4575，935×5=4675，955×5=4775，975×5=4875，995×5=4975，745×6=4470，695×6=4170，795×6=4770，625×7=4375，475×9=4275．（3）由有余数的除法可知，除数是3，余数可能是1，2，当余数是1时，被除数是23×3+1=70；当余数是2时，被除数是23×3+2=71，所以答案是：70÷3=23…1，71÷3=23…2；（4）由有余数的除法可知，余数是1，除数只要大于1就可以，当除数是2时，被除数是21×2+1=43，当除数是3时，被除数是21×3+1=64，当除数是4时，被除数是21×4=85，当除数是5时，被除数是21×5+1=106，是三位数，与题目不符；所以，答案是：43÷2=21...1，64÷3=21...1，85÷4=21 (1)14．根据题干分析可以把竖式补充完整如下所示：故答案为：7；4；4；2；3；8；8；9；5；1；1；9；5；9；1；1；0；5．15．解：（1）当A=3时，39×8=312，即D=1；39×28=1092＞999，故B=1；39×1=39，所以F=3，G=9；39×18=702，故H=7，I=0．（2）当A=4时，49×8=392，即D=9；39×28=1092＞999，故B=1；49×1=49，所以F=4，G=9；49×18=882，故故答案为：16．解：（1）根据竖式可知：第一个因数乘第二个因数的个位数字是三位数，第一个因数乘第二个因数的十位数字4是四位数，由此可得，第一个因数的百位数字大于等于3，再根据第一个因数乘第二个因数的个位数字是3□□，因为3×1=3，所以，可以得出，第一个因数的百位数字是3，第二个因数的个位数字是1，3□5×4=□2□□，由305×4=1220，315×4=1260，325×4=1300，可得，第一个因数的十位数字是0或1；305×41=12505，315×41=12915；由以上分析可得竖式是：或（2）根据竖式可知：商的百位数字乘8是48，6×8=48，可得，商的百位数字是6，商的个位数字乘8是1□，2×8=16，可得，商的个位数字是2，那么商就是：602，那么被除数是：602×8=4816．由以上推算可得竖式是：17．根据题干分析可得，一位数因数最小是7，即一位数因数可以是7、8、9，经过推算可得，一位数因数只能是8，2×8=16，则三位数的十位上是3，据此可得：432×8=3456，故答案为：3；8；4；618．根据竖式可知，除数□7乘商的十位数字的积是三位数，并且末尾是6，7×8=56，可以得知商的十位数字是8；4□□﹣□□6=□，可知，□7×8的结果接近4□□，57×8=456，所以，除数是57；由57乘商的个位数字的积是两位数，可得商的给位数字是1，即商是81；由被除数=商×除数+余数可得，被除数是：81×57+3=4620．故填：462019．根据题意，由除数的个位是7，再根据竖式中给出的数，7×5=35，可知商的十位是5，7×3=21，可以推知商的个位是3，可知商是53，由5×27=135，推出除数是27，可知被除数是53×27=1431．故算式是：1431÷27=5320．（1）根据竖式可知，除数2□乘商的个位数是46，23×2=46，所以除数是23，商是22，被除数是：22×23=506，竖式是：2 24 6﹣﹣﹣﹣﹣﹣﹣﹣4 64 6﹣﹣﹣﹣﹣﹣﹣﹣（2）根据竖式可知，□4×商的个位数的末尾是0，4×5=20，所以商是15，□4×5=1□0，24×5=120，34×5=170，所以，除数是24或34；当除数是24时，被除数是：24×15=360，竖式是：1 52 4﹣﹣﹣﹣﹣﹣﹣﹣1 2 01 2 0﹣﹣﹣﹣﹣﹣﹣﹣当除数是34时，被除数是：34×15=510，竖式是：1 53 4﹣﹣﹣﹣﹣﹣﹣﹣1 7 01 7 0﹣﹣﹣﹣﹣﹣﹣﹣21．根据题干分析可得：，93786﹣91756=2030，答：这两个乘积的差是2030．故答案为：2030．22．23．（1）根据除法竖式可得，商的末尾是0；6除被除数的百位上的数，够商1，并且只能商1，并且有余数，可得，被除数百位上的数大于6，即7，8，9；当被除数百位上的数是7时，百位上的余数是1，由6×2=12，可得十位上的数是2；因此被除数是720．由以上推算可得竖式是：当被除数百位上的数是8时，百位上的余数是2，由6×4=24，可得十位上的数是4；因此被除数是840．由以上推算可得竖式是：当被除数百位上的数是9时，百位上的余数是3，由6×6=36，可得十位上的数是6；因此被除数是960．由以上推算可得竖式是：（2）根据乘法竖式可得，第一个因数个位上的数与第二个因数的十位数9相乘的积的末尾是4；由9×6=54，可得，第一个因数个位上的数是6；第一个因数个位上的数6与第二个因数的个位数相乘的积的末尾是8；由6×3=18，6×8=48，可得，第二个因数个位上的数是3或8；当第二个因数个位上的数是3，□6×3的积不可能是6□□，因此，第二个因数个位上的数是6，即第二个因数是98；第一个因数□6×8的积是6□8，由76×8=608，86×8=688，可得，第一个因数十位上的数是7或8；即第一个因数是76或78；当第一个因数是76时，76×9=684，符合题意；由以上推算可得竖式是：当当第一个因数是86时，86×9=774，与6□4不符合．所以，只有上面一种情况24．25．除数399÷7=57，被除数37×57=2109，所以算式为：2109÷57=37．故答案为：2109，3726．设这个算式是：ab5（1）首先考虑被乘数的百位数字，由×3是十位数字为0的三位数知a≤3．若a=3，由×3的十位数字为0知b=3，此时×3=1005不是三位数，故a≠3；若a=1，则×□＜200×9=1800，不会是千位为2的四位数，故a≠1，因此a=2．×3==，乘积的十位上是0，易知b=3；那么被乘数就是235；（2）再考虑乘数的个位数字d，它与235的积的末尾是0，而且是一个三位数，所以d是2或4；如果d=2，那么算式就是：235；4+5+h+1=15；h=5，c=5；235×5=1175，不足2000，所以c≠5，那么d≠2；那么只有d=4；（3）再讨论乘数的十位数字c，c与被乘数235的乘积是，那么c是一个奇数，一位奇数与235的乘积超过2000，那么这个数只能是9；由此可知乘数是394，这个算式就是：235；即乘法算式为：235×394=92590．乘积是92590．故答案为：9259027．解：过程如下：或28．解：图中1号线所指的5是由商的十位数与除数相乘得到的，与7相乘得到积的尾数是5的个位数只有5．因此可以1确定商的十位数是5．同样通过2号线所指的4，咱们可以确定4上方两个方格中也应该是4．同时也能确定出商的个位数是2（2×ϖ7=ϖ4）．如图：那么通过被除数的前三位数减去除数ϖ7与商的十位上5的乘积是一位数，可以确定除数的十位上是3．如果是2则有27×5=135，那么19ϖ减去135肯定是两位数，与题意矛盾．如果是4则有47×5=235，235＞19ϖ，同样与题意矛盾．故除数必是37．由：37×5=185，可以推出1号线5前面的两个数字是1，8．由：37×2=74，可以推出2号线4前面的数字是7．接着7上面的方格也是7．由：7+185=192，推出被除数的十位上的方格是2．故本题答案如下图：29．30．解：（1）由竖式可得：6□×4的末尾是6，4×4=16，4×9=36．可知，因数6□可能是64，69，又因为64×5=320，不符合，69×5=345，符合，所以，因数6□是69；由以上推算可得竖式是：（2）由竖式可知，除数乘7的积是两位数，那么除数的最高位只能是1，由11×7=77，12×7=84，13×7=91，14×7=98，那么除数可能是11、12、13、14；又因为除数乘商的个位数的积是三位数，那么商的个位上的数是8或9；除数乘商的个位上的数的积是□2□，只有14×9=126符合，所以，除数是14，商是79，被除数是：79×14=1106；由以上推算可得竖式是：。

小学奥数—乘除法数字谜(一)

5-1-2-2.乘除法数字谜（一）
教学目标
数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突
1.数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．
模块一、乘法数字谜
是一个残缺的乘法竖式，其中
下面残缺的算式中，只写出了3个数字1，其余的数字都不是1，那么这个算式的乘积是？
，不同汉字代表不同数字．美。

填数字使等式成立的数学题规律

填数字使等式成立的数学题规律一、引言数学题中常常会涉及到填数字使等式成立的问题，这类问题既考验了学生对基本数学运算规律的掌握，也拓展了他们的逻辑思维能力。

本文将从加法、减法、乘法和除法等基本数学运算展开讨论，探究填数字使等式成立的数学题规律。

二、加法运算对于填数字使等式成立的加法运算题，一般有以下几种常见的情况：1. 相同数字相加：例如填数字使等式成立：4+4=？当然答案就是8。

2. 逐位相加：例如填数字使等式成立：143+___=300此时需要填入157，即143+157=300。

3. 进位相加：例如填数字使等式成立：68+___=100根据十进制进位规则，填入32，即68+32=100。

三、减法运算填数字使等式成立的减法运算题同样有一定的规律性：1. 相同数字相减：例如填数字使等式成立：9-9=？此时答案为0。

2. 逐位相减：例如填数字使等式成立：750-___=482可填入268，即750-268=482。

3. 借位相减：例如填数字使等式成立：64-___=25需要借位，填入39，即64-39=25。

四、乘法运算在填数字使等式成立的乘法运算题中，也有其独特的规律：1. 乘法交换律：例如填数字使等式成立：7×___=42答案为6，即7×6=42。

2. 乘法配分配律：例如填数字使等式成立：___×8=32答案为4，即4×8=32。

3. 乘法进位：例如填数字使等式成立：12×___=84答案为7，即12×7=84。

五、除法运算填数字使等式成立的除法运算题同样具有一定的规律性：1. 除法的定义：例如填数字使等式成立：16÷___=4此时填入4，即16÷4=4。

2. 余数的概念：例如填数字使等式成立：25÷___=5此时填入5，即25÷5=5。

3. 除尽的情况：例如填数字使等式成立：54÷___=6此时填入9，即54÷9=6。

小学一年级综合算式专项测题填入正确的数字与未知数使乘除法算式成立

小学一年级综合算式专项测题填入正确的数字与未知数使乘除法算式成立一、填数字，使等式成立1. 3 × 4 = × 42. ÷ 6 = 7 ÷3. 2 × = 124. ÷ 5 = 6 ÷ 25. 4 × = 20二、填数字或未知数，使等式成立1. 5 × = 02. ÷ 4 = 33. 9 ÷ 3 = ÷ 14. 10 ÷ = 15. × 2 = 6三、填数字或未知数组成正确的算式并计算结果1. 某数 × 5 = 45，请计算这个数。

2. 某数 ÷ 3 = 8，请计算这个数。

3. 4 × = 24，请计算这个数。

4. 16 ÷ = 8，请计算这个数。

5. × 7 = 21，请计算这个数。

四、填数字或未知数，使等式成立1. 8 ÷ = 4 ÷ 22. × 9 = 273. ÷ 7 = 34. 20 ÷ = 45. 5 × = 35五、挑战题：填数字或未知数组成正确的算式并计算结果1. 某数 × 7 = 0，请计算这个数。

2. 某数 ÷ 4 = 12，请计算这个数。

3. × 8 = 56，请计算这个数。

4. 36 ÷ = 6，请计算这个数。

5. ÷ 9 = 2，请计算这个数。

六、填数字，使等式成立1. 21 ÷ = 3 ÷ 12. × 3 = 03. 3 × = 244. ÷ 6 = 15. 9 ÷ = 3七、填数字或未知数，使等式成立1. 15 ÷ = 32. 8 × = 83. ÷ 2 = 94. 16 ÷ = 45. × 6 = 42八、填数字或未知数，使等式成立1. × 10 = 802. 36 ÷ = 63. ÷ 9 = 14. 28 ÷ = 45. 7 × = 63以上是小学一年级综合算式专项测题，你可以根据题目的要求填入正确的数字和未知数，完成算式，并计算出结果。

数字谜02_三上08_乘除法填空格

三年级上学期第八讲，数字谜第02讲乘除法填空格【内容概述】利用竖式运算法则和推理，通过观察、判断、推理、尝试把较简单的乘除法竖式算式中缺少的数填出．【典型问题】【基础题】1.【10801】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★）把1至9这9个不同的数字分别填在图7-1的各个方格内，可使加法和乘法两个算式都成立．现有3个数字的位置已确定，请你填上其他数字．图7-12.【10802】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★）图7-2是一个乘法算式．当乘积最大时，方框内所填的4个数字之和是多少？3.【10803】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★）请补全图7-3所示的残缺算式，问其中的被乘数是多少？4.【10804】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-4是一个残缺的乘法竖式，那么乘积是多少？5.【10805】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-5是一个残缺的乘法算式，只知道其中一个位置上数字为8，那么这个算式的乘积是多少？6.【10806】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-6是一个残缺的乘法算式，补全后它的乘积是多少？7.【10807】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★★）在图7-7所示的残缺算式中只知道3个位置上的数字是4，那么补全后它的乘积是多少？8.【10808】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-8是一个残缺的乘法算式，补全后这个算式的乘积应是多少？9.【10809】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-9是一个残缺的乘法算式，补全后这个算式的乘积应是多少？10. 【10810】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）图7-10中的竖式由1，2，3，4，5，6，7，8中的7个数码组成，请将空缺的数码填上，使得竖式成立．11. 【10811】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★）在图7-11所示除法竖式的每个方框中，填入适当的数字，使算式成立．那么算式中的被除数是多少？12. 【10812】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）补全图7-12所示的除法算式．图7-117213. 【10813】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★）补全图7-13所示的残缺除法算式，问其中的被除数应是多少？14. 【10814】（导引偶数题，三上第08讲，乘除法填空格，数字谜第02讲★★）按照图7-14中给出的各数字的奇偶性补全这个除法算式．图7-12 图7-1315. 【10815】（导引奇数题，三上第08讲，乘除法填空格，数字谜第02讲★★★★）一个四位数被一个一位数除得图7-15中的①式，而被另一个一位数除得图7-15中的②式，求这个四位数．16. 【10816】（汪岩、三上第08讲，乘除法填空格，数字谜第02讲★★）在下面的乘法竖式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字，请将这个竖式补充完。

(小学奥数)乘除法数字谜(二)

乘除法数字谜(一)(含详细解析)

乘除法找规律填数题

小学奥数系列：第07讲 乘除法填空格

小学奥数教程：乘除法数字谜(二)全国通用(含答案)

小学思维数学讲义乘除法数字谜-带详解

(完整版)三年级数字谜加减法,乘除法

乘除法数字谜(一)

乘除法数字谜(一)

乘除法数字谜

乘除法算式谜

华数思维训练导引 三年级上学期 第07讲 数字谜问题第02讲 乘除法填空格

小学奥数填算式(乘除法)专项练习30题(有答案)

小学奥数—乘除法数字谜(一)

填数字使等式成立的数学题规律

小学一年级综合算式专项测题填入正确的数字与未知数使乘除法算式成立

数字谜02_三上08_乘除法填空格

小学奥数系列：第07讲乘除法填空格

华数思维训练导引三年级上学期第07讲数字谜问题第02讲乘除法填空格