132立方根(2)
实用的平方根表立方根表.pdf

,检查合同的履行情况;
4.5.4 保管法人代表授权委托书、合同专用章,并按编号归口使用;
4.5.5 建立合同管理台帐,对合同文本资料进行编号统计管理;
4.5.6 组织对法规、制度的学习和贯彻执行,定期向有关领导和部门报告工作;
4.5.7 在总经理领导下,做好合同管理的其他工作,
4.6 工程技术部:专职合同管理员及材料、燃料供应部兼职合同管理员履行以下职责:
4.2 工程部:是发电厂建设施工安装等工程合同签订管理部门;负责签订管理基建、安装、人工技术的工程合同。
4.3 经营部:是合同签订管理部门,负责管理设备、材料、物资的订购合同。
4.5 合同管理部门履行以下职责:
4.5.1 建立健全合同管理办法并逐步完善规范;
4.5.2 参与合同的洽谈、起草、审查、签约、变更、解除以及合同的签证、公证、调解、诉讼等活动,全程跟踪和检查合同的履行质量; 4.5.3 审查、登记合同对方单位代表资格及单位资质,包括营业执照、经营范围、技术装备、信誉、越区域经营许可等证件及履约能力(必要时要求对方提供担保)
立方根 √3 1 = 1 √ 2 = 1.260 √ 3 = 1.442 √ 4 = 1.587 √ 5 = 1.710 √ 6 = 1.817 √ 7 = 1.913 √8 = 2 √ 9 = 2.080 √ 10 = 2.154 √ 11 = 2.224 √ 12 = 2.289 √ 13 = 2.351 √ 14 = 2.410 √ 15 = 2.466 √ 16 = 2.520 √ 17 = 2.571 √ 18 = 2.621 √ 19 = 2.668 √ 20 = 2.714
平方根 √1=1 √2= 1.414 √3= 1.732 √4=2 √5= 2.236 √6= 2.449 √7= 2.646 √8= 2.828 √9=3 √10=3.162 √11 = 3.317 √12 = 3.464 √13 = 3.606 √14 = 3.742 √15 = 3.873 √16 = 4 √17 = 4.123 √18 = 4.243 √19 = 4.359 √20 = 4.472
山东省八年级数学《132 立方根 》学案 精品

立方根学习目标1. 掌握立方根的概念,立方根的性质,立方根的表示,立方根的公式2.能利用立方根解决实际问题重点:立方根的性质难点:立方根的公式一:知识频道:预习课本77页填一填1.立方根的概念一般地,如果即x3=a,那么x 叫做a的立方根(也叫三次方根)2..立方根的性质都有立方根,而且只有一个。
正数的立方根是,负数的立方根是,0的立方根是想一想填一填:平方根与立方根的区别与联系⑴⑵⑶3.立方根的表示每个数都有一个立方根,记作3a读作,其中a叫做,3叫做,数3 省略。
4.开立方的运算叫开立方。
到现在为止学过的运算有5.立方根的公式(3a)3=a 33a=a想一想a的取值范围是探究3a-与- 3a的关系是二:方法频道:1.求一个数的立方根⑴0.729 ⑵-1 ⑶-22710⑷10 ⑸-64解:(由学生完成)⑴⑵⑶⑷⑸2.根式求值问题⑴.327105-⑵36432+-⑶32004524⨯⨯⑷3271+解:(由学生完成)3.下列说法正确的是()A64的立方根是2 B-3是27的负的立方根C 8的立方根是+2和-2D -(-3)3的立方根是-3 4.一个数的立方根是它本身,则这个数是()A 1B -1C 0D ±1 05.-3216-的立方根是( )A –6B ±3C 36D -36. 若a<0,则a的立方根为()A 3aB - 3aC 3a -D ±3a 7.观察下列各式,思考并填空: 因为31-=-1 -31=-1 所以 31- = -31 因为 38-=-2 -38=-2 所以38-=-38以上各式有什么规律,用式子表示为 8.如果3x+16的立方根为4, 那么2x+4的算术平方根为9.一个正方体的体积为729厘米3, 则它的表面积为 10.求下列各式的值⑴ 364÷(1-81) ⑵323178+11.若m<0 则2m -33m = 12.若(2x-1)3=0.018 则x=13.求x ⑴(3x+2)3–1=6461 ⑵ 31(2x+1)3-81=114.若x 是320的整数部分,y 是320的小数部分. 求x, y。
重庆市万州区丁阳中学八年级数学上册《132立方根(2)》

重庆市万州区丁阳中学八年级数学上册《13.2立方根(2)》学案 人
教新课标版
引入
1. 立方根及开立方的概念
2. 平方根与立方根有什么不同? 被正数
零3、(1) 64的平方根是________立方根是________.
(2) 的立方根是________. (3) 37-是_______的立方根.
(4) 若 ,则 x=_______, 若 ,则 x=________. (5) 若 , 则x 的取值范围是__________
合作探究
1、完成教科书78页探究,总结规律
求负数的立方根,可以先求出这个负数的 的立方根,再取其 ,即 思考:立方根是它本身的数是 ,平方根是它本身的数是
2、一些计算机设有 键,用它可以求出一个立方根(或其近似值)。
有些计算器需要用 键求一个数的立方根。
精讲精练
例1、 求下列各式的值:
(1)3125-; (2)311
102- (3)310001-; 例2、求满足下列各式的未知数x :
(1) 364x 1250+=
练习
1.完成79页练习
2、计算: 327
102--- 3、计算:()2
3122⎛⎫-- ⎪⎝⎭327()92=-x ()93
=-x x
x -=2
课堂小结:求负数的立方根,可以先求出这个负数的的立方根,再取
其,即
思考:立方根是它本身的数是,平方根是它本身的数是
2、一些计算机设有键,用它可以求出一个立方根(或其近似值)。
有些计算器需要用键求一个数的立方根。
实用的平方根表立方根表
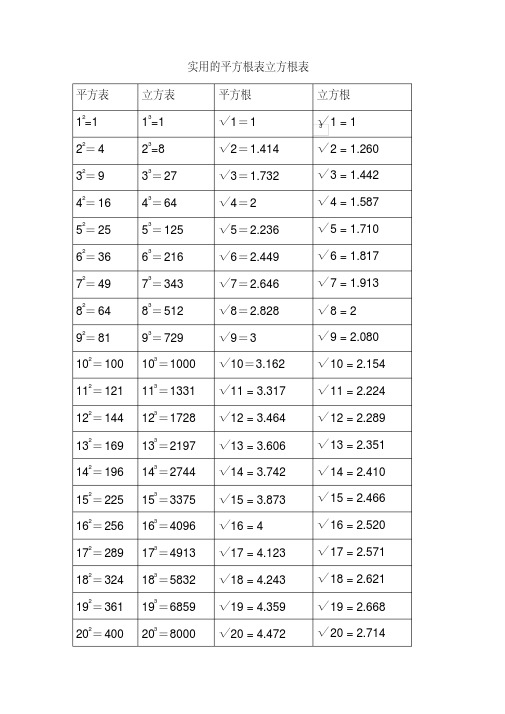
3 实用的平方根表立方根表平方表立方表平方根立方根12=1 13=1 √1=1 √1 = 1 22=4 23=8 √2=1.414 √2 = 1.260 32=9 33=27 √3=1.732 √3 = 1.442 42=16 43=64 √4=2 √4 = 1.587 52=25 53=125 √5=2.236 √5 = 1.710 62=36 63=216 √6=2.449 √6 = 1.817 72=49 73=343 √7=2.646 √7 = 1.913 82=64 83=512 √8=2.828 √8 = 2 92=81 93=729 √9=3 √9 = 2.080 102=100 103=1000 √10=3.162 √10 = 2.154 112=121 113=1331 √11 = 3.317 √11 = 2.224 122=144 123=1728 √12 = 3.464 √12 = 2.289 132=169 133=2197 √13 = 3.606 √13 = 2.351 142=196 143=2744 √14 = 3.742 √14 = 2.410 152=225 153=3375 √15 = 3.873 √15 = 2.466 162=256 163=4096 √16 = 4 √16 = 2.520 172=289 173=4913 √17 = 4.123 √17 = 2.571 182=324 183=5832 √18 = 4.243 √18 = 2.621 192=361 193=6859 √19 = 4.359 √19 = 2.668 202=400203=8000√20 = 4.472√20 = 2.7143√0 = 0(表示根号0等于0,下平方根表立方根表√1 = 1√2 = 1.414√3 = 1.732√4 = 2√5 = 2.236√6 = 2.449√7 = 2.646√8 = 2.828√9 = 3√10 = 3.162√11 = 3.317√12 = 3.464√13 = 3.606√14 = 3.742√15 = 3.873√16 = 4√17 = 4.123√18 = 4.243√19 = 4.359√20 = 4.472其中专业理论知识内容包括:保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1、 求下列各式的值:
(1) ;(2) (3) ;
例2、求满足下列各式的未知数x:
(1)
1.完成79页练习
2、计算:
(
1、这节课你学到的知识有
2、这节课你的收获有
3、这节课应注意的问题有
板
书
设
计
13.2立方根(2)
一、
二、
三、
四、
教
学
反
思
(1)通过估算检验计算结果的合理性,主要是依据两个公式:⑴ ;(2) (a为任意数).
估算一个根号表示的无理数所采用的方法可概括为“逐步逼近”.例如要估算 的大小,要求精确到小数点后一位.首先找出与43邻近的两个完全平方数,如36<43<49,则___< <___,由此可得 的整数部分是____,然后再由6.52=42.25,6.62=43.56,得6.5< <6.6,从而知 的一位小数应为5,即 ≈6.5或6.6.
13.2立方根(2)
金银滩复兴学校 殷志强
教
学
内
容
分
析
教
学
目
标
1、了解立方根的概念,会用根号表示一个数的立方根.
2、能用立方运算求某些数的立方根,了解开立方与立方ቤተ መጻሕፍቲ ባይዱ为逆运算,了解立方根的性质.
3、能通过估算检验计算结果的合理性,能估计一个无理数的大致范围,并能通过估算比较两个数的大小。
4、能应用立方根的概念及性质解决实际问题。
(3)用计算器开方
(这是重、难点)开方运算要用到键“ ”和键“ ”。对于开平方运算,按键顺序为:“ ”,被开方数,“=”;对于开立方运算,按键顺序为:“ ”,被开方数,“=”。
(2)的立方根是________. (3) 是_______的立方根.
(4)若,则x=_______,若,则x=________.
(5)若,则x的取值范围是__________
1、完成教科书78页探究,总结规律
求负数的立方根,可以先求出这个负数的的立方根,再取其,即
思考:立方根是它本身的数是,平方根是它本身的数是
重
点
1、立方根的概念、表示、求法
2、用估算的方法求无理数的近似值
难
点
用计算器进行开方运算
设
计
思
路
教学
环节
教师活动
学生活动
设计意图
创设情境
探索新知
课堂练习
巩固练习
课堂小结
1. 立方根及开立方的概念
2. 平方根与立方根有什么不同?
被开方数
平方根
立方根
正数
负数
零
3、(1) 64的平方根是________立方根是________.
