分类与整理统计表、统计图共33页文档

应用统计学第2章统计表统计图

对数图可以直观反映时间序列的环比变化趋势
可以在Office图表类型中选择自定义类型中的“对数图” ，也可通过将一般折线图纵轴“坐标轴格式” 中的“刻度” 设为“对数刻度”来绘制对数图。
例：某公司总成本和劳动成本的增长
该公司总成本和劳动成本每年增加相同的数量，因而用绝对数据作图时两条线是平行的，不小心可能会得出劳动成本占总成本固定比例的误解。实际上第1年占40%，第6年占60%。使用对数图就可以清晰反映劳动成本有更高的增长率。
“平滑线”复选框，就将折线图转换为曲线图。
⑵经济管理中几种常见的频数分布曲线
①正态分布曲线 ——这是客观事物数量特征上表现得最为普遍的一
类频数分布曲线。如人的身高、体重、智商，钢的含碳量、抗拉强度
，某种农作物的产量等等。
正态分布曲线
②偏态曲线
——按其长尾拖向哪一方又可分为右偏(正偏)和左偏(负偏)两类。
1.频数分布表
频数分布表列出了一系列分类数据的频率、总数或百分比，可以看出不同类别数据间的区别。
表2-1 1 000美元用途的频数分布表
用钱做什么购买奢侈品、旅游或礼物向慈善机构捐款还贷储蓄购买必需品其他
百分比/% 20 2 24 31 16 7
2.条形图
3.圆饼图
4.帕累托图
L = [ 10 × log 10 n ] 茎叶图类似于横置的直方图，但又有区别
直方图可大体上看出一组数据的分布状况，但没有给出具体的数值茎叶图既能给出数据的分布状况，又能给出每一个原始数值，保留了原始数据的信息
未分组数据—茎叶图（茎叶图的制作）
树茎树叶
数据个数
10 788
3
11 022347778889

统计图表

表号表号指表的序号，位于表的
左上方，一般以出现的先后顺序排列。
名称

名称又称标题，是一个表格的名称，应写在表的上方。标题用语要简练扼要，准确得体，一望即知该表的内容。

表的序号和标题之间留一个汉字的空格。二者居中
排在顶线的上方，长度不宜超过表的宽度，若标题
字数过多，应转行排列。
标目

标目即分类的项目。标目的好坏决定统计表的质量，要认真酌定。标目一般在表的上面一行或左侧一列。如果分类的标志只有一个，写在表的上行或左列都可以。如果分类的标志有两个，且二者没有隶属关系，则左列与上行各一个。如果两个分类标志有隶属关系，则要放在一个方向（或上面或左侧）分两行分述。标目确立了数据组织的逻辑，并确定了栏目下数据栏的性质。

2、数量类别。这是以数据的取值大小为分类标志，把数据按数值大小以分组或不分组的形式排出一个顺序来。（等距、比率）
对原始数据排序和分类以后，数量小的就可以直接计算，数量大时再做进一步分组，编制统计表、统计图为以后的分析打下基础。

三、统计表

1、定义：统计表是用来表达统计指标与被说明事物之间数量关系的表格。统计指标：在对数据进行统计分类以后，得到的各种数量结果称为统计指标。 2、作用：简洁、清晰、准确、一目了然，明显地反映出事物的全貌及其蕴含的特征，省去冗长的文字叙述，便于分析、比较、计算和记忆。 3、结构

图题的文字要言简意赅，具有说明性和专指性，使
人一看就能知道该图所要显示的是何事、何物，发生于何时、何地。如果图示资料比较复杂，这时图
题可用大标题与小标题呈现。图题的字体要与整个
图形的大小相称，一般是图中使用的最大号的文字。

第四节统计表与统计图(1)

ò ¼¼ ±¼ ×¼ ± í é í
1979¡ 1982Ä ± ¶ Ñ Á ¶ Í É · Ä Ô ± Ö £ CM£ « ê É ¼ §ä ù ¯ í ß ê ö ¤µ ¨ ©
统计表
Ë ý È Ê
80 60 40 20 0
ê ä Ä Á ¨ê © £ Ë £
Ð Ä
72 198 322 351 356 322 296 266
1.层次不清，结构混乱，难于理解。 2.线条过多。
修改后
表2 病变性质良性肿瘤恶性肿瘤﹡ 囊肿瘤样病变合计口腔颌面部不同病变构成情况例数 674 558 192 168 1592 构成比（%） 42.34 35.05 12.06 10.55 100.00
﹡包括癌437例，肉瘤101例，其他恶性肿瘤20例。
….
家政人员合计
….
725 6904
…..
63（8.7） 2130（30.9）
….
537 5974
…..
34（6.3） 1293（21.6）
（三）编制统计表应注意的事项
1、重点突出，简单明了。 2、合理安排主语和谓语的位置。横标目上的主语是所分析研究事物，纵标目上的谓语则是所研究的指标，两者相互联系，才能表达一个完整的意思。 3、表内数据要准确可靠。
4）圆中各部分用线分开，各部分可注明简要文字和百分比，也可用不同颜色或线条表示，并用图例加以说明。
5% 4% 10% 肠道传染病呼吸道传染病血液传播疾病虫媒传染病其他
22%
59%
图8-4某医院2004年收治传染病构成
4、线图（line graph）是用线段的升降来表示统计指标的变化趋势，或某现象随另一现象的变化情况。适用资料：描述统计量随另一连续性数值变量变化而变化的趋势。绘制方法： 1）横轴表示动态的事物，如时间，年龄等；纵轴表示频数或率。 2）坐标内点的位置要适当，并用短线依次将相邻的点连接。 3）单式线图和复式线图，≤4 图例

第02讲常用的统计表与图

依据它所显示的次数如何产生，次数分布可以区分为简单次数分布、分组简单次数分布、相对次数分布、累积次数分布等。次数分布表和次数分布图就是各种次数分布的列表形式和图示形式。
二、次数分布表——简单次数分布表
简单次数分布表（simple frequency table）就是依据每一个分数值在一列数据中出现的次数编制成的统计表。
根本目标
形象化的方式把事物的特性、规律显示出来。使人能获得全面与深刻的直观形象。便于说明问题与比较。
三、常用的统计图——统计图的种类
统计图的种类
条形图(Bar chart) 圆形图(Pie chart)
百分条图（percentage chart）
线图（ line chart，次数多边图、累积次数分布图）
Ð¡ Êý Î» Êý Ò» ÖÂ ¡¢ Î» ´Î ¶Ô Æë
²» ÄÜ ÓÐ ¿Õ
¸±×¢
Ø±Òª Ê±
Í¼ Àý
·Å ÔÚ Í¼ ÓÒ ÉÏ ½Ç »ò ±ê Ìâ µÄ ÉÏ ·½
下次上课再见！
一般统计表的常见错误举例1
表 2-15 第三组病人各年存活及死亡情况 (原表)
年份 (1)
病例数 (2)
存活数 (3)
住院期死亡总例数
急性期死亡数
住院期总病死率(%)
急性期病死率(%)
(4)=(2)+(3) (5) (6)=(4)/(2) (7)=(5)/(2)
1964 17
9
8
7
47.1
41.2
1965 13
8
5
4
38.5
30.8
1966 15
8
7

应用统计学第2章--统计表统计图

①利用 Excel 的 FREQUENCY 函数语法规则：格式：FREQUENCY(<数据区域>,<接收区间>)
接收区间——各组上限值组成的一列区域功能：返回各组的频数。
②使用【工具】→“数据分析”→“直方图”功能
其它数值数据统计图
统计图可以形象、直观、生动、简洁地显示数据的特征。常用的统计图有以下几种： 1.折线图 ——通常用来描述时间序列数据，用以表示某些指标的变化趋势。制作折线图时应正确选择坐标轴轴的刻度。对同样的统计资料，延伸或压缩某一坐标轴可能传达不同的甚至是误导的印象。
0—9 10—19 20—29 30—39 40—49 50—59 60—69 70—79 80—89 90以上
未分组数据的茎叶图
• 用于显示未分组的原始数据的分布
• 由“茎”和“叶”两部分构成，其图形是由数字组成的
• 以该组数据的高位数值作树茎，低位数字作树叶 • 对于n(20≤n≤300)个数据，茎叶图最大行数不超
标签下选“平滑线”复选框，就将折线图转换为曲线图。
⑵经济管理中几种常见的频数分布曲线
①正态分布曲线 ——这是客观事物数量特征上表现得最为普遍的
一类频数分布曲线。如人的身高、体重、智商，钢的含碳量、抗拉强
度，某种农作物的产量等等。
正态分布曲线
②偏态曲线
——按其长尾拖向哪一方又可分为右偏(正偏)和左偏(负偏)两类。
排序是把数据从小到大(或从大到小)进行排列。 (2) 茎叶图
茎叶图就是将数据分成几组(称为茎)，每组中数据的值(称为叶)放置在每行的右边。结果可以显示出数据是如何分布的，以及数据中心在哪里。
为了制作茎叶图，可以将整数作为茎，把小数(叶) 化整。例如，数值5.40，它的茎(行)是5，叶是4；数值 4.30，它的茎(行)是4，叶是3。也可以将数据的十位数作为茎，个位数作为叶。

统计表与统计图

小学六年级小升初数学专题复习（23）——统计表与统计图一、简单的统计表知识归纳1．统计表定义：是表现数字资料整理结果的最常用的一种表格．是由纵横交叉线条所绘制的表格来表现统计资料的一种形式．统计调查所得来的原始资料，经过整理，得到说明社会现象及其发展过程的数据，把这些数据按一定的顺序排列在表格中，就形成“统计表”．2．统计表构成及格式：一般由表头、行标题、列标题和数字资料四个主要部分组成，必要时可以在统计表的下方加上表外附加．（1）表头应放在表的上方，它所说明的是统计表的主要内容．（2）行标题和列标题通常安排在统计表的第一列和第一行，它所表示的主要是所研究问题的类别名称和指标名称，通常也被称为“类”．（3）表外附加通常放在统计表的下方，主要包括资料来源、指标的注释、必要的说明等内容．统计表分类：统计表形式繁简不一，通常是按项目的多少，分为单式统计表与复式统计表两种．只对某一个项目数据进行统计的表格，称为单式统计表，也称之为简单统计表．统计项目在2个或2个以上的统计表格，称之为复式统计表．1．按作用不同：统计调查表、汇总表、分析表．2．按分组情况不同：简单表、简单分组表、复合分组表．（1）简单表：即不经任何分组，仅按时间或单位进行简单排列的表．（2）简单分组表：即仅按一个标志进行分组的表．（3）复合分组表：即按两个或两个以上标志进行层叠分组的表．常考题型例1：六一儿童节，学校进行歌咏比赛，7位评委给张华的打分如下：评委 1 2 3 4 5 6 7打分92 90 95 88 85 97 90去掉一个最高分，一个最低分，张华的平均分是分．分析：根据平均数的应用和求平均数的方法解答即可．解：去掉一个最高分97分，最低分85分；其他五位评委打的平均分是：（92+90+95+88+90）÷5=455÷5=91（分）；答：张华的平均分是91分；故答案为：91．点评：此题属于简单的统计和求平均数问题，根据求平均数的方法，总数÷份数=平均数，列式计算即可．二、两种不同形式的单式条形统计图知识归纳1．条形图定义：用一个单位长度表示一定的数量，根据数量的多少画成长短不同的条形，条形的宽度必须保持一致，然后把这些条形排列起来，这样的统计图叫做条形统计图．它可以表示出每个项目的具体数量．2．单式条形统计图只表示一种数据的变化情况，比较简单．常考题型例：看图回答问题．（1）哪个季度的月平均销售量多？多多少？（2）从统计图中你还能发现什么信息？分析：（1）先分别求出第一季度和第三季度的月平均销售量，再比较哪个季度的月平均销售量多，进而求出多的具体的数量即可；（2）从统计图中我还能发现以下信息：一月销售120箱，二月销售110箱，三月销售130箱，七月销售195箱，八月销售190箱，九月销售185箱；其中二月销售的箱数最少，七月销售的箱数最多；等等．解：（1）第一季度的月平均销售量：（120+110+130）÷3，=360÷3，=120（箱），第三季度的月平均销售量：（195+190+185）÷3，=570÷3，=190（箱），190＞120，190-120=70（箱）；答：第三季度的月平均销售量多，多70箱．（2）从统计图中我还能发现以下信息：一月销售120箱，二月销售110箱，三月销售130箱，七月销售195箱，八月销售190箱，九月销售185箱；其中二月销售的箱数最少；七月销售的箱数最多；等等．点评：此题主要考查从条形统计图中获取信息，并根据信息解决问题；也考查了求平均数的方法：平均数=总数量÷总份数．三、单式折线统计图知识归纳1．折线统计图：用一个单位长度表示一定数量，用折线的上升或下降表示数量的多少和增减变化．容易看出数量的增减变化情况．2．折现统计图制作步骤：（1）标题：根据统计表所反映的内容，在正上方写上统计图的名称；（2）画出横、纵轴：先画纵轴，后画横轴，横、纵轴都要有单位，按纸面的大小来确定用一定单位表示一定的数量；（3）描点、连线：根据数量的多少，在纵、横轴的恰当位置描出各点，然后把各点用线段顺序连接起来．常考题型例：如图，电车从A站经过B站到达C站，然后返回．去时B站停车，而返回时不停，去时的车速为每小时48千米，返回时的车速是每小时千米．分析：从统计图中可知电车从A站到达B站用了4分钟，并在B站休息了1分钟，从B站到达C站用了5分钟，所以电车从A站到达C站共行驶了4+5=9（分钟），根据“速度×时间=路程”求出从A站到C站的距离；电车在C站休息了3分钟，从第13分钟开始行驶到第19分钟返回A站，根据“速度=路程÷时间”即可得出答案．解：48×（4+5）÷（19-13），=48×9÷6，=72（千米）；答：汽车从C站返回A站的速度是每小时行72千米．故答案为：72．点评：此题首先根据问题从图中找出所需要的信息，然后根据数量关系式：“速度×时间=路程”和“速度=路程÷时间”即可作出解答．四、扇形统计图知识归纳1．扇形统计图的特点：扇形统计图是用整个圆的面积表示总数，用圆内的扇形面积表示各部分数量占总数的百分比．2．读懂扇形统计图：（1）获取信息的方法：运用综合、对比等多种观察方法，可以从扇形统计图中获取信息，还可以利用这些信息提出相应的问题．（2）扇形统计图的优点：它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系．3．利用扇形统计图解决问题，就是解决有关不同类型的百分数应用题，按照百分数应用题的解题思路和解题方法进行解答．常考题型例：如图是某小学六年级学生视力情况统计图．①视力正常的有76人，视力近视的有人；②假性近视的同学比视力正常的人少%；（百分号前保留一位小数）③视力正常的学生与视力非正常学生人数的比是．分析：由图可知：把总人数看成单位“1”，视力正常的人数占总人数的38%，近视的人数占总人数的30%，假性近视的人数占总人数的32%；①视力正常的有76人，它对应的百分数是38%，由此用除法求出总人数，再求出总人数的30%就是近似的人数；②用视力正常占的百分数减去假性近视人数占的百分数，然后用求得的差除以视力正常占的百分数即可；③先求出视力非正常学生人数占总人数的百分数，然后作比．解：①76÷38%×30%，=200×30%，=60（人）；答：视力近视的有60人．②（38%-32%）÷38%，=6%÷38%，≈15.8%；答：假性近视的同学比视力正常的人少15.8%．③38%：（32%+30%），=38%：62%，=38：62，=19：31；答：视力正常的学生与视力非正常学生人数的比是19：31．故答案为：60，15.8%，19：31．点评：解决本题关键是从图中读出数据，找出单位“1”，再根据基本的数量关系求解．一．选择题（共6小题）1．如图，（）可以表示下面哪种情况的统计．A．4个学生期末数学考试成绩B．四年级喜欢各项运动的男女生人数C．小明1﹣﹣8岁的身高D．蛋糕店的草莓蛋糕和芒果蛋糕最近5天的销售情况2．下图表示的是甲班和乙班男、女生人数的情况．如果每个班都是36人，那么甲班的男生比乙班多（）人．A．4 B．11 C．18 D．433．5、如图是两个厂男、女职工人数的统计图，甲厂和乙厂的女职工人数相比，（）。

第三章统计整理

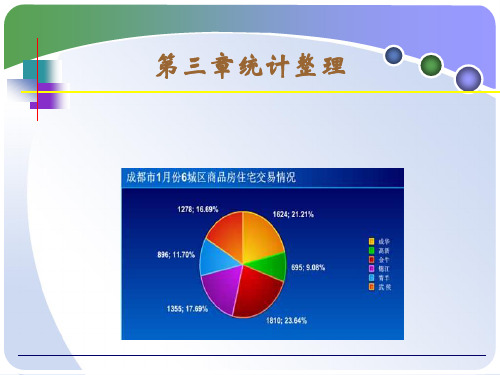
按照习惯，成绩一般分为不及格、及格、按照习惯，成绩一般分为不及格、及格、中良好、等、良好、优秀
即组限 60分以下 60~70 70~80 80~90 90分以上 65 75 85 组中值
上组限不在内
利用Excel Excel进行分组㈢利用Excel进行分组
数据分析” 直方图直方图” 选“工具”-“数据分析”-“直方图” 工具” 数据分析定义“输入区域” 数据定义“输入区域”—数据分组中每组上限， “接收区域”—分组中每组上限，包括在本组接收区域” 分组中每组上限内 “输出区域”—结果输出区域” 结果
编制结果如下：编制结果如下：
日产量（件）X 日产量（件）X 20 21 22 23 24 25 26 合计工人数（人) 工人数（人) f 3 5 6 4 3 2 1 24
组距数列
指每个组的变量值用一个区间来表现的变量数列
编制条件:
变量是连续变量；变量是连续变量；或：总体单位数较多，变量不同取值个数总体单位数较多，也较多的离散变量。也较多的离散变量。
复合分组
按性别分类
对教师的分类
共计12组共计组 × × 男 2×3×2
女高级中级初级青年中年
按职称分类按年龄分类
第三节次数分布 ★ 一、分布数列的概念及种类
二、组距数列的编制三、累计次数与累计频率
将总体各单位按分组标志分组后，将总体各单位按分组标志分组后，次数分布形成的各单位在各组的分布
地位
统计整理的步骤
拟定统计整理方案统计资料的预处理数据处理制作统计表或统计图
第二节统计分组
将总体中所有单位按一定的标志划统计分组分为类型或性质不同的若干部分的过程统计分组的作用: 划分现象的类型反映现象内部结构分析现象之间的依存关系

统计数据的整理及其显示(ppt-107页)(共106张PPT)全篇

2、统计分组的原则
穷尽原则
互斥原则
注意：统计分组是对总体认识深化的手段，它是一切统计研究的基础，应用于统计工作的全过程，是统计研究的基本方法。
⑴ 类型分组
揭露社会经济现象的类型，反映各类型的特点。
例
单位：亿元
类型 1999年 2000年 2001年 2002年
农业 14 106.2 13 873.6 14 462.8 14 931.5
审核
对第二手数据：完整性：准确性：适用性：数据的来源、口径以及
有关背景资料；时效性：尽可能使用最新的数据。
（2）数据筛选
当数据中的错误不能予以纠正，或者有些数据不符合调查的要求而又无法弥补时，需要对数据进行筛选。
数据筛选的内容：
▪ 将某些不符合要求的数据或有明显错误的数
据予以剔除；
例如：企业按人数分组
499及以下
500 ～ 999
1000 ～ 2999 3000及以上
工人按工资分组
600 ～ 700 700 ～ 800 800 ～ 1200
1200 ～ 1500
适用条件：它适用于变量值变化范围较大、不同变量值个数
较多的离散型变量及连续型变量的场合。
注意：连续型变量的数值不能一一列举，故
例如：按以五分制计分的成绩对全班100名学生进行分组，宜单变量数列；按以百分制计分的成绩对全班100名学生进行分组，宜组距式数列；
1. 定类数据的排序
▪ 字母型数据，排序有升序降序之分，但习惯
上用升序
▪ 汉字型数据，可按汉字的首位拼音字母排列
，也可按笔画排序，其中也有笔画多少的升序降序之分
2. 定距和定比数据的排序
递递增增排排序序：后设可一表组示数为据：为X(1X)1<，X(X2)2<，……<X，(NX) N，递减排序可表示为：X(1)>X(2)>…>X(N)

统计学原理4.4统计表与统计图

在绘制茎叶图时要注意以下几个问题。一是根据数据的特点设定叶的单位，本例中的叶的单位是1，如果数据的值较大或较小，可以将叶的单位设为10或0.1等等。二是叶的数据上下要对齐，这样可以突出分布的特点。三是重复出现的数据要重复计算。
5.箱线图箱线图也称箱须图，是利用数据中的五个统计量：最小值、下四分位数、中位数、上四分位数与最大值来描述数据的一种方法。箱线图描述了数据的分布和分散程度的特征，也可以用来判断数据是否具有对称性，特别可以用于对多个样本的比较。绘制箱线图要把握二个要点：一是将数据在同一数轴上表示出来；二是在数轴上找出五个统计量的值。
【例2】市场研究部门为了调查啤酒市场的销售情况，在一家超市抽取了50次购买记录，统计结果如下：
啤酒品牌
购买次数
A
20
B
13
C
8
D
4
EHale Waihona Puke 5试用条形图描述不同品牌的啤酒销售状况。
解：这个问题是进行比较，故应该绘制比较条形图。
a) 横向条形图
b) 纵向条形图
图 2 比较条形图由图2 可以非常清楚地看出A 品牌的啤酒的销售量是领先的。
2、按主词的结构分类：
（1）简单表：对总体未经任何分组（2）分组表：对总体仅按一个变量进行分组（3）复合表：对总体按两个或以上变量进行层叠分组
3、按宾词设计
（1）平行排列表
分类：
（2）分层排列表
4
统计表的设计要求：
简练、明确、实用、美观、便于比较。
2020/5/31
5
2020/5/31
次数分布直方图，纵坐标为频率的直方图称为频率分布直方图。
a)频数分布直方图
图1 直方图

人教版七下数学第20讲数据的收集与整理统计图表的综合运用(学生版)

第20讲统计图表的综合运用（原卷版）类型一统计表与统计图的综合（1）统计表与扇形统计图的综合典例1（2020•大连二模）2020年初我国爆发了新冠肺炎疫情，为了增加学生对疫情和肺炎的预防知识的了解，某学校利用网络开展了相关知识的宣传教育活动，为了解这次的宣传效果，学校从全校3600名学生中随机抽取200名学生进行知识测试（满分100分，得分均为整数），并根据这200人的测试成绩，制订如下统计图表：200名学生成绩的频数表等级成绩/分频数/人E50≤a＜6020D60≤a＜7030C70≤a＜80mB80≤a＜90nA90≤a≤10030（1）被抽取的学生中，成绩为A的人数为30人，成绩等级为B的人数占被抽取的学生总人数的百分比为%．（2）m＝，n＝；（3）如果80分以上为优秀，请估计全校3600名学生中成绩优秀的人数．针对练习11．（2020•绍兴）一只羽毛球的重量合格标准是5.0克～5.2克（含5.0克，不含5.2克），某厂对4月份生产的羽毛球重量进行抽样检验，并将所得数据绘制成如图统计图表．4月份生产的羽毛球重量统计表组别重量x（克）数量（只）A x＜5.0mB 5.0≤x＜5.1400C 5.1≤x＜5.2550D x≥5.230（1）求表中m的值及图中B组扇形的圆心角的度数．（2）问这些抽样检验的羽毛球中，合格率是多少？如果购得4月份生产的羽毛球10筒（每筒12只），估计所购得的羽毛球中，非合格品的羽毛球有多少只？（2）统计表与条形统计图的综合典例2（2021秋•崂山区期末）某校对七年级300名学生进行了教学质量检测（满分100分），现从中随机抽取部分学生的成绩进行整理，并绘制成如图不完整的统计表和统计图：等级频数频率（频率＝频数÷总数）不及格10.05及格20.10良好a0.45优秀8b注：60分以下为：“不及格”，60～69分为“及格”，70～79分为“良好，80分以上为“优秀”请根据以上信息回答下列问题：（1）求出a，b值，并补全统计图；（2）若用扇形统计图表示统计结果，则“良好”所对应扇形的圆心角为多少度？（3）请估计该校七年级本次监测成绩为70分以上的学生共有多少人？针对练习23．（2021秋•金水区校级期末）今年12月4日是第八个国家宪法日，宪法是国家的根本大法，是治国安邦的总章程．为贯彻落实习近平总书记关于宪法学习宣传教育的系列重要指示精神，某校开展了丰富多彩的宪法宣传教育活动，并分别在活动前后举办了有关学宪法的知识竞赛（百分制），活动结束后，在七年级随机抽取25名学生活动前后的竞赛成绩进行整理和描述，下面给出部分信息：活动后被抽取学生竞赛成绩为：82，88，96，98，84，86，89，99，94，90，79，91，99，98，87，92，86，99，98，84，93，88，94，89，98．活动后被抽取学生竞赛成绩频数分布表成绩x（分）频数（人）75≤x＜80180≤x＜85385≤x＜90790≤x＜95m95≤x＜100n请你根据以上信息解决下列问题：（1）本次调查的样本容量是，表中m＝；n＝；（2）若想直观地反映出活动前后被抽取学生竞赛成绩的变化情况，应该把数据整理，绘制成折线统计图；（填“扇形”“条形”或“折线”）（3）若90分及以上都属于A等级，根据调查结果，请估计该校2000名同学中活动后的竞赛成绩为A 等级的学生有多少人？。

六年级上册数学课件 - 统计图的选择北师大版(共33页)

统计图的选择
大房身小学
第31届夏季奥运会在巴西举办
中国体育代表团获得26枚金牌
描述材料中的数据，选择哪种统计图比较合适？为什么？
材料1：第24届～第31届奥运会我国获得金牌情况：第24届获得5枚，第25届获得16枚，第26届获得16枚，第27届获得28枚，第28届获得32枚，第29届获得51枚，第30届获得38枚，第31届获得 26枚。
1.你能从下面三幅图中读出哪些信息？
人数
百分比
上升下降
2.下面数据分别用哪种统计图表示比较合适？
氧化 14%
食物 39%
喝水 47%
乐乐从一年级到五年级每年体检的身高记录如下。要表示乐乐身高的变化情况。
你想从哪个角度描述以下数据，并选择适合的统计图？
（1）小明家2011年的四个季度的用电量如下：
40 36 32
条形统计图能清楚地表示
28
24
16 12
出每个项目的具体数目。
8
4
0
第24届第25届第26届第27届第28届第29届第30届第31届
52 48 44 40 36 32 28
24 20 16 12
8 4 0
第24届第25届第26届第27届第28届第29届第30届第31届
材料2：2008年，第29届奥运会在我国首都北京举办。在这届奥运会上，我国共获得100枚奖牌，其中金牌51枚，银牌21枚，铜牌28枚。
第29届奥运会我国获奖牌情况统计图
60
50
40
30
20
10
0
金牌
银牌
铜牌
第29届奥运会我国获奖牌情况统计图
铜牌 28%