欧几里得证明勾股定理简化版

合集下载

勾股定理两种主要证明方法

勾股定理两种主要证明方法勾股定理是一个基本的几何定理，是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释，又给出了另外一个证明。

“勾三，股四，弦五”是勾股定理的一个最著名的例子。

当整数a,b,c满足a^2;+b^2;=c^2;这个条件时，(a,b,c)叫做勾股数组。

也就是说，设直角三角形两直角边为a和b，斜边为c，那么a^2;+b^2;=c^2;。

在中国数学史中同样源远流长，是中算的重中之重。

《周髀算经》中已有“勾三股四弦五”的记述，赵爽的《周髀算经》中将勾股定理表述为“勾股各自乘，并之，为弦实。

开方除之，即弦。

”勾股定理现辨认出约有种证明方法，就是数学定理中证明方法最少的定理之一。

下面我们一起来观赏其中一些证明方法：方法一：赵爽“弦图”三国时期吴国数学家赵爽在为《周髀算是经》并作注释时，编定了一幅“勾股圆方图”，也称作“弦图”，这就是我国对勾股定理最早的证明。

年世界数学家大会在北京召开，这届大会会标的中央图案正是经过艺术处理的“弦图”，标志着中国古代数学成就。

方法二：刘徽“青朱进出图”约公元年，三国时代魏国的数学家刘徽为古籍《九章算术》作注释时，用“出入相补法”证明了勾股定理。

方法三：欧几里得“公理化证明”希腊数学家欧几里得（euclid，公元前～公元前）在巨著《几何原本》给出一个公理化的证明。

年希腊为了纪念二千五百年前古希腊在勾股定理上的贡献，发售了一张邮票，图案就是由三个棋盘排序而变成。

方法四：毕达哥拉斯“拼图”毕达哥拉斯（公元前—前年），古希腊知名的哲学家、数学家、天文学家.将4个全等的直角三角形拼成边长为(a＋b)的正方形abcd，使中间留下边长c的一个正方形洞．画出正方形abcd．移动三角形至图2所示的位置中，于是留下了边长分别为a与b的`两个正方形洞。

如何证明勾股定理

如何证明勾股定理勾股定理是数学中的一个基本定理，它描述了直角三角形三边之间的关系。

勾股定理的表述为：在直角三角形中，直角边的平方和等于斜边的平方。

也就是说，如果直角三角形的两个直角边长度分别为a和b，斜边长度为c，那么a² + b² = c²。

勾股定理的证明方法有很多种，下面介绍其中两种常见的证明方法：方法一：赵爽弦图证明赵爽是中国古代数学家，他在《周髀算经》中给出了勾股定理的详细证明。

其中，他使用了“勾股圆方图”进行证明。

证明过程如下：1.画两个边长为a和b的正方形，分别作为勾股形两直角边。

2.在两个正方形中，各画一个边长为c的正方形，作为股方。

3.连接两个小正方形的对角线，形成四个全等的直角三角形。

4.通过面积计算，可以证明a² + b² = c²。

方法二：欧几里得证明欧几里得是古希腊数学家，他在《几何原本》中给出了勾股定理的证明。

证明过程如下：1.画一个直角三角形ABC，其中∠C=90°。

2.作CD⊥AB于点D，交AC于点E。

3.由于△ADC和△BDE都是直角三角形，并且∠CAD=∠EBD=90°-∠A，所以△ADC∽△BDE。

4.根据相似三角形的性质，有AD/BD = AC/BE = CD/DE。

5.由于CD=DE（因为它们都是直角三角形的高），所以AD/BD = AC/BE = 1。

6.因此，AD=BD且AC=BE。

7.所以，AB² = AD² + BD² = 2AD² = AE² + BE² = AE² + AC²。

这两种证明方法虽然不同，但都能有效地证明勾股定理的正确性。

在实际应用中，我们可以根据需要选择合适的证明方法。

中外勾股定理的证明方法赏析

二、刘徽的“出入相补法”
即：ｎ＋６ｃ。；
三国时代魏国的数学家刘徽在魏景元四年（即公元２６３年）为古籍《九章算术》作注
三、欧几里得对毕达哥拉斯定理的证明在西方，人们认为是毕达哥拉斯最早发现并证明这一定理的，但遗憾的是，他的证明
股／
，／
妙的证明．《勾股圆方图注》一开首就说：“勾股各自
，茕她
乘，并之为弦实．开方除之，即弦． ”这实际上给出了如下两个公式：
图２
图３
对于刘徽的 “出入相补法 ”，我们可以作
（１）勾 ×勾＋股Ｘ股＝弦 ×弦（ａ＋ｂ＝ｃ）；图给出证明：
释，也提出了一个证明勾股定理的方法，即以方法已经失传．关于对毕达哥拉斯定理的证
，形证数．刘徽的证明原也有一幅图，可惜图已明，现在人类保存下来的最早的文字资料是
，失传，只留下一段文字：“勾自乘为朱方，股自欧几里得所著的《几何原本》第一卷中的命题
Ｒｔ△ＡＪ／，ＪＩ＝ＦＨ＝ａ，
‘
‘
５＝／３＝９０。一Ａ，３：４，
．
‘
．
．
Ｌ４＝Ｌ５，ＤＡ＝＝Ⅱ，ＡＤＬ＝ＬＩＪＫ＝９０。，
‘ Ｒｔ△ＡＤＬ￣ｔＬｔ△ＩＪＫ．
．
．
４× 一＋（６一。）．
图１
‘
‘
６＝１＝９０。一Ｅ日Ｆ，１＝２，

几何原本中的勾股定理及其逆定理的现代数学证明

几何原本中的勾股定理及其逆定理的现代数学证明作者：张胜持来源：《科学与财富》2020年第20期摘要：本文对《几何原本》中欧几里得关于勾股定理及其逆定理的证明方法运用现代数学的公式进行了详细证明，简明扼要，简单直观，非常符合于现代人的书写和阅读习惯。

关键词：勾股定理;证明;欧几里得;初等数论。

0引言：勾股定理是一个古老的数学定理，其勾股数计算历来受到人们的重视。

古希腊著名数学家欧几里得在他所著的《几何原本》予以了证明，是人类历史上最早的一种证明方法。

但是在这本书中，其证明几乎是文字叙述性的，现代人阅读起来非常困难，甚至困惑不解。

本人试将这些文字叙述转换为现代数学公式，然后进行推导证明。

其中勾股定理证明是第一卷1.47命题，逆定理是1.48命题。

下面分别予以详细讨论。

1;;;;;; 勾股定理证明：1.47命题对勾股定理的描述：在直角三角形中，直角所对的边上的正方形的面积等于夹直角两边上的正方形面积的和。

为了证明这个命题，他还画了一个图，如图1所示，图中的 R 点是本人为叙述方便所加的，它是位于 BC 和 AL 的交点处。

该图为书中的图1.47。

证明如下所述。

求证：BC2= BA2+ AC2。

证明：在△FBC 和△ABD 中，∠FBC = ∠FBA + ∠ABC ，∠ABD = ∠CBD + ∠ABC ，∵∠FBA = ∠CBD =90°，∴∠FBC = ∠ABD .∵FA = AB， BC = BD ，∴△FBC ≌△ABD （两条边及一个角相等）。

即SFBC = SABD （面积相等）。

∵SFBC = SABFG÷2，亦即 SABFG =2SFBC （同底同高三角形的面积等于其上正方形面积的一半【*】）。

（因为∠BAC 和∠BAG 同为直角，故 CA 与 AG 在同一条直线上，这样有BF∥CG，使三角形同底同高条件成立）。

另有 SABD = SBDLR/2，亦即 SBDLR =2SFBC （原因同【*】）。

勾股定理的九种证明方法(附图)

勾股定理的证明方法一、传说中毕达哥拉斯的证法（图1）左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、，斜边为的直角三角形拼成的。

右边的正方形是由1个边长为的正方形和4个直角边分别为、，斜边为的直角三角形拼成的。

因为这两个正方形的面积相等(边长都是)，所以可以列出等式，化简得。

二、美国第20任总统茄菲尔德的证法（图3）这个直角梯形是由2个直角边分别为、，斜边为的直角三角形和1个直角边为的等腰直角三角形拼成的。

因为3个直角三角形的面积之和等于梯形的面积，所以可以列出等式，化简得。

三、相似三角形的证法：4.相似三角形的方法：在学习了相似三角形以后，我们知道在直角三角形中，斜边上的高把这个直角三角形所分成的两个三直角角形与原三角形相似。

如图，Rt△ABC中，∠ACB=90°。

作CD⊥AB，垂足为D。

则△BCD∽△BAC，△CAD∽△BAC。

由△BCD∽△BAC可得BC2=BD ×BA，①由△CAD∽△BAC可得AC2=AD ×AB。

②我们发现，把①、②两式相加可得BC2+AC2=AB（AD+BD），而AD+BD=AB，因此有BC2+AC2=AB2，这就是a2+b2=c2。

这也是一种证明勾股定理的方法，而且也很简洁。

它利用了相似三角形的知识。

四、古人的证法：CABD如图，将图中的四个直角三角形涂上深红色，把中间小正方形涂上白色，，以弦为边的正方形称为弦实，然后经过拼补搭配，“令出入相补，各从其类”，他肯定了勾股弦三者的关系是符合勾股定理的。

即“勾股各自乘，并之为弦实，开方除之，即弦也”。

赵爽对勾股定理的证明，显示了我国数学家高超的证题思想，较为简明、直观。

五、项明达证法：作两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP∥BC，交AC于点P.过点B作BM⊥PQ，垂足为M；再过点F作FN⊥PQ，垂足为N.∵∠BCA = 90°，QP∥BC，∴∠MPC = 90°，∵ BM⊥PQ，∴∠BMP = 90°，∴ BCPM是一个矩形，即∠MBC = 90°.∵∠QBM + ∠MBA = ∠QBA =90 °，∠ABC + ∠MBA = ∠MBC = 90°，∴∠QBM = ∠ABC，又∵∠BMP = 90°，∠BCA = 90°，BQ = BA = c，∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.即a^2+b^2=c^2六、欧几里德射影定理证法：如图，Rt△ABC中，∠ABC=90°，AD是斜边BC上的高，通过证明三角形相似则有射影定理如下：1）（BD）^2;=AD·DC，（2）（AB）^2;=AD·AC ，（3）（BC）^2;=CD·AC 。

勾股定理的证明方法欧几里得证法

勾股定理的证明方法欧几里得证法针对小学生的文章《神奇的勾股定理欧几里得证法》小朋友们，今天我们要一起来探索一个超级神奇的数学定理——勾股定理！特别是它的欧几里得证法哦。

比如说，我们有一个直角三角形，两条直角边分别是 3 和 4，斜边是 5。

那为什么 3 的平方加上 4 的平方就等于 5 的平方呢？欧几里得爷爷就想出了一个聪明的办法来证明。

他就像一个聪明的魔术师，用一些巧妙的图形和推理，让我们一下子就明白了这个道理。

想象一下，我们有两个一样的直角三角形，把它们拼在一起，就会出现一个新的图形。

通过这个新图形，我们就能清楚地看到勾股定理是怎么回事啦！是不是很有趣呢？小朋友们，数学的世界就像一个大大的魔法乐园，勾股定理就是其中一颗闪亮的星星，让我们一起去发现更多的奇妙吧！《一起来了解勾股定理的欧几里得证法》小朋友们，你们知道吗？在数学的王国里，有一个非常重要的定理，叫做勾股定理。

而欧几里得爷爷有一种特别厉害的方法来证明它。

咱们先来讲个小故事。

有一天，小明在纸上画了一个直角三角形，两条直角边分别是 2 和 3，他想知道斜边是多少。

这时候，欧几里得爷爷的方法就派上用场啦！欧几里得爷爷说，我们可以通过一些巧妙的图形变换来找到答案。

就好像是在玩拼图游戏一样。

比如说，我们把四个这样的直角三角形拼在一起，就能得到一个大正方形。

然后通过计算这个大正方形的面积，就能算出斜边的长度啦！小朋友们，快来和我一起探索这个神奇的数学世界吧！《有趣的勾股定理欧几里得证法》亲爱的小朋友们，今天我们要讲一个有趣的数学知识——勾股定理的欧几里得证法。

假设我们有一块大大的三角形蛋糕，它是直角三角形哦，两条直角边分别是 1 和 2。

那怎么知道斜边有多长呢？这时候，欧几里得爷爷就来帮忙啦！他告诉我们，可以用一些特别的方法来算。

他让我们想象把这个三角形蛋糕切成几块，然后重新拼起来。

拼完之后，我们就能发现其中的秘密，知道勾股定理是怎么回事啦！小朋友们，是不是觉得很神奇？让我们一起在数学的海洋里快乐地玩耍吧！《欧几里得证法与勾股定理》小朋友们好呀！今天我们来聊聊勾股定理，特别是欧几里得爷爷的证明方法。

勾股定理的证明

勾股定理的证明据不完全统计，勾股定理的证明方法已经多达400多种了。

下面我便向大家介绍几种十分著名的证明方法。

【证法1】（赵爽证明）以a、b 为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于. 把这四个直角三角形拼成如图所示形状.∵RtΔDAH ≌RtΔABE,∴∠HDA = ∠EAB.∵∠HAD + ∠HAD = 90º，∴∠EAB + ∠HAD = 90º，∴ABCD是一个边长为c的正方形，它的面积等于c2.∵EF = FG =GH =HE = b―a ,∠HEF = 90º.∴EFGH是一个边长为b―a的正方形，它的面积等于.∴∴.【证法2】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b，所以面积相等. 即，整理得.【证法3】（1876年美国总统Garfield证明）以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵RtΔEAD ≌RtΔCBE,∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠DEC = 180º―90º= 90º.∴ΔDEC是一个等腰直角三角形，它的面积等于.又∵∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形，它的面积等于∴.∴.【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。

他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。

欧几里得证明勾股定理的详细步骤

欧几里得证明勾股定理的详细步骤全文共四篇示例，供读者参考第一篇示例：欧几里得证明勾股定理是几何学中的一个重要定理，也是古代数学中的经典问题之一。

欧几里得通过几何分析和推理，证明了勾股定理的正确性。

下面我们来详细介绍欧几里得的证明步骤。

欧几里得证明勾股定理的基本思路是利用几何特性和几何运算来推导结论。

在证明过程中，我们假设有一个直角三角形，三边分别为a、b、c，并且假设c为斜边，a、b为直角边。

根据勾股定理，有a² + b² = c²。

第一步：构造正方形我们首先构造一个正方形，其边长为a+b。

这个正方形可以分成四个小正方形和一个边长为c的正方形。

第二步：利用几何运算根据正方形的性质和几何运算，可以得出以下结论：1. 四个小正方形的面积之和为2ab。

2. 一个边长为c的正方形的面积为c²。

第三步：结合步骤一和步骤二由于正方形的面积等于其边长的平方，所以我们可以得出以下等式：( a + b )² = 2ab + c²第四步：化简将第三步中等式中左边展开，有：a² + 2ab + b² = 2ab + c²将等式两侧的2ab化简，得：a² + b² = c²欧几里得证明勾股定理的步骤主要是通过构造正方形、利用几何运算、化简等方法来推导出结论，从而证明了勾股定理的正确性。

这一证明方法深刻展示了欧几里得的几何思维和推理能力，也为后世数学家提供了许多启发和借鉴。

欧几里得的勾股定理证明是几何学中的经典之作，对后世几何学的发展具有重要意义。

第二篇示例：欧几里得证明勾股定理是一项经典的数学证明，它是欧几里得几何学中最著名的定理之一。

勾股定理指出：直角三角形中，直角边的平方等于其他两条边的平方和。

即对于一个直角三角形ABC，设直角边为AB，斜边为AC，则有AB²+BC²=AC²。

勾股定理的证明(比较全的证明方法)

传说中毕达哥拉斯的证法
证明：从Rt△ABC的三边向外各作一个正方形（如图），作CN⊥DE 交AB于M，那么正方形ABED被分成两个矩形．连结CD和KB． ∵由于矩形ADNM和△ADC同底（AD），等高(即平行线AD和CN间的距离)， ∴S矩形ADNM＝2S△ADC．又∵正方形ACHK和△ABK同底（AK）、等高（即平行线AK和BH间的距离）， ∴S正方形ACHK＝2S△ABK． ∵AD＝AB，AC＝AK，∠CAD＝∠KAB， ∴△ADC≌△ABK．由此可得S矩形ADNM＝S正方形ACHK ．同理可证S矩形MNEB＝S正方形CBFG． ∴S矩形ADNM＋S矩形MNEB＝S正方形ACHK＋S正方形CBFG．
总统巧证勾股定理
D
a
C
c
b
c
b
A
E a B
美国第二十任总统伽菲尔德
返回
向常春的证明方法
S梯形ABCD 1 1 2 1 (a b b)(a b) a ab 2 2 2
S梯形ABCD S四边形AECD SEBC 1 2 1 c (a b )b 2 2 1 2 1 1 2 c ab b 2 2 2
探索勾股定理
数学家毕达哥拉斯的发现：
探索 C 勾股 A、B、C的面积有什么关系？定 SA+SB=SC 理
A
B
设：直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系？
返回
SA+SB=SC
C
A a
c
b B
探 SA=a2 索 SB=b2 勾 SC=c2 股定 2 2 2 a +b =c 理
2
a
以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于 . 把这四个直角三角形拼成如图所示形状，使A、E、 B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上. ∵ RtΔHAE ≌ RtΔEBF, ∴ ∠AHE = ∠BEF. ∵ ∠AEH + ∠AHE = 90º ,∴ ∠AEH + ∠BEF = 90º .∴ ∠HEF = 180º―90º= 90º. ∴ 四边形EFGH是一个边长为c的正方形. 它的面积等于c2. ∵ RtΔGDH ≌ RtΔHAE, ∴ ∠HGD = ∠EHA. ∵ ∠HGD + ∠GHD = 90º ,∴ ∠EHA + ∠GHD = 90º . 又∵ ∠GHE = 90º ,∴ ∠DHA = 90º + 90º = 180º . ∴ ABCD是一个边长为a + b的正方形，它的面积等于（a+b）² ， ∴（a+b）² =4×½ab+c² ， ∴a² +b² =c²

勾股定理的十六种证明方法

勾股定理的几种证明方法我们刚刚学了勾股定理这重要的知识，老师告诉我们，勾股定理的证明方法非常得多，其数量之大足可以撰写出一部书来，我对知识的探求欲望被激发了出来，随即到网络上查找了勾股定理的证明方法，现在我收集到了几种。

【证法1】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等. 即abc ab b a 214214222⨯+=⨯++，整理得 222c b a =+.这是课本上面为我们提供的毕达哥拉斯的证明方法，我在网络上查阅资料发现：毕达哥拉斯是西方公认的发现勾股定理的数学家，因此，我们可以在外国的一些资料上发现，勾股定理在西方被称为毕达格拉斯定理。

【证法2】（邹元治证明）以a 、b 为直角边，以c 为斜边做四个全等的直角三角形，则每个直角三角形的面积等于ab 21.把这四个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上，B 、F 、C 三点在一条直线上，C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形，它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.这个证明对我来讲也很好理解，它利用了全等三角形的性质和因式分解的知识，这对于我们初二的学生来说，是能够领会的。

勾股定理的证明(比较全的证明方法)

∴S矩形ADNM＋S矩形MNEB＝S正方形ACHK＋S正方形CBFG．即S正方形ADEB＝S正方形ACHK＋S正方形CBAFG ，
DN
也就是 a2+b2=c2．
F B
E
12
返回
刘徽的证法
刘徽在《九章算术》中对勾股定理的证明：
勾自乘为朱方，股自乘为青方，令出入相补，各
从其类，因就其余不移动也．合成弦方之幂，开方除之，即弦也．
里德（Euclid，是公元前三百年左右的人）在编著《几何原本》
时，认为这个定理是毕达哥达斯最早发现的，所以他就把这个
定理称为“毕达哥拉斯定理”，以后就流传开了。（为了庆祝这一定理
的发现，毕达哥拉斯学派杀了一百头牛酬谢供奉神灵，因此这个定理又有人叫做
“百牛定理”．）
A
3
走
进
数
学
史
A
4
勾股定理的证明
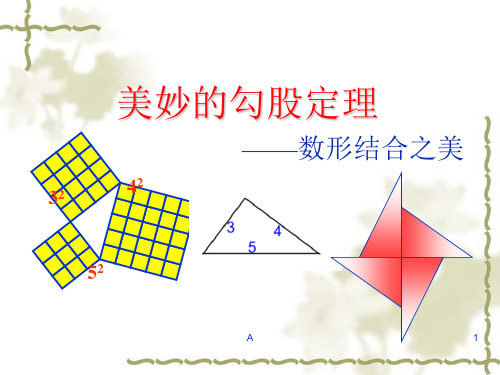
美妙的勾股定理
——数形结合之美
32
42
52
A
1
勾股
勾股弦的定义
在中国古代，人们把弯曲成直角的手臂的上半部分称为
"勾"，下半部分称为"股"。我国古代学者把直角三角形
较短的直角边称为“勾”，较长的直角边称为“股”，
斜边称为“弦”.
A
2
勾股定理的由来
走进数学史
这个定理在中国又称为“商高定理”，在外国称为“毕达哥拉
勾看关砖一
你系铺次
股能，成毕
发同的达
A
现学地哥什们面拉
定么，反斯
？我映去
理们直朋 9
数学家毕达哥拉斯的发现：

勾股定理的多种证明方法

勾股定理的多种证明方法勾股定理的多种证明方法勾股定理是数学史上一个伟大的定理,同时也是一个历史悠久的定理，如何证明勾股定理呢？勾股定理证明方法有哪些呢?下面是的勾股定理证明方法资料，欢迎阅读。

勾股定理的种证明方法(部分)【证法1】(梅文鼎证明)做四个全等的直角三角形，设它们的两条直角边长分别为a、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D、E、F在一条直线上. 过C作AC的延长线交DF于点P.∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD,∴ ∠EGF = ∠BED，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c，∴ ABEG是一个边长为c的正方形.∴ ∠ABC + ∠CBE = 90º.∵ RtΔABC ≌ RtΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则,∴ .【证法2】(项明达证明)做两个全等的直角三角形，设它们的两条直角边长分别为a、b(b>a) ，斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP‖BC，交AC于点P.过点B作BM⊥PQ，垂足为M;再过点F作FN⊥PQ，垂足为N.∵ ∠BCA = 90º，QP‖BC，∴ ∠MPC = 90º，∵ BM⊥PQ，∴ ∠BMP = 90º，∴ BCPM是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴ ∠QBM = ∠ABC，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c，∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.【证法3】(赵浩杰证明)做两个全等的直角三角形，设它们的两条直角边长分别为a、b(b>a) ，斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的`多边形.分别以CF，AE为边长做正方形FCJI和AEIG，∵EF=DF-DE=b-a，EI=b，∴FI=a，∴G,I,J在同一直线上，∵CJ=CF=a，CB=CD=c，∠CJB = ∠CFD = 90º，∴RtΔCJB ≌ RtΔCFD ，同理，RtΔABG ≌ RtΔADE，∴RtΔCJB ≌ RtΔCFD ≌ RtΔABG ≌ RtΔADE∴∠ABG =∠BCJ,∵∠BCJ +∠CBJ= 90º,∴∠ABG +∠CBJ= 90º,∵∠ABC= 90º,∴G,B,I,J在同一直线上，【证法4】(欧几里得证明)做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD. 过C作CL⊥DE，交AB于点M，交DE于点L.∵ AF = AC，AB = AD，∠FAB = ∠GAD，∴ ΔFAB ≌ ΔGAD，∵ ΔFAB的面积等于，ΔGAD的面积等于矩形ADLM的面积的一半，∴ 矩形ADLM的面积 =.同理可证，矩形MLEB的面积 =.∵ 正方形ADEB的面积= 矩形ADLM的面积 + 矩形MLEB的面积∴ ，即 .勾股定理的多种证明方法毕达哥拉斯证法：一、传说中毕达哥拉斯的证法(图1)左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为a、b，斜边为c的直角三角形拼成的。

欧几里得证明勾股定理简化版

欧几里得的证法
设△ABC为一直角三角形，其中A为直角。

从A点划一直线至对边，使其垂直于对边。

延长此线把对边上的正方形一分为二，其面积分别与其余两个正方形相等。

在定理的证明中需要如下四个辅助定理：
▪如果两个三角形有两组对应边和这两组边所夹的角相等，则两三角形全等SAS。

▪三角形面积是任一同底同高之平行四边形面积的一半。

▪任意一个正方形的面积等于其二边长的乘积。

▪任意一个矩形的面积等于其二边长的乘积（据辅助定理3）。

证明的思路为：把上方的两个正方形，透过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形。

其证明如下：
1. AL⊥DE，分别与BC和DE直角相交于K、L。

2. 分别连接CF、AD，形成两个三角形BCF、BDA。

3. AB＝FB,BC＝BD,∠ABC+∠ABF＝∠ABF+∠CBD
4. 因为AB 和BD 分别等于FB 和BC，所以△ABD 必须相等于△FBC。

5. 因为A 与K 和L在同一直线上，所以四方形BDLK 必须二倍面积于
△ABD。

同理正方形BAGF必须二倍面积于△FBC。

6. 正方形面积BAGF = AB2，面积ACIH = AC2。

7. 把这两个结果相加，AB2+ AC2 = BD×BK + KL×KC
8. 由于BD=KL，BD×BK + KL×KC = BD(BK + KC) = BD×BC= BC2
9. 由于CBDE是个正方形，因此AB2 + AC2 = BC2。

勾股定理的多种证明方法

勾股定理的多种证明方法勾股定理是数学史上一个伟大的定理,同时也是一个历史悠久的定理，如何证明勾股定理呢？勾股定理证明方法有哪些呢?下面是的勾股定理证明方法资料，欢迎阅读。

勾股定理的种证明方法(部分)【证法1】(梅文鼎证明)做四个全等的直角三角形，设它们的两条直角边长分别为a、b ，斜边长为c. 把它们拼成如图那样的一个多边形，使D、E、F在一条直线上. 过C作AC的延长线交DF于点P.∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD,∴ ∠EGF = ∠BED，∵ ∠EGF + ∠GEF = 90°，∴ ∠BED + ∠GEF = 90°，∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c，∴ ABEG是一个边长为c的正方形.∴ ∠ABC + ∠CBE = 90º.∵ RtΔABC ≌ RtΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90º.即∠CBD= 90º.又∵ ∠BDE = 90º，∠BCP = 90º，BC = BD = a.∴ BDPC是一个边长为a的正方形.同理，HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S，则,∴ .【证法2】(项明达证明)做两个全等的直角三角形，设它们的两条直角边长分别为a、b(b>a) ，斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.过点Q作QP‖BC，交AC于点P.过点B作BM⊥PQ，垂足为M;再过点F作FN⊥PQ，垂足为N.∵ ∠BCA = 90º，QP‖BC，∴ ∠MPC = 90º，∵ BM⊥PQ，∴ ∠BMP = 90º，∴ BCPM是一个矩形，即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º，∠ABC + ∠MBA = ∠MBC = 90º，∴ ∠QBM = ∠ABC，又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c，∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.【证法3】(赵浩杰证明)做两个全等的直角三角形，设它们的两条直角边长分别为a、b(b>a) ，斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形.分别以CF，AE为边长做正方形FCJI和AEIG，∵EF=DF-DE=b-a，EI=b，∴FI=a，∴G,I,J在同一直线上，∵CJ=CF=a，CB=CD=c，∠CJB = ∠CFD = 90º，∴RtΔCJB ≌ RtΔCFD ，同理，RtΔABG ≌ RtΔADE，∴RtΔCJB ≌ RtΔCFD ≌ RtΔABG ≌ RtΔADE∴∠ABG = ∠BCJ,∵∠BCJ +∠CBJ= 90º,∴∠ABG +∠CBJ= 90º,∵∠ABC= 90º,∴G,B,I,J在同一直线上，【证法4】(欧几里得证明)做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD. 过C作CL⊥DE，交AB于点M，交DE于点L.∵ AF = AC，AB = AD，∠FAB = ∠GAD，∴ ΔFAB ≌ ΔGAD，∵ ΔFAB的面积等于，ΔGAD的面积等于矩形ADLM的面积的一半，∴ 矩形ADLM的面积 =.同理可证，矩形MLEB的面积 =.∵ 正方形ADEB的面积= 矩形ADLM的面积 + 矩形MLEB的面积∴ ，即 .勾股定理的多种证明方法毕达哥拉斯证法：一、传说中毕达哥拉斯的证法(图1)左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为a、b，斜边为c的直角三角形拼成的。

欧几里得几何与勾股定理

欧几里得几何与勾股定理一、欧几里得几何1.欧几里得几何的基本公理：–同一平面内，两点确定一条直线。

–同一平面内，一条直线和该直线外一点确定一个圆。

–连接圆上任意两点的线段，其长度相等。

–圆的半径与圆心到圆上任意一点的距离相等。

2.欧几里得几何的基本概念：–点：几何图形的基本构成部分，没有大小和形状，只有位置。

–线段：连接两点的线，具有长度。

–射线：起点固定，无限延伸的直线。

–直线：无限延伸的线，无起点和终点。

–平面：无限延伸的二维空间。

–圆：平面上所有到圆心距离相等的点的集合。

3.欧几里得几何的基本性质：–平行线的性质：同一平面内，不相交的两条直线称为平行线。

–直线的性质：直线可以无限延伸，两点确定一条直线。

–角度的性质：圆心角等于它所对的圆弧所对应的圆周角。

–三角形的性质：三角形的内角和为180度。

–四边形的性质：四边形的对角线互相平分。

4.欧几里得几何的重要定理：–勾股定理：直角三角形两条直角边的平方和等于斜边的平方。

–Pythagorean theorem：In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equalto the sum of the squares of the lengths of the other two sides.–相似定理：若两个三角形对应角相等，则它们相似。

–平行线定理：若一条直线与两条平行线相交，那么它所截得的对应角相等。

二、勾股定理1.勾股定理的定义：–勾股定理是指直角三角形两条直角边的平方和等于斜边的平方。

2.勾股定理的证明：–证明方法有多种，如几何证明、代数证明、构造法证明等。

–其中，几何证明方法主要包括：面积法、相似三角形法、平行线法等。

3.勾股定理的应用：–在计算直角三角形的边长、面积等方面具有重要作用。

欧几里得证明勾股定理的故事

欧几里得证明勾股定理的故事故事一嘿，朋友！今天我要跟你讲讲欧几里得证明勾股定理的超有趣故事！你知道吗，欧几里得那可是个超级厉害的数学家！当时啊，大家都对直角三角形的三边关系感到好奇，都想弄明白这其中的奥秘。

欧几里得就开始动脑筋啦，他整天埋头思考，写写画画。

他可不是随便试试哦，那是真的下了大功夫。

他先从最简单的图形入手，一点点地分析，不放过任何一个小细节。

就好像在解开一个超级复杂的谜题。

经过好多好多天的努力，终于，他找到了关键！那种感觉，就像是在黑暗中突然看到了亮光。

当他证明出勾股定理的时候，那可真是轰动了整个数学界。

大家都对他佩服得五体投地。

欧几里得的这个证明，让后来的人们在数学的道路上走得更稳、更远。

他就像是个领路人，带着大家探索数学的奇妙世界。

怎么样，是不是觉得欧几里得超厉害？他的故事是不是很鼓舞人心呀！故事二亲爱的，来听我讲讲欧几里得证明勾股定理的事儿！欧几里得啊，那可是数学界的大神！当时大家对直角三角形的边边关系那叫一个迷糊。

可欧几里得不服气，他心里想，我一定要把这个搞清楚！于是乎，他天天闷头琢磨。

有时候饭都忘了吃，觉都忘了睡。

他一会儿看看这个图形，一会儿又算算那个数据。

脑袋里的小算盘打得噼里啪啦响。

有一天，突然灵感就像闪电一样击中了他。

他兴奋得差点跳起来。

他的证明过程那叫一个精彩，就像是一场精心编排的舞蹈，每一步都恰到好处。

后来啊，他的证明成果传遍了各地。

人们都对他竖起大拇指，说他太牛啦！欧几里得的努力让我们明白了，只要坚持，再难的问题也能被解决。

你说，咱们是不是也应该像欧几里得一样，遇到难题不放弃，努力去攻克它？。