跃峰奥数PPT4图论方法3-9(圈分析之同色的单色圈)
数学奥林匹克竞赛解题方法(第9讲 图论方法)

1 第9讲 数学解题方法(图论方法)
课时:3课时
教学课型:理论课
教学目的: 让学生对数学解题方法之一图论方法的知识有个全面的认识,并由此产生兴趣。
教学重点与教学难点:
● 运用图论方法进行有效地解决数学问题。
教学内容:
● 心理学家纽亏尔和西蒙提出:熟悉的知识和技能是问题解决者“可能信步漫游的网络”
● 把现实世界中的某些事情用点和联结点的边(线段或曲线)所组成的图形来描述,并应用这样的图形特征来解答问题.
例1 设R b b b R a a a n n ∈∈+,,,,,,,2121 ,且),,3,2,1(0n i b a i i =>+则有不等式
∑∑∑∑∑=====+≤+n i n i i i
n i n i i i n i i i i i b a b a b a b a 11111,其中等号当1=n 或1>n 有n
n b a b a b a === 2211时成立.(《数学通报》问题974题)
例2 (算术-几何平均值不等式)设+∈R a a a a n ,,,321,对于+∈N n ,则n n n a a a n
a a a 2121≥+++,其中等号当且仅当n a a a === 21时成立.。
图论课件第七章图的着色
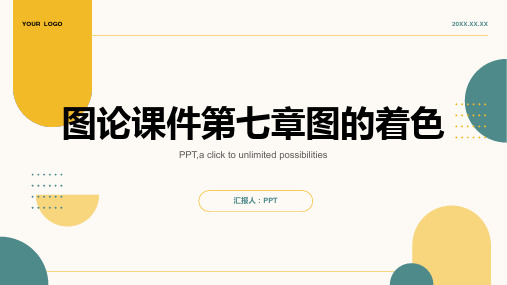
全着色:给每个顶点和每条边都 分配一个颜色,使得相邻顶点、 边都不同色
ቤተ መጻሕፍቲ ባይዱ
添加标题
添加标题
添加标题
添加标题
边着色:给每条边分配一个颜色, 使得相邻边不同色
部分着色:只给部分顶点和边分 配颜色,部分顶点和边不参与着 色
图的着色应用
图的着色概述
图的着色应用
旅行商问题
定义:旅行商问题是一个经典的组合优化问题,指的是给定一组城市和每 对城市之间的距离,要求找到访问每个城市一次并返回到原点的最短路径。
应用场景:旅行商问题在许多领域都有应用,如物流、运输、电路设计等。
图的着色在旅行商问题中的应用:通过给城市着色,可以将问题转化为图 的着色问题,从而利用图的着色算法来求解旅行商问题。
图的着色的应用案
06
例
地图着色问题
定义:地图着色问题是一个经典的组合优化问题,旨在为地图上的 国家或地区着色,使得相邻的国家或地区没有相同的颜色。
背景:地图着色问题在计算机科学、数学和地理学等领域都有广泛 的应用。
应用案例:地图着色问题可以应用于许多实际场景,如地图制作、 交通规划、网络设计等。
图的着色在排课问题中的应用:通过将排课问题转化为图的着色问题,可以运用图的着色算 法进行求解,从而得到最优的排课方案
图的着色算法在排课问题中的优势:通过将排课问题转化为图的着色问题,可以运用图的 着色算法进行求解,从而得到最优的排课方案,避免了传统排课方法的繁琐和主观性
图的着色在排课问题中的实际应用案例:以某高校为例,通过运用图的着色算法进行排课, 成功解决了该校的排课问题,提高了排课效率和教学质量
贪心策略:在图的着色问题中,贪心策略是选择与当前未着色顶点相邻的未使用颜色进行着色。
离散数学——图论PPT课件

• 完全图:一个(n,m)图G,其n个结点中每个结点均与其它n-1个结点相邻接,记为Kn。 • 无向完全图:m=n(n-1)/2 • 有向完全图:m=n(n-1) • 举例说明以上几种图。
第20页/共93页
定义补图
• 设图G=<V,E> , G’=<V,E’> ,若G’’=<V,E∪E’> 是完全图,且E∩E’= 空集,则称G’是G的补图。 • 事实上,G与G’互为补图。
正则图
• 所有结点均有相同次数d的图称为d次正则图。 • 如4阶的完全图是3次正则图,是对角线相连的四边形。 • 试画出两个2次正则图。
第27页/共93页
两图同构需满足的条件
• 若两个图同构,必须满足下列条件: (1)结点个数相同 (2)边数相同 (3)次数相同的结点个数相同
• 例子
第28页/共93页
• 图是人们日常生活中常见的一种信息载体,其突出的特点是直观、形象。图论,顾 名思义是运用数学手段研究图的性质的理论,但这里的图不是平面坐标系中的函数, 而是由一些点和连接这些点的线组成的结构 。
第8页/共93页
• 在图形中,只关心点与点之间是否有连线,而不关心点具体代表哪些对象,也不关 心连线的长短曲直,这就是图的概念。
定义图的子图
• 子图:设G=<V,E> , G’=<V’,E’> ,若V’是V的子集, E’是E的子集,则 G’是G的子图。 • 真子图:若V’是V的子集,E’是E的真子集。 • 生成子图:V’=V,E’是E的子集。 • 举例说明一个图的子图。
第18页/共93页
定义(n,m)图
• (n,m)图:由n个结点,m条边组成的图。 • 零图:m=0。即(n,0)图,有n个孤立点。 • 平凡图:n=1,m=0。即只有一个孤立点。
图论课件-PPT课件

学习方法
目的明确
态度端正 理论和实践相结合
充分利用资源
逐步实现从知识到能力到素质的深化和
升华
课程考核
平时成绩 (30%-40%)
闭卷考试 (60%-70%)
图论模型
为了抽象和简化现实世界,常建立数学模型。图是关 系的数学表示,为了深刻理解事物之间的联系,图 是常用的数学模型。 (1) 化学中的图论模型 19世纪,化学家凯莱用图论研究简单烃——即碳氢 化合物 用点抽象分子式中的碳原子和氢原子,用边抽象原子间 的化学键。
E={w1r1, w1r2, w2r2, w2r3, w2r4, w3r3, w3r5}代表每个仓库和每个 零售店间的关联。则图模型图形为: w1 w2 w3
r1
r2
r3
r4
r5
29
(3) 最短航线问题 用点表示城市,两点连线当且仅当两城市有航线。为了 求出两城市间最短航线,需要在线的旁边注明距离值。 例如:令V={a, b, c, d, e}代表5个城市} E={a b, ad, b c , be, de}代表城市间的直达航线 则航线图的图形为: a 320 500 d 370 b 140 430 e c
图论学科简介 (2)
19世纪末期,图论应用于电网络方程组
和有机化学中的分子结构 20世纪中叶,由于计算机的发展,图论 用来求解生产管理、军事、交通运输、 计算机和网络通信等领域中的离散性问 题 物理学、化学、运筹学、计算机科学、 电子学、信息论、控制论、网络理论、 社会科学、管理科学等领域应用
七桥问题
近代图论的历史可追溯到18世纪的七桥问题:
穿过Kö nigsberg城的七座桥,要求每座桥通过 一次且仅通过一次。
跃峰奥数PPT1代数组合4-3(整体思考之通性叠合)

温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
代数组合4-3(整体思考之等式叠合)●冯跃峰本讲内容本节为第1板块(代数组合)第4专题(研究特例整体思考)的第3小节(等式叠合),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、流畅、简练。
【整体思考】有些问题是从一些个体或局部提出的【1】,但解决它却要从整体入手【1】——将个体放入整体中,通过研究整体性质【1】来发现个体性质。
【1】它有3种主要方式:研究整体发现个体三种整体思考方式平均值估计(构造若干个同类个体)【1】题中给定、或自我构造。
整体函数(通过多元函数刻划整体性质)通式叠合(性质通式叠合一起得出结论)两个趣题:(1)量纸问题:如何量出一张纸的厚度?——取100张(同类个体)纸叠起来量。
(2)追针问题:时针与分针经历多少时间重合一次(口答)■?⇒单个时间段不易计算⇒两个时间段也不易计算⇒…多少时间后容易计算总体时间?⇒12小时后,两针又回到原来位置。
12小时候,时针追上分针多少次?——先看时针追上分针一次两者路程有何关系:追上一次,等价于多跑一圈。
从而分针共追上时针11次,每次经历的时间是12/11小时■。
【追针问题解答(整体思考)】例【代数4-3】平面给定n个不全共线的点,每个点处写上一个实数,如果一条直线通过两个或两个以上的点,则此线通过点处的数的和为零,证明:所有的点处的数都为0。
跃峰奥数PPT2组合几何4-11(染色问题之撒网策略)

温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
【百度文库】跃峰奥数PPT经典原创组合几何4-11(染色问题之撒网策略)●冯跃峰本讲内容本节为第2板块(组合几何)第4专题(染色问题)的第11小节(撒网策略),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、简练。
【百度文库】跃峰奥数PPT经典原创【百度文库】跃峰奥数PPT 经典原创染色问题的就是按一定的规则对相关对象染色,使之具有某种性质。
染色问题常有如下3种思考方法:3种思维方法局部扩展先对局部染色,然后扩展到整体(注意整体目标的分解)研究特例归纳通式、迁移特征、建立递归、操作化归。
拟对象逼近先构造满足部分条件的拟染色,然后改进本节介绍“拟对象逼近”的相关例子■。
【题感】从目标看,所找的m 个凸n 边形要满足2个条件:(1)同色;(2)全等。
其中同色是很容易的,只需“基点”足够多即可。
因此,可采用拟对象逼近策略,先满足全等【1】。
由此想到全等的定义:完全重合【1】。
进一步,全等图形一组“对应点”【2】构成的两个子图形是全等的【2】。
由此想到一个充分条件:作m 条全等的曲线,内接一条曲线的凸n 边形一定与另一条曲线上的对应凸n 边形全等。
为了保证n 边形是凸的,只需此曲线为凸曲线,且任何3点不共线。
这样的曲线很多,比如抛物线,圆等,其中以圆最简单。
【几何4-11】将平面上一个正方形内的所有点2-染色,试证:对任何正整数m 、n ,存在m 个全等的凸n 边形,它们的mn 个顶点互不相同且同色。
跃峰奥数PPT2组合几何4-3(染色问题之区域格点染色)

奥数系列讲座——组合几何4-3(染色问题之区域格点染色)●冯跃峰本讲内容本节为第2板块(组合几何)第4专题(染色问题)的第3小节(区域格点染色),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、简练。
编号与染色的一个共同特征就是分类。
当编号只用到数字的互异性时,编号与染色是等价的。
当编号涉及其他数字特征时,则要发掘图形特征与数字特征的相互关系,由此寻找规律。
编号与染色常有如下3种思考方法:3种思维方法局部扩展先构造局部,然后扩展到整体(注意整体目标的分解)研究特例归纳通式、迁移特征、建立递归、变动化归。
拟对象逼近先构造满足部分条件的拟对象,然后改进本次讲座介绍变若(x ,y )是红色,则T 中所有满足x'≤x 且y'≤y 的点(x',y')均为红色。
如果n 个蓝点的横坐标各不相同,则称这n 个蓝点所成的集合为一个X-集;如果n 个蓝点的纵坐标各不相同,则称这n 个蓝点所成的集合为一个Y-集。
证明:X-集的个数f (X )与Y-集的个数f (Y )相等。
(第43届IMO )【题感】目标很简单,证明两个集合容量相等【1】。
但条件非常复杂【1】,自然想到先将其简化。
它包括两个方面:(1)点集的存在域【1】;(2)染色具有的性质【1】。
其中(1)有明显的几何意义(三角形区域),但为便于计算f (X )等,可将有关格线编号。
别扭的是“染色性质”,这自然想到用相应几何图形来刻画。
【符号化】集合T 是由直线x=0,y=0【1】,及x+y=n-1【1】围成的三角形区域。
为方便,从下至上将直线y=0,y=1,…,y=n-1称为第1行,第2行,…第n 行【1】;从左至右将直线x=0,x=1,…x=n -1称为第1列,第2列,……第n 列【1】;从上至下将直线x+y=n-1,x+y=n-2,…x+y=0称为第1斜行,第2斜行,…第n 斜行【1】。
跃峰奥数PPT2组合几何4-7(染色问题之拟对象逼近)

温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
【百度文库】跃峰奥数PPT经典原创组合几何4-7(染色问题之拟对象逼近)●冯跃峰本讲内容本节为第2板块(组合几何)第4专题(染色问题)的第7小节(拟对象逼近),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、简练。
【百度文库】跃峰奥数PPT经典原创【百度文库】跃峰奥数PPT 染色问题的就是按一定的规则对相关对象染色,使之具有某种性质。
染色问题常有如下3种思考方法:3种思维方法局部扩展先对局部染色,然后扩展到整体(注意整体目标的分解)研究特例归纳通式、迁移特征、建立递归、操作化归。
拟对象逼近先构造满足部分条件的拟染色,然后改进本节介绍“拟对象逼近”的相关例子■。
【题感】从目标看,要找一个特殊的同色直角三角形:(30°,60°,90°)。
它可分解为两个部分:(1)3个同色点;(2)构成(30°,60°,90°)三角形(不好优化)。
先寻找“拟对象”(满足1.5个条件):3个点中有2个同色【1】,且构成(30°,60°,90°)三角形【1】。
先让哪两点同色呢?注意到最重要的是90°【1】,想到让同色点为斜边端点【1】,即找距离为2【1】的同色点,然后作圆【1】。
90°2找距离为2的同色点是很容易的,取3点利用抽屉原理即可■。
图论课件--与色数有关的几类图和完美图

( G )c l( G )
定义5 设G是一个图。若对G的每个点导出子图H,均 有 ( H ) c l ( H ) ,则称G为完美图。
例如Kn, 偶图是完美图,而不含三角形但含奇圈的图不 是完美图。 因为不含三角形的但含奇圈的图的团数为2,但色数为3, 所以,它不能是完美图。 注:完美图问题是点着色的进一步讨论题材,属于比较 高深和困难的问题。
25
补充定理:设G是一个偶图,记h为G的最大匹配包含 的边数,i为G的最大独立集包含的顶点数,j为构成覆盖G 的顶点的G的最小点边集合,则:i = j = m+n-h。
2、关于色数的完美图的主要结论
定理7 偶图的补图是完美图。 分析:欲证 G 是完美图,要证明对任意 H G 有
(H ) c l(G )
证明:设G是k临界图。如果G有割点v, 设G1,G2,…,Gr是 G-v的分支。又设第i个分支顶点集为Vi (1≦i≦r)。
设Hi=G[Vi∪{v}], (1≦i≦r)。则Hi是k-1可正常点着色 的,现对每个Hi进行k-1正常点着色,且v都分配同一种颜色, 那么,将着色后的Hi合在一起,得到G的k-1正常点着色方 案,这与G是k色图矛盾。所以临界图没有割点。
8
以,k(G)≦Δ (G); 情形2, H是完全图Hk
在这种情况下,由于G是连通的非完全图,那么在H 之外,必然有边和H相连,即Δ ≥K(H)=k(G);
情形3, H既不是奇圈又不是完全图,由例3知道, k≥4。H满足例4中条件。 所以,由例4中的结论有:
( H ) n ( H ) 2 m ( H )( n H ) ( k ( H ) 1 ) 1
设g的k临在这种情况下由于g不是奇圈所以h之外必然有边和h相连即g3另一方面kgkh3所在这种情况下由于g是连通的非完全图那么在h之外必然有边和h相连即情形3h既不是奇圈又不是完全图由例3知道k4h满足例4中条件
图论-总结PPT课件

.
16
第三节 割点、桥和割集
3.1 割点和桥(割边)
定义1 设v是图G的一个顶点,若G-v的支数大于 G的支数,则称顶点v为图G的一个割点(如图)。
degu + degv≥p-1,
则G是连通的。[这个定理是一个充分条件]
定理3 设G=(V,E)是至少有一个顶点不是弧立顶 点的图。若对任意v∈V,degv为偶数,则G中 有回路。
定理4 若图G中的两个不同顶点u与v间有两条不 同的路联结,则G中有回路。
.
6
例1 若G是一个恰有两个奇度顶点u和v的无向图,则 G连通G+uv连通。
.
8
第五节 欧拉图(Euler)
5.1 欧拉图
定义1 设(G,V)是一个图,则包含图的所有顶 点和所有边的闭迹称为欧拉闭迹;存在一 条欧拉闭迹的图称为欧拉图。
定理1 图G是欧拉图当且仅当G是连通的且每 个顶点的度都是偶数。
(定理1对多重图也成立)
.
9
第六节 哈密顿图
6.1 哈密顿图 定义1 设G是一个图,则图G中包含G的所有顶
数称为顶点v的度,记为degv。 定理1 (握手定理)设G=(V,E)是一个具有p个顶点q条边的图,
则G中各顶点度的和等于边的条数q的两倍,即∑degv=2q。 推论1任一图中,度为奇数的顶点的数目必为偶数。
.
3
定义3 设G是图,若Δ(G)=δ(G)=r,即G的每个顶点的 度都等于r,则G称为r度正则图。
图论中的圈与块(共79张PPT)精选

程序代码
PROCEDURE DFS(v);
begin
inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign
lowlink[v] := sign; //给lowlink[v]赋初始值
for 寻找一个v的相邻(xiānɡ lín)节点u
if 边uv没有被标记过 then
1:询问某两个点之间的min(u,v)
2:删除一条边
你的任务是对于每个询问,输出min(u,v)的值。 (WC2006)
2024/2/27
5
第五页,共79页。
水管局长(2)
数据范围约定 结点个数N≤1000 图中的边数M≤100000 询问(xúnwèn)次数Q≤100000 删边次数D≤5000
32
第三十二页,共79页。
关键(guānjiàn)网线(2)
朴素算法: 枚举每条边,删除它,然后判断是否有独立
出来的连通区域内没有A属性或者(huòzhě)没 有B属性。复杂度O(M2) 当然,这个复杂度太大了!
2024/2/27
33
第三十三页,共79页。
关键(guānjiàn)网线(3)
a
b
2024/2/27
27
第二十七页,共79页。
嗅探器(2)
数据范围(fànwéi)约定 结点个数N≤100 边数M≤N*(N-1)/2
2024/2/27
28
第二十八页,共79页。
嗅探器(3)
朴素算法: 枚举每个点,删除它,然后(ránhòu)判断a和
b是否连通,时间复杂度O(NM) 如果数据范围扩大,该算法就失败了!
8
第八页,共79页。
水管局长(5)
跃峰奥数PPT4图论方法3-4(圈分析之同色圈问题)

温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
【百度文库】跃峰奥数PPT经典原创图论方法3-4(圈分析之同色圈问题)●冯跃峰本讲内容本节为第4板块(图论方法)第3专题(圈分析)的第4小节(同色圈问题),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、流畅、简练。
通过分析图中的一些点的度的性质,找到解题的突破口,我们称之为“度分析”。
包括如下4个方面:四种分析方法去掉悬挂点(度为1的点)将问题化归到已知情形(通常与归纳法相结合)图论方法1(度分析)考察极端从最大度、最小度突破度与边关联建立度与边的联系引入容量参数设d(A)=k,对k的取值进行讨论。
【图论方法(圈分析)】所谓“圈分析”,就是从图中的圈入手,探索解题途径。
它包括三种常见的思路:三种思路(1)论证有圈:在给定的图中寻找圈,发现图的相关性质;(2)判断是圈:先考察图的最简单情形:是一个圈。
再考虑其它情形:或者化归,或者迁移特征。
(3)主动作圈:先构造一个圈,然后逐步完善其它边,得到合乎要求的图。
本节介绍“论证有圈”的相关例子。
【找“固定长度r”的圈的策略】图论中的定理通常只指存在圈,但并不知道圈的长度。
若要找固定长度r 的圈,可采用以下局部扩充策略:定义:两条有公共顶点的边组成的图称为“2-链”,公共顶点称为2-链的中心,另两个顶点称为2-链的端点。
中心端点端点···(1)由一条“2-链”扩充取2-链ABC ,然后由端点A 、C 向两边扩展(找邻点),最后叠合成圈【3】。
跃峰奥数PPT1代数组合11-3(发掘性质之局部性质)

温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
代数组合11-3(发掘性质之局部性质)●冯跃峰本讲内容本节为第1板块(代数组合)第11专题(发掘性质)的第3小节(局部性质),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、流畅、简练。
【发掘性质】四种发掘性质方式发掘正面性质:从正面构造“合乎要求”的对象,发现其必定含有某种结构。
发掘反面性质:从反面构造“不合乎要求”的对象,发现其必定不含有某种结构。
发掘局部性质:研究条件中的局部对象,发现相关性质,然后迁移或扩展。
所谓发掘性质,就是从题给的条件出发,发掘若干有用的结论,反复运用这些结论,求出参数、指导构造,或用于导出矛盾。
发掘性质有如下三种常见的途径:发掘功能性质:发现条件具有某种功能,它恰好与目标要求相吻合。
本节介绍发掘局部性质的相关例子■。
(i=1,2)中每两个相邻的方格的中心都用一条线段连接,得到的图记为G i 。
试证:如果G 1、G 2都是连续的折线(无环路,不分岔),则棋盘的中心必定是G 1或G 2的端点。
(2017年中国国家集训队测试题第3轮)【述评】本题应该算是一道“难题”,因为当年参加集训的学生中除9人得分外,其余考生都得0分。
“官方”解答也很繁,占用了近2个版面的篇幅。
我们这里给出一个简单的证明,10行就够了。
从这个角度看,本题似乎又不算“难题”。
有趣的是,我们的解答中几乎只用到小学知识,这是本题的一大特色,也是组合问题的魅力所在。
跃峰奥数PPT8组合构造5-9(递归构造之撒网策略)
温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
组合构造5-9(递归构造之撒网策略)●冯跃峰本讲内容本节为第8板块(组合构造)第5专题(递归构造)的第9小节(撒网策略),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、流畅、简练。
涉及到n个对象的构造问题,最直截了当的方法是“通式构造”(对每个1≤i≤n,给出第i个对象的具体表现形式)。
此时,研究特例是一种有效手段。
但有的情况下,通式构造难以发现,这时,递归构造则有奇特效果。
因为构造建立在一种“假设”之下,使构造有“坚实”的基础:只需在“k”的情形中,考虑增加一个元素后如何构造。
最简单的递归构造是:“k”情形中的构造可以考察原封不动,只需考虑新增元素与原来元素之间的关系。
较为复杂的情形是,“k”情形中的构造需要进行适当的改造。
递归构造技巧包括以下“三种情形”与“两个选择”:涉及到n 个对象的构造问题,最直截了当的方法是“通式构造”(对每个1≤i≤n ,给出第i 个对象的具体表现形式)。
此时,研究特例是一种有效手段。
但有的情况下,通式构造难以发现,这时,递归构造则有奇特效果。
因为构造建立在一种“假设”之下,使构造有“坚实”的基础:只需在“k ”的情形中,考虑增加一个元素后如何构造。
三种情形(1)初值递归(穷举初值的所有构造)(2)“定元”递归(适当选取增、减元素)(3)多假设递归(利用假设中多个结论)两个(1)选择归纳对象(多元选一、分批归纳)例【构造5-9】如果最少要用n种赛给图中的顶点染色,才能使相邻的点不同赛,则称之为n-赛构图。
跃峰奥数PPT9竞赛真题0-1(2021年之原创新题限距染)
跃峰奥数系列讲座——温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
奥数系列讲座——竞赛真题0-1(2021年之原创新题限距染型号)●冯跃峰本讲内容本节为第9板块(竞赛真题)第0专题(2021年原创新题)的第1小节(限距染型号),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、简练。
【真题0-1】设X={(x ,y )|x ,y ∈Z}是平面内所有格点的集合,对X 中任意两个格点a=(x 1,y 1)、b=(x 2,y 2),定义它们的距离为:|a-b|=|x 1-x 2|+|y 1-y 2|。
将X 中的点染型号,使对任何两个同型号的格点a 、b ,都有|a-b|≥k ,其中k 是给定的大于1的整数,我们称这种方式的染型号为格点的“k-限距染型号”。
记平面格点的“k-限距染型号”中型号种数为μ(k ),求μ(k )的最小值。
(原创题)例但由于参数k 比较抽象,可先研究k 的一些简单取值情形,从中发现规律。
【题感】从目标看【1】,为求μ(k )的最小值,可先估计μ(k )的下界。
再注意到染型号是由“距离”不等式|a-b|≥k 限定的【1】,其反面容量远远小于正面容量([k ,+∞)与[1,k-1]之间的显著差别),可采用补集思考:如果|a-b|≤k-1,则a 、b 异型号。
由此想到构造两两距离不大于k-1的点集M ,则M 中的点两两异型号,得到μ(k )的下界估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温馨提示为了设计教学场景互动效果的需要,课件中采用了大量“播放后隐藏”的文本,从而导致预览模式下出现诸多文本重叠,影响阅读。
但在放映模式下,这些现象都不会出现。
另外,课件中的图像均不是一次性形成,而是展现了“尝试-修改-成形”等发生过程,这可能导致预览模式下出现诸多乱码,但在放映模式下,图形则非常生动、美观。
【百度文库】跃峰奥数PPT经典原创图论方法3-9(圈分析之同色的单颜色圈)●冯跃峰本讲内容本节为第4板块(图论方法)第3专题(圈分析)的第9小节(同色的单颜色圈),包含如下3个部分内容:第一部分,概述问题涉及的知识方法体系;第二部分,思维过程剖析。
这是课件的核心部分,重在发掘问题特征,分析如何找到解题方法。
按照教师场景授课互动效果设计,立足于启发思维;第三部分,详细解答展示。
提供笔者重新书写的解答(简称“新写”),力求严谨、流畅、简练。
【百度文库】跃峰奥数PPT经典原创通过分析图中的一些点的度的性质,找到解题的突破口,我们称之为“度分析”。
包括如下4个方面:四种分析方法去掉悬挂点(度为1的点)将问题化归到已知情形(通常与归纳法相结合)图论方法1(度分析)考察极端从最大度、最小度突破【百度文库】跃峰奥数PPT 经典原创度与边关联建立度与边的联系引入容量参数设d(A)=k,对k的取值进行讨论。
【图论方法(圈分析)】所谓“圈分析”,就是从图中的圈入手,探索解题途径。
它包括三种常见的思路:三种思路(1)论证有圈:在给定的图中寻找圈,发现图的相关性质;(2)判断是圈:先考察图的最简单情形:是一个圈。
再考虑其它情形:或者化归,或者迁移特征。
(3)主动作圈:先构造一个圈,然后逐步完善其它边,得到合乎要求的图。
跃峰奥数本节介绍“论证有圈”的相关例子■。
【找“固定长度r”的圈的策略】图论中的定理通常只指存在圈,但并不知道圈的长度。
若要找固定长度r 的圈,可采用以下局部扩充策略:定义:两条有公共顶点的边组成的图称为“2-链”,公共顶点称为2-链的中心,另两个顶点称为2-链的端点。
中心端点端点···(1)由一条“2-链”扩充取2-链ABC ,然后由端点A 、C 向两边扩展(找邻点),最后叠合成圈【3】。
A B C (2)由一条边扩充取边AB ,然后由A 、B 向两边扩展(找邻点),最后叠合成圈【3】。
AB(3)由中间点扩充取两个中间点A 、B (不一定相邻),在AB 两侧分别扩充、叠合【5】。
A B(4)由“s 、t-链”拼合证明2条s 、t-链对应同一个“2点组”(叠合)【3】。
A B ····■跃峰奥数【以C3、C4为例,技巧略有不同】找三角形有两种方式由一条“2-链”扩充取点A为“2-链”中心【1】,证明A的邻域中【1】,有2点相邻【1】(通常用到“邻域分块”、“充分条件分类”技巧);PAQ由一条边扩充适当取边AB【1】,证明A、B的邻域有公共点【1】:(|D(A)∩D(B)|≥1)【1】。
AB■跃峰奥数找四边形有四种方式由一条“2-链”扩充取“2-链”中心A【1】,证明有异于A的点P【1】,向A的邻域引两条边【1】;AP由一条边扩充取边AB【1】,证明A的邻域中一点【1】,与B邻域中一点【1】相邻【1】;A B 由对顶点扩充取两点A、B【1】,证明A、B邻域有2个公共点【1】:|D(A)∩D(B)|≥2【1】;A B 两条“2-链”拼合证明有两条2-链【2】对应同一个“2点组”【1】。
AB····■跃峰奥数【图论3-9】对n阶完全图Kn 的边任意2-染色,都有2个单颜色三角形,而且这两个单颜色三角形同色,求n的最小值。
(原创题)【题感】从目标看【1】,本题属于“任意型【1】”最值。
其“论证”用于等式,“构造”用于不等式(下界)。
就等式而言,设n=n0合乎要求,则要找到两个同色【1】的单颜色三角形。
由抽屉原理可知,一个充分条件是:找到3个单颜色的三角形。
这可采用逼近策略,先由局部(单颜色角)扩展得到一个单颜色三角形,在此基础上再“扩展”,直至得到3个单颜色三角形。
就不等式而言,要证明:n≥n0。
一个显然的下界是n≥6,因为熟知2-染色的K5可能没有单颜色三角形:比如红色C5与蓝色C5的并。
再注意到“最小值【1】”也许不会太大,可从n=6开始逐一试验■。
跃峰奥数【构造反例】当n ≤5时,取图G 为红色C 5与蓝色C 5的并【1】,再取G 的n 阶子图【1】,则n 阶子图中没有单颜色三角形,矛盾。
所以n≥6。
A 1A 4A 2A 3A 5跃峰奥数【穷举试验】当n=6时,由拉姆塞定理,2-染色的K 6中必有(2个)单颜色三角形(证明见后)。
现在的问题是,二色K 6中的2个单颜色三角形未必同色。
我们期望能构造一个2-染色的K 6,使其中只有2个单颜色三角形,且这两个单颜色三角形不同色(构造“反例”)。
这可按2个单颜色三角形的位置分布的不同方式分类讨论,通过局部扩展,找到合乎要求的反例构造。
【位置分布】(1)两个单颜色三角形没有公共顶点,设有一个红色△ABC 【1】,和一个蓝色△DEF 【1】。
A 【局部扩展】考察A 向△DEF 引出的3条边,由抽屉原理,必有2条同色,设AD 、AE 同色【1】。
B C D EF若AD 、AE 同为蓝【1】,则有2个蓝三角形DEF 、DEA ,构图不合要求,于是AD 、AE 同为红色【1】。
同理,B 向△DEF 也引出2条红边【1】,必与D 、E 之一连红边,设BD 为红色【1】。
这样,又得到2个红色三角形:△ABC 、△ABD 。
此时,构图也不合要求(不合“反例”要求)■。
(2)两个单颜色三角形有公共顶点,设有一个红色△ABC 和一个蓝色△ADE 【1】。
EF D BCA类似地进行局部扩展,可先考虑F 连的边【1】。
注意同色线段尽可能不共点(同色角),以避免出现新的单颜色三角形。
由对称性,可设FA 为蓝色【1】,则FD 、FE 为红(△FAD 、△FAE )【1】。
因为B 、C 都引出2条红边【1】,为避免红三角形,可取FB 、FC 为蓝色【1】。
继而由对称性,可设EB 为红色【1】,则EC 为蓝色(△EBC )【1】。
最后,DC 为红色(△DEC )【1】,DB 为蓝色(△DCB )【1】,得到构图没有2个同色的单颜色三角形,从而n≠6。
如果n<6,则在上图中去掉6-n 个点及其关联的边,得到的图中也没有2个同色的单颜色三角形,从而n≥7■。
跃峰奥数一个充分条件是找到3个单颜色三角形。
这可采用逼近策略,逐步找到单颜色三角形。
可用的相关知识是:2-染色K 6中一定有单颜色三角形。
但需要避免与后续单颜色三角形重复。
为了避免重复,需要在一个单颜色三角形中去掉“一个点”,则剩下的图为2-染色的K 6,还需在K 6中找到2个单颜色三角形。
所以需要加强命题(用变式),期望证明如下的引理。
6其证明也可以采用逼近策略。
【逼近策略】首先,由拉姆塞定理,2-染色K 6中一定有单颜色三角形,设为红色的△ABC 【1】。
EF D BC A 下面只需在图中再找一个单颜色三角形。
若逐一分析各边的颜色,从正面确定谁为单颜色三角形,则过程较繁;若从反面思考,反设没有单颜色三角形,则可利用相关知识,确定大多数边的颜色,使图的颜色逐步确定,最终产生矛盾。
6【逼近策略】首先,由拉姆塞定理,2-染色K6中一定有单颜色三角形,设为红色的△ABC【1】。
EF DBCA【反面思考】反设没有其它单颜色三角形,去掉点B及其关联的边【1】,得到2-染色的K5【1】,由图论知识可知,它是一个红色C5与一个蓝色C5的并。
注意到AC为红【1】,设红色C5为ACDEF【1】,则蓝色C5为ADFCE【1】。
【局部扩展】由于BC、CD为红色,所以BD为蓝色【1】。
由对称性,BF为蓝色【1】,得到蓝色△BDF【1】,矛盾,引理获证。
利用上述引理,在2-染色K7中找到3个单颜色三角形是轻而易举的■。
下面证明n=7合乎要求,即2色K7中有2个同色的单颜色三角形。
【逼近策略】首先,由引理,2色K7中一定有2个单颜色三角形,取其中一个单颜色△ABC【1】。
EG DBC去掉点A及其关联的边【1】,由引理,在剩下的2色K6又有2个单颜色三角形【1】,连同前面的单颜色△ABC【1】,一共有3个单颜色三角形。
FA由抽屉原理,这3个单颜色三角形中必有2个同色,所以n=7合乎要求。
综上所述,n的最小值为7■。
【新写】先证明引理:2-染色K 6中有2个单颜色三角形(略)。
再证明n=7合乎要求。
首先,由引理知,2色K 7中一定有2个单颜色三角形,取其中一个单颜色△ABC 。
去掉点A 及其关联的边,由引理,在剩下的2色K 6中又一定有2个单颜色三角形,连同前面的单颜色△ABC ,一共有3个单颜色三角形。
由抽屉原理,这3个单颜色三角形中必有2个单颜色三角形同色,所以n=7合乎要求。
最后,在完全6边形ABCDEF 中将AB 、BC 、CA 、CD 、DF 、FE 、EB 染红色,其余边染蓝色,则图中只有2个单颜色三角形,其中一个红△ABC ,一个蓝△ADE 。
当n ≤6时,取上述图的n 阶子图,则子图中没有2个同色的单颜色三角形,矛盾,所以n ≥7。
综上所述,n 的最小值为7。
【发掘引理】【逼近策略】【剔除元素,避免重复】【局部扩展】■■。
