九年级三角函数复习课件PPT.ppt
合集下载
23.一般锐角的三角函数值PPT课件(沪科版)

解:(1)过点C作CD⊥AB于点D, ∵AC=10千米,∠CAB=25°, ∴CD=sin∠CAB·AC=sin25°×10≈0.42×10=4.2(千米), AD=cos∠CAB·AC=cos25°×10≈0.91×10=9.1(千米). ∵∠CBA=45°,∴BD=CD=4.2(千米),
B C = C D 4 .2 5 .9 (千 米 ), sin C BA sin 45
【方法总结】解决问题的关键是作出辅助线,构造直 角三角形,利用三角函数关系求出有关线段的长.
例4:如图,课外数学小组要测量小山坡上塔的高度 DE,DE所在直线与水平线AN垂直.他们在A处测得塔 尖D的仰角为45°,再沿着射线AN方向前进50米到达B 处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡 顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组 算一算塔高DE大约是多少米 (结果精确到个位).
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∵tan25.6°= EF ≈0.5,
BF
∴BF=2x,则DF=AF=50+2x,
故tan61.4°=
DF BF
50 2x 2x
=1.8,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
所以,塔高DE大约是81米.
归纳总结
解决此类问题要了解角之间的关系,找到 与已知和未知相关联的直角三角形,当图形中 没有直角三角形时,要通过作高或垂线构造直 角三角形.
巩固练习
1. 已知下列锐角三角函数值,用计算器求其相应 的锐角: (1)sinA=0.627 5,sinB=0.054 7;
∠A=38°51′57″ ∠B=38°8″
B C = C D 4 .2 5 .9 (千 米 ), sin C BA sin 45
【方法总结】解决问题的关键是作出辅助线,构造直 角三角形,利用三角函数关系求出有关线段的长.
例4:如图,课外数学小组要测量小山坡上塔的高度 DE,DE所在直线与水平线AN垂直.他们在A处测得塔 尖D的仰角为45°,再沿着射线AN方向前进50米到达B 处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡 顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组 算一算塔高DE大约是多少米 (结果精确到个位).
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∵tan25.6°= EF ≈0.5,
BF
∴BF=2x,则DF=AF=50+2x,
故tan61.4°=
DF BF
50 2x 2x
=1.8,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
所以,塔高DE大约是81米.
归纳总结
解决此类问题要了解角之间的关系,找到 与已知和未知相关联的直角三角形,当图形中 没有直角三角形时,要通过作高或垂线构造直 角三角形.
巩固练习
1. 已知下列锐角三角函数值,用计算器求其相应 的锐角: (1)sinA=0.627 5,sinB=0.054 7;
∠A=38°51′57″ ∠B=38°8″
【中考数学考点复习】第六节 锐角三角函数及其应用 课件(共33张PPT)

返回目录
第1题图
第六节 锐角三角函数及其应用
返回目录
改编条件:题干改变“测量点的高度”;“两个非特殊角”改为“两个 特殊角” 2.(2020 贺州)如图,小丽站在电子显示屏正前方 5 m 远的 A1 处看“防溺 水六不准”,她看显示屏顶端 B 的仰角为 60°,显示屏底端 C 的仰角为 45°,已知小丽的眼睛与地面距离 AA1=1.6 m, 3.求电子显示屏高 BC 的值.(结果保留一位小数. 4.参考数据: 2≈1.414, 3≈1.732).
第 6 题图
第六节 锐角三角函数及其应用
解:如解图,延长 BC 交 MN 于点 F, 由题意得 AD=BE=3.5 米,AB=DE=FN=1.6 米,
在 Rt△MFE 中,∠MEF=45°,∴MF=EF,
在 Rt△MFB 中,∠MBF=33°,
∴MF=BF·tan33°=(MF+3.5)·tan33°,
第六节 锐角三角函数及其应用
返回目录
3. .如图,为测量电视塔观景台 A 处的高度,某数学兴趣小组在电视塔 附近一建筑物楼顶 D 处测得塔 A 处的仰角为 45°,塔底部 B 处的俯角为 22°.已知建筑物的高 CD 约为 61 米,请计算观景台的高 AB 的值.(结果 精确到 1 米,参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40)
形的边角 1. 三边关系:a2+b2=c2
关系
2. 两锐角关系:∠A+∠B=90° 3. 边角关系:sinA=cosB= a ;cosA=sinB= b;
tanA=
a
c
;tanB=
b
c
图②用
返回思维导图
返回目录
1.仰角、俯角:如图③,当从低处观测高处的目标时,视线与水平线 锐角三角 所成的锐角称为__仰__角____,当从高处观测低处的目标时,视线与水平 函数的实 线所成的锐角称为___俯__角___ 际应用 2.坡度(坡比)、坡角:如图④,坡面的铅直高度h和水平宽度l的比叫坡
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
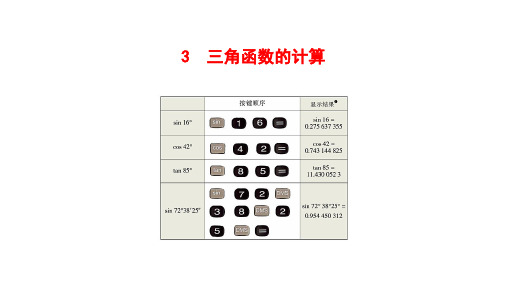
上表的显示结果是以“度”为单位的,再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗?
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″,所以∠A=14˚28′39″.
正弦值随着角度的增大(或减小)而增大(或减小); 余弦值随着角度的增大(或减小)而减小(或增大); 正切值随着角度的增大(或减小)而增大(或减小).
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】(1)由题意,AC=AB=610 米.
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE= BE ,
DE
故BE=DEtan39°. 因为CD=AE,
所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米). 答:大楼的高度CD约为116 米.
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α=1 ,求α,若用科学计算器计算且结果以“度、分、秒
2
”为单位,最后按键(D )
•A.AC/ON
B. SHIFT
C.MODE
(4)sin18°+cos55°-tan59°≈-0.7817.
苏科版数学九年级下7.2锐角三角函数—正弦、余弦课件(共16张PPT)

B
在△ABC中, ∠C=90°.
A C
我们把锐角A的对边a与斜边c的比叫做 ∠A的正弦,记作sinA. 我们把锐角A的邻边b与斜边c的比叫做 ∠A的余弦,记作cosA.
∠A的对边 a sinA = = 斜边 c
∠A的邻边 b cosA = = 斜边 c
整合提升
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB 于D若AC= 5 BC=2 , 求∠A的三角函数值和sin∠ACD的值.
AD 4 tan B . BD 3
个性展示
3. 在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求: △ABC 的周长和面积
5 4 .在△ABC中,∠C=90°,sinA= 13 ,△ABC的周长
为60,求△ABC的面积。
课堂小结
锐角A的正弦、余弦和正切都是∠A的三角函数
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
C
3
C
3
4 ①
B
A
4 ②
B
已知:如图, ∠ACB=90°,CD⊥AB,垂足为D
(1)sinA ( AC ) BC (
( AB
A
)
)
C D B
CD (2)sinB ( )
(3)cosACD
(4)tanA CD (
CD (
( AC
)
, cosBCD
) , tanB (
( BC
)
)
A计算器 ,求值(精确到0.01):
α sinα 10º 20º 30º 40º 50º 60º 70º 80º
0.17 0.34 0.5 0.87 0.64 0.77 0.77 0.64 0.87 0.5 0.94 0.34 0.98 0.17
在△ABC中, ∠C=90°.
A C
我们把锐角A的对边a与斜边c的比叫做 ∠A的正弦,记作sinA. 我们把锐角A的邻边b与斜边c的比叫做 ∠A的余弦,记作cosA.
∠A的对边 a sinA = = 斜边 c
∠A的邻边 b cosA = = 斜边 c
整合提升
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB 于D若AC= 5 BC=2 , 求∠A的三角函数值和sin∠ACD的值.
AD 4 tan B . BD 3
个性展示
3. 在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求: △ABC 的周长和面积
5 4 .在△ABC中,∠C=90°,sinA= 13 ,△ABC的周长
为60,求△ABC的面积。
课堂小结
锐角A的正弦、余弦和正切都是∠A的三角函数
例1.根据图中数据,分别求出∠A, ∠B 的正弦,余弦.
A
C
3
C
3
4 ①
B
A
4 ②
B
已知:如图, ∠ACB=90°,CD⊥AB,垂足为D
(1)sinA ( AC ) BC (
( AB
A
)
)
C D B
CD (2)sinB ( )
(3)cosACD
(4)tanA CD (
CD (
( AC
)
, cosBCD
) , tanB (
( BC
)
)
A计算器 ,求值(精确到0.01):
α sinα 10º 20º 30º 40º 50º 60º 70º 80º
0.17 0.34 0.5 0.87 0.64 0.77 0.77 0.64 0.87 0.5 0.94 0.34 0.98 0.17
《三角函数的计算》直角三角形的边角关系PPT课件

5.一个人由山底爬到山顶,需先爬坡角为40°的山坡300 m,
再爬坡角为30°的山 坡100 m,求山高(结果精确到0.1m).
解:如图,过点C作CE⊥AE于点E,
过点B作BF⊥AE于点F,
过点B作BD⊥CE于点D,则BF=DE.
在Rt△ABF中,BF=AB sin 40°;
在Rt△CDB中,CD=BC sin 30°.
BC 10 1
如图,在Rt△ABC中,sinA=
,
AC 40 4
那么∠A是多少度呢?
要解决这个问题,我们可以借助科学计算器.
已知三角函数值求角度,要用到
“sin”、“cos”、“tan”键
的第二功能“sin־¹,cos־¹,
tan־¹ ”和2ndf 键。
以“度”为单位
按键顺序
sinA=0.9816
(4)sin18°+cos55°-tan59°≈-0.7817.
议一议
当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D
的行驶路线与水平面的夹角为∠β=42°
,由此你还能计算什么?
想一想
为了方便行人推自行车过某天桥,市政府在10m高的天桥两端
修建了40m长的斜道.这条斜道的倾斜角是多少?
故选A.
)
2.下列各式中一定成立的是( A )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°<sin15°
3.某款国产手机上有科学计算器,依次按键: = ,显示
合作学习
如图,在Rt△ABC中,∠ACB=90°
九年级三角函数复习课件PPT(共19张PPT)

则a= 2 ,∠B= 60°,∠A= 30°.
5.如果 cos A 1 3 tan B 3 0
2
那么△ABC是( D )
A.直角三角形 C.钝角三角形
B.锐角三角形 D.等边三角形
6.直角三角形纸片的两直角边BC为6, AC为8,现将△ABC,按如图折叠,使点A 与点B重合,折痕为DE,则tan∠CBE的值
在Rt△PAD中,∵∠PAD=90°-60°=30°,
AD 3PD, 12 x 3x,
x 12 6( 3 1) 18. 3 1
∴渔船不改变航线继续向东航行,有触礁危险.
8.如图,甲船在港口P的北偏西60°方向,距港口80海里的A 处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P 出发,沿北偏东45°方向匀速驶离港口P,现两船同时出发, 2小时后乙船在甲船的正东方向.求乙船的航行速度.
谢 谢!
让我们共同进步
(2)两锐角的关系:∠A十∠B=90°
(3)边角的关系:sin A a cos A b tan A a
c
c
b
归纳:只要知道其中的2个元素(至少有一个是边),
就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角
在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.
视线
铅 直
仰角
线
俯角
水平线
视线
2.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则 i h tan
l
锐角三角函数复习课件九年级中考复习

误的是( A )
A.sin B=
1
3
1
C.tan B=
2
B.sin C=
2 5
5
D.sin2B+sin2C=1
3
8.如图,点 A(x,4)在第一象限,OA 与 x 轴所夹的锐角为 α,cos α= ,
5
则 tan α 的值为( A
A.
4
3
B.
3
4
C.
5
4
)
D.
4
5
3
9.在 Rt△ABC 中,∠C=90°,若 sin A= ,则 cos B 的值是( B )
B
2- 3
2+ 3 2-
=23.类比这种方法,计算
tan
22.5°的
3
)
B. 2-1
C. 2
1
D.
2
14.在如图所示的网格中,小正方形的边长为1,点A,B,C,D都在
格点上,
AB与CD相交于点O,则∠AOC的正切值是( A )
A.
C.
2
3
3
5
3
B.
2
5
D.
3
(1)cos260°+sin260°=
1 ;
cos45°
(2)
-
tan 45°= 0 ;
sin45°
3
(3)1-2sin 30°cos 30°= 1- 2
.
练习题
1.在△ABC 中,∠A=105°,∠B=45°,tan C 的值是
3
3
.
2.在Rt△ABC中,∠C=90°,若△ABC的三边都缩小5倍,则sin
是( D )
新浙教版九年级数学下册第一章《 有关三角函数的计算》课件

D
ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是 高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的 新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
D
太阳光
25° A
F
住 宅
新
楼
w如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°,45°,60°这些特殊角的三角函 数值,可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利 的彼岸
w用科学计算器求锐角的三角函数值,要用到三个键: w例如,求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下: sin cos tan
A
B
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
驶向胜利 的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =
ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是 高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的 新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
D
太阳光
25° A
F
住 宅
新
楼
w如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°,45°,60°这些特殊角的三角函 数值,可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利 的彼岸
w用科学计算器求锐角的三角函数值,要用到三个键: w例如,求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下: sin cos tan
A
B
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
驶向胜利 的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =
数学课件九年级数学锐角三角函数复习共18页

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
数学课件九年级数学锐角三角函数 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
第19讲 三角形 锐角三角函数第二课时 九年级中考数学一轮复习课件(共18张PPT)

c= a2+b2,由tan A= a
⑪___b_____求∠A,∠B=
90°-∠A
已知斜边和一 条直角边(c, a)
b= c2-a2,由⑫_s_i_n__A__ =ac求∠A,∠B=90°-∠A
自学检测1(9分钟)
考点 解直角三角形(6年3考)
1、例 3 如图 4,在△ABC 中,AD⊥BC,
图4
仰角、俯 角
在视线与水平线所成的锐角中,视线在 水平线上方的角叫仰角,视线在水平线 下方的角叫俯角
坡度(坡 比)、坡
坡面的铅直高度 h 和水平宽度 l 的比叫 坡度(坡比),用字母 i 表示;坡面与水
角 平线的夹角α叫坡角,i=tan α=hl
中考几种常考的考查形式:1.以楼房等建筑物为背景,含仰角、俯角; 2.以航海为背景,含方向角;3.以河流为背景的测量;4.以四边形为背景, 含坡度、坡角
解:由题意可知:CD⊥AD,设 CD=x m.
在 Rt△BCD 中,tan∠CBD=CBDD,
∴BD=tan∠CDCBD=
3 3 x.
在 Rt△ACD 中,tan A=ACDD.
∴AD=taCnDA= 3x.
又 AD=AB+BD,
∴ 3x=10+ 33x.
5分
解得 x=5 3≈8.7. 6 分
答:这棵树的高度是 8.7 m.7 分
CD2-DE2= 32-2 22=1.
∴BC=BE-CE=3.
自学指导2(1分钟)
一般指以观测者的位置为中 心,将正北或正南方向作为起 始方向旋转到目标方向线所成 的角(一般指锐角),通常表达成 方向角 北(南)偏东(西)××度,如图, A点位于O点的南偏西20°,B点 位于O点的北偏东75°,C点位于 O点的南偏东45°
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)

观察以上计算结果,你发现了什么?
sinA=cosB ,cosA=sinB (∠A+∠B=90)
tanA·tanB=1
(∠A+∠B=90)
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图,在△ABC中,若AB=5,BC=3,则下列结论正确
锐角A,A′的余弦值的关系为( ) A
A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定 2.如图,已知P是射线OB上的任意一点,PM⊥OA于M,
且PM:OM=3:4,则cosα的值等于( C)
3 A.4
4 B.3
C.4 5
3
D.
5
3.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦,余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine),记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ,记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ,记做tanα.
b,c,则下列各项中正确的是( ) B
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确
4.在Rt△ABC中,∠C=90°,cosA= 2 ,则tanB等于( )
C
浙教版九年级下册 1.3 解直角三角形 课件(共42张PPT)

3.5 5
=0.7,
∴α≈350.
答:斜面钢条a的长度约为6.1米,坡角约为350.
特别强调:
在解直角三角形的过程中,常会遇到近似计
算,本书除特别说明外,边长保留四个有效数 字,角度精确到1′.
解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角 (必须有一个条件是边)
钢条的长度a和倾角a 吗?
L
变化:已知平顶屋面的宽度
L和坡顶的设计倾角α(如
述例题中,我们都是利用直角三角 形中的已知边、角来求出另外一些的边角. 像这样,
******************************** 在直角三角形中,由已知的一些
因此 AB=AE+EF+BF
≈6.72+12.51+7.90 ≈27.13(米).
图 19.4.6
答:路基下底的宽约为27.13米.
如图,沿水库拦水坝的背水坡将坝面加宽两 米,坡度由原来的1:2改成1:2.5,已知原背水坡 长BD=13.4米,
求: (1)原背水坡的坡角 和加宽后的背水
坡的坡角
(1)c=10,∠A=30°
B
(2)b=4,∠B=72°
(3)a=5, c=7
C
A
(4)a=20,sinA= 1
2
应用练习
如图东西两炮台A、B相距2000米,同时发现入侵敌 舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B 测得敌舰C在它的正南方,试求敌舰与两炮台的距离.
(精确到1米)
本题是已知
面的夹角叫做坡角,记作a,有i= h = tan a. l
显然,坡度越大,坡角a就越大,坡面就越陡.
试一试
1、如图
1)若h=2cm, l=5cm,则i= 2 ; 5
人教版九年级数学下册课件:28.1.2特殊角的三角函数值(共30张PPT)

sin A BC 3 2 , AB 6 2
A 45.
B
6
3
A
C
在直角三角形中,根据边的比值反推出角的大小
(2)如图,已知圆锥的高AO等于圆锥的 底面半径OB的 3 倍,求α .
解:在Rt△ABO中
tan AO 3OB 3,
OB OB
60.
A OB
3、计算
二、逆向应用 :通过直角三角形边长求出角的度数。
一、直接应用 :根据特殊角的三角函数值,直接代 入计算即可。
☆ 应用练习
求下列各式的值
1.已知角,求值
1. 2sin30°+3tan30°+tan45°
=2 + d3
2. cos245°+ tan60°cos30°
=2
☆ 应用练习
1.已知角,求值 2.已知值,求角
于 3 时,∠A( D )
(A)0°<∠A<30° (B)30°<∠A<90° (C)0 °<∠A<60° (D)60°<∠A<90
1、如图,在△ABC中,已知BC=1+ 3 , ∠B=60°,∠C=45°,求AB的长.
A
B
D
C
2 (1)如图,在Rt△ABC中,∠C=90°, AB 6, BC 3 ,求∠A的度数.
解:延长BC与AD交于点E。
tan 60 BE BE 2 3 2 3 AB
B
B A
90 60
E
30
C 2
又CDA 90 在RtCDE中
60°
1
A
D
E
tan E CD DE CD 3
《锐角三角函数》PPT优秀课件

斜边c
B ∠A的对边a
sin A= ∠A的对边
斜边
A ∠A的邻边b C
∠A的邻边
cos A=
斜边
tan A= ∠A的对边 ∠A的邻边
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
已知直角三角形两边求锐角三角函数的值
如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,
即tan A= a . b
B
斜边c
∠A的对边a
A
┌ ∠A的邻边b C
再见
在Rt△ABC中,∠C=90°锐角正弦的定义
斜边 A
B
∠A的对边
┌
C
如图,在Rt△ABC中,∠C=90° 我们把锐角A的邻边与对边的比叫做∠A的正切,记作tanA,即
B
斜边 ∠A的对边
┌ A ∠A的邻边 C
例1 如图,在 Rt△ABC 中,∠C =90°,AB=10,BC=6,求
sin A, cos A,tan A的值.
tanA的值. 解:由勾股定理,得
B 10
6
A
C
因此 sin A BC = 6 = 3, AB 10 5
cos A AC 8 4 , tan A BC = 6 = 3 .
AB 10 5
AC 8 4
利用勾股定理求三角函数值方法
已知直角三角形中的两条边求锐角三角函数值的一般思路 是:当所涉及的边是已知时,直接利用定义求锐角三角函数值; 当所涉及的边是未知时,可考虑运用勾股定理的知识求得边的 长度,然后根据定义求锐角三角函数值.
课堂练习
1. 如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:作PD⊥BC,设PD=x,则 BD=x,AD=x+12,根据AD= 3 PD, 得x+12= 3 x,求出x的值,再 比较PD与18的大小关系.
D
解:有触礁危险.
D
理由:过点P作PD⊥AC于D.设PD为x,在Rt△PBD中,
∠PBD=90°-45°=45°.∴BD=PD=x,AD=12+x.
二.特殊角的三角函数值
1
2
3
2
2
2
3
2
1
2
2
2
3
1
3
3
锐角的三角函数值 有何变化规律呢?
三.解直角三角形
1.什么叫解直角三角形?
由直角三角形中,除直角外的已知元素,求出所 有未知元素的过程,叫做解直角三角形.
2.直角三角形中的边角关系:
(1)三边关系: a 2 b2 c 2 (勾股定理)
则a= 2 ,∠B= 60°,∠A= 30°.
5.如果 cos A 1 3 tan B 3 0
2
那么△ABC是( D )
A.直角三角形 C.钝角三角形
B.锐角三角形 D.等边三角形
6.直角三角形纸片的两直角边BC为6, AC为8,现将△ABC,按如图折叠,使点A 与点B重合,折痕为DE,则tan∠CBE的值
解: ∠B=90°- ∠ A=90°-30°=60°,
B
∵tanB=b/a,
∴b=a·tanB=5·tan60°5 =3
5
∵ sinA=a/c,
30°
A
C
∴ c=a/sinA=5/sin30=5/(1/2)=10.
解直角三角形分为两类:一是已知一边一角解直角三 角形;二是已知两边解直角三角形.
例4.如图,在△ABC中,AD是BC边上的高, A 若tanB=cos∠DAC.
视线
铅 直
仰角
线
俯角
水平线
视线
2.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则 i h tan
l
h
l
坡度通常写成 i h tan 的形式.
l
例1.计算2sin30 °+tan45 ° ×cos60°
1
1
解:原式=2×2 +1× 2 步骤:
=1+ 1 2
=
3 2
一“代”二 “算”
例2.若 3 tan 1 0 ,则锐角α= 30°
点拨:本题是由特殊角的三角函数值求角度,首先 将原式变形为tanα= 3 ,从而求得α的度数.
3
例3.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5, 求b、c的大小.
是 7.
24
C
方法点拨:设CE=x,则AE=BE=8-x, 6
E8
利用勾股定理求出x,再求tan∠CBE的值.
B
D
A
例5.海中有一个小岛P,它的周围18海里内有暗礁, 渔船跟踪鱼群由西向东航行,在点A测得小岛P在北 偏东60°方向上,航行12海里到达B点,这时测得小 岛P在北偏东45°方向上.如果渔船不改变航线继续 向东航行,有没有触礁危险?请说明理由.
2.若tan( 20) 3 0 ,则锐角α= 80°
3.计算:
(1)
2 sin 45 tan 60 2 cos30. 2
1 2
2 6 tan2 300 3 sin 600 2 cos 450. 1 2
2
B
A
C
4.如图,在Rt△ABC中,∠C=90,b= 2 3 ,c=4.
BD C
14 2
⑴正弦
1.锐角三角函数的定义 ⑵余弦
锐
⑶正切
角 2.30°、45°、60°特殊角的三角函数值
三
⑴定义
角
①三边间关系
函
3.解直角三角形
⑵解直角三角形的依据 ②锐角间关系
③边角间关系
数
⑶解直角三角形在实际问题中
的应用
放映结束 感谢各位的批评指导!
谢 谢!
让我们共同进步
(1)AC与BD相等吗?说明理由;
B
(2)若sinC= 12 ,BC=12,求AD的长.
13
DC
解:(1)
在Rt △ABD和△ACD中,tanB= AD ,cos∠DAC = AD
BD
AC
因为tanB=cos∠DAC,所以 AD = AD
BD AC
故 BD=AC
1.若 2 sin 2 0 ,则锐角α= 45°
(2)两锐角的关系:∠A十∠B=90°
(3)边角的关系:sin A a cos A b tan A a
c
c
b
归纳:只要知道其中的2个元素(至少有一个是边),
就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角
在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.
B
斜边c
对边a
一.锐角三角函数的概念 A 邻边b C
正弦:把锐角A的对边与斜边的比叫做∠A
的正弦,记作 sin A a
对这些关系式
c
要学会灵活变
余 余弦弦:,记把作锐角coAs的A 邻b边与斜边的式比运叫做用∠A的
c
正切:把锐角A的对边与邻边的比叫做∠A的 正切,记作 tan A a
b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
在Rt△PAD中,∵∠PAD=90°-60°=30°,
AD 3PD, 12 x 3x,
x 12 6( 3 1) 18. 3 1
∴渔船不改变航线继续向东航行,有触礁危险.
8.如图,甲船在港口P的北偏西60°方向,距港口80海里的A 处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P 出发,沿北偏东45°方向匀速驶离港口P,现两船同时出发, 2小时后乙船在甲船的正东方向.求乙船的航行速度.
D
解:有触礁危险.
D
理由:过点P作PD⊥AC于D.设PD为x,在Rt△PBD中,
∠PBD=90°-45°=45°.∴BD=PD=x,AD=12+x.
二.特殊角的三角函数值
1
2
3
2
2
2
3
2
1
2
2
2
3
1
3
3
锐角的三角函数值 有何变化规律呢?
三.解直角三角形
1.什么叫解直角三角形?
由直角三角形中,除直角外的已知元素,求出所 有未知元素的过程,叫做解直角三角形.
2.直角三角形中的边角关系:
(1)三边关系: a 2 b2 c 2 (勾股定理)
则a= 2 ,∠B= 60°,∠A= 30°.
5.如果 cos A 1 3 tan B 3 0
2
那么△ABC是( D )
A.直角三角形 C.钝角三角形
B.锐角三角形 D.等边三角形
6.直角三角形纸片的两直角边BC为6, AC为8,现将△ABC,按如图折叠,使点A 与点B重合,折痕为DE,则tan∠CBE的值
解: ∠B=90°- ∠ A=90°-30°=60°,
B
∵tanB=b/a,
∴b=a·tanB=5·tan60°5 =3
5
∵ sinA=a/c,
30°
A
C
∴ c=a/sinA=5/sin30=5/(1/2)=10.
解直角三角形分为两类:一是已知一边一角解直角三 角形;二是已知两边解直角三角形.
例4.如图,在△ABC中,AD是BC边上的高, A 若tanB=cos∠DAC.
视线
铅 直
仰角
线
俯角
水平线
视线
2.坡度、坡角
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度(坡比):坡面的铅
直高度h和水平距离l的
比叫做坡度,用字母i表
示,则 i h tan
l
h
l
坡度通常写成 i h tan 的形式.
l
例1.计算2sin30 °+tan45 ° ×cos60°
1
1
解:原式=2×2 +1× 2 步骤:
=1+ 1 2
=
3 2
一“代”二 “算”
例2.若 3 tan 1 0 ,则锐角α= 30°
点拨:本题是由特殊角的三角函数值求角度,首先 将原式变形为tanα= 3 ,从而求得α的度数.
3
例3.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5, 求b、c的大小.
是 7.
24
C
方法点拨:设CE=x,则AE=BE=8-x, 6
E8
利用勾股定理求出x,再求tan∠CBE的值.
B
D
A
例5.海中有一个小岛P,它的周围18海里内有暗礁, 渔船跟踪鱼群由西向东航行,在点A测得小岛P在北 偏东60°方向上,航行12海里到达B点,这时测得小 岛P在北偏东45°方向上.如果渔船不改变航线继续 向东航行,有没有触礁危险?请说明理由.
2.若tan( 20) 3 0 ,则锐角α= 80°
3.计算:
(1)
2 sin 45 tan 60 2 cos30. 2
1 2
2 6 tan2 300 3 sin 600 2 cos 450. 1 2
2
B
A
C
4.如图,在Rt△ABC中,∠C=90,b= 2 3 ,c=4.
BD C
14 2
⑴正弦
1.锐角三角函数的定义 ⑵余弦
锐
⑶正切
角 2.30°、45°、60°特殊角的三角函数值
三
⑴定义
角
①三边间关系
函
3.解直角三角形
⑵解直角三角形的依据 ②锐角间关系
③边角间关系
数
⑶解直角三角形在实际问题中
的应用
放映结束 感谢各位的批评指导!
谢 谢!
让我们共同进步
(1)AC与BD相等吗?说明理由;
B
(2)若sinC= 12 ,BC=12,求AD的长.
13
DC
解:(1)
在Rt △ABD和△ACD中,tanB= AD ,cos∠DAC = AD
BD
AC
因为tanB=cos∠DAC,所以 AD = AD
BD AC
故 BD=AC
1.若 2 sin 2 0 ,则锐角α= 45°
(2)两锐角的关系:∠A十∠B=90°
(3)边角的关系:sin A a cos A b tan A a
c
c
b
归纳:只要知道其中的2个元素(至少有一个是边),
就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角
在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.
B
斜边c
对边a
一.锐角三角函数的概念 A 邻边b C
正弦:把锐角A的对边与斜边的比叫做∠A
的正弦,记作 sin A a
对这些关系式
c
要学会灵活变
余 余弦弦:,记把作锐角coAs的A 邻b边与斜边的式比运叫做用∠A的
c
正切:把锐角A的对边与邻边的比叫做∠A的 正切,记作 tan A a
b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
在Rt△PAD中,∵∠PAD=90°-60°=30°,
AD 3PD, 12 x 3x,
x 12 6( 3 1) 18. 3 1
∴渔船不改变航线继续向东航行,有触礁危险.
8.如图,甲船在港口P的北偏西60°方向,距港口80海里的A 处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P 出发,沿北偏东45°方向匀速驶离港口P,现两船同时出发, 2小时后乙船在甲船的正东方向.求乙船的航行速度.
