第八章 幂的运算 单元测试
七年级数学下册第八章《幂的运算》单元测试卷-苏科版(含答案)

七年级数学下册第八章《幂的运算》单元测试卷-苏科版(含答案)一.选择题(共7小题,满分21分)1.若a•2•23=26,则a等于()A.4B.8C.16D.322.已知a≠0,下列运算中正确的是()A.a2•a3=a6B.a5﹣a3=a2C.(﹣a3)2=a5D.a•a3=a43.若10m=5,10n=3,求102m﹣3n的值()A.B.C.675D.4.若(2x﹣1)0有意义,则x的取值范围是()A.x=﹣2B.x≠0C.x≠D.x=5.若(x﹣3)0﹣2(2x﹣4)﹣1有意义,则x取值范围是()A.x≠3B.x≠2C.x≠3且x≠﹣2D.x≠3且x≠2 6.“绿水青山就是金山银山”.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资1.102×108元资金.数据1.102×108用科学记数法可表示为()A.1102亿B.1.102亿C.110.2亿D.11.02亿7.嫦娥五号返回器携带月球样品安全着陆,标志着中国航天业向前又迈出了一大步.嫦娥五号返回器在接近大气层时,飞行1m大约需要0.0000893s.数据0.0000893s用科学记数法表示为()A.8.93×10﹣5B.893×10﹣4C.8.93×10﹣4D.8.93×10﹣7二.填空题(共7小题,满分21分)8.将2x﹣3y(x+y)﹣1表示成只含有正整数指数幂的形式为.9.新型冠状病毒直径约为100nm,计m(用科学记数法表示).10.若有意义,则x的取值范围是.11.若a2n=2(n为正整数),则(4a3n)2÷4a4n的值为.12.目前全国疫情防控形势依旧严峻,我们应该坚持“勤洗手,戴口罩,常通风”.一双没有洗过的手,带有各种细菌约7.5×105个,则科学记数法数据7.5×105的原数为.13.已知x2n=5,则(3x3n)2﹣4(x2)2n的值为.14.已知m x=2,m y=4,则m x+y=.三.解答题(共6小题,满分58分)15.计算:(1)2+(﹣2)×3+(﹣7)0;(2)×12.16.在数学中,我们经常会运用逆向思考的方法来解决一些问题,例如:“若a m=4,a m+n =20,求a n的值.”这道题我们可以这样思考:逆向运用同底数幂的乘法公式,即a m+n =a m•a n,所以20=4•a n,所以a n=5.(1)若a m=2,a2m+n=24,请你也利用逆向思考的方法求出a n的值.(2)下面是小贤用逆向思考的方法完成的一道作业题,请你参考小贤的方法解答下面的问题:小贤的作业计算:89×(﹣0.125)9.解:89×(﹣0.125)9=(﹣8×0.125)9=(﹣1)9=﹣1.①小贤的求解方法逆用了哪一条幂的运算性质,直接写出该逆向运用的公式:.②计算:52023×(﹣0.2)2022.17.(1)若3×27m÷9m=316,求m的值;(2)已知a x=﹣2,a y=3,求a3x﹣2y的值;(3)若n为正整数,且x2n=4,求(3x2n)2﹣4(x2)2n的值.18.我们知道,同底数幂的乘法法则为a m•a n=a m+n(其中a≠0,m、n为正整数),类似地,我们规定关于任意正整数m、n的一种新运算:f(m)•f(n)=f(m+n)(其中m、n为正整数).例如,若f(3)=2,则f(6)=f(3+3)=f(3)•f(3)=2×2=4.f(9)=f(3+3+3)=f(3)•f(3)•f(3)=2×2×2=8.(1)若f(2)=5,①填空:f(6)=;②当f(2n)=25,求n的值;(2)若f(a)=3,化简:f(a)•f(2a)•f(3a)•…•f(10a).19.如表是某河流今年某一周内的水位变化情况,上周末(星期六)的水位已经达到警戒水位33米.(正号表示水位比前一天上升,负号表示水位比前一天下降).(单位:米)星期日一二三四五六水位变化+0.2+0.8﹣0.4+0.2+0.3﹣0.5﹣0.2(1)本周哪一天河流的水位最高?哪一天河流的水位最低?分别是多少?(2)与上周末相比,本周末河流的水位是上升了还是下降了?本周末的水位是多少?(3)若水位每下降1厘米,就有2.5×102吨水蒸发到大气中,请计算这个星期共有多少吨水蒸发到大气中?20.已知10﹣2α=3,,求106α+2β的值.参考答案一.选择题(共7小题,满分21分)1.解:∵a•2•23=26,∴a=26÷24=22=4.故选:A.2.解:A、原式=a5,故不符合题意;B、a5与a3不是同类项,故不能合并,故不符合题意;C、原式=﹣a6,故不符合题意;D、原式=a4,故符合题意.故选:D.3.解:∵10m=5,10n=3,∴102m﹣3n=102m÷103n=.故选:D.4.解:(2x﹣1)0有意义,则2x﹣1≠0,解得:x≠.故选:C.5.解:若(x﹣3)0﹣2(2x﹣4)﹣1有意义,则x﹣3≠0且2x﹣4≠0,解得:x≠3且x≠2.故选:D.6.解:1.102×108=1.102亿.故选:B.7.解:0.0000893=8.93×10﹣5,故选:A.二.填空题(共7小题,满分21分)8.解:原式=•=.故答案为:.9.解:新型冠状病毒的直径约为100nm=100×10﹣9m=1×10﹣7m,故答案为1×10﹣7.10.解:∵有意义,∴0.∴x+2≠0,x﹣2≠0,∴x≠±2.故答案为:x≠±2.11.解:当a2n=2时,(4a3n)2÷4a4n=16(a2n)3÷4(a2n)2=16×23÷(4×22)=16×8÷(4×4)=16×8÷16=8.故答案为:8.12.解:7.5×105=750000,故答案为:750000.13.解:∵x2n=5,∴(3x3n)2﹣4(x2)2n=9x6n﹣4x4n=9(x2n)3﹣4(x2n)2=9×53﹣4×52=1125﹣100=1025.故答案为:1025.14.解:∵m x=2,m y=4,∴m x+y=m x•m y=8,故答案为:8.三.解答题(共6小题,满分58分)15.解:(1)原式=2﹣6+1=﹣3;(2)原式=×12+=5+8﹣1616.解:(1)∵a m=2,∴a2m+n=24,∴a2m×a n=24,(a m)2×a n=24,22×a n=24,∴4a n=24,∴a n=6;(2)①逆用积的乘方,其公式为:a n•b n=(ab)n,故答案为:a n•b n=(ab)n;②52023×(﹣0.2)2022=5×52022×(﹣0.2)2022=5×(﹣0.2×5)2022=5×(﹣1)2022=5×1=5.17.解:(1)∵3×27m÷9m=316,∴3×33m÷32m=316,∴33m+1﹣2m=316,∴3m﹣2m+1=16,解得m=15;(2)∵a x=﹣2,a y=3,∴a3x=﹣8,a2y=9,∴a3x﹣2y=a3x÷a2y=(﹣8)÷9=﹣;(3)∵x2n=4,∴(3x2n)2﹣4(x2)2n=(3x2n)2﹣4(x2n)2=(3×4)2﹣4×42=122﹣4×16=144﹣64=80.18.解:(1)①∵f(2)=5,∴f(6)=f(2+2+2)=f(2)•f(2)•f(2)=125;故答案为:125;②∵25=5×5=f(2)•f(2)=f(2+2),f(2n)=25,∴f(2n)=f(2+2),∴2n=4,∴n=2;(2)∵f(2a)=f(a+a)=f(a)•f(a)=3×3=31+1=32,f(3a)=f(a+a+a)=f(a)•f(a)•f(a)=3×3×3=31+1+1=33,…,f(10a)=310,∴f(a)•f(2a)•f(3a)•…•f(10a)=3×32×33×…×310=31+2+3+…+10=355.19.解:(1)周日:33+0.2=33.2(米),周一:33.2+0.8=34(米),周二:34﹣0.4=33.6(米),周三:33.6+0.2=33.8(米),周四:33.8+0.3=34.1(米),周五:34.1﹣0.5=33.6(米),周六:33.6﹣0.2=33.4(米).答:周四水位最高,最高水位是34.1米,周日水位最低,最低水位是33.2米;(2)33.4﹣33=0.4>0,答:与上周末相比,本周末河流的水位上升了,水位是33.4米;(3)100×(0.4+0.5+0.2)×2.5×102吨=2.75×104(吨),答:这个星期共有2.75×104吨水蒸发到大气中.20.解:∵10﹣2α==3,10﹣β==﹣,∴102α=,10β=﹣5,∴106α+2β=(102α)3•(10β)2,=()3×(﹣5)2,=×25,=.。
幂的运算(经典——含单元测试题)
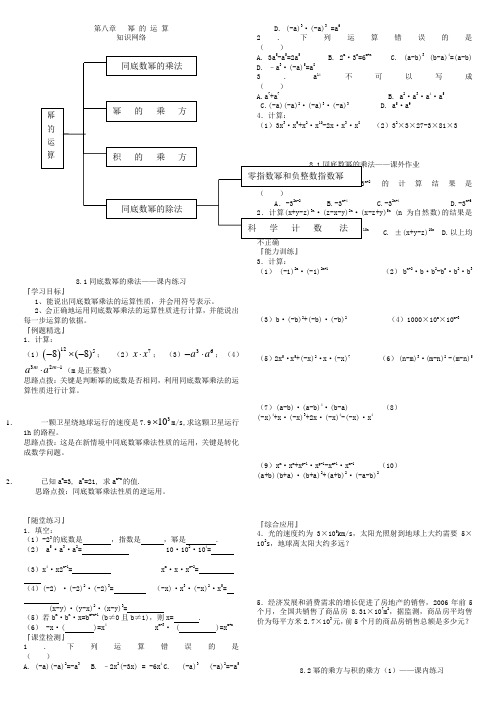
第八章 幂 的 运 算知识网络8.1同底数幂的乘法——课内练习『学习目标』1、能说出同底数幂乘法的运算性质,并会用符号表示。
2、会正确地运用同底数幂乘法的运算性质进行计算,并能说出每一步运算的依据。
『例题精选』1.计算:(1)()1258(8)-⨯-; (2)7x x ⋅; (3)36a a -⋅; (4)321m m a a -⋅(m 是正整数)思路点拨:关键是判断幂的底数是否相同,利用同底数幂乘法的运算性质进行计算。
1. 一颗卫星绕地球运行的速度是7.9310⨯m/s,求这颗卫星运行1h 的路程。
思路点拨:这是在新情境中同底数幂乘法性质的运用,关键是转化成数学问题。
2. 已知a m =3, a n =21, 求a m+n的值. 思路点拨:同底数幂乘法性质的逆运用。
『随堂练习』 1.填空: (1)-23的底数是 ,指数是 ,幂是 . (2) a 5·a 3·a 2= 10·102·104= (3)x 4·x2n-1= x m ·x ·x n-2= (4)(-2) ·(-2)2·(-2)3= (-x)·x 3·(-x)2·x 5= (x-y)·(y-x)2·(x-y)3= (5)若b m ·b n ·x=b m+n+1(b ≠0且b ≠1),则x= . (6) -x ·( )=x 4 x m-3· ( )=x m+n『课堂检测』 1.下列运算错误的是 ( ) A. (-a)(-a)2=-a 3 B. –2x 2(-3x) = -6x 4 C. (-a)3 (-a)2=-a 5 D. (-a)3·(-a)3 =a 62.下列运算错误的是 ( )m+n C. (a-b)3 (b-a)4=(a-b)可以写成 2·a 3·a 4·a 5D. a 5·a 9(2)32×3×27-3×81×3n+2的计算结果是 C.-32n+4 D.-3n+65n(n 为自然数)的结果是C. ±(x+y-z)10n D.以上均『能力训练』 3.计算:(1) (-1)2m ·(-1)2m+1 (2) b n+2·b ·b 2-b n ·b 2·b 3(3)b ·(-b)2+(-b)·(-b)2 (4)1000×10m ×10m-3(5)2x 5·x 5+(-x)2·x ·(-x)7 (6) (n-m)3·(m-n)2 -(m-n)5(7)(a-b)·(a-b)4·(b-a) (8)(-x)4+x ·(-x)3+2x ·(-x)4-(-x)·x 4(9)x m ·x m +x p-1·x p-1-x m+1·x m-1 (10)(a+b)(b+a)·(b+a)2+(a+b)2·(-a-b)2『综合应用』4.光的速度约为3×105km/s ,太阳光照射到地球上大约需要5×102s ,地球离太阳大约多远? 5.经济发展和消费需求的增长促进了房地产的销售,2006年前5个月,全国共销售了商品房8.31×107m 2,据监测,商品房平均售价为每平方米2.7×103元,前5个月的商品房销售总额是多少元? 8.2幂的乘方与积的乘方(1)——课内练习『学习目标』 1、 能说出幂的乘方的运算性质,并会用符号表示; 2、 会运用幂的乘方的运算性质进行运算,并能说出每一步运算的依据。
苏科版七下数学第8章《幂的运算》单元自测题(含答案)培训讲学

第八章 幂的运算 单元自测题时间:45分钟 满分:100分班级: 姓名: 得分:一、选择题(每小题3分,共24分)1.下列各式中错误的是( )A.()[]()623y x y x -=-B.84216)2(a a =-C.363227131n m n m -=⎪⎭⎫ ⎝⎛- D.6333)(b a ab -=- 2.若2=m a ,3=n a ,则n m a +等于 ( )A.5B.6C.8D.93.在等式⋅⋅23a a ( )11a =中,括号里填入的代数式应当是 ( )A.7aB. 8aC.6aD.3a4.计算m m 525÷的结果为 ( )A.5B.20C.m 5D.m 205. 下列4个算式中,计算错误的有 ( )(1)()()-=-÷-24c c 2c (2)336)()(y y y -=-÷-(3)303z z z =÷(4)44a a a m m =÷A.4个B.3个C.2个D.1个6.如果(),990-=a ()11.0--=b ,235-⎪⎭⎫ ⎝⎛-=c ,那么c b a ,,三数的大小为( ) A.c b a >> B.b a c >> C.b c a >> D.a b c >>7.计算3112)(n n x xx +-⋅⋅的结果为( ) A.33+n x B.36+n x C.n x12 D.66+n x 8.已知 n 是大于1的自然数,则 ()()11+--⋅-n n c c 等于 ( ) A.()12--n c B.nc 2- C.n c 2- D. n c 2二、填空题(每空2分,共20分)9.最薄的金箔的厚度为m 000000091.0,用科学记数法表示为_________m ;每立方厘米的空气质量约为g 310239.1-⨯,用小数把它表示为g . 10.()=-⋅⎪⎭⎫ ⎝⎛n n 221 ;=÷-++112n n y y ;=-23])[(m . 11.=+⋅+32)()(a b b a ;=-⋅-23)2()2(m n n m .12.( )242b a =; 32122+-=⨯n n .13.已知: ,=+,,15441544833833322322222⨯⨯=+⨯=+··· , 若ba b a ⨯=21010+(b a 、为正整数),则 =+b a . 三、解答题(共56分)14.计算(每小题4分,共20分):(1)3223)()(a a -⋅- (2)543)()(t t t -⋅-⋅- (3)234)()()(q p p q q p -⋅-÷-(4)23)3()()3(a a a -⋅--- (5)022)14.3(3)2(4π-÷----15.(8分)先化简,再求值:32233)21()(ab b a -+-⋅,其中441==b a ,.16.(8分)已知 1632793=⨯⨯m m ,求m 的值.17.(10分)已知 n x m x ==53,用含有n m 、的代数式表示14x .18.(10分)已知 222444555632---===c b a ,,请用“>”把它们按从小到大的顺序连接起来,并说明理由.第八章 幂的运算 单元自测题 参考答案三、解答题:14.(1)12a -(2)12t (3)3)(p q -(4)318a -(5)415- 15.56 16.3=m 17.n m x314= 18.b c a >>。
苏科新版七年级下册《第8章幂的运算》2024年单元测试卷(4)+答案解析

苏科新版七年级下册《第8章幂的运算》2024年单元测试卷(4)一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.某款手机芯片的面积大约仅有,将用科学记数法表示正确的是()A.B.C.D.2.下列运算正确的是()A. B. C.D.3.将,,这三个数按从小到大的顺序排列,为()A. B. C.D.4.计算,则括号内应填入的式子为()A. B. C.D.5.计算等于()A. B.C.1D.6.若,则n 的值为() A.B.C.0D.17.a 与b 互为相反数,且都不等于0,n 为正整数,则下列各组中一定互为相反数的是()A.与B.与C.与D.与8.王老师有一个实际容量为的U 盘,内有三个文件夹,已知课件文件夹占用了的内存,照片文件夹内有32张大小都是的旅行照片,音乐文件夹内有若干首大小都是的音乐,若该U 盘内存恰好用完,则此时文件夹内有音乐首.()A.28B.30C.32D.34二、填空题:本题共11小题,每小题3分,共33分。
9.计算:______.10.比较与的大小,我们可以采用从“特殊到一般”的思想方法:通过计算比较下列各式中两数的大小:填“>”“<”或“=”①______;②______;③______;④______由可以猜测与正整数的大小关系:当n ______时,;当n______时,根据上面的猜想,则有______填“>”“<”或“=”11.根据数值转换机的示意图,输出的值为,则输入的x值为______.12.计算:______.13.把的结果用科学记数法表示为______.14.若,则______.15.,则______.16.若,则______.17.已知,则______.18.若,,则用x的代数式表示y为______.19.一质点P从距原点1个单位的M点处向原点方向跳动,第一次跳动到OM的中点处,第二次从跳到的中点处,第三次从点跳到的中点处,如此不断跳动下去,则第n次跳动后,该质点到原点O的距离为______.三、解答题:本题共6小题,共48分。
初中数学苏科版七年级下册第八章 幂的运算 单元测试卷【含答案】

初中数学苏科版七年级下册第八章幂的运算单元测试卷一、单选题(本大题共10题,每题3分,共30分)1.化简的结果是()A. B. C. D.2.下列计算正确的是()A. B. C. D.3.下列运算正确的是()A. B. C. D.4.某种细胞的直径是,用科学记数法表示为()A. B. C. D.5.若,,,则()A. B. C. D.6.若(2a m b m+n)3=8a9b15成立,则()A.m=3,n=2B.m=n=3C.m=6,n=2D.m=3,n=57.若,,则的值为()A.12B.20C.32D.2568.计算(-×103)2×(1.5×104)2的结果是()A.-1.5×1011B.×1010C.1014D.-10149.观察等式,其中的取值可能是().A. B.或 C.或 D.或或10.我们常用的十进制数,如,我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量,如图,一位母亲在如下排列的绳子上打结,并采用七进制(如),用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是()A.1326天B.510天C.336天D.84天二、填空题(本大题共8题,每题2分,共16分)11.若,则x=________.12.若2n=8,则3n-1=________。
13.若9×32m×33m=322,则m的值为________.14.若a m=3,a m+n=9,则a n=________.15.已知,则的值为________.16.若m,n均为正整数,且3m﹣1•9n=243,则m+n的值是________.17.若,y=9m–8,用x的代数式表示y,则y=________.18.我们知道下面的结论:若a m=a n(a>0,且a≠1),则m=n.利用这个结论解决下列问题:设2m =3,2n=6,2p=12.现给出m,n,p三者之间的三个关系式:①m+p=2n,②m+n=2p﹣3,③n2﹣mp=1.其中正确的是________.(填编号)三、解答题(本大题共10题,共84分)19.计算:(1);(2).20.已知n是正整数,且,求的值.21.已知(x3)n+1=(x n-1)4·(x3)2,求(-n2)3的值。
苏教版七年级数学下册第8章《幂的运算》单元检测(含答案)

第8章《幂的运算》单元检测一、选择题1.计算的结果是()A. B. C. D.2.等于()A. B. C. D.3.下列运算错误的是()A. B.C. D.4.若,,则的结果为()A. 6B. 3C. 9D. 125.下列运算正确的是()A. B.C. D.6.已知,,,则a、b、c的大小关系是()A. B. C. D.7.可写成()A. B. a C. D.8.如果,那么x的值为()A. 2或B. 0或1C. 2D.9.若,则n的值是()A. B. 0 C. D.10.如果,那么m应取()A. B. C. D. ,4或2二、填空题11.己知,,用含x的式子表示y为:______ .12.如果,那么的值为______.13.计算的结果等于______.14.若,,则______ .15.禽流感病毒的形状一般为球形,直径大约为,该直径用科学记数法表示为________m.16.计算:______ .17.若,,则的值是______.18.若,则的结果是_________.19.若,则________.20.若有意义,则x的取值范围是________.三、计算题21.计算下列各题:四、解答题22.已知,求m的值.23.已知,,、b都是正整数,用含m、n或p的式子表示下列各式:;.24.已知,,。
(1)求与的值;(2)试说明:。
25.(1)已知:,求n的值(2)计算:.26.阅读:为了求的值,令,则,因此________,所以________.应用:仿照以上推理计算出的值.答案和解析1.【答案】A【解析】【分析】本题主要考查了积的乘方运算,积的乘方等于积中每个因式分别乘方,然后再将所得的幂相乘解答此题根据积的乘方的法则计算即可.【解答】解:.故选A.2.【答案】A【解析】【分析】本题主要考查同底数幂的乘法的法则,熟练掌握法则是解题的关键.根据同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加,即计算即可.【解答】解:.故选A.3.【答案】D【解析】【分析】本题考查积的乘方与幂的乘方运算法则以及单项式乘以单项式的法则,掌握这些法则是解决问题的关键运用这些法则逐一判断即可.【解答】解:,本选项正确,不符合题意;B.,本选项正确,不符合题意;C.,本选项正确,不符合题意;D.,本选项错误,符合题意.故选D.4.【答案】B【解析】解:,,.故选:B.根据同底数幂的除法法则进行计算即可.本题考查的是同底数幂的除法,熟知同底数幂的除法法则:底数不变,指数相减,是解答此题的关键.5.【答案】B【解析】【分析】本题考查了合并同类项、积的乘方、单项式乘单项式、完全平方公式,掌握运算法则是解答本题的关键.结合选项分别进行合并同类项、积的乘方、单项式乘单项式、完全平方公式的运算,选出正确答案.【解答】解:,故本选项错误;B.,故本选项正确;C.,故本选项错误;D.,故本选项错误.故选B.6.【答案】C【解析】解:,,,,故选:C.根据幂的乘方法则:底数不变,指数相乘.n是正整数分别计算得出即可.此题主要考查了幂的乘方计算,熟练掌握运算法则是解题关键.7.【答案】C【解析】【分析】根据同底数幂的乘法法则求解.本题考查了同底数幂的乘法,掌握同底数幂的乘法法则是解题的关键.【解答】解:,故ABD错误,C正确.故选C.8.【答案】C【解析】解:,,即,解得:,,当时,,故,故选:C.首先利用零指数幂的性质整理一元二次方程,进而利用因式分解法解方程得出即可.此题主要考查了因式分解法解一元二次方程以及零指数幂的性质,注意是解题关键.9.【答案】C【解析】【分析】本题考查的是同底数幂的乘法和有理数的乘方运算首先根据有理数的乘方运算把原式变形为,再由同底数幂的运算得到,解出n的值即可.【解答】解:,,,,.故选C.10.【答案】D【解析】解:,,,,,,故选:D.根据任何非零数的0次幂为1和的偶次幂为1进行解答即可.本题考查的是零指数幂和有理数的乘方,掌握任何非零数的0次幂为1和有理数的乘方法则是解题的关键.11.【答案】【解析】解:,,;故答案为:.首先根据得出,再把要求的式子进行变形得出,然后把代入进行整理即可得出答案.此题考查了幂的乘方与积的乘方,熟练掌握运算法则并对要求的式子进行变形是解题的关键.12.【答案】27【解析】解:.故答案为:27.根据幂的乘方,即可解答.本题考查了幂的乘方,属于基础题.13.【答案】【解析】解:原式,故答案为:.根据同底数幂的乘法,可得答案.本题考查了同底数幂的乘法,熟记法则并根据法则计算是解题关键.14.【答案】6【解析】解:,,,,,,.故答案为:6.先把81,9化为,的形式,求出mn的值即可.本题考查的是幂的乘方与积的乘方法则,先根据题意把81,9化为,的形式是解答此题的关键.15.【答案】【解析】【分析】本题考查用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.绝对值小于1的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:.故答案为.16.【答案】3【解析】解:原式,故答案为:3.根据负整数指数幂,非零的零次幂等于1,可得答案.本题考查了负整数指数幂,利用负整数指数幂,非零的零次幂等于1是解题关键.17.【答案】2【解析】【分析】本题主要考查了同底数幂的除法法则以及积的乘方法则,解决问题的关键是逆用这两个法则.同底数幂的除法法则:底数不变,指数相减.逆用同底数幂的除法法则以及积的乘方法则,即可得到结果.【解答】解:,,,故答案为2.18.【答案】8【解析】【分析】本题考查了幂的乘方运算以及同底数幂的乘法运算,正确将原式变形是解题的关键.直接利用幂的乘方运算法则以及同底数幂的乘法运算法则将原式变形即可得出答案.【解答】,,.故答案为8.19.【答案】22【解析】【分析】本题考查了同底数幂的除法及幂的乘方逆用同底数幂的除法及幂的乘方的法则列方程是解题的关键.先根据幂的乘方将,化成底数为3的幂,再根据同底数幂的除法法则即可列出方程求解.【解答】解:,,,,.故答案为22.20.【答案】且【解析】【分析】本题主要考查负整数指数幂和零指数幂有意义的条件.根据底数不等于零解答.【解答】解:根据题意得,,且,解得,且.故答案为且.21.【答案】解:原式,原式.【解析】本题是对积的乘方和幂的乘方,同底数幂的乘法,同底数幂的除法,负整指数幂,零指数幂等的考查.依据积的乘方和幂的乘方,同底数幂的乘法、同底数幂的除法计算即可;依据负整指数幂、零指数幂,数的乘方计算各项,然后进行加减运算.22.【答案】解:,,,,所以,.【解析】先利用幂的乘方把幂的底数都化为2,再把等式左边利用同底数幂的乘除法则计算,然后根据指数相等列关于m的方程,再解方程即可.本题考查了幂的乘方和同底数幂的乘法,解决本题的关键是转化同底数幂.23.【答案】解:..【解析】本题考查的是同底数幂的乘法与幂的乘方有关知识,与分别逆运用同底数幂的乘法,幂的乘方的运算法则计算即可.24.【答案】解:;;因为,所以;又因为,所以,所以.【解析】本题考查同底数幂的运算,解题的关键是熟练运用运算法则,本题属于基础题型根据同底数幂的运算法则即可求出答案.把变形为,把变形为,然后计算即可;因为,所以;又因为,所以,所以.25.【答案】解:,,,,..【解析】本题考查了幂的运算性质,平方差公式的运用,提公因式法的运用.解题关键是逆用幂的运算性质.运用平方差公式依次把相邻两项分解因式.把写成,然后运用提取公因式法进行变形得出,求出,即可求出n的值.先运用平方差公式依次把相邻两项分解因式,得出,然后运用求和即可.26.【答案】解:;;应用:令,则,因此,所以,.【解析】【分析】此题考查了同底数幂的乘法,弄清题中的推理,利用错位相减法,消掉相关值,是解题的关键.学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.依照题目中类似推理,找出其中规律,利用错位相减法求解本题.6S与S之间的差就是s的值,即可得到结果.【解答】解:阅读:,所以,故答案为;;应用:见答案.。
(完整版)第8章幂的运算综合测试卷(含答案),推荐文档

1第8章 幂的运算 单元综合卷(B)一、选择题。
(每题3分,共21分)1.可以写成 ()31m a +A .B .C .·D .()31()m a +3()1m a +a a3mm a 21m +2.下列是一名同学做的6道练习题:①;②;③÷=(3)1-=336a a a +=5()a -3()a - ;④4m=;⑤;⑥其中做对的题有 ( )2a -2-214m2336()xy x y =225222+= A .1道B .2道C .3道D .4道3.2013年,我国发现“H 7N 9”禽流感,“H 7N 9”是一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012 m ,这一直径用科学记数法表示为 ( )A .1.2×10m B .1.2×10m C .12 X 10m D .1.2×10m9-8-8-7-4.若、为正整数,且·=2;,则、的值有 ()x y 2x2y5x y A .4对 B .3对C .2对D .1对5.若<一1。
则之间的大小关系是 ( )x 012x x x --、、 A .> > B .>>C .>>D ..>>0x 2x -1x -2x -1x -0x 0x 1x -2x -1x -2x -0x 6.当=一6,y =时,的值为 ( )x 1620132014x y A .B .C .6D .一61616-7.如果(··)=,那么、的值分别为 ( )m a n b b 3915a b m n A .=9,=一4 B .=3,n =4C .=4,=3D .=9,=6m n m m n m n2二、填空题。
(每空2分,共16分)8.将()、(一2) 、(一3) 、一︱-10 ︱这四个数按从小到大的顺序排为 ·161-029.() =;()×=2242a b 12n -23n +10.若=×,则=.35)x (152153x 11.如果÷=64,且a <0,那么a = .43(a )25(a )12.若=2,,则的值为 .3n 35m =2313m n +-13.已知2=,4=y ,用含有字母的代数式表示y ,则y.mx 3mx 14.如果等式(2一1) =1,则的值为.a 2a +a 三、解答题。
第八章幂的运算单元基础测试卷(含答案)-精品

第八章幂的运算单元基础测试卷(含答案)-精品2020-12-12【关键字】问题、发现、基础、关系、解决(60分钟,满分100分)一、填空题(6题,每题3分,共18分)1.计算:(1)x 3·x 4=_______; (2) x n ·x n -1 =_______;(3)(—m )5·(—m )·m 3=_______; (4)(x 2)3÷x 5=_______.2.计算:(1)4()3xy -·(—3x 2y )2=_______; (2)(π-)0+2-2=________.3.氢原子中电子和原子核之间的距离为0.00000000529厘米.用科学记数法表示这个距离为_______厘米.4.若a x =2,则a 3x =_______.5.若3n =2,3m =5,则32m +3n -1=_______.6.计算:2013201252()(2)125-⨯=__________. 二、选择题(6题,每题3分,共18分)7.在下列四个算式:(—a )3·(—a 2)2=—a 7,(—a 3)2=—a 6,(—a 3)3÷a 4=a 2,(—a )6÷(—a )3=—a 3,正确的有 ( )A .1个B .3个C .2个D .4个8.若(a m b n )3=a 9b 15,则m 、n 的值分别为 ( )A .9;5B .3;5C .5;3D .6;129.[—(-x )2]5= ( )A .—x 10B .x 10C .x 7D .—x 710.若a =—0.32,b =—3-2,c =21()3--,d =01()5-,则 ( ) A .a <b <c <dB .b <a <d <cC .a <d <c <bD .c <a <d <b11.已知| x | =1,|y |=12,则(x 20)3—x 3y 2等于 ( ) A .34-或54-B .34或54C .34D .54- 12.如果等式(2a —1)a +2=1成立,则a 的值可能有 ( )A .4个B .1个C .2个D .3个三、解答题(8题,共64分)13.(本题8分)计算:2(x 3)4+x 4(x 4)2+x 5·x 7+x 6(x 3)2.14.(本题8分)计算:(—2×1012)÷(—2×103)3÷(0.5×102)2.15.(本题8分)计算:—10—2—1×3—1×[2—(—3)2].16.(本题8分)已知83=a 9=2b 求222111()()2()5525a b a b b a b -++-+的值. 17.(本题8分)我们知道:因为4<5,所以4n <5n (n 为正整数),用你所学过的知识来比较3108与2144的大小关系?18.(本题6分)厂次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A 、B 、C 、D 、E 、F 分别藏在六张大纸牌的后面,如图所示,A 、B 、C 、D 、E 、F 所持的纸牌的前面分别写有六个算式:66;63+63;(63) 3;(2×62)×(3×63);(22×32) 3;(64) 3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A 来找他的朋友,他可以找谁呢?说说你的看法.19.(本题6分)有一句谚语说:“捡了芝麻,丢了西瓜.”意思是说有些人办事只抓一些无关紧要的小事,却忽略了具有重大意义的大事.据测算,5万粒芝麻才200克,你能换算出1粒芝麻有多少克吗?可别“占小便宜吃大亏”噢!(把你的结果用科学记数法表示)20.(本题12分)阅读下列一段话,并解决后面的问题.观察下面一列数:l ,2,4,8,…我们发现,这列数从第二项起,每一项与它前一项的比值都是2.我们把这样的一列数叫做等比数列,这个共同的比值叫做等比数列的公比.(1)等比数列5,一15,45,…的第4项是_______;(2)如果一列数a 1,a 2,a 3,…是等比数列,且公比是q ,那么根据上述规定有21a q a = 32a q a =,43a q a =,…所以a 2=a 1q ,a 3=a 2q =a 1q ·q =a 1q 2,a 4=a 3q =a 1q 2·q =a 1q 3, … 则a n =______;(用a 1与q 的代数式表示)(3)一个等比数列的第2项是10,第3项是20,求它的第1项和第4项.参考答案一、填空题1.(1)x 7 (2)x 2n -1 (3)m 9 (4)x2.(1)—12x5y3(2)5 43.5.29×10-94.8 5.20036.512二、选择题7.C 8.B 9.A 10.B 11.B 12.D 三、解答题13.【解】原式=5x1214.【解】原式=1 1015.原式=1 616.原式=一6417.19.4×10-3(克)20.(1)一135 (2)a l·q n-1(3)第一项是5,第二项是40。
第八章幂的运算单元综合测试卷

第八章幂的运算单元综合测试卷第八章幂的运算综合测试卷一、填空题:1.104×107=______,(-5)7×(-5)3=_______,b2m·b4n-2m=_________。
2. (x4)3=_______,(a m)2=________ ,m12=()2=()3=()4。
3.(a2)n·(a3)2n=_______, 27a·3b=_______, (a -b)4·(b-a)5=_______。
4.(2x2y)2=______, ( - 0.5mn)3=_______,(3 ×102)3=______,86 2 ,a6 6 6 ,5.x y=()b=()0.0920122012120122×(-2)×(-4 )=_______,6.若 4x=5,4y=3,则 4x+y=________ 。
7.若 a-b=3,则[(a-b)2]3·[(b-a)3]2=________。
(用幂的形式表示)8.氢原子中电子和原子核之间的距离为0.00000000529厘米。
用科学记数法表示这个距离为.9. (-2)64+(-2)63=_________,( )0 2 2的结果是.10.若a x2,则a3 x =.11.计算:(5)2012(22)2013 =.12512. 3108与2144的大小关系是.13.如果等式(2a 1)a 21,则a的值为。
二、选择题;1. 已知: 24×8n=213,那么 n 的值是()A. 2B.3C. 5D. 82.以下计算:(1)a n·a n=2a n; (2) a6+a6=a12; (3) c·c5=c5; (4) 3b3·4b4=12b12;(5) (3xy3)2=6x2y6.中正确的个数为()A. 0B. 1C. 2D. 33.已知 (a x·a y)5=a20 (a>0,且 a≠ 1),那么x、y 应知足()A. x+y=15B. x+y=4C. xy=4D.y=4x4.已知 a=266,b=355,c=444,那么 a、b、c 的大小关系是()A. a>b>cB. b> c>aC. a<b<c D. c>a>b5.已知 a m=3,a n=2,那么 a m+n+2的值为()A. 8B. 7C. 6a2D. 6+a26.x 2 5=()A.x10B.-x10C. x7 D.-x77.若a 3 2,c20)0.32 , b1, d 1 ,则(35A.a<b<c<d B.b<a<d<c C.a <d<c<b D.c<a<d<b8.已知x 1, y 1 ,则x203x3 y2等于()2A .3或5B .3或5C .44443 4D.54三、计算:1. a2·a3+a·a52.y m+2·y·y m-1-y2m+23.(-2x·x2·x3)24.a3·a3·a2+(a4)2+(-2a2)45.1(0.25)14 (- 4)146.23×8×16×32 (结果用幂的形式表示)(x-y)5·(y-x)4·(x-y)38. ( 271 )15×(315)3( 2 1012 ) ( 2 103 )3(0.510 2 )2.四、解答题 :1.已知 23x+2=64,求 x 的值;假如 x 知足方程 33x-1=27×81,求 x 的值。
七年级下第8章幂的运算单元自测题含答案.docx

算255m的结果为B.5(-)*(-)=- -列4个算式中,计算错误的有20 C. 5m D. 20m⑴ c4 c2 2 3 Z° Z34m a m a4七年级下第8章幕的运算单元自测题含答案第八章幕的运算单元自测题时间:45分钟满分:100分一、选择题(每小题3分,共24分)1 •下列各式中错误的是()A.班级: 姓名: 得分:C. / y-4J 2 2丿° m nB.m2•若a = --1-6 3m n27 +m na 等于(3,贝【JD.—3)3 = 一(ab aA.5B.6C.8D.93.在等式11a中, 括号里填入的代数式应当是A・a C. D.二、填空题(每空2分,共20分)每立方厘米的空气质量约为1.239x10^g ,用小数把它表示为(4) ( 3a)3 ( a) ( 3a)2 (5)3] 2 [(耐—(a b) b a—• 一3=( 2 )2;(2m n) n m—+________________ X n 1 =22n 3.2•—2 _ X —2 +3 := X —-----3 4X 一42 2 213.已知:_2=•2,3 3 ,4+ =4=,3 3 8 8 15 •••915a 有10+210a(a、b为正整数),则 a bb b三、解答题(共56分)• ■■ •12.(——) --------- 2 = a4bj14•计算(每小题4分,共20分):(1) 3)2(a3 ( t) ( t)4 5t4 ( )3 ( )2(p q) q p p qg・4 ( 2p 32 (3.14 )o15. (8分)先化简,再求值:Q3 2a (b )16. (8分)已知3 m9 27 ,求m的值.3 1 1)2 3ab ,其中a ,b 4.2 4-2-Y3Y 5“用含有m> n的代数式表示X14.X = ill X = ri18. (10分)已知a 2少,b 3上44, C 6些2请用“ >"把它们按从小到大的顺序连接起来, 并说明理由第八章幕的运算单元自测题参考答案仃.(10分)已知一、选择题:1・D 2・B 3.C 4.C 5.C 6.C 7.D 8.D二填空题:9・0.001239 10. - 1;fn611. (a+6)';(2櫛-12. a 甥13. 10912 12 3 31一a ( 2) t (3) (q- p) (4) -48a (5) -5—15. 564= 14 = 18. a c b3 16. m 3 17. x m n 三、解答题:(1)。
第八章 幂的运算 单元测试(一)

第八章 幂的运算单元测试一.填空题(20×1’)1.102·107 = ,(m 4)3= ,(2a)4= ;a 5÷(-a 2 )·a =2. (-a)3·(-a)= ,(-b 2)3= , (-3xy)2= ; x 2+x ·x =3. (21)·(-2 n )= ,-y 3n+1÷y n+1= ,[(-m)3]2= ; 4. (a +b)2·(b +a)3= ,(2m -n)3·(n -2m)2= ;5. ( )2=a 4b 2; ×2 n-1=2 2n+3;6.最薄的金箔的厚度为0.000000091m ,用科学记数法表示为 ;每立方厘米的空气质量为1.239×10-3g ,用小数把它表示为 ;7. 0.25×55= ; 0.125 2004×(-8)2005= ;8已知:。
二.判断题(6×2’)1.a 2·a 3=a 6 ( )2.a 3+a 3=a 6 ( )3.3 n ·(-3)2=3 n+2 ( )4.(x 5) 8=x 13 ( )5.(-2x 2y 3)2=-4x 4y 6 ( )6.32m ×9m ×27=34m+3 ( )三.选择题(6×3’)1. 若a m =2,a n =3,则a m+n 等于( )(A)5 (B)6 (C)8 (D)92. n n 2)(-a 的结果是( )(A)-a 3n (B) a 3n (C)2n 2a - (D) 2n 2a3.在等式a 3·a 2·( )=a 11中,括号里面人代数式应当是( ).(A)a 7 (B)a 8 (C)a 6 (D)a 34. 计算25m ÷5m 的结果为 ( )(A) 5 (B)20 (C) 5m (D )20m5. (x 2·x n-1·x 1+n)3结果为( ) (A)x 3n+3 (B) x 6n+3 (C)x 12n (D)x 6n+66.计算(-8)2×0.253的结果是( ).=则为正整数),,(=若=,=+,=+ba b a b a 10b a 10,...,15441544833833 3223222222+⨯+⨯+⨯⨯(A)1 (B)-1 (C)-41 (D) 41 四.计算题 (6×5’)1. (-a 3)2·(-a 2)3 2. -t 3·(-t)4·(-t)53. (p -q)4÷(q -p)3·(p -q)2 4 . (-3a)3-(-a)·(-3a)25. 4-(-2)-2-32÷(3.14-π)0 6 化简求值a 3·(-b 3)2+(-21ab 2)3 ,其中a =41,b =4。
第八章幂的运算单元测试

第八章幂的运算单元测试一.填空题1.计算:(1)某24(2)某2y3(3)a24a3(4)a4a2.填上适当的指数:(1)a4aa5(2)a5aa4(3)a4a8(4)ab3aba3b33.填上适当的代数式:(1)某3某4某8(2)a12a6(3)某y5某y434.计算:(1)ab4ab4.(2)某n2某2(3)aa3ama8,则m=(4)(4107)21055.用小数表示3.141046.一种细菌的半径是0.00003厘米,用科学计数法表示为厘米二.选择题1.下列各式中,正确的是()A.m4m4m8B.m5m52m25C.m3m3m9D.y6y62y122.下列各式中错误的是()A.某y32某y6B.(2a2)4=16a8C.13m2n1m6n3D.ab33273-a3b63.下列各式(1)3某34某27某5;(2)2某33某36某9(3)(某5)2某7(3某y)3=9某3y3,其中计算正确的有()A.0个B.1个C.2个D.3个4.下列各式(1)b5b52b5(2)(-2a2)2=4a4(3)(an1)3=a3n1345某2y364125某6y9,其中计算错误的有()A.1个B.2个C.3个D.4个(4)(4)5.下列4个算式(1)c4c2c2(2)y6y4y2(3)z3z0z3(4)a4mama4其中,计算错误的有()A.4个B.3个C.2个D.1个6.某k12等于()A.某2k1B.某2k2C.某2k2D.2某k17.已知n是大于1的自然数,则cn1cn1等于()8.计算某43某7的结果是()A.某12B.某14C.某19D.某849.如果a990,b0.11,c253,那么a,b,c三数的大小为()A.abcB.cabC.acbD.cba10.下列等式正确的是()A.某23某5B.某8某4某2C.某3某32某3D.(某y)3某y3211.计算30122的结果是()A.1B.-1C.3D.9812.下列运算中与a4a4结果相同的是()A.a2a8B.a24C.a44D.a24a2413.下列计算正确的是()A.a3a2a5B.a3aa3C.a23a5D.(3a)33a314.下列计算正确的是A.某2某32某5B.某2某3某6C.(某3)2某6D.某6某3某315.下列计算正确的是()A.143341B.510201C.252102D.12981(三.解答题1.计算(1)(ab)ab322(2)某2某m3某2m123223(3)某yz(4)y某某y++2(某y)2y某(某y)22.计算311323012105)(155(2)10(-1023910(3)某(某)某3.计算(1)(ab)5mba(2)nm2m7mba(m为偶数,ab)mn3202m12某n1(4)babaab353mn(mn)pp54.用简便方法计算22000791.5199911999(2)1(1)(1)()39165.已知3927mm1111113,求m的值。
第八章幂的运算单元测试卷(讲+练)(原卷版)

2022-2023学年第二学期七年级下册第八章单元测试卷姓名 班级 得分一.选择题(共8小题)1.医学研究发现一种病毒的直径约为0.00000012米,则这个数用科学记数法表示为( )A .0.12×10﹣6B .1.2×10﹣7C .1.2×10﹣6D .12×10﹣8 2.下列计算错误的是( )A .x +x +x +x =4xB .x ﹣x ﹣x ﹣x =﹣2xC .x •x •x •x =x 4D .x ÷x ÷x ÷x =1 3.若2a =5,2b =3,则2a﹣b 的值为( ) A .53 B .2 C .4 D .154.计算:(﹣0.25)12×413( )A .﹣1B .1C .4D .﹣45.已知25a •52b =56,4b ÷4c =4,则代数式a 2+ab +3c 值是( )A .3B .6C .7D .8 6.若一个正方体的棱长为2×10﹣2米,则这个正方体的体积为( ) A .6×10﹣6立方米 B .8×10﹣6立方米 C .2×10﹣6立方米D .8×106立方米 7.若a 为正整数,则(a ⋅a ⋅⋯⋅a ︸a 个)2=( )A .a 2aB .2a aC .a aD .a a 28.我们知道,同底数幂的乘法法则为a m •a n =a m +n (其中a ≠0,m 、n 为正整数),类似地我们规定关于任意正整数m 、n 的一种新运算:h (m +n )=h (m )•h (n );比如h (2)=3,则h (4)=h (2+2)=3×3=9,若h (2)=k (k ≠0),那么h (2n )•h (2020)的结果是( )A .2k +2021B .2k +2022C .k n +1010D .2022k二.填空题(共8小题)9.计算:2﹣2﹣(﹣2)0= . 10.0.000000358用科学记数法可表示为 .11.将2x ﹣3y (x +y )﹣1表示成只含有正整数指数幂的形式为 .12.若(a +3)a +1=1,则a 的值是 .13.已知4×8m×16m=29,则m的值是.14.已知2a=3,2b=6,2c=12,则2a+b=;a+c﹣2b=.15.有一个棱长10cm的正方体,在某种物质的作用下,棱长以每秒扩大为原来的102倍的速度膨胀,则3秒后该正方体的体积是立方厘米.16.已知m=154344,n=54340,那么2016m﹣n=.三.解答题(共11小题)17.计算:(1)−12030+|−6|−(π−3.14)0+(−13)−2;(2)x3y(12x−1y3)−2.18.计算:(1)−(512)6×(−4)5×(225)6×0.256;(2)a5•(﹣a)3+(﹣2a2)4.19.若a+b+c=3,求22a﹣1•23b+2•2a+3c的值.20.若a m=a n(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:(1)如果2÷8x•16x=25,求x的值;(2)如果2x+2+2x+1=24,求x的值;21.若a m=a n(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:(1)如果2÷8x•16x=2,求x的值;(2)如果2y+2+2y+1=24,求y的值.22.我们知道,同底数幂的乘法法则为a m•a n=a m+n(其中a≠0,m、n为正整数),类似地,我们规定关于任意正整数m、n的一种新运算:f(m)•f(n)=f(m+n)(其中m、n为正整数).例如,若f(3)=2,则f(6)=f(3+3)=f(3)•f(3)=2×2=4.f(9)=f(3+3+3)=f(3)•f(3)•f(3)=2×2×2=8.(1)若f(2)=5,①填空:f(6)=;②当f(2n)=25,求n的值;(2)若f(a)=3,化简:f(a)•f(2a)•f(3a)•…•f(10a).23.若a m=a n(a>0且a≠l,m、n是正整数),则m=n.利用上面结论解决下面的问题:(1)如果8x=25,求x的值;(2)如果2x+2+2x+1=24,求x的值;(3)若x=5m﹣3,y=4﹣25m,用含x的代数式表示y.24.(1)已知a=2﹣4444,b=3﹣3333,c=5﹣2222,请用“<”把它们按从小到大的顺序连接起来,说明理由.(2)请探索使得等式(2x+3)x+2021=1成立的x的值.25.如果x n=y,那么我们规定(x,y)=n.例如:因为32=9,所以(3,9)=2.(1)(理解)根据上述规定,填空:(2,8)=,(2,14)=;(2)(说理)记(4,12)=a,(4,5)=b,(4,60)=c.试说明:a+b=c;(3)(应用)若(m,16)+(m,5)=(m,t),求t的值.26.阅读下列材料:一般地,n个相同的因数a相乘a•a…,记为a n.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).(1)计算以下各对数的值:log24=,log216=,log264=.(2)写出(1)log24、log216、log264之间满足的关系式.(3)由(2)的结果,请你能归纳出一个一般性的结论:log a M+log a N=(a>0且a≠1,M>0,N>0).(4)设a n=N,a m=M,请根据幂的运算法则以及对数的定义说明上述结论的正确性.27.比较2021﹣2022与2022﹣2021的大小,我们可以采用从“特殊到一般”的思想方法:(1)通过计算比较下列各式中两数的大小:(填“>”,“<”或“=”)①1﹣22﹣1,②2﹣33﹣2,③3﹣44﹣3,4﹣55﹣4.(2)由(1)可以猜测n﹣(n+1)与(n+1)﹣n(n为正整数)的大小关系:当n时,n﹣(n+1)>(n+1)﹣n;当n时,n﹣(n+1)<(n+1)﹣n.(3)根据上面的猜想,则有2021﹣20222022﹣2021(填“>”,“<”或“=”).。
七年级数学_第八章_幂的运算_单元测试卷

七年级数学第八章 幂的运算 单元测试(满分150分)第Ⅰ卷(选择题,共30分)一、选择题(每题3分,共30分) 1. 若23==nmaa ,,则)(=+nm aA.5B.6C.8D.9 2. 22=nx ,则)(6=nxA.6B.8C.9D.12 3. 如果1623)9(=n ,则n 的值为( )A.3B.4C.5D.6 4. n x -与n x )(-的正确关系是( )A.相等B.当n 为奇数时它们互为相反数,当n 为偶数时相等C.互为相反数D.当n 为奇数时相等,当n 为偶数时互为相反数5. 1221)()(-+∙n n a a 等于( )A.34+n aB. 14+n aC. 14-n aD. n a 4 6. 若n 为正整数,且72=nx ,则nnx x2223)(4)3(-的值为( )A.833B.2891C.3283D.1225 7. 若2=-b a ,1=-c a ,则22)()2(a c c b a -+--等于( )A.9B.10C.2D.1 8. ()[])(32=--a学校:____ 班级:_____ 姓名:_______ 学号:____ 考场号:____ 。
装。
订。
线。
内。
请。
勿。
答。
题。
A.6a -B.6aC.61a-D.61a9. 下列四个算式:⑴84444)(xxx ==+,⑵()[]8222222yyy ==⨯⨯,⑶()632yy =-,⑷()[]()6623xx x =-=-,其中正确的有( )A.0个B.1个C.2个D.3个 10. 把-2360000用科学计数法表示,应是( )A.41036.2⨯-B.61036.2⨯-C.71036.2⨯-D.71036.2-⨯- 选择题 1 2 3 4 5 6 7 8 9 10 答案第Ⅱ卷(非选择题,共120分)二、填空题(每空2分,共20分)11.=∙-+1n mxx , =∙-∙∙27393322,12.若22=n x ,则=nx 6,已知22=x ,3=ny,则=nxy 3)(13.计算:=-⨯-20062005)125.0(814.=++--21)2.022(,=÷÷÷)()(6735m m m m15.=÷-81812)2(,()=∙⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛333222116.()36216.0=-x ,()56244=⨯17. 已知8∙∙mmaa =211,则m= .18.用小数表示=⨯-41014.3 19.一种细菌的半径是00003.0厘米,用科学计数法表示为 厘米;20.若x=2m +1,y=4m +3,则用x 的代数式表示y 为_________. 三、解答题(21题40分、22-25每题7分,共68分) 21.计算(40分) ⑴()()2222266--⨯--- ⑵mn n xx xx÷∙∙-+11(n >m )⑶2010225.0⨯ ⑷()[]()()532232334babab a -∙-∙-⑸-102n×100×(-10)2n -1(6)()[]()()522343225xxxx-÷-∙-÷(7)(-9)3×(-23)2×(13)3(8)()()()52b a a b b a nn-∙-∙-(其中n 为正整数)22.先化简,再求值:()3233212a b ab ⎛⎫-+- ⎪⎝⎭, 其中a=14, b=4.23. 已知x+y=a, 试求(x+y)3(2x+2y)3(3x+3y)324.一种电子计算机每秒可做810次运算,它工作2105⨯秒可做多少次 运算?(结果用科学记数法表示)25.若3-=a ,25=b 。
(完整版)第八章幂的运算单元测试B卷(含答案)

七(下)数学第八章幕的运算B 卷、选择题(每题3分,共15分)1. 下列各式中(n 为正整数),错误的有①a n +a n =2 a 2n :② a n -a n =2a 2n ; A . 4个 B . 3个2. 下列计算错误的是A . (- a )2(- a )= - a 3 C . a 7-a 8=1 3. 宀3等于A .x 5B .45x201120122 320134.计算g - g 1的结果3223A —B—325.已知 a m =2,a n=3,则a2m+3 n 等于A. 54B.108填空题(每题3分,共21分)()③ a n + a n = a 2n ; ④ a n -a n =a 2nC . 2个D . 1个()B . (xy 9) 2=x 10 11y 4D . 2a 43a 2=6a4( )7•计算:[(—n 3)] 2= ________ ; 92X9 X81 — 310= ___________________ . &若 2a +3b=3,贝U 9a 27b 的值为 __________________ . 9 .计算: a 2 -a a 3 = ____________ ; (x 2) 3—x x 2) 2= _______________________ 10. _________________________________________计算:[(m 2) 3 (— m 4) 3]十m m 2) 2-m 12 _______________________ .11. 用科学记数法表示 0. 000 507,应记作 .C . x 12 13 14 15D . x 16( )12. 有一道计算题:(—a 4) 2,李老师发现全班有以下四种解法,①(—a 4) 2=( — a 4)(— a 4)= a 4a 4=a 8 ②(—a 4) 2=— a 4x2=— a 8④ (—a4)2=( — 1 x a4)2= (— 1)2(a4)2=a8 你认为其中完全正确的是 (填序号) ___________ 、解答题洪64分) 13. (本题满分12分)计算: 后1 2天加利福尼亚发生了 7级地震.问加利福尼亚的地震强度是荷兰地2 3c.——D.—-3 2( ) C. 36 D. 18震强度的⑴ a 3+a -a 2;(2)( — 2 a )3 — ( — a ) (3 a )2 b ;(3)t 8说t 215);⑷x 5x 3—x 7 x+x 2 x 6+x 4 x 4.14.(本题满分 16 分)计算:(1)0. 252012N —4)2013(3)2(a 4) 3+( a 3) 2 (a 2) 3+a 2a 10木星的质量约是多少吨 ?(结果用科学记数法表示 ) 16 17 * 1817. (本题满分6分)已知5m =2 , 5n =4,求16 (本题满分 6 分)一般地,我们说地震的震级为 10 级,是指地震的强度是 1010,地震的震级为 8级,是指地震的强度是 108. 1992年 4月,荷兰发生了 5级地震,其 多少倍 ?③(—a 4) 2=( — a )4X2=( — a )8= a 8(2)(a —b) 2 (a —b) 10 (b —a );⑷ x 3n+y —x n+i2)2^x n .15. (本题满分 6 分 )地球的质量约是 5. 98 XI021吨,木星的质量约是地球质量的318 倍,252^n+125m+n的值.18.(本题满分8 分)(1)观察下列各式:①104十103=104「3=101;②104十102=104「2=102;③104-101=10^1=103;④104十100=104「0=104;由此可以猜想:⑤104-10^ 1= ________ = __________ ;⑥104+10「2= ________ = __________ ;(2)由上述式子可知,使等式a m+a n=a m_n成立的m、n除了可以是正整数外,还可以是 .⑶利用⑵中所得的结论计算:①22+f8;②x n+x「n.19.观察、分析、猜想并对猜想的正确性予以说明.1 >2 X3 M+I =522 X3 X4 ^5+1=11 2 3 X4 X5 X6+1=1924X)X5X7+1=292n(n+1)(n+2)(n+3)+仁____________ ( n 为整数).参考答案— 、 1 . B 2. D 3. C 4. D 5. B二、 6. a 6, 1 7 . n 6,0 8. 27 9. -2a 3b 210.- 111 . 5.07 XI0_412.①③④三、 13 .(1)a 4;(2)a3;(3)t ;(4)2x 814. (1)-4 ;(2)-(a -b) 13;(3)4a 12;(4)115. 1. 90 XI024 吨 16.100倍仃.提示:252m_n +125m+n =(52)2m _n +(53)m+n =54m ^52n +53n 53n=(5m) 4说5n ) 2+(5m ) 3 (5n ) 3=24詔2+23 43=51318. (1)104-(-1)=105,104-(-2)=106; (2 )负整数和零; (3)210,x 2n .19.[n(n+3)+1]9. 若x3= —8a9b6,贝V x= ____________ .。
苏科版七年级下册幂的运算单元检测2份1

第八章幂的运算测试姓名: 得分: ( 总分:100分;时间:100分钟)一、选择题(每小题2分,共16分)1.下列各式中错误的是( )A.()[]()623y x y x -=- B.84216)2(a a =- C.363227131n m n m -=⎪⎭⎫⎝⎛- D.6333)(b a ab -=-2.若2=ma,3=n a ,则n m a +等于 ( )A.5B.6C.8D.9 3.在等式⋅⋅23a a ( )11a =中,括号里填入的代数式应当是 ( )A.7aB.8aC.6aD.3a 4.计算mm 525÷的结果为 ( )A.5B.20C.m 5D.m20 5. 下列4个算式中,计算错误的有 ( )(1)()()-=-÷-24c c 2c (2)336)()(y y y -=-÷-(3)33z z z =÷(4)44a a a m m =÷A.4个B.3个C.2个D.1个6.如果(),990-=a ()11.0--=b ,235-⎪⎭⎫⎝⎛-=c ,那么c b a ,,三数的大小为( )A.c b a >>B.b a c >>C.b c a >>D.a b c >>7.计算3112)(n n x x x +-⋅⋅的结果为( )A.33+n xB.36+n x C.nx12 D.66+n x8.已知 n 是大于1的自然数,则 ()()11+--⋅-n n c c 等于 ( )A.()12--n c B.nc 2- C.nc 2- D.nc2二、填空题(每题3分,共30分)9.最薄的金箔的厚度为 m 000000091.0,用科学记数法表示为 m ;10.()=-⋅⎪⎭⎫⎝⎛n n221 ;=÷-++112n n y y ;=-23])[(m . 11.=+⋅+32)()(a b b a ;=-⋅-23)2()2(m n n m ;(-21)100×2101= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 幂的运算 单元测试
姓名:______ 得分:_____-
一.填空题(24分) 1.计算:(1)()
=-4
2
x 2)()
=3
2y x (3)()()=-÷-a a 4
2.填上适当的指数: (1)()
54
a a
a =∙ (2)()()8
4
a
a = (3)()()
()
334
b a ab ab =÷
3.填上适当的代数式: (1)(
)84
3
x x x =∙∙
(2)()612
a a
=÷ (3) ()()(
)345
-=-∙-y x y x
4. 计算:
(1) ()=÷4
4ab ab (2) =÷+22
x x
n (3) 8
3a a a a m =∙∙,则m=
5.(7
104⨯)()
5102⨯÷= 6.若2,x
a =则3x
a = 7、若32,35n m ==,则231
3
m n +-=
8、计算:2007
2006
522125⎛⎫⎛⎫-⨯ ⎪
⎪⎝⎭⎝⎭=
二.选择题(30分)
1.下列各式中,正确的是( )
A .8
4
4
m m m = B.25
5
5
2m m m =
C.9
3
3
m m m = D.66y y 12
2y =
2. 下列各式中错误的是( ) A.()
[
]
()6
2
3y x y x -=- B.(22a -)4=816a C.363
227131n m n m -=⎪⎭
⎫
⎝⎛- D.()
=-3
3
ab -b a 36
3.下列各式(1) 523743x x x =∙; (2) 933632x x x =∙ (3) (5x )7
2x = (4) (3xy)3
=933y x ,其中计算正确的有 ( ) A.0个 B.1个 C.2个 D.3个
4.下列各式(1)55b b ∙52b = (2) (-2a
2
)
2
=4-4a (3) (1-n a )3=1
3-n a (4)
963
32125
6454y x y x =⎪⎭⎫
⎝⎛,其中计算错误的有 ( ) A.1个 B.2个 C.3个 D.4个
5.()2
1--k x 等于 ( )
A.1
2--k x
B.2
2--k x
C.2
2-k x
D.1
2-k x
6.已知n 是大于1的自然数,则()c -1
-n ()
1
+-∙n c 等于 ( )
A. ()
1
2--n c B.nc 2- C.c -n
2 D.n
c
2
7.计算()
73
4
x x ∙的结果是 ( )
A. 12
x B. 14
x C. x 19
D.84
x
8.下列等式正确的是 ( ) A.()
53
2
x x -=- B. 248x x x =÷ C.3332x x x =+ D.(xy )33xy =
9.下列运算中与4
4
a a ∙结果相同的是 ( ) A.8
2
a a ∙ B.()
2
a 4
C.()4
4
a D.()()
2
4
2a a ∙4
10.下列计算正确的是 ( ) A.5
2
3
a a a =∙ B.a a a =÷3
3
C.()
a a =3
2
5 D.(a 3)333a =
三.解答题(66分) 1.计算(16分) (1) (b a 2
)()
3ab ∙2
(2) ()
m m
x x x 23
2÷∙
(3)3
2
3221⎥⎥⎦
⎤
⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-z xy (4)()
1132)(--∙÷∙n m n m x x x x
2.计算(10分)
(1)()a b - ()3a b -()5b a - (2) ()()y x x y --2
+3
)
(y x -+()x y y x -∙-2)(2
3.用简便方法计算(10分)
(1)()5.1)32(2000⨯1999()19991-⨯ (2) )1(16997111
11-⎪⎭
⎫
⎝⎛⎪⎭⎫ ⎝⎛11
4.若的值求n m n m b a b b a +=2,)(1593(6分)
5.已知2793⨯⨯m
m
3=,求m 的值。
(6分)
6.已知a n =3,a m =2,求a
2n+3m
的值。
(6分)
7. 已知 222444555
632===c b a ,,请用“>”把它们按从小到大的顺序连接起来,并说明理
由. (6分)
8.已知 n x m x ==53,用含有n m 、的代数式表示14
x . (6分)。
