4.2-常用符号计算函数
Matlab中的符号计算方法

Matlab中的符号计算方法在数学和科学领域,符号计算是一个重要的工具。
它可以帮助我们进行精确的数学计算和推理,而不仅仅是依赖计算机的数值近似。
Matlab作为一个强大的数值计算软件,也提供了丰富的符号计算功能,用于代数运算、微积分和代数方程求解等方面。
本文将介绍Matlab中的一些常用的符号计算方法和技巧。
一、符号变量在Matlab中,我们可以通过声明符号变量来表示符号对象。
符号变量通常用小写字母表示,例如x、y、z等。
使用符号变量,我们可以进行各种代数运算,例如加法、减法、乘法和除法等。
下面是一些示例:syms x y zf = x^2 + y^2 - z^2;g = (x + y + z)^3;h = sin(x) * cos(y);通过声明符号变量,并使用这些变量进行计算,我们可以得到精确的结果,而不是使用数值近似。
二、符号表达式在Matlab中,符号表达式是由符号变量和运算符组成的一种数据类型。
使用符号表达式,我们可以构建复杂的代数表达式和方程。
例如,我们可以定义一个符号表达式f表示一个多项式函数,并对其进行运算:f = x^3 - 2*x^2 + x - 1;我们可以对符号表达式进行加减乘除等运算,并得到一个新的符号表达式。
三、代数方程求解在解决数学问题时,我们经常需要求解代数方程。
Matlab提供了强大的符号求解工具,可以帮助我们求解各种类型的代数方程。
例如,我们可以使用solve函数求解一元方程:syms xeqn = x^2 - 3*x + 2 == 0;sol = solve(eqn, x);通过solve函数,我们可以找到满足方程eqn的所有解,并将其存储到sol变量中。
除了一元方程,Matlab还支持多元方程的求解。
例如,我们可以使用solve函数求解一个二元方程组:syms x yeqn1 = x + 2*y == 5;eqn2 = x - y == 1;sol = solve([eqn1, eqn2], [x, y]);通过solve函数,我们可以找到满足方程组eqn1和eqn2的所有解,并将其存储到sol变量中。
三角函数公式表(初中物理公式)
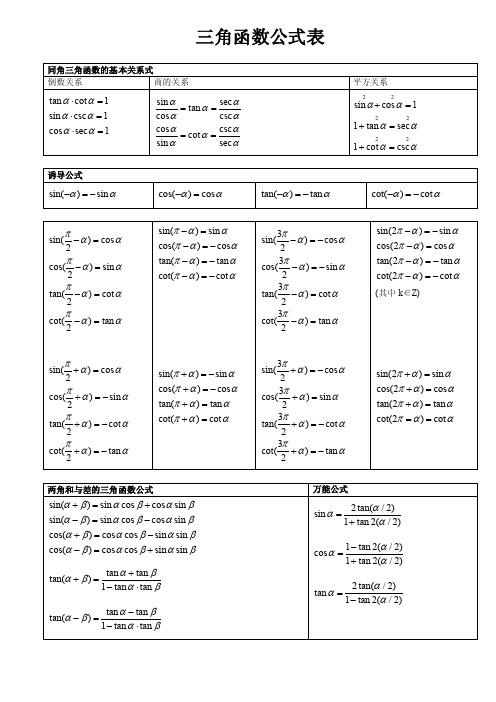
三角函数公式表物理量计算公式备注速度υ= S / t1m / s = 3.6 Km / h声速υ= 340m / s光速C = 3×108 m /s密度ρ= m / V 1 g / c m3 = 103 Kg / m3合力 F = F1 - F2F = F1 + F2 F1、F2在同一直线线上且方向相反F1、F2在同一直线线上且方向相同压强p = F / Sp =ρg h p = F / S适用于固、液、气p =ρg h适用于竖直固体柱p =ρg h可直接计算液体压强1标准大气压= 76 cmHg柱= 1.01×105 Pa = 10.3 m水柱浮力①F浮= G – F②漂浮、悬浮:F浮= G③F浮= G排=ρ液g V排④据浮沉条件判浮力大小(1)判断物体是否受浮力(2)根据物体浮沉条件判断物体处于什么状态(3)找出合适的公式计算浮力物体浮沉条件(前提:物体浸没在液体中且只受浮力和重力):①F浮>G(ρ液>ρ物)上浮至漂浮②F浮=G(ρ液=ρ物)悬浮③F浮<G(ρ液<ρ物)下沉杠杆平衡条件F1 L1 = F2 L 2 杠杆平衡条件也叫杠杆原理滑轮组 F = G / nF =(G动+ G物)/ nSF = n SG 理想滑轮组忽略轮轴间的摩擦n:作用在动滑轮上绳子股数功W = F S = P t 1J = 1N•m = 1W•s功率P = W / t = Fυ1KW = 103 W,1MW = 103KW有用功W有用= G h(竖直提升)= F S(水平移动)= W总– W额=ηW总额外功W额= W总– W有= G动h(忽略轮轴间摩擦)= f L(斜面)总功W总= W有用+ W额= F S = W有用/ η机械效率η= W有用/ W总η=G /(n F)= G物/(G物+ G动)定义式适用于动滑轮、滑轮组中考物理所有的公式特点或原理串联电路并联电路时间:t t=t1=t2 t=t1=t2电流:I I = I 1= I 2 I = I 1+ I 2电压:U U = U 1+ U 2 U = U 1= U 2电荷量:Q电Q电= Q电1= Q电2 Q电= Q电1+ Q电2电阻:R R = R 1= R 2 1/R=1/R1+1/R2 [R=R1R2/(R1+R2)]电功:W W = W 1+ W 2 W = W 1+ W 2电功率:P P = P 1+ P 2 P = P 1+ P 2电热:Q热Q热= Q热1+ Q热 2 Q热= Q热1+ Q热 2物理量(单位)公式备注公式的变形速度V(m/S)v= S:路程/t:时间重力G(N)G=mg m:质量g:9.8N/kg或者10N/kg密度ρ(kg/m3)ρ=m:质量V:体积合力F合(N)方向相同:F合=F1+F2方向相反:F合=F1—F2 方向相反时,F1>F2浮力F浮(N) F浮=G物—G视G视:物体在液体的重力浮力F浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F浮(N) F浮=G排=m排g=ρ液gV排G排:排开液体的重力m排:排开液体的质量ρ液:液体的密度V排:排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1:动力 L1:动力臂F2:阻力 L2:阻力臂定滑轮F=G物S=h F:绳子自由端受到的拉力G物:物体的重力S:绳子自由端移动的距离h:物体升高的距离动滑轮F= (G物+G轮)S=2 h G物:物体的重力G轮:动滑轮的重力滑轮组F= (G物+G轮)S=n h n:通过动滑轮绳子的段数机械功W(J)W=Fs F:力s:在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs 适用滑轮组竖直放置时机械效率η= ×100%功率P(w)P=W:功t:时间压强p(Pa)P=F:压力S:受力面积液体压强p(Pa)P=ρgh ρ:液体的密度h:深度(从液面到所求点的竖直距离)热量Q(J)Q=cm△t c:物质的比热容 m:质量△t:温度的变化值燃料燃烧放出的热量Q(J)Q=mq m:质量q:热值常用的物理公式与重要知识点一.物理公式单位)公式备注公式的变形串联电路电流I(A)I=I1=I2=…… 电流处处相等串联电路电压U(V)U=U1+U2+…… 串联电路起分压作用串联电路电阻R(Ω)R=R1+R2+……并联电路电流I(A)I=I1+I2+…… 干路电流等于各支路电流之和(分流)并联电路电压U(V)U=U1=U2=……并联电路电阻R(Ω)= + +……欧姆定律I=电路中的电流与电压成正比,与电阻成反比电流定义式I=Q:电荷量(库仑)t:时间(S)电功W(J)W=UIt=Pt U:电压 I:电流t:时间 P:电功率电功率P=UI=I2R=U2/R U:电压 I:电流R:电阻电磁波波速与波长、频率的关系C=λν C:波速(电磁波的波速是不变的,等于3×108m/s)λ:波长ν:频率二.知识点1.需要记住的几个数值:a.声音在空气中的传播速度:340m/s b光在真空或空气中的传播速度:3×108m/sc.水的密度:1.0×103kg/m3 d.水的比热容:4.2×103J/(kg•℃)e.一节干电池的电压:1.5V f.家庭电路的电压:220Vg.安全电压:不高于36V2.密度、比热容、热值它们是物质的特性,同一种物质这三个物理量的值一般不改变。
EXCEL学生成绩统计的常用函数公式

1、统计不同分数段的学生人数统计不同分数段的学生人数是非常常见的需求,其所需结果如图1中A16~E16所示。
这里,假设需要统计90~100、80~89、70~79、60~69及低于60分五个不同分数段的人数。
通常,统计不同分数段最好的方法是利用COUNTIF(X,Y)函数。
其中有两个参数,第一个参数X为统计的范围,一般最好用绝对引用;第二个参数Y为统计条件,要加引号。
对于小于60分的人数只要用一个COUNTIF( )函数,如在E16单元格中输入公式:=COUNTIF($C$2:$C$13,"<60")。
对于其他在两个分数之间的分数段的人数统计,需要用两个COUNTIF( )函数相减。
如在A16单元格中输入公式:=COUNTIF($C$2:$C$13,"<=100")-COUNTIF($C$2:$C$13, "<90"),即用小于等于100的人数减去小于90的人数。
如果要统计80~89、70~79与60~69分数段的人数,只要利用自动填充柄将该公式复制到右边三个单元格,再把"<=100"与"<90"作相应的修改,就可以得到正确的结果。
2.保持学号顺序不变的前提下进行成绩排名学生成绩排定在学生成绩统计中经常用到。
特别要强调的是,这里所谈的方法不是一般的排序,因为那样会使学生的学号顺序发生变化。
这里所需要的是在保持学号顺序不变的情况下进行学生成绩名次排定的功能,其所需结果如图1中F2~F13所示。
要进行保持学号顺序不变的情况下进行学生成绩名次的排定,最好使用RANK(X,Y,Z)函数。
其中有三个参数,第一个参数X为某个学生的成绩所在单元格;第二个参数Y为整个班级成绩所在的区域;第三个参数Z是可选的,表示统计方式,若省写或写0,则成绩高的名次靠前,一般都使用这种方式,如果写1,则成绩高的名次靠后,这种情况一般较少用。
符号计算系统Mathematica的常用系统函数

符号计算系统Mathematica的常用系统函数Mathematica是一个很大的用计算机作数学的软件系统,仅在2.0版的系统中就定义了800多个函数。
这里摘选了Mathematica2.0版的部分函数和命令,其中不包括Mathematica软件包中的函数定义,因篇幅所限,对于一些函数只作了简要说明,可在任意版本中用“??函数名”或“??命令名”的形式得到该版本中函数和命令的更详细的使用说明.所提供的函数和命令对Mathematica2.0以后的版本仍然适用.(一)数学常数ComplexInfinity 复无穷大Degree 1°对应的弧度值,为π/180 DirectedInfinity 有方向的无穷E 自然对数的底e≈2.718 28I 虚单位i=1Indeterminate 不定值Infinity 正无穷Pi 圆周率π≈3.141 59…(二)数学函数Abort[ ] 产生中止运算过程的急停。
AbortProtect[expr ] expr的运算完成后执行中止运算过程的Abort[ ]命令.Abs[x] 给出实数x的绝对值,或给出复数x的模。
如果x不是数,则Abs[x]不作运算..AbsoluteDashing[{d1,d2,…}] 图形的样式指令,虚线线段重复循环使用d1,d2,…的长度.AbsolutePointSize[d] 图形的样式指令,d是图形上点的半径.AbsoluteThickness[d] 图形的样式指令,d是图形上直线的绝对宽度.Accuracy[x] 给出x的小数点以后的位数,如果x不是一个数,Accuracy[x]给出x 中所有数的精度的最小值,整数的精度为无穷大.Apart[expr] 将有理式写成一系列最简分式之和.Apart[expr,var] 将var以外的变量都作为常数.Append[expr,elem] 给出将元素elem追加到expr后的结果,expr的值不变.AppendTo[s,elem] 将元素elem追加到s中.Apply[f,expr] f作用于expr.例如,Apply[Plus,2,3]的值为5.ArcCos[z] 复数z的反余弦arccos z.ArcaCosh[z] 复数z的反双曲余弦arccosh z.ArcCot[z] 复数z的反余切arccot z.ArcCoth[z] 复数z的反双曲余切arccoth z.ArcCsc[z] 复数z的反余割arccsc z.ArcCsch[z] 复数z的反双曲余割arccsch z.ArcSec[z] 复数z的反正割arcsec z.ArcSech[z] 复数z的反双曲正割arcsech z.ArcSin[z] 复数z的反正弦arcsin z.ArcSinh[z] 复数z的反双曲正弦arcsinh z.ArcTan[z] 复数z的反正切arctan z.ArcTanh[z] 复数z的反双曲正切arctanh z.Arg[z] 给出复数z的辐角。
计算数据(课件)--2024—2025学年高教版(2021)中职信息技术(基础模块下册)

计算每位员工的月销售提成(月销售提成=(月销售-400)*10%); 计算每位员工的实发工资(实发工资=基本工资+销售提成-扣发工资); 在表格下方增加行,分别计算所有员工的基本工资、月销售提成、扣发工
资和实发工资之和、平均值、最大值、最小值; 在表格右侧增加一列R,在R2单元格输入“工资排名”,使用RANK函数
思考1:所有员工的基本工资的计算方法是一样的,第一位员工 的数据计算出来后,如何快速计算其他员工的基本工资?
复习导入 学习新知 实战演练 总结作业
问4 如何使用函数计算数据?
4.2.1 计算数据
格式:=函数名(参数) 常用函数:求和SUM、求平均值AVERAGE、计数COUNT、最大值MAX、
数据处理 4.2.1 计算数据
信息技术
学习内容
Learning content
使用公式计算数据 使用函数计算数据
4.2.1 计算数据 2
任务1:计算北极小屋员工工资; 任务2:计算六一节目评分表/计算车展销售目标表/公司产品月销售情况表。
复习导入 学习新知 实战演练 总结作业
4.2.1 计算数据
>=、<=、<>
大于运算符
>
比较
运算 小于运算符
<
符
大于等于运算符 >=
小于等于运算符 <= 不等于运算符 <>
类型
名称
符号
作用
文本
运算
&
连接文本
符
=“a”&”b”运算结果对为两个”引a用b之”
区域运算符 : 前的所有单元
格的引用
引用 运算 联合运算符 符
excel常用公式笔记

excel常用公式笔记
SUM函数:用于求和,可以将多个数值相加。
VLOOKUP函数:用于垂直查找,可以在一个表格中查找与指定值匹配的数据。
HLOOKUP函数:用于水平查找,可以在一个表格中查找与指定值匹配的数据。
CONCATENATE函数:用于拼接字符串,可以将多个字符串连接起来。
LEFT函数:用于提取左侧的字符,可以从一个字符串中获取指定长度的左侧字符。
RIGHT函数:用于提取右侧的字符,可以从一个字符串中获取指定长度的右侧字符。
AVERAGE函数:用于求平均值,可以计算一组数据的平均数。
MAX函数:用于求最大值,可以找出一组数据中的最大值。
MIN函数:用于求最小值,可以找出一组数据中的最小值。
COUNT函数:用于计数,可以统计一组数据中非空单元格的数量。
COUNTA函数:用于计数非空单元格,可以统计一组数据中非空单元格的数量。
IF函数:用于条件判断,可以根据给定的条件返回不同的结果。
LEN函数:用于计算字符串长度,可以统计一个字符串的字符数。
UPPER函数:用于将字符串转换为大写,可以将一个字符串中的字符转换为大写字母。
LOWER函数:用于将字符串转换为小写,可以将一个字符串中的字符转换为小写字母。
计算机中的函数公式

计算机中的函数公式
计算机中的函数公式是一种用于描述两个或多个变量之间关系的数学表达式。
函数公式通常由一个或多个数学运算符、常数和变量组成,用于计算并返回一个特定的值。
函数公式可以应用于各种计算机程序和算法中,用于执行各种任务,例如数据处理、数值计算和逻辑判断等。
以下是一些常见的函数公式示例:
线性函数:f(x) = ax + b
指数函数:f(x) = a^x
对数函数:f(x) = log_a(x)
三角函数:f(x) = sin(x)、cos(x)、tan(x)
幂函数:f(x) = x^n
分段函数:根据不同的x值范围,定义不同的f(x)值。
这些函数公式可以根据需要进行组合和修改,以适应不同的应用场景。
在编写计算机程序时,可以使用各种编程语言提供的数学库或函数来调用这些函数公式,以方便地
实现各种计算和数据处理任务。
MATLAB程序设计实验指导书

MATLAB程序设计实验指导书MATLAB是集数值计算、符号运算及图形处理等强大功能于一体的科学计算语言。
作为强大的科学计算平台,它几乎能满足所有的计算需求。
在美国及其他发达国家的理工科院校里,MATLAB已经作为一门必修的课程;在科研院所、大型公司或企业的工程计算部门,MATLAB也是最普遍的计算工具之一。
有鉴于此,我院开设了《MATLAB程序设计》这门课程,它需要一定的理论基础,同时又具有很强的实践性。
如何加强理论课程的学习、加深学生对本课程中的基本理论知识及基本方法的理解,如何培养学生实践动手能力是教学的当务之急。
而MATLAB程序设计实验课程就是一种重要的教学手段和途径。
实验将MATLAB程序设计的基本方法灵活地运用在数学、电路等课程中,重点突出,内容丰富。
同时,注重理论分析与实际动手相结合,以理论指导实践,以实践验证基本原理,旨在提高学生分析问题、解决问题的能力及动手能力,使学生进一步巩固基本理论知识,建立比较全面的MATLAB程序设计的概念。
实验注意事项1、实验系统接通电源前请确保电源插座接地良好。
2、完成实验后请确保关闭电脑电源及插座电源。
实验一 矩阵及其运算一、实验目的1、熟悉MATLAB 工作环境2、掌握矩阵和数组的创建、寻访和运算 二、实验内容验证欧姆定律:iur ,其中i u r , ,分别是电阻(欧姆)、电压(伏特)、电流(安培)。
已知u=[0.89, 1.20, 3.09, 4.27, 3.62, 7.71, 8.99, 7.92, 9.70, 10.41],i=[0.028, 0.040, 0.100, 0.145, 0.118, 0.258, 0.299, 0.257, 0.308, 0.345]。
三、实验器材PC 机 (装有 MA TLAB 软件 ) 1台 四、实验原理 4.1 Desktop 简介MATLAB R2006a 版的Desktop 操作桌面,是一个高度集成的MATLAB 工作界面。
lindo常用的基本语法

2、 min Z x1 3 x2 x1 2 x2 6 s.t. 3 x1 x2 15 x , x 0 1 2
2、lingo的优点 (1)可以用于求线性规划及非线性规划问 题,包括非线性整数规划问题。
(2)lingo包含内置的建模语言(常称矩阵 生成器),允许以简练、直观的方式描述 较大规模的优化模型(成千万个约束条件 和变量), 模型中所需的数据可以用一定格 式保存在独立的文件中,需要时再读取数据。
在Lingo中,所有的系统函数都必须是以“@”开头。
2、集合循环函数
集合循环函数是指对集合中的所有元素(下标) 进行循环操作的函数,如@sum,@for等。
具体的使用格式:
@循环函数名(循环变量所在的集 (循环变量)│ 过滤条件:循环表达式) 其中,如果在操作过程中没有过滤条件,可 以省略过滤条件;如果表达式是对集合的所有循 环变量进行操作,循环变量也可以省略。
LINGO软件的使用规则(3)
(6) 约束条件中的符号“≥”用 “> = ”或“>”表示, “≤”用“<=”或 “<”表示。
(7) 计算机把输入程序中的第一行默认为目标函数, 其它各约束条件可以用[_1],[_2]标明它的行号。 (8) 虽然决策变量可以放在约束条件的右端,但为 了提高Lingo的求解效率,应尽可能采用线性表达 式定义目标函数和约束条件。 (9) 在lingo中以感叹号“!”开始的是说明语句, 并且说明语句也需要以分号“;”结束,并且除 了“!”和“;”之外,说明语句中的其它字符 可以是任何字符。
3、 lingo中的灵敏度分析
在lindo中的目标函数最优值、最优解与灵敏度 而在lingo中,最优解、最 分析是一起显示出来, 优值与灵敏度分析是分别用不同的命令显示出来。 lingo中的灵敏度分析的数据输出结果与lindo 中的灵敏性分析中输出结果是相同的。 因为lingo的求解结果中是没有灵敏度分析的, 所以如果需要灵敏度分析的数据,可以通过修改 选项来实现。
函数所有符号的意思

函数所有符号的意思
函数中的符号具有特定的含义。
例如,“∑”表示求和,“∏”表示求积,“∝”表示成比例,“∞”表示无穷大,“∧”表示逻辑“或”,“∨”表示逻辑“与”,“∩”表示“交集”,“∪”表示“并集”,“∈”表示“属于”,“⊂”表示“包含于”,“⊃”表示“包含”,“∣”表示“整除”,“÷”表示“除”。
此外,在Excel中,$是引用符号,用于绝对引用和混合引用。
比如$A$2,就是对A2的绝对引用,行列都不会发生变化。
一般用于将多个单元格内的数据连接起来。
比如A2=”我爱”,B2=”中国”,则A2&B2=”我爱中国”。
<>是不等于符号,比如IF(A2<>1,2,0),此函数意思是如果A2不等于1,则返回2,反之返回0。
是通配符或乘法符号,比如
=COUNTIF(A:A,"车间"),意思是统计A列中包含有车间字符的个数。
只要在A列中的单元格中含有车间二字或者在车间前后面有其他文字,也统一算作包含车间。
双引号可以表示空值,在Excel中要想表示空值,要在英文输入法状态下输入双引号。
空值经常应用于容错函数中,让函数避免返回错误值。
>=是大于或等于符号,经常用于逻辑判断函数中。
以上内容仅供参考,建议查阅函数相关书籍或咨询专业技术人员以获取更全面和准确的信息。
2023年新高考数学一轮复习4-2 应用导数研究函数的单调性(知识点讲解)解析版

专题4.2 应用导数研究函数的单调性(知识点讲解)【知识框架】【核心素养】考查利用导数求函数的单调区间或讨论函数的单调性以及由函数的单调性求参数范围,凸显数学运算、逻辑推理的核心素养.【知识点展示】(一)导数与函数的单调性1.在(,)a b 内可导函数()f x ,'()f x 在(,)a b 任意子区间内都不恒等于0.'()0()f x f x ≥⇔在(,)a b 上为增函数.'()0()f x f x ≤⇔在(,)a b 上为减函数.2.利用导数研究函数的单调性的方法步骤:①确定函数f(x)的定义域;②求导数f ′(x);③由f ′(x)>0(或f ′(x)<0)解出相应的x 的取值范围,当f ′(x)>0时,f(x)在相应区间上是增函数;当f ′(x)<0时,f(x)在相应区间上是减增函数.特别提醒:讨论函数的单调性或求函数的单调区间的实质是解不等式,求解时,要坚持“定义域优先”原则.(二)常用结论1.在某区间内f ′(x )>0(f ′(x )<0)是函数f (x )在此区间上为增(减)函数的充分不必要条件.2.可导函数f (x )在(a ,b )上是增(减)函数的充要条件是对∀x ∈(a ,b ),都有f ′(x )≥0(f ′(x )≤0)且f ′(x )在(a ,b )上的任何子区间内都不恒为零.【常考题型剖析】题型一:判断或证明函数的单调性例1.(2017·山东·高考真题(文))若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是( )A .()2xf x -= B .()2f x x = C .()-3xf x = D .()cos f x x =【答案】A 【解析】 【详解】对于A,令()e 2x x g x -=⋅,11()e (22ln )e 2(1ln )022x x x x xg x ---'=+=+>,则()g x 在R 上单调递增,故()f x 具有M 性质,故选A.例2.(2021·全国·高考真题(文))设函数22()3ln 1f x a x ax x =+-+,其中0a >. (1)讨论()f x 的单调性;(2)若()y f x =的图象与x 轴没有公共点,求a 的取值范围.【答案】(1)()f x 的减区间为10,a ⎛⎫ ⎪⎝⎭,增区间为1,+a ⎛⎫∞ ⎪⎝⎭;(2)1a e >.【解析】 【分析】(1)求出函数的导数,讨论其符号后可得函数的单调性.(2)根据()10f >及(1)的单调性性可得()min 0f x >,从而可求a 的取值范围. 【详解】(1)函数的定义域为()0,∞+, 又()23(1)()ax ax f x x+-'=,因为0,0a x >>,故230ax +>, 当10x a<<时,()0f x '<;当1x a >时,()0f x '>;所以()f x 的减区间为10,a ⎛⎫ ⎪⎝⎭,增区间为1,+a ⎛⎫∞ ⎪⎝⎭.(2)因为()2110f a a =++>且()y f x =的图与x 轴没有公共点,所以()y f x =的图象在x 轴的上方,由(1)中函数的单调性可得()min 1133ln 33ln f x f a a a ⎛⎫==-=+ ⎪⎝⎭,故33ln 0a +>即1a e>.例3.(2021·全国·高考真题(文))已知函数32()1f x x x ax =-++.(1)讨论()f x 的单调性;(2)求曲线()y f x =过坐标原点的切线与曲线()y f x =的公共点的坐标. 【答案】(1)答案见解析;(2) 和()11a ---,. 【解析】 【分析】(1)首先求得导函数的解析式,然后分类讨论导函数的符号即可确定原函数的单调性;(2)首先求得导数过坐标原点的切线方程,然后将原问题转化为方程求解的问题,据此即可求得公共点坐标. 【详解】(1)由函数的解析式可得:()232f x x x a '=-+,导函数的判别式412a ∆=-,当14120,3a a ∆=-≤≥时,()()0,f x f x '≥在R 上单调递增,当时,的解为:12113113,33a ax x --+-==, 当113,3a x ⎛⎫--∈-∞ ⎪ ⎪⎝⎭时,单调递增;当113113,33a a x ⎛⎫--+-∈ ⎪ ⎪⎝⎭时,单调递减;当113,3a x ⎛⎫+-∈+∞ ⎪ ⎪⎝⎭时,单调递增;综上可得:当时,在R 上单调递增,当时,在113,3a ⎛⎫---∞ ⎪ ⎪⎝⎭,113,3a⎛⎫+-+∞ ⎪ ⎪⎝⎭上单调递增,在⎣⎦上单调递减. (2)由题意可得:()3200001f x x x ax =-++,()200032f x x x a '=-+,则切线方程为:()()()322000000132y x x ax x x a x x --++=-+-,切线过坐标原点,则:()()()32200000001320x x ax x x a x --++=-+-,整理可得:3200210x x --=,即:()()20001210x x x -++=,解得:,则,()0'()11f x f a '==+切线方程为:()1y a x =+, 与联立得321(1)x x ax a x -++=+,化简得3210x x x --+=,由于切点的横坐标1必然是该方程的一个根,()1x ∴-是321x x x --+的一个因式,∴该方程可以分解因式为()()2110,x x --=解得121,1x x ==-,()11f a -=--,综上,曲线过坐标原点的切线与曲线的公共点的坐标为和()11a ---,. 【总结提升】1.利用导数研究函数的单调性的关键在于准确判定导数的符号,易错点是忽视函数的定义域.2.当f (x )含参数时,需依据参数取值对不等式解集的影响进行分类讨论.讨论的标准有以下几种可能:(1)f ′(x )=0是否有根;(2)若f ′(x )=0有根,求出的根是否在定义域内; (3)若在定义域内有两个根,比较两个根的大小. 题型二:求函数的单调区间例4.(2012·辽宁·高考真题(文))函数y=12x 2-㏑x 的单调递减区间为( ) A .(-1,1] B .(0,1] C .[1,+∞) D .(0,+∞)【答案】B 【解析】 【详解】对函数21ln 2y x x =-求导,得211x y x x x='-=-(x>0),令210{0x x x -≤>解得(0,1]x ∈,因此函数21ln 2y x x =-的单调减区间为(0,1],故选B例5.(2016·北京·高考真题(理))设函数()a x f x xe bx -=+,曲线()y f x =在点(2,(2))f 处的切线方程为(1)4y e x =-+, (1)求a ,b 的值;(2)求()f x 的单调区间.【答案】(Ⅰ)2a =,b e =;(2)()f x 的单调递增区间为(,)-∞+∞. 【解析】 【详解】试题分析:(Ⅰ)根据题意求出,根据(2)22,(2)1f e f e =+=-'求a,b 的值即可;(Ⅱ)由题意判断的符号,即判断1()1x g x x e -=-+的单调性,知g(x)>0,即>0,由此求得f(x)的单调区间.试题解析:(Ⅰ)因为()a x f x xe bx -=+,所以()(1)a x f x x e b -=-+'. 依题设,(2)22,{(2)1,f e f e =+=-'即222222,{1,a a eb e e b e --+=+-+=- 解得2,e a b ==.(Ⅱ)由(Ⅰ)知2()x f x xe ex -=+. 由21()(1)x x f x e x e --=-+'及20x e ->知,与11x x e --+同号.令1()1x g x x e -=-+,则1()1x g x e -=-+'. 所以,当时,,在区间上单调递减; 当时,,在区间上单调递增. 故是在区间上的最小值,从而.综上可知,,.故的单调递增区间为.【总结提升】1.利用导数求函数单调区间的方法(1)当导函数不等式可解时,解不等式f ′(x )>0或f ′(x )<0求出单调区间.(2)当方程f ′(x )=0可解时,解出方程的实根,按实根把函数的定义域划分区间,确定各区间f ′(x )的符号,从而确定单调区间.(3)若导函数的方程、不等式都不可解,根据f ′(x )结构特征,利用图象与性质确定f ′(x )的符号,从而确定单调区间.温馨提醒:所求函数的单调区间不止一个,这些区间之间不能用并集“∪”及“或”连接,只能用“,”“和”字隔开.2.解决含参数的函数的单调性问题应注意两点(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论.(2)划分函数的单调区间时,要在函数定义域内讨论,还要确定导数为0的点和函数的间断点. 题型三: 利用函数的单调性解不等式例6.(2015·全国·高考真题(理))设函数'()f x 是奇函数()f x (x ∈R )的导函数,(1)0f -=,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围是( ) A .(,1)(0,1)-∞- B .(1,0)(1,)C .(,1)(1,0)-∞--D .(0,1)(1,)⋃+∞【答案】A 【解析】 【详解】构造新函数()()f xg x x=,()()()2'xf x f x g x x -=',当0x >时()'0g x <. 所以在()0,∞+上()()f xg x x=单减,又()10f =,即()10g =.所以()()0f x g x x=>可得01x <<,此时()0f x >,又()f x 为奇函数,所以()0f x >在()(),00,-∞⋃+∞上的解集为:()(),10,1-∞-⋃. 故选A.点睛:本题主要考查利用导数研究函数的单调性,需要构造函数,例如()()xf x f x '-,想到构造()()f xg x x=.一般:(1)条件含有()()f x f x '+,就构造()()x g x e f x =,(2)若()()f x f x -',就构造()()xf xg x e =,(3)()()2f x f x +',就构造()()2x g x e f x =,(4)()()2f x f x -'就构造()()2xf xg x e =,等便于给出导数时联想构造函数.例7.(2017·江苏·高考真题)已知函数()3x x 1f x =x 2x+e -e-,其中e 是自然数对数的底数,若()()2f a-1+f 2a 0≤,则实数a 的取值范围是_________.【答案】1[1,]2-【解析】 【详解】因为31()2e ()ex x f x x x f x -=-++-=-,所以函数()f x 是奇函数,因为22()32e e 320x x f 'x x x -=-++≥-+,所以数()f x 在R 上单调递增,又2(1)(2)0f a f a -+≤,即2(2)(1)f a f a ≤-,所以221a a ≤-,即2210a a +-≤, 解得112a -≤≤,故实数a 的取值范围为1[1,]2-. 【总结提升】比较大小或解不等式的思路方法(1)根据导数计算公式和已知的不等式构造函数,利用不等关系得出函数的单调性,即可确定函数值的大小关系,关键是观察已知条件构造出恰当的函数.(2)含有两个变元的不等式,可以把两个变元看作两个不同的自变量,构造函数后利用单调性确定其不等关系.题型四:利用函数的单调性比较大小 例8.(2022·全国·高考真题(理))已知3111,cos ,4sin 3244a b c ===,则( ) A .c b a >> B .b a c >>C .a b c >>D .a c b >>【答案】A 【解析】 【分析】 由14tan 4c b =结合三角函数的性质可得c b >;构造函数21()cos 1,(0,)2f x x x x =+-∈+∞,利用导数可得b a >,即可得解. 【详解】因为14tan 4c b =,因为当π0,,sin tan 2x x x x ⎛⎫∈<< ⎪⎝⎭ 所以11tan 44>,即1cb >,所以c b >;设21()cos 1,(0,)2f x x x x =+-∈+∞,()sin 0f x x x '=-+>,所以()f x 在(0,)+∞单调递增,则1(0)=04f f ⎛⎫> ⎪⎝⎭,所以131cos 0432->,所以b a >,所以c b a >>, 故选:A例9.(2007·陕西·高考真题(理))已知f (x )是定义在(0,+∞) 上的非负可导函数,且满足xf ′(x )+f (x )≤0,对任意的0<a <b ,则必有( ). A .af (b )≤bf (a ) B .bf (a )≤af (b ) C .af (a )≤f (b ) D .bf (b )≤f (a )【答案】A【解析】 【详解】因为xf ′(x )≤-f (x ),f (x )≥0,所以()f x x ⎡⎤⎢⎥⎣⎦′=2'()()xf x f x x -≤22()f x x -≤0, 则函数()f x x在(0,+∞)上单调递减.由于0<a <b ,则()()f a f b a b≥,即af (b )≤bf (a ) 例10.(2013·天津·高考真题(文))设函数()2x f x e x =+-,2()ln 3g x x x =+-若实数,a b 满足()0f a =,()0g b =则( )A .()0()g a f b <<B .()0()f b g a <<C .0()()g a f b <<D .()()0f b g a <<【答案】A 【解析】 【详解】试题分析:对函数()2x f x e x =+-求导得()=1x f x e '+,函数单调递增,()()010,110f f e =-=+,由()0f a =知01a <<,同理对函数2()ln 3g x x x =+-求导,知在定义域内单调递增,(1)-20g =<,由()0g b =知1b >,所以()0()g a f b <<.例11.(2022·全国·高考真题)设0.110.1e ,ln 0.99a b c ===-,,则( )A .a b c <<B .c b a <<C .c a b <<D .a c b <<【答案】C 【解析】 【分析】构造函数()ln(1)f x x x =+-, 导数判断其单调性,由此确定,,a b c 的大小. 【详解】设()ln(1)(1)f x x x x =+->-,因为1()111x f x x x'=-=-++, 当(1,0)x ∈-时,()0f x '>,当,()0x ∈+∞时()0f x '<,所以函数()ln(1)f x x x =+-在(0,)+∞单调递减,在(1,0)-上单调递增, 所以1()(0)09f f <=,所以101ln 099-<,故110ln ln 0.999>=-,即b c >,所以1()(0)010f f -<=,所以91ln +01010<,故1109e 10-<,所以11011e 109<,故a b <,设()e ln(1)(01)xg x x x x =+-<<,则()()21e 11()+1e 11xx x g x x x x -+'=+=--, 令2()e (1)+1x h x x =-,2()e (21)x h x x x '=+-,当01x <<时,()0h x '<,函数2()e (1)+1x h x x =-单调递减,11x <<时,()0h x '>,函数2()e (1)+1x h x x =-单调递增, 又(0)0h =,所以当01x <<时,()0h x <,所以当01x <<时,()0g x '>,函数()e ln(1)x g x x x =+-单调递增, 所以(0.1)(0)0g g >=,即0.10.1e ln 0.9>-,所以a c > 故选:C. 【总结提升】1.在比较()1f x ,()2f x ,,()n f x 的大小时,首先应该根据函数()f x 的奇偶性与周期性将()1f x ,()2f x ,,()n f x 通过等值变形将自变量置于同一个单调区间,然后根据单调性比较大小.2.构造函数解不等式或比较大小一般地,在不等式中若同时含有f (x )与f ′(x ),常需要通过构造含f (x )与另一函数的和、差、积、商的新函数,再借助导数探索新函数的性质,进而求出结果.常见构造的辅助函数形式有:(1)f (x )>g (x )→F (x )=f (x )-g (x ); (2)xf ′(x )+f (x )→[xf (x )]′; (3)xf ′(x )-f (x )→()[]'f x x; (4)f ′(x )+f (x )→[e x f (x )]′; (5)f ′(x )-f (x )→()[]'x f x e. 题型五:根据函数的单调性求参数范围例12.(2014·全国·高考真题(文))若函数()ln f x kx x =-在区间()1,+∞上单调递增,则实数k 的取值范围是A .(],2-∞-B .(],1-∞-C .[)2,+∞D .[)1,+∞【答案】D 【解析】 【详解】 试题分析:,∵函数()ln f x kx x =-在区间()1,+∞单调递增,∴在区间()1,+∞上恒成立.∴,而在区间()1,+∞上单调递减,∴.∴的取值范围是[)1,+∞.故选D .例13.(2019·北京·高考真题(理))设函数f (x )=e x +a e −x (a 为常数).若f (x )为奇函数,则a =________;若f (x )是R 上的增函数,则a 的取值范围是___________. 【答案】 -1; (],0-∞. 【解析】 【分析】首先由奇函数的定义得到关于a 的恒等式,据此可得a 的值,然后利用导函数的解析式可得a 的取值范围. 【详解】若函数()x xf x e ae -=+为奇函数,则()()(),x x x x f x f x e ae e ae ---=-+=-+,()()1 0x x a e e -++=对任意的x 恒成立.若函数()x x f x e ae -=+是R 上的增函数,则()' 0x xf x e ae -=-≥恒成立,2,0x a e a ≤≤.即实数a 的取值范围是(],0-∞例14.(2014·全国·高考真题(理))若函数()cos 2sin f x x a x =+在区间(,)62ππ内是减函数,则实数a 的取值范围是_______. 【答案】2a ≤ 【解析】()()2sin 2cos 4sin cos cos cos 4sin .,62f x x a x x x a x x x a x ππ⎛⎫=-+=-+=-+∈ ⎪⎝'⎭时,()f x 是减函数,又cos 0x >,∴由()0f x '≤得4sin 0,4sin x a a x -+≤∴≤在,62ππ⎛⎫⎪⎝⎭上恒成立,()min 4sin ,,262a x x a ππ⎛⎫⎛⎫∴≤∈∴≤ ⎪ ⎪⎝⎭⎝⎭.【总结提升】由函数的单调性求参数的取值范围的方法(1)可导函数在区间(a ,b )上单调,实际上就是在该区间上f ′(x )≥0(或f ′(x )≤0)恒成立,得到关于参数的不等式,从而转化为求函数的最值问题,求出参数的取值范围.(2)可导函数在区间(a ,b )上存在单调区间,实际上就是f ′(x )>0(或f ′(x )<0)在该区间上存在解集,从而转化为不等式问题,求出参数的取值范围.(3)若已知f (x )在区间I 上的单调性,区间I 上含有参数时,可先求出f (x )的单调区间,令I 是其单调区间的子集,从而求出参数的取值范围. 题型六:利用导数研究函数的图象例15.(2021·浙江·高考真题)已知函数21(),()sin 4f x xg x x =+=,则图象为如图的函数可能是( )A .1()()4y f x g x =+-B .1()()4y f x g x =--C .()()y f x g x =D .()()g x y f x =【答案】D 【解析】 【分析】由函数的奇偶性可排除A 、B ,结合导数判断函数的单调性可判断C ,即可得解.【详解】对于A ,()()21sin 4y f x g x x x =+-=+,该函数为非奇非偶函数,与函数图象不符,排除A ; 对于B ,()()21sin 4y f x g x x x =--=-,该函数为非奇非偶函数,与函数图象不符,排除B ;对于C ,()()21sin 4y f x g x x x ⎛⎫==+ ⎪⎝⎭,则212sin cos 4y x x x x ⎛⎫'=++ ⎪⎝⎭,当4x π=时,2102164y ππ⎛⎫'=+> ⎪⎝⎭,与图象不符,排除C. 故选:D.例16.(2018·全国·高考真题(文))函数()2e e x xf x x --=的图像大致为 ( )A .B .C .D .【答案】B 【解析】 【详解】分析:通过研究函数奇偶性以及单调性,确定函数图像.详解:20,()()()x xe e xf x f x f x x --≠-==-∴为奇函数,舍去A,1(1)0f e e -=->∴舍去D;243()()2(2)(2)()2,()0x x x x x xe e x e e x x e x ef x x f x x x ---+---++=='∴>'>, 所以舍去C ;因此选B.例17.(2017·浙江·高考真题)函数y ()y ()f x f x ==,的导函数的图象如图所示,则函数y ()f x =的图象可能是A .B .C .D .【答案】D 【解析】 【详解】原函数先减再增,再减再增,且0x =位于增区间内,因此选D .【名师点睛】本题主要考查导数图象与原函数图象的关系:若导函数图象与x 轴的交点为0x ,且图象在0x 两侧附近连续分布于x 轴上下方,则0x 为原函数单调性的拐点,运用导数知识来讨论函数单调性时,由导函数'()f x 的正负,得出原函数()f x 的单调区间.【规律方法】函数图象的辨识主要从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象. 题型七:与函数单调性相关的恒成立问题例18.(2022·广东·执信中学高三阶段练习)已知函数 ()e xf x x =-,则 ()f x 的单调递增区间为________; 若对任意的()0,x ∞∈+, 不等式 ln 2e 1xx ax+-≥恒成立, 则实数 a 的取值范围为________.【答案】 (0,)+∞(填[)0,∞+亦可) 1(,]2-∞【解析】 【分析】求出函数导数,利用导数求函数单调区间,不等式恒成立可分离参数后求函数()e ln x g x x x x =⋅--的最小值,令ln t x x =+换元后可根据单调性求最值. 【详解】 ()1x f x e =-',令()0f x '>,可得()f x 的单调递增区间(0,)+∞ (或[)0+∞,亦可); ln 2e 1x x ax+-≥可化为2e ln x a x x x ≤⋅--. 令()e ln x g x x x x =⋅--=ln e e ln x x x x ⋅--=ln e (ln )x x x x +-+, 设ln t x x =+,则()e =-t h t t ,由()e xf x x =-在[)0+∞,上单调递增可知, 0()(0)e 01h t h ≥=-=,则21a ≤, 故解得12a ≤.故答案为:(0,)+∞(填[)0,∞+亦可);12a ≤例19.(2022·全国·高三专题练习)已知函数()()e ln xf x m x m =+∈R ,若对任意正数12,x x ,当12x x >时,都有()()1212f x f x x x ->-成立,则实数m 的取值范围是______. 【答案】[)0,∞+ 【解析】 【分析】令()()g x f x x =-,进而原题等价于()g x 在()0,∞+单调递增,从而转化为()e 10x mg x x'=+-≥,在()0,∞+上恒成立,参变分离即可求出结果.【详解】由()()1212f x f x x x ->-得,()()1122f x x f x x ->- 令()()g x f x x =-,∴()()12g x g x > ∴()g x 在()0,∞+单调递增,又∵()()e ln xg x f x x m x x =-=+-∴()e 10xmg x x'=+-≥,在()0,∞+上恒成立,即()1e x m x ≥- 令()()1e x h x x =-,则()()e 110xh x x '=-++<∴()h x 在()0,∞+单调递减,又因为()()01e 00h =-⨯=,∴0m ≥.故答案为:[)0,∞+.例20.(2010·全国·高考真题(理))设函数()21x f x e x ax =---.(1)若0a =,求()f x 的单调区间;(2)若当0x ≥时()0f x ≥恒成立,求a 的取值范围.【答案】(1) f (x )在(-∞,0)单调减少,在(0,+∞)单调增加;(2) a 的取值范围为(-∞,12]. 【解析】 【分析】 (1)a =0时,()1x f x e x=--,()1x f x e '=-.分别令f ′(x )<0,f ′(x )>0可求()f x 的单调区间;(2求导得到)f ′(x )=e x -1-2ax .由(1)知e x ≥1+x ,当且仅当x =0时等号成立.故问题转化为f ′(x )≥x -2ax =(1-2a )x ,从而对1-2a 的符号进行讨论即可得出结果. 【详解】 (1)a =0时,()1x f x e x=--,()1x f x e '=-.当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0.故f (x )在(-∞,0)单调减少,在(0,+∞)单调增加 (2)()12x f x e ax'-=-.由(1)知1x e x ≥+,当且仅当x =0时等号成立.故f ′(x )≥x -2ax =(1-2a )x ,从而当1-2a ≥0,即a ≤时,f ′(x )≥0(x ≥0),而f (0)=0,于是当x ≥0时,f (x )≥0.由1x e x ≥+ (x ≠0)得1x e x -≥- (x ≠0),从而当a >时,f ′(x )< 1x e -+2a (1x e --)=x e - (1x e -)(x e -2a ),故当x ∈(0,ln2a )时, f ′(x )<0,而f (0)=0,于是当x ∈(0,ln2a )时,f (x )<0, 综上可得a 的取值范围为(-∞,]. 【规律方法】处理此类问题,往往利用“构造函数法”、“分离参数法”.。
高考数学总复习 第四章4.2 同角三角函数的基本关系及三角函数的诱导公式教案 理 北师大版

2013年高考第一轮复习数学北师(江西版)理第四章4.2 同角三角函数的基本关系及三角函数的诱导公式考纲要求1.理解同角三角函数的基本关系式:sin 2α+cos 2α=1,sin αcos α=πtan π2k αα⎛⎫≠ ⎪⎝⎭+(k ∈Z )).2.能利用单位圆中的三角函数线推导出π2α±,π±α的正弦、余弦、正切的诱导公式,并能灵活运用.知识梳理1.同角三角函数的基本关系式 (1)平方关系:__________; (2)商数关系:__________; (3)倒数关系:__________. 2.诱导公式总口诀为:奇变偶不变,符号看象限,其中“奇”“偶”是指“k ·π2±α(k ∈Z )”中k 的奇偶性;“符号”是指把任意角α看作锐角时,原函数值的符号.即α+k ·2π(k ∈Z ),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成__________时原函数值的符号;π2±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.1.已知cos(α-π)=-513,且α是第四象限角,则sin α=( ).A .-1213B .1213C .±1213D .5122.已知sin x =2cos x ,则sin 2x +1=( ).A .65B .95C .43D .533.已知α是第四象限角,tan α=-512,则sin α等于( ).A .15B .-15C .513D .-5134.已知sin α+3cos α3cos α-sin α=5,则sin 2α-sin αcos α的值是________.思维拓展1.有人说sin(k π-α)=sin(π-α)=sin α(k ∈Z ),你认为正确吗?提示:不正确.当k =2n (n ∈Z )时,sin(k π-α)=sin(2n π-α)=sin(-α)=-sin α;当k =2n +1(n ∈Z )时,sin(k π-α)=sin[(2n +1)·π-α]=sin(2n π+π-α)=sin(π-α)=sin α.2.“符号看象限”中,符号是否与α的大小有关?提示:无关,只是把α从形式上看作锐角,从而2k π+α(k ∈Z ),π+α,-α,π-α,π2-α,π2+α分别是第一,三,四,二,一,二象限的角.一、同角三角函数关系式的应用【例1-1】已知tan α=14,则cos 2α+sin 2α的值为__________.【例1-2】已知α是三角形的内角,且sin α+cos α=15.(1)求tan α的值;(2)把1cos 2α-sin 2α用tan α表示出来,并求其值. 方法提炼1.利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用sin αcos α=tan α⎝ ⎛⎭⎪⎫α≠k π+π2,k ∈Z 可以实现角α的弦切互化.2.注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.请做[针对训练]1二、诱导公式的应用 【例2-1】化简:sin(540°-x )tan(900°-x )·1tan(450°-x )tan(810°-x )·cos(360°-x )sin(-x )=__________.【例2-2】化简:cos(π+θ)cos θ[cos(π-θ)-1]+cos(θ-2π)sin ⎝ ⎛⎭⎪⎫θ-3π2cos(θ-π)-sin ⎝⎛⎭⎪⎫3π2+θ.【例2-3】已知cos(π+α)=-12,且α是第四象限角,计算:sin[α+(2n +1)π]+sin[α-(2n +1)π]sin(α+2n π)·cos (α-2n π)(n ∈Z ).方法提炼利用诱导公式化简求值时的原则为:1.“负化正”,运用公式三将任意负角的三角函数化为任意正角的三角函数.2.“大化小”,利用公式一将大于360°的角的三角函数化为0°到360°的三角函数,利用公式二将大于180°的角的三角函数化为0°到180°的三角函数.3.“小化锐”,利用公式六将大于90°的角化为0°到90°的角的三角函数.4.“锐求值”,得到0°到90°的三角函数后,若是特殊角直接求得,若是非特殊角可由计算器求得.请做[针对训练]2三、sin x ±cos x 与方程思想【例3】已知sin θ-cos θ=12,求:(1)sin θcos θ;(2)sin 3θ-cos 3θ;(3)sin 4θ+cos 4θ.方法提炼1.已知a sin x +b cos x =c 可与sin 2x +cos 2x =1联立,求得sin x ,cos x ,一般此法不常用,原因是计算麻烦.2.sin x +cos x ,sin x -cos x ,sin x cos x 之间的关系为:(sin x +cos x )2=1+2sin x cos x ,(sin x -cos x )2=1-2sin x cos x ,(sin x +cos x )2+(sin x -cos x )2=2.因此已知上述三个代数式中的任意一个代数式的值可求其余两个代数式的值.请做[针对训练]3考情分析从近几年的高考试题来看,同角三角函数的基本关系和诱导公式中是高考的热点,题型既有选择题、填空题,又有解答题.主要考查诱导公式在三角函数式求值,化简的过程中与同角三角函数的关系式,和差角公式及倍角公式的综合应用,在考查基本运算的同时,注重考查等价转化的思想方法.预测2013年高考仍将以诱导公式为主要考点,重点考查考生的运算能力与恒等变形能力.针对训练 1.(2011重庆高考,文12)若cos α=-35,且α∈⎝⎛⎭⎪⎫π,3π2,则tan α=__________.2.已知A =sin(k π+α)sin α+cos(k π+α)cos α(k ∈Z ),则A 的值构成的集合是__________.3.已知关于x 的方程2x 2-(3+1)x +m =0的两根为sin θ和cos θ,θ∈(0,2π),求m 的值.参考答案基础梳理自测 知识梳理1.(1)sin 2α+cos 2α=1(2)tan α=sin αcos α⎝ ⎛⎭⎪⎫α≠k π+π2,k ∈Z(3)tan α·cot α=12.sin α -sin α -sin α sin α cos αcos α cos α -cos α cos α -cos α sin α -sin α tan α tan α -tan α -tan α 锐角3.0 π6 π4 π3 π2 2π3 56ππ 3π2 0 12 22 32 1 32 120 -1 132 22 12 0 -12-32 -1 0 0 331 3 不存在 - 3 -33不存在基础自测1.A 解析:cos(α-π)=-cos α=-513,cos α=513.sin α=±1-cos 2α=±1213,∵α是第四象限角,∴sin α=-1213.2.B 解析:∵sin 2x +cos 2x =1,∴sin 2x +⎝ ⎛⎭⎪⎫12sin x 2=1,∴sin 2x =45,∴sin 2x +1=95.3.D 解析:由tan α=sin αcos α=-512,sin 2α+cos 2α=1及α是第四象限角,解得sin α=-513.4.25 解析:由sin α+3cos α3cos α-sin α=5得,tan α+33-tan α=5,即tan α=2.所以sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α=tan 2α-tan αtan 2α+1=25. 考点探究突破【例1-1】1617 解析:cos 2α+sin 2α=1-2sin 2α+sin 2α=cos 2α=cos 2αcos 2α+sin 2α=11+tan 2α=1617. 【例1-2】解:(1)联立方程 ⎩⎪⎨⎪⎧ sin α+cos α=15,sin 2α+cos 2α=1.①②由①得cos α=15-sin α,将其代入②.整理得25sin 2α-5sin α-12=0. ∵α是三角形的内角,∴⎩⎪⎨⎪⎧sin α=45,cos α=-35.∴tan α=-43.(2)1cos 2α-sin 2α=sin 2α+cos 2αcos 2α-sin 2α=sin 2α+cos 2αcos 2αcos 2α-sin 2αcos 2α=tan 2α+11-tan 2α.∵tan α=-43, ∴1cos 2α-sin 2α=tan 2α+11-tan 2α=⎝ ⎛⎭⎪⎫-432+11-⎝ ⎛⎭⎪⎫-432=-257. 【例2-1】sin x 解析:原式=sin(180°-x )tan(180°-x )·1tan(90°-x )tan(90°-x )·cos x-sin x=sin x-tan x ·ta n x ·tan x ⎝ ⎛⎭⎪⎫-1tan x =sin x . 【例2-2】解:原式=-cos θcos θ(-cos θ-1)+cos θcos θ(-cos θ)+cos θ=11+cos θ+11-cos θ=2sin 2θ. 【例2-3】解:∵cos(π+α)=-12.∴-cos α=-12,cos α=12.则sin[α+(2n +1)π]+sin[α-(2n +1)π]sin(a +2n π)·cos (α-2n π)=sin(2n π+π+α)+sin(-2n π-π+α)sin(2n π+α)·cos (-2n π+α)=sin(π+α)+sin(-π+α)sin α·cos α=-sin α-sin(π-α)sin α·cos α=-2sin αsin αcos α=-2cos α=-4.【例3】解:(1)∵sin θ-cos θ=12,∴(sin θ-cos θ)2=14,即sin 2θ-2sin θcos θ+cos 2θ=14.由平方关系sin 2θ+cos 2θ=1,可得sin θcos θ=38.(2)sin 3θ-cos 3θ=(sin θ-cos θ)(sin 2θ+cos θsin θ+cos 2θ).由平方关系及sin θ-cos θ=12,可得sin 3θ-cos 3θ=12×⎝⎛⎭⎪⎫1+38=1116.(3)由(sin 2θ+cos 2θ)2=sin 4θ+2sin 2θ·cos 2θ+cos 4θ=1,可得sin 4θ+cos 4θ=1-2sin 2θ·cos 2θ=1-2×964=2332.演练巩固提升 针对训练1.43 解析:由1+tan 2α=1cos 2α,则tan 2α=169.又因α∈⎝ ⎛⎭⎪⎫π,3π2,故tan α>0,则tan α=43.2.{-2,2} 解析:当k 为偶数时,A =sin αsin α+cos αcos α=2;k 为奇数时,A =-sin αsin α-cos αcos α=-2.3.解:由韦达定理可知⎩⎪⎨⎪⎧sin θ+cos θ=3+12,sin θcos θ=m 2.①②由①式平方得1+2sin θcos θ=2+32,∴sin θcos θ=34,由②得m 2=34.∴m =32.。
符号计算的常用调用函数

符号计算的常用调用函数vpa %变量精度算法vpa Variable precision arithmetic.R = vpa(S) numerically evaluates each element of the double matrix S using variable precision floating point arithmetic with D decimaldigit accuracy, where D is the current setting of DIGITS.The resulting R is a SYM.vpa(S,D) uses D digits, instead of the current setting of DIGITS.D is an integer or the SYM representation of a number.It is important to avoid the evaluation of an expression using double precision floating point arithmetic before it is passed to VPA.For example,phi = vpa((1+sqrt(5))/2)phi =1.6180339887498949025257388711907first computes a 16-digit approximation to the golden ratio, thenconverts that approximation to one with d digits, where d is the current setting of DIGITS. To get full precision, use unevaluated string orsymbolic arguments,phi = vpa('(1+sqrt(5))/2')phi =1.6180339887498948482045868343656ors = sym('sqrt(5)')phi = vpa((1+s)/2)s =5^(1/2)phi =1.6180339887498948482045868343656Additional examples:vpa(pi,780) shows six consecutive 9's near digit 770 in thedecimal expansion of pi.vpa(hilb(2),5) returns[ 1., .50000][.50000, .33333]symvar %在符号表达式中或矩阵中寻找符号变量Find symbolic variables in symbolic expression or matrixSyntaxsymvar(s)symvar(s,n)Descriptionsymvar(s) returns a vector containing all the symbolic variables in s. The variables are returned in the alphabetical order with uppercase letters preceding lowercase letters. If there are no symbolic variables in s, then symvar returns the empty vector. symvar does not consider the constants pi, i, and j to be variables.symvar(s,n) returns a vector containing the n symbolic variables in s that are alphabetically closest to 'x':The variables are sorted by the first letter in their names. The ordering is x y w z v u ... a X Y W Z V U ... A. The name of a symbolic variable cannot begin with a number.For all subsequent letters, the ordering is alphabetical, with all uppercase letters having precedence over lowercase: 0 1 ... 9 A B ... Z a b ...z.Examplessyms wa wb wx yx ya ybf = wa + wb + wx + ya + yb + yxf =wa + wb + wx + ya + yb + yxsymvar(f)ans =[ wa, wb, wx, ya, yb, yx]The result is:ans =[ wa, wb, wx, ya, yb, yx]syms x y z a bw = x^2/(sin(3*y - b))w =x^2/sin(3*y - b)symvar(w)ans =[ b, x, y]The result is:ans =[ b, x, y]symvar(w, 3)ans =[ x, y, b]The result is:ans =[ x, y, b]symvar(s,1) returns the variable closest to x. When performing differentiation, integration, substitution or solving equations, MATLAB uses this variable as a default variable.syms v zg = v + zg =v + zsymvar(g, 1)ans =zThe result is:ans =zsyms aaa aabg = aaa + aab;symvar(g, 1)ans =zThe result is:ans =aaasyms X1 x2 xa xbg = X1 + x2 + xa + xbg =X1 + x2 + xa + xbsymvar(g, 1)ans =x2The result is:ans =x2digits %设置变量精度位数digits Set variable precision digits.Digits determines the accuracy of variable precision numeric computations.digits, by itself, displays the current setting of Digits.digits(D) sets Digits to D for subsequent calculations. D is aninteger, or a string or sym representing an integer.D = digits returns the current setting of Digits. D is an integer.double %转换为双精度Convert to double precisionSyntaxdouble(x)Descriptiondouble(x) returns the double-precision value for X. If X is already a double-precision array, double has no effect.Remarksdouble is called for the expressions in for, if, and while loops if the expression isn't already double-precision. double should be overloaded for any object when it makes sense to convert it to a double-precision value.who, whos %列出工作区中的变量List variables in workspaceGraphical InterfaceAs an alternative to whos, use the Workspace browser. Or use the What Is the Current Folder Browser? to view the contents of MAT-files without loading them.Syntaxwhowhoswho(variable_list)whos(variable_list)who(variable_list, qualifiers)whos(variable_list, qualifiers)s = who(variable_list, qualifiers)s = whos(variable_list, qualifiers)who variable_list qualifierswhos variable_list qualifiersEach of these syntaxes applies to both who and whos:Descriptionwho lists in alphabetical order all variables in the currently active workspace.whos lists in alphabetical order all variables in the currently active workspace along with their sizes and types. It also reports the totals for sizes.who(variable_list) and whos(variable_list) list only those variables specified in variable_list, where variable_list is a comma-delimited list of quoted strings: 'var1','var2', ..., 'varN'. You can use the wildcard character * to display variables that match a pattern. For example, who('A*') finds all variables in the current workspace that start with A.who(variable_list, qualifiers) and whos(variable_list, qualifiers) list those variables in variable_list that meet all qualifications specified in qualifiers. You can specify any or all of the following qualifiers, and in any order.s = who(variable_list, qualifiers) returns cell array s containing the names of the variables specified in variable_list that meet the conditions specified in qualifiers.s = whos(variable_list, qualifiers) returns structure s containing the following fields for the variables specified in variable_list that meet the conditions specified in qualifiers:who variable_list qualifiers and whos variable_list qualifiers are the unquoted forms of the syntax. Both variable_list and qualifiers are space-delimited lists of unquoted strings. RemarksNested Functions. When you use who or whos inside of a nested function, MATLAB returns or displays all variables in the workspace of that function, and in the workspaces of all functions in which that function is nested. This applies whether you include calls to who or whos in your M-file code or if you call who or whos from the MATLAB debugger.If your code assigns the output of whos to a variable, MATLAB returns the information in a structure array containing the fields described above. If you do not assign the output to a variable, MATLAB displays the information at the Command Window, grouped according to workspace.If your code assigns the output of who to a variable, MATLAB returns the variable names in a cell array of strings. If you do not assign the output, MATLAB displays the variable names at the Command Window, but not grouped according to workspace. Compressed Data. Information returned by the command whos -file is independent of whether the data in that file is compressed or not. The byte counts returned by this command represent the number of bytes data occupies in the MATLAB workspace, and not in the file the data was saved to. See the function reference for save for more information on data compression.MATLAB Objects. whos -file filename does not return the sizes of any MATLAB objects that are stored in file filename.ExamplesExample 1Show variable names starting with the letter a:who a*Your variables are:a aaa aab ansShow variables stored in MAT-file mydata.mat:who -file mydataExample 2Return information on variables stored in file mydata.mat in structure array s:s = whos('-file', 'mydata1')s =6x1 struct array with fields:namesizebytesclassglobalsparsecomplexnestingpersistentDisplay the name, size, and class of each of the variables returned by whos:for k=1:length(s)disp([' ' s(k).name ' ' mat2str(s(k).size) ' ' s(k).class])endA [1 1] doublespArray [5 5] doublestrArray [2 5] cellx [3 2 2] doubley [4 5] cellExample 3Show variables that start with java and end with Array. Also show their dimensions and class name:whos -file mydata2 -regexp \<java.*Array\>Name Size Bytes ClassjavaChrArray 3x1 ng.String[][][]javaDblArray 4x1 ng.Double[][]javaIntArray 14x1 ng.Integer[][]Example 4The function shown here uses variables with persistent, global, sparse, and complex attributes:function show_attributespersistent pglobal go = 1 g = 2s = sparse(eye(5))c = [4+5i 9-3i 7+6i]whosWhen the function is run, whos displays these attributes:show_attributesName Size Bytes Class Attributesc 1x3 48 double complexg 1x1 8 double globalp 1x1 8 double persistents 5x5 84 double sparseExample 5Function whos_demo contains two nested functions. One of these functions calls whos; the other calls who:function whos_demodate_time = datestr(now);[str pos] = textscan(date_time, '%s%s%s', ...1, 'delimiter', '- :');get_date(str);str = textscan(date_time(pos+1:end), '%s%s%s', ...1, 'delimiter', '- :');get_time(str);function get_date(d)day = d{1}; mon = d{2}; year = d{3};whosendfunction get_time(t)hour = t{1}; min = t{2}; sec = t{3};whoendendWhen nested function get_date calls whos, MATLAB displays information on the variables in all workspaces that are in scope at the time. This includes nested function get_date and also the function in which it is nested, whos_demo. The information is grouped by workspace:whos_demoName Size Bytes Class---- get_date -----------------------------------------d 1x3 378 cellday 1x1 64 cellmon 1x1 66 cellyear 1x1 68 cell---- whos_demo ----------------------------------------ans 0x0 0 (unassigned)date_time 1x20 40 charpos 1x1 8 doublestr 1x3 378 cellWhen nested function get_time calls who, MATLAB displays names of the variables in the workspaces that are in scope at the time. This includes nested function get_time and also the function in which it is nested, whos_demo. The information is not grouped by workspace in this case:Your variables are:hour min sec t ans date_timepos strisa %确定输入的量是否是给定的类型Determine whether input is object of given classSyntaxK = isa(obj, 'class_name')DescriptionK = isa(obj, 'class_name') returns logical 1 (true) if obj is of class (or a subclass of) class_name, and logical 0 (false) otherwise.The argument obj is a MATLAB object or an object of the Java programming language. The argument class_name is the name of a MATLAB (predefined or user-defined) or a Java class. Predefined MATLAB classes includelogical Logical array of true and false valueschar Characters arraynumeric Integer or floating-point arrayinteger Signed or unsigned integer arrayint8 8-bit signed integer arrayuint8 8-bit unsigned integer arrayint16 16-bit signed integer arrayuint16 16-bit unsigned integer arrayint32 32-bit signed integer arrayuint32 32-bit unsigned integer arrayint64 64-bit signed integer arrayuint64 64-bit unsigned integer arrayfloat Single- or double-precision floating-point arraysingle Single-precision floating-point arraydouble Double-precision floating-point arraycell Cell arraystruct Structure arrayfunction_handle Function handle'class_name' MATLAB class or Java classTo check for a sparse array, use issparse. To check for a complex array, use ~isreal. Examplesisa(rand(3,4),'double')ans =1The following example creates an instance of the user-defined MATLAB class named polynom. The isa function identifies the object as being of the polynom class. polynom_obj = polynom([1 0 -2 -5]);isa(polynom_obj, 'polynom')ans =1is* %检测状态Detect stateDescriptionThese functions detect the state of MATLAB entities:findsym %在符号表达式中或矩阵寻找变量Determine variables in symbolic expression or matrixSyntaxfindsym(S)findsym(S,n)Descriptionfindsym(S) for a symbolic expression or matrix S, returns all symbolic variables in S in lexicographical order, separated by commas. If S does not contain any variables, findsym returns an empty string.findsym(S,n) returns the n variables alphabetically closest to x:The variables are sorted by the first letters in their names. The ordering is x y w z v u ... a X Y W Z V U ... A. The name of a symbolic variable cannot begin with a number.For all subsequent letters the ordering is alphabetical, with all uppercase letters having precedence over lowercase: 0 1 ... 9 A B ... Z a b ...z.Examplessyms a x y z t X1 x2 xa xbfindsym(sin(pi*t))ans =tfindsym(x+i*y-j*z)ans =x,y,zfindsym(a+y,1)ans =yfindsym(X1 + x2 + xa + xb)ans =X1,x2,xa,xbfindsym(X1 + x2 + xa + xb,4)ans =x2,xa,xb,X1collect %合并同类项Collect coefficientsSyntaxR = collect(S)R = collect(S,v)DescriptionR = collect(S) returns an array of collected polynomials for each polynomial in the array S of polynomials.R = collect(S,v) collects terms containing the variable v.ExamplesThe following statementssyms x yR1 = collect((exp(x)+x)*(x+2))R1 =x^2 + (exp(x) + 2)*x + 2*exp(x)R2 = collect((x+y)*(x^2+y^2+1), y)R2 =y^3 + x*y^2 + (x^2 + 1)*y + x*(x^2 + 1)R3 = collect([(x+1)*(y+1),x+y])R3 =[ y + x*(y + 1) + 1, x + y]expand %对指定项展开Symbolic expansion of polynomials and elementary functionsSyntaxexpand(S)Descriptionexpand(S) writes each element of a symbolic expression S as a product of its factors. expand is often used with polynomials. It also expands trigonometric, exponential, and logarithmic functions.ExamplesExpand the expression:syms x;expand((x-2)*(x-4))ans =x^2 - 6*x + 8The result is:ans =x^2 - 6*x + 8Expand the trigonometric expression:syms x y;expand(cos(x+y))ans =cos(x)*cos(y) - sin(x)*sin(y)The result is:ans =cos(x)*cos(y) - sin(x)*sin(y)Expand the exponent:syms a b;expand(exp((a+b)^2))ans =exp(2*a*b)*exp(a^2)*exp(b^2)The result is:ans =exp(2*a*b)*exp(a^2)*exp(b^2)Expand the expressions that form a vector:syms t;expand([sin(2*t), cos(2*t)])ans =[ 2*cos(t)*sin(t), cos(t)^2 - sin(t)^2]The result is:ans =[ 2*cos(t)*sin(t), cos(t)^2 - sin(t)^2]numden %分子和分母Numerator and denominatorSyntax[N,D] = numden(A)Description[N,D] = numden(A) converts each element of A to a rational form where the numerator and denominator are relatively prime polynomials with integer coefficients. A is a symbolic or a numeric matrix. N is the symbolic matrix of numerators, and D is the symbolic matrix of denominators.ExamplesFind the numerator and denominator of the symbolic number:[n, d] = numden(sym(4/5))n =4d =5The result is:n =4d =5Find the numerator and denominator of the symbolic expression:syms x y;[n,d] = numden(x/y + y/x)n =x^2 + y^2d =x*yThe result is:n =x^2 + y^2d =x*yThe statementssyms a bA = [a, 1/b]A =[ a, 1/b][n,d] = numden(A)n =[ a, 1]d =[ 1, b]returnA =[a, 1/b]n =[a, 1]d =[1, b]factor %进行因式或因子分解FactorizationSyntaxfactor(X)Descriptionfactor(X) can take a positive integer, an array of symbolic expressions, or an array of symbolic integers as an argument. If N is a positive integer, factor(N) returns the prime factorization of N.If S is a matrix of polynomials or integers, factor(S) factors each element. If any element of an integer array has more than 16 digits, you must use sym to create that element, for example, sym('N').ExamplesFactorize the two-variable expression:syms x y;factor(x^3-y^3)ans =(x - y)*(x^2 + x*y + y^2)The result is:ans =(x - y)*(x^2 + x*y + y^2)Factorize the expressions that form a vector:syms a b;factor([a^2 - b^2, a^3 + b^3])ans =[ (a - b)*(a + b), (a + b)*(a^2 - a*b + b^2)]The result is:ans =[ (a - b)*(a + b), (a + b)*(a^2 - a*b + b^2)]Factorize the symbolic number:factor(sym('12345678901234567890'))ans =2*3^2*5*101*3541*3607*3803*27961The result is:ans =2*3^2*5*101*3541*3607*3803*27961horner %转换成嵌套形式Horner nested polynomial representationSyntaxhorner(P)DescriptionSuppose P is a matrix of symbolic polynomials. horner(P) transforms each element of P into its Horner, or nested, representation.ExamplesFind nested polynomial representation of the polynomial:syms xhorner(x^3-6*x^2+11*x-6)ans =x*(x*(x - 6) + 11) - 6The result isans =x*(x*(x - 6) + 11) - 6Find nested polynomial representation for the polynomials that form a vector:syms x yhorner([x^2+x;y^3-2*y])ans =x*(x + 1)y*(y^2 - 2)The result is:ans =x*(x + 1)y*(y^2 - 2)simplify %恒等式简化Symbolic simplificationSyntaxR = simplify(S)R = simplify(S, n)DescriptionR = simplify(S) simplifies each element of the symbolic matrix S using MuPAD simplification rules.R = simplify(S, n) uses the positive integer n to control how many steps of simplification the simplify function attempts. The default value (without n) is n = 100.ExamplesSimplify the trigonometric expression:syms x;simplify(sin(x)^2 + cos(x)^2)ans =1Simplify the expression:syms a b c;simplify(exp(c*log(sqrt(a+b))))ans =(a + b)^(c/2)Simplify the expressions from the list:S = [(x^2 + 5*x + 6)/(x + 2), sqrt(16)]S =[ (x^2 + 5*x + 6)/(x + 2), 4]R = simplify(S)R =[ x + 3, 4]simple %化简因式Search for simplest form of symbolic expressionSyntaxr = simple(S)[r, how] = simple(S)Descriptionr = simple(S) tries several different algebraic simplifications of the symbolic expression S, displays any that shorten the length of S's representation, and returns the shortest. S is a sym. If S is a matrix, the result represents the shortest representation of the entire matrix, which is not necessarily the shortest representation of each individual element. If no return output is given, simple(S) displays all possible representations and returns the shortest.[r, how] = simple(S) does not display intermediate simplifications, but returns the shortest found, as well as a string describing the particular simplification. r is a sym. how is a string.ExamplesSimplify the expressions:syms x;f = cos(x)^2 + sin(x)^2f =cos(x)^2 + sin(x)^2f = simple(f)f =1g = cos(3*acos(x))g =cos(3*acos(x))g = simple(g)g =4*x^3 - 3*xSimplify the expressions displaying all possible simplifications:syms x;f = cos(x) + i*sin(x)f =cos(x) + i*sin(x)simple(f)simplify:cos(x) + i*sin(x)radsimp:cos(x) + i*sin(x)simplify(100):cos(x) + i*sin(x)combine(sincos):cos(x) + i*sin(x)combine(sinhcosh):cos(x) + i*sin(x)combine(ln):cos(x) + i*sin(x)factor:cos(x) + i*sin(x)expand:cos(x) + i*sin(x)combine:cos(x) + i*sin(x)rewrite(exp):exp(i*x)rewrite(sincos):cos(x) + i*sin(x)rewrite(sinhcosh):cosh(-i*x) - sinh(-i*x)rewrite(tan):(2*i*tan(x/2))/(tan(x/2)^2 + 1) - (tan(x/2)^2 - 1)/(tan(x/2)^2 + 1) mwcos2sin:- 2*sin(x/2)^2 + i*sin(x) + 1collect(x):cos(x) + i*sin(x)ans =exp(i*x)The result is:simplify:cos(x) + i*sin(x)radsimp:cos(x) + i*sin(x)simplify(100):cos(x) + i*sin(x)combine(sincos):cos(x) + i*sin(x)combine(sinhcosh):cos(x) + i*sin(x)combine(ln):cos(x) + i*sin(x)factor:cos(x) + i*sin(x)expand:cos(x) + i*sin(x)combine:cos(x) + i*sin(x)rewrite(exp):exp(i*x)rewrite(sincos):cos(x) + i*sin(x)rewrite(sinhcosh):cosh(-i*x) - sinh(-i*x)rewrite(tan):(2*i*tan(x/2))/(tan(x/2)^2 + 1) - (tan(x/2)^2 - 1)/(tan(x/2)^2 + 1)mwcos2sin:- 2*sin(x/2)^2 + i*sin(x) + 1collect(x):cos(x) + i*sin(x)ans =exp(i*x)Simplify the expression and display the simplification method:syms x;f = (x + 1)*x*(x - 1);[f, how] = simple(f)f =x^3 - xhow =simplify(100)pretty %习惯方式显示Pretty-print symbolic expressionsSyntaxDescriptionThe pretty function prints symbolic output in a format that resembles typeset mathematics. ExamplesThe following statementsA = sym(pascal(2))A =[ 1, 1][ 1, 2]B = eig(A)B =3/2 - 5^(1/2)/25^(1/2)/2 + 3/2pretty(B)+- -+| 1/2 || 3 5 || - - ---- || 2 2 || || 1/2 || 5 3 || ---- + - || 2 2 |+- -+subs %符号表达式或矩阵的符号替换Symbolic substitution in symbolic expression or matrixSyntaxR = subs(S)R = subs(S, new)R = subs(S, old, new)DescriptionR = subs(S) replaces all occurrences of variables in the symbolic expression S with values obtained from the calling function, or the MATLAB workspace.R = subs(S, new) replaces the default symbolic variable in S with new.R = subs(S, old, new) replaces old with new in the symbolic expression S. old is a symbolic variable or a string representing a variable name. new is a symbolic or numeric variable or expression. That is, R = subs(S,old,new) evaluates S at old = new. The substitution is first attempted as a MATLAB expression resulting in the computation being done in double precision arithmetic if all the values in new are double precision. Convert the new values to sym to ensure symbolic or variable precision arithmetic.If old and new are vectors or cell arrays of the same size and type, each element of old is replaced by the corresponding element of new. If S and old are scalars and new is an array or cell array, the scalars are expanded to produce an array result. If new is a cell array of numeric matrices, the substitutions are performed elementwise (i.e.,subs(x*y,{x,y},{A,B}) returns A.*B when A and B are numeric).If subs(s,old,new) does not change s, subs(s,new,old) is tried. This provides backwards compatibility with previous versions and eliminates the need to remember the order of the arguments. subs(s,old,new,0) does not switch the arguments if s does not change.ExamplesSingle InputSuppose a = 980 and C2 = 3 exist in the workspace.The statementy = dsolve('Dy = -a*y')y =C2/exp(a*t)Then the statementsa = 980; C2 = 3; subs(y)ans =3/exp(980*t)Single Substitutionsyms a b;subs(a + b, a, 4)ans =b + 4Multiple Substitutionssyms a b;subs(cos(a) + sin(b), {a, b}, {sym('alpha'), 2})ans =sin(2) + cos(alpha)Scalar Expansion Casesyms t;subs(exp(a*t), 'a', -magic(2))ans =[ 1/exp(t), 1/exp(3*t)][ 1/exp(4*t), 1/exp(2*t)]Multiple Scalar Expansionsyms x y;subs(x*y, {x, y}, {[0 1; -1 0], [1 -1; -2 1]})ans =0 -12 0subexpr %用常见的符号表达式重写符号表达式Rewrite symbolic expression in terms of common subexpressionsSyntax[Y, SIGMA] = subexpr(X, SIGMA)[Y, SIGMA] = subexpr(X, 'SIGMA')Description[Y, SIGMA] = subexpr(X, SIGMA) or [Y, SIGMA] = subexpr(X, 'SIGMA') rewrites the symbolic expression X in terms of its common subexpressions.ExamplesThe statementsh = solve('a*x^3+b*x^2+c*x+d = 0');[r,s] = subexpr(h,'s')r =s^(1/3) - b/(3*a) - (c/(3*a) - b^2/(9*a^2))/s^(1/3)(c/(3*a) - b^2/(9*a^2))/(2*s^(1/3)) - s^(1/3)/2 - b/(3*a) -(3^(1/2)*i*(s^(1/3) + (c/(3*a) - b^2/(9*a^2))/s^(1/3)))/2(c/(3*a) - b^2/(9*a^2))/(2*s^(1/3)) - s^(1/3)/2 - b/(3*a) +(3^(1/2)*i*(s^(1/3) + (c/(3*a) - b^2/(9*a^2))/s^(1/3)))/2s =((d/(2*a) + b^3/(27*a^3) - (b*c)/(6*a^2))^2 + (c/(3*a) -b^2/(9*a^2))^3)^(1/2) - b^3/(27*a^3) - d/(2*a) + (b*c)/(6*a^2)return the rewritten expression for t in r in terms of a common subexpression, which is returned in s:r =s^(1/3) - b/(3*a) - (c/(3*a) - b^2/(9*a^2))/s^(1/3)(c/(3*a) - b^2/(9*a^2))/(2*s^(1/3)) - s^(1/3)/2 - b/(3*a) - (3^(1/2)*i*(s^(1/3) + ...(c/(3*a) - b^2/(9*a^2))/s^(1/3)))/2(c/(3*a) - b^2/(9*a^2))/(2*s^(1/3)) - s^(1/3)/2 - b/(3*a) + (3^(1/2)*i*(s^(1/3) + ...(c/(3*a) - b^2/(9*a^2))/s^(1/3)))/2s =((d/(2*a) + b^3/(27*a^3) - (b*c)/(6*a^2))^2 + (c/(3*a) - b^2/(9*a^2))^3)^(1/2) - ...b^3/(27*a^3) - d/(2*a) + (b*c)/(6*a^2)limit %计算符号表达式的极限Compute limit of symbolic expressionSyntaxlimit(expr, x, a)limit(expr, a)limit(expr)limit(expr, x, a, 'left')limit(expr, x, a, 'right')Descriptionlimit(expr, x, a) computes bidirectional limit of the symbolic expression expr when x approaches a.limit(expr, a) computes bidirectional limit of the symbolic expression expr when the default variable approaches a.limit(expr) computes bidirectional limit of the symbolic expression expr when the default variable approaches 0.limit(expr, x, a, 'left') computes the limit of the symbolic expression expr when x approaches a from the left.limit(expr, x, a, 'right') computes the limit of the symbolic expression expr when x approaches a from the right.ExamplesCompute bidirectional limits for the following expressions:syms x h;limit(sin(x)/x)ans =1limit((sin(x + h) - sin(x))/h, h, 0)ans =cos(x)The results areans =1ans =cos(x)Compute the limits from the left and right for the following expressions: syms x;limit(1/x, x, 0, 'right')ans =Inflimit(1/x, x, 0, 'left')ans =-InfThe results areans =Infans =-InfCompute the limit for the functions presented as elements of a vector: syms x a;v = [(1 + a/x)^x, exp(-x)]v =[ (a/x + 1)^x, 1/exp(x)]limit(v, x, inf)ans =[ exp(a), 0]The result isans =[ exp(a), 0]diff %微分符号表达式Differentiate symbolic expressionSyntaxdiff(expr)diff(expr, v)diff(expr, sym('v'))diff(expr, n)diff(expr, v, n)diff(expr, n, v)Descriptiondiff(expr) differentiates a symbolic expression expr with respect to its free variable as determined by symvar.diff(expr, v) and diff(expr, sym('v')) differentiate expr with respect to v.diff(expr, n) differentiates expr n times. n is a positive integer.diff(expr, v, n) and diff(expr, n, v) differentiate expr with respect to v n times. ExamplesDifferentiate the following single-variable expression one time:syms x;diff(sin(x^2))ans =2*x*cos(x^2)The result isans =2*x*cos(x^2)Differentiate the following single-variable expression six times:syms t;diff(t^6,6)ans =720The result isans =720Differentiate the following expression with respect to t:syms x t;diff(sin(x*t^2), t)ans =2*t*x*cos(t^2*x)The result isans =2*t*x*cos(t^2*x)jacobian %计算雅可比矩阵Compute Jacobian matrixSyntaxjacobian(f, v)Descriptionjacobian(f, v) computes the Jacobian of the scalar or vector f with respect to v. The (i, j)-th entry of the result is . If f is scalar, the Jacobian of f is the gradient of f. If v is a scalar, the result equals to diff(f, v).ExamplesCompute the Jacobians of the following vectors:syms x y zf = [x*y*z; y; x + z]f =x*y*zyx + zv = [x, y, z]v =[ x, y, z]R = jacobian(f, v)R =[ y*z, x*z, x*y][ 0, 1, 0][ 1, 0, 1]b = jacobian(x + z, v)b =[ 1, 0, 1]The result isR =[ y*z, x*z, x*y][ 0, 1, 0][ 1, 0, 1]b =[ 1, 0, 1]symsum %计算符号多项式的和Evaluate symbolic sum of seriesSyntaxr = symsum(expr)r = symsum(expr, v)r = symsum(expr, a, b)r = symsum(expr, v, a, b)Description。
第四讲符号运算

-5-
1 ans = 1 (5)利用 whos 观察内存变量的类别和其它属性 >> whos Mn Mc Ms % 观察三个变量的类别和属性 Name Size Bytes Class Mc 1x9 18 char array Mn 2x2 32 double array Ms 2x2 408 sym object Grand total is 21 elements using 458 bytes
-3-
例 4.1.3 用符号计算验证三角等式 sin ϕ1 cos ϕ 2 − cos ϕ 1 sin ϕ 2 = sin(ϕ1 − ϕ 2 ) 。 >> syms fai1 fai2; >> y=simple(sin(fai1)*cos(fai2)-cos(fai1)*sin(fai2)) y= sin(fai1-fai2)
4.1.2 符号计算中的算符和基本函数
由于新版 MATLAB 采用了重载技术,使得用来构成符号计算表达式的算符和基本函 数,无论在形状、名称上,还是在使用方法上,都与数值计算中的算符和基本函数几乎完全 相同。这无疑给编程带来极大的便利。 下面就符号计算中的基本算符和函数作简单的归纳。 (1) 基本运算符 算符“+”,“-”,“*”,“\”,“/”, “^”分别实现矩阵的加、减、乘、左除、右除、求 幂运算。 算符“.*”,“./”,“.\”,“.^”分别实现“元素对元素”的数组乘、除、求幂。 算符“’”,“.’”分别实现矩阵的共轭转置、非共轭转置。 (2) 关系运算符 在符号对象的比较中,没有“大于”、“大于等于”、“小于”、“小于等于”的概念, 而只有是否“等于”的概念。 算符“= =”,“~ =”分别对算符两边的对象进行“相等”、“不等”的比较。当事实 为“真”时,比较结果用 1 表示;当事实为“假”时,比较结果则用 0 表示。 (3) 三角函数、双曲函数及它们的反函数 除 atan2 仅能用于数值计算外,其余的三角函数(如 sin) 、双曲函数(如 cosh) 及它们的反函数(如 asin,acosh) ,无论在数值计算还是符号计算中,它们的使 用方法相同。 (4) 指数、对数函数 在数值、符号计算中,函数 sqrt,exp,expm 的使用方法完全相同。至于对数函 数,符号计算中只有自然对数 log(即一般教材中用 ln),而没有数值计算中的 log2,log10。 (5) 复数函数 涉及复数的共轭 conj、求实部 real、求虚部 imag 和求模 abs 函数,在符号、数 值计算中的使用方法相同。但注意,在符号计算中,MATLAB 没有提供求相 角的命令。
高三数学考点-同角三角函数的基本关系及诱导公式
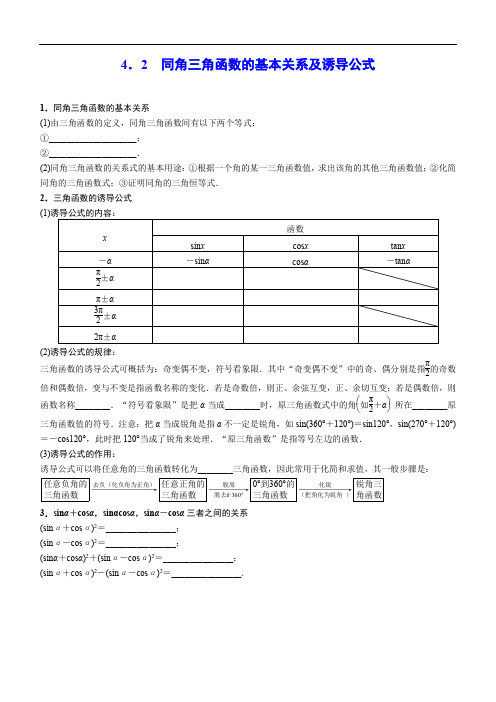
4.2 同角三角函数的基本关系及诱导公式1.同角三角函数的基本关系(1)由三角函数的定义,同角三角函数间有以下两个等式: ①____________________; ②____________________.(2)同角三角函数的关系式的基本用途:①根据一个角的某一三角函数值,求出该角的其他三角函数值;②化简同角的三角函数式;③证明同角的三角恒等式. 2.三角函数的诱导公式 (1)(2)诱导公式的规律:三角函数的诱导公式可概括为:奇变偶不变,符号看象限.其中“奇变偶不变”中的奇、偶分别是指π2的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则正、余弦互变,正、余切互变;若是偶数倍,则函数名称________.“符号看象限”是把α当成________时,原三角函数式中的角⎝⎛⎭⎫如π2+α 所在________原三角函数值的符号.注意:把α当成锐角是指α不一定是锐角,如sin(360°+120°)=sin120°,sin(270°+120°)=-cos120°,此时把120°当成了锐角来处理.“原三角函数”是指等号左边的函数. (3)诱导公式的作用:诱导公式可以将任意角的三角函数转化为________三角函数,因此常用于化简和求值,其一般步骤是: 任意负角的三角函数―――――――――→去负(化负角为正角)任意正角的三角函数―――――→脱周脱去k ·360°0°到360°的三角函数―――――――→化锐(把角化为锐角 )锐角三角函数 3.sin α+cos α,sinαcos α,sin α-cos α三者之间的关系 (sin α+cos α)2=________________; (sin α-cos α)2=________________;(sin α+cos α)2+(sin α-cos α)2=________________; (sin α+cos α)2-(sin α-cos α)2=________________.自查自纠1.(1)①sin 2α+cos 2α=1 ②sin αcos α=tan α2.(1)x 函数sin x cos x tan x -α -sin α cos α -tan α π2±α cos α ∓sin α π±α ∓sin α -cos α ±tan α 3π2±α -cos α ±sin α 2π±α±sin αcos α±tan α(2)不变 锐角 象限 (3)锐角3.1+sin2α 1-sin2α 2 2sin2α(2017·全国卷Ⅲ)已知sin α-cos α=43,则sin2α=( )A .-79B .-29 C.29 D.79解:sin2α=2sin αcos α=(sin α-cos α)2-1-1=-79.故选A .(2016·贵州4月适应性考试)若sin ⎝⎛⎭⎫π2+α=-35,且α∈⎝⎛⎭⎫π2,π,则sin(π-2α)=( ) A.2425 B.1225 C .-1225 D .-2425解:由sin ⎝⎛⎭⎫π2+α=-35得cos α=-35,又α∈⎝⎛⎭⎫π2,π,则sin α=45,所以sin(π-2α)=sin2α=2sin αcos α=-2425.故选D . (2017·重庆检测)已知α是第四象限角,且sin α+cos α=15,则tan α2=( )A.13 B .-13 C.12 D .-12解:因为sin α+cos α=15,α是第四象限角,所以sin α=-35,cos α=45,则tan α2=sinα2cos α2=2sin 2α22sin α2cosα2=1-cos αsin α=-13.故选B .(2016·四川)sin750°=________.解:因为sin θ=sin(k ·360°+θ)(k ∈Z ),所以sin750°=sin(2×360°+30°)=sin30°=12.故填12.(2017·郑州质检)已知cos ⎝⎛⎭⎫π2+α=2sin ⎝⎛⎭⎫α-π2,则sin 3(π-α)+cos (α+π)5cos ⎝⎛⎭⎫5π2-α+3sin ⎝⎛⎭⎫7π2-α的值为________. 解:因为cos ⎝⎛⎭⎫π2+α=2sin ⎝⎛⎭⎫α-π2,所以-sin α=-2cos α,则sin α=2cos α,代入sin 2α+cos 2α=1,得cos 2α=15.所以sin 3(π-α)+cos (α+π)5cos ⎝⎛⎭⎫52π-α+3sin ⎝⎛⎭⎫72π-α=sin 3α-cos α5sin α-3cos α=8cos 3α-cos α7cos α=87·cos 2α-17=335.故填335.类型一 利用同角三角函数的基本关系式进行化简和求值(1)(2017·全国卷Ⅰ)已知a ∈⎝⎛⎭⎫0,π2,tan α=2,则cos ⎝⎛⎭⎫α-π4=________; (2)已知sin α=13,求tan α;(3)已知sin α=m (m ≠0,m ≠±1),求tan α. 解:(1)由tan α=2得sin α=2cos α.又sin 2α+cos 2α=1,所以cos 2α=15.因为α∈⎝⎛⎭⎫0,π2,所以cos α=55,sin α=255. 因为cos ⎝⎛⎭⎫α-π4=cos αcos π4+sin αsin π4, 所以cos ⎝⎛⎭⎫α-π4=55×22+255×22=31010. 故填31010.(2)因为sin α=13,所以α是第一或第二象限角.当α是第一象限角时, cos α=1-sin 2α=1-⎝⎛⎭⎫132=223,所以tan α=sin αcos α=24;当α是第二象限角时,tan α=-24. (3)因为sin α=m (m ≠0,m ≠±1),所以cos α=±1-sin 2α=±1-m 2(当α为第一、四象限角时取正号,当α为第二、三象限角时取负号).所以当α为第一、四象限角时,tan α=m1-m 2;当α为第二、三象限角时,tan α=-m1-m 2 .【点拨】给值求值的关键是找出已知式与待求式之间的联系及函数的差异.①一般可以适当变换已知式,求得另外函数式的值,以备应用;②变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.(1)设sin α2=45,且α是第二象限角,则tan α2的值为________.解:因为α是第二象限角,所以α2是第一或第三象限角.①当α2是第一象限角时,有cos α2=1-sin 2α2=1-⎝⎛⎭⎫452=35,所以tan α2=sinα2cosα2=43;②当α2是第三象限角时,与sin α2=45矛盾,舍去.综上,tan α2=43.故填43.(2)已知sin α-cos α=2,α∈(0,π),则tan α=________. 解法一:由⎩⎨⎧sin α-cos α=2,sin 2α+cos 2α=1,得2cos 2α+22cos α+1=0,即(2cos α+1)2=0,所以cos α=-22.又α∈(0,π),所以α=3π4,tan α=tan 3π4=-1.解法二:因为sin α-cos α=2,所以(sin α-cos α)2=2,得sin2α=-1.因为α∈(0,π),所以2α∈(0,2π),2α=3π2,所以α=3π4,tan α=-1.故填-1.类型二 诱导公式的应用(1)(2016·全国卷Ⅰ)已知θ是第四象限角,且sin ⎝⎛⎭⎫θ+π4=35,则tan ⎝⎛⎭⎫θ-π4=________. 解:由题意知,θ+π4是第一象限角,得cos ⎝⎛⎭⎫θ+π4=45, 根据同角三角函数关系式可得tan ⎝⎛⎭⎫θ+π4=34. 所以tan ⎝⎛⎭⎫θ-π4=tan ⎝⎛⎭⎫θ+π4-π2=-1tan ⎝⎛⎭⎫θ+π4=-43.故填-43. (2)化简sin (2π-α)cos (π+α)cos ()π2+αcos ()11π2-αcos (π-α)sin (3π-α)sin (-π-α)sin ()9π2+α. 解:原式=(-sin α)(-cos α)(-sin α)(-sin α)(-cos α)·sin α·sin α·cos α=-tan α. 【点拨】①三角式的化简通常先用诱导公式,将角度统一后再用同角三角函数关系式,这可以避免交错使用公式时导致的混乱.②在运用公式时正确判断符号至关重要.③三角函数的化简、求值是三角函数中的基本问题,也是高考常考的问题,要予以重视.④正确理解“奇变偶不变,符号看象限”可以提高解题效率.(1)化简sin 2(π+α)-cos(π+α)·cos(-α)+1.解:原式=sin 2α-(-cos α)·cos α+1=sin 2α+cos 2α+1=2.(2)(2017·北京)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若sin α=13,则cos(α-β)=________. 解:因为α和β的终边关于y 轴对称,所以α+β=π+2k π,k ∈Z ,那么sin β=sin α=13,cos α=-cos β,这样cos(α-β)=cos αcos β+sin αsin β=-cos 2α+sin 2α=2sin 2α-1=-79.故填-79.类型三 关于sin α,cos α的齐次式问题已知tan αtan α-1=-1,求下列各式的值.(1)sin α-3cos αsin α+cos α; (2)sin 2α+sin αcos α+2.解:由已知得tan α=12.(1)sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.(2)sin 2α+sin αcos α+2=sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝⎛⎭⎫122+12⎝⎛⎭⎫122+1+2=135. 【点拨】(1)形如a sin α+b cos α和a sin 2α+b sin αcos α+c cos 2α的式子分别称为关于sin α,cos α的一次齐次式和二次齐次式,对涉及它们的三角变换通常转化为正切(分子分母同除以cos α或cos 2α)求解.如果分母为1,可考虑将1写成sin 2α+cos 2α.(2)已知tan α=m 的条件下,求解关于sin α,cos α的齐次式问题,必须注意以下几点:①一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式.②因为cos α≠0,所以可以用cos n α(n ∈N *)除之,这样可以将被求式化为关于tan α的表示式,可整体代入tan α=m 的值,从而完成被求式的求值运算.③注意1=sin 2α+cos 2α的运用.(荆州2017届质量检测)已知tan(5π-x )=2,则2cos 2x2-sin x -1sin x +cos x=________.解:tan(5π-x )=2,即tan(π-x )=2,得tan x =-2.又因为2cos 2x2-1=cos x ,所以2cos 2x2-sin x -1sin x +cos x =cos x -sin x sin x +cos x=1-tan x tan x +1=-3.故填-3.1.诱导公式用角度制和弧度制表示都可,运用时应注意函数名称是否要改变以及正负号的选取.2.已知一个角的某一个三角函数值,求这个角的其他三角函数值,这类问题用同角三角函数的基本关系式求解,一般分为三种情况:(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的,此类情况只有一组解. (2)一个角的某一个三角函数值是已知的,但这个角所在的象限或终边所在的位置没有给出,解答这类问题,首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置,然后分不同的情况求解.(3)一个角的某一个三角函数值是用字母给出的,此类情况须对字母进行讨论,并注意适当选取分类标准,一般有两组解.3.计算、化简三角函数式常用技巧(1)减少不同名的三角函数,或化切为弦,或化弦为切,如涉及sin α,cos α的齐次分式问题,常采用分子分母同除以cos n α(n ∈N *),这样可以将被求式化为关于tan α的式子. (2)巧用“1”进行变形,如1=sin 2α+cos 2α=tan45°等. (3)平方关系式需开方时,应慎重考虑符号的选取.(4)熟悉sin α+cos α,sin α-cos α,sin αcos α三者之间的内在联系,利用(sin α±cos α)2=1±2sin αcos α进行和积转换,可知一求二.1.sin585°的值为( )A .-22 B.22 C .-32 D.32解:sin585°=sin ()90°×6+45°=-sin45°=-22.故选A .2.(福建四地六校2017届月考)已知cos ⎝⎛⎭⎫θ+π2=45,-π2<θ<π2,则sin2θ的值等于( ) A .-2425 B.2425 C .-1225 D.1225解:由cos ⎝⎛⎭⎫θ+π2=45,-π2<θ<π2,得sin θ=-45,cos θ=35,则sin2θ=2sin θcos θ=-2425.故选A . 3.(江西上饶2017届一模)已知sin ⎝⎛⎭⎫α-π12=13,则cos ⎝⎛⎭⎫α+17π12 的值等于( ) A.13 B.223 C .-13 D .-223解:由cos ⎝⎛⎭⎫α+17π12=cos ⎝⎛⎭⎫α-π12+3π2=sin ⎝⎛⎭⎫α-π12=13.故选A . 4.(2016·全国卷Ⅲ)若tan α=34,则cos 2α+2sin2α=( )A.6425B.4825 C .1 D.1625解法一:cos 2α+2sin2α=cos 2α+2sin2αsin 2α+cos 2α=1+4tan α1+tan 2α=6425. 解法二:由tan α=34,得sin α=34cos α,sin α=35,cos α=45或sin α=-35,cos α=-45,所以cos 2α+2sin2α=1625+4×1225=6425.故选A .5.(2016·长春质检)已知tan α=2,α为第一象限角,则sin2α+cos α=( )A. 5B.4+255C.4+55D.5-25解:由三角函数定义sin α=255,cos α=55,故sin2α+cos α=2sin αcos α+cos α=4+55.故选C .6.(2016·淮南二模)已知sin α+cos α=12,α∈(0,π),则1-tan α1+tan α=( )A .-7 B.7 C. 3 D .-3解:因为(sin α+cos α)2=1+2sin αcos α=14,所以sin αcos α=-38,又α∈(0,π),所以sin α>0,cos α<0.因为(sin α-cos α)2=1-2sin αcos α=74,所以cos α-sin α=-72.所以1-tan α1+tan α=cos α-sin αcos α+sin α=-7212=-7.故选A .7.(2016江苏冲刺卷)已知θ是第三象限角,且sin θ-2cos θ=-25,则sin θ+cos θ=________.解:由平方关系得⎝⎛⎭⎫2cos θ-252+cos 2θ=1,且cos θ<0,解得cos θ=-725,从而sin θ=-2425,故sin θ+cos θ=-3125.故填-3125.8.(2015·四川)已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________.解:因为sin α+2cos α=0,所以sin α=-2cos α,由同角三角函数关系式得cos 2α+4cos 2α=1,所以cos 2α=15,所以2sin αcos α-cos 2α=-4cos 2α-cos 2α=-5cos 2α=-1.故填-1.9.已知sin(3π+θ)=13,求值:cos (π+θ)cos θ[cos (π-θ)-1]+cos (θ-2π)sin ⎝⎛⎭⎫θ-3π2cos (θ-π)-sin ⎝⎛⎭⎫3π2+θ.解:因为sin(3π+θ)=-sin θ=13,所以sin θ=-13.所以原式=-cos θcos θ(-cos θ-1)+cos θcos θ·(-cos θ)+cos θ=11+cos θ+11-cos θ=21-cos 2θ=2sin 2θ =2⎝⎛⎭⎫-132=18. 10.已知sin θ-cos θ=12,求:(1)sin θcos θ; (2)sin 3θ-cos 3θ; (3)sin 4θ+cos 4θ.解:(1)将sin θ-cos θ=12两边平方得:1-2sin θcos θ=14,sin θcos θ=38.(2)sin 3θ-cos 3θ=(sin θ-cos θ)(sin 2θ+sin θcos θ+cos 2θ)=12×⎝⎛⎭⎫1+38=1116. (3)sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ =1-2×⎝⎛⎭⎫382=2332.11.(1)已知tan α=3,求23sin 2α+14cos 2α的值.(2)已知1tan α-1=1,求11+sin αcos α的值.解:(1)23sin 2α+14cos 2α=23sin 2α+14cos 2αsin 2α+cos 2α=23tan 2α+14tan 2α+1=23×32+1432+1=58.(2)由1tan α-1=1得tan α=2,11+sin αcos α=sin 2α+cos 2αsin 2α+cos 2α+sin αcos α=tan 2α+1tan 2α+tan α+1=22+122+2+1=57. (黄冈2017届期末)已知函数y =sin(πx +φ)-2cos(πx +φ)(0<φ<π)的图象关于直线x =1对称,则sin2φ=( ) A.35 B .-35 C.45 D .-45解:y =f (x )=sin(πx +φ)-2cos(πx +φ)=5sin(πx +φ-α),其中sin α=25,cos α=15, 因为函数的图象关于x =1对称,所以y =f (1)=±5,即π+φ-α=π2+k π,k ∈Z ,sin2φ=sin2⎝⎛⎭⎫α-π2+k π=sin(2α-π+2k π)=sin(2α-π)=-sin2α=-2sin αcos α=-2×25×15=-45 .故选D .。
第四章 MATLAB符号计算

Ezpolar函数实现极坐标中二维曲 线图象的绘制,它的调用格式:
ezpolar(f,[a,b])
说明: 绘图表达式为rho=f(theta)极坐标曲线,
theta的取值范围为,缺省时为[0,2*pi]
例:p83
4.5.2三维绘图函数
ezplot3是实现三维绘图的函数,它的 调用格式:
ezplot3(x,y,z,[tmin,tmax]) ezplot3(x,y,z,[tmin,tmax ],'animate')
3.符号表达式的提取分子和分母运算
在matlab中可利用numden函数来提取符号表达式 中的分子或分母。其一般调用格式为:
[n,d]=numden(s)
说明:
参数s是符号表达式是一个 有理分式或可以展开为有理
例: s=sym('2/5+3/7')
n= 29
分式,numden函数把有理分 式的分子返回给n,分母返回
dsolve在求常微分方程组时 的调用格式为:
dsolve('eq1,eq2,...','cond1,cond2...','v')
说明: 该函数求解常微分方程组eq1,…,eqn在初值条件或边界 条件为cond1,…,condn下的符号特解,若不给出初值 条件,则求方程组的通解,v为指定的返回值中的变量 表示。
例4-9解超越方程组
sin(x+y)-y*exp(x)=0 x^2-y=2
syms x y
[x,y]=solve('sin(x+y)-y*exp(x)=0','x^2-y=2')
x =-.66870120500236202933135901833637
Excel常用的函数计算公式大全(免费) excel公式计算

excel公式计算(免费)EXCEL的常用计算公式大全一、单组数据加减乘除运算:①单组数据求加和公式:=(A1+B1)举例:单元格A1:B1区域依次输入了数据10和5,计算:在C1中输入 =A1+B1 后点击键盘“Enter(确定)”键后,该单元格就自动显示10与5的和15。
②单组数据求减差公式:=(A1-B1)举例:在C1中输入 =A1-B1 即求10与5的差值5,电脑操作方法同上;③单组数据求乘法公式:=(A1*B1)举例:在C1中输入 =A1*B1 即求10与5的积值50,电脑操作方法同上;④单组数据求乘法公式:=(A1/B1)举例:在C1中输入 =A1/B1 即求10与5的商值2,电脑操作方法同上;⑤其它应用:在D1中输入=A1^3 即求5的立方(三次方);在E1中输入 =B1^(1/3)即求10的立方根小结:在单元格输入的含等号的运算式,Excel中称之为公式,都是数学里面的基本运算,只不过在计算机上有的运算符号发生了改变---- “×”与“*”同、“÷”与“/”同、“^”与“乘方”相同,开方作为乘方的逆运算,把乘方中和指数使用成分数就成了数的开方运算。
这些符号是按住电脑键盘“Shift”键同时按住键盘第二排相对应的数字符号即可显示。
如果同一列的其它单元格都需利用刚才的公式计算,只需要先用鼠标左键点击一下刚才已做好公式的单元格,将鼠标移至该单元格的右下角,带出现十字符号提示时,开始按住鼠标左键不动一直沿着该单元格依次往下拉到你需要的某行同一列的单元格下即可,即可完成公司自动复制,自动计算。
二、多组数据加减乘除运算:①多组数据求加和公式:(常用) 举例说明:=SUM(A1:A10),表示同一列纵向从A1到A10的所有数据相加; =SUM(A1:J1),表示不同列横向从A1到J1的所有第一行数据相加;②多组数据求乘积公式:(较常用)举例说明:=PRODUCT(A1:J1)表示不同列从A1到J1的所有第一行数据相乘;=PRODUCT(A1:A10)表示同列从A1到A10的所有的该列数据相乘;③多组数据求相减公式:(很少用) 举例说明:=A1-SUM(A2:A10)表示同一列纵向从A1到A10的所有该列数据相减;=A1-SUM(B1:J1)表示不同列横向从A1到J1的所有第一行数据相减;④多组数据求除商公式:(极少用) 举例说明:=A1/PRODUCT(B1:J1)表示不同列从A1到J1的所有第一行数据相除; =A1/PRODUCT(A2:A10)表示同列从A1到A10的所有的该列数据相除;三、其它应用函数代表:①平均函数 =AVERAGE(:);②最大值函数 =MAX (:);③最小值函数 =MIN (:);④统计函数 =COUNTIF(:):举例:Countif ( A1:B5,”>60”) 说明:统计分数大于60分的人数,注意,条件要加双引号,在英文状态下输入。
python微分方程

Python微分方程一、介绍微分方程是数学中的一个重要分支,用于描述自然界中许多现象和过程的数学模型。
Python作为一种功能强大且易于学习的编程语言,提供了许多用于求解微分方程的工具和库。
本文将介绍如何使用Python求解微分方程,并提供一些实例和应用。
二、Python求解微分方程的工具和库Python中有许多用于求解微分方程的工具和库,包括SciPy、SymPy、NumPy等。
下面将介绍其中两个常用的库。
2.1 SciPySciPy是Python中用于科学计算的一个库,其中包含了许多用于求解微分方程的函数和工具。
它提供了scipy.integrate模块,其中包含了许多用于数值积分和求解常微分方程的函数。
2.2 SymPySymPy是一个用于符号计算的Python库,它提供了强大的符号计算功能,可以用于求解微分方程。
SymPy中的sympy.dsolve模块提供了用于求解常微分方程的函数。
三、数值方法求解微分方程数值方法是求解微分方程的一种常用方法,它将微分方程转化为一个数值问题,并通过数值计算得到近似解。
Python中的SciPy库提供了多种数值方法用于求解微分方程,包括Euler方法、Runge-Kutta方法等。
3.1 Euler方法Euler方法是一种简单而常用的数值方法,它通过将微分方程中的导数用差分近似表示,从而得到递推的近似解。
Euler方法的基本思想是将求解区间分割成若干个小区间,然后在每个小区间上用线性近似来逼近解的变化。
Euler方法的步骤如下:1.将求解区间分割成若干个小区间,确定步长h。
2.从初始条件开始,根据微分方程和差分近似计算下一个点的值。
3.重复上述步骤,直到达到所需的精度或求解区间的末尾。
3.2 Runge-Kutta方法Runge-Kutta方法是一种常用的数值方法,它通过使用多个差分近似来逼近解的变化。
Runge-Kutta方法的基本思想是在每个小区间上进行多次计算,通过加权平均来得到更精确的近似解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用符号计算函数
●主要用法:
●compose(f, g) 返回复合函数f(g(y)),其中f=f(x),g=g(y).
x和y分别为findsym从f、g中找到的符号变量.
●compose(f, g, z) 返回复合函数f(g(z)), f=f(x), g=g(y),
x,y含义同上一种用法. 最后用指定变量z代替变量y.
●compose(f, g, x, y, z) 返回复合函数f(g(z)). 将x=g(y)代入f(x)中, 最后用
指定的变量z代替变量y
●示例:
●syms x y t
●f = 1/(1+x);
●g = sin(y)^2
●h = compose(f,g,x,y,t)●运行结果:
●f = 1/(x + 1)
●g = sin(y)^2
●h = 1/(sin(t)^2 + 1)
计算极限函数:limit
●函数一般使用格式:
●limit(f,x,a): 计算f(x)当x趋向于a的极限●limit(f,x,a,'right'): 计算右极限
●limit(f,x,a,'left'): 计算左极限
示例:求一元函数极限,并绘图观察函数在变量x 趋于0时函数的变化趋势。
x x x )sin(lim 0 编程实现:
syms x
y=sin(x)/x;
s=limit(y,x,0)% 求函数y 的极限
x=-1:0.02:1;
y=sin(x)./x; %计算离散点的坐标
plot(x,y,'k.’); %绘制黑色的散点图
●示例:计算数列的极限。
●
编程实现:
●syms n
●an=(1+1/n)^n;
●S=limit(an,n,inf) %计算数列极限●
返回结果:
●S = exp(1)n n n
a )11(+=
求导计算diff
●
用法:
●diff(s,'v') 求s 对自变量v 的1阶导数
●diff(s,'v',n) 求s 对自变量v 的n 阶导数
●注:'v' 可以为符号变量已知求和.222),(y
xy y x y x f ++=x f ∂∂y f ∂∂编写程序:
syms x y
f= x^2*y + 2*x*y + y*y
d1 = diff(f,x,1)
d2 = diff(f,y,1)运行结果:d1 = 2*y + 2*x*y d2 = x^2 + 2*x + 2*y
练习
求下列函数的一阶导数:22x
a ae
y x +=编写程序:
syms x a
f1=a*exp(x)/sqrt(a^2+x^2);
d1=diff(f1,x,1)
运行结果:
d1=
(a*exp(x))/(a^2+x^2)^(1/2)-(a*x*exp(x))/(a^2+x^2)^(3/2)
符号积分函数int
●用法:
●s=int(expr,var):以expr表达式中的变量var为积分变量计算不定积分●s=int(expr,var,a,b)
以expr表达式中的变量var为积分变量计算定积分,积分上下限分别为b和a。
●示例. 使用符号工具箱函数解下列不定积分:
⎰-dx
x)1
ln(2
x
●编写程序:
●syms x a
●f=int(x*log(x*x-1))
泰勒多项式函数taylor 一般用法:
●taylor(f) 计算f 的5阶麦克劳林多项式●taylor(f,v,Name,Value)●taylor(f,v,a) 计算f 在点a 展开的麦克考林多项式●taylor(f,v,a,Name,Value) 指定属性名称,属性值的调用方法●f 为函数的表达式或者符号变量v 为函数的自变量●Name 为属性名(用字符串表示);Value 为属性值。
200000()00()()()()()()2!
()()()!
n n n f x f x f x f x x x x x f x x x R x n '''=+-+-++-+
泰勒多项式函数taylor
求e x的7阶泰勒多项式.
>>taylor(exp(x),x,0,'order',8)
ans =
x^7/5040 + x^6/720 + x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 >>taylor(exp(x),x,'expansionpoint',0,'order',8)
ans =
x^7/5040 + x^6/720 + x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1说明:以上两个语句效果相同。
