弹性力学平面问题的极坐标解答优秀课件
合集下载
《弹塑性力学》第七章 弹性力学平面问题的极坐标系解答.ppt

x
应力:r, ,r= r 应变:r, ,r= r
P
y
位移:u r , u
2020/10/9
3
§7-1平面极坐标下的基本公式
直角坐标与极坐标之间关系:
x=rcos, y=rsin
r cos sin
x r x x
r r
r sin cos
y r y y
r
r
2 r
r )( f r
r
f 1
r
fr 0 0 f
fr ) r
2= 2 1 1 2
r 2 r r r 2 2
力的边界条件如前所列。
2020/10/9
14
§7-1平面极坐标下的基本公式
1.8 应力函数解法
当体力为零 fr=f=0时, 应力法基本方程中的应
力分量可以转为一个待求的未知函数 ( r, ) 表示,而应力函数 ( r, ) 所满足方程为
16
§7-2 轴对称问题
2.1 轴对称问题的特点
1.截面的几何形状为圆环、圆盘。
2.受力和约束对称于中心轴,因此,可知体 积力分量 f=0 ; 在边界上 r=r0 :F 0, u (0 沿环向的受力和约束为零) 。
3.导致物体应力、应变和位移分布也是轴 对称的:
2020/10/9
17
§7-2 轴对称问题
上式代入平衡微分方程可得到用位移表 示的平衡微分方程,即位移法的基本方程。
r
r
1 r r
( r
r
)
Kr
0
r
r
1 r
2 r
r
K
0
力的边界条件也同样可以用位移表示。
2020/10/9
第4章 (弹力)平面问题的极坐标解答13

圆孔的孔口应力集中
§4-8
圆孔的孔口应力集中
本节课小结 掌握压力隧洞的求解方法,了解工程 中的四类接触问题; 关键:径向变形连续,径向应力连续 理解应力集中的概念,掌握圆孔孔口 应力集中的求解方法,了解任意荷载任 意薄板的应力求解; 关键:坐标转换,叠加法
本节课小结 掌握压力隧洞的求解方法,了解工程 中的四类接触问题; 关键:径向变形连续,径向应力连续 理解应力集中的概念,掌握圆孔孔口 应力集中的求解方法,了解任意荷载任 意薄板的应力求解; 关键:坐标转换,叠加法
求解A、B、C、D,然后令 a / b = 0,得
Hale Waihona Puke qa q 2 A 0, B , C qa , D 4 4
4
§4-8
圆孔的孔口应力集中
代入应力分量式, 有
q a2 3a 2 r (1 2 )(1 2 ) cos 2 2 r r q a4 1 3 4 cos 2 2 r
q r 2
r 0
§4-8
圆孔的孔口应力集中
q r r b cos 2 2 q r r b sin 2 2
a
问题2求解 (非轴对称问题)
内边界
r r a 0
r
r a
外边界
0
b
r
r
乘以 cos 2 ; r 为r 的某一函数乘以
圆孔的孔口应力集中
a
问题2求解 (非轴对称问题)
可假设应力函数为: 将其代入相容方程:
f (r ) cos 2
2 2
b
r
r
1 1 r 2 r r r 2 2 0
弹性力学 第四章 平面问题的极坐标解答

s = sσ
(3) 多连体中的位移单值条件
§ 4-4 应力分量的坐标变换式
·问题的提出
工程中有些问题, 用极坐标计算方便, 但应力分量用直角坐 标表述更直观. 反之也存在.
由此需要对应力分量进行坐标变换.
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ?
y
fρ τ + ∂τρυdρ ρυ ∂ρ ∂συ dυ συ+ ∂σρ ∂υ σρ+ dρ ∂τυρ C ∂ρ dυ τυρ+ ∂υ
B
fυ
§ 4-1 极坐标中的平衡微分方程
·平衡微分方程
x
υ dυ ρ
Σ Fρ = 0 :
συ
A
σρ τρυ P τυρ
∂σρ σρ+ dρ (ρ+dρ)dυ - σρ ρdυ ∂ρ ∂συ dυ - συ+ dυ dρ sin ∂υ 2 + τυρ+ - συ dρ sin
Σ Fυ = 0 :
συ = ?
§ 4-4 应力分量的坐标变换式
·坐标变换
συ = ?
将两坐标系下微元体组合
τyx σy σx συ
τυρ τxy
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ?
O x
υ
τyx
σy σx
συ y
τυρ τxy
Σ Fυ = 0 :
O h/2 h/2 lqx源自(v)x=0, l = 0
应力边界条件: ( σy ) y=-h/2 = - q (τyx ) y=-h/2 = 0 ( σy ) y= h/2 = 0 (τyx ) y= h/2 = 0
弹性力学:第四章 平面问题的极坐标解答

两 面面积不等,分别为 ρd φ , ρ d ρ d φ 。
从原点出发为正, 从 x 轴向 y 轴方向 转动为正。
微分体上的作用力有:
体力-- f ρ , fφ , 以坐标正向为正。 应力-- ρ面, φ面分别表示应力及其 增量。
应力同样以正面正向,负面负向的应力为正,反 之为负 。
平衡条件:
(b)
u u sin v cos。
导数的变换:
将对 x, y 的导数,变换为对 , 的导数:
F (x, y) 可看成是 F (, ),而 , 又是 x, y
的函数,即 F 是通过中间变量 , 为 x, y
的复合函数。
有: F
Φ Φ ρ Φ φ , x ρ x φ x
Φ y
Φ ρ
ρ y
d
2
f ρ ρddρ
0
上式中一阶微量相互抵消,保留到二阶微量,得
1
f
0。
(a)
式( a )中 1、2、4 项与直角坐标的方向相似; 而
σρ
ρ -- 是由于 面ρ面积大于 面的ρ面
积而引起的,
σφ ρ
-- 是由于 面上的
在C点的
向有 投影。
Fφ 0 --通过形心C的 φ向合力为0,
故物理方程形式相似。
平面应力问题的物理方程:
1 E
(
),
1 E
(
),
2(1 E
)
。
对于平面应变问题,
只须作如下同样变换,
E
1
E
2
,
。 1
泰勒展开
Exercise : Chap 4
Today: 4-1, 4-2 End of Lecture 9
边界条件
从原点出发为正, 从 x 轴向 y 轴方向 转动为正。
微分体上的作用力有:
体力-- f ρ , fφ , 以坐标正向为正。 应力-- ρ面, φ面分别表示应力及其 增量。
应力同样以正面正向,负面负向的应力为正,反 之为负 。
平衡条件:
(b)
u u sin v cos。
导数的变换:
将对 x, y 的导数,变换为对 , 的导数:
F (x, y) 可看成是 F (, ),而 , 又是 x, y
的函数,即 F 是通过中间变量 , 为 x, y
的复合函数。
有: F
Φ Φ ρ Φ φ , x ρ x φ x
Φ y
Φ ρ
ρ y
d
2
f ρ ρddρ
0
上式中一阶微量相互抵消,保留到二阶微量,得
1
f
0。
(a)
式( a )中 1、2、4 项与直角坐标的方向相似; 而
σρ
ρ -- 是由于 面ρ面积大于 面的ρ面
积而引起的,
σφ ρ
-- 是由于 面上的
在C点的
向有 投影。
Fφ 0 --通过形心C的 φ向合力为0,
故物理方程形式相似。
平面应力问题的物理方程:
1 E
(
),
1 E
(
),
2(1 E
)
。
对于平面应变问题,
只须作如下同样变换,
E
1
E
2
,
。 1
泰勒展开
Exercise : Chap 4
Today: 4-1, 4-2 End of Lecture 9
边界条件
弹性力学第4章-平面问题的极坐标解答

两面不平行, d 夹角为 φ; 两
ρ 面面积不等,分别为 ρdφ, ( ρ + d ρ) dφ. ρ从原点出发为正, 从 x 轴向 y 轴方向转动为正.
微分体上的作用力有: 微分体上的作用力有
体力-- f ρ , f φ , 以坐标正向为正. -应力---
作用力
±ρ
面, φ 面分别表示应力及其增量. ±
第一节 第二节 第三节 第四节 第五节
极坐标中的平衡微分方程 极坐标中的几何方程及物理方程 极坐标中的应力函数与相容方程 应力分量的坐标变换式 轴对称应力和相应的位移
第六节 第七节 第八节 第九节 第十节 例题
圆环或圆筒受均布压力 压力隧洞 圆孔的孔口应力集中 半平面体在边界上受集中力 半平面体在边界上受分布力
基本方程的区别. 对于圆形,弧形,扇形及由径向线和环向围成的物 体,宜用极坐标求解.用极坐标表示边界简单,使边界条 件简化.
在A内任一点(ρ, )取出一个微分体,考虑其平 衡条件. 微分体:由夹 角为d φ的两 径向线和距离 为d ρ的两环 向线围成.
§4-1 极坐标中的平衡微分方程
注意: 注意:
即 Φ是通过中间变量 ρ,φ ,为 x, y 的复合函数. 有: Φ = Φ ρ + Φ φ, Φ=Φρ +Φφ. 而
ρ x φ x y ρ y φ y sin cos ρ ρ = , = sin; = cos, . = ρ x y ρ y x x
代入,即得一阶导数的变换公式,
Φ sin Φ sinφ Φ=cosφ =(cosφ )Φ x ρ ρ φ ρ ρ φ
u = uρ cos u sin, v = uρ sin + u cos.
(c) (d)
弹性力学 第七章平面问题的极坐标解答

x r cos
arctan y
x
y r sin
x
y
r x
y
两种坐标系下位移分量坐标转换公式:
ur u
v sin u cos
v
cos
u
sin
u v
ur ur
cos sin
u u
sin cos
r
u
x
u
v
ur y
2、极坐标下的平衡微分方程
•几何描述
PB面积:rd AC面积:(r+dr)d
第七章 平面问题的极坐标解答
•本质上坐标系的选择并不影响弹性力学问题的求 解。 •但是影响边界条件的描述和表达,从而关系问题 的求解难易程度。 •圆形,楔形,扇形等物体,采用极坐标系求解比 较方便。
采用极坐标可更方便几何定位描述。
§7-1 平面问题的极坐标方程
1、极坐标与直角坐标之间的关系式:
r2 x2 y2
rds 1 xds cos 1 cos yds sin 1 sin
xyds cos 1 sin yxds sin 1 cos 0
用 xy 代替 yx 简化以后,得
r x cos2 y sin2 2 xy sin cos
o
yx y
x
y
B x
y
r
xy xya
c
A
x
b r r
同样可由三角板A的平衡条件F=0,得到 r ( y x )sin cos xy (cos2 sin2 )
和y分别改换为r和 。
r
1
E
2
( r
1
)
1 2
E
(
1
r
)
r
arctan y
x
y r sin
x
y
r x
y
两种坐标系下位移分量坐标转换公式:
ur u
v sin u cos
v
cos
u
sin
u v
ur ur
cos sin
u u
sin cos
r
u
x
u
v
ur y
2、极坐标下的平衡微分方程
•几何描述
PB面积:rd AC面积:(r+dr)d
第七章 平面问题的极坐标解答
•本质上坐标系的选择并不影响弹性力学问题的求 解。 •但是影响边界条件的描述和表达,从而关系问题 的求解难易程度。 •圆形,楔形,扇形等物体,采用极坐标系求解比 较方便。
采用极坐标可更方便几何定位描述。
§7-1 平面问题的极坐标方程
1、极坐标与直角坐标之间的关系式:
r2 x2 y2
rds 1 xds cos 1 cos yds sin 1 sin
xyds cos 1 sin yxds sin 1 cos 0
用 xy 代替 yx 简化以后,得
r x cos2 y sin2 2 xy sin cos
o
yx y
x
y
B x
y
r
xy xya
c
A
x
b r r
同样可由三角板A的平衡条件F=0,得到 r ( y x )sin cos xy (cos2 sin2 )
和y分别改换为r和 。
r
1
E
2
( r
1
)
1 2
E
(
1
r
)
r
弹性力学平面问题的极坐标解答课件
b
a
2
ln
a
b2
a
2
0
位移的确定
H, I, K待定
u
1 E
(1 )
A
(1 3 )B
2(1 )B(ln
1)
2(1
)C
I
sin
K
cos
u
4B
E
H
I
cos
K
sin
左端固定:(u )0 0
0,
(u ) 0 0
0,
u
0
0
0
常数的确定:
H
I
0,
K
1 E
极坐标下的双调和方程
代入协调方程,得到应力函数U需满足
的双调和方程
2
2
1
1
2
2
2
2U
2
1
U
1
2
2U
2
0
§7-2 轴对称应力及其位移
应力函数与无关,双调和方程为
d2
d 2
1
d
d
d2 U
d 2
1
dU
d
0
4
d4 U
d 4
23
d3 U
d 3
2
d2 U
d 2
dU
问题描述 任一截面上的弯矩:
M () F cos R tan F R sin
应力函数:
U f () sin
O
m
ba
F
x
n
y
f()的求解及应力表达式
微分方程及其通解
d2
d 2
1
d
d
1
2
d2 f
弹性力学 第4章 1-5 极坐标解答

(4 12)
u H
若适当给定约束条件,无刚体位移
u | 0 , u | / 2 0 F K I 0
A 1 C u (1 ) (1 ) E E u 0
R2
•五. 特例
1.只受内压
R ( )2 1
2
1 qr
A ln B 2 ln C 2 D (4 10)
2.应力分量的通解
A
2
B(1 2 ln ) 2C B(3 2 ln ) 2C (4 11)
0
A
2
3.位移分量的通解
I cos K sin
§4.5 轴对称应力和对应的位移
构件的几何形状,受力都关于通过Z轴对称。则为 轴对称应力问题,应力分量和应力函数均与无关。
( )
( )
( )
1.应力分量(不计体力,与无关)
1 d d d 2 2 d
0
2.相容方程:(采用应力函数,不计体力)
d2 d 2 ( 2 ) d d d2 d 2 ( 2 ) 0 d d
3.这是一个常微分方程,可以求得通解为:
A ln B 2 ln C 2 D
(4 10)
轴对称应力问题的求解
1.应力函数的通解:
(4)针孔问题(应力集中) 受外压qb内径a0时:
| r
2 q 2q2 r 2 2 1 ( ) R
孔虽然很小,但孔边应力却提高了近2倍, 这就是应力集中现象。如果外力为拉力, 则此处为2倍的拉力实际问题中,孔边发 生开裂,就是这个原因。
弹性力学-04平面问题的极坐标解答 (2)PPT

ur , u 为边界上已知的位移分量。
应力边界条件:
lrsm rsfr m slrsf
f r , f 为边界上已知的面力分量。lcos(N,r) mcos(N,)
特别地,对r =常数的边界,应力边界条件简化为:
r r常数=pn
r r常数=pt
对 =常数的边界,应力边界条件简化为:
常数=pn
y
x r2
cos
r
x y
x r xr xcos r sinr cosrsinr
y r yr ysin r cors sinrcors
2 x 2 c o s r sin r c o s r sin r
x x
cos2 2 r 2 sin21 r rr12 2 2
r 常数=pt
0
r l
q0
r 0 0
0 r 0
r ra 0 r ra 0
r rb 0 r rb 0
b
a 0 dr0
b
a r 0 dr 0
b
a
0
rd
rM
ur /2 0 u /2 0
lr
r
r
0 0 r0
0 180 r0
r 0 0 r0
r 180 0 r0
r r
1 r r
r
r
fr
0
y
F 0,
d r
r
P r
x
(rdr)d
r
rd B
dr
fr
f
A
r
r
r
d
C
r
r
r
d
r
r
dr dr
dd
r
dr
弹性力学03平面问题的直角坐标解答PPT课件

2
h
h
(2)
2 h
x
y
dy
M
2
x
12M h3
y
2 h
6dy2dy
M
2
x
M (h3 /12)
y
h
2 h
6dy
dy
0
2
d 2
h3
M
(或d 2M) h3
x
M I
y
可见:此结果与材力中结果相同,说明材力中纯弯曲梁的应力结果是正确的。
说明:
l
l
(1) 组成梁端力偶 M 的面力须线性 分布,且中心处为零,结果才
(2) 检验φ(x,y) 是否满足双调和方程
4
x4
24a
4
2 xy4 8c
4 y 4 24 e
代入:4 0
得 2a 4 8 c 2e4 0 3ac3e0
可见,对于函数:
a4 x b3 y x c2 y x 2 d3 x ey 4y
其待定系数,须满足下述关系才能作为应函数: 3ac3e0
l
l
x 6dy y 0 xy 0
h
图示梁对应的边界条件:
yh: 2
y 0,xy0
M min3dh
2
M x
xl: x6d,yxy0 1 max3dh y
h
2
可见: dy3 —— 对应于矩形截面梁的纯弯曲问题应力分布。
常数 d 与弯矩 M 的关系: h
由梁端部的边界条件:
(1n3dh
h 2
M
是精确的。
x
(2) 若按其它形式分布,如:
则此结果不精确,有误差;
1 max3dh y
h
弹性力学课件chapter7-(1-5)

16
应用弹性力学
APPLIED ELASTO-PLASTICITY OF SOLIDS
〈2〉位移分量: 由几何方程:
r ur
r
ur 1 u
r r
r 1 ur u u 0
r r r
积分: ur 1 [(1 ) A (1 3 )Br
7-2 轴对称问题
对轴对称问题,应力,应变和位移分量都不随 而变。 1. 应力函数 : <1>由于轴对称, = (r),与 无关
<2>相容方程为:
2 (
1 )2 0 即
d2 (
1 d )2 0
r 2 r r
dr 2 r dr
展开:( d 4 2 d 3
r 2
r r r 2 2
2 sin
c
os
(
1 r2
1 r
2 )
r
于是有:
2 2
2 1 1
2
x2 y 2 r 2 r r r 2 2
2
相容方程: ▽2▽=0
表达成:
2 ( r 2
1 r
r
1 r2
2 2 2 )( r 2
<3> 物理方程:
(平面应力)
APPLIED ELASTO-PLASTICITY OF SOLIDS
r 1 (r )
1 ( r)
r 2(1 ) r
对平面应变问题:
以 E 代替E,
1 2
以 代替 。
3.极坐标系下的应力函数与相容方程: <1> 以极坐标表示的变形协调方程: 10. 坐标系间的变换关系:
弹性力学 第四章

(τ ρϕ ) ρ =R = 0 (σ ρ ) ρ = R = −q2
上面的两个边界条件是自然满足的。 上面的两个边界条件是自然满足的。 下面的两个边界条件只能确定两个常数。 下面的两个边界条件只能确定两个常数。 由多连体的位移单值条件,可以确定 。(P63) 由多连体的位移单值条件,可以确定B=0。( 。( 于是由下面的两个边界条件得: 于是由下面的两个边界条件得:
γ ρϕ
仅有切向位移时: 仅有切向位移时:
ερ = 0
α=
∂uϕ ∂ϕ
1 ∂uϕ εϕ = ρ ∂ϕ
β =−
∂uϕ ∂ρ
uϕ
ρ
uρ
γ ρϕ = α + β =
于是
−
ρ
ερ =
∂u ρ ∂ρ
1 ∂uϕ εϕ = + ρ ρ ∂ϕ uρ
γ ρϕ
1 ∂u ρ ∂uϕ u ρ − = + ρ ∂ϕ ∂ρ ρ
σρ =
ρ
1+
q
r2
1−
r R2
σϕ =
ρ2
2
R远大于 ,得 远大于r, 远大于
σ ρ = (1 −
r2
r 1− 2 R
q
ρ
2
)q
σ ϕ = (1 +
r2
ρ
2
)q
τ ρϕ = τ ϕρ = 0
应力分量: 应力分量:
σx = q
σ y = −q
τ xy = 0
外环边界条件: 外环边界条件:
(σ ρ ) ρ = R = q cos 2 ϕ − q sin 2 ϕ = q cos 2ϕ
A
ρ
2
+ B(1 + 2 ln ρ ) + 2C + B(3 + 2 ln ρ ) + 2C
工程弹塑性力学课件:第七章极坐标解答

Φ f (ρ)cos 2φ.
(d)
代入相容方程,
d4 f 2 d3 f 9 d2 f 9 d f cos2φ[ d ρ4 ρ d ρ3 ρ2 d ρ2 ρ3 d ρ ]0,
双向受拉压
除去 cos2φ ,为欧拉方程,得解
f
( ρ)
Aρ4
Bρ2
C
D ρ2
.
(e)
由式 (d),(e) 得 Φ ,并求出应力。
PA线应变
0,(略去高阶小量).
PB线应变
εφ
PB PB PB
(u
φ
uφ φ
dφ)
u
ρdφ
1 ρ
uφ φ
;
PA转角
α
DA
uφ ρ
d
ρ
uφ
,
PA d ρ ρ
几何方程
PB转角 变形前切线 OP,变形后切线 OP,
POP u .
(使直角扩大,为负值)
切应变为
u
u 。
几何方程
3.当 u和ρ 同uφ时存在时,几何方程为
平衡条件
平衡条件: 应用假定:(1)连续性,(2)小变形。
考虑通过微分体形心 C 的 , 向及矩的平
衡,列出3个平衡条件:
F 0, F 0, M c 0。
Fρ 0--通过形心C的 ρ向合力为0,
(
)(
d )d
d
(
d)d sin
d
2
d
sin
d
2
(
d)d cos
换,
E
1
E
2
,
。 1
边界条件
边界条件--应用极坐标时,弹性体的 边界面通常均为坐标面,即:
弹性力学--平面问题的极坐标解答2
(a2) )
uρ 1 ∂uϕ ∂uρ 1 ∂uρ ∂uϕ uϕ εϕ = + γρϕ = + − = 0 ερ = ρ ρ ∂ϕ ∂ρ ρ ∂ϕ ∂ρ ρ
(a3) )
1 ∂uρ ∂uϕ uϕ γρϕ = + − ρ ∂ϕ ∂ρ ρ
积分式(a)中的第一式,有 积分式( )中的第一式,
1 A uρ = −(1+µ) +2(1−µ)Bρ(ln ρ −1 +(1−3µ)Bρ ) E ρ +2(1−µ)Cρ] + f (ϕ)
o
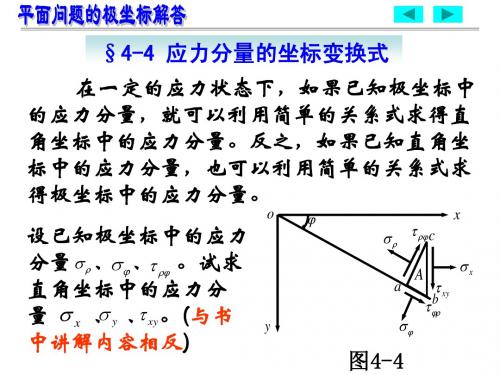
设已知极坐标中的应力 分量 σ ρ 、 ϕ 、 ρϕ 。试求 σ τ 直角坐标中的应力分 σ τ 量 σ x 、y 、xy 。(与书 中讲解内容相反) 中讲解内容相反)
ϕ
σ ρ τ ρϕ c
a
x
A
y
σϕ
b τϕρ
τ xy
σx
图4 - 4
如图4-4,在弹性体中取微小三角板 , 如图 ,在弹性体中取微小三角板A, 各边上的应力如图所示。三角板的厚度取为 各边上的应力如图所示。 一个单位。 边的长度为ds, 边及ac 一个单位。令bc边的长度为 ,则ab边及 边的长度为 边及 边的长度分别为 ds sin ϕ 及 ds cos ϕ 。
A
y
另取微小三角板B 如图4-4, 另取微小三角板 ,如图 ,根据平衡条 得到: 件 ∑ Fy = 0 ,得到:
σϕ
b τ
τ xy
σx
ϕρ
σ y = σ ρ sin ϕ + σ ϕ cos ϕ + 2τ ρϕ sin ϕ cos ϕ
2 2
综合以上结果, 综合以上结果,得出应力分量由极坐标向直角坐 标的变换式为: 标的变换式为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r
r
r
2 r
r
f
fr 0
0
y
rd
B
方程说明:
(4-1)
d
Pr
x
(r dr)d
dr
fr f
A
r
r
r
C
r
r
r
d
r
r
dr dr
两方程三个未知量,是一次超静定问题,须应用几何学和物
理学方面的条件才能求解。
弹性力学
平面问题的极坐标解答
7
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
)
r
平面问题的极坐标解答
(4-3) (4-4)
13
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
1 r
r
r
2 r
r
f
0 y
d
C
r
r
r
d
r
r
dr
弹性力学
平面问题的极坐标解答
6
一 极坐标中的平衡微分方程
M 0 r
r
O
—— 剪应力互等定理
于是,极坐标下的平衡方程为:
r
d r r
r
r
1
r
1 r
r r
F 0: d d cr d 2 o s d cr d 2 o s r r r d r r d d r
rrd r rd dsrid 2 n O
rdsrid n2 frdd r0
r
d r r
两边同除以 rdrd ,并略去高阶小量: rd B
弹性力学平面问题 的极坐标解答
弹性力学
平面问题的极坐标解答
1
第四章 平面问题的极坐标解答
本章要点
徐芝纶院士(1911-1999)
要点:
(1)极坐标中平面问题的基本方程: —— 平衡方程、几何方程、物理方程、 相容方程、边界条件。
(2)极坐标中平面问题的求解方法及应用
应用: 圆盘、圆环、厚壁圆筒、楔形 体、半无限平面体等的应力与 变形分析。
PB PB (r ur )d rd ur (c)
PB
rd
r
环向线段PB的转角:
弹性力学 1 tan 1
BB PP
(ur
ur
d ) ur
PB 平面问题的极坐标解答 rd
1 ur
r
(d)
9
二 极坐标中的几何方程与物理方程
径向线段PA的相对伸长:
ur
r1
r (a)
径向线段PA的转角:
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
弹性力学简明教程(第三版)
二 极坐标中的几何方程与物理方程
1. 几何方程
O
(1) 只有径向变形,无环向变形。
径向线段PA的相对伸长:
r1
ur
PA PA
PA
ur r
dr
ur
dr
AA PP
PA y
ur r
(a)
ur
d
r
P
ur
B
B
ur d
x
dr ur
A
P
A
1
(r ur )d
ur r
dr
径向线段PA的转角: 1 0 (b)
线段PB的相对伸长: 1
1 0
(b)
环向线段PB的相对伸长:
1
ur r
(c)
环向线段PB的转角:
O
d
r
P
ur
dr P
x
A
ur
ur r
dr
A
B
1
y
B
ur
ur
d
(r ur )d
剪应变为:
1
1 r
ur
(d)
r 1
1
1
1 r
ur
(e)
弹性力学
平面问题的极坐标解答
10
二 极坐标中的几何方程与物理方程
(2) 只有环向变形,无径向变形。O
弹性力学简明教程(第三版)
一 极坐标中的平衡微分方程
极坐标中的微元体
体力: fr , f
应力:
PA面 ,r
PB面 r , r
BC面
d
r
r
d
AC面
弹性力学
r
r
r
dr
r
r
r
dr
O
r
d r r
rd B
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
y
d
C
r
r
r
r
r
dr
d
应力正向规定:
r、θ的正面上,与坐标方向一致时为正;
平面r问、题θ的的极负坐标面解上答 ,与坐标方向相反时为正。4
一 极坐标中的平衡微分方程
考虑微元体平衡(厚度为1),将力投影到中心径向轴上:
Fr 0:
rrd
( r
r
r
dr)(r
dr)d
r dr
cos
d
2
( r
r
d )dr
cos
d
2
d
dr
sin
d
2
dr sin
d
2
f r rdrd
0
O
r
d r r
两边同除以 rdrd ,并略去高阶小量: rd B
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
r
r
1 r
r
r
r
fr
0
y
d
C
r
r
r
r
r
dr
d
弹性力学
平面问题的极坐标解答
5
一 极坐标中的平衡微分方程
将力投影到中心环向轴上:
u
1 r
u
(h)
剪应弹变性力为学:
r 2
2
2
u u 平面问题的极坐标解答 r r
(j)
11
二 极坐标中的几何方程与物理方程
(3)
Байду номын сангаас
总应变
r r1 r2
ur r
0
ur r
1
2
ur r
1 r
u
r r1 r 2
1 ur
r
u r
u r
r
ur r
ur r
1 r
u
(4-2)
r
弹性力学简明教程(第三版)
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
1 r
ur
u r
u r
—— 极坐标下的几何方程
弹性力学
平面问题的极坐标解答
12
二 极坐标中的几何方程与物理方程
2. 物理方程
平面应力情形:
平面应变情形:
弹性力学
r
1 E
( r
)
1 E
(
r )
r
1 G
r
2(1 E
)
r
r
1 2
E
( r
1
)
1 2
E
(
1
r
)
r
1 G
r
2(1 E
径向线段PA的相对伸长:
r2
PA PA PA
dr dr dr
0(f)
径向线段PA的转角:
y
2
u
u r
dr
u
dr
u r
(g)
d
B
B
x
r P dr
2
P
u
2
A
A u
u r
dr
u
u
d
环向线段PB的相对伸长:
2
PB PB PB
BB PP PB
环向线段PB的转角:
2
u r
u
(i)
u d rd
r
r
2 r
r
f
fr 0
0
y
rd
B
方程说明:
(4-1)
d
Pr
x
(r dr)d
dr
fr f
A
r
r
r
C
r
r
r
d
r
r
dr dr
两方程三个未知量,是一次超静定问题,须应用几何学和物
理学方面的条件才能求解。
弹性力学
平面问题的极坐标解答
7
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
)
r
平面问题的极坐标解答
(4-3) (4-4)
13
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
1 r
r
r
2 r
r
f
0 y
d
C
r
r
r
d
r
r
dr
弹性力学
平面问题的极坐标解答
6
一 极坐标中的平衡微分方程
M 0 r
r
O
—— 剪应力互等定理
于是,极坐标下的平衡方程为:
r
d r r
r
r
1
r
1 r
r r
F 0: d d cr d 2 o s d cr d 2 o s r r r d r r d d r
rrd r rd dsrid 2 n O
rdsrid n2 frdd r0
r
d r r
两边同除以 rdrd ,并略去高阶小量: rd B
弹性力学平面问题 的极坐标解答
弹性力学
平面问题的极坐标解答
1
第四章 平面问题的极坐标解答
本章要点
徐芝纶院士(1911-1999)
要点:
(1)极坐标中平面问题的基本方程: —— 平衡方程、几何方程、物理方程、 相容方程、边界条件。
(2)极坐标中平面问题的求解方法及应用
应用: 圆盘、圆环、厚壁圆筒、楔形 体、半无限平面体等的应力与 变形分析。
PB PB (r ur )d rd ur (c)
PB
rd
r
环向线段PB的转角:
弹性力学 1 tan 1
BB PP
(ur
ur
d ) ur
PB 平面问题的极坐标解答 rd
1 ur
r
(d)
9
二 极坐标中的几何方程与物理方程
径向线段PA的相对伸长:
ur
r1
r (a)
径向线段PA的转角:
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
弹性力学简明教程(第三版)
二 极坐标中的几何方程与物理方程
1. 几何方程
O
(1) 只有径向变形,无环向变形。
径向线段PA的相对伸长:
r1
ur
PA PA
PA
ur r
dr
ur
dr
AA PP
PA y
ur r
(a)
ur
d
r
P
ur
B
B
ur d
x
dr ur
A
P
A
1
(r ur )d
ur r
dr
径向线段PA的转角: 1 0 (b)
线段PB的相对伸长: 1
1 0
(b)
环向线段PB的相对伸长:
1
ur r
(c)
环向线段PB的转角:
O
d
r
P
ur
dr P
x
A
ur
ur r
dr
A
B
1
y
B
ur
ur
d
(r ur )d
剪应变为:
1
1 r
ur
(d)
r 1
1
1
1 r
ur
(e)
弹性力学
平面问题的极坐标解答
10
二 极坐标中的几何方程与物理方程
(2) 只有环向变形,无径向变形。O
弹性力学简明教程(第三版)
一 极坐标中的平衡微分方程
极坐标中的微元体
体力: fr , f
应力:
PA面 ,r
PB面 r , r
BC面
d
r
r
d
AC面
弹性力学
r
r
r
dr
r
r
r
dr
O
r
d r r
rd B
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
y
d
C
r
r
r
r
r
dr
d
应力正向规定:
r、θ的正面上,与坐标方向一致时为正;
平面r问、题θ的的极负坐标面解上答 ,与坐标方向相反时为正。4
一 极坐标中的平衡微分方程
考虑微元体平衡(厚度为1),将力投影到中心径向轴上:
Fr 0:
rrd
( r
r
r
dr)(r
dr)d
r dr
cos
d
2
( r
r
d )dr
cos
d
2
d
dr
sin
d
2
dr sin
d
2
f r rdrd
0
O
r
d r r
两边同除以 rdrd ,并略去高阶小量: rd B
Pr
x
(r dr)d
dr
fr f
A
r
r
r
dr
r
r
1 r
r
r
r
fr
0
y
d
C
r
r
r
r
r
dr
d
弹性力学
平面问题的极坐标解答
5
一 极坐标中的平衡微分方程
将力投影到中心环向轴上:
u
1 r
u
(h)
剪应弹变性力为学:
r 2
2
2
u u 平面问题的极坐标解答 r r
(j)
11
二 极坐标中的几何方程与物理方程
(3)
Байду номын сангаас
总应变
r r1 r2
ur r
0
ur r
1
2
ur r
1 r
u
r r1 r 2
1 ur
r
u r
u r
r
ur r
ur r
1 r
u
(4-2)
r
弹性力学简明教程(第三版)
第四章 平面问题的极坐标解答
内容提要
徐芝纶院士(1911-1999)
一、极坐标中的平衡微分方程 二、极坐标中的几何方程与物理方程 三、极坐标中的应力函数与相容方程 四、应力分量的坐标变换式 五、轴对称应力与相应的位移 六、圆环或圆筒受均布压力 七、压力隧洞 八、圆孔的孔边应力集中 九、半平面体在边界上受集中力 十、半平面体在边界上受分布力
1 r
ur
u r
u r
—— 极坐标下的几何方程
弹性力学
平面问题的极坐标解答
12
二 极坐标中的几何方程与物理方程
2. 物理方程
平面应力情形:
平面应变情形:
弹性力学
r
1 E
( r
)
1 E
(
r )
r
1 G
r
2(1 E
)
r
r
1 2
E
( r
1
)
1 2
E
(
1
r
)
r
1 G
r
2(1 E
径向线段PA的相对伸长:
r2
PA PA PA
dr dr dr
0(f)
径向线段PA的转角:
y
2
u
u r
dr
u
dr
u r
(g)
d
B
B
x
r P dr
2
P
u
2
A
A u
u r
dr
u
u
d
环向线段PB的相对伸长:
2
PB PB PB
BB PP PB
环向线段PB的转角:
2
u r
u
(i)
u d rd
