组合图形的面积练习题
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
五年级组合图形的面积精选32题
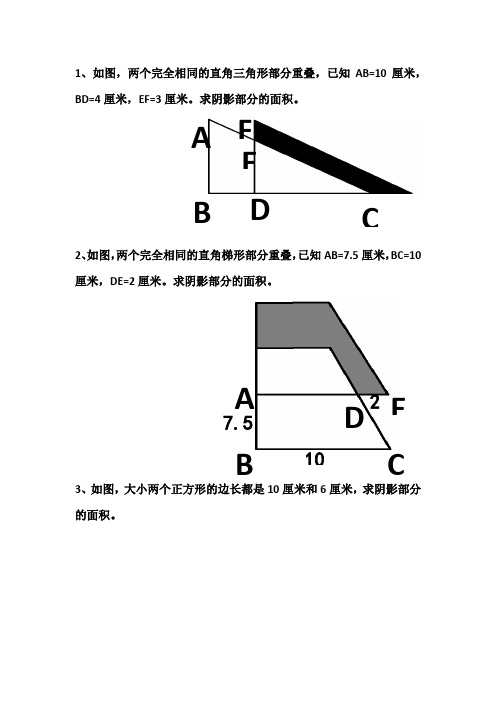
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
六年级数学组合图形的面积试题答案及解析

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少?【答案】18【解析】图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).2.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.3.如图,平行四边形,,,,,平行四边形的面积是,求平行四边形与四边形的面积比.【答案】1/18【解析】连接、.根据共角定理∵在和中,与互补,∴.又,所以.同理可得,,.所以.所以.4.如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.5.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.6.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.7.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).8.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.9.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.10.如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).11.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.12.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.15.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少.【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.16.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.17.在长方形内部有一点,形成等腰的面积为16,等腰的面积占长方形面积的,那么阴影的面积是多少?【答案】3.5【解析】先算出长方形面积,再用其一半减去的面积(长方形面积的),再减去的面积,即可求出的面积.根据模型可知,所以,又与的面积相等,它们的面积和等于长方形面积的一半,所以的面积等于长方形面积的,所以.18.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.19.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.20.如图,长方形的面积是36,是的三等分点,,求阴影部分的面积.【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.。
(完整版)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题1:一个等腰直角三角形,最长的边是10 厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12 厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的 2 倍。
求中间长方形的面积。
2:求右面平行四边形的周长。
5412巩固练习2】:求右面三角形的AB上的高典型例题3:求右图等腰直角三角形中阴影部分的面积。
单位:厘米)10巩固练习3】:求四边形ABCD的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和 6 厘米,求阴影部分的面积。
【巩固练习5】:图中两个正方形的边长分别是阴影部分的面积。
巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7 厘米,求正方形EFGH的面积A下两个3、求下图长方形ABCD的面积(单位:厘米)4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?A【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)例2 】下图中甲和乙都是正方形,求阴影部分的面积。
单位:厘米)【练一练】平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长8厘米,已知阴影部分的面积比三角形EFG 的面积大10 平方厘米。
求CF 的长。
【例4】两条对角线把梯形ABCD 分割成四个三角形。
组合图形的面积练习题5道

组合图形的面积练习题5道2、求下面图形的面积。
你能想出几种方法。
、求下面图形的面积。
2、计算下面图形中阴影部分的面积。
30dm25dmm七、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
8dm16cm8dm②已知S平=48dm2,求S阴。
④求S阴。
312cm三、“实践操作”显身手:10分16cm2、求下面图形的面积。
组合图形面积计算练习姓名:1、计算下列组合图形的面积2、求下列阴影部分的面积。
③已知:阴影部分的面积为24平方厘米,求梯形的面积。
12cm②已知S平=48dm2,求S阴。
dm ④求S阴。
dm组合图形面积计算练习姓名:1、求下面各图形的面积。
3、求下面图形的面积。
16cm4、已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
5、计算右边图形的面积。
发展题:如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
组合图形的面积如图,ABCD是直角梯形,求阴影部分的面积和。
下图1的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
下图2中,边长为10和15的两个正方体并放在一起,求三角形ABC的面积。
下图3中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
下图1中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
下图2中三角形ABC面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影的面积。
下图3中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
下图1求四边形ABCD的面积。
下图2已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
下图3图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
下图4中两个完全一样的三角形重叠在一起,求阴影部分的面积。
下图1中,甲三角形的面积比乙三角形的面积大多少平方厘米?下图2中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?如下图3,正方形ABCD 中,AB=4厘米,EC=10厘米,求阴影部分的面积。
组合图形的面积小学奥数专题
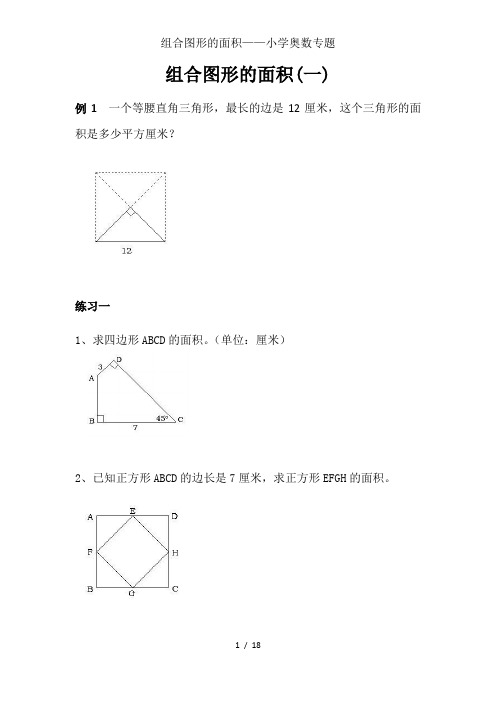
组合图形的面积(一)例1一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习一1、求四边形ABCD的面积。
(单位:厘米)2、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
例2正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习二1、已知大正方形的边长是12厘米,求中间最小正方形的面积。
2、如下图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
例3四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习三1、图中两个正方形的边长分别是6厘米和4厘米,求阴影部分面积。
2、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
3、下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?例4下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习四1、如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
2、在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)3、图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
例5图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
练习五1、如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。
求AH长多少厘米?2,图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影部分的面积。
五年级数学组合图形的面积试题
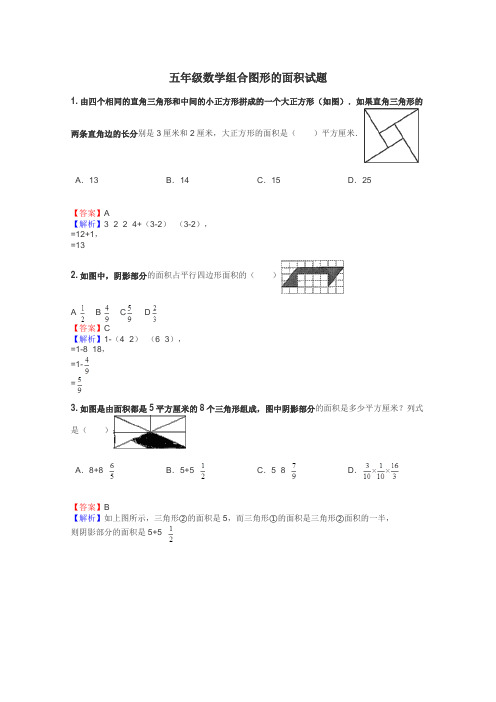
五年级数学组合图形的面积试题1.由四个相同的直角三角形和中间的小正方形拼成的一个大正方形(如图).如果直角三角形的两条直角边的长分别是3厘米和2厘米,大正方形的面积是()平方厘米.A.13B.14C.15D.25【答案】A【解析】3×2÷2×4+(3-2)×(3-2),=12+1,=132.如图中,阴影部分的面积占平行四边形面积的()A B C D【答案】C【解析】1-(4×2)÷(6×3),=1-8÷18,=1-=3.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是()A.8+8×B.5+5×C.5×8×D.【答案】B【解析】如上图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×4.下列图形的面积是()A.800B.700C.750D.600【答案】A【解析】观察图形可知,这个图形的面积等于上面的三角形的面积与下面的平行四边形的面积之和,据此利用三角形和平行四边形的面积公式计算即可解答问题。
32×10÷2+32×20=160+640=8005.图中图形的面积最大的是()A.A B.B C.C【答案】B【解析】设三个图形的高都是h,则:三角形的面积=12h÷2=6h;平行四边形的面积=7h;梯形的面积=(8+3)h÷2=5.5h;7h>6h>5.5h,所以平行四边形的面积最大。
6.用同一条铁丝围成下列图形,围成的图形()的面积最大。
A.圆 B.长方形 C.正方形【答案】A【解析】假设铁丝的长度为12.56分米,则围成的正方形的边长是:12.56÷4=3.14(分米),正方形的面积是:3.14×3.14=9.8596(平方分米);长方形的长和宽的和是:12.56÷2=6.28(分米),长和宽越接近面积越大,若长可为3.15分米,宽为3.13分米,长方形的面积是:3.15×3.13=9.8595(平方分米);圆的半径是:12.56÷2÷3.14=2(分米),圆的面积是:3.14×22=12.56(平方分米);9.8595<9.8596<12.56;所以围成的圆的面积最大。
新青岛版小学数学五年级上册组合图形的面积计算 练习题

新青岛版小学数学五年级上册组合图形的面积计算练习题组合图形的面积计算练题1.填表图形名称 | 长方形 | 正方形 | 平行四边形 | 三角形 | 梯形 |面积公式(文字) | 底乘高 | 边长的平方 | 底乘高 | 底乘高除以二 | 上底加下底乘高除以二 |面积公式(字母) | $A=ab$ | $A=a^2$ | $A=bh$ |$A=\frac{1}{2}bh$ | $A=\frac{(a+b)h}{2}$ |2.求下面图形的面积(单位:m)。
你能想出几种方法?长方形:$A=5\times2=10\text{ }m^2$正方形:$A=3^2=9\text{ }m^2$平行四边形:$A=6\times5=30\text{ }m^2$三角形:$A=\frac{1}{2}\times4\times8=16\text{ }m^2$ 梯形:$A=\frac{(3+7)\times4}{2}=20\text{ }m^2$3.计算下面图形中阴影部分的面积。
先求整个图形的面积,再减去未阴影部分的面积:A=30\times12.5=375\text{ }dm^2$未阴影部分的面积为:A=25\times12.5=312.5\text{ }dm^2$阴影部分的面积为:A=375-312.5=62.5\text{ }dm^2$7.求下列阴影部分的面积。
①先求整个图形的面积,再减去未阴影部分的面积:A=8.13+0.16+3=11.29\text{ }dm^2$未阴影部分的面积为:A=8.13\text{ }dm^2$阴影部分的面积为:A=11.29-8.13=3.16\text{ }dm^2$②已知$S_{平}=48\text{ }dm^2$,求$S_{阴}$。
由于图形是对称的,阴影部分的面积等于未阴影部分的面积,因此:S_{阴}=S_{平}=48\text{ }dm^2$③已知:阴影部分的面积为$24\text{ }cm^2$,求梯形的面积。
五年级数学上册《组合图形的面积》测试卷及答案-北师大版

五年级数学上册《组合图形的面积》测试卷及答案-北师大版一.选择题(共8小题)1.如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比()A.甲的面积大B.乙的面积大C.相等2.点A是长方形内任意一点,阴影部分的总面积与空白部分总面积比较,哪个的面积较大?A.阴影部分面积大B.空白部分面积大C.一样大D.无法确定3.图中每个小方格的面积是1cm2.请你估计一下,这个脚印的面积约是()A.45B.35C.254.下面图形中涂色部分面积与其它不同的一个是()5.中心广场的占地面积约为5公顷,()个中心广场的面积约为1平方千米.A.2 B.20 C.2006.丫丫家的面积有110平方分米.她家所在的小区有300平方千米.丫丫最喜欢楼下的游乐场了,它有10公顷那么大呢.这段话里有()处错误.A.1 B.2 C.37.“6平方千米〇601公顷”,比较大小,在〇里应填的符号是()A.>B.<C.=D.×8.如图:树叶的面积约是()(每个小方格的面积是1cm2)A.15cm2~25cm2B.35cm2~45cm2C.55cm2~65cm2二.填空题(共8小题)9.如图是一个不规则的土地,估测一下,它的面积大约是平方米.10.如图,平行四边形中,阴影部分的面积是36.5dm2,平行四边形的面积是平方分米.11.右图平行四边形的面积是25平方厘米,阴影部分的面积是平方厘米.12.如果1平方米能站9人,那么1公顷能站人,1平方千米能站人.13.260000000平方米=公顷=平方千米800平方千米=公顷=平方米14.如下图所示,平行四边形的面积是28cm2,阴影部分的面积是cm2.15.如图中这片树叶的面积约是cm2.16.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)17.200个50平方米的教室面积是1公顷.(判断对错)18.100个1角的硬币大约重1千克.(判断对错)19.一张床的周长估计是2米.(判断对错)20.计算的面积,只能把它分成一个正方形和一个三角形来计算.(判断对错)21.如图中阴影部分的面积是14平方厘米.(判断对错)四.计算题(共2小题)22.求下面组合图形的面积.(单位:dm)23.如图,阴影部分是两个正方形,周长分别为12厘米和32厘米.求空白部分的总面积是多少平方厘米?五.操作题(共2小题)24.先估计下面图形的面积,再用1平方厘米的正方形学具量一量,填在括号里.25.分割组合图形(不计算):你有哪几种分割方法便于计算其面积,请画出分割示意图.六.应用题(共6小题)26.某街心广场有一块地(如图所示),李叔叔要在这块地上铺满草坪.(1)他需要购买多少平方米草皮?(2)如果每平方米草皮需要68元,请你估计一下,李叔叔要带多少元钱才能一次性把草皮买够?请写出你的估计过程.27.王大伯从平行四边形菜地中划出一块三角形地种西红柿,其余地方种黄瓜(如图),这块黄瓜地的面积是多少平方米?28.一个果园形状如图,一棵果树占地5m2,这个果园一共可以种多少棵树?29.李阿姨家有一块菜地,(如图)这块菜地的面积有多少平方米?30.王村有一块梯形果园,村里进行道路规划时,有一条公路穿过了这个果园.这个果园的实际面积是多少平方米?31.下面三个大正方形的边长都是32厘米,先计算每个正方形中一个小方格的面积,再估计出荷叶的面积.你觉得哪幅图估计得最接近实际面积?参考答案一.选择题(共8小题)1.解:两个阴影三角形的底等于正方形的边长,三角形的高也等于正方形的边长,因此两个三角形等底等高,所以面积相等;故选:C.2.解:阴影部分两个三角形的高等于长方形宽,底等于长方形的长,空白部分两个三角形的高等于长方形的长,底等于长方形的宽,所以阴影部分的面积与空白部分的面积相等。
小学五年级数学组合图形的面积试题及答案

小学五年级数学组合图形的面积试题及答案集团档案编码:[YTTR-YTPT28-YTNTL98-UYTYNN08]五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷212×3÷2=20×8.5÷2=36÷2=170÷2=18(cm2)=85(cm2)图形面积=梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+正方形面积(2×2)图形面积=长方形面积-梯形面积6×(5-2)+2×210×6–[(3+6)×2÷2]=6×3+4=60-[9×2÷2]=18+4=60-9=22(m2)=51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高=49÷(6+8)×2直角三角形面积=6×7÷2=49÷14×2=42÷2=3.5×2=21(dm2)=7(dm2)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2=45÷12×2=17×7.5÷2=3.75×2=127.5÷2=7.5(cm2)=63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75-45=18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2=40÷10×2=16×8÷2=4×2=128÷2=8(m2)=64(m2)空白部分面积=梯形面积–阴影部分面积:64–40=24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
(完整版)《组合图形的面积》练习题(含答案)

(完整版)《组合图形的面积》练习题(含答
案)
-CAL-FENGHAI.-(YICAI)-Company One1
组合图形的面积
测试题
1、下面的图形是由两个三角形组成的,请画出这两个三角形。
A
B D
C
2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm
8dm
3、求下面个图形的面积、(单位:分米)
(1)(2) 14
8
6 6
12
3 6
12
(3)(4) 8
2.5
5.4 4 1.5
4.2 6
3
4、如图所示,梯形的周长是52厘米,求阴影部分的面积。
16
5、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)
6 2
2
5
6、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)
7
7
22
7、有一块土地如图所示,你能用几种方法求出它的面积(
单位:米)
12
15
8
22
7、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?
B
A
8米
【参考答案】。
五年级组合图形的面积精选32题

1、如图,两个完全相同的直角三角形部分重叠,已知
AB=10厘米,
BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分的面积。
A B C
D E
F A
D
E B C
107.52
4、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分
的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?
A
B
C D E F
A
B C D F E G。
组合图形的面积小学奥数专题e
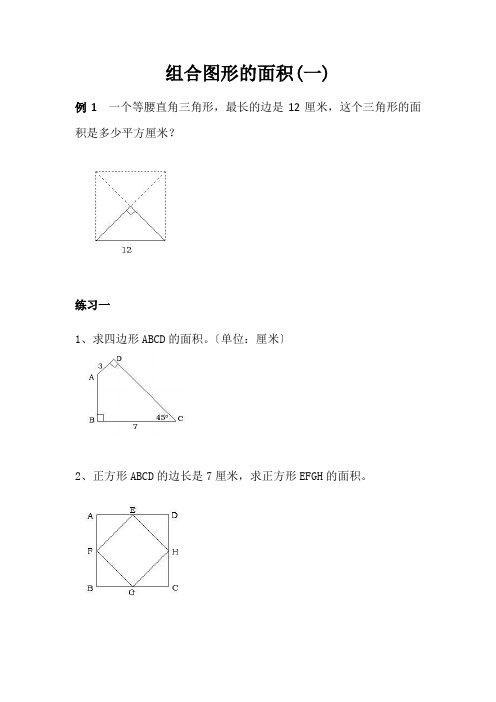
组合图形的面积(一)例1一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习一1、求四边形ABCD的面积。
〔单位:厘米〕2、正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
例2正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习二1、大正方形的边长是12厘米,求中间最小正方形的面积。
2、如下列图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3、求下列图长方形ABCD的面积〔单位:厘米〕。
例3四边形ABCD和四边形DEFG都是正方形,三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习三1、图中两个正方形的边长分别是6厘米和4厘米,求阴影局部面积。
2、下列图中两个完全一样的三角形重叠在一起,求阴影局部的面积。
3、下列图中,甲三角形的面积比乙三角形的面积大多少平方厘米?例4下列图中正方形的边长为8厘米,CE为20厘米,梯形BCDF 的面积是多少平方厘米?练习四1、如下列图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影局部的面积。
2、在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?〔单位:厘米〕3、图中BC=10厘米,EC=8厘米,且阴影局部面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
例5图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
练习五1、如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影局部面积比三角形ADH的面积大8平方厘米。
求AH长多少厘米?2,图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影局部的面积。
(原创)人教版五年级上册组合图形的面积专项练习含参考答案

组合图形的面积1一、图形计算题(每题分,计分)1.计算下面组合图形的面积。
(单位:cm)2.计算如图所示各图中阴影部分的面积.3.如图,梯形的面积为40cm 2,求阴影部分的面积.4.求下面阴影部分的面积。
(单位:m)5.求下面图形中阴影部分的面积。
(单位:厘米)6.计算组合图形的面积。
(单位:cm)7.计算下面组合图形的面积。
(单位:cm)8.右图所示,梯形的面积是90cm2,上底是12cm,下底是18cm,求阴影部分的面积。
9.求下列图形的面积.(每个小方格的边长表示1cm)______cm2______cm2二、解答题(每题分,计分)10.下面是一幢楼房占地的平面图,算一算它的占地面积有多大?(单位:m)11.下图阴影部分是实验小学门前的一个花坛,你能算出这个花坛占地多少平方米吗?(单位:m)12.张爷爷家有一块平行四边形菜地,地的底长80米,高是50米,张爷爷准备在地中间修一条宽3米的路,修完路后,这块地实际种菜面积是多少平方米?13.王大伯家有一块梯形的菜地,中间有一个三角形的水池(单位:米),这块菜地种菜的面积是多少平方米? 14.一块玉米地的形状如图(单位:米)。
它的面积是多少平方米。
15.少先队大队部做了两个标语牌(如下图),请算出它们各用了多少铁板?(单位:m)16.求下图阴影部分(平行四边形)的面积。
17.如图是一种边长为4dm的正方形地板砖,图中阴影部分是地板砖上的花纹,A. B. C. D是各边中点,请你求出花纹部分的面积.18.如图,长方形的长是8,宽是6,A和B是宽的中点,求长方形内阴影部分的面积.参考答案:一、计算题(每题分,计分)1.(35+45)×15÷2+45×14÷2=600+315=915(cm2)(8+14)×6÷2+14×7=66+98=164(cm2)2. (1)(9+14)×10÷2-9×10÷2,=23×10÷2-9×10÷2,=115-45,=70(cm2),答:阴影部分面积是70cm2(2)(5+10)×12÷2-5×12÷2,=15×12÷2-5×12÷2,=90-30,=60(cm2),3. 40×2÷4-8,=80÷4-8,=20-8,=12(厘米),12×4÷2=24(平方厘米);答:阴影部分的面积是24平方厘米.4.(1)8×10÷2=40(m2)(2)52×28-(20+30)×10÷2=1206( m2)5. 300cm26. 5×3.6-5×1.4÷2=18-3.5=14.5(cm2)20×16-(3+9)×5÷2=320一30=290(cm2)7.(1)10×15÷2+(10+15)×12÷2=225(cm2)(2)(10+14)×6÷2=72(cm2)14×8=112(cm2)72+112=184 (cm2)(3)2.4×6÷2=7.2(cm2)5×6-7.2=22.8(cm2)8.36cm29.①画图表示如下:(2+3)×3÷2+(2+3)×1÷2×2,=7.5+5,=12.5(平方厘米);②4×2+(1+3)×1÷2,=8+2,=10(平方厘米);故答案为:12.5,10.二、解答题(每题分,计分)10. 30×48+(48+72)×(60-30)÷2=1440+1800=3240(m2)答:它的占地面积有3240平方米。
求组合图形面积专项练习30题 不含曲线图形(有答案)ok
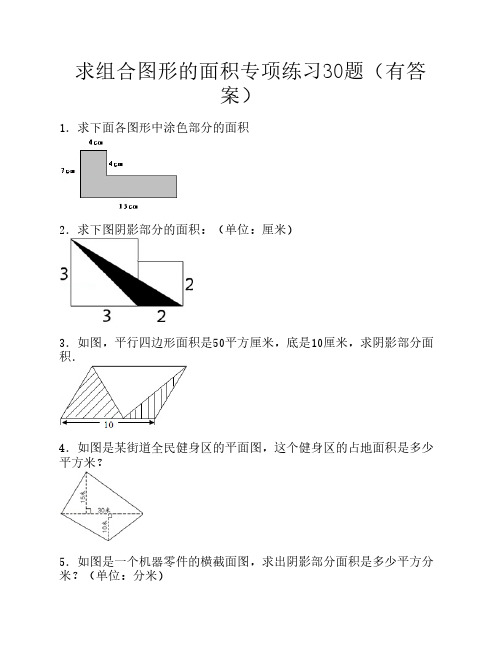
求组合图形的面积专项练习30题(有答案) 1.求下面各图形中涂色部分的面积2.求下图阴影部分的面积:(单位:厘米)3.如图,平行四边形面积是50平方厘米,底是10厘米,求阴影部分面积.4.如图是某街道全民健身区的平面图,这个健身区的占地面积是多少平方米?5.如图是一个机器零件的横截面图,求出阴影部分面积是多少平方分米?(单位:分米)6.求阴影部分的面积(单位:厘米)7.计算图中阴影部分的面积.(单位:厘米)8.图中梯形的面积是144cm2,求阴影部分的面积.9.边长分别为3厘米与5厘米的两个正方形拼在一起(如图).求阴影部分的面积?10.一块长方形草地,长方形的长是15米,宽是10米,中间铺了一条石子路(如图).那么草地部分面积有多大?11.求如图中阴影部分的面积(单位:分米)12.求如图阴影部分的面积(单位:厘米)13.求组合图形的面积.(在图中标出割补方法后再计算).14.如图中平行四边形的面积是90平方分米.求阴影部分的面积.15.如图是一块长方形草坪,长是16米,宽是10米,中间有两条小路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?(单位:米)16.计算阴影部分面积(单位:厘米).17.图中三个正方形的边长分别是4厘米、6厘米、5厘米.求涂色部分的面积.18.计算图形中阴影部分的面积.(单位:厘米)19.火车站广场长95米,宽80米.中间留下边长12米的正方形花坛,其余都铺彩色地砖.彩色地砖铺了多少平方米?20.下面梯形中空白部分的面积是25平方厘米,求梯形的面积.21.图中阴影部分的面积是多少?22.如图,一个正方形中套着一个长方形,已知正方形的边长是16分米,长方形的四个角的顶点恰好把正方形四条边都分成两段,其中长的一段是短的3倍.阴影部分的面积是多少?23.求图中阴影部分的面积24.如图,正方形ABCD的面积为1,M是AD边上的中点,求图中阴影部分的面积.25.如图,梯形ABCD的面积是35平方厘米,AE=ED,图中三角形甲、乙、丙的面积相等,求阴影部分的面积.26.如图,在长方形ABCD中,AB=6厘米,BE=8厘米,EC=2厘米,F是DE 的中点.求四边形ABFD(阴影部分)的面积是多少平方厘米?27.图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积.28.求图形阴影部分的面积29.已知△ABC和△DEF是两个完全相等的直角三角形,根据图中所标数据,求图中阴影部分的面积(单位:厘米)30.求图中阴影部分的面积.参考答案:1.如图,4×4+15×(7﹣4)=16+45=61(平方厘米);答:涂色部分的面积是61平方厘米.2.2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.3. 如图:平行四边形ABDC与三角形ABF等底等高,所以三角形ABF的面积是平行四边形ABDC的面积的一半,所以阴影部分的面积是平行四边形ABDC面积的一半.50÷2=25(平方厘米),答:阴影部分的面积是25平方厘米4.30×15÷2+30×10÷2=225+150=375(平方米);答:这个健身区的占地面积是375平方米5.10×10﹣(5+10)×5÷2=100﹣37.5=62.5(平方分米),答:阴影部分面积是62.5平方分米 6.4.5×4.5+8.2×8.2﹣(4.5+8.2)×4.5÷2=20.25+67.24﹣28.575=58.915(平方厘米);答:阴影部分的面积是58.915平方厘米 7.4×8÷2=16(平方厘米);答:阴影部分的面积是16平方厘米8. 由题意可知:图形的面积已知,于是可以求出梯形的高,也就是阴影部分的高,从而利用三角形的面积公式即可求解144×2÷(8+12)=288÷20=14.4(厘米),8×14.4÷2=115.2÷2=57.6(平方厘米);答:阴影部分的面积是57.6平方厘米.9.由图意可知:阴影部分的面积就等于两个正方形的面积和减去两个空白三角形的面积,利用正方形和三角形的面积公式即可求解3×3+5×5﹣3×(3+5)÷2﹣5×5÷2=9+25﹣12﹣12.5=9.5(平方厘米);答:阴影部分的面积是9.5平方厘米 10. 由题意可知:草地部分的面积就等于长方形草地的面积减去小路的面积,长方形草地的面积可以利用长方形的面积公式求出,而小路是一个平行四边形,于是可以利用平行四边形的面积公式求出小路的面积,问题即可得解. 15×10﹣1×15=150﹣15=135(平方米);答:草地部分面积是135平方米.11.由题意可知:如图所示,阴影部分面积=平行四边形ABCD的面积﹣三角形ADE的面积,依据题目中的数据即可求解.4×7﹣4×(7﹣5)÷2=28﹣8÷2=28﹣4=24(平方分米);答:阴影部分的面积是24平方分米. 12.如图所示:阴影部分的面积=S△DBG+S△GBE,将已知数据分别代入此等量关系即可求解.阴影部分的面积:(20﹣10)×20÷2+10×(20﹣10)÷2=10×20÷2+10×10÷2=200÷2+100÷2=150(平方厘米);答:阴影部分的面积是150平方厘米13.画图如下:5×6+(5+10)×5÷2=30+37.5=67.5(平方厘米);答:组合图形的面积是67.5平方厘米 14. 观察图形可知:图中有平行四边形ADEF,长方形ABCF,等腰直角三角形ABD和CDG;而阴影部分是一个梯形:只要求出这个梯形的上下底CG、AB和高BC的长度即可解答问题.AB的长度是:90÷6=15(分米),则BD的长度也是15分米,因为BC=AF=6分米,所以CD=DG=15﹣6=9(分米),所以阴影部分的面积是:(9+15)×6÷2=24×3=72(平方分米);答:阴影部分的面积是72平方分米 15.由题意可知:求阴影部分的面积,实际上就是求长为(16﹣2)米,宽为(10﹣2)米的长方形的面积,利用长方形的面积公式即可求解(16﹣2)×(10﹣2)=14×8=112(平方米);答:阴影部分的面积是112平方米.16.如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.10×15﹣10×(15﹣7)÷2=150﹣40=110(平方厘米);答:阴影部分的面积是110平方厘米17.(5+4+6+5)×6÷2﹣5×(6﹣5)÷2﹣(4+6+5)×5÷2=60﹣2.5﹣37.5=20(平方厘米);答:阴影部分的面积是20平方厘米.18.(2+2.5)×2÷2=4.5(平方厘米);答:阴影部分的面积是4.5平方厘米. 19.95×80﹣12×12=7600﹣144=7456(平方米);答:彩色地砖铺了7456平方米20.25×2÷5=10(厘米),所以梯形的面积是(5+9)×10÷2=14×5=70(平方厘米),答:这个梯形的面积是70平方厘米 21.2×2×7=28(平方米);答:阴影部分的面积是28平方米 22.由题意可得:BC=CD=FG=HG=AB=AC=×16=4(厘米),AB=AH=EF=DE=AC=×16=12(厘米),所以长方形DBHF的面积是:16×16﹣4×4﹣12×12=196﹣16﹣144=36(平方厘米);答:长方形的面积是36平方厘米23.9×6÷2=27(平方厘米);答:图中阴影部分的面积是27平方厘米24.AM=MD,则AM=AD=BC,即AM:BC=1:2,则ME:BE=1:2,S△BAE=S△BAM,又因S△BAM=S正方形ABCD,则S△BAE=×S正方形ABCD=,而S△BAE=S△EMC,所以阴影部分的面积为:×2=;答:图中阴影部分的面积是25.因为AE=ED,又因为甲的面积=乙的面积,所以甲和乙一定等底等高,所以AD∥BF,又因为ABCD是梯形,所以AB∥CD,所以ABFD是平行四边形,所以阴影的面积=2个乙的面积,把梯形ABCD的面积分成5份,阴影占2份,所以阴影的面积=35÷5×2=14(平方厘米).答:阴影部分的面积是14平方厘米26.(8+2)×6﹣8×(6÷2)÷2﹣2×6÷2=60﹣12﹣6=42(平方厘米);答:阴影部分的面积是42平方厘米27.因为CE:AB=FE:FB=5:9,则FE=BE=×5=(厘米),所以阴影部分的面积=S△AFD+S△CDE=×(9﹣5)×5+×(9﹣5+)×9=10+=36(平方厘米);答:阴影部分的面积约是36平方厘米28.①(10+20)×12÷2﹣10×12÷2=180﹣60=120;②5×3÷2=15÷2=7.5;③5×5+4×4﹣(2+5)×(5+4)÷2=41﹣7×9÷2=41﹣31.5=9.5 29. [(25﹣5)+25]×15÷2=(20+25)×15÷2=45×15÷2=675÷2=337.5 (平方厘米);答:图中阴影部分的面积是337.5平方厘米30.如图所示,阴影部分的面积=S平行四边形ABCD﹣S△ABE,又因平行四边形的底和高分别为10和15,三角形ABE的底和高分别为10和(15﹣7),分别利用平行四边形和三角形的面积公式即可求解.10×15﹣10×(15﹣7)÷2,=150﹣40,=110;答:阴影部分的面积为110。
人教版五年级数学上册课后分层作业6.4组合图形的面积(附答案)

6.4组合图形的面积(同步练习)一、填空题1.如图,AC长10厘米,BD长6厘米,且AC垂直BD,那么四边形ABCD的面积为平方厘米。
2.如下图所示的直角三角形ABC中,AB=6厘米,BC=8厘米,AC=10厘米,正方形BFGE的边长为1厘米,则GD=( )厘米。
3.图是一个长方形,长为10厘米,宽为6厘米,则阴影部分面积为( )平方厘米.4.如图,平行四边形ABCD的边长BC为10厘米,直角三角形BCE的直角边EC为8厘米,已知阴影部分的面积比三角形EFG的面积大4.8平方厘米,则CF的长是( ) 厘米.5.街心花园有一个正方形的花坛,四周有一条宽1.5米的甬道(如图),如果甬道的面积是27平方米,那么中间的花坛面积是( )平方米.二、判断题6.用正八边形可以密铺。
( )7.计算组合图形的面积也要用到基本图形的面积公式。
( )8.估算一片树叶的面积,可以先在方格纸上描出叶子的轮廓,再根据叶子轮廓的形状转化成近似的规则平面图形进行计算。
( )9.如图,阴影甲的面积大于阴影乙的面积.( )三、选择题10.如下图所示,每个小正方形面积是1cm²,阴影部分的面积是()cm².A.5.5B.7.5C.8D.8.511.比较下图中甲、乙阴影部分的面积,结果是( ).A.甲>乙B.甲<乙C.甲=乙D.不确定12.下图中每个小正方形的面积表示1平方厘米,芳芳2岁时脚印(阴影部分)的面积可能是()平方厘米。
A.20~25B.35~38C.40~45D.50~5513.如图所示,每个小方格的面积是1平方厘米,则阴影部分的面积大约是()平方厘米。
A.5B.8C.6D.20四、解答题14.如图,梯形的下底为8厘米,高为4厘米.阴影部分的面积是多少平方厘米?15.两个长12厘米、宽8厘米的长方形(如图)摆放后,组合图形的面积是多少?16.李叔叔准备在这块地里种郁金香(如图),每棵郁金香占地0.25平方米,这块地大约可种多少棵郁金香?17.下图是房屋的一面墙。
人教版小学数学组合图形的面积 (经典例题含答案)

班级小组姓名成绩(满分120)一、组合图形的面积(一)组合图形的面积计算(共4小题,每题3分,共计12分)例1.求下面图形的面积。
(单位:cm)32×10÷2+32×203×4÷2+(5+10)×5÷210×12-(4+8)×2÷2=160+640=6+37.5=120-12=800(cm²)=43.5(cm²)=108(cm²)例1.变式1.先回答问题,再计算图形的面积。
(单位:cm)(1)组合图形的面积=(长方形)面积+(三角形)面积36×24+24×21÷2=1116(平方厘米)(2)52阴影部分的面积=(梯形)面积-(三角形)面积(30+52)×28÷2-30×28÷2=728(cm²)例1.变式2.计算下面图形的面积,你能用不同的计算方法吗?5×2.5+(3+5)×(5-2.5)÷2=5×2.5+8×2.5÷2=12.5+10=22.5(平方米)5×3+(2.5+5)×(5-3)÷2=5×3+7.5×2÷2=15+7.5=22.5(平方米)例1.变式3.如图,左边阴影部分的面积是60平方厘米。
求右边空白部分(梯形)的面积。
(单位:厘米)60×2÷8=15(厘米)(16+16+8)×15÷2=40×15÷2=300(平方厘米)答:空白部分的面积是300平方厘米.(二)组合图形的面积计算(共4小题,每题3分,共计12分)例2.计算下列组合图形的面积。
(单位:cm)(8.5+15)×13÷2-8.5×4÷2=135.75(cm²)例2.变式1.解决问题。
五年级数学 组合图形的面积 练习题(含答案)

人教版数学五年级上册6.4 组合图形的面积练习卷一、选择题1.如图,阴影部分的面积是16dm2,平行四边形的面积是()dm2.A.48B.32C.642.下图为一幅图形的密铺方案,则此影阴部分的面积与空白部分的面积比为()A.2∶1B.7∶9C.1∶1D.3∶43.如图,长方形ABCD中,AB=12厘米,BC=8厘米,平行四边形BCEF的一边BF 交CD于G,若梯形CEFG的面积为64平方厘米,则DG长为()A.3B.4C.5D.64.图中每个小方格的面积为1cm2,脚印的面积大约是()。
A.5cm2——50cm2B.10cm2——28cm2C.28cm2——50cm2 5.如下图,每个方格的面积为1平方厘米。
请你估一估,这个图案的面积约为()。
A.20平方厘米B.11平方厘米C.9平方厘米D.7平方厘米6.估计一下,下图不规则土地的面积约是()。
A.216m 36m B.224m C.2二、图形计算7.[多种思路求面积].你能计算出图中这个多边形的面积吗?8.计算下面图形的面积。
(单位:厘米)三、填空题9.如图,两个正方形的边长分别是6厘米、4厘米,阴影部分的面积是_____平方厘米。
10.如图,A是平行四边形BC边上的中点,阴影部分面积是2平方厘米,则平行四边形的面积是平方厘米.11.下图中,长方形长10厘米,宽6厘米,E为AB边上任一点,三角形EDC(即阴影部分)的面积是________平方厘米.12.如图,5个相同的小长方形拼成一个周长是88厘米的大长方形,那么大长方形的面积是_____平方厘米。
13.下图中每个小方格的面积表示21cm,估算一下,阴影部分的面积大约是( )2cm。
14.如图中三个正方形的边长分别为10,20,30,那么图中阴影部分的面积是.15.如图,大小两个正方形拼在一起,阴影部分面积为28平方厘米,小正方形边长为4厘米,则图中空白部分的面积是平方厘米.16.如图,四边形ABCD是一个梯形,由三个直角三角形拼成;它的面积是_____cm2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•5m •答:一共需要4255块砖
如图,有一面墙,粉刷这面墙每平方米需要 0.15 千克涂料,一共需要多少千克涂料?
•1.6m
•4m
•10m
• 4x10+1.6x10÷2 •=40+16÷2
•=40+8
•=48(㎡)
48x0.15=7.2(千克)
•20c m
• 20x26—4x4x4
•=520—16x4
•=520—64 •=456(c㎡) •答:这张硬纸还 剩下456 c㎡
•26c m
•下图是房屋的一堵墙,如果砌这面墙每平方 米用砖185块,一共需要多少块砖?
•它的面积 = 三角形的面积+长方形的面积.
•5×4+5×1.2÷2
•=20+3
组合图形的面积练习题
2020年7月12日星期日
•3cm •3cm
• 练一练 •分成两个长方形
•4cm •6cm
•4×3+3×7 •=12+21 •=33(cm2)
•7c m
• 练一练 •分割成一个长方形和一个正方 形
•4cm
•3cm •6c m
•7cm
•3cm
•4×6+3×3 •=24+9
•=33(cm2 )
•12 •4 •8 •4
•12
这是我们学校将要开辟的一块草坪 ,如下图。你能算出它的面积吗?
• 现在有两家公司联系,A公司说 种一平方米草要5元,B公司说种同样 的草一共需要2500元。如果让你决定 ,你会选择哪家公司?
•45cm •60cm
•45cm •60cm
•学校开运动会要制作一些锦旗,式样如图所示 。一面锦旗需要多少平方厘米的布料?
•4cm •6cm
•4cm
•6c m
•4cm •6cm
•3cm
•7cm
•7cm
•4cm •3cm •分割法
•7cm
•3cm •3cm
•6cm
•添补法
•7c
•练一练
•求下列图形的面积。 (单位:cm)
•12 •4
•12 •4 •8 •4
•12
•12 •4
•12 •4 •8 •4
•12
•12 •4
•答:一共需要7。2千克 涂料
•有一块菜地的形状如图所示。①这块地 的面积是多少?②如果每平方米需施肥 0.25kg,这块菜地共需施肥多少kg?
•40m
•36m
•24m •60m
•2.2dm
•求阴影部分的面积。
•4dm
思考 计算下面图形中阴影部分的面积
• (4+8)x4÷2 •=12x4÷2 •=48÷2 •=24(c㎡) •答:阴影部分面积是24c㎡
• 把两个梯形面积相加 •长方形的面积加上两个三角形的面积
•在一块梯形的地中间有一个长方形的游 泳池,其余的地方是草地。草地的面积
是多少平方米?
•40m
•15m
•30m
•30m •70m
•下图是一个零件的横截面, 计算它的面积
。
•54mm
•20mm
•10mm
•27m m
•30m m
•试一试: 如图,一张硬纸板剪下4个边长 是4厘米的小正方形后,可以做成一个没 有盖子的盒子.这张硬纸板还剩下多大的面 积?
• 练一练
•分割成两个梯形 •4cm
•3c m
•3c m
•3cm •6c m
•7cm
•(3+7)×3÷2+(3+6)×4÷2
பைடு நூலகம்
• 练一练
•分割成一个长方形和一个正方形
•4cm •3cm •6cm
•7cm
•3cm •3cm
•7×6-3×3
•=42-9
•=33(cm2 )
•3cm
•3cm •3c m
