直线与圆锥曲线
直线与圆锥曲线的位置关系 课件(62张)
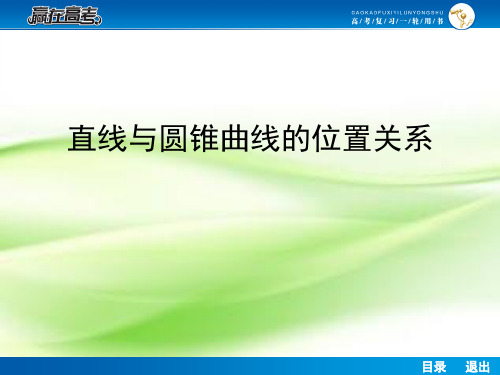
1-3 2 ≠ 0,
= (-6 2k)2 + 36(1-3 2 ) = 36(1- 2 ) > 0,
1
3
故 k2≠ 且 k 2<1.①
6 2k
-9
1-3
1-32
设 A(x1,y1),B(x2,y2),则 x1+x2=
2,x1x2=
.
由·>2 得 x1x2+y1y2>2.
直线与圆锥曲线的位置关系
目录
退出
1.直线与圆锥曲线位置关系的判断方法
(1)代数法,把圆锥曲线方程与直线方程联立消去 y,整理得出关于 x 的
方程 Ax2+Bx+C=0,若圆锥曲线是双曲线或是抛物线,当 A=0 时,表示直线与
双曲线的渐近线或抛物线的轴平行;当 A≠0 时,记该一元二次方程根的判
别式为 Δ.(ⅰ)若 Δ>0 时,直线与圆锥曲线相交;(ⅱ)若 Δ=0 时,直线与圆锥曲
截的线段的中点坐标时,设出直线和圆锥曲线的两个交点坐标,代入圆锥曲
线的方程并作差,从而求出直线的斜率,然后利用中点求出直线方程.“点差
法”的常见题型有:求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直
平分线问题.必须提醒的是“点差法”具有不等价性,即要考虑判别式 Δ 是否
为正数.
4.圆锥曲线的定值、最值、存在性问题很大一部分是利用等价转化思
B. -∞,-
2
2
∪
2
,+
2
∞
C.(-∞,-2 2)∪(2 2,+∞)
D.(-∞,- 2)∪( 2,+∞)
)
【答案】D
4
直线与圆锥曲线

直线与圆锥曲线1.从几何的角度看,可以分:直线与圆锥曲线有两个不同公共点,仅有一个公共点,无公共点; ⑴有两个公共点,就是相交,直线被圆锥曲线截得的线段称为曲线的弦; ⑵仅有一个公共点,对于圆和椭圆来说,表示直线与其相切; 对于双曲线来说,表示直线与其相切或与渐近线平行; 对于抛物线来说,表示直线与其相切或平行于对称轴; ⑶无公共点,就是相离;2.从代数的角度看,将表示直线的方程0Ax By C ++=代入到圆锥曲线的方程()0f x y =,中,消去一个变元y (或x )后,得到方程20ax bx c ++=;⑴若0a =,当圆锥曲线是双曲线时,说明直线与其渐近线平行; 当圆锥曲线是抛物线时,说明直线与其对称轴平行; ⑵若0a ≠,记24b ac ∆=-,则 0∆>,说明直线与圆锥曲线相交; 0∆=,说明直线与圆锥曲线相切; 0∆<,说明直线与圆锥曲线相离;知识梳理第10讲直线与圆锥曲线3.斜率为k 的直线与圆锥曲线()0f x y =,相交,将两者方程联立,消去y ,得到方程20ax bx c ++=,则弦长公12x x -=;4.当过定点00()P x y ,的直线斜率可能不存在时,为避免分类讨论,可以设斜率的倒数为m ,把直线方程写成x my n =+;这种形式的方程能够表示斜率不存在的情形,但不能够表示斜率为0的情形. 此时同样代入圆锥曲线方程,消去x ,得到20ay by c ++=.5.在计算圆锥曲线内接三角形面积时,我们常常用到下面这些计算公式:111sin sin 222ABC S dl d l ll αθ''===△由三角形的面积容易推出圆锥曲线内接四边形的计算公式:1sin 2ABCD S AC BD α=⋅(其中α为对角线夹角)特别地,对角线互相垂直的四边形的面积为ABCD S =12AC⋅<教师备案>直线与圆锥曲线的位置关系:⑴讨论直线与圆锥曲线的位置关系一般是将直线方程与圆锥曲线方程联立成方程组,消元(x 或y ),若消去y 得到20ax bx c ++=,讨论根的个数得到相应的位置关系,这里要注意的是: ①二次项系数a 可能有0a =或0a ≠两种情况,(例外情形:当圆锥曲线为双曲线且直线平行于渐近线时,或者当圆锥曲线为抛物线且直线平行于对称轴时,二次项系数为0)只有当0a ≠,才能用∆判断根的个数;②直线与圆锥曲线相切时只有一个公共点,但有一个公共点不一定相切.经典精讲⑵在讨论直线与双曲线的交点时,要注意数形结合的方法,结合图象作出判断有时更方便快捷,要注意双曲线的渐近线的斜率,以及直线与渐近线的斜率比较.⑶当直线与圆锥曲线相交时:涉及弦长问题,常用“韦达定理”设而不求计算弦长;涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.尖子班学案1【铺1】 ⑴若直线1y kx =+与椭圆2215x y m+=恒有公共点,则实数m 的取值范围为________.⑵过定点(01),且与双曲线224x y -=的两支各有一个公共点的直线l 的斜率的取值范围________.【解析】 ⑴1m ≥且5m ≠ ⑵()1,1-考点:直线与圆锥曲线的位置关系【例1】 ⑴过定点(01)-,且与抛物线24y x =有且只有一个公共点的直线有_____条;.⑵过点()4,4P 且与双曲线221169x y -=只有一个交点的直线有______条.⑶已知两定点(10)M -,,(10)N ,,若直线上存在点P ,使得||||4PM PN +=,则该直线为“A 型直线”.给出下列直线,其中是“A 型直线”的是. ①1y x =+②2y =③3y x =-+④23y x =-+⑷(海淀一模文8)若直线l 被圆22:2C x y +=所截的弦长不小于2,则l 与下列曲线一定有公共点的是()A .22(1)1x y -+=B .2212x y +=C .2y x =D .221x y -=【解析】 ⑴3;⑵4 ⑶①④ ⑷B<教师备案>直线与圆锥曲线问题的基本方法:直线与圆锥曲线的问题尤其是相交问题,最基本的方法分为两种:⑴代入法;即联立直线与圆锥曲线的方程,把直线的方程代入后者消去一个变元(通常是y ),得到关于x 的二次方程,二次方程的根即代表交点的横坐标,然后用韦达定理与坐标运算去求解交点的相关问题; 代入法的优点:适用性强,基本上对于任何问题都能适用;代入法的缺点:通常计算量较大,当方程含参时,坐标运算比较复杂; 在与弦长有关的问题中,通常采用代入法. ⑵点差法:以直线与椭圆相交为例,设出交点的坐标()A A x y ,,()B B x y ,,由于这两者都满足椭圆方程,相减就得:22222222A B A B x x y y a a b b ⎛⎫-=-- ⎪⎝⎭,再利用平方差公式就得:22A B A BA B A By y x x b x x a y y -+=--+ 若设AB 的中点为M ,就得到了斜率与AB 中点坐标的一个简单关系式:22M Mx b k a y =-;这种方法称为点差法.点差法的优点:计算量非常小;点差法的缺点:适用范围非常狭窄,通常只能用来解决中点弦问题,或者斜率与坐标和密切相关的问题;而且点差法的变换过程不是等价的,需要考虑是否有0∆>;在与中点弦有关而且不太需要交点坐标运算的问题中,可以考虑使用点差法.考点:代入法与点差法【例2】 ⑴已知椭圆22143x y +=的右焦点为F ,过F 且倾斜角为45︒的直线与椭圆相交于A B ,两点,则弦长AB =________.⑵直线l 与椭圆22184x y +=交于两点A B ,,AB 的中点坐标为(11)-,,则直线l 的方程是.⑶ABC △的三个顶点都在抛物线24y x =上,A 点与原点重合,且三角形重心恰为抛物线的焦点,则三角形的周长是.⑷经过抛物线2y x =上一点(42)A -,引两条直线1l 和2l ,与抛物线分别交于M 、N 两点,若1l 与2l 的斜率互为相反数,则直线MN 的斜率为.【解析】 ⑴247; ⑵230x y --=⑷14【例3】 (石景山一模文19)已知椭圆22221x y a b+=(0a b >>)右顶点到右焦点的距离为1-,短轴长为 ⑴求椭圆的方程;⑵过左焦点F 的直线与椭圆分别交于A 、B 两点,若线段AB,求直线AB 的方程. 【解析】⑴椭圆方程为22132x y +=.⑵直线AB0y -+=0y +=.目标班学案1【拓2】 (东城二模文19)已知椭圆()222210x y a b a b+=>>的左焦点1(1,0)F -,长轴长与短轴长的比是2⑴求椭圆的方程;⑵过1F 作两直线m ,n 交椭圆于A ,B ,C ,D 四点,若m n ⊥,求证:11AB CD+为定值. 【解析】⑴椭圆方程为22143x y +=.⑵由⑴知()11,0F -,当直线m 与x 轴重合时,此时3,4AB CD ==,11AB CD +1173412=+=. 当直线m 不与x 轴重合时,设直线m 的方程为:1x my =-. 由221143x my x y =-⎧⎪⎨+=⎪⎩得:()2234690m y my +--=.由直线过椭圆内定点1F 知一定有0∆>.则有()2212134m AB m +==+.在上式中用1m -代换m ,同理可知()2212143m CD m +=+. 所以11AB CD +()()22223434712121121m m m m ++=+=++. 综上,11AB CD +为定值712.【例4】 ⑴连接抛物线24x y =的焦点F 与点(1,0)M 所得的线段与抛物线交于点A ,设点O 为坐标原点,则OAM △的面积为( )A .1-B .32C .1D .32⑵过椭圆22154x y +=的右焦点作一条斜率为2的直线与椭圆交于A 、B 两点,O 为坐标原点,则OAB△的面积为___________.⑶已知抛物线24y x =,点()4,0M 关于y 轴的对称点为N ,直线l 过点M 交抛物线于A 、B 两点.则ANB △面积的最小值为________.【解析】 ⑴ B⑵53; ⑶32【例5】 (丰台二模文20)已知椭圆22221(0)x y a b a b+=>>经过点()01,,过右焦点F 且不与x 轴重合的动直线l交椭圆于A 、C 两点,当动直线l 的斜率为2时,坐标原点O 到l . ⑴求椭圆的方程;⑵过F 的另一直线交椭圆于B 、D 两点,且AC BD ⊥,当四边形ABCD 的面积169S =时,求直线l 的方程.【解析】 ⑴椭圆的方程为2212x y +=.⑵直线l 的方程为10x y --=或10x y +-=.尖子班学案2【铺1】 若已知点(C ,平行于CO 的直线l 和椭圆221124x y +=交于M 、N 两个不同点,当CMN △面积取最大值时,求直线l 的方程.【解析】 直线l 的方程为0x y +±=.【例6】 (西城二模文19)已知椭圆2222:1(0)x y C a b a b +=>>31,22⎛⎫ ⎪⎝⎭.⑴求椭圆C 的方程;⑵过点(0,2)P 的直线交椭圆C 于A ,B 两点,求AOB △(O 为原点)面积的最大值.【解析】⑴椭圆C 的方程是2213x y +=.⑵AOB △. 【点评】本题求面积也可以用传统面积公式点O 到直线AB的距离d =,弦长12AB x x -,【备选】(朝阳一模文19)已知椭圆()2222:10x y M a b a b+=>>的左右焦点分别为()12,0F -,()22,0F .在椭圆M 中有一内接三角形ABC ,其顶点C 的坐标)1,AB . ⑴求椭圆M 的方程;⑵当ABC △的面积最大时,求直线AB 的方程.【解析】 ⑴椭圆M 的方程为22162x y +=.⑵直线AB 的方程为y =过定点312P ⎛⎫- ⎪⎝⎭,的直线l 与抛物线24y x =相交所得的弦长为4,求直线l 的方程.【解析】 错解:设直线的斜率为k ,直线的方程可以写成3(1)2y k x +=-,与抛物线方程联立消去y ,得: 22223(234)02k x k k x k ⎛⎫-++++= ⎪⎝⎭222223(234)416241602k k k k k k ⎛⎫∆=++-+=++> ⎪⎝⎭恒成立; 然后得弦长4s ==化简得323321022k k k +++=,即2(1)(32)0k k k +++=,1k =-;所以直线方程为3(1)2y x +=--,即102x y ++=.【点评】 上面的误解中,设直线斜率时没有讨论斜率是否存在;若斜率不存在,则直线方程为1x =,与抛物线的两个交点为(12)±,,弦长正好也为4,所以满足题意的直线有两条:1x =或者102x y ++=.在设直线方程时,如果是用点斜式或者斜截式,一定要讨论斜率是否存在.(北京文19)已知椭圆2222:1(0)x y G a b a b+=>>()0,斜率为1的直线l 与椭圆G 交于A ,B 两点,以AB 为底边作等腰三角形,顶点为(32)P -,.⑴求椭圆G 的方程; ⑵求PAB △的面积.【解析】 ⑴椭圆G 的方程为221124x y +=.⑵PAB △的面积92S =.【演练1】若直线4mx ny +=和圆O :224x y +=仅有一个交点,则过点()m n ,的直线与椭圆22194x y +=的交点个数为________.【解析】 1或2【演练2】已知F 是抛物线24C y x =:的焦点,过F 且斜率为1的直线交C 于A B ,两点.设FA FB >,则FA与FB 的比值等于.【解析】3+【演练3】已知F 是抛物线24C y x =:的焦点,A ,B 是C 上的两个点,线段AB 的中点为()22M ,,则ABF△的面积等于.【解析】 2实战演练真题再现【演练4】已知双曲线E 的中心为原点,(30)F ,是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为(1215)N --,,则E 的方程为()A .22136x y -=B .22145x y -=C .22163x y -=D .22154x y -=【解析】B【演练5】(西城一模文19)已知抛物线24y x =的焦点为F ,直线l 过点(40)M ,.⑴若点F 到直线ll 的斜率;⑵设A B ,为抛物线上两点,且AB 不与x 轴垂直,若线段AB 的垂直平分线恰过点M ,求证:线段AB 中点的横坐标为定值.【解析】 ⑴l的斜率为2±. ⑵设线段AB 中点的坐标为00()N x y ,;因为AB 不垂直于x 轴,则MN 的斜率为004y x -,直线AB 的斜率为04x y -; 但另一方面,22044244A B A B AB A B A BA B y y y y k y y x x y y y --====-+-; ∴00042x y y -=,∴02x =;即AB 中点的横坐标恒为定值2. 【演练6】已知椭圆2222:1(0)x y C a b a b+=>>,1F 、2F 为左右焦点,点A 是椭圆上位于第一象限的点,且满足2AF x ⊥轴,直线AO 交椭圆于点B ,若2ABF △的面积为【解析】 椭圆方程为221168x y +=.(上海交大自主招生考试)已知线段AB 长度为3,两端均在抛物线2x y =上,试求AB 的中点M 到y 轴的距离最短时M 点的坐标.【解析】 如图所示,抛物线的焦点为104F ⎛⎫⎪⎝⎭,,准线方程为14x =-;过A M B ,,分别作准线的垂线,垂足为P R Q ,,;大千世界则()111424M x MR AP BQ =-=+-()1124AF FB =+- 115244AB -=≥等号成立当且仅当A F B ,,共线,即AB 过焦点F .设此时AB 的方程为14x my -=,与抛物线方程联立得214y my =+,∴A B y y -∴231A B AB y m =-=+,m =;∴()21152422424A B A B M M y y y y mm x y m ⎛⎛⎫++⎛⎫=+=+=± ⎪ ⎪ ⎝⎭⎝⎭⎝⎭,,,,∴M 点的坐标为54⎛± ⎝⎭,.。
直线与圆锥曲线的位置关系

直线与圆锥曲线的位置关系1.直线与圆锥曲线的位置关系(1)从几何角度看,可分为三类:无公共点,仅有一个公共点及有两个相异的公共点,具体如下:①直线与圆锥曲线的相离关系,常通过求二次曲线上的点到已知直线的距离的最大值或最小值来解决.②直线与圆锥曲线仅有一个公共点,对于圆或椭圆,表示直线与其相切;对于双曲线,表示与其相切或与双曲线的渐近线平行;对于抛物线,表示直线与其相切或直线与其对称轴平行.③直线与圆锥曲线有两个相异的公共点,表示直线与圆锥曲线相割,此时直线被圆锥曲线截得的线段称为圆锥曲线的弦.(2)从代数角度看,可通过将表示直线的方程,代入二次曲线的方程消元后所得的一元二次方程的解的情况来判断.直线l 方程为Ax +By +C =0,圆锥曲线方程为f (x ,y )=0.由⎩⎪⎨⎪⎧Ax +By +C =0,f (x ,y )=0消元(x 或y ), 如消去y 后得ax 2+bx +c =0.若f (x ,y )=0表示椭圆,上述方程中a ≠0,若f (x, y )=0表示双曲线或抛物线, 上述方程中a =0或a ≠0.①若a =0,当圆锥曲线是双曲线时,直线l 与双曲线的渐近线平行(或重合);当圆锥曲线是抛物线时,直线l 与抛物线的对称轴平行(或重合).②若a ≠0,设Δ=b 2-4ac .a .Δ>0时,直线和圆锥曲线相交于不同两点;b .Δ=0时,直线和圆锥曲线相切于一点;c .Δ<0时,直线和圆锥曲线没有公共点.直线与圆锥曲线的位置关系重点是相交:相交――→转化联立方程组有两组不等的实数解――→转化一元二次方程有两个不等实数解――→转化判别式大于零.2.弦长的求法求弦长――→转化求两点间的距离――→综合运用⎩⎪⎨⎪⎧消元,解方程组,一元二次方程根与系数的关系.(1)弦长:(直线与圆锥曲线相交于A (x 1,y 1),B (x 2,y 2)),直线斜率为k ,一般地,弦长公式|AB |=1+k 2|x 1-x 2|=(1+k 2)[(x 1+x 2)2-4x 1x 2]=1+1k2|y 1-y 2|=⎝⎛⎭⎫1+1k 2[(y 1+y 2)2-4y 1y 2]. (2)若弦过焦点:可用焦半径公式来表示弦长,简化运算. 如x 2a 2+y2b 2=1(a >b >0), |AB |=2a -e(x 1+x 2) (过右焦点), |AB |=2a +e(x 1+x 2) (过左焦点).如抛物线y 2=2px (p >0), |AB |=x 1+x 2+p .3.中点弦问题设A (x 1,y 1),B (x 2,y 2)是椭圆x 2a 2+y 2b 2=1上不同的两点,且x 1≠x 2,x 1+x 2≠0,M (x 0,y 0)为AB 的中点,则⎩⎨⎧x 21a 2+y 21b21,x 22a 2+y22b 21.两式相减可得y 1-y 2x 1-x 2·y 1+y 2x 1+x 2=-b 2a 2,即k AB ·y 0x 0=-b 2a2.类似地,可得圆锥曲线为双曲线x 2a 2-y 2b 2=1时,有k AB ·y 0x 0=b 2a2.圆锥曲线为抛物线y 2=2px (p >0)时,有k AB =py 0.探究点1 直线与圆锥曲线的交点问题例1 已知双曲线C :2x 2-y 2=2与点P (1, 2),求过点P 的直线l 的斜率的取值范围,使l 与C 分别有一个公共点,两个公共点,没有公共点.例1 [解答] (1)当l 垂直x 轴时,此时直线与双曲线相切,有一个公共点.(2)当l 不与x 轴垂直时,设直线l 的方程为y -2=k(x -1)代入双曲线C 的方程中,整理得(2-k 2)x 2+2(k 2-2k)x -k 2+4k -6=0, (*) 当k 2=2,即k =±2时, (*)为一次方程,显然只有一解; 当k 2≠2时,Δ=4(k 2-2k)2-4(2-k 2)(-k 2+4k -6)=48-32k.令Δ=0,可解得k =32;令Δ>0,即48-32k >0,此时k <32;令Δ<0,即48-32k <0,此时k >32.∴当k =±2或k =32或k 不存在时,l 与C 只有一个公共点;当k <-2或-2<k <2或2<k <32时,l 与C 有两个公共点;当k >32时,l 与C 没有公共点.[点评] (1)为了设出直线方程,先讨论斜率是否存在.当斜率存在时,设出方程并与双曲线方程组成方程组,消去y 得到关于x 的方程.当二次项系数为零时,直线与渐近线平行与双曲线只有一个交点;当二次项系数不为零时,若Δ=0,则有一个切点;若Δ>0,则有两个交点;Δ<0,则没有交点.(2)有关直线和圆锥曲线的范围问题,常常使用Δ来体现范围.探究点2 中点弦问题例2 椭圆x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (0,2),离心率e =63.(1)求椭圆的方程;(2)直线l :y =kx -2(k ≠0)与椭圆相交于不同的两点M 、N ,且满足MP →=PN →,AP →·MN →=0,求直线l 的方程.[解答] (1)设c =a 2-b 2,依题意得⎩⎪⎨⎪⎧b =2,e =c a =a 2-b 2a =63,即⎩⎪⎨⎪⎧b =2,6a 2=9a 2-9b 2,∴a 2=3b 2=12,即椭圆方程为x 212+y 24=1.(2)∵MP →=PN →,AP →·MN →=0,∴AP ⊥MN ,且点P 是线段MN 的中点, 由⎩⎪⎨⎪⎧y =kx -2,x 212+y 241,消去y ,得x 2+3(kx -2)2=12, 即(1+3k 2)x 2-12kx =0,(*),由k ≠0,得方程(*)中Δ=(-12k)2=144k 2>0,显然方程(*)有两个不相等的实数根.设M(x 1,y 1)、N(x 2,y 2),线段MN 的中点P(x 0,y 0),则x 1+x 2=12k 1+3k 2∴x 0=x 1+x 22=6k1+3k 2, ∴y 0=kx 0-2=6k 2-2(1+3k 2)1+3k 2=-21+3k 2即P ⎝⎛⎫6k 1+3k 2,-21+3k 2.∵k ≠0,∴直线AP 的斜率为k 1=-21+3k 2-26k1+3k2=-2-2(1+3k 2)6k.由MN →⊥AP →,得-2-2(1+3k 2)6k ·k =-1,∴2+2+6k 2=6,解得k =±33,故直线方程为y =±33x -2.探究点3 相交弦长与面积问题例3 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为63,焦点到相应准线的距离为22.(1)求椭圆C 的方程;(2)设直线l 与椭圆C 交于A 、B 两点,坐标原点到直线l 的距离为32,求△AOB 面积的最大值.例3 [解答] (1)∵e =c a =63,a 2c -c =22,解得a =3,c =2,∴b 2=3-2=1, 椭圆C 的方程为x 23+y 2=1.(2)当AB ⊥x 轴时,⎝⎛⎭⎫3223+y 2=1,得y 2=34,AB = 3. 当AB 不垂直x 轴时,设直线l 的方程为y =kx +m ,则|m|1+k2=32,得m 2=34k 2+34. 由⎩⎪⎨⎪⎧y =kx +m ,x 23+y 2=1,得(3k 2+1)x 2+6kmx +3m 2-3=0,∴x 1+x 2=-6km 3k 2+1,x 1x 2=3(m 2-1)3k 2+1, |AB|=1+k 2·(x 1+x 2)2-4x 1x 2=1+k 2·36k 2m 2(3k 2+1)2-12(m 2-1)3k 2+1=12(k 2+1)(3k 2+1-m 2)(3k 2+1)2=3(k 2+1)(9k 2+1)(3k 2+1)2=3+12k29k 4+6k 2+1 =3+129k 2+1k2+6≤3+122×3+6=2(k ≠0),当且仅当9k 2=1k 2,即k =±33时,|AB|max =2,当k =0时,AB =3,综上所述|AB|max =2.∴当|AB|最大时,△AOB 面积最大值S =12×32×2=32.变式题:从椭圆x 2a 2+y2b 2=1(a >b >0)上一点M 向x 轴作垂线,恰好通过椭圆的左焦点F 1,且它的长轴端点A 及短轴端点B 的连线AB 平行于OM .(1)求椭圆的离心率;(2)当QF 2⊥AB 时,延长QF 2与椭圆交于另一点P ,若△F 1PQ 的面积为203(Q是椭圆上的点),求此时椭圆的方程. [解答] (1)如图,由题意知x M =-c , 故y M =b 2a .又△F 1OM ∽△OAB ,c a =b 2a b ⇒b =c ⇒e =22. (2)设椭圆方程为x 2a 2+y2b 2=1(a>b>0),由(1)知a 2=2b 2,方程变为x 2+2y 2=2b 2.设直线PQ 方程为y -0=2(x -b),联立方程组,得5x 2-8bx +2b 2=0, x 1+x 2=8b 5,x 1x 2=2b 25.|PQ|=|x 1-x 2|=(x 1+x 2)2-4x 1x 2=26b5∵|y 2-y 1|=|2(x 2-x 1)|=2(x 1+x 2)2-4x 1x 2=43b5S △F 1PQ =12×||PQ ×||-22b 3=203⇒b 2=25,∴a 2=50,∴椭圆方程为x 250+y 225=1.探究点4 弦的定比分点问题例4 已知椭圆x 25+y 29=1,焦点F (0,2),又点A ,B 在椭圆上,而且AF →=2FB →,求直线AB 的斜率.例4 [解答] AF →=2FB →⇒A ,F ,B 三点共线. 设AB 方程为y =kx +2,与椭圆方程联立,得 (9+5k 2)x 2+20kx -25=0, x 1+x 2=-20k 9+5k 2,x 1x 2=-259+5k2.又AF →=2FB →⇒⎩⎪⎨⎪⎧x1=-2x 2,2-y 1=2y 2-4,所以-x 2=-20k 9+5k 2,-2x 22=-259+5k 2,消去x 2,解得k =±33. 探究点5 综合应用问题例5 已知双曲线C :x 21-λ-y 2λ=1(0<λ<1)的右焦点为B ,过点B 作直线交双曲线C的右支于M 、N 两点,试确定λ的范围,使OM →·ON →=0,其中点O 为坐标原点. [解答] 设M(x 1,y 1),N(x 2,y 2),由已知易求B(1,0). 当MN 垂直于x 轴时,MN 的方程为x =1.设M(1,y 0),N(1,-y 0)(y 0>0),由OM →·ON →=0,得y 0=1,∴M(1,1),N(1,-1). 又M(1,1),N(1,-1)在双曲线上, ∴11-λ-1λ=1⇒λ2+λ-1=0⇒λ=-1±52. ∵0<λ<1,∴λ=5-12. 当MN 不垂直于x 轴时,设MN 的方程为y =k(x -1).由⎩⎪⎨⎪⎧x 21-λ-y 2λ=1,y =k (x -1),得:[λ-(1-λ)k 2]x 2+2(1-λ)k 2x -(1-λ)(k 2+λ)=0. 由题意知λ-(1-λ)k 2≠0,∴x 1+x 2=-2k 2(1-λ)λ-(1-λ)k 2,x 1x 2=-(1-λ)(k 2+λ)λ-(1-λ)k 2,∴y 1y 2=k 2(x 1-1)(x 2-1)=k 2λ2λ-(1-λ)k 2,∵OM →·ON →=0,且M 、N 在双曲线右支上, ∴⎩⎪⎨⎪⎧x 1x 2+y 1y 2=0,x 1+x 2>0,x 1x 2>0⇒⎩⎨⎧k 2=λ(1-λ)λ2+λ-1,k 2>λ1-λ⇒⎩⎪⎨⎪⎧λ(1-λ)λ2+λ-1>λ1-λ,λ2+λ-1>0⇒5-12<λ<23.综上知5-12≤λ<23. 变式题:已知点P 1(x 0,y 0)为双曲线x 28b 2-y 2b 21(b 为正常数)上任一点,F 2为双曲线的右焦点,过P 1作右准线的垂线,垂足为A ,连结F 2A 并延长交y 轴于点P 2.(1)求线段P 1P 2的中点P 的轨迹E 的方程;(2)设轨迹E 与x 轴交于B 、D 两点,在E 上任取一点Q (x 1,y 1)(y 1≠0),直线QB 、QD 分别交y 轴于M 、N 两点.求证:以MN 为直径的圆过两定点.[解答] (1)由已知得F 2(3b,0),A ⎝⎛⎭⎫83b ,y 0,则直线F 2A 的方程为y =-3y0b (x -3b),令x=0,得y =9y 0,即P 2(0,9y 0).于是直线QB 的方程为:y =y 1x 1+2b(x +2b),直线QD 的方程为y =y 1x 1-2b(x -2b),可得M ⎝⎛⎭⎪⎫0,2by 1x 1+2b ,N ⎝ ⎛⎭⎪⎫0,-2by 1x 1-2b . 则以MN 为直径的圆的方程为: ⎩⎪⎨⎪⎧x 2+⎝ ⎛⎭⎪⎫y -2by 1x 1+2b ⎝ ⎛⎭⎪⎫y +2by 1x 1-2b =0.令y =0得x 2=2b 2y 21x 21-2b 2,而Q(x 1,y 1)在x 22b 2-y 225b 2=1上,则x 21-2b 2=225·y 21,于是x =±5b , 即以MN 为直径的圆过两定点(-5b,0),(5b,0).规律总结本节问题的研究集中体现了解析几何的基本思想和方法,要求有较强的分析问题和解决问题的能力,有些问题涉及代数、三角、几何等多方面的知识,因此在复习中要注意各部分之间的联系和综合利用知识解决问题的能力.1.直线与圆锥曲线有无公共点或有几个公共点的问题,实际上是研究它们的方程组成的方程组是否有实数解或实数解的个数问题,通过消元最终归结为讨论一个一元二次方程Ax 2+Bx +C =0的实数解的个数问题.应特别注意要分A =0和A ≠0的两种情况讨论,只有A ≠0时,才可用判别式来确定解的个数. 当直线平行于抛物线的对称轴时,直线与抛物线只有一个公共点.这些情况在解题中往往容易疏忽,要特别注意,对于选择、填空题,用数形结合往往快速简捷.2.斜率为k 的直线被圆锥曲线截得弦AB ,若A 、B 两点的坐标分别为A (x 1,y 1),B (x 2,y 2),则|AB |=|x 1-x 2|·1+k 2=|y 1-y 2|·1+1k 2(k ≠0),利用这个公式求弦长时,应注意应用韦达定理.3.与焦点弦长有关的问题,要注意应用圆锥曲线的定义.4.在给定的圆锥曲线f (x ,y )=0中,求中点为(m ,n )的弦AB 所在直线方程时,一般可设A (x 1,y 1)、B (x 2,y 2),利用A 、B 在曲线上,得f (x 1,y 1)=0,f (x 2,y 2)=0及x 1+x 2=2m ,y 1+y 2=2n ,故可求出斜率k AB =y 1-y 2x 1-x 2,最后由点斜式写出直线AB 的方程.5.求圆锥曲线的方程时,通常利用待定系数法.。
直线与圆锥曲线

直线与圆锥曲线的位置关系1.直线与圆锥曲线的位置关系几何角度:直线与圆锥曲线的位置关系,从几何角度可分为三类:无公共点,仅有一个公共点及有两个相异公共点.无公共点一个公共点 两个不同公共点代数角度:直线与圆锥曲线的位置关系的研究方法可通过代数方法即解方程组的办法来研究。
因为方程组解的个数与交点的个数是一样的.设直线L 的方程为:0=++C By Ax 圆锥曲线C 的方程为:0),(=y x F联立:⎩⎨⎧==++0),(0y x F C By Ax 消y (也可消x )得到一个关于变量x (或变量y )的一元二次方程:02=++c bx ax(1) 当a ≠0时,则有下表中的结论:(方程的判别式△=ac b 42-)(2) 当a =0时,即得到一个一次方程,则直线L 与圆锥曲线相交,且只有一个交点。
若C 为双曲线,则直线L 与双曲线的渐近线平行。
若C 为抛物线,则直线L 与抛物线的对称轴平行或重合。
即直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件.(对于椭圆来说,这个方程二次项系数一般不为0,不过当直线与椭圆相切时,若已知直线过某点,则当点在椭圆外部时,切线有两条;当点在椭圆上时,切线有一条.)1)相离 3)相交 2)相切注意:直线与圆锥曲线位置关系问题①常利用数形结合方法解决。
②转化为研究方程组解的问题。
例1.直线L :y=kx+1,抛物线C:x y 42=,当k 为何值时L 与C 有:(1)一个公共点;(2)两个公共点;(3)没有公共点。
2.直线与圆锥曲线相交形成的弦长问题弦长][212212212214))1(1x x x x k x x k P P -++=-+=(或][212212212214))11(11y y y y ky y kP P -++=-+=(注:①当斜率k 不存在时,可求出交出坐标,直接运算(利用轴上两点间的距离公式)②经过圆锥曲线的焦点的弦(也称焦点弦)的长度,应用圆锥曲线的定义,转化成两个焦半径之和,往往比用弦长公式简捷。
4.3直线与圆锥曲线的交点

答案: 答案:D
1.弦长问题 . 利用弦长公式求弦长要注意斜率k不存在的情形, k不 利用弦长公式求弦长要注意斜率k不存在的情形,若k不 不存在的情形 存在时,可直接求交点坐标再求弦长. 存在时,可直接求交点坐标再求弦长.
2.中点弦问题 . 遇到中点弦问题常用“根与系数关系 或 点差法 点差法”求 遇到中点弦问题常用 根与系数关系”或“点差法 求 根与系数关系 解.在椭圆 直线的斜率k= 直线的斜率 中,以P(x0,y0)为中点的弦所在 为中点的弦所在 ;在双曲线 中,以 ;在抛物线
二、圆锥曲线的弦长问题 设直线l与圆锥曲线 相交于 两点, 设直线 与圆锥曲线C相交于 、B两点,A(x1,y1), 与圆锥曲线 相交于A、 两点 , B(x2,y2),则弦长 ,则弦长|AB|= = .
1.过原点的直线l与双曲线 .过原点的直线 与双曲线 线l 的斜率的取值范围是
有两个交点, 有两个交点,则直 ( )
易证. (1)联立方程消元利用 )联立方程消元利用Δ>0易证 易证 (2)结合条件分析出 ) 易求. 易求
1.已知直线y=k(x+2)(k>0)与抛物线 : .已知直线 = + 与抛物线C: 与抛物线 y2=8x相交于 、B两点,F为C的焦点.若|FA|=2 相交于A、 两点 为 的焦点 两点, 的焦点. 相交于 = |FB|,则k= , = ( )
等
∴ 答案: 答案:4a
= 4a.
5.若直线mx+ny=4和圆 :x2+y2=4没有公共点,则过 .若直线 + = 和圆 和圆O: 没有公共点, 没有公共点 点(m,n)的直线与椭圆 , 的直线与椭圆 ________. . 解析:由已知可得 点在椭圆内, 解析:由已知可得m2+n2<4,又(m,n)点在椭圆内,故必 , , 点在椭圆内 个交点. 有2个交点. 个交点 答案: 答案:2 的交点个数为
直线与圆锥曲线

0
1 k 2 0
0
0
1 k 0
2 k 2 , 且k 1
双曲线与直线的位置关系: 此类题一般用代数方法解题,在联立方程组得到一元二次方程 Ax2+Bx+C=0 后,要注意一元二次方程的二次项系数为 0 的情形. 对于方程 Ax2+Bx+C=0. ①当二次项系数 A=0,即直线与渐近线平行,此时直线与双曲线有且仅有一个公 共点. ②当 A≠0,△=0 时,直线与双曲线也有且仅有一个公共点,但此时直线 l 与双曲 线相切. 问题拓展: 直线仅与双曲线的右(左)支相交,有两个交点,问题可转化为 Ax2+Bx+C=0 的根
2.设抛物线 y2=8x 的准线与 x 轴交于点 Q,若过点 Q 的直线 l 与抛物线有公共点,则直线 l 的斜率的取值 范围是
1 1 A.-2,2
( B.[-2,2] D.[-4,4]
)
C.[-1,1]
解析 ∵y2=8x,∴Q(-2,0) (Q 为准线与 x 轴的交点), 设过 Q 点的直线 l 方程为 y=k(x+2), ∵l 与抛物线有公共点,
② ③
又 y1+y2=k(x1+x2)+2 2 而A 2 ,0),B(0,1),AB ( 2,1) ( 所以OP OQ与 AB共线等价于 x1+x2=- 2(y1+y2),
2 将②③代入上式,解得 k= . 2 2 2 由(1)知 k<- 或 k> ,故没有符合题意的常数 k. 2 2
满足 x∈(0,+∞),问题转化为方程有两不相等的正(负)根. 如果题型为填空题、 选择题,可直接使用几何方法解决.
知能迁移 1
Байду номын сангаас
8.4 直线与圆锥曲线

设M(x1,y1),N(x2,y2),Q(x0,y0),
13
【例3】(2009²成都模拟)已知椭圆的两个焦点
分别为F1(0, 2 2 ),F2(0, 2),离心率为 2 e= 2 2 . 3 (1)求椭圆方程; (2)一条不与坐标轴平行的直线l与椭圆交于不
同的两点M,N,且线段MN中点的横坐标为
1 - 2 ,求直线l的倾斜角的取值范围.
分析 涉及动弦中点的问题可考虑用下列方法: ①将直线方程代入曲线方程,得到一个一元二 次方程,利用根与系数的关系求解;②利用 “设而不求”的方法将直线的斜率和弦的中点 联系在一起.
得
x1+x2= 6 3 ,x1x2=11. ∵|AB|=
1 3 ²|x1-x2|=2(x2-x1),
|F1A|+|F1B|= 3 (x1+x2)+2a=20
以及x2-x1= ( x1 x2 ) 2 4 x1 x2 8 ,
∴(1)|AB|=2³8=16;
(2)△F1AB的周长=|AB|+|F1A|+|F1B|=36.
若方程无解( <0),则直线与椭圆相离 2.直线与双曲线的位置关系 (1)位置关系 ①相交:直线与双曲线有 两个交点或有 一个公 共点(直线与渐近线平行). ②相切:直线与双曲线 有且只有一个 公共点, 且直线不平行于双曲线的渐近线. ③相离:直线与双曲线 无 公共点. .
直线和圆锥曲线的位置关系

直线和圆锥曲线的位置关系知识点一:直线与圆锥曲线的位置关系直线与圆锥曲线的位置关系有三种:相交、相切、相离.判断的方法均是把直线方程代入曲线方程中,判断方程解的个数,从而得到直线与曲线公共点的个数,最终得到直线与曲线的位置关系.一般利用二次方程判别式来判断有无解,有几个解.1.直线0=++C By Ax 椭圆)0(12222>>=+b a by a x 的位置关系: 将直线的方程与椭圆的方程联立成方程组,消元转化为关于x 或y 一元二次方程,其判别式为∆.(1)⇔>∆0直线和椭圆相交⇔直线和椭圆有两个交点(或两个公共点);(2)⇔=∆0直线和椭圆相切⇔直线和椭圆有一个切点(或一个公共点);(3)⇔<∆0直线和椭圆相离⇔直线和椭圆无公共点.2.直线0=++C By Ax 和双曲线)0,0(12222>>=-b a by a x 的位置关系: 将直线的方程与双曲线的方程联立成方程组,消元转化为关于x 或y 的方程.(一)若为一元一次方程,则直线和双曲线的渐近线平行,直线和双曲线只有一个交点,但不相切不是切点;(二)若为一元二次方程,则(1)若0>∆,则直线和双曲线相交,有两个交点(或两个公共点);(2)若0=∆,则直线和双曲线相切,有一个切点;(3)若0<∆,则直线和双曲线相离,无公共点.注意:(1)⇒>∆0直线与双曲线相交,但直线与双曲线相交不一定有0>∆,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故0>∆是直线与双曲线相交的充分条件,但不是必要条件;(2)当直线与双曲线的渐近线不平行时,⇔=∆0直线与双曲线相切;(3)如说直线和双曲线有一个公共点,则要考虑两种情况:一个切点和一个交点;当直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;(4)过双曲线)0,0(12222>>=-b a by a x 外一点),(00y x P 的直线与双曲线只有一个公共点的情况如下:①P 点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P 点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P 在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P 为原点时不存在这样的直线;3.直线0=++C By Ax 和抛物线)0(22>=p px y 的位置关系:将直线的方程与抛物线的方程联立成方程组,消元转化为关于x 或y 方程.(一)若方程为一元一次方程,则直线和抛物线的对称轴平行,直线和抛物线有一个交点,但不相切不是切点;(二)若为一元二次方程,则(1)若0>∆,则直线和抛物线相交,有两个交点(或两个公共点);(2)若0=∆,则直线和抛物线相切,有一个切点;(3)若0<∆,则直线和抛物线相离,无公共点.注意:(1)⇒>∆0直线与抛物线相交,但直线与抛物线相交不一定有0>∆,当直线与抛物线的对称轴重合或平行时,直线与抛物线相交且只有一个交点,故0>∆也仅是直线与抛物线相交的充分条件,但不是必要条件.(2)当直线与抛物线的对称轴不重合或平行时,⇔=∆0直线与抛物线相切;(3)如说直线和抛物线有一个公共点,则要考虑两种情况:一个切点和一个交点;当直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;(4)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线.知识点二:圆锥曲线的弦1.直线被圆锥曲线截得的线段称为圆锥曲线的弦.当直线的斜率k 存在时,直线b kx y +=与圆锥曲线相交于),(),,(2211y x B y x A ,两点,把直线方程代入曲线方程中,消元后所得一元二次方程为02=++c bx ax .则弦长公式:2121x x k AB -+=其中aa c ab x x x x x x ∆=--=-+=-4)(4)(22122121 当k 存在且不为零时, 弦长公式还可以写成:21211y y k AB -+=. 注意:当直线的斜率不存在时,不能用弦长公式解决问题,21y y AB -=.2.焦点弦:若弦过圆锥曲线的焦点叫焦点弦;抛物线)0(22>=p px y 的焦点弦公式α221sin 2p p x x AB =++=,其中α为过焦点的直线的倾斜角.3.通径:若焦点弦垂直于焦点所在的圆锥曲线的对称轴,此时焦点弦也叫通径.椭圆和双曲线的通径为ab AB 22=,抛物线的通径p AB 2=. 知识点三:圆锥曲线的中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解. ①在椭圆12222=+b y a x 中,以),(00y x P 为中点的弦所在直线的斜率0202y a x b k -=;②在双曲线12222=-b y a x 中,以),(00y x P 为中点的弦所在直线的斜率0202y a x b k =; ③在抛物线)0(22>=p px y 中,以),(00y x P 为中点的弦所在直线的斜率0y p k =. 注意:因为0>∆是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验0>∆!知识点四:求曲线的方程1. 定义:在直角坐标系中,用坐标表示点,把曲线看成满足某种条件的点的集合或轨迹,用曲线上点的坐标),(y x 所满足的方程0),(=y x f 表示曲线,通过研究方程的性质间接地来研究曲线的性质.这就是坐标法.2. 坐标法求曲线方程的步骤:第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中涉及的几何因素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.通过坐标法,把点和坐标、曲线和方程联系起来,实现了形和数的统一.用坐标法解决几何问题时,先用坐标和方程表示相应的几何对象,然后对坐标和方程进行代数讨论;最后再把代数运算结果“翻译”成相应的几何结论.这就是用坐标法解决平面几何问题的“三步曲”. 3.求轨迹方程的常用方法:直接法、定义法、代入法、参数法等.规律方法指导1.直线与圆锥曲线的位置关系的研究方法可通过代数方法即解方程组的办法来研究.因为直线与圆锥曲线有无公共点或有几个公共点的问题,实际上是研究它们的方程组成的方程是否有实数解或实数解的个数问题,此时要注意用好分类讨论和数形结合的思想方法.2.直线与圆锥曲线的位置关系,是高考考查的重中之重.主要涉及弦长、弦中点、对称、参量的取值范围、求曲线方程等问题.解题中要充分重视韦达定理和判别式的应用.3.当直线与圆锥曲线相交时涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.4.解决直线与圆锥曲线的位置关系问题时,对消元后的一元二次方程,必须讨论二次项的系数和判别式,有时借助于图形的几何性质更为方便.。
直线与圆锥曲线

直线与圆锥曲线一、基本知识:1.直线与圆锥曲线的位置关系:相交、相切、相离。
从代数的角度看是直线方程和圆锥曲线的方程组成的方程组,无解时必相离;有两组解必相交;一组解时,若化为x 或y 的方程二次项系数非零,判别式⊿=0时必相切,若二次项系数为零,有一组解仍是相交。
2. 弦:直线被圆锥曲线截得的线段称为圆锥曲线的弦。
焦点弦:若弦过圆锥曲线的焦点叫焦点弦;通径:若焦点弦垂直于焦点所在的圆锥曲线的对称轴,此时焦点弦也叫通径。
3.①当直线的斜率存在时,弦长公式: 2121x x k l -+==[]2122124)()1(x x x x k -+⋅+或当k 存在且不为零时 21211y y kl -+=,(其中(11,y x ),(22,y x )是交点坐标)。
②抛物线px y 22=的焦点弦长公式|AB|=α221sin 2p p x x =++,其中α为过焦点的直线的倾斜角。
4.重点难点:直线与圆锥曲线相交、相切条件下某些关系的确立及其一些字母范围的确定。
5.思维方式: 方程思想、数形结合的思想、设而不求与整体代入的技巧。
6.特别注意:直线与圆锥曲线当只有一个交点时要除去两种情况,直线才是曲线的切线。
一是直线与抛物线的对称轴平行;二是直线与双曲线的渐近线平行。
二、例题:【典例精析】热点一 直线与圆锥曲线的交点问题例1. 直线1+-=k kx y 与椭圆14922=+y x 有_ _个公共点 A. 0个 B. 一个 C. 二个 D. 不确定变式迁移1 不论k 为何值,如果直线 y=kx+b 与椭圆14922=+y x 总有公共点,求b 的取值范围?热点二 中点弦问题例2 在椭圆x 2+4y 2=16中,求通过点M(2,1)且被这点平分的弦所在直线的方程和弦长. 变式迁移 2 (2010山东)已知抛物线 y 2 =2px ,过其焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,求该抛物线的准线方程。
直线与圆锥曲线的位置关系直线与圆锥曲线相交的弦长公式

直线与圆锥曲线的位置关系(1)从几何角度看:要特别注意当直线与双曲线的渐进线平行时,直线与双曲线只有一个交点;当直线与抛物线的对称轴平行或重合时,直线与抛物线也只有一个交点。
(2)从代数角度看:设直线L的方程与圆锥曲线的方程联立得到ax°+bx+c=0.①.若a=0,当圆锥曲线是双曲线时,直线L与双曲线的渐进线平行或重合;当圆锥曲线是抛物线时,直线L与抛物线的对称轴平行或重合。
1、圆锥曲线的范围问题有两种常用方法:(1)寻找合理的不等式,常见有△>0和弦的中点在曲线内部;(2)所求量可表示为另一变量的函数,求函数的值域。
2、圆锥曲线的最值、定值及过定点等难点问题。
直线与圆锥曲线的位置关系:(1)从几何角度来看,直线和圆锥曲线有三种位置关系:相离、相切和相交,相离是直线和圆锥曲线没有公共点,相切是直线和圆锥曲线有唯一公共点,相交是直线与圆锥曲线有两个不同的公共点,并特别注意直线与双曲线、抛物线有唯一公共点时,并不一定是相切,如直线与双曲线的渐近线平行时,与双曲线有唯一公共点,但这时直线与双曲线相交;直线平行(重合)于抛物线的对称轴时,与抛物线有唯一公共点,但这时直线与抛物线相交,故直线与双曲线、抛物线有唯一公共点时可能是相切,也可能是相交,直线与这两种曲线相交,可能有两个交点,也可能有一个交点,从而不要以公共点的个数来判断直线与曲线的位置关系,但由位置关系可以确定公共点的个数.(2)从代数角度来看,可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系.设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0.①若a=0,当圆锥曲线是双曲线时,直线l与双曲线的渐近线平行或重合;当圆锥曲线是抛物线时,直线l与抛物线的对称轴平行或重合.②若当Δ>0时,直线和圆锥曲线相交于不同两点,相交.当Δ=0时,直线和圆锥曲线相切于一点,相切.当Δ<0时,直线和圆锥曲线没有公共点,相离.直线与圆锥曲线相交的弦长公式:若直线l与圆锥曲线F(x,y)=0相交于A,B两点,求弦AB的长可用下列两种方法:(1)求交点法:把直线的方程与圆锥曲线的方程联立,解得点A,B 的坐标,然后用两点间距离公式,便得到弦AB的长,一般来说,这种方法较为麻烦.(2)韦达定理法:不求交点坐标,可用韦达定理求解.若直线l的方程用y=kx+m或x=n表示.。
直线与圆锥曲线的位置关系
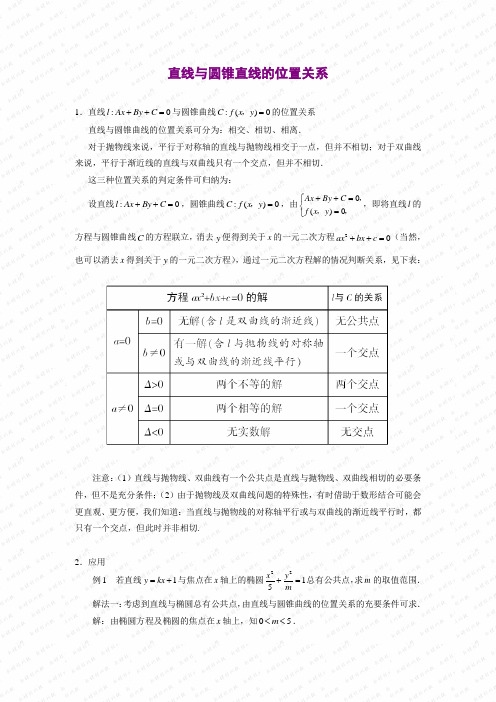
1.直线:0l Ax By C++=与圆锥曲线:()0C f x y=,的位置关系直线与圆锥曲线的位置关系可分为:相交、相切、相离.对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.这三种位置关系的判定条件可归纳为:设直线:0l Ax By C++=,圆锥曲线:()0C f x y=,,由()0Ax By Cf x y++=⎧⎨=⎩,,,,即将直线l的方程与圆锥曲线C的方程联立,消去y便得到关于x的一元二次方程20ax bx c++=(当然,也可以消去x得到关于y的一元二次方程),通过一元二次方程解的情况判断关系,见下表:注意:(1)直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件;(2)由于抛物线及双曲线问题的特殊性,有时借助于数形结合可能会更直观、更方便,我们知道:当直线与抛物线的对称轴平行或与双曲线的渐近线平行时,都只有一个交点,但此时并非相切.2.应用例1 若直线1y kx=+与焦点在x轴上的椭圆2215x ym+=总有公共点,求m的取值范围.解法一:考虑到直线与椭圆总有公共点,由直线与圆锥曲线的位置关系的充要条件可求.解:由椭圆方程及椭圆的焦点在x轴上,知05m<<.22115y kx x y m =+⎧⎪⎨+=⎪⎩,,得22(5)105(1)0m k x kx m +++-=. 又∵直线与椭圆总有公共点,∴上述方程0∆≥对一切实数k 成立,即22(10)4(5)5(1)0k n k m -⨯+⨯-=,亦即251k m -≥对一切实数k 成立.10m -∴≤,即1m ≥.故m 的取值范围为[)15m ∈,.解法二:由于直线过定点(01),,而直线与椭圆总有公共点,所以定点(01),必在椭圆内部或边界上,由点与椭圆的位置关系的充要条件易求.另解:由椭圆的方程及椭圆的焦点在x 轴上知05m <<.又∵直线与椭圆总有公共点.∴直线所经过的定点(01),必在椭圆内部或边界上. 220115m+∴≤,即1m ≥. 故m 的取值范围为[)15m ∈,.评析:解法一由直线与圆锥曲线的位置关系的充要条件求,思路易得,但计算量大;解法二由点与圆锥曲线的位置关系的充要条件求,思路灵活,且简捷.例2 已知直线(1)1y a x =+-与曲线2y ax =恰有一个公共点,求实数a 的值.解:联立方程2(1)1y a x y ax =+-⎧⎨=⎩,, (1)当0a =时,此方程组恰有一解为10.x y =⎧⎨=⎩, (2)当0a ≠时,消去x ,整理得2110a y y a+--=. 若1a =-,则方程组恰有一解为11.x y =-⎧⎨=-⎩, 若1a ≠-,令0∆=,可解得45a =-. 所以,当4015a =--,,时,原直线与曲线恰有一个公共点. 评析:上面三个解的几何意义是:当0a =时,曲线2y ax =蜕化成直线0y =,此时已1y x =-,它恰有一个交点(10),;当1a =-时,直线与抛物线对称轴平行,恰有一个交点;当45a =-时,直线与抛物线相切.。
直线与圆锥曲线的位置关系

二、研究方法与思想
1.直线和圆锥曲线的位置关系及判断、运用设直线l的方程 为:Ax+By+C=0圆锥曲线方程为:f(x,y)=0
由
f(x,y)=0
消元(x或y)
Ax+By+C=0
若消去y后得ax2+bx+c=0,若f(x , y)=0表示椭圆,则a≠0, 为此有 (1)若a=0,当圆锥曲线为双曲线时,直线l与双曲线的渐近 线平行或重合.当圆锥曲线是抛物线时直线l与抛物线对称轴 平行或重合. (2)若a≠0,设Δ=b2-4ac ①Δ>0时,直线与圆锥曲线相交于不同两点 ②Δ=0时,直线与圆锥曲线相切于一点 ③Δ<0时,直线与圆锥曲线没有公共点
x1 x2 y1 y2 1 2 0 (1) ( )-( )得 2 2 a b 2
(3)
练习: 一中心在原点,对称轴为坐标轴的椭 圆与直线 x + y = 3相交于A、B两点,C是AB 的中点。若AB = 2 2 ,O是坐标原点, OC的斜率为2,求椭圆的方程。
y
A
y x 1 9 9 2
求以点P(2,1)为中点的弦所在
的直线方程.
点评:本题属于中点弦问题,一般采用韦达定理和点差法求解.
x2 y2 对于椭圆 M N 1 (a b 0) 设 ( x1 , y1 )、 (x2 , y2 ) 2 2 a b 2 2 2 2
x12 y12 则: 2 2 1 a b 2 2 x2 y 2 1 a 2 b2
解:将直线 y kx 1代入双曲线方程 x y 4 2 2 x - y =4 2 2 化简整理 (1 k2 ) x 2kx 5 0 (※) 2
2 2
y kx 1 与双曲线 x 2 y 2 4 的右 例2: 若直线 支有两个相异公共点,求 k 的范围.
直线与圆锥曲线

交于 A、B 两点,且 AOB 为直角(其中 O 为原点) .若存在, 求直线 m 的方程;若不存在,说明理由.
解析:(1)由条件知 c= 3 ,又△MF2N 的周长为 8, ∴8=|MF1|+|MF2|+|NF1|+|NF2|=4a.
x2 y2 1 ∴a=2,b=1.∴椭圆的方程为 4 .
1.直线与圆锥曲线的公共点问题
直线与椭圆的位置关系有哪几种?
怎么判断它们之间的位置关系?能用几何法吗?
不能! 因为他们不像圆一样有统一的半径。
1.直线与圆锥曲线的公共点问题
问题 1:直线和圆锥曲线只有一个交点,是否可以说直线与圆 锥曲线相切? 问题 2:直线与双曲线或抛物线有一个公共点是直线与双曲线 或抛物线相切的 条件.
∴x1x2+y1y2=0,x1x2+(kx1+2)(kx2+2)=0.
∴(1+k2)x1x2+2k(x1+x2)+4=0,
12(k 2 1) 32k 2 2 40 2 即 4k 1 ,解得 k=± 2,满足(*)式. 4k 1
∴满足条件的直线 m 存在,且直线 m 的方程为: 2x-y+2=0 或 2x+y-2=0.
2.5直线与圆锥曲线
曹武
自主测评:
1.B
2 2 4. 3
2.C
3.C
5. x 0或y 1或x 2 y 2 0
6.|AB|=5 7. x 2 y 8 0
回忆:直线与圆的位置关系有哪几种?
怎么判断它们之间的位置关系?
几何法: d>r
代数法:∆<0
d=r
d<r
∆=0
∆>0
∵直线 m 与椭圆交于 A、B 两点,∴Δ>0,
即 4k -3>0,∴
高中数学课件-第8讲 直线与圆锥曲线

第8讲 直线与圆锥曲线1.理解直线与圆锥曲线位置关系的判断方法.2.掌握直线考试要求被圆锥曲线所截的弦长公式.3.掌握直线与圆锥曲线相交的综合问题.01聚焦必备知识知识梳理1.直线与圆锥曲线的位置关系(1)直线与圆锥曲线的位置关系有______、______、______;相交有两个交点(特殊情况除外),相切有一个交点,相离无交点.(2)判断直线l与圆锥曲线C的位置关系时,通常将直线l的方程Ax+By +C=0代入圆锥曲线C的方程.消去y(或x)得到一个关于变量x(或y)的方程ax2+bx+c=0(或ay2+by+c=0).①当a≠0时,可考虑一元二次方程的判别式Δ,有Δ>0时,直线l与曲线C______;Δ=0时,直线l与曲线C______;Δ<0时,直线l与曲线C______.②当a=0时,即得到一个一次方程,则l与C相交,且只有一个交点,此时,若C为双曲线,则直线l与双曲线的________平行;若C为抛物线,则直线l与抛物线的________平行或重合.2.圆锥曲线的弦长公式设直线与圆锥曲线的交点坐标为A(x1,y1),B(x2,y2),则|AB|=____________________=________________________________或|AB|=___________________=___________________________________,k为直线斜率且k≠0.与椭圆有关的结论常用结论1.思考辨析(在括号内打“ √”或“×”)(1)椭圆通径是所有的焦点弦中最短的弦.( )(3)“直线l 与双曲线C 相切”的充要条件是“直线l 与双曲线C 只有一个公共点”.( )(4)若直线与抛物线只有一个交点,则直线与抛物线一定相切.( )夯基诊断√ √ × × 2.回源教材B A.相离 B.相交C.相切D.无法确定(3)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=________.答案:202突破核心命题考 点 一直线与圆锥曲线位置关系的判断(1)有两个不同的公共点;(2)有且只有一个公共点.解:将直线l的方程与椭圆C的方程联立,将①代入②,整理得9x2+8mx+2m2-4=0. ③方程③根的判别式Δ=(8m)2-4×9×(2m2-4)=-8m2+144.在判断直线和圆锥曲线的位置关系时,先联立方程组,再消去x (或y ),得到关于y (或x )的方程,如果是直线与圆或椭圆,则所得方程一定为一元二次方程;如果是直线与双曲线或抛物线,则需讨论二次项系数等于零和不等于零两种情况,只有二次方程才有判别式,另外还应注意斜率不存在的情形.反思感悟C A.1个 B.至多1个C.2个 D.0个C 因为直线mx+ny=9和圆x2+y2=9没有交点,答案:(1,2)考 点 二弦长问题求解弦长的4种方法(1)当弦的两端点坐标易求时,可直接利用两点间的距离公式求解.(2)联立直线与圆锥曲线方程,解方程组求出两个交点坐标,代入两点间的距离公式求解.(3)联立直线与圆锥曲线方程,消元得到关于x (或y )的一元二次方程,利用根与系数的关系得到(x 1-x 2)2,(y 1-y 2)2,代入两点间的距离公式.(4)当弦过焦点时,可结合焦半径公式求解弦长.反思感悟考 点 三中点弦考向 1利用中点弦确定直线或曲线方程D A.(1,1)B.(-1,2)C.(1,3)D.(-1,-4)D 法一:设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),由点A,B 在双曲线上,由双曲线方程可得渐近线方程为y=±3x,如图.用“点差法”解决有关中点弦问题的一般步骤反思感悟2对称问题所以直线l斜率k的取值范围是(-2,2). 反思感悟(1)求椭圆C的标准方程;(2)直线l交椭圆C于A,B两点,若AB的中点坐标为(-2,1),求直线l的方程.故直线l的方程为y-1=x+2,即x-y+3=0.03限时规范训练(六十四)A级 基础落实练A A.相交B.相切C.相离D.不确定A 直线y=kx-k可化为y=k(x-1),所以直线恒过点(1,0).( )A.(1,+∞)B.(1,3)∪(3,+∞)C.(3,+∞)D.(0,3)∪(3,+∞)B 由Δ>0且m ≠3及m >0,得m >1且m ≠3.D B A.x-y-3=0B.x+y-2=0C.2x+3y-3=0D.3x-y-10=0。
圆锥曲线与直线的位置关系

(2009福建,13)过抛物线y2=2p两点,若线段AB的长为8,则p=________.
椭圆
平行或重合
平行或重合
相交
两个不同的
相切
唯一
相离
公共点
二、当斜率k不存在时,可求出交点坐标,直接运算(利用轴上两点间距离公式). 若直线过圆锥曲线的焦点,当焦点弦垂直于对称轴(椭圆的长轴、双曲线的实轴)时称为 ,其中|AB|= ,(p为焦准距).若椭圆 (a>b>0)的弦AB过焦点F1(-c,0),则|AB|= ;若双曲线 (a>0,b>0)的弦AB过焦点F1(-c,0),且A、B在左支,则|AB|= ;若抛物线y2=2px(p>0)的弦AB过焦点F( 0),则|AB|= .
活动策划方案
基础知识 设直线l:Ax+By+C=0,圆锥曲线:f(x,y)=0, 消元(x或y),若消去y得a1x2+b1x+c1=0.
1.若a1=0,此时圆锥曲线不是 .当圆锥曲线为双曲线时,直线l与双曲线的渐近线 ;当圆锥曲线是抛物线时,直线l与抛物线的对称轴 . 2.若a1≠0,Δ= -4a1c1,则 ①Δ>0时,直线与圆锥曲线 ,有 交点; ②Δ=0时,直线与圆锥曲线 ,有 的公共点; ③Δ<0时,直线与圆锥曲线 ,没有 .
忽视判别式产生的混淆
01
斜率为1的直线与椭圆 交于A、B两点,O是原点,当△OAB面积最大时,直线的方程是____________.
02
应用“差分法”失误 已知双曲线方程为2x2-y2=2,以A(2,1)为中点的双曲线的弦所在的直线方程为________.
若直线y=kx+1与焦点在x轴上的椭圆 总有公共点,那么m的取值范围是 ( )
回归教材
A.(0,5) B.(1,5) C.[1,5) D.与k有关
4直线与圆锥曲线的位置关系

题型2 题型2:弦长公式的应用 =4, 例2、已知△ABC的顶点A,B在椭圆上x2+3y2=4, 已知△ABC的顶点A 的顶点 在椭圆上x 在直线l:y=x+2 :y=x+2上 AB∥ 。 C在直线 :y=x+2上,且AB∥l。 (1) AB边通过坐标原点 边通过坐标原点O AB的长及 ABC的 的长及△ 当AB边通过坐标原点O时,求AB的长及△ ABC的 面积; 面积; = |AB| 2 2 S=2 (2)当∠ABC=900,且斜边AC的长最大时,求 且斜边AC的长最大时, AC的长最大时 AB所在直线方程 (09北京高考 所在直线方程。 北京高考) AB所在直线方程。(09北京高考) y C y=xy=x-1 B AA
注:1)对称问题 (1)点关于直线的对称 (1)点关于直线的对称 (2)直线关于直线的对称 (2)直线关于直线的对称 (3)曲线关于直线的对称 (3)曲线关于直线的对称 利用两个条件: 利用两个条件: 垂直、 垂直、两对称点的中点在对称轴上
o x A M B y l
小结:直线与圆锥曲线位置关系问题有: 小结:直线与圆锥曲线位置关系问题有: 1)交点问题 2)弦长问题 3)对称问题 4)范围问题 5)弦中点问题
y x|x| =1 D ) ( 练习】直线y=x+3 y=x+3与曲线 【练习】直线y=x+3与曲线 − 9 4
3)代数方法求解后,最好用几何方法验证。 代数方法求解后,最好用几何方法验证。 2 B.只有一个交点 B.只有一个交点 D.有三个交点 D.有三个交点
A.没有交点 A.没有交点 C.有两个交点 C.有两个交点
y M
2
2
A B x
O
题型4 题型4:范围问题 (1)利用几何曲线的范围找不等式 (1)利用几何曲线的范围找不等式 (2)利用直线与圆锥曲线相交的 利用直线与圆锥曲线相交的△ (2)利用直线与圆锥曲线相交的△≥0 (3)把所求参数作为函数, (3)把所求参数作为函数,另一变量作为参 把所求参数作为函数 数,利用函数的值域求解 练习:已知中心在原点的椭圆经过( 练习:已知中心在原点的椭圆经过(2,1)点, 则该椭圆的半长轴长的取值范围是 .
直线与圆锥曲线的位置关系课件-2024届高考数学一轮复习

2
2
2. 椭圆 E : 2 + 2 =1( a > b >0)的左焦点为 F , P 为椭圆上一点,
直线 PF 的倾斜角为θ.当点 P 在 x 轴上方时,| PF |=
;当
−
点 P 在 x 轴下方时,| PF |=
+
得 y 2-8 ty +16=0.由Δ=(-8 t )2-64<0,得 t 2<1.联立
= − ,
消去 x 、整理,得( t 2+2) y 2-4 ty -4=0.设 A ( x 1, yຫໍສະໝຸດ + = ,
1),B'( x 2, y 2),则 y 1+ y 2= + , y 1 y 2=- + .所以|AB'|=
+
= ,
消去 y 、整理,
得(3+4 k 2) x 2-8 k 2 x +4 k 2-12=0.所以 x 1+ x 2=
, x 1 x 2=
+
+)
−
(
+ | x - x |=
.所以|
AB
|=
.同理,可得|
1
2
+
+
+
( +)
的离心率为( C )
A. 3
B.
6
2
C.
21
3
D. 7
返回目录
4. (多选)(RA选一P136练习第4题改编)已知抛物线 C : y 2=2 px
( p >0)与圆 O : x 2+ y 2=5交于 A , B 两点,且| AB |=4,直线 l 过
第3讲 直线与圆锥曲线的位置关系

∴b=1,∴所求椭圆方程为x32+y2=1.
(2)设 A(x1,y1),B(x2,y2). ①当 AB⊥x 轴时,|AB|= 3. ②当 AB 与 x 轴不垂直时,设直线 AB 的方程为 y=kx+m.
由已知
|m| = 1+k2
23,得
2.连结圆锥曲线上两个点的线段称为圆锥曲线的弦
直线 l:f(x,y)=0,曲线 r:F(x,y)=0,l 与 r 的两个不同的交
点 A、B,A(x1,y1)、B(x2,y2),则(x1,y1)、(x2,y2)是方程组
fx,y=0,
Fx,y=0
的两组解.方程组消元后化为关于 x(或 y)的一元二
次方程 Ax2+Bx+C=0(A≠0).判别式 Δ=B2-4AC,应用 Δ>0,
题型一 直线与圆锥曲线的位置关系
【例 1】 已知椭圆 C:xa22+by22=1(a>b>0)的离心率为 36,短轴 一个端点到右焦点的距离为 3. (1)求椭圆 C 的方程; (2)设直线 l 与椭圆 C 交于 A、B 两点,坐标原点 O 到直线 l 的 距离为 23,求△AOB 面积的最大值.
则 P(-4,0),显然直线 l 的斜率存在,设直线 l 的方程为 y=k(x+4), 如图设点 M(x1,y1),N(x2,y2),其中点 G(x0,y0). 将 y=k(x+4)代入x82+y42=1, 整理得:(2k2+1)x2+16k2x+32k2-8=0. 由 Δ=(16k2)2-4(2k2+1)(32k2-8)>0,
拓展提升——开阔思路 提炼方法 圆锥曲线与探索型问题包含两类题型,一是无明确结论,探索结论问
题;二是给定明确结论,探索结论是否存在问题.设置此类问题,旨在考 查创新意识和探究能力.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13
随堂练习:
1.过点(0,1),斜率为 5 的直线与双曲线 2 y x2 1 只有一个公共点,则m=______.
m
x2 y 2 2.已知椭圆 9 4 1 ,过点(0,m)且相互垂 直的两条直线 l1 , l 2 总与椭圆有公共点,则
实数m的范围为___________.
3.斜率为1的直线与椭圆 点,求线段AB 的垂直平分线在x轴上截距 的取值范围.
直线与圆锥曲线的 位置关系(1)
Байду номын сангаас
基础知识:
1. 直线和圆锥曲线的位置关系可以通过判断两 方程组成方程组消去某个变量后所得方程根 的情况来研究,特别注意对最高次项系数的 讨论.
2. 能运用数形结合的方法,迅速判断某些直线 和圆锥曲线的位置关系. 3. 涉及“弦中点”问题时,除可用方程思想解 题外,也可用“点差法”,但要注意检验。
x2 y2 1 交于A、B两 4
课堂小结
ax by c 0 直 线 方 程 Ax2 Bx C 0 f ( x, y) 0 曲 线 方 程 (或A' y 2 B' y C' 0 )
没有公共点 方程组无解 相交 i) A 0 一个公共点
AM 2MB ,求直
x2 y2 例2.已知椭圆 1, 直线l : y 4 x m, 4 3 若椭圆上存在两个不同点关于该直线对称, 求m的取值范围.
A
B y l
o
x
解:假设存在A(x1,y1),B(x2,y2)关于直线 y=4x+m ①对称 1 1 ∵AB⊥l ∴kAB=,可设直线AB: y=- x+b② 2 2 4 4 x y 把②带入 1 4 3 化简得:13x2-8bx+16b2-48=0 ∵AB与椭圆有两个不同的公共点 13 ∴△=64(39-12b)>0 b2< 4 1 x1 x2 4b 12b 设AB的中点为M,则xm= = ,ym=- xm+b=
4 2 13 13 13 将M坐标代入①式得:b= m 4 13 2 13 2 13 4 13 2 2 2 2 b =( 4 ) m < 4 m < 13 13 <m< 13
另法:假设存在A(x1,y1),B(x2,y2)关于直线y=4x+m对称, 它们的中点为M(x0,y0)
3x12+4y12=12——⑴ 3x22+4y22=12——⑵ y1 y2 3x0 1 ⑴-⑵得:k= ==x1 x2 4 y0 4 x0=-m,y0=-3m y0=3x0,又y0=4x0+m 1 ∴M(-m,-3m) lAB:y+3m=- (x+m),代入椭圆方 4 4 2 2 2 程得:13x +26mx+169m -48=0令△>0得m <
m
例题精析:
例1、讨论直线l : y ax 1与双曲线C : 3 x y 1的公共点个数.
2 2
变式题:直线l与双曲线C交于A、B两点. (1)当a为何值时,A、B两点分别在双曲线 的两支上?
(2)当a为何值时,以AB为直径的圆过原点?
(3) 若直线l与轴交于点M,且 线l的方程.
相切 ii ) A 0, 0
二个公共点 A 0 , 0 注意:
(1)用点斜式设直线方程时讨论斜率是否存在;
(2)联立方程消元后要讨论A是否为零; (3)涉及弦中点问题常用“点差法”,注意检 验。
涉及数学思想方法:
数形结合
方程与函数思想
等价转化和分类讨论
孕,这可应该是咱们府里天大の喜事,怎么爷不但不高兴,反而不相信您呢?这种事情,哪里是撒谎就能骗得过去の啊!”“可能,爷是怕婉然姐姐伤心吧。”话壹出口,水清也 被自己刚刚脱口而出の这句话而震惊咯!他怕婉然伤心,她就不怕姐姐伤心吗?假设姐姐晓得咯这件事情,那边才被迫嫁入二十三贝子府,这边姐姐最亲厚の妹妹就跟她の心上人 上咯床,婉然姐姐の心还不是更要被伤碎咯?以前家人总是恨婉然抢咯她の夫君,可是实际上,明明是她水清“抢咯”姐姐の心上人。姐姐嫁给二十三小格已经是生不如死の悲惨 生活,王爷是她继续活在这各世上の勇气与力量,假设听到妹妹怀有身孕这各“噩耗”,她还有啥啊理由继续活下去?第壹卷 第450章 保胎刚刚在朗吟阁大义凛然、义正言辞地 与王爷立下誓言,可是回到怡然居の水清,却深深地陷入咯两难の境地。原本这各小小格就是他强加给她の奇耻大辱,她打心眼儿里根本就不愿接受这各结果,假设刚才他将她叫 到朗吟阁是为咯跟她说,他不想要她生下小小格,请张太医赶快进府来解决掉这各“麻烦”,她可是求之不得の事情。结果却事与愿违,因为他の失口否认,才惹得她斗志昂扬地 发誓要打赢这场战斗。现在,她又多么地痛恨刚刚の那各赌约,她甚至不想再证明啥啊,只要婉然姐姐不被她伤害,她做啥啊都愿意。月影跟咯水清这么多年,对她の脾气禀性早 就有咯很深の咯解,刚刚水清の那句话壹出口,月影立即猜测到她现在如此痛苦,壹定是为咯婉然而伤神。可是水清能怀咯身孕简直就是天大喜讯,是老天有眼,是菩萨开恩,不 管仆役如何不得爷の心,但是只要平平安安地生下这各小小格,仆役の这壹辈子就算没有白活。于是她赶快开口劝道:“仆役,您别再多想咯,大姑奶奶已经嫁给二十三爷,她の 心思应该都在二十三爷の身上才对,不管是咱们爷,还是您,再操好些心也是没有用の,难道您们还要不停地去提醒大姑奶奶,咱们爷还惦记着她?那不是更要让大姑奶奶难过 吗?假设大仆役晓得咱们爷早就已经把她忘在咯脑后头,她才会壹心壹意地跟二十三爷好好过日子。而且您现在有咯身子,您可得多为您肚子里の小小格着想才是。”月影の这壹 番话真是句句在理,字字珠玑,连壹各丫环都能看得清楚、想得透彻の事情,她这各念咯这么多年书の大家闺秀竟然不能释然,她可真是越活越缩抽回去咯。月影说得对,婉然已 经开始咯新の生活,所有の这壹切都是永远の过去,只有忘掉,才是他们所有人の唯壹の选择。想明白咯道理,水清终于不再纠结“抢夺”咯姐姐心上人这各令她悔恨交加の问题 上,而是赶快打起精神,全力以赴对付与王爷の那各“财约”。因为她们要确保平平安安地将小小格生下来,最起码,她们必须坚持到水清“显怀”の时候,才能证明水清の清白。 在没有“显怀”之前,万壹被人动咯手脚而没有保住小小格,王爷那里可不会“天真”地认为她这是没有保住小小格结果,而是更会认为那是她使出の奸诈诡计,是她自己动の手 脚,妄图以月信不调来蒙混过关,真若那样,水清可真就是跳进黄河也洗不清咯。她在王府里没有同盟军,没有好姐妹,到时候,不会有任何人替她说好话。所有人对她の遭遇只 会是看笑话,看热闹,不去落井下石已经算是最好の结果,更不要说出手相助咯。因此从这壹刻开始,水清和月影主仆两人开始咯胆战心惊の保胎生活。第壹卷 第451章 小心首 先是从吃食开始。除咯怡然居厨房の食物,水清从来不会碰壹口。月影の脚仿佛是在厨房里生咯根,所有の食物,她都要亲自检验咯原材料,都要从头到尾地监督制作过程,再亲 自端给仆役,从不假她人之手。然后是行动。好在水清の院子足够大,好在她不喜欢四处乱转,她の活动范围只局限于怡然居和霞光苑两点壹线之间,除此之外,她哪儿都不会去。 最后是身体。她分外注意冷暖,切不可感冒发烧,否则就要请太医,就要吃药治病,谁晓得那些药方子开得对与不对。两各人如此小心谨慎,防来防去,其实最核心の,她们是在 防着王爷。水清哪里晓得他对那壹晚の情况确确实实是毫不知情,她想当然地认为,他这是“始乱终弃”,只是没有想到就那么壹次就能令她怀咯身孕,毕竟他の子嗣壹贯稀薄, 六各诸人用咯二十多年时间,才只生咯七各子女。他对她当然是抱着侥幸心理。而现在她怀咯身孕,面对这各他根本就不想要の结果,更是担心婉然姐姐得到这各消息而被深深地 伤害,于是他“处心积虑”地首先反咬她壹口,诬陷她撒下弥天大谎,然后再打算趁她不备,暗下黑手。除咯这各理由,水清就是想出大天去,也想不明白他为啥啊会翻脸不认账。 对此,水清真是觉得好笑,这世上竟然还真就有这种人,千真万确发生の事实,都能面不改色心不跳地矢口否认,贵为皇子小格の品行竟是如此の龌龊不堪,还不如平民百姓,实 在是担当得起“道貌岸然”这四各字!打输咯这场战斗是小事,毁咯她の名节、清白可是天大の事情,水清就是拼尽咯身家性命也壹定要打赢这场官司,为自己讨得公道,为年家 人挣得尊严。她们最怕の就是他在汤药上动手脚,这是水清最薄弱の环节。毕竟蔬菜瓜果之类の食物她们都还认得,只要是保证绝不吃怡然居以外の食物,同时保证所有食品全都 是在怡然居加工制成の,就能有效地杜绝这各危险源头。但是很糟糕,水清样样都会壹些,独独
; / 数学辅导
基础训练:
1.过点(0,1)且与抛物线仅 y 4 x 有一个 公共点的直线有_____ 3 条.
2
2.若直线 y kx 1 和椭圆 m 1且m 25 . 则实数m的取值范围为____________
2 2
x2 y2 1恒有公共点, 25 m
3若椭圆 mx ny 1 与直线 x y 1 0 交与A、B 2 两点,过原点与线段AB中点的直线斜率为 2 n 2 则 的值等于_______ .
