恒定总流的能量方程PPT课件
合集下载
流体力学课件 第4章恒定总流基本方程

如图:qv1=0.004m3/s, qv1=0.0005m3/s,h=5m,D=0.0 5m,忽略损失,修正系数取1, 求作用水头H,以及真空室的 真空值pv2 解 : 如图 , 取喷嘴轴线 0-0 为 计 算 基 准 , 渐 变 流 断 面 11,2-2,3-3,4-4,5-5 为 计 算 断面 , 计算点取在轴线及液 面上,压强取相对压强.
qV 3 qV 2 v1 0, v3 , v4 A3 A4 qV 3 qV 1 qV 2
Ai
D
qV 1
qV 3
qV 2
d i
4
2
带入数据解得:H
0.927 m
列断面4-4,5-5的能量方程,近似认为p5=p2,则
1 qV 2 2 p2 h ( ) 2 g A5 g
8
2.1恒定总流伯努利方程适用条件 *、不可压缩流体的恒定流动; *、质量力只有重力;
*、过流断面必须是渐变流或均匀流断面; *、总流的流量沿程不变;
*、两过流断面间除水头损失外,无能量输出或输入。
2.2总流伯努利方程的物理及几何意义(P94)
9
总流伯努利方程的物理及几何意义
项目 名称 位置水头 压强水头 物理意义 单位重量流体的位置势能 单位重量流体的压强势能
19
讨论:
2 v12 v2 p1 ( a ) g ( z1 z2 ) p2 pw 2 2
*、流体密度与外界密度相同时,或两计算点高度相同时:
p1
v12
2
p2
全压
2 v2
2
pw
全压
*、当气流密度远大于外界空气密度时,相当于液体总流, 空气密度忽略不计,认为各点的当地压强相同:
水力学课件 第三章_水动力学基础

(1) 渐变流过水断面近似为平面;
(2) 恒定渐变流 过水断面上,动水压强近似 地按静水压强分布。
z p C
取过水断面上任意两相邻流线 间的微小液柱。轴向受力分析:
1) 表面力
液柱上、下底面 的动水压力 pdω与(p+dp)dω
液柱侧面
的动水压力及摩擦力趋于零;
液柱底面的 摩擦力,与液柱垂直。
2) 质量力 自重分力:γdωdn cosα 惯性力:恒定渐变流条件下略去不计。
用欧拉法描述液体运动时,液体运动质点的加速度是当地加速 度与迁移加速度之和。
当地加速度: 固定点速度随时间的变化,
第一项:
ux
/ t,u y
/ t,uz
/ t
迁移加速度:等号右边括号内项反映了在同一时刻因地 点变更而形成的加速度。
§3—2 欧拉法的若干基本概念
1. 迹线和流线 迹线则是同一质点在一个时段内运动的轨迹线。
活学活用
பைடு நூலகம்
恒定渐变流中,同一过水断面上的动水压强近似按地静水压强分布 恒定均匀流中,同一过水断面上的动水压强精确地按静水压强分布
对恒定均匀流, z p C
同一过水断面上:
对于断面AB
pA
zA
pB
zB
C1
pA ? pB ?
对于断面CD
pC
zC
pD
zD
C2
pC ? pD ?
pA
zA
pB
zB
pC
zC
C
pA ? pB ? pC ?
§3—3 恒定总流的连续性方程
考虑到: (1)在恒定流条件下,元流的形状与位置不随时间改变; (2)不可能有液体经元流侧面流进或流出; (3)液流为连续介质,元流内部不存在空隙。
(2) 恒定渐变流 过水断面上,动水压强近似 地按静水压强分布。
z p C
取过水断面上任意两相邻流线 间的微小液柱。轴向受力分析:
1) 表面力
液柱上、下底面 的动水压力 pdω与(p+dp)dω
液柱侧面
的动水压力及摩擦力趋于零;
液柱底面的 摩擦力,与液柱垂直。
2) 质量力 自重分力:γdωdn cosα 惯性力:恒定渐变流条件下略去不计。
用欧拉法描述液体运动时,液体运动质点的加速度是当地加速 度与迁移加速度之和。
当地加速度: 固定点速度随时间的变化,
第一项:
ux
/ t,u y
/ t,uz
/ t
迁移加速度:等号右边括号内项反映了在同一时刻因地 点变更而形成的加速度。
§3—2 欧拉法的若干基本概念
1. 迹线和流线 迹线则是同一质点在一个时段内运动的轨迹线。
活学活用
பைடு நூலகம்
恒定渐变流中,同一过水断面上的动水压强近似按地静水压强分布 恒定均匀流中,同一过水断面上的动水压强精确地按静水压强分布
对恒定均匀流, z p C
同一过水断面上:
对于断面AB
pA
zA
pB
zB
C1
pA ? pB ?
对于断面CD
pC
zC
pD
zD
C2
pC ? pD ?
pA
zA
pB
zB
pC
zC
C
pA ? pB ? pC ?
§3—3 恒定总流的连续性方程
考虑到: (1)在恒定流条件下,元流的形状与位置不随时间改变; (2)不可能有液体经元流侧面流进或流出; (3)液流为连续介质,元流内部不存在空隙。
流体力学课件_第3章_一元流体动力学基础(下)

A
2. 急变流
动压强特性:在断面上有
3.控制断面的选取: 控制断面一般取在渐变流过水断面或其 极限情况均匀流断面上。
想一想
为什么在总流分析法中需引入断面平均 流速? 即目的所在?
因为总流过水断面上各点的流速是不相等的。为了 简化总流的计算,所以引入了断面平均流速来代替 各点的实际流速。
第五节 恒定总流连续性方程
取距基准面的铅直距离来分别表示相应断面的总水头与测 压管水头。 • 测压管水头线是根据总水头线减去流速水头绘出的。
第十一节 恒定气流能量方程式
虽然恒定总流伯努利方程是在不可压缩这样 的流动模型基础上提出的,但在流速不高(小于 68m / s ) ,压强变化不大的情况下,同样可以应 用于气体。
p1 α v p2 α v z1 + + = z2 + + + hw γ 2g γ 2g
二、控制断面的选取
1、渐变流的性质 渐变流过水断面近似为平面,即 渐变流是流线接近于平行直线的流动。均匀流是渐变 流的极限。 2、动压强特性:在渐变流同一过水断面上, 各点动 压强按静压强的规律(2-11)式分布,如图的c-c断面, 即
想一想
图中,过水断面上的动压强分布符合静 压强分布规律的为: A 直管处 B 弯管处
第3章 一元流体动力学基础(下)
重点内容: 1、总流分析方法; 2、恒定总流能量方程 1)恒定总流能量方程 2)能量方程的扩展 3)能量方程的应用 掌握内容: 1、连续性方程 2、实际流体元流能量方程
第五节 补充内容 (伯努利方程基础概念)
一、概念 1.控制体:即在流场中划定的一个固定的 空间区域,该区域完全被流动流体所充满。 2.控制断面:即控制体(流管)有流体流 进流出的两个断面,如图中的1-1,2-2断面。
高二物理竞赛课件:恒定总流能量方程

能量守恒定律:流体系统中能量随时间的变化率等于作用于控制体
上的表面力、系统内流体受到的质量力对系统内流体所作的功和外
界与系统交换的热量之和。
输运公式为
dN dt
t
dV
CV
n dA
CS
=u
2 2
,
N
V
u
2 2
dV
η表示单位质量流体具有的能量;
N 为系统内流体具有的总能量。
能 量
d dt
V
(u
2
2
)dV
t
CV
(u
2
2
)dV
CS
n (u
2
2
)dA
守
恒
定 律
d dt
V
(u
2
2
)dV
Байду номын сангаас
CV
f
dV
CS
pn
dA Q
2023/12/25
外界与系统单位
D质on量gh力ua功U率niversity表面力功率
时间交换的热量
2
一般形式的能量方程:
t
CV
(u
2
2
)dV
CS
n (u
2
2
)dA
里管就是利用这个原理,在管道中造成流速差,引起压强变化,通过压差的测 量来求出流速和流量。
2023/12/25
Donghua University
7
※皮托管 —— 测量流速
测压管
法国人皮托,1773年
皮托管
沿流线B – A 列伯努利方程:
2 B
pB
pA
2
pB gH0 pA g(H 0 h)
第四章 能量方程

(1)渐变流过水断面近似为 平面;
(2)恒定渐变流过水断面上, 动水压强的分布与静水压 强的分布规律相同。
现证明如下:
在过水断面上、任意两相邻流线间取微小柱体,长为dn ,底面 积为 dA 。(如图示)。分析该柱体所受轴线方向的作用力:
上下底面的压强: p与p dp
柱体自重沿轴线方向的投影dAdncos ,其中: 为重力
1
H v0
c
渐变流断面
d 2
A
0
vc
0
c 1
水箱的来流断面和收缩断面是渐变流断面
渐变流断面上动水压强分布规律: 水流射入大气中时的渐变流断面,动水压强
不服从静水压强分布规律 孔口出流收缩断面,其上流线近似平行, 各点均与大气接触,压强约为大气压强。
固体边界约束的渐变流过水断面,动水压强符合静水压 强分布规律.
伯诺力方程中的三项分别表示单位重量液体的 三种不同的能量形式:
Z1
p1
u12 2g
Z2
p2
u22 2g
hw
z为单位重量液体的位置势能(位能)。
u2/2g为单位重量液体的动能。
p/为单位重量液体的压能(压强势能) z+p/ =该质点所具有的势能
z+p/ + u2/2g=总机械能
hw'为单位重量的流体从断面1-1流到2-2过程中由 于克服流动的阻力作功而消耗的机械能。这部分 机械能转化为热能而损失,因此称为水头损失。
将⑥⑦⑧代入⑤。并注意到Q1=Q2=Q 再两边除以rQ,则
Z1
p1
1V12
2g
Z2
p2
2V22
2g
hw12
三、能量(伯诺力)方程的几何表示——水头线 总流伯诺力方程的量纲:
(2)恒定渐变流过水断面上, 动水压强的分布与静水压 强的分布规律相同。
现证明如下:
在过水断面上、任意两相邻流线间取微小柱体,长为dn ,底面 积为 dA 。(如图示)。分析该柱体所受轴线方向的作用力:
上下底面的压强: p与p dp
柱体自重沿轴线方向的投影dAdncos ,其中: 为重力
1
H v0
c
渐变流断面
d 2
A
0
vc
0
c 1
水箱的来流断面和收缩断面是渐变流断面
渐变流断面上动水压强分布规律: 水流射入大气中时的渐变流断面,动水压强
不服从静水压强分布规律 孔口出流收缩断面,其上流线近似平行, 各点均与大气接触,压强约为大气压强。
固体边界约束的渐变流过水断面,动水压强符合静水压 强分布规律.
伯诺力方程中的三项分别表示单位重量液体的 三种不同的能量形式:
Z1
p1
u12 2g
Z2
p2
u22 2g
hw
z为单位重量液体的位置势能(位能)。
u2/2g为单位重量液体的动能。
p/为单位重量液体的压能(压强势能) z+p/ =该质点所具有的势能
z+p/ + u2/2g=总机械能
hw'为单位重量的流体从断面1-1流到2-2过程中由 于克服流动的阻力作功而消耗的机械能。这部分 机械能转化为热能而损失,因此称为水头损失。
将⑥⑦⑧代入⑤。并注意到Q1=Q2=Q 再两边除以rQ,则
Z1
p1
1V12
2g
Z2
p2
2V22
2g
hw12
三、能量(伯诺力)方程的几何表示——水头线 总流伯诺力方程的量纲:
流体力学第四章能量方程ppt完美版

tCV u 2 g d z V CS v n u 2 g d z A Cp S n v dA
pnvd A pnd v A vdA
CS
CS
CS
为0
管道流动
tCV u v 2 2 g d z V CS v n u v 2 2 g z p d A 0
例题
• 自然排烟锅炉,烟囱直径d=1m,烟气流
量Q=7.135m3/s。烟气密度ρ=1.2kg/m3
,烟囱的压强损失Pl=0.035(H/d)( v2/2g),为使烟囱底部入口断面的真空度
不小于10mm水柱。求烟囱的高度。
2
H
1
例题
• 消防喷枪如图所示,已知管道直径
d1=150mm,喷嘴出口直径d2=50mm, 测得水管相对压强为105Pa, (1)如果倾斜角为30度,求射程高度h; (2)要使射程高达h=6m,则倾斜角是多少?
总流的伯努利方程与元流的伯努利方程区别 (1)z1、z2——总流过流断面上同一流线上的两个 计算点相对于基准面的高度; (2)p1、p2——对应z1、z2点的压强(同为绝对压 强或同为相对压强); (3)v1a、v2a——断面的平均流速
计算点相对于基准面的高度;
流体力学第四章能量方程
11黏性流体总流的伯努利方程
A
gv z
p g
dA
gq V z
p g
缓变流,Z+P/ρg为常数
A
gv
v2 dA
2g
1 A
3
A
v va
dA gq V
v2 a
2g
gq V
v2 a
2g
3
1 A
A
v va
dA
连续性方程能量方程ppt课件

压强标准要相同。 ⑶ 动能修正系数α:
一般可以取α1=α2= 1.0 计算。
22
4.应用注意事项:
⑷ 注意水头损失hw的取舍。 ⑸ 当一个问题中有2-3个未知数的时 候,能量方程需要和连续方程、动量 方程组成方程组联合求解。
⑹ 列方程时,不遗漏物理量。
23
5.能量方程的特点:
没有涉及边界对水流的作用力。 是一个动力学方程。
渐变流 断面
5
推导中,产生三类积分: • (1) ∫Q(z+ p/γ)γdQ • (2) ∫Q(u12/2g )γdQ • (3) ∫Q(hw’ )γdQ
6
1.方程的建立:
势能+动能=总能量
αv2 2g
—— 单位动能
7
实际不可压缩恒定总流的能量方程:
z1
p1
α1v12 2g
z
2
p2
H0= Z+p/γ+v2/2g —— 总水头
H01=H02 +hw ,即H01 > H02
10
各断面的位置水头、测压管水头和 总水头端点的连线分别称为位置水头线、 测压管水头线和总水头线。
11
12
J — 水力坡度,
hw J=
l
13
14
对于实际液体(hw>0),总水头线总 是一条下降的曲线或直线,它下降的数值 等于两个过水断面之间水流的水头损失。
24
6.能量方程的主要应用:
(a) 求解:平均流速,动水压强,
作用水头,水头损失,流向等
(b) 毕托管(流速仪) (c) 文丘里流量计 (d) 孔口出流,水泵与虹吸管 计算等
25
例2:输水圆管全管路 hw =3.5m。已知
一般可以取α1=α2= 1.0 计算。
22
4.应用注意事项:
⑷ 注意水头损失hw的取舍。 ⑸ 当一个问题中有2-3个未知数的时 候,能量方程需要和连续方程、动量 方程组成方程组联合求解。
⑹ 列方程时,不遗漏物理量。
23
5.能量方程的特点:
没有涉及边界对水流的作用力。 是一个动力学方程。
渐变流 断面
5
推导中,产生三类积分: • (1) ∫Q(z+ p/γ)γdQ • (2) ∫Q(u12/2g )γdQ • (3) ∫Q(hw’ )γdQ
6
1.方程的建立:
势能+动能=总能量
αv2 2g
—— 单位动能
7
实际不可压缩恒定总流的能量方程:
z1
p1
α1v12 2g
z
2
p2
H0= Z+p/γ+v2/2g —— 总水头
H01=H02 +hw ,即H01 > H02
10
各断面的位置水头、测压管水头和 总水头端点的连线分别称为位置水头线、 测压管水头线和总水头线。
11
12
J — 水力坡度,
hw J=
l
13
14
对于实际液体(hw>0),总水头线总 是一条下降的曲线或直线,它下降的数值 等于两个过水断面之间水流的水头损失。
24
6.能量方程的主要应用:
(a) 求解:平均流速,动水压强,
作用水头,水头损失,流向等
(b) 毕托管(流速仪) (c) 文丘里流量计 (d) 孔口出流,水泵与虹吸管 计算等
25
例2:输水圆管全管路 hw =3.5m。已知
恒定总流能量方程(伯努利方程)

恒定总流能量方程(伯努利方程)
恒定总流能量方程式也称作恒定总流伯努利方程式,是流体力学领域极其适用的一个公式,其表达式以下:
式中, h1、 h2——流体截面被研究点相关于选定基准面的高度;
p 1、p2——流体截面被研究点的压强;
v 1、v2——流体截面被研究点的均匀流速;
h l1-2——流体在两截面被研究点之间的水头损失。
注意:截面上的被研究点能够为截面上的随意点。
伯努利方程的合用性剖析:
(1)方程是在恒定流速前提下推导获得。
从理论大将讲,没有绝对的恒定流;可是,关于多半流动,流速随时间变化迟缓,由此所致使的惯性力较小,方程仍旧合用。
(2)方程的推导以不行压缩流体为基础。
当在工程应用中,它仍旧合用于压缩性极小的液体流动,也合用于惯例的大部分气体流动。
只有当气体压强变化较大、流速很高时,才需要考虑气体的可压缩性。
(3)方程推导所选流体截面处于渐变流段。
渐变流是指各流线靠近于平行直线的流动。
这在一般条件下是要恪守的,特别是断面流速特别大时,更应当严格恪守。
伯努利方程的扩展应用:
(1)关于两截面之间有能量输出(水轮机或汽轮机)或输入(水泵或风机)的场合。
(2)关于两截面之间有分流或合流的场合。
方程的推导是依据两截面间没有分流或合流的状况下推获得的。
可是,关于两截面间存在两分流或合流的状况,方程仍旧合用。
恒定总流的能量方程 PPT

u22 γdQ 2g
hw 'γdQ
Q
dA1 Q
Q
Q
Q
1(z1
p1 γ
)γu1dA1
u12 2g
γu1dA1
(z2
p2 γ
)γu2dA2
u22gd2 Aγu22dA2 hw 'γdQ
A1
A1
A2
A2
Q
2
p1/γ z1
u1
Ⅰ类积分
Ⅱ类积分
u2
p2/γ
Ⅲ类积分 2
3.4.1.2 实际液体恒定元流的能量方程
对于实际液体,因为存在粘性, 在流动过程中,要消耗一部分能量用 于克服摩擦力,液体的机械能沿程减 少,即存在能量损失。
在重力作用下,实际元流从1运动到2
p u2
p u2
z 1 1 z 2 2
1 2g 2 2g
2 1
令: hw’ = 单位重量的液体 从断面1-1运动至断面2-2所损失的能量,则
3.4.2 实际液体恒定总流的能量方程
3.4.2.1 实际液体恒定总流能量方程的推导 3.4.2.2 能量方程物理意义和几何意义 3.4.2.3 总水头线和测压管水头线 3.4.2.4 能量方程的应用 3.4.2.5 注意事项 3.4.2.6 应用举例
不可压缩实
dA
际液体、恒
定元流的能
量方程
图 闸孔出流
γ
Q 2g
γdQ hw 'γdQ
Q
(z1
Q
p1 γ
)γu1dA1
Q
u12 2g
γu1dA1
(z2
水力学系统讲义课件第三章水动力学基础

ux t
ux
ux x
uy
ux y
uz
ux z
ay
uy t
ux
uy x
uy
uy y
uz
uy z
az
uz t
ux
uz x
uy
uz y
uz
uz z
4
a du du(x, y, z,t) u u dx u dy u dz
z p C
g
中,各项都为长度量纲。
位置势能(位能): Z 位置水头(水头) : Z
pA /
pB /
压强势能(压能): p
测压管高度(压强水头) : g
zA
O
zB
O
单测位压势管能水:头:z
p
g
35
恒定总流的能量方程
理想液体恒定微小流束能量方程推导
动能定理:某物体在运动过程中动能的改变等于其在同 一时间内所有外力所做的功。
解:ax
ux t
ux
ux x
uy
ux y
4y 6x 4y 6xt 6t 6y 9xt 4t
4y 6x 1 6t2 6t2
将t 2, x 2, y 4代入得,ax 4m / s2 同理可得, ay (6 y 9x) (4 y 6x)9t 2 (6 y 9t)6t 2
Q A
49 60
umax
24
(2)过流断面上,速度等于平均流速的点距管壁的距离。
1/ 7
第四章--恒定总流基本方程PPT优秀课件

k mv
元流单位时间内通过过流断面的动量:
dKdm u(ud)A u
教师:朱红钧
总流单位时间通过整个过流断面其相应的动量值为:
d K (u) d u A (u 2 d)i A
Av 2 A i q A v v i q v v
为了将上式中的积分用断面平均流速v来表达
引入动量修正系数
v3
或
z 1 p g 12 1 v g 1 2 z 3p g 32 3 v g 3 2 h w 图1 4,-3 11 分流
教师:朱红钧
(2)汇流
满足总流的总能量守恒 ,即
g qV 1 ( z1
p
g1
1v
2 1
2g
)
gqV 2 (z2
p
g2
2v 2g
2 2
)
gqV 3 (z3
二、分叉流的总流连续性方程
在有分流汇入及流出的情况下, 连续性方程只需做相应变化, 流量的总流入=流量的总流出。
Q1
Q1= Q2+ Q3
Q3 Q2
教师:朱红钧
v1A 1v2A 2v3A 3
或
q V1q V2q V3 1
2
qV2
2
节点连续性方程:
n
qV i 0
i1
qV1
3
1 节点 3
qV3
式中: n—支管数。流出节点的流量为“-”,流
p
3
g
3v
2 3
2g
)
g q V 1 h w 1 , 3 g q V h2 w 2 , 3
1
3
1
v1
v3 2
v2
3 2
图4-12 汇流
元流单位时间内通过过流断面的动量:
dKdm u(ud)A u
教师:朱红钧
总流单位时间通过整个过流断面其相应的动量值为:
d K (u) d u A (u 2 d)i A
Av 2 A i q A v v i q v v
为了将上式中的积分用断面平均流速v来表达
引入动量修正系数
v3
或
z 1 p g 12 1 v g 1 2 z 3p g 32 3 v g 3 2 h w 图1 4,-3 11 分流
教师:朱红钧
(2)汇流
满足总流的总能量守恒 ,即
g qV 1 ( z1
p
g1
1v
2 1
2g
)
gqV 2 (z2
p
g2
2v 2g
2 2
)
gqV 3 (z3
二、分叉流的总流连续性方程
在有分流汇入及流出的情况下, 连续性方程只需做相应变化, 流量的总流入=流量的总流出。
Q1
Q1= Q2+ Q3
Q3 Q2
教师:朱红钧
v1A 1v2A 2v3A 3
或
q V1q V2q V3 1
2
qV2
2
节点连续性方程:
n
qV i 0
i1
qV1
3
1 节点 3
qV3
式中: n—支管数。流出节点的流量为“-”,流
p
3
g
3v
2 3
2g
)
g q V 1 h w 1 , 3 g q V h2 w 2 , 3
1
3
1
v1
v3 2
v2
3 2
图4-12 汇流
11-3、恒定流能量方程

p
h
2.理想流体稳定流动能量方程
伯努利方程
1kg流体带入1—1截面的总机械能为
v12 p1 E入 gz1 2 1
1kg流体在2—2截面处带出的总机械能为
2 v2 p 2 E出 gz2 2 2
能量守恒定律,对稳定流动系统应有:
E入 E出
2 v12 p1 v2 p2 gz1 gz2 2 1 2 2
§11-3、恒定流能量方程
一、均匀流过流断面上的压强分布 二、恒定元流能量方程 三、恒定总流能量方程 四、能量方程的应用 五、恒定气流能量方程
一、均匀流过流断面上的压强分布
均匀流:质点流速大小和方向沿流向不发生变化 的流动。 非均匀流:质点流速大小和方向沿流向发生变化 的流动。
急变流:质点流速大小和方向沿流向变化显著的流动。 渐变流:质点流速大小和方向沿流向变化缓慢的流动。
p1
位置 速度 压强 水头 流体在管道中流动时,不同断面上的位置高度、 水头 水头 水头 损失 测压管高度和测速管高度可以互相转换,但后一 断面的三种高度和与前一个断面的三种高度和之 差总是等于该两断面上测速管的液面高差。
四、能量方程的应用
1、应用能量方程时应注意的问题 2、能量方程的应用实例 3、应用能量方程解题的步骤
理想流体稳定流动:
从截面1—1流入,截面2—2流出。
基准水平面:0—0水平面(可任意选定)。
流 压 标 速 力 高
v2 p2 z2
截面面积
流 压 标 速 力 高
A2
2
v1 p1 z1 A 1
流体密度
截面面积 流体密度
1.流体所具有的机械能
流体的机械能是指由流体的位置、运动和压力所决 定的位能、动能和压力能,单位为J或kJ。
第四章 恒定总流基本方程 PPT
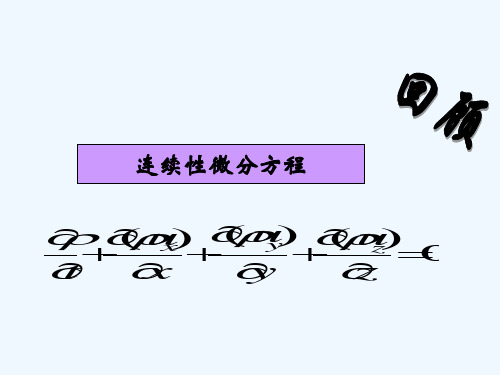
二、恒定总流伯努利方程
元流(Element Flow) 过流断面无限小的流束,元流的极限是流线。 断面上的各点的运动要素均相同。
积 分
总流(Total Flow)
元流 总流
过流断面有限大小的流束,是由无数元流构成的。
断面上各点的运动要素一般情况下不相同。
1、恒定总流伯努利方程的推导
s
z1p g 12 u 1 g 2z2p g 22 u g 2 2h w dA
u1 dA1 A1
u2 dA2 A2
u1 dA1 A1
入口面: - A1 u 1d A
u2
dA2
出口面:
A2 u 2 d A
A2
Байду номын сангаас
u
外表面: 0
A1u1dA A2u2dA
即
v1A1v2A2 或 qV1 qV2
物理意义:对于不可压缩流体,v与A成反比,即流 线密集(A小)的地方流速大,而流线稀疏(A大) 的地方流速小。 适用范围:固定边界内的不可压缩流体。
1、以元流为基础
总流是无限多元流的总和,因此,在分析总
流前,先分析元流流动,然后将元流积分就可推
广到总流。
元流 总流
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
教师:朱红钧
2、控制断面恒选在渐变流上
什么是渐变流呢?
在总流分析法中,其控制断面恒取在渐变流, 或其极限情况(均匀流)。
想一想 为什么控制断面恒选在渐变流上?
本章学习要点:
1)掌握流体运动的总流分析法; 2)掌握恒定总流的连续性方程、伯努利方程和动
量方程(三大方程)及其综合应用 。
第一节 总流分析法
一、概念
水力学--恒定总流的动量方程 ppt课件

tv11
dQ
Q
1Qtv1
动量修正系数α':
1
MQ1t1v1
tQQut1vd1Q
A1u1u1dA1 v1v1 A1
由于所取断面在渐变流上,流
速几乎平行且和平均流速的
方向基本一致.
ppt课件
7
5.7 恒定总流的动量方程
一、恒定总流动量方程的推导
所以, 动量修正系数α':
1
A1u1u1dA1 v1v1 A1
(2)作用于流体上的质量力只有重力,所研究的流 体边界是静止的.
(3)所取的两个过流断面必须是均匀流断面或渐 变流断面,但两个断面之间可以不是渐变流.
(4)一般地,所取两个断面间没有流量的汇入和分
出;也无能量的输入和输出.
ppt课件
11
5.7.2 恒定总流动量方程的应用
动量方程的应用步骤和注意事项: (1)依题意,选断面,取脱离体.
(8)应尽可能选择未知量较少的断面,这样易于求 得过程的解.
ppt课件
14
5.7.2 恒定总流动量方程的应用
例5.5 水平射流从喷嘴射出冲击一个与之成角的 斜置固定平板,如图,试求:沿S方向的分流量及射 流对平板的冲击力.
ppt课件
15
例题:如图,有一水平放置的变直径弯 曲管道,d1=500mm,d2=400mm,转角 α=45º,断面1-1处流速v1=1.2m/s,压强 p1=245kPa,求水流对弯管的作用力(不 计弯管能量损失)。
(2)全面分析作用于脱离体上的所有力.
(a)相邻水流作用于两端渐变流断面上的动水总 压力(相对压强). (b)固壁边界对脱离体内水体上的作用力
(c)作用于脱离体内水体上的重力. (3)选定坐标系.
第三章 水动力学基础 ppt课件

M12 M12 M 22
故有 ΔM M 22 M11
任取一微小流束MN,微小流束1-1′流段内液体的动量
ρu1dtdA1 u1
对断面A1积分有 M11' A1 ρ u1 u1dtdA1 ρdt A1 u1 u1dA1
同理
5
ppt课件
M 22' A2 ρ u2 u2dtdA2 ρdt A2 u2 u2dA2
Fx Fy
ρQ(β2ν2z β1ν1z )
Fz
实际液体恒定总流的动量方程式
依动量定律:
F
M t
1′ t+△t时刻2
2′
1 t时刻
即:单位时间内,物体动量
的增量等于物体所受的合外力
u1
u2
dA2
2
2′
△t时段内,动量的增量: dA1
1
M M M
M 1 2
F y
Q( 2v2z 1v1z )
F z
11
ppt课件
恒定总流动量方程建 立了流出与流进控制体 的动量流量之差与控制 体内流体所受外力之间 的关系,避开了这段流 动内部的细节。对于有 些水力学问题,能量损 失事先难以确定,用动 量方程来进行分析常常 是方便的。
水排
12
ppt课件
水排简介
M 1 2
22
11
1′ dm u1dtdA1 dM u1 dm u1 u1dtdA1
在均匀流或渐变流过水断面上
u2 u2dtdA2 u1 u1dtdA1
A2
A1
单位时间内,u 通V 过所研究流段
作V2用 于u2总dt流dA流2 段上V1所 有u1dtdA1
故有 ΔM M 22 M11
任取一微小流束MN,微小流束1-1′流段内液体的动量
ρu1dtdA1 u1
对断面A1积分有 M11' A1 ρ u1 u1dtdA1 ρdt A1 u1 u1dA1
同理
5
ppt课件
M 22' A2 ρ u2 u2dtdA2 ρdt A2 u2 u2dA2
Fx Fy
ρQ(β2ν2z β1ν1z )
Fz
实际液体恒定总流的动量方程式
依动量定律:
F
M t
1′ t+△t时刻2
2′
1 t时刻
即:单位时间内,物体动量
的增量等于物体所受的合外力
u1
u2
dA2
2
2′
△t时段内,动量的增量: dA1
1
M M M
M 1 2
F y
Q( 2v2z 1v1z )
F z
11
ppt课件
恒定总流动量方程建 立了流出与流进控制体 的动量流量之差与控制 体内流体所受外力之间 的关系,避开了这段流 动内部的细节。对于有 些水力学问题,能量损 失事先难以确定,用动 量方程来进行分析常常 是方便的。
水排
12
ppt课件
水排简介
M 1 2
22
11
1′ dm u1dtdA1 dM u1 dm u1 u1dtdA1
在均匀流或渐变流过水断面上
u2 u2dtdA2 u1 u1dtdA1
A2
A1
单位时间内,u 通V 过所研究流段
作V2用 于u2总dt流dA流2 段上V1所 有u1dtdA1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
1点
2
2点
9
伯努利方程(瑞士,1738)
z1
p1
g
u12 2g
z2
p2
g
u22 2g
z ----单位重量液体的位能
位置水头
p ----单位重量液体的压能
g
压强水头
u 2 ----单位重量液体具有的的动能
2g
流速水头
10
z1
p1
g
u12 2g
z2
p2
g
u22 2g
dp dA gdA dz dA d (u2 )
2
gdz dp d (u2 ) 0
2
z
p
g
u2 2g
C
z1
p1
g
u12 2g
z2
p2
g
u22 2g
8
1
dA 1
d z g 2g zQ1
p1 γ
u12 )dQ
2g
( z2
Q
p2 γ
p2u/2γ2g2
hw ')γdQ
2
z2
(z1
Q
p1 γ
)γdQ
1Q
u12 2g
γdQ
Q
( z2
p2 )γdQ γ
u22 γdQ 2g
hw 'γdQ
Q
Q
21
dA1 1
dA2 2
方程物理意义: 在不可压缩理想液体恒定流情况下,微小流束 内不同的过水断面上,单位重量液体所具有机 械能保持相等(守恒)。
11
3.4.1.2 实际液体恒定元流的能量方程
对于实际液体,因为存在粘性, 在流动过程中,要消耗一部分能量用 于克服摩擦力,液体的机械能沿程减 少,即存在能量损失。
12
在重力作用下,实际元流从1运动到2
3.4.2.1 实际液体恒定总流能量方程的推导 3.4.2.2 能量方程物理意义和几何意义 3.4.2.3 总水头线和测压管水头线 3.4.2.4 能量方程的应用 3.4.2.5 注意事项 3.4.2.6 应用举例
15
3.4.2 实际液体恒定总流的能量方程
3.4.2.1 实际液体恒定总流能量方程的推导 3.4.2.2 能量方程物理意义和几何意义 3.4.2.3 总水头线和测压管水头线 3.4.2.4 能量方程的应用 3.4.2.5 注意事项 3.4.2.6 应用举例
3.4.2 实际液体恒定总流的能量方程
4
3.4.1 恒定元流的能量方程
3.4.1.1 理想液体恒定元流的能量方程 3.4.1.2 实际液体恒定元流的能量方程
5
3.4.1.1 理想液体恒定元流的能量方程
2
dA
P+dP
S
dS
1
2
dG
Z+dZ
P 1
Z
6
原理:
根据牛顿第二定律,作用ds在流段上的外力沿s方向的合力,
=z
2
p2 γ
u2 2 2g
hw'
p1/γ z1
p2/γ
1
z1
p1 γ
u12 2g
=z2
p2 γ
u2 2 2g
2
hw'
u2 z2
19
dA1 1
dA2 2
u1
z1
p1 γ
u12 2g
=z
2
p2 γ
u2 2 2g
hw'
p1/γ z1
p2/γ
1
z1
p1 γ
u12 2g
沿u着x 元u流y 的各u个z 过水断面,则 the integralzone is limiedin thesamestreamline,then
z1
p1 γ
u12 2g
z2
p2 γ
u2 2 2g
1-1-1 元流过水断面(上游) 2-2-2 元流过水断面(下游)
1-1-1 元流过水断面的形心点 2-2-2 元流过水断面的形心点
=z2
p2 γ
u2 2 2g
2
hw'
u2 z2
20
沿总流过水断面积分
dA1 1
z1
p1 γ
u12 = 2g
z2
p2 γ
u22 2g
hw '
dA2
2
p1/γ
u1 dQ = u1dA1
z1
p1 γ
u12 2g
=z
2
p2 γ
u2 2 2g
hw'
dQ = u2dA2 u2
3 流体动力学理论基础
1
第3章 作业
• P46 2,4,5,9,12,16,18
2
3.1 描述液体运动的两种方法 3.2 流体运动的基本概念 3.3 恒定总流的连续性方程 3.4 恒定总流的能量方程 3.5 恒定总流的动量方程
3
3.4.1 恒定元流的能量方程
3.4.1.1 理想液体恒定元流的能量方程 3.4.1.2 实际液体恒定元流的能量方程
(z1
p1 γ
u12 2g
)dQ=u(1z2dQpγ2=uu212gd2 A 1hw
'
)γdQ
dQ = u2dA2
Q
u2
p(1z1/γ (z1
p1 γ
p1 γ
)γdQ
z1
)γu1dA1
u12 γdQ= 2g
(z2
Q
Q
Q
u12
21g
γu1dA1=
应该等于该流段质量
dA与d加s 速度
的du乘积。
dt
dG cos gdAds cos
受力:
pdA
( p dp)dA
且 cos dz
ds
7
pdA ( p dp)dA gdAdz gdAds du
dt
其中:du dt
du ds
ds dt
u
du ds
d u2 ds 2
Q
(
p2 γ
z2
)γdQ u22
p2/γ Q 2g
p2 γ
)γu2dA2
γdQ hw 'γdQ
Q
u2 2 2g
2
γu2dA2
Q
Q
hw
z2
'γdQ
22
(z1
p1 )γdQ γ
u12 γdQ 2g
(z2
p2 )γdQ γ
u22 γdQ 2g
hw 'γdQ
Q
Q
Q
Q
dA1
(z11
p1 γ
)γu1dA1
u12 2g
p u2
p u2
z 1 1 z 2 2
1 2g 2 2g
2 1
13
令: hw’ = 单位重量的液体 从断面1-1运动至断面2-2所损失的能量,则
z1
p1
u12 2g
=z2
p2
u2 2 2g
hw '
2
1
不可压缩实际液体恒定流元流的伯努利方程
14
3.4.2 实际液体恒定总流的能量方程
16
不可压缩实
dA
际液体、恒
定元流的能
量方程
图 闸孔出流
dA
z1
p1 γ
u12 2g
=z
2
p2 γ
u2 2 2g
hw'
微小流管→微小流束,或元流
17
1
2
2
1
在有压管流中,任取
一段1-1和2-2断面之间
的总流,并把它放大进
行分析。
18
dA1 1
dA2 2
u1
z1
p1 γ
u12 2g
