选修21空间向量单元测试
空间向量单元测试题及答案

空间向量单元测试题及答案# 空间向量单元测试题及答案一、选择题1. 空间向量\( \overrightarrow{AB} \)与\( \overrightarrow{CD} \)平行,那么\( \overrightarrow{AB} + \overrightarrow{CD} \)与\( \overrightarrow{AB} \)的关系是什么?A. 垂直B. 平行C. 共线D. 无法确定答案:B. 平行2. 已知空间向量\( \overrightarrow{a} = (2, 3, 1) \),\( \overrightarrow{b} = (1, -1, 2) \),求\( \overrightarrow{a} \times \overrightarrow{b} \)的模。
A. 0B. 3C. 5D. 6答案:C. 53. 空间中任意两点A和B,它们之间的向量\( \overrightarrow{AB} \)的模长是两点间的距离,这个说法:A. 正确B. 错误答案:A. 正确二、填空题4. 若空间向量\( \overrightarrow{a} \)与\( \overrightarrow{b} \)的夹角为90°,则\( \overrightarrow{a} \)与\( \overrightarrow{b} \)的点积\( \overrightarrow{a} \cdot\overrightarrow{b} \)等于______。
答案:05. 空间向量\( \overrightarrow{a} = (x, y, z) \),若\( \overrightarrow{a} \)的模长为1,则\( x^2 + y^2 + z^2 =______。
答案:1三、简答题6. 解释空间向量的基本性质,并给出两个例子。
答案:空间向量的基本性质包括:- 向量加法满足交换律和结合律。
- 向量的数乘满足分配律。
高中数学选修2-1 第三章《空间向量与立体几何》单元测试题(含答案)

这时Q ⎝ ⎛⎭⎪⎫43,43,83.答案:C二、填空题:本大题共4小题,每小题5分,共20分.13.若A (x,5-x,2x -1),B (1,x +2,2-x ),则当|AB →|取最小值时,x 的值等于________.解析:AB →=(1-x,2x -3,-3x +3),则 |AB →|=1-x2+2x -32+-3x +32=14x 2-32x +19=14⎝⎛⎭⎪⎫x -872+57,故当x =87时,|AB →|取最小值.答案:8714.正方体ABCD -A 1B 1C 1D 1中,直线BC 1与平面A 1BD 夹角的正弦值是________. 解析:如图,以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则A (1,0,0),B (1,1,0),C 1(0,1,1), 易证AC 1→是平面A 1BD 的一个法向量.AC 1→=(-1,1,1),BC 1→=(-1,0,1). cos 〈AC 1→,BC 1→〉=1+13×2=63. 所以BC 1与平面A 1BD 夹角的正弦值为63.答案:63设AC ∩BD =N ,连结NE ,则N ⎝ ⎛⎭⎪⎫22,22,0,E (0,0,1), ∴NE →=⎝ ⎛⎭⎪⎫-22,-22,1. 又A (2,2,0),M ⎝ ⎛⎭⎪⎫22,22,1, ∴AM →=⎝ ⎛⎭⎪⎫-22,-22,1. ∴NE →=AM →,且NE 与AM 不共线.∴NE ∥AM .又NE ⊂平面BED ,AM ⊄平面BDE ,∴AM ∥平面BDE .(2)设P (t ,t,0)(0≤t ≤2),则PF →=(2-t ,2-t,1),CD →=(2,0,0).又∵PF →与CD →所成的角为60°,|2-t ·2|2-t2+2-t 2+1·2=12, 解之得t =22,或t =322(舍去). 故点P 为AC 的中点.22.(本小题满分12分)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,C 是AB 的中点,D 为AC 的中点.。
高二数学选修2-1空间向量试卷及答案
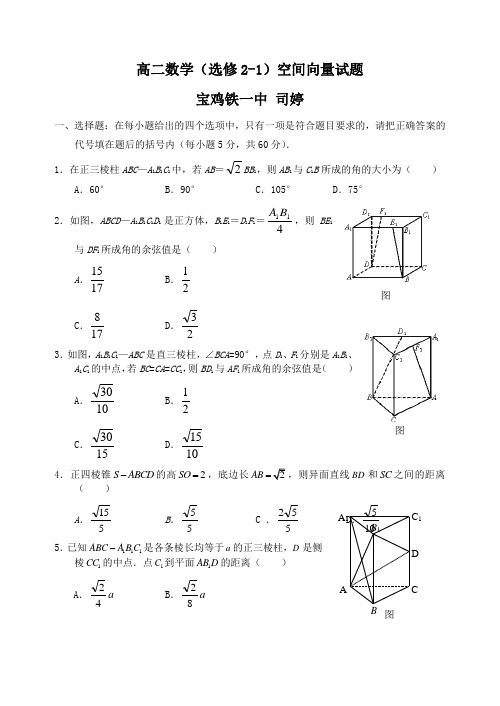
AA 1 DCB B 1C 1图高二数学(选修2-1)空间向量试题宝鸡铁一中 司婷一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共60分). 1.在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的角的大小为( )A .60°B .90°C .105°D .75°2.如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( )A .1715 B .21 C .178 D .23 3.如图,A 1B 1C 1—ABC 是直三棱柱,∠BCA =90°,点D 1、F 1分别是A 1B 1、A 1C 1的中点,若BC =CA =CC 1,则BD 1与AF 1所成角的余弦值是( )A .1030B .21C .1530D .10154.正四棱锥S ABCD -的高2SO =,底边长2AB =,则异面直线BD 和SC 之间的距离( )A .515 B .55 C .552 D .1055.已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点.点1C 到平面1AB D 的距离( )A .a 42 B .a 82 图图C .a 423 D .a 22 6.在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11A C D 间的距离( )A .63 B .33 C .332 D .23 7.在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =21PA ,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC ,则直线OD 与平面PBC 所成角的正弦值( )A .621B .338 C60210 D .302108.在直三棱柱111C B A ABC -中,底面是等腰直角三角形,ο90=∠ACB ,侧棱21=AA ,D ,E 分别是1CC 与B A 1的中点,点E 在平面AB D 上的射影是ABD ∆的重心G .则B A 1与平面AB D 所成角的余弦值( )A .32B .37C .23 D .73 9.正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是C B 延长线上一点,且BC BD =,则二面角B AD B --1的大小( )A .3π B .6πC .65πD .32π10.正四棱柱1111D C B A ABCD -中,底面边长为22,侧棱长为4,E ,F 分别为棱AB ,CD 的中点,G BD EF =⋂.则三棱锥11EFD B -的体积V ( )A .66 B .3316 C .316D .1611.有以下命题:①如果向量b a ,与任何向量不能构成空间向量的一组基底,那么b a ,的关系是不共线; ②,,,O A B C 为空间四点,且向量OC OB OA ,,不构成空间的一个基底,则点,,,O A B C一定共面;③已知向量c b a ,,是空间的一个基底,则向量c b a b a ,,-+也是空间的一个基底。
高中数学选修2-1测试题—空间向量

高中数学选修2-1测试题—空间向量班别:_________ 姓名:__________ 学号:_____ 评分:________ 一.选择题:(10小题共40分)1.已知A 、B 、C 三点不共线,对平面ABC 外的任一点O,下列条件中能确定点M 与点A 、B 、C 一 定共面的是 ( ) A.OC OB OA OM ++= B.OC OB OA OM --=2C.OC OB OA OM 3121++=D.OC OB OA OM 313131++=2.直三棱柱ABC —A 1B 1C 1中,若====B A C CC b CB a CA 11,,,则 ( )A.c b a -+B.c b a +-C.c b a ++-D.c b a -+-3.若向量λμλμλ且向量和垂直向量R b a n b a m ∈+=,(,、则)0≠μ ( )A.n m //B.n m ⊥C.n m n m 也不垂直于不平行于,D.以上三种情况都可能4.以下四个命题中,正确的是 ( ) A.若OB OA OP 3121+=,则P 、A、B三点共线B.设向量},,{c b a 是空间一个基底,则{a +b ,b +c ,c +a }构成空间的另一个基底C.c b a c b a ⋅⋅=⋅)(D.△ABC 是直角三角形的充要条件是0=⋅AC AB 5.对空间任意两个向量b a o b b a //),(,≠的充要条件是( )A.b a =B.b a -=C.a b λ=D.b a λ= 6.已知向量b a b a 与则),2,1,1(),1,2,0(--==的夹角为( )A.0°B.45°C.90°D.180°7.在平行六面体1111D C B A ABCD -中,M 为AC 与BD 的交点,若c A A b D A a B A ===11111,,, 则下列向量中与M B 1相等的是 ( ) A.c b a 212121++-B.c b a 212121++C.c b a +-2121 D.-c b a +-21218.已知的值分别为与则若μλμλλ,//),2,12,6(),2,0,1(b a b a -=+= ( )A.21,51 B.5,2 C.21,51--D.-5,-2 9.已知的数量积等于与则b a k j i b k j i a 35,2,23+-=-+= ( )A.-15B.-5C.-3D.-110.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN所成角的余弦值是( )A.52-B.52C.53D.1010二.填空题: (4小题共16分)11.若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n= . 12.已知A (0,2,3),B (-2,1,6),C (1,-1,5),若a AC a AB a a 则向量且,,,3||⊥⊥=的坐标为 .13.已知b a ,是空间二向量,若b a b a b a 与则,7||,2||,3||=-==的夹角为 .14.已知点G 是△ABC 的重心,O 是空间任一点,若的值则λλ,OG OC OB OA =++为 . 三.解答题:(10+8+12+14=44分)15.如图:ABCD 为矩形,PA ⊥平面ABCD ,PA=AD ,M 、N 分别是PC 、AB 中点, (1)求证:MN ⊥平面PCD ;(2)求NM 与平面ABCD 所成的角的大小.16.一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是300,求这条线段与这个二面角的棱所成的角的大小.17.正四棱锥S —ABCD 中,所有棱长都是2,P 为SA 的中点,如图. (1)求二面角B —SC —D 的大小;(2)求DP 与SC 所成的角的大小.18.如图,直三棱柱ABC —A 1B 1C 1,底面△ABC 中,CA=CB=1,∠BCA=90°,棱AA 1=2,M 、N 分别是A 1B 1,A 1A 的中点; (1)求;的长BN(2)求;,cos 11的值><CB BA (3).:11M C BA⊥求证(4)求CB 1与平面A 1ABB 1所成的角的余弦值.高中数学选修2-1测试题(10)—空间向量(1)参考答案DDBB DCDA AB 11.0 12.(1,1,1) 13.60014.3 15.(1)略 (2)45016.45017.(1) 13-(2) π18.(1)3 (2)3010(3) 略 (4)3101018.如图,建立空间直角坐标系O —xyz.(1)依题意得B (0,1,0)、N (1,0,1) ∴|BN |=3)01()10()01(222=-+-+-.(2)依题意得A 1(1,0,2)、B (0,1,0)、C (0,0,0)、B 1(0,1,2) ∴1BA ={-1,-1,2},1CB ={0,1,2,},1BA ·1CB =3,|1BA |=6,|1CB |=5∴cos<1BA ,1CB >=30101||||1111=⋅⋅CB BA CB BA .(3)证明:依题意,得C 1(0,0,2)、M (21,21,2),B A 1={-1,1,2},M C 1={21,21,0}.∴B A 1·M C 1=-2121++0=0,∴B A 1⊥M C 1,∴A 1B ⊥C 1M.评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件.图选校网高考频道专业大全历年分数线上万张大学图片大学视频院校库(按ctrl 点击打开)选校网()是为高三同学和家长提供高考选校信息的一个网站。
空间向量单元测试题(原卷版)

2021-2022年度高二第一学期单元测试空间向量与立体几何一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 如图所示,正方体1111ABCD A B C D -的棱长为a ,M ,N 分别为1A B 和AC 上的点,123aA M AN ==,则MN 与平面11BB C C 的位置关系是( )A .相交B .平行C .垂直D .不能确定2. 已知正四面体ABCD 的棱长为1,点E 、F 分别是AD 、DC 中点,则(EF AB = )A .14B .14-C .34D .34-3. 三棱柱111ABC A B C -的侧棱与底面垂直,11AA AB AC ===,AB AC ⊥,N 是BC 的中点,点P 在11A B 上,且满足111A P A B λ=,当直线PN 与平面ABC 所成的角取最大值时,λ的值为( )A .12B 2C 3D 254. 如图,在长方体1111ABCD A B C D -中,2AB =,3BC =,16AA =,则异面直线1AB 与1BC 所成角的大小为( )A .60︒B .45︒C .30︒D .15︒5. 如图,60︒的二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4AB =,6AC =,8BD =,则CD 的长为( )A 17B .7C .217D .96. 在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为11A D ,11D C 的中点,则过B ,E ,F 三点的平面截该正方体,所得截面的周长为( )A .52B .62C 2213D 24137. 在长方体1111ABCD A B C D -中,2AB =11BC AA ==,点M 为1AB 的中点,点P 为对角线1AC 上的动点,点Q 为底面ABCD 上的动点(点P 、Q 可以重合),则MP PQ +的最小值为( ) A 2B 3C .34D .18. 把正方形ABCD 沿对角线BD 折成直二面角,对于下列结论:①AC BD ⊥;②ADC ∆是正三角形;③AB 与CD 成60︒角;④AB 与平面BCD 成60︒角. 则其中正确结论的个数是( ) A .1个 B .2个C .3个D .4个三、填空题:本题共4小题,每小题5分,共20分.13. 如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上,过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M ,N 两点,设BP x =,MN y =,则函数()y f x =的图象大致是 ② .(在横线上填上正确的序号,多选少选都不得分)14.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成△1A DE .若M 为线段1A C 的中点,则在ADE ∆翻折过程中,下列命题正确的是 .(写出所有正确的命题的编号) ①线段BM 的长是定值; ②点M 在某个球面上运动; ③存在某个位置,使1DE AC ⊥; ④存在某个位置,使//MB 平面1A DE .15.正方体1111ABCD A B C D -中,E 、F 分别是棱11A B ,BC 上的动点,且1A E BF =,P 为EF 的中点,则点P 的轨迹是 .16.正方体1111ABCD A B C D -的棱长为4,E ,F 分别是BC 和11C D 的中点,经过点A ,E ,F 的平面把正方体1111ABCD A B C D -截成两部分,则截面的周长为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 如图,直线AQ ⊥平面α,直线AQ ⊥平行四边形ABCD ,四棱锥P ABCD -的顶点P 在平面α上,7AB =3AD ,AD DB ⊥,AC BD O =,//OP AQ ,2AQ =,M ,N分别是AQ 与CD 的中点. (1)求证://MN 平面QBC ; (2)求二面角M CB Q --的余弦值.18. 如图所示,该几何体是由一个直三棱柱ADE BCF -和一个正四棱锥P ABCD -组合而成,AD AF ⊥,2AE AD ==. (Ⅰ)证明:平面PAD ⊥平面ABFE ;(Ⅱ)求正四棱锥P ABCD -的高h ,使得二面角C AF P --的余弦值是223.19. 如图,已知长方形ABCD 中,2AB =,1AD =,M 为DC 的中点.将ADM ∆沿AM 折起,使得平面ADM ⊥平面ABCM . (1)求证:AD BM ⊥;(2)若点E 是线段DB 上的一动点,问点E 在何位置时,二面角E AM D --的余弦值为55.20. 如图,PD 垂直于梯形ABCD 所在的平面,90ADC BAD ∠=∠=︒.F 为PA 中点,2PD =,112AB AD CD ===. 四边形PDCE 为矩形,线段PC 交DE 于点N .(Ⅰ)求证://AC 平面DEF ; (Ⅱ)求二面角A BC P --的大小;(Ⅲ)在线段EF 上是否存在一点Q ,使得BQ 与平面BCP 所成角的大小为6π?若存在,求出Q 点所在的位置;若不存在,请说明理由.21. 已知长方形ABCD 中,1AB =,2AD =,现将长方形沿对角线BD 折起,使AC a =,得到一个四面体A BCD -,如图所示.(1)试问:在折叠的过程中,异面直线AB 与CD ,AD 与BC 能否垂直?若能垂直,求出相应的a 值;若不垂直,请说明理由.(2)当四面体A BCD -体积最大时,求二面角A CD B --的余弦值.22. 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且1==,PO OB(Ⅰ)若D为线段AC的中点,求证:AC⊥平面PDO;(Ⅱ)求三棱锥P ABC-体积的最大值;(Ⅲ)若2BC=,点E在线段PB上,求CE OE+的最小值.。
选修2-1空间向量单元测试卷

第三章 单元测试卷第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.已知A (2,-4,-1),B (-1,5,1),C (3,-4,1),令a =CA →,b =CB →,则a +b 对应的点为( )A .(5,-9,2)B .(-5,9,-2)C .(5,9,-2)D .(5,-9,-2)答案 B2.已知a =(-3,2,5),b =(1,x ,-1)且a ·b =2,则x 的值是( ) A .3 B .4 C .5 D .6答案 C解析 (-3)×1+2x +5×(-1)=2,解得x =5.3.已知三点A (0,1,1),B (1,2,1),C (1,1,2),则a =AB →与b =AC →的夹角为( )A.π2B.π3 C.π6 D.π4 答案 B4.在以下命题中,不正确的个数为( ) ①|a |-|b |=|a +b |是a ,b 共线的充要条件; ②若a ∥b ,则存在唯一的实数λ,使a =λ·b ;③对空间任意一点O 和不共线的三点A ,B ,C ,若OP →=2OA →-2OB →-OC →,则P ,A ,B ,C 四点共面;④若{a ,b ,c }为空间的一个基底,则{a +b ,b +c ,c +a }构成空间的另一个基底;⑤|(a ·b )c |=|a |·|b |·|c |. A .2 B .3 C .4 D .5答案 C5.已知正方体ABCD -A 1B 1C 1D 1中,点E 为上底面A 1B 1C 1D 1的中心,若AE →=AA 1→+xAB →+yAD →,则x ,y 的值分别为( )A .x =1,y =1B .x =1,y =12 C .x =12,y =12 D .x =12,y =1 答案 C6.若直线l 的方向向量为a ,平面α的法向量为n ,则能使l ∥α的是( )A .a =(1,0,0),n =(-2,0,0)B .a =(1,3,5),n =(1,0,1)C .a =(0,2,1),n =(-1,0,-1)D .a =(1,-1,3),n =(0,3,1) 答案 D解析 A :a ·n =-2≠0;B :a·n =1+5≠0; C :a·n =-1≠0;D :a·n =-3+3=0.7.已知A (1,-2,11),B (6,-1,4),C (4,2,3),则△ABC 是( )A .锐角三角形B .等腰三角形C .直角三角形D .钝角三角形答案 C解析 ∵BA →·BC →=(-5,-1,7)·(-2,3,-1)=10-3-7=0,∴∠ABC =90°.8.已知空间三点A (0,2,3),B (-2,1,6),C (1,-1,5).若|a |=3,且a 分别与AB →,AC →垂直,则向量a 为( )A .(1,1,1)B .(-1,-1,-1)C .(1,1,1)或(-1,-1,-1)D .(1,-1,1)或(-1,1,-1) 答案 C9.在正方体ABCD -A 1B 1C 1D 1中,M 是AB 的中点,则DB 1与CM 所成角的余弦值等于( )A.12B.1515C.23D.21015答案 B解析 以D 为坐标原点,DA →,DC →,DD 1→分别为x 轴,y 轴,z 轴正方向建立空间直角坐标系.设正方体的棱长为1,则D (0,0,0),B 1(1,1,1),C (0,1,0),M (1,12,0),则cos<DB 1→CM →>=DB 1→·CM→|DB 1→||CM →|=(1,1,1)·(1,-12,0)3×1+14=1515.∴DB 1与CM 的夹角的余弦值为1515. 10.如图,在直二面角α-l -β中,A ,B ∈l ,AC ⊂α,AC ⊥l ,BD ⊂β,BD ⊥l ,AC =6,AB =8,BD =24,则线段CD 的长是( )A .25B .26C .27D .28答案 B11.在正方体ABCD -A 1B 1C 1D 1中,BB 1与平面ACD 1所成角的余弦值为( )A.23B.33C.23D.63 答案 D解析 BB 1与平面ACD 1所成角等于DD 1与平面ACD 1所成的角,在三棱锥D -ACD 1中,由三条侧棱两两垂直得点D 在底面ACD 1内的射影为等边△ACD 1的垂心即中心H ,则∠DD 1H 为DD 1与平面ACD 1所成角,设正方体棱长为a ,则cos ∠DD 1H =63a a =63,故选D.12.在直角坐标系中,A (-2,3),B (3,-2),沿x 轴把直角坐标系折成120°的二面角,则AB 的长度为( )A. 2 B .211 C .3 2 D .4 2答案 B解析 作AM ⊥x 轴于M ,BN ⊥x 轴于N .则AM =3,BN =2,MN =5.又AB →=AM →+MN →+NB →, ∴AB →2=AM →2+MN →2+NB →2+2(AM →·MN →+AM →·NB →+MN →·NB →). 又AM ⊥MN ,MN ⊥NB ,,<AM →,NB →>=60°, 故AB →2=9+25+4+6=44. ∴AB =|AB →|=211.故选B.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知A ,B ,C ,D 是平面上四点,O 是空间任一点,{a n }为等差数列,若OA →=a 1OB →+a 8OC →+a 15OD →,求a 8=________.答案 13解析 ∵A ,B ,C ,D 共面, ∴a 1+a 8+a 15=3a 8=1,∴a 8=13.14.在四面体OABC 中,OA →=a ,OB →=b ,OC →=c ,D 为BC 的中点,E 为AD 中点,则OE →=________.(用a ,b ,c 表示)答案 12a +14b +14c15.在平行六面体ABCD -A 1B 1C 1D 1中,AB =2,AA 1=2,AD =1,且AB ,AD ,AA 1夹角都是60°,则AC 1→·BD 1→=________.答案 316.如图所示,在直三棱柱ABC -A 1B 1C 1中,∠ABC =90°,AB =BC =AA 1=2,点D 是A 1C 1的中点,则异面直线AD 和BC 1所成角的大小为________.答案 π6三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知a =(1,2,-2). (1)求与a 共线的单位向量b ;(2)若a 与单位向量c =(0,m ,n )垂直,求m ,n 的值.思路分析 (1)若a 与b 共线,则b =(λ,2λ,-2λ),根据|b |=1,可求得λ;(2)若a ⊥c ,则a ·c =0且|c |=1,注意讨论解的情况.解析 (1)设b =(λ,2λ,-2λ),而b 为单位向量, ∴|b |=1,即λ2+4λ2+4λ2=9λ2=1.∴λ=±13. ∴b =(13,23,-23)或b =(-13,-23,23).(2)由题意,知⎩⎪⎨⎪⎧ a ·c =0,|c |=1,∴⎩⎪⎨⎪⎧1×0+2m -2n =0,m 2+n 2+02=1.解得⎩⎨⎧m =22,n =22或⎩⎨⎧m=-22,n =-22.18.(12分)如图所示,在直三棱柱ABC -A 1B 1C 1中,底面是等腰直角三角形,∠ACB =90°,侧棱AA 1=2,CA =2,D 是CC 1的中点,试问在A 1B上是否存在一点E 使得点A 1到平面AED 的距离为263?解析 以CA ,CB ,CC 1所在直线为x 轴,y 轴和z 轴,建立如图所示的空间直角坐标系,则A (2,0,0),A 1(2,0,2),D (0,0,1),B (0,2,0),设BE →=λBA 1→,λ∈(0,1),则E (2λ,2(1-λ),2λ).又AD →=(-2,0,1),AE →=(2(λ-1),2(1-λ),2λ), 设n =(x ,y ,z )为平面AED 的法向量,则⎩⎨⎧n ·AD →=0,n ·AE →=0⇒⎩⎪⎨⎪⎧-2x +z =0,2(λ-1)x +2(1-λ)y +2λz =0. 取x =1,则y =1-3λ1-λ,z =2,即n =(1,1-3λ1-λ,2).由于d =|AA 1→·n ||n |=263,∴263=45+(1-3λ1-λ)2.又λ∈(0,1),解得λ=12.所以当点E 为A 1B的中点时,A 1到平面AED 的距离为263. 19.(12分)如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB =4,点E 在CC 1上且C 1E =3EC .(1)证明:A 1C ⊥平面BED ; (2)求二面角A 1-DE -B 的余弦值.解析 (1)以D 为坐标原点,射线DA 为x 轴的正半轴,射线DC 为y 轴的正半轴,射线DD 1为z 轴的正半轴,建立如图所示的空间直角坐标系D -xyz .依题设B (2,2,0),C (0,2,0),E (0,2,1),A 1(2,0,4).DE →=(0,2,1),DB →=(2,2,0),A 1C →=(-2,2,-4),DA 1→=(2,0,4). 因为A 1C →·DB →=0,A 1C →·DE →=0, 故A 1C ⊥BD ,A 1C ⊥DE . 又BD ∩DE =D , 所以A 1C ⊥平面BED .(2)设向量n =(x ,y ,z )是平面DA 1E 的法向量,则 n ⊥DE →,n ⊥DA 1→. 故2y +z =0,2x +4z =0.令y =1,则z =-2,x =4,所以n =(4,1,-2). 设θ等于二面角A 1-DE -B 的平面角, cos<n ,A 1C →>=n ·A 1C →|n ||A 1C →|=1442.所以二面角A 1-DE -B 的余弦值为1442.20.(12分)如图,已知点P 在正方体ABCD -A ′B ′C ′D ′的对角线BD ′上,∠PDA =60°.(1)求DP 与CC ′所成角的大小;(2)求DP 与平面AA ′D ′D 所成角的大小.解析(1)如图所示,以D 为原点,DA 为单位长建立空间直角坐标系D -xyz .则DA →=(1,0,0),CC ′→=(0,0,1).连接BD ,B ′D ′.在平面BB ′D ′D 中,延长DP 交B ′D ′于H .设DH →=(m ,m,1)(m >0),由已知<DH →,DA →>=60°,由DA →·DH →=|DA →||DH →|cos<DH →,DA →>,可得2m =2m 2+1.解得m =22或m =-22(舍),所以DH →=(22,22,1).因为cos<DH →,CC ′→>=22×0+22×0+1×11×2=22,所以<DH →,CC ′→>=45°,即DP 与CC ′所成的角为45°.(2)平面AA ′D ′D 的一个法向量是DC →=(0,1,0),因为cos<DH →,DC →>=22×0+22×1+1×01×2=12, 所以<DH →,DC →>=60°.可得DP 与平面AA ′D ′D 所成的角为30°.21.(12分)如图所示,四棱锥P -ABCD 的底面ABCD 是边长的1的菱形,∠BCD =60°,E 是CD 的中点,P A ⊥底面ABCD ,P A =2.(1)证明:平面PBE ⊥平面P AB ;(2)求平面P AD 和平面PBE 所成二面角(锐角)的余弦值.解析(1)如图所示,以A 为原点,建立空间直角坐标系,则相关各点的坐标分别是A (0,0,0),B (1,0,0),C (32,32,0),D (12,32,0),P (0,0,2),E (1,32,0).因为BE →=(0,32,0),平面P AB 的一个法向量是n 0=(0,1,0),所以BE →和n 0共线.从而BE ⊥平面P AB .又因为BE ⊂平面PBE ,故平面PBE ⊥平面P AB .(2)易知PB →=(1,0,-2),BE →=(0,32,0),P A →=(0,0,-2),AD →=(12,32,0).设n 1=(x 1,y 1,z 1)是平面PBE 的一个法向量,则由⎩⎨⎧n 1·PB →=0,n 1·BE →=0得⎩⎨⎧ x 1+0×y 1-2z 1=0,0×x 1+32y 1+0×z 1=0.所以y 1=0,x 1=2z 1,故可取n 1=(2,0,1).设n 2=(x 2,y 2,z 2)是平面P AD 的一个法向量,则由⎩⎨⎧n 2·P A →=0,n 2·AD →=0得⎩⎨⎧ 0×x 2+0×y 2-2z 2=0,12x 2+32y 2+0×z 2=0.所以z 2=0,x 2=-3y 2,故可取n 2=(3,-1,0).于是cos<n 1,n 2>=n 1·n 2|n 1||n 2|=235×2=155. 故平面P AD 和平面PBE 所成二面角(锐角)的余弦值为155.22.(12分)如图所示,设动点P 在棱长为1的正方体ABCD -A 1B 1C 1D 1的对角线BD 1上,记D 1P D 1B =λ.当∠APC 为钝角时,求λ的取值范围.解析 由题设可知,以DA →,DC →,DD 1→为单位正交基底,建立如右图所示的空间直角坐标系D -xyz ,则有A (1,0,0),B (1,1,0),C (0,1,0),D 1(0,0,1).由D 1B →=(1,1,-1),得D 1P →=λD 1B →=(λ,λ,-λ),所以P A →=PD 1→+D 1A →=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),PC →=PD 1→+D 1C →=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1).显然∠APC 不是平角,所以∠APC 为钝角等价于cos ∠APC=cos<P A →,PC →>=P A →·PC →|P A →||PC →|<0, 这等价于P A →·PC →<0.即(1-λ)(-λ)+(-λ)(1-λ)+(λ+1)2=(λ-1)(3λ-1)<0,解得13<λ<1.1因此,λ的取值范围为(3,1).。
空间向量单元测试卷

空间向量单元测试卷第一部分:选择题1. 下列哪个不是空间向量的表示方法?A. 箭头表示法B. 行向量表示法C. 列向量表示法D. 数量表示法2. 空间向量的模长是指什么?A. 向量的长度B. 向量的方向C. 向量的大小D. 向量的起点和终点的距离3. 空间向量的方向角是指什么?A. 向量与$x$轴正向的夹角B. 向量的长度C. 向量与$y$轴正向的夹角D. 向量与$z$轴正向的夹角4. 下列哪个不是向量的线性运算?A. 加法B. 减法C. 乘法D. 数乘5. 向量$\vec{a}(1, 2, 3)$和向量$\vec{b}(4, 5, 6)$的点积是多少?A. $32$B. $35$C. $38$D. $41$6. 两个向量的叉积为零,则它们的关系是什么?A. 平行B. 垂直C. 重合D. 倾斜7. 两个向量平行,则它们的叉积是什么?A. 零向量B. 原向量C. 单位向量D. 无法确定8. 空间中三个相互垂直的向量长度分别为$\sqrt{2}$,$\sqrt{3}$,$\sqrt{6}$,则它们的信部角余弦分别为多少?A. $\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{2}$B. $\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$,$\frac{1}{\sqrt{2}}$C. $\frac{1}{\sqrt{6}}$,$\frac{1}{\sqrt{3}}$,$\frac{1}{\sqrt{2}}$D. $\frac{\sqrt{6}}{6}$,$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$第二部分:填空题1. 空间向量的数量表示法是用______个实数表示。
2. 向量$\vec{a}=(x_1, y_1, z_1)$和向量$\vec{b}=(x_2, y_2,z_2)$的点积为$x_1x_2+y_1y_2+z_1z_2$,也可以表示为$\|\vec{a}\|\cdot\|\vec{b}\|\cos\theta$,其中$\theta$为向量$\vec{a}$和向量$\vec{b}$的______角。
高中新课标数选修(21)空间向量与立体几何测试题

高中新课标数学选修(2-1)空间向量与立体几何测试题一、选择题1.空间的一个基底{},,a b c 所肯定平面的个数为( ) A.1个B.2个C.3个D.4个以上答案:C2.已知(121)A -,,关于面xOy 的对称点为B ,而B 关于x 轴的对称点为C ,则BC =( ) A.(042),, B.(042)--,,C.(040),,D.(202)-,,答案:B3.已知向量111222()()x y z x y z ==,,,,,a b ,若≠a b ,设a b -=R ,则a b -与x 轴夹角的余弦值为( )A.12x x R- B.21x x R- C.12x x R- D.12()x x R-±答案:D4.若向量MA MB MC ,,的起点与终点M A B C ,,,互不重合且无三点共线,O 是空间任一点,则能使MAMB MC ,,成为空间一组基底的关系是( ) A.111333OM OA OB OC =++B.MA MB MC ≠+C.1233OM OA OB OC =++D.2MA MB MC =- 答案:C5.正方体1111ABCD A B C D -的棱长为1,E 是11A B 的中点,则E 是平面11ABC D 的距离是( ) A.32B.22C.12D.33答案:B6.一条长为a 的线段,夹在彼此垂直的两个平面之间,它和这两个平面所成的角别离是45°和30°,由这条线段两头向两平面的交线引垂线,垂足的距离是( )A.2a B.3a C.22a D.23a 答案:A7.若向量a 与b 的夹角为60°,4=b ,(2)(3)72a b a b +-=-,则a =( ) A.2 B.4C.6D.12答案:C8.设P 是60°的二面角l αβ--内一点,PA ⊥平面α,PB ⊥平面β,A B ,为垂足,42PA PB ==,,则AB 的长为( )A.42 B.23 C.25 D.27答案:D9.ABCD 为正方形,P 为平面ABCD 外一点,2PD AD PD AD ⊥==,,二面角P AD C --为60°,则P 到AB 的距离为( ) A.22 B.3 C.2 D.7答案:D 10.已知()()(00)x y z a b c xyz abc ==≠≠,,,,,,p q ,如有等式2222222()()()x y z a b c ax by cz ++++=++成立,则,p q 之间的关系是( )A.平行 B.垂直 C.相交 D.以上都可能答案:A11.已知平面α与β所成二面角为80°,P 为αβ,外必然点,过点P 一条直线与αβ,所成的角都是30°,则这样的直线有且仅有( ) A.1条 B.2条 C.3条 D.4条 答案:D12.如图1,梯形ABCD 中,AB CD ∥,且AB ⊥平面α,224AB BC CD ===,点P 为α内一动点,且APB DPC ∠=∠,则P 点的轨迹为( ) A.直线 B.圆 C.椭圆 D.双曲线 答案:B二、填空题13.已知(11)(2)t t t t t =--=,,,,,a b ,则-b a 的最小值是 .答案:35514.在棱长为a 的正方体1111ABCD A B C D -中,向量1BA 与向量AC 所成的角为 . 答案:120°15.如图2,在正三棱柱111ABC A B C -中,已知1AB D =,在棱1BB 上,且1BD =,若AD 与平面11AAC C 所成的角为α,则sin α= . 答案:6416.已知m l ,是异面直线,那么: ①必存在平面α过m 且与l 平行; ②必存在平面β过m 且与l 垂直; ③必存在平面γ与m l ,都垂直; ④必存在平面δ与m l ,距离都相等. 其中正确命题的序号是 . 答案:①④三、解答题17.设空间两个不同的单位向量122(0)(0)x y x y ==,,,,,a b 与向量(111)=,,c 的夹角都等于π4. 解:(1)由π6cos 42==ac a c ,且11a c =+·x y , 1162+=∴x y . 又22111x y =+=a ,222111111113()2122x y x y x y x y +=++=+=∴. 1114x y =∴. (4)同理可得22226124x y x y +==,, 11x y ,∴是方程261024x x -+=的两根,同理22x y ,也是. 又≠∵a b ,1221==,∴x y x y .cos ==,·∴·a b a b a b a b 1212112212=+=+=x x y y x y x y ,60a b =,∴°.18.如图3,已知直四棱柱1111ABCD A B C D -中,12AA =,底面ABCD 是直角梯形,ADC ∠是直角,421AB CD AB AD DC ===,,,∥,求异面直线1BC 与DC 所成角的大小. 解:以D 为原点,1DA DC DD ,,所在直线别离为x 轴,y 轴,z 轴成立空间直角坐标系D xyz -, 则1(012)(240)(010)C B A ,,,,,,,,.1(232)BC =--,,∴,(010)CD =-,,.设1BC 与CD 所成角为θ, 则11317cos 17BC CD BC CDθ==·. 317arccos17θ=∴. ∴异面直线1BC 与DC 所成角的大小为317arccos17.19.如图4,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动,问AE 等于何值时,二面角1D EC D --的大小为π4. 解:设AE x =,以D 为原点,直线1DA DC DD ,,所在直线别离为x y z ,,轴成立空间直角坐标系, 则11(101)(001)(10)(100)(020)A D E x A C ,,,,,,,,,,,,,,. 11(120)(021)(001)CE x D C DD =-=-=,,,,,,,,∴.设平面1D EC 的法向量为()a b c =,,n , 由1020(2)00n n⎧=-=⎧⎪⇒⎨⎨+-==⎩⎪⎩,,,··D C b c a b x CE 令1b =,22c a x ==-,∴.(212)x =-,,∴n .依题意121π222cos 422(2)5DD DD x ==⇒=-+n n ·.23x =-∴(23x =+不合题意,舍去). 23AE =-∴.20.如图5所示的多面体是由底面为ABCD 的长方体被截面1AEC F 所截而取得的,其中14231AB BC CC BE ====,,,. (1)求BF ;(2)求点C 到平面1AEC F 的距离.解:(1)以D 为原点,DAF DC DF ,,所在直线为x 轴, y 轴,z 轴成立空间直角坐标系D xyz -, 1(000)(240)(200)(040)(241)(043)D B A C E C ,,,,,,,,,,,,,,,,,, 设(00)F z ,,. 由1AF EC =,得(20)(202)z -=-,,,,,2z =∴.(002)(242)F BF =--,,,,,∴.26BF =∴.(2)设1n 为平面1AEC F 的法向量,1(1)x y =,,n ,由1100AE AF ⎧=⎪⎨=⎪⎩,,··n n 得410220y x +=⎧⎨-+=⎩,.114x y =⎧⎪⎨=-⎪⎩,.∴ 又1(003)CC =,,,设1CC 与1n 的夹角为α, 则111433cos 33CC CC α==·n n. C ∴到平面1AEC F 的距离1433cos 11d CC α==.21.如图6,在三棱锥P ABC -中,AB BC ⊥,AB BC kPA ==,点O D ,别离是AC PC ,的中点,OP ⊥底面ABC .(1)求证:OD ∥平面PAB ;(2)当12k =时,求直线PA 与平面PBC 所成角的大小;(3)当k 为何值时,O 在平面PBC 内的射影恰好为PBC △的重心? 解:(1)证明:OP ⊥∵平面ABC OA OC AB BC ==,,, OA OB OA OP OB OP ⊥⊥⊥,,∴.以O 为原点,成立如图所示空间直角坐标系O xyz -.设AB a =,则222000000222A a B a C a ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,,,,,. 设OP h =,则(00)P h ,,.D ∵为PC 的中点,21042OD a h ⎛⎫=- ⎪ ⎪⎝⎭,,∴.202PA a h ⎛⎫=- ⎪ ⎪⎝⎭,,,12OD PA =-∴. OD PA ∴∥,OD ∴∥平面PAB .(2)12k =,即2PA a =,72h a =∴,27022PA a a ⎛⎫=- ⎪ ⎪⎝⎭,,∴ 可求得平面PBC 的法向量1117⎛⎫=-- ⎪ ⎪⎝⎭,,n . 210cos 30PA PA PA ==,·∴n n n. 设PA 与平面PBC 所成的角为θ, 则210sin cos 30PA θ==,n . PA ∴与平面PBC 所成的角为210arcsin30. (3)PBC △的重心221663G a a h ⎛⎫- ⎪ ⎪⎝⎭,,,221663OG a a h ⎛⎫=- ⎪ ⎪⎝⎭,,∴, OG ⊥∵平面PBC ,OG PB ⊥∴.又202PB a h ⎛⎫=- ⎪ ⎪⎝⎭,,,2211063OG PB a h =-=∴·. 22h a =∴. 22PA OA h a =+=∴,即1k =.反之,当1k =时,三棱锥O PBC -为正三棱锥. O ∴在平面PBC 内的射影为PBC △的重心.22.如图7,已知向量OA OB OC ===,,a b c ,可组成空间向量的一个基底,若123()a a a =,,,a123123()()b b b c c c ==,,,,,b c ,在向量已有的运算法则的基础上,新概念一种运算233231131221()a b a b a b a b a b a b ⨯=---,,a b ,显然⨯a b 的结果仍为一贯量,记作p .(1) 求证:向量p 为平面OAB 的法向量;(2) 求证:以OA OB ,为边的平行四边形OADB 的面积等于⨯a b ;(3) 将四边形OADB 按向量OC =c 平移,取得一个平行六面体111OADB CA D B -,试判断平行六面体的体积V 与()⨯·a b c 的大小. 解:(1)233213113212213()()()0a b a b a a b a b a a b a b a =-+-+-=p a ·, ⊥p a ∴,同理⊥p b . p ∴是平面OAB 的法向量.(2)设平行四边形OADB 的面积为S ,OA 与OB 的夹角为θ, 则sin θ=S OA OB 21⎛⎫=- ⎪ ⎪⎝⎭·a b a b a b 222()a b a b a b -=⨯·.∴结论成立.(3)设C 点到平面OAB 的距离为h ,OC 与平面OAB 所成的角为α, 则=V Sh sin α=⨯a b c ,又()cos sin α⨯=⨯⨯=⨯,·a b c a b c a b c a b c , ∴V ()a b c =⨯·.。
高二数学选修2-1空间向量与立体几何单元测试卷

高二数学选修2-1空间向量与立体几何课标要求一、空间向量及其运算课标要求1.理解空间向量的概念,了解空间向量的基本定理及其意义,理解空间向量的正交分解及其坐标表示。
2.掌握空间向量的线性运算及其坐标表示。
3.掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。
二、空间向量及其运算课标要求的具体化和深广度分析1.经历向量及其运算由平面向量向空间向量推广的过程,理解空间向量的概念。
2.掌握空间向量的加法、减法运算。
3.掌握空间向量的数乘运算。
4.理解共线向量定理及其推论。
5.理解共面向量定理及其推论。
6.掌握空间向量夹角的概念及表示方法,掌握两个向量的数量积的概念、性质和计算方法及运算规律。
7.掌握两个向量的数量积的主要用途,会用它解决立体几何中的一些简单的问题。
8.了解空间向量基本定理,并能用基本定理解决一些几何问题。
9.理解基底、基向量及向量的线性组合的概念。
10.掌握空间向量的坐标表示,能在适当的坐标系中写出向量的坐标。
11.理解空间向量坐标的概念,会确定一些简单几何体的顶点坐标。
12.掌握空间向量的坐标运算规律,会判断两个向量的共线或垂直。
13.掌握空间向量的模、夹角公式和两点间距离公式,并能运用这些知识解决一些相关问题。
三、立体几何中的向量方法课标要求1.理解直线的方向向量与平面的法向量。
2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系。
3.能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理、直线与平面垂直的判定定理)和一些简单命题。
4.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角计算问题,了解向量方法在研究立体几何问题中的应用。
四、立体几何中的向量方法具体化和深广度分析1.理解直线的方向向量和平面的法向量。
2.能用向量语言表述线线、线面、面面平行于垂直关系。
3.能利用平面法向量证明两个平面垂直。
4.能利用直线的方向向量和平面的法向量判定并证明空间中的垂直关系。
2-1空间向量与立体几何单元测试

1数学选修2-1第三章《空间向量与立体几何》单元测试一、选择题(本大题共10个小题,每小题3分,共30分)1.若a 、b 、c 为任意向量,∈m R ,下列等式不一定成立的是( ) A .)()(c b a c b a ++=++ B .)(b a +·a c =·b c +·c C .b m a m b a m +=+)( D .(a ·b a c b ()=·)c 2.已知ABCD 是四面体,O 为△BCD内一点,则)(31++=是O 为△BCD 的重心的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件3.若向量),2,1,2(),2,,1(-==λ、夹角的余弦值为98,则λ等于( ) A .2 B .-2 C .-2或552 D .2或-5524.在以下命题中,不正确的个数为( ) +=-是、共线的充要条件; ②.若a ∥b ,则存在唯一的实数λ,使λ=a ·b ;③.对空间任意一点O 和不共线的三点A 、B 、C ,若OC OB OA OP --=22,则P 、A 、B 、C 四点共面;④.若{,,}为空间的一个基底,则{+++,,}构成空间的另一个基底; ⑤.│(a ·b )c │=│a │·│b │·│c │A .2B .3C .4D .5 5.设),2,3(),3,4,(z x ==,且∥,则xz 等于( ) A .-4 B .9 C .-9 D .9646.在正三棱柱111C B A ABC -中,若12BB AB =,则1AB 与B C 1所成角的大小为( )A .60°B .90°C .105°D .75°7.在△ABC 中,⊥===PA BC AC AB ,6,5平面8,=PA ABC ,则P 到BC 的距离是2( ) A .5 B .54 C .53 D .52 8.一条长为 a 的线段,夹在互相垂直的两个平面之间,它和这两个平面所成的角分别是45°和30°,由这条线段两端向两平面的交线引垂线,垂足间的距离( ) A .2a B .3a C .a 22 D .a 32 9.空间四点A 、B 、C 、D 每两点的连线长都等于a ,动点P 在线段AB 上,动点Q 在线段CD 上,则点P 与Q 的最小距离为( ) A .2a B .3a C .a 22 D .a 3210.如右图所示,在正方体''''D C B A ABCD -的侧面''A ABB 内有一动点P ,点P 到直线''B A 的距离与到直线BC 的距离相等,则动点P 所在曲线的形状为( )二、填空题(本大题共4小题,每小题3分,共12分)11.1A 、2A 、3A 是空间不共线的三点,则=++133221A A A A A A ;类比上述性质得到一般性的结论是 . 12.已知平行六面体1111D C B A ABCD -中,A B C D 是边长为a 的正方形,=∠=∠=AD A AB A b AA 111,120°,则1AC 的长= .13.已知a =(3,1,5),b =(1,2,-3),向量c 与z 轴垂直,且满足c ·a =9,c ·,4-=,则= .14.在长方体1111D C B A ABCD -中,C B 1和D C 1与 底面所成的角分别为60°和45°,则异面直线C B 1 和D C 1所成角的余弦值为 .'A'B 'C 'DBA DCP'A 'B B A P A 'A 'B B A P B 'A 'B B A P C 'A'BBAPDD CBA1A1B1C1D3三、解答题(本大题共6小题,共58分)15.(9分)如右图,E 是正方体1111D C B A ABCD -的棱11D C 的中点,试求向量11C A 与所成角的余弦值.16.(10分)设a a a a 523,32,23,24321++=-+-=-+=+-=,试问是否存在实数λ、μ、v ,使3214a v a a a ++=μλ成立?如果存在,求出λ、μ、v ;如果不存在,请给出证明.17. (9分)如图,在长方体1111ABCD A BC D -中,,E P 分别是11,BC A D 的中点,,M N 分别是1,AE CD 的中点,1,2AD AA a AB a === (Ⅰ)求证://MN 面11ADD A ; (Ⅱ)求二面角P AE D --的大小。
高二数学选修2-1空间向量与立体几何单元测试题

东升学校《空间向量与立体几何》单元测试题一、选择题(本大题8 小题 , 每小题 5 分,共 40 分)1、若a ,b , c是空间任意三个向量 ,R ,下列关系式中,不成立的是()A.a b b a B. a b a bC.a b c a b c D.b a2、给出下列命题①已知 a b ,则 a b c c b a b c ;②A、B、M 、N 为空间四点 ,若BA, BM , BN不构成空间的一个基底 ,则 A、B、M、N 共面 ;③已知 a b ,则 a, b 与任何向量不构成空间的一个基底;④已知a,b, c 是空间的一个基底,则基向量a, b可以与向量m a c 构成空间另一个基底 .正确命题个数是()A.1B.2C.3D.43、已知a, b均为单位向量 ,它们的夹角为 60 ,那么a3b 等于()A.7B.10C.13D.44、a1, b 2, c a b, 且 c a ,则向量 a与b 的夹角为()A.30B.60C.120D.1505、已知a3,2,5 , b 1, x, 1 , 且 a b 2 ,则x的值是()A.3B.4C.5D.66、若直线 l 的方向向量为a ,平面的法向量为n,则能使l //的是()A.a1,0,0 , n2,0,0B.a1,3,5 , n 1,0,1C.a0,2,1 , n1,0, 1D.a1, 1,3 , n0,3,17、在平面直角坐标系中 ,A( 2,3), B(3, 2) ,沿x轴把平面直角坐标系折成120第1页共15页的二面角后 ,则线段 AB 的长度为()A.2B.2 11C.3 2D.4 2、正方体ABCD-AB11C1D1的棱长为 1,E 是 A中点 ,则 E 到平面 ABC的距离8 1 B11D1是()A.3B.2C.1D.3 2223二、填空题(本大题共 6 小题,每空 5 分,共 30 分)9、已知F1i 2 j3k, F22i 3 j k , F33i 4 j5k ,若 F1 , F2 , F3共同作用于一物体上,使物体从点M(1,-2,1)移动到 N( 3,1,2),则合力所作的功是.10 、在平行六面体 ABCD-A1B1C1D1中 , 已知∠ BAD= ∠ A1AB= ∠A1AD=60 ,AD=4,AB=3,AA1=5, AC1 =.11、△ABC和△ DBC所在的平面互相垂直,且 AB=BC=BD,∠CBA=∠DBC=60,则 AD 与平面 BCD所成角的余弦值为.12、若直线l 的方向向量为(4,2,m),平面的法向量为 (2,1,-1),且 l⊥ ,则 m =.13、已知 A(-3,1,5),B(4,3,1),则线段 AB 的中点 M 的坐标为.三、解答题(本大题共 6 小题,共 80 分)14、(本题满分 12分 )设空间两个不同的单位向量a x1, y1 ,0,b x2 , y2 ,0 与向量 c1,1,1的夹角都等于 45 .(1)求x1y1和 x1 y1的值;(2)求a,b的大小 .15、(本题满分 12 分)已知四棱锥 P-ABCD的底面是边长为 a 的正方形 ,侧棱 PA⊥底面 ABCD,E为 PC上的点且 CE:CP=1:4,则在线段 AB上是否存在点 F 使 EF// 平面 PAD?第2页共15页17、(本题满分 14 分) 如图 ,四棱锥 S-ABCD的底面是矩形 ,AB=a,AD=2,SA=1,且SA ⊥底面 ABCD,若边 BC上存在异于 B,C的一点 P,使得PS PD .(1)求 a 的最大值 ;(2)当 a 取最大值时 ,求异面直线 AP 与 SD所成角的大小 ;(3)当 a 取最大值时 ,求平面 SCD的一个单位法向量n及点 P 到平面 SCD的距离 .18、 (本题满分14 分)已知正方形ABCD 和矩形ACEF 所在的平面互相垂直, AB2, AF=1,M是线段EF的中点.(1)求证: AM// 平面 BDE;(2)求证: AM⊥平面 BDF.第3页共15页19、(本题满分14 分)如图所示 ,矩形 ABCD 的边 AB=a,BC=2,PA⊥平面 ABCD,PA=2,现有数据 :① a 3;②a 1;③a 3 ;④ a 2 ;⑤ a 4 ; 2(1)当在 BC边上存在点⊥QD 时,a 可能取所给数据中的哪些值 ?请说明理由 ; Q,使 PQ(2)在满足 (1)的条件下 ,a 取所给数据中的最大值时,求直线 PQ与平面 ADP所成角的正切值 ;(3)记满足 (1)的条件下的Q 点为 Q n(n=1,2,3, ⋯ ),若 a 取所给数据的最小值时,这样的点Q n有几个 ?试求二面角Q n-PA-Q n+1的大小 ;20、 (本题满分14 分 )如图所示,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60 ,PA=AC=a,PB=PD= 2a,点E在PD上,且PE:ED=2:1.(1)证明: PA⊥平面ABCD;(2)求以 AC 为棱 ,EAC与 DAC为面的二面角θ的大小;(3)棱 PC上是否存在一点F,使 BF∥平面 AEC?证明你的结论 .第4页共15页参考答案: 一、选择题题号 1 23 4 5 6 7 8 答案 DCCCCDBB二、 填空题题号 9 1011 121314答案1497302-212, 2,32三、 解答题x 12 y 121x2y 21x y611112 ;15、解:( 1)依题意,x 1 y 12 x 1 y 16322x 1 y 114(2)∵单位向量 ax 1, y 1 ,0 ,bx 2 , y 2 ,0与向量 c 1,1,1 的夹角都等于45.x y 6x 162x 162112 4 或4 , ∴由x 1 y 11y 162 y 162444∴ a62 ,6 2,0 ,b62 ,6 2,04444x 1x 2y 1 y 26 2 6262 6 2 1由 cos a, b a b44442∴ a, b.316、解:建立如图所示的空间直角坐标系,设 PA=b ,则 A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,b),则 CPa, a, b ,∵E 为 PC 上的点且 CE : CP=1: 3,第5页共15页∴ CE1CP1a, a, b a , a , b44444∴由 CE AE AC AE CE AC3a , 3a , b,444设点 F 的坐标为 (x,0,0,) (0≤x≤a),则 EFx3a ,3a ,b,444又平面 PAD的一个法向量为AB a,0,0,依题意 , EF AB x3a a0 x3a ,443∴在线段 AB 上存在点 F,满足条件 ,点 F 在线段 AB 的处.17、解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,,0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设 P(a,x,0). (0<x<2)(1) ∵PS a, x,1 , PD a, 2x,0∴由 PS PD 得: a2x(2 x)0即:a2x(2 x) (0 x 2)∴当且仅当 x=1 时,a 有最大值为 1.此时 P 为 BC中点 ;(2)由(1)知 : AP (1,1,0), SD (0,2, 1),AP SD210,∴ cos AP, SD2 55AP SD∴异面直线 AP 与 SD所成角的大小为arc cos10 .5(3) 设n1x, y, z 是平面SCD的一个法向量,∵DC (1,0,0), SD(0, 2,1),第6页共15页∴由n1DC n1DC0x0x02 y z 0y 1 得 n1 (0,1, 2),n1SD n1SD0取 y1z2n11∴平面 SCD的一个单位法向量 n0,1,2n155又 CP CP n5(0, 1,0), 在 n 方向上的投影为1n∴点 P 到平面 SCD的距离为 5 .518、解:建立如图的直角坐标系,则各点的坐标分别为:O(0,0,0),A(0,1,0),B(-1,0,0),C(0,-1,0,),D(1,0,0,),E(0,-1,1),F(0,1,1),M(0,0,1).(1) ∵AM(0, 1,1),OE (0,1,1)∴ AM OE ,即AM//OE,又∵ AM平面BDE, OE平面BDE,∴A M// 平面 BDE;(2) ∵BD(2,0,0), DF(1,1,1),∴ AM BD 0, AM DF0,∴AM⊥BD,AM⊥DF,∴AM⊥平面BDF.19、解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0,),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2),设 Q(a,x,0).(0≤ x≤2)(1) ∵PQ a, x, 2 ,QD a,2x,0 ,∴由 PQ⊥QD 得PQ QD a2x(2x)0a2x(2 x)∵ x0, 2 , a2x(2x)0,1525 (0,,),555,5第7页共15页∴在所给数据中 ,a 可取 31两个值 .a和 a2(2) 由 (1)知 a 1,此时 x=1,即 Q 为 BC 中点 , ∴点 Q 的坐标为 (1,1,0)从而 PQ1,1, 2 , 又 AB 1,0,0为平面 ADP 的一个法向量 ,∴ cos PQ, ABPQ AB 1 6PQAB6 1,6∴ 直线 PQ 与平面 ADP 所成角的正切值为5 .5(3) 由(1)知 a31 或 x3,此时 x,,即满足条件的点 Q 有两个 ,222其坐标为 3 13 3Q 1, ,0 和Q 2 , ,02 22 2∵PA ⊥平面 ABCD,∴ PA ⊥AQ ⊥1,PA AQ 2,∴∠ Q 1AQ 2 就是二面角 Q 1-PA-Q 2 的平面角 .AQ 1 AQ 23 3 3由 cos AQ 1 , AQ 2 4 4AQ 1AQ 2 13,得∠Q 1AQ 2=30 ,2∴二面角 Q 12 的大小为 30 .-PA-Q20、解:( 1) ∵PA=AC=a ,PB=PD= 2a∴ PA 2 AB 2 PB 2 , PA 2 AD 2 PD 2,∴ PA ⊥AB 且 PA ⊥AD , ∴ PA ⊥平面 ABCD ,( 2)∵底面 ABCD 是菱形, ∴ AC ⊥BD ,设 AC ∩ BD=O ,∴以 O 为原点,建立如图所示的空间直角坐标系,则各点坐标分别为:A 0, a,0 , B3a ,0,0 , C 0, a ,0 , D 3a,0,0 ,P 0,a, a ,22 222∵ 点 E 在 PD 上,且 PE :ED=2:1.∴ DP3DE ,即: DP3 OEOD第8页共15页∴ OE3a, a , a ,即点 E 的坐标为 E 3a, a , a3 6 33 63又平面 DAC 的一个法向量为 n 10,0,1EAC 个 法 向 量 为 n 2x, y, z , OC0,a 设 平 面的 一 ,0 ,23 a aOEa,,36 3ay 02x 1n 2OCn 2 OC3a a由y, 得axyz 0n 2OEn 2 OE3 63z3取x=1n 2 1 , 0 , 3 ,n 1 n 2 3 3 ,n 2∴cos n 1, n 2n 21 2n 1 6n 1 2∴由图可知二面角 E-AC-D 的大小为.6( 3)设在 CP 上存在点 F ,满足题设条件,由 CFCP (01) ,得 OF OCCP0,12 a, a2 ∴ BF0,12 a, a 3a,0,03 a,1 2 a, a2222依题意,则有 BFn 2∴3 a,1 2a, a 1,0, 3 03 a 3 a 012222∴点 F 为 PC 中点时 ,满足题设条件 .第9页共15页一 . 选择题: (10 小题共 40 分 )1. 已知 A、B、C 三点不共线,对平面ABC外的任一点O,下列条件中能确定点M与点 A、B、C 一定共面的是( )A. OM OA OB OCB. OM2OA OB OCC. OM OA 1OB1OC D. OM1OA1OB1OC 233332. 直三棱柱 ABC— A1B1C1中,若 CA a,CB b,CC1C,则 A1 B( )A. a b cB. a b cC. a b cD. a b c3. 若向量m垂直向量 a和 b,向量 na b( ,R且、0)则()A. m// nB. m nC.m不平行于 n, m也不垂直于 nD. 以上三种情况都可能4.以下四个命题中,正确的是( )A.若 OP 1 OA 1OB,则P、A、B三点共线2 3B.设向量 { a,b, c} 是空间一个基底,则{ a +b , b +c , c + a }构成空间的另一个基底C. (a b) c a b cD. △ ABC是直角三角形的充要条件是AB AC05. 对空间任意两个向量a,b(b o), a // b 的充要条件是( )第10页共15页A. a bB. a bC. b aD. a b6.已知向量 a(0,2,1), b(1,1,2),则 a与 b 的夹角为()A.0 °B.45°C.90°D.180 °7.在平行六面体ABCDA1B1C1D1中,M为 AC与 BD的交点,若A1 B1 a, A1D1b, A1 A c ,则下列向量中与B1M相等的是()A. 1 a 1 b1c B. 1 a 1 b1c C. 1 a1b c D.- 1 a1b c22222222228.已知a(1,0,2), b(6,21,2), 若 a // b, 则与的值分()A.11B.5 ,2C. 1 ,1D.-5 , -2 5,2529.已知 a3i 2 j k, b i j2k, 则5a与 3b的数量积等于()A.-15B.-5C.-3D.-110. 在棱长为1 的正方体 ABCD— A1B1C1D1中, M和 N 分别为 A1B1和 BB1的中点,那么直线AM与CN所成角的余弦值是()A.2B.2C. 3D.1055510二. 填空题 : (4 小题共 16 分)11. 若 A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n=.第11页共15页12. 已知 A(0,2,3),B( -2 ,1,6),C( 1,-1 ,5),若| a |3,且 a AB, a AC ,则向量 a的坐标为.13.已知a,b是空间二向量,若| a |3, | b | 2, | a b |7,则 a与b 的夹角为.14. 已知点G 是△ ABC 的重心, O 是空间任一点,若OA OB OC OG ,则的值为.三. 解答题 :(10+8+12+14=44 分 )15.如图: ABCD为矩形, PA⊥平面 ABCD, PA=AD, M、 N 分别是 PC、AB中点,(1)求证: MN⊥平面 PCD;(2) 求 NM与平面 ABCD所成的角的大小 .16. 一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是300,求这条线段与这个二面角的棱所成的角的大小.17. 正四棱锥S— ABCD中,所有棱长都是2, P 为 SA的中点,如图.第12页共15页(1)求二面角 B— SC— D 的大小; (2) 求 DP与 SC所成的角的大小 .18.如图,直三棱柱 ABC— A1B1C1,底面△ ABC中, CA=CB=1,∠ BCA=90°,棱 AA1=2,M、 N分别是 A1B1, A1A 的中点;(1)求 BN的长 ;(2)求 cos BA1 , CB1的值 ;(3)求证 : A1B C1M .(4)求 CB1与平面 A1ABB1所成的角的余弦值 .第13页共15页高中数学选修2-1 测试题 (10)—空间向量 (1) 参考答案DDBB DCDA AB 11.012.(1, 1,1)13.60014.315.(1)略016.45017.(1)1(2)45(2)318.(1)3(2)30(3)略310 10(4)1018.如图,建立空间直角坐标系O— xyz. ( 1)依题意得 B( 0, 1,0)、 N( 1,0, 1)∴| BN |=(1 0)2(0 1)2(1 0)23.( 2)依题意得 A ( 1,0, 2)、B( 0, 1,0)、 C( 0, 0, 0)、 B ( 0,1, 2)11∴ BA ={-1,-1,2}, CB ={0,1,2,}, BA · CB =3,| BA |= 6 ,11111| CB1 |= 5 ∴cos< BA1, CB1>=BA1 CB11|BA1 | |CB1 |30 .10图第14页共15页1,1, C1M ={1,1( 3)证明:依题意,得 C( 0,0,2)、M(,2),A1B ={ -1,1,2},1222211⊥ C1M ,∴AB⊥CM.0}. ∴A1B·C1M =-+0=0,∴A1B2211评述:本题主要考查空间向量的概念及运算的基本知识. 考查空间两向量垂直的充要条件.第15页共15页。
选修2_1空间向量单元测试

空间向量单元测试(一)本试卷分第Ⅰ卷和第II 卷两部分.共150分.第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.在下列命题中:①若a 、b 共线,则a 、b 所在的直线平行;②若a 、b 所在的直线是异 面直线,则、一定不共面;③若、、三向量两两共面,则、、三向量一定 也共面;④已知三向量a 、b 、c ,则空间任意一个向量p 总可以唯一表示为 z y x ++=.其中正确命题的个数为( ) A .0 B .1 C .2D .32.在平行六面体ABCD -A 1B 1C 1D 1中,向量1D A 、1D C 、11C A 是 ( )A .有相同起点的向量B .等长向量C .共面向量D .不共面向量 3.若向量λμλμλ且向量和垂直向量R b a n b a m ∈+=,(,、则)0≠μ ( )A .//B .⊥C .也不垂直于不平行于,D .以上三种情况都可能4.已知a =(2,-1,3),b =(-1,4,-2),c =(7,5,λ),若a 、b 、c 三向量共 面,则实数λ等于 ( )A .627B .637C .647D .6575.直三棱柱ABC —A 1B 1C 1中,若c CC b CB a CA ===1,,, 则1A B =( )A .a +b -cB .a -b +cC .-a +b +cD .-a +b -c6.已知++=,||=2,||=3,||=19,则向量与之间的夹角><b a ,为( ) A .30° B .45° C .60° D .以上都不对7.若a 、b 均为非零向量,则b a =⋅是a 与b 共线的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件8.已知△ABC 的三个顶点为A (3,3,2),B (4,-3,7),C (0,5,1),则BC 边上的 中线长为 ( )A .2B .3C .4D .5 9.已知与则35,2,23+-=-+= ( ) A .-15 B .-5 C .-3 D .-110.已知(1,2,3)OA =,(2,1,2)OB =,(1,1,2)OP =,点Q 在直线OP 上运动,则当QA QB ⋅取得最小值时,点Q 的坐标为( ) A .131(,,)243B .123(,,)234C .448(,,)333D .447(,,)333第Ⅱ卷(非选择题,共100分)二、填空题(本大题共4小题,每小题6分,共24分)11.若A(m+1,n-1,3),B(2m,n,m-2n),C(m+3,n-3,9)三点共线,则m+n= .12.已知S是△ABC所在平面外一点,D是SC的中点,若BD=xAB y AC z AS++,则x+y+z=.13.在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{AB,AC,AD}为基底,则GE=.14.设|m|=1,|n|=2,2m+n与m-3n垂直,a=4m-n,b=7m+2n,则<a,b>=.三、解答题(本大题满分76分)15.(12分) 如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是DC的中点,取如图所示的空间直角坐标系.(1)写出A、B1、E、D1的坐标;(2)求AB1与D1E所成的角的余弦值.17.(12分)如图,已知矩形ABCD 所在平面外一点P ,P A ⊥平面ABCD ,E 、F 分别是AB 、 PC 的中点.(1)求证:EF ∥平面P AD ; (2)求证:EF ⊥CD ;(3)若∠PDA =45︒,求EF 与平面ABCD 所成的角的大小.18.(12分)在正方体1111D C B A ABCD -中,如图E、F分别是 1BB ,CD的中点,(1)求证:⊥F D 1平面ADE ; (219.(14分)如图,在四棱锥ABCD P -中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD , DC PD =,E 是PC 的中点,作PB EF ⊥交PB 于点F. (1)证明 ∥PA 平面EDB ; (2)证明⊥PB 平面EFD ;(3)求二面角D -PB -C 的大小.20.(14分)如图,直三棱柱ABC —A 1B 1C 1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA 1=2,D 、E 分别是CC 1与A 1B 的中点,点E 在平面ABD 上的射影是△ABD 的垂心G. (1)求A 1B 与平面ABD 所成角的正弦; (2)求点A 1到平面AED 的距离.空间向量单元测验(二)本卷满分150分,时间120分钟一、选择题:(本大题共10小题,每小题5分,共50分)1、已知向量a = (2, 4, 5) , b = (3, x, y) , 若 a ∥b ,则 ( )A. x = 6, y = 15B. x = 3, y = 15/2C. x = 3, y = 15D. x = 6, y = 15/2 2、已知向量a = (-3, 2, 5) , b = (1, x, -1) , 且 a ·b =2,则x 的值为A. 3B. 4C. 5D. 6 3.若向量λμλμλ且向量和垂直向量R ∈+=,(,、则)0≠μ ( ) A .n m //B . n m ⊥C .也不垂直于不平行于,D .以上三种情况都可能4.设向量},,{c b a 是空间一个基底,则一定可以与向量b a q b a p -=+=,构成空间的另一个基底的向量是( )NB1A1BAA .aB .bC .cD .b a 或 5.对空间任意两个向量//),(,≠的充要条件是( )A .=B .-=C .λ=D .λ= 6.已知向量b a b a 与则),2,1,1(),1,2,0(--==的夹角为 ( ) A .0° B .45°C .90°D .180°7、3.如图,在一个60°的二面角的棱上有两个点A 、B ,直线AC 、BD 分别在这个二面角的两个面内,且垂直于AB 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间向量单元测试(一)本试卷分第Ⅰ卷和第II 卷两部分.共150分.第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.在下列命题中:①若a 、b 共线,则a 、b 所在的直线平行;②若a 、b 所在的直线是异 面直线,则、一定不共面;③若、、三向量两两共面,则、、三向量一定 也共面;④已知三向量a 、b 、c ,则空间任意一个向量p 总可以唯一表示为 z y x ++=.其中正确命题的个数为( ) A .0 B .1 C .2D .32.在平行六面体ABCD -A 1B 1C 1D 1中,向量1D A 、1D C 、11C A 是 ( )A .有相同起点的向量B .等长向量C .共面向量D .不共面向量 3.若向量λμλμλ且向量和垂直向量R b a n b a m ∈+=,(,、则)0≠μ ( )A .//B .⊥C .也不垂直于不平行于,D .以上三种情况都可能4.已知=(2,-1,3),=(-1,4,-2),=(7,5,λ),若、、三向量共 面,则实数λ等于 ( )A .627B .637C .647D .6575.直三棱柱ABC —A 1B 1C 1中,若CC ===1,,, 则1A B =( )A .a +b -cB .a -b +cC .-a +b +cD .-a +b -c6.已知++=,||=2,||=3,||=19,则向量与之间的夹角><b a ,为( ) A .30° B .45° C .60° D .以上都不对 7.若a 、b 均为非零向量,则b a b a =⋅是a 与b 共线的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件8.已知△ABC 的三个顶点为A (3,3,2),B (4,-3,7),C (0,5,1),则BC 边上的 中线长为 ( )A .2B .3C .4D .5 9.已知与则35,2,23+-=-+= ( ) A .-15 B .-5 C .-3 D .-110.已知(1,2,3)OA =,(2,1,2)OB =,(1,1,2)OP =,点Q 在直线OP 上运动,则当QA QB ⋅ 取得最小值时,点Q 的坐标为 ( )A .131(,,)243B .123(,,)234C .448(,,)333D .447(,,)333第Ⅱ卷(非选择题,共100分)二、填空题(本大题共4小题,每小题6分,共24分)11.若A(m+1,n -1,3),B(2m,n,m-2n),C(m+3,n-3,9)三点共线,则m+n= .12.已知S是△ABC所在平面外一点,D是SC的中点,++,则x+y+z=.若BD=xAB y AC z AS13.在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{AB,AC,AD}为基底,则GE=.14.设|m|=1,|n|=2,2m+n与m-3n垂直,a=4m-n,b=7m+2n,则<a,b>=.三、解答题(本大题满分76分)15.(12分) 如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是DC的中点,取如图所示的空间直角坐标系.(1)写出A、B1、E、D1的坐标;(2)求AB1与D1E所成的角的余弦值.17.(12分)如图,已知矩形ABCD所在平面外一点P,P A⊥平面ABCD,E、F分别是AB、PC的中点.(1)求证:EF∥平面P AD;(2)求证:EF⊥CD;(3)若∠PDA=45︒,求EF与平面ABCD所成的角的大小.18.(12分)在正方体1111DCBAABCD-中,如图E、F分别是1BB,CD的中点,(1)求证:⊥FD1平面ADE;(2)求1,CBEF.19.(14分)如图,在四棱锥ABCDP-中,底面ABCD是正方形,侧棱⊥PD底面ABCD,DCPD=,E是PC的中点,作PBEF⊥交PB于点F.(1)证明∥PA平面EDB;(2)证明⊥PB平面EFD;(3)求二面角D-PB-C的大小.20.(14分)如图,直三棱柱ABC —A 1B 1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA 1=2,D 、E 分别是CC 1与A 1B 的中点,点E 在平面ABD 上的射影是△ABD 的垂心G. (1)求A 1B 与平面ABD 所成角的正弦; (2)求点A 1到平面AED 的距离.空间向量单元测验(二)本卷满分150分,时间120分钟一、选择题:(本大题共10小题,每小题5分,共50分)1、已知向量a = (2, 4, 5) , b = (3, x, y) , 若 a ∥b ,则 ( )A. x = 6, y = 15B. x = 3, y = 15/2C. x = 3, y = 15D. x = 6, y = 15/2 2、已知向量a = (-3, 2, 5) , b = (1, x, -1) , 且 a ·b =2,则x 的值为A. 3B. 4C. 5D. 6 3.若向量λμλμλ且向量和垂直向量R b a n b a m ∈+=,(,、则)0≠μ ( ) A .n m //B . n m ⊥C .n m n m 也不垂直于不平行于,D .以上三种情况都可能4.设向量},,{c b a 是空间一个基底,则一定可以与向量b a q b a p -=+=,构成空间的另一个基底的向量是( )NMB1A1CBAA .aB .bC .cD .b a 或 5.对空间任意两个向量//),(,≠的充要条件是( )A .=B .-=C .λ=D .λ= 6.已知向量与则),2,1,1(),1,2,0(--==的夹角为 ( ) A .0° B .45°C .90°D .180°7、3.如图,在一个60°的二面角的棱上有两个点A 、B ,直线AC 、BD 分别在这个二面角的两个面内,且垂直于AB 。
已知AB=4cm ,AC=6cm ,BD=8cm ,则CD 的长为( )A 314cmB 341cmC 412cmD 217cm8.已知的值分别为与则若μλμλλ,//),2,12,6(),2,0,1(b a b a -=+= ( ) A .21,51 B .5,2C .21,51--D .-5,-29、8.如图,在直三棱柱111C B A ABC -的底面ABC 中,CA=CB=1,∠BCA=90°,棱1AA =2,M ,N 分别是A A B A 111,的中点。
则:A .CB 1⊥MC 1 B. B A 1⊥M C 1 C. B A 1⊥C B 1D . BN ⊥C B 110.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( )A .52-B .52C .53 D .1010 二、填空题(本大题共4小题,每小题6分,共24分) CDBA11.若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n=.12.已知A (0,2,3),B (-2,1,6),C (1,-1,5),若a AC a AB a a 则向量且,,,3||⊥⊥=的坐标为 .13、. △ABC 和△DBC 所在的平面互相垂直,且AB=BC=BD ,∠CBA=∠DBC=120°,则二面角A-BD-C 的正切为_____________.14.已知点G 是△ABC 的重心,O 是空间任一点,若的值则λλ,OG OC OB OA =++为.三、解答题(本大题共6题,共76分)15.如图,M 、N 、E 、F 、G 、H 分别是四面体ABCD 中各棱的中点,若此四面体的对棱相等,求)()2(;)1(MG NH EF GH EF +⋅的夹角与(12分)16.如图:ABCD 为矩形,PA ⊥平面ABCD ,PA=AD ,M 、N 分别是PC 、AB 中点, 求证:MN ⊥平面PCD.(12分)17.直三棱柱ABC —A 1B 1C 1中,BC 1⊥AB 1,BC 1⊥A 1C 求证:AB 1=A 1C (12分)18.一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是30°,求这条线段与这个二面角的棱所成的角。
(12分)19.正四棱锥S —ABCD 中,所有棱长都是2,P 为SA 的中点,如图 (1)求二面角B —SC —D 的大小;(2)如果点Q 在棱SC 上,那么直线BQ 与PD 能否垂直? 请说明理由(14分)20.如图,直三棱柱ABC —A 1B 1C 1,底面△ABC 中,CA=CB=1,∠BCA=90°,棱AA 1=2,M 、N 分别是A 1B 1,A 1A 的中点, (1)求;的长BN(2)求;,cos 11的值><CB BA (3).:11M C B A ⊥求证(14分)。
