两等量同种(异种)电荷场强分布特点
等量异种同种电荷总结

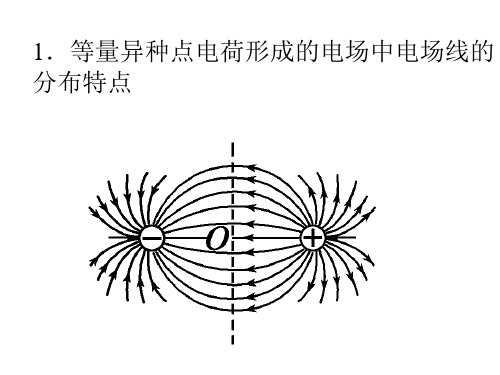
一.等量异种同种电荷产生电场电场线场强关系1.等量异种点电荷形成的电场中电场线的分布特点(1)两点电荷连线上各点,电场线方向从正电荷指向负电荷.(2)两点电荷连线的中垂面(中垂线)上,电场线方向均相同,即场强方向均相同,且总与中垂面(线)垂直.在中垂面(线)上到O点等距离处各点的场强相等(O为两点电荷连线中点).(3)在中垂面(线)上的电荷受到的静电力的方向总与中垂面(线)垂直,因此,在中垂面(线)上移动电荷时静电力不做功.(4) 等量异种点电荷连线上以中点O场强最小,中垂线上以中点O的场强为最大;(5)等量异种点电荷连线和中垂线上关于中点对称处的场强相同;2.等量同种点电荷形成的电场中电场线的分布特点(1)两点电荷连线中点O处场强为零,此处无电场线.(2)中点O附近的电场线非常稀疏,但场强并不为零.(3)两点电荷连线中垂面(中垂线)上,场强方向总沿面(线)远离O(等量正电荷).(4)在中垂面(线)上从O点到无穷远,电场线先变密后变疏,即场强先变强后变弱.(5)等量同种点电荷连线上以中点电场强度最小,等于零.因无限远处场强E∞=0,则沿中垂线从中点到无限远处,电场强度先增大后减小,之间某位置场强必有最大值.(6)等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.PS:等量异种电荷和等量同种电荷连线上以及中垂线上电场强度各有怎样的规律?(1)等量异种点电荷连线上以中点O场强最小,中垂线上以中点O的场强为最大;等量同种点电荷连线上以中点电场强度最小,等于零.因无限远处场强E∞=0,则沿中垂线从中点到无限远处,电场强度先增大后减小,之间某位置场强必有最大值.(2)等量异种点电荷连线和中垂线上关于中点对称处的场强相同;等量同种点电荷连线和中垂线上关于中点对称处的场强大小相等、方向相反.二.等量异种同种电荷产生电场电势等势面1.等量异种点电荷的电场:是两簇对称曲面,两点电荷连线的中垂面是一个等势面.如图1-4-6所示.在从正电荷到负电荷的连线上电势逐渐降低,φA>φA′;在中垂线上φB=φB′.2.等量同种点电荷的电场:是两簇对称曲面,如图1-4-7所示,在AA′线上O点电势最低;在中垂线上O点电势最高,向两侧电势逐渐降低,A、A′和B、B′对称等势.-三、练习1.如图所示,在真空中有两个固定的等量异种点电荷+Q和-Q。
对等量异种点电荷和等量同种点电荷电场中电场强度的变化情况的研究
对等量异种点电荷和等量同种点电荷电场中电场强度变化情况的研究[摘要]:本文用点电荷电场强度的计算公式以及场强的叠加原理,讨论了等量异种点电荷和等量同种点电荷电场中电场强度变化的情况。
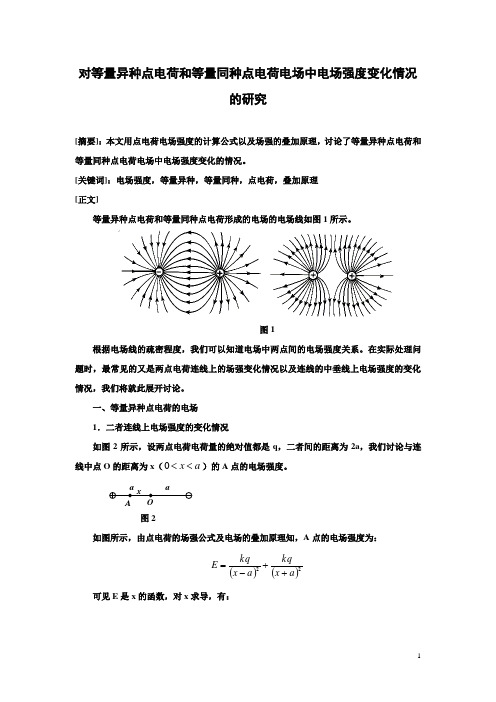
[关键词]:电场强度,等量异种,等量同种,点电荷,叠加原理[正文]等量异种点电荷和等量同种点电荷形成的电场的电场线如图1所示。
图1根据电场线的疏密程度,我们可以知道电场中两点间的电场强度关系。
在实际处理问题时,最常见的又是两点电荷连线上的场强变化情况以及连线的中垂线上电场强度的变化情况,我们将就此展开讨论。
一、等量异种点电荷的电场1.二者连线上电场强度的变化情况如图2所示,设两点电荷电荷量的绝对值都是q ,二者间的距离为2a ,我们讨论与连线中点O 的距离为x (a x <<0)的A 点的电场强度。
如图所示,由点电荷的场强公式及电场的叠加原理知,A 点的电场强度为: ()()22a x kq a x kq E ++-= 可见E 是x 的函数,对x 求导,有:图2()()()()[]()()⎥⎦⎤⎢⎣⎡+--=+-+---=-3323112212'x a x a kq x a x a kq E 由于,所以0'>E ,所以在a x <<0上,E 是增函数。
这说明x 的数值越大,即A 点离两点电荷连线的中点O 越远,场强越大。
由对称性可知,当A 位于O 点右边时,有同样的结果。
总之,从连线中点沿连线向两电荷移动时,电场强度逐渐增大,二者连线上中点位置的场强最小。
2.二者连线的中垂线上电场强度的变化情况如图3所示,我们研究二者连线的中垂线上与垂足O 相距x 的点A 的电场强度。
由对称性知,两点电荷在此处产生的场强的大小相等,方向如图所示。
由点电荷的场强公式和场的叠加原理知: θcos 222⋅+⋅=x a kq E 而 22cos x a a+=θ由上面两式可得:()23222x a kqaE +=从上式可以看出,当x 增大时,E 减小。
(完整版)电荷电场线分布示意图及场强电势特点

等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零(以无穷远处为零电势点,场强为零)(以无穷远处为零电势点,场强为零)注意:电场线、等势面的特点和电场线与等势面间的关系:①电场线的方向为该点的场强方向,电场线的疏密表示场强的大小。
等量电荷两条线的场强分布特点

等量电荷两条线上的场强分布特点等量同种(异种)点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q,两电荷连线AB长度为L,中点为O.一、等量异种电荷1、两电荷连线上如图1所示,在两电荷连线上任取一点G,设AG长度为x,则G点场强EG为两点电荷分别在该点的场强EA、EB的矢量和,方向从A指向B(由正电荷指向负电荷一侧),由点电荷场强公式知:EG= EA+ EB=∵x+(L-x)等于定值L,∴当x=(L-x),即x= 时,x与(L-x)乘积最大,EG有最小值,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称。
2、中垂线上如图2所示,在中垂线上,任取一点H,设OH=x,根据对称性知:EH沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H点的场强EH=,∴在O点,即x=0处,EH最大,x越大,即距O点越远EH越小,两侧电场强度数值关于O 点对称。
二、等量同种电荷1、电荷连线上如图3所示,在两电荷连线上任取一点N,设AN长度为x,则N点场强EN为两点电荷在该点的场强EA、EB的矢量和,方向沿AB连线,O点左侧从A指向B,右侧从B指向A(沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之),N点电场强度大小知:EN = ,∴当x= 时,EN =0,,即在两电荷连线中点O处场强最小,从O点向两侧逐渐增大,数值关于O点对称,方向相反。
2、中垂线上如图4所示,根据对称性知:在O点两侧,电场强度方向均沿中垂线方向从O点指向无限远(若两电荷为等量负电荷则反之),由极限分析法易得:在O点处,E =0;在距O点无限远处,E =0。
说明中间某位置有极大值,可见:合电场强度的大小随着距O点的距离增大,先从零增大到最大,然后逐渐减小。
同异种电荷的电场线分布
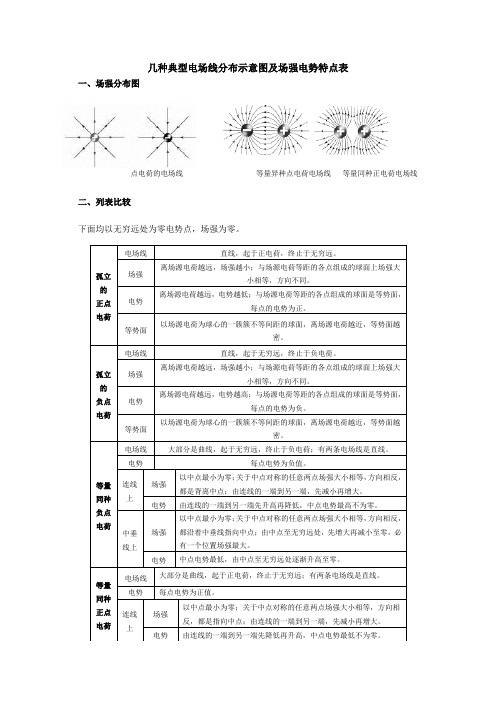
几种电荷电场线分布示意图及场强电势特点

点场强大小相等,方向
场
连
相同,都是由正电荷指 强
线
向负电荷;由连线的一
上
端到另一端,先减小再
增大。
电 由正电荷到负电荷逐渐 势 降低,中点电势为零。
以中点最大;关于中点
对称的任意两点场强大
小相等,方向相同,都
中
场 是与中垂线垂直,由正
垂
强 电荷指向负电荷;由中
线
点至无穷远处,逐渐减
上
小。
电 中垂面是一个等势面, 势 电势为零
(以无穷远处为零电势点,场强为零)
孤立点电荷电场线分布示意图及场强电 势特点
电场 直线,起于正电荷,终止于无 线 穷远。
离场源电荷越远,场强越小;
孤
与场源电荷等距的各点组成的 场强
立
球面上场强大小相等,方向不
的
同。
正
离场源电荷越远,电势越低;
点
与场源电荷等距的各点组成的
电
电势 球面是等势面,每点的电势为
荷
正。
等势 面
以场源电荷为球心的一簇簇不 等间距的球面,离场源电荷越 近,等势面越密。
电场 直线,起于无穷远,终止于负 线 电荷。
离场源电荷越远,场强越小;
孤
与场源电荷等距的各点组成的
场强
立
球面上场强大小相等,方向不
的
同。
负
离场源电荷越远,电势越高;
点
与场源电荷等距的各点组成的
电
电势 球面是等势面,每点的电势为
垂
穷远处,先增大再减小
线
至零,必有一个位置场
上
强最大。
中点电势最高,由中点 电
至无穷远处逐渐降低至 势
两个等量异种电荷和电场强度变化

两个等量异种电荷和电场强度变化摘要:一、引言二、两个等量异种电荷连线上的电场强度变化1.连线上以中点最小不等于零2.关于中点对称的任意两点场强大小相等,方向相同3.由连线的一端到另一端,先减小再增大三、等量异种电荷连线中垂线上的电场强度变化1.由中点向外侧逐渐减小2.无穷远处为零四、两个点电荷之间连线上的变化规律1.在两个点电荷之间,由大到小,再到大2.两个点电荷之外,由大到小五、结论正文:一、引言电场强度是描述电场力的作用效果的物理量,它是由电荷所产生的电场在空间中的分布情况。
对于两个等量的异种电荷,它们之间的电场强度变化规律是物理学中的基本问题之一。
本文将从电场强度变化的角度,探讨两个等量异种电荷之间的相互作用。
二、两个等量异种电荷连线上的电场强度变化在两个等量异种电荷连线上,电场强度的变化具有一定的规律。
首先,在连线上以中点为最小值,不等于零。
这是因为两个电荷之间的电场强度在中点处相互抵消,导致场强为零。
其次,关于中点对称的任意两点,场强大小相等,方向相同,都是由正电荷指向负电荷。
最后,在由连线的一端到另一端的过程中,电场强度会先减小后增大。
三、等量异种电荷连线中垂线上的电场强度变化在等量异种电荷连线中垂线上,电场强度的变化也具有规律。
从中点向外侧,电场强度逐渐减小,直至无穷远处为零。
这是因为在中垂线上,两个电荷产生的电场强度方向相同,使得场强叠加,从而导致场强逐渐减弱。
四、两个点电荷之间连线上的变化规律在两个点电荷之间,电场强度的变化规律是先由大到小,再到大。
在两个点电荷之外,电场强度会逐渐减小。
这些规律可以通过电场线的分布情况进行直观的观察和分析。
五、结论综上所述,两个等量异种电荷之间的电场强度变化具有规律性。
两等量同种(异种)电荷场强分布特点

两等量同种(异种)电荷场强分布特点 等量同种(异种)点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其 中垂线)上仍有其规律性,为研究方便,设它们带电量为 Q ,两电荷连线 AB 长度为 L,中点 为 O.1、 两电荷连线上如图 1 所示,在两电荷连线上任取一点 G ,设 AG 长度为 x ,则 G 点场强 E G 为两点电荷分别在该点的场强 E A 、E B 的矢量和,方向从A 指向 B (由正电 ∵x+(L-x )等于定值 L ,∴当 x=(L-x ),即x= L 时,x 与 (L-x )乘积最大, E G 有最小值,2即在两电荷连线中点 O 处场强最小,从 O 点向两侧逐渐增大,数值关于 O 点对称。
2、 中垂线上∴在 O 点,即 x=0 处,E H 最大,x 越大,即距 O 点越远E H 越小,两侧电场强度数值关于 O 点对称。
一、 等量异种电荷荷指向负电荷一侧),由点电荷场强公式知: E G = E A + E B = +x 2kQL 2 -2(L -x )xx (L - x )O图 1如图 2 所示,在中垂线上,任取一点 H ,设 OH=x ,根据对称性知:E H 沿水 平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷 一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一 等势线,与无限远处等势,即各点电势为零。
H 点的场强 E H =cos =kQ B2kQL2+ x 2H二、等量同种电荷1、电荷连线上如图3 所示,在两电荷连线上任取一点N,设AN 长度为x,则N 点场强E N为两点电荷在该点的场强E A、E B的矢量和,方向沿AB连线,O 点左侧从 A 指向B,右侧从 B 指向A(沿两电荷连线指向较远一侧电荷,图3若两电荷为等量负电荷则反之),N 点电场强度大小知:E NkQ kQ=x2 -(L- x)2∴当x= 时,E N =0,,即在两电荷连线中点O 处场强最小,2从O 点向两侧逐渐增大,数值关于O 点对称,方向相反。
等量同种、异种电荷电场强度和电势的定量比较

等量同种、异种电荷电场强度和电势的定量比较作者:杨杰来源:《理科考试研究·高中》2015年第02期平常教学中,关于等量同种、异种电荷连线上电场强度和电势的比较,往往更多地根据电场线的方向和分布定性地说明.由于电场线本身并不是客观存在的,而是人为引入的,再加上电场概念本身又比较抽象,不少同学对结论心存疑惑,更希望能够通过定量计算得出更具说服力的结论.笔者尝试着进一步分析发现,的确也可以通过定量计算进行说明,教学中也收到了理想的效果.一、等量同种电荷的电场强度和电势1.等量同种电荷的连线上①电场强度从电场线分布定性分析,a→o→b,由于电场线先变疏,后变密,所以电场强度先减小后增大.定量计算:设︱ab︱=L,︱aA︱=x,EA=kQx2,kQ(L-x)2,a→o过程中(x≤L2),x 变大, kQx2减小,kQ(L-x)2增大,∴EA减小.当x=L2时,Emin=Eo=0.由对称性可知,o→b过程中,电场强度不断增大.所以,a→o→b电场强度先减小后增大.②电势从电场方向定性分析,a→o,电场方向向右,o→b,电场方向向左.沿电场线方向电势降低.所以a→o→b,电势先减小后增大.定量计算:取无穷远处Ep=0,WA→∞=EPA-0,距电荷+Q距离为r处的A点的点电荷+q 的电势能,等于把它从这点移动到零势能位置时静电力做的功.EPA=WA→∞=∫∞rkQqr2dr=kQqr,则A点的电势φA=kQr.所以,到点电荷Q距离为r处的电势为φ=kQr(Q含正负,即正电荷在其周围产生的电势为正,负电荷在其周围产生的电势为负).在A点,a处的+Q在A点产生的电势为φ=kQx,b处的+Q在C点产生的电势为φ=kQL-x,所以等量同种电荷连线上的A点的电势φA=kQx+kQL-x=kQLx(L-x)=kQLL24-(L2-x)2,a→o过程中(x≤L2),x变大,φA减小,当x=L2时,φmin=4kQL.由对称性可知,o→b过程中,电势不断增大.所以,a→o→b,电势先减小后增大.2.等量同种电荷的中垂线上①电场强度从电场线分布定性分析,o→∞,电场线先变密,后变疏,所以,电场强度先增大后减小.定量计算:EC=2E1cosθ=8kQL2sin2θcosθ=42kQL22cos2θsin2θsin2θ.当2cos2θ=sin2θ时,即tanθ=2,场强有最大值Emax=1630kQL2.所以o→∞,电场强度先增大后减小.②电势从电场方向定性分析,电场方向沿o→∞方向.o→∞,电势降低.定量计算:a、b处的+Q在C点产生的电势均为kQL2sinθ=2kQsinθL所以φC=4kQsinθL,θ减小,φC减小,当θ=90°时,电势最高,φ0=φmax4kQL.所以o→∞,电势一直减小.二、等量异种电荷的电场强度和电势1.等量异种电荷的连线上①电场强度从电场线分布定性分析,a→o→b,由于电场线先变疏,后变密,所以电场强度先减小后增大.定量计算:同样设︱ab︱=L,︱aA︱=x,则EA-EO=kQx2 +kQ(L-x)2-8k QL2≥kQ[2x (L-x)2-8L2]=2kQ(L-2x)2x(L-x)L2≥0,所以EA≥EO,o点的电场强度最小,由对称性可知,a→o→b电场强度先减小后增大.②电势从电场方向定性分析,电场方向沿a→b方向,所以,a→b电势一直减小.定量计算:+Q在A点产生的电势为φ=kQx,-Q在C点产生的电势为φ=-kQL-x,所以φA=-kQx-kQL-x=kQ(L-2x)x(L-x),x增大,x(L-x)增大,(L-2x)减小,φA减小.所以,a→b电势一直减小.2.等量异种电荷的中垂线上①电场强度从电场线分布定性分析,o→∞,由于电场线越来越疏,所以,电场强度一直减小.定量计算:中垂线上任取一点C,Ec=8kQL2sin3θ,θ越小,EC越小.∴o→∞,E一直减小.②电势从电场方向定性分析,电场方向垂直于中垂线,沿o→∞方向移动电荷,电场力不做功,所以,o→∞,电势不变,且与无穷远处电势相等(电势为零).定量计算:+Q在C点产生的电势为φ=2kQsinθL,-Q在C点产生的电势为φ=-2kQsinθL.所以φC=0,o→∞,电势始终为0,中垂线为等势线.由此可见,无论通过定量计算还是定性分析,都会得出同样的结论.而定量分析能让学生经历概念规律的探究过程,使得原本抽象难懂的知识真实地呈现在学生眼前,加深了学生对同种、等量异种电荷的电场强度和电势的理解,有助于学生更好地解决与此相关的各类问题.下面笔者以一道典型的高考题为例,说明相关知识在解决实际问题中的重要作用.例1(2010年江苏单科第5题)空间有一沿x轴对称分布的电场,其电场强度E随x变化的图象如图所示.下列说法中正确的是().A.O点的电势最低B.x2点的电势最高C.x1和-x1两点的电势相等D.x1和x3两点的电势相等解析由题图知,该图象所反映的电场的特点:①在O处,场强为零,但电势最高;②在x1和-x1两点处,场强大小相等,方向相反,电势相等;③在x1和x3两点处,场强相同,但电势不同.由此可知,这个电场不是一个点电荷的电场,可能是两个点电荷形成的电场;从x=0到正负无穷远,场强有一个最大值,电势逐渐减小;当x趋近于正负无穷远时,场强和电势均为零.说明这是两个等量同种正电荷中垂线上的电场分布(如图所示).如果画出图象如右图所示,这就是09年江苏高考的第8题.同一个物理情境可以从不同的角度考查,但只要对等量同种、异种点电荷的电场、电势有准确的理解,问题自然就迎刃而解.答案C例2(2013年天津理综第6题)两个带等量正电的点电荷,固定在图中P、Q两点,MN 为PQ连线的中垂线,交PQ于O点,A点为MN上的一点.一带负电的试探电荷q,从A点由静止释放,只在静电力作用下运动.取无限远处的电势为零,则().A.q由A向O的运动是匀加速直线运动B.q由A向O运动的过程电势能逐渐减小C.q运动到O点时的动能最大D.q运动到O点时电势能为零解析等量正电荷连线的中垂线上,电场方向由O指向A,o→∞,电场强度先变大后变小,O点电场强度为零,A点电场强度大于零.又由于A点是中垂线上的任意一点,不一定是电场最强的特殊点,所以A到O的过程加速度是变化的,但不能确定是如何变化的,可能是一直减小,也可能先增大后减小.所以,A错误.带负电的试探电荷q,从A点由静止释放,所受静电力由A指向O,只在静电力作用下运动,A向O运动,电场力做正功,动能增加,电势能减小.取无限远处的电势为零,到O点时电势能为负,动能最大,所以,选项D错误,BC 正确.电场力减小,加速度逐渐减小的加速运动,q由A向O运动的过程电势能逐渐减小,q运动到O点时的动能最大,电势能不为零,AD错误.答案BC。
等量电荷两条特殊线上的场强、电势分布特点

等量电荷两条特殊线上的场强、电势分布特点一、等量异种电荷1、两电荷连线上如图1所示,在两电荷连线上任取一点G ,设AG 长度为x ,则G 点场强E G 为两点电荷分别在该点的场强E A 、E B 的矢量和,方向从A 指向B (由正电荷指向负电荷一侧)E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ,∴当x=(L-x),即x=2L时,x 与 (L-x)乘积最大 ∴这时E G 有最小值,即在两电荷连线中点O 处场强最小,将x=2L带入上式,可求得E G 最小值E Gmin =28L kQ,方面由A 指向B 。
从O 点向两侧逐渐增大,数值关于O 点对称。
小结;等量异种电荷连线中点场强最小,靠近点电荷场强渐强,方向从正点荷指向负电荷。
2、中垂线上如图2所示,在中垂线上,任取一点H ,设OH=x ,根据对称性知:E H 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H 点的场强图1GO B图2E H=232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ∴在O 点,即x=0处,E H 最大,x 越大,即距O 点越远E H 越小,两侧电场强度数值关于O 点对称。
小结:等量异种电荷的中垂线上电场强度由中点向上向下减小,方向与两点电荷的连线平行且由正电荷指向负电荷。
1)连线上:由于沿着电场线的方向电势降低,所以连线上从正点电荷到负点电荷电势降低。
(2)两点电荷连线中垂线上:由于中垂线上场强方向与中垂线垂直,所以某检验荷在中垂线上移动时,电场力不做功,由0==qW U AB AB 知,中垂线上任意两点的电势差为零,即中垂线上电势均为零。
两等量点电荷的场强、电势、电势能的情况分析

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析高中物理“电场”这个内容的概念很抽象,学生往往感到很困惑,导致对两点电荷连线及中垂线上的电场强度、电势、电势能的变化情况感到模糊不清,现就将我对这个问题的分析小结如下:这里所指的两点电荷是指靠得很近的两等量同种点电荷和等量异种点电荷。
一、两正点电荷连线及中垂线上的电场强度、电势、电势能的变化1、电场强度(1)两点电荷的连线上两点电荷在空间的电场是由这两个点电荷分别在该点的场强叠加而成。
根据电场强度的决定式2rQ k E =,可知E 与r 2成反比,与Q 成正比,而对于正电荷E 的方向背离点电荷。
在其连线上的中点,由于Q 相等,r 相等,即E 大小相等,而两点电荷在的场强方向相反,故合场强为零,如图1所示。
图1由||||212212r Q k r Q k E E E -=-=知,从中点往两边合场强增大,且关于中点对称。
小结:连线中点场强为零,靠近点电荷场强渐强,且关于中点对称,场强方向沿较近点电荷的场强方向。
(2)两点电荷的中垂线上中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。
由于中垂线上的点到线两端的距离相等,由2r Q kE =知|E 1|=|E 2|,即大小相等,方向如图2所示:图2分别把E 1、E 2分解在连线上和中垂线上,连线上的分量大小相等,方向相反,相互抵消,故合场强E 如图2所示。
所以从中垂线上中点往两边场强先是由零增大,但由2rQ k E =可知。
r 越大,E 减小,所以合场强又开始减小。
小结:两正电荷的中垂线上电场强度先从中点时的零逐渐增大,当增大到某个值时,又逐渐减小,且两边对称。
2、电势(1)可根据电势与电场线的关系(沿着电场线的方向电势降低)直接判断:连接上,从中点往两边电势升高;中垂线上从中点往两边电势降低。
电场线的分布如图3所示。
图3(2)也可由电势差的定义qW U AB AB =判断。
先看两点电荷的连线上:设一正检验电荷由连线上某点A 向中点O 运动时,如图4所示图4根据W=FS cos θ知,F 与S 的方向相同,故F 做正功,q 又为正电荷,所以 0>=qW U AO AO 即 0>-=O A Ao U ϕϕ故 O A ϕϕ>可知连线上从O 到点电荷电势升高,又由于两边对称,故连线上O 点电势最低。
几种典型电场线分布示意图及场强电势特点表
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最高,由中点至无穷远处逐渐降低至零。
等量异种点电荷电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线。
电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负。
连线上场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大。
电势由正电荷到负电荷逐渐降低,中点电势为零。
中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小。
电势中垂面是一个等势面,电势为零。
等势面(1)定义:电场中电势相等的点构成的面(2)等势面的性质:①在同一等势面上各点电势相等,所以在同一等势面上移动电荷,电场力不做功②电场线跟等势面一定垂直,并且由电势高的等势面指向电势低的等势面。
③等势面越密,电场强度越大④等势面不相交,不相切(3)等势面的用途:由等势面描绘电场线,判断电场中电势的高低。
(4)几种电场的电场线及等势面①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示。
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
等量同种电荷和异种电荷连线的垂直平分线上的电势,电势能,场强的变化

等量同种电荷和异种电荷连线的垂直平分线上的电势,电势
能,场强的变化
等量同种电荷连线的垂直平分线上的电势:在垂直平分线上,两侧的电荷是等量的,所以电场的强度也是一样的,也就是说,其电势也是一样的。
等量异种电荷连线的垂直平分线上的电势:在垂直平分线上,两侧的电荷是等量但异种的,由于两侧电荷的电荷量不同,所以其电场强度也是不同的,也就是说,其电势也会有不同。
电势能:当等量电荷连线时,其电势能会减少;而当异种电荷连线时,其电势能会增大。
场强:对于等量同种电荷连线时,由于电荷量、电场强度都是一样的,所以其场强也是一样的;而对于等量异种电荷连线时,由于电荷量、电场强度都是不同的,所以其场强也是不同的。
两等量同种(异种)电荷场强分布特点讲课稿

两等量同种(异种)电荷场强分布特点两等量同种(异种)电荷场强分布特点等量同种(异种)点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q,两电荷连线AB长度为L,中点为O.一、等量异种电荷1、两电荷连线上如图1所示,在两电荷连线上任取一点G,设AG长度为x,则G点场强E G为两点电荷分别在该点的场强E A、E B的矢量和,方向从A指向BE G=E A+E B=()[]()[]22222)(xLxxxLLkQxLkQxkQ---=-+图1x∵x+(L-x)等于定值L ,∴当x=(L-x),即x=2L时,x 与 (L-x)乘积最大, E G 有最小值,即在两电荷连线中点O 处场强最小,从O 点向两侧逐渐增大,数值关于O 点对称。
2、中垂线上如图2所示,在中垂线上,任取一点H ,设OH=x ,根据对称性知:E H 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ,∴在O 点,即x=0处,E H 最大,x 越大,即距O 点越远E H 越小,两侧电场强度数值关于O 点对称。
二、 等量同种电荷1、电荷连线上如图3所示,在两电荷连线上任取一点N ,设AN 长度为x , 则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和,方向沿图3图2HAB连线,O 点左侧从A 指向B ,右侧从B 指向A (沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之),N 点电场强度大小知:E N =22)(x L kQx kQ --, ∴当x=2L时,E N =0,,即在两电荷连线中点O 处场强最小, 从O 点向两侧逐渐增大,数值关于O 点对称,方向相反。
两等量同种(异种)电荷场强分布特点

两等量同种(异种)电荷场强分布特点等量同种(异种)点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q ,两电荷连线AB 长度为L,中点为O.一、 等量异种电荷1、 两电荷连线上如图1所示,在两电荷连线上任取一点G ,设AG 长度为x ,则G 点场强E G 为两点电荷分别在该点的场强E A 、E B荷指向负电荷一侧),由点电荷场强公式知:E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ,∴当x=(L-x),即x=2L时,x 与 (L-x)乘积最大, E G 有最小值,即在两电荷连线中点O 处场强最小,从O 点向两侧逐渐增大,数值关于O 点对称。
2、 中垂线上如图2所示,在中垂线上,任取一点H ,设OH=x ,根据对称性知:E H 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ,∴在O 点,即x=0处,E H 最大,x 越大,即距O 点越远E H 越小,两侧电场强度数值关于O 点对称。
图1G O B图2H二、 等量同种电荷1、 电荷连线上如图3所示,在两电荷连线上任取一点N ,设AN 长度为x ,则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和,方向沿AB 连线,O 点左侧从A 指向B ,右侧从B 指向A (沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之),N 点电场强度大小知:E N =22)(x L kQx kQ --, ∴当x=2L时,E N =0,,即在两电荷连线中点O 处场强最小, 从O 点向两侧逐渐增大,数值关于O 点对称,方向相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两等量同种(异种)电荷场强分布特点等量同种(异种)点电荷在空间的场强分布比较复杂,但在两条线(点电荷连线及其中垂线)上仍有其规律性,为研究方便,设它们带电量为Q ,两电荷连线AB 长度为L,中点为O.一、 等量异种电荷1、 两电荷连线上如图1所示,在两电荷连线上任取一点G ,设AG 长度为x ,则G 点场强E G 为两点电荷分别在该点的场强E A 、E B荷指向负电荷一侧),由点电荷场强公式知:E G = E A + E B =()[]()[]22222)(xL x xx L L kQ x L kQ x kQ ---=-+∵x+(L-x)等于定值L ,∴当x=(L-x),即x=2L时,x 与 (L-x)乘积最大, E G 有最小值,即在两电荷连线中点O 处场强最小,从O 点向两侧逐渐增大,数值关于O 点对称。
2、 中垂线上如图2所示,在中垂线上,任取一点H ,设OH=x ,根据对称性知:E H 沿水平方向向右,即在中垂线上各点场强水平向右(垂直于中垂线指向负电荷一侧),沿中垂线移动电荷,电场力不做功,由电势差定义知:中垂线为一等势线,与无限远处等势,即各点电势为零。
H 点的场强E H =232222222222222cos 22⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛=⋅+⎪⎭⎫ ⎝⎛x L kQL x L L x L kQ x L kQ θ,∴在O 点,即x=0处,E H 最大,x 越大,即距O 点越远E H 越小,两侧电场强度数值关于O 点对称。
图1G O B图2H二、 等量同种电荷1、 电荷连线上如图3所示,在两电荷连线上任取一点N ,设AN 长度为x ,则N 点场强E N 为两点电荷在该点的场强E A 、E B 的矢量和,方向沿AB 连线,O 点左侧从A 指向B ,右侧从B 指向A (沿两电荷连线指向较远一侧电荷,若两电荷为等量负电荷则反之),N 点电场强度大小知:E N =22)(x L kQx kQ --, ∴当x=2L时,E N =0,,即在两电荷连线中点O 处场强最小, 从O 点向两侧逐渐增大,数值关于O 点对称,方向相反。
2、 中垂线上如图4所示, 根据对称性知:在O 点两侧, 电场强度方向均沿中垂线方向从O 点指向 无限远(若两电荷为等量负电荷则反之),由极限分析法易得:在O 点处,E =0;在距O 点无限远处,E =0。
说明中间某位置有极大值,可见:合电场强度的大小随着距O 点的距离增大,先从零增大到最大,然后逐渐减小。
在中垂线上,任取一点P ,设OP=x ,由点电荷场强公式, P 点场强 E P =2 E A cos θ=23222222222222cos 2⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⋅⎪⎭⎫ ⎝⎛+=⋅L x kQx L x x L x kQ rkQ θ,运用数学方法,令y=232222⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+L x kQx,求导可得:y,=322212223222222321⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯L x xL x x L x令y ,=0,则212222322232⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+L x x L x ,即22232x L x =⎪⎭⎫ ⎝⎛+,∴当L x 42±=时, E P 有最大值29316LkQ ,∴从中点沿中垂线向两侧,电场强度的数值先增大后减小,两侧方向相反,关于O 点对称的点数值相等。
图3NO BE1(09·上海物理·3)两带电量分别为q和-q的点电荷放在x轴上,相距为L,能正确反映两电荷连线上场强大小E与x关系是图(A)2.(09·江苏物理·8)空间某一静电场的电势在轴上分布如图所示,轴上两点B、C点电场强度在方向上的分量分别是Ebx、Ecx,下列说法中正确的有( AD ) A.Ebx的大小大于Ecx的大小 B.Ebx的方向沿x轴正方向 C.电荷在O点受到的电场力在方向上的分量最大 D.负电荷沿轴从移到的过程中,电场力先做正功,后做负功3 .(09·山东·20)如图所示,在x轴上关于原点O对称的两点固定放置等量异种点电荷+Q 和-Q,x轴上的P点位于的右侧。
下列判断正确的是()A.在x轴上还有一点与P点电场强度相同B.在x轴上还有两点与P点电场强度相同C.若将一试探电荷+q从P点移至O点,电势能增大D.若将一试探电荷+q从P点移至O点,电势能减小4.如图,一个带负电的粒子沿着异种电荷的中垂线从A点匀速运动到B点,如果粒子重力不计,则带电粒子受到的除电场力外的另一个力大小和方向正确的是(A)A、先变大后变小,方向水平向右B、先变小后变大,方向水平向左C、大小不变,方向水平向左D、大小不变,方向水平向右5.如图所示,A、B为两个固定的等量的同种正电荷,在它们连线的中点处有一个可以自由运动的正电荷C,现给电荷C一个垂直于连线的初速度v0,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( BD ) A.加速度始终增大B.加速度先增大后减小C.速度始终增大,最后趋于无穷大D.速度始终增大,最后趋于某有限值(AB)7.(2009年高考江苏卷)空间某一静电场的电势φ在x轴上分布如图1-7所示,x轴上两点B、C的电场强度在x方向上的分量分别是EBx、ECx.下列说法中正确的有( D )A.EBx的大小大于ECx的大小B.EBx的方向沿x轴正方向C.电荷在O点受到的电场力在x 方向上的分量最大D.负电荷沿x轴从B移到C的过程中,电场力先做正功,后做负功8.空间有一沿x轴对称分布的电场,其电场强度E随X变化的图像如图所示。
下列说法正确的是( C )(A)O点的电势最低(B)X2点的电势最高(C)X1和- X1两点的电势相等(D)X1和X3两点的电势相等AC10.(09·山东·20)如图所示,在x 轴上关于原点O 对称的两点固定放置等量异种点电荷+Q和-Q ,x 轴上的P 点位于的右侧。
下列判断正确的是 ( AC )A .在x 轴上还有一点与P 点电场强度相同B .在x 轴上还有两点与P 点电场强度相同C .若将一试探电荷+q 从P 点移至O 点,电势能增大 D .若将一试探电荷+q 从P 点移至O 点,电势能减小 11.(2011朝阳一模)如图所示,在真空中有两个固定的等量异种点电荷+Q 和-Q 。
直线MN 是两点电荷连线的中垂线,O 是两点电荷连线与直线MN 的交点。
a 、b 是两点电荷连线上关于O 的对称点,c 、d 是直线MN 上的两个点。
下列说法中正确的是( )A .a 点的场强大于b 点的场强;将一检验电荷沿MN 由c 移动到d ,所受电场力先增大后减小B .a 点的场强小于b 点的场强;将一检验电荷沿MN 由c 移动到d ,所受电场力先减小后增大C .a 点的场强等于b 点的场强;将一检验电荷沿MN 由c 移动到d ,所受电场力先增大后减小D .a 点的场强等于b 点的场强;将一检验电荷沿MN 由c 移动到d ,所受电场力先减小后增大12. (2011昌平二模)等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a 点沿直线移到b 点,再从b 点沿直线移到c 点.则( )A .从a 点到b 点,电势逐渐增大B .从a 点到b 点,检验电荷受电场力先增大后减小C .从a 点到c 点,检验电荷所受电场力的方向始终不变D .从a 点到c 点,检验电荷的电势能先不变后增大13.(2011石景山一模)如图所示,在矩形ABCD 的AD 边和BC 边的中点M 和N 各放一个点电荷,它们分别带等量的异种电荷。
E 、F 分别是AB 边和CD 边的中点,P 、Q 两点在MN 的连线上,且MP =QN 。
在图中,电场强度相同、电势相等的两点是( )A .E 和FB .P 和QC .A 和CD .C 和D14.(2011•福州模拟)如图9所示,在x 轴上关于原点O 对称的两点固定放置在等量异种点电荷+Q 和—Q ,x 轴上的P 点位于—Q 的右侧。
下列判断正确的是 ( ) A .P 点电势比O 点高B .在x 轴上没有点与P 点电场强度相同C .在x 轴上还有一点与P 点电场强度相同D .若将一试探电荷+q 从P 点移至O 点,电势能减小15. (09年山东卷)20.如图所示,在x 轴上关于原点O 对称的两点固定放置等量异种点电荷+Q 和-Q ,x 轴上的P 点位于的右侧。
下列判断正确的是( )A .在x 轴上还有一点与P 点电场强度相同B .在x 轴上还有两点与P 点电场强度相同C .若将一试探电荷+q 从P 点移至O 点,电势能增大D .若将一试探电荷+q 从P 点移至O 点,电势能减小16.【2011•济南模拟】两个固定的异号点电荷,电量给定但大小不等,用E 1和E 2分别表示两个点电荷产生的电场强度的大小,则在通过两点电荷的直线上,E 1=E 2的点( )A .有三个,其中两处合场强为零B .有三个,其中一处合场强为零C .只有两个,其中一处合场强为零D .只有一个,该处合场强不为零17.(2011朝阳期末)如图所示,真空中有直角坐标系xOy ,在x 轴上固定着关于O 点对称的等量异号点电荷+Q 和-Q ,C 是y 轴上的一个点,D 是x 轴上的一个点,DE 连线垂直于x 轴。
将一个点电荷+q 从O 移动到D ,电场力对它做功为W 1,将这个点电荷从C 移动到E ,电场力对它做功为W 2。
下列判断正确的是( )A .两次移动电荷电场力都做正功,并且W 1=W 2B .两次移动电荷电场力都做正功,并且W 1>W 2C .两次移动电荷电场力都做负功,并且W 1=W 2D .两次移动电荷电场力都做负功,并且W 1>W 218.(2011山东第21题).如图所示,在两等量异种点电荷的电场中,MN 为两电荷连线的中垂线,a 、b 、c 三点所在直线平行于两电荷的连线,且a 与c 关于MN 对称,b 点位于MN 上,d 点位于两电荷的连线上。
以下判断正确的是 ( ) A .b 点场强大于d 点场强 B .b 点场强小于d 点场强C .a 、b 两点的电势差等于b 、c 两点间的电势差D .试探电荷+q 在a 点的电势能小于在c 点的电势能19.【2011•焦作模拟】某静电场的电场线分布如图所示,P 、Q 为电场中的两点.则下列说法正确的是( )A.P 点电势一定高于Q 点电势B.P 点场强一定小于Q 点场强C.负电荷在P 点的电势能大于在Q 点的电势能D.若将一试探电荷+q 由P 点释放,它将沿电场线运动到Q 点20. 一对等量正点电荷电场的电场线(实线)和等势线(虚线)如图所示,图中A 、B 两点电场强度分别是E A 、E B ,电势分别是ΦA 、ΦB ,负电荷q 在A 、B 时的电势能分别是E PA 、E PB ,下列判断正确的是( )A .E A >EB ,ΦA >ΦB ,E PA <E PB B .E A >E B ,ΦA <ΦB ,E PA <E PBC .E A < E B ,ΦA >ΦB ,E PA >E PBD .E A <E B ,ΦA <ΦB ,E PA >E PB 21.(09年安徽卷)18. 在光滑的绝缘水平面上,有一个正方形的abcd ,顶点a 、c 处分别固定一个正点电荷,电荷量相等,如图所示。
