(完整版)六年级数学上册组合图形的周长和面积
六年级数学上册组合图形的周长和面积讲解

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:切圆面积减去等腰直角三角形的面积,石沖2 X1=1.14 (平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)II解:这也是一种最基本的方法用正方形的面积减去■■圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以+=7,所以阴影部分的面积为:7-亍.丄=7-一X7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)(2) 解:最基本的方法之一。
用四个-I圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2X2- n= 0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16- n()=16-4n=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为叶形”,是用两个圆减去一个正方形,n() >2-16=8 n -16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2X 1=2平方厘米 (注: 8、9、10三题是简单割、补或平移)这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求50 7(n - n ) X 预=6 X 3.14=3.66 平方厘米例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积 多多少厘米? 解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分) n :-n ()=100.48 平方厘米 (注:这和两个圆是否相交、交的情况如何无关) 例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长冷寸角线长吃,求)正方形面积为:5X5^2=12.5 所以阴影面积为: 0 *12.5=7.125平方厘米 (注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
六年级数学上册组合图形的周长和面积[1]汇编
![六年级数学上册组合图形的周长和面积[1]汇编](https://img.taocdn.com/s3/m/2640e421a58da0116d17496f.png)
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法: 1圆面积减去等腰直角三角形的面积,4拓-2 X1=1.14 (平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)£解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以?=7,所以阴影部分的面积为:7- ^「=7-丨X7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)£解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积:2X2- n= 0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16- n()=16-4n=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为叶形”,是用两个圆减去一个正方形,n() >2-16=8n -16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)n :-n()=100.48 平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长 >对角线长煜,求)正方形面积为:5X5^2=12.5(5)2所以阴影面积为:n ^4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)£解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,£所以阴影部分面积为:n()=3.14平方厘米例9.求阴影部分的面积。
人教版六年级上册数学圆的组合图形的面积(课件)(共16页PPT)

方法一:分割法
求阴影部分的面积
3
S阴 S圆 S正
4
r=5cm
方法二:补缺法
求阴影部分的面积
S 阴=S正 – S半圆
10m
方法三:割补法
求阴影部分的面积①r= Nhomakorabeam②
S阴= S三角形
方法四:平移法
求阴影部分的面积
①
②
5cm
10cm
S阴=S正
方法五:对称法
求阴影部分的面积
①
②
S阴=S大三+S小三
人教版六年级数学上册
圆的组合图形的面积
长 方 形 的 面 积 = 长 ×宽
S=ab
正 方 形 的 面 积 = 边长×边长
平行四边形的面积= 底×高
S=a×a
S=ah
三 角 形 的 面 积 = 底×高÷2
S=ah÷2
梯 形 的 面 积 = (上底+下底)×高÷2 S=(a+b)h÷2
圆的面积:
S=
③
④
5cm
方法六:重叠法
求阴影部分的面积
S阴 2S扇 S正
练习:(想一想:用什么方法计算阴影
部分的面积呢?)
2厘米
3厘米
6厘米
4厘米
10cm
6cm
4dm
20cm
4m
六年级周长和面积知识点

六年级周长和面积知识点在数学学科中,周长和面积是我们学习的基本概念之一。
六年级的学生正是在这个阶段开始接触和学习相关的知识点。
下面,我们将深入探讨六年级周长和面积的知识。
一、周长知识点周长是指封闭图形的边界长度。
具体来说,我们可以根据不同的图形计算其周长。
1. 矩形的周长计算公式:矩形的周长等于两个相对边的长度之和乘以2,即P = (a + b) ×2。
其中,a和b分别代表矩形的两个边长。
2. 正方形的周长计算公式:正方形的周长是其四条边的长度之和,即P = a × 4。
其中,a代表正方形的边长。
3. 三角形的周长计算公式:三角形的周长等于三条边的长度之和,即P = a + b + c。
其中,a、b和c分别代表三角形的三条边长。
二、面积知识点面积是指封闭图形所占据的区域的大小。
不同的图形有不同的计算公式。
1. 矩形的面积计算公式:矩形的面积等于矩形的长乘以宽,即A = a × b。
其中,a和b分别代表矩形的两个边长。
2. 正方形的面积计算公式:正方形的面积是其边长的平方,即A = a²。
其中,a代表正方形的边长。
3. 三角形的面积计算公式:三角形的面积等于底边长度乘以高,再除以2,即A = (b × h) / 2。
其中,b代表三角形的底边长度,h代表三角形的高。
三、实际应用了解周长和面积的知识,可以帮助我们应用到各种实际问题中。
下面举几个例子来说明。
例1:围墙的周长如果我们要给一个形状为矩形的花园建造围墙,那么我们需要计算其周长。
首先,我们需要测量花园的长度和宽度,然后应用矩形的周长计算公式P = (a + b) × 2来计算围墙的长度。
例2:涂料的面积当我们准备涂刷一面墙时,我们需要知道墙的面积,从而购买足够的涂料。
如果墙的形状是矩形,我们可以应用矩形的面积计算公式A = a × b来计算其面积。
如果墙的形状是三角形,则需要应用三角形的面积计算公式A = (b × h) / 2来计算其面积。
《组合图形的面积》六年级上册
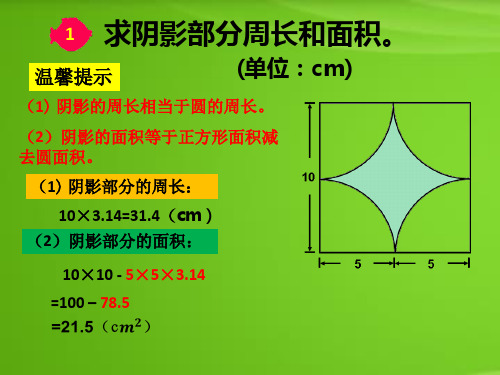
两个内圆面积:
5×5×3.14+2×2×3.14 =78.5+12.56
4 10
3 求阴影部分周长和面积(单位:dm)
温馨提示
(1)阴影的周长=大圆周长的一半 + 两
个小圆周长的一半
(2)阴影的面积=大圆面积的一半 — 两
个小圆面积的一半
3
5
阴影的周长:8×3.14÷2+3×3.14÷2+5×3.14÷2=25.12(dm)
阴影面积=(扇形面积 – 三角形 面积形面积)×2
10cm
13 求阴影部分面积。(单位:cm)
温馨提示:
1)正方形面积 – 圆面积=等于4
角的空白面积。
8
2)正方形面积 – 4个角的扇形
面积(也就是一个圆的面积)=
圆中间的空白面积。
8
14 跑道长多少米?(两端各是半圆)跑道 面积是多少?
跑道长: 10×2×3.14+100×2 =62.8+200 =262.8(米)
100米
15 求阴影部分面积。
温馨提示:
(1)做辅助线把圆心连起来呈现
出一个正方形,正方形的边长
是半径的2倍。
(2)正方形的面积 - 4个空白扇形
2cm
的面积(也就是一个圆面积)=
中间的阴影面积
16 求阴影部分面积。
温馨提示:
(1)正方形面积-外圆面积
=4个角的阴影面积
4cm
(2)4个角的阴影面积+小
=9×4.5÷2 =20.25(平方厘米)
阴影面积:
42-20.25 =21.75(平方厘米)
30 求阴影部分面积。(单位:厘米)
温馨提示:
完整版六年级54组合图形的周长与面积练习题

趁自己年纪,好好把握时光六年级上册数学组合图形(圆)的周长和面积练习题一、基础训练:) 1.求阴影部分的面积(单位:厘米。
43.14x2x2÷2X2÷2-平方厘米,求阴影部分的面积。
正方形面积是16 2.43.14x4x4÷16-16÷4=4(cm)cm)求图中阴影部分的面积及周长。
(单位3. 3.14x1x1=0.86(平方厘米)面积:2x2-)周长:3.14x1x1=3.14(cm)(单位:厘米4.求阴影部分的面积及周长。
(x4÷2))4÷4x4-3.14x面积:(24x2+3.14x4周长:1趁自己年纪,好好把握时光5.求阴影部分的面积。
) 厘米求阴影部分的面积。
(单位:7.如图(8),:厘米) 98.如图()求阴影部分的面积。
(单位2+1)X2=6(平方厘米)(S=) 厘米求阴影部分的面积。
如图(11)(单位:9.3.14x4x4-3.14x3x3〖〗6÷2趁自己年纪,好好把握时光10.在如图(12)是正三角形中求阴影部分的面积及周长。
(单位:厘米)面积:3.14x3x3÷2 周长:3.14x3+3x612. 如图(13)求阴影部分的面积。
(单位:厘米))厘米单位:)13.如图(14求阴影部分的面积。
() 单位右图(16.如33),求阴影部分的面积及周长。
(:厘米二、能力提升:19如17.右图()正方形边长为厘米,求阴影部分的面积及周长。
4 3 趁自己年纪,好好把握时光平方厘米,求阴影部分的面积。
ABCD的面积是3618.如图(20),正方形厘米,求阴影部分的面积。
如图(22),正方形边长为819.单位:厘米)(2820.如图()求阴影部分的面积。
4趁自己年纪,好好把握时光求阴影部分的面积。
)如图(3321. 5。
六年级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级上册数学教案-第九讲组合图形的周长与面积人教版

六年级上册数学教案第九讲组合图形的周长与面积人教版教学内容本讲主要介绍组合图形的周长与面积的计算方法。
学生需要掌握组合图形的构成,理解组合图形可以分解为简单的几何图形,如三角形、矩形、圆形等。
学生需要学习如何计算组合图形的周长和面积,包括分解图形、计算各部分周长和面积、求和等步骤。
本讲还将介绍一些常见的组合图形的周长与面积的求解技巧和注意事项。
教学目标1. 理解组合图形的构成,能够将组合图形分解为简单的几何图形。
2. 学会计算组合图形的周长和面积,能够熟练运用相关公式和定理。
3. 掌握一些常见的组合图形的周长与面积的求解技巧和注意事项。
4. 培养学生的观察能力、分析能力和解决问题的能力。
教学难点1. 如何正确地将组合图形分解为简单的几何图形。
2. 如何准确地计算组合图形的周长和面积,特别是涉及到多个几何图形的情况。
3. 如何灵活运用求解技巧和注意事项,解决实际问题。
教具学具准备1. 教师准备:组合图形的模型或图片,用于讲解和演示。
2. 学生准备:直尺、圆规、计算器等学习工具。
教学过程1. 导入:通过展示一些组合图形的图片或模型,引起学生的兴趣和好奇心,激发他们的学习欲望。
2. 讲解:讲解组合图形的构成,如何分解为简单的几何图形,以及如何计算组合图形的周长和面积。
通过示例和练习,让学生理解和掌握相关的概念和计算方法。
3. 练习:让学生进行一些练习题,巩固所学知识,提高计算能力。
同时,教师可以给予指导和解答,帮助学生解决遇到的问题。
4. 应用:通过解决实际问题,让学生将所学知识应用到实际中,提高解决问题的能力。
同时,教师可以给予指导和评价,帮助学生提高解题能力。
板书设计1. 组合图形的周长与面积2. 内容:包括组合图形的构成、分解方法、周长和面积的计算公式、示例和练习题等。
作业设计1. 基础题:计算给定组合图形的周长和面积。
2. 提高题:解决实际问题,应用所学知识。
3. 挑战题:探索一些特殊的组合图形的周长和面积的计算方法。
六年级数学上册《几何公式大全》

六年级数学上册
《几何公式大全》暑假预习
几何公式
►长方形的周长=(长+宽)×2 C=(a+b)×2 长方形的面积=长×宽S=ab
►正方形的周长=边长×4 C=4a
正方形的面积=边长×边长S=a.a=a²
►三角形的面积=底×高÷2 S=ah÷2
三角形的内角和=180度
►平行四边形的面积=底×高S=ah
►梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
►直径=半径×2(d=2r)半径=直径÷2(r=d÷2)圆的周长=圆周率×直径=圆周率×半径×2
C=πd =2πr
圆的面积=圆周率×半径×半径S=πr²
►长方体的体积=长×宽×高V=abh
长方体(或正方体)的体积=底面积×高V=abh
►正方体的体积=棱长×棱长×棱长V=aaa
►圆柱侧面积:圆柱的侧面积等于底面的周长乘高S=ch=πdh=2πrh
圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积S=ch+2s=ch+2πr×r 圆柱的体积:圆柱的体积等于底面积乘高V=Sh。
六年级数学上册教材解析面积与周长的计算

六年级数学上册教材解析面积与周长的计算六年级数学上册教材解析面积与周长的计算在六年级数学上册教材中,面积与周长的计算是一个重要的学习内容。
通过学习面积和周长的计算,可以帮助学生进一步理解几何图形的性质与变化规律,提高他们的数学运算和推理能力。
本文将对六年级数学上册教材中的面积和周长的计算进行详细解析。
一、矩形的面积和周长计算矩形是最简单的四边形之一,也是最常见的几何图形之一。
我们首先来学习如何计算矩形的面积和周长。
1. 矩形的面积计算公式矩形的面积等于两条相邻边的长度相乘,即S = a x b,其中a和b分别表示矩形的两个相邻边的长度。
例如,如果一个矩形的长为4米,宽为3米,则它的面积为12平方米。
2. 矩形的周长计算公式矩形的周长等于四条边的长度之和,即C = 2a + 2b,其中a和b分别表示矩形的两个相邻边的长度。
例如,如果一个矩形的长为4米,宽为3米,则它的周长为14米。
二、正方形的面积和周长计算正方形是一种特殊的矩形,其四条边的长度相等。
我们来学习如何计算正方形的面积和周长。
1. 正方形的面积计算公式正方形的面积等于边长的平方,即S = a²,其中a表示正方形的边长。
例如,如果一个正方形的边长为5厘米,则它的面积为25平方厘米。
2. 正方形的周长计算公式正方形的周长等于4条边的长度之和,即C = 4a,其中a表示正方形的边长。
例如,如果一个正方形的边长为5厘米,则它的周长为20厘米。
三、三角形的面积计算三角形是另一种常见的几何图形,其面积的计算与矩形和正方形有所不同。
1. 三角形的面积计算公式三角形的面积等于底边乘以高的一半,即S = 0.5ab,其中a表示三角形的底边长度,b表示三角形到底边的高。
例如,如果一个三角形的底边长为6厘米,高为4厘米,则它的面积为12平方厘米。
四、圆的面积和周长计算圆是几何中一个特殊的图形,其面积和周长的计算有其独特的方法。
1. 圆的面积计算公式圆的面积等于半径的平方乘以π(pi),即S = πr²,其中r表示圆的半径。
六年级数学上册组合图形地周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
小学六年级几何图形基本周长面积公式

几何图形及计算公式查询1.公园里菊花365盆,比月季花的2倍多13盆,月季花有多少盆?2.少先队员参加植树活动,六(1)班第一小队种4行树,每行15棵。
第二小队也种了一些树,现在共有105棵树,第二小队种了多少棵树?3.家电商场第一天卖30台冰箱,第二天卖38台冰箱,第二天比第一天多卖20000元,平均每台冰箱多少钱?4.少先队员采集植物标本和昆虫标本共84件,昆虫标本的件数是植物标本的2/5,两种标本个采集多少件?5.小红买了一本书和一支钢笔价格16元书的价格比钢笔的8元.一本书的价格是多少元?★ 6.有一根绳子长五分之三米,把它剪成三段。
其中一段占全长的三分之一,第二段长四分之一米。
这3段绳子中最长的是哪一段?7.求阴影部分的面积.1. 一辆汽车每行8千米要耗油4/5千克,平均每千克汽油可行多少千米.行1千米路程要耗油多少千克?2.一辆车从甲地到乙地,行了全程的2/5还多20千米,这时候离乙地还有70千米,甲乙两地相距多少千米3.小明看一本书,第一天看了28页,第二天看了全书的1/5(5分之1),两天共看了全书的3/8(3分之8),这本书共有多少页?4.一桶油,吃了7/10后,又添进了15千克,这时桶中的油正好是一桶油的一半,这桶油重多少千克?5.水果店在两天内卖完一批水果,第一天卖出水果总重量的3/5,比第二天多卖了30千克,这批水果共有多少千克?6.西街小学共有学生910人,其中女生占4/7,女生有多少人?男生有多少人?7.一块长方形地,长60米,宽是长的2/5,这块地的面积是多少平方米?8.金鱼池里红金鱼与黑金鱼条数的比是7:3,黑金鱼有9条,红金鱼有多少条?9.6年级有学生132人,其中男学生与女学生人数的比是6:5,6年级男.女学生各有多少人?10.解放路小学今年植树的棵数是去年的1.2倍.写出这个小学今年植树棵数和去年植树棵数的比.化简.11.一块地,长和宽的比是8:5,长比宽多24米。
六年级组合图形的周长和面积
学员姓名:学科教师:年级:辅导科目:授课日期××年××月××日时间A / B / C / D / E / F段主题组合图形的周长和面积教学内容1.熟练掌握基本图形(圆、扇形、三角形、长方形、正方形、梯形等)的面积计算公式;2.会利用基本图形的面积公式求组合图形的面积。
(此环节设计时间在10-15分钟)教法指导:根据上次课的预习思考中的一些常见公式,完成以下几题。
可以设置为学生间相互PK。
1.圆的周长是直径的()A、3.14159倍;B、3.14倍;C、3倍;D、 倍2.圆的半径扩大为原来的3倍()A、周长扩大为原来的9倍B、周长扩大为原来的6倍C、周长扩大为原来的3倍D、周长不变3.圆的半径不变,圆心角扩大为原来的2倍,则()A、弧长扩大为原来的4倍B、弧长扩大为原来的2倍C、弧长不变D、弧长缩小为原来的一半4.圆的半径扩大为原来的3倍()A、面积扩大为原来的9倍B、面积扩大为原来的6倍C、面积扩大为原来的3倍D、面积不变5.周长相等,面积最大的图形是()A、正方形;B、长方形;C、圆;D、它们的面积也相等6.圆的面积扩大为原来的四倍,则半径()A、扩大为4倍;B、扩大为16倍;C、不变;D、扩大为2倍7.一个扇形的半径扩大2倍,圆心角扩大3倍,则扇形的面积( ) A 、扩大5倍 B 、扩大6倍 C 、扩大18倍 D 、扩大12倍 8.一个扇形的圆心角扩大3倍,弧长扩大6倍,则扇形的面积( ) A 、扩大5倍 B 、扩大6倍 C 、扩大18倍 D 、扩大12倍9.扇形的面积是157平方厘米,它所在的圆面积是1256平方厘米,则扇形的圆心角是 度。
10.已知圆心角为120°的扇形弧长为12.56厘米,则扇形的面积是 平方厘米。
答案:1、D ; 2、C ; 3、B ; 4、A ; 5、C ; 6、D ;7、D ; 8、D ; 9、45°; 10、37.68;(此环节设计时间在50-60分钟)例题1:如图,有一只狗被缚在建筑物的墙角,这个建筑物是边长600厘米的正方形,缚狗的绳子长20米,现狗从A 点出发,将绳拉紧顺时针跑,可跑多少米?220666建筑物A教法指导:要求学生利用圆规来进行画图,通过画图来理解本题281420666建筑物A解:113.14202=31.4 3.14142=21.9844⨯⨯⨯⨯⨯⨯113.1482=12.563.1422=3.1444⨯⨯⨯⨯⨯⨯路程全长:31.4+21.98+12.56+3.1469.08()=米 答:狗从A 点出发,将绳拉紧顺时针跑,可跑69.08米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(单位:厘米) 解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求。
(π-π)×=×3.14=3.66平方厘米例12.求阴影部分的面积。
(单位:厘米)解:三个部分拼成一个半圆面积.π()÷2=14.13平方厘米例13.求阴影部分的面积。
(单位:厘米)解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例14.求阴影部分的面积。
(单位:厘米)解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 .例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π。
圆内三角形的面积为12÷2=6,阴影部分面积为:(3π-6)×=5.13平方厘米例16.求阴影部分的面积。
(单位:厘米) 解:[π+π-π]=π(116-36)=40π=125.6平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
解:阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为:2×3.14×3÷2=9.42厘米例19.正方形边长为2厘米,求阴影部分的面积。
解:右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形。
所以面积为:1×2=2平方厘米例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
解:设小圆半径为r,4=36, r=3,大圆半径为R,=2=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π(-)÷2=4.5π=14.13平方厘米例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22.如图,正方形边长为8厘米,求阴影部分的面积。
解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和.π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以阴影部分的面积为:π()-8π+16=41.12平方厘米例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部分的面积为:4π-8(π-1)=8平方厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成3个整圆,而正方形中的空白部分合成两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4×4+π=19.1416平方厘米例25.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π=22-4π=9.44平方厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积。
解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π÷4=12.25-3.14=9.36平方厘米例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
解:因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28.求阴影部分的面积。
(单位:厘米)解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空白部分为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部分面积,为:10×5÷2-(25-π)=π=19.625平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部分甲比乙面积小多少?解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为:π×-×4×6=5π-12=3.7平方厘米例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=(5×10+5×5)=37.5两弓形PC、PD面积为:π-5×5所以阴影部分的面积为:37.5+π-25=51.75平方厘米例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部分可补成圆ABE的面积,其面积为:π÷4=9π=28.26平方厘米例33.求阴影部分的面积。
(单位:厘米)解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6=4.205平方厘米例34.求阴影部分的面积。
(单位:厘米)解:两个弓形面积为:π-3×4÷2=π-6阴影部分为两个半圆面积减去两个弓形面积,结果为π+π-(π-6)=π(4+-)+6=6平方厘米例35.如图,三角形OAB 是等腰三角形,OBC 是扇形,OB=5厘米,求阴影部分的面积。
解:将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2=(π-)÷2=3.5625平方厘米例36.如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO 1O 的面积。
B解:因为两圆的半径相等,所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图19-10右图所示)。
所以3.14×12×14 ×2=1.57(平方厘米)答:长方形长方形ABO 1O 的面积是1.57平方厘米。
