1-2-1、2 中心投影与平行投影 空间几何体的三视图
1.2.1-1.2.2中心投影与平行投影、空间几何体的三视图
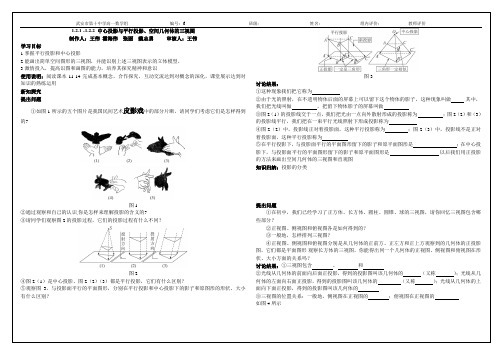
图1
你是怎样来理解投影的含义的?
的投影过程,它们的投影过程有什么不同?
图2
)是中心投影、图2(2)(3)都是平行投影,它们有什么区别?
,与投影面平行的平面图形,分别在平行投影和中心投影下的影子和原图形的形状、大小
图3
②由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做
,把留下物体影子的屏幕叫做.
图4
的位置关系,即反映了物体的
(1) (2)
的位置关系,即反映了物体的
的位置关系,即反映了物体的
所示的矿泉水瓶的三视图.
引导学生认识这种容器的结构特征.矿泉水瓶是我们熟悉的一种容器,这种容器是简单的组合体,
其主要结构特征是从上往下分别是圆柱、圆台和圆柱
图6
7所示的几何体的三视图
图7
课堂小结。
1.2.1 中心投影与平行投影&1.2.2 空间几何体的三视图

结论: “长对正”, “高平齐”, “宽相等”
基本几何体三视图
上一节学习的棱柱、棱锥、棱台以及圆台的三视图是
怎样的?
棱柱的三视图
俯
侧
六棱柱
正
棱锥的三视图
俯
正三棱锥
棱锥的三视图
俯
正四棱锥
棱台的三视图
俯
侧
正四棱台
圆台的三视图
俯
侧
圆台
探究点3
简单组合体的三视图
画出右图所示物体的俯视图. 该物体可以看作是由两个圆台组合而成的,俯
1.2
空间几何体的三视图和直观图
1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图
在前一节中我们主要学习了柱、锥、台、球的结构
特征,对空间几何体有了一个直观性、概念性的认识. 本节我们将要学习如何将空间几何体用平面图形表 示出来,同时能够根据平面图形想象空间几何体的形状 和结构. 我们将在了解投影知识的基础上,学习空间几何体 的三视图和直观图.
1. 位置 正视图 侧视图 俯视图 2.运用长对正、高平齐、宽 相等的原则画出其它视图 俯视图方向
侧视图方向
正视图方向
三视图表达的意义
从前面正对着物体观察,画出正视图,正视图反映了物
体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在正视图的 正下方,俯视图反映了物体的长和宽及上下两个面的实形. 从左向右正对着物体观察,画出侧视图,布置在正视图 的正右方,侧视图反映了物体的宽和高及左右两个面的实形
是良药,音乐是秘方,睡觉则可以让你忘
掉一切。祝天天快乐!
高平齐
正视图
侧视图
高度
正视图
侧 视 图
中心投影与平行投影 空间几何体的三视图 课件

课前自学
课堂互动
课堂达标
1.下列说法正确的是( ) A.任何物体的三视图都与物体的摆放位置有关 B.任何物体的三视图都与物体的摆放位置无关 C.有的物体的三视图与物体的摆放位置无关 D.正方体的三视图一定是三个全等的正方形 解析 对于A,球的三视图与物体摆放位置无关,故A错;对 于B,D,正方体的三视图与摆放位置有关,故B,D错;故 选C. 答案 C
课前自学
课堂互动
课堂达标
2.三视图
(1)定义:光线从几何体的_前__面向_后__面正投影,得到投影图, 这种投影图叫做几何体的正视图;光线从几何体的_左__面向_右__ 面正投影,得到投影图,这种投影图叫做几何体的侧视图;光 线从几何体的_上__面向_下__面正投影,得到投影图,这种投影图 叫做几何体的俯视图.几何体的正视图、侧视图、俯视图统称为 几何体的__三__视__图___,三视图是正投影.
课前自学
课堂互动
课堂达标
2.如图,网格纸的各小格都是正方形,粗实线画出的是一个 几何体的三视图,则这个几何体是( )
A.三棱锥
B.三棱柱
解析 如图,几何体为三棱柱.
C.四棱锥
D.四棱柱
答案 B
课前自学
课堂互动
课堂达标
3.如图所示,正三棱柱ABC-A1B1C1的正视图是边长为4的正 方形,则此正三棱柱的侧视图的面积为________.
解析 由正视图可知三棱柱的高为 4,底面边长为 4,所以底 面正三角形的高为 2 3,所以侧视图的面积为 4×2 3=8 3. 答案 8 3
课前自学
课堂互动
课堂达标
4.画出如图所示空间图形的三视图(阴影部分为正面). 解 如图所示.
课前自学
课堂互动
1.2.1-1.2.2中心投影与平行投影、空间几何体的三视图

空间想象力.
上页 下页 结束
问题探究点一 中心投影与平行投影 导引:在建筑、机械等工程中,需要用平面图形反映空间 几何体的形状和大小,在作图技术上这也是一个几何问 题,把一个空间几何体投影到一个平面上,可以获得一个 平面图形.从多个角度进行投影就能较好地把握几何体
的形状和大小,通常选择三种正投影,即正面、侧面和上
①正方体
②圆锥
③三棱台
④正四棱锥
解: 在各自的三视图中 ①正方体的三个视图都相同;
②圆锥的两个视图相同; ③三棱台的三个视图都不同;
④正四2(3):下图是底面为等腰直角三角形,等腰梯形的 直三棱柱,直四棱柱的俯视图,尝试画出它的正视图,侧 视图(高自己确定).
正视图 侧视图
侧(左)视图
A
B
C
D
上页 下页 结束
例4(1)下列是某个几何体的三视图,你能说出它对应的几何体的名称?
(1)
(2)
(3)
圆锥
圆台
三棱锥
(4)
(5)
(6)
四棱锥
六棱锥
六棱柱
上页
下页
结束
(2)三视图如下图的几何体是 A.三棱锥 B.四棱锥 C.四棱台 D.三棱台
(B )
正视图
侧视图
直观图
俯视图
解: 由三视图知该几何体为一四棱锥,其中有一侧棱垂直 于底面, 底面为一直角梯形.
上页 下页 结束
平行投影:在一束平行光线照射下形成的投影,叫做平行投 影. D
D A B a b A C B H a b C d
d c
c
H
斜投影
正投影
注: 平行投影的投影线平行.
斜投影: 投影线与投影面相互倾斜的平行投影叫做斜投影.
1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图

2-2:如图,在正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A,E,C1的平 面截去该正方体的上部分,则剩余几何体的正视图为( )
解析:设过点A,E,C1的截面与棱DD1相交于点F,则F是棱DD1的中点,截去 正方体的上部分,剩余几何体的直观图如图所示,则其正视图为C.故选C.
题型三 由三视图还原几何体 【例3-1】 如图所示为一个简单几何体的三视图,则其对应的实物图是 ()
自我检测(教师备用)
1.已知△ABC,选定的投影面与△ABC所在的平面平行,则经过中心投影后
(投影线与投影面相交)所得的三角形与△ABC( B )
(A)全等
(B)相似
(C)不相似
(D)以上均有可能
2.在三棱锥、正方体、长方体、圆柱、圆锥、圆台、球中,正视图、俯视
图、侧视图都相同的几何体有( B )
3-3:某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
(A)1
(B) 2
(C) 3
(D)2
解析:该几何体是底面为正方形,一侧棱垂直于底面的四棱锥,最长棱的 棱长为 12 12 12 = 3 ,故选C.
点击进入 课时作业
解析:根据三种视图的对角线的位置,可以判断A是正确的.故选A.
变式探究:本例中三视图对应的几何体是一个什么样的组合体?
解:因为实物图为A,所以该几何体是由一个直三棱柱和一个四棱锥组成的.
【3-2】 某多面体的三视图如图所示,其中正视图和侧视图都由正方形 和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该 多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
(A)10 (B)12 (C)14 (D)16
解析:由三视图可知该多面体是一个组合体,下面是一个底面是等腰直角三角形 的直三棱柱,上面是一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰 长为 2,直三棱柱的高为 2,三棱锥的高为 2,易知该多面体有 2 个面是梯形,这些
§1.2中心投影和平行投影及空间几何体的三视图

三视图的画法。
教
学
设
计
教学内容
教学环节与活动设计
一、创设情景,揭开课题
“横看成岭侧看成峰”,这说明从不同的角度看同一物体视觉的效果可能不同,要比较真实反映出物体,我们可从多角度观看物体,这堂课我们主要学习中心投影与平行投影及空间几何体的三视图。
二、知识探究
1.中心投影与平行投影:
我们知道,物体在灯光或日光的照射下,就会在地面或墙壁上产生影子,这是一种自然现象。投影就是由这类自然现象抽象出来的。所谓投影,是光线(投射线)通过物体,向选定的面(投影面)投射,并在该面上得到图形的方法。生活中有许多利用投影的例子,如手影表演,皮影戏等。
(2)我们把在一束平行光线照射下形成的投影,称为平行投影。平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种
2.空间几何体的三视图
主视图(正视图)――光线从物体的前面向后投射所得的投影。
俯视图――光线从物体的上面向下投射所得的投影。
左视图――光线从物体的左面向右投射所得的投影。
用这三种视图刻画空间物体的结构,我们称之为三视图。
请同学们观察下面的投影图,并将它们进行比较:
结论:(1)我们把光由一点向外散射形成的投影称为中心投影。
中心投影的优缺点:它能非常逼真的反映原来的物体,主要应用于绘画领域,也常用来概括的描绘一个结构或一个产品的外貌。由于投影中心,投影面和物体的相对位置改变时,
1
教
学
设
计
教学内容
教学环节与活动设计
直观图的大小和形状亦将改变,因此在另外的一些领域,比如工程制图或技术图样,一般不采用中心投影。。
作三视图之前应当细心观察,认识了它的基本结构特征后,再动手作图。
数学必修2——1.2.1-1.2.2《中心投影与平行投影、空间几何体的三视图》导学导练

高中数学必修2第1页 解密佛山吉红勇老师扣扣:一0七669八11高中数学必修二1.21-1.2.2《中心投影与平行投影与空间几何体的三视图》【知识要点】1、中心投影与平行投影(重点)(1)平行投影的概念: (2)平行投影的性质:性质1.直线或线段的平行投影仍是直线或线段; 性质2.平行直线的平行投影是平行或重合的直线; 性质3.平行于投射面的线段,它的投影与这条线段平行且等长;性质4.与投射面平行的平面图形,它的投影与这个图形全等; 性质5.在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比.2、空间几何体的三视图①正投影:在平行投影中,如果投射线与投射面垂直,这样的平行投影叫做正投影. ②三视图:主视图: 俯视图: 左视图: ③三视图:将空间图形向这三个平面做正投影,然后把三个投影按右图所示的布局放在一个水平面内,这样构成的图形叫空间图形的三视图.④三视图的基本原则:“主左一样高,主俯一样长,俯左一样宽”. 3、简单组合体的三视图【范例析考点】考点一.中心投影与平行投影例1:正方体ABCD-A 1B 1C 1D 1中,E,F 分别是A 1A ,C 1C 的中点,则下列判断正确的有(1)四边形BFD 1E 在底面ABCD 内的投影是正方形; (2)四边形BFD 1E 在面A 1D 1DA 内的投影是菱形;(3)四边形BFD 1E 在面A 1D 1DA 内的投影与在面ABB 1A 1内的投影是全等的平行四边形. 【针对练习】1、下列说法正确的是( )A 水平放置的正方形的直观图可能是梯形B 两条相交直线的直观图可能是平行直线C 平行四边形的直观图仍然是平行四边形D 互相垂直的两条直线的直观图仍然互相垂直 2、两条相交直线的平行投影是( )A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线3、有下列结论:①角的水平放置的直观图一定是角②相等的角在直观图中仍然相等③相等的线段在直观图中仍然相等④若两条线段平行,则在直观图中对应的两条线段仍然平行 其中正确的是————————————4、①如果一个几何体的三视图是完全相同的,则这个几何体一定是正方体。
空间几何体1.2.1中心投影与平行投影1.2.2空间几何体的三视图教案新人教A版必修2

1.2.1 中心投影与平行投影122 空间几何体的三视图1.2.1 中心投影与平行投影122 空间几何体的三视图②通过观察和自己的认识,你是怎样来理解投影的含义的④图2(2)(3)都是平行投影,它们有什么区别?⑤观察图3,与投影面平行的平面图形,分别在平行投影和中心投影下的影子和原图形的形状、大小有什么区别?活动:①教师介绍中国的民间艺术皮影戏,学生观察图片②从投影的形成过程来定义•③从投影方向上来区别这三种投影•④根据投影线与投影面是否垂直来区别•⑤观察图3并归纳总结它们各自的特点•讨论结果:①这种现象我们把它称为是投影•②由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影•其中,我们把光线叫做投影线,把留下物体影子的屏幕叫做投影幕.③图2(1)的投影线交于一点,我们把光由一点向外散射形成的投影称为中心投影;图2(2)和(3)的投影线平行,我们把在一束平行光线照射下形成投影称为平行投影•④图2( 2)中,投影线正对着投影面,这种平行投影称为正投影;图2(3)中,投影线不是正对着投影面,这种平行投影称为斜投影⑤在平行投影下,与投影面平行的平面图形留下的影子和原平面图形是全的三视图和直观图• 知识归纳:投影的分类如图提出问题①在初中,我们已经学习了正方体、长方体、圆柱、圆锥、球的三视图,请你回忆三视图包含哪些部分?②正视图、侧视图和俯视图各是如何得到的?③一般地,怎样排列三视图?④正视图、侧视图和俯视图分别是从几何体的正前方、正左方和正上你能得出同一个几何体的正视图、侧视图和俯视图在形状、大小方面的关系吗?讨论结果:①三视图包含正视图、侧视图和俯视图②光线从几何体的前面向后面正投影,得到的投影图叫该几何体的正视图(又称主视图);光线从几何体的左面向右面正投影,得到的投影图叫该几何体的侧视图(又称左视图);光线从几何体的上面向下面正投影,得到的投影图叫该几何体的俯视图③三视图的位置关系:一般地,侧视图在正视图的右边;俯视图在正视图的下边•如图5 所示.俯视图等的平面图形;在中心投影下, 与投影面平行的平面图形留下的影子和原平面图形是相似的平面图形.以后我们用正投影的方法来画出空间几何体方观察到的几何体的正投影图,它们都是平面图形.观察长方体的三视图,4所示.图4点评:本题主要考查简单几何体的三视图和空间想象能力 •有关三视图的题目往往依赖于丰富的空间想象能力 •要做到边想着几何体的实物图边画 着三视图,做到想图(几何体的实物图)和画图(三视图)相结合 变式训练说出下列图7中两个三视图分别表示的几何体例2试画出图8所示的矿泉水瓶的三视图活动:引导学生认识这种容器的结构特征 •矿泉水瓶是我们熟悉的一种容 器,这种容器是简单的组合体,其主要结构特征是从上往下分别是圆柱、 圆台和圆柱解:图6 (1)是圆柱的三视图,图 疋视圏 侧观图答案: 图7( 1)是正六棱锥;图 7( 2)是两个相同的圆台组成的组合体 正观图 测視图 正视图 测观图俯视图 俯观图正视圈侧视图俯视图图8解:三视图如图9所示.点评:本题主要考查简单组合体的三视图•对于简单空间几何体的组合体, 一定要认真观察,先认识它的基本结构,然后再画它的三视图变式训练图10 图11答案:三视图如图11 所示.课堂小结:本节课学习了:1.中心投影和平行投影•2.简单几何体和组合体的三视图的画法及其投影规律3.由三视图判断原几何体的结构特征.布置作业:习题1.2 A组第1、2题.。
学案5:1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图

1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图知识点一中心投影与平行投影提出问题《泰坦尼克号》是一部浪漫的爱情灾难电影,于1997年11月1日,在全球上映,票房收入超过18亿美元,并获得了多项奥斯卡奖项.15年之后,《泰坦尼克号》再次被搬上了荧屏,而这次的宣传噱头则是3D.《泰坦尼克号(3D)》让观众在明知下一步剧情发展的情况下,仍然会因为发生在“眼前”的真实爱情悲歌热泪盈眶.从上图中我们可以清楚地看到3D电影是怎么一回事:两个投影机会从不同的方向错开一定距离,把画面中有距离区别的部分投射到荧幕上.而观众所佩戴的3D眼镜也会选择不同的光线进入左右眼,这样你就能看到物体“前于画面”或“后于画面”的视觉假象了.电影的播放实质是利用了小孔成像原理,而太阳光下地面上人的影子是阳光照射到人后留下的影像.放电影和太阳光照射成影像都具备光线、不透明物体和投影面这些相同的条件.问题1:放电影成像与太阳光照射成像原理一样吗?问题2:放电影成像中的光线有何特点?问题3:太阳光照人成影像的光线又有何特点?导入新知1.投影的定义由于光的照射,在物体后面的屏幕上可以留下这个物体的,这种现象叫做投影.其中,把叫做投影线,把的屏幕叫做投影面.2.中心投影与平行投影平行投影和中心投影都是空间图形的一种画法,但二者又有区别 (1)中心投影的投影线交于一点,平行投影的投影线互相平行.(2)平行投影下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小完全相同;而中心投影则不同. 知识点二 三视图 提出问题如梦似幻!——这是无数来自全世界的游客对国家游泳中心“水立方”的第一印象.同天安门、故宫、长城等北京标志性建筑一样,“水立方”成了游客在北京的必到之地.问题1:“水立方”的外观形状是什么?问题2:假如你站在“水立方”入口处的正前方或在“水立方”的左侧看“水立方”,你看到的是什么?问题3:若你在“水立方”的正上方观察“水立方”看到的是什么?问题4:根据上述三个方向观察到的平面,能否画出“水立方”的形状? 导入新知1.每个视图都反映物体两个方向上的尺寸.正视图反映物体的上下和左右尺寸,俯视图反映物体的前后和左右尺寸,侧视图反映物体的前后和上下尺寸.2.画几何体的三视图时,能看见的轮廓线和棱用实线表示,看不见的轮廓线和棱用虚线表示.考点突破题型一中心投影与平行投影例1下列说法中:①平行投影的投影线互相平行,中心投影的投影线相交于一点;②空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线;③两条相交直线的平行投影是两条相交直线.其中正确的个数为()A.0B.1C.2 D.3类题通法1.判定几何体投影形状的方法.(1)判断一个几何体的投影是什么图形,先分清楚是平行投影还是中心投影,投影面的位置如何,再根据平行投影或中心投影的性质来判断.(2)对于平行投影,当图形中的直线或线段不平行于投影线时,平行投影具有以下性质:①直线或线段的投影仍是直线或线段;②平行直线的投影平行或重合;③平行于投影面的线段,它的投影与这条线段平行且等长;④与投影面平行的平面图形,它的投影与这个图形全等;⑤在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比.2.画出一个图形在一个平面上的投影的关键是确定该图形的关键点,如顶点、端点等,方法是先画出这些关键点的投影,再依次连接各投影点即可得此图形在该平面上的投影.活学活用1.如图,在正方体ABCD A′B′C′D′中,E,F分别是A′A,C′C的中点,则下列判断正确的序号是________.①四边形BFD′E在底面ABCD内的投影是正方形;②四边形BFD′E在平面A′D′DA内的投影是菱形;③四边形BFD′E在平面A′D′DA内的投影与在平面ABB′A内的投影是全等的平行四边形.题型二画空间几何体的三视图例2画出如图所示的四棱锥的三视图.类题通法画三视图的注意事项(1)务必做到长对正,宽相等,高平齐.(2)三视图的安排方法是正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.(3)若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.活学活用2.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧视图为()题型三由三视图还原空间几何体例3如图所示的三视图表示的几何体是什么?画出物体的形状.(1)(2)(3)类题通法由三视图还原几何体时,一般先由俯视图确定底面,由正视图与侧视图确定几何体的高及位置,同时想象视图中每一部分对应实物部分的形状.活学活用3.如图(1)(2)(3)(4)为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为()A.三棱台、三棱柱、圆锥、圆台B.三棱台、三棱锥、圆锥、圆台C.三棱柱、正四棱锥、圆锥、圆台D.三棱柱、三棱台、圆锥、圆台随堂即时演练1.将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为()2.如图,在正方体ABCDA1B1C1D1中,M,N分别是BB1,BC的中点,则图中阴影部分在平面ADD1A1上的投影为()3.直线的平行投影可能是________.4.如图,在多面体ABCA′B′C′中,底面ABC为正三角形,三条侧棱AA′,BB′,CC′分别平行,侧棱垂直于底面ABC,且3AA′=32BB′=CC′=AB,则下面图形可视为多面体ABCA′B′C′的正视图的是________.5.画出如图所示几何体的三视图.参考答案知识点一中心投影与平行投影问题1:【答案】不一样.问题2:【答案】光是由一点向外散射.问题3:【答案】一束平行光线.导入新知1.不透明影子光线留下物体影子2.一点交于一点平行光线互相平行正投影斜投影知识点二三视图问题1:【答案】长方体.问题2:【答案】“水立方”的一个侧面.问题3:【答案】“水立方”的一个表面.问题4:【答案】可以.导入新知前面后面左面右面上面下面高度长度宽度考点突破题型一中心投影与平行投影例1【答案】B活学活用1. 【答案】①③题型二画空间几何体的三视图例2解:几何体的三视图如下:活学活用2.【答案】B题型三由三视图还原空间几何体例3解:(1)该三视图表示的是一个四棱台,如图.(2)由俯视图可知该几何体是多面体,结合正视图、侧视图可知该几何体是正六棱锥.如下图.(3)由于俯视图有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体,结合侧视图和正视图,可知该几何体上面是一个圆柱,下面是一个四棱柱,所以该几何体的形状如图所示.活学活用3. 【答案】C随堂即时演练1. 【答案】B2. 【答案】A3.【答案】直线或点4. 【答案】④5.解:图①为正六棱柱,可按棱柱的画法画出;图②为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状.三视图如图所示.。
必修2课件:1-2-1、2 中心投影与平行投影 空间几何体的三视图

自主预习 阅读教材P11-15,回答: 1.投影
由于光的照射,在不透明物体后面的屏幕上 可以留下这个物体的 影子 ,这种现象叫做 定义 投影,其中,我们把光线叫做 投影线 ,把 留下物体影子的屏幕叫做 投影面
第一章 空间几何体
中心 光由 一点 向外散射形成的投影,叫做中
投影 心投影.中心投影的投影线交于 一点
下面是两个几何体的三视图.
第一章 空间几何体
则(1)中几何体是______,(2)中几何体是________. [答案] (1)三棱柱 (2)四棱锥
第一章 空间几何体
[解析] (1)中几何体是三棱柱,(2)中几何体是四棱锥, 如图.
第一章 空间几何体
名师辨误做答
第一章 空间几何体
易错点 虚线漏画或画为实线 [例 5] 画出如图所示几何体的正视图和俯视图.
成才之路·数学
人教A版 ·必修2
路漫漫其修远兮 吾将上下而求索
第一章
空间几何体
第一章 空间几何体
第一章
1.2 空间几何体的三视图和直观图
第一章 空间几何体
第一章
1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图
第一章 空间几何体
课前自主预习 思路方法技巧 名师辨误做答
基础巩固训练 能力强化提升
第一章 空间几何体
探索延拓创新
第一章 空间几何体
由三视图还原空间几何体 由三视图还原空间几何体的步骤:
第一章 空间几何体
[例4] 某几何体的三视图如图所示,试分析该几何体的 结构特征.
[分析] 由三视图,知该几何体是由一个柱体和一个锥体 组合而成.
第一章 空间几何体
[解析] 由正视图和侧视图可知,该物体的下半部分为柱 体,上半部分为锥体,又因俯视图为一个正六边形,故该几 何体是由一个正六棱柱和一个正六棱锥组合而成的,如图所 示.
1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图

超级记忆法--故 • 鲁迅本名:周事树法人
• 主要作品:《阿Q正传》、、 《药 》、
• 《狂人日记》、《呐喊》、《孔 乙己》
• 《故乡》、《社戏》、《祝福》(图片来自网络) 。
超级记忆法-记忆 方法 TIP1:NPC代入,把自己想成其中的人物,会让自己的记忆过程更加有趣
(比如你穿越回去,成为了岳飞的母亲,你会在什么背景下怀着怎样的心情在 背 上刺下“精忠报国”四个字);
TIP3:认知获取是学习的开始,而不是结束。
为啥总是听懂了, 但不会做,做不好?
高效学习模型-内外脑 模型
2
内脑- 思考内化
思维导图& 超级记忆法& 费曼学习法
1
外脑- 体系优化
知识体系& 笔记体系
内外脑高效学习模型
超级记忆法
超级记忆法-记忆 规律
记忆前
选择记忆的黄金时段
前摄抑制:可以理解为先进入大脑的信息抑制了后进 入大脑的信息
棱柱的三视图
俯
侧
六棱柱
正视图
侧视图
俯视图
棱锥的三视图
俯
正视图
侧视图
正四棱锥
俯视图
棱台的三视图
俯
侧
正四棱台
正视图
侧视图
俯视图
圆台的三视图
俯 正视图 侧视图
侧
圆台
俯视图
探究点3 简单组合体的三视图 画出如图所示物体的俯视图. 该物体可以看作是由两个圆台 组合而成的,俯视图有不可见 边界轮廓线(用虚线表示).
几何体的正视图、侧视图、俯视图统称为几何体的
三视图.
根据长方体的模型,请你画出它的三视图, 并观察三种图形之间有什么关系?
学案10:1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图

1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图1.投影的概念及分类思考:画三视图时一定要求光线与投射面垂直吗?初试身手1.哪个实例不是中心投影()A.工程图纸B.小孔成像C.相片D.人的视觉2.如图,小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能是()A B C D3.有一个几何体的三视图如图所示,这个几何体应是一个________.4.水平放置的下列几何体,正视图是长方形的是________.(填序号)①②③④合作探究A.矩形的平行投影一定是矩形B.梯形的平行投影一定是梯形C.两条相交直线的投影可能平行D.一条线段的中点的平行投影仍是这条线段投影的中点(2)如图所示,在正方体ABCDA1B1C1D1中,M、N分别是BB1、BC的中点,则图中阴影部分在平面ADD1A1上的正投影是()A B C D【规律方法】判断几何体投影形状的方法及画投影的方法:(1)判断一个几何体的投影是什么图形,先分清楚是平行投影还是中心投影,投影面的位置如何,再根据平行投影或中心投影的性质来判断.(2)画出一个图形在一个平面上的投影的关键是确定该图形的关键点,如顶点、端点等,方法是先画出这些关键点的投影,再依次连接各投影点即可得出此图形在该平面上的投影.跟踪训练1.已知△ABC,选定的投影面与△ABC所在平面平行,则经过中心投影后所得的△A′B′C′与△ABC()A.全等B.相似C.不相似D.以上都不对()(2)画出如图所示几何体的三视图:①②【规律方法】1.画组合体三视图的“四个步骤”(1)析:分析组合体的组成形式;(2)分:把组合体分解成简单几何体;(3)画:画分解后的简单几何体的三视图;(4)拼:将各个三视图拼合成组合体的三视图.2.画三视图时要注意的“两个问题”(1)务必做到“正侧一样高,正俯一样长,俯侧一样宽”.(2)把可见轮廓线画成实线,不可见轮廓线要画成虚线,重合的线只画一条.跟踪训练2.螺栓是棱柱和圆柱构成的组合体,如图,画出它的三视图.1.如何由三视图确定几何体的长、宽、高?2.如图所示的三视图,其几何体是什么?其正视图、侧视图中的三角形的腰是几何体的侧棱长吗?例3(1)若一个几何体的正视图和侧视图都是等腰三角形,俯视图是带圆心的圆,则这个几何体可能是()A.圆柱B.三棱柱C.圆锥D.球体(2)若某几何体的三视图如图所示,则这个几何体的直观图可以是()A B C D【规律方法】由三视图确定几何体一般分两步:第一步:通过正视图和侧视图确定是柱体、锥体还是台体.若正视图和侧视图为矩形,则原几何体为柱体;若正视图和侧视图为等腰三角形,则原几何体为锥体;若正视图和侧视图为等腰梯形,则原几何体为台体.第二步:通过俯视图确定是多面体还是旋转体.若俯视图为多边形,则原几何体为多面体;若俯视图为圆,则原几何体为旋转体.跟踪训练3.根据下列图中所给出的几何体的三视图,试画出它们的形状.①②课堂小结1.三视图的正视图、侧视图、俯视图是分别从几何体的正前方、正左方、正上方观察几何体画出的轮廓线,画几何体三视图的要求是正视图、俯视图长对正,正视图、侧视图高平齐,俯视图、侧视图宽相等,前后对应,画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征.2.画组合体的三视图的步骤特别提醒:画几何体的三视图时,能看见的轮廓线和棱用实线表示,看不见的轮廓线和棱用虚线表示.当堂达标1.中心投影的投影线()A.相互平行B.交于一点C.是异面直线D.在同一平面内2.如图网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱3.一个正三棱柱(俯视图为正三角形)的三视图如图所示,则这个三棱柱的高和底面边长分别为________.4.画出如图所示的几何体的三视图.参考答案新知初探1.影子投影线投影面一点一点平行平行正对2.思考:[提示]正确.由画三视图的规则要求可知正确.初试身手1.【答案】A【解析】根据中心投影的概念可知A不是中心投影.2.【答案】A【解析】矩形的投影可以是线段,矩形,平行四边形,但不会是梯形.3.【答案】棱台【解析】从俯视图来看,上、下底面都是正方形,但大小不一样,可以判断是棱台.4.【答案】③④【解析】①③④的正视图均是长方形,②是等腰三角形.合作探究【解析】矩形的平行投影可能是线段、平行四边形或矩形,梯形的平行投影可能是线段或梯形,两条相交直线的投影还是相交直线.因此A、B、C均错,故D正确.(2)【答案】A【解析】由正投影的定义知,点M、N在平面ADD1A1上的正投影分别是AA1、DA的中点,D在平面ADD1A1上的投影还是D,因此A正确.跟踪训练1.【答案】B【解析】本题主要考查对中心投影的理解.根据题意画出图形,如图所示.由图易得OAOA′=ABA′B′=OBOB′=BCB′C′=OCOC′=ACA′C′,则△ABC∽△A′B′C′.【解析】依题意,侧视图中棱的方向是从左上角到右下角.故选B.(2) [解]①此几何体的三视图如图③所示;②此几何体的三视图如图④所示.①④跟踪训练2.[解]它的三视图如图所示.类型3由三视图还原几何体1.[提示]由正视图可确定几何体的长、高;由俯视图可确定几何体的宽.2.[提示]由三视图可知,该几何体为正四棱锥,如图所示.正视图、侧视图中三角形的腰长不是四棱柱的侧棱长,应为四棱椎的侧面高线.【例3】【答案】(1) C【解析】正视图和侧视图都是等腰三角形,俯视图是带圆心的圆说明此几何体是圆锥.(2)【答案】D【解析】对于选项A,B,正视图均不符合要求;对于选项C,俯视图显然不符合要求.只有D符合要求.跟踪训练3.[解]由三视图的特征,结合柱、锥、台、球及简单组合体的三视图逆推.图①对应的几何体是一个正六棱锥,图②对应的几何体是一个三棱柱,则所对应的空间几何体的图形分别如下:当堂达标1.【答案】B【解析】由中心投影的定义知,中心投影的投影线交于一点,故选B.2.【答案】B【解析】由题意知,该几何体的三视图为一个三角形,两个四边形,经分析可知该几何体为三棱柱.3.【答案】2,4【解析】由正三棱柱三视图中的数据,知三棱柱的高为2,底面边长为23×23=4.4.[解]该几何体的三视图如图所示.。
1.2.1中心投影与平行投影 1.2.2 空间几何体的三视图

A
投射线
B
D
C 特点: 特点:中心投影的投影大小与物体和 投影面之间的距离有关. 投影面之间的距离有关
二、平行投影: 平行投影:
在一束平行光线照射下形 成的投影,叫做平行投影 成的投影,叫做平行投影. 平行投影
1.正投影:投影线与投影面垂直 正投影: 正投影 2.斜投影:投影线与投影面斜交 斜投影: 斜投影
基本几何体的三视图: 基本几何体的三视图
棱柱的三视图: 棱柱的三视图
俯
侧
正三棱锥的三视图: 正三棱锥的三视图
俯
侧
思考: 侧视图是等腰三角形吗?
正四棱锥的三视图: 正四棱锥的三视图
俯
侧
思考: • 1.它的正视图是等腰三角形吗? • 2.它的正视图和侧视图一样吗?
思考:先画出三视图, 思考:先画出三视图, 你能否作出一个截面使它与正视图相同? 你能否作出一个截面使它与正视图相同? 你能否作出一个截面使它与侧面相同? 你能否作出一个截面使它与侧面相同?
回忆初中已经学过的正方体、长方体、 回忆初中已经学过的正方体、长方体、 圆柱、圆锥、球的三视图. 圆柱、圆锥、球的三视图.
正方体的三视图: 正方体的三视图
俯
侧
圆柱的三视图: 圆柱的三视图
俯
侧
圆锥的三视图: 圆锥的三视图
俯
侧
球的三视图: 球的三视图
俯
侧
长
正视图
方 体 的 三 视
视
图
c(高) 高 b(宽) 宽 a(长) 长
圆台的三视图: 圆台的三视图
俯
侧
圆台的三视图: 圆台的三视图
俯
侧
三视图的作图原则: 三视图的作图原则:
1.2.1中心投影与平行投影1.2.2空间几何体的三视图4

三、新知建构,交流展示
题型四
易错点 虚线漏画或画为实线
易错辨析
【例 4】 画出如图所示几何体的正视图和俯视图.
错解:正视图和俯视图,如图所示.
错因分析:正视图的上边矩形中缺少几何体中间小圆柱的轮廓线(用虚线表示); 俯视图中的三个圆都应画为实线,因为三个圆都是可见的.
三、新知建构,交流展示
正解:正视图与俯视图如图所示.
三角板在中心投影和不同方向的平行投影下的投影效果
S
投 射 方 向
物体上某一点与其投影面上的投影点的连线是平行的,则 为平行投影,如果聚于一点,则为中心投影.
中心投影:投射线交于一点 投影的分类 斜投影 平行投影 投射线平行 正投影
三视图的形成原理
正 投 影
视图:是指将物体按正投影向 投影面投射所得到的图形.
侧视图
正视图
侧视图
俯视图
俯视图
请同学们试试画出立白 洗洁精塑料瓶的三视图
正视图
侧视图
俯视图
正视图
侧视图
俯视图
(1)
(2)
圆柱 俯
正 视 图
侧 视 图
侧
正
俯视图
正视图
侧视图
俯视图
题型一
判断投影的形状
【例 1】 如图所示,正方体 ABCD-A1B1C1D1 中,E,F 分别是 AA1,C1D1 的中 点,G 是正方形 BCC1B1 的中心,则四边形 AGFE 在该正方体的各个面上的投影 可能是图中的 .
变式训练3-1:根据三视图说出组合体有哪些几何体组成?
正视图
侧视图
俯视图
正视图
侧视图
俯视图
答案:一个四棱柱和 一个球组成的简单组 合体。
1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图

方体求解.
新知探究 题型探究 感悟提升
解析
由正视图和俯视图可知几何体
是正方体切割后的一部分(四棱锥 C1ABCD),还原在正方体中,如图所 示.
多面体最长的一条棱即为正方体的体对角线,由正方体棱 长 AB=2 知最长棱的长为 2 3.
答案 2 3
[规律方法]
(1)由三视图想象出几何体是关键.(2)由几何体
新知探究
题型探究
感悟提升
4.如图是一个几何体的三视图,则可以判断此几何体是
________.
解析
由三视图可知,此几何体为一个四棱锥.
答案
四棱锥
新知探究 题型探究 感悟提升
5.说出下面的三视图表示的几何体的结构特征.
解
几何体为三棱台,结构特征如下图:
新知探究
题型探究
感悟提升
课堂小结
(1)画三视图时要注意正侧等高,正俯等长,侧俯等宽.画
答案
2
6
新知探究
题型探究
感悟提升
方法技巧
三视图间的推断问题
利用正、俯视图长相等,正、侧视图宽相等,俯、侧视图高相 等进行推断三视图之间的推断,是高考对视图考查的新热点. 的俯视图不可能是 ( ).
【示例】 某几何体的正视图和侧视图均如图所示,则该几何体
新知探究
题型探究
感悟提升
[思路分析] 解析
由正视图、侧视图相同按其上、下部分分别考
观察,先认识它的基本结构,然后再画它的三视图. (2)画简单组合体的三视图应注意两个问题:首先,确定正 视、侧视、俯视的方向,同一物体放置的位置不同,所画的 三视图就可能不同;其次,简单组合体是由哪几个基本几何
体构成的,并注意它们的构成方式 ,特别是它们的交线位
§1.2中心投影和平行投影及空间几何体的三视图

14页简单组合体的三视图
(强调注意点,顺带解决练习1)
4.三视图与几何体之间的相互转化。
13页思考
14页思考
学生推出
学生思考
并总结
2
教
学
设
计
教学内容
教学环节与活动设计
15页练习2,3,4
补充:根据下列三视图,说出立体图形的形状
(2)正四棱锥;(3)螺帽。
(2)我们把在一束平行光线照射下形成的投影,称为平行投影。平行投影按照投射方向是否正对着投影面,可以分为斜投影和正投影两种
2.空间几何体的三视图
主视图(正视图)――光线从物体的前面向后投射所得的投影。
俯视图――光线从物体的上面向下投射所得的投影。
左视图――光线从物体的左面向右投射所得的投影。
用这三种视图刻画空间物体的结构,我们称之为三视图。
2.三视图
3.如何准确画几何体的三视图:
长对正、宽相等、高平齐.
课后
反思
3
课本13页圆柱,圆锥的三视图
注意点:长对正,高平齐,宽相等
3.实践动手作图
1.讲台上放球、长方体实物,要求学生画出它们的三视图,教师巡视,学生画完后可交流结果并讨论;
2.教师引导学生用类比方法画出简单组合体的三视图
(1)画出球放在长方体上的三视图
(2)画出矿泉水瓶(实物放在桌面上)的三视图
学生画完后,可把自己的作品展示并与同学交流,总结自己的作图心得。
河北武邑中学课堂教学设计
备课人
授课时间
课题
§1.2中心投影和平行投影及空间几何体的三视图
教
学
目
标
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1.一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其圆心,那么这个几何体为()
A.棱锥B.棱柱
C.圆锥D.圆柱
[答案] C
2.已知某空间几何体的三视图如图所示,则此几何体为()
A.圆台B.四棱锥
C.四棱柱D.四棱台
[答案] D
3.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是()
A.(1)(2) B.(2)(3)
C.(3)(4) D.(1)(4)
[答案] D
4.(2012-2013·安徽淮南高三模拟)下列几何体各自的三视图中,
有且仅有两个视图相同的是()
A.①②B.①③C.①④D.②④
[答案] D
[解析]①正方体,三视图均相同;②圆锥,正视图和侧视图相
同;③三棱台,三视图各不相同;④圆台,正视图和侧视图相同.
[点评]熟悉常见几何体的三视图特征,对于画几何体的直观图
是基本的要求.
下图是最基本的常见几何体的三视图.
[答案] C
[解析]结合俯视图的定义,仔细观察,易得答案C.
6.一个几何体的三视图如图,则组成该组合体的简单几何体为()
A.圆柱与圆台B.四棱柱与四棱台
C.圆柱与四棱台D.四棱柱与圆台
[答案] B
[解析]该几何体形状如图.上部是一个四棱柱,下部是一个四棱台.
7.如图所示几何体的正视图和侧视图都正确的是()
[答案] B
8.(2011·新课标全国高考)在一个几何体的三视图中,主视图和俯视图如右图所示,则相应的侧视图可以为()
[答案] D
[解析]此几何体为一个半圆锥和一个半三棱锥的组合体,只有D项符合题意.
二、填空题
9.下列图形:①三角形;②直线;③平行四边形;④四面体;
⑤球.其中投影不可能是线段的是________.
[答案]②④⑤
[解析]三角形的投影是线段成三角形;直线的投影是点或直线;平行四边形的投影是线段或平行四边形;四面体的投影是三角形或四边形;球的投影是圆.
10.由若干个小正方体组成的几何体的三视图如下图,则组成这个组合体的小正方体的个数是________.
[答案] 5
[解析]由三视图可作出直观图,由直观图易知共有5个小正方体.
11.(2012~2013·烟台高一检测)已知某一几何体的正视图与侧视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有________.
[答案]①②③④
12.(2012-2013·湖南高三“十二校联考”)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,则用________个这样的几何体可以拼成一个棱长为4的正方体.
[答案] 3
[解析]该几何体是四棱锥,其底面是边长为4的正方形,高等于4,如图(1)所示的四棱锥A-A1B1C1D1,
如图(2)所示,三个相同的四棱锥A-A1B1C1D1,A-BB1C1C,A -DD1C1C可以拼成一个棱长为4的正方体.
三、解答题
13.如图,四棱锥的底面是正方形,顶点在底面上的射影是底面正方形的中心,试画出其三视图.
[解析]所给四棱锥的三视图如下图.
[点评](1)画三视图时,务必做到正视图与侧视图的高度一致
(即所谓的高平齐)、正视图与俯视图的长度一致(即所谓的“长对正”)、侧视图与俯视图的宽度一致(即所谓的“宽相等”).
(2)习惯上将侧视图放在正视图的右侧,将俯视图放在正视图的下方.
[拓展提高]
1.三视图中各种数据的对应关系:
(1)正视图中AB的长对应原四棱锥底面多边形的左右方向的长度,AC、BC的长则不对应侧棱的长,它们对应四棱锥的顶点到底面左、右两边的距离.
(2)侧视图中,EF的长度对应原四棱锥底面的前后长度,GE、GF的长度则是四棱锥顶点与底面前后两边的距离.
(3)俯视图中HIJK的大小与四棱锥底面的大小形状完全一致,而OK,OI,OJ,OH的大小,则为四棱锥的顶点在底面上的投影到底面各顶点的距离.
2.误区警示:正视图、侧视图中三角形的腰长有的学生会误认为是棱锥的侧棱长,实则不然.弄清一些数据的对应关系,是后面进行相关计算的前提.
14.依所给实物图的形状,画出所给组合体的三视图.
[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:
15.说出下列三视图表示的几何体:
[解析]
16.根据下列图中所给出的一个物体的三视图,试画出它的形状.
[答案]所对应的空间几何体的图形为:。
