企业生产函数与成本函数全面概述
经济学的生产和成本理论

经济学的生产和成本理论经济学是一门研究资源配置和决策的科学。
在市场经济中,生产和成本是最基本的概念之一。
生产是指将一定数量的资源转化成一定数量的产品或服务的过程,而成本则是为了生产这些产品或服务必须支出的全部费用。
本文将重点探讨经济学的生产和成本理论。
一、生产函数生产函数是经济学中最基本的生产理论之一。
它描述了一定数量的投入如何转化为一定数量的产出的关系。
生产函数的形式通常为:Y = f(K,L)其中,Y代表产出,K代表资本投入,L代表劳动投入。
生产函数可以用不同的数学形式来表示,比如线性函数、对数函数和指数函数等。
生产函数的图形化描绘可以用等产线来表示。
等产线代表在不同的投入下,可以生产出相同的产出。
图1展示了一个等产线图。
在图中,等产线是曲线,它代表了将劳动和资本的不同组合用于产出时,可以获得相同的产出。
图1:等产线图生产函数的概念也可以用边际产出的概念来解释。
边际产出是指增加一单位投入所带来的额外产出。
边际产出可能随着投入的增加而递减。
这是因为当投入增加到一定程度时,每单位投入会带来较少的额外产出。
二、成本成本是生产中的一个基本概念。
它包括直接成本和间接成本。
直接成本是生产特定产品或服务的直接支出,如劳动力、原材料和设备等。
间接成本是与生产过程相关的费用,但不是直接用于生产特定产品或服务的支出,如场地租金、水电费和管理费用等。
成本还可以分为固定成本和变动成本。
固定成本是指一些不随产量而变化的支出,如场地租金和机器折旧等。
变动成本是指随产量变化而变化的支出,如原材料和劳动力等。
三、成本函数成本函数是将生产函数和成本联系在一起的函数。
它描述了对于不同的生产水平,不同的生产成本。
成本函数的一般形式为:C = f(Y, W)其中,C代表成本,Y代表产出,W代表成本因素。
成本函数也可以用各种数学形式来表示。
一种常见的形式是线性的,如:C = a + bY其中,a代表固定成本,b代表变动成本。
这个线性成本函数的图形化表示如图2所示。
生产和成本决策分析

◈若生产函数属于规模收益递增,即产量 增加的速度大于投入量增加的速度,那 么,它的成本函数是:总成本的增加速 度随产量的增加而递减。
◈若生产函数属于规模收益递减,即产量 增加的速度小于投入量增加的速度,那 么,它的成本函数是:总成本的增加速 度随产量的增加而递增。
2、短期成本函数和长期成本函数
第三阶段: 边际产量<0,边际产量<平均产量 特点:随着投入要素的增加,总产量、平均产量 均呈下降趋势 管理重点:减少要素投入量
生产三阶段原理对管理 的启示: ◆投入与产出并不成正比。 ◆投入要素之间必须保持合理比例关系 ◆管理决策必须面向整体、面向未来
4、单一可变要素最优投入量的确定 ◈边际产量收入:是指增加一个单位的可
素的投入量不变。增加一种要素的投入量 ,开始时会使产量增加,当产量增加到一 定程度后,在增加该要素的投入量,产量 反而下降。 特别注意:边际收益递减规律的假设前提: ◆技术不变 ◆其他要素投入量不变 问题思考:请举出边际收益递减规律的实例
3、生产三阶段理论
产 量
TP
第一阶段 (管“量”区) 第二阶段 第三阶段
式中,
分别为投入要素
的边际产量,它们相应的价格分
别为
。
例题分析: 某出租汽车公司有小轿车100辆,大轿
车15辆,如果再增加一辆小轿车可增加 收入10000元,但要增加开支1250元;如 果再增加一辆大轿车可增加收入30000元 ,但要增加开支2500元,问目前两种车 的比例是否合适?
(四)规模经济性分析
会计成本不能用于决策,只有机会成 本才是决策的基础。
2、隐性成本与显性成本 显性成本:是指企业向生产要素供给
方支付的那些成本。它是记在帐面上的 ,看得见的实际支出,是偿付资金的实 际现金流出量。
生产函数与成本

不同等成本线与投入品组合 Y
与B国相比,A国
要素稀缺度与相对价
格不同:X(资本或
土地?)要素价格较
YA
贵,Y(劳动?)比
较便宜,因而选择“
劳动密集型”的生产
技术,而B国则相反
。
YB
A国(地、时) 等成本线
等产量线
B国(地、时) 等成本线
0 XA
X XB
长期与短期假定
经济学家用短期和长期(Short term and long term) 来 表示微观经济主体调节行为的受时间限制程度:短期表示 受到调整限制而无法完成全部调整的时间周期。如在短期 内厂商很容易对于劳动,原料投入数量进行调节,却难以 迅速调节设备及厂房等投入;长期则指厂商有充分调节所 有投入的时间周期。如通过固定资本投资来改变企业最大 产出能力通常只能在较长的时间中解决。不同行业不同企 业的“长期”对应的具体时间长度有显著差别。
边际收益递减规律的原因
生产中各要素的使用通常都有一个最佳匹配比例。生 产函数指的就是各要素的投入接近这一比例时将产生的最 大可能产量。当某些要素的投入保持不变而仅增加另一些 要素的投入时,各要素的投入将偏离这那个“最佳匹配比 例”。这样,当某些要素投入的增加使总投入规模增加时 ,由于受到那些投入保持不变的生产要素的牵制,产量的 将不会同步增加。
从经济学家的视角看,企业的成本是所用资源的机 会成本,而不论这些资源是归其他人所有还是归企业自 己所有。因此,经济学家把吸引资源并使其保持在某个 特定生产行业内所需要的所有成本(显性成本和隐性成 本,其中包括正常利润)都归入到生产成本之中。
经济利润 = 总收入
-
所有投入品的 机会成本
对经济学家来说的利润
在只考虑两种投入的情况下,“劳动和资本两种投入 都可以变化”代表了经济分析的长期情况,面对的问题应理 解为投资决策。而仅有一种要素可变则代表了经济分析的 短期情况,其所面对的问题应理解为生产决策。
生产函数与成本分析

MC
AC AVC AFC
因為 AFC = TFC/Q,隨著產量 增加,平均每單位產量所分攤 的固定成本愈少,AFC 線必然 不斷下降。
AC 線 在 任 一 點 的 高 度 , 是 AVC、AFC 兩線對應點高度加 總的結果。
隨著產量增加,AFC 線下降的 趨勢先會主導 AC 線下降,但 當產量增加到一定程度後, MC 的上升會帶動 AC 上升, 使 AC 線呈正斜率,因此 AC 線亦可能呈 U 字形。
A
w /r
0
L0
C0
w
Q0
C 1 勞動
w
長期之中,所有的生產要素 數量均可以調整,因此不需 要區分變動成本與固定成本。
長期生產函數 Q = f (L, K) 可 以用等產量線在 L-K 平面上 刻劃;同理,我們可以用等 成本線在 L-K 平面上表現要 素組合與成本間的關係。
等成本線的概念與消費者的 預算線相近;在同一條等成 本線上的任意 L-K 組合,具 有相同的成本水準。
5-15
產量分析-長期分析 (三)
邊際技術替代率的另一種表示法:
MPL :勞動邊際產量。 MPK :資本邊際產量。 邊際技術替代率可以刻劃兩種要素在生產上的替代關係, 如果邊際技術替代率愈高,表示兩種要素在生產上的替 代性愈強。 隨著某種生產要素使用量的增加,用這種生產要素替代 另一種要素的可能性會愈來愈弱,這表示邊際技術替代 率具有遞減的特性。
數量的增加而增加,當勞
動數量增加到一定程度後,
AP
MP 開始遞減,甚或可能
出現負值。
隨著勞動雇用量的增加,勞
MP
動的邊際產量終會出現遞減
圖 5.1 總產量、平均產量與邊際產量的範例 的現象,現象稱為邊際報酬 遞減法則 (law of diminishing
成本函数的名词解释

成本函数的名词解释在经济学中,成本函数是一种用于分析和描述企业生产成本的数学工具。
成本函数可以帮助我们理解企业的生产决策以及不同生产要素对成本的影响程度。
在本文中,我将对成本函数进行详细解释,并探讨其与企业经营和决策的关系。
一、成本函数的概念和基本形式成本函数是一种描述企业成本与生产要素之间关系的函数。
它通常以产出数量和生产要素的价格为自变量,以成本为因变量。
一般情况下,成本函数可以表示为C(x) = f(P1, P2, ..., Pn, x),其中x表示产出数量,P1、P2、...、Pn表示生产要素的价格,C表示成本。
这个函数描述了在给定产出数量和生产要素价格的情况下,企业需要支付的成本。
在经济学中,我们常常使用生产函数来描述产出与各种生产要素(如劳动力、资本、原材料等)之间的关系,而成本函数则是生产函数的衍生概念。
生产函数告诉我们,在给定生产要素下,企业可以生产多少产出;而成本函数则告诉我们,在给定产出下,企业需要支付多少成本。
二、成本函数的特征成本函数具有以下几个重要特征:1. 成本函数随产出数量的增加而增加。
这是因为随着产出数量的增加,企业需要增加生产要素的使用,以满足产出的增长需求,从而导致成本的上升。
2. 成本函数随生产要素价格的增加而增加。
生产要素价格的上升会导致生产成本的增加,因为企业需要支付更高的价格来购买所需的生产要素。
3. 成本函数具有递增递凸的特性。
递增性表示当产出数量增加时,附加成本也在增加;而递凸性表示随着产出数量的增加,成本增加的速度逐渐减缓。
这是因为随着产出数量增加,企业逐渐实现规模经济,生产效率提高,从而导致成本增长的速度减缓。
三、成本函数与经营决策的关系成本函数对企业的经营决策具有重要的影响。
通过分析成本函数,企业可以获得以下信息:1. 边际成本:成本函数的导数表示边际成本,即当产出数量增加一个单位时,额外需要支付的成本。
了解边际成本的变化情况,可以帮助企业决定是否继续生产更多产出,以及何时停止生产。
生产与成本函数分析

生产与成本函数分析摘要生产与成本函数分析是管理经济学中一个重要的主题。
通过研究生产函数和成本函数,可以帮助企业决策者了解生产过程中的效率和成本。
本文将对生产函数和成本函数进行详细介绍,并探讨它们之间的关系。
此外,还将介绍生产与成本函数的应用,并讨论它们在管理决策中的重要性。
1. 生产函数生产函数是描述生产过程中输入和输出之间关系的函数。
它表达了生产所需要的输入(劳动、资本等)与输出(产品或服务)的数量之间的关系。
生产函数通常表示为:Y = f(K, L)其中,Y代表产量(输出),K代表资本投入,L代表劳动投入。
函数f(K, L)表示生产函数的具体形式,它可以是线性函数、二次函数、指数函数等等。
生产函数的形式取决于具体的生产过程。
生产函数有几个重要的性质:•递增边际产量:生产函数通常具有递增边际产量的性质。
也就是说,增加一单位的输入(如劳动或资本)会带来更多的产出。
然而,递增边际产量通常在某一点开始递减。
•边际产量递减:随着输入的增加,生产函数的边际产量通常递减。
也就是说,增加一单位的输入会带来递减的额外产出。
了解生产函数对企业决策至关重要。
企业可以通过分析生产函数来确定最优的生产组合,以最大化产出。
2. 成本函数成本函数是描述生产成本与输入数量之间关系的函数。
它表达了生产所需的投入成本与投入数量之间的关系。
成本函数通常表示为:C = g(K, L)其中,C代表成本,K代表资本投入,L代表劳动投入。
函数g(K, L)表示成本函数的具体形式,它可以是线性函数、二次函数等等。
成本函数的形式取决于企业的生产过程和要素价格。
成本函数有几个重要的性质:•递增边际成本:成本函数通常具有递增边际成本的性质。
也就是说,增加一单位的输入会带来递增的额外成本。
然而,递增边际成本通常在某一点开始递减。
•边际成本递减:随着输入的增加,成本函数的边际成本通常递减。
也就是说,增加一单位的输入会带来递减的额外成本。
了解成本函数对企业决策也非常重要。
供给函数,生产函数和成本函数的名词解释

一、供给函数1. 供给函数是指在某一时期内,各种商品或服务的供给数量与商品或服务的价格之间的关系。
它反映了在不同价格水平下的供给情况,通常用数学函数的形式进行表达,其一般形式可以表示为Qs = f(P),其中Qs表示商品或服务的供给数量,P表示商品或服务的价格,f(P)表示价格P下的供给函数。
2. 供给函数可以帮助市场参与者了解和预测供给方面的情况,如在价格上涨时供给数量的增加情况,或在价格下跌时供给数量的减少情况。
供给函数也是市场经济中决定市场平衡价格和数量的重要工具,通过对供给函数的分析可以得出供给曲线,帮助市场参与者做出合理的决策。
3. 供给函数在经济学理论中具有重要意义,它不仅可以用来分析商品或服务的供给情况,还可以用来研究税收政策、补贴政策等对供给数量的影响,是经济学领域中的基础理论之一。
二、生产函数1. 生产函数是指在一定时间内,生产者通过投入一定数量的生产要素(如劳动力、资本、土地等)来生产出一定数量的产品或服务的关系。
它通常用数学函数的形式表示,一般形式可以表示为Q = f(K, L),其中Q表示生产的产量,K表示资本投入,L表示劳动力投入,f(K, L)表示生产函数。
2. 生产函数是生产理论中的一个重要工具,它可以帮助生产者了解和预测生产过程中的产出情况,如在投入增加时产出的增加情况,或在投入减少时产出的减少情况。
生产函数也是确定合理生产要素投入组合、提高生产效率的基础。
3. 生产函数的研究对于生产计划、生产组织、生产管理等方面具有重要意义,通过对生产函数的分析可以帮助生产者优化资源配置,提高生产效率,实现经济增长和社会发展。
三、成本函数1. 成本函数是指在一定时间内,生产者在生产一定数量的产品或服务过程中所用到的各种成本与生产数量之间的关系。
它通常用数学函数的形式表示,一般形式可以表示为C = f(Q),其中C表示生产成本,Q表示生产数量,f(Q)表示成本函数。
2. 成本函数是生产理论中的一个重要工具,它可以帮助生产者了解和预测生产过程中的成本情况,如在产量增加时成本的增加情况,或在产量减少时成本的减少情况。
企业生产函数与成本函数全面概述

TP
• MPL递增阶段(OL1);
TP
• MPL递减阶段(L1L3);
• MPL为负阶段(L3以后)。
O
L
MP
I
II
III
AP
MP
17.12.2019
AP
O
L L1 L2 L3 16
6、一种变动投入的最优选择
• 边际要素投入的边际产量产值 VMPL=MPL PX ( PX为产品价格)
• 产品的边际成本 MC=w/MPL ,w= MPL MC( W为要素 价格)
17.12.2019
4
一、生产函数
在一定的技术条件下,各种生产要素投 入量的某一组合与其可能生产的最大产量 之间的关系,称为生产函数,即投入和产
出之间的关系:劳动、资本、土地是任 何生产活动的最基本投入,称原始投入。
17.12.2019
5
生产函数
可与原始投入相配合而作生产投入之用的称为中间 投入,生产要素常泛指原始投入和中间投入。
17.12.2019
7
二、一种可变投入生产函数
技术条件不变,一种可变动投入(劳 动)与另一种固定投入(通常是资 本)相结合,只生产一种产品,可 能生产的最大产量(Q),通常又称 作短期生产函数:
Q =f (L)
17.12.2019
8
1. 实物产量
可能的最大产量和变动投入之间的关系, 可表示为:
TP = Q = f (L)
17.12.2019
11
一种可变投入生产函数
150
100
50
Q
0
0
2
4
6
8
10
30
20
10
AP
已知生产函数求成本函数

已知生产函数求成本函数已知生产函数求成本函数一、引言在现代经济学中,生产函数是研究商品生产过程的重要工具。
在生产过程中,我们需要考虑投入和产出之间的关系,那么如何确定成本函数呢?本文将带大家了解已知生产函数求成本函数的方法。
二、生产函数概述生产函数是由经济学家使用的一个重要的工具,在宏观经济中具有广泛的应用。
在生产过程中,生产函数描述了使用特定技术和生产资源进行生产所能生产的最大产量。
生产函数通常表示为:Y = f(K,L)其中,Y代表产量,K代表资本,L代表劳动力。
生产函数也可以写成: Y = A × f(K,L)其中,A代表技术进步或者生产效率等外在因素。
三、成本函数的概述为了生产商品,企业需要消耗各种生产要素,如资本和劳动力。
这些生产要素的成本会影响商品的生产成本。
成本函数是指一定产出水平下,生产所需要的最小成本。
成本函数通常表示为:C = wL + rK其中,w代表单位劳动力的成本,r代表资本的机会成本。
L和K分别代表使用的劳动力和资本的数量。
四、已知生产函数求成本函数的方法已知生产函数,我们可以通过下面的步骤来求解成本函数:1. 对生产函数进行对数化转换,得到:ln Y = ln A + α ln K + (1-α) ln L其中,α代表产出弹性。
我们假设生产函数来自某家企业,且该企业所有的输入要素的成本是已知的,即wL + rK = C2. 对式子进行求导:d(ln Y)/d(ln K) = αd(ln Y)/d(ln L) = 1-α3. 代入成本函数,得到:ln Y = ln A + d(ln Y)/d(ln K) ln K + d(ln Y)/d(ln L) ln Lln Y - ln A = α ln K + (1-α) Lln(Y/A) = α ln K + (1-α) ln Lln(Y/A)-ln L^(1-α) = α ln K4. 求解K:K = (Y/A)/(L^(1-α) × exp(α ln K))5. 将K代入成本函数中,得到:C = wL + r(Y/A)/(L^(1-α) × exp(α ln K))至此,我们就求得了成本函数的表达式。
成本函数知识点总结

成本函数知识点总结在经济学中,成本函数通常被用来描述生产过程中所用资源的成本与产出之间的关系。
成本函数的一般形式可以表示为:C = f(x1, x2, ..., xn)其中,C 表示成本总额,x1, x2, ..., xn 分别表示不同的资源投入,f 表示生产函数或成本函数的具体形式。
一般来说,成本函数可以分为总成本函数和平均成本函数两种形式。
总成本函数表示的是生产一定数量的产品所需要的总成本,通常表示为:TC = f(x1, x2, ..., xn, Q)其中,TC 表示总成本,Q 表示产出量,x1, x2, ..., xn 表示各种生产要素的投入量。
总成本函数可以帮助生产者了解在不同产出量下所需要的总成本,从而帮助其做出生产规模的决策。
平均成本函数表示的是单位产出所需要的平均成本,通常表示为:AC = TC / Q其中,AC 表示平均成本,TC 表示总成本,Q 表示产出量。
平均成本函数可以帮助生产者了解在不同产出量下单位产品的平均成本,从而帮助其确定最优的产出量和生产规模。
成本函数的知识点总结包括但不限于以下内容:1. 成本函数的分类:总成本函数和平均成本函数2. 成本函数的形式:通常表示为关于生产要素和产出量的函数3. 成本函数的性质:通常具有经济学意义的性质,如递增成本、递减成本等4. 成本函数的应用:帮助生产者了解生产过程中的成本结构,从而帮助其做出合理的决策成本函数的分类成本函数主要可以分为总成本函数和平均成本函数两种形式。
总成本函数表示的是生产一定数量的产品所需要的总成本,通常表示为:TC = f(x1, x2, ..., xn, Q)其中,TC 表示总成本,Q 表示产出量,x1, x2, ..., xn 表示各种生产要素的投入量。
总成本函数可以帮助生产者了解在不同产出量下所需要的总成本,从而帮助其做出生产规模的决策。
平均成本函数表示的是单位产出所需要的平均成本,通常表示为:AC = TC / Q其中,AC 表示平均成本,TC 表示总成本,Q 表示产出量。
企业生产函数与成本函数全面概述

企业生产函数与成本函数全面概述引言企业生产函数与成本函数是微观经济学中非常重要的概念,它们对于理解企业生产决策和经济效率有着重要的意义。
本文将全面概述企业生产函数和成本函数的概念、性质以及它们之间的关系。
企业生产函数企业生产函数描述了企业如何将投入转化为产出的关系。
它是一种描述企业生产过程的函数,通常用数学形式表示。
企业生产函数的一般形式如下:Q=f(K,L)其中,Q代表产出,K代表资本投入,L代表劳动投入。
企业生产函数可以取多种形式,常见的有线性生产函数、凸生产函数和Cobb-Douglas生产函数等。
线性生产函数线性生产函数是企业生产函数的一种简单形式,它假设产出与资本和劳动之间的关系是线性的。
线性生产函数的形式如下:Q=aK+bL其中,a和b是正常数,代表了单位资本和单位劳动的产出数量。
线性生产函数假设资本和劳动是完全可替代的,即单位资本和单位劳动的边际产出是相等的。
凸生产函数凸生产函数是企业生产函数的一种常见形式,它假设产出与资本和劳动之间的关系是凸形的。
凸生产函数的特点是边际产出递减,即每增加一单位的投入,产出的增加量越来越小。
凸生产函数的形式如下:Q=f(K,L)其中,Q代表产出,K代表资本投入,L代表劳动投入。
凸生产函数的曲率程度可以根据具体情况进行调整,以适应不同行业和企业的生产特点。
Cobb-Douglas生产函数Cobb-Douglas生产函数是一种常用的凸生产函数形式,它的形式如下:$$Q = AK^{\\alpha}L^{\\beta}$$其中,Q代表产出,K代表资本投入,L代表劳动投入,A是常数,$\\alpha$和$\\beta$是正常数,称为资本弹性和劳动弹性。
Cobb-Douglas生产函数假设资本和劳动是具有固定配比的,且边际产出递减。
成本函数成本函数描述了企业生产过程中的成本与产出、投入之间的关系。
它是企业经济决策过程中必不可少的工具,能够帮助企业确定最佳的生产和投入组合,以实现最大的利润。
知识点二成本函数

【知识点二】成本函数1.成本函数的含义和类型成本函数就是表示企业总成本与产量之间关系的公式。
分为短期成本函数和长期成本函数。
(1)短期成本函数可分为固定成本与可变成本C=b+f(q),其中b―――――固定成本f(q)―――可变成本C-----------总成本(2)长期成本函数没有固定成本(从长期看一切生产要素都是可变的)C=f(q)【注】短期成本函数和长期成本函数的区别在于是否含有固定成本。
2.短期成本函数分析(1)短期总成本TC =总固定成本TFC +总可变成本TVC①固定成本是指在短期内不随产量增减而变动的那部分成本,如厂房设备的折旧,以及管理人员的工资费用。
②可变成本是随产量变动而变动的那部分成本,如原材料、燃料和动力以及生产工人的工资费用。
【例题10:2008年多选】固定成本包括的项目有()A厂房和设备折旧B管理人员的工资费用C原材料费用D燃料和动力费用E生产工人的工资费用【答案】AB【例题11:2011年多选】下列项目中,从短期来看,属于企业可变成本的有( )。
A.原材料费用B.燃料和动力费用C.厂房和设备折旧D.生产工人的工资E.银行借款利息【答案】ABD(2)平均成本:单位产品成本,是生产每一单位产品的成本,是总成本除以总产量所得之商。
(3)边际成本:边际成本是增加一个单位产量时总成本的增加额【提示】边际成本是产量变动引起的可变成本的变动(因为短期内固定成本不随产量的变化而变化)【例题12:2008年单选题】当某企业的产量为2个单位时,其总成本、总固定成本、总可变成本、平均成本分别为2000元、1200元、800元和1000元;当产量为3个单位时,其总成本、总固定成本、总可变成本、平均成本分别是2100元、1200元、900元和700元,则该企业的边际成本是()元A 0B 150C 100D 300【答案】C【解析】考核边际成本概念的理解。
边际成本是指增加一个单位产量时总成本的增加额,产量由2个单位增加到3个单位,总成本由2000元增加到2100元,所以边际成本是100元。
经济学原理第四章生产与成本理论

第四章 生产与成本理论
劳动的平均产量(APL)指平均每一单位可变要素劳动的 投入量所生产的产量。它的定义公式为
APL
TPL(L,K) L
(4.5)
劳动的边际产量(MPL)指增加一单位可变要素劳动的投 入量所增加的产量。它的定义公式为
MPL
TPL(L,K) L
(4.6)
第四章 生产与成本理论
或
M P L lL i0 m TL P (L L,K)dT L d(L L P ,K) (4.7)
假设等产量曲线的生产函数为
第四章 生产与成本理论
Q=f(L,K)=Q0
在等式两边取全微分得
f dLf dKdQ0 L K
整理得
第四章 生产与成本理论
f dK L MPL dL f MPK
K
由边际技术替代率定义公式可得
MRTLR KddK LM MK LPP
第四章 生产与成本理论
2. 边际技术替代率递减规律 在两种生产要素相互替代的过程中,普遍存在这么一种 现象:在维持产量不变的前提下,当一种生产要素的投入量 不断增加时,每一单位的这种生产要素所能替代的另一种生 产要素的数量是递减的。这一现象被称为边际技术替代率递 减规律。以图4-4为例。
在图4-6中,有一条等成本线AB和三条等产量曲线Q1 、 Q2和Q3。等成本线AB的位置和斜率取决于既定的成本量C
和两种生产要素的价格比例 P L 。 PK
第四章 生产与成本理论
图4-6 既定成本条件下的产量最大化
第四章 生产与成本理论
总之,在均衡点E,等产量曲线Q2与等成本线AB相切。
由于等产量曲线的斜率可用边际技术替代率MRTS表示,等
第四章 生产与成本理论
第三章-企业的生产和成本ppt课件

销售额是一个标志企业健康状态的晴雨表,销售收入最大化可能超 越利润最大化成为企业占统治地位的目标。
3. 长期规模增长的最大化
指管理者寻求销售收入或企业资本价值在一定时期内的最大增长。
第二节 生产函数
一、生产和生产函数 二、短期和长期 三、生产函数的例子
一、生产和生产函数
资本(K)
生产过程中投入的物品和货币资金等。资本的价格表现为租用价格。
土地(N)
泛指一切自然资源。使用土地的价格也表现为租用价格。
企业家才能(E)
指建立、组织和经营企业的企业家的发现市场机会并组织各种投入的能力。就 一般性的技术讨论而言,可以此归于劳动。
一、生产和生产函数
2. 生产函数
第二节 生产函数
L
第三节 短期生产函数
一、总产量、平均产量和边际产量
L
Q
MP AP
0
0
---
---
1
20
20
20
2
46
26
23
3
70
24
23.33
4
92
22
ቤተ መጻሕፍቲ ባይዱ
23
5
110
18
22
Average Product = Q / L Marginal Product =△ Q / △ L = dQ / dL 观察表中数值的数字特征。
资本投入不变,劳动投入可变。
Qf L,K
资本投入和劳动投入都可变。
三、生产函数的例子
第二节 生产函数
1. 固定比例的生产函数
• 含义:指生产要素按固定比例搭配的生产函数,如公交车和公
交车司机。
经济学原理(中级)

A aL
(1 a)K
1
第二节 短期分析——具有一种可变 生产要素的生产函数
一、总产量,平均产量和边际产量及其相互关系 总产量(total product,简写为TP)
Q=TP=ƒ(L) 平均产量(average product,简写为AP)
AP= TP/L 边际产量(marginal product,简写为MP)
经济学专业学位
经济学原理(中级)
郑长德 教授 (西南民族大学经济学院)
第二部分
第一节 生产与生产函数
一、生产集(production set) 是指一定技术条件下企业的投入与产出
之间的各种组合的集合。
生产集反映了企业所面临的所有可能的技术选择,
二、生产函数
生产集的上边界点的集合就叫生产函数
w r
第五节 生产弹性
一、产出弹性(elasticity of output) 指在技术水平和生产要素价格不变的条
件下,若保持其他投入要素使用量不变, 单独变动一种投入要素使用量 的变化百分 率所引起的产量变化的百分率,它反映了 产量的相对变化对于该种投入要素的相对 变化的敏感性。
设生产函数为Q=ƒ(L,K),则劳动L和资本K的产出弹性分别为:
如果生产函数满足下列性质:
f (tx1, tx2 ) t K f (x1, x2,) 其中t指任何正实数,k 为常数,称该生产函数为K次齐次生产函数。
t 1, K 1 →递增
t 1, K 1 →不变
t 1, K 1 →递减
对上式两边对t求导:x1 f1 x2 f2 kt k1 f
(a)成本既定求产量最大
(b)产量既定求成本最小
成本函数
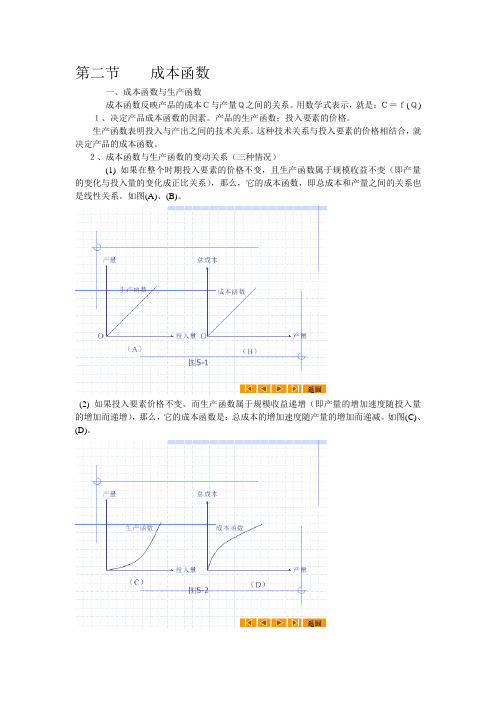
第二节成本函数一、成本函数与生产函数成本函数反映产品的成本C与产量Q之间的关系。
用数学式表示,就是:C=f(Q) 1、决定产品成本函数的因素。
产品的生产函数;投入要素的价格。
生产函数表明投入与产出之间的技术关系。
这种技术关系与投入要素的价格相结合,就决定产品的成本函数。
2、成本函数与生产函数的变动关系(三种情况)(1) 如果在整个时期投入要素的价格不变,且生产函数属于规模收益不变(即产量的变化与投入量的变化成正比关系),那么,它的成本函数,即总成本和产量之间的关系也是线性关系。
如图(A)、(B)。
(2) 如果投入要素价格不变,而生产函数属于规模收益递增(即产量的增加速度随投入量的增加而递增),那么,它的成本函数是:总成本的增加速度随产量的增加而递减。
如图(C)、(D)。
(3) 如果要素价格不变,而生产函数属于规模收益递减(即产量的增长速度随投入量的增加而递减),那么,它的成本函数是:总成本的增加速度随产量的增加而递增。
如图(E)、(F)。
由上可见,成本函数导源于它的生产函数,只要知道某种产品的生产函数,以及投入要素的价格,就可以推导出它的成本函数。
二、总成本、平均成本与边际成本1、总成本(TC):指企业为生产一定量产品所消耗(或支付)的全部成本(费用)。
从短期看,总成本包括:(1) 总固定成本(TFC):即使产量为零也必须支付的费用总额。
(2) 总变动成本(TVC):总成本中随产量增加而增加的费用总额。
即:TC=TFC+TVC。
当然,从长期看,不存在任何固定成本,一切成本都是可变的。
例如,对一家已经建成的钢铁厂来说,无论产量如何变化,厂房和设备总是固定不变的,可变的只是劳力和原材料的数量。
在这种条件下形成的产量和成本之间的关系,就叫做短期成本函数。
其几何表现(或图形)就是短期成本曲线。
显然,在短期成本中,因为有一部分投入要素固定不变,所以,它除了包括变动成本之外,还包括固定成本。
短期成本函数通常用来反映现有企业中产量与成本的关系,所以,它主要用于日常的经营决策。
生产和成本决策分析

二、生产决策分析
(一)生产函数的概念 生产函数是指在一定的技术条件下,
各种生产要素投入量的组合与所能生产 的最大产量之间的对应关系。其一般数 学表达式为:
Q=f(X1,X2,…,Xn) 式中,Q为产量;X1,X2,…,Xn 为诸投
入要素,如原材料、资金、劳动量等。
1、短期生产函数 短期生产函数,是指企业在此期间内,
(四)规模经济性分析
1、规模与收益的关系 ◆规模收益递增(事半功倍) ◆规模收益不变 ◆规模收益递减(事倍功半) 2、促使规模收益递增的原因 ◆工人可以专业化 ◆使用专门化的设备和较先进的技术 ◆大设备单位能力的制造和运转费用通常
比小设备要低 ◆生产要素具有不可分割性
3、促使规模收益递减的原因 主要是管理问题
(管“理”区)(管“条件”区)
AP
O
A
B MP 要素投入量
第一阶段:边际产量>0,边际产量>平均产量 特点:随着投入要素的增加,总产量、平均产量 均呈上升趋势 管理重点:扩大要素投入量
第二阶段: 边际产量>0,边际产量<平均产量 特点:随着投入要素的增加,总产量呈上升趋势, 平均产量呈下降趋势 管理重点:优化要素投入量
生产与成本决策分析
一、对生产的全面理解 二、生产决策分析 三、成本决策分析 四、生产函数与成本函数的应用
问题讨论与交流 1、高投入能否带来高产出?是否投入越多、
产出越大? 2、高产出能否带来高收益?是否产出越多、
效益越好?
一、对生产的全面理解
所谓生产,就是投入与产出之间的转换 关系。 特别强调: ◆任何企业的生产都离不开要素的投入。 ◆任何企业的生产都必须经过相应的转换。 ◆任何企业生产的结果都是产品。
成 本 函 数

成本函数
成本函数
一、成本函数的含义 二、边际收益递减规律 三、生产阶段的划分
一、成本函数的含义
(一)成本函数概念 生产函数是表示产出与成本之间的数量关 系 ,如果反过来研究成本与产出之间的关
系,即把成本作为因变量,把产出作为自变量, 那么成本就是产出的函数。反映成本与产出之间 的数量关系的函数即为成本函数。
产
量
生产函
数
总
成
成本函
本
数
O
(a)
要素投入 量
O 产量
(b量增 加的速度大于投入量增加的速度,那么,它的 总成本的增加速度随产量的增加而递减,如图 所示:
产量
成本
生产函数
成本函数
0 (a)
投入量 0
(b)
投入量
一、成本函数的含义
3.若生产函数规模收益递减,即产量增 加的速度入量增加的速度那么,它的总成本的 增加速度随产量的增加而递增。如图所示:
三、长期成本函数
长期成本函数可以表示为以产量为横轴.以成本为 纵轴的坐标图上的长期成本曲线。长期看。企业各 种投入要素都是可变的,因此,在长期中,企业所 有的成本都是可变的。企业的长期成本可分为长期总 成本、长期平均成本、长期边际成本。 1.长期总成本(LTC)
长期总成本是指企业在长期中在每一个产量水平 上通过选择最优的生产规模所能达到的最低总成本。 长期总成本曲线说明在企业可以自由选定投入 要素组合比例的条件下,当企业达到各个最优 规模时可能的最低的总成本。
TC(Q) TFC TVC(Q)
二、短期成本函数
3.总成本 总成本(TC)指短期内生产一定量所付出
的全部成本,是企业总固定成本与总变动成本 之和。由于TVC是产量的函数,因此TC也是产 量的函数。其公式表示为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MP=0时,TP达到最大。
05.05.2020
O
生产函数分析
TP
L MP
AP L
L1 L2 L3 15
5、 生产三阶段
TP
• MPL递增阶段(OL1);
TP
• MPL递减阶段(L1L3);
• MPL为负阶段(L3以后)。
O
L
MP
I
II
III
AP
MP
05.05.2020
O
生产函数分析
AP L
L1 L2 L3 16
C-D 生产函数反映了两种投入要素之间相互影 响。
05.05.2020
生产函数分析
39
柯布—道格拉斯生产函数
• MRTS = MPL/MPK = αK/ βL • EL = α • EK = β • Ee = α+ β • 从α+β是大于1、等于1、还是小于1
就可以知道生产是处于规模报酬递增、 规模报酬不变、还是规模报酬递减。
27
生产者最优选择
某一确定总成本所能购 到劳动和资本各种可 K
能的组合轨迹为等成
本线,只有当等产量
线和等成本线正好相
切时实现产量最大化。
E
(对偶问题是成本最小) O
q C
L
05.05.2020
生产函数分析
28
生产者最优选择
等产量线与等成本线相切的切点斜率,
等产量线上切点的斜率等于两种投入的边 际技术替代率的相反数:- MPL/ MPK
05.05.2020
生产函数分析
2
企业分类
• 业主制; • 合伙制; • 公司制:
• 无限责任公司; • 有限责任公司; • 两合公司; • 股份责任公司。
05.05.2020
生产函数分析
3
第一节 生产函数分析
人类经济活动的四个环节 生产环节起决定性作用;
生产力是社会发展的第一杠杆, 从实物形态研究是生产函数, 从货币形态研究是成本函数。
例题
• 某产品的生产函数为Q=KL-0.8K2-0.2L2, 求:当K=10时,画出劳动的总产出与平均
产出曲线、边际曲线。
05.05.2020
生产函数分析
18
三、长期生产函数
只要考察的时间足够长,就不只一种投入 在变动,两种或两种以上的投入可以变 动,甚至所有的投入都可以变动。
如投入的劳动和资本都可以变动,投入和 产出之间的关系:
05.05.2020
生产函数分析
7
二、一种可变投入生产函数
技术条件不变,一种可变动投入(劳 动)与另一种固定投入(通常是资 本)相结合,只生产一种产品,可 能生产的最大产量(Q),通常又称 作短期生产函数:
Q =f (L)
05.05.2020
生产函数分析
8
1. 实物产量
可能的最大产量和变动投入之间的关系, 可表示为:
当L上升,MPL下降; 同时K下降, MPK上升; 于是有MRTS= MPL/ MPK下降。
05.05.2020
生产函数分析
25
特殊生产函数
不同的两种投入,彼此间替代程度不同: 完全替代,等产量线是一族倾斜的直线; 完全不替代,等产量线是一族直角线。
K
完全替代
K
完全不替代
O
05.05.2020
L
O
生产要素一般分为四类: 1. 自然资源 2. 资本资源 3. 劳动(人力)资源 4. 信息资源
05.05.2020
生产函数分析
6
生产函数
投入和产出之间的关系可表示为
Q =f (L,K,···,T)
投入又可分固定投入和变动投入;
生产函数分一个可变投入生产函数(短期生 产函数)和两个可变投入生产函数(长期 生产函数)。
Q = f ( L,K)
05.05.2020
生产函数分析
19
1、等产量线
不同的投入要素组合可以生产同样的产量
Q
K
L
05.05.2020
生产函数分析
20
等产量线
等产量线表示具有相同产量的各种可能的 要素组合的轨迹; K
等产量线的性质:
1) 斜率为负, 2) 凸向原点, 3) 互不相交。
q4
ΔK
ΔL
同时生产多种产品所产生的节约,称 作为范围经济(Economics of cope)。
05.05.2020
生产函数分析
36
四、 经验生产函数
使用的生产函数是经验生产函数,是从实 际生产的数据中模拟出来,反映了在一 定的技术条件下,投入和平均产出之间 的关系。
05.05.2020
生产函数分析
37
1. 多项式生产函数
TP = Q = f (L)
平均产量 AP ( Average Product) 也 随着变动投入的变动而变动 APL = Q / L
05.05.2020
生产函数分析
9
2、边际产量
在一定技术条件下,面其它诸投入要素都 保持不变,每增加一个单位变动投入所 引起的总产量的变动,称为边际产量 MP(Marginal Product):
05.05.2020
生产函数分析
43
6、对数生产函数
对柯布—道格拉斯生产函数取对数,即可 转换成线性函数: ln Q = ln A +αlnL + βlnK
生产函数分析
23
边际技术替代率
两可变投入生产函数,增加投入劳动 引起的产量的增加,必然等于减少 投入资本引起的产量的减少:
dL·MPL = -dK·MPK MRTSLK = -dK/ dL MRTSLK = MPL/MPK
05.05.2020
生产函数分析
24
2) 边际技术替代率递减法则
沿着同一条等产量线,以一种投入要 素替代另一种投入要素,可替代的 数量是越来越少,这称边际技术替 代率递减法则。
MPL =ΔTP/ΔL = dTP/ dL
05.05.2020
生产函数分析
10
一种可变投入生产函数
L
K
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
10
10
10
ቤተ መጻሕፍቲ ባይዱ
Q 0 10 30 60 80 95 108 112 112 108 100
APL -
10 15 20 20 19 18 16 14 12 10
05.05.2020
生产函数分析
22
边际技术替代率
边际技术替代率记作MRTSLK
(Marginal rate of technical
substitution)
K
MRTSLK = -ΔK/ΔL = - dK/ dL
k1 k2
绝对值等于等产量线上该点的
q
切线斜率。
O L1 L2
L
05.05.2020
33
规模报酬
• 当Ee > 1时,规模报酬递增阶段;(由于
大规模生产带来明显的规模上的好处,称规模经济, 因此在扩张阶段出现规模报酬递增。)
• Ee = 1时,规模报酬不变阶段; • Ee < 1时,规模报酬递减阶段。(但有
时规模太大也有不利因素,这称规模不经济,这样在 扩张阶段会出现规模报酬递减。)
05.05.2020
生产函数分析
4
一、生产函数
在一定的技术条件下,各种生产要素投 入量的某一组合与其可能生产的最大产量 之间的关系,称为生产函数,即投入和产
出之间的关系:劳动、资本、土地是任 何生产活动的最基本投入,称原始投入。
05.05.2020
生产函数分析
5
生产函数
可与原始投入相配合而作生产投入之用的称为中间 投入,生产要素常泛指原始投入和中间投入。
q3
q2
假定L、K之间可以替代。
q1
O
L
05.05.2020
生产函数分析
21
2、边际技术替代率
1)边际技术替代率
不同投入要素之间有一定的技术替代关系; 在技术水平不变的条件下,维持同样的产 量,增加一个单位的某一种投入可以替代 另一种投入的数量,叫作这一种投入要素 对另一种投入要素的边际技术替代率。
05.05.2020
生产函数分析
14
4、总产量、平均产量、边际产量
TP
总产量、平均产量、边际产 量间的关系:
当MP > AP时,AP 上升;
MP < AP时,AP 下降;
MP = AP时,AP达到最大值。 O
边际产量曲线必然通过平均产量
曲线的最高点,
MP
当MP>0时,TP上升;
AP
MP<0时,TP下降;
05.05.2020
生产函数分析
40
3、C —D生产函数的一般形式
技术进步的影响日益增大,对C —D生产 函数可改进为更一般的形式:
Q=X1α1X 2 α2 ···Xn αne λt λ 是技术进步因子 t 为时间, X 是广义的投入要素, αn 是回归系数。
05.05.2020
生产函数分析
41
例题
• 已知函数Q=K0.5L0.5,C=wL+rK, 当w=r=1时, 求 短期(K=1,4,9时)成本函数STC、 SAC、SMC。
05.05.2020
生产函数分析
42
其他生产函数
• 4、线性生产函数
• Q = A(αL + βK) • MRTS = β/ α
