网络分析与综合-4.3 图解法
合集下载
运筹学:第6章 图与网络分析

给图中的点和边赋以具体的含义和权值,我们称 这样的图为网络图(赋权图)
2021/4/18
6
图中的点用 v 表示,边用 e 表示,对每条边可用
它所联结的点表示,如图,则有:
e1 = [v1 , v1], e2 = [v1 , v2]或e2= [v2 , v1]
2021/4/18
7
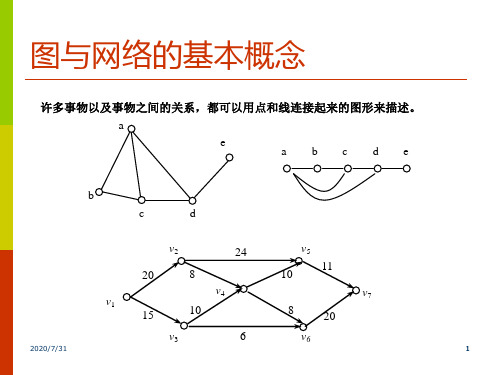
用点和点之间的线所构成的图,反映实际生产和 生活中的某些特定对象之间的特定关系。
第一种解法:
1. 在点集中任选一点,不妨取 S,令 V={S} 2. 找到和 S 相邻的边中,权值最小的 [S , A] 。
2021/4/18
22
3.V={S , A} 4. 重复第2,3步,找到下一个点。
2021/4/18
23
第二种做法求解过程:
2021/4/18
24
破圈法求解步骤:
1. 从图 N 中任取一回路,去掉这个回路中边 权最大的边,得到原图的一个子图 N1。
Dijkstra 算法假设:
1.设 dij 表示图中两相邻点 i 与 j 的距离,若 i 与 j 不相邻,令 dij =∞,显然 dii =0。 2. 设 Lsi 表示从 s 点到 i 点的最短距离。
2021/4/18
31
求从起始点 s 到终止点 t 的最短路径。 Dijkstra 算法步骤:
1.对起始点 s ,因 Lss =0 ,将 0 标注在 s 旁的小 方框内,表示 s 点已标号;
终点重合的链称为圈,起点和终点重合的路称为回
路,若在一个图中,每一对顶点之间至少存在一条
链,称这样的图为连通图,否则称该图为不连通的。
2021/4/18
12
2021/4/18
链
2021/4/18
6
图中的点用 v 表示,边用 e 表示,对每条边可用
它所联结的点表示,如图,则有:
e1 = [v1 , v1], e2 = [v1 , v2]或e2= [v2 , v1]
2021/4/18
7
用点和点之间的线所构成的图,反映实际生产和 生活中的某些特定对象之间的特定关系。
第一种解法:
1. 在点集中任选一点,不妨取 S,令 V={S} 2. 找到和 S 相邻的边中,权值最小的 [S , A] 。
2021/4/18
22
3.V={S , A} 4. 重复第2,3步,找到下一个点。
2021/4/18
23
第二种做法求解过程:
2021/4/18
24
破圈法求解步骤:
1. 从图 N 中任取一回路,去掉这个回路中边 权最大的边,得到原图的一个子图 N1。
Dijkstra 算法假设:
1.设 dij 表示图中两相邻点 i 与 j 的距离,若 i 与 j 不相邻,令 dij =∞,显然 dii =0。 2. 设 Lsi 表示从 s 点到 i 点的最短距离。
2021/4/18
31
求从起始点 s 到终止点 t 的最短路径。 Dijkstra 算法步骤:
1.对起始点 s ,因 Lss =0 ,将 0 标注在 s 旁的小 方框内,表示 s 点已标号;
终点重合的链称为圈,起点和终点重合的路称为回
路,若在一个图中,每一对顶点之间至少存在一条
链,称这样的图为连通图,否则称该图为不连通的。
2021/4/18
12
2021/4/18
链
新编第6章图与网络分析精选文档PPT课件
有向图
由点和弧组成的图称为有向图。
有向图是一个有序二元组(V,A),记为 D=(V,A),其中 V=(v1,v2,…….vp)是 p 个点 的集合,A={a1,a2,……aq}是 q 条弧的集合,并且 ai 是一个有序二元组,记为 aij=(vi,vj)≠ (vj,vi),vi,vj∈V,并称 aij 是以 vi 为始点,vj 为终点的弧, i, j 的顺序不能颠倒,图中弧的方 向用箭头标识。
上图中的{ v1,v2,v3 },{ v2,v4,v5},{ v1,v2,v4,v5}都是链。 闭链或圈:两个端点重合的链,称为圈。上图中的{ v1,v2,v3 , v1}就是圈。 简单链与初等链:若链μ中,若含的边数均不相同,则称之为简
单链;若链μ中,顶点 vi1,vi2,…,vik 都不相同,则称此链为初等链。 除非特别交代,以后我们讨论的均指初等链。
V=(v1,v2,v3,v4,v5) E={e1,e2,e3,e4,e5,e6,e7,e8}
e1
v2
e2
v1
e6
e4
e5
e3 v3
e7
2020/7/31
v4
e8
v5
4
无向图
点集 V 中元素的个数成为图 G 的点数,记为 p(G)=| V |。如上图中,p(G)=5。 边集 E 中元素的个数成为图 G 的边数,记为 q(G)=| E |。如上图中,q(G)=8。 边 e=[vi,vj]∈E,称 vi,vj 为 e 的端点,e 为 vi,vj 的关联边。上图中,v1,v2 为 e2 的端点,e2 为 v1,v2 的关联边。 若边 ei,ej 有一公共端点,则称 ei,ej 相邻。如上图中中,e7,e8 相邻。 若点 vi,vj 有边相连,即[vi,vj]∈E,则称 vi,vj 相邻。如上图中中,v3,v5 相 邻。
第6章图与网络分析PPT课件

有向图:图是由点和弧所构成的,
记 作 D={V ,A}(V 是 点 的 集 合 , A 是 弧 的 集 合 ) ,
一条方向从vi指向vj的弧,记作(vi,vj)。
网络图:给图中的点和边赋予具体的含义和权数,如距离, 费用,容量等,记作N.
第8页
图的相关概念
若边eij=[vi,vj]∈E,称vi,vj是eij的端点,也称vi,vj是 相邻的。称eij是点vi(及点vj)的关联边。
若两条边有一个公共的端点,则称这两条边相邻。
点与点
相邻
vi
e
vj
vi,vj相邻
e 与vi,vj关联
边与边相邻
vi e1 vk e2
v
j
点与边关联
第9页
图的相关概念
若某条边两个端点相同,称这条边为环。 若两点之间有多于一条的边,称这些边为多重边。
v1
v5 v4
e1 e2
e4
v2
e3 v3
e5
无环、无多重边的 图称为简单图。
无环、但允许有多 重边的图称为多重 图。
注:无特别声明我们今后讨论的图都是简单图
第10页
图的相关概念
图G中以点v为端点的边的数目,称为v在G中
的次(度), 记为d(v)。
v1
v5 v4
e1 e2
e4
d(v1)=2 d(v2)=3 d(v3)=4 d(v4)=1
v2
e3 v3
e5
次为1 的点为悬挂点,悬挂点的关联边称为悬
第7章 图与网络分析
• 图的基本概念与模型 • 树图和图的最小部分树 • 最短路问题 • 网络最大流问题
第1页
概述
1
点击输入简要文字内容,文字内容需概括精炼,不用多余 的文字修饰,言简意赅的说明分项内容……
记 作 D={V ,A}(V 是 点 的 集 合 , A 是 弧 的 集 合 ) ,
一条方向从vi指向vj的弧,记作(vi,vj)。
网络图:给图中的点和边赋予具体的含义和权数,如距离, 费用,容量等,记作N.
第8页
图的相关概念
若边eij=[vi,vj]∈E,称vi,vj是eij的端点,也称vi,vj是 相邻的。称eij是点vi(及点vj)的关联边。
若两条边有一个公共的端点,则称这两条边相邻。
点与点
相邻
vi
e
vj
vi,vj相邻
e 与vi,vj关联
边与边相邻
vi e1 vk e2
v
j
点与边关联
第9页
图的相关概念
若某条边两个端点相同,称这条边为环。 若两点之间有多于一条的边,称这些边为多重边。
v1
v5 v4
e1 e2
e4
v2
e3 v3
e5
无环、无多重边的 图称为简单图。
无环、但允许有多 重边的图称为多重 图。
注:无特别声明我们今后讨论的图都是简单图
第10页
图的相关概念
图G中以点v为端点的边的数目,称为v在G中
的次(度), 记为d(v)。
v1
v5 v4
e1 e2
e4
d(v1)=2 d(v2)=3 d(v3)=4 d(v4)=1
v2
e3 v3
e5
次为1 的点为悬挂点,悬挂点的关联边称为悬
第7章 图与网络分析
• 图的基本概念与模型 • 树图和图的最小部分树 • 最短路问题 • 网络最大流问题
第1页
概述
1
点击输入简要文字内容,文字内容需概括精炼,不用多余 的文字修饰,言简意赅的说明分项内容……
图与网络分析 胡运权 第四版 运筹学PPT课件

4
3.关联与相邻
❖关联(边与点的关系):若e是v1、v2两点间
的边,记e=[v1,v2 ],称v1、v2 与e关联。
v1
e
v2
❖相邻(有公共边,称点v1与v2相邻;
边e1与e2 有公共点,称边e1与e2相邻。
e1
V2
V1
e2
V3
5
4. 链、圈与连通图
■链:由图G中的某些点与边相间构成的序列 {V1,e1,V2,e2, ……,Vk,ek},若满足 ei=[Vi, Vi ],则称此
(4)A={v1,v2,v4}
[0,v1]
[2,v1]
2
6
v1
v2
v3
1 [1,v1]10
5
9
3
v4
7
v5
6
5
2
3
4
v6
v7
4
[3,v1]
v8 8
考虑边(v1,v6),(v2,v3),(v2,v5),(v4,v7)
计算min { 0+3, 2+6, 2+5, 1+2}=min {3,8,7,3}=3
70
费用、容量等),则称这样 1
4
的图为网络图。
20
45
3
4.2 最小支撑树问题
C1 根
C2
C3
C4
叶
❖树:无圈的连通图,记为T。
8
❖树的性质
■ 树中任意两个节点间有 且只有一条链。
2
3
1
5
4
■ 在树中任意去掉一条边, 1
则不连通。
2
3
5
4
■如果树T有m个结点,则 边的个数为m-1。
3.关联与相邻
❖关联(边与点的关系):若e是v1、v2两点间
的边,记e=[v1,v2 ],称v1、v2 与e关联。
v1
e
v2
❖相邻(有公共边,称点v1与v2相邻;
边e1与e2 有公共点,称边e1与e2相邻。
e1
V2
V1
e2
V3
5
4. 链、圈与连通图
■链:由图G中的某些点与边相间构成的序列 {V1,e1,V2,e2, ……,Vk,ek},若满足 ei=[Vi, Vi ],则称此
(4)A={v1,v2,v4}
[0,v1]
[2,v1]
2
6
v1
v2
v3
1 [1,v1]10
5
9
3
v4
7
v5
6
5
2
3
4
v6
v7
4
[3,v1]
v8 8
考虑边(v1,v6),(v2,v3),(v2,v5),(v4,v7)
计算min { 0+3, 2+6, 2+5, 1+2}=min {3,8,7,3}=3
70
费用、容量等),则称这样 1
4
的图为网络图。
20
45
3
4.2 最小支撑树问题
C1 根
C2
C3
C4
叶
❖树:无圈的连通图,记为T。
8
❖树的性质
■ 树中任意两个节点间有 且只有一条链。
2
3
1
5
4
■ 在树中任意去掉一条边, 1
则不连通。
2
3
5
4
■如果树T有m个结点,则 边的个数为m-1。
第二章 电网络分析与综合

u 回路l1 u 回路l2 u l3 回路
0 0 0
BU=0
对图1-4所示的基本割集依次列写KCL方程并写成矩阵形式得
c3
4 2
5 3 6 c1
0 1 1 i4 i1 1 1 1 i i 5 2 1 1 0 i3 i6
说明连支电压可以用树支电压的线性组合表示。 在全部支路电压中,树支电压是一组独立变量, (n 1) 个数等于树支数 取基本回路是列写独立KVL方程的一个充分非 必要条件 。
u 6 u1 u 2
推广到一般情况:在基本回路上列写的基尔霍夫 电压定律方程是一组独立方程,方程的数目等于 连支数,基本回路是一组独立回路。
推广,b条支路,n个节点,第n号节点为参考节点,支路电压和节 点电压列矢量分别记作 则基尔霍夫电压定律的关联矩阵形式是
ATU n U
四、基尔霍夫定律的基本回路矩阵形式
基本回路矩阵(fundamental loop matrix):描述基本回路与各支路的 关联关系,用B表示。B的行对应基本回路、列对应支路,B 是
c2
1
图 1-4 基本割集
连支电流列矢量为
I l [il1 il 2 il ,bl ]T
则基尔霍夫电流定律的基本回路矩阵形式为 B T I l I
五、基尔霍夫定律的基本割集矩阵形式
基本割集矩阵(fundamental cut-set matrix) :基本割集与各支 路的关联关系,用C表示。矩阵的行对应基本割集,列对应支 路,其元素为:
第二章 网络图论和网络方程
本章是通过线图既点和线联结而成 的几何图形,抽象模拟比较复杂的电网 络,从而对形象直观的线图性质进行研 究,得到各种系统的分析综合方法。
第5章图与网络分析163页PPT

bi j 0wi j
(vi ,vj)E (vi ,vj)E
例6.4 下图所表示的图可以构造权矩阵B如下:
v1 4
v2
36
72
v6 4
3
3
v3
5
2
v5
v4
v1 0 4 0 6 4 3
v
2
4
0
2
7
0
0
B
v3
0
2
0
5
0
3
v4 6 7 5 0 2 0
v
5
4
17
v4
树与图的最小树
v1 23 v6
20
v2
1
4
v7
9
15 v3
28 25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7
9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23 v6
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
16 3
v5
17
v4
v1
②
15
9
7 ④ 14
⑤
①
10
19
20
6 ⑥
③
25
图的矩阵描述: 邻接矩阵、关联矩阵、权矩阵等。
1. 邻接矩阵 对于图G=(V,E),| V |=n, | E |=m,有nn阶方矩阵
图与网络分析

图与网络分析
引言 第一节 图与网络的基本概念 第二节 树 第三节 最短路径问题 第四节 网络最大流问题 第五节 最小费用最大流问题
引言
图论(Graph Theory)是研究图的理论, 是运筹学中一重要 的分支. 有200多年历史, 大体可划分为三个阶段.
图论发展的三个阶段
第一阶段
第二阶段
第三阶段
从十八世纪中叶 到十九世纪中叶
e1
v1
e2
v2
v6
e5
e6
e3
v4
e8
e4
图-9
v3 e7 v5
定义4: 若图G=(V,E)的点集V可分为两个非空子集X, Y, 满 足: XY=V, XY=, 使得E中的每条边的两上顶点必有 一个端点属于X,而另一个端点Y,则称G为二部图(偶图)
v1
e1
v2
v1
U1
e4
e2
v2
v3
U2
v4
C
River
7
5
3
D
2
B 图-1
Euler在1736年发表了一篇题为“依据几何位置的解题 方法”论文,有效解决了Konigsber七桥难题,这是有记 载的第一篇图论论文,Euler也被公认为图论的创始人.
A
C
D
B
例2: Hamilton回路是19世纪英国数学家Hamilton提出
给出一个正12面体图形,共有20个顶点,分别表示全球20个主 要城市,要求从某个城市出发沿着棱线寻找一条经过每个城 市一次而且仅一次,最后回到原处的周游世界线路(并不要求 经过每条边).-环球旅行问题.
定义9 无向图G=(V, E), 连接 vi0与vik 的一条链是同一 个点时, 称为圈(circle). 若圈中没有重复的点与重复边者称为初等圈
引言 第一节 图与网络的基本概念 第二节 树 第三节 最短路径问题 第四节 网络最大流问题 第五节 最小费用最大流问题
引言
图论(Graph Theory)是研究图的理论, 是运筹学中一重要 的分支. 有200多年历史, 大体可划分为三个阶段.
图论发展的三个阶段
第一阶段
第二阶段
第三阶段
从十八世纪中叶 到十九世纪中叶
e1
v1
e2
v2
v6
e5
e6
e3
v4
e8
e4
图-9
v3 e7 v5
定义4: 若图G=(V,E)的点集V可分为两个非空子集X, Y, 满 足: XY=V, XY=, 使得E中的每条边的两上顶点必有 一个端点属于X,而另一个端点Y,则称G为二部图(偶图)
v1
e1
v2
v1
U1
e4
e2
v2
v3
U2
v4
C
River
7
5
3
D
2
B 图-1
Euler在1736年发表了一篇题为“依据几何位置的解题 方法”论文,有效解决了Konigsber七桥难题,这是有记 载的第一篇图论论文,Euler也被公认为图论的创始人.
A
C
D
B
例2: Hamilton回路是19世纪英国数学家Hamilton提出
给出一个正12面体图形,共有20个顶点,分别表示全球20个主 要城市,要求从某个城市出发沿着棱线寻找一条经过每个城 市一次而且仅一次,最后回到原处的周游世界线路(并不要求 经过每条边).-环球旅行问题.
定义9 无向图G=(V, E), 连接 vi0与vik 的一条链是同一 个点时, 称为圈(circle). 若圈中没有重复的点与重复边者称为初等圈
运筹学课件-第六章图与网络分析

运筹学课件-第六章 图与网络分析
contents
目录
•的算法 • 图的应用
01
CATALOGUE
图的基本概念
图的定义
总结词
图是由顶点(或节点)和边(或弧) 组成的数据结构。
详细描述
图是由顶点(或节点)和边(或弧) 组成的数据结构,其中顶点表示对象 ,边表示对象之间的关系。根据边的 方向,图可以分为有向图和无向图。
04
CATALOGUE
图的算法
深度优先搜索
要点一
总结词
深度优先搜索是一种用于遍历或搜索树或图的算法。
要点二
详细描述
该算法通过沿着树的深度遍历树的节点,尽可能深地搜索 树的分支。当节点v的所在边都己被探寻过,搜索将回溯到 发现节点v的那条边的起始节点。这一过程一直进行到已发 现从源节点可达的所有节点为止。如果还存在未被发现的 节点,则选择其中一个作为源节点并重复以上过程,整个 进程反复进行直到所有节点都被访问为止。
物流网络设计的应用
在物流规划、供应链管理、运输优化等领域有广泛应用,例如通过物 流网络设计优化货物运输路径、提高仓储管理效率等。
生物信息学中的图分析
生物信息学中的图分析
利用图论的方法对生物信息进 行建模和分析,以揭示生物系 统的结构和功能。
生物信息学中的节点
代表生物分子、基因、蛋白质 等。
生物信息学中的边
Dijkstra算法
总结词:Dijkstra算法是一种用于在有向图中查找单源 最短路径的算法。
详细描述:Dijkstra算法的基本思想是从源节点开始, 逐步向外扩展,每次找到离源节点最近的节点,并更新 最短路径。该算法使用一个优先级队列来保存待访问的 节点,并将源节点加入队列中。然后,从队列中取出具 有最小优先级的节点进行访问,并将其相邻节点加入队 列中。这一过程一直进行,直到队列为空,即所有可到 达的节点都已被访问。Dijkstra算法的时间复杂度为 O((V+E)logV),其中V是节点的数量,E是边的数量。
contents
目录
•的算法 • 图的应用
01
CATALOGUE
图的基本概念
图的定义
总结词
图是由顶点(或节点)和边(或弧) 组成的数据结构。
详细描述
图是由顶点(或节点)和边(或弧) 组成的数据结构,其中顶点表示对象 ,边表示对象之间的关系。根据边的 方向,图可以分为有向图和无向图。
04
CATALOGUE
图的算法
深度优先搜索
要点一
总结词
深度优先搜索是一种用于遍历或搜索树或图的算法。
要点二
详细描述
该算法通过沿着树的深度遍历树的节点,尽可能深地搜索 树的分支。当节点v的所在边都己被探寻过,搜索将回溯到 发现节点v的那条边的起始节点。这一过程一直进行到已发 现从源节点可达的所有节点为止。如果还存在未被发现的 节点,则选择其中一个作为源节点并重复以上过程,整个 进程反复进行直到所有节点都被访问为止。
物流网络设计的应用
在物流规划、供应链管理、运输优化等领域有广泛应用,例如通过物 流网络设计优化货物运输路径、提高仓储管理效率等。
生物信息学中的图分析
生物信息学中的图分析
利用图论的方法对生物信息进 行建模和分析,以揭示生物系 统的结构和功能。
生物信息学中的节点
代表生物分子、基因、蛋白质 等。
生物信息学中的边
Dijkstra算法
总结词:Dijkstra算法是一种用于在有向图中查找单源 最短路径的算法。
详细描述:Dijkstra算法的基本思想是从源节点开始, 逐步向外扩展,每次找到离源节点最近的节点,并更新 最短路径。该算法使用一个优先级队列来保存待访问的 节点,并将源节点加入队列中。然后,从队列中取出具 有最小优先级的节点进行访问,并将其相邻节点加入队 列中。这一过程一直进行,直到队列为空,即所有可到 达的节点都已被访问。Dijkstra算法的时间复杂度为 O((V+E)logV),其中V是节点的数量,E是边的数量。
4-8 计算机辅助分析《网络分析与综合》课件

牛顿—拉夫逊法流程框图
开始
Байду номын сангаас
输入非线性方程组信息 形成右端项矩阵B
设定一个值e和迭代次数n
计算雅可比矩阵A
k =1
输入一组初始值 X k
将 X k 带入矩阵B中 计算各项的值
Y B中各项小于e?
N k =k+Y1
k >n? N
计算 X k
Y 迭代失败
输出结果 结束
牛顿拉夫逊法流程框图计算开始输入非线性方程组信息形成右端项矩阵b设定一个值e和迭代次数n计算雅可比矩阵ak1b中各项小于e
§4-8 计算机辅助分析
讨论非线性电阻电路的牛顿-拉夫逊迭代解法的计算机实 现。
基本思想
输入非线性方程组的信息,包括方程个数及最高阶数,然 后计算其对应的雅可比矩阵,随后迭代求解。
4-3 图解法《网络分析与综合》课件

例4-3 如图(a)所示非线性电阻电路,图(b)是非线性电阻R的特 性曲线。试求非线性电阻R两端的电压u 和通过的电流i。
解 根据KVL 有:u U s Rsi
Q(i,是u) 静态工作点,该点的坐标即为 电阻R两端的电流和电压。
曲线相交法
u
Us Q1 Q2 Q3
u=f(i)
Rs
+
Us
-
u/V Us
§4-3 图解法
图解法是通过在u-i平面上作出元件的特性曲线进行求解的 一种方法,通常只适用于简单非线性电路的分析。
I
+
+
u/V
U=f(I)
U
-U1
+
U2
-
-
。 。
0
U1=f1(I1) U2=f2(I2)
i/A
串联电路,电流值相同,所以,在同一电流值下电压进行 相加即得端口的电压。
并联电路,电压值相同,所以,在同一电压值下电流进行 相加即得端口的电流。
i +
+ u R u=f(i)
-
(a)
u=f(i)
0
i Us/Rs
Q
0
(bU)s/Rs i/A
《图与网络分析》课件

网络的定义与分类
总结词
网络的定义与分类是理解图与网络分析的关键。
详细描述
网络是由节点和边构成的集合,用于描述系统中各个组成部分之间的关系。根据 不同的分类标准,网络可以分为多种类型,如无向网络和有向网络、单层网络和 多层网络等。
图与网络的应用领域
总结词
图与网络的应用领域广泛,包括计算机科学、交通运输、生物信息学等。
从任意一个顶点开始,每次选择一条与已选顶点集合相连的边中权 重最小的边,将其加入最小生成树中。
最短路径算法
Dijkstra算法
01
用于求解图中从一个顶点到其他所有顶点的最短路径。
Bellman-Ford算法
02
用于求解图中所有顶点之间的最短路径。
Floyd-Warshall算法
03
用于求解图中所有顶点之间的最短路径,时间复杂度较低。
网络流算法
01
Ford-Fulkerson算法
用于求解最大网络流问题,通过不断寻找增广路径来增加网络的流量。
02
Dinic算法
基于层次搜索和增广路径的算法,用于求解最大网络流问题。
03
Edmonds-Karp算法
基于广度优先搜索的算法,用于求解最大网络流问题。
03
网络分析与应用
网络中心性分析
节点中心性
社区结构特征
包括社区大小、社区密度、社区连通性等。
社区结构分析的应用
在社交网络中识别用户群体,在组织结构中划分部门和团队等。
网络动态分析
网络动态模型
常见的网络动态模型有随机游走、马尔科夫链和自组 织映射等。
网络动态特征
包括节点的活跃度、网络的演化规律和网络的鲁棒性 等。
网络动态分析的应用
图与网络分析-(共34张PPT)

4、环:某一条孤起点=终点,称为环。 5、基础图:给定一个有向图D=(V,A) ,从D中去掉所有
弧上的箭头,所得到的无向图。记之为G(D)。
第九页,共34页。
6、链:设(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的
一个点弧交错序列,如果这个序列在基础图G(D)中
所对应的点边序列是一条链,则称这个点弧交错序列
v(f) fij–fji= 0
–v(f)
i=s is,t
i=t
且使v(f)达到最大。
第二十三页,共34页。
3、增广链 给定可行流f={fij},使fij=cij的弧称为饱和弧,使
fij<cij的弧称为非饱和弧,把fij=0的弧称为零流弧, fij>0
的弧称为非零流弧。
若是网络中连接发点vs和收点vt的一条链,定义链
22
21
44
(0,Vvs)1
89
62
31
32 63
45
24
47
(44,V1) v4
37 27
(78,V3)
v6
32
v3 (31, V1) 34
第十九页,共34页。
v5 (62,V1)
第三节 最大流问题
如下是一运输网络,弧上的数字表示每条弧上 的容量,问:该网络的最大流量是多少?
4 vs
3
v1
3
1 2
2
v2
v3 3
2
vt
4 v4
第二十页,共34页。
一、基本概念和基本定理
1、网络与流
定义1:给定一个有向图D=(V,A),在V中有一个发点 vs和一收点vt,其余的点为中间点。对于每一条弧 (vi,vj),对应有一个c(vi,vj)0,(cij)称为弧的容量。这 样的有向图称为网络。记为D=(V,A,C)。
弧上的箭头,所得到的无向图。记之为G(D)。
第九页,共34页。
6、链:设(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的
一个点弧交错序列,如果这个序列在基础图G(D)中
所对应的点边序列是一条链,则称这个点弧交错序列
v(f) fij–fji= 0
–v(f)
i=s is,t
i=t
且使v(f)达到最大。
第二十三页,共34页。
3、增广链 给定可行流f={fij},使fij=cij的弧称为饱和弧,使
fij<cij的弧称为非饱和弧,把fij=0的弧称为零流弧, fij>0
的弧称为非零流弧。
若是网络中连接发点vs和收点vt的一条链,定义链
22
21
44
(0,Vvs)1
89
62
31
32 63
45
24
47
(44,V1) v4
37 27
(78,V3)
v6
32
v3 (31, V1) 34
第十九页,共34页。
v5 (62,V1)
第三节 最大流问题
如下是一运输网络,弧上的数字表示每条弧上 的容量,问:该网络的最大流量是多少?
4 vs
3
v1
3
1 2
2
v2
v3 3
2
vt
4 v4
第二十页,共34页。
一、基本概念和基本定理
1、网络与流
定义1:给定一个有向图D=(V,A),在V中有一个发点 vs和一收点vt,其余的点为中间点。对于每一条弧 (vi,vj),对应有一个c(vi,vj)0,(cij)称为弧的容量。这 样的有向图称为网络。记为D=(V,A,C)。
第二节网络分析

截集(割集):将V分为二非空互补集V 与V ,
1
1
使v V ,v V 。称弧集( v ,v )v V ,v V
1
1
1
1
为D的一个截集,记为(V ,V )。
1
1
截量:截集上的容量和,记为 C(V ,V )。
例3.4 对于下图,若V1={vs,v1},请指出相应的截
集与截量。
v2 (4,3) v4
集,A为弧集,C={cij}为容量集, cij 为弧(vi,vj ) 上的容量。现D上要通过一个流f={fij},其中fij 为弧 (vi,vj )上的流量。问应如何安排流量fij可使D上 通过的总流量v最大?
v2
4
例如:
3
vs
1
1
v4 5
3
vt
2019/10/24
5
2
v1
2 v3
2. 数学模型
问题:最大流问题的决策变量、目标函数、约束条件各是什么?
零流弧:f 0
如:在前面例举的网络流问题中,若已给定一个可行流 (如括号中后一个数字所示),请指出相应的弧的类型。
v2 (4,3) v4
(3,3)
(5,3)
vs
(1,1)(1,1)(3,0)
vt
(5,1)(2,1)2019/10/24v1 (2,2) v3
(2)可增值链(增广链)
D中由v
至v
(1,1)(1,1)(3,0)
vt
(5,1)
(2,1)
v1 (2,2) v3
最大流最小割定理:
Maxv (f) MinC (V ,V )
2019/10/24
(5) 最大流的判别条件 可行流f是最大流的充要条件是D中不存在 关于f的可增值链。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i +
Rs
+ u R
+ u=f(i) -
Us
-
(a)
u/V Us Q 0 u=f(i)
(b)
Us/Rs i/A
例4-3 如图(a)所示非线性电阻电路,图(b)是非线性电阻R的特 性曲线。试求非线性电阻R两端的电压u 和通过的电流i。
解 根据KVL 有:u U s Rs i Q(i, u ) 是静态工作点,该点的坐标即 为电阻R两端的电流和电压。
曲线相交法
u Us Q1 Q2 0 Q3 Us/Rs i u=f(i)
§4-3 图解法
图解法是通过在 u-i 平面上作出元件的特性曲线进行求解 的一种方法,通常只适用于简单非线性电路的分析。
I
+ + + -
u/V
。 。
U=f(I) U1=f1(I1) U2=f2(I2) i/A
U1
U
-
U2
ቤተ መጻሕፍቲ ባይዱ
0
串联电路,电流值相同,所以,在同一电流值下电压进行 相加即得端口的电压。 并联电路,电压值相同,所以,在同一电压值下电流进行 相加即得端口的电流。
