定弦定角最值问题 (1)

合集下载

线段最值系列之（一）——定弦定角，定最值

线段最值系列之（一）——定弦定角，定最值一条线段的两个端点和该线段外一动点构成的角（动点是角的顶点），不随点的运动而变化，即该动角的度数恒定不变，称为“定弦定角”问题。

该线段称“定弦”，该运动的定值角称“定角”。

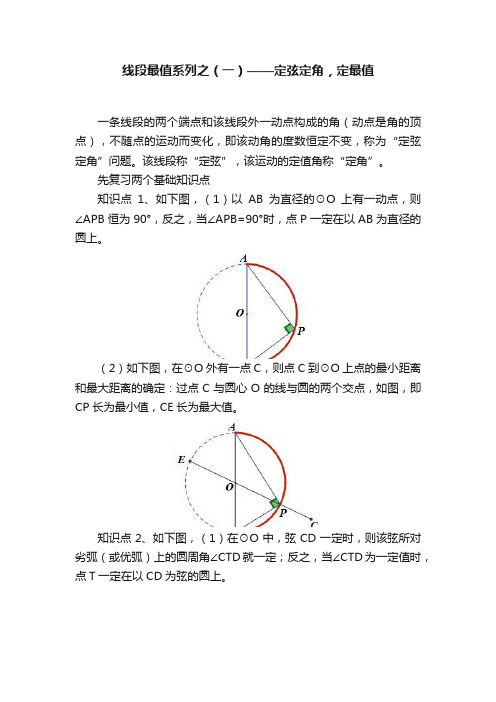
先复习两个基础知识点知识点1、如下图，（1）以AB为直径的⊙O上有一动点，则∠APB恒为90°，反之，当∠APB=90°时，点P一定在以AB为直径的圆上。

（2）如下图，在⊙O外有一点C，则点C到⊙O上点的最小距离和最大距离的确定：过点C与圆心O的线与圆的两个交点，如图，即CP长为最小值，CE长为最大值。

知识点2、如下图，（1）在⊙O中，弦CD一定时，则该弦所对劣弧（或优弧）上的圆周角∠CTD就一定；反之，当∠CTD为一定值时，点T一定在以CD为弦的圆上。

（2）如下图，在⊙O外有一点A，射线AO与圆的交点分别为点T和点E，则点A到圆的最小距离是AT的长，最大距离是AE的长。

下面，以两道典型例题来说明定弦定角在解一类线段最值题目中的应用。

例1：如图，在Rt△ABC ,∠ABC=90° ，AB=4, BC=6 ,P是△ABC 内部的一个动点，且满足∠PAB=∠PBC , 则线段CP的长度的最小值是 .(您的点赞，就是给予作者一份信心，别忘了，给作者一个鼓励，点个赞哦！)下面还有，继续……变式练习：如图，在Rt△ABC ,∠ABC=90° ，AB=4,BC=6, P是△ABC所在平面上的一个动点，且满足∠APB=90° , 则线段CP长度的取值范围是 .例2：如图，已知点E , F为等边△ABC边AB 、AC上的两动点，且AF=BE ,:连接CE , BF交于点T, 若等边△ABC的边长为6 ，则AT的长度的最小值是 .。

最值问题(定弦定角定线段)

最值问题专题训练一、定弦定角最值问题【例1】如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）A．1 B．2 C．2D．241-4【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）16A．213+C．5 D．13-B．29【练习1】如图，在△ABC中，AC＝3，BC＝24，∠ACB＝45°，AM∥BC，点P在射线AM 上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1 B．2 C．2D．34-2【例3】如图，⊙O的半径为2，弦AB的长为32，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的面积的最大值是（）A．3612+B．346+12+D．336+C．33【练习2】如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21B ．22C ．23D ．43【例4】如图，边长为3的等边△ABC ，D 、E 分别为边BC 、AC 上的点，且BD ＝CE ，AD 、BE 交于P 点，则CP 的最小值为_________【例5】如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________【练习3】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________4．如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22 AB DE ，则点C 到AB 的距离的最大值是_________OABCDP5．如图，已知以BC为直径的⊙O，A为»BC中点，P为»AC上任意一点，AD⊥AP交BP于D，连CD．若BC＝8，则CD的最小值为___________二、定角、定线段与定圆问题主要是体现在题目中出现了固定度数的角对着固定长度的线段时隐含着一个固定大小的圆，此时定线段为隐圆的一条弦，定角为弦所对的一个圆周角，借助隐圆来分析问题极其方便，关键是要先发现隐含着的特殊度数的角。

定弦定角最值问题

定弦定角最值问题【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题，一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等，定弦的同侧两个圆周角相等，则四点共圆，因此动点的轨迹是圆。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

②寻找不变的张角（这个时候一般是找出张角的补角，这个补角一般为45°、60°或者一个确定的三角函数的对角等）③找张角所对的定弦，根据三点确定隐形圆。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】（2016 ·新观察四调模拟1）如图，△ABC中，AC＝3，BC＝4 2 ，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD 的最小值为（）A．1 B．2 C．2 D．41 4 2解：∵∠CDP＝∠ACB＝45°∴∠BDC＝135°（定弦定角最值）如图，当AD过O′时，AD有最小值∵∠BDC＝135°∴∠BO′ C＝90°∴△BO′C为等腰直角三角形∴∠ACO′＝45 °＋45°＝90°∴AO′＝5又O′ B＝O′C＝4 ∴AD＝5－4＝1【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD 交圆于E 点，连CE，则CE的最小值为（）A．13 2 B．13 2 C．5 D．169解：连接AE∵AD为⊙O的直径∴∠AEB＝∠AED＝90°∴E点在以AB为直径的圆上运动当CE过圆心O′时，CE有最小值为13 2【练】（2015 ·江汉中考模拟1）如图，在△ABC中，AC＝3，BC＝4 2 ，∠ACB＝45°，AM∥BC，点P 在射线AM上运动，连BP 交△APC的外接圆于D，则AD的最小值为（）A．1 B．2C．2 D．4 2 3解：连接CD∴∠PAC＝∠PDC＝∠ACB＝45°∴∠BDC＝135°如图，当AD过圆心O′时，AD有最小值∵∠BDC＝135°∴∠BO′ C＝90°∴O′ B＝O′ C＝4又∠ACO′＝90 °∴ AO ′＝ 5∴AD 的最小值为 5－ 4＝ 1【例 3】（2016 ·勤学早四调模拟 1）如图，⊙ O 的半径为 2，弦 AB 的长为 2 3 ，点 P 为优弧 AB 上一动点， AC ⊥ AP 交直线 PB 于点 C ，则△ ABC 的面积的最大值是（） A ．12 6 3 B ． 6 3 3 C ．12 3 3 D ． 6 4 3【练】（2014 ·洪山区中考模拟 1）如图，⊙ O 的半径为 1，弦 AB ＝1，点 P 为优弧 AB 上一动点， AC ⊥ AP 交直线 PB 于点 C ，则△ ABC 的最大面积是（）A ．【例 5】如图，A （1，0）、B （3，0），以 AB 为直径作⊙ M ，射线 OF 交⊙ M 于E 、 F 两点， C 为弧 AB 的中点， D 为 EF 的中点．当射线绕 O 点旋转时， CD 的最小值为 ______ 解：连接 DM∵ D 是弦 EF 的中点∴DM ⊥EF∴点 D 在以 A 为圆心的， OM 为直径的圆上运动当 CD 过圆心 A 时， CD 有最小值连接 CM∵ C 为弧 AB 的中点∴ CM ⊥ AB∴ CD 的最小值为 2 1练】如图， AB 是⊙ O 的直径， AB ＝2，∠ABC ＝60°， P 是上一动点， D 是 AP 的中点，连接 CD ，则 CD 的最小值为 _________ 解：连接 OD∵ D 为弦 AP 的中点∴OD ⊥AP∴点 D 在以 AO 为直径的圆上运动当 CD 过圆心 O ′时， CD 有最小值过点 C 作 CM ⊥ AB 于 M ∵OB ＝OC ，∠ ABC ＝60°∴△ OBC 为等边三角形∴ OM ＝ 1 ， CM ＝ 322∴ O ′ C ＝ 74∴ CD 的最小值为 7 142 B ． C ．D ． 2。

九年级讲义：定弦定角最值问题秘籍

九年级讲义：定弦定角最值问题令狐采学【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】如图，△ABC中，AC＝3，BC＝，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）A．1B．2C．D．【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）A．B．C．5D．【练】如图，在△ABC中，AC＝3，BC＝，∠ACB＝45°，AM∥BC，点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1B．2C．D．【例3】如图，⊙O的半径为2，弦AB的长为，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的面积的最大值是（）A．B．C．D．【练】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）A．B．C．D．【例4】如图，边长为3的等边△ABC，D、E分别为边BC、AC上的点，且BD＝CE，AD、BE交于P点，则CP的最小值为_________例题4 例题5 图8【例5】如图，A(1，0)、B(3，0)，以AB为直径作⊙M，射线OF交⊙M于E、F两点，C为弧AB的中点，D为EF的中点．当射线绕O点旋转时，CD的最小值为__________【练】如图8，AB是⊙O的直径，AB＝2，∠ABC＝60°，P是上一动点，D是AP的中点，连接CD，则CD的最小值为__________针对练习：1．如图，在动点C与定长线段AB组成的△ABC中，AB＝6，AD⊥BC于点D，BE⊥AC于点E，连接DE．当点C在运动过程中，始终有，则点C到AB的距离的最大值是_________2．如图，已知以BC为直径的⊙O，A为弧BC中点，P为弧AC上任意一点，AD⊥AP交BP于D，连CD．若BC＝8，则CD的最小值为___________。

定弦定角最值问题含答案

定弦定角最值问题【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】(2016·新观察四调模拟1)如图，△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，D 为△ABC 内一动点，⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（）A ．1B ．2C ．2D ．2441-解：∵∠CDP ＝∠ACB ＝45°∴∠BDC ＝135°（定弦定角最值）如图，当AD 过O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴△BO ′C 为等腰直角三角形∴∠ACO ′＝45°＋45°＝90°∴AO ′＝5又O ′B ＝O ′C ＝4∴AD ＝5－4＝1【例2】如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（）A ．213-B ．213+C ．5D ．916解：连接AE∵AD 为⊙O 的直径∴∠AEB ＝∠AED ＝90°∴E 点在以AB 为直径的圆上运动当CE 过圆心O ′时，CE 有最小值为213-【练】(2015·江汉中考模拟1)如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-解：连接CD∴∠P AC ＝∠PDC ＝∠ACB ＝45°∴∠BDC ＝135°如图，当AD 过圆心O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴O ′B ＝O ′C ＝4又∠ACO ′＝90°∴AO ′＝5∴AD 的最小值为5－4＝1【例3】(2016·勤学早四调模拟1)如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+【练】(2014·洪山区中考模拟1)如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21B ．22C ．23 D ．43 【例5】如图，A (1，0)、B (3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________解：连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的，OM 为直径的圆上运动当CD 过圆心A 时，CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________解：连接OD∵D 为弦AP 的中点∴OD ⊥AP∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时，CD 有最小值过点C 作CM ⊥AB 于M∵OB ＝OC ，∠ABC ＝60°∴△OBC 为等边三角形∴OM ＝21，CM ＝23 ∴O ′C ＝47∴CD 的最小值为2147。

(完整版)定弦定角最值问题(含答案)

定弦定角最值问题【定弦定角题型的鉴别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

【题目种类】图形中一般求一个从动点到一个定点线段长度最值问题，一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等，定弦的同侧两个圆周角相等，则四点共圆，因此动点的轨迹是圆。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

②搜寻不变的张角（这个时候一般是找出张角的补角，这个补角一般为 45°、 60°也许一个确定的三角函数的对角等）③找张角所对的定弦，依照三点确定隐形圆。

④确定圆心地址，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，依照点到圆的距离求最值（最大值或最小值）。

【例 1】(2016 ·新观察四调模拟1) 如图，△ ABC 中， AC＝ 3，BC＝ 42 ，∠ ACB ＝ 45°，D 为△ABC 内一动点，⊙ O 为△ ACD 的外接圆，直线BD 交⊙ O 于 P 点，交BC 于 E 点，弧 AE＝ CP，则 AD 的最小值为（）A ． 1B． 2C．2D．41 4 2解：∵∠ CDP ＝∠ ACB ＝ 45°∴∠ BDC ＝135 °（定弦定角最值）如图，当AD 过 O′时， AD 有最小值∵∠ BDC ＝135 °∴∠ BO′C＝ 90 °∴ △ BO′C 为等腰直角三角形∴∠ ACO ′＝ 45 °＋ 45 °＝ 90 °∴AO′＝ 5又O′B＝O′C＝ 4∴AD ＝5－ 4＝1【例 2】如图， AC＝ 3， BC ＝ 5，且∠ BAC ＝90°，D 为 AC 上一动点，以AD 为直径作圆，连接BD 交圆于 E 点，连 CE，则 CE 的最小值为（）A ． 13 2B． 13 2C． 516 D．9解：连接 AE∵AD 为⊙ O 的直径∴∠AEB＝∠ AED ＝ 90 °∴ E 点在以 AB 为直径的圆上运动当 CE 过圆心O′时， CE 有最小值为13 2【练】(2015 ·江汉中考模拟1) 如图，在△ ABC 中， AC ＝ 3，BC ＝ 4 2 ，∠ ACB ＝ 45°，AM ∥ BC，点 P 在射线 AM 上运动，连BP 交△ APC 的外接圆于D，则 AD 的最小值为（）A ． 1B． 2C．2 D ． 4 2 3解：连接 CD∴∠ PAC ＝∠ PDC ＝∠ ACB＝ 45 °∴∠ BDC ＝135 °如图，当AD 过圆心 O′时， AD 有最小值∵∠ BDC ＝135°∴∠ BO′C＝ 90°∴O′B＝ O′C＝ 4又∠ ACO ′＝ 90°∴AO′＝ 5∴AD 的最小值为 5－4＝ 1【例3】 (2016 ·勤学早四调模拟1) 如图，⊙ O的半径为2，弦AB的长为 2 3 ，点 P 为优弧AB 上一动点， AC ⊥ AP交直线 PB 于点C，则△ ABC的面积的最大值是（）A ． 12 6 3B． 6 33C． 12 33D． 6 4 3【练】 (2014·洪山区中考模拟1)如图，⊙ O 的半径为1，弦 AB＝ 1，点 P 为优弧 AB 上一动点，AC ⊥ AP 交直线 PB 于点 C，则△ ABC 的最大面积是（）A ．1B．2 22C．3D ．3 24【例 5】如图， A(1 ， 0) 、 B(3， 0) ，以 AB 为直径作⊙ M，射线 OF 交⊙ M 于 E 、 F 两点， C 为弧AB 的中点， D 为 EF 的中点．当射线绕 O 点旋转时， CD 的最小值为 __________解：连接 DM∵D 是弦 EF 的中点∴DM ⊥ EF∴点 D 在以 A 为圆心的，OM 为直径的圆上运动当CD 过圆心 A 时， CD 有最小值连接 CM∵C 为弧 AB 的中点∴ CM⊥ AB∴ CD 的最小值为 2 1【练】如图， AB 是⊙ O 的直径， AB＝ 2，∠ ABC＝ 60°， P 是上一动点， D 是 AP 的中点，连接CD ，则 CD 的最小值为 __________解：连接 OD∵ D 为弦 AP 的中点∴OD⊥ AP∴点 D 在以 AO 为直径的圆上运动当CD 过圆心 O′时， CD 有最小值过点 C 作 CM ⊥ AB 于 M∵OB＝OC ，∠ ABC ＝ 60°∴△ OBC 为等边三角形∴OM ＝1， CM ＝3 22∴O′C＝747 1∴ CD 的最小值为42。

完整版定弦定角最值问题教师版

定弦定角最值问题（答案版）△45°＝【例1】(2016·新观察四调模拟1)如图，△ABC中，AC3，BC为＝＝，∠，ACBD24，CP于E点，弧AE＝△ACD的外接圆，直线BD交⊙O于P点，交BCABC内一动点，⊙O为的最小值为（）则AD．B．2CD．A．12241?4＝45°：∵∠CDP＝∠ACB解135°（定弦定角最值）∴∠BDC＝AD有最小值过O′时，如图，当AD 135°∵∠BDC＝＝BO90°′C∴∠BO′C∴△为等腰直角三角形∴∠ACO′＝45°＋45°＝90°∴AO′＝5又O′B＝O′C＝4∴AD＝5－4＝1【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）162?21313?．D．B．5A．C 9解：连接AE∵AD为⊙O的直径∴∠AEB＝∠AED＝90°∴E点在以AB为直径的圆上运动13?2 CE有最小值为CE过圆心O′时，当42，∠ACB＝45°，3，BC＝AM∥BC，AC如图，在(2015【练】·江汉中考模拟1)△ABC中，＝点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1B．2242?3 ．D ．CCD解：连接＝∠ACB＝45°∴∠PAC＝∠PDC135°BDC＝∴∠AD有最小值如图，当AD过圆心O′时，135°∵∠BDC＝90°∴∠BO′C＝4 B′＝O′C＝∴O又∠＝90°ACO′5′＝∴AO1＝5－4∴AD的最小值为32AB例【3】(2016·勤学早四调模拟1)如图，的长为P，点的半径为2，弦AB为优弧⊙O ABC的面积的最大值是（）C上一动点，AC⊥AP交直线PB于点，则△3633?12312?66?334?．．AC．B ． D·洪山区中考模拟1)如图，⊙O的半径为1，弦AB＝1，点P为优弧【练】(2014AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）12．A． B 2233．．C D 24为弧于E、F两点，CAB(3，0)，以为直径作⊙M，射线OF交⊙M，【例5】如图，A(10)、B__________的中点．当射线绕O点旋转时，CD的最小值为AB的中点，D为EF解：连接DM的中点D是弦EF∵EF∴DM⊥为直径的圆上运动为圆心的，OM∴点D在以A有最小值时，CD当CD过圆心A连接CM AB 的中点∵C为弧⊥AB∴CM CD的最小值为∴12?的中点，连接AP是60°，P是上一动点，D，∠AB【练】如图，是⊙O的直径，AB＝2ABC＝__________ 的最小值为CD，则CDOD解：连接D为弦AP的中点∵OD⊥AP∴在以AO为直径的圆上运动∴点D CD有最小值′当CD过圆心O时，过点C作CM⊥AB于M∵OB＝OC，∠ABC＝60°∴△OBC为等边三角形13，CM＝∴OM＝22．7＝C∴O′417的最小值为CD∴?24练习：如图，在动点C与定长线段AB组成的△ABC中，AB＝6，AD⊥BC于点D，BE⊥AC于点E，DE2 _________AB 的距离的最大值是到CDE连接．当点在运动过程中，始终有，则点C?AB2。

轨迹问题之定角对定边定弦定角最值问题(含答案) (PDF版)

定弦定角最值问题----20190828【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】(2019·模拟)如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E 点，弧AE＝CP，则AD的最小值为（）A．1 B．2 C．2D．241-4解：∵∠CDP＝∠ACB＝45°∴∠BDC＝135°（定弦定角最值）如图，当AD过O′时，AD有最小值∵∠BDC＝135°∴∠BO′C＝90°∴△BO′C为等腰直角三角形∴∠ACO′＝45°＋45°＝90°∴AO′＝5又O′B＝O′C＝4∴AD＝5－4＝1【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为16（）A．213-B．213+C．5 D．9解：连接AE∵AD为⊙O的直径∴∠AEB＝∠AED＝90°∴E点在以AB为直径的圆上运动当CE过圆心O′时，CE有最小值为213-【练】(2015·江汉中考模拟1)如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-解：连接CD∴∠P AC ＝∠PDC ＝∠ACB ＝45°∴∠BDC ＝135°如图，当AD 过圆心O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴O ′B ＝O ′C ＝4又∠ACO ′＝90°∴AO ′＝5∴AD 的最小值为5－4＝1【例3】(2016·勤学早四调模拟1)如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+2019【练】(·洪山区中考模拟 1)如图，⊙O 的半径为 1，弦 AB ＝1，点 P 为优弧 AB 上一动点， AC ⊥AP 交直线 PB 于点 C ，则△ABC 的最大面积是（）A ．21B ．22C ．23D ．43【例5】如图，A (1，0)、B (3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________解：连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的，OM 为直径的圆上运动当CD 过圆心A 时，CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12-【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________解：连接OD ∵D 为弦AP 的中点∴OD ⊥AP ∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时，CD 有最小值过点C 作CM ⊥AB 于M∵OB ＝OC ，∠ABC ＝60° ∴△OBC 为等边三角形∴OM ＝21，CM ＝23∴O ′C ＝47∴CD 的最小值为2147-定弦定角1.（安徽）如图，Rt △ABC 中，AB ⊥BC ，AB=6，BC=4，P 是△ABC 内部的一个动点，且满足∠PAB=∠PBC ，则线段CP 长的最小值为（）A ．23B ．2C ．13138D ．131312故选B.3.（宜兴模拟）如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P从点P向半径OA引垂线PH交OA于点H，设△OPH的内心为I，当点P在弧AB上从点A 运动到点B时，内心I所经过的路径长为．4.等腰直角△ABC 中，∠C ＝90°，AC ＝BC ＝4，D 为线段AC 上一动点，连接BD ，过点C 作CH ⊥BD 于H ，连接AH ，则AH 的最小值为．答案：2-52（点H 在以BC 为直径的圆上）5.直线y ＝x ＋4分别与x 轴、y 轴相交与点M 、N ，边长为2的正方形OABC 一个顶点O 在坐标系的原点，直线AN 与MC 相交与点P ，若正方形绕着点O 旋转一周，则点P 到点（0，2）长度的最小值是．A.1B.2C.332 D.3答案：D （点C 在以AB 为弦的圆上）8.（外国语模拟）如图，以正方形ABCD 的边BC 为一边向内部做一等腰△BCE ，BE=BC ，过E 做EH ⊥BC ，点P 是Rt △BEH 的内心，连接AP ，若AB=2，则AP 的最小值为________.答案：22π（点P 在以BC 为弦的圆上）9.（江阴期中）如图，以G （0，1）为圆心，半径为2的圆与x 轴交于A 、B 两点，与y 轴交于C 、D 两点，点E 为⊙G 上一动点，CF ⊥AE 于F ，当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为________．答案：π33（点F 在以AC 为直径的圆上）10.（南长区二模）如图，矩形OABC 的边OA 、OC分别在x 轴、y 轴上，点B 的坐标为(7，3)，点E 在边AB 上，且AE=1，已知点P 为y 轴上一动点，连接EP ，过点O 作直线EP 的垂线段，垂足为点H ，在点P 从点F(0，254)运动到原点O 的过程中，点H 的运动路径长为________．答案：π425（点H 在以OE 为直径的圆上）。

九年级讲义：定弦定角最值问题秘籍

九年级道义：定弦定角最值问题之阳早格格创做【定弦定角题型的辨别】有一个定弦，一个主动面，一个从动面，定弦所对于的弛角牢固没有变.【题目典型】图形中普遍供一个从动面到一个定面线段少度最值问题，普遍波及定弦定角最值问题【解题本理】共弧所对于的圆周角相等，定弦的共侧二个圆周角相等，则四面共圆，果此动面的轨迹是圆.（线段共侧的二面对于线段的弛角相等，则那二面以及线段的二个端面共圆.）【普遍解题步调】①让主动面动一下，瞅察从动面的疏通轨迹，创造从动面的疏通轨迹是一段弧.②觅找没有变的弛角（那个时间普遍是找出弛角的补角，那个补角普遍为45°、60°大概者一个决定的三角函数的对于角等）③找弛角所对于的定弦，根据三面决定隐形圆.④决定圆心位子，估计隐形圆半径.⑤供出隐形圆圆心至所供线段定面的距离.⑥估计最值：正在此前提上，根据面到圆的距离供最值（最大值大概最小值）.【例1】如图，△ABC中，AC＝3，BC＝，∠ACB＝45°，D为△ABC内一动面，⊙O为△ACD的中接圆，曲线BD接⊙O于P面，接BC于E面，弧AE＝CP，则AD的最小值为（）A．1B．2C．D．【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC 上一动面，以AD为曲径做圆，对接BD接圆于E面，连CE，则CE的最小值为（）A．B．C．5D．【练】如图，正在△ABC中，AC＝3，BC＝，∠ACB＝45°，AM∥BC，面P正在射线AM上疏通，连BP接△APC的中接圆于D，则AD的最小值为（）A．1B．2C．D．【例3】如图，⊙O的半径为2，弦AB的少为，面P为劣弧AB上一动面，AC⊥AP接曲线PB于面C，则△ABC 的里积的最大值是（）A．B．C．D．【练】如图，⊙O的半径为1，弦AB＝1，面P为劣弧AB 上一动面，AC⊥AP接曲线PB于面C，则△ABC的最大里积是（）A．B．C．D．【例4】如图，边少为3的等边△ABC，D、E分别为边BC、AC上的面，且BD＝CE，AD、BE接于P面，则CP 的最小值为_________例题4 例题5 图8 【例5】如图，A(1，0)、B(3，0)，以AB为曲径做⊙M，射线OF接⊙M于E、F二面，C为弧AB的中面，D为EF 的中面．当射线绕O面转动时，CD的最小值为__________【练】如图8，AB是⊙O的曲径，AB＝2，∠ABC＝60°，P是上一动面，D是AP的中面，对接CD，则CD的最小值为__________针对于训练：1．如图，正在动面C取定少线段AB组成的△ABC中，AB＝6，AD⊥BC于面D，BE⊥AC于面E，对接DE．当面C正在疏通历程中，末究有，则面C到AB的距离的最大值是_________2．如图，已知以BC为曲径的⊙O，A为弧BC中面，P为弧AC上任性一面，AD⊥AP接BP于D，连CD．若BC＝8，则CD的最小值为___________。

九年级讲义：定弦定角最值问题

九年级讲义：定弦定角最值问题【例1】如图，△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，D 为△ABC 内一动点，⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（）A ．1B ．2C ．2D ．2441-【例2】如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（）A ．213-B ．213+C ．5D ．916 【练】如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-【例3】如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+【练】如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21 B ．22 C ．23 D ．43 【例4】如图，边长为3的等边△ABC ，D 、E 分别为边BC 、AC 上的点，且BD ＝CE ，AD 、BE 交于P 点，则CP 的最小值为_________【例5】如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________针对练习：1．如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22 AB DE ，则点C 到AB 的距离的最大值是_________O ABC DP2．如图，已知以BC 为直径的⊙O ，A 为 BC 中点，P 为 AC 上任意一点，AD ⊥AP 交BP 于D ，连CD ．若BC ＝8，则CD 的最小值为___________3.直线y=x+4分别与x轴、y轴相交于点M、N，边长为2的正方形OABC一个顶点O在坐标系的顶点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点（0，2）长度的最小值是_______4、已知∠MON=300，矩形ABCD的顶点A、D分别是OM、ON上的动点，且AD=2，AB=3，则线段OB长度的最大值为___________变式：已知∠MON=450，矩形ABDC的顶点A、C分别是OM、ON上的动点，且AC=2，AB=1，则线段OB长度的最大值为___________。

初中数学：定弦定角最值问题

九年级讲义：定弦定角最值问题【例1】如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD 的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）【练】如图，在△ABC中，AC＝3，BC＝24，∠ACB＝45°，AM∥BC，点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）【例3】如图，⊙O的半径为2，弦AB的长为32，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的面积的最大值是（）【练】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）【例4】如图，边长为3的等边△ABC ，D 、E 分别为边BC 、AC 上的点，且BD ＝CE ，AD 、BE 交于P 点，则CP 的最小值为_________【例5】如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________针对练习：1．如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22 AB DE ，则点C 到AB 的距离的最大值是_________ABCDP2．如图，已知以BC为直径的⊙O，A为»BC中点，P为»AC上任意一点，AD⊥AP交BP于D，连CD．若BC＝8，则CD的最小值为___________定角、定线段与定圆问题主要是体现在题目中出现了固定度数的角对着固定长度的线段时隐含着一个固定大小的圆，此时定线段为隐圆的一条弦，定角为弦所对的一个圆周角，借助隐圆来分析问题极其方便，关键是要先发现隐含着的特殊度数的角。

九年级讲义：定弦定角最值问题

九年级讲义：定弦定角最值问题【例1】如图，△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，D 为△ABC 内一动点，⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（）A ．1B ．2C ．2D ．2441-【例2】如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（）A ．213-B ．213+C ．5D ．916 【练】如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-【例3】如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+【练】如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21 B ．22 C ．23 D ．43 【例4】如图，边长为3的等边△ABC ，D 、E 分别为边BC 、AC 上的点，且BD ＝CE ，AD 、BE 交于P 点，则CP 的最小值为_________【例5】如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________针对练习：1．如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22 AB DE ，则点C 到AB 的距离的最大值是_________O ABC DP2．如图，已知以BC 为直径的⊙O ，A 为BC 中点，P 为AC 上任意一点，AD ⊥AP 交BP 于D ，连CD ．若BC ＝8，则CD 的最小值为___________。

九年级讲义：定弦定角最值问题秘籍之欧阳家百创编

九年级讲义：定弦定角最值问题欧阳家百（2021.03.07）【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】如图，△ABC中，AC＝3，BC＝，∠ACB＝45°，D 为△ABC内一动点，⊙O为△ACD的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）A．1B．2C．D．【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）A．B．C．5D．【练】如图，在△ABC中，AC＝3，BC＝，∠ACB＝45°，AM∥BC，点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1B．2C．D．【例3】如图，⊙O的半径为2，弦AB的长为，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的面积的最大值是（）A．B．C．D．【练】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）A．B．C．D．【例4】如图，边长为3的等边△ABC，D、E分别为边BC、AC 上的点，且BD＝CE，AD、BE交于P点，则CP的最小值为_________例题4 例题5 图8【例5】如图，A(1，0)、B(3，0)，以AB为直径作⊙M，射线OF 交⊙M于E、F两点，C为弧AB的中点，D为EF的中点．当射线绕O点旋转时，CD的最小值为__________【练】如图8，AB是⊙O的直径，AB＝2，∠ABC＝60°，P是上一动点，D是AP的中点，连接CD，则CD的最小值为__________针对练习：1．如图，在动点C与定长线段AB组成的△ABC中，AB＝6，AD⊥BC于点D，BE⊥AC于点E，连接DE．当点C在运动过程中，始终有，则点C到AB的距离的最大值是_________ 2．如图，已知以BC为直径的⊙O，A为弧BC中点，P为弧AC 上任意一点，AD⊥AP交BP于D，连CD．若BC＝8，则CD的最小值为___________。

初中数学：定弦定角最值问题

九年级讲义：定弦定角最值问题【例1】如图，△ABC中，AC＝3，BC＝24，∠ACB＝45°，D为△ABC内一动点，⊙O为△ACD 的外接圆，直线BD交⊙O于P点，交BC于E点，弧AE＝CP，则AD的最小值为（）【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）【练】如图，在△ABC中，AC＝3，BC＝24，∠ACB＝45°，AM∥BC，点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）【例3】如图，⊙O的半径为2，弦AB的长为32，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的面积的最大值是（）【练】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）【例4】如图，边长为3的等边△ABC ，D 、E 分别为边BC 、AC 上的点，且BD ＝CE ，AD 、BE 交于P 点，则CP 的最小值为_________【例5】如图，A(1，0)、B(3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________针对练习：1．如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22 AB DE ，则点C 到AB 的距离的最大值是_________ABC DP2．如图，已知以BC为直径的⊙O，A为»BC中点，P为»AC上任意一点，AD⊥AP交BP于D，连CD．若BC＝8，则CD的最小值为___________定角、定线段与定圆问题主要是体现在题目中出现了固定度数的角对着固定长度的线段时隐含着一个固定大小的圆，此时定线段为隐圆的一条弦，定角为弦所对的一个圆周角，借助隐圆来分析问题极其方便，关键是要先发现隐含着的特殊度数的角。

定弦定角(1)

定弦定角(1)定弦定角整理解题技巧：构造隐圆圆形中，当需要求一个定点到一动点线段长度的最小值时，一般会涉及到定弦定角问题。

解决这类问题的步骤如下：1.让动点移动，观察另一个动点的运动轨迹，发现另一个动点的运动轨迹为一段弧。

2.找到不变的张角，通常是找出张角的补角，这个补角一般为60度或45度。

3.找到张角所对的定弦，根据三点确定隐形圆，确定圆心位置。

4.计算隐形圆的半径。

5.圆心与所求线段上定点的距离可以求出。

6.最小值等于圆心到定点之间的距离减去半径。

例题讲解：例1、（2016深圳二模）如图，在等腰直角三角形ABC 中，AB=AC=BC=42，D是AC边上一动点，连接BD，以AD 为直径的圆交BD于点E，则线段CE长度的最小值为多少？例2、（2014洪山区一模）如图，⊙O的半径为1，弦AB=1，点P为优弧AB上的一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积为多少？例3、（2013呼和浩特）在平面直角坐标系中，已知点A （4，0）、B（-6，0），点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为多少？例4、（2016黄冈二模）如图，△ABC，△EFG均是边长为2的等边三角形，D是边BC、EF的中点，直线AG、FC相交于点M．当△EFG绕点D旋转时，线段BM长的最大值为多少？巩固练：1.在直角三角形ABC中，∠C=90°，AC=10，BC=12，点D为线段BC上的一动点．以CD为直径，作AD交⊙O于点E，连BE，则BE的最小值为多少？2.直线y=x+4分别与x轴、y轴相交于点M，N，边长为2的正方形OABC一个顶点O在坐标系的原点，直线AN与MC相交于点P，若正方形绕着点O旋转一周，则点P到点(0,2)长度的最小值是多少？3.如图，半径为2cm，圆心角为90°的扇形OAB的AB上有一运动的点P．从点P向半径OA引垂线PH交OA于点H．设△OPH的内心为I，当点P在AB上从点A运动到点B 时，内心I所经过的路径长为多少？4.如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是多少？5.如图，以G(0,1)为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E为⊙G上的一动点，CF⊥AE于F．若点E从在圆周上运动一周，则点F所经过的路径长为多少？6、在以扇形OAB的顶点O为原点，半径OB所在的直线为x轴的平面直角坐标系中，点B的坐标为（2，0），若抛物线y=k的取值范围是使得2x+k与扇形OAB的边界总有两个公共点的实数范围。

定弦定角最值问题 (1)

线段最值系列之（一）——定弦定角，定最值

最值问题(定弦定角定线段)

定弦定角最值问题

九年级讲义：定弦定角最值问题秘籍

定弦定角最值问题含答案

(完整版)定弦定角最值问题(含答案)

完整版定弦定角最值问题教师版

轨迹问题之定角对定边 定弦定角最值问题(含答案) (PDF版)

九年级讲义：定弦定角最值问题秘籍

九年级讲义：定弦定角最值问题

初中数学：定弦定角最值问题

九年级讲义：定弦定角最值问题

最新九年级讲义定弦定角最值问题秘籍

九年级讲义：定弦定角最值问题秘籍之欧阳家百创编

初中数学：定弦定角最值问题

定弦定角(1)

轨迹问题之定角对定边定弦定角最值问题(含答案) (PDF版)