四年级加法交换和结合律、乘法交换律、结合律、分配律练习
运算律,交换律,分配率,结合律专项练习试题附答案_四年级上册北师大,人教版等版本通用

运算律练习试题附答案_四年级上册北师大,人教版等版本通用1一、选择题1.用简便方法计算25×44,不恰当的方法是(()A.25×44=25×(40+4)B.25×44=25×4×11C.25×44=25×40×42.与25×6结果相等的式子是()A.25×2×4 B.24×6+6 C.25×5+13.与125×2×4得数相等的算式是()A.125×8 B.125×6 C.125×4 D.125×24.求54减35与5的商,差是多少?列式是()A.54﹣(35÷5)B.54﹣35÷5 C.(54﹣35)÷55.乐乐和他的3个好朋友每人折了9只纸鹤,送给幼儿园的小朋友19只,还剩多少只?列式正确的是()。
A.3×9-19 B.4×9-19 C.4×9+196.篮球有6个,排球的个数是篮球的4倍,排球比篮球多()个.A.18 B.24 C.307.2337÷3×5=()A.3895 B.4775 C.3032 D.33258.与45×6×11的积相等的算式是()。
A.45×6+11 B.11×(6×45) C.(45+6)×119.347-98用简便方法计算是()。
A.347-100-2 B.347-(100+2)C.347-100+210.下面运用了乘法分配律的是()。
A.125×61×8=125×8×61 B.78×(23+7)=78×30C.15×(8+6)=15×8+15×6二、填空题11.275+332+725=332+(275+725),这是运用了加法_____律和加法_____律.12.32-8÷4=________ (32-8)÷4=________13.根据16×62=992,直接写出下面算式得数。
小学数学四年级四则混合运算及运算法则知识点整理附练习题

小学数学四年级四则混合运算及运算法则知识点整理附练习题文章目录四则运算(一)加法运算定律:1、两个加数交换位置,和不变,这叫做加法交换律。
字母公式:a+b=b+a2、先把前两个数相加,或者先把后两个数相加,和不变,这叫做加法结合律。
字母公式:(a+b) +c=a+(b+c)(二)乘法运算定律:1、交换两个因数的位置,积不变,这叫做乘法交换律。
字母公式:a×b=b×a2、先乘前两个数,或者先乘后两个数,积不变,这叫做乘法结合律。
字母公式:(a×b)×c=a×(b×c)3、两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
用字母公式:(a+b)×c=a×c+b×c或a×(b+c) =a×b+a×c拓展:(a-b)×c=a×c-b×c或a×(b-c) =a×b-a×c(三)减法简便运算:1、一个数连续减去两个数,可以用这个数减去这两个数的和。
用字母表示:a-b-c=a-(b+c)2、一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
用字母表示:a-b-c=a—c-b(四)除法简便运算:1、一个数连续除以两个数,可以用这个数除以这两个数的积。
用字母表示:a÷b÷c=a÷(b×c)2、一个数连续除以两个数,可以用这个数先除以后一个数再除以前一个数。
用字母表示:a÷b÷c=a÷c÷b小学四年级数学“四则运算”知识点详解知识点一:四则运算的概念和运算顺序1、加法、减法、乘法和除法统称四则运算。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
3、在没有括号的算式里,既有乘、除法又有加、减法的,要先算乘除法,再算加减法。
(完整)四年级运算定律练习题

运算定律练习题(1)乘法交换律:a×b=b×a 乘法结合律:(a×b)×c=a×(b×c)38×25×4 42×125×8 25×17×4 (25×125)×(8×4)49×4×538×125×8×3 (125×25)×4 5 ×289×2 (125×12)×8 125×(12×4)(2) 乘法交换律和结合律的变化练习125×64 125×88 44×25 125×24 25×28(3)加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c)357+288+143 158+395+105 167+289+33 129+235+171+165 378+527+73 169+78+22 58+39+42+61 138+293+62+107(4)乘法分配律:(a+b)×c=a×c+b×c 正用练习(80+4)×25 (20+4)×25 (125+17)×8 25×(40+4)15×(20+3)(5)乘法分配律正用的变化练习:36×3 25×41 39×101 125×88 201×24 (6)乘法分配律反用的练习:34×72+34×28 35×37+65×37 85×82+85×1825×97+25×3 76×25+25×24(7)乘法分配律反用的变化练习:38×29+38 75×299+75 64×199+64 35×68+68+68×64☆思考题:(8)其他的一些简便运算。
四年级上册数学计算题简便计算

四年级上册数学的简便计算主要包括加法交换律、结合律,乘法交换律、结合律和分配律的应用,以及一些常见的速算技巧。
以下是一些示例:
1. 加法交换律与结合律:
简便计算:98 + 45 + 2 = (98 + 2)+ 45 = 100 + 45 = 145
2. 乘法交换律与结合律:
简便计算:125 ×8 ×4 = (125 ×8)×4 = 1000 ×4 = 4000
3. 乘法分配律:
简便计算:25 ×(40 + 4) = 25 ×40 + 25 ×4 = 1000 + 100 = 1100
4. 其他简便计算方法:
利用“凑整”策略:如计算375 + 218 + 625时,可以先计算375 + 625 = 1000,再加218得到1218。
分解因数:例如计算25 ×12,可以将12分解为4×3,然后利用乘法结合律进行简便计算:25 ×12 = 25 ×(4×3) = (25×4)×3 = 100×3 = 300。
以上仅为示例,实际题目可能需要根据具体情况进行分析,找出合适的简便运算方式。
在教学过程中,老师会逐步引导学生理解和掌握这些简便计算方法,并通过大量练习来巩固。
四年级运算律计算题100道

四年级运算律计算题100道一、加法交换律和结合律。
1. 25 + 36+75- 解析:- 根据加法交换律a + b=b + a,先交换36和75的位置,得到25+75 + 36。
- 再根据加法结合律(a + b)+c=a+(b + c),先计算25+75 = 100,最后100+36 = 136。
2. 13+42+58+87- 解析:- 利用加法交换律将42和87交换位置,变为13 + 87+42+58。
- 然后利用加法结合律(13 + 87)+(42+58)。
- 先算13+87 = 100,42 + 58=100,最后100+100 = 200。
3. 34+(66 + 29)- 解析:- 根据加法结合律a+(b + c)=(a + b)+c,先计算34+66 = 100,再100+29 = 129。
4. 52+37+48+63- 解析:- 利用加法交换律得到52+48+37+63。
- 再利用加法结合律(52 + 48)+(37+63)。
- 先算52+48 = 100,37+63 = 100,最后100+100 = 200。
二、乘法交换律和结合律。
5. 25×4×8- 解析:- 根据乘法结合律(a× b)× c=a×(b× c),先计算25×4 = 100,再100×8 = 800。
6. 125×8×5- 解析:- 根据乘法结合律,先算125×8 = 1000,再1000×5 = 5000。
7. 5×17×2- 解析:- 根据乘法交换律a× b = b× a,交换17和2的位置,得到5×2×17。
- 先算5×2 = 10,再10×17 = 170。
8. 25×13×4- 解析:- 利用乘法交换律将13和4交换位置,得到25×4×13。
四年级交换律、结合律和分配律的算术题

四年级交换律、结合律和分配律的算术题在四年级的数学研究中,交换律、结合律和分配律是非常重要的概念。
这些法则可以帮助我们更好地理解和解决算术题。
本文将为大家提供一些与交换律、结合律和分配律相关的算术题。
交换律交换律是指在加法和乘法中,交换两个操作数的位置不改变结果。
以下是一些关于交换律的算术题例子:例子 1::如果 a = 3,b = 5,求 a + b 和 b + a 的结果。
解答::根据交换律,a + b 的结果和 b + a 的结果应该相等。
因此,a + b = b + a。
代入具体的数值,得到 3 + 5 = 5 + 3,结果都是 8。
例子 2::如果 a = 4,b = 2,求 a × b 和 b × a 的结果。
解答::根据交换律,a × b 的结果和 b × a 的结果应该相等。
因此,a ×b = b × a。
代入具体的数值,得到 4 × 2 = 2 × 4,结果都是 8。
结合律结合律是指在加法和乘法中,无论操作数的顺序如何,结果都是相同的。
以下是一些关于结合律的算术题例子:例子 3::如果 a = 2,b = 3,c = 4,求 (a + b) + c 和 a + (b + c) 的结果。
解答::根据结合律,(a + b) + c 的结果和 a + (b + c) 的结果应该相等。
因此,(a + b) + c = a + (b + c)。
代入具体的数值,得到 (2 + 3) + 4 = 2 + (3 + 4),结果都是 9。
例子 4::如果 a = 5,b = 6,c = 7,求 (a × b) × c 和 a × (b × c) 的结果。
解答::根据结合律,(a × b) × c 的结果和 a × (b × c) 的结果应该相等。
四年级计算题简便运算

四年级计算题简便运算一、加法交换律和结合律的简便运算。
1. 加法交换律:a + b=b + a例题:25+36+75解析:观察式子发现25和75相加可以得到整百数,根据加法交换律,将36和75交换位置,得到25 + 75+36。
先计算25+75 = 100,再加上36,结果为136。
2. 加法结合律:(a + b)+c=a+(b + c)例题:12 + 35+65+88解析:根据加法交换律,将35和88交换位置,式子变为12+88 + 35+65。
再根据加法结合律,将(12 + 88)和(35+65)分别结合起来先计算,12+88=100,35 + 65 = 100,最后100+100 = 200。
二、乘法交换律、结合律和分配律的简便运算。
1. 乘法交换律:a× b = b× a例题:25×13×4解析:观察到25和4相乘可以得到100,根据乘法交换律,将13和4交换位置,得到25×4×13。
先计算25×4 = 100,再乘以13,结果为1300。
2. 乘法结合律:(a× b)× c=a×(b× c)例题:25×17×4×2解析:根据乘法交换律,将17和4交换位置,式子变为25×4×17×2。
再根据乘法结合律,将(25×4)和(17×2)分别结合起来先计算,25×4 = 100,17×2 = 34,最后100×34 = 3400。
3. 乘法分配律:a×(b + c)=a× b+a× c或a×(b c)=a× b a× c例题1(乘法分配律正向应用):25×(40 + 4)解析:根据乘法分配律,将25分别与40和4相乘,再将结果相加,即25×40+25×4。
四年级交换律和结合律的计算题

四年级交换律和结合律的计算题# 一、加法交换律和结合律(一)知识点回顾1. 加法交换律定义:两个数相加,交换加数的位置,和不变。
用字母表示为公式。
2. 加法结合律定义:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
用字母表示为公式。
(二)例题1. 加法交换律例题计算公式和公式。
解析:对于公式,按照正常的加法运算顺序,先计算个位公式,向十位进1,再计算十位公式,结果是公式。
对于公式,同样先计算个位公式,向十位进1,再计算十位公式,结果也是公式。
这就验证了加法交换律公式。
2. 加法结合律例题计算公式和公式。
解析:先计算公式,先算括号内公式,再算公式,个位公式,向十位进1,十位公式,结果是公式。
再计算公式,先算括号内公式,再算公式。
这就验证了加法结合律公式。
(三)练习题1. 用加法交换律计算下面各题。
公式解析:根据加法交换律公式,公式,计算公式,个位公式,十位公式,结果是公式。
公式解析:根据加法交换律公式,计算公式,个位公式,十位公式,结果是公式。
2. 用加法结合律计算下面各题。
公式解析:根据加法结合律公式,公式,先算括号内公式,再算公式。
公式解析:根据加法结合律公式,先算括号内公式,再算公式。
# 二、乘法交换律和结合律(一)知识点回顾1. 乘法交换律定义:两个数相乘,交换因数的位置,积不变。
用字母表示为公式。
2. 乘法结合律定义:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。
用字母表示为公式。
(二)例题1. 乘法交换律例题计算公式和公式。
解析:对于公式。
对于公式,按照乘法口诀“三四十二”,结果也是公式。
这就验证了乘法交换律公式。
2. 乘法结合律例题计算公式和公式。
解析:先计算公式,先算括号内公式,再算公式。
再计算公式,先算括号内公式,再算公式。
这就验证了乘法结合律公式。
(三)练习题1. 用乘法交换律计算下面各题。
公式解析:根据乘法交换律公式,公式,按照乘法口诀“五六三十”,结果是公式。
小学四年级上加法交换律 结合律 乘法交换结合分配律及商不变规律汇总
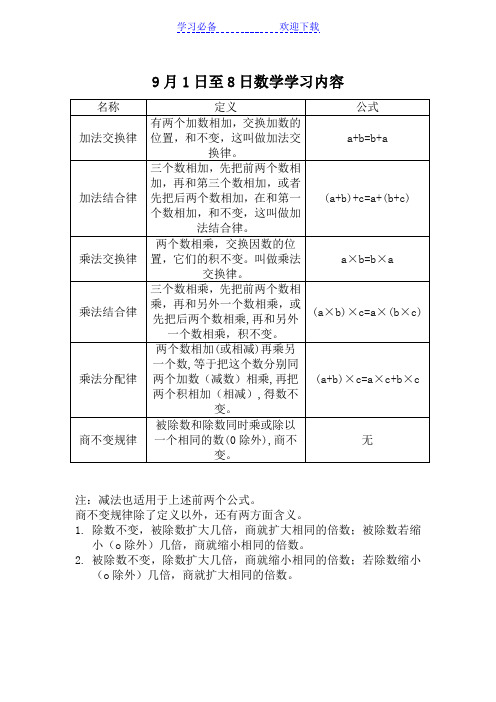
9月1日至8日数学学习内容注:减法也适用于上述前两个公式。
商不变规律除了定义以外,还有两方面含义。
1.除数不变,被除数扩大几倍,商就扩大相同的倍数;被除数若缩小(o除外)几倍,商就缩小相同的倍数。
2.被除数不变,除数扩大几倍,商就缩小相同的倍数;若除数缩小(o除外)几倍,商就扩大相同的倍数。
一.用简便方法运算。
355+260+140+2451022-478-422 987-(287+135)478-256-144 672-36+64 36+64-36+64 1814-378-422568-(68+178) 561-19+58382+165+35-82 155+256+45-98512+(373—212)228+(72+189) 169+199 109+(291—176)二. 判断。
1、56+72+28=56+(72+28)运用了加法交换律。
()2、83+63+27=83+27+63运用了加法交换律。
()三.应用题。
1.小明买了88斤苹果,10斤雪梨,12斤李子,总共买了多少斤水果!2.小明有3条数学题要做,5条英语题要做,2条语文题要做,今天一共需要做多少题?3.小明,小红,小芳分别有68支铅笔,小明先给小芳26支,小红给小芳32支,问芳芳现在有多少支铅笔?一、用简便方法计算下面各题23×15×2 125×7×8 250×56×4 75×9×2二、在□里填上适当的数35×8=35×(□×□) 45×12=45×(□×□) 16×15=16×(□×□) 18×25=18×(□×□) 125×32=125×(□×□) 25×24=25×(□×□)三、用简便方法计算:45×8 28×15 25×12 125×32 75×24四、判断18×12×5=18×(12×5),这应用了乘法结合律。
小学四年级上加法交换律,结合律,乘法交换结合分配律及商不变规律汇总剖析

9月1日至8日数学学习内容注:减法也适用于上述前两个公式。
商不变规律除了定义以外,还有两方面含义。
1.除数不变,被除数扩大几倍,商就扩大相同的倍数;被除数若缩小(o除外)几倍,商就缩小相同的倍数。
2.被除数不变,除数扩大几倍,商就缩小相同的倍数;若除数缩小(0除外)几倍,商就扩大相同的倍数。
加法交换律和结合律练习题一.用简便方法运算。
355+260+140+245 1022-478-422 987-(287+135)478-256-144 672-36+64 36+64-36+641814-378-422 568-(68+178)561-19+58382+165+35-82 155+256+45-98 512+(373—212)228+(72+189)169+199 109+(291—176)二. 判断。
1、56+72+28=56+(72+28)运用了加法交换律。
()2、83+63+27=83+27+63运用了加法交换律。
()三.应用题。
1.小明买了88斤苹果,10斤雪梨,12斤李子,总共买了多少斤水果!2.小明有3条数学题要做,5条英语题要做,2条语文题要做,今天一共需要做多少题?3.小明,小红,小芳分别有68支铅笔,小明先给小芳26支,小红给小芳32支,问芳芳现在有多少支铅笔?乘法交换律和结合律练习题一、用简便方法计算下面各题23X15X2 125X7X8 250X56X4 75X9X2 二、在口里填上适当的数35X8=35X (DXD) 16X15=16X (DXD) 45X 12=45X (DXD) 18X25=18X (DXD)125X32=125X (DXD) 25X24=25X (DXD)三、用简便方法计算:45X8 28X15 25X12 125X32 75X24四、判断18X12X5=18X(12X5),这应用了乘法结合律。
()25X(9X4) = (25X4)X9,这是应用了乘法交换律。
运算律,交换律,分配率,结合律专项练习试题附答案_四年级上册北师大,人教版等版本通用

运算律练习试题附答案_四年级上册北师大,人教版等版本通用4一、选择题1.下面的变化错误的是( )。
A.25×44=(25×4)×(25×40)B.25×44=25×4×11C.25×44=25×4+25×402.用简便方法计算,选出正确答案。
=()A.0 B.1 C.2 D.3.1000枚1元的硬币大约重6千克,2000000枚硬币大约重()。
A.6吨B.12吨C.120千克D.60吨4.35×5×6=35×(5×6),这道等式符合()。
A.乘法分配律B.乘法交换律C.乘法结合律5.25×140的简便运算是()。
A.25×100×4B.100+25×4C.25×100+25×406.428+157+72+△,△是( )时计算简便。
A.28 B.75 C.437.用简便方法计算.=()A.B.0 C.1 D.二、填空题8.从1000里连续减去5个98,结果是________。
9.口算28+5×4=________.42-42÷7=________.36÷(3+6)=________.10.在横线上可以填哪些数.36÷6-________=011.计算.34×+34×=________.12.计算.(15+2-7)×3=________.13.计算,并用计算器检验.4987+113×33=________.14.计算.12-4+3=________.15.计算64×26后,可以交换两个数的位置验算,是用了(_______)律。
16.两个数相加,交换加数的(_______),结果不变,这叫做(______________)。
四年级加法交换和结合律、乘法交换律、结合律、分配律练习汇编

加法交换律、结合律加法交换律:多个加数相加,可以任意交换加数的位置。
a+b=b+a加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176)43+189+57 591+482+118986+1999 216+89+11 473+79—63645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-1321814-378-422 155+264+36+45 698-291-9568-(68+178) 382+165+35-82 169+199184+507 236+189+64 759—126—259569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457) 68+24+32+76 425+64+75+36235+102 902-98 634-273+466-127(337+464)+536 727-194-106 374-(35+174)765-(96+65)247-185+53-15 384-297乘法交换律、结合律乘法交换律:多个因数相乘,可以任意交换因数的位置。
a×b=b×a乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
小学四年级乘法分配律的练习题

加法交换律:a+b=b+a加法结合律:a+b+c=(a+b)+c=a+(b+c) 乘法分配律:(a+b)×c=a×c+b×c乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律练习题类型一:(注意:一定要括号外的数分别乘括号里的两个数,再把积相加)(40+8)×25 125×(8+80)36×(100+50)24×(2+10)86×(1000-2)15×(40-8)类型二:(注意:两个积中相同的因数只能写一次)36×34+36×66 75×23+25×23 63×43+57×6393×6+93×4 325×113-325×13 28×18-8×28类型三:(提示:把102看作100+2;81看作80+1,再用乘法分配律)78×102 69×102 56×10152×102 125×81 25×41类型四:(提示:把99看作100-1;39看作40-1,再用乘法分配律)31×99 42×98 29×9985×98 125×79 25×39类型五:(提示:把83看作83×1,再用乘法分配律)83+83×99 56+56×99 99×99+99 75×101-75 125×81-125 91×31-91运算定律与简便计算测试题(一)一、判断题。
(10分)1、27+33+67=27+100 ()2、125×16=125×8×2 ()3、134-75+25=134-(75+25)()4、先乘前两个数,或者先乘后两个数,积不变,这是乘法结合律。
四年级加法交换和结合律、乘法结合律和交换律、分配律练习

四年级加法交换和结合律、乘法结合律和交换律、分配律练习1. 加法交换律加法交换律是指加法运算中,交换加法顺序不改变结果的性质。
例如,对于任意的两个数a和b,a + b的结果与b + a的结果相同。
练题:- 1 + 2 =- 3 + 4 =- 5 + 6 =2. 加法结合律加法结合律是指加法运算中,无论运算顺序如何改变,结果都相同。
例如,对于任意的三个数a、b和c,(a + b) + c的结果与a + (b + c)的结果相同。
练题:- (1 + 2) + 3 =- 1 + (2 + 3) =- (4 + 5) + 6 =3. 乘法结合律乘法结合律是指乘法运算中,无论运算顺序如何改变,结果都相同。
例如,对于任意的三个数a、b和c,(a * b) * c的结果与a * (b * c)的结果相同。
练题:- (2 * 3) * 4 =- 2 * (3 * 4) =- (5 * 6) * 7 =4. 乘法交换律乘法交换律是指乘法运算中,交换乘法顺序不改变结果的性质。
例如,对于任意的两个数a和b,a * b的结果与b * a的结果相同。
练题:- 2 * 3 =- 4 * 5 =- 6 * 7 =5. 分配律分配律是指乘法运算对加法具有分配性质。
例如,对于任意的三个数a、b和c,a * (b + c)的结果等于a * b + a * c。
练题:- 2 * (3 + 4) =- 5 * (6 + 7) =- 8 * (9 + 10) =以上是四年级加法交换和结合律、乘法结合律和交换律、分配律的练习。
通过这些练习题,学生可以巩固和加深对这些数学性质的理解和运用能力。
使用交换律、结合律和分配律解决的四年级数学题

使用交换律、结合律和分配律解决的四年级数学题问题描述在四年级数学课上,学生们遇到了以下数学题目:题目1:计算 13 + 7 + 2 + 18 + 5 + 9题目2:将 5 × 6 + 7 与 10 + 5 × 6 分别计算出来,然后求这两个结果的和解决方法交换律交换律是数学中的一个基本运算法则,根据交换律,同样的数进行加法或乘法运算,结果是相同的,只是顺序不同。
对于题目1,我们可以使用交换律来简化计算。
根据交换律,我们可以重新排列数字的顺序,将相同的数靠在一起计算,这样可以简化计算过程。
题目1变为:13 + 7 + 2 + 18 + 5 + 9 = 13 + 18 + 7 + 2 + 9 + 5结合律结合律也是数学中的一个基本运算法则,根据结合律,同样的数进行多次加法或乘法运算,结果是相同的,只是括号的位置不同。
对于题目2,我们可以使用结合律来简化计算。
根据结合律,我们可以改变计算顺序,将括号的位置调整,这样可以简化计算过程。
题目2变为:(5 × 6) + 7 和 10 + (5 × 6)分配律分配律也是数学中的一个基本运算法则,它描述了乘法运算与加法运算的关系。
根据分配律,我们可以将乘法运算先进行,然后再进行加法运算。
对于题目2,我们先计算乘法运算,然后再进行加法运算。
题目2进一步简化为:30 + 7 和 10 + 30计算结果经过简化后的计算,我们得到以下结果:题目1计算结果:13 + 18 + 7 + 2 + 9 + 5 = 54题目2计算结果:30 + 7 = 37,10 + 30 = 40总结通过使用交换律、结合律和分配律,我们可以简化复杂的数学题目。
交换律可以改变数字的顺序,结合律可以改变括号的位置,而分配律则可以先进行乘法运算,再进行加法运算。
这些基本运算法则帮助我们更快地计算数学题目,提高计算效率。
四年级数学必考乘法交换律结合律分配律(附专项练习及答案)

四年级数学必考乘法交换律、结合律、分配律(附专项练习及答案)什么是乘法交换律?三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
它是一种简算定律,在小学四年级均有涉及。
乘法交换律是乘法运算的一种运算定律。
主要公式为ab=ba(注意,在乘法与数字中,乘号用·表示,列:a·b=b·a或:ab=ba)。
作用:它可以改变乘法运算当中的运算顺序,在日常生活中乘法交换律运用的不是很多,主要是在一些较复杂的运算中起到简便的作用。
应用:(1)因数中间有零或者未尾有零交换位置相乘一般情况下可以简便计算过程。
(2)其中一个因数由重复的数字组成的,利用交换律计算也有简便。
运算例题如: 3×4×5=3×5×4=605.5×9×10=5.5×10×9=55×9=495什么是乘法结合律?定义:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
运算方法:主要公式为(a×b)×c=a×(b×c),它可以改变乘法运算当中的运算顺序 .在日常生活中乘法结合律运用的不是很多,主要是在一些较复杂的运算中起到简便的作用。
乘法结合律是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
注意:乘法结合律不适用于向量的计算。
例子:69×125×8=69×(125×8)=69×1000=6900什么是乘法分配律?两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),得数不变。
用字母表示:(a+b)x c=axc+bxc还有一种表示法:ax(b+c)=ab+ac示例25×404=25×(400+4)=25×400+25×4=10000+100=10100乘法分配律的逆运用25×37+25×3=25×(37+3)=25×40=1000乘法分配律还可以用在小数、分数的计算上。
(完整)四年级加法交换和结合律、乘法交换律、结合律、分配律练习

(完整)四年级加法交换和结合律、乘法交换律、结合律、分配律练习加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176)43+189+57 591+482+118986+1999 216+89+11 473+79—63645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-1321814-378-422 155+264+36+45 698-291-9568-(68+178) 382+165+35-82 169+199184+507 236+189+64 759—126—259569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457) 68+24+32+76 425+64+75+36235+102 902-98 634-273+466-127(337+464)+536 727-194-106 374-(35+174)765-(96+65)247-185+53-15 384-297乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
小学四年级上加法交换律-结合律-乘法交换结合分配律及商不变规律汇总

小学四年级上加法交换律-结合律-乘法交换结合分配律及商不变规律汇总加法交换律,结合律,乘法结合律,分配律,商不变规律汇总注:减法也适用于上述前两个公式。
商不变规律除了定义以外,还有两方面含义。
1. 除数不变,被除数扩大几倍,商就扩大相同的倍数;被除数若缩小(o 除外)几倍,商就缩小相同的倍数。
2. 被除数不变,除数扩大几倍,商就缩小相同的倍数;若除数缩小(o 除外)几倍,商就扩大相同的倍数。
加法交换律和结合律练习题一.用简便方法运算。
355+260+140+245 1022-478-422 987-(287+135)名称 定义公式加法交换律有两个加数相加,交换加数的位置,和不变,这叫做加法交换律。
a+b=b+a加法结合律三个数相加,先把前两个数相加,再和第三个数相加,或者先把后两个数相加,在和第一个数相加,和不变,这叫做加法结合律。
(a+b)+c=a+(b+c)乘法交换律两个数相乘,交换因数的位置,它们的积不变。
叫做乘法交换律。
a ×b=b ×a乘法结合律三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
(a ×b)×c=a ×(b ×c)乘法分配律两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),得数不变。
(a+b)×c=a ×c+b ×c 商不变规律被除数和除数同时乘或除以一个相同的数(0除外),商不变。
无1814-378-422 568-(68+178) 561-19+58382+165+35-82 155+256+45-98 512+(373—212)228+(72+189) 169+199 109+(291—176)二. 判断。
1、56+72+28=56+(72+28)运用了加法交换律。
()2、83+63+27=83+27+63运用了加法交换律。
四年级:四则运算交换律、结合律、分配律及去括号汇总

四年级:四则运算交换律、结合律、分配律及去括号汇总!例题:3X8÷2=3×(8÷2)✔8÷2×3=8÷(2×3)✘一、交换律①加法:A+ B+ C=A+ C+ B例子:9 6 1=9 1 6②减法:A-B-C=A-C-B例子:15-9-5=15-5-9③乘法:A×B×C=A×C×B例子:1×2×3=1×3×2④除法:A÷B÷C=A÷C÷B例子:6÷2÷3=6÷3÷2二、结合律①加法:A +B+ C=A+ (B+ C)例子:6 +9 +1=6+ (9+ 1)②减法:A-B-C=A-(B +C)例子:15-1-4=15-(1+ 4)③乘法:A×B×C=A×(B×C)例子:9×5×2=9×(5×2)④除法:A÷B÷C=A÷(B×C)例子:90÷5÷2=90÷(5×2)三、分配率①乘法:A×(B+ C)=A×B+A×C例子:5×(6 8)=5×6 5×8A×B+ A×C=A×(B C)例子:5×17 5×3=5×(17 3)A×(B-C)=A×B-A×C例子:5×(8-6)=5×8-5×6A×B-A×C=A×(B-C)例子:5×24-5×4=5×(24-4)②除法:(A +B)÷C=A÷C+ B÷C例子:(9 +6)÷3=9÷3 +6÷3A÷C +B÷C=(A +B)÷C例子:9÷3+6÷3=(9+ 6)÷3(A-B)÷C=A÷C-B÷C例子:(9-6)÷3=9÷3-6÷3A÷C-B÷C=(A-B)÷C例子:9÷3-6÷3=(9-6)÷3四、去括号①只有“+”“-”算式里,括号在“+ ”后面,去括号后,括号里面所有符号不变:A+ (B+C)=A+ B+ C例子:9 +(2+ 1)=9+ 2+ 1A+ (B-C)=A+ B-C例子:9 (2-1)=9 2-1②只有“+ ”“-”算式里, 括号在“-”后面,去括号后,括号里面的所有符号变相反:A-(B-C)=A-B +C例子:9-(5-1)=9-5+1A-(B +C)=A-B-C例子:9-(1+8)=9-1-8③只有“×”“÷”算式里, 括号在“×”后面,去括号后,括号里面的所有符号不变:A×(B×C)=A×B×C例子:3×(2×6)=3×2×6A×(B÷C)=A×B÷C例子:3×(6÷2)=3×6÷2④只有“×”“÷”算式里,括号在“÷”后面,去括号后,括号里面的所有符号变相反:A÷(B×C)=A÷B÷C例子:12÷(2×6)=12÷2÷6A÷(B÷C)=A÷B×C例子:12÷(6÷2)=12÷6×2去括号法则添括号法则去括号法则括号前面是“+”号,去掉“+”号和括号,括号里的各项不变号;括号前面是“-”,去掉“-”号和括号,括号里的各项都变号.添括号法则所添括号前面是“+”号,括到括号里的各项都不改变符号;所添括号前面是“-”号,括到括号里的各项都改变符号.★要点提示★1.去括号法则,实质要连同括号前的“+”号或“-”号同时去掉.2.去括号法则可简记为:去正不变,去负全变.3.括号前有数字因数,去括号时应把它与括号内各项相乘,切忌漏乘.4.去多重括号一般先去小括号,再去中括号比较简单,每去掉一层括号,如果有同类项,应随时合并,这样可使下一步运算简便,减少差错.5.添括号时,无论括号前是“+”还是“-”,都是根据需要添上的.6.去括号和添括号都是恒等变形,在数与式的运算、化简、变形、求值中经常用到,务必掌握.解题时要注意观察、比较、归纳和总结.整式的加减运算整式的加减运算是求几个整式的和、差的运算,其实质就是去括号,合并同类项.运算的结果仍然是整式.一般步骤为:(1)如果有括号,先去括号;(2)如果有同类项,再合并同类项.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
加法交换律、结合律
加法交换律:多个加数相加,可以任意交换加数的位置。
a+b=b+a
加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)
连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b
598+99 396—28—22 355+260+140+245
109+(291—176)43+189+57 591+482+118
986+1999 216+89+11 473+79—63
645—180—245 1022-478-422 987-(287+135)
478-256-144 672-36-64 36+64-36+64
487-287-139-61 500-257-143 2000-368-132
1814-378-422 155+264+36+45 698-291-9
568-(68+178) 382+165+35-82 169+199
184+507 236+189+64 759—126—259
569—256—44 514+189—214 228+(72+189)
28+45+72 123+38+62 1+13+85+7+99
100-57-23 37+56+63+44 574-398
1457-(185+457) 68+24+32+76 425+64+75+36
235+102 902-98 634-273+466-127
(337+464)+536 727-194-106 374-(35+174)
765-(96+65)247-185+53-15 384-297
乘法交换律、结合律
乘法交换律:多个因数相乘,可以任意交换因数的位置。
a×b=b×a
乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)
(25×4=100、125×8=1000)
连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
a÷b÷c= a÷(b×c)可以任意交换除数的位置。
a÷b÷c= a÷c÷b
35×125×8 97×25×4 1250×24
38×250×4 25×28 25×17×4
49×4×5 44×25 (25×125)×(8×40)
(125×25)×4 5 ×289×2 (125×12)×8
125×64 125×250×32 3×125×80×3
125×18×8 42×125×8 125×88
195×25×4 2×1250×8×5 125×489×8
125×16 16×250 42×125×8
2000 ÷ 125 ÷ 8 3200 ÷(32 × 5)240 ÷(24 ×2)
270÷(9×5)240÷ 5 ÷ 8 600÷24
330÷ 5 ÷ 2 540÷(54×2)300÷ 25 ÷ 4
720÷ 45 350÷ 14 800÷(20×8)
540÷ 5 ÷ 54 480÷32 720÷ 45 ÷ 2
48×125×9 7800÷(78×4)470÷(47×2)
乘法分配律
两个数的和或差与一个数相乘,可以把这两个数分别与这个数相乘,再将积相加或相减。
(正用)
(a±b)×c=a×c±b×c
两个数分别与同一个数相乘,且积相加或相减,可以把这两个数的和或差与这个数相乘。
(反用)
a×c±b×c=(a±b)×c
正用乘法分配律,对算式进行变形
(4+8)×25 (43+25)×40 8×(125+7)
5×(40-4)125×(80+8)(80+8)×25
(43+25)×40 8×(125+7)(40+8)×25
125×(8+80) 36×(100+50)24×(2+10)
86×(1000-2) 15×(40-8)35×(100-1)
(200-4)×25 125×(8+80)(57+140)×4
正用乘法分配律,对算式进行变形
135×6+65×6 4×24+26×24 30×2-25×2
135×6+65×6 35×37+65×37 16×256-16×56
69×45+31×45 124×25-25×24 135×37+165×37
123×99 +123 299 ×120+120 38×29+38
125×7+125 18×82+18×47+18×71 124×36-36×24
9 ×99+79 25×188+25×12 38×101-38
(40+8)×25 125×(8+80) 16×(100+50)
24×(2+10) 52×102 28×18-8×28
36×34+36×66 75×23+25×23 398×25
201×25 25×113-325×13 48×23+48×26+51×48 35×(100-1)78×102 56+56×99
69×102 125×79 99×99+99
42×98 25×41 (200-4)×25
56×101 15×(40-8) 125×81
19×16+19×84 31×99 83+83×99
36×198 201×38-38 63×43+57×63 75×101-75 125×81-125 91×31
93×6+93×4 102×76 25×34。
