工程光学课件
合集下载
《工程光学与技术》课件

智能制造
智能制造需要高精度、高效率的光学检测和测量技术,工程光学将大有可为。
医疗健康
光学成像、光谱分析等技术将为医疗健康领域带来更多创新。
THANK YOU
感谢各位观看
《工程光学与技术》ppt课件
目录
• 工程光学概述 • 光学基础知识 • 工程光学技术 • 现代光学技术 • 工程光学实验 • 工程光学前沿与展望
01
工程光学概述
光学的基本概念
光的本质
光是一种电磁波,具有波粒二象性。
光的传播
光在真空中沿直线传播,在其他介质中传播方向会发生改变。
光的反射、折射和散射
04
现代光学技术
非线性光学
非线性光学效应
非线性光学效应是光与物质相互作用时产生的非线性现象,如倍频 、和频、差频等。
非线性光学材料
非线性光学材料是实现非线性光学效应的关键,如晶体、玻璃、聚 合物等。
非线性光学应用
非线性光学在激光技术、光电子学、光通信等领域有广泛的应用,如 光参量振荡器、光倍频器等。
光子学与光子技术
ቤተ መጻሕፍቲ ባይዱ光子学基本概念
光子学是研究光子的产生、传播、相互作用和应 用的科学。
光子器件
光子器件是实现光子技术的关键,如激光器、光 放大器、光调制器等。
光子技术的应用
光子技术在通信、信息处理、传感等领域有广泛 的应用,如光纤通信、光计算等。
光学信息存储与处理
01
光学信息存储
光学信息存储是利用光的干涉、 衍射等光学效应实现信息的存储 和读取。
工程光学的研究内容
光学系统设计
研究光学系统的基本理论和设 计方法,涉及光学仪器、摄影
镜头、显微镜等。
光学材料与制造
智能制造需要高精度、高效率的光学检测和测量技术,工程光学将大有可为。
医疗健康
光学成像、光谱分析等技术将为医疗健康领域带来更多创新。
THANK YOU
感谢各位观看
《工程光学与技术》ppt课件
目录
• 工程光学概述 • 光学基础知识 • 工程光学技术 • 现代光学技术 • 工程光学实验 • 工程光学前沿与展望
01
工程光学概述
光学的基本概念
光的本质
光是一种电磁波,具有波粒二象性。
光的传播
光在真空中沿直线传播,在其他介质中传播方向会发生改变。
光的反射、折射和散射
04
现代光学技术
非线性光学
非线性光学效应
非线性光学效应是光与物质相互作用时产生的非线性现象,如倍频 、和频、差频等。
非线性光学材料
非线性光学材料是实现非线性光学效应的关键,如晶体、玻璃、聚 合物等。
非线性光学应用
非线性光学在激光技术、光电子学、光通信等领域有广泛的应用,如 光参量振荡器、光倍频器等。
光子学与光子技术
ቤተ መጻሕፍቲ ባይዱ光子学基本概念
光子学是研究光子的产生、传播、相互作用和应 用的科学。
光子器件
光子器件是实现光子技术的关键,如激光器、光 放大器、光调制器等。
光子技术的应用
光子技术在通信、信息处理、传感等领域有广泛 的应用,如光纤通信、光计算等。
光学信息存储与处理
01
光学信息存储
光学信息存储是利用光的干涉、 衍射等光学效应实现信息的存储 和读取。
工程光学的研究内容
光学系统设计
研究光学系统的基本理论和设 计方法,涉及光学仪器、摄影
镜头、显微镜等。
光学材料与制造
工程光学课件第03章

第三节 反射棱镜
(二)屋脊棱镜
奇数次反射使得物体成镜像,偶数次反射使物体成原像。 如果需得到与物体一致的像,而又不宜增加反射棱镜时,可用交线位 于棱镜光轴面内的两个相互垂直的反射面取代其中一个反射面,使垂直 于主截面的坐标被这二个相互垂直的反射面依次反射而改变方向,从而 得到物体的一致像。这两个相互垂直的反射面叫做屋脊面,带有屋脊面 的棱镜称为屋脊棱镜。 常用的屋脊棱镜有直角屋脊棱镜、半五角屋脊棱镜、五角屋脊棱镜、 斯密特屋脊棱镜等。
亦即同心光束经平行平板后变成了非同心光束。因此平行
平板不能成完善像。
L2 L1 L1 d
第二节 平行平板
二、平行平板的等效光学系统
平行平板在近轴区内以细光束成像时,由于I1及I1'都很小,其 余弦值可用1代替,于是近轴区内的轴向位移为
l d (1 1 )
n
平行平板在近轴区以细光束成像是
L
完善的。不管物体位置如何,其像 P
2
ß只与α有关
出射光线 不稳定
第二节 平行平板
一、平行平板的成像特性
n1 sin I1 n1 sin I1 n2 sin I2 n2 sin I2
B
n1 n2 1,n1 n2 n
I 2
I2
E
F
I1
nsisninI1I
2
n
s s
in in
I1 I 2
I1 U1 U2
A1( A2 ) A1 A2
(四)棱镜的组合——复合棱镜 1、分光棱镜
第三节 反射棱镜
2、分色棱镜
3、转向棱镜
第三节 反射棱镜
第三节 反射棱镜
第三节 反射棱镜
4、双像棱镜
第三节 反射棱镜
第二版工程光学分解课件

详细描述:当光从光密介质射向光疏介质时,如 果入射角大于临界角,光波将被完全反射回原介 质,不进入光疏介质,这种现象称为全反射。全 反射是光的波动性的一种表现。
02
光学系统与元件
透镜与光学镜头
透镜的分类
光学镜头的应用
根据透镜的形状和焦距,透镜可以分 为球面透镜、非球面透镜、双凸透镜 、双凹透镜和凸凹透镜等。
折反镜由反射镜和折射镜 组成,通过改变光路,将 光线聚焦在一点上。
折反镜的应用
在望远镜、显微镜和照相 机等光学仪器中广泛应用 ,用于改变光路和聚焦光 线。
滤光片与分光仪
滤光片的分类
根据滤光片的透过光谱, 滤光片可以分为可见光滤 光片、红外滤光片、紫外 滤光片等。
分光仪的结构
分光仪由棱镜或光栅等分 光元件和探测器组成,可 以将光谱分成不同的波段 。
非线性光学材料
研究和发展新型非线性光学材料,如有机晶体、 无机晶体、光折变晶体等,以提高非线性光学效 应的转换效率。
非线性光学应用
非线性光学在光通信、光信息处理、光计算等领 域有广泛应用,如光参量振荡、倍频、和频等。
光子学与光子技术
光子学基础
01
研究光子的产生、传播、相互作用等基本规律,以及光子与物
在摄影、摄像、显微镜、望远镜等领 域广泛应用,用于聚焦光线、改变光 路等。
光学镜头的基本参数
包括焦距、光圈、视场角、相对孔径 等,这些参数决定了镜头的光学性能 和使用范围。
反射镜与折反镜
01
02
03
反射镜的分类
根据反射面的形状,反射 镜可以分为平面反射镜、 凹面反射镜和凸面反射镜 等。
折反镜的结构
质的相互作用机制。
光子器件
02
02
光学系统与元件
透镜与光学镜头
透镜的分类
光学镜头的应用
根据透镜的形状和焦距,透镜可以分 为球面透镜、非球面透镜、双凸透镜 、双凹透镜和凸凹透镜等。
折反镜由反射镜和折射镜 组成,通过改变光路,将 光线聚焦在一点上。
折反镜的应用
在望远镜、显微镜和照相 机等光学仪器中广泛应用 ,用于改变光路和聚焦光 线。
滤光片与分光仪
滤光片的分类
根据滤光片的透过光谱, 滤光片可以分为可见光滤 光片、红外滤光片、紫外 滤光片等。
分光仪的结构
分光仪由棱镜或光栅等分 光元件和探测器组成,可 以将光谱分成不同的波段 。
非线性光学材料
研究和发展新型非线性光学材料,如有机晶体、 无机晶体、光折变晶体等,以提高非线性光学效 应的转换效率。
非线性光学应用
非线性光学在光通信、光信息处理、光计算等领 域有广泛应用,如光参量振荡、倍频、和频等。
光子学与光子技术
光子学基础
01
研究光子的产生、传播、相互作用等基本规律,以及光子与物
在摄影、摄像、显微镜、望远镜等领 域广泛应用,用于聚焦光线、改变光 路等。
光学镜头的基本参数
包括焦距、光圈、视场角、相对孔径 等,这些参数决定了镜头的光学性能 和使用范围。
反射镜与折反镜
01
02
03
反射镜的分类
根据反射面的形状,反射 镜可以分为平面反射镜、 凹面反射镜和凸面反射镜 等。
折反镜的结构
质的相互作用机制。
光子器件
02
工程光学(光阑)ppt课件

入射窗
出瞳
入瞳
L1
L2
像
物
主光线
视场光阑 出射窗
孔径光阑
以上只讨论了入射光瞳口径为无限小的情况。实际上,光学系统的入射
光瞳总是有一定大小。有时还可能很大。此时系统小光束被限制的情况就变
得复杂一些。下面我们就一般情况作精简品课要件分析。
15
当入射光瞳有一定大小时,由轴外物点发出的充满入瞳的光束,有时会 被某些透镜框所遮拦。如图所示,透镜L1、L2分别位于孔径光阑D的两侧。 由轴外物点B发出的充满入瞳的光束,其中只有一部分(画有阴影线部分) 通过系统成像,而其上下各有一部分分别被透镜L2与L1的镜框所遮拦。因此, 轴外物点成像光束的孔径显然要比轴上物点小。致使像面上从中央到边缘, 光照度逐渐下降,这种现象称为“惭晕”。
B
C A
精品课件
4
(二)入射光瞳、出射光瞳 入射光瞳:孔径光阑经其前面的光组在物空间的像。也就是从透镜左向右方 观察所看到的孔径光阑的像。 出射光瞳:孔径光阑经其后面的光组在像空间成的像。 入射光瞳、出射光瞳和孔径光阑三者是共轭关系。 入射光瞳是光束进入系统的公共入口,出射光瞳是光束射出系统的公共出口。
“光阑”。
在光学系统中,不单用装夹光学零件的金属框的内孔来限制光束,有
时还要专门设置一些带孔的金属薄片来限制光束,这些就是专用光阑。专
用光阑的通光孔一般为圆形,其中心线和光轴重合。多数专用光阑的孔径
是固定的,但也有可变的。孔径可变的光阑称为可变光阑,常用于照相物
镜中。又如人眼的瞳孔也是一个可变光阑,其孔径能随外界光线的强弱
视场光阑——决定物平面或物空间成像范围的光阑。在多数光学系统 如照相机、显微系统中,视场光阑的位置常被设置在系统物镜的像平面上, 这样,视场才能具有清晰的边界。
课件工程光学-08典型光学系统.ppt

1.0
0.8
光谱光效率
为什么暗环境下能
0.6
做饭、洗衣,但不
0.4
能描龙绣凤?
0.2
2024/10/8
0.0 400 500 600 700 800
l(nm)
光谱光效率函数曲线
第七章 光度学基础
7
§8.1.5 眼睛的分辨率
眼睛刚能分辨开二个很靠近点的能力称为眼睛的分辨率。 二者成反 比
刚能分辨的二个点对眼睛物方节点的张角称为极限分辨角。
瞄准精度和前面讲到的分辨率是不是一个概念?
瞄准精度随所选取的瞄准标志而异,最高精度可达人眼分辨率的1/6到1/10。
二实线重合 60
2024/10/8
二直线端部对准 叉线对准单线
(10~20)
10
第七章 光度学基础
双线对称夹单线 (5~10)
9
§8.1.7 眼睛的立体视觉
眼睛观察空间物体时,能区别它们的相对远近而具有立体视觉。简称体视。 C
若以50%渐晕点为界来决定线视场2 y
F
2 y 2B2F
f tanW2
f h d
250 f
2 y 500h d
W F
f 眼瞳
W3W2 W1 2a 2h
眼瞳
d
2024/10/8
第七章 光度学基础
14
讨论:
逢年过节,要买放大镜孝敬老人, 该如何选择其放大倍率?
2y h
2y 1
2y 1 d
(2)与照明光谱成份有关:单色光分辨率高(眼睛有色差); (3)与视网膜上成像位置有关,黄斑处分辨率最高。
对眼睛张角小物体的要借助望远镜或显微镜等仪器,仪器 应有适当的放大率,使能被仪器分辨的也能被眼睛分辨。
工程光学实验PPT课件

后将成为一束平行光。若用与主光轴垂直的平面镜将此平行光反 射回去,反射光再次通过透镜后仍会聚于透镜的焦平面上,其会 聚点将在发光点相对于光轴的对称位置上。 • 三、实验仪器
• 1、带有毛玻璃的白炽灯光源S • 2、品字形物屏P: SZ-14 • 3、凸透镜L: f=190mm(f=150mm) • 4、二维调整架: SZ-07 • 5、平面反射镜M • 二维调整架: SZ-07 • 7、通用底座: SZ-04 • 8、二维底座: SZ-02 • 9、通用底座: SZ-04
• 光学表面上如有灰尘,用实验室专备的干燥脱脂棉轻轻拭去或 用橡皮球吹掉。
• 光学表面上若有轻微的污痕或指印,用清洁的镜头纸轻轻拂去, 但不要加压擦拭,
• 更不准用手帕、普通纸片、衣服等擦拭。若表面有较严重的污 痕或指印,应由实验室人员用丙酮或酒精清洗。所有镀膜面均 不能接触或擦拭。
• 防止唾液或其溶液溅落在光学表面上。
F1经Lo后成一放大实像F’1,然后再用目镜Le作为放大镜观察 这个中间像F’1,F’1应成像在Le的第一焦点Fe之内,经过目镜 后在明视距离处成一放大的虚像F’’1。 • 三、实验仪器 • 1、带有毛玻璃的白炽灯光源S • 2、1/10mm分划板F1
•
mx=(像宽/实宽)÷20 (20为测微目镜的放大倍数)
• 像距改变量:s=(a1-a2)+(b2-b1)
• 被测目镜焦距:fe=s/(m2-m1)
• 实验四 自组显微镜
返回
• 一、实验目的 • 了解显微镜的基本原理和结构,并掌握其调节、使用和测量它的
放大率的一种方法。
• 二、实验原理 • 物镜Lo的焦距fo很短,将F1放在它前面距离略大于fo的位置,
2 F 3 4 Le 5
• 1、带有毛玻璃的白炽灯光源S • 2、品字形物屏P: SZ-14 • 3、凸透镜L: f=190mm(f=150mm) • 4、二维调整架: SZ-07 • 5、平面反射镜M • 二维调整架: SZ-07 • 7、通用底座: SZ-04 • 8、二维底座: SZ-02 • 9、通用底座: SZ-04
• 光学表面上如有灰尘,用实验室专备的干燥脱脂棉轻轻拭去或 用橡皮球吹掉。
• 光学表面上若有轻微的污痕或指印,用清洁的镜头纸轻轻拂去, 但不要加压擦拭,
• 更不准用手帕、普通纸片、衣服等擦拭。若表面有较严重的污 痕或指印,应由实验室人员用丙酮或酒精清洗。所有镀膜面均 不能接触或擦拭。
• 防止唾液或其溶液溅落在光学表面上。
F1经Lo后成一放大实像F’1,然后再用目镜Le作为放大镜观察 这个中间像F’1,F’1应成像在Le的第一焦点Fe之内,经过目镜 后在明视距离处成一放大的虚像F’’1。 • 三、实验仪器 • 1、带有毛玻璃的白炽灯光源S • 2、1/10mm分划板F1
•
mx=(像宽/实宽)÷20 (20为测微目镜的放大倍数)
• 像距改变量:s=(a1-a2)+(b2-b1)
• 被测目镜焦距:fe=s/(m2-m1)
• 实验四 自组显微镜
返回
• 一、实验目的 • 了解显微镜的基本原理和结构,并掌握其调节、使用和测量它的
放大率的一种方法。
• 二、实验原理 • 物镜Lo的焦距fo很短,将F1放在它前面距离略大于fo的位置,
2 F 3 4 Le 5
工程光学介绍课件

04
继续教育:加强继续教育和 培训,提高工程光学人才的 综合素质和技能水平
谢谢
3
相机:用于记录影像 的仪器,如数码相机、 手机相机等
望远镜:用于观察遥远 天体的仪器,如天文观 测、卫星通信等
2
投影仪:用于显示图像 的仪器,如电影放映、 会议演示等
4
光学测量系统
应用领域:工业、医疗、科研等
01
领域 功能:测量物体的几何形状、尺
02
寸、位置等参数 技术原理:利用光学原理,如激
03
于导航、教育和娱乐
上,用于游戏、电影和训练
4
工程光学的未来 展望
光学技术的创新
超材料:具有特殊 光学性质的人造材 料,如光子晶体、 超透镜等
01
纳米光学:利用纳 米尺度的光学现象, 如表面等离子体、 量子点等
02
04
集成光学:将光学 元件集成在芯片上, 如光子集成电路、 光通信系统等
03
生物光学:研究生 物系统中的光学现 象,如生物成像、 生物传感器等
05
光的衍射:光 在传播过程中 遇到障碍物时
发生衍射
06
光的偏振:光 在传播过程中 具有偏振特性
07
光的吸收与散 射:光在传播 过程中被吸收
或散射
08
光的色散:光 在传播过程中 发生色散,形
成彩色光谱
工程光学的应用领域
01
光学仪器:如显微镜、 望远镜、照相机等
02
光学通信:如光纤通信、 激光通信等
工程光学的应用拓展
虚拟现实(VR)和增强现实(AR)技术:工程光学在虚拟现实 和增强现实技术中发挥着重要作用,如光学元件的设计和制造。
自动驾驶汽车:工程光学在自动驾驶汽车领域具有广泛的应用, 如激光雷达(LiDAR)、摄像头和传感器等。
工程光学课件第01章

波面:发光点发出的光波向四周传播时, 某一时刻其振动位相相同的点所构成的 面称为波阵面,简称波面。光的传播即 为光波波阵面的传播。 光束:几何波面与几何光线的关系:在 各项同性介质中,波面上某点的法线即 代表了该点处光的传播方向,即光沿着 波面法线方向传播,因此,波面法线即 为光线。与波面对应的所有光线的集合, 称为光束。
时,可以全反射传送,
i i0
时,光线将会透过内壁进入包层
26
定义 na sin i0 为光纤的数值孔径
够传送的光能越多。
i0
越大,可以进入光纤的光能就越多,也就是光纤能
这意味着光信号越容易耦合入光纤。
27
三、费马原理
费马原理与几何光学的基本定律一样,也是描 述光线传播规律的基本理论。 它以光程的观点描述光传播的规律,涵盖了光 的直线传播和光的折、反射规律,具有更普遍 的意义。 根据物理学,光在介质中走过的几何路程与该 介质折射率的乘积定义为光程。设介质的折射 率为n,光在介质中走过的几何路程为l,则光程 s表示为
同心光束:通常波面可分为平面波、
球面波和任意曲面波。与平面波对应的光
束成为平行光束,与球面波对应的光束称
为同心光束。
平行光束与同心光束
平面波面
球形波面
同心光束
平行光束
各类光束及对应的波面
返回
折射率:折射率是表征透明介质光学 性质的重要参数。我们知道,各种波长的 光在介质中的传播速度会减慢。介质的折 射率正是用来描述介质中光速减慢程度的 物理量,即:
c n v
这就是折射率的定义。
10
二、几何光学的基本定律
几何光学的基本定律决定了光线在一般 情况下的传播方式,也是我们研究光学 系统成像规律以及进行光学系统设计的 理论依据。 几何光学的基本定律有三大定律:
工程光学 典型光学系统PPT课件
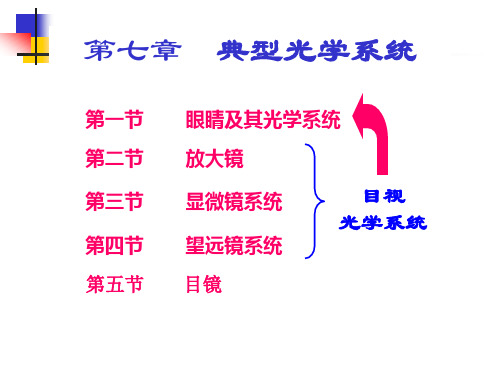
眼睛及其光学系统
放大镜 显微镜系统 望远镜系统
目视 光学系统
目镜
第一节 眼睛及其光学系统
一、眼睛(Eyes)的结构
调节肌
1、巩膜:包围眼球的白色 不透明外层,D≈25mm.
2、角膜(Cornea):眼球前突出的透明球面膜,
r≈8mm,n ≈1.38;
——主要折射成像界面(角膜—空气)
眼球横切面
3、前室:角膜后水晶体前的空间,充满透明水状液n =1.336。
1、调焦(对准)平面上的物点——视网膜上的点像
2、远景、近景平面上的物点——视网膜上的像为弥散斑
若弥散斑可看作一像点, 则要求其对人眼张角小于极限分辨角。
八、双目立体视觉
1,视差角
A
A
A
B
l
B
a1
a2 b2a2源自b1 a1b视觉基线
2,视差、体视锐度
视差:
视差越大,两物体的纵向 深度越大,反之越小
二、瑞利判据 :等亮度的两个物点,其一衍射图样的中央 极大与另一衍射图样的第一级极小重合时,认 为刚好能分辨这两个物点。
——能分辨的两个等亮度点间的距离对应于艾里斑半径。
无限远物点被理想光学系统成衍射图案: 第一暗环半径对出瞳中心的张角:
=1.22 / D,入瞳直径D的函数
——能分辨的二点间的最小角距离
2、眼睛+目视光学仪器:视角可被目视光学仪器放大。 观察物体所需分辨率×目视光学仪器的放大率=眼睛分辨率
★ 不同的目视光学仪器,通常选择的物距为: 1)放大镜、显微镜:观察物位于明视距离附近; 2)望远镜:观察物位于远处或无穷远。
第二节 放大镜 (The Magnifying Glass)
一、放大镜的成像原理
《工程光学》课件

光学信号处理原理
光学信号处理概述 简要介绍了光学信号处理的基本 概念和原理,包括光波的干涉、 衍射、傅里叶变换等方面的知识 。
全息术与光学信息处理 简要介绍了全息术的基本原理和 应用,以及光学信息处理技术的 发展和应用前景。
干涉测量技术 详细介绍了干涉测量技术的基本 原理和应用,包括干涉仪的结构 和工作原理、干涉图样的分析和 解释等方面的知识。
的发展提供了新的机遇和挑战。
工程光学在各领域的应用
能源领域
太阳能利用、激光焊接、激光切割等 。
通信领域
光纤通信、光网络技术等。
环境监测领域
光谱分析、大气污染监测等。
生物医学领域
医学成像、光谱诊断、激光医疗等。
CHAPTER 02
工程光学基础知识
光的本质与传播
光的本质
光是一种电磁波,具有波粒二象性。 其电磁场振动方向与传播方向垂直, 表现出横波的特征。
显微镜
介绍了显微镜的基本原理和结构,包括透射光显微镜和反 射光显微镜等类型,以及显微镜的性能参数和选择方法。
激光器
简要介绍了激光器的基本原理和结构,包括气体激光器、 固体激光器、光纤激光器等类型,以及激光器的性能参数 和应用领域。
光学系统设计原理
光学系统设计基础
介绍了光学系统设计的基本概念和原则, 包括光学材料、光学镀膜、光学元件加工
光学信息处理实验
研究光学信息处理技术,如傅里叶 变换、光学图像处理等,掌握光学 信息处理系统的基本构成和操作方 法。
光学系统设计与制造实践
光学系统设计实践
通过实践了解光学系统设计的基本原理和方法,掌握光学设 计软件的使用技巧,熟悉光学元件的选择和加工工艺。
光学制造工艺实践
大学工程光学课件

光学微纳加工技术
通过微纳加工技术制造微小尺度的光学元件 ,实现高精度、高效率的光学系统。
光学传感技术
利用光学原理对物理量进行测量,具有高精 度、高灵敏度的特点。
工程光学发展趋势预测与展望
集成化与智能化
多学科交叉融会
随着微纳加工技术的发展,工程光学将更 加重视元件的集成化和智能化,提高系统 的性能和效率。
光的本质与传播特性
光的本质
光是一种电磁波,具有波粒二象 性。其波动性质表现为光的干涉 、衍射等现象,粒子性质则体现 为光电效应等。
光的传播特性
光在均匀介质中沿直线传播,遇 到不同介质界面时会产生反射、 折射等现象。
光的反射、折射与干涉
光的反射
光在遇到物体表面时,会改变传 播方向并返回原介质的现象。反 射过程中遵循反射定律,即入射
工程光学在各领域的应用
航空领域
用于飞机导航、着 陆系统、气象观测 等。
能源领域
用于太阳能电池板 、风力发电叶片的 检测与设计等。
国防领域
用于制造精确的武 器瞄准系统、夜视 仪等。
航天领域
用于卫星通讯、空 间探测、天文观测 等。
通讯领域
用于光纤通讯、光 交换、光网络等。
CHAPTER 02
光学基础知识
光的吸取、散射与色散
01 02
光的吸取
光在传播过程中被物质吸取转化为热能或其他情势能量的现象。不同物 质对不同波长光的吸取程度不同,因此可以利用这一特性进行光谱分析 等。
光的散射
光在传播过程中遇到微小颗粒时,产生散射的现象。散射程度与颗粒大 小和入射光的波长有关,可以利用这一现象进行大气污染检测等。
感谢您的观看
大、缩小、旋转等功能。
《工程光学》课件第4章

第4章 平面与平面系统
4.1 平面反射镜 4.2 平行平板 4.3 反射棱镜 4.4 折射棱镜 4.5 光楔
4.1 平面反射镜
4.1.1 单平面镜成像
如图4-1所示,PP′为平面反射镜,由物点A发出的光 束被平面反射镜反射,其中任意一条光线AO经平面镜PP′ 反射后,沿OB方向射出;另一条光线AP垂直于镜面入射, 并沿原路反射,这两条反射光线的反向延长线交于A′, A′点即为物点A被平面镜反射后所成的像。
折射后,射向第二面,经折射后沿EB 方向射出。出射光线的 延长线与光轴交于点A2 ,此即为物点A 经平行平板后的虚像 点。光线在第一、第二两面上的入射角和折射角分别为I1 I、1 和 I 2 、 I 2 ,按折射定律有
sin I1 nsin I1 n sin I 2 sin I 2
因 两 折 射 面 平 行 , 所 以 I 2 I1 ,I 2 I1 , 故 U1 U 2 ,可见出射光线EB 和入射光线AD 相互平
垂直。根据反射面数目的不同,简单棱镜又分为一次反射棱 镜、二次反射棱镜和三次反射棱镜。
1)一次反射棱镜 一次反射棱镜具有一个反射面,相当于单块平面镜,对 物成镜像,即垂直于主截面的坐标方向不变,位于主截面内 的坐标方向改变。 最常用的一次反射棱镜是等腰直角棱镜,如图4-10(a) 所示为等腰直角棱镜,光线从一直角面入射,从另一直角面 出射,使光轴折转90°。图4-10(b)所示的等腰棱镜可以使 光轴折转任意角度。确定反射面角度时,只需使反射面的法 线方向处于入射光轴与出射光轴夹角的平分线上即可。这两 种棱镜的入射面与出射面都与光轴垂直,在反射面上的入射 角大于临界角,能够发生全反射,反射面上无需镀反射膜。
l2 l1 d l
(4-6)
而无需对平行玻璃平板逐面进行计算。因此,在进行光
4.1 平面反射镜 4.2 平行平板 4.3 反射棱镜 4.4 折射棱镜 4.5 光楔
4.1 平面反射镜
4.1.1 单平面镜成像
如图4-1所示,PP′为平面反射镜,由物点A发出的光 束被平面反射镜反射,其中任意一条光线AO经平面镜PP′ 反射后,沿OB方向射出;另一条光线AP垂直于镜面入射, 并沿原路反射,这两条反射光线的反向延长线交于A′, A′点即为物点A被平面镜反射后所成的像。
折射后,射向第二面,经折射后沿EB 方向射出。出射光线的 延长线与光轴交于点A2 ,此即为物点A 经平行平板后的虚像 点。光线在第一、第二两面上的入射角和折射角分别为I1 I、1 和 I 2 、 I 2 ,按折射定律有
sin I1 nsin I1 n sin I 2 sin I 2
因 两 折 射 面 平 行 , 所 以 I 2 I1 ,I 2 I1 , 故 U1 U 2 ,可见出射光线EB 和入射光线AD 相互平
垂直。根据反射面数目的不同,简单棱镜又分为一次反射棱 镜、二次反射棱镜和三次反射棱镜。
1)一次反射棱镜 一次反射棱镜具有一个反射面,相当于单块平面镜,对 物成镜像,即垂直于主截面的坐标方向不变,位于主截面内 的坐标方向改变。 最常用的一次反射棱镜是等腰直角棱镜,如图4-10(a) 所示为等腰直角棱镜,光线从一直角面入射,从另一直角面 出射,使光轴折转90°。图4-10(b)所示的等腰棱镜可以使 光轴折转任意角度。确定反射面角度时,只需使反射面的法 线方向处于入射光轴与出射光轴夹角的平分线上即可。这两 种棱镜的入射面与出射面都与光轴垂直,在反射面上的入射 角大于临界角,能够发生全反射,反射面上无需镀反射膜。
l2 l1 d l
(4-6)
而无需对平行玻璃平板逐面进行计算。因此,在进行光
哈工大《工程光学》课件

※ 入射光线AE与光轴的夹角为物方倾斜角也叫物方 孔径角,用U 表示。
Engineering Optics
授课:任秀云
n
E n’
A
-U
h
C U’
A’
O r
-L
L’
折射光线EA’ 由以下参量确定:
※像方截距:顶点O到折射光线与光轴交点,用L’表示。
※像方倾斜角:折射光线EA’ 与光轴的夹角,也叫像方 孔径角,用U’ 表示。
(5)r = -40mm, L = -100mm, U = -10°, L’= -200mm
Engineering Optics
授课:任秀云
2.1.3 单折射球面成像的光路计算
一、实际光路的计算公式(追迹公式或大L公式):
nE
n’
A
-U
C O
r
-L
当结构参数 r , n , n’ 给定时,只要知道 L 和 U ,就可求L’ 和 U’
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
-y’ B’
L’
Engineering Optics
授课:任秀云
×
×
√
×
L = 100mm, U = 30°
Engineering Optics
授课:任秀云
同学们一定要记住上面 的符号规则!
Engineering Optics
授课:任秀云
Engineering Optics
n
授课:任秀云
I
E
n’
-U A
-L
φC
O
r
Engineering Optics
授课:任秀云
n
E n’
A
-U
h
C U’
A’
O r
-L
L’
折射光线EA’ 由以下参量确定:
※像方截距:顶点O到折射光线与光轴交点,用L’表示。
※像方倾斜角:折射光线EA’ 与光轴的夹角,也叫像方 孔径角,用U’ 表示。
(5)r = -40mm, L = -100mm, U = -10°, L’= -200mm
Engineering Optics
授课:任秀云
2.1.3 单折射球面成像的光路计算
一、实际光路的计算公式(追迹公式或大L公式):
nE
n’
A
-U
C O
r
-L
当结构参数 r , n , n’ 给定时,只要知道 L 和 U ,就可求L’ 和 U’
光轴 为起始边。
B
y -U
A
-L
E I
h
I’
φ
C
U’
A’
O
r
-y’ B’
L’
Engineering Optics
授课:任秀云
×
×
√
×
L = 100mm, U = 30°
Engineering Optics
授课:任秀云
同学们一定要记住上面 的符号规则!
Engineering Optics
授课:任秀云
Engineering Optics
n
授课:任秀云
I
E
n’
-U A
-L
φC
O
r
工程光学讲稿(平面)(完整)课件

详细描述
折射望远镜使用透镜作为主反射镜,能够观测可见光波段的天体。反射望远镜使用凹面反射镜作为主反射镜,能够观测红外线和射电波段的天体。射电望远镜则专门用于观测射电波段的天体。
01
02
03
04
总结词
摄影镜头是一种光学仪器,用于拍摄照片或录制视频。
总结词
摄影镜头的种类繁多,根据用途和功能可分为多种类型,如定焦镜头、变焦镜头、鱼眼镜头等。
光的衍射
平面镜与透镜
平面镜是反射面为平面的镜子,具有反射光线的能力,且入射角等于反射角。
用于日常生活、光学仪器和科学实验中,如化妆镜、眼镜、显微镜、望远镜等。
平面镜的用途
平面镜的性质
中间厚边缘薄的透镜,具有汇聚光线的能力,可以用于制作放大镜、显微镜、望远镜等。
凸透镜Βιβλιοθήκη 凹透镜透镜的焦距中间薄边缘厚的透镜,具有发散光线的能力,可以用于制作近视眼镜、散光眼镜等。
光学仪器在科研领域的应用也十分广泛,主要用于物理、化学、生物等学科的研究。例如,利用光谱仪研究物质的结构和性质,使用干涉仪测量微小距离和角度,以及通过光学仪器观测天体和微观粒子等。
科研中常用的光学仪器还包括分光仪、干涉仪、光谱分析仪等,这些仪器在推动学科发展和科技进步方面发挥着重要作用。
光的干涉与衍射实验
通过双缝干涉实验,观察光波的干涉现象,了解干涉的条件和特点。
双缝干涉实验是研究光波干涉现象的基础实验之一。在实验中,通过调整光源、双缝和屏幕的距离,观察到明暗相间的干涉条纹。通过测量干涉条纹的间距和双缝的间距,可以计算出光波的波长。
通过圆孔衍射实验,观察光波的衍射现象,了解衍射的条件和特点。
工程光学应用
光学仪器在工业中应用广泛,主要用于检测、测量和控制等方面。例如,利用光学显微镜对产品表面进行微观检测,使用激光测量仪对生产线上的产品进行高精度测量,以及通过光束控制系统实现自动化生产。
折射望远镜使用透镜作为主反射镜,能够观测可见光波段的天体。反射望远镜使用凹面反射镜作为主反射镜,能够观测红外线和射电波段的天体。射电望远镜则专门用于观测射电波段的天体。
01
02
03
04
总结词
摄影镜头是一种光学仪器,用于拍摄照片或录制视频。
总结词
摄影镜头的种类繁多,根据用途和功能可分为多种类型,如定焦镜头、变焦镜头、鱼眼镜头等。
光的衍射
平面镜与透镜
平面镜是反射面为平面的镜子,具有反射光线的能力,且入射角等于反射角。
用于日常生活、光学仪器和科学实验中,如化妆镜、眼镜、显微镜、望远镜等。
平面镜的用途
平面镜的性质
中间厚边缘薄的透镜,具有汇聚光线的能力,可以用于制作放大镜、显微镜、望远镜等。
凸透镜Βιβλιοθήκη 凹透镜透镜的焦距中间薄边缘厚的透镜,具有发散光线的能力,可以用于制作近视眼镜、散光眼镜等。
光学仪器在科研领域的应用也十分广泛,主要用于物理、化学、生物等学科的研究。例如,利用光谱仪研究物质的结构和性质,使用干涉仪测量微小距离和角度,以及通过光学仪器观测天体和微观粒子等。
科研中常用的光学仪器还包括分光仪、干涉仪、光谱分析仪等,这些仪器在推动学科发展和科技进步方面发挥着重要作用。
光的干涉与衍射实验
通过双缝干涉实验,观察光波的干涉现象,了解干涉的条件和特点。
双缝干涉实验是研究光波干涉现象的基础实验之一。在实验中,通过调整光源、双缝和屏幕的距离,观察到明暗相间的干涉条纹。通过测量干涉条纹的间距和双缝的间距,可以计算出光波的波长。
通过圆孔衍射实验,观察光波的衍射现象,了解衍射的条件和特点。
工程光学应用
光学仪器在工业中应用广泛,主要用于检测、测量和控制等方面。例如,利用光学显微镜对产品表面进行微观检测,使用激光测量仪对生产线上的产品进行高精度测量,以及通过光束控制系统实现自动化生产。
工程光学完整课件1

述观点
光学测量技 术的特点与 优势 光学 测量技术的
应用
光学测量技术的应 用
光学测量技 术在工业领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
述观点
光学测量技 术在医疗领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
述观点
光学测量技 术在军事领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
实践环节的安排与要求
实验课程设置:包括实验项目、 实验内容、实验目的等
实验要求:实验前的准备、实验 过程中的注意事项、实验报告的 撰写等
添加标题
添加标题
添加标题
添加标题
实验时间安排:每周实验时间、 实验周期等
实践环节的考核方式:考核内容、 考核方式、评分标准等
YOUR LOGO
THANK YOU
实验设备:光学仪器、光 源、光电探测器等
实验步骤:搭建实验装置、 调整光学参数、记录实验 数据、分析实验结果
注意事项:遵守实验室规 定,注意安全操作,保护 光学仪器
实验设备与操作方法
实验设备介绍:包括光学实验箱、显微镜、望远镜等 操作方法演示:通过图文并茂的方式展示实验步骤和操作技巧 注意事项提醒:强调实验过程中的安全问题和注意事项 实验报告撰写:说明实验报告的撰写方法和要求
述观点
光学检测技术的种类与特点
干涉测量技术:利用光的干涉现象进行测量,具有高精度、高分辨率 和高灵敏度的特点。
衍射测量技术:利用光的衍射现象进行测量,具有测量范围广、测 量精度高和抗干扰能力强的特点。
光学显微技术:利用光学显微镜对微小物体进行观察和测量,具有直 观、快速和简便的特点。
光学测量技 术的特点与 优势 光学 测量技术的
应用
光学测量技术的应 用
光学测量技 术在工业领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
述观点
光学测量技 术在医疗领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
述观点
光学测量技 术在军事领
域的应用
输入你的正文,文 字是您思想提炼请 尽量言简意赅的阐
实践环节的安排与要求
实验课程设置:包括实验项目、 实验内容、实验目的等
实验要求:实验前的准备、实验 过程中的注意事项、实验报告的 撰写等
添加标题
添加标题
添加标题
添加标题
实验时间安排:每周实验时间、 实验周期等
实践环节的考核方式:考核内容、 考核方式、评分标准等
YOUR LOGO
THANK YOU
实验设备:光学仪器、光 源、光电探测器等
实验步骤:搭建实验装置、 调整光学参数、记录实验 数据、分析实验结果
注意事项:遵守实验室规 定,注意安全操作,保护 光学仪器
实验设备与操作方法
实验设备介绍:包括光学实验箱、显微镜、望远镜等 操作方法演示:通过图文并茂的方式展示实验步骤和操作技巧 注意事项提醒:强调实验过程中的安全问题和注意事项 实验报告撰写:说明实验报告的撰写方法和要求
述观点
光学检测技术的种类与特点
干涉测量技术:利用光的干涉现象进行测量,具有高精度、高分辨率 和高灵敏度的特点。
衍射测量技术:利用光的衍射现象进行测量,具有测量范围广、测 量精度高和抗干扰能力强的特点。
光学显微技术:利用光学显微镜对微小物体进行观察和测量,具有直 观、快速和简便的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fringes can be observed visually,
projected on a screen, or recorded
photoelectrically. 返回24
2
S
y x r1 S1 O
S2
P(x,y,D)
x
r2
z
d D
2 k ( r2 r1 ) k
2
( r2 r1 ) 2 ( r2 r ) 1 则:I=4 I 0 cos k 4 I 0 cos 2
光强 I 的强弱取决于光程差 (r2 r1 )
d I=4 I 0 cos x D
2
D 当 xm 时 d D xm 有最大值:I MAX 4 I 0 , 为亮条纹; d , I MAX 1 D 当 x (m ) 时 2 d 有最小值:I MIN 0, 为暗条纹; 其中:m 0, 1, 2,
r22 r12 2 xd
2 xd 2 xd d x 光程差: r2 r1 r2 r1 2 D D
kd 2 d 则:I=4 I 0 cos x 4 I 0 cos x 2D D
2
7
3、干涉条纹(Interference fringes) 及其意义
在同一条纹上 的任意一点到 两个光源的光 程差是恒定的。
P(x,y,D)
x
结论:
1、干涉条纹代表着光程差的等值线。
2、相邻两个干涉条纹之间其光程差
变化量为一个波长,位相差变 9 化2。
10
Interference fringes
Zeroth-order maximum
axial First-order maximum First-order minimum
干涉项 I12 与两个光波的振动方向(A1, A2 ) 和位相有关。
4
干涉条件(必要条件): I12 A1 A2 cos
k1 r1 k 2 r2 1 2 1 2 t
(1)频率相同,1 2 0; (2)振动方向相同, 1 A 2 A1 A2 cos A (3)位相差恒定,1 2 常数
2、相干光波(Coherent wave)和相干光源 (Coherent light source) 能够产生干涉的光波,叫相干光波; 其光源称为相干光源。
2
二、干涉条件
一般情况下,
两个振动E1和E 2 叠加后的光强为: I E E E 1 E 2 E 1 E 2 1t I ( E E )dt E1 E 2 E1 E 2 T0 E1 E1 E 2 E 2 2 E1 E 2 I1 I 2 I 12
11
I
1 .0 0 .8
4、干涉条纹的间隔
条纹间隔:
0 .6
0 .4
0 .2
0 .0 -4 -2
e
0
e
2
4
D D D e ( m 1) m d d d
m-1
m
m+2 m+1
定义:两条相干光线的夹角为 相干光束的会聚角,用表示。
y 会聚角 x
y
在杨氏实验中: d 条纹的间隔: e
x
4I 0
I MIN 0
1 D x (m ) , 2 d
对于接收屏上相同的x值,光强I相等。条纹垂直于x轴。
8
(r2 r1 ) I=4 I 0 cos
2
用光程差表示:
y
r2 r1 m
1 2
时 时 S
S2
y x r1 S1 O r2
z
I MAX 4 I 0 , 为亮条纹; r2 r1 ( m ) I MIN 0, 为暗条纹;
y2 z2
2
对于m级亮条纹,=m;有: m
x2
d 2 m 2 2
2
2
1
15
局部位置条纹
在三维空间中,干涉结果:
等光程差面
16
本课内容回顾
1、干涉现象和干涉条件 2、P点的干涉条纹强度: I I1 I 2 2 I1I 2 cos
2 xd 2 xd d x 3、光程差的计算: r2 r1 r2 r1 2 D D
干涉条纹间隔与波长的关系
条纹间隔 e ,
e 1 。
白光条纹 0 白条纹 白条纹
14
x
二、两个点源在空间形成的干涉场
两点源形成的干涉场是空间分布的; 干涉条纹应是空间位置对点光源等光程差的轨迹。 =r2 r1 ( x d ) 2 y 2 D 2 ( x d ) 2 y 2 D 2 2 2
注意:干涉的光强分布 只与光程差 k r1 k r2 有关。
补充条件: 叠加光波的光程差不超过波列的长度
5
第二节 杨氏干涉实验
(Young’s double-slit experiment)
一、干涉图样的计算
y
1、P点的干涉条纹强度
I I1 I 2 2 I1 I 2 cos 设I1 I 2 I 0 则: I 4 I 0 cos
6
2、光程差的计算
y
d r1 ( x ) 2 y 2 D 2 2 d 2 r2 ( x ) 2 y 2 D 2 S 2
2Байду номын сангаас
y x r1 S1 O S2 d D r2 z P(x,y,D) x
r r ( r2 r1 )(r2 r1 )
2 2 2 1
20
干涉现象实例(Interference Examples)
21
2
返回
22
Thomas Young (1773-1829)
• A British physician and physicist. He could read at age 2, at 6 began studying Latin, and at 13 had also mastered Greek, Hebrew, Italian and French. At 19 he entered medical school, correctly explained the accommodation of the eye and was elected Fellow of the Royal Society. In 1796, he graduated from the University of Gottingen Medical School, opened a practice in London, and 5 years later became professor of Natural Philosophy at the Royal Institution. That same year,1801, he read the first of several papers presenting the wave theory of light and the principle of interference, much to the opposition of Newton’s followers. Young made noteworthy contributions also to acoustics, atmospheric refraction, elasticity, fluid dynamics and color vision. 返回23
4、干涉条纹的意义: 光程差的等值线。
5、干涉条纹的间隔:
e
6、干涉条纹间隔与波长:多色光的干涉
7、两个点源在空间形成的干涉场:等光程差面
17
Key words
1. Path difference 2. Phase difference 3. The order of interference 4. The light distribution 5. A maximum amount of light (maxima) 6. A minimum amount of light (minima)
下一节 19
干涉现象(Interference)
• 在两个(或多个)光波叠加的区域形成 强弱稳定的光强分布的现象,称为光的
干涉现象。
The term Interference refers to the phenomenon that waves, under certain conditions, intensify or weaken each other.
第十一章 光的干涉和干涉系统
• 干涉现象是光波波动性的重要特征
• 1801年杨氏干涉实验—波动理论—部分相干理论
• 应用:测量光谱线的细微结构、测量长度 • 多种干涉装置:杨氏双缝干涉、迈克尔逊干涉仪等
• 本章内容:干涉现象、干涉理论和干涉装置
1
第一节 光波的干涉条件
一、干涉现象
1、什么是干涉现象(Interference)
Interference fringes
The light of distribution resulting from a superposition of waves will consist of alternately bright and dark bands
called interference fringes. Such
18
Homework (11-1&2)
1. Light passes through two narrow slits of d=0.8mm. On screen 1.6m away the distance between the two second-order maxima is 5mm. What is the wavelength of the light? P243 1&2
projected on a screen, or recorded
photoelectrically. 返回24
2
S
y x r1 S1 O
S2
P(x,y,D)
x
r2
z
d D
2 k ( r2 r1 ) k
2
( r2 r1 ) 2 ( r2 r ) 1 则:I=4 I 0 cos k 4 I 0 cos 2
光强 I 的强弱取决于光程差 (r2 r1 )
d I=4 I 0 cos x D
2
D 当 xm 时 d D xm 有最大值:I MAX 4 I 0 , 为亮条纹; d , I MAX 1 D 当 x (m ) 时 2 d 有最小值:I MIN 0, 为暗条纹; 其中:m 0, 1, 2,
r22 r12 2 xd
2 xd 2 xd d x 光程差: r2 r1 r2 r1 2 D D
kd 2 d 则:I=4 I 0 cos x 4 I 0 cos x 2D D
2
7
3、干涉条纹(Interference fringes) 及其意义
在同一条纹上 的任意一点到 两个光源的光 程差是恒定的。
P(x,y,D)
x
结论:
1、干涉条纹代表着光程差的等值线。
2、相邻两个干涉条纹之间其光程差
变化量为一个波长,位相差变 9 化2。
10
Interference fringes
Zeroth-order maximum
axial First-order maximum First-order minimum
干涉项 I12 与两个光波的振动方向(A1, A2 ) 和位相有关。
4
干涉条件(必要条件): I12 A1 A2 cos
k1 r1 k 2 r2 1 2 1 2 t
(1)频率相同,1 2 0; (2)振动方向相同, 1 A 2 A1 A2 cos A (3)位相差恒定,1 2 常数
2、相干光波(Coherent wave)和相干光源 (Coherent light source) 能够产生干涉的光波,叫相干光波; 其光源称为相干光源。
2
二、干涉条件
一般情况下,
两个振动E1和E 2 叠加后的光强为: I E E E 1 E 2 E 1 E 2 1t I ( E E )dt E1 E 2 E1 E 2 T0 E1 E1 E 2 E 2 2 E1 E 2 I1 I 2 I 12
11
I
1 .0 0 .8
4、干涉条纹的间隔
条纹间隔:
0 .6
0 .4
0 .2
0 .0 -4 -2
e
0
e
2
4
D D D e ( m 1) m d d d
m-1
m
m+2 m+1
定义:两条相干光线的夹角为 相干光束的会聚角,用表示。
y 会聚角 x
y
在杨氏实验中: d 条纹的间隔: e
x
4I 0
I MIN 0
1 D x (m ) , 2 d
对于接收屏上相同的x值,光强I相等。条纹垂直于x轴。
8
(r2 r1 ) I=4 I 0 cos
2
用光程差表示:
y
r2 r1 m
1 2
时 时 S
S2
y x r1 S1 O r2
z
I MAX 4 I 0 , 为亮条纹; r2 r1 ( m ) I MIN 0, 为暗条纹;
y2 z2
2
对于m级亮条纹,=m;有: m
x2
d 2 m 2 2
2
2
1
15
局部位置条纹
在三维空间中,干涉结果:
等光程差面
16
本课内容回顾
1、干涉现象和干涉条件 2、P点的干涉条纹强度: I I1 I 2 2 I1I 2 cos
2 xd 2 xd d x 3、光程差的计算: r2 r1 r2 r1 2 D D
干涉条纹间隔与波长的关系
条纹间隔 e ,
e 1 。
白光条纹 0 白条纹 白条纹
14
x
二、两个点源在空间形成的干涉场
两点源形成的干涉场是空间分布的; 干涉条纹应是空间位置对点光源等光程差的轨迹。 =r2 r1 ( x d ) 2 y 2 D 2 ( x d ) 2 y 2 D 2 2 2
注意:干涉的光强分布 只与光程差 k r1 k r2 有关。
补充条件: 叠加光波的光程差不超过波列的长度
5
第二节 杨氏干涉实验
(Young’s double-slit experiment)
一、干涉图样的计算
y
1、P点的干涉条纹强度
I I1 I 2 2 I1 I 2 cos 设I1 I 2 I 0 则: I 4 I 0 cos
6
2、光程差的计算
y
d r1 ( x ) 2 y 2 D 2 2 d 2 r2 ( x ) 2 y 2 D 2 S 2
2Байду номын сангаас
y x r1 S1 O S2 d D r2 z P(x,y,D) x
r r ( r2 r1 )(r2 r1 )
2 2 2 1
20
干涉现象实例(Interference Examples)
21
2
返回
22
Thomas Young (1773-1829)
• A British physician and physicist. He could read at age 2, at 6 began studying Latin, and at 13 had also mastered Greek, Hebrew, Italian and French. At 19 he entered medical school, correctly explained the accommodation of the eye and was elected Fellow of the Royal Society. In 1796, he graduated from the University of Gottingen Medical School, opened a practice in London, and 5 years later became professor of Natural Philosophy at the Royal Institution. That same year,1801, he read the first of several papers presenting the wave theory of light and the principle of interference, much to the opposition of Newton’s followers. Young made noteworthy contributions also to acoustics, atmospheric refraction, elasticity, fluid dynamics and color vision. 返回23
4、干涉条纹的意义: 光程差的等值线。
5、干涉条纹的间隔:
e
6、干涉条纹间隔与波长:多色光的干涉
7、两个点源在空间形成的干涉场:等光程差面
17
Key words
1. Path difference 2. Phase difference 3. The order of interference 4. The light distribution 5. A maximum amount of light (maxima) 6. A minimum amount of light (minima)
下一节 19
干涉现象(Interference)
• 在两个(或多个)光波叠加的区域形成 强弱稳定的光强分布的现象,称为光的
干涉现象。
The term Interference refers to the phenomenon that waves, under certain conditions, intensify or weaken each other.
第十一章 光的干涉和干涉系统
• 干涉现象是光波波动性的重要特征
• 1801年杨氏干涉实验—波动理论—部分相干理论
• 应用:测量光谱线的细微结构、测量长度 • 多种干涉装置:杨氏双缝干涉、迈克尔逊干涉仪等
• 本章内容:干涉现象、干涉理论和干涉装置
1
第一节 光波的干涉条件
一、干涉现象
1、什么是干涉现象(Interference)
Interference fringes
The light of distribution resulting from a superposition of waves will consist of alternately bright and dark bands
called interference fringes. Such
18
Homework (11-1&2)
1. Light passes through two narrow slits of d=0.8mm. On screen 1.6m away the distance between the two second-order maxima is 5mm. What is the wavelength of the light? P243 1&2
