奥数讲座搭配问题ppt课件
合集下载
二年级奥数第2讲:搭配问题-课件
12
3种
3
3种
3种
2+1=3(种) 3×3=9(种) 答:一共有9种不同的扎法。
练习五(选做)
为了让大家的伙食更丰富,芭啦啦综合教育学校食堂提
供了以下几种食物和水果,每个学生可以从中选择2种食物
和1种水果,有多少种不同的选择?
4种
3种
5种
2种
1种
4+3+2+1=10(种)
10×5=50(种)
答:有50种不同的选择。
5次 4次 3次 2次 1次
1
2
3
4
5
6
5+4+3+2+1=15(场) 答:一共要进行15场比赛。
小结
解决组合问题的主要方法是用列举法。 一般可以借助图形来描述,更加生动形象清 晰,并且不容易遗漏。
密码要求:
(1)是两位数。 (2)十位上的数字是3、4中的任意一个,个位上的数
字是2、5中的任意一个。 (3)必须要把组成的两位数全找齐了,才能通过密码。
搭配问题
例题一
阿派准备放学后回家换上运动鞋再去爬山,已知从学校 有2条路可以回家,从家有4条路可以去爬山。阿派有多少种 不同的走法? (学校、家、山的位置如下图)
学校
1 2
家
3
4 5 6
山
4种 4种
4×2=8(种) 答:阿派有8种不同的走法。
练习一
欧拉回乡下看望奶奶,从家到中转站有3种公交可以 选择,从中转站到奶奶家有2种公交可以选择,那么欧拉去 奶奶家有多少条不同的路线?
择孩
在子
冬是
天荷
开花
放,
选
择
在
《搭配问题》课件

)种不
1.面包和饮料搭配。
(1)有两种面包、两种饮料,各选其中的一种,有(4 )种不
同的搭配方法。
1.面包和饮料搭配。
(2)有三种面包、三种饮料,各选其中的一种,有( 9)种不
同的搭配方法。
3×3=9
2.饭菜搭配。
(1)选一种主食和一种菜有多少种搭配方法。
3×2=6或2×3=6
有6种不同的搭配方法。
搭配问题
2+2+2=6(种)
3+3=6(种)
3×2=6(种)或2×3=6(种)
搭配时要注意按照一定的顺序,不重复、不遗漏。
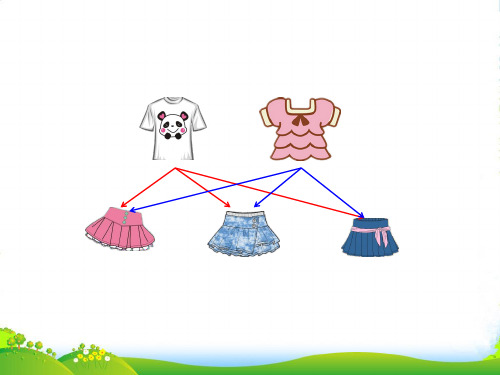
再加一件上衣,丫丫每天穿一套衣服, 一周不重复能做到吗?
2×4=8(种)或4×2=8(种)
1.面包和饮料搭配。 (1)有两种面包、两种饮料,各选其中的一种,有( 同的搭配方法。
《搭配问题》
1件上衣+1条裤子
丫丫每天要搭配一套不同的衣服,有几种不同的搭配方法?
帮丫丫想一想,怎样搭配?
方法一:先确定上衣,再确定裤子。 有6种不同的搭配方法。
2+2+2=6(种)
2×3=6(种)或3×2=6(种)
方法二:先确定裤子,再确定上衣。 有6种不同的搭配方法。
3+3=6(种)
3×2=ቤተ መጻሕፍቲ ባይዱ(种)或2×3=6(种)
2.饭菜搭配。
(2)选一种主食和两种菜有多少种搭配方法。 3×2=6或2×3=6 有6种不同的搭配方法。
丫丫又买了2顶帽子,选择一顶帽子、一件上衣和一条裤子, 有几种不同的搭配方法?
2×(2×3)=12(种)
解决搭配问题的方法 1.搭配过程中可以先固定一个事物,再按照顺序 和另一个事物搭配,做到不重复、不遗漏。 2.搭配m件A类物品和n件B类物品,就有m×n种 搭配方法。
数学广角──搭配(一) 课件(共28张PPT)

数学广角——搭配(一)
课前准备: 1.0-9数字卡片 2.红、黄、蓝彩色笔各一支 3.学习任务单
十位
个位
密码是用1、2组成的两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?密码就在其中。
密码是两个数中较大的一个
数学广角—搭配(一)
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
探究任务一:摆一摆、写一写或用自己喜欢的方法解决问题,把结果记录在任务单1。
21
13
小丽
1
2
3
2
1
3
3
1
2
搭配
交换位置法
固定十位
固定个位
固定数位法
不重不漏
ቤተ መጻሕፍቲ ባይዱ有序思考
能组成(6)个两位数。
在数字0-9中任选三个数摆一摆、写一写,验证你的猜想。
探究任务二:验证猜想把验证过程记录在任务单2。
探究任务三:设计排队方案用自己喜欢的方法记录在任务单3。
回顾课本,这节课你学到了什么?
搭配
交换位置法
固定十位法
固定个位法
不重复不遗漏
有序
生活中处处有数学,只要你带着数学的眼光去观察,带着数学的思维去思考,一定会发现和创造更多的美好!
同学们再见!
授课老师:
时间:2024年9月15日
4
30
能组成( 4 )个两位数。
39
93
90
怎样做才能不重不漏
数学课本第97页
学以致用:涂一涂完成数学课本第97页做一做。
北城
南城
答:一共有6种涂色方法。
3名同学要在数学王国门口排成一排合影,有多少种排法?
最新《找规律(搭配)》课件

四年级下册 执教:高乃国
馒头
包子
牛奶
豆浆
小丽吃一种点心,喝一种饮料,
她的早餐有多少种不同的搭配方法?
饮料: 心:
先选饮料
先选点心
先选饮料: 返回
先选点心:
返回
把两类物体进行搭配,用第一
类的个数去乘第二类的个数,就能 求出搭配的总数。这就是搭配的规 律。
小丽家
2×4=8(种)
穿衬衣和裤子,有几种不同的穿法?
3×2=6(种)
穿衬衣和裙子,有几种不同的穿法?
3×3=9(种)
一共有多少种不同的穿法?
3×5=15(种) 3×2+3×3=15(种)
游戏:剪刀、石头、布
两人玩剪刀、石头、布的游戏, 一共会出现多少种不同的情况?
馒头
包子
牛奶
豆浆
小丽吃一种点心,喝一种饮料,
她的早餐有多少种不同的搭配方法?
饮料: 心:
先选饮料
先选点心
先选饮料: 返回
先选点心:
返回
把两类物体进行搭配,用第一
类的个数去乘第二类的个数,就能 求出搭配的总数。这就是搭配的规 律。
小丽家
2×4=8(种)
穿衬衣和裤子,有几种不同的穿法?
3×2=6(种)
穿衬衣和裙子,有几种不同的穿法?
3×3=9(种)
一共有多少种不同的穿法?
3×5=15(种) 3×2+3×3=15(种)
游戏:剪刀、石头、布
两人玩剪刀、石头、布的游戏, 一共会出现多少种不同的情况?
《数学广角—搭配》PPT(第1课时)

人民教育出版社 二年级 | 上册
小丽
小清
小红
小结
今天这节课有趣吗? 同学们在数学广角里学到 了什么?你有什么收获? 以后在解决这类问题时应 注意什么?
人民教育出版社 二年级 | 上册
可爱的同学,找资料眼 睛累了吧!长时间屏幕,眼 睛会干涩、酸痛、疲劳的。
不过现在教同学们一个 小办法,左边我为大家准备 了一张视力保健“远眺图” ,看看图就能缓解眼疲劳, 起到远眺解乏的作用。
新课导入
一天,狮子大王带来了一个超级密码箱,赶快看看吧!
这个密码箱的 密码是由1、2两个 数字组成的两位数 ,猜一猜密码箱的 密码可能是多少?
新课导入
密码 是两个数 中较大的 一个
人民教育出版社 二年级 | 上册
人民教育出版社 二年级 | 上册
教学例1
用1、2和3组成两位数,每个两位数的十位数和个位 数不能一样,能组成几个两位数?
远眺图是利用心理学 空间知觉原理,在一张二维 空间平面上,强烈显示出三 维空间的向远延伸的立体图 形,远视和视力良好的人在 长时间近距离用眼情况下引 起的视力疲劳,可以通过此 种方法获得一定的缓解。
因绿色为最佳感受色, 可使睫状体放松,图案从里 到外大小不等,不断变化图 案可不断改变眼睛晶状体的 焦距,使调节他们的睫状体 放松而保护视力。
“十位数和个位数不能 一样”是什么意思? 你要用什么办法解决这 个问题呢?
人民教育出版社 二年级 | 上册
教学例1:排列
1、 交换位置:有顺序的从这3个数字中选择2个数字, 组成两位数,再把位置交换,又组成另外一个两位数。
人民教育出版社 二年级 | 上册
教学例1:排列
2、 固定十位:先确定十位,再将个位变动。
奥数讲座 搭配问题PPT课件

.
3
1.5 个小朋友,互相握一次手,他 们共握多少次手?
4+3+2+1=10(次)
.
4
2.小英有 8 本不同的书, 小莉向她借 2 本,有几种 不同的借法?
7+6+5+4+3+2+1
=28(种)
.
5
3.用 2 、 3 、 4 能写出多少个不同的三位 数?其中最大的是多少?最小的是多少?
234 243
搭配问题
.
1
例1.北京到广州的火车如果只考虑京广铁路上 的北京、郑州、武汉、广州这 4 个车站,那么 这 4 个车站间的往返火车票共需多少种?这 4 个车站中,任何一个车站既可以作起点站也可以 作终点站。
( 1 )以北京为起点站,则终点站是(郑州 ) ( 武汉)(广州 ),有( 3 )种不同的票;
.
8
例4.小青有两件毛衣:一件黄的、一件白的; 她有 3 条裤子:一条蓝的、一条咖啡色的、 一条红的。算一算,要使她的毛衣和裤子有 不同的搭配,能有几种搭配方法?
2×3 = 6 (种)
因为上衣有两种不同的选择方法,裤 子木块:红、蓝、黄、白, 取出三块排成一横排,共有多少种不同的取 法?
共有车票的种数是: 8×9 = 72 (种)。
.
14
例6. 有 6 个小朋友,要互相通一次电话, 你能算出,他们一共打了多少次电话?
【 思路分析 】我们把 6 个小朋友分别编号: A、B、C、D、E、F。 A 应与其他小朋友打电话 5 次,这 5 次是: A一B , A 一 C , A一D , A一E , A一F 。同 样, B 也应打 5 次电话, B 打的 5 次电话是: B一A , B一C , B一D , B一E , B一F 。
奥数讲座搭配问题ppt课件

解 :3 x4 = 12 (种)
答:有 12 种不同的搭配方法。
精选PPT课件
26
15.从红霞的家到学校有两条路,从学校到少 年科技馆有 3 条路,如果红霞从家先到学校, 再去少年科技馆,一共有几种不同的走法?
解: 2 x3 = 6 (条)
答:红霞从家经过学校到科技馆有 6 种
不同的走法。
精选PPT课件
27
16.用数字 1 、 2 、 3 可以组成多少个没有 重复数字的三位数?
123 213
132 321
231 312
3×2 × 1=6(个)
精选PPT课件
28
17.用数字 0 、 1 、 2 可以组成多少个没 有重复数字的三位数?
120 102 210 201
2×2×1=4(个)
精选PPT课件
解 :4 + 2 + 1 = 7 (场)
答:一共要进行 7 场比赛。 精选PPT课件
18
8. ( 1 )魔术师有一个大盒子,大盒子里有 5 个中盒子,每个中盒子里有 2 个小盒子, 间魔术师一共有多少个盒子?
1 + 5 + 2×5 = 16 (个)
精选PPT课件
19
( 2 )两颗药丸装一袋, 1 个小盒装 2 袋,1 个大盒装 4 个小盒, 2 个大盒可装多 少颗药丸?
种走法;
(4 )从甲地到丙地共有( 2 )+ ( 2 ) + ( 2 )
= ( 6 ) (种)不同的走法;
( 5 )用乘法计算: ( 2 ) ×( 3 ) = ( 6 )种。
精选PPT课件
23
12.陈华有尼龙袜、毛线袜、丝光袜共 3 双,还有 4 种不同的鞋子。如果她要穿上鞋和袜,可有几种
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
432 423
3 × 2 = 6 (种) 最大数是 432 ,最小数是 234
6
例2.用0、 1 、 2 、 3 能写出多少个不 同的四位数?其中最大的是多少?最小 的是多少?
1023 1032 1203 1230 1320 1302
2031 2013 2103 2130 2310 2301
3012 3021 3201 3210 3120 3102
共有车票的种数是: 8×9 = 72 (种)。
14
例6. 有 6 个小朋友,要互相通一次电话, 你能算出,他们一共打了多少次电话?
【 思路分析 】我们把 6 个小朋友分别编号: A、B、C、D、E、F。 A 应与其他小朋友打电话 5 次,这 5 次是: A一B , A 一 C , A一D , A一E , A一F 。同 样, B 也应打 5 次电话, B 打的 5 次电话是: B一A , B一C , B一D , B一E , B一F 。
15
同样, C 、 D 、 E 、 F 也应该各打 5 次电话。 这样, 6 个小朋友,一共要打: 5 x6 = 30 (次)电话。但是,题目要求两个小 朋友之间只能通一次电话,当 A 打电话给 B 时 ( A-B ) , A 、 B 两人已通了一次电话, B 没有必要再打电话给 A (去掉 B -A 这一次)。 如果把打电话的情况排列出来,我们就会发现, 这 30 次电话中,有一半是重复计算的。所以实 际打电话的次数是:
可以组成 4 十 6 + 4 十 1 二 15 (种)不同的币值11。
6.要从某班数学学习优秀的 5 个同学中,选 出 4 个同学参加一次数学竞赛,间共有多少 种不同的选法?
ABC DE
ABCD BCDE CDEA
DEAB EABC
共5种
12
7.从甲地到乙地有 2 条路可走,从乙地到丙地有 3 条路可走,从丙地到丁地有 4 条路可走,试问 从甲地到丁地共有多少种不同的走法?
搭配问题
1
例1.北京到广州的火车如果只考虑京广铁路上 的北京、郑州、武汉、广州这 4 个车站,那么 这 4 个车站间的往返火车票共需多少种?这 4 个车站中,任何一个车站既可以作起点站也可 以作终点站。
( 1 )以北京为起点站,则终点站是(郑州 ) ( 武汉)(广州 ),有( 3 )种不同的票;
( 2 )以郑州为起点站,则终点站是(北京) (武汉 )(广州 ),有(3 )种不同车票:
5 ×6 ÷ 2 = 15 (次)。
解: 5 ×6 ÷ 2 = 15 (次)
答:他们一共打了 15 次电话。
16
例7. 某校举行乒乓球单打比赛,把参赛选手分为 2 组,每组 7 个同学,每个同学都要与本组其他同 学比赛一场,这次比赛共要进行多少场?
3
1.5 个小朋友,互相握一次手,他 们共握多少次手?
4+3+2+1=10(次)
4
2.小英有 8 本不同的书, 小莉向她借 2 本,有几种 不同的借法?
7+6+5+4+3+2+1 =28(种)
5
3.用 2 、 3 、 4 能写出多少个不同的三位 数?其中最大的是多少?最小的是多少?
234 243 324 342
2×3 = 6 (种)
因为上衣有两种不同的选择方法,裤 子有 3 种不同的选择方法。
9
4.四块不同颜色的木块:红、蓝、黄、白, 取出三块排成一横排,共有多少种不同的 取法?
以红色的作为第一块,可以排出: 3×2 =6 (种)不同的形式。 这四种颜色的木块都可作为第一块,而且 各种颜色作为第一块时都可以排出 6 种不 同形式。因此不同的取法共有:
1一 7 , 1一 8 , 1一 9 。同样, 2 号站到其他车站的车票也有 8 种。
如 2 ? 1 , 2 一 3 , 2 一 4 , 2一 5 , 2 一 6 , 2一 7 , 2一 8 , 2一 9 。(注意 1一 2 , 2一 1 的车票是 不相同的。)每个车站必须准备 8 种不同的车票。所以,
(3)以武汉为起点站,则终点站是(北京 ) (郑州 )(广州 ),有( 3 )种不同车票:
2
(4)以广为起点站,则终点站是(北京) (郑州)(武汉),有( 3 )种不同车票:
( 5 )一个起点和一个终点间对应一种车票, 因此,这四个车站间的往返火车票共需( ) ×(3 ) = ( 4 )1(2种)不同的车票。
2 × 3×4 = 24 (条)
13
例5. 从上海到南京有 9 个火车站(包括上海和 南京)。各火车站售票处要为这条路线准备几种 不同的火车票?(往返车票是不相同的。)
【 思路分析]我们假设这些火车站的编号分别是 1 号、 2 号、 3 号、 4 号、 5 号、 6 号、 7 号、 8 号、 9 号。那么 1 号站到其他车站的车票有8种。 如:1 一 2 , 1一 3 , 1一 4 , 1 一 5 , 1一 6 ,
6×4 = 24 (种)。
10
5.有一张 10 元、一张 5 元、一张 2 元、一张 1 元的人民币,可以组成多少种不同的币值?
( 1)四张人民币就有四种币值: 1 元、 2 元、 5 元、 10 元。 ( 2 )每次取两张人民币,可以组成的币值有:
1 + 2 = 3 (元)、 1 + 5 二 6 (元)、 1 + 10 = 11 (元)、 2 + 5 = 7 (元)、 2 + 10 = 12 (元)、 5 + 10 = 15 (元) ; ( 3 )每次取 3 张人民币,可以组成的币值有: 1 + 2 + 5 = 8(元)、 2 + 5 + 10 = 17 (元)、 1 + 2 + 10 = 13 (元)、 l + 5 + 10 = 16 (元) ; ( 4 )每次取四张人民币,有一种币值: 1 + 2 十 5 + 10 = 18 (元)所以,
3×6=18(个) 最大数是 3210 ,最小数是 1023。
7
例3.用 3 、 0 、 0 、 5 四个数字可以组成 多少个不同的四位数?请你全部写出来?
可以组成 6 个不同的四位数,它们分别是:
3005 、 3050 、 3500 、 5003 、5030 、 5300 。
8
例4.小青有两件毛衣:一件黄的、一件白 的;她有 3 条裤子:一条蓝的、一条咖啡色 的、一条红的。算一算,要使她的毛衣和裤 子有不同的搭配,能有几种搭配方法?
