多服务台排队系统的仿真
MG1型排队系统分析与仿真

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究,得出这些数量指标(等待时间、排队长度、忙期长短等)的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优。
它是数学运筹学的分支学科。
也是研究服务系统中排队现象随机规律的学科。
广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。
排队论研究的内容有3个方面:统计推断,根据资料建立模型;系统的性态,即和排队有关的数量指标的概率规律性;系统的优化问题。
其目的是正确设计和有效运行各个服务系统,使之发挥最佳效益。
一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中虚线所包括的部分。
排队系统又称服务系统。
服务系统由服务机构和服务对象(顾客)构成。
服务对象到来的时刻和对他服务的时间(即占用服务系统的时间)都是随机的。
描述一个排队系统一般需要分析其三个组成部分:输入过程、排队规则和服务机构。
输入过程输入过程考察的是顾客到达服务系统的规律。
它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述,一般分为确定型和随机型两种。
例如,在生产线上加工的零件按规定的间隔时间依次到达加工地点,定期运行的班车、班机等都属于确定型输入。
随机型的输入是指在时间t内顾客到达数n(t)服从一定的随机分布。
如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布,即式中λ为单位时间顾客期望到达数,称为平均到达率;1/λ为平均间隔时间。
在排队论中,讨论的输入过程主要是随机型的。
排队规则排队规则分为等待制、损失制和混合制三种。
一个基于VC++的多台多队仿真系统

厂 ) e‘ 去 一 ≥0 ( =A =p , e
其 中 , =_ 为到达 时 间f 卢 1 M隔均值 .
^
1 2 服务模 式 .
其 特征 可 以是一 个或 多个 服务 台 , 务 时间 的分 布与时 间有 关或无 关 , 服 服务 台为 顾客 服务 的时 间可
收 稿 日期 :0 5—1 20 2—1 6
策略 , 为用户的正确决策提供参考. 本文介绍的排 队系统仿真软件能较好地实现 以上三种服务方式 的计
算机 仿 真.
1 排 队系统 中的一些概念
因为排队现象是一个随机现象 , 因此在研究排队现象 的时候 , 主要采用的是研究随机现象的概率论
作为 主要 工具 . 在排 队系统 的仿 真 中 , 常用 到 的一 些 概念有 :
关键词 : 队系统 ; 排 队列 ; 服务 ; 计算机仿真
中图分类号 :P 1 T 31 文献标 识码 : A 文章编号 : 0 26 (0 6 0 0 2 0 1 0— 12 20 )4— 0 6— 0 4
排 队论 是 运筹 学 的主要 分支 , 现代社 会生 活 中 , 多 问题 可 以归为 排 队 系统 , 队 系统 是 研究 服 在 很 排 务 台 的工作 效率 问题 . 队论研 究 的 内容包 括 :1 数 量指标 : 排 () 队长 、 态 实 体等 待 时 间和 逗 留时 间 的分 动
稳 态平 均延 迟 时间 d
d = lm i
, 一 *
D l /,
。
其 中, 为第 个实体 的延迟时间( 即在队中排队的时间) n , 为已接受服务的实体总数 , 也就是 n d 个实 体的平均等待时间. 实 体通 过系 统 的稳态 平均 滞 留时 间 w
数学建模论文(蒙特卡罗的多服务台和单服务台排队系统)

课程名称:数学建模与数学实验学院:专业:姓名:学号:指导老师:利用Monte Carlo方法模拟单服务台排队系统和多服务台排队系统摘要蒙特卡罗方法(Monte Carlo)又称统计模拟法随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。
本文通过两个具体的服务机构为例,分别说明如何利用蒙特卡洛方法模拟单服务台排队系统和多服务台排队系统。
单服务台排队系统(排队模型之港口系统):通过排队论和蒙特卡洛方法解决了生产系统的效率问题,通过对工具到达时间和服务时间的计算机拟合,将基本模型确定在//1M M排队模型,通过对此基本模型的分析和改进,在概率论相关理论的基础之上使用计算机模拟仿真(蒙特卡洛法)对生产系统的整个运行过程进行模拟,得出最后的结论。
多服务台排队系统(开水供应模型):为了解决水房打水时的拥挤问题。
根据相关数据和假设推导,最终建立了多服务窗排队M/G/n模型,用极大似然估计和排队论等方法对其进行了求解,并用Matlab软件对数据进行了处理和绘图。
用灵敏度分析对结果进行了验证。
本模型比较完美地解决了水房排队拥挤问题,而且经过简单的修改,它可以用于很多类似的排队问题。
关键词:蒙特卡洛方法,排队论,拟合优度,泊松流,灵敏度分析。
一、问题重述港口排队系统:一个带有船只卸货设备的小港口,任何时间仅能为一艘船只卸货。
船只进港是为了卸货,响铃两艘船到达的时间间隔在15分钟到145分钟变化。
一艘船只卸货的时间有所卸货物的类型决定,在15分钟到90分钟之间变化。
开水供应系统:学院开水房的供水时间有限,水房面积有限,水管易受水垢堵塞。
根据调查数据可知:通畅时几乎无人排队,堵塞时水房十分拥挤。
由此可以看出水房设计存在问题,我们可以把开水房看成是一个随即服务系统,应用排队论的方法对系统运行状态做定量的描述。
优先级队列的应用——多服务台排队系统的模拟

多服务台排队系统的模拟一、与单服务台排队系统相比1.在多服务台系统中,先到达的顾客先获得服务,这个规则仍然存在;但后获得服务的顾客可能先离开,这是因为每个顾客要求的服务时间是不一样的。
如果各科i要求的是一个复杂业务,服务台j提供服务;而顾客i+1要求的是一个简单业务,服务台k提供服务,那么顾客i+1虽然比顾客i晚到达,却比顾客i先离开。
2.在单服务台系统中,到达次序和离开次序是一致的,所以只需要一个先进先出的队列;在多服务台系统中,离开事件不再与到达事件保持一致,先处理的到达事件对应的离开事件可能比后处理的到达事件对应的离开事件发生得晚,因此需要一个优先级队列,将事件发生得时间作为优先级,发生时间早的事件先处理,发生时间晚的事件后处理。
二、多服务台排队系统模拟过程1.模拟开始时,产生所有的到达事件,存入优先级队列,此时队列只有到达事件。
2.模拟器开始处理事件。
首先从队列中取出一个事件,这是第一个顾客的到达事件,根据各科的服务要求生成对应的服务时间,当前时间+服务时间=这个顾客的离开时间,生成一个这个时候离开的事件插入队列,这样在队列中就有了两类事件:到达事件和离开事件。
3.这样模拟器从队列中取出的事件也可能是离开事件,这时只要将这个离开事件从队列中删去,为它服务的服务台就可以为别的顾客服务。
综上:(1)产生所有的顾客到达事件,存入事件队列;(2)模拟器从事件队列中取事件,按照不同的事件类型处理事件。
①若是到达事件,先检查有没有空闲的服务台,如果有,则为此顾客生成服务时间,并产生一个离开事件,插入事件队列。
②如果处理到达事件时,没有空闲的服务台,则该顾客进入到等待队列排队。
等待队列是一个普通的先进先出的队列。
(3)如果处理的是离开事件,则释放该服务台。
如果此时等待队列有人排队,则服务台为他服务,并统计等待时间,如果等待队列没有人排队则置服务台为空闲。
三、伪代码产生CustomNum个顾客的到达事件,按时间的大小存入事件队列;置等待队列为空;置所有柜台为空闲;设置等待时间为0;While(事件队列非空){队头元素出列;设置当前时间为该事件发生的时间;switch(事件类型){case 到达:if(柜台有空){柜台数-1;生成所需的服务时间;修改事件类型为“离开”;设置事件发生时间为当前时间+服务时间;重新存入事件队列;}else 将该事件存入等待队列;case 离开:if(等待队列非空){队头元素出队;统计该顾客的等待时间;生成所需的服务时间;修改事件类型为“离开”;设置事件发生时间为当前时间+服务时间;存入事件队列;}else 空闲柜台+1;}}计算平均等待时间;返回;四、代码分析代码清单6-9 模拟类的定义class simulator{//以下定义了保存模拟参数的数据成员int noOfServer; //服务台的个数int arrivalLow; //到达间隔时间的下界int arrivalHigh; //到达间隔时间的上界int serviceTimeLow; //服务间隔时间的下界int serviceTimeHigh; //服务间隔时间上界int customNum; //模拟的顾客数struct eventT//定义了一个私有内嵌类eventT,用于保存一个事件信息,是事件队列和等待队列中的元素类型,eventT有两个数据成员,time表示事件发生的时间,type表示事件类型{int time; //事件的大小取决于事件发生的时间,发生时间早的事件优先级高,发生时间晚的事件优先级低int type; //事件类型,0为到达,1为离开bool operator<(const eventT &e)const{return time<e.time;}};public: //两个公有函数simulator();//模拟类的构造函数int avgWaitTime();//模拟类的平均等待时间函数};代码清单6-10 构造函数的实现simulator::simulator()//模拟参数的输入{ cout<<"请输入柜台数:"; cin>>noOfServer;cout<<"请输入到达时间间隔的上下界(最小间隔时间最大间隔时间):";cin>>arrivalLow>>arrivalHigh;cout<<"请输入服务时间的上下界(服务时间上界服务时间下界):";cin>>serviceTimeLow >>serviceTimeHigh;cout<<"请输入模拟的顾客数:";cin>>customNum;srand(time(NULL)); //完成随机数发生器的初始化}代码清单6-11 avgWaitTime函数的实现int simulator::avgWaitTime()//根据模拟参数进行模拟,并统计出平均等待时间{ int serverBusy=0; //正在工作的服务台数int currentTime; //表示现在模拟到了什么时间int totalWaitTime=0; //记录整个模拟过程中所有顾客的等待时间总和linkQueue<eventT>waitQueue; //定义了一个类型为eventT的链接队列waitQueue,这个队列是等待队列,用来保存正在排队的顾客信息priorityQueue<eventT>eventQueue; //定义了一个类型为eventT的优先级队列eventQueue,保存的是整个模拟过程中发生的所有事件eventT currentEvent;//根据模拟参数中指定的顾客数生成所有顾客的到达事件,并存入事件队列int i;currentEvent.time=0;currentEvent.type=0;for(i=0;i<customNum;++i){ currentEvent.time+=arrivalLow+(arrivalHigh-arrivalLow+1)*rand()/(RAND_MAX+1); //每个顾客的到达时间为前一顾客的到达时间加上随机生成的到达时间间隔eventQueue.enQueue(currentEvent);}while(!eventQueue.isEmpty())//只要队列非空,就要处理事件,直到队列为空{currentEvent=eventQueue.deQueue();//先从事件队列中取出一个事件currentTime=currentEvent.time; //把模拟时钟直接拨到事件发生的时间switch(currentEvent.type) //然后根据事件发生类型进行不同的处理{case 0: //如果是到达事件if(serverBusy!=noOfServer) //首先检查有没有空闲的服务台{++serverBusy; //如果有空闲的,则分配服务台currentEvent.time+=serviceTimeLow+(serviceTimeHigh-serviceTimeLow+1)*rand()/(RAND_MAX+1); //离开时间=服务时间+当前时间currentEvent.type=1; //服务完后,生成一个离开事件eventQueue.enQueue(currentEvent); //入队,事件队列}else waitQueue.enQueue(currentEvent);//否如果没有空闲的服务台,这位顾客要到等待队列排队,入队,等待队列break;case 1: //若是离开事件if(!waitQueue.isEmpty())//检查有没有顾客在排队,即等待队列是否为空{currentEvent=waitQueue.deQueue();//若有顾客在排队,则为等待队列队头的顾客服务,即让等待队列队头元素出队totalWaitTime+=currentTime-currentEvent.time; //把这位顾客的等待时间加入到总的等待时间,currentTime为当前时间,currentEvent.time为顾客进入到等待队列的时间,即事件发生的事件currentEvent.time=currentTime+serviceTimeLow+(serviceTimeHigh-serviceTimeLow+1)*rand()/(RAND_MAX+1);//currentEvent.time在这指离开时间=当前时间+随机数生成的服务时间currentEvent.type=1; //服务完后,生成一个离开事件eventQueue.enQueue(currentEvent); //入队,事件队列}else--serverBusy; //若没有人排队,则服务台可以休息,所以正在工作的服务台-1}}return totalWaitTime/customNum; //计算并返回平均等待时间}。
第六章 排队系统仿真

6.2 排队系统的组成部分
– 6.2.1 输入过程 – 6.2.2 排队规则 – 6.2.3 服务机构
6.3 排队系统的特性 6.4 排队系统的类型
– 6.4.1 最简单的排队系统 – 6.4.2 M/M/n成批到达队列 – 6.4.3 M/M/1串联服务系统 – 6.4.4 M/M/n系统
Page 2
Page 8
第六章 排队系统仿真
6.2 排队系统的组成部分 排队系统又称服务系统。服务系统由服务机构和服务对象(顾客)构 成。服务对象到来的时刻和对他服务的时间(即占用服务系统的时间)都 是随机的。排队系统包括三个组成部分:输入过程、排队规则和服务机构 。
Page 9
第六章 排队系统仿真
6.2 排队系统的组成部分 输入过程 输入过程描述了顾客来源和顾客按怎样的规律到达排队系统。 顾客的来源可能是有限的,也可能是无限的;顾客是单个到达还是成 批到达;相继到达的顾客的时间服从什么样的概率分布,分布的参数是什 么,到达的间隔时间之间是否独立。 输入过程考察的是顾客到达服务系统的规律。它可以用一定时间内顾 客到达数或前后两个顾客相继到达的间隔时间来描述,一般分为确定型和 随机型两种。
∑µ
i =1 k
i
P 该顾 客在 k 个顾 客中 排在第 i个 位置 =
∞
∑µ
i =1
k
i 1 k +1 = k 2µ
平均逗留时间为 W = ∑ µ + 2µ P = µ = 2µ L = λ k (W ) ,带入上式,解出 W = k + 1 , µ > λ k 。
第六章 排队系统仿真
排队系统是由顾客和为顾客提供服务的服务台组成的系统。 排队系统是由顾客和为顾客提供服务的服务台组成的系统。顾客先进 入等待队列排队,然后接受服务台提供的服务。排队系统在服务业、物流 业及生产制造等行业有广泛的应用。例如,顾客到银行办理业务时先排队 ,然后在柜台(服务台)接受服务;物流系统中车辆(顾客)在装卸点排 队,然后接受装卸机械(服务台)的装卸服务;生产系统中产品(顾客) 在加工机器前排队,然后接受机器(服务台)的加工服务等。 排队系统由两方构成,一方要求得到服务,另一方设法给予服务。 排队系统由两方构成,一方要求得到服务,另一方设法给予服务。把 要求得到服务的人或物(设备)统称为顾客,给予服务的服务人员或服务机 构统称为服务员或服务台(有时服务员专指人,而服务台是指给予服务的设 备)。顾客与服务台就构成一个排队系统,或称为随机服务系统。显然,缺 少顾客和服务台任何一方都不会形成排队系统。
多服务台排队系统的仿真

实验3---多服务台排队系统的仿真姓名:学号:一、目标任务已知一个系统有N个服务员,能力相等,服务时间服从指数分布。
顾客的到达时间间隔服从指数分布。
用Monte-Carlo仿真,分别求按下列方案的总体平均排队时间:① M|M|N。
② N个单通道系统并列,按1/N概率分裂到达流。
③ N个单通道并列,挑选最短的队。
要求:①给出程序设计的过程。
②如果采用固定的N,则要求N>2。
③至少取ρ=0.3和ρ=0.7两种强度运行程序。
④对结果进行分析。
二、编程语言Matlab三、关键代码方案一:N = 3; % 服务员人数r = 6; % 顾客到达流强度u = 20; % 服务员服务强度T = 1000000; % 仿真运行时间avg_wait_time = []; % 平均等待时间for i=1:100% 模拟排队函数server_time = [0.0, 0.0, 0.0]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为0client_num = 0; % 顾客总数,初始为0CRTime = 0; % 顾客到达时间间隔ServeTime = 0; % 顾客服务时间server_id = 0; % 当前进入排队窗口的服务员编号total_wait_time = 0;% 系统中到达顾客的总等待时间while 1CRTime = exprnd(1/r); % 按指数分布产生顾客到达时间间隔time = time + CRTime; % 更新系统的绝对时钟if time > Tbreak;endclient_num = client_num + 1; % 顾客数加1ServeTime = exprnd(1/u); % 按指数分布产生顾客服务间隔server_id = mod(client_num, N); % 按1..N的顺序循环排入服务员窗口if server_id ==0server_id = N;endif server_time(1, server_id) <= time % 如果当前server_id号服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; % 服务员下一空闲时间为当前绝对时钟加上当前服务时间else % 否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; % 顾客排队等候时间为当前服务员下一空闲时间减去绝对时钟server_time(1, server_id) = server_time(1, server_id) + ServeTime;endendavg_wait_time = [avg_wait_time, total_wait_time/client_num];end% 计算平均等待时间mean_avg_wait_time = mean(avg_wait_time);fprintf('ρ=%2.1f平均等待时间%6.5f\n', r/u, mean_avg_wait_time); % 打印平均等待时间% 绘制每次仿真的平均等待时间和总体平均等待时间线状图x = 1:100;%plot(x, avg_wait_time, x, mean_avg_wait_time);scatter(x, avg_wait_time, '.');方案二:N = 3; % 服务员人数r = 6; % 顾客到达流强度u = 20; % 服务员服务强度T = 1000; % 仿真运行时间avg_wait_time = []; % 平均等待时间for i=1:100% 模拟排队函数server_time = [0.0, 0.0, 0.0]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为0client_num = 0; % 顾客总数,初始为0CRTime = 0; % 顾客到达时间间隔ServeTime = 0; % 顾客服务时间server_id = 0; % 当前进入排队窗口的服务员编号total_wait_time = 0;% 系统中到达顾客的总等待时间while 1CRTime = exprnd(1/r); % 按指数分布产生顾客到达时间间隔time = time + CRTime; % 更新系统的绝对时钟if time > Tbreak;endclient_num = client_num + 1; % 顾客数加1ServeTime = exprnd(1/u); % 按指数分布产生顾客服务时间间隔server_id = randi([1 N]); % 按1/N的概率排入服务员窗口if server_time(1, server_id) <= time % 如果当前server_id号服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; % 服务员下一空闲时间为当前绝对时钟加上当前服务时间else % 否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; % 顾客排队等候时间为当前服务员下一空闲时间减去绝对时钟server_time(1, server_id) = server_time(1, server_id) + ServeTime;endendavg_wait_time = [avg_wait_time, total_wait_time/client_num];end% 计算平均等待时间mean_avg_wait_time = mean(avg_wait_time);fprintf('ρ=%2.1f平均等待时间%6.5f\n', r/u, mean_avg_wait_time); % 打印平均等待时间% 绘制每次仿真的平均等待时间散点图x = 1:100;scatter(x, avg_wait_time, '.');方案三:N = 3; % 服务员人数r = 6; % 顾客到达流强度u = 20; % 服务员服务强度T = 1000; % 仿真运行时间avg_wait_time = []; % 平均等待时间for i=1:100% 模拟排队函数server_time = [0.0, 0.0, 0.0]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为0client_num = 0; % 顾客总数,初始为0CRTime = 0; % 顾客到达时间间隔ServeTime = 0; % 顾客服务时间server_id = 0; % 当前进入排队窗口的服务员编号total_wait_time = 0;% 系统中到达顾客的总等待时间while 1CRTime = exprnd(1/r); % 按指数分布产生顾客到达时间间隔time = time + CRTime; % 更新系统的绝对时钟if time > Tbreak;endclient_num = client_num + 1; % 顾客数加1ServeTime = exprnd(1/u); % 按指数分布产生顾客服务时间间隔temp = min(server_time); % 寻找排队时间最短的服务员窗口[x, y] = find(temp == min(min(server_time)));server_id = y; % 按队伍最短排入服务员窗口if server_time(1, server_id) <= time % 如果当前server_id号服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; % 服务员下一空闲时间为当前绝对时钟加上当前服务时间else % 否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; % 顾客排队等候时间为当前服务员下一空闲时间减去绝对时钟server_time(1, server_id) = server_time(1, server_id) + ServeTime;endendavg_wait_time = [avg_wait_time, total_wait_time/client_num];end% 计算平均等待时间mean_avg_wait_time = mean(avg_wait_time);fprintf('ρ=%2.1f平均等待时间%6.5f\n', r/u, mean_avg_wait_time); % 打印平均等待时间% 绘制每次仿真的平均等待时间散点图x = 1:100;scatter(x, avg_wait_time, '.');四、实验结果与分析方案一:图1 方案一仿真的平均等待时间散点图图2 方案一平均等待时间M|M|N1. 输入参数:服务员人数N,顾客到达流强度r,服务员服务强度u,仿真运行时间T;2. 各变量初始值置0:绝对时钟time,服务员下一空闲时刻数组server_time[](其中按顺序保存每一个服务员的下一空闲时刻),顾客总数client_num,顾客到达时间间隔CRTime,顾客服务时间ServeTime,当前进入排队窗口的服务员编号server_id,系统中顾客总等待时间total_wait_time;3. 按照指数分布产生下一顾客到达的时间间隔CRTime,time+=CRTime。
第六章-排队系统建模与仿真(New)
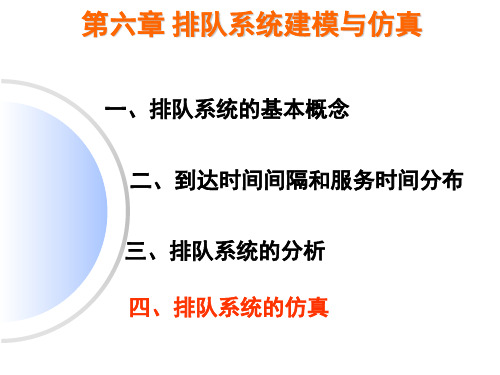
出现的次数ft 38 25 17 9 6 5 0 100
三、排队系统的分析
解:(1)计算 平均到达速度:
nfn 2.1人 / 小时
100
平均手术时间: 平均服务速度:
Ts
tft 100
0.37小时 / 人
1 1 2.5人 / 小时
Ts 0.4
(2)取λ=2.1,μ=2.5,通过统计检验方法的检验,可以认 为病人到达数服从参数为2.1的泊松分布,手术时间服从参数 为2.5的负指数分布。
服务员空闲否?
Y
开始服务
经过Si
服务完毕
N
排队等待
顾客离去
四、排队系统的仿真
仿真方法:手工仿真 仿真初始条件:系统中没有顾客,即:排队的队列中没有顾客等待,服务台 无服务对象。 仿真开始:以第一个顾客到达时刻为仿真的起始点。
四、排队系统的仿真
? 事件何时出现?
在仿真中,通过随机数来产生!
四、排队系统的仿真
• M——负指数分布 • M/M/1表示相继到达时间为负指数分布,服务时 间为负指数分布,单服务设备的模型。
三、排队系统的分析
1 单服务台M/M/1模型(M/M/1/∞/ ∞/FCFS)
(1)到达模式。动态实体源是无限的,动态实体单个 到达,相互独立,一定时间的到达数服从泊松分布。
(2)排队规则。单对,且队列长度没有限制,先到先 服务。
混合制
队列的度量
队列的度量
(1)服务强度
1
T0
n
1 Ts
ns
(2)实际业务强度u‘
u' ' 1
(3)服务设备利用率
n
三、排队系统的分析
随机排队系统的运行指标: 在系统中动态实体数量的期望值Ls, 在系统队列中等待的动态实体数量(队列长度)的 期望值Lq。 在系统中动态实体逗留时间的期望值Ws, 在队列中动态实体等待时间(排队时间)的 期望值Wq。
服务台单队列排队系统仿真

服务台单队列排队系统仿真1. 引言排队是我们日常生活中常见的现象之一。
每当我们去银行、超市、餐厅等地方,总会看到人们在服务台前排长队等待接受服务。
而排队系统的效率直接影响到我们的等待时间和满意度。
为了改善排队系统的效率,许多地方引入了服务台单队列排队系统。
这种系统中,所有顾客都将排在同一个队伍中,然后按照先后顺序依次接受服务。
这种系统相比于多个队列排队系统,能够有效减少空闲时间和服务延迟。
为了对服务台单队列排队系统进行评估和优化,我们可以使用仿真技术来模拟系统的运行情况,并对其进行分析。
2. 仿真模型设计在服务台单队列排队系统的仿真模型中,我们需要考虑到以下几个方面的因素:2.1 顾客到达规律在实际排队系统中,顾客的到达时间往往是随机的,我们可以使用随机数生成器来模拟此过程。
通过设定到达时间的概率分布函数,我们可以生成一系列随机数来模拟顾客的到达间隔。
2.2 服务时间每个顾客在服务台的服务时间也是随机的。
同样地,我们可以使用随机数生成器来模拟服务时间。
通过设定服务时间的概率分布函数,我们可以生成一系列随机数来模拟顾客在服务台的停留时间。
2.3 服务台数量为了简化仿真模型,我们假设只有一个服务台。
在实际情况中,可以根据实际需求增加服务台数量,以提高系统的整体效率。
2.4 排队规则在服务台单队列排队系统中,顾客按照先后顺序依次接受服务。
当一个顾客结束服务后,下一个顾客将开始接受服务。
为了模拟这个过程,我们可以使用队列数据结构来管理顾客的排队顺序。
3. 仿真过程在进行仿真过程时,我们可以按照以下步骤进行操作:3.1 初始化仿真参数根据实际情况,我们可以设定好仿真的时间段、顾客到达规律和服务时间的概率分布函数等参数。
3.2 创建顾客队列根据顾客到达规律,我们可以按照一定的间隔时间将顾客加入到队列中。
3.3 顾客进入服务台当顾客队列不为空时,服务台将接受当前队列中的第一个顾客,并开始对其进行服务。
3.4 更新服务时间和队列在服务过程中,服务单位时间递减,直到达到零时,服务结束,当前顾客离开服务台,下一个顾客开始接受服务。
数学建模:排队系统仿真

4、外部信号分路形式:需添加外部信号产生器和 分路器进行连接,根据外部信号产生器产生结果, 决策出口。
2、带概率分路形式:等概率的随机 选择分路模块的各出口。
Exopential:指数分布。(Mean:数
学期望值,即顾客达到平均间隔时间)
Uniform:均匀分布。(Mean:均匀
分布的数学期望值)
Constant:常数值。(Mean:对应常
数值,每隔常数值时间发出一个顾客)
打开“Time-Based Entity Generator”对话框
双击“Time-Based Entity Generator”模块(基 于时间的实体生成器)
双击“Discrete Event Signal to Workspace” 模块打开对话框
把排队离开顾客数记录信息赋值给变量 paiduilikaigukeshujilu 存储格式为数组(Array)
在Matlab窗口下敲入变量名称”paiduilikaigukeshujilu”打回车,即显示模拟时间 内的顾客累计离开数。
服务台模块(共 3 种)
打开“Single Server”对话框
双击“Single Server”模块
服务时间,所有顾客服务时间均一样
Service time from(服务时间形式):选择”signal port t”时,需要为其指定服务时间分布。
随机数产生器
将随机数产生器 (Events-Based random number)拖 动到模型编辑器中, 并同服务器(Single Server)的 t 端口建立 输入连接。
多服务台混合制排队模型M_G_s_K的仿真研究_陈实

( 2) 矩阵初始化 在仿真开始之前, 队列中无顾客在等候, 所以将该 矩阵初始化为 2 @ ( K - s) 的零矩阵。 ( 3) 矩阵的更新算法 等待队列信息矩阵中的元素应随着仿真时钟的推 进而不断更新 , 每次仿真时钟刷新之后 , 矩阵就应按照 如下算法进行更新 : ¹ 若仿真时钟所指时刻刚好有顾客结束服务离开 系统或此时有服务台处于空闲状态, 如果等待队列中仍 有乘客在等待 , 则此服务台接受占据等待矩阵第一列的 乘客 , 并将等待矩阵中所有其他顾客的信息前移一列。 用 0 元素填充不存储有等待顾客信息的矩阵列。如果 等待队列中没有顾客在等待 , 即此时等待队列信息矩阵 为一个零矩阵 , 则不对等待队列信息矩阵做任何变换。 143
过离散化处理仿真时间方 法 , 并借 鉴时间步长法的思想 , 给出一 种基于 M at lab 编程的仿 真算法 。 通过实验说明 了该方法的 有效性 。 对于处理此类排队问题提供了一个新的方法 。 关键词 : 多服务台混合制排队模型 ; M / G/ s/ K 排队模型 ; 时间步长法 ; M atlab 编程 中图分类号 : T N911 - 34; T P274 文献标识 码 : A 文章编号 : 1004 - 373X( 2010) 17 - 0142 -04
自动化技术
陈
实 : 多服务台混合制排队模型 M /G /s /K 的仿真研究
多服务台混合制排队模型 M /G /s /K 的仿真研究
陈 实
200241) ( 华东师范大学 金融与统计学院 , 上海 摘
要 : 为更快 、 更方便地得到一般服务时间的多服务台混 合制中 M / G/ s/ K 排队系统 在达到 稳定之 后的系 统状态 , 通
表2 等待队列信息矩阵 矩阵行存放的信息 顾客进入等待队列的时刻 顾客接受服务台服务所要花费的时间
排队论系统仿真

于零,即
dPn (t ) 0, 对一切n 。 dt 因为稳态和时间无关,所以将符号简化,用 Pn 代替 Pn(t),于是
Pn n 1 n 2 0 P0 n n 1 1
i 0 n i 1
——平均服务率,即单位时间内接受服务的顾客数;
C——并列服务台的个数;
——服务强度。
通常,排队论研究的相关问题可大体分成统计问题和最优化问题两大类。 统计问题是排队系统建模中的一个组成部分,它主要研究对现实数据的处理 问题, 在输入数据的基础上, 首先要研究顾客相继到达的间隔时间是否独立同分
布,如果是独立同分布,还要研究分布类型以及有关参数的确定问题.类似地, 对服务时间也要进行相应的研究。 排队系统的优化问题涉及到系统的设计、控制以及有效性评价等方面的内 容。 排队论本身不是一种最优化方法,它是一种分析工具。常见的系统最优设计 问题是在系统设置之前, 根据已有的顾客输入与服务过程等资料对系统的前景进 行估计或预测,依此确定系统的参数。 系统最优控制问题是根据顾客输入的变化而对现有服务系统进行的适度调 整,即根据系统的实际情形,制定一个合理的控制策略,并据此确定系统运行的 最佳参数。作为一种分析工具,处理排队问题的过程可以概括为以下四步: (1)确定排队问题的各个变量,建立它们之间的相互关系; (2)根据已知的统计数据, 运用适当的统计检验方法以确定相关的概率分布; (3)根据所得到的概率分布,确定整个系统的运行特征; (4)根据服务系统的运行特征,按照一定的目的,改进系统的功能。
P0 (t ) e t
T 小于等于 t 的概率 P(T≤t)表示为 F(t) (累积分布函数) ,有
F (t ) 1 et
排队系统的仿真与应用论文

摘要排队系统是一个应用很广泛的课题。
它可以应用于各个部门,比如:银行储蓄柜的排队管理,医院门诊挂号,电信营业厅排队管理,财政营业厅,税务报税大厅,工商注册,海关业务大厅,邮政业务,民航、铁路、车站售票处等任何窗口服务需要排队等候的场所。
在这些场所,使用排队管理系统的意义重大。
首先,它可以提升服务机构的形象,提高服务质量;其次,减少客户的等待时间,杜绝大厅的纷乱现象;最后,它也为部门有关决策提供依据,增加对工作人员的考核依据。
此外利用排队系统的原理结合预测算法和大量历史数据来设计系统,用它来预测顾客的到来和顾客的订单。
利用本系统可以科学的预测将来的某一天中顾客的到达情况和他所要的订单,为公司生产多少产品提供了依据。
除了以上的基本功能外,本系统还提供了对历史数据和库存基本操作,更方便了用户的使用。
希望对朋友们有所启发,也希望同朋友们一起完善它,使之更实用。
【关键词】排队系统预测数据库操作历史数据随机数AbstractQueueing system is an applied very extensive lesson. It can apply in the each department,for example,the queueing system using in the cashomart of bank, the hospital out-patient service registers,the system using in the telecommunication business hall,public finance business hall,tax administration tax reporting hall,industry and business register, maritime customs business hall, postal service business, and civil , railroad, station box office etc. any places which provide server windows and demand waiting in line. In these places, it is very important to use the queueing system. First, it can promote the image of the service organization,and increase service quantity; Second, it also can reduce the customer's time spending on waiting, and eradicate completely the confusion phenomenon of the hall; Finally, it can provide grounds for some relevant decisions, and increase to investigate to the worker basis. In addition,making use of the principle of the queueing system ,predictive algorithm, and a flood of history data,we can design a system,with which to predict when the next customer will come and how many products he will order.Making use of this system,you can predict scientifically the situation of the arrives of customers and their orders on some day in the future,which could provide the basis on how many products should be produce in the future. In addition to above basic function, this system still provided the basic operations for the history data in stock,making it more convenient. I hope this system to have to inspire to the friends.I also hope to make it perfect with friends, let it more practical. 【Key Words】Queueing system;Pretect;Operate on database; History data;Random number目录引言 (2)第一章系统概述及其体系结构 (3)1.1系统概述 (3)1.2系统体系结构 (4)第二章开发环境介绍 (6)2.1 Microsoft Visual C++ 6.0简介 (7)2.2开发过程中所用到的组件及其介绍 (12)2.3开发过程中所用到的数据库及其简介 (13)第三章系统功能的实现 (15)3.1预测算法的原理 (15)3.2 Visual C++环境下数据库与应用程序的连接 (19)3.3 各个功能模块的实现简介 (21)第四章开发过程中遇到的问题及其解决方法 (36)第五章系统的改进方案 (37)第六章心得体会 (38)致谢 (39)参考文献 (40)附录 (41)引言离散事件系统中,由于顾客到来时间间隔与服务台服务时间都是随机的,所以在系统中会产生顾客排队现象,排队是该类系统的特征. 离散系统仿真技术是研究该类系统的有效方法,在计算机上模拟逐个顾客的来到、排队、服务及离开,统计得到整个系统的运行参数,即根据顾客到来及服务台结构、服务时间的分与参数得到了顾客的等待时间与服务台效率,从而有效地分析各类排队系统的性能。
多服务台指数分布排队系统

• 引言 • 引言 • 引言 • 多服务台指数分布排队系统概述 • 多服务台指数分布排队系统的性能指
标
• 多服务台指数分布排队系统的优化设 计
• 多服务台指数分布排队系统的应用实 例
• 结论与展望
01
引言
平均等待时间
• 平均等待时间表示顾客在进入系统后等待接受服务的平均 时间。
系统参数的优化调整
等待时间
过长可能导致客户不满,过短可能造成资源浪 费。
忙期持续时间
过长可能导致服务台超负荷运行,过短可能造 成资源闲置。
优化建议
通过实时监控和数据分析,调整系统参数,以实现服务质量和经济效益的平衡。
05
多服务台指数分布排队系统的应用实
例
银行服务排队系统
总结词
适用于银行服务的多服务台指数分布排队系统能够有效地解决客户等待时间过长的问题, 提高服务效率。
详细描述
在机场安检过程中,乘客需要经过多个环节的检查才能进入候机区。为了提高安检效率,机场通常会设置多个安 检通道,并采用多服务台指数分布排队系统来分配乘客到各个通道。该系统能够根据乘客到达时间和安检流程的 复杂程度,动态调整每个通道的服务速率,使得乘客能够快速、有序地完成安检。
医院挂号排队系统
要点一
04
本文还探讨了系统在不同负载情况下的性能表现,发 现系统在高负载下容易出现性能瓶颈,因此需要合理 设计系统以应对高负载情况。
研究展望
未来研究可以进一步探讨多服务台指 数分布排队系统在不同类型任务和复 杂环境下的性能表现,以更好地适应 实际应用需求。
此外,可以考虑将多服务台指数分布 排队系统与其他排队模型进行比较研 究,以进一步了解其优势和局限性。
排队论讲义-2

5⎤−1
[M/M/c]:[∞/m/FCFS
由(63)可以计算得到(算式略): P1=0.394,P2=0.197,P3=0.074,P4=0.018,P5=0.002 由此,计算系统的各项运行指标如下:
(1) Lq =
n=c+1
. ∑ (n − c)Pn = P3 + 2P4 + 3P5 = 0118
]
(58)
(59) (60)
Wq =
Lq λ (1 − P N )
q
(61) 特别,当N=c时,系统的队列最大长度为0,即顾客到达时,如果服务台有空闲 ,则进入服务台接受服务,如果服务台没有空,顾客则当即离去。这样的系统 成为“即时制”。许多服务设施,如旅馆、停车场等都具有这样的性质。
W = W
+
[M/M/c]:[N/∞/FCFS
[M/M/c]:[∞/∞/FCFS]
这个系统的特点是,系统的服务速率与系统中的顾客数有关。当系统 中的顾客数k不大于服务台个数,即1≤k≤c时,系统中的顾客全部在服 务台中,这时系统的服务速率为kμ;当系统中的顾客数k>c时,服务 台中正在接受服务的顾客数仍为c个,其余顾客在队列中等待服务,这 时系统的服务速率为cμ。为了求得系统的状态概率,先作出系统的状 态转移图。 P0 P1 P2 Pc-1 Pc Pc+1
正在修理的机器 修理速率μ
顾客到达
修理速率μ 发生故障等待修理的机器 修理速率μ
到达速率 (m-n)λ 运行的机器数 m-n
修理速率cμ
[M/M/c]:[∞/m/FCFS
用状态转移图可以得到状态概率与运行指标(推导过程从略): 1 7.6.3.1 状态概率 P = 1 ⋅
第四章多服务窗排队模型MMn….ppt

p
k 0
k
1
n 1 1k 1n 1- m n 1 1 ] [ 1 k 0 k ! n ! p0 k n n 1 n 1 [ ( m n 1)] k 0 k ! n !
1 1
3 多服务窗混合制排队模型M/M/n/m
0 1 2
n-1
n n
n+1 n
n+2 n
2
3
(n-1)
n
服务窗还有空闲
n个服务窗全忙
2 多服务窗等待制排队模型M/M/n
求平稳分布
令1 , , 1 n
1k nk k p0 p0 k! k! pk k n n 1 p k p 0 0 n! n !n k n
(n 1)!(n 1 )
1n p0
2
n n!(1 )2
1n p0
平均系统内逗留时间
Ws Ls
Ws Wq W服 Wq
1
2 多服务窗等待制排队模型M/M/n
来到系统的顾客必须排队等待的概率
nn k C (n, ) C (n, 1 ) pk p0 k n k n n !
p
k 0
m
k
1
n 1
k C k! k p0 [ Cm 1k m k n 1k ]1 k 0 k n n !n
4 多服务窗闭合式排队模型M/M/n/m/m
目标参量
Lq (k n) pk
k n m m
Ls kpk
k 0
在Excel中应用随机函数模拟多服务台多队列排队系统

务 台两 队列为例 . 模拟排队系统 。如果需要更专业更精确 的模拟 研究 , 使用 Fes A eaPo oe、 t s、 推荐 l i x m、 rn 、rm d l n s Wi e
负熵流抵消系统内部熵的产生 ,使整个系统熵值减少 , 系 容易, 创造力也就越高 , 与此 同时, 其情报活动也会更加有 统逐步向有序的方向转化 。因此 。 开放是系统从无序走 向 效。
晶 晶
( 天津科 技大 学 经 济 与管理 学 院 , 津 30 2 ) 天 0 2 2
[ 要] 摘 在多 服务台的排队系 统中, 客户排成单队列比排成多队列更有效率。因此, 不论是理论研究还是 系 统模拟
研究 , 究人 员很 少关注多台多队列的情况。本文提供 了一种基于 E cl 研 xe 的简便 方法 。 以两服务 台两队列 为例 。 模拟 排队 系统 。
有 序的必要 条件 。 报用 户必须 使其 自身知识 结构 系统对 情 知 识是 产生创 见 的基础 和原料 . 何领域 的创 新 活动 任
外界环境能保持较高的动态适应能力 , 要注重随时补充吸 都要以该领域中的已有知识和成果为起点。 而知识对创新 收、 更新重组知识结构, 以保证情报活动的效率和效果 。 的作用 . 不仅仅在于知识的数量 , 更重要的在于知识 的组 c 注重协同, 2 ) 充分发挥整体功能。 根据耗散结构理论 , 织结构。因为创造力本身可以看成是对跨越时空的各种知
系统 中存在 复杂 的非线 性关 系 。 要素 之 间会产 生 相关 性 识 的全 新 意 义 的调 用 、 各 重组 、 品化 ( 中还 包 括 人 际 知 产 其
联系。系统的整体功能不再是各要素功能 的简单线性加 识 、 情绪智力的运用等 ) 一个合理的知识结构中的知识成 。 和。 而是一种各要素所不具有的新质 , 是在更高的能量层 分 , “ ” 知识 , 是 活 的 不是 一 般意 义 上 的堆 砌 在头 脑 中的东
一个基于VC + +的多台多队仿真系统

一个基于VC + +的多台多队仿真系统
傅廷亮;李春生;汪鑫
【期刊名称】《安徽大学学报(自然科学版)》
【年(卷),期】2006(030)004
【摘要】排队系统是离散系统中常见的一大类研究对象,尤其是多服务台多队列服务方式较难得到满意的解决.本文讨论了排队系统和排队系统的计算机仿真,开发了一个基于VC + +的多台多队仿真系统软件,用户可选择服务台数和队列数以及与两者有关的参数.通过多次仿真结果的比较,可对较复杂的排队系统提供一组应对策略,为用户的正确决策提供参考.
【总页数】4页(P26-29)
【作者】傅廷亮;李春生;汪鑫
【作者单位】中国科学技术大学,计算机系,安徽,合肥,230027;中国科学技术大学,计算机系,安徽,合肥,230027;安徽医科大学,医药卫生管理学院,安徽,合肥,230022【正文语种】中文
【中图分类】TP311
【相关文献】
1.基于VC++6.0的PC机与多台单片机的串行通信 [J], 宋向荣;韩克敏;陈梦华
2.基于规范形方法的多台SVC交互影响分析 [J], 邹振宇;江全元;曹一家;王海风
3.基于VC6.0的多台MSP430单片机和PC机串口通讯实现方案 [J], 周辉军;许亮;韩瑞宁
4.基于VCS的固存坏块仿真系统设计与应用 [J], 刘国斌;祝周荣;宁静;刘攀;陈恩耀
5.基于事件调度的飞机供油多队多台系统仿真 [J], 顾毓;施毅
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3--- 多服务台排队系统的仿真姓名:学号:一、目标任务已知一个系统有N 个服务员,能力相等,服务时间服从指数分布。
顾客的到达时间间隔服从指数分布。
用Monte-Carlo 仿真,分别求按下列方案的总体平均排队时间:①M|M|N 。
②N 个单通道系统并列,按1/N 概率分裂到达流。
③N 个单通道并列,挑选最短的队。
要求:①给出程序设计的过程。
②如果采用固定的N,则要求N>2。
③至少取p二和p二两种强度运行程序。
④对结果进行分析。
二、编程语言Matlab三、关键代码N = 3; % 服务员人数 r = 6; % 顾客到达流强度 u = 20; % 服务员服务强度 T = 1000000; % 仿真运行时间avg_wait_time = []; %平均等待时间for i=1:100% 模拟排队函数server_time =[, , ]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为 0 client_num = 0; % 顾客总数,初始为 0 CRTime = 0;%顾客到达时间间隔 ServeTime = 0; % 顾客服务时间server_id = 0 ; % 当前进入排队窗口的服务员编号total_wait_time = 0;%系统中到达顾客的总等待时间while 1按 1..N 的顺序循环排入服务员窗口if server_id ==0 server_id = N; endif server_time(1, server_id) <= time % 如果当前 server_id 号 服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; % 服务员下 一空闲时间为当前绝对时钟加上当前服务时间else % 否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; %顾客排队等候时间为当前服务员下一空闲时间减去绝对时 钟server_time(1, server_id) = server_time(1, server_id) + ServeTime; end endavg_wait_time = [avg_wait_time, total_wait_time/client_num]; end% 计算平均等待时间 mean_avg_wait_time = mean(avg_wait_time);CRTime = exprnd(1/r); % 按指数分布产生顾客到达时间间隔 time = time + CRTime; % 更新系统的绝对时钟if time > Tbreak;endclient_num = client_num + 1; % 顾客数加 1ServeTime = exprnd(1/u); %按指数分布产生顾客服务间隔server_id = mod(client_num, N); %fprintf(' p 二%平均等待时间%\n', r/u, mean_avg_wait_time); % 打印平均等待时间% 绘制每次仿真的平均等待时间和总体平均等待时间线状图x = 1:100;%plot(x, avg_wait_time, x, mean_avg_wait_time); scatter(x, avg_wait_time, '.');方案二:N = 3; % 服务员人数 r = 6; %顾客到达流强度u = 20; % 服务员服务强度 avg_wait_time = []; %平均等待时间for i=1:100% 模拟排队函数server_time =[, , ]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为 0 client_num = 0; % 顾客总数,初始为 0 CRTime = 0;%顾客到达时间间隔 ServeTime = 0; % 顾客服务时间server_id = 0 ; % 当前进入排队窗口的服务员编号total_wait_time = 0;%系统中到达顾客的总等待时间while 1按指数分布产生顾客到达时间间隔 time = time + CRTime;更新系统的绝对时钟T = 1000; % 仿真运行时间 CRTime = exprnd(1/r); %服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; %一空闲时间为当前绝对时钟加上当前服务时间else %否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; %顾客排队等候时间为当前服务员下一空闲时间减去绝对时钟server_time(1, server_id) = server_time(1, server_id) +ServeTime;end endavg_wait_time = [avg_wait_time, total_wait_time/client_num]; end % 计算平均等待时间 mean_avg_wait_time = mean(avg_wait_time); fprintf(' p 二%平均等待时间 %\n', r/u, mean_avg_wait_time); %等待时间endclient_num = client_num + 1; % ServeTime = exprnd(1/u); % server_id = randi([1 N]); % if server_time(1, server_id) <= time %顾客数加 1 按指数分布产生顾客服务时间间隔 按 1/N 的概率排入服务员窗口如果当前 server_id 号服务员下打印平均% 绘制每次仿真的平均等待时间散点图 x = 1:100;scatter(x, avg_wait_time, '.');〉' 丿 2 £ 方案三:N = 3; % 服务员人数 r = 6; %顾客到达流强度u = 20; % 服务员服务强度 avg_wait_time = []; %平均等待时间for i=1:100% 模拟排队函数server_time =[, , ]; % 用来保存服务员下一空闲时间time = 0; % 绝对时钟,初始为 0 client_num = 0; % 顾客总数,初始为 0 CRTime = 0;%顾客到达时间间隔 ServeTime = 0; % 顾客服务时间server_id = 0 ; % 当前进入排队窗口的服务员编号total_wait_time = 0;%系统中到达顾客的总等待时间while 1按指数分布产生顾客到达时间间隔 time = time + CRTime;更新系统的绝对时钟T = 1000; % 仿真运行时间 CRTime = exprnd(1/r); %[x, y] = find(temp == min(min(server_time))); server_id = y; %按队伍最短排入服务员窗口if server_time(1, server_id) <= time % 如果当前 server_id 号 服务员空闲,则直接接收服务server_time(1, server_id) = time + ServeTime; %服务员下一空闲时间为当前绝对时钟加上当前服务时间else %否则所有服务员都在忙碌,顾客要排队等候total_wait_time = total_wait_time + server_time(1, server_id) - time; %顾客排队等候时间为当前服务员下一空闲时间减去绝对时 钟server_time(1, server_id) = server_time(1, server_id) +ServeTime;end endavg_wait_time = [avg_wait_time, total_wait_time/client_num]; end % 计算平均等待时间 mean_avg_wait_time = mean(avg_wait_time);endclient_num = client_num + 1; % ServeTime = exprnd(1/u); % temp = min(server_time); %顾客数加 1按指数分布产生顾客服务时间间隔 寻找排队时间最短的服务员窗口fprintf(' p 二%平均等待时间%\n', r/u, mean_avg_wait_time); % 打印平均等待时间% 绘制每次仿真的平均等待时间散点图x = 1:100;scatter(x, avg_wait_time, '.');四、实验结果与分析图 1 方案一仿真的平均等待时间散点图图2 方案一平均等待时间M|M|N1.输入参数:服务员人数N,顾客到达流强度r,服务员服务强度u,仿真运行时间T;2.各变量初始值置0:绝对时钟time ,服务员下一空闲时刻数组server_time[](其中按顺序保存每一个服务员的下一空闲时刻),顾客总数client_num ,顾客到达时间间隔CRTime,顾客服务时间ServeTime,当前进入排队窗口的服务员编号server_id ,系统中顾客总等待时间total_wait_time ;3.按照指数分布产生下一顾客到达的时间间隔CRTime,time+=CRTime。
若time>T ,输出total_wait_time/client_num ;4.Client_num ++ ;5.按照指数分布产生顾客到达时间间隔ServeTime;6.按服务员的顺序生成当前服务员的server_id ;7.如果当前server_id 号服务员空闲,则更新服务员下一空闲时间为当前绝对时钟加上当前服务时间并存入server_time[] 对应数组。
否则所有服务员都在忙碌,顾客要排队等候,总的排队时间加上顾客排队等候时间,等候时间为当前服务员下一空闲时间减去绝对时钟。
再更新当前服务员下一空闲时间加上服务时间ServeTime 。
8.转到3;二:图 3 方案二仿真的平均等待时间散点图图 4 方案二平均等待时间N 个单通道系统并列,按1/N 概率分裂到达流1.输入参数:服务员人数N,顾客到达流强度r ,服务员服务强度u,仿真运行时间T;2.各变量初始值置0:绝对时钟time ,服务员下一空闲时刻数组server_time[] (其中按顺序保存每一个服务员的下一空闲时刻),顾客总数client_num ,顾客到达时间间隔CRTime,顾客服务时间ServeTime ,当前进入排队窗口的服务员编号server_id ,系统中顾客总等待时间total_wait_time ;3.按照指数分布产生下一顾客到达的时间间隔CRTime,time+=CRTime 。
