C·A上传 【理论力学】第十一章 动能定理

P 2 1 P 2 1 P 2 2 1 P 2 Rω + T带 = v + ( 2v ) = v 2 4g g 2 2g 2 2g
T= 1 3W + 2 P 2 v g 2
例4:均质杆 长l,质量为 ,滑块 :均质杆AB长 ,质量为m,滑块B 的质量为m,圆柱A的质量为 的质量为M, 的质量为 ,圆柱 的质量为 ,半径 为R.在运动过程中θ =θ(t).试写出在 . ) θ =45° 瞬时的系统动能. ° 瞬时的系统动能.
dT = ∑dWi
动能定力的元功之和 质点系动能的增量 等于作用于质点系的力的元功之和 两边积分: 两边积分:
T2 T = ∑W 1 i
e
动能定理的积分形式
i
T2 T1 = ∑Wi + ∑Wi = ∑Wi + ∑W i
A A
N
质点系动能的改变 等于作用于质点系的所有力所做功的总和 质点系动能的改变 等于作用于质点系的所有力所做功的总和
1 2 1 T = mυC + JCω2 2 2
例2:空心轮重为 ,半径为 ,写出空心轮的动能. :空心轮重为P,半径为R,写出空心轮的动能. 如为匀质实心轮,写出实心轮的动能. 如为匀质实心轮,写出实心轮的动能.
1 2 1 解: T空 = mυC + JCω2 2 2
轮幅 轮缘
P 2 1 P 2 vc 2 P 2 P 2 vc + R 2 = vc = R 2g 2 g g R g JC =1 mi ρi2 1 2 ∑ 2 T实 = mυC + JCω 2 2 P 2 P 2 1 vc 2 3 P 2 P 2 = vc + + R = vc R 2 1 2g 2g 2R 4 g T = JPω2 1 2 2 JC = mR 2 JP = JC + mR2
柯尼希定理: 柯尼希定理:
质点系的动能 等于随同其质心平动 等于随同其质心平动 的动能与相对其质心运动的动能之和 的动能与相对其质心运动的动能之和
三,刚体的动能: 刚体的动能:
1 1 1 2 1,平行移动刚体的动能: T = ∑ mi vi = ∑ mi v2 = mv2 的动能: ,平行移动刚体的动能 2 2 2 υi = ρiω 2,定轴转动刚体的动能: 的动能: ,定轴转动刚体的动能 1 1 1 2 2 2 T = ∑ mi vi = (∑mi ρi )ω = J zω 2 2 2 2
3,刚体平面运动的动能: ,刚体平面运动的动能: 的动能 设刚体上任一质点到瞬心的垂直距离为 ρi 则该点的速度为 υi = ρiω
1 1 T = ∑miυi = (∑mi ρi2 )ω2 2 2 2 JP = JC + mρC 1 2 T = (JC + mρC )ω2 2
1 T = JPω2 2
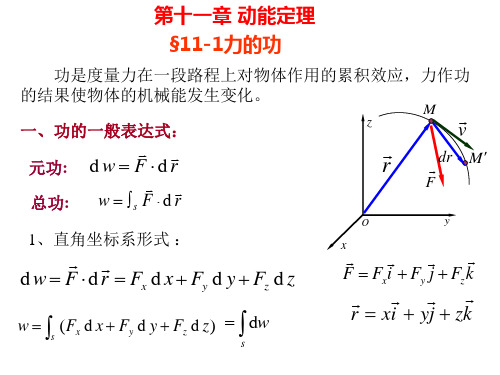
dW = F dS 元功
z
M
v
dr dW = F dr 总功: 总功: W = ∫ s F dr
O
r
dr M ′
F
y
dS
1,直角坐标形式 直角坐标形式: 直角坐标形式
dW = F dr = Fx dx + Fy dy + Fz dz
W=
x
F = Fxi + Fy j + Fzk
∫s dW = ∫ ( F dx + F dy + F dz )
代入 W = ∫ F d x + Fy d y + F d z x z
s
M
z1
O
mg
z2
M2
= ∫ mg d z = mg( z1 z2 )
z1
z2
重力的功取决于重力大小和过程始末的质点位置, 重力的功取决于重力大小和过程始末的质点位置, 取决于重力大小和过程始末的质点位置 而与质点在其间运动的轨迹无关. 而与质点在其间运动的轨迹无关. 对于质点系
1 2 T = ∑ mi vi 2
1 2 T = mv 2
平动动系 在质心
速度合成定理: 速度合成定理: vi = vC + vri
2 2 vi2 = vi vi = (vC + vri ) (vC + vri ) = vC + 2 vC vri + vri 1 1 1 n 2 2 2 T = ∑ mi vi = ∑m i v C + ∑m i v ri + ∑m i v C v ri 2 2 2 i =1 1 1 2 2 = mvC + ∑mi v ri + v C ∑mi v ri 2 2 1 2 1 2 ∵vC ∑mivri = vC mvrC = 0 ∴T = mvC + ∑mivri 2 2
例3:图示为坦克履带轮.已知:履带重 ,各轮重 ,半径 :图示为坦克履带轮.已知:履带重P,各轮重W, R,写出整个系统的动能. ,写出整个系统的动能. πR 1 = JPω2 v = Rω 解: 2v 2 ω 1 3W 2 2 3W 2 v T轮 = 2 v = Rω + 22 g 2 g T带 = T轮履质心 + T轮履转动 + T水平履带 轮履质心 轮履转动
dr
I
F
包括:光滑面约束;光滑铰链;不可伸长的绳索; 包括:光滑面约束;光滑铰链;不可伸长的绳索; 刚体纯滚动;刚性连接约束等. 刚体纯滚动;刚性连接约束等. P41 习题:1,2 习题: ,
§11-2 动能 一,质点的动能: 质点的动能 质点的质量为m 速度值为 速度值为v 质点的质量为 二,质点系的动能: 质点系的动能
t = 0,
v0 = 0 , ,T1 = 0
动能定理
Pv2 Wr 2ω2 + 2 = Px 2g 2 g
ω
W
v ω= r
Pgx v =4 2P + W
2
Pgx v=2 2P + W
v P F a P x
2 Pg Pg 2va = 4 x, a = 2P + W 2P + W
P dv a = PF 轿厢 = g dt
例1:固定圆环半经为 ,小球套在圆环上,被长度为 = 2 R 的 :固定圆环半经为R,小球套在圆环上,被长度为l 弹簧约束在O点 小球从A到 的功 又从B到 的功 的功, 的功. 弹簧约束在 点.求:小球从 到B的功,又从 到C的功. 解: 的功: 从A到B的功 到 的功 A
δ1 = 0
δ 2 = 2 R 2 R) (
s x y z
r = xi + yj + zk
2,自然坐标形式 : ,
W =∫
M2 M1
F dr
∵ dr = ds
z
M
v
∴W = ∫ s F cos( F,v )ds = ∫ s Fτ ds
3,合力的功 ,
r
O
dr
M′
F
y
n个力: F1, 2, , n F F
x
FR = ∑ Fi
....... W = ∫ FR dr = ∫ F1dr + ....... = ∑ Wi
3,作用于转动刚体的力及力偶的功: ,作用于转动刚体的力及力偶的功:
Fz
d
dW = Fτ ds = Fτ rd
dW = M z d
4,刚体内力的功: ,刚体内力的功:
自然坐标形式
F
ds = r d Fτ r = M z (F) = M z
2 W = ∫1 Mz d
ds
F τ
Fr
常力偶
∑dW = F d rA + F′ d rB
= F d rA cosα + F d rB cos β
= F( d rB cos β d rA cosα)
d rB cos β = d rA cosα
B
d rA α
F
A
F′
β
d rB
由于刚体上任意两点之间的距离始终保持不变. 由于刚体上任意两点之间的距离始终保持不变. 因此
∑d′W = 0
5,约束反力的功: ,约束反力的功 (1)光滑固定面反力的功 )
W = ∑mi g(zi1 zi2 ) = (∑mi zi1)g (∑mi zi2 )g
W = mg(zC1 zC2 )
2,弹性力的功: ,弹性力的功
自然坐标形式
M1
设弹簧原长为l 弹簧刚度系数为k, 设弹簧原长为 0,弹簧刚度系数为 , lO +δ1 r 弹性力 F = k(r l0 )
vB
I
ωA
A
θ,
C
B
vC
θ =45° °
vA
2 2 l 解: vC = θ, vA = lθ, , vB = lθ , 2 2 2
1 1 2 T AB = mv C + J C θ 2 2 2 1 l 2 1 ml 2 2 1 2 2 θ = ml θ = m( θ ) + 2 2 2 12 6 1 2 1 2 1 TB = mv B = m( θ ) 2 = ml 2θ 2 2 2 2 4
O
k 2 W = [0 (2 R 2 R) 2 ] = 0.171kR 2 2
的功: 从B到C的功 到 的功
45° ° 22.5° °
B C
δ1 = 2 R 2 R) δ 2 = OC 2 R ) ( (
OC = 2 R cos 22.5° = 1.84776R
k 2 2 W = (δ1 δ 2 ) = 0.077kR 2 2
动能定理 §13-3 质点系动能定理 - 质点系动能
dvi = Fi 个质点所组成的质点系: 由n个质点所组成的质点系: 第 i个质点 mi 个质点所组成的质点系 dt 1 分别点乘 vi dt = dri mi vi dvi = Fi dri d( mi vi2 ) = dWi 分别点乘 2 1 1 2 质点系: 质点系: ∑d ( m i v i ) = ∑dWi d(∑ mi vi2 ) = ∑dWi 2 2