7-1描述函数法分析
合集下载
第二节 描述函数法
第二节 描述函数法
18
作业：7-1(b)
2020/10/18
第二节 描述函数法
19
(A )
2020/10/18
第二节 描述函数法
16
2) 非线性环节的串联 当两个非线性环节串联，其总的描述函数不等于两个非
线性环节描述函数乘积。
非线性环节串联
必须首先求出这两个非线性环节串联后的等效非线性特性， 然后根据等效的非线性特性求出总的描述函数。 例7-2 求下图所示两个非线性环节串联总的描述函数N(A)。
一、描述函数的概念
针对一任意非线性系统，设输入x(t)=Asinωt,输出波形为
y(t)，则可以将y(t)表示为富氏级数形式：
y(t) A0 ( An cos nt Bn sin nt) n1
A0 Yn sin(nt n ) n 1
2020/10/18
第二节 描述函数法
2
y(t) A0 ( An cos nt Bn sin nt)
N ( A) N1( A) N2( A)
2020/10/18
第二节 描述函数法
12
3、组合非线性特性的描述函数
当非线性系统中含有两个或两个以上线性环节时： 一般不能按照线性环节的串并联方法求总的描述函数； 应按非线性的并联、串联方法计算。
1）非线性特性的并联 设系统中有两个并联的非线性环节，其非线性特性都是
A
AA A A A
2020/10/18
第二节 描述函数法
9
⑦ 非线性增益I 非线性特性
描述函数
N ( A)
k2
2
(k1
k2 )[sin1
a A
a A
1 ( a )2 ] A
自动控制原理__(13)
x0 e t , 其中x0 x(0) t 1 x0 x 0 e
江南大学物联网工程学院——自动控制原理
（2）会产生自激振荡 非线性系统即使无外界作用，往往也会产生具有一定振幅 和频率的稳定性振荡，称为自激（自持）振荡。在有的非线性 系统中，还可能产生不止一种振幅和频率的自激振荡。自激振 荡是非线性系统一种特有的运动形式，其振幅和频率由系统本 身特性决定。 说明：
江南大学物联网工程学院——自动控制原理
2. 典型的非线性特性
常见的非线性特性有饱和、死区、间隙（回环）、继电等。 (1)饱和特性 特点：当输入信号超过某一范围后，输出信号不再随输 入信号而变化，将保持某一常数值不变。可将饱和非线性元 件看作为一个变增益的比例环节。
x2 f ( x1 ) tan , x1 ＜s 如图： x2 f ( x1 ) K x1 x1 0, x1 ＞s
作用：饱和特性将使系 统等效增益减小，因此可用 来改善系统的稳定性，但会 降低稳态精度。在有些系统 中利用饱和特性起信号限幅 作用。
（a）理想饱和特性
（b）实际饱和特性
图7-2 理想与实际饱和特性
江南大学物联网工程学院——自动控制原理
（2）死区（不灵敏区）特性 特点：是当输入信号在零值附近的某一小范围之内变化 时，没有相应的输出信号，只有当输入信号大于此范围时， 才有信号输出。 常见于测量、放大、变换元件中，执行机构中静摩擦的 影响往往也可用死区来表示。 影响：控制系统中死区特性的存 在，将导致系统稳态误差增大，而测 量元件死区的影响尤为显著。摩擦死 区会造成系统低速运动的不均匀，导 致随动系统不能准确地跟踪目标。
3. 非线性系统的分析方法
目前，对于非线性系统的分析与设计，工程上常用的近似方法有：小 偏差线性化法、分段线性化法、反馈线性化法、描述函数法、相平面法及 计算机仿真等。本章将重点介绍应用较多的相平面法和描述函数法。 （1） 相平面法 相平面法是基于时域的图解分析方法。特点是保留非线性特性，将高 阶的线性部分近似地化为二阶，利用二阶系统的状态方程，绘制由状态变 量所构成的的相轨迹图。可用来分析系统的稳定性及运动特性。 只适用于一、二阶的简单非线性系统分析。
江南大学物联网工程学院——自动控制原理
（2）会产生自激振荡 非线性系统即使无外界作用，往往也会产生具有一定振幅 和频率的稳定性振荡，称为自激（自持）振荡。在有的非线性 系统中，还可能产生不止一种振幅和频率的自激振荡。自激振 荡是非线性系统一种特有的运动形式，其振幅和频率由系统本 身特性决定。 说明：
江南大学物联网工程学院——自动控制原理
2. 典型的非线性特性
常见的非线性特性有饱和、死区、间隙（回环）、继电等。 (1)饱和特性 特点：当输入信号超过某一范围后，输出信号不再随输 入信号而变化，将保持某一常数值不变。可将饱和非线性元 件看作为一个变增益的比例环节。
x2 f ( x1 ) tan , x1 ＜s 如图： x2 f ( x1 ) K x1 x1 0, x1 ＞s
作用：饱和特性将使系 统等效增益减小，因此可用 来改善系统的稳定性，但会 降低稳态精度。在有些系统 中利用饱和特性起信号限幅 作用。
（a）理想饱和特性
（b）实际饱和特性
图7-2 理想与实际饱和特性
江南大学物联网工程学院——自动控制原理
（2）死区（不灵敏区）特性 特点：是当输入信号在零值附近的某一小范围之内变化 时，没有相应的输出信号，只有当输入信号大于此范围时， 才有信号输出。 常见于测量、放大、变换元件中，执行机构中静摩擦的 影响往往也可用死区来表示。 影响：控制系统中死区特性的存 在，将导致系统稳态误差增大，而测 量元件死区的影响尤为显著。摩擦死 区会造成系统低速运动的不均匀，导 致随动系统不能准确地跟踪目标。
3. 非线性系统的分析方法
目前，对于非线性系统的分析与设计，工程上常用的近似方法有：小 偏差线性化法、分段线性化法、反馈线性化法、描述函数法、相平面法及 计算机仿真等。本章将重点介绍应用较多的相平面法和描述函数法。 （1） 相平面法 相平面法是基于时域的图解分析方法。特点是保留非线性特性，将高 阶的线性部分近似地化为二阶，利用二阶系统的状态方程，绘制由状态变 量所构成的的相轨迹图。可用来分析系统的稳定性及运动特性。 只适用于一、二阶的简单非线性系统分析。
王建辉《自动控制原理》(名校考研真题 非线性系统分析)【圣才出品】
第7章 非线性系统分析一、选择题1．非线性系统的无穷多条相轨迹相交的点称为（）。
[华中科技大学研]A．奇点B．会合点C．分离点D．终点【答案】A2．输出信号的一次谐波分量和输入信号的复数比定义为非线性环节的（）。
[华中科技大学研]A．传递函数B．描述函数C．谐波函数D．频率特性【答案】B二、解答题1．已知非线性系统如图7-1所示，其中，T＞0，K＞0，现要求系统输入量c（t）的ωc＝10，试确定参数T和K的数值。
（非线性环节自振振幅X c＝0.1，角频率为）[上海交通大学研]图7-1解：由已知ωc ＝10，线性部分传递函数为即又由于ωc ＝10，自振振幅X c ＝0.1得因此有2．已知某非线性系统结构如图所示，试用描述函数法分析K （K ＞0）值对系统稳定性的影响。
[南京航空航天大学2006研]图7-2 非线性系统结构图解：该饱和特性的描述函数为负倒描述函数当A ＝1时，，当A→＋∞时，，因此位于负实轴上的－1~－∞区段。
线性部分频率特性为令ImG （j ω）＝0，得G （j ω）与负实轴交点的频率为，且在复平面上绘制G （j ω）曲线以及曲线如下图所示。
由图可见，当时，即0＜K ＜6系统稳定；当时，即K ＞6系统产生自振。
自振频率，振幅A 由求得。
图7-33．某单位负反馈非线性系统如图所示，非线性环节的描述函数为，线性部分的传递函数如图所示。
试分析：（1）系统是否存在自振。
（2）若产生自振，计算自振频率及振幅，并讨论极限环的稳定性。
[浙江大学2008研]图7-4 非线性系统结构图解：非线性环节负倒描述函数为线性部分频率特性为且在复平面上绘制G（jω）曲线以及曲线如下图所示，相交于B点，有解得即系统存在自振的频率为1.155，振幅为11.246。
图7-54．已知非线性控制系统的结构图如图7-6所示。
为了使系统不产生自持振荡，试采用描述函数法确定图中非线性环节的特性参数a和b的数值。
[长安大学研][南京理工大学研][华中科技大学研]图7-6解：由题知非线性环节为死区继电器特性，则图形如图7-8所示。
描述函数法讲解
0
Ka sintd(t)
KA s in2
td(t
)
2
KAsin1
a
a
1
a
2
AA
A
则饱和特性的描述函数为：
N ( A)
B1
2
K sin1
a
a
1
a
2
A
AA
A
式中，
Asin
a,
sin1
a
A
x(t) k
由于输出波形为奇函数，
A1＝0,（单值奇对称）
1
tg1
A1 B1
0
a
t
x(t)
e(t)
e(t)
10
B1
2
x(t)sint d(t)
0
2
KAsin2 td(t)
N ( A)
A12 B12
j arctg A1
e
B1
B1
j
A1
A
AA
用N(A)代替非线性环节，建立起非线性系统的数学描述，可
以将线性系统频率法扩展到非线性系统中，用来分析非线性
系统。
7
说明：
一般情况下，描述函数 N 是输入正弦振幅A和振荡频率的
函数，应表示成 N ( A,) 。
但实际大多数非线性环节中不包含储能元件，它们的输出 与输入信号的频率无关，因此常见NL的描述函数 N 仅是输 入信号幅值A的函数，表示成 N(A)。
Ka sintd(t)
KA s in2
td(t
)
2
KAsin1
a
a
1
a
2
AA
A
则饱和特性的描述函数为：
N ( A)
B1
2
K sin1
a
a
1
a
2
A
AA
A
式中，
Asin
a,
sin1
a
A
x(t) k
由于输出波形为奇函数，
A1＝0,（单值奇对称）
1
tg1
A1 B1
0
a
t
x(t)
e(t)
e(t)
10
B1
2
x(t)sint d(t)
0
2
KAsin2 td(t)
N ( A)
A12 B12
j arctg A1
e
B1
B1
j
A1
A
AA
用N(A)代替非线性环节，建立起非线性系统的数学描述，可
以将线性系统频率法扩展到非线性系统中，用来分析非线性
系统。
7
说明：
一般情况下，描述函数 N 是输入正弦振幅A和振荡频率的
函数，应表示成 N ( A,) 。
但实际大多数非线性环节中不包含储能元件，它们的输出 与输入信号的频率无关，因此常见NL的描述函数 N 仅是输 入信号幅值A的函数，表示成 N(A)。
非线性系统
若在线性部分的频率特性G l(jω)曲线与非线性元件的负倒
下一页 返回
§7-3 描述函数分析
描述函数-1/N(X)曲的交点处，沿振幅X增加方向，-1/N(X)上的 点不被G l(jω)曲线所包围，则这个交点是稳定的自激振荡点， 其线性元件的输出波形为正弦波，振荡频率为交点处G l(jω)的 ω值，现行元件输入信号一次谐波的复制为交点处-1/N(X)曲线 的X值。
振荡线性化是在非线性元件的输入端除加输入信号外，还 加一个辅助的高频振荡信号，在非线性元件的输出端接一个低 通滤波器，如图7-20所示。图中x1(t)为输入信号，x2(ωt)为附 加高频振荡，y(t)为非线性元件的输出，z(t)为低通滤波器的 输出。当输入信号x1(t)等于常数时，y(t)为频率等于ω的周期 波，其波形与x1(t)、x2(ωt)及非线性特性f(x)有关。如果低通 滤波器能滤去频率等于和高于ω的所有谐波，则低通滤波器输 出仅保留了与输入信号有关的直流分量。这样z(t)对于x1(t)而 言，可能得到近似的线性关系。
第七章 非线性系统
§7-1 概述 §7-2 描述函数法 §7-3 描述函数分析 §7-4 非线性特性的振荡线性化
§7-1 概述
一、反馈系统的非线性特性 在反馈系统中，常见的非线性特性有：
1)据有光滑曲线形式的非线性较大时，必须考 虑其非线性特性。
三、非线性系统的研究方法 1.相平面法 应用相平面图可以分析非线性系统的稳定性、过
渡过程即自振荡等问题。 2.描述函数法 描述函数法不受系统阶次的限制，但必需满足
假设条件。 3.系统仿真
上一页 返回
§7-2 描述函数法
一、描述函数的基本概念 描述函数法基于下述情况：如果非线性元件输出的周期函
数信号加到另一个线性元件的输入端，当线性元件有滤除非 线性元件输出y(t)中二次及二次以上谐波的低通滤波特性时， 那么线性元件的输出为与非线性元件输入同频率的正弦函数， 如图7-4所示。 二、描述函数计算举例
下一页 返回
§7-3 描述函数分析
描述函数-1/N(X)曲的交点处，沿振幅X增加方向，-1/N(X)上的 点不被G l(jω)曲线所包围，则这个交点是稳定的自激振荡点， 其线性元件的输出波形为正弦波，振荡频率为交点处G l(jω)的 ω值，现行元件输入信号一次谐波的复制为交点处-1/N(X)曲线 的X值。
振荡线性化是在非线性元件的输入端除加输入信号外，还 加一个辅助的高频振荡信号，在非线性元件的输出端接一个低 通滤波器，如图7-20所示。图中x1(t)为输入信号，x2(ωt)为附 加高频振荡，y(t)为非线性元件的输出，z(t)为低通滤波器的 输出。当输入信号x1(t)等于常数时，y(t)为频率等于ω的周期 波，其波形与x1(t)、x2(ωt)及非线性特性f(x)有关。如果低通 滤波器能滤去频率等于和高于ω的所有谐波，则低通滤波器输 出仅保留了与输入信号有关的直流分量。这样z(t)对于x1(t)而 言，可能得到近似的线性关系。
第七章 非线性系统
§7-1 概述 §7-2 描述函数法 §7-3 描述函数分析 §7-4 非线性特性的振荡线性化
§7-1 概述
一、反馈系统的非线性特性 在反馈系统中，常见的非线性特性有：
1)据有光滑曲线形式的非线性较大时，必须考 虑其非线性特性。
三、非线性系统的研究方法 1.相平面法 应用相平面图可以分析非线性系统的稳定性、过
渡过程即自振荡等问题。 2.描述函数法 描述函数法不受系统阶次的限制，但必需满足
假设条件。 3.系统仿真
上一页 返回
§7-2 描述函数法
一、描述函数的基本概念 描述函数法基于下述情况：如果非线性元件输出的周期函
数信号加到另一个线性元件的输入端，当线性元件有滤除非 线性元件输出y(t)中二次及二次以上谐波的低通滤波特性时， 那么线性元件的输出为与非线性元件输入同频率的正弦函数， 如图7-4所示。 二、描述函数计算举例
自动控制原理 第七章 非线性系统
实质上是应用谐波线性化的方法，将非线性特性线性化， 然后用频域法的结论来研究非线性系统，它是线性理论 中的频率法在非线性系统中的推广，不受系统阶次的限 制。
（2）相平面法（本质非线性）：图解法。通过在相平 面上绘制相轨迹，可以求出微分方程在任何初始条件下 的解。是一种时域分析法，仅适用于一阶和二阶系统。
1
ωt
y1 (t ) B1 sint
由式（7-15）可得饱和特性的描述函数为
B1 2k a a a 2 N ( A) arcsin 1 ( ) A A A A
M sin td ( t )
yMFra bibliotek0 π2π
ωt
所以基波分量为：
y1 ( t )
4M
sin t
故理想继电器特性的描述函数为
Y1 4M N ( A) 1 A A
2.饱和特性
请牢记！
即 N(A)的相位角为零度,幅值是输入正弦信号A的函数.
当输入为x(t)＝Asinωt，且A大于线性区宽度a 时， 饱和特性的输出波形如图7-10所示。
7.1.3
非线性系统的分析方法
非线性的数学模型为非线性微分方程，大多数尚无
法直接求解。到目前为止，非线性系统的研究还不成熟， 结论不能像线性系统那样具有普遍意义，一般要针对系 统的结构，输入及初始条件等具体情况进行分析。工程 上常用的方法有以下几种：
（1）描述函数法（本质非线性）：是一种频域分析法，
r(t)=0 x
N
y
G(s)
c(t)
图7-8 非线性系统典型结构图
（2）非线性环节的输入输出静特性曲线是奇对称的，即 y(x)=-y(-x)，以保证非线性元件在正弦信号作用下的输出不 包含直流分量。 （3）系统的线性部分具有良好的低通滤波特性。能较好的滤 除非线性环节在正弦输入下输出中的高次谐波，于是可以认 为在闭环通道中只有基波分量在流通，此时应用描述函数法 所得的分析结果才是比较准确的。实际系统基本都能满足。
自动控制原理第七章
条件下的时间响应曲线如图所示。
四、非线性控制系统的特点
3.稳定性 3.稳定性 从曲线及方程中可以看出， 系统有两个平衡状态，即 x=0和 x=1 。 按稳定性的定义对平衡状 态 x=1来说，系统只要有一 个很小的偏离，就再也不会 回到这一平衡状态上来。 因此，x=1的平衡状态是一个不稳定的平衡状态。
第七章 非线性系统的分析
§7
非线性系统的分析
教学内容：
§7-1 非线性控制系统概述 §7-2 描述函数法 §7-3 相平面法
§7-1 非线性控制系统概述
一、引言 二、研究非线性系统的一般方法 三、典型非线性特性 四、非线性控制系统的特点
一、引言
包含一个或一个以上非线性元件或环节的系统为非线性系 统。 实际上自动控制系统的各个环节不可避免的带有某种程度 的非线性，线性系统只是非线性系统的近似。 非线性系统程度不严重时，在一定范围内或特定条件下， 可采用微偏法进行线性化，这种非线性称为非本质非线性。 如果系统的非线性具有间断点、折断点，称为本质非线性。 这时采用线性系统分析方法去研究会引起很大的误差甚至导 致错误的结论。
四、非线性控制系统的特点
3.稳定性 3.稳定性
线性系统的稳定性取决于系统的结构与参数，与起始 状态无关。 非线性系统的稳定性不仅仅和系统的结构与参数有关， 还和起始状态有直接关系。 一个非线性系统，他的某些平衡状态可能是稳定的， 某些平衡状态可能是不稳定的。因此对于非线性系统， 不存在系统是否稳定的笼统概念，要研究的是非线性系 统平衡状态的稳定性。
2 n
A +B
2 n
An ϕn = arctan Bn
一 描述函数的基本概念
非线性特性为奇对称，则直流分量 A0= 0； 同时，各谐波分量的幅值与基波相比一般都比较小； 因此，可以忽略式中的高次谐波分量，只考虑基波分量， 这种近似也称为谐波线性化。则
第七章非线性控制系统分析习题答案.
解： y(t) = A3 sin3 ωt
∫ ∫ 1
B=
2π
A3 sin 4 ωt
4 A3
dωt =
π
2
1
(1
− cos
2ωt) 2
dωt
1
π0
π 04
∫ [ ] A3
=
π
2 (1 − 2 c os 2ω t + c os 2 2ω t )
A3
dωt =
π
A3
π
− sin 2ωt 2
π0
π2 π
0
A 3 π c o s 4ω t + 1
G1 ( s) +G1 ( s)
4 、 判 断 题 7 -2 图 中 各 系 统 是 否 稳 定 ； −1 N( A) 与 G ( j ω ) 两 曲 线 交 点 是 否 为 自 振 点 。
2
解 ：（ a ） 不 是 ； （ b） 是 ； （c）是；
（ d） a、c 点 是， b 点 不 是；
（ e） 是 ；
（ 2 ） 由 图 解 7 -5 可 见 ， 当 −1 N( A) 和 G ( j ω ) 相 交 时 ， 系 统 一 定 会 自 振 。 由 自 振 条 件
A + 6 −K −( A + 6) K
N ( A)G( jω ) =
=
= −1
ω =1 A + 2 2
2( A+2)
( A +6) K = 2 A +4
10
−1 0
10
G( jω ) =
=
−j
j ω( j ω + 1) ω2 + 1
ω( ω2 + 1)
∫ ∫ 1
B=
2π
A3 sin 4 ωt
4 A3
dωt =
π
2
1
(1
− cos
2ωt) 2
dωt
1
π0
π 04
∫ [ ] A3
=
π
2 (1 − 2 c os 2ω t + c os 2 2ω t )
A3
dωt =
π
A3
π
− sin 2ωt 2
π0
π2 π
0
A 3 π c o s 4ω t + 1
G1 ( s) +G1 ( s)
4 、 判 断 题 7 -2 图 中 各 系 统 是 否 稳 定 ； −1 N( A) 与 G ( j ω ) 两 曲 线 交 点 是 否 为 自 振 点 。
2
解 ：（ a ） 不 是 ； （ b） 是 ； （c）是；
（ d） a、c 点 是， b 点 不 是；
（ e） 是 ；
（ 2 ） 由 图 解 7 -5 可 见 ， 当 −1 N( A) 和 G ( j ω ) 相 交 时 ， 系 统 一 定 会 自 振 。 由 自 振 条 件
A + 6 −K −( A + 6) K
N ( A)G( jω ) =
=
= −1
ω =1 A + 2 2
2( A+2)
( A +6) K = 2 A +4
10
−1 0
10
G( jω ) =
=
−j
j ω( j ω + 1) ω2 + 1
ω( ω2 + 1)
自动控制7-1描述函数法.详解
当x0<1时，x(t) 递减并趋于0。
x0 t ln x -1 0
由上例可见，初始条件不同，自由运动的稳定性 亦不同。因此非线性系统的稳定性不仅与系统的结构 和参数有关，而且与系统的初始条件有直接的关系。
11
所谓自激振荡是指没有外界周期变化信号的作用 时，系统内产生的具有固定振幅和频率的稳定周期运 动，简称自振。 考虑著名的范德波尔方程 - 2 ρ(1 - x 2 ) x x 0 >0 x
6
2
4
14
7.1.3 非线性系统的分析方法
到目前为止，非线性系统的研究还缺乏成熟，结论不能像 线性系统那样具有普遍意义，一般要针对系统的结构，输入及 初始条件等具体情况进行分析。工程上常用的方法有以下几种：
（1）小偏差线性化（非本质非线性） （2）描述函数法（本质非线性）
这是一种频域分析方法，其实质是应用谐波线性化的方法， 将非线性特性线性化，然后用频率法的结论来研究非线性系统。 它是线性理论中的频率法在非线性系统中的推广，这种方法不 受系统阶次的限制。
4
7.1.1 典型非线性特性的种类
1．饱和特性
-a
y
M k 0 -M a x
a为线性区宽度，k为线性区斜率。 饱和特性在控制系统中是普遍存在的，放大器及 执行机构受电源电压或功率的限制导致饱和。
5
2．死区特性 死区又称不灵敏区，在死区内虽有输入信号，但 其输出为零
y k
-a
0
a
x
| x | a 0, y = k ( x - a ), x>a k ( x + a ), x < -a
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使 x <1时，因为 - (1- x2 )<0，系统具有负阻 尼，此时系统从外部获得能量， x(t)的运动呈发散形式； 当x>1时，因为-(1-x2 )>0，系统具有正阻尼，此 时系统消耗能量，x(t)的运动呈收敛形式； 而当 x=1时，系统为零阻尼，系统运动呈等幅振荡 形式。上述分析表明，系统能克服扰动对 x的影响，保 持幅值为1的等幅振荡。 12
x0 t ln x -1 0
由上例可见，初始条件不同，自由运动的稳定性 亦不同。因此非线性系统的稳定性不仅与系统的结构 和参数有关，而且与系统的初始条件有直接的关系。
11
所谓自激振荡是指没有外界周期变化信号的作用 时，系统内产生的具有固定振幅和频率的稳定周期运 动，简称自振。 考虑著名的范德波尔方程 - 2 ρ(1 - x 2 ) x x 0 >0 x
6
2
4
14
7.1.3 非线性系统的分析方法
到目前为止，非线性系统的研究还缺乏成熟，结论不能像 线性系统那样具有普遍意义，一般要针对系统的结构，输入及 初始条件等具体情况进行分析。工程上常用的方法有以下几种：
（1）小偏差线性化（非本质非线性） （2）描述函数法（本质非线性）
这是一种频域分析方法，其实质是应用谐波线性化的方法， 将非线性特性线性化，然后用频率法的结论来研究非线性系统。 它是线性理论中的频率法在非线性系统中的推广，这种方法不 受系统阶次的限制。
4
7.1.1 典型非线性特性的种类
1．饱和特性
-a
y
M k 0 -M a x
a为线性区宽度，k为线性区斜率。 饱和特性在控制系统中是普遍存在的，放大器及 执行机构受电源电压或功率的限制导致饱和。
5
2．死区特性 死区又称不灵敏区，在死区内虽有输入信号，但 其输出为零
y k
-a
0
a
x
| x | a 0, y = k ( x - a ), x>a k ( x + a ), x < -a
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使 x <1时，因为 - (1- x2 )<0，系统具有负阻 尼，此时系统从外部获得能量， x(t)的运动呈发散形式； 当x>1时，因为-(1-x2 )>0，系统具有正阻尼，此 时系统消耗能量，x(t)的运动呈收敛形式； 而当 x=1时，系统为零阻尼，系统运动呈等幅振荡 形式。上述分析表明，系统能克服扰动对 x的影响，保 持幅值为1的等幅振荡。 12
自动控制原理考试试题第七章习题及答案
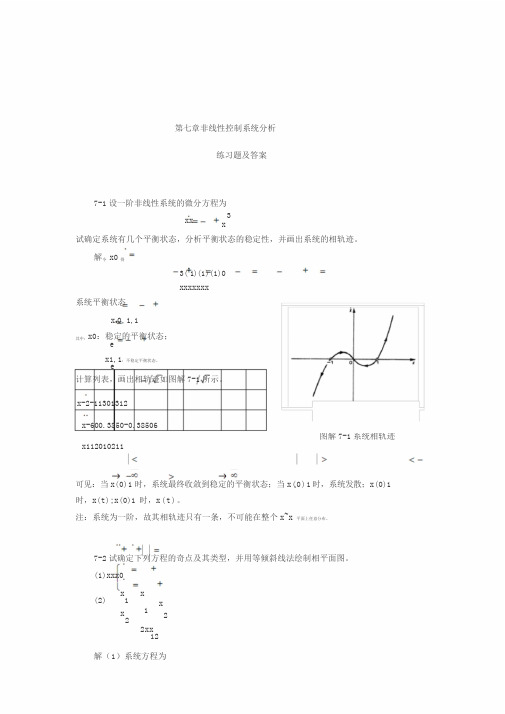
第七章 非线性控制系统分析练习题及答案7-1 设一阶非线性系统的微分方程为3x x x+-=& 试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。
解 令 x =0 得-+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中：0=e x ：稳定的平衡状态；1,1+-=e x ：不稳定平衡状态。
计算列表，画出相轨迹如图解7-1所示。
可见：当x ()01<时，系统最终收敛到稳定的平衡状态；当x ()01>时，系统发散；1)0(-<x 时，x t ()→-∞; 1)0(>x 时，x t ()→∞。
注：系统为一阶，故其相轨迹只有一条，不可能在整个 ~x x 平面上任意分布。
7-2 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。
(1) x x x ++=0 (2) ⎩⎨⎧+=+=2122112x x xx x x &&解 （1） 系统方程为x -2 -1 -13 0 13 1 2x -6 0 0.385 0 -0.385 0 6 x11 2 0 1 0211图解7-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x &&&&&&令0x x ==&&&，得平衡点：0e x =。
系统特征方程及特征根：21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxx x xdx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解7-2（a ）所示。
自动控制原理考试试题第七章习题与答案
第七章非线性控制系统分析练习题及答案7-1设一阶非线性系统的微分方程为xx3 x试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。
解令x0得3(21)(1)(1)0xxxxxxx系统平衡状态x e0,1,1其中：x0：稳定的平衡状态；ex1,1：不稳定平衡状态。
e计算列表，画出相轨迹如图解7-1所示。
x-2-11301312x-600.3850-0.38506x112010211图解7-1系统相轨迹可见：当x(0)1时，系统最终收敛到稳定的平衡状态；当x(0)1时，系统发散；x(0)1 时，x(t);x(0)1时，x(t)。
注：系统为一阶，故其相轨迹只有一条，不可能在整个x~x平面上任意分布。
7-2试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。
(1)xxx0(2) x1x2xx122xx12解（1）系统方程为1:xxx0(x0):xxx0(x0)令xx0，得平衡点：x e0。
系统特征方程及特征根：132:ss10,sj(稳定的焦点)1,2222:ss10,s1.618,0.618(鞍点)1,2xf(x,x)xx, d xdxxxxdx dx 1xx,1xxx11I:1(x0)1II:1(x0)计算列表-∞-3-1-1/301/313∞x0:11-1-2/302-∞-4-2-4/3-1x0:11-1-4/3-2-4∞20-2/3-1用等倾斜线法绘制系统相平面图如图解7-2（a）所示。
2图解7-2（a）系统相平面图（2）xxx112①x22xx②12由式①：x2x1x1③式③代入②：(x1x1)2x1(x1x1)即x12x1x10④令x1x10得平衡点：x e0由式④得特征方程及特征根为2.4142ss2101,2（鞍点）0.414画相轨迹，由④式xx 11 d x1dxx12x1x1x 1 x1 2计算列表322.53∞11.52=1/(-2)∞210-1-2∞用等倾斜线法绘制系统相平面图如图解7-2（b）所示。
自动控制原理-第七章 非线性系统分析
p p p ( x1 , x 2 ) ( x1 x 10 ) ( x 2 x 20 ) x1 x 2 Q ( x , x ) Q ( x x ) Q ( x x ) 1 2 1 10 2 20 x1 x 2
p ( x1 , x 2 ) a ( x1 x10 ) b( x 2 x 20 ) Q( x1 , x 2 ) c( x1 x10 ) d ( x 2 x 20 )
c 区域： a Tc c k m
c k m c 1 （k m c) T T ct 0 由奇点定义： k m c 0 c 常数 c k m 1 k m c dc T dc c 区域： c 常数 奇线： c k m
§7-4
奇点及极限环
dx 0 奇点概念：相轨迹上满足 dx 0 不定式的特殊点，称为奇点。
在奇点处有多条相轨迹穿过或趋于该奇点，相当于系统处于 平衡状态 一 奇点分类：(线性系统)
2 2 n x n x 0 x 2 2 n x n x x dx 2 x dx 2 n x n x dt (*) 相轨迹方程 dx x dx x dt
介绍：典型非线性特性、相平面法、描述 函数法
§7-1引言
稳定性 1．线性系统与非线性系统区别： 输出曲线 等幅振荡 稳态输出
2．非线性特性（典型） 1）死区
0 x a y k ( x a ) x a k ( x a ) x a
0 = k ( x aSignx)
x1 a ( x1 x 10 ) b( x 2 x 20 ) x 2 c( x1 x10 ) d ( x 2 x 20 )
自动控制原理第七章
解：1．将继电特性的参数代入相应公式得到：
4B 12 a 1 N ( A) 1 1 A A A A
2 2
1 πA N(A) 12 1 - 1 2 A
根据
( N (1A) ) ( )
a A
0，求得
1 π 的极值为 6 N ( A)
7.4.2 非线性系统结构的简化
非线性环节串联 若两个非线性环节串联，可将两个环节 的特性归化为一个特性，即以第一个非线性 环节的输入和第二个非线性环节的输出分别 作为归化后非线性特性的输入和输出，从而 作出等效非线性特性。注意，若两个非线性 特性的描述函数分别为 N1 ( A)和 N 2 ( A，等效非 ) 线性的描述函数为 N ( A)绝不等于 N1 ( A和 的 ) ) N2 (A 乘积，并且串联非线性环节的次序不可交换。 对于多个非线性环节串联，其处理方法可以 按照串联的次序，先归化前两个非线性环节， 等效后的非线性特性再与第三个环节进行归 化变换。 非线性环节并联 若两个并联的非线性环节其描述 函数分别为 和 N ( A) ，则并联后的 N 2 ( A) 1 等效非线性环节的描述函 数 。
7.2 典型非线性特性及其对系统的影响
间隙特性
也称回环，机械传动中为保证齿轮转动灵活不卡齿，主动轮、从动 轮齿轮之间必须有适当的间隙存在，使得两者不能同步运转，即从 动轮滞后主动轮。含有间隙特性的系统，其输出相位滞后于输入相 位，从而减小了系统的相稳定裕度，使系统的稳定性变坏，同时增 大了系统的稳差。
7.3 描述函数法
7.3.2 非线性特性的描述函数
非线性特性 描 述 函 数
7.3 描述函数法 描 述 函 数
非线性特性
7.4 用描述函数法分析非线性控制系统
第七章非线性系统的分析
2、死区非线性
x1 ≤ ∆ 0, x2 = k ( x1 − ∆signx1 ), x1 > ∆
1 signx1 = −1
x1 > 0 x1 < 0
在实际系统中死区可由众多原因引起，它对系统可产生不同的 影响：一方面它使系统不稳定或者产生自振荡；另一方面有时 人们又人为的引入死区特性，使系统具有抗干扰能力。
第七章 非线性控制系统
7-2
1、饱和非线性
kx1 = x2 = ka x2 m −ka = − x 2m
典型非线性环节
x1 < a x1 ≥ a x1 ≤ −a
x2m
x2
−a
0
k
a
x1
此处：输入 x1 − − − − x2 − − − −输出 k − − − −比例系数
− x2m
第七章 非线性控制系统
第七章 非线性控制系统
4）混沌(Chaos)
蝴蝶效应（ The Butterfly Effect） 是指在一个动力系统中，初始条 件下微小的变化能带动整个系统 的长期的巨大的连锁反应。这是 一种混沌现象。 核心理念：看似微不足道的细小 变化，却能以某种方式对社会产 生微妙的影响，甚至影响整个社 会系统的正常运行。
第七章 非线性控制系统
r(t)
e(t)
N(A,ω) NLS
x(t)
G(s)
c(t)
非线性系统的闭环“传递函数”：
G ( jω ) N ( A, ω ) Φ ( jω ) = 1 + G ( jω ) N ( A, ω )
0 闭环“特征方程”： 1 + G ( jω ) N ( A, ω ) =
即
1 G ( jω ) = − N ( A, ω )
7-1描述函数法
（3）相平面法（本质非线性）
相平面法是求解一、二阶常微分方程的图解法。通过在相
平面上绘制相轨迹，可以求出微分方程在任何初始条件下的解。 这是一种时域分析法，但仅适用于一阶和二阶系统。
（4）计算机求解法
用模拟计算机或数字计算机直接求解非线性微分方程，对于12 分析和设计复杂的非线性系统是非常有效的方法。
1
第七章 非线性系统
内容提要 7.1 典型非线性特性 7.2 描述函数法 7.3 相平面法 学习指导与小结
2
※7.1 典型非线性特性
前面各章研究的都是线性系统，或者虽然是非线 性系统，仍可进行线性化处理，从而可视为线性系统。 事实上，几乎所有的实际控制系统，都不可避免地带 有某种程度的非线性、系统中只要具有一个非线性环 节，就称为非线性系统。因此实际的控制系统大都是 非线性系统。本章将主要讨论关于非线性系统的基本 概念，以及两种基本分析方法：描述函数法和相平面 法。
0
14
由于在傅氏级数中n越大，谐波分量的频率越高，An, Bn越小。此时若系统又满足第三个条件，则高次谐波 分量又进一步被充分衰减，故可认为非线性环节的稳
态输出只含基波分量，即
y(t) y1(t) A1 cost B1 sin t Y1 sin(t 1)
式中
A1
1
x 2(1 x 2 )x x 0 >0
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使x<1时，因为(1x2 )<0，系统具有负阻
尼，此时系统从外部获得能量，x(t)的运动呈发散形式；
当x>1时，因为(1x2 )>0，系统具有正阻尼，此
时系统消耗能量，x(t)的运动呈收敛形式；而当x=1时， 系统为零阻尼，系统运动呈等幅振荡形式。上述分析表 明，系统能克服扰动对x的影响，保持幅值为1的等幅振 荡。
相平面法是求解一、二阶常微分方程的图解法。通过在相
平面上绘制相轨迹，可以求出微分方程在任何初始条件下的解。 这是一种时域分析法，但仅适用于一阶和二阶系统。
（4）计算机求解法
用模拟计算机或数字计算机直接求解非线性微分方程，对于12 分析和设计复杂的非线性系统是非常有效的方法。
1
第七章 非线性系统
内容提要 7.1 典型非线性特性 7.2 描述函数法 7.3 相平面法 学习指导与小结
2
※7.1 典型非线性特性
前面各章研究的都是线性系统，或者虽然是非线 性系统，仍可进行线性化处理，从而可视为线性系统。 事实上，几乎所有的实际控制系统，都不可避免地带 有某种程度的非线性、系统中只要具有一个非线性环 节，就称为非线性系统。因此实际的控制系统大都是 非线性系统。本章将主要讨论关于非线性系统的基本 概念，以及两种基本分析方法：描述函数法和相平面 法。
0
14
由于在傅氏级数中n越大，谐波分量的频率越高，An, Bn越小。此时若系统又满足第三个条件，则高次谐波 分量又进一步被充分衰减，故可认为非线性环节的稳
态输出只含基波分量，即
y(t) y1(t) A1 cost B1 sin t Y1 sin(t 1)
式中
A1
1
x 2(1 x 2 )x x 0 >0
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使x<1时，因为(1x2 )<0，系统具有负阻
尼，此时系统从外部获得能量，x(t)的运动呈发散形式；
当x>1时，因为(1x2 )>0，系统具有正阻尼，此
时系统消耗能量，x(t)的运动呈收敛形式；而当x=1时， 系统为零阻尼，系统运动呈等幅振荡形式。上述分析表 明，系统能克服扰动对x的影响，保持幅值为1的等幅振 荡。
7-1 离散系统的基本概念
e*(t) A(t) τ
e*(t)
理想化后： τ→0
t T t
T
矩形面积：s=A(t)×τ
τ ：脉冲宽度 A(t)：幅度
由定义： B(t ) (t )dt A(t )
0－
0＋
由脉冲函数定义，在0－～0+脉冲强 0 度B(t)可视为不变数。而 0 (t )dt 1
所以：B(t)= A(t)×τ
a.开环采样系统：采样器位于系统闭合回路之外， 或系统本身不存在闭合回路。 b.闭环采样系统：采样器位于系统闭合回路之内。 而在实践中用得最多的是：误差采样控制的闭环系统。 误差采样：采样开关设在误差比较点之后。 s:采样开关，τ→0
r(t) e(t) S e*(t) eh(t) c(t)
Gh(s)
e*(t)
e*(t) 信号复现滤波器
(保持器）
eh(t)
e*(t)(t) eh
保持器输入信号
t
保持器输出信号
t
图7-3 保持器的输入与输出信号
保持器可把脉冲信号e*(t)复现为阶梯信号eh(t)； 当采样频率足够高时，eh(t)接近于连续信号。
(2) 采样系统的典型结构图
根据采样器在系统中所处的位置不同，可以构成各种采 样系统。
第七章 线性离散系统的分析与校正
7-1 离散系统的基本概念 7-2 信号的采样与保持 7-3 z变换理论 7-4 离散系统的数学模型 7-5 离散系统的稳定性与稳态误差 7－6 离散系统的动态性能分析 7－7 离散系统的数字校正
学习目的
由于数字技术的迅速发展，特别是计算机技术的 发展，数字控制在许多场合取代了模拟控制器，作为 分析与设计数字控制系统的理论基础，离散系统控制 理论发展也非常迅速。 离散控制系统与连续控制系统既有本质上的不同， 又有分析研究方面的相似性，利用z变换法研究离散 系统，可以把连续系统中的许多概念和方法推广到线 性离散系统。 通过本章学习，建立有关离散控制系统的概念， 掌握数字控制中采样和保持这二个信号变换过程及数 学描述，了解z变换理论，建立离散系统的数学模型， 掌握离散系统的分析和校正方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M k 0 -M 饱和特性在控制系统中是普遍存在的，常见的调节 器就具有饱和特性。
4
-a
a
x
2．死区特性 死区又称不灵敏区，在死区内虽有输入信号，但 其输出为零。
y k
-a
0
a
x
0,| x | a y k ( x a ), x a k ( x a ), x a
6
y b x -a
y b 0 -b a x -a
y
b
0
-b
0
a
x
-b
(1) 若a＝0，称这种特性为理想继电器特性所示。 (2) 若m=1，称为死区继电器特性。 (3) 若m=-1，滞环继电器特性。
实际系统中，各种开关元件都具有继电器特性。
7
7.1.2 非线性系统的若干特征
由于上述非线性特性的存在，与线性系统相比， 非线性系统具有如下特点：
n 1
非线性环节奇对称，则有A0=0
1 An 1 Bn
2
0 2
y (t ) cos n td t y (t ) sin n td t
1
第七章 非线性系统
内容提要
7.1
7.2 7.3
典型非线性特性
描述函数法 相平面法
学习指导与小结
2
※7.1
典型非线性特性
前面各章研究的都是线性系统，或者虽然是非线 性系统，仍可进行线性化处理，从而可视为线性系统。 事实上，几乎所有的实际控制系统，都不可避免地带 有某种程度的非线性、系统中只要具有一个非线性环
9
所谓自激振荡是指没有外界周期变化信号的作用 时，系统内产生的具有固定振幅和频率的稳定运动， 简称自振。 考虑著名的范德波尔方程 2 (1 x 2 ) x x 0 >0 x
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使 x<1 时，因为 (1x2 )<0 ，系统具有负阻 尼，此时系统从外部获得能量， x(t) 的运动呈发散形式； 当 x>1时，因为 (1x2 )>0，系统具有正阻尼，此 时系统消耗能量，x(t)的运动呈收敛形式；而当x=1时， 系统为零阻尼，系统运动呈等幅振荡形式。上述分析表 明，系统能克服扰动对x的影响，保持幅值为1的等幅振 荡。 10
（1）小偏差线性化（非本质非线性） （2）描述函数法（本质非线性）
这是一种频域分析方法，其实质是应用谐波线性化的方法， 将非线性特性线性化，然后用频率法的结论来研究非线性系统。 它是线性理论中的频率法在非线性系统中的推广，这种方法不 受系统阶次的限制。
（3）相平面法（本质非线性）
相平面法是求解一、二阶常微分方程的图解法。通过在相 平面上绘制相轨迹，可以求出微分方程在任何初始条件下的解。 这是一种时域分析法，但仅适用于一阶和二阶系统。
非线性系统对于正弦输入信号的响应则比较复杂， 会产生一些比较奇特的现象。例如跳跃谐振和多值响 应、波形畸变、倍频振荡和分频振荡等。 考虑有名的杜芬方程
fx k1 x k3 x 3 p cos t m x
x 1
6 5
2
3
4
11
7.1.3 非线性系统的分析方法
到目前为止，非线性系统的研究还缺乏成熟，结论不能像 线性系统那样具有普遍意义，一般要针对系统的结构，输入及 初始条件等具体情况进行分析。工程上常用的方法有以下几种：
3. 滞环特性 滞环特性表现为正向与反向特性不是重叠在一起 ，而是在输入—输出曲线上出现闭合环路。又称为间 隙特性。
5
b -a 0
y
a -b
x
k ( x asign x ) y 0 y y0 bsignx
4 继电器特性
y b
-a -ma
0 ma -b a
ma x a, x 0 0 a x ma, x 0 0 y bsignx | x | a x b x ma, x 0 x ma, x 0 b
（1）稳定性的复杂性。
（2）可能存在自激振荡现象 。
x(t)
（3）频率响应。
x 2 x x( x 1) x
1
x0>1
x0<1
设t = 0，系统的初始状态为x0 0
dx dt x( x 1)
x0 e t x(t ) 1 x 0 x 0 e t
x0 t ln x 1 0
节，就称为非线性系统。因此实际的控制系统大都是
非线性系统。本章将主要讨论关于非线性系统的基本 概念，以及两种基本分析方法：描述函数法和相平面 法。
3
7.1
典型非线性特性
在控制系统中，若控制装置或元件其输入输出 间的静特性曲线，不是一条直线，则称为非线性特 性。如果这些非线性特性不能采用线性化的方法来 处理，称这类非线性为本质非线性。为简化对问题 的分析，通常将这些本质非线性特性用简单的折线 y 来代替，称为典型非线性特性。 7.1.1 典型非线性特性的种类 1．饱和特性
c( t )
（2）非线性环节的输入输出3
2.描述函数的定义 设系统的非线性环节输入信号是正弦信号 x(t) = Asint 则其输出一般为周期性的非正弦信号，可以展成傅 氏级数 y (t ) A0 ( An cos n t B n sin n t )
8
相应的时间响应随初始条件而 变。
x(t) x0>1
当x0 >1，t <lnx0/(x0 1) 时，随t 1 增大，x(t) 递增；t = lnx0 /(x0 1) 时，x(t)为无穷大。
0
x0<1
当x0<1时，x(t) 递减并趋于0。
x0 t ln x 1 0
由上例可见，初始条件不同，自由运动的稳定性 亦不同。因此非线性系统的稳定性不仅与系统的结构 和参数有关，而且与系统的初始条件有直接的关系。
（4）计算机求解法
用模拟计算机或数字计算机直接求解非线性微分方程，对于 12 分析和设计复杂的非线性系统是非常有效的方法。
※7.2
描述函数
7.2.1 描述函数的定义 1. 描述函数的应用条件 （1）非线性系统的结构图可简化成一个非线性环 节N和一个线性部分G(s)串联的闭环结构。
r(t)=0
x
y
N G(s)
4
-a
a
x
2．死区特性 死区又称不灵敏区，在死区内虽有输入信号，但 其输出为零。
y k
-a
0
a
x
0,| x | a y k ( x a ), x a k ( x a ), x a
6
y b x -a
y b 0 -b a x -a
y
b
0
-b
0
a
x
-b
(1) 若a＝0，称这种特性为理想继电器特性所示。 (2) 若m=1，称为死区继电器特性。 (3) 若m=-1，滞环继电器特性。
实际系统中，各种开关元件都具有继电器特性。
7
7.1.2 非线性系统的若干特征
由于上述非线性特性的存在，与线性系统相比， 非线性系统具有如下特点：
n 1
非线性环节奇对称，则有A0=0
1 An 1 Bn
2
0 2
y (t ) cos n td t y (t ) sin n td t
1
第七章 非线性系统
内容提要
7.1
7.2 7.3
典型非线性特性
描述函数法 相平面法
学习指导与小结
2
※7.1
典型非线性特性
前面各章研究的都是线性系统，或者虽然是非线 性系统，仍可进行线性化处理，从而可视为线性系统。 事实上，几乎所有的实际控制系统，都不可避免地带 有某种程度的非线性、系统中只要具有一个非线性环
9
所谓自激振荡是指没有外界周期变化信号的作用 时，系统内产生的具有固定振幅和频率的稳定运动， 简称自振。 考虑著名的范德波尔方程 2 (1 x 2 ) x x 0 >0 x
该方程描述具有非线性阻尼的非线性二阶系统。
当扰动使 x<1 时，因为 (1x2 )<0 ，系统具有负阻 尼，此时系统从外部获得能量， x(t) 的运动呈发散形式； 当 x>1时，因为 (1x2 )>0，系统具有正阻尼，此 时系统消耗能量，x(t)的运动呈收敛形式；而当x=1时， 系统为零阻尼，系统运动呈等幅振荡形式。上述分析表 明，系统能克服扰动对x的影响，保持幅值为1的等幅振 荡。 10
（1）小偏差线性化（非本质非线性） （2）描述函数法（本质非线性）
这是一种频域分析方法，其实质是应用谐波线性化的方法， 将非线性特性线性化，然后用频率法的结论来研究非线性系统。 它是线性理论中的频率法在非线性系统中的推广，这种方法不 受系统阶次的限制。
（3）相平面法（本质非线性）
相平面法是求解一、二阶常微分方程的图解法。通过在相 平面上绘制相轨迹，可以求出微分方程在任何初始条件下的解。 这是一种时域分析法，但仅适用于一阶和二阶系统。
非线性系统对于正弦输入信号的响应则比较复杂， 会产生一些比较奇特的现象。例如跳跃谐振和多值响 应、波形畸变、倍频振荡和分频振荡等。 考虑有名的杜芬方程
fx k1 x k3 x 3 p cos t m x
x 1
6 5
2
3
4
11
7.1.3 非线性系统的分析方法
到目前为止，非线性系统的研究还缺乏成熟，结论不能像 线性系统那样具有普遍意义，一般要针对系统的结构，输入及 初始条件等具体情况进行分析。工程上常用的方法有以下几种：
3. 滞环特性 滞环特性表现为正向与反向特性不是重叠在一起 ，而是在输入—输出曲线上出现闭合环路。又称为间 隙特性。
5
b -a 0
y
a -b
x
k ( x asign x ) y 0 y y0 bsignx
4 继电器特性
y b
-a -ma
0 ma -b a
ma x a, x 0 0 a x ma, x 0 0 y bsignx | x | a x b x ma, x 0 x ma, x 0 b
（1）稳定性的复杂性。
（2）可能存在自激振荡现象 。
x(t)
（3）频率响应。
x 2 x x( x 1) x
1
x0>1
x0<1
设t = 0，系统的初始状态为x0 0
dx dt x( x 1)
x0 e t x(t ) 1 x 0 x 0 e t
x0 t ln x 1 0
节，就称为非线性系统。因此实际的控制系统大都是
非线性系统。本章将主要讨论关于非线性系统的基本 概念，以及两种基本分析方法：描述函数法和相平面 法。
3
7.1
典型非线性特性
在控制系统中，若控制装置或元件其输入输出 间的静特性曲线，不是一条直线，则称为非线性特 性。如果这些非线性特性不能采用线性化的方法来 处理，称这类非线性为本质非线性。为简化对问题 的分析，通常将这些本质非线性特性用简单的折线 y 来代替，称为典型非线性特性。 7.1.1 典型非线性特性的种类 1．饱和特性
c( t )
（2）非线性环节的输入输出3
2.描述函数的定义 设系统的非线性环节输入信号是正弦信号 x(t) = Asint 则其输出一般为周期性的非正弦信号，可以展成傅 氏级数 y (t ) A0 ( An cos n t B n sin n t )
8
相应的时间响应随初始条件而 变。
x(t) x0>1
当x0 >1，t <lnx0/(x0 1) 时，随t 1 增大，x(t) 递增；t = lnx0 /(x0 1) 时，x(t)为无穷大。
0
x0<1
当x0<1时，x(t) 递减并趋于0。
x0 t ln x 1 0
由上例可见，初始条件不同，自由运动的稳定性 亦不同。因此非线性系统的稳定性不仅与系统的结构 和参数有关，而且与系统的初始条件有直接的关系。
（4）计算机求解法
用模拟计算机或数字计算机直接求解非线性微分方程，对于 12 分析和设计复杂的非线性系统是非常有效的方法。
※7.2
描述函数
7.2.1 描述函数的定义 1. 描述函数的应用条件 （1）非线性系统的结构图可简化成一个非线性环 节N和一个线性部分G(s)串联的闭环结构。
r(t)=0
x
y
N G(s)