Excel求置信区间的方法-excel置信区间
[重点]EXCEL区间估计
![[重点]EXCEL区间估计](https://img.taocdn.com/s3/m/e94a9ca7f021dd36a32d7375a417866fb84ac0d7.png)
区间估计计算置信区间的本质是输入两个公式，分别计算置信下限与置信上限．当熟悉了数据输入方法及常见统计函数后，变得十分简单。
1、单一总体均值的区间估计在2σ未知时，均值μ的置信区间：),(22n sz x n s z x αα+-例1：一家保险公司收集到由36位投保人组成的随机样本，得到每位投保人的年龄数据如下图7-1所示。
试建立投保人年龄95%的置信区间。
图7-1 36个投保人年龄的数据具体操作步骤如下：①在单元格C3输入样本数(n)=36。
②计算平均数和标准差。
在单元格C4输入平均数公式：= A VERAGE （E1:J6），在单元格C5输入样本标准差公式：= STDEV （E1:J6）。
③在单元格C6输入置信度（1-α）=95%，在单元格C7中输入显著水平(α)=5%。
④计算Z 值，在单元格C8中输入 =NORMSINV （1-C7/2）⑤计算置信区间上限和下限。
在单元格C9输入求置信区间下限公式：=C4-C8*C5/SQRT(C3)，在单元格C10输入求置信区间上限公式：= C4+C8*C5/SQRT(C3)。
⑥在单元格C11输入求置信区间公式：=CONCA TENA TE("(",C9,",",C10,")")。
由上可得置信区间为（36.96, 42.04），如图7-2所示。
图7-2 单一总体均值的区间估计2、单一总体比例的区间估计： 置信区间为：)/)1(,/)1((2/2/n q q z q n q q z q -+--αα 例2：美国某调查机构想了解美国民众对政府某项税收议案的态度，调查了1000位美国人，结果发现5成人表示支持，4成人表示反对，1成人既不支持，也不反对。
试估计支持比例的95%置信区间。
操作步骤如下：①在单元格C3输入样本数(n)=1000。
②在单元格C4输入样本中支持百分比(q)=0.5。
③在单元格C5输入置信度(1-α)=95%，在单元格C6输入显著水平(α)=5%。
excel表格如何计算溶出曲线非模型依赖多变量置信区间
excel表格如何计算溶出曲线非模型依赖多变量置信区间
在Excel中计算溶出曲线非模型依赖多变量置信区间，可以通过以下步骤实现：
1.准备数据：将溶出曲线的原始数据输入Excel表格中，确保数据格式正确。
2.添加辅助列：在数据表的旁边，添加一列用于计算置信区间，假设为“置信区间”。
3.计算均值和标准差：在另一列中计算每组数据的均值和标准差，假设分别为“均值”和“标准差”。
4.计算置信区间：使用以下公式计算置信区间。
假设要计算的置信水平为95%，则公式为“(均值-t
标准差/sqrt(n), 均值+t标准差/sqrt(n))”，其中n为样本数量，t为t分布的临界值，可以通过Excel 中的函数TINV()或T.INV()计算。
5.填充公式：将上述公式复制到“置信区间”列的每个单元格中，填充整个列。
6.查看结果：完成上述步骤后，即可在“置信区间”列中查看每组数据的非模型依赖多变量置信区间。
需要注意的是，以上步骤仅供参考，实际操作可能因Excel版本和具体数据情况而有所不同。
如果数据量较大，建议使用专业的统计软件进行计算。
excel计算回归模型的置信区间
excel计算回归模型的置信区间回归模型的置信区间是在统计学中常用的一种方法，用于评估回归模型的预测结果的准确性和可靠性。
在实际应用中，我们经常需要使用回归模型来预测某个变量的取值，并对预测结果进行评估。
通过计算回归模型的置信区间，我们可以得到一个范围，该范围内包含了预测结果的真实值的概率。
让我们先了解一下回归模型的基本概念。
回归模型是一种用于研究变量之间关系的统计模型，它可以帮助我们理解和预测一个变量（因变量）与其他变量（自变量）之间的关系。
回归模型的基本形式可以表示为：Y = β0 + β1X1+ β2X2 + ... + βnXn + ε，其中Y是因变量，X1、X2、...、Xn是自变量，β0、β1、β2、...、βn是回归系数，ε是误差项。
在实际应用中，我们通常使用最小二乘法来估计回归系数，即通过最小化观测值与回归模型预测值之间的差距来确定回归系数的值。
然而，由于样本数据的限制，我们无法得到准确的回归系数值，因此需要进行统计推断来评估回归模型的预测结果的准确性。
回归模型的置信区间是一种常用的统计推断方法，用于估计回归模型预测结果的不确定性。
置信区间表示了对于给定置信水平的情况下，预测结果的真实值落在一个区间内的概率。
通常，我们使用95%的置信水平，即置信区间的宽度为95%。
计算回归模型的置信区间需要考虑多个因素，包括样本的大小、回归系数的估计值、自变量的取值以及残差的方差等。
在进行计算之前，我们需要对回归模型做一些假设，包括误差项服从正态分布、观测值之间独立等。
一种常用的计算回归模型置信区间的方法是基于t分布。
根据中心极限定理，当样本容量足够大时，回归系数的估计值近似服从正态分布。
因此，我们可以使用t分布来计算回归系数的置信区间。
具体而言，回归模型的置信区间可以表示为：估计值±t值×标准误差，其中估计值是回归系数的估计值，t值是与给定置信水平和自由度相关的临界值，标准误差反映了回归系数估计值的不确定性。
excel 斜率置信区间 -回复
excel 斜率置信区间-回复Excel 斜率置信区间是用来衡量回归分析的斜率参数的可靠性和确定性的。
在统计学中，回归分析是研究变量之间关系的一种方法，而斜率是描述这种关系强度和方向的重要指标。
通过计算斜率的置信区间，我们可以判断斜率参数的可靠性，以及此参数估计的波动范围。
斜率置信区间是指在给定置信水平下，斜率的真实值有多大概率落在某个区间内。
通常情况下，我们可以使用Excel来计算斜率置信区间，以下是一步一步的说明。
1. 收集数据：首先，我们需要收集相关变量的数据，这些变量应该存在某种联系。
例如，如果我们想研究身高和体重之间的关系，我们可以收集一组样本数据，包括身高和体重的观测值。
2. 插入数据：一旦数据收集完毕，我们可以将这些数据插入Excel中的数据表。
我们需要确保每个变量都有相应的列，并将数据以适当的格式输入。
3. 绘制散点图：为了可视化变量之间的关系，我们可以使用Excel中的散点图功能绘制出数据的散点图。
选择身高作为自变量（X轴），体重作为因变量（Y轴），然后选择散点图类型。
4. 添加趋势线：为了更好地描述变量之间的关系，我们可以为散点图添加趋势线。
选择散点图上的任意散点，然后右键单击选择“添加趋势线”。
在弹出的对话框中，选择合适的线性趋势线。
5. 计算斜率：一旦趋势线添加完成，我们可以通过点击趋势线上的右键，选择“趋势线的格式设置”来查看趋势线参数。
其中一个参数就是斜率。
6. 计算标准误差：标准误差是衡量斜率参数估计的准确性的指标之一。
在Excel中，标准误差可以通过参考计算斜率的公式和相关数据来计算。
标准误差可以使用“STERR”函数完成。
7. 确定置信水平：在计算斜率置信区间之前，我们需要确定置信水平。
通常，常见的置信水平包括95和99。
我们可以根据实际需求选择适当的置信水平。
8. 计算置信区间：一旦有了标准误差和置信水平，我们可以使用Excel 中的T分布或Z分布来计算斜率的置信区间。
excel 拟合 置信区间
excel 拟合置信区间摘要：一、背景介绍1.Excel 在数据分析中的应用2.拟合函数在Excel 中的重要性3.置信区间的概念二、Excel 中拟合函数的应用1.线性拟合2.多项式拟合3.指数拟合4.对数拟合5.其他拟合函数三、Excel 中计算置信区间的步骤1.选择数据2.确定置信水平3.使用内置函数计算置信区间4.结果解读四、拟合函数与置信区间的实际应用案例1.数据分析2.预测趋势3.市场调研4.科学研究正文：在当今这个大数据时代，Excel 作为一款功能强大的数据处理软件，被广泛应用于各个领域。
在数据分析过程中，拟合函数和置信区间的应用尤为重要，它们可以帮助我们更好地理解数据，从而做出更准确的决策。
本文将详细介绍Excel 拟合函数在置信区间计算中的应用。
首先，我们需要了解Excel 中拟合函数的应用。
Excel 提供了丰富的拟合函数，包括线性拟合（SLOPE 和INTERCEPT）、多项式拟合（POLY）、指数拟合（EXPONENTIAL）和对数拟合（LOGARITHMIC）等。
这些拟合函数可以帮助我们更好地理解数据之间的关系，从而为后续的数据分析提供便利。
其次，我们需要了解如何在Excel 中计算置信区间。
计算置信区间的步骤如下：首先选择需要计算置信区间的数据，然后确定置信水平（通常为95%），接着使用Excel 内置的函数（如STDEV.S、VAR.S 等）计算标准误差，最后使用公式计算置信区间。
需要注意的是，计算置信区间的过程中要确保数据的可靠性。
在实际应用中，拟合函数和置信区间可以帮助我们更好地分析数据、预测趋势和进行市场调研。
例如，在市场调研中，我们可以使用Excel 的拟合函数预测产品的销售趋势，并根据置信区间评估预测结果的可靠性。
在科学研究中，拟合函数可以帮助我们建立实验模型，而置信区间则可以用于评估实验结果的准确性。
总之，Excel 中的拟合函数和置信区间在数据分析中具有重要意义。
excel置信区间计算
excel置信区间计算Excel置信区间计算一、什么是置信区间？置信区间是统计学中用于估计总体参数的一种方法。
在实际应用中，我们通常无法获得总体的全部数据，只能通过对样本数据进行统计分析来推断总体的特征。
而置信区间就是在某个置信水平下，对总体参数的一个区间估计。
二、如何使用Excel计算置信区间？在Excel中，计算置信区间需要使用到两个函数：平均值函数（AVERAGE）和标准误差函数（STDEVP）。
下面以一个实例来说明如何在Excel中进行置信区间的计算。
假设我们有一组样本数据，包含10个观测值。
我们想要计算该样本数据的均值的95%置信区间。
1. 首先，在Excel的一个单元格中输入样本数据，例如A1到A10。
2. 然后，在另外一个单元格中输入平均值函数，即在B1单元格中输入=AVERAGE(A1:A10)，回车。
3. 接下来，在第三个单元格中输入标准误差函数，即在C1单元格中输入=STDEVP(A1:A10)/SQRT(COUNT(A1:A10))，回车。
4. 最后，在第四个单元格中输入置信区间的下限，即在D1单元格中输入=B1-1.96*C1，回车。
在第五个单元格中输入置信区间的上限，即在E1单元格中输入=B1+1.96*C1，回车。
5. 到此，我们就得到了该样本数据均值的95%置信区间。
三、如何解读置信区间的结果？在上述实例中，我们得到了样本数据均值的95%置信区间。
这意味着，如果我们重复抽取样本数据，并计算其均值的置信区间，有95%的概率使得该区间包含总体的真实均值。
具体解读时，我们可以说“在95%的置信水平下，样本数据的均值的置信区间为[下限，上限]”。
其中，下限和上限即为Excel计算得到的结果。
四、注意事项在使用Excel进行置信区间计算时，需要注意以下几点：1. 样本数据必须是随机抽取的，并且符合总体分布的假设。
2. 置信水平的选择需要根据实际需求进行。
常用的置信水平有90%、95%和99%。
Excel求置信区间的方法-excel置信区间
Excel求置信区间的方法-excel置信区间什么是置信区间在研究统计问题时，往往需要对总体的某个特征参数进行估计，但是由于样本数据的随机性，导致我们的估计值并不完全准确。
这时我们需要确定一个范围，认为真实值有一定的概率落在这个范围内，这个范围就是置信区间。
换句话说，置信区间是指，以样本数据作为基础，对总体的某个参数进行估计时，给出的一个范围，该范围内含有总体参数真实值的概率就是置信水平。
常见的置信水平有90%、95%和99%，其中90%的置信水平代表在总体参数真实值不变的情况下，我们进行100次估计，会有90次的估计值落在该置信区间范围内。
Excel如何求置信区间Excel提供了STDEV.S、T.INV.2T和NORM.S.INV三个函数帮助用户求解置信区间。
STDEV.S函数用于求样本标准差，T.INV.2T函数用于求T分布累积分布函数的反函数，NORM.S.INV函数用于求标准正态分布累积分布函数的反函数。
以95%的置信水平和样本大小为10的样本数据为例，下面介绍Excel求置信区间的具体方法：1. 打开Excel，从A1单元格到A10单元格输入样本数据，如下图所示：4. 在D1单元格输入=T.INV.2T(0.05,9)，函数T.INV.2T(0.05,9)表示将0.05分位点与T分布进行比较，参数9表示样本大小-1，如下图所示：5. 在E1单元格输入=B1-D1*C1/SQRT(10)，函数B1-D1*C1/SQRT(10)代表置信区间下限，其中C1/SQRT(10)是标准误差，SQRT(10)表示样本大小的平方根，如下图所示：7. 最终得到的结果如下图所示，表示95%的置信水平下，总体均值的真实值有95%的概率落在6.95到11.65之间：以上就是Excel求置信区间的方法，需要注意的是，对于不同的置信水平和样本大小，求解置信区间的步骤略有不同，但求解方法是类似的。
对于用户而言，只需要熟悉求解方法，再根据需要进行参数设置即可。
在Excel中求回归分析的预测区间置信区间
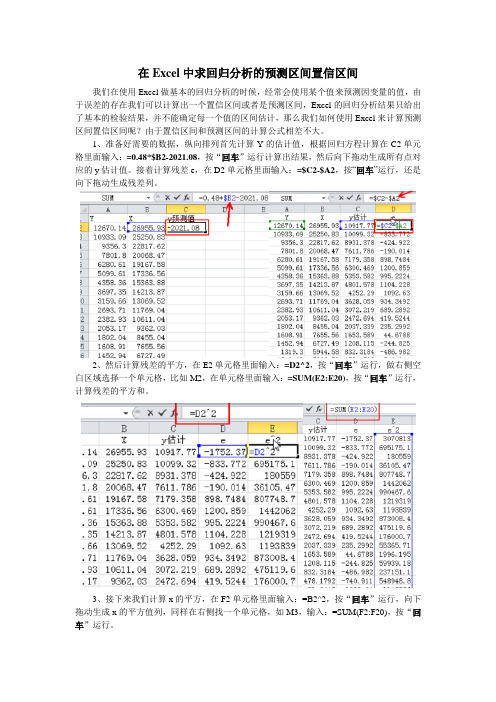
在Excel中求回归分析的预测区间置信区间我们在使用Excel做基本的回归分析的时候，经常会使用某个值来预测因变量的值，由于误差的存在我们可以计算出一个置信区间或者是预测区间，Excel的回归分析结果只给出了基本的检验结果，并不能确定每一个值的区间估计，那么我们如何使用Excel来计算预测区间置信区间呢？由于置信区间和预测区间的计算公式相差不大。
1、准备好需要的数据，纵向排列首先计算Y的估计值，根据回归方程计算在C2单元格里面输入：=0.48*$B2-2021.08，按“回车”运行计算出结果，然后向下拖动生成所有点对应的y估计值。
接着计算残差e，在D2单元格里面输入：=$C2-$A2，按“回车”运行，还是向下拖动生成残差列。
2、然后计算残差的平方，在E2单元格里面输入：=D2^2，按“回车”运行，做右侧空白区域选择一个单元格，比如M2，在单元格里面输入：=SUM(E2:E20)，按“回车”运行，计算残差的平方和。
3、接下来我们计算x的平方，在F2单元格里面输入：=B2^2，按“回车”运行，向下拖动生成x的平方值列，同样在右侧找一个单元格，如M3，输入：=SUM(F2:F20)，按“回车”运行。
4、接下来我们计算估计误差，先在K2单元格计算出x的均值，输入：=AVERAGE(B2:B20)，按“回车”运行。
在K3输入需要计算得X值，比如这里的3000，在K5单元格里面输入：=SQRT($M$2/17*(1/18+($K$3-$K$2)^2/$M$3))，按“回车”运行输出误差值。
如果计算得是置信区间的话，可以另外选择单元格输入：=SQRT($M$2/17*(1+1/18+($K$3-$K$2)^2/$M$3))，按“回车”运行。
5、计算预测区间的上限和下限在J9单元格里面输入：=$M$5-TINV(0.05,17)*$K$5，按“回车”运行，作为下限值。
在K9单元格里面输入：=$M$5+TINV(0.05,17)*$K$5，按“回车”运行，作为上限值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
应用Excel求置信区间
一、总体均值的区间估计
（一）总体方差未知
例：为研究某种汽车轮胎的磨损情况，随机选取16只轮胎，每只轮胎行驶到磨坏
假设汽车轮胎的行驶里程服从正态分布，均值、方差未知。
试求总体均值卩的置信度为0.95的置信区间。
步骤:
1.在单元格A1中输入样本数据”，在单元格B4中输入指标名称”，在单元格C4 中输入指标数值”，并在单元格A2:A17中输入样本数据。
2. 在单元格B5中输入样本容量”，在单元格C5中输入“1&”
3. 计算样本平均行驶里程。
在单元格B6中输入样本均值”，在单元格C6中输入
公式：“ =AVERAGEA2, A17) ”，回车后得到的结果为41116.875”
4. 计算样本标准差。
在单元格B7中输入样本标准差”，在单元格C7中输入公
式： =STDEV(A2 A17)”，回车后得到的结果为1346.842771。
5. 计算抽样平均误差。
在单元格B8中输入抽样平均误差”，在单元格C8中输入
公式：=C7SQRT(C5)”，回车后得到的结果为336.7106928 ”
6. 在单元格B9中输入置信度”，在单元格C9中输入“ 0.95 ”
7. 在单元格B10中输入自由度”，在单元格C10中输入“15。
8. 在单元格B11中输入“分布的双侧分位数”，在单元格C11中输入公式：“=
TINV(1-C9, CIO) ”回车后得到a= 0.05的t分布的双侧分位数t = 2.1315。
9•计算允许误差。
在单元格B12中输入允许误差”，在单元格C12中输入公
式：=C11*C8，回车后得到的结果为717.6822943。
10. 计算置信区间下限。
在单元格B13中输入置信下限”，在单元格
C13中输
入置信区间下限公式：=C6- C12”回车后得到的结果为40399.19271。
11. 计算置信区间上限。
在单元格B14中输入置信上限”，在单元格C14中输入置
信区间上限公式：=C6+ C12”回车后得到的结果为41834.55729。
(二)总体方差已知
仍以上例为例，假设汽车轮胎的行驶里程服从正态总体，方差为体均值
10002,试求总
卩的置信度为0.95的置信区间。
1样本数据
241250
340187
443175指标名称指标数值
5.J41010样本容量16 __|
639265样本均值41116. 875
741872标准差1000 1
842654抽样平均误差250
941287置信度CL 95
1038970自由度15 _______ 1140200标准正态分布的双侧分位数L 96 \ 1242550允许误差
1341095置信下限40636.875 I 1440680置信上限4:1606. 875
1543500
1639775
1740400
18
19
1. 在单元格A1中输入样本数据”，在单元格B4中输入指标名称”，在单元格C4 中输入指标数值”，并在单元格A2:A17中输入样本数据。
2. 在单元格B5中输入样本容量”，在单元格C5中输入“1&”
3. 计算样本平均行驶里程。
在单元格B6中输入样本均值”，在单元格C6中输入
公式：“ =AVERAGEA2, A17) ”，回车后得到的结果为41116.875。
4. 在单元格B7中输入标准差”，在单元格C7中输入“ 1000。
5. 计算抽样平均误差。
在单元格B8中输入抽样平均误差”，在单元格C8中输入
公式：=C7SQRT(C5)”，回车后得到的结果为250。
6. 在单元格B9中输入置信度”，在单元格C9中输入“ 0.95 ”
7. 在单元格B10中输入自由度”，在单元格C10中输入“15'
8. 在单元格B11中输入标准正态分布的双侧分位数”，在单元格C11中输入公式：=NORMSINV(0.975)，回车后得到a= 0.05的标准正态分布的双侧分位数
Z0.052=1.96。
9. 计算允许误差。
在单元格B12中输入允许误差”，在单元格C12中输入公式：
=C11*C8 ”，回车后得到的结果为490。
10. 计算置信区间下限。
在单元格B13中输入置信下限”，在单元格C13中输入置
信区间下限公式：=C6- C12',回车后得到的结果为40626.875。
11. 计算置信区间上限。
在单元格B14中输入置信上限”，在单元格C14中输入置
信区间上限公式：=C6+ C12，回车后得到的结果为41606.875。
二、总体方差的区间估计(卩未知)
例：假设从加工的同一批产品中任意抽取20件，测得它们的平均长度为12厘米，方差为0.0023平方厘米，求总体方差的置信度为95%的置信区间。
为构造区间估计的工作表，我们应在工作表的A列输入计算指标，B列输入计算
公式，C列输入计算结果。
①本表C列为B列的计算结果，当在B列输入完公式后，即显示出C列结果，这里只是为了让读者看清楚公式，才给出了B列的公式形式。
②统计函数 =CHINV(a df) ”给出概率水平为a自由度为v的X分布上侧分位数。
具体使用方法，可以在Excel的函数指南中查看。
综上所述，我们有95%的把握认为该批零件平均长度的方差在0.00133至0.00491
之间。
三、总体比例的区间估计
—450 小 _
p 0.3, np
1500 例：某研究机构欲调查某市大专以上学历的从业人员专业不
对口的比率。
于是随机抽取了一个由1500人组成的样本进行调查，其中有450人说
他们从事的工作与所学专业不对口。
试在95%的置信度下构造出该市专业不对口人员
所占比率的置信区间。
n(1_P)由于样本容量很大，n = 1500，样本比例
都大于5,故可用正态分布逼近。
构造区间估计的工作表，我们应在工作表的C列输入计算指标，D列输入计算公
为了让读者看清楚公式，才给出了D列的计算公式。
②统计函数=CONFIDENCE(a, 3, § )，”给出置信水平为1-a样本比例标准差为B和样本容量为§的总体比例的误差范围。
具体使用方法，可以在Excel的函数指南中查看。