渐开线方程
proe 齿轮渐开线方程

第一组关系式 sd17=df/2
sd16=db/2 sd15=d/2 sd12=da/2 sd18=b sd11=delta sd10=90
第二组关系式 sd0=d/cos(delta) sd1=da/cos(delta) sd2=db/cos(delta) sd3=df/cos(delta)
第三组关系式 sd0=(d-2*b*sin(delta))/cos(delta) sd1=(da-2*ba*sin(delta_a))/cos(delta) sd2=(db-2*bb*sin(delta_b))/cos(delta) sd3=(df-2*bf*sin(delta_f))/cos(delta)
斜齿齿轮齿廓渐开线生成方程为笛卡儿坐标系输入参数方 程,根据 t (将从0变到1) 对 x, y 和 z 例如:对在 x-y 平面的一个圆,中心在原点 , 半径 = 4,参数方程将是:
x = 4*cos(t*360) y = 4*sin(t* 360) z=0 delta=atan(z/z_asm) d=m*z db=d*cos(alpha) da=d+2*ha*cos(delta) df=d-2*hf*cos(delta) hb=(d-db)/(2*cos(delta)) rx=d/(2*sin(delta)) theta_a=atan(ha/rx) theta_b=atan(hb/rx) delta_a=delta+theta_a delta_b=delta-theta_b delta_f=delta-theta_f ba=b/cos(theta_a) bb=b/cos(theta_b) bf=b/cos(theta_f) d1=d/(2*tan(delta))
齿轮渐开线方程图解
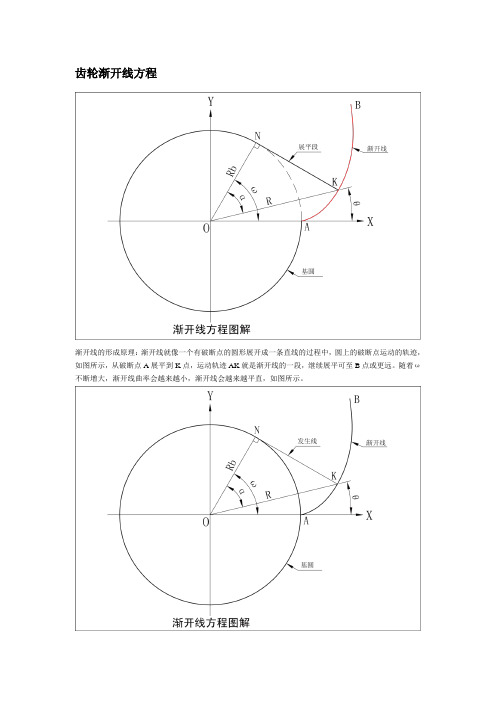
建立方法同大端,但球面半径rx变为rx-bc
大端齿根圆:
以默认的笛卡尔坐标为基准,用从方程功能建立基准曲线,方程关系式如下:
x=bb1*cos(t*360)
y=bb1*sin(t*360)
z=ob1
小端齿根圆:
建立方法同大端,但半径bb1变为b2b3,x方向尺寸ob1变为ob3。
齿根过度曲线:
3.齿顶圆压力角为参数控制的“极坐标”表示的渐开线方程B:
FAI=T*TAN(ACOS(DB/DW))*180/PI
Rb=DB/2
R=Rb/COS(ATAN(FAI*PI/180))
THETA=FAI-ATAN(FAI*PI/180)
Z=0
B.设ω为滚角参数,设定一个参数值,如45°,将ω用个人习惯的字母符号代替,如FAI。根据“勾股定理”,极轴R的长度R=( Rb^2+NK^2)^0.5。因式中NK=Rb*FAI*PI/180,将其代入。即可写成:
Z=0
滚角为参数“笛卡尔”坐标表示的渐开线:
A=T*45
X=DB/2*COS(A)+DB/2*SIN(A)*A*PI/180
Y=DB/2*SIN(A)-DB/2*COS(A)*A*PI/180
Z=0
所以创建齿轮模型时,如果对渐开线方程不熟悉,尽可能采用“极坐标”方程表达式:式1。
控制渐开线长度的方法:
C.在所有的“极坐标”渐开线方程表达式中,式1是最直接最简单的表达方法,公式简单,容易理解或记忆。而直角渐开线方程式表达式比较繁琐,不容易理解或记忆,如以下两种方程式的比较:
压力角为参数“极坐标”表示的渐开线方程1:
FAI=T*45
Rb=DB/2
R=Rb/COS(FAI)
平面螺旋线方程

平面螺旋线方程
螺旋线早在古希腊及古埃及就已有所见证,它们在世界历史上占有重要地位。
螺旋线是一种特殊的平面曲线,它们以不断改变的方向旋转来围绕一个轴心,其中有很多旋转曲线通常被分类为螺旋线。
如阿基米德桃花曲线,卡塔尔曲线,贝塞尔曲线等等。
但本文重点介绍的是平面螺旋线,也称渐开线。
渐开线的方程是按照风格给出的,以二次函数的形式表示。
根据渐开线中心点和半径的定义,可以得出以下方程:
$${displaystyle x=Rcostheta ,quad y=Rsintheta +c}$$ 其中,$R$表示渐开线的半径;$c$表示渐开线中心点到原点的距离;$theta$表示渐开线的弧度参数,用来描述渐开线的旋转情况。
平面螺旋线的构造是由一个圆或椭圆的旋转弧线构成的,它以不断改变的方向旋转来围绕一个轴心。
- 1 -。
渐开线方程

渐开线方程
1渐开线方程
渐开线方程是一种微分方程,在几何方面它表示了两个曲线之间的关系,并且可以用来求解复杂的函数关系。
它具有有趣的数学特性,在数学中有重要的应用。
渐开线方程由两个曲线组成,一条曲线是称为渐开线的曲线,而另一条曲线是称为渐开线法则的曲线。
一般来说,渐开线的曲线表示第一个函数的极限值,而渐开线法则的曲线则表示第二个函数的极限值。
当两个函数的极限值相等时,渐开线方程就成立了。
渐开线方程有多种形式,最常用的两种形式分别为渐近线方程和凸线方程。
渐近线方程也可以表示两个几何图形的关系,凸线方程也表示几何图形的关系,但是它的表示性比渐近线方程要强一些。
渐开线方程在微积分中具有重要的应用,用它可以更好地理解复杂的函数关系,从而推导出更正确的解决方案。
当被求解的方程形式特别复杂时,渐开线方程也可以用来进行解析求解。
渐开线方程既有科学价值,又具有数学智力。
它不仅可以用来解决实际问题,还可以帮助我们更好地理解函数关系,它是解决数学问题的一种重要方法。
渐开线方程
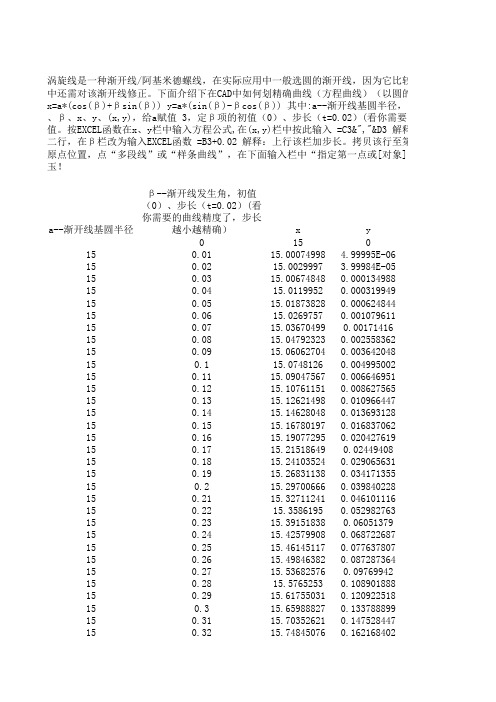
a--渐开线基圆半径β--渐开线发生角,初值(0)、步长(t=0.02)(看你需要的曲线精度了,步长越小越精确)xy 015150.0115.00074998 4.99995E-06150.0215.0029997 3.99984E-05150.0315.006748480.000134988150.0415.01199520.000319949150.0515.018738280.000624844150.0615.02697570.001079611150.0715.036704990.00171416150.0815.047923230.002558362150.0915.060627040.003642048150.115.07481260.004995002150.1115.090475670.006646951150.1215.107611510.008627565150.1315.126214980.010*********.1415.146280480.013693128150.1515.167801970.016837062150.1615.190772950.020*********.1715.215186490.024********.1815.241035240.029*********.1915.268311380.034171355150.215.297006660.0398********.2115.327112410.046101116150.2215.35861950.052982763150.2315.391518380.06051379150.2415.425799080.068722687150.2515.461451170.0776********.2615.498463820.0872********.2715.536825760.0976*******.2815.57652530.108901888150.2915.617550310.120922518150.315.659888270.133788899150.3115.703526210.147528447150.3215.748450760.162168402涡旋线是一种渐开线/阿基米德螺线,在实际应用中一般选圆的渐开线,因为它比较容品中还需对该渐开线修正。
渐开线方程

α
标准齿轮为20°
模数
m
m=p/π
齿厚
s
s=p/2
齿槽宽
e
e=p/2
齿距
p
p=mπ
基圆齿距
pb
pb=pcosα
齿顶高
ha
ha=ha*m=m
齿根高
hf
hf=(ha*+c*)m=1.25m
齿高
h
h=ha+hf=2.25m
分度圆直径
d
d=mz
齿顶圆直径
da
da=m(z+2)
齿根圆直径
渐开线方程为:
x=r×cos(θ+α)+(θ+α)×r×sin(θ+α)
y=r×sin(θ+α)-(θ+α)×r×cos(θ+α)
z=0
式中,r为基圆半径;θ为展角,其单位为弧度
展角θ和压力角α之间的关系称为渐开线函数
θ=inv(α)=tan(α)-α
式中,inv为渐开线involute的缩写
外啮合标准直径圆柱齿轮的几何尺寸的计算公式
df
df=d-2hf=m(z-2.5)
基圆直径
db
db=dcosα
标准中心距
a
a=m(z1+z2)/2
齿数
Z
举例:
模数m:4
齿数z:10
压力角:20
D=mz=40
Da=48
Df=30
为展角其单位为弧度invtan式中inv为渐开线involute的缩写外啮合标准直径圆柱齿轮的几何尺寸的计算公式代号计算公式齿形角标准齿轮为20模数pbpbhaha齿根高hfhfhahahf225m分度圆直径mz齿顶圆直径dadamz2齿根圆直径dfdfd2hfmz25基圆直径dbdbcos标准中心距举例
渐开线方程式推导
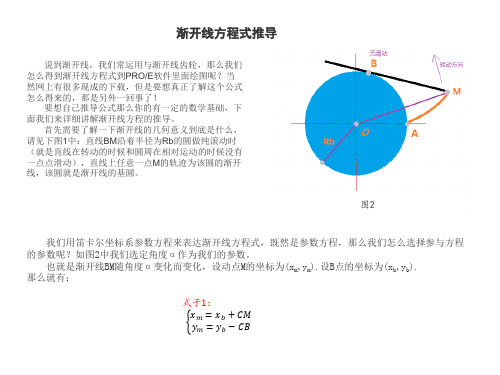
渐开线方程推导

渐开线方程推导(直角坐标系)鱼板主在前面对渐开线的极坐标方程进行了推导,使大家受益匪浅。
直角坐标方程在本论坛上也出现了很多次,但一些朋友对其中的参数理解上还有一定的偏差。
本贴通过对渐开线直角坐标方程(参数方程)推导,使朋友们对其中的参数更加深入的了解,以便在工作中能很好的使用它。
如果大家觉得没有什么意义的话,本贴就当是灌水。
如图:在渐开线上有一点P(X,Y),X=OB+BC,Y=AB-AN由渐开线特点可知,弧长AD=AP=r.βOB=rcosβBC=AP.sinβ=r.β.sinβ所以X=r.cosβ+r.β.sinβ同理Y=r.sinrβ-r.β.cosβ因此,渐开线的直角坐标参数方程就是:X=r.cosβ+r.β.sinβY=r.sinrβ-r.β.cosβ其中r为基圆半径在这里大家可以和渐开线的极坐标方程推导进行比较,直角坐标方程中的β就是压力角和展角的和,β=α+θ图片附件:渐开线.jpg(2005-7-622:40,26.33K)使用autocadvba绘制渐开线齿轮Dim mAsDouble'齿轮模数Dim zAsInteger'齿数Dim rAsDouble'分度圆半径Dim raAsDouble'齿顶圆半径Dim rbAsDouble'基圆半径Dim rfAsDouble'齿根圆半径Dim PIAsDouble'定义常数πPrivateSubCommand1_Click()PI=4*Atn(1)m=Val(TextBox1.text)z=Val(TextBox2.text)r=m*z/2ra=r+mrb=r*Cos(20*PI/180)rf=r-1.25*mDim cobrAsAcadCircle'分度圆Dim cobraAsAcadCircle'齿顶圆Dim cobrbAsAcadCircle'基圆Dim cobrfAsAcadCircle'齿根圆Dim cp1(0To2)AsDoublecp1(0)=0:cp1(1)=0:cp1(2)=0Setcobr=ThisDrawing.ModelSpace.AddCircle(cp1,r)Setcobra=ThisDrawing.ModelSpace.AddCircle(cp1,ra)Setcodrb=ThisDrawing.ModelSpace.AddCircle(cp1,rb)Setcodrf=ThisDrawing.ModelSpace.AddCircle(cp1,rf)Dim colorAsAcadAcCmColorSetcolor=AcadApplication.GetInterfaceObject("AutoCAD.AcCmColor.17")Callcolor.SetRGB(80,100,244)cobr.TrueColor=color'创建splineDim theta0 As Double'定义渐开线展角与压力角之和Dim InvPoint(0To32) As Double'定义拟合点坐标Dim SPtan(0To2) As Double'定义起点切线方向Dim EPtan(0To2) As Double'定义终点切线方向theta0=Sqr(ra^2-rb^2)/rb'将展角与压力角之和角度转换为弧度theta1=theta0-Atn(theta0)'展角delta_theta=theta0/10'单位角For j=0 To 10theta=j*delta_thetaInvPoint(j*3)=rb*(Sin(theta)-theta*Cos(theta))InvPoint(j*3+1)=rb*(Cos(theta)+theta*Sin(theta))InvPoint(j*3+2)=0Next jEPtan(0)=1:EPtan(1)=1/Tan(theta0):EPtan(2)=0Setinvobj=ThisDrawing.ModelSpace.AddSpline(InvPoint,SPtan,EPtan)'创建半个齿顶圆弧Dim center1(0To2) As DoubleDim radius1 As DoubleDim startangle As Double,endangle As DoubleDim arc1 As AcadArccenter1(0)=0:center1(1)=0:center1(2)=0radius1=rastartangle=PI/2-(Tan(PI/9)-PI/9+PI/2/z)endangle=PI/2-(Atn((Sin(theta)-theta*Cos(theta))/(Cos(theta)+theta*Sin(theta)))) Setarc1=ThisDrawing.ModelSpace.AddArc(center1,radius1,startangle,endangle)'齿根圆Dim myplineAsAcadLWPolylineDim vpoint(0To5)AsDoublevpoint(0)=0:vpoint(1)=rbvpoint(2)=-(rb-rf)*Tan(PI/2/z+Tan(PI/9)-PI/9)/2:vpoint(3)=(rb+rf)/2vpoint(4)=-rf*Sin(PI/2/z-Tan(PI/9)+PI/9):vpoint(5)=rf*Cos(PI/2/z-Tan(PI/9)+PI/9) Setmypline=ThisDrawing.ModelSpace.AddLightWeightPolyline(vpoint)mypline.SetBulge1,-1/3mypline.Update'镜像spline、齿根曲线和齿顶圆弧,形成一个齿廓Dim mirror_point1(0 To 2) As DoubleDim mirror_point2(0 To 2) As Doublemirror_point1(0)=0:mirror_point1(1)=0:mirror_point1(2)=0mirror_point2(0)=1:mirror_point2(1)=1/Tan(Tan(PI/9)-PI/9+PI/2/z):mirror_point2(2 )=0Dim mirrorinvobj As AcadSplineDim mirrorarc1 As AcadArcDim mirror_mypline As AcadLWPolylineSetmirrorarc1=arc1.Mirror(mirror_point1,mirror_point2)086Setmirrorinvobj=invobj.Mirror(mirror_point1,mirror_point2)087Setmirror_mypline=mypline.Mirror(mirror_point1,mirror_point2)088'环形阵列齿轮轮齿各部分线段089Dim noOfObjectsAsInteger090Dim angleToFillAsDouble091Dim basePnt(0To2)AsDouble092noOfObjects=z093angleToFill=2*PI*(z-1)/z094basePnt(0)=0#:basePnt(1)=0#:basePnt(2)=0#095096Dim retobjAsVariant097Dim retobj1AsVariant098Dim retobjarc1AsVariant099Dim retobjarcAsVariant100Dim retobj_myplineAsVariant101Dim retobj_mirror_myplineAsVariant102retobj=invobj.ArrayPolar(noOfObjects,angleToFill,basePnt)103retobj1=mirrorinvobj.ArrayPolar(noOfObjects,angleToFill,basePnt)104retobjarc1=mirrorarc1.ArrayPolar(noOfObjects,angleToFill,basePnt)105retobjarc=arc1.ArrayPolar(noOfObjects,angleToFill,basePnt)106retob_mypline=mypline.ArrayPolar(noOfObjects,angleToFill,basePnt)107retobj_mirror_mypline=mirror_mypline.ArrayPolar(noOfObjects,angleToFill,basePnt) 108ZoomAll109110111Command1.Enabled=False112113114EndSub。
creo齿轮渐开线曲线方程

creo齿轮渐开线曲线方程渐开线是指在齿轮啮合过程中,齿轮上任意一点的轨迹,也被称为齿轮曲面。
渐开线具有特殊的几何形态,使得齿轮在传动和运动过程中产生稳定和平滑的运动。
Creo(起初为Pro/ENGINEER)是一款由PTC公司开发的三维建模软件,广泛应用于机械设计和制造领域。
在Creo中,我们可以借助数学方程来定义齿轮的渐开线曲线。
一、齿轮渐开线曲线定义齿轮的渐开线曲线由齿数和齿轮尺寸确定。
Creo中的渐开线曲线方程如下:r = t / m - (1/m + B / m) * sin(t / m) + C,其中,r是渐开线曲线的半径,t是渐开线曲线的角度,m是齿数模数,B和C是与齿轮尺寸相关的常数。
二、参数的含义1. 齿数模数(m):齿数模数是齿轮的尺寸参数,它代表了齿轮齿数和齿轮的直径的比值。
齿数模数决定了渐开线曲线的形状。
一般情况下,齿数模数越大,渐开线曲线越平缓。
2. 常数B和C:常数B和C取决于齿轮的尺寸和几何特征。
它们可以通过齿轮的几何参数计算得出。
三、渐开线曲线的应用1. 传动平稳:齿轮的渐开线曲线可以使得齿轮之间的啮合更加平稳,降低传动过程中的噪声和振动。
这对于高精度和高速传动装置尤为重要。
2. 避免轴向力:渐开线曲线还可以帮助减小齿轮之间的轴向力,避免齿轮轴承的过早损坏。
这对于提高齿轮传动的寿命和可靠性有着重要的影响。
3. 改善齿轮效率:渐开线曲线可以减小齿轮的滚动摩擦,提高齿轮传动的效率。
总结:Creo软件提供了方便的功能来定义齿轮的渐开线曲线方程。
通过准确定义和计算齿轮的渐开线曲线,可以实现高效、稳定和精确的齿轮传动。
在实际的机械设计和制造过程中,掌握和应用齿轮渐开线曲线方程是非常重要的。
在使用Creo软件进行齿轮设计时,我们可以根据具体的齿轮参数来确定渐开线曲线方程,并进行相应的模拟和验证。
通过合理地选择齿轮渐开线曲线方程,可以提高齿轮传动的性能和可靠性。
渐开线曲线方程的应用不仅局限于齿轮设计,还可以在其他领域中使用。
利用复数求圆的渐开线和摆线方程

利用复数求圆的渐开线和摆线方程
渐开线(Rolle’s Theorem)是微积分中的一种重要的思想,其用复数方程求解圆的渐开线和摆线的方程也是一个重要的方法。
首先要知道,一般来说,用抛物线求解圆的渐开线和摆线的方法只适用于椭圆和偏心的椭圆,如果要求解圆的渐开线和摆线,就要用复数求解。
圆的渐开线方程可以由复平面内针对某一点的曲线定义得到。
当此曲线由一个复数写成渐开线(Rolle’s Theorem)的形式时,就可以得到圆的渐开线方程:
设某点M(z)在圆C上,以z0为圆心,以R为半径:
那么从z=z0开始,沿着半径R从M(z)点出发,到圆心z0的实轴上方及圆心z0的虚轴上方表示:
圆的渐开线:
圆的摆线方程也可以用复数求解,当复数表示为eθ 的形式时,可以得到圆的摆线方程:
其中,R为圆的半径,θ为复数eθ在复平面上的实虚圆弧长。
另外,也可以使用复数式方程求解圆的外切线和内切线的方程,圆的外切线方程可以写成:
其中,R为圆的半径,z0为圆心,f(z)自变量的函数值,将f (z)的导数等于0,如果取得极值,就可以得到圆的外切线方程。
圆的内切线方程可以写成:
在这里,R为圆的半径,z0为圆心,f(z)是自变量的函数值,将f(z)的导数等于1,如果取得极值,就可以得到圆的内切线方程。
总而言之,用复数求解圆的渐开线和摆线方程,相比用抛物线方法求解椭圆和偏心椭圆的渐开线和摆线,也是一种很好的求解方法,也可以求出圆的外切线和内切线方程。
齿轮齿面方程

齿轮齿面方程一、概述齿轮是机械传动中常用的零部件,其作用是将动力从一个轴传递到另一个轴上。
齿轮的设计需要考虑多个因素,其中之一就是齿面方程。
二、齿面方程的定义齿面方程是描述齿轮齿形几何形状的数学公式,它包含了齿顶高度、模数、压力角等参数。
通过解析齿面方程,可以获得各种重要的几何参数,如法向厚度、径向距离等。
三、常见的齿面方程1. 渐开线渐开线是最常用的齿面曲线之一,它具有良好的传动特性和低噪音水平。
渐开线方程可以表示为:x = m * (cos(theta) + theta * sin(theta))y = m * (sin(theta) - theta * cos(theta)) + h其中m为模数,theta为角度,h为顶高。
2. 圆弧曲线圆弧曲线也是一种常见的齿面曲线,在低速大扭矩应用中表现良好。
圆弧曲线方程可以表示为:x = r * sin(theta)y = r - r * cos(theta)其中r为半径,theta为角度。
3. 阿基米德螺线阿基米德螺线是一种特殊的曲线,其斜率为常数,因此在制造时易于加工。
阿基米德螺线方程可以表示为:x = r * cos(theta)y = r * sin(theta) + h * theta / (2 * pi)其中r为半径,theta为角度,h为顶高。
四、齿面方程的应用齿面方程是齿轮设计中非常重要的一部分。
通过解析齿面方程,可以计算出各种重要参数,如法向厚度、径向距离等。
这些参数对于齿轮的性能和寿命都有着至关重要的影响。
此外,在制造过程中,齿面方程也起着至关重要的作用。
通过使用数控加工设备和CAD软件,可以精确地制造出符合设计要求的齿轮。
五、总结齿面方程是描述齿轮几何形状的数学公式。
常见的齿面曲线包括渐开线、圆弧曲线和阿基米德螺线等。
通过解析齿面方程,可以计算出各种重要参数,并精确地制造符合设计要求的齿轮。
齿面方程在齿轮设计和制造中起着至关重要的作用。
渐开线方程

圆柱齿轮齿廓的渐开线方程渐开线的问题,这是用 Pro/ENGINEER 建立理论上精确的圆柱齿轮的基础,以下是站长推导的卡笛尔坐标系和圆柱坐标系的渐开线方程,在Pro/E 2000i 里已经测试成功,现公布给大家。
我还没时间做一个完整的齿轮,等以后有时间做好了再升级这篇文章。
1.卡笛尔坐标下的渐开线参数方程卡笛尔坐标系下的渐开线参数方程如下(设压力角 afa 由0到60度,基圆半径为 10):afa=60*tx=10*cos(afa)+pi*10*afa/180 * sin(afa)y=10*sin(afa)-pi*10*afa/180 * cos(afa)z=02.圆柱坐标下的渐开线参数方程圆柱坐标系下的渐开线参数方程如下(设基圆半径为10,压力角 afa 从0到60度):afa = 60*tr = (10^2 + (pi*10*afa/180)^2)^0.5theta = afa-atan((pi*10*afa/180)/10)z = 0在 Pro/ENGINEER 里使用 Feature > Creat > Datum > Curve > From Equation 命令,选择一个坐标系,然后选择坐标类型(卡笛尔坐标/圆柱坐标/球坐标),在窗口里输入以上方程即可生成一段精确的渐开线直齿渐开线齿轮画法讲座(一)发布日期:2010-4-14 [ 收藏评论没有找到想要的知识 ]齿轮传动是最重要的机械传动之一。
齿轮零件具有传动效率高、传动比稳定、结构紧凑等优点。
因而齿轮零件应用广泛,同时齿轮零件的结构形式也多种多样。
根据齿廓的发生线不同,齿轮可以分为渐开线齿轮和圆弧齿轮。
根据齿轮的结构形式的不同,齿轮又可以分为直齿轮、斜齿轮和锥齿轮等。
本章将详细介绍用Pro/E创建标准直齿轮、斜齿轮、圆锥齿轮、圆弧齿轮以及蜗轮蜗杆的设计过程。
3.1直齿轮的创建3.1.1渐开线的几何分析直齿渐开线齿轮画法讲座(二)发布日期:2010-4-14 [ 收藏评论没有找到想要的知识 ]4.镜像渐开线(1)在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“点”→“点”,系统弹出“基准点”对话框,如图3-15所示;图3-15“基准点”对话框(2)单击分度圆曲线作为参照,按住Ctrl键,单击渐开线作为参照,如图3-16所示。
渐开线方程式

渐开线方程式
工作中总是要用到渐开线方程式,但每次都要拿书来抄袭,总记不住,死记不是好的记忆方法,理解记忆才是正确之方法.因此问题就出在我没有理解方程式的求解
过程.因为马上就要换新的工作环境了,如果去那里还是拿着公式来抄,那不就糗大了.所以昨天在网上找了一些资料,整理成章,与大家分享.希望可以给大家带
来便利.
设<XOB=theta OB=r A⌒B=S
分别过B,M点作OX的垂线BC,ME.分别交于C,E点;
过M点作BC的垂线,交BC于D点.
由渐开线之定义可得以下等式:A⌒B=BM=渐开线
AM=S=2r*pi/360*theta
因为BC平行于OY
所以<YOB=<OBC,DM=CE
又因为MB垂直于OB(渐开线的定义)
所以<MBO-<OBC=<YOX-<YOB
所以<MBC=<XOB=theta
所以
OE=OC+CE=OC+DM=OB*cos(theta)+BM*sin(theta)=r*co
s(theta)+S*sin(theta)
EM=CD=CB-BD=OB*sin(theta)-BM*cos(theta)=r*sin(theta) -S*cos(theta)
即方程式为:x=r*cos(theta)+S*sin(theta)
y=r*sin(theta)-S*cos(theta)
z=0。
高中数学第二章参数方程第4节渐开线与摆线课件新人教A版选修4

坐标只需把φ=π4 代入曲线的参数方程,得 x= 22+ 28π,y
= 22- 28π,由此可得对应的坐标为( 22+ 28π, 22- 28π).
答案:2
( 22+
28π, 22-
2π 8)
6.我们知道关于直线 y=x 对称的两个函数互为反函数,
3.当
φ=π2 、π时,求出渐开线xy==scions
φ+φsin φ-φcos
φ, φ
上对应的点 A、B,并求出 A、B 间的距离.
解:将 φ=π2 代入xy==scions
φ+φsin φ-φcos
φ, φ,
得 x=cos π2 +π2 ·sin π2 =0+π2 =π2 ,
ππ
π
y=sin 2 - 2 ·cos 2 =1.
向量 =(2α,2),向量 =(2sin α,2cos α), = (-2sin α,-2cos α),
=(2α-2sin α,2-2cos α)
=(2(α-sin α),2(1-cos α)).
动点 M 的坐标为(x,y),向量 =(x,y).
所以xy==22((1α--csoins
α), α).
∴点 M 的坐标分别是(10π+6 3 3,12r)、(12r(7π+2),r).
10.如图 ABCD 是边长为 1 的正方形,曲线 AEFGH… 叫做“正方形的渐开线”,其中 AE、EF、FG、GH…的圆 心依次按 B、C、D、A 循环,它们依次相连接,求曲线 AEFGH 的长.
解:根据渐开线的定义可知,A︵E是半径为 1 的14圆周长, 长度为π2 ,继续旋转可得E︵F是半径为 2 的14圆周长,长度为π; F︵G是半径为 3 的14圆周长,长度为3π 2 ;G︵H是半径为 4 的14圆 周长,长度为 2π.所以曲线 AEFGH 的长是 5π.
proe笛卡尔坐标渐开线以及常用方程

proe笛卡尔坐标渐开线以及常⽤⽅程⼀、圆柱直齿轮1、渐开线1theta=t*60x=DB/2*cos(theta)+DB/2*sin(theta)*theta*pi/180y=DB/2*sin(theta)-DB/2*cos(theta)*theta*pi/180z=02、渐开线2ang=90*tr=db/2s=pi*r*t/2xc=r*cos(ang)yc=r*sin(ang)x=xc+s*sin(ang)y=yc-s*cos(ang)3、关系ha=(hax+x)*mhf=(hax+cx-x)*md=m*zda=d+2*hadf=d-2*hfdb=d*cos(alpha)⼆、圆柱斜齿轮d96=asin(2*b*tan(beta/d))d10=beta其余渐开线和关系同圆柱直齿轮三、圆锥齿轮关系ha=(hax+x)*mhf=(hax+cx-x)*mH=(2*HAX+CX)*MDELTA=ATAN(Z/Z_D)d=m*zda=d+2*ha*COS(DELTA)df=d-2*hf*COS(DELTA)db=d*cos(alpha)HB=(D-DB)/(2*COS(DELTA))RX=D/(2*SIN(DELTA))THETA_A=ATAN(HA/RX)THETA_B=ATAN(HB/RX)THETA_F=ATAN(HF/RX)DELTA_A=DELTA+THETA_ADELTA_B=DELTA-THETA_BDELTA_F=DELTA-THETA_FBA=B/COS(THETA_A)BB=B/COS(THETA_B)BF=B/COS(THETA_F)/*DTM1⾯与TOP⾯距离:D1=d/(2*tan(delta))D8=90D6=deltaD2=df/2D3=db/2D4=d/2D5=da/2D7=b/*齿轮⼤端圆关系式:D15=d/cos(delta)D16=da/cos(delta)D17=db/cos(delta)D18=df/cos(delta)/*齿轮⼩端圆关系式:D24=(df-2*bf*sin(delta_f))/cos(delta)D25=(db-2*bb*sin(delta_b))/cos(delta)D26=(d-2*b*sin(delta))/cos(delta)D27=(da-2*ba*sin(delta_a))/cos(delta)/*坐标关系式:d32=360*cos(delta)/(4*z)+180*tan(alpha)/pi-alpha d64=360*cos(delta)/(4*z)+180*tan(alpha)/pi-alpha /*DTM4与DTM5夹⾓:D50=360-360*cos(delta)/(4*z)D55=360-360*cos(delta)/(4*z)/*旋转体:d69=hd68=0.8*h/*阵列:d91=360/zp94=z渐开线r=db/cos(delta)/2theta=t*60x=r*cos(theta)+r*sin(theta)*theta*pi/180y=r*sin(theta)-r*cos(theta)*theta*pi/180z=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱齿轮齿廓的渐开线方程渐开线的问题,这是用 Pro/ENGINEER 建立理论上精确的圆柱齿轮的基础,以下是站长推导的卡笛尔坐标系和圆柱坐标系的渐开线方程,在Pro/E 2000i 里已经测试成功,现公布给大家。
我还没时间做一个完整的齿轮,等以后有时间做好了再升级这篇文章。
1.卡笛尔坐标下的渐开线参数方程卡笛尔坐标系下的渐开线参数方程如下(设压力角 afa 由0到60度,基圆半径为 10):afa=60*tx=10*cos(afa)+pi*10*afa/180 * sin(afa)y=10*sin(afa)-pi*10*afa/180 * cos(afa)z=02.圆柱坐标下的渐开线参数方程圆柱坐标系下的渐开线参数方程如下(设基圆半径为10,压力角 afa 从0到60度):afa = 60*tr = (10^2 + (pi*10*afa/180)^2)^0.5theta = afa-atan((pi*10*afa/180)/10)z = 0在 Pro/ENGINEER 里使用 Feature > Creat > Datum > Curve > From Equation 命令,选择一个坐标系,然后选择坐标类型(卡笛尔坐标/圆柱坐标/球坐标),在窗口里输入以上方程即可生成一段精确的渐开线直齿渐开线齿轮画法讲座(一)发布日期:2010-4-14 [ 收藏评论没有找到想要的知识 ]齿轮传动是最重要的机械传动之一。
齿轮零件具有传动效率高、传动比稳定、结构紧凑等优点。
因而齿轮零件应用广泛,同时齿轮零件的结构形式也多种多样。
根据齿廓的发生线不同,齿轮可以分为渐开线齿轮和圆弧齿轮。
根据齿轮的结构形式的不同,齿轮又可以分为直齿轮、斜齿轮和锥齿轮等。
本章将详细介绍用Pro/E创建标准直齿轮、斜齿轮、圆锥齿轮、圆弧齿轮以及蜗轮蜗杆的设计过程。
3.1直齿轮的创建3.1.1渐开线的几何分析图3-1 渐开线的几何分析渐开线是由一条线段绕齿轮基圆旋转形成的曲线。
渐开线的几何分析如图3-1所示。
线段s 绕圆弧旋转,其一端点A划过的一条轨迹即为渐开线。
图中点(x1,y1)的坐标为:x1=r*cos(ang),y1=r*sin(ang) 。
(其中r为圆半径,ang为图示角度)对于Pro/E关系式,系统存在一个变量t,t的变化范围是0~1。
从而可以通过(x1,y1)建立(x,y)的坐标,即为渐开线的方程。
ang=t*90s=(PI*r*t)/2x1=r*cos(ang)y1=r*sin(ang)x=x1+(s*sin(ang))y=y1-(s*cos(ang))z=0以上为定义在xy平面上的渐开线方程,可通过修改x,y,z的坐标关系来定义在其它面上的方程,在此不再重复。
3.1.2直齿轮的建模分析本小节将介绍参数化创建直齿圆柱齿轮的方法,参数化创建齿轮的过程相对复杂,其中要用到许多与齿轮有关的参数以及关系式。
直齿轮的建模分析(如图3-2所示):(1)创建齿轮的基本圆这一步用草绘曲线的方法,创建齿轮的基本圆,包括齿顶圆、基圆、分度圆、齿根圆。
并且用事先设置好的参数来控制圆的大小。
(2)创建渐开线用从方程来生成渐开线的方法,创建渐开线,本章的第一小节分析了渐开线方程的相关知识。
(3)镜像渐开线首先创建一个用于镜像的平面,然后通过该平面,镜像第2步创建的渐开线,并且用关系式来控制镜像平面的角度。
(4)拉伸形成实体拉伸创建实体,包括齿轮的齿根圆实体和齿轮的一个齿形实体。
这一步是创建齿轮的关键步骤。
(5)阵列轮齿将上一步创建的轮齿进行阵列,完成齿轮的基本外形。
这一步同样需要加入关系式来控制齿轮的生成。
(6)创建其它特征创建齿轮的中间孔、键槽、小孔等特征,并且用参数和关系式来控制相关的尺寸。
图3-2 齿轮的建模分析3.1.3直齿轮的建模过程1.输入基本参数和关系式(1)单击,在新建对话框中输入文件名“gear”,然后单击;(2)在主菜单上单击“工具”→“参数”,系统弹出“参数”对话框,如图3-3所示;图3-3 “参数”对话框(3)在“参数”对话框内单击按钮,可以看到“参数”对话框增加了一行,依次输入新参数的名称、值、和说明等。
需要输入的参数如表3-1所示;名称值说明名称值说明M 3 模数DB ___ 基圆直径Z 25 齿数DF ___ 齿根圆直径ALPHA 20 压力角 D ___ 分度圆直径HAX 1 齿顶高系数DD0 ___ 凹槽直径CX 0.25 顶系系数BB0 ___ 凹槽深度B 10 齿轮宽度DD1 15 轴孔直径HA ___ 齿顶高LL1 ___ 键槽高HF ___ 齿根高LL2 ___ 键槽宽X 0 变位系数LL3 ___ 小孔到原点DA ___ 齿顶圆直径DD2 ___ 小孔直径表3-1 创建齿轮参数注意:表3-1中未填的参数值,表示是由系统通过关系式将自动生成的尺寸,用户无需指定。
完成后的参数对话框如图3-4所示:图3-4 “参数”对话框(4)在主菜单上依次单击“工具”→“关系”,系统弹出“关系”对话框,如图3-5所示;(5)在“关系”对话框内输入齿轮的分度圆直径关系、基圆直径关系、齿根圆直径关系和齿顶圆直径关系。
由这些关系式,系统便会自动生成表3-1所示的未指定参数的值。
输入的关系式如下:ha=(hax+x)*mhf=(hax+cx-x)*md=m*zda=d+2*hadb=d*cos(alpha)df=d-2*hf完成后的“关系”对话框如图3-5所示;图3-5 “关系”对话框2.创建齿轮基本圆(1)在工具栏内单击按钮,系统弹出“草绘”对话框;(2)选择“FRONT”面作为草绘平面,选取“RIGHT”面作为参考平面,参考方向为向“左”,如图3-6所示。
单击【草绘】进入草绘环境;图3-6 “草绘”对话框(3)在绘图区以系统提供的原点为圆心,绘制一个任意大小的圆,并且标注圆的直径尺寸。
在工具栏内单击按钮,完成草图的绘制;(4)在模型中右键单击刚刚创建的草图,在弹出的快捷菜单中单击选取“编辑”;(5)在主菜单上依次单击“工具”→“关系”,系统弹出关系对话框,如图3-7所示;(6)在“关系”对话框中输入尺寸关系如下:D11=d其中D11为圆的直径尺寸代号,注意尺寸代号视具体情况会有所有同。
d为用户自定义的参数,即为分度圆直径。
通过该关系式创建的圆即为分度圆;图3-7 “关系”对话框(7)继续在工具栏内单击按钮,系统弹出“草绘”对话框;(8)在“草绘”对话框内单击按钮,进入草绘环境;(9)在绘图区以系统提供的原点为圆心,绘制一个任意大小的圆,并且标注圆的直径尺寸。
在工具栏内单击按钮,完成草图的绘制;(10)在模型中右键单击刚刚创建的草图,在弹出的快捷菜单中单击选取“编辑”;(11)在主菜单上依次单击“工具”→“关系”,系统弹出关系对话框;(12)在“关系”对话框中输入尺寸关系如下:D12=da其中D12为圆的直径尺寸代号,da为用户自定义的参数,即为齿顶圆直径。
通过该关系式创建的圆即为齿顶圆;(13)重复7—12步骤,创建另外两个齿轮的基本圆,分别为齿根圆和基圆,基中齿根圆的尺寸关系式为:D13=df基圆的尺寸代号为:D14=db完成后的基本圆曲线如图3-8所示,完成后的“关系”对话框如图3-9所示。
图3-8 完成后的基本圆曲线图3-9 完成后的关系式3.创建渐开线(1)依次在主菜单上单击“插入”→“模型基准”→“曲线”,或者在工具栏上单击按钮,系统弹出“曲线选项”菜单管理器,如图3-10所示;图3-10 “曲线选项”菜单管理器(2)在“曲线选项”菜单管理器上依次单击“从方程”→“完成”,弹出“得到坐标系”菜单管理器,如图3-11所示;图3-11“得到坐标系”菜单管理器(3)在绘图区单击选取系统坐标系为曲线的坐标系,弹出“设置坐标类型”菜单管理器,如图3-12所示;图3-12 “设置坐标系类型”菜单管理器(4)在“设置坐标类型”菜单管理器中单击“笛卡尔”,系统弹出一个记事本窗口;(5)在弹出的记事本窗口中输入曲线的方程,如下:ang=90*tr=db/2s=PI*r*t/2xc=r*cos(ang)yc=r*sin(ang)x=xc+s*sin(ang)y=yc-s*cos(ang)z=0渐开线的创建是齿轮创建过程中的一个难点,渐开线方程的推导已经在本章第一节中做了详细的介绍;(6)保存数据,退出记事本,单击“曲线:从方程”对话框中的【确定】,如图3-13所示;图3-13“曲线:从方程”对话框(7)完成后的曲线如图3-14所示;图3-14 完成后的渐开线直齿渐开线齿轮画法讲座(二)发布日期:2010-4-14 [ 收藏评论没有找到想要的知识 ]4.镜像渐开线(1)在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“点”→“点”,系统弹出“基准点”对话框,如图3-15所示;图3-15“基准点”对话框(2)单击分度圆曲线作为参照,按住Ctrl键,单击渐开线作为参照,如图3-16所示。
在“基准点”对话框内单击【确定】,完成基准点“PNT 0”的创建;图3-16选取参照曲线(3)在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“轴”,系统弹出“基准轴”对话框,如图3-17所示;(4)在绘图区单击选取“TOP”面作为参考平面,按住Ctrl键,单击选取“RIGHT”面作为参考,在“基准轴”对话框内单击【确定】,完成轴“A_ 1”的创建;(5)在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”,系统弹出“基准平面”对话框;(6)在绘图区单击选取“A_ 1”轴作为参照,按住Ctrl键,继续单击基准点“PNT 0”作为参照,如图3-17所示;图3-17“基准平面”对话框(7)继续在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”,系统弹出“基准平面”对话框,如图3-18所示;图3-18“基准平面”对话框(8)在绘图区单击选取刚刚创建的“DTM 1”面作为参考平面,按住Ctrl键选取“A_ 1”轴作为参考。
在偏距文本框内输入旋转角度为“360/(4*z)”,系统提示是否要添加特征关系,单击“是”;(9)在“基准平面”对话框内单击【确定】,完成基准平面的创建;(10)将关系式添加到“关系”对话框。
在绘图区右键单击刚刚创建的基准平面“DTM 2”,在弹出的快捷菜单上单击“编辑”。
(11)在主菜单上单击“工具”→“关系”,系统弹出“关系”对话框。
此时系统显示“DTM 1”面和“DTM 2”面间的夹角尺寸代号。
单击该尺寸代号,尺寸代号将自动显示在“关系”对话框中,输入的关系式为:d202=360/(4*z)在“关系”对话框内单击【确定】完成添加关系式;(12)在绘图区单击渐开线特征,然后在工具栏内单击按钮,或者依次在主菜单上单击“编辑”→“镜像”。
