(完整版)2018初三中考数学复习平行线的证明专题复习练习含答案
中考数学专题复习全等三角形之辅助线做平行线

中考数学专题复习全等三角形(辅助线做平行线)学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,△ABC是边长为4的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC至点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.1B.1.8C.2D.2.52.如图,⊥ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC,垂足为E,延长BC到点Q,使CQ=P A,连接PQ交AC于点D,则DE的长为()A.0.5B.0.9C.1D.1.25评卷人得分二、填空题3.如图,四边形ABCD中,AC与BD相交于点O,且AC⊥BD,AC=BD=CD,点P 是⊥OCD角平分线的交点,点M是AB的中点,给出下列结论:⊥⊥CPD=135°;⊥BA=BP;⊥⊥P AC⊥⊥PDB;⊥S△ABP=S△DCP;⊥PM=12CD.其中正确的是___.(填序号)评卷人得分三、解答题4.如图,⊥ABC中,点D,E在边AB上,点F在边BC上,且AD=AC,EF=EC,⊥CEF=⊥A,连接DF.(1)在图1中找出与⊥ACE相等的角,并证明;(2)求证:⊥BDF=⊥EFC;(3)如图2,延长FD,CA交于点G,连接EG,若EG=AG,DE=kAE,求DG DF的值(用含k的代数式表示).5.如图所示:ABC是等边三角形,D、E分别是AB及AC延长线上的一点,且BD CE=,连接DE交BC于点M.求让:MD ME=6.P为等边△ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.7.P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,且P A=CQ,连PQ交AC 边于D.(1)证明:PD=DQ.(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.8.如图,点P为等边⊥ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,(1)求证:DP=DQ;(2)过P作PE⊥AC于E,若BC=4,求DE的长.9.已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;(3)如图(3),当点E在CA的延长线上,点D在线段AB上(点D不与A,B重合),DE所在直线与直线BC交于点M,若CE=2BD,请直接写出线段MD与线段ME的数量关系.10.读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DB上,且⊥BAE=⊥CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明.图(1):延长DE到F使得EF=DE图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F图(3):过C点作CF⊥AB交DE的延长线于F.参考答案:1.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD⊥QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴△是等边三角形,AP PF∴=,⊥CQ=P A,⊥PF CQ=在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴⊥()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF∴=,=AE DC EF FD ED∴+=+,12DE AC∴=,4AC=,2DE∴=,故选:C.【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键.2.C【解析】【分析】过P作BC的平行线交AC于F,通过AAS证明PFD≌QCD,得FD CD=,再由APF 是等边三角形,即可得出12DE AC=.【详解】解:过P作BC的平行线交AC于F,Q FPD∴∠=∠,ABC是等边三角形,60APF B∴∠=∠=︒,60AFP ACB∠=∠=︒,APF∴是等边三角形,AP PF∴=,在PFD中和QCD中,FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,PFD∴≌()QCD AAS,FD CD∴=,PE AC⊥于E,APF是等边三角形,AE EF ∴=,AE DC EF FD ∴+=+,12DE AC ∴=, 2AC =, 1DE ∴=,故选:C . 【点睛】本题主要考查了等边三角形的判定与性质,全等三角形的判定与性质,作辅助线构造全等三角形是解题的关键. 3.⊥⊥⊥⊥ 【解析】 【分析】由角平分线的定义,可得⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,进而即可判断⊥;先证ACP DCP ≌,可得APD △是等腰直角三角形,进而得PAC PDB ≌,即可判断⊥;过点A 作AN ⊥BP 交PM 的延长线于点N ,可得AMN BMP ≌,再证明APN PDC ≌,从而得PM =12CD ,即可判断⊥;由ABP APM BMP APM AMN APN S S S S S S +=+==,即可判断⊥. 【详解】解:⊥AC ⊥BD ,点P 是⊥OCD 角平分线的交点,⊥⊥DOC =90°,⊥ODC +⊥OCD =90°,⊥CDP =12⊥CDO ,⊥DCP =12⊥DCO , ⊥⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°,⊥⊥CPD =180°-(⊥CDP +⊥DCP )=135°,故⊥正确; ⊥CP ,DP 分别平分⊥DCO ,⊥CDO , ⊥⊥DCP =⊥ACP ,⊥CDP =⊥BDP , ⊥AC =CD ,PC =PC , ⊥ACP DCP ≌,⊥AP =DP ,⊥CAP =⊥CDP =⊥BDP ,⊥APC =⊥DPC =135°, ⊥⊥DP A =360°-135°-135°=90°,⊥APD △是等腰直角三角形, 又⊥AC =BD ,⊥CAP =⊥BDP,AP =DP , ⊥PAC PDB ≌,故⊥正确; ⊥⊥DPB =⊥APC=135°,PB =PC , ⊥⊥BPC =360°-135°-135°=90°,⊥BPC △是等腰直角三角形,找不到证明BA =BP 的条件,故⊥错误; 过点A 作AN ⊥BP 交PM 的延长线于点N ,⊥⊥N =⊥BPM ,⊥P AN +⊥APB =180°, ⊥点M 是AB 的中点,即AM =BM , 又⊥⊥AMN =⊥BMP , ⊥AMN BMP ≌,⊥MN =PM =12PN ,AN =PB =PC ,AMNBMPSS=,⊥⊥DP A =⊥BPC =90°, ⊥⊥APB +⊥DPC =180°, 又⊥⊥P AN +⊥APB =180°, ⊥⊥P AN =⊥DPC , 又⊥AP =DP ,AN =PC , ⊥APN PDC ≌,⊥CD =PN =2PM ,即:PM =12CD ,故⊥正确; ⊥APNPDCSS=,AMNBMPSS=,⊥ABPAPMBMPAPMAMNAPNS SSSSS+=+==,⊥ABPDCPSS=,故⊥正确.故正确的是⊥⊥⊥⊥. 【点睛】本题主要考查全等三角形的判定和性质,平行线的性质,等腰直角三角形的判定和性质,熟练掌握中线倍长模型和旋转全等模型,是解题的关键. 4.(1)⊥DEF =⊥ACE ,证明见解析;(2)见解析;(3)k 【解析】 【分析】(1)由三角形外角的性质可得出答案;(2)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥DEF ⊥⊥MEC (SAS ),由全等三角形的性质可得出⊥EDF =⊥EMC ,证出⊥EMD =⊥EFC ,则可得出结论;(3)连接CD ,过点E 作AC 的平行线与CD 交于点M ,证明⊥EFG ⊥⊥ECD (ASA ),由全等三角形的性质可得出GF =DC ,证出GD =DM ,则根据平行线分线段成比例即可得出答案. 【详解】解:(1)⊥DEF =⊥ACE . 证明:⊥⊥DEC 是⊥ACE 的外角, ⊥⊥DEC =⊥A +⊥ACE , ⊥⊥DEC =⊥DEF +⊥CEF , ⊥⊥DEC +⊥CEF =⊥A +⊥ACE , ⊥⊥CEF =⊥A , ⊥⊥DEF =⊥ACE ;(2)证明:连接CD ,过点E作AC 的平行线与CD 交于点M ,⊥AD =AC ,⊥⊥ADC=⊥ACD,⊥EM⊥AC,⊥⊥EMD=⊥ACD,⊥CEM=⊥ACE,⊥⊥EDM=⊥EMD,⊥DEF=⊥CEM,⊥ED=EM,又⊥EF=EC,⊥⊥DEF⊥⊥MEC(SAS),⊥⊥EDF=⊥EMC,⊥⊥BDF+⊥EDF=⊥EMD+⊥EMC=180°,⊥⊥BDF=⊥EMC,⊥EM⊥AC,⊥⊥DEM=⊥A,⊥⊥A=⊥CEF,⊥⊥DEM=⊥CEF,⊥⊥DEM中,⊥EMD=1802DEM︒-∠,⊥FEC中,⊥EFC=1802CEF︒-∠,⊥⊥EMD=⊥EFC,⊥⊥BDF=⊥EFC;(3)连接CD,过点E作AC的平行线与CD交于点M,⊥EG=AG,⊥⊥GAE=⊥GEA,⊥⊥DAC+⊥GAE=⊥GEA+⊥GED=180°,⊥⊥DAC=⊥GED,⊥⊥CEF=⊥DAC,⊥⊥DEG=⊥CEF,⊥⊥DEG+⊥DEF=⊥CEF+⊥DEF,即⊥GEF=⊥DEC,⊥⊥DEF⊥⊥MEC,⊥⊥EFG=⊥ECD,DF=MC,又⊥EF=EC,⊥⊥EFG⊥⊥ECD(ASA),⊥GF=DC,⊥DC﹣MC=GF﹣DF,即GD=DM,⊥EM⊥AC,⊥DM DEk MC AE==,⊥GD DMk DF MC==.【点睛】本题考查了全等三角形的性质与判定,平行线分线段成比例,三角形的内角和定理,三角形的外角性质,添加辅助线证明三角形全等是解题的关键.5.见详解【解析】【分析】过点D作DE⊥AC,交BC于点E,根据等边三角形和平行线的性质得⊥MDE=⊥MEC,DE=CE,从而证明∆EMD≅∆CME,进而即可得到结论.【详解】过点D作DE⊥AC,交BC于点E,⊥ABC是等边三角形,⊥⊥B=⊥ACB=60°,⊥DE⊥AC,⊥⊥DEB=⊥ACB=60°,⊥MDE=⊥MEC,⊥BDE是等边三角形,⊥BD=DE,⊥DE=CE,又⊥⊥EMD=⊥CME,⊥∆EMD≅∆CME,⊥MDME =.【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理,添加辅助线,构造等边三角形和全等三角形,是解题的关键.6.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出△APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明△PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明△PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在△PDF和△QDC中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,△ABC是等边三角形,⊥⊥PFD=⊥QCD,△APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在△PFD和△QCD中,PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质,解题的关键是掌握等边三角形的判定与性质、全等三角形的判定(AAS)与性质、平行线的性质,熟练掌握等边三角形的性质.7.(1)证明见解析;(2)DE=3.【解析】【分析】(1)过点P作PF⊥BC交AC于点F;证出⊥APF也是等边三角形,得出AP=PF=AF=CQ,由AAS证明⊥PDF⊥⊥QDC,得出对应边相等即可;(2)过P作PF⊥BC交AC于F.同(1)由AAS证明⊥PFD⊥⊥QCD,得出对应边相等FD=CD,证出AE+CD=DE12=AC,即可得出结果.【详解】(1)如图1所示,点P作PF⊥BC交AC于点F.⊥⊥ABC是等边三角形,⊥⊥APF也是等边三角形,AP=PF=AF=CQ.⊥PF⊥BC,⊥⊥PFD=⊥DCQ.在⊥PDF和⊥QDC中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PDF⊥⊥QDC(AAS),⊥PD=DQ;(2)如图2所示,过P作PF⊥BC交AC于F.⊥PF⊥BC,⊥ABC是等边三角形,⊥⊥PFD=⊥QCD,⊥APF是等边三角形,⊥AP=PF=AF.⊥PE⊥AC,⊥AE=EF.⊥AP=PF,AP=CQ,⊥PF=CQ.在⊥PFD和⊥QCD中,PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩,⊥⊥PFD⊥⊥QCD(AAS),⊥FD=CD.⊥AE=EF,⊥EF+FD=AE+CD,⊥AE+CD=DE12=AC.⊥AC=6,⊥DE=3.【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.8.(1)详见解析(2)ED=2【解析】【分析】(1)过P作PF⊥BQ,可得△APF为等边三角形,所以AP=PF,再证△DCQ⊥⊥DFP,即可得PD=DQ;(2)根据等腰三角形三线合一的性质可得AE=EF,根据全等三角形对应边相等可得FD =CD,然后求出2DE=AC,代入数据进行计算即可得解.(1)证明:如图,过点P作PF⊥BC,则⊥DPF=⊥Q,⊥⊥ABC为等边三角形,⊥⊥APF是等边三角形,⊥AP=PF,又⊥AP=CQ,⊥PF=CQ,在△DPF和△DQC中,DPF QPDF QDC PF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DPF⊥⊥DQC(AAS),⊥DP=DQ;(2)⊥⊥P AF为等边三角形,PE⊥AC,可得AE=EF,由(1)知,⊥DPF⊥⊥DQC⊥FD=CD,⊥AC=AE+EF+FD+CD,⊥AC=2EF+2FD=2(EF+FD)=2ED,⊥AC=BC=4,⊥2ED=4,⊥ED=2.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线构造出等边三角形和全等三角形是解题的关键,也是本题的难点.9.(1)DM=EM.理由见详解;(2)成立,理由见详解;(3)MD=12ME.【解析】【分析】(1)DM=EM;过点E作EF//AB交BC于点F,然后利用平行线的性质和已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(2)成立;过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质与已知条件可以证明△DBM⊥⊥EFM,接着利用全等三角形的性质即可证明题目的结论;(3)MD=12ME.过点E作EF//AB交CB的延长线于点F,然后利用平行线的性质和已知条件得到△DBM⊥⊥EFM,接着利用相似三角形的性质即可得到结论;(1)解:DM=EM;证明:过点E作EF//AB交BC于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDM FEMBMD FMEBD EF∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥DBM⊥⊥EFM,⊥DM=EM.(2)解:成立;证明:过点E作EF//AB交CB的延长线于点F,⊥AB=AC,⊥⊥ABC=⊥C;又⊥EF//AB,⊥⊥ABC=⊥EFC,⊥⊥EFC=⊥C,⊥EF=EC.又⊥BD=EC,⊥EF=BD.又⊥EF//AB,⊥⊥ADM=⊥MEF.在△DBM和△EFM中BDE FEM BMD FME BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩⊥⊥DBM ⊥⊥EFM ;⊥DM =EM ;(3)解:过点E 作EF //AB 交CB 的延长线于点F ,⊥⊥DBM =⊥EFM ,⊥DMB =⊥EMF⊥⊥DBM ⊥⊥EFM ,⊥BD :EF =DM :ME ,⊥AB =AC ,⊥⊥ABC =⊥C ,⊥⊥F =⊥ABC ,⊥⊥F =⊥C ,⊥EF =EC ,⊥BD :EC =DM :ME =1:2,⊥MD =12ME . 【点睛】本题主要考查了三角形综合,涉及了等腰三角形性质和判定、全等三角形的判定与性质、相似三角形的判定和性质,利用平行构造全等三角形是解题关键.10.选择(1)(3)证明,证明见解析【解析】【分析】如图(1)延长DE 到F 使得EF=DE,证明△DCE⊥⊥FBE,得到⊥CDE=⊥F,BF=DC,结合题干条件即可得到结论;如图3,过C 点作CF⊥AB 交DE 的延长线于F,得到△ABE⊥⊥FCE,AB=FC,结合题干条件即可得到结论,【详解】如图(1)延长DE 到F 使得EF=DE在△DCE 和△FBE 中,EF DE DEC FEB BE EC =∠=∠=⎧⎪⎨⎪⎩⊥△DCE⊥⊥ FBE (SAS)⊥⊥CDE=⊥F,BF=DC⊥⊥BAE=⊥CDE⊥BF=AB⊥AB= CD如图3,过C 点作CF⊥AB 交DE 的延长线于F在△ABE 和△FCE 中B ECF BE ECBAE F ∠=∠=∠=∠⎧⎪⎨⎪⎩⊥△ABE⊥⊥ FCE(AAS),⊥AB=FC⊥⊥BAE=⊥CDE⊥⊥F=⊥CDE⊥CD=CF⊥AB=CD【点睛】此题考查全等三角形的判定与性质和等腰三角形的性质,解题关键在于利用三角形全等的性质证明。
中考数学专题复习平行线问题骨折型

中考数学专题复习平行线问题骨折型学校:___________姓名:___________班级:___________考号:___________评卷人得分一、填空题1.如图,如果AB∥EF,EF∥CD,则∥1,∥2,∥3的关系式__________.2.如图所示,AB∥CD,∥E=37°,∥C=20°,则∥EAB的度数为__________.3.如图,已知//AB DE,∥ABC=80°,∥CDE=140°,则∥BCD=_____.4.如图,直线MA∥NB,∥A=70°,∥B=40°,则∥P=___________度.5.如图,AB∥CD,则∥1+∥3—∥2的度数等于__________.评卷人得分二、解答题6.(1)如图,AB//CD,CF平分∥DCE,若∥DCF=30°,∥E=20°,求∥ABE的度数;(2)如图,AB//CD,∥EBF=2∥ABF,CF平分∥DCE,若∥F的2倍与∥E的补角的和为190°,求∥ABE的度数.(3)如图,P为(2)中射线BE上一点,G是CD上任一点,PQ平分∥BPG,GN//PQ,GM平分∥DGP,若∥B=30°,求∥MGN的度数.7.已知直线AB∥CD,P为平面内一点,连接P A、PD.(1)如图1,已知∥A=50°,∥D=150°,求∥APD的度数;(2)如图2,判断∥P AB、∥CDP、∥APD之间的数量关系为.(3)如图3,在(2)的条件下,AP∥PD,DN平分∥PDC,若∥P AN+12∥P AB=∥APD,求∥AND的度数.8.如图1,MN∥PQ,点C、B分别在直线MN、PQ上,点A在直线MN、PQ之间.(1)求证:∥CAB=∥MCA+∥PBA;(2)如图2,CD∥AB,点E在PQ上,∥ECN=∥CAB,求证:∥MCA=∥DCE;(3)如图3,BF平分∥ABP,CG平分∥ACN,AF∥CG.若∥CAB=60°,求∥AFB的度数.9.(1)如图1,l1∥l2,求∥A1+∥A2+∥A3=______.(直接写出结果)(2)如图2,l1∥l2,求∥A1+∥A2+∥A3+∥A4=_____.(直接写出结果)(3)如图3,l1∥l2,求∥A1+∥A2+∥A3+∥A4+∥A5=_______.(直接写出结果)(4)如图4,l1∥l2,求∥A1+∥A2+…+∥An=_______.(直接写出结果)10.已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∥BME、∥E、∥END的数量关系为:;(不需要证明)如图2中,∥BMF、∥F、∥FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∥FND,MB平分∥FME,且2∥E+∥F=180°,求∥FME的度数;(3)如图4中,∥BME=60°,EF平分∥MEN,NP平分∥END,且EQ∥NP,则∥FEQ 的大小是否发生变化,若变化,请说明理由,若不变化,求出∥FEQ的度数.11.综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动(1)如图1,//EF MN,点A、B分别为直线EF、MN上的一点,点P为平行线间一点,请直接写出PAF∠、PBN∠和APB∠之间的数量关系;【问题迁移】(2)如图2,射线OM与射线ON交于点O,直线//m n,直线m分别交OM、ON于点A、D,直线n分别交OM、ON于点B、C,点P在射线OM上运动,∥当点P 在A 、B (不与A 、B 重合)两点之间运动时,设ADP α∠=∠,BCP β∠=∠.则CPD ∠,α∠,β∠之间有何数量关系?请说明理由.∥若点P 不在线段AB 上运动时(点P 与点A 、B 、O 三点都不重合),请你画出满足条件的所有图形并直接写出CPD ∠,α∠,β∠之间的数量关系.12.已知AB //CD ,求证:∥B =∥E +∥D13.为更好地理清平行线与相关角的关系,小明爸爸为他准备了四根细直木条AB 、BC ,CD 、DE ,做成折线ABCDE ,如图1,且在折点B 、C 、D 处均可自由转出.(1)如图2,小明将折线调节成50,75,25B C D ∠=︒∠=︒∠=︒,判别AB 是否平行于ED ,并说明理由;(2)如图3,若25C D ∠=∠=︒,调整线段AB 、BC 使得//AB CD ,求出此时B 的度数,要求画出图形,并写出计算过程.(3)若85,25,//C D AB DE ∠=︒∠=︒,求出此时B 的度数,要求画出图形,直接写出度数,不要求计算过程.参考答案:1.∥2+∥3﹣∥1=180°【解析】【分析】根据平行线的性质和平角定义求解即可.【详解】解:∥AB∥EF,EF∥CD,∥∥2+∥BOE=180°,∥3+∥COF=180°,∥∥2+∥3+∥BOE+∥COF=360°,∥∥BOE+∥COF+∥1=180°,∥∥BOE+∥COF=180°﹣∥1,∥∥2+∥3+(180°﹣∥1)=360°,即∥2+∥3﹣∥1=180°.故答案为:∥2+∥3﹣∥1=180°.【点睛】本题考查平行线的性质、平角定义,熟练掌握平行线的性质是解答的关键.2.57°【解析】【分析】根据三角形内角和180°以及平行线的性质:1、如果两直线平行,那么它们的同位角相等;2、如果两直线平行,那么它们的同旁内角互补;3、如果两直线平行,那么它们的内错角相等,据此计算即可.【详解】解:设AE、CD交于点F,∥∥E=37°,∥C=20°,∥∥CFE=180°-37°-20°=123°,∥∥AFD=123°,∥AB∥CD,∥∥AFD+∥EAB=180°,∥∥EAB=180°-123°=57°,故答案为:57°.【点睛】本题主要考查三角形内角和定理以及平行线的性质,熟知平行的性质是解题的关键.3.40︒【解析】【分析】∠,延长ED交BC于M,根据两直线平行,内错角相等证明∥BMD=∥ABC,再求解CMD再利用三角形的外角的性质可得答案.【详解】解:延长ED交BC于M,∥//AB DE,∥∥BMD=∥ABC=80°,∥180100∠=︒-∠=︒;CMD BMD又∥∥CDE=∥CMD+∥C,∥14010040∠=∠-∠=︒-︒=︒.BCD CDE CMD故答案是:40°【点睛】本题考查了平行线的性质.三角形的外角的性质,邻补角的定义,掌握以上知识是解题的关键.4.30【解析】【分析】要求∥P的度数,只需根据平行线的性质,求得其所在的三角形的一个外角,根据三角形的外角的性质进行求解.【详解】解:根据平行线的性质,得∥A的同位角是70°,再根据三角形的外角的性质,得∥P=70°−40°=30°.故答案为30.【点睛】本题考查了平行线的性质以及三角形的一个外角等于和它不相邻的两个内角和,可以牢记此题中的结论:∥P=∥A−∥B.5.180°【解析】【详解】解:∥AB∥CD∥∥1=∥EFD∥∥2+∥EFC=∥3∥EFD=180°-∥EFC∥∥1+∥3—∥2=180°故答案为:180°6.(1)∥ABE=40°;(2)∥ABE=30°;(3)∥MGN=15°.【解析】【分析】(1)过E作EM∥AB,根据平行线的判定与性质和角平分线的定义解答即可;(2)过E作EM∥AB,过F作FN∥AB,根据平行线的判定与性质,角平分线的定义以及解一元一次方程解答即可;(3)过P作PL∥AB,根据平行线的判定与性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义解答即可.【详解】解:(1)过E作EM∥AB,∥AB∥CD,∥CD∥EM∥AB,∥∥ABE=∥BEM,∥DCE=∥CEM,∥CF平分∥DCE,∥∥DCE=2∥DCF,∥∥DCF=30°,∥∥DCE=60°,∥∥CEM=60°,又∥∥CEB=20°,∥∥BEM=∥CEM﹣∥CEB=40°,∥∥ABE=40°;(2)过E作EM∥AB,过F作FN∥AB,∥∥EBF=2∥ABF,∥设∥ABF=x,∥EBF=2x,则∥ABE=3x,∥CF平分∥DCE,∥设∥DCF=∥ECF=y,则∥DCE=2y,∥AB∥CD,∥EM∥AB∥CD,∥∥DCE=∥CEM=2y,∥BEM=∥ABE=3x,∥∥CEB=∥CEM﹣∥BEM=2y﹣3x,同理∥CFB=y﹣x,∥2∥CFB+(180°﹣∥CEB)=190°,∥2(y﹣x)+180°﹣(2y﹣3x)=190°,∥x=10°,∥∥ABE=3x=30°;(3)过P作PL∥AB,∥GM平分∥DGP,∥设∥DGM=∥PGM=y,则∥DGP=2y,∥PQ平分∥BPG,∥设∥BPQ=∥GPQ=x,则∥BPG=2x,∥PQ∥GN,∥∥PGN=∥GPQ=x,∥AB∥CD,∥PL∥AB∥CD,∥∥GPL=∥DGP=2y,∥BPL=∥ABP=30°,∥∥BPL=∥GPL﹣∥BPG,∥30°=2y﹣2x,∥y﹣x=15°,∥∥MGN=∥PGM﹣∥PGN=y﹣x,∥∥MGN=15°.【点睛】此题考查平行线的判定与性质,角平分线的定义,三角形的内角和定理,解题关键在于作辅助线和掌握判定定理.7.(1)∥APD=80°;(2)∥P AB+∥CDP-∥APD=180°;(3)∥AND=45°.【解析】【分析】(1)首先过点P作PQ∥AB,则易得AB∥PQ∥CD,然后由两直线平行,同旁内角互补以及内错角相等,即可求解;(2)作PQ∥AB,易得AB∥PQ∥CD,根据平行线的性质,即可证得∥P AB+∥CDP-∥APD=180°;(3)先证明∥NOD=12∥P AB,∥ODN=12∥PDC,利用(2)的结论即可求解.【详解】解:(1)∥∥A=50°,∥D=150°,过点P作PQ∥AB,∥∥A=∥APQ=50°,∥AB∥CD,∥PQ∥CD,∥∥D+∥DPQ=180°,则∥DPQ=180°-150°=30°,∥∥APD=∥APQ+∥DPQ=50°+30°=80°;(2)∥P AB+∥CDP-∥APD=180°,如图,作PQ∥AB,∥∥P AB=∥APQ,∥AB∥CD,∥PQ∥CD,∥∥CDP+∥DPQ=180°,即∥DPQ=180°-∥CDP,∥∥APD=∥APQ-∥DPQ,∥∥APD=∥P AB-(180°-∥CDP)=∥P AB+∥CDP-180°;∥∥P AB+∥CDP-∥APD=180°;(3)设PD交AN于O,如图,∥AP∥PD,∥∥APO=90°,由题知∥P AN+12∥P AB=∥APD,即∥P AN+12∥P AB=90°,又∥∥POA+∥P AN=180°-∥APO=90°,∥∥POA=12∥P AB,∥∥POA=∥NOD,∥∥NOD=12∥P AB,∥DN平分∥PDC,∥∥ODN=12∥PDC,∥∥AND=180°-∥NOD-∥ODN=180°-12(∥P AB+∥PDC),由(2)得∥P AB+∥CDP-∥APD=180°,∥∥P AB+∥PDC=180°+∥APD,∥∥AND=180°-12(∥P AB+∥PDC)=180°-12(180°+∥APD)=180°-12(180°+90°)=45°,即∥AND=45°.【点睛】本题考查了平行线的性质以及角平分线的定义.注意掌握辅助线的作法,注意掌握数形结合思想的应用.8.(1)证明见解析;(2)证明见解析;(3)120°.【解析】【分析】(1)过点A作AD∥MN,根据两直线平行,内错角相等得到∥MCA=∥DAC,∥PBA=∥DAB,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∥、∥CAB+∥ACD=180°,由邻补角定义得到∥ECM+∥ECN=180°,再等量代换即可得解;(3)由平行线的性质得到,∥F AB=120°﹣∥GCA,再由角平分线的定义及平行线的性质得到∥GCA﹣∥ABF=60°,最后根据三角形的内角和是180°即可求解.【详解】解:(1)证明:如图1,过点A作AD∥MN,∥MN∥PQ,AD∥MN,∥AD∥MN∥PQ,∥∥MCA=∥DAC,∥PBA=∥DAB,∥∥CAB=∥DAC+∥DAB=∥MCA+∥PBA,即:∥CAB=∥MCA+∥PBA;(2)如图2,∥CD∥AB,∥∥CAB+∥ACD=180°,∥∥ECM+∥ECN=180°,∥∥ECN=∥CAB∥∥ECM=∥ACD,即∥MCA+∥ACE=∥DCE+∥ACE,∥∥MCA=∥DCE;(3)∥AF∥CG,∥∥GCA+∥F AC=180°,∥∥CAB=60°即∥GCA+∥CAB+∥F AB=180°,∥∥F AB=180°﹣60°﹣∥GCA=120°﹣∥GCA,由(1)可知,∥CAB=∥MCA+∥ABP,∥BF平分∥ABP,CG平分∥ACN,∥∥ACN=2∥GCA,∥ABP=2∥ABF,又∥∥MCA=180°﹣∥ACN,∥∥CAB=180°﹣2∥GCA+2∥ABF=60°,∥∥GCA﹣∥ABF=60°,∥∥AFB+∥ABF+∥F AB=180°,∥∥AFB=180°﹣∥F AB﹣∥FBA=180°﹣(120°﹣∥GCA)﹣∥ABF=180°﹣120°+∥GCA﹣∥ABF=120°.【点睛】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.9.(1)360°;(2)540°;(3)720°;(4)(n-1)180 °【解析】【分析】(1)过点A2作A2B∥l1,根据平行线的性质,即可求解;(2)过点A2作A2B∥l1,过点A3作A3C∥l1,根据平行线的性质,即可求解;(3)根据平行线的性质,即可求解;(4)根据平行线的性质,即可求解.【详解】解:(1)过点A2作A2B∥l1,∥l1∥l2,∥A2B∥l1∥l2,∥∥A1+∥A1A2B=180°,∥A3+∥A3A2B=180°,∥∥A1+∥A1A2A3+∥A3=∥A1+∥A1A2B+∥A3+∥A3A2B=180°+180°=360°,故答案是:360°;(2)过点A2作A2B∥l1,过点A3作A3C∥l1,∥l1∥l2,∥A3C∥A2B∥l1∥l2,∥∥A1+∥A1A2B=180°,∥A4+∥A4A3B=180°,∥BA2A3+∥CA3A2=180°,∥∥A1+∥A1A2A3+∥A2A3A4+∥A4=∥A1+∥A1A2B+∥A4+∥A4A3B+∥BA2A3+∥CA3A2=180°+180°+180°=540°,故答案是:540°;(3)同理可得:∥A1+∥A2+∥A3+∥A4+∥A5=180°+180°+180°+180°=720°,故答案是:720°;(4)同理可得:∥A1+∥A2+…+∥An=(n-1)180 °,故答案是:(n-1)180 °.【点睛】本题主要考查平行线的性质,添加辅助线,构造平行线,是解题的关键.10.(1)∥BME=∥MEN﹣∥END;∥BMF=∥MFN+∥FND;(2)120°;(3)不变,30°【解析】【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∥BME+∥END)+∥BMF-∥FND=180°,可求解∥BMF=60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∥FEQ=12∥BME,进而可求解.【详解】解:(1)过E作EH∥AB,如图1,∥∥BME=∥MEH,∥AB∥CD,∥HE∥CD,∥∥END=∥HEN,∥∥MEN=∥MEH+∥HEN=∥BME+∥END,即∥BME=∥MEN﹣∥END.如图2,过F作FH∥AB,∥∥BMF=∥MFK,∥AB∥CD,∥FH∥CD,∥∥FND=∥KFN,∥∥MFN=∥MFK﹣∥KFN=∥BMF﹣∥FND,即:∥BMF=∥MFN+∥FND.故答案为∥BME=∥MEN﹣∥END;∥BMF=∥MFN+∥FND.(2)由(1)得∥BME =∥MEN ﹣∥END ;∥BMF =∥MFN +∥FND .∥NE 平分∥FND ,MB 平分∥FME ,∥∥FME =∥BME +∥BMF ,∥FND =∥FNE +∥END ,∥2∥MEN +∥MFN =180°,∥2(∥BME +∥END )+∥BMF ﹣∥FND =180°,∥2∥BME +2∥END +∥BMF ﹣∥FND =180°,即2∥BMF +∥FND +∥BMF ﹣∥FND =180°,解得∥BMF =60°,∥∥FME =2∥BMF =120°;(3)∥FEQ 的大小没发生变化,∥FEQ =30°.由(1)知:∥MEN =∥BME +∥END ,∥EF 平分∥MEN ,NP 平分∥END ,∥∥FEN =12∥MEN =12(∥BME +∥END ),∥ENP =12∥END , ∥EQ ∥NP ,∥∥NEQ =∥ENP ,∥∥FEQ =∥FEN ﹣∥NEQ =12(∥BME +∥END )﹣12∥END =12∥BME ,∥∥BME =60°,∥∥FEQ =12×60°=30°. 【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键. 11.(1)360PAF PBN APB ∠+∠+∠=°;(2)∥CPD αβ∠=∠+∠,理由见解析;∥图见解析,CPD βα∠=∠-∠或CPD αβ∠=∠-∠【解析】【分析】(1)作PQ ∥EF ,由平行线的性质,即可得到答案;(2)∥过P 作//PE AD 交CD 于E ,由平行线的性质,得到DPE α∠=∠,CPE β∠=∠,即可得到答案;∥根据题意,可对点P 进行分类讨论:当点P 在BA 延长线时;当P 在BO 之间时;与∥同理,利用平行线的性质,即可求出答案.【详解】解:(1)作PQ ∥EF ,如图:∥//EF MN ,∥////EF MN PQ ,∥180PAF APQ ∠+∠=°,180PBN BPQ ∠+∠=°,∥APB APQ BPQ ∠=∠+∠∥360PAF PBN APB ∠+∠+∠=°;(2)∥CPD αβ∠=∠+∠;理由如下:如图,过P 作//PE AD 交CD 于E ,∥//AD BC ,∥////AD PE BC ,∥DPE α∠=∠,CPE β∠=∠,∥CPD DPE CPE αβ∠=∠+∠=∠+∠;∥当点P 在BA 延长线时,如备用图1:∥PE ∥AD ∥BC ,∴∴EPC=β,∥EPD=α,∥CPDβα∠=∠-∠;当P在BO之间时,如备用图2:∥PE∥AD∥BC,∥∥EPD=α,∥CPE=β,∥CPDαβ∠=∠-∠.【点睛】本题考查了平行线的性质,解题的关键是熟练掌握两直线平行同旁内角互补,两直线平行内错角相等,从而得到角的关系.12.见解析【解析】【分析】过点E作EF∥CD,根据平行线的性质即可得出∥B=∥BOD,根据平行线的性质即可得出∥BOD=∥BEF、∥D=∥DEF,结合角之间的关系即可得出结论.【详解】证明:过点E作EF∥CD,如图∥AB∥CD,∥∥B=∥BOD,∥EF∥CD(辅助线),∥∥BOD=∥BEF(两直线平行,同位角相等);∥D=∥DEF(两直线平行,内错角相等);∥∥BEF=∥BED+∥DEF=∥BED+∥D(等量代换),∥∥BOD=∥E+∥D(等量代换),即∥B=∥E+∥D.【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出相等或互补的角.13.(1)AB∥DE,理由见解析;(2)25°或155°,画图见解析;(3)60°或120°或70°或110°【解析】【分析】(1)过点C作CF∥AB,利用平行线的判定和性质解答即可;(2)分别画图3和图4,根据平行线的性质可计算∥B的度数;(3)分别画图,根据平行线的性质计算出∥B的度数.【详解】解:(1)AB∥DE,理由是:如下图,过点C作CF∥AB,∥∥B=∥BCF=50°,∥∥BCD=75°,∥∥DCF=25°,∥∥D=25°,∥∥D=∥DCF=25°,∥CF∥DE,∥AB∥DE;(2)如下图,∥AB∥CD,∥∥B=∥BCD=25°;如图4:∥AB∥CD,∥∥B+∥BCD=180°,∥∥ABC=180°-25°=155°;(3)由(1)得:∥B=85°-25°=60°;如图5,过C作CF∥AB,则AB∥CF∥CD,∥∥FCD=∥D=25°,∥∥BCD=85°,∥∥BCF=85°-25°=60°,∥AB∥CF,∥∥B+∥BCF=180°,∥∥B=120°;如图6,∥∥C=85°,∥D=25°,∥∥CFD=180°-85°-25°=70°,∥AB∥DE,∥∥B=∥CFD=70°,如图7,同理得:∥B=25°+85°=110°,综上所述,∥B的度数为60°或120°或70°或110°.【点睛】本题主要考查了平行线的性质和三角形内角和的运用,解决问题的关键是作辅助线构造同位角以及内错角,依据平行线的性质及三角形外角性质进行推导计算.。
人教中考数学综合题专题复习【平行四边形】专题解析附详细答案
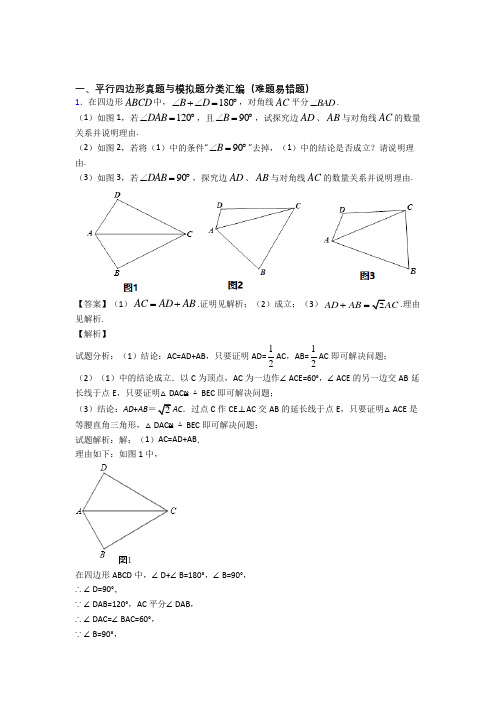
一、平行四边形真题与模拟题分类汇编(难题易错题)1.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB AC +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB =2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD 中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC 平分∠DAB ,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°.∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.在Rt△ACE中,∠CAB=45°,∴AE=245ACACcos︒=∴2AD AB AC+=.2.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)3【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB223BD AD-,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF22AB AF+3.3.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).【答案】(1)作图参见解析;(2)作图参见解析.【解析】试题分析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN即可;(2)根据勾股定理画出图形即可.试题解析:(1)过点O向线段OM作垂线,此直线与格点的交点为N,连接MN,如图1所示;(2)等腰直角三角形MON面积是5,因此正方形面积是20,如图2所示;于是根据勾股定理画出图3:考点:1.作图﹣应用与设计作图;2.勾股定理.4.(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;请运用上述解答中所积累的经验和方法完成下列两题:(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD =16,CF=6,求PG+PH的值.(迁移拓展)(3)在直角坐标系中,直线l1:y=-43x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】(﹣1,6),(1,10)【解析】【变式探究】连接AP,同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得;【结论运用】过点E作EQ⊥BC,垂足为Q,根据勾股定理和矩形的性质解答即可;【迁移拓展】分两种情况,利用结论,求得点P到x轴的距离,再利用待定系数法可求出P的坐标.【详解】变式探究:连接AP,如图3:∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ACP﹣S△ABP,∴12AB•CF=12AC•PE﹣12AB•PD.∵AB=AC,∴CF=PD﹣PE;结论运用:过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是长方形,∴AD=BC,∠C=∠ADC=90°.∵AD=16,CF=6,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF.∴DF=5.∵∠C=90°,∴DC2222106DF CF-=-8.∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC.∴四边形EQCD是长方形.∴EQ=DC=4.∵AD∥BC,∴∠DEF=∠EFB.∵∠BEF=∠DEF,∴∠BEF=∠EFB.∴BE=BF,由问题情境中的结论可得:PG+PH=EQ.∴PG+PH=8.∴PG+PH的值为8;迁移拓展:如图,由题意得:A(0,8),B(6,0),C(﹣4,0)∴AB2268+10,BC=10.∴AB=BC,(1)由结论得:P1D1+P1E1=OA=8∵P1D1=1=2,∴P1E1=6 即点P1的纵坐标为6又点P1在直线l2上,∴y=2x+8=6,∴x=﹣1,即点P1的坐标为(﹣1,6);(2)由结论得:P2E2﹣P2D2=OA=8∵P2D2=2,∴P2E2=10 即点P1的纵坐标为10又点P1在直线l2上,∴y=2x+8=10,∴x=1,即点P1的坐标为(1,10)【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点,利用面积法列出等式是解决问题的关键.5.(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在∠的度数为______.点C'处,若42ADB=∠,则DBE(2)小明手中有一张矩形纸片ABCD ,4AB =,9AD =.(画一画)如图2,点E 在这张矩形纸片的边AD 上,将纸片折叠,使AB 落在CE 所在直线上,折痕设为MN (点M ,N 分别在边AD ,BC 上),利用直尺和圆规画出折痕MN (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);(算一算)如图3,点F 在这张矩形纸片的边BC 上,将纸片折叠,使FB 落在射线FD 上,折痕为GF ,点,A B 分别落在点A ',B '处,若73AG =,求B D '的长.【答案】(1)21;(2)画一画;见解析;算一算:3B D '=【解析】【分析】(1)利用平行线的性质以及翻折不变性即可解决问题;(2)【画一画】,如图2中,延长BA 交CE 的延长线由G ,作∠BGC 的角平分线交AD 于M ,交BC 于N ,直线MN 即为所求;【算一算】首先求出GD=9-72033=,由矩形的性质得出AD ∥BC ,BC=AD=9,由平行线的性质得出∠DGF=∠BFG ,由翻折不变性可知,∠BFG=∠DFG ,证出∠DFG=∠DGF ,由等腰三角形的判定定理证出DF=DG=203,再由勾股定理求出CF ,可得BF ,再利用翻折不变性,可知FB′=FB ,由此即可解决问题.【详解】 (1)如图1所示:∵四边形ABCD 是矩形,∴AD∥BC,∴∠ADB=∠DBC=42°,由翻折的性质可知,∠DBE=∠EBC=12∠DBC=21°,故答案为21.(2)【画一画】如图所示:【算一算】如3所示:∵AG=73,AD=9,∴GD=9-72033=,∵四边形ABCD是矩形,∴AD∥BC,BC=AD=9,∴∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,∴∠DFG=∠DGF,∴DF=DG=203,∵CD=AB=4,∠C=90°,∴在Rt△CDF中,由勾股定理得:22222016433 DF CD⎛⎫-=-=⎪⎝⎭,∴BF=BC-CF=9161133-=,由翻折不变性可知,FB=FB′=11 3,∴B′D=DF-FB′=2011333-=.【点睛】四边形综合题,考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题.6.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.7.如图,在正方形ABCD中,点E在CD上,AF⊥AE交CB的延长线于F.求证:AE=AF.【答案】见解析【解析】【分析】根据同角的余角相等证得∠BAF=∠DAE,再利用正方形的性质可得AB=AD,∠ABF=∠ADE=90°,根据ASA判定△ABF≌△ADE,根据全等三角形的性质即可证得AF=AE.【详解】∵AF⊥AE,∴∠BAF+∠BAE=90°,又∵∠DAE+∠BAE=90°,∴∠BAF=∠DAE,∵四边形ABCD是正方形,∴AB=AD,∠ABF=∠ADE=90°,在△ABF和△ADE中,,∴△ABF≌△ADE(ASA),∴AF=AE.【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质等知识点,证明△ABF≌△ADE是解决本题的关键.8.已知点O是△ABC内任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作▱OBFC,连接OF与BC交于点H,再连接EF.(1)如图1,若△ABC为等边三角形,求证:①EF⊥BC;②EF=BC;(2)如图2,若△ABC为等腰直角三角形(BC为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图3,若△ABC是等腰三角形,且AB=AC=kBC,请你直接写出EF与BC之间的数量关系.【答案】(1)见解析;(2)EF⊥BC仍然成立;(3)EF=BC【解析】试题分析:(1)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等边三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(2)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰直角三角形的性质得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可;(3)由平行四边形的性质得到BH=HC=BC,OH=HF,再由等腰三角形的性质和AB=AC=kBC得到AB=BC,AH⊥BC,根据勾股定理得到AH=BC,即可.试题解析:(1)连接AH,如图1,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等边三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2,∴AH==BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(2)EF⊥BC仍然成立,EF=BC,如图2,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC是等腰三角形,∴AB=BC,AH⊥BC,在Rt△ABH中,AH2=AB2﹣BH2=(BH)2﹣BH2=BH2,∴AH=BH=BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=EF,AH∥EF,∴EF⊥BC,BC=EF,∴EF⊥BC,EF=BC;(3)如图3,∵四边形OBFC是平行四边形,∴BH=HC=BC,OH=HF,∵△ABC 是等腰三角形, ∴AB=kBC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2﹣BH 2=(kBC )2﹣(BC )2=(k 2-)BC 2,∴AH=BH=BC ,∵OA=AE ,OH=HF , ∴AH 是△OEF 的中位线, ∴AH=EF ,AH ∥EF , ∴EF ⊥BC ,BC=EF ,∴EF=BC .考点:四边形综合题.9.已知ABC ,以AC 为边在ABC 外作等腰ACD ,其中AC AD =. (1)如图①,若AB AE =,60DAC EAB ∠=∠=︒,求BFC ∠的度数. (2)如图②,ABC α∠=,ACD β∠=,4BC =,6BD =.①若30α=︒,60β=︒,AB 的长为______.②若改变,αβ的大小,但90αβ+=︒,ABC 的面积是否变化?若不变,求出其值;若变化,说明变化的规律.【答案】(1)120°;(2)55【解析】试题分析:(1)根据SAS ,可首先证明△AEC ≌△ABD ,再利用全等三角形的性质,可得对应角相等,根据三角形的外角的定理,可求出∠BFC 的度数;(2)①如图2,在△ABC 外作等边△BAE ,连接CE ,利用旋转法证明△EAC ≌△BAD ,可证∠EBC=90°,EC=BD=6,因为BC=4,在Rt △BCE 中,由勾股定理求BE 即可;②过点B 作BE ∥AH ,并在BE 上取BE=2AH ,连接EA ,EC .并取BE 的中点K ,连接AK ,仿照(2)利用旋转法证明△EAC ≌△BAD ,求得EC=DB ,利用勾股定理即可得出结论. 试题解析:解:(1)∵AE=AB,AD=AC,∵∠EAB=∠DAC=60°,∴∠EAC=∠EAB+∠BAC,∠DAB=∠DAC+∠BAC,∴∠EAC=∠DAB,在△AEC和△ABD中{AE ABEAC BAD AC AD=∠=∠=∴△AEC≌△ABD(SAS),∴∠AEC=∠ABD,∵∠BFC=∠BEF+∠EBF=∠AEB+∠ABE,∴∠BFC=∠AEB+∠ABE=120°,故答案为120°;(2)①如图2,以AB为边在△ABC外作正三角形ABE,连接CE.由(1)可知△EAC≌△BAD.∴EC=BD.∴EC=BD=6,∵∠BAE=60°,∠ABC=30°,∴∠EBC=90°.在RT△EBC中,EC=6,BC=4,∴22EC BC-2264-∴5②若改变α,β的大小,但α+β=90°,△ABC的面积不变化,以下证明:如图2,作AH⊥BC交BC于H,过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK.∵AH⊥BC于H,∴∠AHC=90°.∵BE∥AH,∴∠EBC=90°.∵∠EBC=90°,BE=2AH,∴EC2=EB2+BC2=4AH2+BC2.∵K为BE的中点,BE=2AH,∴BK=AH.∵BK∥AH,∴四边形AKBH为平行四边形.又∵∠EBC=90°,∴四边形AKBH为矩形.∠ABE=∠ACD,∴∠AKB=90°.∴AK是BE的垂直平分线.∴AB=AE.∵AB=AE,AC=AD,∠ABE=∠ACD,∴∠EAB=∠DAC,∴∠EAB+∠EAD=∠DAC+∠EAD,即∠EAC=∠BAD,在△EAC与△BAD中{AB AEEAC BAD AC AD=∠=∠=∴△EAC≌△BAD.∴EC=BD=6.在RT△BCE中,BE=22EC BC-=25,∴AH=12BE=5,∴S△ABC=12BC•AH=25考点:全等三角形的判定与性质;等腰三角形的性质10.(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.小明应用这个结论进行了下列探索活动和问题解决.问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造□APBQ,求对角线PQ的最小值及PQ最小时的值.(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为,当PQ最小时= _____ __;(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时的值;问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图4,若为上任意一点,以,为边作□.试求对角线长的最小值和PQ最小时的值.(2)若为上任意一点,延长到,使,再以,为边作□.请直接写出对角线长的最小值和PQ最小时的值.【答案】问题1:(1)3,;(2)PQ=,=.问题2:(1)=4,.(2)PQ的最小值为..【解析】试题分析:问题1:(1)首先根据条件可证四边形PCBQ是矩形,然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC,从而可求的值.(2)由题可知:当QP⊥AC 时,PQ最小.过点C作CD⊥AB于点D.此时四边形CDPQ为矩形,PQ=CD,在Rt△ABC中,∠C=90°,AC=4,BC=3,利用面积可求出CD=,然后可求出AD=,由AE=nPA可得PE=,而PE=CQ=PD=AD-AP=,所以AP=.所以=.问题2:(1)设对角线与相交于点.Rt≌Rt.所以AD=HC,QH=AP.由题可知:当QP⊥AB时,PQ最小,此时=CH=4,根据条件可证四边形BPQH为矩形,从而QH=BP=AP.所以.(2)根据题意画出图形,当AB 时,的长最小,PQ的最小值为..试题解析:问题1:(1)3,;(2)过点C作CD⊥AB于点D.由题意可知当PQ⊥AB时,PQ最短.所以此时四边形CDPQ为矩形.PQ=CD,DP=CQ=PE.因为∠BCA=90°,AC=4,BC=3,所以AB=5.所以CD=.所以PQ=.在Rt△ACD中AC=4,CD=,所以AD=.因为AE=nPA,所以PE==CQ=PD=AD-AP=.所以AP=.所以=.问题2:(1)如图2,设对角线与相交于点.所以G是DC的中点,作QH BC,交BC的延长线于H,因为AD//BC,所以.所以.又,所以Rt≌Rt.所以AD=HC,QH=AP.由图知,当AB时,的长最小,即=CH=4.易得四边形BPQH为矩形,所以QH=BP=AP.所以.(若学生有能力从梯形中位线角度考虑,若正确即可评分.但讲评时不作要求)(2)PQ的最小值为..考点:1.直角三角形的性质;2.全等三角形的判定与性质;3.平行四边形的性质;4矩形的判定与性质.。
备考2023年中考数学一轮复习-图形的性质_相交线与平行线_垂线段最短-综合题专训及答案

备考2023年中考数学一轮复习-图形的性质_相交线与平行线_垂线段最短-综合题专训及答案垂线段最短综合题专训1、(2016徐州.中考真卷) 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣),C(2,0),其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;(2)若P为y轴上的一个动点,连接PD,则PB+PD的最小值为;(3)M(x,t)为抛物线对称轴上一动点①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N 共有个;②连接MA,MB,若∠AMB不小于60°,求t的取值范围.2、(2017广东.中考模拟) 如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=,BC= .(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.3、(2018无锡.中考模拟) 如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD 的长;若不能,请说明理由;(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作▱ADEF.①▱ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.4、(2020宁波.中考模拟) 已知,在平面直角坐标系xoy中,点A的坐标为(0,2),点P(m,n)是抛物线上的一个动点.(1)如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA 与PB的大小关系:PAPB(直接填写“>”“<”或“=”,不需解题过程);(2)请利用(1)的结论解决下列问题:①如图2,设C的坐标为(2,5),连接PC,AP+PC是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP 的解析式.5、(2018湖南.中考真卷) 如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.(1)求景点B与C的距离;(2)为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)6、(2017郴州.中考真卷) 如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从O点出发,沿OM的方向以1cm/s的速度运动,当D 不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连结DE.(1)求证:△CDE是等边三角形;(2)如图2,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;(3)如图3,当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.7、(2016南山.中考模拟) 如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).(1)求以C为顶点,且经过点D的抛物线解析式;(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;(3)求(2)中N1N2的最小值;(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.8、(2014成都.中考真卷) 如图,已知抛物线y= (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?9、(2019岐山.中考模拟) 问题探究:(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.10、(2020青羊.中考模拟) 已知四边形ABCD为矩形,对角线AC、BD相交于点O,AD =AO.点E、F为矩形边上的两个动点,且∠EOF=60°.(1)如图1,当点E、F分别位于AB、AD边上时,若∠OEB=75°,求证:DF =AE;(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE 的数量关系;(3)如图3,当点E、F同时在AB边上运动时,将△OEF沿OE所在直线翻折至△OEP,取线段CB的中点Q.连接PQ,若AD=2a(a>0),则当PQ最短时,求PF之长.11、(2020石家庄.中考模拟) 如图,和中,,,,边与边交于点(不与点,重合),点,在异侧,为的内心.(1)求证:;(2)设,用含的式子表示为,则求的最大值为.(3)当时,的取值范围为,则,.12、(2020信阳.中考模拟)(1)问题发现:如图1,在平面直角坐标系中,A点的坐标为(2 ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:①OP与CQ的大小关系是________.②OP的最小值为________.(2)解决问题:在(1)的条件下,点Q运动的过程中当△ACQ为直角三角形时,求OP的长?(3)拓展探究:如图2,当点B为直线x=﹣1上一动点,点A(2 ,0),连接AB,以AB为一边向下作等边△AB P,连接OP,请直接写出OP的最小值.13、(2020西安.中考模拟) 问题探究(1)请在图①的的边上求作一点,使最短;(2)如图②,点为内部一点,且满足.求证:点到点、、的距离之和最短,即最短;(3)问题解决:如图③,某高校有一块边长为400米的正方形草坪,现准备在草坪内放置一对石凳及垃圾箱在点处,使点到、、三点的距离之和最小,那么是否存在符合条件的点?若存在,请作出点的位置,并求出这个最短距离;若不存在,请说明理由.14、(2020滨州.中考真卷) 如图,抛物线的顶点为A(h,-1),与y轴交于点B ,点F(2,1)为其对称轴上的一个定点.(1)求这条抛物线的函数解析式;(2)已知直线l是过点C(0,-3)且垂直于y轴的定直线,若抛物线上的任意一点P(m,n)到直线l的距离为d,求证:PF=d;(3)已知坐标平面内的点D(4,3),请在抛物线上找一点Q,使△DFQ的周长最小,并求此时DFQ周长的最小值及点Q的坐标.15、如图(1)问题发现如图1,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,直线BD,CE交于点F,直线BD,AC交于点G.则线段BD和CE的数量关系是,位置关系是;(2)类比探究如图2,在△ABC和△ADE中,∠ABC=∠ADE=α,∠ACB=∠AED=β,直线BD,CE交于点F,AC与BD相交于点G.若AB=kAC,试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数,并说明理由;(3)拓展延伸如图3,在平面直角坐标系中,点M的坐标为(3.0),点N为y轴上一动点,连接MN.将线段MN绕点M逆时针旋转90得到线段MP,连接NP,OP.请直接写出线段OP长度的最小值及此时点N的坐标.垂线段最短综合题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。
九年级数学中考一轮复习知识点基础达标测评:相交线与平行线(附答案)

2021年九年级数学中考一轮复习知识点基础达标测评:相交线与平行线(附答案)1.下列说法正确的是()A.直线AB和直线BA是同一条直线B.直线是射线的2倍C.射线AB与射线BA是同一条射线D.三条直线两两相交,有三个交点2.如图,直线AB,CD交于点O,射线OM平分∠AOC,如果∠AOD=104°,那么∠BOM 等于()A.38°B.104°C.140°D.142°3.如图,OA⊥OB,若∠1=55°16′,则∠2的度数是()A.35°44′B.34°84′C.34°74′D.34°44′4.如图,AC⊥BC于点C,点D是线段BC上任意一点,若AC=6,则AD的长不可能是()A.5.5B.6C.7D.85.已知点P在直线MN外,点A、B、C均在直线MN上,P A=2.5cm,PB=3cm,PC=2.2cm,则点P到直线MN的距离()A.等于3cm B.等于2.5cmC.不小于2.2cm D.不大于2.2cm6.下列说法错误的是()A.对顶角相等B.两点之间所有连线中,线段最短C.等角的补角相等D.不相交的两条直线叫做平行线7.下列说法:①相等的角是对顶角;②同位角相等;③过一点有且只有一条直线与已知直线平行;④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;其中正确的有()个.A.0B.1C.2D.38.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是()A.①②③④B.①③C.②③④D.①②9.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是()A.∠α+∠β﹣∠γ=90°B.∠α+∠γ﹣∠β=180°C.∠γ+∠β﹣∠α=180°D.∠α+∠β+∠γ=180°10.如图所示,下列推理及括号中所注明的推理依据错误的是()A.∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行)B.∵AB∥CD,∴∠BCD+∠ABC=180°(两直线平行,同旁内角互补)C.∵AD∥BC,∴∠BAD+∠D=180°(两直线平行,同旁内角互补)D.∵∠DAM=∠CBM,∴AD∥BC(同位角相等,两直线平行)11.观察下列图形,2条直线相交,有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,…,像这样,10条直线相交最多有个交点.12.如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3=.13.如图,已知AO⊥BC于O,∠BOD=120°,那么∠AOD=°.14.如图,为了把河中的水引到C处,可过点C作CD⊥AB于D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是.15.如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是.16.如图,∠B的内错角是.17.在同一平面内,不重合的两条直线的位置关系是.18.若直线a∥b,a∥c,则直线b与c的位置关系是.19.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是.20.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为度.21.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.请你比照上述方法,解决下列问题:(要求作图分析)(1)平面上的20条直线最多有多少个交点?(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?22.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.(1)求∠BOE的度数;(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.23.如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.24.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l 上画出车站的位置(用点M表示),依据是;(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是.25.已知点A,B,C如图所示,根据要求完成下列各题.(1)画直线BC,线段AB和射线CA.(以(2)过点A画BC的垂线段AD,垂足为D,并量出点A到直线BC的距离为cm.答题纸为测量依据,结果精确到0.1cm).26.如图,已知AB∥CD,直线MN与AB,CD分别交于点E、F,EG平分∠MEB,FH平分∠MFD.∵AB∥CD,根据可知∠MEB=∠MFD.又∵EG平分∠MEB,FH平分∠MFD,于是可得∠MEG和∠MFH的大小关系是∠MEG ∠MFH.而∠MEG和∠MFH是EG、FH被直线MN所截得的角,根据,可判断角平分线EG、FH的位置关系是.27.(1)补全下面的图形,使之成为长方体ABCD﹣EFGH的直观图,并标出顶点的字母;(2)图中与棱AB平行的棱有;(3)图中棱CG和面ABFE的位置关系是.28.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?29.如图,已知:∠DGA=∠FHC,∠A=∠F.求证:DF∥AC.(注:证明时要求写出每一步的依据)30.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.(1)请完成下列书写过程.∵AO∥CD(已知)∴∠O==40°()又∵OB∥DE(已知)∴=∠1=°()(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=°.参考答案1.解:A、直线AB和直线BA是同一条直线,故本选项说法正确.B、直线和射线不能度量,故本选项说法不正确.C、射线AB与射线BA方向相反,不是同一条射线,故本选项说法不正确.D、三条直线两两相交有三个或一个交点,故本选项说法不正确.故选:A.2.解:∵∠AOD=104°,∴∠AOC=76°,∵射线OM平分∠AOC,∴∠AOM=∠AOC=×76°=38°,∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.故选:D.3.解:∵OA⊥OB,∴∠AOB=90°,∵∠1=55°16′,∴∠2=90°﹣55°16′=34°44′.故选:D.4.解:∵AC⊥BC于点C,点D是线段BC上任意一点,AC=6,∴AD≥6,故选:A.5.解:当PC⊥MN时,PC的长是点P到直线MN的距离,即点P到直线MN的距离等于2.2cm,当PC不垂直于MN时,点P到直线MN的距离小于PC的长,即点P到直线MN的距离小于2.2cm,综上所述:点P到直线MN的距离不大于2.2cm,故选:D.6.解:A、对顶角相等,正确;B、两点之间所有连线中,线段最短,正确;C、等角的补角相等,正确;D、在同一平面内,不相交的两条直线叫做平行线,故本选项错误;故选:D.7.解:①相等的角不一定是对顶角,故说法错误;②同位角不一定相等,故说法错误;③过直线外一点有且只有一条直线与已知直线平行,故说法错误;④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故说法正确;故选:B.8.解:①∵∠1=∠2,∴a∥b,故本小题正确;②∵4=∠5,∴a∥b,故本小题正确;③∵∠8=∠1,∠8=∠2,∴∠1=∠2,∴a∥b,故本小题正确;④∵∠6+∠7=180°,∠6+∠2=180°,∴∠7=∠2,∴a∥b,故本小题正确.故选:A.9.解:∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠γ+∠α﹣∠β=180°,故选:B.10.解:A.∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行),正确;B.∵AB∥CD,∴∠BCD+∠ABC=180°(两直线平行,同旁内角互补),正确;C.∵AD∥BC,∴∠BCD+∠D=180°(两直线平行,同旁内角互补),故C选项错误;D.∵∠DAM=∠CBM,∴AD∥BC(同位角相等,两直线平行),正确;故选:C.11.解:两条直线相交最多有1个交点,三条直线相交最多有1+2=3个交点,四条直线相交最多有1+2+3=6个交点,五条直线相交最多有1+2+3+4=10个交点,……十条直线相交最多有1+2+3+4+5+6+7+8+9=45个交点;故答案为:45.12.解:∵∠1=∠2,∠1+∠2=220°,∴∠1=∠2=110°,∴∠3=180°﹣110°=70°,故答案为:70°.13.解:∵AO⊥BC,∴∠AOB=90°,∵∠BOD=120°,∴∠AOD=∠BOD﹣∠AOB=120°﹣90°=30°,故答案是:30.14.解:过D点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,这种设计的依据是垂线段最短.故答案为:垂线段最短.15.解:∵AB⊥l1,则点A到直线l1的距离是AB的长=4;故答案为:4.16.解:∠B的内错角是∠BAD;故答案为:∠BAD.17.解:在同一平面内,不重合的两条直线的位置关系是平行和相交,故答案为:平行和相交.18.解:若直线a∥b,a∥c,则直线b与c的位置关系是平行,故答案为:平行.19.解:由图形得,有两个相等的同位角存在,这样做的依据是:同位角相等,两直线平行.故答案为:同位角相等,两直线平行.20.解:∵AB∥CD,∴∠CMF=∠1=57°,∵MF平分∠CME,∴∠CME=2∠CMF=114°.又∵∠CME+∠EMD=180°,∴∠EMD=180°﹣∠CME=180°﹣114°=66°.故答案为:66.21.解:(1)当有2,3,4条直线时最多交点的个数分别是:∴20条直线最多有1+2+3+…+19=190个交点;(2)当有1,2,3条直线时最多可把平面分成的部分分别是:∴100条直线最多可把平面分成1+(1+2+3+…+100)=5051个部分,同理n条直线最多可把平面分成1+(1+2+3+…+n)=1+=.22.解:(1)∵∠AOC=120°,∴∠BOC=180°﹣120°=60°,∵OE平分∠BOC,∴∠BOE=∠BOC=×60°=30°;(2)OA平分∠DOF,理由如下:∵∠BOE=30°,∴∠AOE=180°﹣30°=150°,∵∠AOF:∠EOF=2:3,∴∠AOF=60°,∠EOF=90°,∵∠AOD=∠BOC=60°,∴∠AOD=∠AOF,∴OA平分∠DOF.23.解:∵∠BON=20°,∴∠AOM=20°,∵OA平分∠MOD,∴∠AOD=∠MOA=20°,∵OC⊥AB,∴∠AOC=90°,∴∠COD=90°﹣20°=70°.24.解:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短(2)如图,点N即为所示.依据是两点之间线段最短;故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.25.解:(1)如图所示:(2)经测量AD=1.8cm,故答案为:1.8.26.解:如图,已知AB∥CD,直线MN与AB,CD分别交于点E、F,EG平分∠MEB,FH平分∠MFD.∵AB∥CD,根据两直线平行,同位角相等可知∠MEB=∠MFD.又∵EG平分∠MEB,FH平分∠MFD,于是可得∠MEG和∠MFH的大小关系是∠MEG =∠MFH.而∠MEG和∠MFH是EG、FH被直线MN所截得的同位角,根据同位角相等,两直线平行,可判断角平分线EG、FH的位置关系是平行.故答案为:两直线平行,同位角相等;=;同位、同位角相等,两直线平行、平行.27.解:(1)如图即为补全的图形;(2)图中与棱AB平行的棱有CD、EF、GH;故答案为:CD、EF、GH;(3)图中棱CG和面ABFE的位置关系是:平行.故答案为:平行.28.解:∠BFC等于30度,理由如下:∵AB∥GE,∴∠B+∠BFG=180°,∵∠B=110°,∴∠BFG=180°﹣110°=70°,∵AB∥CD,AB∥GE,∴CD∥GE,∴∠C+∠CFE=180°,∵∠C=100°.∴∠CFE=180°﹣100°=80°,∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.29.证明:∵∠DGA=∠FHC=∠DHB,∴AE∥BF,(同位角相等,两直线平行)∴∠A=∠FBC,(两直线平行,同位角相等)又∵∠A=∠F,∴∠F=∠FBC,(等量代换)∴DF∥AC.(内错角相等,两直线平行)30.解:(1)∵AO∥CD(已知),∴∠O=∠1=40°(两直线平行,同位角相等),又∵OB∥DE(已知),∴∠D=∠1=40°(两直线平行,同位角相等).故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.故答案为:(40或140)。
中考数学常考易错点 角、相交线与平行线 专题练习试题合集(含答案解析)

中考数学常考易错点角、相交线与平行线专题练习试题合集(含答案解析)易错清单1.平行线的性质.【例1】(2014·湖北襄阳)如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于().A.35°B.45°C.55°D.65°【解析】利用“直角三角形的两个锐角互余”的性质求得∠A=35°,然后利用平行线的性质得到∠1=∠A=35°.【答案】∵BC⊥AE,∴∠ACB=90°.∴∠A+∠B=90°.又∵∠B=55°,∴∠A=35°.又CD∥AB,∴∠1=∠A=35°.【误区纠错】本题考查了平行线的性质和直角三角形的性质.此题也可以利用垂直的定义、邻补角的性质以及平行线的性质来求∠1的度数.【例2】(2014·广东梅州)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是().A.15°B.20°C.25°D.30°【解析】根据两直线平行,内错角相等求出∠3,再求解即可.【答案】∵直尺的两边平行,∠1=20°,∴∠3=∠1=20°.∴∠2=45°-20°=25°.【误区纠错】误认为∠1与∠2是内错角来解题.【例3】(2014·湖北孝感)如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数().A.46°B.44°C.36°D.22°【解析】根据两直线平行,内错角相等可得∠3=∠1,再根据直角三角形两锐角互余列式计算即可得解.【答案】∵l1∥l2,∴∠3=∠1=44°.∵l3⊥l4,∴∠2=90°-∠3=90°-44°=46°.故选A.【误区纠错】本题考查了平行线的性质,垂线的定义,要熟记性质并准确识图.例外识别∠3与∠1是同位角很重要.2.平行线的判定.【例4】(2014·湖南湘潭)如图,直线a,b被直线c所截,若满足,则a,b平行.【解析】根据同位角相等两直线平行可得∠1=∠2时,a∥b.其他合理答案亦可.【答案】∵∠1=∠2,∴a∥b(同位角相等两直线平行).故可填∠1=∠2.【误区纠错】分不清三线八角,以及平行线的判定方法是解题的误区,本题属条件开放性题.名师点拨1.能记住点、线、面的概念.2.能利用角的概念判断角的大小及角的表示方法;会进行角的换算;能正确区分角的大小;会进行角的和、差运算.3.能区分补角、余角的概念,记住补角、余角的性质.4.掌握角平分线定理和线段垂直平分线定理并能正确使用.5.会画直线的垂线;能区分垂线、垂线段的联系与区别.6.掌握平行的概念,会进行平行线的判断.7.能利用直尺画直线的平行线;会作两平行线间的距离;能确定并准确度量两平行线间的距离.提分策略1.直线平行与垂直的判定及简单应用.计算角度问题时,要注意挖掘图形中的隐含条件(三角形内角和、互为余角或补角、平行性质、垂直)及角平分线知识的应用.【例1】如图,△ABC中,∠A=90°,点D在边AC上,DE∥BC.若∠1=155°,则∠B的度数为.【解析】由∠1=155°,可求得∠BCD=∠CDE=25°,最后求∠B=65°.【答案】65°2.平行线的性质和判定的应用.主要理解和掌握:(1)平行线的性质;(2)平行线的判定.【例2】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD的关系,请你从所得到的关系中任选一个加以证明.【解析】①∠APC=∠PAB+∠PCD;②∠APC=360°-(∠PAB+∠PCD);③∠APC=∠PAB-∠PCD;④∠APC=∠PCD-∠PAB.如证明①∠APC=∠PAB+∠PCD.证明:过点P作PE∥AB,所以∠A=∠APE.又因为AB∥CD,所以PE∥CD.所以∠C=∠CPE.所以∠A+∠C=∠APE+∠CPE.所以∠APC=∠PAB+∠PCD.同理可证明其他的结论.专项训练一、选择题1.(2014·四川峨眉山二模)如图,已知直线AB,CD相交于点O,OE平分∠CPB.若∠BOD=70°,则∠COE的度数是().A.45°B.70°C.55°D.110°(第1题)(第2题)2.(2014·北京平谷区模拟)如图,AB∥CD,O为CD上一点,且∠AOB=90°.若∠B=33°,则∠AOC的度数是().A.33°B.60°C.67°D.57°3.(2014·山东日照模拟)将一副三角板按图中的方式叠放,则∠α等于().A.75°B.60°C.45°D.30°(第3题)(第4题)4.(2013·广东广州海珠区毕业班综合调研)如图,∠1与∠2是同位角,若∠2=65°,则∠1的大小是().A.25°B.65°C.115°D.不能确定5.(2013·浙江温州一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为().A.9B.6C.4D.3(第5题)(第6题)6.(2012·湖北荆门东宝区模拟)如图,已知直线a∥b,∠1=40°,∠2=60°.则∠3等于().A.100°B.60°C.40°D.20°二、填空题7.(2014·广东模拟)将三角板ABC按下图放置,使其三个顶点分别落在三条平行直线上,其中∠CAB=90°,且CF恰好平分∠ACB.若∠CBA=40°,则∠DAC的度数是.(第7题)(第8题)8.(2014·河南鹿邑一模)如图,∠1=∠2,∠3=40°.则∠4= .9.(2014·湖北鄂州二模)如图AB∥CD,∠1=50°,∠2=110°,则∠3= .(第9题)(第10题)10.(2013·湖北孝感模拟)如图,直线AB,CD相交于点E,EF⊥AB于点E,若∠CEF=59°,则∠AED的度数为.三、解答题11.(2014·河南安阳模拟)已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD.探究下列问题:(1)如图(1),当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图(2),当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图(3),当∠ACB变化,且点D与点C位于直线AB的两侧时,求CD的最大值及相应的∠ACB的度数.(第11题)参考答案与解析1.C[解析]2.D[解析]∠AOC=90°-33°=57°.3.A[解析]∠α=45°+(90°-60°)=75°.4.D[解析]两直线平行同位角相等,如果不能确定两直线是平行线则不能确定同位角之间的关系.5.A[解析]首先利用平行线判定两三角形相似,然后利用相似三角形对应边的比等于相似比求得线段BC的长即可.6.A[解析]∠3=∠1+∠2=100°.8.140°[解析]∠4=180°-∠3=140°.9.60°[解析]∠3=180°-(∠1+180°-∠2)=60°.10.149°[解析]∵EF⊥AB于点E,∠CEF=59°,∴∠AEC=90°-∠CEF=90°-59°=31°.∴∠AED=180°-∠AEC=180°-31°=149°.11.(3)以点D为中心,将△DBC逆时针旋转60°,则点B落在点A,点C落在点E.连接AE,CE.∴CD=ED,∠CDE=60°,AE=CB=a.∴△CDE为等边三角形.∴CE=CD.如图(1),当点E,A,C不在一条直线上时,有CD=CE<AE+AC=a+b;如图(2),当点E,A,C在一条直线上时,CD有最大值,CD=CD=a+b.此时∠CED=∠BCD=∠ECD=60°,∴∠ACB=120°.因此当∠ACB=120°时,CD有最大值a+b.(第11题)。
中考数学复习《平行四边形》专项综合练习含答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.(1)、动手操作:如图①:将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么的度数为 .(2)、观察发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.(3)、实践与运用:将矩形纸片ABCD按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC 边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F 重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.【答案】(1)125°;(2)同意;(3)60°【解析】试题分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.试题解析:(1)、∵在直角三角形ABE中,∠ABE=20°,∴∠AEB=70°,∴∠BED=110°,根据折叠重合的角相等,得∠BEF=∠DEF=55°.∵AD∥BC,∴∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°.;(2)、同意,如图,设AD与EF交于点G由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.由折叠知,∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,即△AEF为等腰三角形.(3)、由题意得出:∠NMF=∠AMN=∠MNF,∴MF=NF,由折叠可知,MF=PF,∴NF=PF,而由题意得出:MP=MN,又∵MF=MF,∴△MNF≌△MPF,∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,即3∠MNF=180°,∴∠MNF=60°.考点:1.折叠的性质;2.等边三角形的性质;3.全等三角形的判定和性质;4.等腰三角形的判定2.如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).(1)当点N落在边BC上时,求t的值.(2)当点N到点A、B的距离相等时,求t的值.(3)当点Q沿D→B运动时,求S与t之间的函数表达式.(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF 与四边形PQMN的面积比为2:3时t的值.【答案】(1)(2)2(3)S=S菱形PQMN=2S△PNQ=t2;(4)t=1或【解析】试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当0≤t≤时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当≤t≤时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题3.如图,矩形ABCD 中,AB =6,BC =4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,求EF 的长.【答案】(1)证明见解析;(2)133. 【解析】 分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD ,∴∠OBE=∠ODF ,在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ),∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE=x ,则 DE=x ,AE=6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得:x=133, ∵22AD AB +13 ∴OB=1213 ∵BD ⊥EF ,∴EO=22BE OB=2133,∴EF=2EO=4133.点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题5.△ABC 为等边三角形,AF AB =.BCD BDC AEC ∠=∠=∠.(1)求证:四边形ABDF 是菱形.(2)若BD 是ABC ∠的角平分线,连接AD ,找出图中所有的等腰三角形.【答案】(1)证明见解析;(2)图中等腰三角形有△ABC ,△BDC ,△ABD ,△ADF ,△ADC ,△ADE .【解析】【分析】(1)先求证BD ∥AF ,证明四边形ABDF 是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD 平分∠ABC ,得到BD 垂直平分线段AC ,进而证明△DAC 是等腰三角形,根据BD ⊥AC,AF ⊥AC ,找到角度之间的关系,证明△DAE 是等腰三角形,进而得到BC =BD =BA =AF =DF ,即可解题,见详解.【详解】(1)如图1中,∵∠BCD =∠BDC ,∴BC =BD ,∵△ABC 是等边三角形,∴AB =BC ,∵AB =AF ,∴BD =AF ,∵∠BDC =∠AEC ,∴BD ∥AF ,∴四边形ABDF 是平行四边形,∵AB =AF ,∴四边形ABDF是菱形.(2)解:如图2中,∵BA=BC,BD平分∠ABC,∴BD垂直平分线段AC,∴DA=DC,∴△DAC是等腰三角形,∵AF∥BD,BD⊥AC∴AF⊥AC,∴∠EAC=90°,∵∠DAC=∠DCA,∠DAC+∠DAE=90°,∠DCA+∠AEC=90°,∴∠DAE=∠DEA,∴DA=DE,∴△DAE是等腰三角形,∵BC=BD=BA=AF=DF,∴△BCD,△ABD,△ADF都是等腰三角形,综上所述,图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.【点睛】本题考查菱形的判定,等边三角形的性质,等腰三角形的判定等知识,属于中考常考题型,熟练掌握等腰三角形的性质是解题的关键.6.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF 与BE交于点O.(1)求证:△AOB和△AOE是“友好三角形”;(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的,请直接写出△ABC的面积.【答案】(1)见解析;(2)12;探究:2或2.【解析】试题分析:(1)利用一组对边平行且相等的四边形是平行四边形,得到四边形ABFE是平行四边形,然后根据平行四边形的性质证得OE=OB,即可证得△AOE和△AOB是友好三角形;(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中点,则可以求得△ABE、△ABF的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.探究:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;②求出高CQ,求出△A′DC的面积.即可求出△ABC的面积.试题解析:(1)∵四边形ABCD是矩形,∴AD∥BC,∵AE=BF,∴四边形ABFE是平行四边形,∴OE=OB,∴△AOE和△AOB是友好三角形.(2)∵△AOE和△DOE是友好三角形,∴S△AOE=S△DOE,AE=ED=AD=3,∵△AOB与△AOE是友好三角形,∴S△AOB=S△AOE,∵△AOE≌△FOB,∴S△AOE=S△FOB,∴S△AOD=S△ABF,∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12.探究:解:分为两种情况:①如图1,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OB,A′O=CO,∴四边形A′DCB是平行四边形,∴BC=A′D=2,过B作BM⊥AC于M,∵AB=4,∠BAC=30°,∴BM=AB=2=BC,即C和M重合,∴∠ACB=90°,由勾股定理得:AC=,∴△ABC的面积是×BC×AC=×2×2=2;②如图2,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OA′,BO=CO,∴四边形A′BDC是平行四边形,∴A′C=BD=2,过C作CQ⊥A′D于Q,∵A′C=2,∠DA′C=∠BAC=30°,∴CQ=A′C=1,∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2;即△ABC的面积是2或2.考点:四边形综合题.7.如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.8.(1)问题发现如图1,点E. F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;(2)类比引申如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E. F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系时,仍有EF=BE+DF;(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC 满足的等量关系,并写出推理过程。
中考数学专题复习题 命题与证明(含解析)

2017-2018年中考数学专题复习题:命题与证明一、选择题1.下列命题中是假命题的A. 在同一平面内,垂直于同一条直线的两条直线平行B. 三角形的三个内角中至少有一个角不大于C. 三角形的一个外角等于两个内角之和D. 平行于同一条直线的两条直线平行2.如图,有下列命题:若,则;若,则;若,则;若,,则,其中正确的个数为A. 1B. 2C. 3D. 43.对于命题“如果,那么”,说明它是假命题的反例可以是A. ,B. ,C. ,D.4.用反证法证明“三角形中至少有一个内角大于或等于”时,应先假设A. 有一个内角小于B. 每一个内角都小于C. 有一个内角大于D. 每一个内角都大于5.对于命题“若,则”,下面四组关于a,b的值中,能说明这个命题是假命题的是A. ,B. ,C., D. ,6.下列命题的逆命题是真命题的是A. 如果,那么B. 如果,那么C. 对顶角相等D. 对角线相等的四边形是矩形7.下列命题:负数没有立方根;一个实数的立方根不是正数就是负数;一个正数或负数的立方根与这个数的符号一致;如果一个数的立方根等于它本身,那么它一定是1或0.其中正确的是A. 1B. 2C. 3D. 48.在足球、篮球、网球和垒球中,小张、小王、小李和小刘分别喜欢其中的一种,根据下面的提示,判断小刘喜欢的是小张不喜欢网球;小王不喜欢足球;小王和小李都是既不喜欢篮球也不喜欢网球.A. 足球B. 篮球C. 网球D. 垒球9.一个大矩形按如图方式分割成九个小矩形,且只有标号为和的两个小矩形为正方形,在满足条件的所有分割中若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是A. 3B. 4C. 5D. 610.如图所示,小圆圈表示网络的结点,结点之间的线段表示它们有网线相连连线标注的数字表示该段网线单位时间内可以通过的最大信息量现从结点A向结点B传递信息,信息分开可以从不同的路线同时传递,则单位的时间内传递的最大信息量为A. 19B. 20C. 24D. 25二、填空题11.用反证法证明“一个三角形不能有两个角是直角”时应首先假设______ .12.小红为奶奶冲杯热牛奶,她需要做下列事情:烧开水分钟,洗杯子分钟,冲奶粉分钟她至少要用______ 分钟才能让奶奶喝上热牛奶.13.甲、乙、丙、丁、戊与小强六位同学参加乒乓球比赛,每两人都要比赛一场,到现在为止,已知甲赛了5场,乙赛了4场,丙赛了3场,丁赛了2场,戊赛了1场,则小强赛了______ 场14.把命题“对顶角相等”改写成“如果那么”的形式:______.15.给出四个命题:若,,则;若,则;若,则;若,则.正确的是______填序号16.证明“为实数”是假命题的一个反例是______.17.命题:“如果m是整数,那么它是有理数”,则它的逆命题为:______ .18.若,则,它的逆命题是______真或假命题.19.字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形的连接方式为______ .20.在数学课上,林老师在黑板上画出如图所示的图形其中点B、F、C、E在同一直线上,并写出四个条件:,,,请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.条件:______ ;结论:______ 均填写序号三、计算题21.某次数学竞赛,共有40道选择题,规定答对一题得5分,不答得1分,答错倒扣1分证明:不论有多少人参赛,全体学生的得分总和一定是偶数.22.判断下列命题是真命题还是假命题,如果是假命题,举一个反例.两条直线被第三条直线所截,同旁内角互补;如果,那么;两个锐角的和是钝角.23.某商店有5只分别装有麻油、豆油、菜油,其重量如图,其中麻油一桶,豆油的公斤数恰好是菜油的两倍,五只桶分别装的是哪种油?并请说明推理过程.24.我们的数学教材中有一个“抢30的游戏”,现在改为“甲、乙二人抢20”的游戏游戏规则是:甲先说“1”或“1、2”乙接着甲的数往下说一个或两个数,然后又轮到甲再接着乙的数往下说一个或两个数,甲、乙反复轮流说,每次每人说一个或两个数都可以,但不能连续说三个数,也不能一个数也不说谁先抢到20,谁就获胜因为甲先说,你认为谁会获胜?请你分析获胜策略、推理说明获胜的道理.【答案】1. C2. B3. D4. B5. B6. D7. A8. C9. A10. A11. 这个三角形中有两个角是直角12. 613. 314. 如果两个角是对顶角,那么它们相等15.16. 当时,17. “如果m是有理数,那么它是整数”18. 假19.20. ;21. 证明:我们证明每一个学生的得分都是偶数.设某个学生答对了a道题,答错了b道题,那么还有道题没有答于是此人的得分是,这是一个偶数.所以,不论有多少人参赛,全体学生的得分总和一定是偶数.22. 解:两条直线被第三条直线所截,同旁内角互补是假命题,如:三角形三边可看作为两条直线被第三条直线所截,则同旁内角不互补;如果,那么是假命题,如:当,则;两个锐角的和是钝角是假命题,如:和的和为锐角.23. 解:商店有5只分别装有麻油、豆油、菜油,其中麻油一桶,豆油、菜油各两桶,且麻油重量一定不是60kg,又豆油的公斤数恰好是菜油的两倍,豆油的公斤数至少是的2倍,豆油公斤数是:,菜油的公斤数是:120,五只桶分别装的是:60kg菜油,60kg菜油,80kg麻油,90kg豆油,150kg豆油.24. 解:第一个人必胜;因为是第一个人先说,所以主动权在第一个人,他肯定按2,5,8,11,17,20,报数,故第一个人必胜.。
中考数学总复习训练 平行线的判定与性质(含解析)(2021-2022学年)

平行线的判定与性质1.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有个.2.如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有()A.4对B.8对C.12对ﻩ D.16对3.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°求证:AB∥EF.4.如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.5.探究:(1)如图a,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请证明;ﻬ(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;(4)若将E点移至图c所示位置,情况又如何?(5)在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?(6)在图e中,若AB∥CD,又得到什么结论?6.如图所示,已知AB∥CD,EF交AB于M交CD于F,MN⊥EF于M,MN交CD于N,若∠BME=110°,则∠MND=.7.如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3=.8.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α=度.9.已知两个角的两边分别平行,其中一个角为40°,那么另一角是度.ﻬ10.如图,下列条件中,不能判断直线l1∥l2的是( )A.∠1=∠3ﻩ B.∠2=∠3ﻩ C.∠4=∠5D.∠2+∠4=180°11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )A.1条ﻩB.2条 C.3条D.4条12.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是()A.①③ﻩB.②④C.①③④ﻩD.①②③④13.如图所示,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有()A.6个ﻩB.5个 C.4个ﻩD.2个14.如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.15.如图,已知∠1十∠2=180°,∠A=∠C,AD平分∠BDF.求证:BC平分∠DBE.16.在同一平面内有2002条直线a1,a2,…,a2002,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2002的位置关系是.17.若平面上4条直线两两相交且无三线共点,则共有同旁内角对.18.如图,已知l1∥l2,AB⊥l1,∠ABC=130°,则∠α= .19.如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是.20.如图,D、G是△ABC中AB边上的任意两点,DE∥BC,GH∥DC,则图中相等的角共有( )A.4对ﻩ B.5对ﻩC.6对 D.7对21.如图,若AB∥CD,则( )A.∠1=∠2+∠3B.∠1=∠3﹣∠2C.∠1+∠2+∠3=180°ﻩD.∠l﹣∠2+∠3=180°22.如图:已知AB∥CD∥EF,EH⊥CD于H,则∠BAC+∠ACE+∠CEH等于()A.180°B.270°ﻩ C.360°ﻩ D.450°23.如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )A.β=α+γB.α+β+γ=180°C.α+β﹣γ=90°D.β+γ﹣α=180°24.如图,已知AB∥CD,P为HD上任意一点,过P点的直线交HF于O点,试问:∠HOP、∠AGF、∠HPO有怎样的关系?用式子表示并证明.25.如图,AB∥ED,α=∠A+∠E,β=∠B+∠C+∠D.证明:β=2α26.平面上有7条不同的直线,如果其中任何三条直线都不共点.(1)请画出满足上述条件的一个图形,并数出图形中各直线之间的交点个数;(2)请再画出各直线之间的交点个数不同的图形(至少两个);(3)你能否画出各直线之间的交点个数为n的图形,其中n分别为6,21,15?(4)请尽可能多地画出各直线之间的交点个数不同的图形,从中你能发现什么规律?27.如图,直线CB∥OA,∠C=∠BAO=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.平行线的判定与性质参考答案与试题解析1.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有 3 个.【考点】平行线的性质;余角和补角.【分析】本题考查互余的概念,和为90度的两个角互为余角,结合图形和平行线的性质作答.【解答】解:AB∥CD,AC⊥BC,则图中与∠CAB互余的角有3个,∠CBA,∠BCD,和∠CBA的对顶角.【点评】此题属于基础题,较简单,主要记住互为余角的两个角的和为90度.2.如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有( )A.4对ﻩ B.8对 C.12对D.16对【考点】同位角、内错角、同旁内角.【专题】几何图形问题.【分析】每一个“三线八角"基本图形都有两对同旁内角,从对原图形进行分解入手可知同旁内角共有对数.【解答】解:直线AB、CD被EF所截有2对同旁内角;直线AB、CD被GH所截有2对同旁内角;直线CD、EF被GH所截有2对同旁内角;直线CD、GH被EF所截有2对同旁内角;直线GH、EF被CD所截有2对同旁内角;直线AB、EF被GH所截有2对同旁内角;ﻬ直线AB、GH被EF所截有2对同旁内角;直线EF、GH被AB所截有2对同旁内角.共有16对同旁内角.故选D.【点评】本题考查了同旁内角的定义.注意在截线的同旁找同旁内角.要结合图形,熟记同旁内角的位置特点.两条直线被第三条直线所截所形成的八个角中,有两对同旁内角.3.如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°求证:AB∥EF.【考点】平行线的判定与性质.【专题】证明题.【分析】解本例的困难在于图形中没有“三线八角”,考虑创造条件,在图中添置“三线八角"或作出与AB或CD平行的直线,利用平行线的性质和判定求证.【解答】解:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,∵∠B=25°,∴∠BCG=25°,∵∠BCD=45°,∴∠GCD=20°,∵CG∥HD,∴∠CDH=20°,∵∠CDE=30°,∴∠HDE=10°∴∠HDE=∠E=10°,∴DH∥EF,∴DH∥AB,∴AB∥EF.【点评】此题考查平行线的判定和性质,辅助线是常见的作法,证明过程注意选用有用的条件作为证明的依据.4.如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.【考点】平行线的性质;垂线.【分析】先运用垂直于同一条直线的两直线平行,得出∠BDF=∠BCE,∠FDE=∠DEC,再根据平行线的性质得出∠DEC=∠ACE,然后利用角平分线等量代换即可得出两角的关系.【解答】解:∠EDF=∠BDF.∵CE⊥AB于E,DF⊥AB于F∴DF∥CE (垂直于同一条直线的两直线平行),∴∠BDF=∠BCE (两直线平行,同位角相等),∠FDE=∠DEC(两直线平行,内错角相等)又∵AC∥ED,∴∠DEC=∠ACE(两直线平行,内错角相等),∵CE是∠ACB的角平分线,∴∠ACE=∠ECB(角平分线的定义),∴∠EDF=∠BDF(等量代换).【点评】本题主要运用了平行线的性质和垂线的性质,解答本题的关键是熟练掌握平行线的性质:两直线平行内错角、同位角相等.ﻬ5.探究:(1)如图a,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请证明;(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;(4)若将E点移至图c所示位置,情况又如何?(5)在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?(6)在图e中,若AB∥CD,又得到什么结论?【考点】平行线的判定与性质.【分析】已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.【解答】解:(1)过E作EF∥AB,则∠B=∠BEF,∵AB∥CD,∴EF∥CD,∴∠D=∠DEF,∴∠BED=∠BEF+∠DEF=∠B+∠D.(2)若∠B+∠D=∠E,由EF∥AB,∴∠B=∠BEF,∵∠E=∠BEF+∠DEF=∠B+∠D,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;(3)若将点E移至图b所示位置,过E作EF∥AB,∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,∠E+∠B+∠D=360°;(4)∵AB∥CD,∴∠B=∠BFD,∵∠D+∠E=∠BFD,∴∠D+∠E=∠B;(5)∵AB∥CD,∴∠E+∠G=∠B+∠F+∠D;(6)由以上可知:∠E1+∠E2+…+∠E n=∠B+∠F1+∠F2+…+∠Fn﹣1+∠D;【点评】本题考查了平行线的性质与判定,属于基础题,关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.6.如图所示,已知AB∥CD,EF交AB于M交CD于F,MN⊥EF于M,MN交CD于N,若∠BME=110°,则∠MND=20° .【考点】平行线的性质.【分析】根据对顶角相等求出∠AMF,再求出∠AMN,然后根据两直线平行,内错角相等求解即可.【解答】解:∵∠BME=110°,∴∠AMF=∠BME=110°,∵MN⊥EF于M,∴∠NMF=90°,∴∠AMN=∠AMF﹣∠NMF=110°﹣90°=20°,∵AB∥CD,∴∠MND=∠AMN=20°.故答案为:20°.【点评】本题考查了平行线的性质,对顶角相等的性质,以及垂直的定义,是基础题,熟记性质并准确识图是解题的关键.7.如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3= 65°.【考点】平行线的判定与性质.【专题】计算题.【分析】由∠1+∠3=90°,∠2﹣∠3=90°,可得∠1+∠2=180°,则可得出a∥b,根据同旁内角互补即可得出答案.【解答】解:∵∠1+∠3=90°,∠2﹣∠3=90°,∴∠1+∠2=180°,∴∠1的对顶角+∠2=180°,∴a∥b,∴∠3+∠4的对顶角=180°,∵∠4=115°,∴∠3=180°﹣∠4=65°,故答案为:65°.【点评】本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.8.如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α=40度.ﻬ【考点】平行线的性质.【专题】计算题.【分析】过点F作EF∥AB,由平行线的性质可先求出∠3与∠4,再利用平角的定义即可求出∠α.【解答】解:如图,过点F作EF∥AB,∴∠1+∠3=180°.∵∠1=100°,∴∠3=80°.∵AB∥CD,∴CD∥EF,∴∠4+∠2=180°,∵∠2=120°,∴∠4=60°.∴∠α=180°﹣∠3﹣∠4=40°.故应填40.【点评】本题的难点在于用辅助线构造平行线;关键点在于利用平行线的性质进行角的转化.9.已知两个角的两边分别平行,其中一个角为40°,那么另一角是 40或140 度.【考点】平行线的性质.【分析】两个角的两边分别平行,则两个角可能是同位角,也可能是同旁内角,所以应分情况讨论.【解答】解:当两个角是同位角时,则另一个角也等于40°;若两个角是同旁内角时,则另一个角是140°.故应填:40或140.【点评】会利用平行线性质求解角的大小,能够分析讨论一些简单的问题.ﻬ10.如图,下列条件中,不能判断直线l1∥l2的是()A.∠1=∠3B.∠2=∠3ﻩ C.∠4=∠5D.∠2+∠4=180°【考点】平行线的判定.【分析】根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行分别进行分析即可.【解答】解:A、根据内错角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;B、∠2=∠3,不能判断直线l1∥l2,故此选项符合题意;C、根据同位角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;D、根据同旁内角互补,两直线平行可判断直线l1∥l2,故此选项不合题意;故选:B.【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.11.已知线段AB=10cm,点A,B到直线l的距离分别为6cm,4cm.符合条件的直线l有( )A.1条 B.2条ﻩ C.3条D.4条【考点】点到直线的距离.【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.画出图形进行判断.【解答】解:在线段AB的两旁可分别画一条满足条件的直线;作线段AB的垂线,将线段AB分成6cm,4cm两部分,所以符合条件的直线l有3条,故选C.【点评】此题主要考查了从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离的定义.12.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )A.①③ﻩB.②④ﻩC.①③④ D.①②③④【考点】平行线的判定;对顶角、邻补角.【分析】在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【解答】解:①∵∠1=∠2,∴a∥b(同位角相等,两直线平行).②∵∠3=∠6,∴a∥b(内错角相等,两直线平行).③∵∠4+∠7=180°,∵∠4=∠6(对顶角相等),∴∠6+∠7=180°,∴a∥b(同旁内角互补,两直线平行).④同理得,a∥b(同旁内角互补,两直线平行).故选D.【点评】正确识别“三线八角"中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.13.如图所示,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有()A.6个ﻩB.5个C.4个 D.2个【考点】平行线的性质.ﻬ【分析】由AB∥EF得∠FEG=∠1,由EG∥DB可得∠DBG=∠1;设BD与EF相交于点P,由AB∥EF得到∠FPB=∠DBG=∠1,∠DPE=∠DBG=∠1,又AB∥DC可以得到∠CDB=∠DBG=∠1,由此得到共有5个.【解答】解:∵AB∥EF,∴∠FEG=∠1,∵EG∥DB,∴∠DBG=∠1,设BD与EF相交于点P,∵AB∥EF,∴∠FPB=∠DBG=∠1,∠DPE=∠DBG=∠1,∵AB∥DC,∴∠CDB=∠DBG=∠1.∴共有5个.故选B.【点评】本题主要利用了由平行得到的内错角相等以及同位角相等,注意不要漏解.14.如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.【考点】平行线的性质.【专题】探究型.【分析】由图中题意可先猜测∠AED=∠C,那么需证明DE∥BC.题中说∠1+∠2=180°,而∠1+∠4=180°所以∠2=∠4,那么可得到BD∥EF,题中有∠3=∠B,所以应根据平行得到∠3与∠ADE之间的关系为相等.就得到了∠B与∠ADE之间的关系为相等,那么DE∥BC.【解答】证明:∵∠1+∠4=180°(邻补角定义)∠1+∠2=180°(已知)∴∠2=∠4(同角的补角相等)∴EF∥AB(内错角相等,两直线平行)∴∠3=∠ADE(两直线平行,内错角相等)又∵∠B=∠3(已知),∴∠ADE=∠B(等量代换),∴DE∥BC(同位角相等,两直线平行)∴∠AED=∠C(两直线平行,同位角相等).【点评】本题是先从结论出发得到需证明的条件,又从所给条件入手,得到需证明的条件.属于典型的从两头往中间证明.15.如图,已知∠1十∠2=180°,∠A=∠C,AD平分∠BDF.求证:BC平分∠DBE.【考点】平行线的判定与性质.【专题】证明题.【分析】由已知易得∠1=∠BDC,则AE∥CF,所以∠EBC=∠BCD,又∠BAD=∠BCD,故∠EBC=∠BAD,可得AD∥BC,再用角平分线的定义和平行线的性质求证即可.【解答】证明:∵∠1十∠2=180°,∠1+∠EBD=180°,∴∠2=∠EBD,∴AE∥CF,∴∠FDB=∠DBE,∠BAD=∠ADF,又∵∠BAD=∠BCD,∴∠BCD=∠ADF,∴AD∥BC,∴∠DBC=∠BDA=∠FDB=∠DBE,∴BC平分∠DBE.ﻬ【点评】此题考查了平行线的判定和性质,综合利用了角平分线的定义,要充分利用已知条件.16.在同一平面内有2002条直线a1,a2,…,a2002,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2002的位置关系是垂直.【考点】垂线;平行线.【专题】压轴题;规律型.【分析】a1与后面的直线按垂直、垂直、平行、平行每4条直线一循环.根据此规律可求a1与a2002的位置关系是垂直.【解答】解:∵a1与后面的直线按垂直、垂直、平行、平行每4条直线一循环.∴(2002﹣1)÷4=500余1,故答案为:垂直.【点评】本题难点在规律的探索,要认真观察即可得出规律.17.若平面上4条直线两两相交且无三线共点,则共有同旁内角24对.【考点】同位角、内错角、同旁内角.【专题】几何图形问题.【分析】一条直线与另3条直线相交(不交于一点),有3个交点.每2个交点决定一条线段,共有3条线段.4条直线两两相交且无三线共点,共有3×4=12条线段.每条线段两侧各有一对同旁内角,可知同旁内角的总对数.【解答】解:∵平面上4条直线两两相交且无三线共点,∴共有3×4=12条线段.又∵每条线段两侧各有一对同旁内角,∴共有同旁内角12×2=24对.故答案为:24.【点评】本题考查了同旁内角的定义.注意在截线的同旁找同旁内角.要结合图形,熟记同旁内角的位置特点.两条直线被第三条直线所截所形成的八个角中,有两对同旁内角.ﻬ18.如图,已知l1∥l2,AB⊥l1,∠ABC=130°,则∠α=40°.【考点】平行线的性质.【专题】计算题.【分析】过点B作EF∥l1∥l2,再根据平行线的性质不难求得∠α的度数.【解答】解:过点B作EF∥l1∥l2∵EF∥l1∥l2,AB⊥l1∴∠ABF=90°∵∠ABC=130°∴∠FBC=40°∵EF∥l1∥l2∴∠FBC=∠α=40°故答案为:40°【点评】此题主要考查平行线的性质定理:定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.19.如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是40°.【考点】平行线的性质;三角形的外角性质;多边形内角与外角.【专题】计算题.【分析】作辅助线:延长PM、EG交于点K;PM延长线交AB于点L.利用平行线性质进行求解.【解答】解:辅助线延长PM、EG交于点K,PM延长线交AB于点L.如图:∵AB∥CD,∴∠ALM=∠LND=50°;∴∠MKG=∠BFG+∠ALM=80°.∵∠HMN=30°,∴∠HMK=150°;∵∠FGH=90°,∴∠GHM=360°﹣∠HMK﹣∠MKG﹣∠MGH=360°﹣150°﹣80°﹣90°=40°.【点评】考查了平行线的性质的应用.本题综合性较强.20.如图,D、G是△ABC中AB边上的任意两点,DE∥BC,GH∥DC,则图中相等的角共有( )A.4对B.5对 C.6对D.7对【考点】平行线的性质.【分析】可利用平行线内错角相等,同位角相等的性质得出图中相等的角.【解答】解:由DE∥BC,可得∠ADE=∠ABC,∠AED=∠ACB,∠EDC=∠DCB,由GH∥DC,可得∠BDC=∠BGH,∠HGD=∠ADC,∠DCB=∠GHB,∵∠EDC=∠DCB,∠DCB=∠GHB,∴∠EDC=∠BHG,∴题中共有7对相等的角.故选D.【点评】本题主要考查平行线的性质,即同位角相等,内错角相等,所以熟练掌握平行线的性质.21.如图,若AB∥CD,则( )A.∠1=∠2+∠3 B.∠1=∠3﹣∠2C.∠1+∠2+∠3=180°ﻩD.∠l﹣∠2+∠3=180°【考点】平行线的性质.【分析】先根据平行线的性质由AB∥CD得到∠3=∠4,再根据三角形外角性质得∠1=∠2+∠4,等量代换后得到∠1=∠2+∠3.【解答】解:延长BA交EC于F,如图,∵AB∥CD,∴∠3=∠4,∵∠1=∠2+∠4,∴∠1=∠2+∠3.故选A.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形外角性质.22.如图:已知AB∥CD∥EF,EH⊥CD于H,则∠BAC+∠ACE+∠CEH等于()A.180°ﻩB.270°C.360°D.450°【考点】平行线的性质.【专题】计算题.【分析】根据平行线的性质可以求得:∠BAC与∠ACD,∠DCE与∠CEF的度数的和,再减去∠HEF的度数即可.【解答】解:∵AB∥CD,∴∠BAC+∠ACD=180°,同理∠DCE+∠CEF=180°,∴∠BAC+∠ACE+∠CEF=360°;又∵EH⊥CD于H,∴∠HEF=90°,∴∠BAC+∠ACE+∠CEH=∠BAC+∠ACE+∠CEF﹣∠HEF=360°﹣90°=270°.故选B.【点评】本题主要考查了平行线的性质:两直线平行同旁内角互补.23.如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )A.β=α+γﻩB.α+β+γ=180° C.α+β﹣γ=90°ﻩ D.β+γ﹣α=180°【考点】平行线的性质.【分析】此题可以构造辅助线,利用三角形的外角的性质以及平行线的性质建立角之间的关系.【解答】解:延长DC交AB与G,延长CD交EF于H.在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,∵AB∥EF,∴∠1=∠2,∴90°﹣α=β﹣γ,即α+β﹣γ=90°.故选:C.【点评】本题考查的是平行线的性质,根据题意作出辅助线是解答此题的关键.24.如图,已知AB∥CD,P为HD上任意一点,过P点的直线交HF于O点,试问:∠HOP、∠AGF、∠HPO有怎样的关系?用式子表示并证明.【考点】平行线的性质;三角形的外角性质.【分析】可过点O作OM∥CD,利用内错角相等,再通过转化即可得出结论.【解答】解:∠HOP=∠AGF﹣∠HPO,过点O作OM∥CD,如图,则∠AGF=∠HOM,∠HPO=∠POM,∠HOP=∠HOM﹣∠POM,∴∠HOP=∠AGF﹣∠HPO.【点评】本题主要考查平行线的性质,能够熟练运用平行线的性质求解角之间的关系问题.25.如图,AB∥ED,α=∠A+∠E,β=∠B+∠C+∠D.证明:β=2α【考点】平行线的判定与性质;多边形内角与外角.【专题】证明题.【分析】此题的关键是过点C作AB的平行线,再利用平行线的性质和判定,得出∠A+∠E=180°,∠B+∠C+∠D=360°,即可证明.【解答】证法1:∵AB∥ED,∴α=∠A+∠E=180°(两直线平行,同旁内角互补)过C作CF∥AB(如图1)∵AB∥ED,∴CF∥ED(平行于同一条直线的两条直线平行)∵CF∥AB,∴∠B=∠1,(两直线平行,内错角相等)又∵CF∥ED,∴∠2=∠D,(两直线平行,内错角相等)∴β=∠B+∠C+∠D=∠1+∠BCD+∠2=360°(周角定义)∴β=2α(等量代换)证法2:∵AB∥ED,∴α=∠A+∠E=180°(两直线平行,同旁内角互补)过C作CF∥AB(如图2)∵AB∥ED,∴CF∥ED(平行于同一条直线的两条直线平行)∵CF∥AB,∴∠B+∠1=180°,(两直线平行,同旁内角互补)又∵CF∥ED,∴∠2+∠D=180°,(两直线平行,同旁内角互补)∴β=∠B+∠C+∠D=∠B+∠1+∠2+∠D=180°+180°=360°,∴β=2α(等量代换)【点评】此题考查平行线的判定和性质,辅助线的作法很关键,也是常见作法,需掌握.26.平面上有7条不同的直线,如果其中任何三条直线都不共点.(1)请画出满足上述条件的一个图形,并数出图形中各直线之间的交点个数;(2)请再画出各直线之间的交点个数不同的图形(至少两个);(3)你能否画出各直线之间的交点个数为n的图形,其中n分别为6,21,15?(4)请尽可能多地画出各直线之间的交点个数不同的图形,从中你能发现什么规律?【考点】平行线;相交线.【专题】规律型.【分析】从平行线的角度考虑,先考虑六条直线都平行,再考虑五条、四条,三条,二条直线平行,都不平行作出草图即可看出.ﻬ从画出的图形中归纳规律即可得到答案.【解答】解:(1)如图1所示;交点共有6个,(2)如图2,3.(3)当n=6时,必须有6条直线平行,都与一条直线相交.如图4,当n=21时,必须使7条直线中的每2条直线都相交(即无任何两条直线平行)如图5,当n=15时,如图6,(4)当我们给出较多答案时,从较多的图形中,可以总结出以下规律:①当7条直线都相互平行时,交点个数是0,这是交点最少,②当7条直线每两条均相交时,交点个数为21,这是交点最多.ﻬ【点评】此题主要考查了平行线与相交线,关键是根据一定的规律画出图形,再再根据图形归纳规律.27.如图,直线CB∥OA,∠C=∠BAO=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.【考点】平行线的性质;三角形内角和定理;角平分线的性质;平移的性质.【专题】几何图形问题.【分析】(1)根据两直线平行,同旁内角互补求出∠AOC,再根据角平分线的定义求出∠EOB=∠AOC,代入数据即可得解;(2)根据两直线平行,内错角相等可得∠OBC=∠BOA,从而得到∠OBC=∠FOB,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OFC=2∠OBC,从而得解;(3)设∠AOB=x,根据两直线平行,内错角相等表示出∠CBO=∠AOB=x,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC,然后利用三角形的内角和等于180°列式表示出∠OBA,然后列出方程求解即可.【解答】解:(1)∵CB∥OA,∴∠AOC=180°﹣∠C=180°﹣120°=60°,∵∠FOB=∠AOB,OE平分∠COF,∴∠EOB=∠AOC=×60°=30°;(2)∠OBC:∠OFC的值不会发生变化,为1:2,ﻬ∵CB∥OA,∴∠OBC=∠BOA,∵∠FOB=∠AOB,∴∠OBC=∠FOB,∴∠OFC=∠OBC+∠FOB=2∠OBC,∴∠OBC:∠OFC=1:2;(3)当平行移动AB至∠OBA=45°时,∠OEC=∠OBA.设∠AOB=x,∵CB∥AO,∴∠CBO=∠AOB=x,∵∠OEC=∠CBO+∠EOB=x+30°,∠OBA=180°﹣∠A﹣∠AOB=180°﹣120°﹣x=60°﹣x,∴x+30°=60°﹣x,∴x=15°,∴∠OEC=∠OBA=60°﹣15°=45°.【点评】本题考查了平行线的性质,平移的性质,角平分线的定义,三角形的内角和定理,图形较为复杂,熟记性质并准确识图是解题的关键.。
2018 初三中考数学复习 平行线的证明 专题复习练习 含答案

2018 初三中考数学复习平行线的证明专题复习练习1. 下列说法正确的是( D )A.经验、观察或试验完全可以判断一个数学结论的正确与否B.推理是科学家的事,与我们没有多大的关系C.对于自然数n,n2+n+37一定是质数D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个2. “两条平行直线被第三条直线所截,同位角相等”这句话是( C )A.定义 B.假命题 C.公理 D.定理3. 下列语句中,是命题的是( C )A.直线AB和CD垂直吗B.过线段AB的中点C画AB的垂线C.同旁内角不互补,两直线不平行D.连接A,B两点4.如图,AB∥CD,CB⊥DB,∠D=65°,则∠ABC的大小是( A ) A.25°B.35°C.50°D.65°5.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于( B )A.90°B.100°C.130°D.180°6.如图,已知△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( A )A .∠DCE>∠ADB B .∠ADB>∠DBCC .∠ADB>∠ACBD .∠ADB>∠DEC7.如图,AB ∥CD ,直线EF 交AB 于点E ,交CD 于点F ,EG 平分∠BEF ,交CD 于点G ,∠1=50°,则∠2等于( C )A .50°B .60°C .65°D .90°8.如图,已知直线AB ∥CD ,BE 平分∠ABC ,且BE 交CD 于点D ,∠CDE =150°,则∠C 的度数为( C )A .150°B .130°C .120°D .100°9.如图,直线a ∥b ,∠A =38°,∠1=46°,则∠ACB 的度数是( C )A .84°B .106°C .96°D .104°10.适合条件∠A =12∠B =13∠C 的三角形ABC 是( B )A .锐角三角形 B. 直角三角形 C .钝角三角形 D .都有可能11.如图,在折纸活动中,小明制作了一张△ABC 纸片,点D ,E 分别在边AB ,AC 上,将△ABC 沿着DE 折叠压平,A 与A ′重合.若∠A =75°,则∠1+∠2等于( A )A.150° B. 210°C.105°D.75°12.已知直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( B )A.30° B. 35°C.40°D.45°13.如图,DAE是一条直线,DE∥BC,则x=__64°__.14.如图,已知AB∥CD,∠DEF=50°,∠D=80°,∠B的度数是__50°__.15.如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=__70°__,∠CED=__110°__.16.已知如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠DAC =100°,则∠BAC=__120°__.17.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为__22°__.18.已知等腰三角形的一腰上的高与另一腰的夹角为40°,则这个等腰三角形的顶角为__50°或130°__.19.如图所示,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A=__10__度.20.如图,∠C=∠1,∠2和∠D互余,BE⊥FD,求证:AB∥CD.解:∵∠C=∠1,∴CF∥BE,又BE⊥FD,∴CF⊥FD,∴∠CFD=90°,则∠2+∠BFD=90°,又∠2+∠D=90°,∴∠D=∠BFD,则AB∥CD21.一天,爸爸带着小刚到建筑工地去玩,看见有如图所示的人字架,爸爸说:“小刚,我考考你,这个人字架的夹角∠1等于130°,你能求出∠3比∠2大多少吗?”小刚马上得到了正确答案,他的答案是多少?请说明理由.解:50°,因为∠1=130°,所以与∠1相邻的内角为50°,所以∠3-∠2=50°22.如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.解:∵BE∥DF,∴∠ABE=∠D,又AB=FD,∠A=∠F,∴△ABE≌△FDC(ASA),∴AE=FC23.如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,又∠BDC=∠BCD,且∠1=∠2,求∠3的度数.解:由∠BAC=90°,∠ABC=∠ACB易求∠ACB=45°,设∠1=x,可得∠BCD=∠2+45°=x+45°=∠3,∴x+(x+45°)+(x+45°)=180°,x=30,则∠3=x+45°=75°24.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.解:∵∠A+∠B+∠C=180°,∴∠B+∠C=110°,∵∠B=∠DEB,∠C=∠DFC ,∴∠B +∠DEB +∠C +∠DFC =220°,∵∠B +∠DEB +∠C +∠DFC +∠EDB +∠FDC =360°,∴∠EDB +∠FDC =140°,即∠EDF =180°-140°=40°25.如图,已知∠1+∠2=180°,∠3=∠B ,试判断∠AED 与∠C 的大小关系,并对结论进行证明.解:∠AED =∠C.∵∠1+∠2=180°,∠1+∠EFD =180°,∴∠2=∠EFD ,∴AB ∥EF ,∴∠3=∠ADE ,又∵∠3=∠B ,∴∠ADE =∠B ,∴DE ∥BC ,∴∠AED =∠C26.【问题】如图①,在△ABC 中,BE 平分∠ABC ,CE 平分∠ACB ,若∠A =80°,则∠BEC =__130°__;若∠A =n °,则∠BEC =__90°+12n °__.【探究】(1)如图②,在△ABC 中,BD ,BE 三等分∠ABC ,CD ,CE 三等分∠ACB.若∠A =n °,则∠BEC =__60°+23n °__;(2)如图③,O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点,试分析∠BOC和∠A 有怎样的关系?请说明理由;(3)如图④,O 是外角∠DBC 与外角∠BCE 的平分线BO 和CO 的交点,则∠BOC 与∠A 有怎样的关系?(只写结论,不需证明)解:(2)∠BOC =12∠A.理由:∠BOC =∠2-∠1=12∠ACD -12∠ABC =12(∠ACD-∠ABC)=12∠A(3)∠BOC =90°-12∠A。
九年级中考数学平行四边形专题复习(含答案)

九年级中考数学平行四边形专题复习一、选择题:1.已知四边形ABCD是平行四边形,再从①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ) A.选①② B.选②③ C.选①③ D.选②④2.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )A.△EBD是等腰三角形,EB=ED B.折叠后∠ABE和∠CBD一定相等C.折叠后得到的图形是轴对称图形 D.△EBA和△EDC一定是全等三角形3.有下列说法:①由许多条线段连接而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;④半圆是扇形.其中正确的结论有( )A.1个 B.2个 C.3个 D.4个4.如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )95°D D.85°105°C C.95°A.115°115°B B.105°5.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )A.1.8B.2.4C.3.2D.3.66.现有纸片:4张边长为a的正方形,3张边长为b的正方形,8张宽为a、长为b的长方形,用这15张纸片重新拼出一个长方形,那么该长方形的长为( )A.2a+3b B.2a+b C.a+3b D.无法确定7.如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形 ENCM 的面积之比为( )A.9:4 B.12:5 C.3:1 D.5:28.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )A. B.2 C. +1 D.2+19.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )A.1 B.2 C.3 D.410.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )A.6cm2 B.8cm2 C.10cm2 D.12cm2二、填空题:11.如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形______.12.如图,在▱ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD度数为 .13.如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG 木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为______m.14.如图,正方形ABCD的长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是 cm2.15.在中,,其面积为,则的最大值是.16.已知平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+0.5m-0.25=0的两个实数根.当m= 时,四边形ABCD是菱形.三、解答题:17.如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求平行四边形ABCD的周长.18.如图,已知在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.19.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上, 顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;(2)求这个正方形的边长与面积.20.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的九分之一?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.21.下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为 ;(2)在图中画出两条裁剪线,并画出将此六边形剪拼成的正方形.22.如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.探究:当点E在边AB上,求证:EF=AE+CF.应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是 .(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是 .参考答案1.B2.B3.B4.C5.D6.A7.D8.B9.C10.A11.答案为:△AFE(答案不唯一).12.答案为:120°.13.答案为:.14.答案为:32.15.答案为:16.答案为:1.17.解:在平行四边形ABCD中,∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABE=∠EBC,∠BCE=∠ECD.,∴∠EBC+∠BCE=90°,∴∠BEC=90°, ∴BC22=BE22+CE22=1222+522=1322∴BC=13cm,∵AD∥BC,∴∠AEB=∠EBC,∴∠AEB=∠ABE,∴AB=AE,同理CD=ED,∵AB=CD,∴AB=AE=CD=ED=0.5BC=6.5cm,∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm18.提示:取BE的中点P,证明四边形EFPC是平行四边形.19.(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.(2)解:如图设AD与EH交于点M.∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴=,∴=,∴x=,∴正方形EFGH的边长为cm,面积为cm2.20.21.答案为:(1);(2)如图:22.探究:证明:如图,延长BA到G,使AG=CF,连接DG,∵四边形ABCD 是正方形,∴DA=DC ,∠DAG=∠DCF=90°, ∴△DAG ≌△DCF (SAS ),∴∠1=∠3,DG=DF ,∵∠ADC=90°,∠EDF=45°,∴∠EDG=∠1+∠2=∠3+∠2=45°2=45°==∠EDF , ∵DE=DE ,∴△GDE ≌△FDE (SAS ),∴EF=EG=AE+AG=AE+CF ; 应用:解:(1)△BEF 的周长=BE+BF+EF ,由探究得:EF=AE+CF , ∴△BEF 的周长=BE+BF+AE+CF=AB+BC=2+2=4,故答案为:4; (2)当点E 不在边AB 上时,分两种情况:①点E 在BA 的延长线上时,如图2,EF=CF ﹣AE ,理由是:在CB 上取CG=AE ,连接DG , ∵∠DAE=∠DCG=90°,AD=DC ,∴△DAE ≌△DCG (SAS )∴DE=DG ,∠EDA=∠GDC ∵∠ADC=90°,∴∠EDG=90°∴∠EDF+∠FDG=90°,∵∠EDF=45°,∴∠FDG=90°﹣45°45°=45°=45°,∴∠EDF=∠FDG=45°, 在△EDF 和△GDF 中,∵,∴△EDF ≌△GDF (SAS ),∴EF=FG ,∴EF=CF ﹣CG=CF ﹣AE ;②当点E 在AB 的延长线上时,如图3,EF=AE ﹣CF ,理由是:把△DAE 绕点D 逆时针旋转90°至△DCG ,可使AD 与DC 重合,连接DG , 由旋转得:DE=DG ,∠EDG=90°,AE=CG ,∵∠EDF=45°,∴∠GDF=90°﹣45°45°=45°=45°,∴∠EDF=∠GDF , ∵DF=DF ,∴△EDF ≌△GDF ,∴EF=GF ,∴EF=CG ﹣CF=AE ﹣CF ;综上所述,当点E 不在边AB 上时,EF ,AE ,CF 三者的数量关系是:EF=CF ﹣AE 或EF=AE ﹣CF ;故答案为:EF=CF ﹣AE 或EF=AE ﹣CF .。
中考数学模拟题汇总《平行线的证明》专项练习(附答案解析)

中考数学模拟题汇总《平行线的证明》专项练习(附答案解析)一、综合题1.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.2.如图,在矩形ABCD中,E是BC边上的点,AE=BC ,DF⊥AE,垂足为F,连接DE。
(1)求证:AB=DF;(2)若CE=1,AF=3,求DF的长。
3.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D在同一直线上,且AB∥DE,连接AE.(1)求证:△ABC≌△DCE.(2)当BC=5,AC=12时,求AE的长.4.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是.(2)猜想论证当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.(3)拓展探究已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使SΔDCF=SΔFDE,请直接写出相应的BF的长.5.如图, ∠1+∠2=180° , ∠DEF=∠A , ∠BED=70° .(1)求证: EF//AB :(2)求∠ACB的度数.6.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.7.在△ABC中,点D在直线AB上,在直线BC上取一点E,连接AE,DE,使得 AE=DE,DE交AC于点G,过点D作DF∥AC,交直线BC于点F,∠EAC=∠DEF.(1)当点E在BC的延长线上,D为AB的中点时,如图1所示.①求证:∠EGC=∠AEC;②若DF=3,求BE的长度;(2)当点E在BC上,点D在AB的延长线上时,如图2所示,若CE=10,5EG=2DE,求AG的长度.8.如图1,在Rt△ABC中,∠C=90°,AC=BC=2√2,点D、E分别在边AC、AB上,AD=DE=12AB,连接DE .将△ADE绕点A顺时针方向旋转,记旋转角为θ .(1)(问题发现)①当θ=0°时,BECD =;②当θ=180°时,BECD=;(2)(拓展研究)试判断:当0°≤θ<360°时,BECD的大小有无变化?请仅就图2的情形给出证明;(3)(问题解决)在旋转过程中,求出BE的最大值.9.如图,已知AB是圆O的直径,F是圆O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.(1)求证:DE是⊙O的切线;(2)若DE=3,CE=2,的值;①求BCAEEG最小值.②若点G为AE上一点,求OG+ 1210.如图,已知在菱形ABCD中,AB=5,cosB=3,点E、F分别在边BC、CD上,AF的延长5∠BAD.线交BC的延长线于点G,且∠EAF=12(1)求证:AE2=EC⋅EG;(2)如果点F是边CD的中点,求S△ABE的值;(3)延长AE、DC交于点H,联结GH、AC,如果△AGH与△ABC相似,求线段BE的长.11.如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心的圆恰好经过A、B、C三点,⌢=CE⌢,连接OA、OF.⊙O交BD于E,交AD于F,且AE(1)求证:四边形ABCD是菱形;(2)若∠AOF=3∠FOE,求∠ABC的度数.,过点C作CD∥AB,点E在边AC上,AE=CD,联结12.在△ABC中,AB=AC=10,sin∠BAC= 35AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.(1)求证:∠ABE=∠CAD.(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.(3)若△DFG是直角三角形,求△CEF的面积.13.在ΔABC中,∠A=90°,AB=8cm,AC=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s 的速度向点C运动(点M不与A,B重合,点N不与A,C重合),设运动时间为xs .(1)求证:ΔAMN∽ΔABC;(2)当x为何值时,以MN为直径的⊙O与直线BC相切?(3)把ΔAMN沿直线MN折叠得到ΔMNP,若ΔMNP与梯形BCNM重叠部分的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?14.如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作CD∥AB,且CD=OB .连接AD,分别交OC,BC于点E,F,与⊙O交于点G,若∠ABC=45∘ .(1)求证:①△ABF∽△DCF;②CD是⊙O的切线.(2)求EF的值.FG15.小东在做九上课本123页习题:“1:√2也是一个很有趣的比.已知线段AB(如图1),用直尺和圆规作AB上的一点P,使AP:AB=1:√2.”小东的作法是:如图2,以AB为斜边作等腰直角三角形ABC,再以点A为圆心,AC长为半径作弧,交线段AB于点P,点P即为所求作的点.小东称点P为线段AB的“趣点”.(1)你赞同他的作法吗?请说明理由.(2)小东在此基础上进行了如下操作和探究:连结CP,点D为线段AC上的动点,点E在AB的上方,构造△DPE,使得△DPE∽△CPB.①如图3,当点D运动到点A时,求∠CPE的度数.②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.16.在等腰△ABC中,AB=BC,点D,E在射线BA上,BD=DE,过点E作EF//BC,交射线CA于点F.请解答下列问题:(1)当点E在线段AB上,CD是△ACB的角平分线时,如图①,求证:AE+BC=CF;(提示:延长CD,FE交于点M.)(2)当点E在线段BA的延长线上,CD是△ACB的角平分线时,如图②;当点E在线段BA的延长线上,CD是△ACB的外角平分线时,如图③,请直接写出线段AE,BC,CF之间的数量关系,不需要证明;(3)在(1)、(2)的条件下,若DE=2AE=6,则CF=.参考答案与解析1.【答案】(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,∴OE=OC,OC=OF,∴OE=OF(2)解:当O运动到AC中点时,四边形AECF是矩形,∵AO=CO,OE=OF,∴四边形AECF是平行四边形,∵∠ECA+∠ACF= 12∠BCD,∴∠ECF=90°,∴四边形AECF是矩形2.【答案】(1)证明:在矩形ABCD中∴BC=AD AD∥BC,∠B=∠C=90°∴∠DAF=∠AEB∵DF⊥AE,AE=BC,∴∠AFD=90°=∠B,AE=AD∴△ABE≌△DFA,∴AB=DF(2)解:由(1)可得△ABE≌△DFA,∴AF=BE=3,DF=AB=CD∴∠DFE=∠DCE∴△DFE≌△DCE,∴CE=EF=1,AE=4在Rt△ABE中,AB= √42−32 = √73.【答案】(1)证明:∵AB∥DE,∴∠BAC=∠D.在△ABC和△DCE中,{∠B=∠DCE∠BAC=∠DAC=DE∴△ABC≌△DCE(AAS)(2)解:由(1)可得△ABC≌△DCE,∴CE=BC=5,在Rt△ACE中,AE=√AC2+CE2=√122+52=13.4.【答案】(1)DE∥AC;S1=S2(2)解:如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,{∠ACN=∠DCM∠CMD=∠N=90°AC=CD,∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2(3)解:如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,所以BE=DF1,且BE、DF1上的高相等,此时S△DCF1=S△BDE;过点D作DF2⊥BD,∵∠ABC=60°,F1D∥BE,∴∠F2F1D=∠ABC=60°,∵BF1=DF1,∠F1BD= 12∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°,∴△DF1F2是等边三角形,∴DF1=DF2,∵BD=CD,∠ABC=60°,点D是角平分线上一点,∴∠DBC=∠DCB= 12×60°=30°,∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,∠CDF2=360°﹣150°﹣60°=150°,∴∠CDF1=∠CDF2,∵在△CDF1和△CDF2中,{DF1=DF2∠CDF1=∠CDF2CD=CD,∴△CDF1≌△CDF2(SAS),∴点F2也是所求的点,∵∠ABC=60°,点D是角平分线上一点,DE∥AB,∴∠DBC=∠BDE=∠ABD= 12×60°=30°,又∵BD=4,∴BE= 12×4÷cos30°=2÷√32= 4√33,∴BF1= 4√33,BF2=BF1+F1F2= 4√33+ 4√33= 8√33,故BF的长为4√33或8√33.5.【答案】(1)解:∵∠1+∠DFE=180°,∴∠1+∠2=180°.∴∠DFE=∠2,∴EF//AB;(2)解:∵EF//AB , ∴∠DEF=∠BDE. 又∵∠DEF=∠A , ∴∠BDE=∠A , ∴DE//AC , ∴∠ACB=∠DEB. 又∵∠DEB=70°, ∴∠ACB=70°.6.【答案】(1)解:连接OF ;根据切线长定理得:BE=BF ,CF=CG ,∠OBF=∠OBE ,∠OCF=∠OCG ; ∵AB ∥CD ,∴∠ABC+∠BCD=180°, ∴∠OBE+∠OCF=90°, ∴∠BOC=90°(2)解:由(1)知,∠BOC=90°.∵OB=6cm ,OC=8cm ,∴由勾股定理得到:BC= √OB 2+OC 2 =10cm ,∴BE+CG=BC=10cm(3)解:∵OF ⊥BC ,∴∠BFO=∠OFC=90°∵∠BOC=90°∴∠BOF+∠COF=90°,∠COF+∠FCO=90°。
中考数学一轮复习平行四边形(讲义及答案)含答案

中考数学一轮复习平行四边形(讲义及答案)含答案一、解答题1.如图, 平行四边形ABCD 中,3AB cm =,5BC cm =,60B ∠=, G 是CD 的中点,E 是边AD 上的动点,EG 的延长线与BC 的延长线交于点F ,连接CE ,DF . (1) 求证:四边形CEDF 是平行四边形;(2) ①当AE 的长为多少时, 四边形CEDF 是矩形;②当AE = cm 时, 四边形CEDF 是菱形, (直接写出答案, 不需要说明理由).2.已知:如图,在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过点A 作BC 的平行线交于BE 的延长线于点F ,且AF=DC ,连接CF .(1)求证:D 是BC 的中点;(2)如果AB=AC ,试判断四边形ADCF 的形状,并证明你的结论.3.如图所示,四边形ABCD 是正方形, M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A B 、重合),另一直角边与CBM ∠的平分线BF 相交于点F .(1)求证: ADE FEM ∠=∠;(2)如图(1),当点E 在AB 边的中点位置时,猜想DE 与EF 的数量关系,并证明你的猜想;(3)如图(2),当点E 在AB 边(除两端点)上的任意位置时,猜想此时DE 与EF 有怎样的数量关系,并证明你的猜想.4.我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.(发现与证明..)ABCD 中,AB BC ≠,将ABC ∆沿AC 翻折至'AB C ∆,连结'B D . 结论1:'AB C ∆与ABCD 重叠部分的图形是等腰三角形;结论2:'B D AC .试证明以上结论.(应用与探究)在ABCD 中,已知2BC =,45B ∠=,将ABC ∆沿AC 翻折至'AB C ∆,连结'B D .若以A 、C 、D 、'B 为顶点的四边形是正方形,求AC 的长.(要求画出图形)5.直线1234,,,,l l l l 是同一平面内的一组平行线.(1)如图1.正方形ABCD 的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点A ,点C 分别在直线1l 和4l 上,求正方形的面积;(2)如图2,正方形ABCD 的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为123h h h ,,.①求证:13h h =;②设正方形ABCD 的面积为S ,求证222211 2 2 S h h h h =++.6.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.7.如图,ABC ADC ∆≅∆,90,ABC ADC AB BC ︒∠=∠==,点F 在边AB 上,点E 在边AD 的延长线上,且,DE BF BG CF =⊥,垂足为H ,BH 的延长线交AC 于点G .(1)若10AB =,求四边形AECF 的面积;(2)若CG CB =,求证:2BG FH CE +=.8.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD ,(1)如图1,求证:△AMC ≌△AND ;(2)如图1,若3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AG AF 是否为定值,若是定值,则求出该值;若不是,请说明理由.9.如图,已知正方形ABCD与正方形CEFG如图放置,连接AG,AE.(1)求证:AG AE=(2)过点F作FP AE⊥于P,交AB、AD于M、N,交AE、AG于P、Q,交BC于H,.求证:NH=FM10.在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF,GH分别交边AB、CD,AD、BC于点E、F、G、H.(1)观察发现:如图①,若四边形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG,又因为S△AOB=14S四边形ABCD,所以S四边形AEOG=S正方形ABCD;(2)类比探究:如图②,若四边形ABCD是矩形,且S四边形AEOG=14S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);(3)拓展迁移:如图③,若四边形ABCD是平行四边形,且S四边形AEOG=14S▱ABCD,若AB=3,AD=5,BE=1,则AG=.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)证明见解析;(2)①当AE=3.5时,平行四边形CEDF 是矩形;②2【分析】(1)证明△FCG ≌△EDG (ASA ),得到FG=EG 即可得到结论;(2)①当AE=3.5时,平行四边形CEDF 是矩形.过A 作AM ⊥BC 于M ,求出BM=1.5,根据平行四边形的性质得到∠CDA=∠B=60°,DC=AB=3,BC=AD=5,求出DE=1.5=BM ,证明△MBA ≌△EDC(SAS),得到∠CED=∠AMB=90°,推出四边形CEDF 是矩形;②根据四边形CEDFCEDF 是菱形,得到CD ⊥EF ,DG=CG=1212CD=1.5,求出∠DEG=30°,得到DE=2DG=3,即可求出AE=AD-DE=5-3=2.【详解】(1)证明:∵ 四边形ABCD 是平行四边形,∴ CF ∥ED ,∴ ∠FCG =∠EDG ,∵ G 是CD 的中点,∴ CG =DG ,在△FCG 和△EDG 中,FCG EDG CG DG CGF DGE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ △FCG ≌△EDG (ASA ),∴ FG =EG ,∵ CG =DG ,∴ 四边形CEDF 是平行四边形;(2)解:①当AE=3.5时,平行四边形CEDF 是矩形,理由是:过A 作AM ⊥BC 于M ,∵∠B=60°,∴∠BAM=30°,∵AB=3,∴BM=1.5,∵四边形ABCD 是平行四边形,∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,∵AE=3.5,∴DE=1.5=BM ,在△MBA 和△EDC 中,BM DE B CDE AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△MBA ≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF 是平行四边形,∴四边形CEDF 是矩形;②∵四边形CEDFCEDF 是菱形,∴CD ⊥EF ,DG=CG=1212CD=1.5,∵∠CDE=∠B=60∘∠B=60∘,∴∠DEG=30°,∴DE=2DG=3,∴AE=AD-DE=5-3=2,故答案为:2.【点睛】此题考查了平行四边形的性质,矩形的判定定理,菱形的性质定理,直角三角形30度角所对的直角边等于斜边的一半,三角形全等的判定及性质定理,熟练掌握各定理并运用解答问题是解题的关键.2.(1)见详解;(2)四边形ADCF 是矩形;证明见详解.【分析】(1)可证△AFE ≌△DBE ,得出AF=BD ,进而根据AF=DC ,得出D 是BC 中点的结论; (2)若AB=AC ,则△ABC 是等腰三角形,根据等腰三角形三线合一的性质知AD ⊥BC ;而AF 与DC 平行且相等,故四边形ADCF 是平行四边形,又AD ⊥BC ,则四边形ADCF 是矩形.【详解】(1)证明:∵E 是AD 的中点,∴AE=DE .∵AF ∥BC ,∴∠FAE=∠BDE ,∠AFE=∠DBE .在△AFE 和△DBE 中,FAE BDE AFE DBE AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△DBE (AAS ).∴AF=BD .∵AF=DC ,∴BD=DC .即:D 是BC 的中点.(2)解:四边形ADCF 是矩形;证明:∵AF=DC ,AF ∥DC ,∴四边形ADCF 是平行四边形.∵AB=AC ,BD=DC ,∴AD ⊥BC 即∠ADC=90°.∴平行四边形ADCF 是矩形.【点睛】此题主要考查了全等三角形的判定和性质,等腰三角形的性质,平行四边形、矩形的判定等知识综合运用.解题的关键是熟练掌握矩形的判定方法,以及全等三角形的判定和性质进行证明.3.(1)详见解析;(2)DE EF =,理由详见解析;(3)DE EF =,理由详见解析【分析】(1)根据90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,等量代换即可证明;(2)DE=EF ,连接NE ,在DA 边上截取DN=EB ,证出△DNE ≌△EBF 即可得出答案;(3)在DA 边上截取DN EB =,连接NE ,证出()DNE EBF ASA ≌即可得出答案.【详解】(1)证明:∵90DAB DEF ∠=∠=︒,∴90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,∴ADE FEM ∠=∠;(2) ;DE EF =理由如下:如图,取AD 的中点N ,连接NE ,∵四边形ABCD 为正方形,∴AD AB = ,∵,N E 分别为,AD AB 中点 ∴11,22AN DN AD AE EB AB ====, ∴,DN BE AN AE == 又∵90A ∠=︒∴45ANE ∠=︒∴180135DNE ANE ∠=︒-∠=︒,又∵90CBM ∠=︒,BF 平分CBM ∠∴45,135CBF EBF ∠=︒∠=︒.∴DNE EBF ∠=∠在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩()DNE EBF ASA ≌,∴DE EF =(3) DE EF =.理由如下:如图,在DA 边上截取DN EB =,连接NE ,∵四边形ABCD 是正方形, DN EB =,∴AN AE =,∴AEN △为等腰直角三角形,∵45ANE ∠=︒∴18045135DNE ∠=︒-︒=︒,∵BF 平分CBM ∠, AN AE =,∴9045135EBF ∠=︒+︒=︒,∴DNE EBF ∠=∠,在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DNE EBF ASA ≌,∴DE EF =.【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE ≌△EBF .4.【发现与证明..】结论1:见解析,结论2:见解析;【应用与探究】AC 2或2. 【分析】【发现与证明..】由平行四边形的性质得出∠EAC=∠ACB ,由翻折的性质得出∠ACB=∠ACB ′,证出∠EAC=∠ACB ′,得出AE=CE ;得出DE=B ′E ,证出∠CB′D=∠B′DA=12(180°-∠B′ED),由∠AEC=∠B′ED,得出∠ACB′=∠CB′D,即可得出B′D∥AC;【应用与探究】:分两种情况:①由正方形的性质得出∠CAB′=90°,得出∠BAC=90°,再由三角函数即可求出AC;②由正方形的性质和已知条件得出AC=BC=2.【详解】【发现与证明..】:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠EAC=∠ACB,∵△ABC≌△AB′C,∴∠ACB=∠ACB′,BC=B′C,∴∠EAC=∠ACB′,∴AE=CE,即△ACE是等腰三角形;∴DE=B′E,∴∠CB′D=∠B′DA=12(180°−∠B′ED),∵∠AEC=∠B′ED,∴∠ACB′=∠CB′D,∴B′D∥AC;【应用与探究】:分两种情况:①如图1所示:∵四边形ACDB′是正方形,∴∠CAB′=90°,∴∠BAC=90°,∵∠B=45°,∴AC=222BC ;②如图2所示:AC=BC=2;综上所述:AC2或2.【点睛】本题考查平行四边形的性质, 正方形的性质, 翻折变换(折叠问题).【发现与证明..】对于结论1,要证明三角形是等腰三角形,只需要证明它的两条边相等,而在同一个三角形内要证明两条线段相等只需要证明它们所对应的角相等(即用等角对等边证明).结论2:要证明两条线段平行,本题用到了内错角相等,两直线平行.所以解决【发现与证明..】的关键是根据已知条件找到对应角之间的关系. 【应用与探究】折叠时,因为正方形的四个角都是直角,所以对应线段之间存在共线情况,所以分BA 和AB’共线和BC 和B’C 两种情况讨论,能根据题意画出两种情况对应的图形,是解题关键.5.(1)9或5;(2)①见解析,②见解析【分析】(1)分两种情况:①如图1-1,得出正方形ABCD 的边长为3,求出正方形ABCD 的面积为9;②如图1-2,过点B 作EF ⊥l 1于E ,交l 4于F ,则EF ⊥l 4,证明△ABE ≌△BCF (AAS ),得出AE=BF=2由勾股定理求出AB=225AE BE +=,即可得出答案;(2)①过点B 作EF ⊥l 1于E ,交l 4于F ,作DM ⊥l 4于M ,证明△ABE ≌△BCF (AAS ),得出AE=BF ,同理△CDM ≌△BCF (AAS ),得出△ABE ≌△CDM (AAS ),得出BE=DM 即可; ②由①得出AE=BF=h 2+h 3=h 2+h 1,得出正方形ABCD 的面积S=AB 2=AE 2+BE 2,即可得到答案.【详解】解:(1)①如图,当点B D ,分别在14,l l 上时,面积为:339⨯=;②如图,当点B D ,分别在23,l l 上时,过点B 作EF ⊥l 1于E ,交l 4于F ,则EF ⊥l 4,∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∴∠ABE+∠CBF=180°-90°=90°,∵∠CBF+∠BCF=90°,∴∠ABE=∠BCF ,在△ABE 和△BCF 中90ABE BCF AEB BFC AB BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABE ≌△BCF (AAS ),∴AE=BF=2,∴AB=2222215AE BE +=+=,∴正方形ABCD 的面积=AB 2=5;综上所述,正方形ABCD 的面积为9或5;(2)①证明:过点B 作EF ⊥l 1于E ,交l 4于F ,作DM ⊥l 4于M ,如图所示:则EF ⊥l 4,∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∴∠ABE+∠CBF=180°-90°=90°,∵∠CBF+∠BCF=90°,∴∠ABE=∠BCF ,在△ABE 和△BCF 中,90ABE BCF AEB BFC AB BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABE ≌△BCF (AAS ),∴AE=BF ,同理△CDM ≌△BCF (AAS ),∴△ABE ≌△CDM (AAS ),∴BE=DM ,即h 1=h 3.②解:由①得:AE=BF=h 2+h 3=h 2+h 1,∵正方形ABCD 的面积:S=AB 2=AE 2+BE 2,∴S=(h 2+h 1)2+h 12=2h 12+2h 1h 2+h 22.【点睛】本题考查了正方形的性质、全等三角形的判定和性质、勾股定理等知识;熟练掌握正方形的性质,证明三角形全等是解题的关键.6.(1)15,8;(2)PE PF CG +=,见解析;(3)534)4【分析】解决问题(1)只需运用面积法:ABC ABP ACP S S S ∆∆∆=+,即可解决问题;(2)解法同(1);(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,由等边三角形的性质得出152BM BC ==,由勾股定理得出2253AM AB BM =-=,得出ABC ∆的面积12532BC AM =⨯=,由ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2532222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++=,即可得出答案; (4)过点E 作EQ BC ⊥,垂足为Q ,易证BE BF =,过点E 作EQ BF ⊥,垂足为Q ,由解决问题(1)可得PG PH EQ +=,易证EQ DC =,BF DF =,只需求出BF 即可.【详解】解:(1)∵PE AB ⊥,10AB =,3PE =,∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=, ∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴358CG PE PF =+=+=.故答案为:15,8.(2)∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴CG PE PF =+.(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,如图2所示:∵10AB AC BC ===,∴ABC ∆是等边三角形,∵AM BC ⊥,∴152BM BC ==, ∴222210553AM AB BM =-=-=,∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯=, ∵PE BC ⊥,PF AC ⊥,PG AB ⊥,∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=,∴22535310PE PF PG ⨯++==. (4)过点E 作EQ BC ⊥,垂足为Q ,如图3所示:∵四边形ABCD 是矩形,∴AD BC =,90C ADC ∠=∠=︒,∵8AD =,3CF =,∴5BF BC CF AD CF =-=-=,由折叠可得:5DF BF ==,BEF DEF ∠=∠,∵90C ∠=︒,∴2222534DC DF FC =-=-=,∵EQ BC ⊥,90C ADC ∠=∠=︒,∴90EQC C ADC ∠=︒=∠=∠,∴四边形EQCD 是矩形,∴4EQ DC ==,∵//AD BC ,∴DEF EFB ∠=∠,∵BEF DEF ∠=∠,∴BEF EFB ∠=∠,∴BE BF =,由解决问题(1)可得:PG PH EQ +=,∴4PG PH +=,即PG PH +的值为4.【点睛】本题是四边形综合题目,考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.7.(1)100;(2)见解析.【分析】(1)先证明四边形ABCD 是正方形,再根据已知条件证明△BCF ≌△DCE ,即可得到四边形AECF 的面积=正方形ABCD 的面积;(2) 延长BG 交AD 于点M ,作AN ⊥MN ,连接FG ,先证明四边形BCEM 是平行四边形,得到BM=CE ,证明△BCF ≌△GCF ,得到BF=GF ,∠FGC=∠FBC=90︒,由AN ⊥MN ,得GM=2MN ,根据∠BAC=45︒,BC ∥AD 得到AM=BF ,再证△BFH ≌△AMN,得到GM=2FH , 由此得到结论.【详解】(1)∵9,0ABC AB BC ︒∠==,∴△ABC 是等腰直角三角形,∵ABC ADC ∆≅∆,∴AB=AD=BC=DC ,∴四边形ABCD 是菱形,∵90ABC ADC ︒∠=∠=,∴四边形ABCD 是正方形,∴∠BCD=90ABC ADC ︒∠=∠=,∴∠CDE=90ABC ADC ︒∠=∠=,∵BF=DE,BC=DC ,∴△BCF ≌△DCE ,∴四边形AECF 的面积=S 正方形ABCD =AB 2=102=100.(2)延长BG 交AD 于点M ,作AN ⊥MN ,连接FG,∵△BCF ≌△DCE ,∴∠BCF=∠DCE ,∴∠FCE=∠BCD=90︒,∵BG ⊥CF ,∴∠FHM=∠FCE=90︒,∴BM ∥CE,∵BC ∥AD,∴四边形BCEM 是平行四边形,∴BM=CE.∵CG CB =,BG ⊥CF ,∴∠BCH=∠GCH,∠CBM=∠CGB,∴△BCF ≌△GCF,∴BF=GF,∠FGC=∠FBC=90︒,∵∠BAC=45︒,∴∠AFG=∠BAC=45︒,∴FG=AG,∵BC ∥AD,∴∠CBM=∠AMB,∴∠AGM=∠CGB=∠CBM=∠AMB,∴AM=AG,∵AN ⊥MN ,∴GM=2MN,∵∠BAD=∠ANM=90︒,∴∠ABM+∠AMN=∠MAN+∠AMN=90︒,∴∠ABM=∠MAN,∵AM=AG=FG=BF,∠BHF=∠ANM=90︒,∴△BFH ≌△AMN,∴FH=MN,∴GM=2FH,∵BG+GM=CE,∴2BG FH CE +=.【点睛】此题是四边形的综合题,考查正方形的判定及性质,全等三角形的判定及性质,等腰三角形的性质,平行四边形的性质,解题中注意综合思想的方法积累.8.(1)见解析;(2)AE =33)(3)122AG AF =,理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x 3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可.【详解】(1)证明:∵四边形AMFN 是正方形,∴AM=AN ∠AMC=∠N=90°∴△AMC,△AND 是Rt △∵△ABC 是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x则AE=2x 3x易得△GBE 是等腰直角三角形∴BG=EG 3x∴AB=BC=31)x易得∠DHF=30°∴HD=2DF=3,HF=3∴BF=BH+HF=233∵Rt △AMC ≌Rt △AND(HL)∴易得3∴BC=BF-CF=233333=+∴(31)33x =∴3x =∴AE =223x=(3)12AG AF =; 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,则GMB ∆≌11GFC ∆,∴111BM FC DF == 1BMG GFN ∠=, ∴BM ∥1F N ,∴MBA N ∠=∠∵0190NAO OF D ∠=∠= 1AON DOF ∠=∠∴1N ADF ∠=∠∴1ABM ADF ∠=∠,∵AB AD = ∴ABM ∆≌1ADF ∆(SAS )∴1AM AF = 1MAB DAF ∠=∠∴0190MAF BAD ∠=∠=∴1AMF ∆是等腰直角三角形∴1AG MF ⊥ 1AG GF =∴12AF∴122AG AF = 【点睛】本题考查正方形的性质、三角形全等、以及勾股定理等知识点,综合性强,难度较大,但解答的关键是正确做出辅助线.9.(1)证明见解析;(2)证明见解析.【分析】(1)根据正方形的性质证得BG=DE ,利用SAS 可证明ABG ≌ADE ,再利用全等的性质即可得到结论;(2)过M 作MK ⊥BC 于K ,延长EF 交AB 于T ,根据ASA 可证明MHK △≌AED ,得到AE=MH ,再利用AAS 证明TNF △≌DAE △,得到NF=AE ,从而证得MH=NF ,即可得到结论.【详解】证明:(1)∵四边形ABCD 与四边形CEFG 均为正方形,∴AB=AD=BC=CD ,CG=CE ,∠ABG=∠ADE=90°,∴BC -GC=CD -EC ,即BG=DE ,∴ABG ≌ADE ,∴AG=AE ;(2)过M 作MK ⊥BC 于K ,则四边形MKCD 为矩形,∴∠MKH=∠ADE=90°,MK=CD ,∠AMK=90°,∴MK=AD ,∠AMP+∠HMK=90°,又∵FP AE ,∴∠EAD+∠AMP=90°,∴∠HMK=∠EAD ,∴MHK △≌AED ,∴MH=AE ,延长EF 交AB 于T ,则四边形TBGF 为矩形,∴FT=BG ,∠FTN=∠ADE=90°,∵ABG ≌ADE ,∴DE=BG ,∴FT=DE ,∵FP ⊥AE ,∠DAB=90°,∴∠N+∠NAP=∠DAE+∠NAP=90°,∴∠N=∠DAE ,∴TNF △≌DAE △,∴FN=AE ,∴FN=MH ,∴FN-FH=MH-FH,∴NH=FM.【点睛】本题考查了正方形的性质,矩形的判定与性质,及全等三角形的判定与性质,熟练掌握各性质、判定定理是解题的关键.10.(1)14;(2)mbAGa;(3)53【分析】(1)如图①,根据正方形的性质和全等三角形的性质即可得到结论;(2)如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到14mb=14AG•a,于是得到结论;(3)如图③,同理:过O作QM⊥AB,PN⊥AD,先根据平行四边形面积可得OM和ON 的比,同理可得S△BOE=S△AOG,根据面积公式可计算AG的长.【详解】解:(1)如图①,∵四边形ABCD是正方形,∴OA=OC,∠OAG=∠EBO=45°,∠AOB=90°,∵EF⊥GH,∴∠EOG=90°,∴∠BOE=∠AOG(SAS),∴△BOE≌△AOG,∴S△BOE=S△AOG,又∵S△AOB=14S四边形ABCD,∴S四边形AEOG=14S正方形ABCD,故答案为:14.(2)解:如图②,过O作OM⊥AB于M,ON⊥AD于N,∴S△AOB=S△AOD=14S矩形ABCD,∵S四边形AEOG=14S矩形ABCD,∴S△AOB=S四边形AEOG,∴S△BOE=S△AOG,∵S△BOE=12BE•OM=14mb,S△AOG=12AG•ON=14AG•a,∴mb=AG•a,∴AG=mba;(3)如图③,过O作OM⊥AB于M,ON⊥AD于N,∵S△AOB=S△AOD=14S▱ABCD,S四边形AEOG=14S▱ABCD,∴S△AOB=S四边形AEOG,∴S△BOE=S△AOG,∵S△BOE=12BE•OM=12OM,S△AOG=12AG•ON,∴OM=AG•ON,∵S▱ABCD=3×2OM=5×2 ON,∴53 OMON,∴AG=53;【点睛】本题是四边形综合题,考查了正方形、矩形、平行四边形的性质及三角形、四边形的面积问题,认真阅读材料,理解并证明S△BOE=S△AOG是解决问题的关键.。
中考数学复习专题11平行线与三角形

平行线与三角形一、单选题1.(2021·山东临沂市)如图,在//AB CD 中,40AEC ∠=︒,CB 平分DCE ∠,则ABC ∠的度数为( )A .10︒B .20︒C .30D .40︒【答案】B 【分析】根据平行线的性质得到∠ABC =∠BCD ,再根据角平分线的定义得到∠ABC =∠BCD ,再利用三角形外角的性质计算即可.【详解】解:∵AB ∥CD ,∴∠ABC =∠BCD ,∵CB 平分∠DCE ,∴∠BCE =∠BCD ,∴∠BCE =∠ABC ,∵∠AEC =∠BCE +∠ABC =40°,∴∠ABC =20°,故选B .【点睛】本题考查了平行线的性质,角平分线的定义和外角的性质,掌握平行线的性质:两直线平行,内错角相等是解题的关键.2.(2021·四川眉山市)如图,将直角三角板放置在矩形纸片上,若148∠=︒,则2∠的度数为( )A .42°B .48°C .52°D .60°【答案】A 【分析】先通过作辅助线,将∠1转化到∠BAC ,再利用直角三角形两锐角互余即可求出∠2.【详解】解:如图,延长该直角三角形一边,与该矩形纸片一边的交点记为点A ,由矩形对边平行,可得∠1=∠BAC ,因为BC ⊥AB ,∴∠BAC +∠2=90°,∴∠1+∠2=90°,因为∠1=48°,∴∠2=42°;故选:A.【点睛】本题考查了矩形的性质、平行线的性质、直角三角形的性质等内容,要求学生能根据题意理解其中的隐含关系,解决本题的关键是对角进行的转化,因此需要牢记并能灵活应用相关性质等.3.(2021·四川乐山市)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为()A.3 B.72C.2 D.52【答案】A【分析】根据由边长为4的正方形分割制作的七巧板,可得共5种图形,然后根据阴影部分的构成图形,计算阴影部分面积即可.【详解】解:如下图所示,由边长为4的正方形分割制作的七巧板,共有以下几种图形:○1腰长是2的等腰直角三角形,的正方形,⑤边长分别是245和135的平行四边形,根据图2可知,图中抬起的“腿”的等腰直角三角形,和一个边长分别是2,顶角分别是45和135的平行四边形组成,如下图示,根据平行四边形的性质可知,顶角分别是45和135的平行四边形的高是DB,且DB=,的等腰直角三角形的面积是:112=,顶角分别是45和135的平行四边形的面积是:2=,∴阴影部分的面积为:123+=,故选:A.【点睛】本题考查了七巧板中的图形的构成和面积计算,熟悉七巧板中图形的分类是解题的关键.4.(2021·湖南岳阳市)下列命题是真命题的是()A.五边形的内角和是720︒B.三角形的任意两边之和大于第三边C.内错角相等D.三角形的重心是这个三角形的三条角平分线的交点【答案】B【分析】根据相关概念逐项分析即可.【详解】A 、五边形的内角和是540︒,故原命题为假命题,不符合题意;B 、三角形的任意两边之和大于第三边,原命题是真命题,符合题意;C 、两直线平行,内错角相等,故原命题为假命题,不符合题意;D 、三角形的重心是这个三角形的三条中线的交点,故原命题为假命题,不符合题意;故选:B .【点睛】本题考查命题判断,涉及多边形的内角和,三角形的三边关系,平行线的性质,以及三角形的重心等,熟记基本性质和定理是解题关键.5.(2021·安徽)两个直角三角板如图摆放,其中90BAC EDF ∠=∠=︒,45E ∠=︒,30C ∠=︒,AB 与DF 交于点M .若//BC EF ,则BMD ∠的大小为( )A .60︒B .67.5︒C .75︒D .82.5︒【答案】C【分析】根据//BC EF ,可得45FDB F ∠=∠=︒,再根据三角形内角和即可得出答案.【详解】由图可得6045B F ∠=︒∠=︒,,∵//BC EF ,∴45FDB F ∠=∠=︒, ∴180180456075BMD FDB B ∠=︒-∠-∠=︒-︒-︒=︒,故选:C .【点睛】本题考查了平行线的性质和三角形的内角和,掌握平行线的性质和三角形的内角和是解题的关键.6.(2021·浙江金华市)某同学的作业如下框,其中※处填的依据是( )A .两直线平行,内错角相等B .内错角相等,两直线平行C .两直线平行,同位角相等D .两直线平行,同旁内角互补【答案】C 【分析】首先准确分析题目,已知12//l l ,结论是34∠=∠,所以应用的是平行线的性质定理,从图中得知∠3和∠4是同位角关系,即可选出答案.【详解】解:∵12//l l ,∴34∠=∠(两直线平行,同位角相等).故选C .【点睛】本题主要考查了平行线的性质的应用,解题的关键是理解平行线之间内错角的位置,从而准确地选择出平行线的性质定理.7.(2021·云南)如图,直线c 与直线a 、b 都相交.若//a b ,155∠=︒,则2∠=( )A .60︒B .55︒C .50︒D .45︒【答案】B 【分析】直接利用平行线的性质:两直线平行,同位角相等,即可得出答案.【详解】解:如图,1=55∠︒, 3=55,∴∠︒ ∵a ∥b ,∠3=55°,∴∠2=∠3=55°.故选B .【点睛】此题主要考查了平行线的性质,正确掌握平行线的基本性质是解题关键.8.(2021·山东)如图,AB ∥CD ∥EF ,若∠ABC =130°,∠BCE =55°,则∠CEF 的度数为( )A .95°B .105°C .110°D .115°【答案】B 【分析】由//AB CD 平行的性质可知ABC DCB ∠=∠,再结合//EF CD 即可求解.【详解】解://AB CD 130ABC DCB ∴∠=∠=︒1305575ECD DCB BCE ∴∠=∠-∠=︒-︒=︒//EF CD 180ECD CEF ∴∠+∠=︒18075105CEF ∴∠=︒-︒=︒故答案是:B .【点睛】本题考查平行线的性质和角度求解,难度不大,属于基础题.解题的关键是掌握平行线的性质.9.(2021·山东泰安市)如图,直线//m n ,三角尺的直角顶点在直线m 上,且三角尺的直角被直线m 平分,若160∠=︒,则下列结论错误的是( )A .275∠=︒B .345∠=︒C .4105∠=︒D .5130∠=︒【答案】D 【分析】根据角平分线的定义求出∠6和∠7的度数,再利用平行线的性质以及三角形内角和求出∠3,∠8,∠2的度数,最后利用邻补角互补求出∠4和∠5的度数.【详解】首先根据三角尺的直角被直线m 平分,∴∠6=∠7=45°;A 、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m ∥n ,∴∠2=∠8=75°结论正确,选项不合题意;B 、∵∠7=45°,m ∥n ,∴∠3=∠7=45°,结论正确,选项不合题意;C 、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;D 、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.故选:D .【点睛】本题考查了角平分线的定义,平行线的性质,三角形内角和,邻补角互补,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补. 10.(2021·四川资阳市)如图,已知直线//,140,230m n ∠=︒∠=︒,则3∠的度数为( )A .80︒B .70︒C .60︒D .50︒【答案】B 【分析】如图,由题意易得∠4=∠1=40°,然后根据三角形外角的性质可进行求解.【详解】解:如图,∵//,140m n ∠=︒,∴∠4=∠1=40°,∵230∠=︒,∴34270∠=∠+∠=︒;故选B .【点睛】本题主要考查平行线的性质及三角形外角的性质,熟练掌握平行线的性质及三角形外角的性质是解题的关键.11.(2021·四川广元市)如图,在ABC 中,90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,点P 是AC 边上一个动点,连接PD ,以PD 为边在PD 的下方作等边三角形PDQ ,连接CQ .则CQ 的最小值是( )A .2B .1CD .32【答案】B【分析】以CD 为边作等边三角形CDE ,连接EQ ,由题意易得∠PDC =∠QDE ,PD =QD ,进而可得△PCD ≌△QED ,则有∠PCD =∠QED =90°,然后可得点Q 是在QE 所在直线上运动,所以CQ 的最小值为CQ ⊥QE 时,最后问题可求解.【详解】解:以CD 为边作等边三角形CDE ,连接EQ ,如图所示:∵PDQ 是等边三角形,∴60,,CED PDQ CDE PD QD CD ED ∠=∠=∠=︒==,∵∠CDQ 是公共角,∴∠PDC =∠QDE ,∴△PCD ≌△QED (SAS ),∵90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,∴∠PCD =∠QED =90°,122CD DE CE BC ====,∴点Q 是在QE 所在直线上运动, ∴当CQ ⊥QE 时,CQ 取的最小值,∴9030QEC CED ∠=︒-∠=︒,∴112CQ CE ==;故选B . 【点睛】本题主要考查等边三角形的性质、含30°直角三角形的性质及最短路径问题,熟练掌握等边三角形的性质、含30°直角三角形的性质及最短路径问题是解题的关键.12.(2021·河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,ACD ∠是ABC 的外角.求证:ACD A B ∠=∠+∠.下列说法正确的是( )A .证法1还需证明其他形状的三角形,该定理的证明才完整B .证法1用严谨的推理证明了该定理C .证法2用特殊到一般法证明了该定理D .证法2只要测量够一百个三角形进行验证,就能证明该定理【答案】B【分析】根据三角形的内角和定理与平角的定义可判断A 与B ,利用理论与实践相结合可判断C 与D .【详解】解:A . 证法1给出的证明过程是完整正确的,不需要分情况讨论,故A 不符合题意;B . 证法1给出的证明过程是完整正确的,不需要分情况讨论,故选项B 符合题意;C . 证法2用量角器度量两个内角和外角,只能验证该定理的正确性,用特殊到一般法证明了该定理缺少理论证明过程,故选项C 不符合题意;D . 证法2只要测量够一百个三角形进行验证,验证的正确性更高,就能证明该定理还需用理论证明,故选项D 不符合题意.故选择:.B【点睛】本题考查三角形外角的证明问题,命题的正确性需要严密推理证明,三角形外角分三种情形,锐角、直角、和钝角,证明中应分类才严谨.13.(2021·四川凉山州)如图,ABC 中,90,8,6ACB AC BC ∠=︒==,将ADE 沿DE 翻折,使点A 与点B 重合,则CE 的长为( )A .198B .2C .254D .74【答案】D【分析】先在RtABC 中利用勾股定理计算出AB =10,再利用折叠的性质得到AE =BE ,AD =BD =5,设AE =x ,则CE =AC -AE =8-x ,BE =x ,在Rt △BCE 中根据勾股定理可得到x 2=62+(8-x )2,解得x ,可得CE .【详解】解:∵∠ACB =90°,AC =8,BC =6,∴AB ,∵△ADE 沿DE 翻折,使点A 与点B 重合,∴AE =BE ,AD =BD =12AB =5, 设AE =x ,则CE =AC -AE =8-x ,BE =x ,在Rt △BCE 中∵BE 2=BC 2+CE 2,∴x 2=62+(8-x )2,解得x =254,∴CE =2584-=74,故选:D . 【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.14.(2021·陕西)如图,点D 、E 分别在线段BC 、AC 上,连接AD 、BE .若35A ∠=︒,25B ∠=︒,50C ∠=︒,则1∠的大小为( )A .60°B .70°C .75°D .85°【答案】B 【分析】由题意易得105BEC ∠=︒,然后根据三角形外角的性质可进行求解.【详解】解:∵25B ∠=︒,50C ∠=︒,∴在Rt △BEC 中,由三角形内角和可得105BEC ∠=︒,∵35A ∠=︒,∴170BEC A ∠=∠-∠=︒;故选B .【点睛】本题主要考查三角形内角和及外角的性质,熟练掌握三角形内角和及外角的性质是解题的关键.15.(2021·安徽)在△ABC 中,90ACB ∠=︒,分别过点B ,C 作BAC ∠平分线的垂线,垂足分别为点D ,E ,BC 的中点是M ,连接CD ,MD ,ME .则下列结论错误的是( ) A .2CD ME =B .//ME ABC .BD CD = D .ME MD = 【答案】A【分析】设AD 、BC 交于点H ,作HF AB ⊥于点F ,连接EF .延长AC 与BD 并交于点G .由题意易证△CAE ≌△FAE ,从而证明ME 为△CBF 中位线,即//ME AB ,故判断B 正确;又易证△AGD ≌△ABD ,从而证明D 为BG 中点.即利用直角三角形斜边中线等于斜边一半即可求出CD BD =,故判断C 正确;由90HDM DHM ∠+∠=︒、90HCE CHE ∠+∠=︒和DHM CHE ∠=∠可证明HDM HCE ∠=∠.再由90HEM EHF ∠+∠=︒、EHC EHF ∠=∠和90EHC HCE ∠+∠=︒可推出 HCE HEM ∠=∠,即推出HDM HEM ∠=∠,即MD ME =,故判断D 正确;假设2CD ME =,可推出2CD MD =,即可推出30DCM ∠=︒.由于无法确定DCM ∠的大小,故2CD ME =不一定成立,故可判断A 错误.【详解】如图,设AD 、BC 交于点H ,作HF AB ⊥于点F ,连接EF .延长AC 与BD 并交于点G .∵AD 是BAC ∠的平分线,HF AB ⊥,HC AC ⊥,∴HC =HF ,∴AF =AC .∴在△CAE 和△FAE 中,AF AC CAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△CAE ≌△FAE ,∴CE FE =,∠AEC =∠AEF =90°,∴C 、E 、F 三点共线,∴点E 为CF 中点.∵M 为BC 中点,∴ME 为△CBF 中位线,∴//ME AB ,故B 正确,不符合题意;∵在AGD △和ABD △中,90GAD BAD AD AD ADG ADB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△AGD ≌△ABD , ∴12GD BD BG ==,即D 为BG 中点.∵在BCG 中,90BCG ∠=︒,∴12CD BG =, ∴CD BD =,故C 正确,不符合题意;∵90HDM DHM ∠+∠=︒,90HCE CHE ∠+∠=︒,DHM CHE ∠=∠,∴HDM HCE ∠=∠. ∵HF AB ⊥,//ME AB ,∴HF ME ⊥,∴90HEM EHF ∠+∠=︒.∵AD 是BAC ∠的平分线,∴EHC EHF ∠=∠.∵90EHC HCE ∠+∠=︒, ∴HCE HEM ∠=∠,∴HDM HEM ∠=∠,∴MD ME =,故D 正确,不符合题意;∵假设2CD ME =,∴2CD MD =,∴在Rt △CDM 中,30DCM ∠=︒.∵无法确定DCM ∠的大小,故原假设不一定成立,故A 错误,符合题意.故选A .【点睛】本题考查角平分线的性质,三角形全等的判定和性质,直角三角形的性质,三角形中位线的判定和性质以及含30角的直角三角形的性质等知识,较难.正确的作出辅助线是解答本题的关键.16.(2021·重庆)如图,在△ABC 和△DCB 中,ACB DBC ∠=∠ ,添加一个条件,不能..证明和△ABC 和△DCB 全等的是( )A .ABC DCB ∠=∠ B .AB DC = C .AC DB =D .A D ∠=∠【答案】B【分析】根据已知条件和添加条件,结合全等三角形的判断方法即可解答.【详解】选项A ,添加ABC DCB ∠=∠,在△ABC 和△DCB 中,ABC DCB BC CB ACB DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DCB (ASA ), 选项B ,添加AB DC =, 在△ABC 和△DCB 中,AB DC =,BC CB =,ACB DBC ∠=∠,无法证明△ABC ≌△DCB ; 选项C ,添加AC DB =,在ABC 和DCB 中,BC CB ACB DBC AC DB =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (SAS ); 选项D ,添加A D ∠=∠,在ABC 和DCB 中,A D ACB DBC BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (AAS ); 综上,只有选项B 符合题意.故选B .【点睛】本题考查了全等三角形的判定方法,熟知全等三角形的判定方法是解决问题的关键.17.(2021·浙江丽水市)如图,在Rt ABC △纸片中,90,4,3ACB AC BC ∠=︒==,点,D E 分别在,AB AC 上,连结DE ,将△ADE 沿DE 翻折,使点A 的对应点F 落在BC 的延长线上,若FD 平分EFB ∠,则AD 的长为( )A .259B .258C .157D .207【答案】D【分析】先根据勾股定理求出AB ,再根据折叠性质得出∠DAE=∠DFE ,AD=DF ,然后根据角平分线的定义证得∠BFD=∠DFE =∠DAE ,进而证得∠BDF=90°,证明Rt △ABC ∽Rt △FBD ,可求得AD 的长.【详解】解:∵90,4,3ACB AC BC ∠=︒==,∴AB ==, 由折叠性质得:∠DAE=∠DFE ,AD=DF ,则BD =5﹣AD ,∵FD 平分EFB ∠,∴∠BFD =∠DFE=∠DAE ,∵∠DAE +∠B =90°,∴∠BDF +∠B =90°,即∠BDF =90°,∴Rt △ABC ∽Rt △FBD ,∴BD BC DF AC =即534AD AD -=,解得:AD =205,故选:D . 【点睛】本题考查折叠性质、角平分线的定义、勾股定理、相似三角形的判定与性质、三角形的内角和定理,熟练掌握折叠性质和相似三角形的判定与性质是解答的关键.18.(2021·四川自贡市)如图,()8,0A ,()2,0C -,以点A 为圆心,AC 长为半径画弧,交y 轴正半轴于点B ,则点B 的坐标为( )A .()0,5B .()5,0C .()6,0D .()0,6【答案】D 【分析】先根据题意得出OA =8,OC =2,再根据勾股定理计算即可【详解】解:由题意可知:AC =AB ∵()8,0A ,()2,0C -∴OA =8,OC =2∴AC =AB =10在Rt △OAB 中,6OB ==∴B (0,6)故选:D【点睛】本题考查勾股定理、正确写出点的坐标,圆的半径相等、熟练进行勾股定理的计算是关键19.(2021·重庆)如图,点B ,F ,C ,E 共线,∠B =∠E ,BF =EC ,添加一个条件,不等判断△ABC ≌△DEF 的是( )A .AB =DEB .∠A =∠DC .AC =DFD .AC ∥FD【答案】C 【分析】根据全等三角形的判定与性质逐一分析即可解题. 【详解】解:BF =EC ,BC EF ∴=A. 添加一个条件AB =DE ,又,BC EF B E =∠=∠()ABC DEF SAS ∴△≌△ 故A 不符合题意;B. 添加一个条件∠A =∠D ,又,BC EF B E =∠=∠,∴△ABC ≌△DEF (AAS ),故B 不符合题意;C. 添加一个条件AC =DF ,不能判断△ABC ≌△DEF ,故C 符合题意;D. 添加一个条件AC ∥FD , ACB EFD ∴∠=∠,又,BC EF B E =∠=∠,△ABC ≌△DEF (ASA ),故D 不符合题意,故选:C .【点睛】本题考查添加条件使得三角形全等即全等三角形的判定,是重要考点,难度较易,掌握相关知识是解题关键.20.(2021·江苏扬州市)如图,在44⨯的正方形网格中有两个格点A 、B ,连接AB ,在网格中再找一个格点C ,使得ABC 是等腰直角....三角形,满足条件的格点C 的个数是( )A .2B .3C .4D .5【答案】B 【分析】根据题意,结合图形,分两种情况讨论:①AB 为等腰直角△ABC 底边;②AB 为等腰直角△ABC 其中的一条腰.【详解】解:如图:分情况讨论:①AB 为等腰直角△ABC 底边时,符合条件的C 点有0个; ②AB 为等腰直角△ABC 其中的一条腰时,符合条件的C 点有3个.故共有3个点,故选:B .【点睛】本题考查了等腰三角形的判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合的思想是数学解题中很重要的解题思想.21.(2021·浙江宁波市)如图,在△ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,BD =若E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D .2【答案】C【分析】根据条件可知△ABD 为等腰直角三角形,则BD =AD ,△ADC 是30°、60°的直角三角形,可求出AC 长,再根据中位线定理可知EF =2AC . 【详解】解:因为AD 垂直BC ,则△ABD 和△ACD 都是直角三角形,又因为45,60,B C ∠=︒∠=︒所以AD =BD =sin ∠C =AD AC =AC =2, 因为EF 为△ABC 的中位线,所以EF =2AC =1,故选:C .【点睛】本题主要考查了等腰直角三角形、锐角三角形函数值、中位线相关知识,根据条件分析利用定理推导,是解决问题的关键.22.(2021·青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为()A.7.5 B.8 C.15 D.无法确定【答案】A【详解】如图,过点D作DE⊥BC于点E.∵∠A=90°,∴AD⊥AB.∴AD=DE=3.又∵BC=5,∴S△BCD=12BC•DE=12×5×3=7.5.故选A.考点:角平分线的性质;全等三角形的判定与性质.二、填空题1.(2021·浙江)由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB的长应是______.1【分析】据裁剪和拼接的线段关系可知CD =,1BD CE ==,在Rt ACD △中应用勾股定理即可求解.【详解】解:∵地毯平均分成了3=,∴CD =在Rt ACD △中,根据勾股定理可得AD =,根据裁剪可知1BD CE ==,∴1AB AD BD =-=1.【点睛】本题考查勾股定理,根据裁剪找出对应面积和线段的关系是解题的关键. 2.(2021·河北)下图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且A ∠,B ,E ∠保持不变.为了舒适,需调整D ∠的大小,使110EFD ∠=︒,则图中D ∠应___________(填“增加”或“减少”)___________度.【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系,进行计算即可判断.【详解】解:∵∠A +∠B =50°+60°=110°,∴∠ACB =180°-110°=70°,∴∠DCE =70°,如图,连接CF 并延长,∴∠DFM =∠D +∠DCF =20°+∠DCF ,∠EFM =∠E +∠ECF =30°+∠ECF ,∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD=110°,则∠EFD减少了10°,若只调整∠D的大小,由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°,因此应将∠D减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.3.(2021·青海)如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是_____.【答案】40°【分析】由EF⊥BD,∠1=50°,结合三角形内角和为180°,即可求出∠D的度数,再由“两直线平行,同位角相等”即可得出结论.【详解】解:在△DEF中,∠1=50°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=40°.∵AB∥CD,∴∠2=∠D=40°.故答案为40°.【点睛】本题考查平行线的性质以及三角形内角和为180°,解题关键是求出∠D=40°.解决该题型题目时,根据平行线的性质,找出相等或互补的角是解题技巧.4.(2021·山东聊城市)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD 与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF 值为____________.【答案】12:15:10【分析】由题意得:BF ⊥AC ,再根据三角形的面积公式,可得5432ABC SAD CE BF ===,进而即可得到答案.【详解】解:∵在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为点D 和点E ,AD 与CE 交于点O ,∴BF ⊥AC ,∵AB =5,BC =4,AC =6,∴111222ABC SBC AD AB CE AC BF =⋅=⋅=⋅, ∴5432ABC S AD CE BF ===,∴CE :AD :BF =12:15:10,故答案是:12:15:10. 【点睛】本题主要考查三角形的高,掌握“三角形的三条高交于一点”是解题的关键. 5.(2021·江苏南京市)如图,在四边形ABCD 中,AB BC BD ==.设ABC α∠=,则ADC ∠=______(用含α的代数式表示).【答案】11802α︒- 【分析】由等腰的性质可得:∠ADB =1902ABD ︒-∠,∠BDC =1902CBD ︒-∠,两角相加即可得到结论.【详解】解:在△ABD 中,AB =BD ∴∠A =∠ADB =11(180)9022ABD ABD ︒-∠=︒-∠ 在△BCD 中,BC =BD ∴∠C =∠BDC =11(180)9022CBD CBD ︒-∠=︒-∠ ∵ABC ABD CBD α∠=∠+∠= ∴ADC ADB CBD ∠=∠+∠ =11909022ABD CBD ︒-∠+︒-∠=1180()2ABD CBD ︒-∠+∠=11802ABC ︒-∠=11802α︒-故答案为:11802α︒-. 【点睛】此题主要考查了等腰三角形的性质和三角形内角和定理,分别求出∠ADB=1902ABD ︒-∠,∠BDC=1902CBD ︒-∠是解答本题的关键. 6.(2021·江苏连云港市)如图,BE 是ABC 的中线,点F 在BE 上,延长AF 交BC 于点D .若3BF FE =,则BD DC=______. 【答案】32【分析】连接ED ,由BE 是ABC 的中线,得到BE BCE S S =△A △,AED EDC S S =,由3BF FE =,得到3,3ABFBFDAFE FED S S S S ==,设=,AEF EFD S x S y =,由面积的等量关系解得53x y =,最后根据等高三角形的性质解得ABDADC S BD S DC =,据此解题即可. 【详解】解:连接EDBE 是ABC 的中线,ABE BCE S S ∴=,AED EDC S S = 3BF FE =3,3ABF BFD AFE FED S S S S ∴==设=,AEF EFD S x S y =,33ABF BFD S x S y ∴==, 4,4,4ABE BEC BED S x S x S y ∴===44EDC BECBED S S S x y ∴=-=-ADE EDC S S =44x y x y ∴+=-53x y ∴=ABD 与ADC 是等高三角形,53+33333833=516445325333ABD ADC y y SBD x y x y y S DC x y x y x y y y y ⨯++∴=====++--⨯-,故答案为:32. 【点睛】本题考查三角形的中线、三角形面积等知识,是重要考点,难度一般,掌握相关知识是解题关键.7.(2021·浙江绍兴市)如图,在ABC 中,AB AC =,70B ∠=︒,以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,连结AP ,则BAP ∠的度数是_______.【答案】15︒或75︒【分析】分①点P 在BC 的延长线上,②点P 在CB 的延长线上两种情况,再利用等腰三角形的性质即可得出答案.【详解】解:①当点P 在BC 的延长线上时,如图∵AB AC =,70B ∠=︒,∴70B ACB ∠=∠=︒∴40CAB ∠=︒ ∵以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,∴AC =PC ∴∠=∠P CAP∵70∠=∠+∠=︒ACB B CAP ∴35∠=∠=P CAP ∴403575∠=∠+∠=+=BAP BAC CAP②当点P 在CB 的延长线上时,如图由①得70C ∠=︒,40CAB ∠=︒∵AC =PC ∴=55∠=∠P CAP∴-55-4015∠=∠∠==BAP CAP BAC 故答案为:15︒或75︒【点睛】本题主要考查了等腰三角形的性质,分类讨论不重不漏是解题的关键.8.(2021·四川广安市)如图,将三角形纸片ABC 折叠,使点B 、C 都与点A 重合,折痕分别为DE 、FG .已知15ACB ∠=︒,AE EF =,DE =BC 的长为_______.【答案】4+【分析】由折叠的性质得出BE =AE ,AF =FC ,∠F AC =∠C =15°,得出∠AFE =30°,由等腰三角形的性质得出∠EAF =∠AFE =30°,证出△ABE 是等边三角形,得出∠BAE =60°,求出AE =BE =2,证出∠BAF =90°,利用勾股定理求出AF ,即CF ,可得BC .【详解】解:∵把三角形纸片折叠,使点B 、点C 都与点A 重合,折痕分别为DE ,FG , ∴BE =AE ,AF =FC ,∠F AC =∠C =15°,∴∠AFE =30°,又AE =EF ,∴∠EAF =∠AFE =30°,∴∠AEB =60°,∴△ABE 是等边三角形,∠AED =∠BED =30°,∴∠BAE =60°,∵DE =AE =BE =AB =cos30DE ︒=2,∴BF =BE +EF =4,∠BAF =60°+30°=90°,∴FC =AF =BC =BF +FC =4+,故答案为:4+.【点睛】此题考查了翻折变换的性质、等腰三角形的性质、等边三角形的判定与性质、直角三角形的性质;根据折叠的性质得出相等的边和角是解题关键.9.(2021·四川遂宁市)如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是_____ .【答案】12.=,根据三角形的周长公式计算即可.【分析】根据线段的垂直平分线的性质得到DB DC=,【详解】解:∵直线DE垂直平分BC,∴DB DC∴△ABD的周长5712=++=++=+=+=,故答案为:12.AB AD BD AB AD DC AB AC【点睛】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.10.(2021·江苏宿迁市)《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为__尺.【答案】12【分析】依题意画出图形,设芦苇长AB=AB'=x尺,则水深AC=(x﹣1)尺,因为B'E=10尺,所以B'C=5尺,利用勾股定理求出x的值即可得到答案..【详解】解:依题意画出图形,设芦苇长AB =AB '=x 尺,则水深AC =(x ﹣1)尺,因为B 'E =10尺,所以B 'C =5尺,在Rt △AB 'C 中,52+(x ﹣1)2=x 2,解之得x =13,即水深12尺,芦苇长13尺.故答案为:12.【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键.三、解答题1.(2021·湖北武汉市)如图,//AB CD ,B D ∠=∠,直线EF 与AD ,BC 的延长线分别交于点E ,F .求证:DEF F ∠=∠.【答案】见解析【分析】根据已知条件//AB CD ,B D ∠=∠,得到DCF D ∠=∠,从而得到//AD BC ,即可证明DEF F ∠=∠.【详解】证明:∵//AB CD ,∴DCF B ∠=∠.∵B D ∠=∠,∴DCF D ∠=∠.∴//AD BC .∴DEF F ∠=∠.【点睛】本题考查平行线的性质和判定.平行线的性质:两直线平行,内错角相等.平行线的判定:同位角相等,两直线平行.2.(2021·浙江温州市)如图,BE 是ABC 的角平分线,在AB 上取点D ,使DB DE =. (1)求证://DE BC .(2)若65A ∠=︒,45AED ∠=︒,求EBC ∠的度数.【答案】(1)见解析;(2)35°【分析】(1)直接利用角平分线的定义和等边对等角求出BED EBC ∠=∠,即可完成求证; (2)先求出∠ADE ,再利用平行线的性质求出∠ ABC ,最后利用角平分线的定义即可完成求解.【详解】解:(1)BE 平分ABC ∠,∴ABE EBC ∠=∠.DB DE =,∴ABE BED ∠=∠,∴BED EBC ∠=∠,∴//DE BC .(2)65A ∠=︒,45AED ∠=︒,∴18070ADE A AED ∠=︒-∠-∠=︒.//DE BC .∴70ABC ADE ∠=∠=︒.BE 平分ABC ∠,∴1352EBC ABC ∠=∠=︒,即35EBC ∠=︒. 【点睛】本题综合考查了角平分线的定义、等腰三角形的性质、平行线的判定与性质等内容,解决本题的关键是牢记概念与性质,本题的解题思路较明显,属于几何中的基础题型,着重考查了学生对基本概念的理解与掌握.3.(2021·四川南充市)如图,90BAC ∠=︒,AD 是BAC ∠内部一条射线,若AB AC =,BE AD⊥于点E ,CF AD ⊥于点F .求证:AF BE =.【答案】见详解【分析】根据AAS 证明△BAE ≌△ACF ,即可得AF BE =.【详解】证明:∵90BAC ∠=︒,∴∠BAE +∠CAF =90°,∵BE ⊥AD ,CF ⊥AD ,∴∠BEA =∠AFC =90°,∴∠BAE +∠EBA =90°,∴∠CAF =∠EBA ,∵AB =AC ,∴△BAE ≌△ACF ,∴AF BE =.【点睛】本题主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.4.(2021·浙江绍兴市)如图,在ABC 中,40A ∠=︒,点D ,E 分別在边AB ,AC 上,BD BC CE ==,连结CD ,BE .(1)若80ABC ∠=︒,求BDC ∠,ABE ∠的度数.(2)写出BEC ∠与BDC ∠之间的关系,并说明理由.【答案】(1)50BDC ∠=︒;20ABE ∠=︒;(2)110BEC BDC ∠+∠=︒,见解析【分析】(1)利用三角形的内角和定理求出ACB ∠的大小,再利用等腰三角形的性质分别求出BDC ∠,ABE ∠.(2)利用三角形的内角和定理、三角形外角的性质和等腰三角形的性质,求出用含ABE ∠分别表示BEC ∠,BDC ∠,即可得到两角的关系.【详解】(1)80ABC ∠=︒,BD BC =,50BDC BCD ∴∠=∠=︒.在ABC 中,180A ABC ACB ∠+∠+∠=︒,40A ∠=︒,60ACB ∠=︒∴,CE BC =,60EBC ∴∠=︒.20ABE ABC EBC ∴∠=∠-∠=︒.(2)BEC ∠,BDC ∠的关系:110BEC BDC ∠+∠=︒.理由如下:设BEC α∠=,BDC β∠=.在ABE △中,40A ABE ABE α=∠+∠=︒+∠,CE BC =,CBE BEC α∴∠=∠=.2402ABC ABE CBE A ABE ABE ∴∠=∠+∠=∠+∠=︒+∠, 在BDC 中,BD BC =,2402180BDC BCD DBC ABE β∴∠+∠+∠=+︒+∠=︒.70ABE β︒∴=-∠.4070110ABE ABE αβ∴+=︒+∠+︒-∠=︒.110BEC BDC ∴∠+∠=︒.【点睛】本题主要通过求解角和两角之间的关系,考查三角形的内角和定理、三角形外角的性质和等腰三角形的性质.三角形的内角和等于180︒ .三角形的外角等于与其不相邻的两个内角之和.等腰三角形等边对等角.5.(2021·陕西中考真题)如图,//BD AC ,BD BC =,点E 在BC 上,且BE AC =.求证:D ABC ∠=∠.【答案】见解析【分析】由题意易得EBD C ∠=∠,进而可证EDB ABC ≌△△,然后问题可求证. 【详解】证明:∵//BD AC ,∴EBD C ∠=∠.∵BD BC =,BE AC =,∴()EDB ABC SAS ≌.∴D ABC ∠=∠.【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.6.(2021·湖南衡阳市)如图,点A 、B 、D 、E 在同一条直线上,,//,//AB DE AC DF BC EF =.求证:ABC DEF △≌△.【答案】见解析【分析】根据//,//AC DF BC EF ,可以得到,A FDE ABC DEF ∠=∠∠=∠,然后根据题目中的条件,利用ASA 证明△ABC ≌△DEF 即可.【详解】证明:点A ,B ,C ,D ,E 在一条直线上∵//,//AC DF BC EF ∴,A FDE ABC DEF ∠=∠∠=∠在△ABC 与△DEF 中CAB FDE AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△ 【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目.7.(2021·浙江)已知在ACD △中,Р是CD 的中点,B 是AD 延长线上的一点,连结,BC AP .(1)如图1,若90,60,,ACB CAD BD AC AP ︒∠=︒∠===,求BC 的长.(2)过点D 作//DE AC ,交AP 延长线于点E ,如图2所示.若60,CAD BD AC ∠︒==,求证:2BC AP =.(3)如图3,若45CAD ∠=︒,是否存在实数m ,当BD mAC =时,2BC AP =?若存在,请直接写出m 的值;若不存在,请说明理由.【答案】(1)(2)见解析;(3)存在,m =【分析】(1)先解直角三角形ABC 得出2AB AC =,从而得出△ADC 是等边三角形,再解直角三角形ACP 即可求出AC 的长,进而得出BC 的长;(2)连结BE ,先利用AAS 证出△CPA ≌△DPE ,得出AE =2PE ,AC =DE ,再得出△ADC 是等边三角形,然后由SAS 得出△CAB ≌△EBA ,得出AE =BC 即可得出结论;(3)过点D 作//DE AC ,交AP 延长线于点E ,连接BE ,过C 作CG ⊥AB 于G ,过E 作EN ⊥AB 于N ,由(2)得AE =2AP ,DE =AC ,再证明△AEN ≌△BCG ,从而得出△CAB ≌△EBA 得出DE =BE ,然后利用勾股定理即可得出m 的值.【详解】(1)解 90,60ACB CAD ∠=∠=︒︒,2cos60AC AB AC ︒==, BD AC =,AD AC =∴,∴△ADC 是等边三角形,60ACD ∴∠=︒Р是CD 的中点,AP CD ∴⊥,在Rt APC 中,AP =2sin 60AP AC ∴==︒,tan 60BC AC =︒=∴ (2)证明:连结BE ,//DE AC ,CAP DEP ∴∠=∠, ,CP DP CPA DPE =∠=∠,∴△CPA ≌△DPE , 1,2AP EP AE DE AC ∴===, BD AC =,BD DE ∴=,又//DE AC ,60BDE CAD ∴∠=∠=︒,。
中考数学【相交线与平行线】考点专项复习教案(含例题、习题、答案)

第五章相交线与平行线本章小结小结1 本章概述本章的主要内容是两条直线的位置关系——相交与平行.特别是垂直和平行关系是平面几何所要研究的基本内容之一.这一章的内容是很重要的基本知识,是几何学习的重要阶段,要引起高度重视.教材在给出对顶角、邻补角、垂线、点到直线的距离等概念的基础上又给出了对顶角、邻补角的性质、垂线的基本性质和平行线的判定和性质,最后给出平移的概念、性质以及利用平移绘制图案.小结2 本章学习重难点【本章重点】了解对顶角、余角、补角的概念;掌握等角的余角相等,等角的补角相等;掌握垂线、垂线段的概念;知道两条直线平行,同位角相等以及同位角相等,两直线平行,进一步探索平行线的性质和判定.【本章难点】掌握垂线段最短的性质,体会点到直线的距离的意义;通过具体实例认识平移;能按要求作出简单平面图形平移后的图形,利用平移进行图案设计,认识和欣赏平移在现实生活中的应用.小结3 中考透视中考所考查的内容主要体现在以下几个方面:1. 对顶角、邻补角、垂线、点到直线的距离等概念的理解,对顶角、邻补角以及垂线性质的应用,包括实际应用.2. 同位角、内错角、同旁内角的含义,能由线找出角、由角说出线.3. 平行线的识别与特征,以及在实际问题中的应用.4. 简单命题的证明.知识网络结构图专题总结及应用一、知识性专题专题1 有关基本图形的问题【专题解读】本章中主要考查数图形的个数问题,构造基本图形以及基本图形的组合,如平行线与角平分线的组合,平行线与平行线的组合等.例1 如图5-132所示,直线AB,CD,EF都经过点O,图中共有几对对顶角?分析数基本图形不能重复,不能遗漏.我们知道两条直线相交有两对对顶角,图中有3组两条直线相交,故对顶角有2×3=6(对).解:共有6对对顶角.【解题策略】数图形个数及书写时,应注意顺序性,这样不易例2 如图5-133所示,图中共有几对同旁内角?分析我们知道两条直线被第三条直线所截共形成八个角,其中有两对同旁内角.图形中有两个“三线八角”,即CD,EF被GH所截,形成两对同旁内角,AB,EF被GH所截,又形成两对同旁内角,所以共有4对同旁内角.解:图中共有4对同旁内角.【解题策略】注意观察同旁内角的特点.例3 如图5-134所示,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.分析此图不是我们所学的“三线八角”的基本图形,需添加一些线(辅助线)把它们转化成我们熟悉的基本图形.解:如图5-134所示,过点P作射线PN∥AB.因为AB∥CD(已知),所以PN∥CD(平行于同一条直线的两直线平行),所以∠4=∠2=25°(两直线平行,内错角相等).因为PN∥AB(已知),所以∠3=∠1=32°(两直线平行,内错角相等).所以∠BPC=∠3+∠4=32°+25°=57°.【解题策略】构造基本图形就是将残缺的基本图AB所以GM∥HN(内错角相等,两直线平行).【解题策略】此题考查平行线的性质、判定以及角平分线的综合应用.例5 如图5-136所示,已知AB∥CD,BC∥DE.试说明∠B=∠D.分析条件为直线平行,故可根据平行线的性质说明.解:因为AB∥CD(已知),所以∠B=∠C(两直线平行,内错角相等).因为BC∥DE(已知),所以∠C=∠D(两直线平行,内错角相等).【解题策略】此题重点考查了平行线的性质的应用.例6 如图5-137所示,已知AB∥CD,G为AB上任一点,GE,GF分别交CD于E,F.试说明∠1+∠2+∠3=180°.分析要说明180°问题,想到了“平角”和“两直线平行,同旁内角互补”这两个知识点,故可用它们解决问题.解:因为AB∥CD(已知),所以∠4=∠2,∠3=∠5(两直线平行,内错角相等).因为∠4+∠1+∠5=180°(平角定义),所以∠2+∠1+∠3=180°(等量代换).【解题策略】此题把说明∠2+∠1+∠3=180°转化为说明∠1+∠5+∠4=180°,应用等量代换解决了问题.例7 如图5-138所示,AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC.试说明OE⊥OF解:因为OE,OF分别平分∠AOC与∠BOC(已知),所以∠1=12∠AOC,∠2=12∠BOC(角平分线定义).所以∠1+∠2=12∠AOC+12∠BOC=12(∠AOC+∠BOC).又因为∠AOC+∠BOC=180°(邻补角定义),所以∠1+∠2=1×180°=90°,∠和°可说明∠1+∠2=90°.例9 如图5-140所示,在三角形ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC.试说明∠1=∠2.解:因为CD⊥AB,FG⊥AB(已知),所以∠CDB=∠FGB=90°(垂直定义),所以∠2=∠3(两直线平行,同位角相等).因为DE∥BC(已知),所以∠1=∠3(两直线平行,内错角相等),所以∠1=∠2(等量代换).【解题策略】多次运用平行线的性质说明∠1,∠2,∠3的关系.二、规律方法专题专题2 基本命题的计算与证明【专题解读】基本命题的计算与证明涉及的题型有(1)有关角的计算;(2)有关角相等的判定;(3)判定平行问题;(4)判定垂直问题;(5)判定共线问题.例10 如图5-141所示,已知∠4=70°,∠3=110°,∠1=46°,求∠2的度数.分析由∠3+∠4=180°,知AB∥CD,故∠2=180°-∠1.解:因为∠4=70°,∠3=110°(已知),所以∠4+∠3=180°,所以AB∥CD(同旁内角互补,两直线平行),所以∠2=180°-∠1=180°-46°=134°(两直线平行,同旁内角互补).【解题策略】此题考查由同旁内角互补判定两直线平行,由两直线平行可行同旁内角互补,从而计算相关的角.例11 如图5-142所示,AB∥CD,EB∥DF.试说明∠1=∠2.解:因为AB∥CD(已知),所以∠1+∠3=∠2+∠4(两直线平行,内错角相等).因为EB∥DF(已知),所以∠3=∠4(两直线平行,内错角相等),所以∠1=∠2(等式性质).【解题策略】判定角相等的方法有:(1)同角(等角)的余角相等;(2)同角(等角)的补角相等;(3)对顶角相等;(4)角平分线定义;(5)两直线平行,同位角相等;(6)两直线平行,内错角相等.例12 如图5-143所示,DF∥AC,∠1=∠2.试说明DE=AB.分析要说明DE∥AB,可说明∠1=∠A,而由DF∥AC,有∠2=∠A.又因为∠1=∠2,故有∠1=∠A,从而得出结论.解:因为DF∥AC(已知),所以∠2=∠A(两直线平行,同位角相等).因为∠1=∠2(已知),所以∠1=∠A(等量代换),所以DE∥AB(同位角相等,两直线平行).【解题策略】判定平行的方法有:(1)平行于同一条直线的两直线平行;(2)垂直于同一条直线的两直线平行;(3)同位角相等,两直线平行;(4)内错角相等,两直线平行;(5)同旁内角互补,两直线平行.例13 如图5-144所示,∠1=∠2,CD∥EF.试说明EF⊥AB.分析要说明EF⊥AB,可说明∠2=90°,而由CD∥EF,可得∠1+∠2=180°,又∠1=∠2,所以有∠1=∠2=90°,从而得出结论.解:因为CD∥EF(已知),所以∠1+∠2=180°(两直线平行,同旁内角互补).又因为∠1=∠2(已知),所以∠1=∠2=90°,所以EF⊥AB(垂直定义).【解题策略】判定垂直的方法有:(1)说明两条相交线的一个交角为90°;(2)说明邻补角相等;(3)垂直于平行线中的一条,也必垂直于另一条.例14 如图5-145所示,直线AB,CD相交于点O,OE平分∠AOC,OF平分∠BOD.试说明E,O,F三点在一条直线上.分析要说明E,O,F三点共线,只需说明∠EOF=180°.解:因为AB,CD相交于点O(已知),所以∠AOC=∠BOD(对顶角相等).因为OE,OF分别平分∠AOC与∠BOD(已知),已知的.例15 如图5-146所示,直线AB,CD相交于点O,OD平分∠AOE,且∠COA:∠AOD=7:2,求∠BOE的度数.分析欲求∠BOE,因为∠BOE与∠AOE互为邻补角,所以可先求∠AOE,而∠AOE=2∠AOD,所以只需求∠AOD即可,由已知条件可求得∠AOD.解:∵∠COA+∠AOD=180°,∠COA:∠AOD=7:2,∴∠COA=79×180°=140°,∠AOD=29×180°=40°.∵OD平分∠AOE,∴∠AOE=2∠AOD=2×40°=80°,∴∠BOE=180°-∠AOE=180°-80°=100°.【解题策略】互为邻补角的两个角的和为180°、对顶角相等是在有关求角的大小的问题中常用的两个等量关系,要注意发现图形中的这两种角,它们常隐藏在直线条件的背后.2011中考真题相交线与平行线精选一、选择题1.(2011云南保山2,3分)如图,l1∥l2,∠1=120°,则∠2= .考点:平行线的性质;对顶角、邻补角。
2018届中考数学复习 专题21 平面几何初步(点、线、面、角、相交线与平行线等)试题(B卷,含解析)

平面几何初步一、选择题1. ( 福建福州,3,3分)如图,直线a ,b 被直线c 所截,∠1和∠2的位置关系是A .同位角B .内错角C .同旁内角D .对顶角【答案】B【逐步提示】本题考查了同位角、内错角、同位角和对顶角的识别,解题的关键是认识三线八角,根据内错角的定义可得答案.【详细解答】解:直线a ,b 被直线c 所截,∠1与∠2是内错角,故选择B .【解后反思】三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线. 【关键词】内错角;同位角;同旁内角;对顶角2. ( 甘肃省武威市、白银市、定西市、平凉市、酒泉市、临夏州、张掖市等9市,6,3分)如图,AB ∥CD ,DE ⊥CE ,∠1=34º,则∠DCE 的度数为( )A . 34º B.54º C. 66º D . 56º1BE第6题图【答案】D 【逐步提示】本题考查了平行线的性质,解题的关键是将线的位置关系转化为角的数量关系,应用平行线的性质:两直线平行线内错角相等得出∠EDC 的度数,再利用直角三角形两锐角互余得出∠DCE 的度数. 【详细解答】解:∵AB ∥CD ,∴ ∠EDC =∠1=34°.∵DE ⊥CE ∴ ∠DEC =90°,∴∠EDC +∠DCE =90°.∴∠DCE =90°-34°=56º,故选择D .【解后反思】本题考查了平行线的性质即两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.【关键词】平行线的性质;垂直的定义;直角三角形的性质; 3. ( 甘肃省天水市,5,4分)如图,直线AB ∥CD ,OG 是∠EOB 的平分线,∠EFD =70°,则∠BOG 的度数是( ) A .70° B .20° C .35° D .40°【答案】C【逐步提示】本题考查了平行线的性质和角平分线的定义,解题关键是注意两直线平行,相关的同位角相等、内错角相等及同旁内角互补.要求∠BOG 的度数,关键是先求∠EOB 的度数,这可根据∠EFD =70°,联想到两直线CO A B D E FG平行,同位角相等解决.【详细解答】解:∵AB∥CD,∴∠EOB=∠EFD=70°.又∵OG平分∠EOB,∴∠BOG=12∠EOB=12×70°=35°.故选择C.【解后反思】平行线间的角离不开同位角、同旁内角,及内错角等知识,另外还要和三角形的内角和定理,及外角等于与它不相邻的两内角和知识相联系,只要从这些方面思考,就不难得到解决.【关键词】平行线的性质;角的平分线.4.(广东茂名,5,3分)如图,直线a、b被直线c所截,若a∥b,∠1=60°,那么∠2的度数为()A.120°B.90°C.60°D.30°【答案】C【逐步提示】本题考查了平行线的性质,解题的关键是识别出图中的∠1、∠2是两条平行直线a、b被第三条直线c截出的一组相等的同位角.直接利用“两直线平行,同位角相等”解题即可.【详细解答】解:∵a∥b,∴∠1=∠2. ∵∠1=60°,∴∠2=60°.故选择C .【解后反思】“两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补”这是由直线的位置关系得出角的数量关系,“同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;”这是由角的数量关系得出直线的位置关系,这里体现了数形结合的思想.【关键词】同位角;平行线的性质5.(贵州省毕节市,8,3分)如图,直线a//b,∠1=85°,∠2=35°,则∠3=()(第8题图)A. 85°B. 60°C. 50°D. 35°【答案】C【逐步提示】本题考查平行线的性质,三角形外角和定理,解题的关键是能从图中发现∠3与∠1、∠2的联系.【详细解答】解:如图,∵a//b,∴∠4=∠3.又∵∠1=∠2+∠4,∴∠4=∠1-∠2=85°-35°=50°,∴∠3=50°,故选择C.【解后反思】此类问题容易出错的地方是找不到图形中角与角之间的数量关系.【关键词】平行线的性质;三角形外角和定理6.(河北省,13,2分)如图,将□ABCD沿对角线AC折叠,使点B落在点B’处.若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°【答案】C【逐步提示】根据平行线的性质和折叠的性质得到∠BAC=12∠B’AB=12∠1=22°,再在△ABC中根据三角形内角和定理求得∠B的度数.【详细解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B’AB=∠1=44°.根据折叠的性质可知∠BAC=12∠B’AB=12×44°=22°.又∵∠2=44°,∴∠B=180°-22°-44°=114°,故答案为选项C.【解后反思】折叠问题是属于轴对称变换,折叠后图形的形状和大小不变,三角形折叠后得到的三角形与原三角形全等,对应边和对应角相等.【关键词】平行四边形的性质;平行线的性质;折叠;三角形内角和定理7.(湖北省黄冈市,3,3分)如图,直线a∥b,∠1=550,则∠2= ()A.350B.450C. 550D.650【答案】C【逐步提示】本题考查了平行线的性质“两直线平行,同位角相等”及对顶角的性质“对顶角相等”,解题的关键是能观察出∠1与∠2之间的联系而不走弯路.由图易发现,∠1的对顶角与∠2是同位角,a∥b是沟通∠1与∠2的桥梁.【详细解答】解:如图,∵a∥b,∴∠3=∠2.∵∠3=∠1,∴∠2=∠1=55°,故选择C.【解后反思】此类题主要考查形式为选择或填空,解决此类题型常用的方法是根据平行线的性质:两直线平行同位角相等、两直线平行内错角相等,两直线平行同旁内角互补,结合对顶角相等或邻补角和为180°,直接求出正确答案后做出选择.【关键词】平行线的性质;对顶角。
【中考冲刺】初三数学培优专题 14 平行线分线段成比例(含答案)(难)

平行线分线段成比例阅读与思考平行线分线段成比例定理是证明比例线段的常用依据之一,是研究比例线段及相似形的最基本、最重要的理论.运用平行线分线段成比例定理解题的关键是寻找题中的平行线.若无平行线,需作平行线,而作平行线要考虑好过哪一个点作平行线,一般是由成比例的两条线段启发而得.此外,还要熟悉并善于从复杂的图形中分解出如下的基本图形:例题与求解【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.(上海市竞赛试题)解题思路:建立含PQ 的比例式,为此,应首先判断PQ 与AD (或BC )的位置关系,关键是从复杂的图形中分解出基本图形,并能在多个成比例线段中建立联系.【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )A .3︰2︰1B .4︰2︰1C .5︰4︰3D .5︰3︰2(“祖冲之杯”邀请赛试题)解题思路:因题设条件没有平行线,故须过M 作BC 的平行线,构造基本图形.A BCDEGH MQA BCDEFP【例3】如图,□ABCD中,P为对角线BD上一点,过点P作一直线分别交BA,BC的延长线于Q,R,交CD,AD于S,T.求证:PQ•PT=P R•PS.(吉林省中考试题)解题思路:要证PQ•PT=P R•PS,需证PQPS=PRPT,由于PQ,PT,P R,PS在同一直线上,故不能直接应用定理,需观察分解图形.【例4】梯形ABCD中,AD//BC,AB=DC.(1)如图1,如果P,E,F分别是BC,AC,BD的中点,求证:AB=PE+PF;(2)如图2,如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.(上海市闵行区中考试题)解题思路:(1)不难证明;对于(2),先假设结论成立,从平行线出发证明AB=PE+PF,即要证明PEAB+PFAB=1,将线段和差问题的证明转化为与成比例线段相关问题的证明.AB CDEFP图2AB CDEFP图1QARBCDSP【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .求证:MN +PQ =2PN .解题思路:考虑延长BA ,EC 构造平行四边形,再利用平行线设法构造有关的比例式.(浙江省竞赛试题)【例6】已知:△ABC 是任意三角形.(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且AM AB =13,AN AC =13,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;(3)如图3,点M ,N 分别在边AB ,AC 上,且P 1,P 2,…,P 2009是边BC 的2010等分点,则∠MP 1N +∠MP 2N +…+∠MP 2009N =____.(济南市中考试题)解题思路:本题涉及的考点有三角形中位线定理、平行四边形的判定、相似三角形的判定与性质.ABCM NP图1A BC MN1P 2P 图2A MNBC1P 2P 2009P 图3QABCDEFGMNP能力训练A 级1.设K =a b c c +-=a b c b -+=a b ca-++,则K =____. (镇江市中考试题)2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____.(杭州市中考试题)4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.(重庆市中考试题)5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则ab 的值为( ) ABCD6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )A .1︰10B .1︰9C .1︰8D .1︰77.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4B .8C .12D .168.如图,EF ∥BC ,FD ∥AB ,BD =35BC ,则BE ︰EA 等于( )A .3︰5B .2︰5C .2︰3D .3︰2A BCD E F 第2题ABCD M N第3题ABCDEFGH 第4题A BCEFG第5题ABCDE F第6题QABCP第7题AB CDEF 第8题9.(1)阅读下列材料,补全证明过程.已知,如图,矩形ABCD 中,AC ,BD 相交于点O ,OE ⊥BC 于E ,连结DE 交OC 于点F ,作FG ⊥BC 于G .求证:点G 是线段BC 的一个三等分点.(2)请你依照上面的画法,在原图上画出BC 的一个四等分点.(要求:保留画图痕迹,不写画法及证明过程)(山西中考试题)10.如图,已知在□ABCD 中,E 为AB 边的中点,AF =12FD ,FE 与AC 相交于G . 求证:AG =15AC .11.如图,梯形ABCD 中,AD ∥BC ,EF 经过梯形对角线的交点O ,且EF ∥AD . (1)求证:OE =OF ; (2)求OE AD +OEBC的值; (3)求证:1AD +1BC =2EF. (宿迁市中考试题)ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题12.如图,四边形ABCD 是梯形,点E 是上底边AD 上的一点,CE 的延长线与BC 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,MB 与AD 交于点N .求证:∠AFN =∠DME .(全国初中数学联赛试题)B 级1.如图,工地上竖立着两根电线杆AB ,CD ,它们相距15cm ,分别自两杆上高出地面4m ,6m 的A ,C 处,向两侧地面上的E ,D 和B ,F 点处,用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD 与BC 的交点P 离地面的高度为____m .(全国初中数学联赛试题)2.如图,□ABCD 的对角线交于O 点,过O 任作一直线与CD ,BC 的延长线分别交于F ,E 点.设BC =a ,CD =b ,CF =c ,则CE =____.(黑龙江省中考试题)3.如图,D ,F 分别是△ABC 边AB ,AC 上的点,且AD ︰DB =CF ︰F A =2︰3,连结DF 交BC 边的延长线于点E ,那么EF ︰FD =____.(“祖冲之杯”邀请赛试题)4.如图,设AF =10,FB =12,BD =14,DC =6,CE =9,EA =7,且KL ∥DF ,LM ∥FE ,MN ∥ED ,则EF ︰FD =____.(江苏省竞赛试题)ABCDEF M NP ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题5.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,那么EF 的值是( ) A .10B .12C .16D .18(全国初中数学联赛试题)6.如图,CE ,CF 分别平分∠ACB ,∠ACD ,AE ∥CF ,AF ∥CE ,直线EF 分别交AB ,AC 于点M ,N .若BC =a ,AC =b ,AB =c ,且c >a >b ,则EM 的长为( )A .2c a- B .2a b- C .2c b- D .2a b c+- (山东省竞赛试题)7.如图,在□ABCD 的边AD 延长线上取一点F ,BF 分别交AC 与CD 于E ,G .若EF =32,GF =24,则BE 等于( )A .4B .8C .10D .12E .16(美国初中数学联赛试题)8.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 是对角线AC 的中点,直线BE 交AD 于点F ,则AF ︰FD 的值是( )A .2B .53C .32D .1(黄冈市竞赛试题)9.如图,P 是梯形ABCD 的中位线MN 所在直线上的任意一点,直线AP ,BP 分别交直线CD 于E ,F .求证:MN NP =1()2AE BFEP FP+. (宁波市竞赛试题)ABCD EFG第7题ABCDE F第8题A BCD E F MNP第9题A BCDE F第5题AB CD E F LKMN第4题AB CDEFM第6题10.如图,在四边形ABCD 中,AC 与BD 相交于O ,直线l 平行于BD 且与AB ,DC ,BC ,AD 及AC 的延长线分别交于点M ,N ,R ,S 和P .求证:PM ·PN =P R ·PS .(山东省竞赛试题)11.如图,AB ⊥BC ,CD ⊥BC ,B ,D 是垂足,AD 和BC 交于E ,EF ⊥BD 于F .我们可以证明:11AB CD +=1EF 成立(不要求证出).以下请回答:若将图中垂直改为AB ∥CD ∥EF ,那么, (1)11AB CD+=1EF 还成立吗?如果成立,请给出证明;如果不成立,请说明理由. (2)请找出S △ABD ,S △BED 和S △BDC 的关系式,并给出证明.(黄冈市竞赛试题)ABCDEF第11题SA R BC DMN OPl第10题12.在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过D点的直线PQ交边AC于点P,交边AB 的延长线于点Q.(1)如图1,当PQ⊥AC时,求证:11AQ AP+;(2)如图2,当PQ不与AD垂直时,(1)的结论还成立吗?证明你的结论;(3)如图3,若∠BAC=60°,其它条件不变,且11AQ AP+=nAD,则n=____(直接写出结果)AQ B CDP图1AQB CDP图2AQB CDP图3专题14 平行线分线段成比例例1aba b+ 提示:由AP DQ a PF QF b ==,推得PQ ∥AD 。
中考数学一轮复习第四章几何初步与三角形第一节线段角相交线与平行线同步测试(含答案)

第四章几何初步与三角形第一节线段、角、相交线与平行线姓名:________ 班级:________ 用时:______分钟1.如图,∠B的同位角可以是( )A.∠1 B.∠2C.∠3 D.∠42.如图,点D在△ABC边AB的延长线上,DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是( )A.24° B.59°C.60° D.69°3.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )A.20° B.30°C.45° D.50°4.如图,直线AB,CD相交于点O,EO⊥CD.下列说法错误的是( )A.∠AOD=∠BOCB.∠AOE+∠BOD=90°C.∠AOC=∠AOED.∠AOD+∠BOD=180°5.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )A.110° B.115°C.120° D.125°6.若∠α=35°,则∠α的补角为__________度.7.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为__________.8.一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=__________.9. 如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG =90°,∠E=35°,求∠EF B的度数.10.如图,AB∥DE,FG⊥BC于点F,∠CDE=40°,则∠FGB=( )A.40° B.50°C.60° D.70°11.如图,已知点P是∠AOB的平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4 cm.如果点C是OB上一个动点,则PC的最小值为( )A.2 cm B.2 3 cm C.4 cm D.4 3 cm12.如图中有四条互相不平行的直线l1,l2,l3,l4所截出的七个角.关于这七个角的度数关系,下列正确的是( )A.∠2=∠4+∠7B.∠3=∠1+∠6C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°13.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=____________.14.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是______.15.如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠B=__________.16.如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E,F分别为DB,BC的中点,连结AE,EF,AF.(1)求证:AE=EF;(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系.17.已知O为直线AB上的一点,OC⊥OE于点O,射线OF平分∠AOE.(1)如图1,∠COF和∠BOE之间有何数量关系?并说明理由;(2)若将∠C OE绕点O旋转至图2的位置,试问(1)中∠COF和∠BOE之间的数量关系是否发生变化?若不发生变化,请你加以证明;若发生变化,请你说明理由;(3)若将∠COE绕点O旋转至图3的位置,继续探究∠COF和∠BOE之间的数量关系,并加以证明.18.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.求∠BON的度数;(2)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.参考答案【基础训练】1.D 2.B 3.D 4.C 5.C 6.145 7.75° 8.75°9.解:∵∠EFG=90°,∠E=35°, ∴∠FGH=55°.∵GE 平分∠FGD,AB∥CD, ∴∠FHG=∠HGD=∠FGH=55°. ∵∠FHG 是△EFH 的外角, ∴∠EFB=55°-35°=20°. 【拔高训练】 10.B 11.C 12.C 13.9.5° 14.3 15.95°16.(1)证明:∵点E ,F 分别为DB ,BC 的中点, ∴EF 是△BCD 的中位线,∴EF=12CD.又∵DB=DC ,∴EF=12DB.在Rt△ABD 中,∵点E 为DB 的中点, ∴AE 是斜边BD 上的中线, ∴AE=12DB ,∴A E =EF.(2)解:如图,∵AE=EF ,AF =AE ,∴AE=EF =AF , ∴△AEF 是等边三角形,∴∠AEF=60°. ∵EF 是△BCD 的中位线, ∴EF∥CD,∴∠BEF=∠CDB=β, ∴β+∠2=60°.又∵∠2=∠1+∠ADB=∠1+α,∴∠1+α+β=60°,∴∠1=60°-α-β. ∵AE 是斜边BD 上的中线, ∴AE=DE ,∴∠1=∠ADB=α, ∴α=60°-α-β,∴2α+β=60°. 17.解:(1)∠BOE=2∠COF.理由如下: ∵∠COE=90°, ∴∠BOE=90°-∠AOC ,∠COF=∠AOF-∠AOC=12(90°+∠AOC)-∠AOC=12(90°-∠AOC),∴∠BOE =2∠COF.(2)不发生变化.证明如下:∵∠COE=90°,∴∠COF=90°-∠EOF,∠BOE=180°-2∠EOF. ∴∠BOE=2∠COF. (3)∠BOE+2∠COF=360°.证明如下:∵∠COE=90°,∴∠COF=90°+∠EOF,∠BOE=90°+∠BOC=90°+90°-2∠EOF=180°-2∠EOF.∴∠BOE+2∠COF=360°. 【培优训练】18.解:(1)∵OM 平分∠BOC, ∴∠MOC=∠MOB.又∵∠BOC=110°,∴∠MOB=55°. ∵∠MON=90°,∴∠BON=∠MON-∠MOB=35°. (2)11或47(3)∠AOM-∠NOC=20°.理由如下:∵∠MON=90°,∠AOC=70°, ∴∠AOM=90°-∠AON,∠NOC=70°-∠AON,∴∠AOM-∠NOC=(90°-∠AON)-(70°-∠AON)=20°, ∴∠AOM 与∠NOC 的数量关系为∠AOM-∠NOC=20°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018 初三中考数学复习平行线的证明专题复习练习
1. 下列说法正确的是( D )
A.经验、观察或试验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个2. “两条平行直线被第三条直线所截,同位角相等”这句话是( C )
A.定义 B.假命题 C.公理 D.定理
3. 下列语句中,是命题的是( C )
A.直线AB和CD垂直吗B.过线段AB的中点C画AB的垂线C.同旁内角不互补,两直线不平行D.连接A,B两点
4.如图,AB∥CD,CB⊥DB,∠D=65°,则∠ABC的大小是( A ) A.25°B.35°C.50°D.65°
5.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于( B )
A.90°B.100°C.130°D.180°
6.如图,已知△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( A )
A.∠DCE>∠ADB B.∠ADB>∠DBC
C.∠ADB>∠ACB D.∠ADB>∠DEC
7.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于( C )
A.50°B.60°C.65°D.90°
8.如图,已知直线AB∥CD,BE平分∠ABC,且BE交CD于点D,∠CDE =150°,则∠C的度数为( C )
A.150°B.130°C.120°D.100°
9.如图,直线a∥b,∠A=38°,∠1=46°,则∠ACB的度数是( C )
A .84°
B .106°
C .96°
D .104°
10.适合条件∠A =12∠B =13∠C 的三角形ABC 是( B )
A .锐角三角形 B. 直角三角形 C .钝角三角形 D .都有可能
11.如图,在折纸活动中,小明制作了一张△ABC 纸片,点D ,E 分别在边AB ,AC 上,将△ABC 沿着DE 折叠压平,A 与A ′重合.若∠A =75°,则∠1+∠2等于( A )
A .150° B. 210° C .105° D .75°
12.已知直线l 1∥l 2,一块含30°角的直角三角板如图所示放置,∠1=25°,
则∠2等于( B )
A.30° B. 35°C.40°D.45°
13.如图,DAE是一条直线,DE∥BC,则x=__64°__.
14.如图,已知AB∥CD,∠DEF=50°,∠D=80°,∠B的度数是__50°__.
15.如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=__70°__,∠CED=__110°__.
16.已知如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠DAC =100°,则∠BAC=__120°__.
17.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为__22°__.
18.已知等腰三角形的一腰上的高与另一腰的夹角为40°,则这个等腰三角形的顶角为__50°或130°__.
19.如图所示,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A=__10__度.
20.如图,∠C=∠1,∠2和∠D互余,BE⊥FD,求证:AB∥CD.
解:∵∠C=∠1,∴CF∥BE,又BE⊥FD,∴CF⊥FD,∴∠CFD=90°,则∠2+∠BFD=90°,又∠2+∠D=90°,∴∠D=∠BFD,则AB∥CD
21.一天,爸爸带着小刚到建筑工地去玩,看见有如图所示的人字架,爸爸说:“小刚,我考考你,这个人字架的夹角∠1等于130°,你能求出∠3比∠2大多少吗?”小刚马上得到了正确答案,他的答案是多少?请说明理由.
解:50°,因为∠1=130°,所以与∠1相邻的内角为50°,所以∠3-∠2=50°
22.如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.
解:∵BE∥DF,∴∠ABE=∠D,又AB=FD,∠A=∠F,∴△ABE≌△FDC(ASA),∴AE=FC
23.如图,△ABC中,∠BAC=90°,∠ABC=∠ACB,又∠BDC=∠BCD,
且∠1=∠2,求∠3的度数.
解:由∠BAC=90°,∠ABC=∠ACB易求∠ACB=45°,设∠1=x,可得∠BCD=∠2+45°=x+45°=∠3,∴x+(x+45°)+(x+45°)=180°,x=30,则∠3=x+45°=75°
24.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
解:∵∠A+∠B+∠C=180°,∴∠B+∠C=110°,∵∠B=∠DEB,∠C=∠DFC,∴∠B+∠DEB+∠C+∠DFC=220°,∵∠B+∠DEB+∠C+∠DFC
+∠EDB +∠FDC =360°,∴∠EDB +∠FDC =140°,即∠EDF =180°-140°=40°
25.如图,已知∠1+∠2=180°,∠3=∠B ,试判断∠AED 与∠C 的大小关系,并对结论进行证明.
解:∠AED =∠C.∵∠1+∠2=180°,∠1+∠EFD =180°,∴∠2=∠EFD ,∴AB ∥EF ,∴∠3=∠ADE ,又∵∠3=∠B ,∴∠ADE =∠B ,∴DE ∥BC ,∴∠AED =∠C
26.【问题】如图①,在△ABC 中,BE 平分∠ABC ,CE 平分∠ACB ,若∠A =
80°,则∠BEC =__130°__;若∠A =n °,则∠BEC =__90°+12n °__.
【探究】
(1)如图②,在△ABC 中,BD ,BE 三等分∠ABC ,CD ,CE 三等分∠ACB.若∠
A =n °,则∠BEC =__60°+23n °__;
(2)如图③,O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点,试分析∠BOC 和∠A 有怎样的关系?请说明理由;
(3)如图④,O 是外角∠DBC 与外角∠BCE 的平分线BO 和CO 的交点,则∠BOC 与∠A 有怎样的关系?(只写结论,不需证明)
解:(2)∠BOC =12∠A.理由:∠BOC =∠2-∠1=12∠ACD -12∠ABC =12(∠ACD
-∠ABC)=12∠A
(3)∠BOC =90°-12∠A。
