粘弹性三维本构关系与解析方法
高分子物理--聚合物的粘弹性ppt课件

粘弹体的应力与应变的相位关系
一、 粘弹性现象 (二) 动态粘弹性
力学损耗:由于滞后,周期性应力应变变化过程将伴随能量消耗, 称之为力学损耗。 损耗的大小同滞后角有关,常以tanδ 表示
橡胶拉伸与回缩的应力-应变关系示意图
一、 粘弹性现象 (二) 动态粘弹性
聚合物的内耗与频率的关系
表示在复平面上的复模量 E* D* ﹦1
一、 粘弹性现象 (三) 粘弹性参数
G*﹦G1+iG2
J* ﹦ J1 - iJ2
tan δ ﹦ E2 / E 1
﹦ D2 / D 1 ﹦ G2 / G 1 ﹦ J2 / J 1
链段运动的松弛时间同 作用频率(速率)相匹 配时(ω ~ 1/τ ),粘 弹性现象最显著。
二、 粘弹性的数学描述
(一) Boltzmann叠加原
在Δ σ31 、、
u2 、 ……
u3 、 Δ σn
……
un时刻,对试样加应力Δ σ1 、 Δ σ2 、
ε(t)﹦ ∑Δσi D(t-ui)
i: 1→ n
连续对试样加应力,变化率为? σ (u)/? u
t﹥ un
ε(t)﹦ ∫ D(t-u)(? σ (u)/? u) du u:- ∞ → t
ηs*﹦ηs1-ηs2 ηs1 ﹦(σ0/γ0 ω)sinδ ηs2 ﹦(σ0/γ0 ω)cosδ
ηs1 ﹦G2/ω
ηs2 ﹦G 1/ω
二、 粘弹性的数学描述
(一) Boltzmann叠加原
1. 数理学表达式
在零时刻,对试样加应力σ0 ε0 (t)﹦σ0 D(t)
在u1时刻,对试样加应力σ1 ε1 (t)﹦σ1 D(t-u1)
粘性响应 理想液体
第10章 粘弹性(固体)材料的本构方程(线性)

第10章 粘弹性(固体)材料的本构方程(线性)1.概述a )基本的典型模型(根据流变学分类法)弹性:没有记忆(与历史无关,没有耗散),可逆的,没有时效,瞬时响应,与加载速率无关。
塑性:有记忆(与历史有关,有耗数),不可逆,没有时效,瞬时响应,与加载速率无关,比拟元件粘性:有记忆,有耗散,不可逆,有时效,比拟元件多数的工程材料,可用上述三者之一,或三者中的某种组合来描述(在一定的条件下)。
b )粘弹性材料该材料既有粘性,又有弹性。
变形=瞬时效应+随时间而变化的变形(后效变,滞后部分)(弹性)(粘性流动) c )两种典型的特性试验弹性:E / ,00σεσσ==,若,10=σ 则 F E ==/1ε(柔度)0 ,εσεεE ==0,若 10=ε,则 E =σ(模量)粘弹性:)() ,t E t 00=(=σεσσ (由于)t (ε增加,则)(t E 减小,材料软化))() ,10t F t =(=εσ蠕变柔量松驰实验:0)()( ,εσεεt E t ==0)() ,10t E t =(=σε 松驰模量线性粘弹性本构方程,用叠加原理。
有三种表述形式:微分算子型,积分型——遗传积分,复数型(本次不介绍)。
2.微分算子型:(a )两个基本的比拟模型(非其正的材料模型,用于定性的说明) ①Maxwell 模型γγεησεσ == e e E 为元件的本构方程 系统的本构方程:(σ与ε的关系)γγεεεσσσ====e e γγεεεεησεσ +===e e E , , 则: ησσε+=E (接近于粘弹性流体) ② Kelvin (V oigt )模型元件的本构方程:γγεησεσ == e e E γγεεεσσσ==+=e e系统的本构方程:则:εηεσ +=E (接近于粘弹性固体) (b )推广到一般情况:定义:0d :d P r pr r p t =∑ 0d :dt Q rpr r q =∑[)][)]P Q t t σε(=(为微分算子型本构方程。
粘弹性

外力的方向运动以减小或者消除内部应力,如果T很高(>>Tg),链运动摩擦
阻力很小,应力很快松弛掉了,所以观察不到,反之,内摩擦阻力很大,链段 运动能力差,应力松弛慢,也观察不到.只有在Tg温度附近的几十度的范围
内应力松弛现象比较明显.(链由蜷曲变为伸展,以消耗外力)
21
第8章 聚合物的粘弹性
0
玻璃态 高弹态 粘流态 t
2 0
0 0
sin tcost - dt
W 0 0sin
又称为力学损耗角,常用tan表示内耗的大小
33
第8章 聚合物的粘弹性
③内耗的表达
当 t 0sin t时, 应力 ( t ) 0sin t
展开 : ( t ) 0 cos sin t 弹性形变的动力 0sin cost 消耗于克服摩擦阻力
27
第8章 聚合物的粘弹性
③滞后现象与哪些因素有关?
a.化学结构:刚性链滞后现象小,柔性链滞后现象大.
b.温度:当不变的情况下,T很高滞后几乎不出现,温度很低, 也无滞后.在Tg附近的温度下,链段既可运动又不太容易,此 刻滞后现象严重。 c. : 外力作用频率低时,链段的运动跟的上外力 的 变化,滞 后现象很小. 外力作用频率不太高时,链段可以运动,但是跟不上外力的变 化,表现出明显的滞后现象.
外力作用频率很高时,链段根本来不及运动,聚合物好像 一块刚性的材料,滞后很小
28
第8章 聚合物的粘弹性
2.内耗:
①内耗产生的原因: 当应力与形变的变化相一致时,没有滞后现象,每次形变所 作的功等于恢复形变时所作的功,没有功的消耗
如果形变的变化跟不上应力的变化,发生滞后现象,则每 一次循环变化就会有功的消耗(热能),称为力学损耗,也叫内 耗. 外力对体系所做的功:一方面用来改变链段的构象(产生 形变),另一方面提供链段运动时克服内摩擦阻力所需要的能量 .
粘弹性基本力学模型

粘弹性基本力学模型粘性:在外力作用下,分子与分子之间发生位移,材料的变形和应力随时间变化的变种特性称为粘性。
理想的粘性流体其流动形变可用牛顿定律来描述:应力与应变速率成正比。
因此,材料的本构关系的数学表达式应是反映应力-应变-时间-温度关系的方程。
粘弹性:塑料对应力的响应兼有弹性固体和粘性流体的双重特性称粘弹性。
材料既有弹性,又有粘性。
粘弹性依赖于温度和外力作用的时间。
其力学性能随时间的变化,称为力学松弛,包括应力松弛、蠕变等。
其力学行为介于理想弹性体和理想粘性体之间。
理想弹性体的形变与时间无关,形变瞬时达到,瞬时恢复。
理想粘性体的形变随时间线性发展。
粘弹性体介于这两者之间,其形变的发展具有时间依赖性,也就是说不仅具有弹性而且有粘性。
这种力学性质随时间变化的现象称为力学松弛现象或粘弹性现象。
橡胶对形变同时具有粘性响应和弹性响应。
粘性响应与形变速率成正比,而弹性响应与形变程度成正比。
粘性响应通常以阻尼延迟器为模型,而弹性响应则以金属弹簧为模型。
采用如下两种基本力学元件,即理想弹簧和理想粘壶。
理想弹簧用于模拟普弹形变,其力学性质符合虎克(Hooke)定律,应变达到平衡的时间很短,可以认为应力与应变和时间无关:σ=Eε其中σ为应力;E为弹簧的模量。
理想粘壶用于模拟粘性形变,其应变对应于充满粘度为η的液体的圆筒同活塞的相对运动,可用牛顿流动定律描述其应力应变关系:将弹簧和粘壶串联或并联起来可以表征粘弹体的应力松弛或蠕变过程。
应力松弛:就是在固定的温度和形变下,聚合物内部的应力随时间增加而逐渐衰减的现象。
这种现象也在日常生活中能观察到,例如橡胶松紧带开始使用时感觉比较紧,用过一段时间后越来越松。
也就是说,实现同样的形变量,所需的力越来越少。
未交联的橡胶应力松弛较快,而且应力能完全松弛到零,但交联的橡胶,不能完全松弛到零。
应力松弛同样也有重要的实际意义。
成型过程中总离不开应力,在固化成制品的过程中应力来不及完全松弛,或多或少会被冻结在制品内。
《高分子物理》课件-第七章粘弹性

第7 章聚合物的粘弹性形变对时间不存在依赖性εσE =虎克定律理想弹性体外力除去后完全不回复dt d εηγησ==.牛顿定律理想粘性体弹性与粘性弹性粘性储能性可逆性σ与ε的关系与t 关系瞬时性依时性储存耗散回复永久形变εσE =dt d εηγησ==.虎克固体牛顿流体粘弹性力学性质兼具有不可恢复的永久形变和可恢复的弹性形变小分子液体–粘性小分子固体–弹性在时间内,任何物体都是弹性体在时间内,任何物体都是粘性体在的时间范围内,任何物体都是粘弹体超短超长一定高分子材料具有显著的粘弹性粘弹性分类静态粘弹性动态粘弹性蠕变、应力松弛滞后、内耗7.1 粘弹性现象7.1.1 蠕变(creep)在一定的温度下,软质PVC丝钩一定的砝码,会慢慢伸长蠕变:指在一定的温度和较小的恒定外力作用下,材料的形变随时间的增加而逐渐增大的现象蠕变反映了材料的尺寸稳定性及长期负荷能力从分子运动和变化的角度分析线性PVC的形变—时间曲线,除去外力后,回缩曲线?11E σε=1ε1t 2t t键长和键角发生变化引起,形变量很小,瞬间响应σ:应力E 1:普弹形变模量1.普弹形变链段运动使分子链逐渐伸展发生构象变化引起τ:松弛时间,与链段运动的粘度η2和高弹模量E 2有关,τ=η2/ E 2)1(/22τσεt eE --=2ε1t t2t 2.高弹形变3ε2t 1t t外力作用造成分子间的相对滑移(线型高聚物)t33ησε=η3——本体粘度3.粘性流动t eE E t t 3/21321)1()(ησσσεεεετ+-+=++=-线型高聚物的蠕变曲线总应变交联聚合物的蠕变曲线1.由于分子链间化学键的键合,分子链不能相对滑移,在外力作用下不产生粘性流动,蠕变趋于一定值2. 无粘性流动部分,能完全回复T<T g 时,主要是(),T>T g 时,主要是()A ε1B ε2C ε3三种形变的相对比例依具体条件不同而不同下列情况那种形变所占比例大?A B聚合物蠕变的危害性蠕变降低了聚合物的尺寸稳定性抗蠕变性能低不能用作工程塑料如:PTFE不能直接用作有固定尺寸的材料硬PVC抗蚀性好,可作化工管道,但易蠕变影响蠕变的因素1.温度2.外力3.分子结构蠕变与T,外力的关系温度外力蠕变T过低外力过小T过高外力过大T g附近适当外力很小很慢,不明显很快,不明显明显(链段能够缓慢运动)23℃时几种高聚物蠕变性能10002000(%)小时2.01.51.00.512345t链的柔顺性主链含芳杂环的刚性高聚物,抗蠕变性能较好12345聚苯醚PCABS(耐热)POM尼龙如何防止蠕变?◆交联橡胶通过硫化来防止由蠕变产生不可逆的形变◆结晶微晶体可起到类似交联的作用◆提高分子间作用力7.1.2 应力松弛(stress relaxation)在一定温度、恒定应变的条件下,试样内的应力随时间的延长而逐渐减小的现象应力松弛的本质加力链段运动使分子链间相对位置的变化分子重排,以分子运动来耗散能量,从而维持一定形变所需要的力逐渐减小交联聚合物和线形聚合物的应力松弛t交联线性高聚物的应力松弛曲线t不同温度下的应力松弛曲线应力松驰与温度的关系温度过高应力松驰很快温度过低内摩擦力很大,应力松驰极慢T g 附近应力松驰最为明显123应力松弛的应用对密封制件,应力松弛行为决定其使用寿命高分子制件加工中,应力松弛行为决定残余应力的大小不变的量变化的量蠕变应力松弛蠕变与应力松弛比较温度力形变根本原因高分子链的构象重排和分子链滑移应力温度形变动态粘弹性在交变应力或交变应变作用下材料的力学行为σωtπ2πεωtδεωtδ正交变化的应力:t sin )t (0ωσσ=无相位差,无能量损耗理想弹性体tsin )t (0ωεε=有相位差,功全部损耗成热理想粘性液体)2-t sin( )t (0πωεε=相位差δ,损耗部分能量)-t sin( )t (0δωεε=聚合物(粘弹性)高聚物在交变应力作用下的应变变化落后于应力变化的现象tt o ωσσsin )(=)sin()(δωεε-=t t o 0<δ<π/2滞后现象原因链段运动时受到内摩擦阻力, 外力变化时,链段运动跟不上外力的变化内摩擦阻力越大,δ 也就越大,滞后现象越严重外力对体系做的功每次形变所作的功= 恢复形变时所作的功无滞后时没有功的消耗每一次循环变化会有功的消耗,称为内耗有滞后时产生形变提供链段运动时克服内摩擦阻力所需要的能量滞后现象的危害σεσ0ε1拉伸硫化橡胶拉伸—回缩应力应变曲线拉伸曲线下面积为外力对橡胶所作的功回缩曲线下面积为橡胶对外力所作的功滞后环面积越大,损耗越大ε0回缩ε2面积之差损耗的功δεπσsin o o W =∆δ :力学损耗角,常用tanδ来表示内耗大小)]dt-t cos(t)[sin ()t (d )t (W Δ020200δωωεωσεσωπωπ⎰⎰==σεσ0回缩拉伸内耗角δεπσsin o o W =∆δ=0,△W=0,所有能量都以弹性能量的形式存储起来滞后的相角δ决定内耗δ=900,△W→max , 所有能量都耗散掉了滞后和内耗对材料使用的利弊?用作轮胎的橡胶制品要求内耗小(内耗大,回弹性差)隔音材料和吸音材料要求在音频范围内有较大的力学损耗防震材料要求在常温附近有较大的力学损耗温度内耗很高很低T g 附近1. 温度影响滞后和内耗的因素高小小小小大大2.外力变化的频率高聚物的内耗与频率的关系频率 内耗很高很低适中小小小小大大橡胶品种内耗顺丁丁苯丁腈3.内耗与分子结构的关系对于作轮胎的橡胶,则选用哪种?内耗大的橡胶,吸收冲击能量较大,回弹性较差较小较大较大7.1.3 粘弹性参数静态粘弹性蠕变应力松弛模量柔量应力,应变与时间的关系模量、柔量与时间的关系蠕变柔量)()(σεt t D =应力松弛模量)()(εσt t E =tsin (t)0ωεε=t cos sin t sin cos (t)00ωδσωδσσ+=)t sin( (t)0δωσσ+=δεσcos '00=E δεσsin "00=E E ′—储能模量,反映材料形变时的回弹能力(弹性)E ″—耗能模量,反映材料形变时内耗的程度(粘性)1.力学损耗角,tg δ动态粘弹性2.动态模量用复数模量的绝对值表示(绝对模量)2''2'*||E E E E +==通常E ″<<E ′,常直接用E ′作为材料的动态模量。
第三章粘弹性流体的本构方程

第三章非线性粘弹流体的本构方程1.本构方程概念本构方程(constitutive equation),又称状态方程——描述一大类材料所遵循的与材料结构属性相关的力学响应规律的方程。
不同材料以不同本构方程表现其最基本的物性,对高分子材料流变学来讲,寻求能够正确描述高分子液体非线性粘弹响应规律的本构方程无疑为其最重要的中心任务,这也是建立高分子材料流变学理论的基础。
两种。
唯象性方法,一般不追求材料的微观结构,而是强调实验事实,现象性地推广流体力学、弹性力学、高分子物理学中关于线性粘弹性本构方程的研究结果,直接给出描写非线性粘弹流体应力、应变、应变率间的关系。
以本构方程中的参数,如粘度、模量、松弛时间等,表征材料的特性。
分子论方法,重在建立能够描述高分子材料大分子链流动的正确模型,研究微观结构对材料流动性的影响。
采用热力学和统计力学方法,将宏观流变性质与分子结构参数(如分子量,分子量分布,链段结构参数等)联系起来。
为此首先提出能够描述大分子链运动的正确模型是问题关键。
根据研究对象不同,象性方法和分子论方法虽然出发点不同,逻辑推理的思路不尽相同,而最终的结论却十分接近,表明这是一个正确的科学的研究基础。
目前关于高分子材料,特别浓厚体系本构方程的研究仍十分活跃。
同时,大量的实验积累着越来越多的数据,它们是检验本构方程优劣的最重要标志。
从形式上分,速率型本构方程,方程中包含应力张量或形变速率张量的时间微商,或同时包含这两个微商。
积分型本构方程,利用迭加原理,把应力表示成应变历史上的积分,或者用一系列松弛时间连续分布的模型的迭加来描述材料的非线性粘弹性。
积分又分为单重积分或多重积分。
判断一个本构方程的优劣主要考察:1)方程的立论是否科学合理,论据是否充分,结论是否简单明了。
2)一个好的理论,不仅能正确描写已知的实验事实,还应能预言至今未知,但可能发生的事实。
3)有承前启后的功能。
例如我们提出一个描写非线性粘弹流体的本构方程,当条件简化时,它应能还原为描写线性粘弹流体的本构关系。
盐岩层井眼缩径粘弹性分析

E
η
σ
σ
图 1 麦克斯韦模型 Fig.1 Maxwell model
因为弹簧(H)和粘壶(N)是串联的,所以弹簧的
应力 σ H 与粘壶的应力 σ N 相等,且都等于模型的总
应力σ ;而模型的总应变 ε 为弹簧的应变 ε H 与粘壶
的应变 ε N 之和,即
ε = εH +εN
(1)
对于弹簧 H,有
σ = σ H = EεH
g/cm3 g/cm3 g/cm3 g/cm3 g/cm3 g/cm3
ur
=
r 4
⎡P
⎢ ⎣
sQ
(2Pm
−σH
−σh )−
图 3 泥浆密度对井眼缩径的影响 Fig.3 Effect of mud density on wellbore shrinkage
第 23 卷 第 14 期
韩建增等. 盐岩层井眼缩径粘弹性分析
1引言
油气钻井工程中,经常遇到厚度从几十米到数 百米不等的盐岩层。在江汉、华北、中原、塔里木 等油田,盐岩层埋深通常在 3 000~5 000 m。这种
处于较高温度和围压环境中的盐岩具有较强的流变 性,井眼钻穿盐岩层后,由于岩石蠕变则会发生井 眼缩径。大量的工程实践表明,盐岩层段钻井工艺 复杂,井下事故频繁[1~3],如果处理不当,可能导 致埋钻具或大段井眼报废,严重阻碍了对盐岩下面 的储集层的勘探开发。因此,深入研究盐岩层井眼
⎤ ⎥ ⎦
Y
σh
Pm
θ
o
(8)
σH X
P (3KP + 7Q sQ (3KP + Q
) )
(σ
H
−
σ
h
)
cos
粘弹性模型

土体动本构模型的研究现状土体实际动本构关系是极其复杂的,它在不同的荷载条件、土性条件及排水条件下表现出极不相同的动本构特性. 要建立一个能适用于各种不同条件的动本构模型的普遍形式是不切实际的,其切实的方法是对于不同的工程问题,应该根据土体的不同要求和具体条件,有选择地舍弃部分次要因素,保留所有主要因素,建立一个能反映实际情况的动本构模型. 目前,具体建立的动本构模型已达数十个,大致可分为两大类,即粘弹性模型和弹塑性模型.曲线模型,均属于等效线性模型[2 ] 。
Masing 类模型以曲线Hardin Drnevich 或Ram2berg Osgood 曲线等为骨干,改用瞬时剪切模量代替前面的平均剪切模量。
为使这类动本构模型更接近实测的动应力应变曲线,很多学者做了大量的工作,以使其能够描述不规则循环荷载作用下土的动本构关系[3 ] 。
Iwan 用一系列具有不同屈服水平的理想弹塑性元件来描述土的动本构关系,它分串联型和并联型2 种构成方式。
串联型和并联型的伊万模型所描述的动应力应变特性基本上一致,只是前者以应变为自变量,后者以应力为自变量[4 ] 。
郑大同在伊万模型的基础上,提出了一个新物理模型,该模型的骨架曲线可为加工硬化状,也可为加工软化状,骨架曲线与滞回曲线的2 个分支既可相同,也可不同[5 ] 。
一般的粘弹性模型不能计算永久变形(残余变形) ,在主要为弹性变形的情况下比较合适。
但实际上,土在往复荷载作用下还会因土粒相互滑移,形成新的排列而产生不可恢复的永久变形。
为此,Mar2tin 等人根据等应变反复单剪试验结果,提出了循环荷载作用下永久体积应变的增量公式[6 ] 。
后来,日本学者八木、大冈和石桥等分别由等应力动单剪试验及扭剪试验各自提出了计算永久体积应变增量的经验公式。
国内的姜朴、徐亦敏、娄炎根据动三轴试验应变与破坏振次的关系式。
沈珠江[7 ] 对等价粘弹性模型进行了较全面的研究,认为一个完整的粘弹性模型应该包含4 个经验公式: (1) 平均剪切模量; (2) 阻尼比; (3) 永久体积应变增量和永久剪切应变增量; (4) 当饱和土体处于完全不排水或部分排水条件下,还需给出孔隙水压力增长和消散模型。
粘弹性流体的本构模型及其应用

粘弹性流体的本构模型及其应用随着人们对物质性质的深入研究,越来越多的特殊性质的物质被人们所发现,粘弹性流体就是其中之一。
粘弹性流体既具有粘性又具有弹性,被广泛运用于化学、医学、生物学和工程等领域中。
而对于粘弹性流体的本构模型的研究,则是这些应用的基础。
本篇文章将对粘弹性流体的本构模型及其应用进行详细的论述。
一、粘弹性流体的性质粘弹性流体是介于粘性流体和弹性体之间的物质,它既具有流变性质,也具有力学弹性。
它的流变特性表现为,当它受到作用力时会出现变形,而当这种作用力减小或消失时,它的变形又会逐渐恢复。
这种特殊的性质使得它在许多领域具有广泛的应用。
二、粘弹性流体的本构模型粘弹性流体的本构模型是用数学方式来描述流体变形特性的模型。
它是通过实验数据和理论推导确定的粘弹性流体性质的一种数学表示,用于预测和计算其在不同外力下的流变特性。
在粘弹性流体的本构模型中,最常见的是Maxwell模型、Kelvin模型以及Jeffreys模型。
1、Maxwell模型Maxwell模型是由Maxwell在1867年提出的一种模型,是最早被使用的粘弹性流体本构模型之一。
它被广泛应用于石油工程、高分子材料工程、生物领域等领域中。
Maxwell模型的基本原理是将粘性流体和弹性体的模型结合而成。
在Maxwell模型中,流体被视为一个简单的线性弹性体,它由一个弹簧和一个阻尼器组成。
当给该模型施加一个外力时,其中的弹簧会产生弹性变形,而其中的阻尼器会产生粘性变形,使模型发生流变。
而在外力消失后,这两种变形也会随之减小或消失。
2、Kelvin模型Kelvin模型是由Lord Kelvin在1855年提出的一种模型,它将Maxwell模型中的一个弹簧换成为一个螺旋状的弹性体。
和Maxwell模型一样,Kelvin模型也是一种线性的本构模型,它可以更好地描述时间依赖性粘弹性流体的行为。
3、Jeffreys模型Jeffreys模型是由Jeffreys在1927年提出的一种模型,它是Maxwell模型的一种变体。
粘弹性方程及其解法

粘弹性方程及其解法粘弹性是指材料在受力下的弹性和黏性的相互作用,其特点是在长时间内承受应力后,材料会有一定程度的形变,而该形变又会影响材料的应力状态,从而影响材料的力学性能。
在实际工程中,许多材料都呈现出明显的粘弹性特征,例如聚合物、胶体、生物体组织等。
因此,研究和解决粘弹性问题具有极其重要的意义。
一、粘弹性方程在传统的弹性理论中,我们使用的是胡克定律,即应力与应变呈线性关系,这种理论适用于短时间内的应力状态变化。
然而在长时间内,材料的弹性常数和形变率都会随时间发生改变,此时我们需要考虑材料的黏性特性。
这就引出了粘弹性方程。
粘弹性方程是一类包含时间导数的偏微分方程,可以用来描述物质的粘弹性行为。
常见的粘弹性方程包括Maxwell模型、Kelvin模型和Jeffreys 模型等。
其中最简单且应用最广泛的是Maxwell模型。
Maxwell模型可以看作是由一根弹性杆和一个粘性阻尼器串联而成的模型。
该模型中,杆的应变和阻尼器的速度同时影响材料的力学性能。
该模型的表达式可以写成以下形式:$$\sigma (t) = E \epsilon (t) + \mu \frac{d\epsilon(t)}{dt}$$其中$\sigma$表示应力,$\epsilon$表示应变,$E$表示弹性模量,$\mu$表示粘性系数。
二、解粘弹性方程对于粘弹性方程的求解,主要有两种方法:解析法和数值法。
解析法是指通过解偏微分方程得到解析解的方法。
对于Maxwell模型,我们可以通过拉普拉斯变换将其转化为一个简单的代数方程,从而得到其完整的解析解。
然而,在实际问题中,由于方程的复杂性和求解方法的限制,大多数情况下我们无法使用解析法来求解粘弹性方程。
数值法是指通过离散化原方程,将其转化为一个有限的代数方程组,并使用数值方法对其进行求解的方法。
常见的数值方法包括有限差分法、有限元法和谱方法等。
其中有限差分法是最为直接、易实现和最常用的方法之一。
弹性材料的本构关系模拟

弹性材料的本构关系模拟一、引言弹性材料在现代工程领域中得到广泛应用,它们在设计和制造中的性能预测和优化是非常重要的。
而弹性材料的本构关系模拟是实现这一目标的关键步骤。
本文将探讨弹性材料的本构关系模拟的原理、方法和应用。
二、基本概念与原理1. 弹性材料:弹性材料是指在外力作用下能够恢复形状和体积的材料。
常见的弹性材料包括金属、塑料和橡胶等。
2. 本构关系:本构关系描述了材料应变与应力之间的关系。
在弹性材料中,存在线弹性和非线弹性两种本构关系。
3. 线弹性材料:线弹性材料的本构关系遵循胡克定律,即应力与应变成正比。
在小应变范围内,线弹性材料的应变与应力之间的关系是线性的。
4. 非线弹性材料:非线弹性材料的本构关系不遵循胡克定律。
在较大应变下,材料的应力-应变曲线表现出非线性特征,例如屈服现象和应力饱和现象。
三、本构关系模拟方法1. 区域分解法:区域分解法将弹性材料划分为多个小区域,通过对每个区域进行本构关系模拟,然后按照一定规则进行组合,得到整体材料的本构关系。
2. 数值模拟方法:数值模拟方法是一种基于数学方程和计算机算法进行模拟的方法。
常用的数值模拟方法包括有限元法、有限差分法和边界元法等。
3. 实验数据拟合法:实验数据拟合法通过对已知的实验数据进行拟合,并提取其中的规律和参数,从而找到适合该材料的本构关系模型。
四、本构关系模拟的应用1. 工程设计优化:通过对弹性材料的本构关系进行模拟,可以更准确地预测材料的性能,进而优化工程设计,提高产品的性能和可靠性。
2. 材料选型和评估:本构关系模拟可以帮助工程师选择合适的材料,并进行材料性能的评估,为产品的设计和制造提供科学依据。
3. 材料加工和成型:通过模拟材料的本构关系,可以预测材料在加工和成型过程中可能发生的变形和应力分布,从而指导加工工艺的优化。
五、挑战与展望1. 复杂材料的模拟:对于复杂结构和组分的材料,其本构关系的模拟可能存在较大的挑战。
如何准确地描述和模拟这些材料的力学行为,仍然是一个亟待解决的问题。
高分子物理chapter7粘弹性讲义

6
第7章 聚合物的黏弹性
7
第7章 聚合物的黏弹性
蠕变:一定温度、较小的恒定外力下,材料的形变随时间增加而逐渐增大
2+3
Creep
1 2 Retraction
1
0
3
t
8
(t)
第7章
普弹形变
聚合物的黏弹性
从分子运动的角度解释:
材料受到外力的作用,链内的键长和 键角立刻发生变化,产生的形变很小, 我们称它普弹形变.
静态的黏弹性
蠕变
力学松弛
应力松弛 滞后现象
动态黏弹性
力学损耗(内耗) 5
第7章 聚合物的黏弹性
二、静态黏弹性 应力或应变恒定,不同时间时,聚合物材料所表现出来的
黏弹现象。
1、蠕变Creep
在一定的温度和恒定应力(拉力,扭力或压力等)作用下, 材料的形变随时间的增长而逐渐增加的现象。
若除掉外力,形变随时间而减小--称为蠕变回复。
3
12
第7章 聚合物的黏弹性
蠕变Creep
•加力瞬间,键长、键角立即产生形变,形变直线上升 •通过链段运动,构象变化,使形变增大 •分子链之间发生质心位移
Creep recovery 蠕变回复
•撤力一瞬间,键长、键角等次级运动立即恢复,形变直线下降 •通过构象变化,使熵变造成的形变恢复 •分子链间质心位移不能恢复
2
0
E2
1 et
推迟时间 2
高弹模量
’ 分子链从一个松弛的平衡态构象变到
一个紧张的平衡态构象所需的时间
t1
t2
t
链段运动,可逐渐恢复
第7章 聚合物的黏弹性
第三章:弹性和粘性本构关系
§3.8 弹性-粘弹性相应原理
利用拉普拉斯积分的正逆变换,线性粘弹性问题 的解可以由对应的线弹性问题的解变换得到。
本构关系小结(由厚到薄)
1. 思想:看线路图回忆查漏。
2. 需要记忆的公式 2.1. 各向同性线性弹性本构方程及其中的物理常数 G、λ、K 与 E、μ的关系式;
(4)对于情况
有何感想!
课后作业:P100:3-1、3-3 下周三上课时交。
柯西弹性和超弹性
线性弹性
各向同性线性弹性
线性粘弹性
§3.5 、3.6 线性粘弹性材料的微分型本构关系
弹性元件 粘性元件
麦克斯韦模型
开尔文模型
伯格斯模型
广义麦克斯韦模型
广义开尔文模型
三维化
§3.7 线性粘弹性材料的积分型本构关系
柯西弹性和超弹性
线性弹性
各向同性线性弹性
线性粘弹性
§3.2 各向同性线性弹性材料的本构关系
本构方程:式(3-22)或(3-29)
扬氏模量: E 拉梅常数:
泊松比: μ
剪切模量: 体积应变:
球量和偏量的本构方程:式(3-32)
体积弹性模量:
五个弹性常数: E、μ、G、λ、K,只有两个独立。
相关性见表3-1。
胡克定理的应用
思想:应力和应变须满足胡克定理
例题:如图所示钢制圆柱,其直径 为d,外面套有一厚度为t的 钢制圆筒(圆柱和圆筒间无 摩擦),沿圆柱轴向施加均 匀压力q,求刚柱内的应力 (E、μ已知)。
解:建立直角坐标如图,分别分析圆柱和圆 筒的应力和应变状态。 对圆柱内的任意一点,有: (1) (2) 式(1-2)代入胡克定理
材料力学中的粘弹性行为与本构模型

材料力学中的粘弹性行为与本构模型粘弹性是材料力学中一个重要而复杂的问题,它指的是材料在受力作用下表现出的弹性和黏性共同存在的特性。
本文将探讨粘弹性的基本概念,其行为与本构模型的关系。
一、粘弹性的基本概念粘弹性是指材料在外力作用下既可以发生形变,又可以恢复原状的性质。
这种性质与材料的分子结构有关,表现为分子固定点之间的相互作用力。
在粘弹性行为中,材料会表现出随时间延迟的形变响应,这是与弹性体和黏性流体的行为有所不同之处。
二、粘弹性行为的特点1. 时间依赖性:粘弹性是一种时间依赖性的现象,即材料的形变响应随时间的推移而变化。
在外力作用结束后,材料仍然会持续发生形变。
2. 复杂的应力-应变关系:粘弹性材料的应力-应变关系通常是非线性的,并且在不同的加载速率下表现出不同的行为。
3. 耗散能量:粘弹性材料在形变过程中会产生内部摩擦,从而导致能量的耗散。
这种能量损失是粘弹性行为的重要特征之一。
三、粘弹性本构模型为了描述粘弹性材料的力学行为,研究者们提出了多种本构模型。
以下介绍几种常见的粘弹性本构模型:1. 弹簧-阻尼器模型:这是最简单的粘弹性模型之一,通过串联连接弹簧和阻尼器来描述材料的粘弹性行为。
该模型基于线性弹簧和线性阻尼器的行为假设,适用于低应变率下的材料。
2. 麦克弗逊模型:麦克弗逊模型是一种常用的粘弹性模型,它由弹性元素和黏性元素组成。
该模型能够较好地描述不同应变速率下的粘弹性行为。
3. 阿米尔-沙魔尔模型:这是一种广泛应用于粘弹性材料的本构模型。
它采用了多项级数的形式来描述应力-应变关系,能够较好地拟合实验数据。
四、粘弹性行为的应用领域粘弹性行为在许多领域都有重要的应用价值,例如生物材料的研究、土壤工程、涂料润滑剂开发等。
通过深入理解粘弹性行为及其本构模型,可以为这些领域的研究和应用提供重要参考和指导。
结论粘弹性行为是材料力学中一个重要且复杂的问题,其研究涉及到材料分子结构和宏观性能的关系。
通过适用的本构模型,我们可以更好地描述和预测粘弹性材料的力学行为。
粘弹性三维本构关系与解析方法

Q ( D) Sij 2 ' eij P ( D)
'
Q ( D) ii 3 '' ii P ( D)
''
如果材料体积变形是弹性变形,则有:
Q (D) K
''
P ( D) 1
''
ii 3K ii
将微分本构方程变换到相空间
2 Maxwell模型: (1 D ) Sij 2 Deij G0
实际应用需要将2.1节中的本构关系推广到二维、三维 空间中。 本节讨论粘弹性三维本构关系、粘弹性准静态边界问 题的解析方法和粘弹塑性三维本构方程。
2.2.1流变微分型本构关系的一维通式 粘弹性流变模型一维本构关系是关于应力、应变、 两者各自对时间导数和材料参数的方程。
2 如:Maxwell模型本构方程 2 E0
课堂思考 1.粘弹性问题基本方程、弹性问题基本方程的区别 与联系是什么? 2如果边界条件是静态的,弹性问题解析解已经得到, 怎么得到粘弹性问题的解? (提示:将两者的基本方程都变换到相空间中)
弹性-粘弹性相应原理:线粘弹性边值问题的求解方 程在拉普拉斯空间具有的形式与线弹性问题完全相 同。
求解思路 1.将线弹性解拉氏变换。 2.用相空间中的粘弹性参数换掉原有参数。 3.整理上面得到的式子,再进行拉普拉斯逆变换。
两边做拉普拉斯变换:
2 (1 s ) Sij 2 seij G0
2 P 1 s G0
'
Q ' 2 s
代入其他模型得到表2.2.2
2.2.3相空间中粘弹性参数变换
Q ' ( D) G ( D)) K ( D) '' P ( D)
弹塑性力学定理和公式

应力应变关系弹性模量 ||广义虎克定律1。
弹性模量对于应力分量与应变分量成线性关系的各向同性弹性体,常用的弹性常数包括:a 弹性模量单向拉伸或压缩时正应力与线应变之比,即b 切变模量切应力与相应的切应变之比,即c 体积弹性模量三向平均应力与体积应变θ(=εx+εy+εz)之比,即d 泊松比单向正应力引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之比,即此外还有拉梅常数λ。
对于各向同性材料,这五个常数中只有两个是独立的。
常用弹性常数之间的关系见表3-1 弹性常数间的关系。
室温下弹性常数的典型值见表3—2 弹性常数的典型值。
2。
广义虎克定律线弹性材料在复杂应力状态下的应力应变关系称为广义虎克定律。
它是由实验确定,通常称为物性方程,反映弹性体变形的物理本质.A 各向同性材料的广义虎克定律表达式(见表3—3 广义胡克定律表达式)对于圆柱坐标和球坐标,表中三向应力公式中的x 、y、z分别用r、θ、z和r、θ、φ代替。
对于平面极坐标,表中平面应力和平面应变公式中的x、y、z用r、θ、z代替。
B 用偏量形式和体积弹性定律表示的广义虎克定律应力和应变张量分解为球张量和偏张量两部分时,虎克定律可写成更简单的形式,即体积弹性定律应力偏量与应变偏量关系式在直角坐标中,i,j=x,y,z;在圆柱坐标中,i,j=r,θ,z,在球坐标中i,j=r,θ,φ。
弹性力学基本方程及其解法弹性力学基本方程|| 边界条件||按位移求解的弹性力学基本方法||按应力求解的弹性力学基本方程|| 平面问题的基本方程 || 基本方程的解法 || 二维和三维问题常用的应力、位移公式1.弹性力学基本方程在弹性力学一般问题中,需要确定15个未知量,即6个应力分量,6个应变分量和3个位移分量。
这15个未知量可由15个线性方程确定,即(1)3个平衡方程[式(2-1—22)],或用脚标形式简写为(2)6个变形几何方程[式(2—1—29)],或简写为(3)6个物性方程[式(3-5)或式(3—6)],简写为或2.边界条件弹性力学一般问题的解,在物体内部满足上述线性方程组,在边界上必须满足给定的边界条件。
第三章:弹性和粘性本构关系

直角坐标系下(广义胡克定理):式(3-16) 和(3-18)
几种特殊情况下的广义胡克定律 分类 一般线弹性 有一个弹性对称平面 广义胡克定律 式(3-16、18) 式(3-19) 独立的弹性常数
21
13 9 5 2
式(3-20) 正交各向异性 (有三个弹性对称平面 ) 横观各向同性 (有一个弹性对称轴 ) 各向同性 式(3-21) 式(3-22)
柯西弹性和超弹性
线性弹性
各向同性线性弹性
线性粘弹性
§3.2 各向同性线性弹性材料的本构关系
本构方程:式(3-22)或(3-29)
扬氏模量: E 拉梅常数:
泊松比: μ
剪切模量: 体积应变:
球量和偏量的本构方程:式(3-32)
体积弹性模量:
五个弹性常数: E、μ、G、λ、K,只有两个独立。
相关性见表3-1。
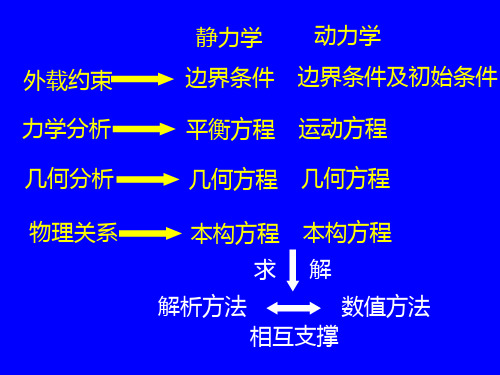
静力学 外载约束
力学分析 几何分析 物理关系 边界条件 平衡方程
动力学 边界条件及初始条件 运动方程
几何方程
本构方程 求 解析方法
几何方程
本构方程 解 数值方法
相互支撑
固体力学基础:傅衣铭、熊慧而编著,中国科学文化出版社,2003年 7月。
第三章:弹性和粘性本构关系
主讲:侯鹏飞
湖南大学工程力学系
柯西弹性和超弹性
线性弹性
各向同性线性弹性
线性粘弹性 重点:线性弹性和各向同性线性弹性。
了解:柯西弹性和超弹性和线性粘弹性。 定位:基础理论部分,属课程学习的重点之一。
柯西弹性和超弹性
线性弹性
各向同性线性弹性
线性粘弹性
§3.1 柯西弹性和超弹性
3.1.1 柯西弹性和超弹性 弹性类别 柯西弹性 (应力和应变一一对应) 弹性系数
第七章聚合物的黏弹性 PPT

7、1、1 蠕变 Creep deformation
❖概念:在恒温下施加一较小得恒定外力时,材 料得应变随时间而逐渐增大得力学现象称 为蠕变
一定力,维持 一段时间
❖ 当外力撤除后,材料形变逐渐回复得过程——蠕变 回复 。
高聚物得蠕变性能就是反映材料得尺寸稳定性与长期负载 能力得量。
❖ 高分子材料蠕变曲线就是由三部分贡献得叠加,如 图所示。
变很小,而且很慢,在短时间内不易 观察到。
(t)
❖ 温度过高(在Tg以上很多)或外力过 大,形变发展很快,也感觉不出蠕变 现象。
❖ 温度在Tg以上不多,链段在外力下
可以运动,但运动时受得内摩擦又
较大,只能缓慢运动,则可观察到蠕
0
t
变。
不同类型高聚物得蠕变行为不同
❖ 线形非晶态高聚物
▪ 如果T<<Tg ,只能瞧到蠕变得起始部分,要观察到全部曲 线要几个月甚至几年。
δ=0
W sin
δ=90°
此外,橡胶试样在每一拉伸-回缩过程中得1/4周期(wt=π/2)时具
有最大得能量储存Wst。 外力做得总功为:
W 2 (t) d (t)dt
0
t
2
(
sin
wt )
d[
sin(wt
)]dt
0
dt
1
cos
sin
2
4
Wst
W
1 4
W
1
2
cos
力学内耗得表达式:
化时,链段得运动还跟不上外力得
变化,所以形变落后于应力,产生一
个位相差。
(t) sin(wt )
σ0
越大说明链段运动越困难、形变
粘弹性材料本构模型的研究

粘弹性材料本构模型的研究第23卷第6期高分子材料科学与工程V o l.23,N o .62020年11月POL Y M ER M A T ER I AL S SC IEN CE AND EN G I N EER I N GN ov .2020粘弹性材料本构模型的研究Ξ路纯红,白鸿柏(军械工程学院,河北石家庄050003摘要:介绍了近年来建立粘弹性材料本构模型的方法。
目前主要有两种方法:利用现有本构模型;对粘弹性材料进行试验研究,拟合实验曲线。
关键词:粘弹性材料;本构模型中图分类号:O 631.2+1文献标识码:A 文章编号:100027555(20200620028204随着化学化工和材料工业的发展,粘弹性材料被广泛应用于航空航天、机械工程、高层建筑、车辆工程以及家用电器等领域。
研究粘弹性材料的力学性能,使其在工程应用中发挥良好的阻尼性能和耗散性能,关键是构建能够精确描述材料本构关系的粘弹性本构模型。
然而粘弹性材料的力学性能如剪切模量、损耗模量、损耗因子等受环境温度、振动频率、应变幅值等影响很大,因此,其本构关系的建立将非常复杂。
本文将对近年来粘弹性材料本构模型的研究成果进行简要的综述,并对今后的研究趋势提出几点建议。
1利用现有模型1.1粘弹性本构模型由于粘弹性材料的力学性能如剪切模量、损耗模量、损耗因子等通常与环境温度、振动频率、应变幅值等有关,因此粘弹性材料的本构关系将是复杂的。
国内外许多学者对此进行了研究,目前常用的粘弹性材料本构模型如下。
1.1.1M axw ll 模型:M axw ell 模型认为,粘弹性材料可以等效为一个弹簧和一个粘壶元件相串联而成,其本构关系为:Σ(t +p 1Σα(t =q 1Χα(t (1式中:Σ(t 和Χ(t ——粘弹性材料的剪应力和剪应变;p 1和q 1——由粘弹性材料性能确定的系数。
在简谐应变的激励下,由本构关系(1式可得:式中:G 1、G 2——储能模量(剪切模量和损耗模量;Γ——损耗因子,用于描述粘弹性材料的阻尼性能,Γ越大,材料阻尼性能越好,Γ越小,材料阻尼性能越差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ˆ [ f (t )] sF ( s ) f (0) L
ˆ[ f ( n ) (t )] s n F ( s ) s n 1 f (0) s n 2 f (0) f ( n 1) (0) s n F ( s ) s n 1i f (i ) (0) L
这些本构关系总能写成下面的形式:
k m k pk k qk k t t k 0 k 0
m
其中 pk , qk 为多项式。
按上述记法, Maxwell模型本构方程可改写成:
2 (1 ) 2 E 0 t t
K 将对时间的微分记为:D K K t 2 D ) 2 D 则(1)式变为 (1 E0
两边做拉普拉斯变换:
2 (1 s ) Sij 2 seij G0
2 P 1 s G0
'
Q ' 2 s
代入其他模型得到表2.2.2
2.2.3相空间中粘弹性参数变换
Q ' ( D) G ( D) ' P ( D)
Q '' ( D) K ( D) '' P ( D)
• 有时会遇到材料参数转换的问题 将 G ( D ), K ( D ) 分别代入 E 9GK
或 ij , j Fi ui
ii 3K ( D) ii
4.边界条件: ij ( xk , t ) n j Ti (t )
ui ( xk , t ) uiS (t )
xk S
5.初始条件: t 0
xk V
ui ( xk , t ) 0
ij ( xk , t ) 0 ij ( xk , t ) 0
物质形态(一切有为法、如梦幻泡影,如露亦如电,应作如是观。 凡所有相,皆是虚妄。--《金刚经》;相,视也。--《尔雅》)
拉普拉斯变换 • [Laplace变换存在定理]若函数 f (t ) 满足下列条件: • (1)当 t 0 时,f (t ) 0 ; • (2) f (t )在t 0的任一有限区间上分段连续, • 间断点的个数是有限个,且都是第一类间断点。 (3) f (t ) 是指数级函数。
L f1 (t ) f 2 ( )d F1 ( s) F2 ( s) 0
拉普拉斯逆变换
i 1 st ˆ f (t ) L [ F ( s )] F ( s )e ds (t 0) 2 i i
1
是复变函数的积分,较为复杂。三种方法: • (1)部分分式法(查表法)满足工程应用 • (2)利用留数定理——围线积分法 • (3)数值计算方法计算机(了解)
• 工程技术中所遇到的函数大部分是存在Laplace变 2 t • 换的,但像 e ,这类函数是不存在Laplace变换的。
拉普拉斯变换
ˆ F ( s ) L[ f (t )] f (t )e st dt 0
• s 是复数, Re s 0 ;
课堂练习 求单位阶跃函数H(t)的拉普拉斯变换
''
'
''
'
'
''
( s)
2.2.4粘弹性问题的解析求解
粘弹性基本方程:
除本构关系外,其他都相同。
1.几何方程: ij 1 [ui , j (t ) u j ,i (t )] 柯西应变
2
2.平衡条件: ij , j Fi 0 3.本构方程: Sij 2G ( D)eij
分别给
E ( D ), ( D ) 做拉普拉斯变换:
E (s)
9Q ( s)Q ( s) 3Q ( s) P ( s) Q ( s) P ( s )
3Q ( s) P ( s) 2Q ( s) P ( s) 2[3P ( s)Q ( s) Q ( s ) P ( s )]
' '' ' '' '' ' ' ''
查表得到逆变换 f (t )
课堂练习 求方程
ty (1 2 t ) y 2 y 0 y (0) 1, y (0) 2 的解。
,满足初始条件:
解: 方程两边进行拉普拉斯变换:
d 2 d [ s Y ( s ) sy (0) y (0)] sY ( s ) y (0) 2 [ sY ( s ) y (0)] 2Y ( s ) 0 ds ds
q(t ) q0 H (t )
做拉普拉斯变换,并用相空间中粘弹性参数代替原 来的参数。整理并做逆变换。 通过代入不同模型的参数,可以比较同一问题各模 型解得差异性。 Maxwell、H-K、和线弹性模型,在t=0瞬时径向位移 相同。
按书中参数,MATLAB作图得到:
总结 应用相应原理时需要注意的几个方面: 1.弹性解容易得到,且能进行拉氏变换。 2.几何方程为柯西应变,只适用于小变形问题。 3.对于接触问题和裂纹扩展,边界、边界条件都随 时间变化,相应条件不能成立。(只能解决准静 态问题) 4.不能用积分变换解决的问题称为非变换问题,存 在拓展的相应原理。可关注相关文献。
i0 n 1
Laplace变换的基本性质
• 1、线性性质 Lf1 (t ) 、相似性质 L f (at ) F ( ) a a • • 3、延迟性质 L f (t ) e s F (s)
(1)
(2)
m
如果令
P ( D ) pk D K
k 0
m
Q ( D ) qk D k
k 0
粘弹性流变模型一维本构方程统一为:
P ( D ) Q ( D )
(3)
P ( D ), Q ( D ) 是算符,代表一种运算。以前学过的算 2 符(算子)如:
对于粘弹塑性模型,当 s 时,一维本构关系 与(3)式相同。当 s 时,变为:
1, t 0 H (t ) 0, t 0
解:
1 st 1 st ˆ L[ H (t )] H (t )e dt e dt e |0 0 0 s s
st
课堂练习
f (t ) 的拉普拉斯为 F ( s ) ,求 f ' (t ) 的拉普拉斯变换
代入初始条件并化简得:
(2 s )Y ( s ) Y ( s ) 0
ln Y ( s ) ln( s 2) C
• 作逆变换得
y (t ) Ce 2 t
y (0) 1; y (t ) e 2 t
2.2三维本构关系与解析方法 实际工程问题一般都是复杂的三维问题,一些情况下 可简化为平面问题。
3K G
3K 2G 2(3K G )
得到:
9Q '' ( D)Q ' ( D) E ( D) '' 3Q ( D) P ' ( D) Q ' ( D) P '' ( D)
3Q '' ( D) P ' ( D) 2Q ' ( D) P '' ( D) ( D) 2[3P ' ( D)Q '' ( D) Q ' ( D) P '' ( D)]
部分分式法 F(s)为多项式: A( s ) am s m am 1s m 1 a1s a0 F (s) B(s) bn s n bn 1s n 1 b1s b0 将上式展开成对照表里,部分分式F(s)之和的形式。
k1 k2 F (s) s p1 s p2 kn s pn
P ( D )( s ) Q ( D )
课堂练习 推导出西原模型对应的算子 P ( D ), Q ( D )
答案:
2 2 1 21 21 ( S ) ( ) 2 E0 E1 E0 E1 E1
2 1 2 21 2 P( D) 1 ( )D D E0 E1 E0 E1 21 2 Q( D) 2 D D E1
直接求解较难,常常将原问题 变换 为易解决问题
积分变换
• 积分变换:通过积分运算,把一个函数变成另一 个函数。
• 积分区间 • 原函数
;积分变换的核 ; ; 称为 的象函数;
选取不同的积分域和变换核时,就得到不同的积 分变换。 傅里叶(Fourier)变换 F ( ) 拉普拉斯(Laplace)变换 F ( s )
0
f (t )e i t dt
f (t )e st dt
Z变换、梅林(Mellin)变换、汉科尔(Hankel)变 换,小波变换;
在积分变换下: 微分运算变为乘法运算; 偏微分方程减少自变量的数目; 常微分方程变为相空间中的代数方程; 从而易于在相空间中求解问题,在经过逆变 换得到原方程的显式解。相空间、像空间、象空间;
材料参数换算
9G0 K E0 3K G0
3K 2G0 2(3K G0 )
E0 G0 2(1 )
E0 K 3(1 2 )
将2.2.1中一维流变微分本构关系推广到三维 偏应力张量的各个分量都符合一维流变微分本构关系。
只需要将一维模型算子中的 E0 换成 G0 , 得到微分算子形式的本构方程:
2.2.5求解示例 《弹性力学上》--徐芝纶,平面极坐标问题课后练习 题。 厚壁筒,受内压q作用,内外半 r q(t ) 径a、b, r=a时, r=b时, r 0 ;求径向位移。
q(t )a 2 1 b2 弹性解: ur (r , t ) 2 [(1 2 )r ] 2 b a E r
